Predicting Miner Localization in Underground Mine Emergencies Using a Hybrid CNN-LSTM Model with Data from Delay-Tolerant Network Databases

Abstract

Underground mining environments are highly hazardous, often prone to gas explosions, cave-ins, and fires that may trap miners during emergencies. The accurate, real-time localization of miners is vital for effective self-escape and rescue operations. Although the Mine Improvement and New Emergency Response (MINER) Act of 2006 mandates communication and tracking systems, most current solutions rely on low-power devices and line-of-sight methods that are ineffective in GPS-denied, dynamic subsurface conditions. Delay-Tolerant Networking (DTN) has emerged as a promising alternative by supporting message relay through intermittent links. In this work, we propose a deep learning framework that combines Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) networks to predict miner locations using simulated DTN-based movement data. The model was trained on a simulated dataset of 1,048,575 miner movement entries, predicting miner locations across 26 pillar classes. It achieved an 89% accuracy, an 89% recall, and an 83% F1-score, demonstrating strong performance for real-time underground miner localization. These results demonstrate the model’s potential for the real-time localization of trapped miners in GPS-denied environments, supporting enhanced self-escape and rescue operations. Future work will focus on validating the model with real-world data and deploying it for operational use in mines.

1. Introduction

Mining contributes significantly to national and global economies by providing minerals and materials for energy, transportation, defense, space exploration, smart technologies, agriculture, medicines, infrastructure, and job opportunities. Strategic, critical, and energy minerals include coal, copper, iron ore, gold, zinc, nickel, and phosphate. The future energy transition into renewable energy with decarbonization and zero emission thrusts would require significant production of these minerals. The production of these minerals must be carried out under the mining industry’s strategic vision of zero fatality by 2050, a grand mining challenge in the near future.

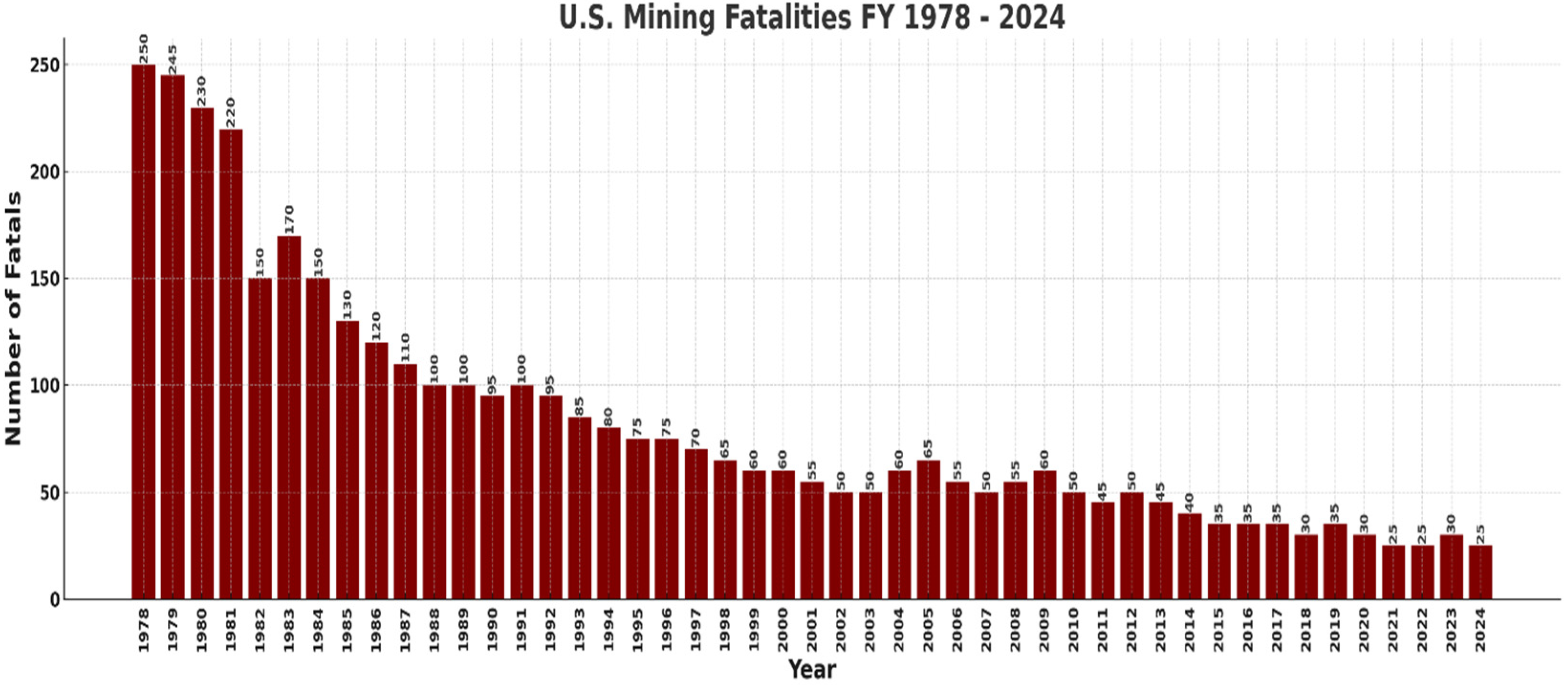
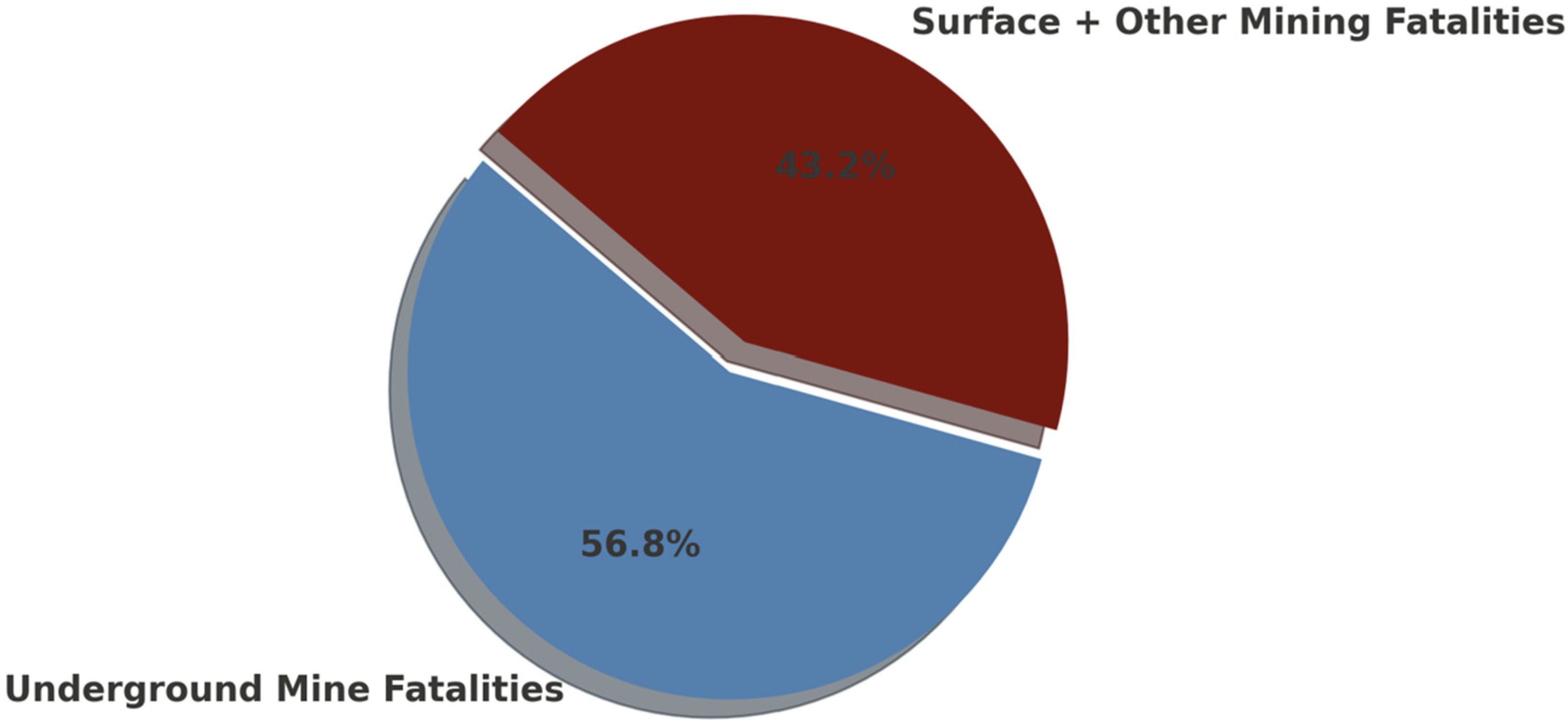
Historical analysis of U.S. mining fatalities clearly demonstrates substantial progress toward this goal. As shown in Figure 1 and Figure 2, U.S. Mining Fatalities FY 1978–2024 [1] and Underground Mine Fatalities in the USA (1978–2023) [2], there has been a significant reduction in both the absolute number of fatalities and the fatality rates over the past four decades. Total mining fatalities have decreased from approximately 250 per year in the late 1970s to below 50 in recent years, while underground mine fatalities have seen a similar downward trend, dropping from over 140 fatalities per year in the early 1980s to fewer than 15 per year in recent years. Furthermore, the pie chart depicting the proportion of underground versus total mining fatalities during the period from 1978 to 2023 illustrates that underground mining accounted for approximately 57% of all mining fatalities. This highlights the critical need for continued improvements in underground mine safety to drive further reductions across the sector.

Several mining events resulting in death or property loss have driven these safety advancements. For instance, the Sago Mine accident in West Virginia in 2006 caused 12 fatalities. The fatalities from the Sago Mine (Figure 3), as well as that from the Dar-by Mine explosion and the Alma Mine fire, forced legislative action to improve miner safety and emergency response capacity [3]. The main goal was to promote safe mining activities and to help miners to effectively self-escape or be assisted in self-escape during underground mine emergencies. A major component of the legislative action included the Mine Improvement and New Emergency Response (MINER) Act of 2006, which re-quires mine operators to implement underground communication and electronic tracking (CT) systems for enhancing miner safety and emergency response in underground coal mines [3]. The MINER Act has two main requirements including (i) implementation of wireless two-way communication systems and electronic tracking systems to locate miners trapped underground; and (ii) development of an emergency response plan (ERP) for post-disaster communication between underground and surface personnel [3]. While mine accidents are unavoidable, measures must be implemented to reduce their occurrences and the associated casualties and fatalities. Conventional methods of locating miners, which rely on manual search techniques, can be erratic, slow, tedious, and inefficient. Thus, there is an urgent need for advanced systems that can enhance the efficiency and reliability of miner localization during underground emergencies [4].

To enhance the robust underground communication system, delay tolerance network (DTN) has been proposed as a feasible alternative for communication during disasters and other emergencies. DTN is designed to operate effectively in challenging environments with very low latency and intermittent connectivity, making it well-suited for underground emergencies with com-promised traditional communication infrastructure. DTN stores and forwards data packets through intermediate nodes until establishing a connection to the destination [5,6,7,8]. This capability is crucial in underground mining environments, where obstacles like debris and rock formations can disrupt direct communication links [9]. The integration of DTN into the emergency response framework can significantly improve the resilience of communication systems in mines. By DTN enhances the chances of successful rescue operations with real-time coordination during emergencies by ensuring that location data and critical messages can still be relayed even when direct paths are unavailable [10]. The adoption of DTN technology aligns with the goals of the MINER Act of 2006, and it provides an additional reliability layer to the mandated communication and tracking systems.

Recent advances in artificial intelligence (AI) and machine learning (ML) present interesting substitutes using predictive models that predict miner movements depending on historical data. A hybrid Convolutional Neural Network (CNN) and Long Short-Term Memory (LSTM) model integrates CNN for spatial feature extraction [11,12,13] with LSTM networks for sequential analysis [14,15], enabling the learning of movement patterns, direction, and velocity to forecast future locations [16]. This design, together with DTN technology, can efficiently process data despite network disruptions, rendering it appropriate for real-time miner localization [12]. Despite its potential, adapting CNN-LSTM models to subsurface mining settings poses obstacles. These include restricted data availability, the need for robust preprocessing techniques, and the necessity for validating the model with real-world data to guarantee predicted accuracy [17,18]. Moreover, interpretation challenges and computing limitations may impede regulatory approval and real-time execution [19,20,21,22,23]. Creating a dependable CNN-LSTM model combined with DTN technology could remarkedly improve emergency response systems, revolutionizing miner safety in the underground mining sector.

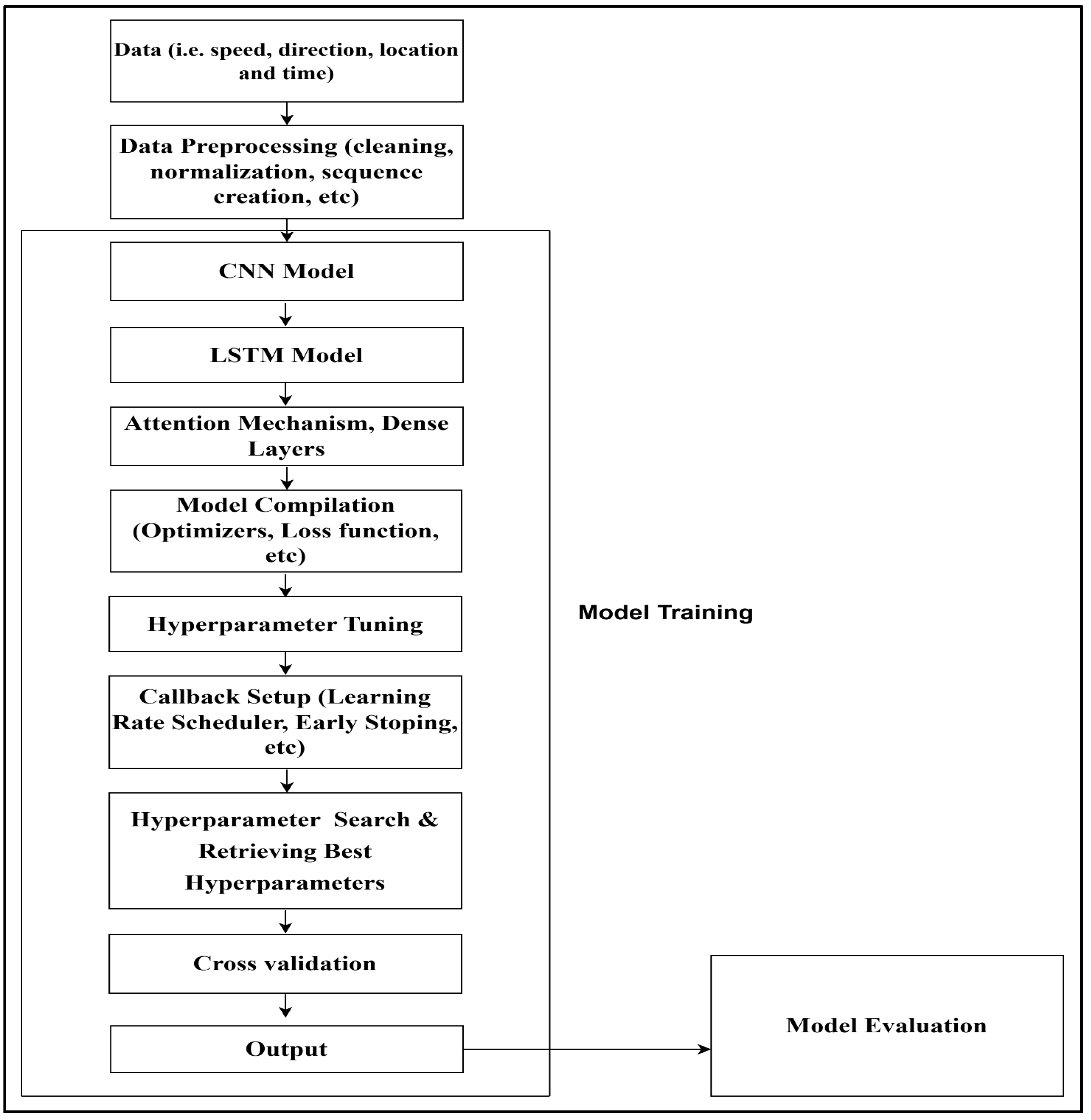
In this paper, we propose a hybrid CNN-LSTM model to predict miner location in an underground mine emergency situation. This was accomplished by collecting historical data (simulated data), which includes the speed, direction, location, and timestamp of a miner. The data were cleaned and normalized. Effective model training was facilitated by the application of normalization to the input features using standardized formulations. The accuracy of the model was enhanced by aggregating the data into sequences of length L, which reflect temporal dependencies. The LSTM component captured sequential dependencies using input, forget, and output gates, while the CNN component conducted spatial feature extraction. The Xavier initialization method was implemented to preserve consistent activations throughout the training process. Overfitting was prevented using regularization techniques, including dropout and L2 regularization. To guarantee precise and dependable predictions of miner locations, the model was trained with backpropagation through time (BPTT) and suitable optimization algorithms. Optimization strategies were employed to improve the computational efficiency and accuracy of the model, with a particular emphasis on hyperparameter tuning, regularization, and sophisticated preprocessing techniques, to enhance real-time performance in underground mining environments.

While this study adopts hybrid CNN-LSTM architecture for underground miner localization, we acknowledge the emergence of more recent and powerful sequence modeling frameworks, including Temporal Convolutional Networks (TCN), XLSTM, Transformer architectures, and Mamba model. Each of these alternatives has demonstrated strong performance across time-series prediction tasks. However, the selection of CNN-LSTM in this work is grounded in several practical considerations relevant to the constraints and safety requirements of underground mining environments.

Interpretability and robustness are essential in safety-critical systems. CNN-LSTM architecture is easier to debug and trust in decision-making pipelines, a significant advantage over Transformer-based models, which often operate as less transparent black boxes [24].

CNN-LSTM structure is highly compatible with Delay-Tolerant Networking (DTN), which produces intermittent sequential data due to communication delays or losses in underground settings.

Computational efficiency is a critical factor for real-time deployment of resource-constrained devices used in underground mines. Transformers and Mamba models require substantial memory and parallel processing power due to attention mechanisms or implicit state-space operations [25,26]. In contrast, CNN-LSTM models offer a balanced trade-off between performance and computational cost, allowing deployment on low-power edge devices and embedded systems without sacrificing critical latency requirements [27].

CNN-LSTM enjoys broad library support and optimization across platforms (e.g., TensorFlow Lite, PyTorch Mobile version 2.7.1), making integration into existing safety-monitoring infrastructure more feasible.

Nonetheless, we recognize the advantages that other architectures might offer in terms of training stability, long-range dependency modeling, and potential accuracy gains.

The remainder of this paper is organized as follows. Section 2 describes a snapshot of the current body of knowledge in this specialty area. Section 3 introduces the architecture of the model with the corresponding mathematics. Section 4 describes data collection and labeling, data pre-processing, models, training, and metrics. Section 5 presents the results from the evaluated metrics. Section 5 discusses the findings presented in Section 4. Section 6 presents the main conclusions and the future research directions.

2. Related Works

Historically, underground localization began with manual tracking and evolved into sensor-based techniques. RFID-based tracking was among the first real-time attempts, enabling the identification of miners through proximity-based tags. However, these systems often failed under cave-in, explosion, or fire scenarios, where tag readers could be destroyed or blocked. ZigBee mesh networks provided an alternative by enabling decentralized, self-healing communication. Yet, ZigBee struggled with mobility handling and degraded performance in the presence of interference or obstructions such as metal machinery or rock falls.

As the need for more adaptive and intelligent systems increased, several probabilistic and learning-based models were introduced. Markov Chain-based models, such as the Continuous-Time Series Markov Model (CTS-MM) proposed by Li et al. [28], introduced temporal awareness by allowing transitions over variable time intervals. However, these models lacked spatial structure representation, limiting their ability to predict movement across spatially diverse tunnel layouts.

Bayesian Networks, like those explored by Hasan and Ukkusuri [29], improved uncertainty modeling and were capable of reconstructing activity-location sequences. Nevertheless, their real-time application was limited by high computational cost and scalability issues, especially in large-scale mining environments.

More recently, deep learning has enabled more sophisticated modeling of spatiotemporal patterns. Graph-based architectures such as the GAE-LSTM introduced by Goyal et al. [30] combined graph autoencoders with LSTM layers to learn embedded spatial representations and sequential behaviors. While effective in open spatial settings, this method depended heavily on global spatial embeddings, which proved inadequate in the highly constrained and variable topology of underground mines.

Spatiotemporal Semantic Neural Networks (STSN), like the model proposed by Wu et al. [31], performed well in predicting the movement of objects across dynamic urban environments. However, these networks required extensive datasets and incurred high computational overhead, making them less practical for emergency response settings.

Our proposed CNN-LSTM model builds upon these foundational efforts by addressing their key limitations. It extracts localized spatial features from miner movement data using 1D convolutional layers and learns sequential dependencies via LSTM. This structure allows the model to adapt to rapid directional changes, pauses, and reroutes—common in emergency scenarios like cave-ins or fire responses.

Unlike global-embedding models, the CNN-LSTM framework can generalize across sparse and noisy datasets typical of underground environments where sensor dropout and communication delays are frequent. The model’s integration with DTN (Delay-Tolerant Networking) further enhances its robustness by ensuring intermittent data can still be used for prediction. This dual-stage hybrid approach offers a practical, generalizable, and computationally efficient solution for real-time miner localization in hazardous underground settings.

Numerous models have been suggested for location prediction, each possessing distinct advantages and drawbacks. Markov Chain-based models, despite their simplicity, fail to adequately capture long-term dependencies. Li et al. [28] advanced this by proposing Continuous-Time Series Markov Models (CTS-MM), which increase real-time accuracy but continue to encounter challenges with state generalization. Bayesian Networks provide strong probabilistic reasoning but are computationally demanding and unsuitable for real-time predictions. Hasan and Ukkusuri [29] mitigated this by combining Bayesian inference with Markov chains. However, scalability remains a difficult challenge. Spatiotemporal Neural Networks (STNN) effectively identify intricate patterns across spatial and temporal dimensions. However, they necessitate extensive datasets and entail significant computational resources [31]. LSTM-integrated polynomial regression can accommodate variable sample intervals in real-time forecasting. However, it raises sensitivity to noise and necessitates human adjustment [32]. Recurrent Neural Networks (RNNs) are constrained by their short-term memory and inadequate spatial modeling, notwithstanding advancements in trajectory prediction identified by Liu et al. [33]. LSTM models alleviate memory challenges in sequential data but encounter difficulties with irregular sampling and fluctuating time intervals [31]. Finally, ref [30] introduced GAE-LSTM for miner localization, integrating graph embeddings with LSTM for spatiotemporal modeling. However, its dependence on global spatial representations undermines its capacity to identify confined movement patterns.

In this study, three baseline models were selected for performance comparison due to their relevance and prior applications in underground miner localization tasks:

(i) CTS-MM Model was chosen for its ability to handle variable time intervals and temporal transitions in miner movement data; (ii) STSN-LSTM was also selected for its demonstrated performance in time-series prediction under constrained environments, though it incurs high computational overhead; and (iii) GAE-LSTM was included due to its integration of graph-based spatial embeddings with LSTM temporal modeling, which is useful for capturing complex, structured movement patterns. These baseline models collectively represent a range of traditional and modern techniques, providing a meaningful benchmark for evaluating the proposed CNN-LSTM + DTN model’s performance in underground emergency scenarios.

3. CNN-LSTM Model for Location Prediction in an Underground Mine

Underground mining environments are inherently constrained by both geological and geometric factors, which significantly influence their structural layout and operational dynamics. Geological constraints arise from the characteristics of the mineral deposit, including its orientation (dip, plunge, and strike), the nature of bedding planes, structural features, such as folds and faults, and the effects of depositional and post-tectonic processes. Geometric constraints are introduced through the engineered layout of the mine, encompassing elements such as pillars, walls, roofs, drifts, and raises, as illustrated in Figure 4. These factors collectively shape a complex and confined setting.

Moreover, environmental conditions such as the accumulation of debris, airborne dust, suspended water vapor, and irregular tunnel curvatures further complicate the physical landscape. These challenges create a hostile environment for conventional communication systems, impeding the reliable propagation of radio signals. This underscores the importance of Delay-Tolerant Networking (DTN) in underground mines. Its ability to store, carry, and forward messages ensures the transmission of critical data—including miner location and movement history—from the depths of the mine to the surface, even under disrupted connectivity. Such resilient data transfer is essential for real-time miner localization using hybrid deep learning models like CNN-LSTM during emergency scenarios. Figure 4 shows the general layout of an underground mine including DTN nodes and miners. Figure 4 also shows a miner traveling with a speed, ${\mathit{S}}_{\mathit{t}}$, in a direction, ${\mathsf{\theta }}_{\mathit{t}}$, towards pillar, P4 at a particular timestamp. The input data comprise T time steps, each containing three features: speed, direction of movement, and time.

This can be represented as a matrix:

$$\mathbf{X} = \left[\begin{array}{ccc}{x}_{\mathrm{1,1}}& x_{\mathrm{1,2}}& x_{\mathrm{1,3}}\\ x_{\mathrm{2,1}}& x_{\mathrm{2,2}}& x_{\mathrm{2,3}}\\ x_{T,1}& x_{T,2}& x_{T,3}\end{array}\right]$$

(1)

$x_{t,1}$: Miner’s speed at time t, $x_{t,2}$: Miner’s direction at time t, $x_{t,3}$: Time at step t, X ∈ ${\mathrm{R}}^{T\times 3}$. Every row in X represents at a given moment the feature vector. Sequential data analysis in neural networks mostly uses this representation [34].

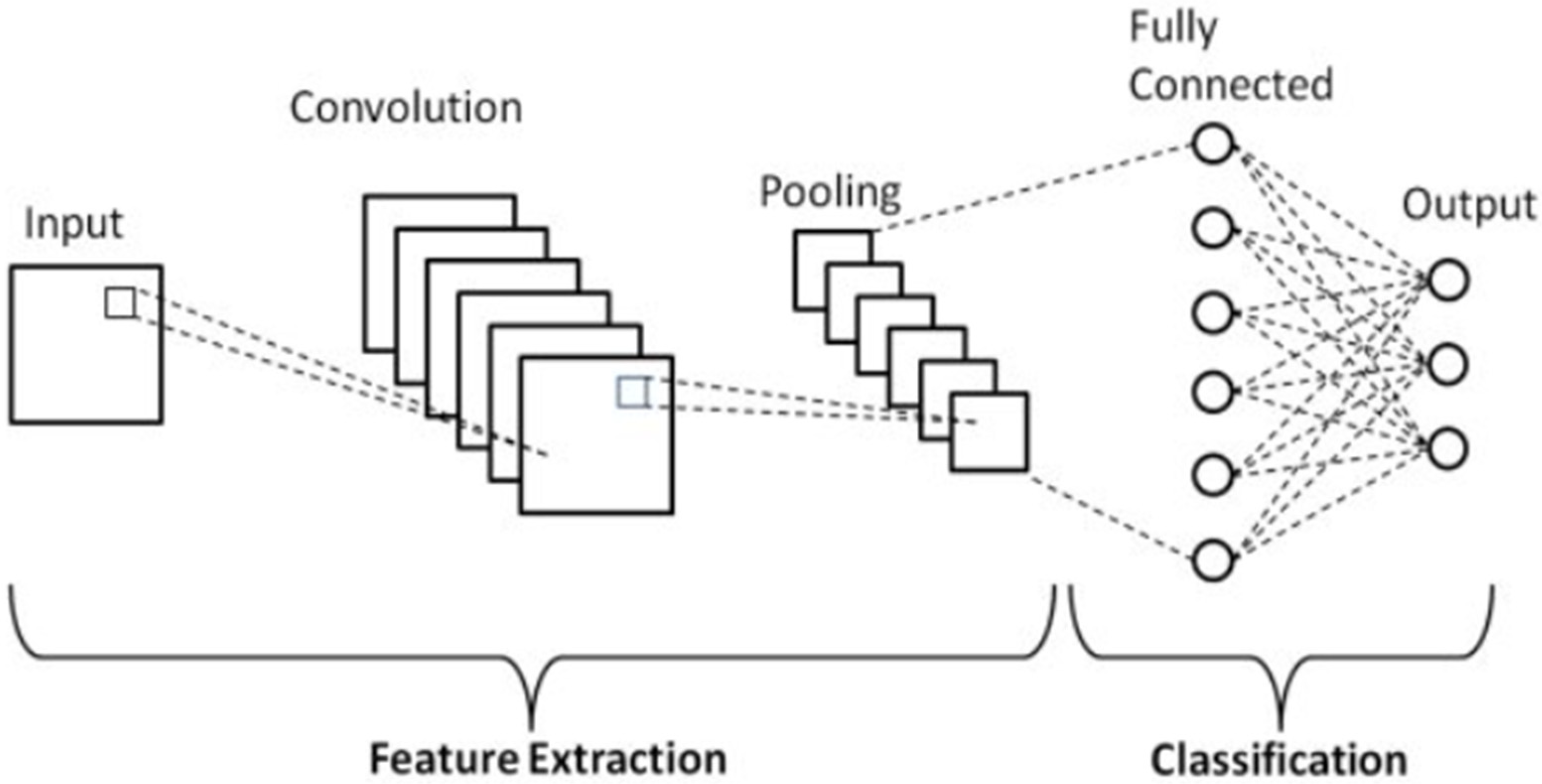
3.1. CNN Component of the Model

Figure 5 represents a basic schematic diagram of a CNN model. This illustrates the basic architecture of a Convolutional Neural Network (CNN), highlighting its two main components: feature extraction and classification. In the context of miner localization during underground emergencies, CNNs are used to automatically extract spatial features from input data—such as miner speed, direction, and location—collected via Delay-Tolerant Networks (DTN). The convolutional layers apply filters to the input data, capturing essential spatial patterns and movement trends relevant to miner behavior in constrained underground environments. Pooling layers then reduce the spatial dimensions, retaining the most significant features while minimizing computational complexity. These extracted features are passed to the fully connected layers, which perform high-level reasoning and classify the miner’s next location or movement pattern.

The convolutional kernel, or filter, is designed to capture localized variations in these features across short temporal windows. Mathematically, the kernel is represented as a matrix, as shown in Equation (2).

$$\mathrm{W}=\left[\begin{array}{ccc}{w}_{\mathrm{1,1}}& w_{\mathrm{1,2}}& w_{\mathrm{1,3}}\\ w_{\mathrm{2,1}}& w_{\mathrm{2,2}}& w_{\mathrm{2,3}}\\ w_{k,1}& w_{k,2}& w_{k,3}\end{array}\right]$$

(2)

K denotes the kernel size (i.e., the number of time steps considered), w (i,j) represents the weight corresponding to the i-th time step and the j-th input feature. This formulation enables the network to detect short-range spatial patterns that may signify miner transitions, stops, or changes in trajectory—particularly valuable in emergency scenarios where abrupt behavior changes are expected.

The convolution operation at a given time step t applies the kernel to a sliding window over the input sequence and is defined as Equation (3).

$$z_t={\sum }_{i=0}^{k-1}{\sum }_{j=1}^3{w}_{i+1,j}·x_{t+i,j}+b$$

(3)

Here, $x_{t+i,j}$ is the input value for feature j at time (t + i), and b is a learnable bias term. The resulting $z_t$ represents the convolved feature at time t, summarizing spatial dynamics across the specified window.

To enhance the non-linear modeling capacity of the network, the output of the convolution is passed through a non-linear activation function, typically ReLU, given by Equation (4).

$${\alpha }_t=\mathrm{ReLU} \left(z_t\right)=\max (0, z_t)$$

(4)

This transformation preserves only the most informative features while introducing sparsity, which is helpful in learning robust representations of miner activity. To further reduce the dimensionality and computational cost, while preserving salient information, max pooling is applied over the activation map.

Given a pooling window size p, the pooling operation is expressed as Equation (5).

$$p_t=\max ({\alpha }_t, {\alpha }_{t+1},. . ., {\alpha }_{t+p-1})$$

(5)

This produces a compact representation:

$$\mathrm{P} = \left[\begin{array}{c}{p}_1\\ \begin{array}{c}{p}_2\\ ⋮\end{array}\\ p_{\lfloor (T-k+1)/p\rfloor }\end{array}\right], \mathrm{P} \in R^{n\times C}$$

(6)

C is the number of convolutional filters used, and $n$ = $\lfloor (T-k+1)/p\rfloor$ is the number of pooled segments.

The pooled output is given by Equation (7).

$${\mathit{F}}_{CNN}=\mathrm{P}, {\mathit{F}}_{CNN}\in R^{n\times C}$$

(7)

Equation (7) represents the final feature map derived from the CNN. This output is subsequently fed into the LSTM layers, which capture temporal dependencies over time, enabling the accurate prediction of future miner locations.

3.2. LSTM Component of the Model

Following the extraction of spatial features using the CNN component, the output sequences ${\mathrm{F}}_{CNN,t}$ are passed to an LSTM network to model temporal dependencies in the sequential behavior of the miner. The LSTM, as illustrated in Figure 6, is particularly suited for handling time-series data due to its ability to retain long-term information while mitigating the vanishing gradient problem common in traditional recurrent networks. This is achieved through gated mechanisms that selectively retain, update, or discard information over time.

At each time step t, the LSTM receives three inputs: the current CNN-derived feature ${\mathbf{F}}_{CNN,t}$, the previous hidden state ${h }_{(t-1)}$ and the previous cell state $C_{t-1}$. These inputs interact through a series of gates, each playing a unique role in the information flow as given by Equations (8)–(13).

$$i_t=\sigma (W_i{\mathit{F}}_{CNN,t}+U_i{h }_{(t-1)}+b_i)$$

(8)

$$f_t=\sigma (W_f{\mathit{F}}_{CNN,t}+U_f{h }_{(t-1)}+b_f)$$

(9)

$${\tilde{c}}_t=\tanh (W_c{\mathit{F}}_{CNN,t}+U_c{h}_{(t-1)}+b_c)$$

(10)

$$c_t=f_t\odot c_{(t-1)}+i_t\odot {\tilde{c}}_t$$

(11)

$$o_t=\sigma (W_o{\mathit{F}}_{CNN,t}+U_o{h}_{(t-1)}+b_o)$$

(12)

$$h_t=o_t\odot \tanh (c_t)$$

(13)

$i_t$, $f_t$, and $o_t$ are the input, forget, and output gates, respectively; ${\tilde{c}}_t$ is the candidate cell state; $c_t$ is the updated cell state; $h_t$ is the current hidden state; ⊙ denotes element-wise multiplication; σ and tanh are the sigmoid and hyperbolic tangent activation functions. $W_i$, $W_f{,W}_o{,W}_c$: Weight matrices for input, forget, output, and cell gates, respectively; $U_i$, $U_f{,U}_o{,U}_c$: Weight matrices for hidden state; $b_i$, $b_f{,b}_o{,b}_c$: bias terms.

Each gate has a well-defined role. The input gate controls the inflow of new information into the memory cell; forget gate regulates the retention of past information; output gate governs how much of the cell memory is exposed to the output; cell state acts as the memory track, preserving long-term information; and the candidate cell state contains potential new content to be added to memory. The hidden state $h_t$ encodes both the past and current contextual knowledge of miner movement and serves as the input to the final classification layer of the model as defined in Equation (14).

In the context of predicting the miner’s next location (e.g., position or pillar ID), the hidden state $h_t$ is passed through a fully connected (dense) layer that projects it into a logit space of dimension K, where K is the number of possible location classes.

$${\widehat{z}}_t=W_{dense}·h_t+b_{dense}$$

(14)

where ${\widehat{z}}_t$ represents the unnormalized log-probabilities (logits) for each class; $W_{dense}$: weight matrix for the dense layer; $b_{dense}$: bias for the dense layer.

These logits are converted into a normalized probability distribution using the SoftMax activation function as in Equation (15).

$${\widehat{y}}_t=\mathrm{Softmax} ({\widehat{z}}_t)={\displaystyle \frac{e^{\widehat{z}t}}{{\sum }_{k=1}^K{e}^{{\widehat{z}}_k}}}$$

(15)

${\widehat{y}}_t$ gives the predicted probabilities over all K location classes.

The predicted class (i.e., the miner’s most likely next location) is determined by selecting the class with the highest probability, as shown in Equation (16).

$$\mathrm{Predicted} \mathrm{Class}=\arg \max \left({\widehat{y}}_t\right)$$

(16)

This final prediction mechanism, informed by both spatial and temporal dynamics, enables the model to anticipate miner movements with high accuracy, even under disrupted communication conditions in underground mine emergencies.

4. Method

4.1. Data Preprocessing

The dataset used in this study was synthetically generated to simulate underground miner movements. We adopted multiple data generation strategies to validate the proposed model. Specifically, we employed the Brinkoff generator, modifying its outputs to accurately simulate movement patterns within an underground mining environment. Datasets were generated for configurations involving 25, 50, and 100 DTN nodes, structured into four distinct operational categories: regular mine workers, supervisory personnel, trolleys, and other mobile equipment. Individual miners were programmed to visit unique sets of locations, with intentional overlaps incorporated to reflect realistic patterns of movement and interaction. Supervisors, while not traversing all locations, exhibited higher movement velocities and were restricted to specific stopping points for task execution. Trolleys and equipment, whose core functions entail the transport of waste and ore, were modeled to exhibit greater speeds and predefined directional flows.

Each DTN node category was assigned a bespoke set of parameters, including velocity constraints, time schedules, and movement paths, thereby capturing the heterogeneous operational behaviors characteristic of underground mine workers. To further enhance realism, movement velocities near certain pillar locations were constrained according to role-based operational norms. Considering the unavailability of real-world DTN data from operational underground mines, we synthesized these data by modeling known movement behaviors of various node types over time. The simulation adhered to a typical underground mining shift (9:00 AM to 5:00 PM), represented within a 12 h time format to maintain temporal consistency with operational practices. Speeds were carefully allocated to each miner (node class) to accurately emulate the movement dynamics of miners and equipment. Post-generation, the dataset was refined to replicate the nuanced temporal and spatial conditions characteristic of real-world underground mining operations. Recognizing that stationary periods form a critical component of underground activities, we incorporated pauses into the movement data to reflect miners stopping for excavation, task performance, and rest breaks. Supervisors were likewise modeled to pause for supervisory tasks such as reporting, while equipment nodes included pauses to simulate operational phenomena such as cooling cycles and loading/unloading intervals.

The dataset consisted of 1,048,575 entries with five primary features: Miner ID, Speed (m/s), Direction (degrees), Timestamp, and Location (Pillar ID). These attributes were chosen to reflect the miner’s movement characteristics and spatial positioning at given time intervals. To ensure high data quality, all missing values were either dropped or replaced with zero, while duplicate records were eliminated to avoid model overfitting and data redundancy. The Timestamp column, originally in seconds, was normalized by converting to hours and subsequently converted to a datetime format to reflect accurate temporal context. The dataset was partitioned using a stratified K-Fold cross-validation technique with five folds. A five-fold configuration was selected to provide a robust estimate of the model performance while maintaining computational efficiency, as this balance is commonly recommended in the literature for typical dataset sizes. Stratification ensured that all folds preserved the class distribution of pillar IDs, thereby minimizing bias and allowing the model to generalize better on unseen data.

Table 1. Sample of the raw dataset before preprocessing.

Miner ID	Speed (m/s)	Direction (Degrees)	Timestamp	Location (Pillar Name)
M001	2.367488	0.0	2025-04-05 14:30:00	P19
M001	2.367488	0.0	2025-04-05 14:30:10	P19
M002	0.0	0.0	2025-04-05 14:30:20	P50
M003	0.695482	0.0	2025-04-05 14:30:30	P30
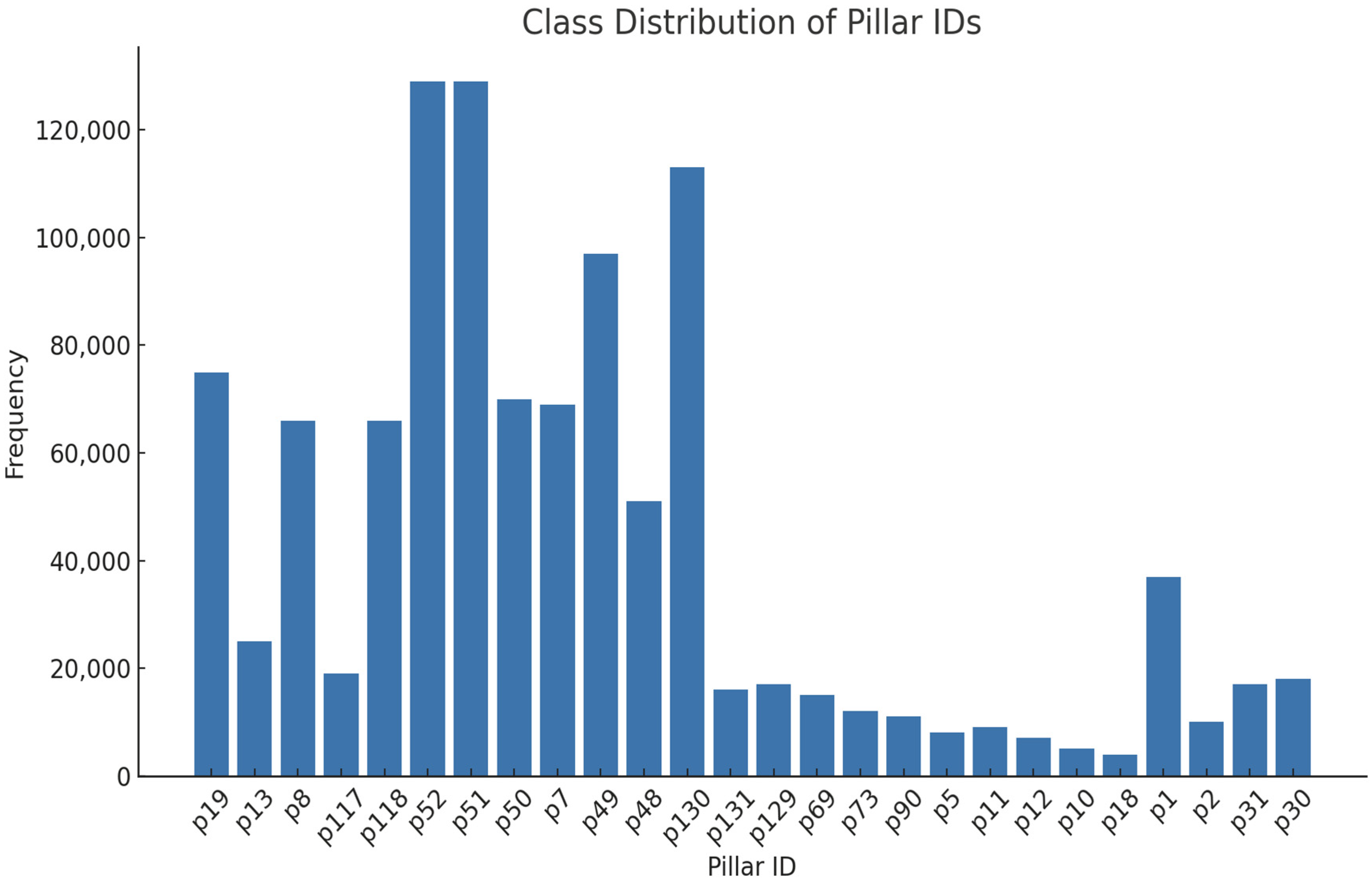
M002	1.352589	0.0	2025-04-05 14:30:40	P48

contains a snapshot of the raw dataset prior to preprocessing. Each row captures an individual miner’s movement data at a given point in time, including their speed, movement direction, timestamp, and associated pillar location. To better understand the distribution of class labels in the dataset, the frequency of miner occurrences across various pillar locations was visualized. Figure 7 illustrates the class distribution of the pillar IDs in the training dataset, representing the ground truth locations that the model is trained to predict. This visualization helps assess the balance of samples across different pillar locations. The distribution is highly imbalanced, with a few pillar IDs (e.g., p51, p52 and p130) accounting for a disproportionately large number of observations, while many other locations have relatively few instances.

4.2. Model Architecture

The CNN component serves to automatically learn local patterns within the sequential input data (such as speed and direction over time). It does this by applying 1D convolutional filters that slide across the time axis, identifying meaningful spatial correlations in short segments of the sequence. This is followed by max-pooling, which reduces the size of the data representation by selecting the most prominent features, thereby preserving key movement patterns while discarding irrelevant details and reducing computational complexity. To further enhance training stability and accelerate convergence, batch normalization is applied after the convolutional layer, helping to maintain consistent feature distributions across training batches. The LSTM layer was then used to capture long-range dependencies in the sequential input, enabling the model to learn the underlying time-series patterns in the miner’s movement. This is essential for modeling the miner’s behavior, as past movements can influence future location transitions. To mitigate overfitting, dropout regularization is applied after the LSTM layer, randomly deactivating a portion of neurons during training to encourage the network to generalize better. The learned features from the LSTM output are then flattened and passed to a fully connected dense layer, which combines these features to make the final prediction. The network concludes with a SoftMax activation function at the output layer, which converts the model’s outputs into a probability distribution over all possible pillar locations which allows the model to assign a confidence score to each potential miner location. This end-to-end architecture is depicted in Figure 8.

4.3. Model Training

Model training was carried out using the Adam optimization algorithm, which is widely used in deep learning for its adaptive learning rate capabilities and efficient convergence. An initial learning rate of 0.001 was chosen to provide a stable starting point for optimization. To further refine the training process as the model approached convergence, the learning rate was configured to decay exponentially during training. This approach allows for larger weight updates in the early stages of learning and progressively smaller updates as the model fine-tunes its weights, helping to avoid overshooting minima in the loss landscape. The batch size was set to 32, meaning that 32 samples were processed in each training iteration. This batch size offers a good trade-off between training speed and convergence stability, making efficient use of GPU memory while ensuring reliable gradient estimates. raining was conducted for a maximum of 100 epochs; however, to prevent unnecessary training cycles and potential overfitting, early stopping was implemented. This technique monitors the validation loss and halts training once the loss stops improving for a predefined number of consecutive epochs (patience). As such, the model is preserved at its best-performing state on the validation set. To further guard against overfitting, a dropout rate of 0.5 was applied during training. Dropout randomly disables 50% of neurons in the relevant layers during each iteration, preventing the network from becoming overly reliant on any particular set of neurons and encouraging it to learn more robust and generalizable patterns. In addition to dropout, L2 regularization (also known as weight decay) was incorporated into the training process. This technique penalizes large weight values by adding a term to the loss function proportional to the squared magnitude of the weights. As a result, the model is encouraged to maintain smaller and more stable weights, which promotes generalization and reduces the risk of overfitting to the training data. The model was trained using the categorical cross-entropy loss function, which is appropriate for the multi-class classification nature of the miner localization problem. Categorical cross-entropy measures the dissimilarity between the true class distribution (ground truth pillar IDs) and the predicted class probabilities output by the model, guiding the optimization process to improve classification accuracy. To fine-tune the model and identify an optimal configuration, Bayesian optimization was employed via the KerasTuner framework. This method systematically explores the hyperparameter space—such as the number of convolution filters, number of LSTM units, dropout rate, and learning rate decay parameters—to discover the combination that yields the best model performance.

Table 2. Hyperparameters used in the CNN-LSTM model.

Hyperparameter	Value
Optimizer	Adam
Initial Learning Rate	0.001
Learning Rate Scheduler	Exponential Decay
Batch Size	32
Number of Epochs	100 (with Early Stopping)
Dropout Rate	0.5
L2 Regularization	Enabled
Loss Function	Categorical Cross-Entropy
CNN Kernel Size	3 (typical, implicitly defined)
Number of CNN Filters	Tuned via Bayesian Optimization
Number of LSTM Units	Tuned via Bayesian Optimization
Activation Functions	eLU (CNN), tanh/sigmoid (LSTM)
Output Activation	SoftMax
Evaluation Metrics	Accuracy, Precision, Recall, F1 Score

summarizes the key hyperparameters and their values used in the proposed CNN-LSTM model during training and optimization. These hyperparameters were determined through Bayesian optimization and regularization strategies to balance accuracy, generalization, and computational efficiency under underground mining constraints.

Bayesian optimization is particularly effective for navigating complex hyperparameter spaces with fewer trials compared to random or grid search. Finally, the entire training process was implemented using the TensorFlow 2.x deep learning framework, which provides robust support for dynamic computational graphs and seamless integration with Keras APIs. Where available, GPU acceleration was leveraged to significantly reduce training time and enable more extensive experimentation with model configurations.

4.4. Evaluation Metrics

Model performance was evaluated using a comprehensive set of metrics suitable for multi-class classification problems. Accuracy was computed to measure the overall percentage of correct predictions. Precision and recall were determined for each class, offering insight into the model confidence and sensitivity in identifying specific pillar locations. The F1 score, defined as the harmonic mean of precision and recall, was used to assess the model balance between false positives and false negatives, especially in the presence of class imbalance. These evaluation metrics are formally defined for precision, recall, and F1, respectively, in Equations (17)–(19).

$$Precision={\displaystyle \frac{True Positives}{True Positives+False Positives}}$$

(17)

$$Recall={\displaystyle \frac{True Positives}{True Positives+False Positives}}$$

(18)

$$F1={\displaystyle \frac{2\times Precision\times Recall}{Precision+Recall}}$$

(19)

The use of these metrics provided a multi-dimensional view of the model’s capacity to detect, classify, and generalize across various underground pillar locations in emergency scenarios.

5. Results and Discussion

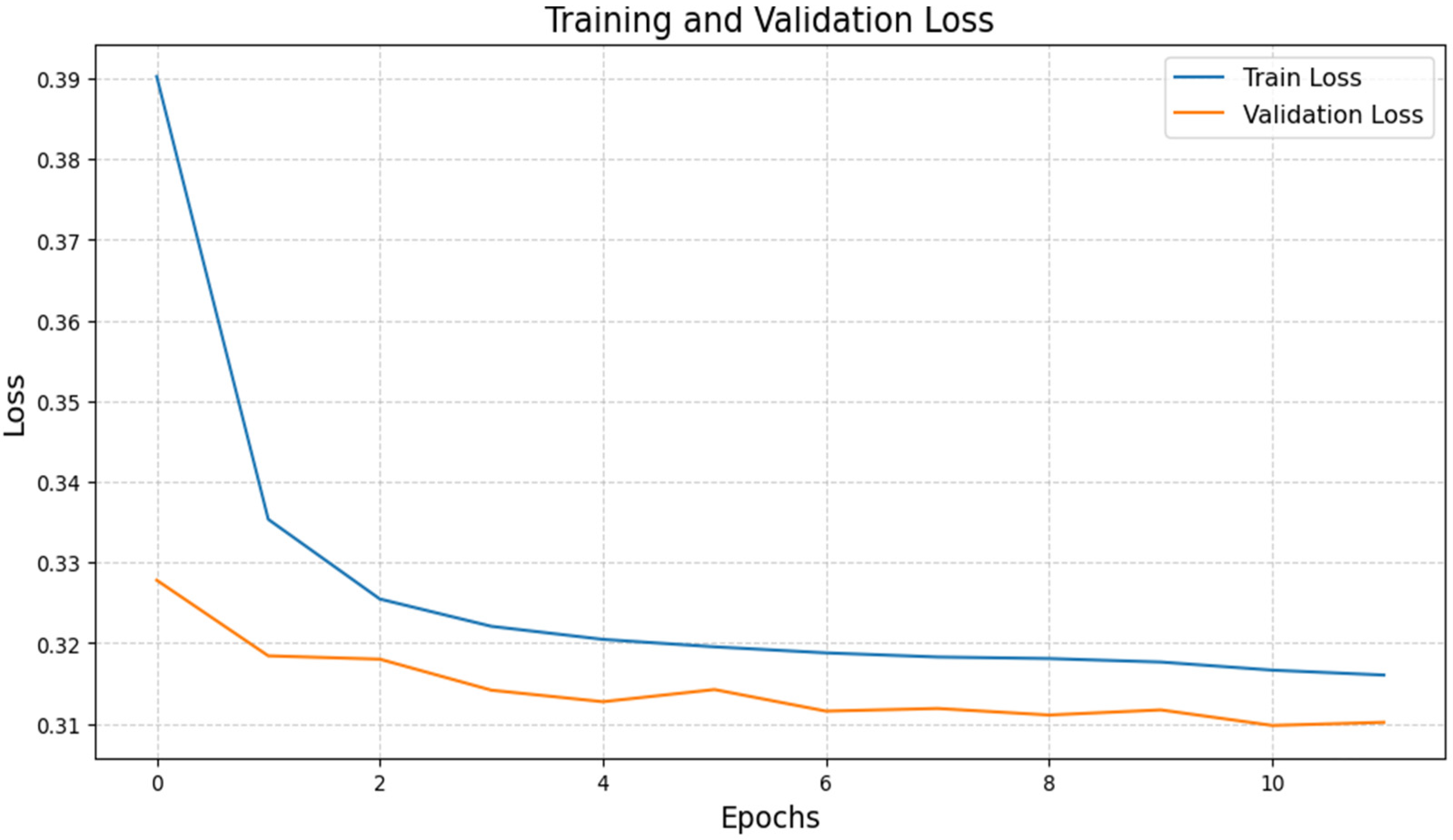
The following results were generated after extensive training of the model. Figure 9 illustrates the loss of the training and validation datasets across epochs. The training loss (blue line) decreases consistently, while the validation loss (orange line) stabilizes and remains lower than the training loss. Consistent training loss reduction suggests that the model is learning patterns in the training data. The continuous drop reflects proper optimization of weights during backpropagation. Also, an important observation is the early stabilization of validation loss around epoch 5. This implies that the model generalizes well to unseen data, with no significant overfitting, indicating that it has effectively learned the underlying spatiotemporal patterns in the data. Such generalization capability is critical in underground mining environments, where models must robustly handle dynamic and variable movement patterns during emergency situations, enabling accurate miner localization even under conditions not explicitly represented in the training data. Furthermore, the small difference between the two losses indicates minimal overfitting. This suggests that the model performs well on the validation and training sets alike. CNN layers extract spatial characteristics, while LSTM layers capture temporal dependencies. These properties enable consistent convergence, as demonstrated in the loss curves. If the loss curves were diverging, it would signal overfitting or underfitting. However, in this case, the curves align closely, indicating balanced model complexity.

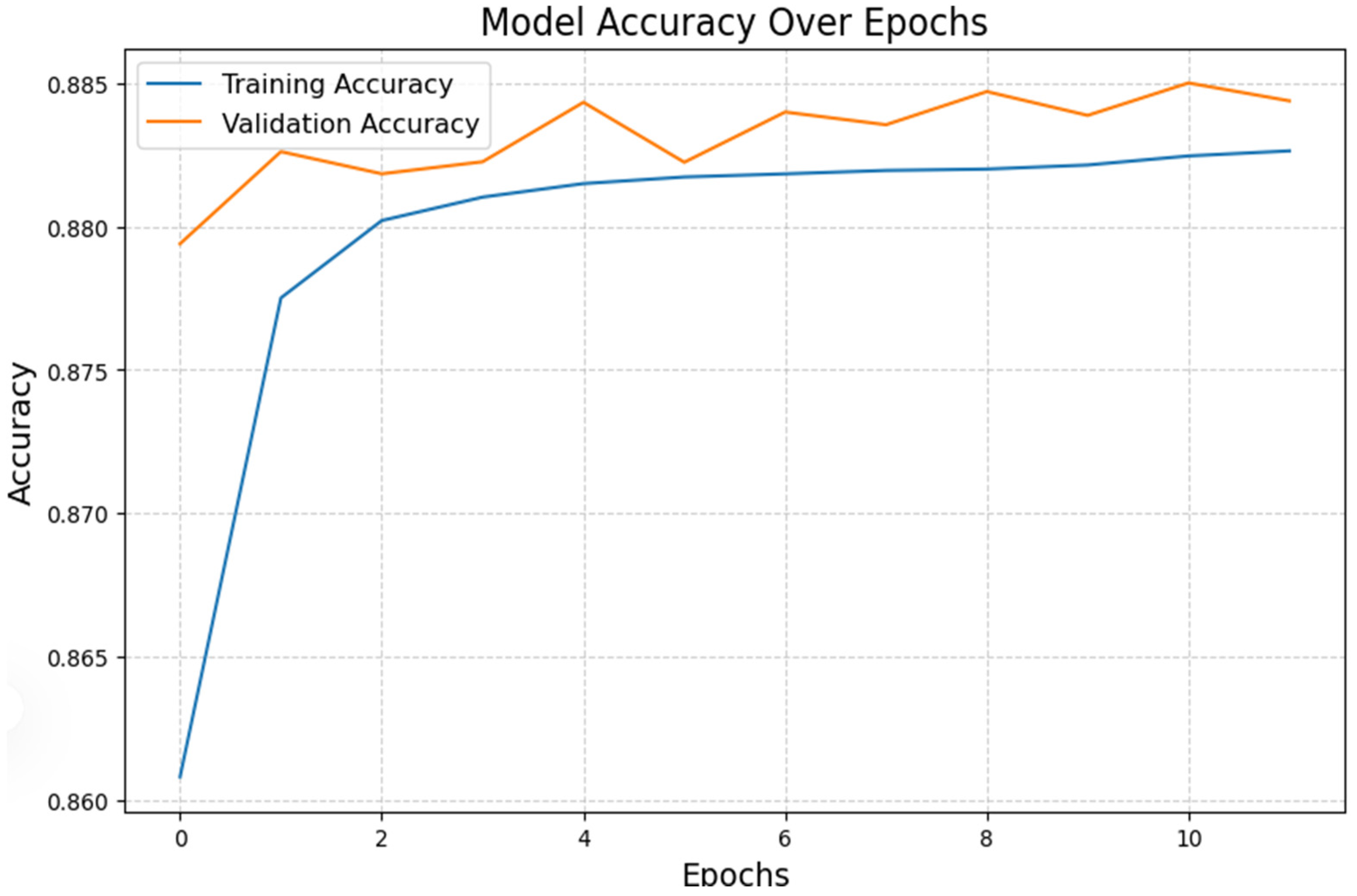
Figure 10 shows the model accuracy on the training and validation sets across epochs. Both metrics improve steadily, with validation accuracy peaking at approximately 88.5%. The training and validation accuracy exhibit a consistent increase, as illustrated in Figure 10. Training accuracy consistently increases, indicating that the model effectively learns from the training data. In addition, the validation accuracy momentarily surpasses the training accuracy in the early epochs, which suggests the effect of dropout regularization and robustness. High validation accuracy (~88.5%) indicates that the CNN-LSTM model effectively captures the spatial and temporal patterns in the data, resulting in strong generalization capabilities. The spatial and temporal patterns in the data are effectively captured by the CNN-LSTM model. After epoch 5, the training and validation accuracies reach a plateau, indicating that the model has attained its maximum learning potential for the specified dataset. The attention mechanism, which enables the model to concentrate on the most pertinent features in sequential data, is likely responsible for the high accuracy. The validation accuracy closely follows the training accuracy, further supported by regularization techniques, such as dropout, that help prevent overfitting.

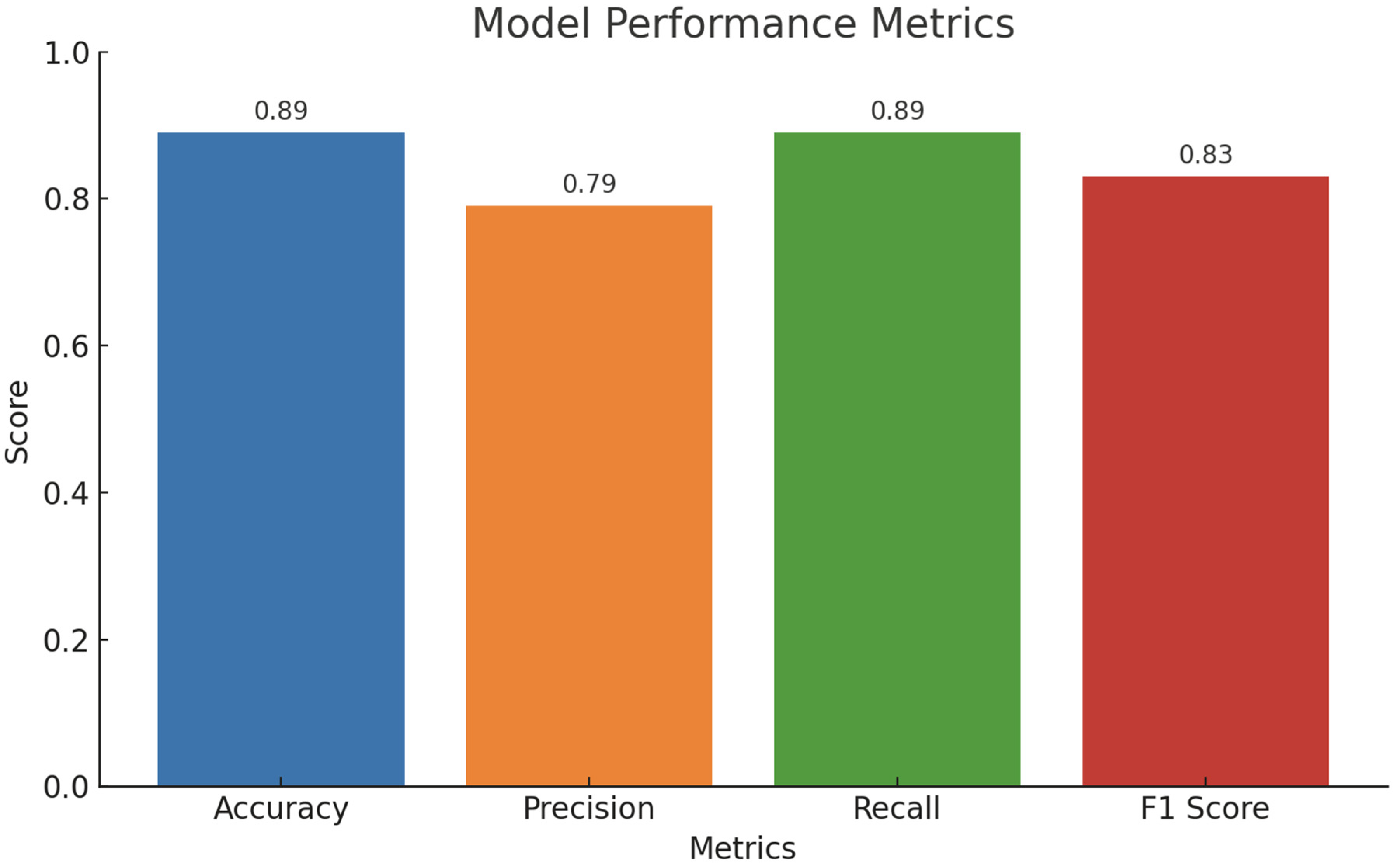
Figure 11 represents the model performance metrics (Accuracy, Precision, Recall, F1-Score). This bar chart compares the overall performance metrics of the model: Accuracy: 89%, Precision: 79%, Recall: 89%, and F1-Score: 83%. High recall indicates the model captures most true positives effectively. Critical for applications where missing a class prediction (false negatives) is more costly than predicting extra classes (false positives). A moderate precision suggests the model occasionally predicts false positives, which could be problematic in high-stakes scenarios.

While accuracy is the most reported performance metric in classification tasks, it is not always the most informative or appropriate, especially in scenarios involving imbalanced class distributions, such as underground miner localization.

In this study, the prediction task involves identifying the correct pillar ID from among many possible classes, some of which are rarely visited (sparse data). In such cases, a model can achieve high accuracy by consistently predicting only the most common classes, while completely ignoring the rare but critical locations (e.g., dead ends, blocked drifts, or emergency escape zones). This would inflate the accuracy score without reflecting the model’s true utility in safety-critical situations.

Metrics such as recall and F1-score are better suited to measure performance under such conditions:

❖

Recall indicates how many of the actual positive cases (true pillar locations) are correctly identified—critical in rescue scenarios.

❖

F1-score balances both precision and recall, giving a better overall view when class distribution is uneven or noisy.

However, we used accuracy for cross-model comparison because:

❖

It is consistently reported across baseline studies (e.g., CTS-MM, STSN-LSTM, GAE-LSTM), enabling direct and fair benchmarking.

❖

Some baseline studies do not report precision, recall, or F1-score, which limits the scope of comparative analysis to accuracy alone.

To mitigate this limitation, we complemented the accuracy-based comparison with a detailed internal performance breakdown of our CNN-LSTM + DTN model using precision (0.79), recall (0.89), and F1-score (0.83) to provide a more robust performance characterization. These additional metrics are particularly relevant to evaluating the model’s real-world applicability in emergency settings.

Generally, a high validation accuracy and low loss indicate strong generalization capabilities. Also, a high recall ensures that the model identifies most true positives, which is critical in underground mining applications. Accurate miner location prediction in underground environments is critical for safety and operational efficiency and the model’s performance metrics suggest it is well-suited for predicting locations with sufficient training data but may need enhancements for underrepresented areas. The proposed CNN-LSTM model, integrated with DTN infrastructure, provides a practical and robust solution for the localization and tracking of miners during underground mine emergencies, where direct communication links may be disrupted. In such scenarios, DTN enables store-carry-forward relay of movement data across nodes, allowing the CNN-LSTM model to continue predicting each miner’s location based on the data received.

The proposed model, integrated with Delay-Tolerant Network (DTN) infrastructure, is well-suited for both routine miner localization and application in simulated trapped-miner scenarios. The CNN component extracts spatial movement patterns from short sequences of input features, while the LSTM captures long-term temporal dependencies, enabling the model to anticipate future miner positions with an accuracy of 89% and recall of 89%. By analyzing recent movement history through a time window of past steps, the model predicts the miner’s next likely location within a given duration and supports multi-step forecasting for dynamic path estimation in real time. Miner movement patterns are shaped by factors such as assigned role (worker, supervisor, equipment operator), the geometric layout of the mine (pillars and tunnels), and task-related behaviors (work zones, break areas), as captured in the synthetic dataset. In simulated emergency scenarios such as a tunnel collapse or explosion, where movement may become constrained or stationary, DTN nodes continue to relay movement features (speed, direction, timestamp).

The CNN-LSTM model can maintain real-time predictions of miner locations even under disrupted communication, accurately localizing trapped miners and enabling rescue teams to dynamically prioritize intervention paths. Furthermore, its ability to forecast possible future movements of miners attempting self-escape enhances situational awareness that is critical for time-sensitive rescue operations. This predictive capability represents a key advancement toward the operational deployment of intelligent miner localization systems to support both routine safety monitoring and emergency response in underground mining environments.

To further validate the effectiveness of the proposed CNN-LSTM model with DTN integration, we compared its performance with three prominent baseline methods commonly used in underground localization tasks: Continuous-Time Series Markov Models (CTS-MM), Spatiotemporal Semantic Neural Networks (STSN-LSTM), and Graph Attention Embedding with LSTM (GAE-LSTM). The comparison metric used was classification accuracy, as it is the most consistently reported across these studies.

As shown in Figure 12, the CTS-MM model by [28] achieved an accuracy of approximately 43%, largely limited by its inability to learn spatial relationships or complex sequential patterns. STSN-LSTM, developed by [31], performed better with an accuracy of about 65%, owing to its use of temporal semantic encoding, though it was constrained by its computational intensity and requirement for dense datasets. The GAE-LSTM model by [30] demonstrated further improvement, reaching around 75% accuracy, by incorporating spatial graph embeddings fused with LSTM networks; however, it struggled with dynamic topologies and confined tunnel environments typical of underground mines.

In contrast, our CNN-LSTM + DTN model achieved the highest accuracy of 89%, reflecting its ability to capture both localized spatial patterns and long-range temporal dependencies, even under sparse, noisy, or disconnected conditions. This improvement confirms the robustness and practical suitability of our dual-stage hybrid architecture for miner localization during underground emergencies.

To supplement the visual summary provided in Figure 12,

Table 3. Accuracy Comparison of Baseline Models and Proposed CNN-LSTM + DTN Model.

Model	Accuracy
CTS-MM	0.43
STSN-LSTM	0.65
GAE-LSTM	0.75
CNN-LSTM + DTN	0.89

presents a concise comparison of the classification accuracy achieved by the baseline models and the proposed CNN-LSTM + DTN model.

This quantitative comparison underscores the contribution of this work not only in terms of architectural novelty but also in significantly advancing predictive accuracy for real-time underground localization under emergency constraints.

CNN-LSTM model handles complexity through a combination of architectural and operational features. The CNN layer extracts localized short-range movement patterns, such as abrupt stops or route detours near obstructions. The LSTM layer captures long-term dependencies, enabling it to learn recurring miner behaviors such as frequent paths or task-based movement cycles. DTN integration ensures continuity of location prediction even when direct communication links are disrupted, allowing stored messages to be processed once connectivity resumes which is crucial for emergencies. Regularization techniques, including dropout and L2 penalties, combined with Bayesian hyperparameter optimization, further improve the model’s robustness against overfitting and enhance generalization across sparse, noisy, or partially missing data. Simulation results confirm that even under challenging conditions, such as irregular time sampling or sudden halts (e.g., due to collapse or entrapment), the model sustains strong performance with F1-scores above 83% and recall above 89%, minimizing false negatives and enhancing rescue reliability.

While CNN-LSTM architecture is suitable for real-time inference due to its efficient sequential structure and relatively small parameter count, this study did not directly measure inference deployment performance on edge devices. Nevertheless, the integration with Delay-Tolerant Networking (DTN) ensures near-real-time prediction continuity during communication gaps. Future work will include an empirical evaluation of the inference time per sample and hardware deployment tests to support real-time performance claims under emergency constraints.

6. Conclusions and Future Work

This study presents the development and evaluation of a deep learning-based location prediction model for underground miners using a hybrid CNN-LSTM architecture. The model was trained on a simulated dataset composed of miner movement data, including timestamped measurements of speed and directional angle, labeled by corresponding pillar IDs to represent physical locations in the mine. Preprocessing steps included timestamp normalization, duplicate removal, handling of missing values, and restructuring of the data for time-series modeling. The CNN-LSTM model was designed to learn both spatial and temporal patterns in miner behavior, which are crucial for anticipating movement and ensuring timely localization in emergency scenarios. The performance evaluation, as illustrated in Figure 11, revealed an accuracy of 89%, a recall of 89%, F1 score of 83%, and a precision of 79%. These results indicate the model’s strong ability to correctly identify miner locations, particularly excelling in recall, an essential metric in safety applications where missed detections could be critical. The overall F1 score reflects a healthy balance between precision and recall, suggesting the model’s reliability in practical applications. However, the class distribution of pillar locations (Figure 7) revealed a high degree of imbalance, with a few classes dominating the dataset. This likely contributed to the relatively lower precision score and indicates the need for strategies to address skewed class representation in future iterations.

It is important to note that the dataset used in this work was synthetically generated to emulate realistic underground movement patterns. While this approach allows controlled experimentation and algorithm development, it may not fully capture the stochastic and environmental complexities of actual underground mining operations. Therefore, future work will focus on validating and adapting the model using real-world underground mine data to ensure its robustness and practical applicability in operational settings. Future work will also focus on deploying the trained model on embedded edge devices for real-time inference and testing in dynamic underground environments. These steps aim to transition the system from proof-of-concept to practical deployment for improving miner safety and spatial awareness in underground emergencies.

In addition to the results achieved in this study, it is important to recognize that CNN-LSTM models—while effective—have encountered several limitations when applied in other domains such as healthcare, energy forecasting, and industrial prognostics. These include high computational demands [20], overfitting on small or imbalanced datasets [21,35], difficulty modeling long-term dependencies in highly variable environments [31], and limited interpretability in safety-critical applications [22,23]. Such challenges are particularly relevant to underground mining, where real-time deployment often requires low-power edge devices and training data may be sparse or unevenly distributed across locations. Future work should therefore explore model compression techniques such as pruning or quantization to enhance deployment feasibility on embedded systems [20]. Incorporating data augmentation strategies and transfer learning from related spatiotemporal datasets may also improve generalization in imbalanced scenarios [35]. Furthermore, integrating attention mechanisms could enhance the model’s ability to capture long-range movement patterns [24], while explainability tools such as SHAP or LIME can help interpret predictions in critical rescue operations [22]. Addressing these limitations is essential to fully harness the model’s potential and ensure robust, transparent, and scalable localization systems for underground mining emergencies.