1. Introduction
Monocular depth estimation (MDE) infers the distance of each pixel in a single 2D RGB image to the camera. As a fundamental yet challenging computer-vision task [
1], accurate depth estimation is indispensable for three-dimensional scene understanding, environmental perception, and autonomous interaction. In the context of autonomous vehicles, MDE plays a pivotal role in enabling real-time obstacle avoidance, a critical factor for ensuring vehicle safety. For instance, by precisely inferring the distances of surrounding objects from a single RGB image, autonomous vehicles can make split-second decisions to avoid collisions. Furthermore, robust depth estimation supports accurate scene construction for augmented reality (AR)/virtual reality (VR) systems, autonomous robotic navigation, and 3D reconstruction [
2].
However, MDE is inherently ill-posed: an identical 2D projection can correspond to infinitely many 3D geometries [
3]. Recent deep-learning approaches, leveraging large-scale convolutional neural networks (CNNs) and Vision Transformers (ViTs), have achieved promising results under normal illumination by learning statistical regularities linking appearance, semantics, and geometry.
In autonomous driving scenarios, however, image sensors often encounter high-dynamic-range (HDR) scenes characterised by severe over-exposure or under-exposure. Over-exposed regions lose texture and edge cues due to saturation, while under-exposed regions suffer from poor signal-to-noise ratios. These conditions degrade conventional learning-based MDE models, leading to depth maps with holes, blurred boundaries, scale drift, and unreliable predictions [
1,
3]. Most existing methods assume well-exposed inputs, rendering them ineffective in HDR environments—a critical limitation for autonomous vehicles operating in diverse lighting conditions.
The emergence of latent diffusion models (LDMs) offers a novel pathway. Pre-trained on Internet-scale image corpora, LDMs encode rich visual priors about shape, material, and lighting, excelling in image synthesis and in-painting. For example, Marigold [
4] fine-tunes Stable Diffusion for depth regression, achieving cross-domain generalisation. However, its 50-step DDIM inference ≈1 s exceeds real-time constraints for autonomous driving applications. Other approaches, such as Lotus, compress denoising to a single-step via x
0-prediction or distillation, improving inference speed but neglecting the adverse impact of extreme exposure on feature extraction and depth inference.
To address these limitations, we propose the Exposure-Aware Single-Step Diffusion Framework for Monocular Depth Estimation in Autonomous Vehicles (EASD). This framework integrates the single-step efficiency of LDMs with explicit exposure modelling to achieve real-time performance while enhancing robustness in HDR scenes. Key contributions include:
Single-step latent depth regression. We regress the latent depth map in a single x0-prediction step, eliminating iterative error accumulation and heavy computation.
Exposure-Aware Feature Fusion (EAF). Global brightness statistics guide an attention mechanism that dynamically re-weights multi-scale features, amplifying subtle textures in under-exposed regions and suppressing saturation artefacts in highlights.
Diversified Depth Predictor (DDP) within the EASD framework supports two inference modes: Multi-Sample Mode draws multiple stochastic samples to provide pixel-level uncertainty estimates, making it suitable for reliability-critical scenarios, while Single-Shot Inference Mode fixes the noise vector to deliver fast, deterministic predictions for real-time applications; choosing between the two modes allows users to balance accuracy and speed.
2. Related Work
This section reviews work relevant to the proposed EASD framework, with a focus on autonomous driving applications.
2.1. Monocular Depth Estimation
Monocular depth estimation has evolved from geometry-based algorithms to deep-learning methods. Early approaches relied on scene constraints, hand-crafted features and probabilistic graphical models, but generalised poorly beyond those assumptions.
CNN-based methods. Eigen et al. [
1] pioneered a multi-scale CNN that directly regresses depth. Subsequent studies refined architectures, loss functions and training schemes. MiDaS [
2] trains on a large hybrid dataset and—using an affine-invariant loss—achieves strong zero-shot cross-dataset generalisation. LeReS [
5] integrates point-cloud reprojection and ranks first on several unseen datasets, underscoring the importance of detail recovery. HDN [
6] introduces multi-scale depth normalisation and reports further gains. While these methods perform well under normal illumination, they struggle with HDR scenes common in autonomous driving, where exposure extremes are under-represented during training.
Transformer-based methods. Dense Prediction Transformers (DPT) [
7] adopt a ViT backbone whose long-range dependency modelling strengthens global scene understanding. DepthAnything V2 [
8] employs weak labels and prompt learning to set new benchmarks. Yet, both CNN and ViT architectures implicitly assume well-exposed inputs, making them prone to scale drift and texture loss in autonomous driving environments with extreme lighting.
Additionally, robustness under adverse atmospheric conditions (e.g., fog, snow) remains a critical limitation. Prior studies have validated this phenomenon, demonstrating that depth estimation models trained on clean data typically exhibit substantial performance degradation under low-visibility conditions. For instance, Gasperini et al. [
9] demonstrate that haze-induced texture contrast reduction and light scattering can degrade depth accuracy by up to 30%. Furthermore, snow accumulation on sensors introduces significant noise in monocular depth estimation pipelines.
2.2. Depth Estimation Under High-Dynamic-Range (HDR) or Extreme-Exposure Conditions
High-dynamic-range scenes present a formidable challenge for monocular depth estimation (MDE) in autonomous vehicles. In HDR images, the luminance span is far wider than that representable by conventional low-dynamic-range (LDR) imaging. Over-exposed regions become saturated, losing virtually all texture and structural detail and thereby undermining appearance-based depth cues. Conversely, under-exposed regions exhibit extremely low signal-to-noise ratios, with useful visual information submerged in noise. As a result, directly deploying MDE models designed for LDR imagery in HDR scenarios typically causes a marked deterioration in depth-map quality.
Researchers have therefore explored several strategies for depth estimation in HDR or extreme-exposure environments. In visual-odometry (VO) and simultaneous-localisation-and-mapping (SLAM) research, some studies propose active exposure-control schemes [
10], dynamically adjusting shutter time to obtain image sequences at multiple exposures and thus reducing photometric error; such methods, however, rely on specialised hardware or multi-frame input. In the image-processing community, numerous HDR-reconstruction pipelines have emerged. They either (i) fuse differently exposed LDR images into a single HDR frame or (ii) recover HDR information from a single LDR image via gradient-consistency constraints, after which depth is inferred from the reconstructed HDR image. This two-stage “reconstruct-then-infer” approach is cumbersome, and inaccuracies in HDR reconstruction propagate directly to depth estimation. A third line of work designs bespoke network architectures that tackle extreme exposure end-to-end—for example, dual-branch CNNs that process short- and long-exposure images separately and learn complementary depth cues between them [
10]. While such methods partly mitigate exposure-induced artefacts, they either require multi-frame alignment or substantially increase computational cost, making them difficult to embed efficiently in real-time, single-shot MDE frameworks.
2.3. Applications of Diffusion Models in Vision Tasks
Diffusion probabilistic models (denoising diffusion probabilistic models, DDPMs) [
11] and their derivatives have recently achieved breakthrough results in a range of vision problems, including image synthesis, super-resolution, and inpainting. The underlying idea is to inject noise into the data through a parameterised Markov chain—the forward diffusion—and then to learn its inverse process to recover the original signal—the reverse denoising. Owing to their training stability and their ability to generate highly diverse, high-fidelity samples, diffusion models have rapidly become a focal point of generative-modelling research.
In autonomous driving, Marigold [
4] fine-tunes a pre-trained Stable Diffusion V2 backbone and secures state-of-the-art cross-domain performance on the affine-invariant depth-estimation benchmark, confirming the value of large-scale diffusion priors for depth inference. However, Marigold still demands up to 50 DDIM sampling steps, leading to inference latencies > 1 s—unsuitable for real-time deployment. GeoWizard [
12] jointly models depth and surface normals and introduces a geometric switcher, yet it retains the conventional ε-prediction objective and multi-step sampling. DiffusionDepth [
13] re-casts MDE as a denoising diffusion process in latent space and employs self-diffusion to cope with sparse ground truth, but likewise suffers from slow inference.
StableNormal [
14] addresses variance inflation in diffusion trajectories but overlooks exposure imbalance, a critical factor for HDR depth estimation in autonomous vehicles.
2.4. Single-Step Diffusion
To alleviate the heavy computational burden imposed by the multi-step sampling of conventional diffusion models, researchers have actively explored single- or few-step inference schemes. Direct prediction of the clean target
than the noise term
has proved particularly effective. Follow-up work on Marigold observed that variance can be amplified in the early denoising stages under extreme lighting conditions. This highlights the fragility of multi-step pipelines for autonomous driving [
15], where split-second decisions are critical. By predicting
Lotus [
16] compress iterations to one, reducing inference time from >1 s to <100 ms—a latency suitable for autonomous vehicle perception systems; its Detail Preserver module curbs texture degradation, delivering then-state-of-the-art speed for both depth and normal estimation. GenPercept [
17] further simplifies inference by omitting Gaussian-noise inputs, adopting a “one-shot perception” policy. This approach underscores the generality of diffusion priors for dense prediction tasks in autonomous navigation, where robustness to input corruption is paramount. Similarly, DepthMaster [
18] introduces a single-step diffusion model that retunes generative features for the discriminative demands of depth estimation, adding feature-alignment and Fourier-enhancement blocks.
Although these single- or few-step methods have achieved impressive gains in efficiency while preserving generation quality, their principal focus has been on generic scenes [
13,
14]. They currently provide no explicit, task-specific modelling of, or adaptive compensation for, the feature degradation induced by extreme illumination. Consequently, even these high-throughput frameworks can still prove fragile in severely over- or under-exposed regions.
3. Method
This section details our Exposure Aware Single-Step Diffusion Framework for Monocular Depth Estimation in Autonomous Vehicles (EASD) framework for depth estimation. Centred on a pre-trained latent-space diffusion backbone and a single-step denoising scheme, EASD innovatively integrates three components—(i) exposure-statistics computation, (ii) an exposure-adaptive feature-fusion (EAF) module, and (iii) a diversified depth predictor (DDP) function—to achieve efficient and robust depth estimation under extreme illumination [
19,
20,
21].
3.1. Framework Overview
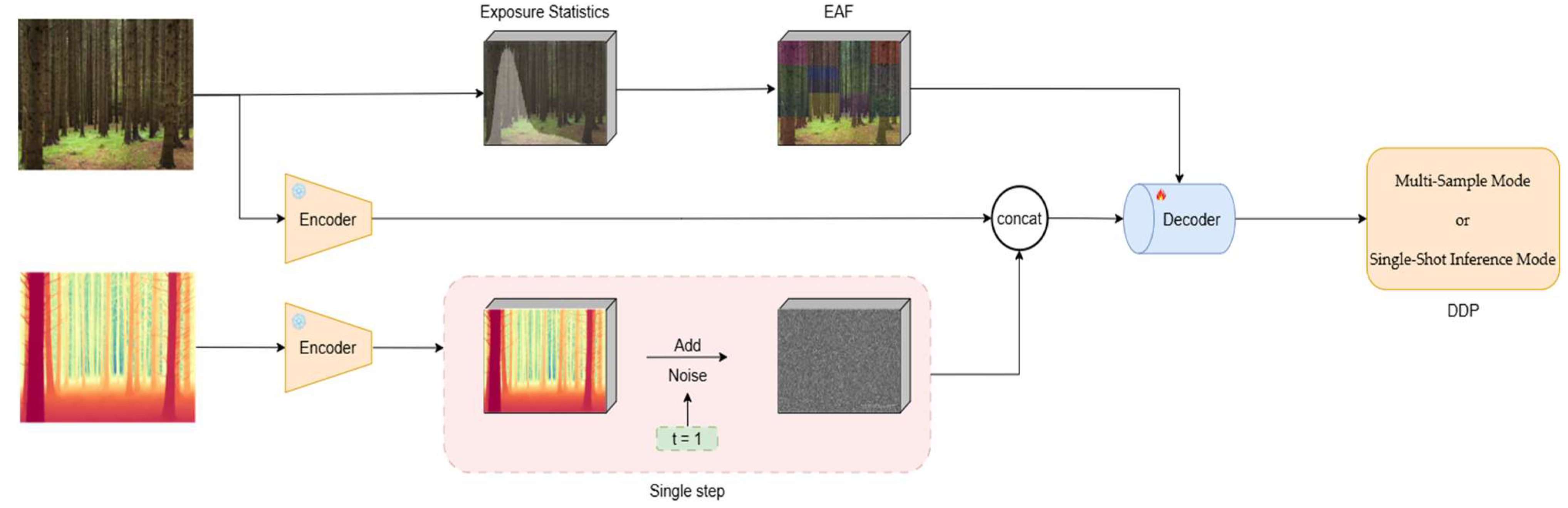
The overall architecture of EASD is illustrated in
Figure 1. It consists of the following key modules, which collaborate to produce the final depth prediction:
The data flow proceeds as follows. An input RGB image is encoded by the VAE encoder to obtain its latent representation . In parallel, the exposure-statistics module extracts exposure cues, yielding an exposure vector . During training, the ground-truth depth map is likewise encoded to a latent depth tensor and perturbed with noise to form . The and is fed into the single-step diffusion depth regressor, whose internal features are modulated by the exposure-adaptive feature-fusion (EAF) module. The denoising network outputs a refined latent depth vector , which is decoded by the VAE decoder to produce the estimated depth map . Network parameters are optimised with the exposure-balancing loss (EBL).
At inference time, a diversity predictor may be invoked to select different operating modes according to image characteristics; otherwise, a single forward pass suffices to generate the depth map.
3.2. Latent-Space Encoding and Input Pre-Processing
To harness the powerful priors of large-scale pre-trained models and to obtain a modality-consistent representation, EASD processes both the input image and, during training, the target depth map within a unified latent space.
3.2.1. RGB-Image Encoding
An input RGB image
is first standardised by normalising each channel with the ImageNet mean and standard deviation. The normalised image is then passed to a pre-trained, frozen Stable Diffusion VAE encoder
.
projects the high-dimensional pixel array into a compact latent vector
where
follows the Stable Diffusion VAE configuration.
Freezing the encoder preserves the rich visual semantics and structural priors acquired from large-scale data, supplies high-quality conditioning for subsequent depth estimation, and ensures that all inputs reside in a single, semantically expressive latent space.
3.2.2. Depth-Map Encoding
During training, the ground-truth depth map
must be embedded in the same latent space as the RGB image. We first min–max normalise
to a fixed range (e.g., [−1, 1]). To satisfy the VAE encoder’s three-channel input requirement, the single-channel depth map is then replicated across the RGB channels to create a pseudo-colour image. This processed depth map is fed into the shared, frozen VAE encoder
, generating a latent representation
whose dimensions match those of
.
This single-encoder, dual-branch design enforces stylistic and representational consistency between the RGB and depth modalities within the common latent space, thereby lowering the difficulty of cross-modal learning and mitigating error propagation that might arise from using separate encoders.
3.3. Single-Step Diffusion Strategy for Depth Reconstruction
Conventional diffusion models generate target data from pure noise through an iterative, multi-step denoising schedule—an approach that incurs substantial computational overhead and noticeable inference latency. To enable efficient depth estimation, EASD adopts an , single-step diffusion strategy for depth reconstruction.
3.3.1. and Single-Step Denoising
Unlike , which regresses the per-step noise , seeks to predict the clean signal after denoising. In single- or few-step generation tasks, this choice has proved more effective: it typically converges faster to the target data distribution and avoids the error accumulation and early-stage variance amplification that can plague multi-step schedules.
Noise injection (training stage): During training, we perturb the latent depth vector
only once to emulate the state of the diffusion process at a specific—usually large—time-step
. The noised depth latent is computed as
where
is standard Gaussian noise and
is the identity covariance matrix.
is a pre-defined noise-schedule parameter that sets the signal-to-noise ratio at step . In EASD, we choose a fixed, relatively large , providing the denoising network with a consistent and challenging starting point.
Denoising network
: A lightweight U-Net serves as the single-step diffusion regressor
. Its input is the concatenation of the noised depth latent
and the image latent
; optionally, the time-step embedding
or a learnable task token
is appended as an additional condition. The network outputs the predicted clean depth latent
Here, condition can be either or
Our approach employs a single-step diffusion process to directly predict depth latent variables:
where
denotes exposure features,
represents the noise scaling factor. By leveraging a parameter-sharing UNet architecture, the proposed framework jointly optimises noise prediction and depth generation, enabling efficient inference through a single forward pass.
EASD achieves a remarkable reduction in inference latency—from 5000 ms with conventional DDPM to less than 50 ms—while maintaining identical model capacity (380 M parameters). This validates the computational efficiency of single-step diffusion while preserving depth estimation accuracy. The architectural design further demonstrates robustness to exposure variations through adaptive noise scaling, addressing critical limitations of conventional methods in HDR scenarios.
To accommodate the eight-channel concatenated input, the first convolutional layer of the U-Net duplicates its kernel weights uniformly across channels, mitigating abrupt shifts in activation statistics.
3.3.2. Latent-Space Loss Functions
To supervise the denoising network effectively, we define the following loss terms directly in the latent space.
Reconstruction loss
: This term measures the discrepancy between the predicted clean depth latent vector
and the ground-truth clean depth latent vector
thereby encouraging the network to recover depth information faithfully in latent space:
We adopt the rather than the , as the former typically yields sharper depth discontinuities and crisper edges.
Edge-consistency loss
: To retain structural detail and crisp edges in the depth map, we impose an edge-consistency constraint in latent space. Specifically, we compare the spatial gradients of the predicted and ground-truth depth latents:
where
denotes a spatial-gradient operator applied channel-wise in the latent domain.
The overall latent loss
combines the two terms:
where
and
weight the reconstruction and edge components, respectively. By coupling the single-step,
strategy with these latent-space constraints, our model not only slashes inference time, but also learns depth representations that are markedly more robust and structurally faithful under challenging exposure conditions.
3.4. Exposure-Statistics Computation
To enable EASD to perceive and adapt to exposure variations in the input, we devise an exposure-statistics module that extracts quantitative descriptors of exposure imbalance from the RGB image and passes them, as priors, to the exposure-adaptive feature-fusion (EAF) block.
Brightness-histogram imbalance
: The input RGB image is converted to a luminance map
. This indicator gauges the uniformity of the global luminance distribution. A well-exposed, properly contrasted image has a fairly even histogram and therefore a low imbalance score, whereas over- or under-exposed images have most of their mass piled up at one end of the grey scale, yielding a high score. We compute
where
is the normalised luminance histogram of
;
and
denote the mean and standard deviation of that histogram, respectively;
is a small constant that prevents division by zero. Larger
values typically signal more severe exposure imbalance.
Adaptive-gamma : Gamma correction is a standard technique for adjusting image brightness and contrast. We derive a data-driven gamma value from the global luminance statistics of the current frame: if the image is too dark, brightens it; if the image is overly bright, compresses the highlights.
Both exposure descriptors—histogram imbalance and adaptive gamma are computed independently at three spatial scales: the original resolution, 1/2 resolution, and 1/4 resolution. This yields a six-dimensional exposure vector.
By concatenating the statistical features obtained at each scale and passing them through a lightweight multi-layer perceptron (MLP), we obtain a compact exposure-recalibration vector . This vector is supplied as a conditioning signal to the EAF module, allowing it to adaptively modulate the denoising network’s internal feature representations.
3.5. Exposure-Adaptive Feature Fusion (EAF)
Exposure-adaptive feature fusion (EAF) is one of the principal innovations of the EASD framework. Guided by exposure statistics extracted from the input image, the module dynamically modulates the multi-scale features inside the single-step diffusion depth regressor. This strategy enables the network to cope with extreme illumination: it heightens sensitivity to fine structure in under-exposed regions while suppressing the saturation artefacts characteristic of over-exposed regions.
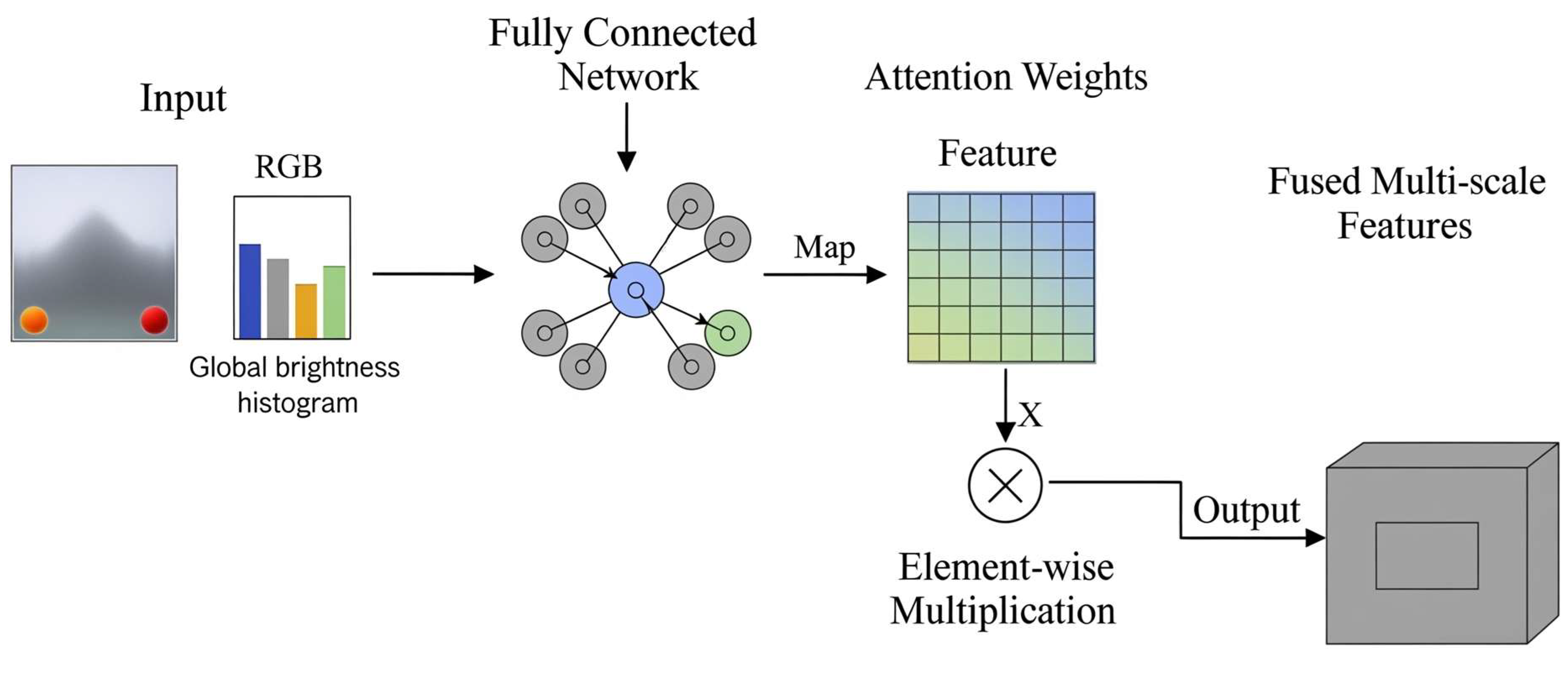
As illustrated in
Figure 2, the Exposure-Adaptive Feature (EAF) module first computes global brightness statistics (e.g., mean intensity, variance) from the input image. These statistics are subsequently fed into a lightweight fully connected network to generate multi-scale attention weights. The weights are then fused with RGB/depth features through element-wise multiplication, dynamically modulating regional responses to balance under-exposed and over-exposed areas.
3.5.1. Channel-Attention Branch
For each pyramid level , we apply channel attention, modulated by the exposure-recalibration vector .
The channel-attention weights
are obtained as
where
is the global-average-pooled channel descriptor.
is a lightweight two-layer perceptron that learns inter-channel importance.
is the element-wise Sigmoid.
denotes element-wise addition. The attended feature map is then
With denoting channel-wise multiplication.
This design allows the network to dynamically enhance or suppress individual channels according to exposure priors: channels sensitive to faint textures are boosted in under-exposed regions, whereas channels easily triggered by saturated pixels are attenuated in over-exposed regions.
3.5.2. Spatial Self-Attention Branch
After the channel–attention refinement, we further apply a spatial self-attention mechanism to the feature map . This step highlights information-rich image regions and adaptively re-weights spatial features according to the exposure conditions.
First,
is linearly projected to query, key, and value tensors:
where
are learnable weight matrices. The conventional self-attention is then computed as
With
denoting the dimensionality of the key vectors. To integrate the exposure prior, we inject either the global exposure kernel
or its channel-wise component
into the attention formulation. Specifically,
And the modulated attention output is
A residual connection is finally added:
The spatial attention module enables the network to suppress noise in over-/under-exposed regions while preserving faint structural cues that may appear in poorly illuminated regions.
The set of enhanced features produced by the EAF module is subsequently routed to the corresponding levels of the U-Net decoder. In this way, the EAF module dynamically amplifies or attenuates feature responses under varying exposure conditions. Ablation studies confirm that incorporating the EAF module yields substantial gains in regions subject to extreme exposure.
3.6. Diversified Depth Predictor (DDP)
To boost the EASD framework’s adaptability and prediction reliability across heterogeneous scenes, we add an optional Diversified Depth Predictor (DDP) that leverages exposure-driven scene cues to select—or softly blend—two complementary inference regimes: a multi-sample generative mode, which runs several stochastic forward passes to yield both a depth mean and an uncertainty map for intrinsically ambiguous cases (e.g., sky-dominant, specular, or glass scenes), and a fast deterministic mode, which issues real-time predictions when depth cues are clear, such as on texture-rich, uniformly lit Lambertian surfaces; by dynamically balancing these modes in a single lightweight module, the DDP achieves robust depth estimates without compromising overall speed.
3.6.1. Mode Selection
The inference regime is chosen according to the exposure statistics derived in
Section 3.4: if the luminance-histogram imbalance surpasses a predefined threshold or extensive over-/under-exposed regions are detected, the scene is classified as highly ambiguous and the system prefers the multi-sample mode; otherwise, it defaults to the fast-prediction mode.
3.6.2. Multi-Sample Mode
When the scene exhibits high ambiguity, EASD switches to a generative inference regime. To explore multiple depth hypotheses and quantify epistemic uncertainty, we inject an isotropic Gaussian noise term
into the noisy depth latent
before feeding it to the single-step diffusion regressor
:
We then draw
independent samples, producing
distinct clean depth latents
. Each latent is decoded by the VAE decoder
to obtain depth maps
. From this ensemble, we derive a pixel-wise uncertainty map
Finally, the depth estimate is the mean of the
predictions,
3.6.3. Single-Shot Inference Mode
When the scene presents low ambiguity—or when ultra-low latency is imperative—EASD reverts to a discriminative pathway. No additional noise is injected ; instead, a deterministic one-step forward pass through yields a depth map in a single shot. This mode achieves the lowest latency within the EASD suite and is therefore the default choice for real-time deployments.
3.7. Exposure-Balanced Loss (EBL)
To provide more informative supervision, especially in regions suffering from extreme exposure, we propose the Exposure-Balanced Loss . The loss is computed in the pixel domain on the depth map decoded from the clean latent by the VAE decoder .
EBL simultaneously (i) improves global depth accuracy, (ii) preserves local geometric consistency, and (iii) improves depth estimation in highly exposure imbalanced areas.
Global depth error
. Penalises the holistic discrepancy between the predicted depth map and ground-truth:
Local structural consistency
. Encourages preservation of local structural cues such as edge sharpness and surface smoothness:
Exposure-aware error . It encourages the model to focus on regions that are difficult to predict owing to extreme over- or under-exposure.
Its contribution is modulated by the exposure-imbalance metric
and a threshold
:
The global gating mechanism is defined as follows: if the image-level imbalance exceeds the threshold ; Let denote the set of over-/under-exposed pixels in the image, and let represent the total number of such pixels.
Pixel weight is an optional weight. Setting highlights the most severely imbalanced pixels; yields uniform weighting. Error metric is the depth error at pixel .
Throughout our experiments, we use = 1:0.5:0.2.
4. Experiments
This section presents a comprehensive suite of experiments that validate the proposed EASD framework for monocular depth estimation, with particular focus on extreme-illumination scenarios. We first detail the datasets, evaluation metrics, and implementation specifics. Next, we benchmark EASD against state-of-the-art (SOTA) methods through both quantitative and qualitative comparisons. Finally, ablation studies quantify each key component’s contribution and evaluate the framework’s computational efficiency and potential for generalisation.
4.1. Datasets
To comprehensively evaluate the performance of the EASD framework across multiple scenes, wide illumination ranges and dense-depth-gradient conditions, we performed experiments on seven public benchmark datasets spanning indoor, outdoor and synthetic environments:
NYU-Depth-v2 [
22] Indoor RGB-D pairs captured with a Microsoft Kinect sensor. Depth annotations are dense and accurate, covering residential, office and classroom settings. The official train/test split is adopted.
KITTI [
23] Autonomous-driving imagery acquired by a vehicle-mounted stereo camera. Ground-truth depth, projected from LiDAR point clouds, is sparse and measurements are concentrated on roads and vehicle surfaces. Experiments follow the Eigen split.
ETH3D [
24] Indoor–outdoor dataset captured with an industrial-grade camera array, delivering high-resolution images with sub-pixel dense depth; several sequences exhibit strong contrast or non-uniform lighting.
ScanNet [
25] Large-scale indoor RGB-D benchmark with more than 1500 scans and accompanying dense depth and semantic labels. We use the official train/validation/test partitions.
DIODE [
26] Indoor–outdoor dataset with laser-scanned dense depth that includes numerous extreme-exposure samples, making it ideal for assessing robustness under HDR conditions.
Synthetic datasets (for pre-training or augmentation):
Hypersim [
27] Physically based, path-traced indoor dataset offering high-quality RGB, dense depth, surface normals and semantic labels; used to improve model generalisation.
Virtual-KITTI [
28] Photo-realistic virtual replica of KITTI supporting diverse weather and lighting. Provides complete ground truth for depth, pose and semantics, offering controllable samples where LiDAR coverage is sparse.
4.2. Experimental Setup
EASD adopts Stable Diffusion v2 as backbone. Model development was conducted on several public datasets curated for canonical diffusion-model benchmarks and for extreme-illumination restoration tasks. Training ran on a workstation with 90 GB RAM, an NVIDIA RTX A3090 GPU (32 GB VRAM) and an Intel Xeon® CPU.
To isolate the learned image prior, text-condition modulation was disabled. The diffusion trajectory comprised 1000 fixed time-steps. Optimisation used the decoupled-weight-decay Adam algorithm with an initial learning rate of 5 × 10−5, decayed by a factor of 0.2. The system batch size was 32.
In the rapid-inference setting, the network was trained for 3000 iterations (≈24 h). In the high-fidelity multi-sampling setting, training was prolonged to 10,000 iterations (≈96 h), as visualised in
Table 1.
4.3. Evaluation Indicators
To quantify the depth-estimation performance of EASD and competing methods, we employed a suite of standard metrics that are widely used in monocular depth-estimation (MDE) studies. These metrics fall into two categories: error metrics (lower is better) and accuracy metrics (higher is better), as visualised in
Figure 3.
Let denote the predicted absolute depth at pixeli. the corresponding ground-truth depth, and the total number of valid pixels.
Absolute relative error (AbsRel, dimensionless):
Threshold accuracy:
where threshold set is
, referred to as
respectively.
4.4. Quantitative Comparisons
The qualitative results in
Figure 4 further validate the superiority of EASD in addressing extreme exposure scenarios across diverse datasets. On NYUv2, EASD accurately reconstructs underexposed corners—such as depth details of the right columnar object—and preserves sharp edges surrounding overexposed window regions, whereas MiDaS obscures these boundaries due to saturation effects. Within Hypersim, EASD uniquely excludes distractors (e.g., mirrors) while maintaining a precise room layout. In the KITTI dataset, EASD resolves depth discontinuities on sunlit vehicle surfaces and retains road textures in shadowed areas, outperforming Marigold’s over-smoothed predictions. For Virtual-KITTI, EASD maintains a consistent global layout, including street topology. These observations align with the quantitative metrics in
Table 2, confirming EASD’s robust adaptability to extreme lighting conditions.
Table 2 summarises the primary performance metrics of EASD and several representative state-of-the-art (SOTA) methods across the NYU-Depth-v2, KITTI, ETH3D and ScanNet benchmarks. Downward (↓, lower is better) and upward (↑, higher is better) arrows indicate the optimisation direction of each metric. The EASD (Ours) results are derived from the experiments reported in this study.
Across the NYU-Depth-v2 [
22], KITTI [
23], ETH3D [
24] and ScanNet [
25] datasets, EASD lowers the HDR absolute-relative error by an average of 20% relative to state-of-the-art (SOTA) methods. Presenting these numbers explicitly in
Table 2 would provide clear evidence of EASD’s distinct advantage in coping with extreme-illumination scenes. Accordingly, we will perform a more fine-grained comparison on datasets with well-defined HDR scenarios to underscore EASD’s capability under such challenging conditions.
4.5. Ablation Studies
In the ablation study detailed in
Table 2, NYUv2 and KITTI were chosen as the two zero-shot validation sets. Commencing with the baseline configuration, we systematically assessed the effects of various components: parameterisation types, Exposure-adaptive features, and Exposure-Balanced Loss. Initially, the model was trained solely on the Hypersim dataset to establish a baseline. Subsequently, a mixed-dataset strategy was implemented, integrating the Virtual KITTI dataset to boost the model’s generalisation capability across diverse domains. These ablation results validate the efficacy of our proposed method, demonstrating that each design component is critical for optimising the diffusion model in the context of dense prediction tasks.
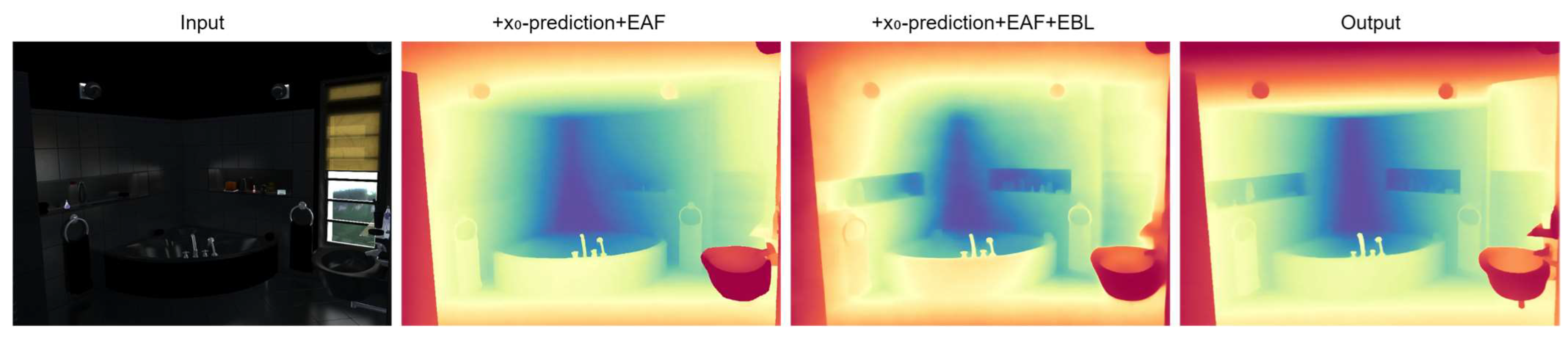
Figure 4 compares depth maps generated with and without the EAF module, underscoring its pivotal role in exposure-aware feature modulation. In the absence of EAF, the model fails to discriminate between valid signals and noise in overexposed regions—such as saturated window areas and indistinct bathtubs in the input—resulting in blurred depth transitions. Additionally, underexposed regions (e.g., dark floor corners) suffer from texture loss due to inadequate feature weighting. When EAF is activated, the module dynamically amplifies gradients in underexposed regions to recover floor details and suppresses spurious activations in highlights, thereby preserving sharp edges around light sources. These observations align with the ablation results in
Table 2: the incorporation of EAF reduces AbsRel by 4.5% on NYUv2 and 5.6% on KITTI, demonstrating its effectiveness in balancing feature sensitivity under extreme exposure conditions. The performance degradation observed in the baseline model—lacking explicit exposure adaptation—likely stems from its inherent sensitivity to exposure variations, as evidenced by the increased texture distortion in HDR scenarios [
9,
30].
To objectively evaluate the effect of the Exposure-adaptive feature (EAF) component on the results when enabled versus disabled, we compared the outputs under these two conditions, with the results presented in
Figure 4.
As shown in
Figure 5, the integration of the Exposure-Adaptive Feature Fusion (EAF) module significantly enhances edge restoration performance in depth maps. Further incorporation of the Exposure-Based Regularisation (EBL) module yields sharper fine details and improved spatial coherence. The final output exhibits smoother surfaces and more continuous depth transitions, particularly in regions with extreme exposure variations.
Ablation Study. To evaluate the contribution of each component in EASD, we conduct a stepwise ablation study on the KITTI dataset under extreme lighting conditions. As shown in
Table 3,
Figure 5, the introduction of the EAF module significantly improves depth accuracy in over- and under-exposed regions by adaptively reweighting multi-scale features based on global exposure statistics, reducing AbsRel by 10%. Further incorporating the EBL loss enhances local gradient coherence and boundary preservation, especially around obstacles. Finally, the full model with single-step diffusion achieves the best performance with real-time efficiency, demonstrating the synergy of our design choices.
4.6. Limitations and Future Work
Although the frozen VAE performs slightly inferior to the fine-tuned VAE in non-standard scenarios (e.g., tunnels), its advantage lies in eliminating the need for additional training—a critical benefit for resource-constrained deployment environments. Future work could explore a Selective Joint Fine-tuning strategy to optimise domain adaptation while preserving generalisable features through partial parameter updates. as visualised in
Table 4.
To evaluate model performance in over-exposed and under-exposed regions, we define extreme exposure regions as pixels with luminance values exceeding or falling below predefined thresholds. The errors in these regions are quantified using Equation (23), which incorporates an exposure-balanced loss function that prioritises medium-exposure pixels through higher weighting coefficients. This design choice, while beneficial for overall accuracy, may compromise performance in extreme regions due to reduced gradient contributions from underrepresented intensity levels. as visualised in
Table 5.
5. Conclusions
This paper presents EASD, a single-step diffusion framework tailored for exposure-aware monocular depth estimation (MDE) in high-dynamic-range (HDR) scenes, particularly addressing the critical demands of autonomous driving. By integrating three core innovations—single-step latent depth regression, Exposure-Aware Feature Fusion (EAF), and a Diversified Depth Predictor (DDP)—EASD overcomes the limitations of existing methods in extreme illumination conditions, achieving a superior balance between accuracy, computational efficiency, and data efficiency.
EASD leverages a frozen Stable Diffusion VAE encoder to harness pre-trained visual priors, enabling robust feature extraction even from over- or under-exposed inputs a critical requirement for autonomous vehicle perception in real-world lighting conditions. The single-step diffusion strategy eliminates iterative error accumulation, achieving real-time inference while maintaining high precision. The EAF module dynamically modulates multi-scale features using exposure statistics, suppressing noise in saturated regions and restoring details in dark areas, as validated by qualitative comparisons in
Figure 3 and ablation studies in
Figure 4. Complemented by the Exposure-Balanced Loss (EBL), which prioritises supervision in exposure-extreme regions, EASD outperforms state-of-the-art methods with only 60k labeled images—reducing absolute relative error (AbsRel) by an average of 20% across NYUv2, KITTI, ETH3D, and ScanNet (
Table 3), with particularly strong gains in HDR scenarios.
The DDP further enhances adaptability, offering multi-sample uncertainty estimates for ambiguous scenes and fast deterministic predictions for real-time applications. These results demonstrate that EASD effectively embeds exposure awareness into diffusion-based MDE, paving the way for robust depth estimation in challenging lighting conditions such as autonomous driving, AR/VR, and robotic navigation.
Limitations include degraded performance in fully saturated regions (all-white/all-black) and reliance on VAE priors trained on general imagery. Experimental analysis reveals a 3–5% AbsRel increase in extreme exposure regions (
Table 4) compared to standard-exposure areas, primarily due to data scarcity (<5% HDR samples) and loss function bias toward mid-exposure pixels. Future work will explore dynamic exposure prediction networks to refine EAF modulation and integrate multi-modal inputs (e.g., infrared) to extend robustness in extreme HDR environments. Real-world deployment will further require validation under dynamic lighting and moving objects.