Unraveling Electrochemical–Thermal Synergy in Lithium-Ion Batteries: A Predictive Framework Based on 3D Modeling and SVAR
Abstract
1. Introduction
2. Model Development and Validation
2.1. Model Assumptions
- (1)
- The particles of the active electrode material are uniformly sized spheres.
- (2)
- The volume change of the electrodes during the charging and discharging processes is ignored.
- (3)
- All side reactions between the solid, the electrolyte, and the separator are ignored.
- (4)
- The current collector has high electrical conductivity.
- (5)
- The heat generation of the current collector is ignored.
- (6)
- The gases that may be generated during the charging and discharging processes are ignored.
- (7)
- The electrodes, current collectors, separators, and electrolytes are regarded as superimposed continua.

2.2. Electrochemical Model
2.2.1. Mass Conservation
2.2.2. Charge Conservation
2.2.3. Electrochemical Kinetics
2.3. Thermal Model
2.4. Electrochemical–Thermal Coupling Model
2.4.1. Solid-Phase Parameters
2.4.2. Electrode Kinetic Parameters
2.4.3. Electrolyte Parameters
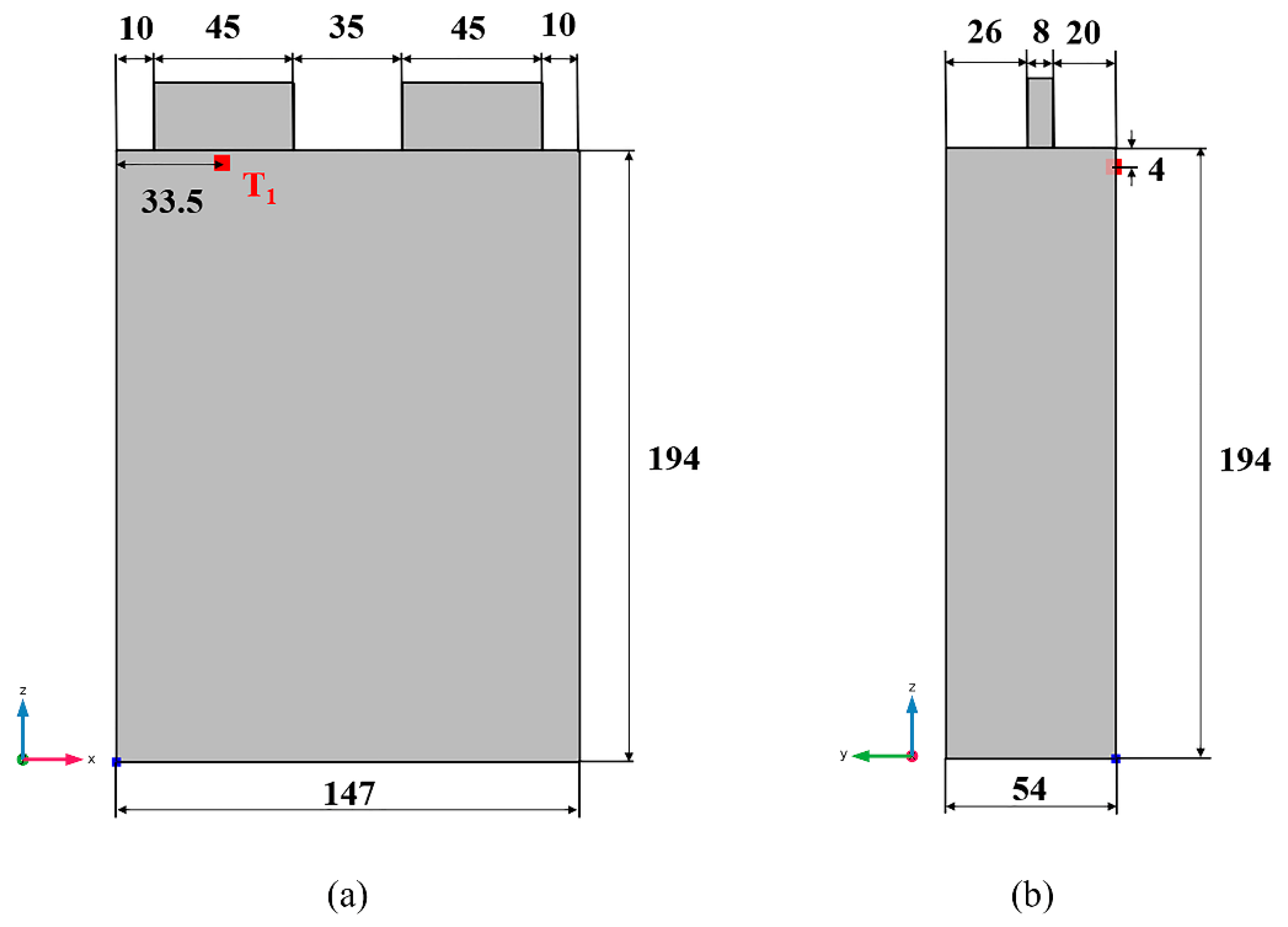
2.5. Model Parameters and Boundary Conditions
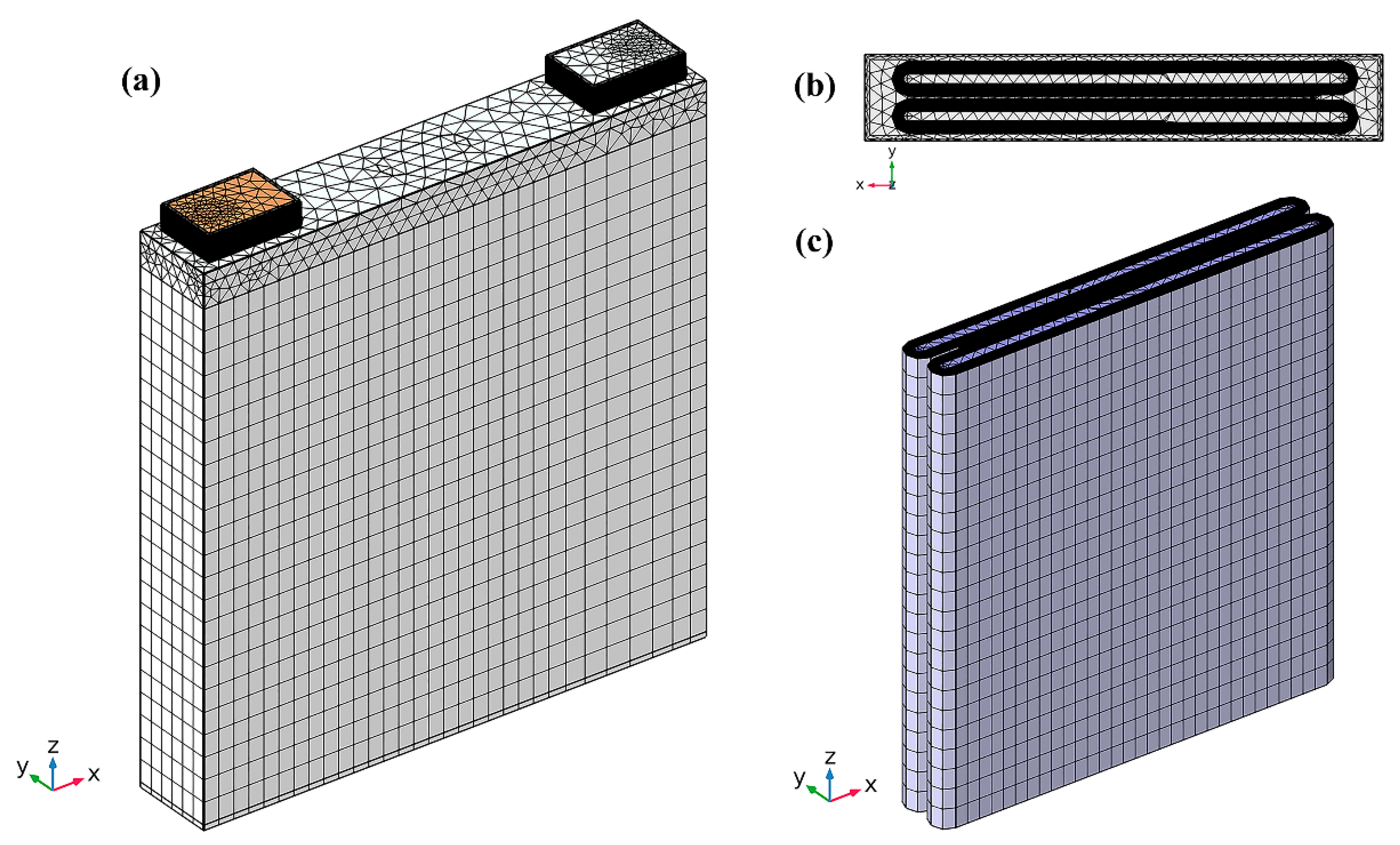
2.6. Grid Independence Test
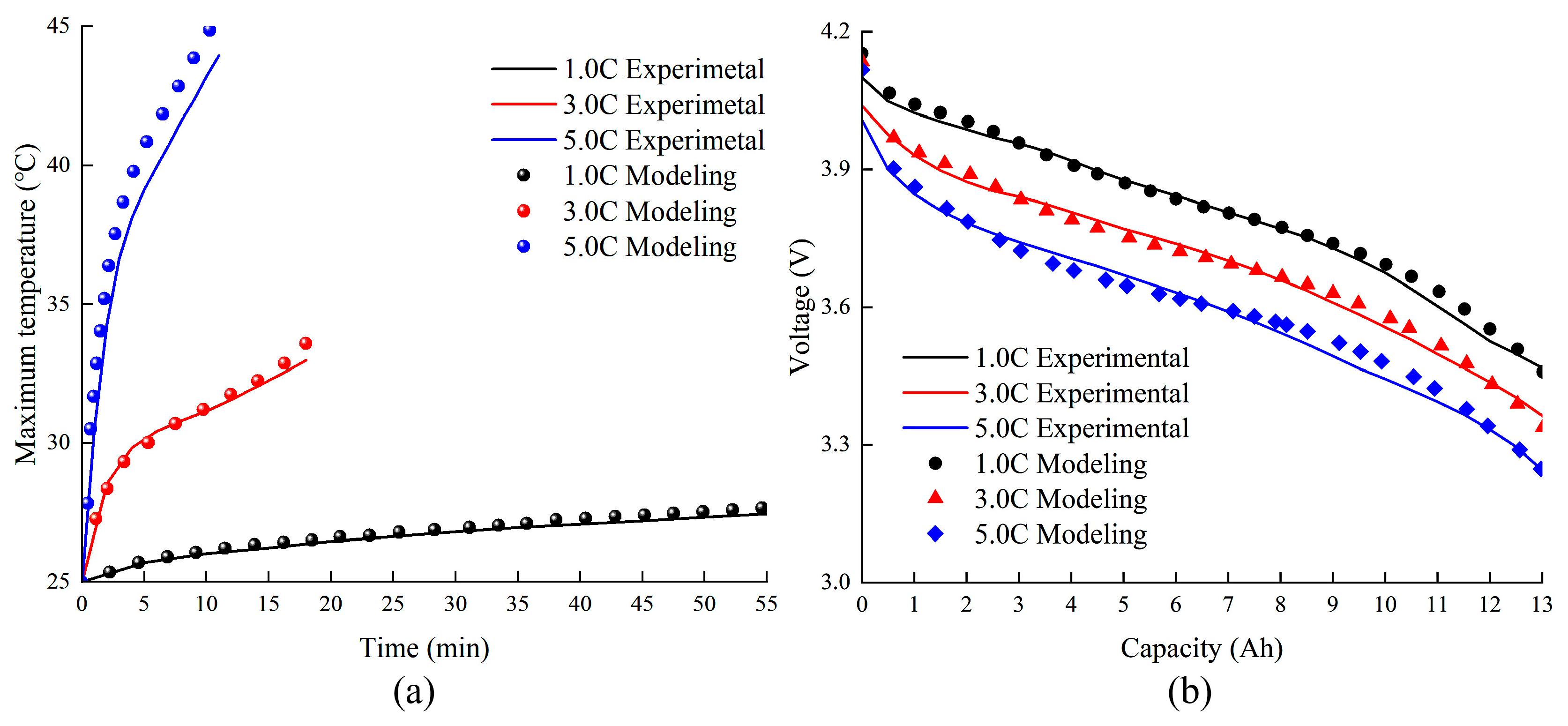
2.7. Experimental Verification
2.8. SVAR Model
2.9. Integrated Learning Regression Prediction System
3. Results
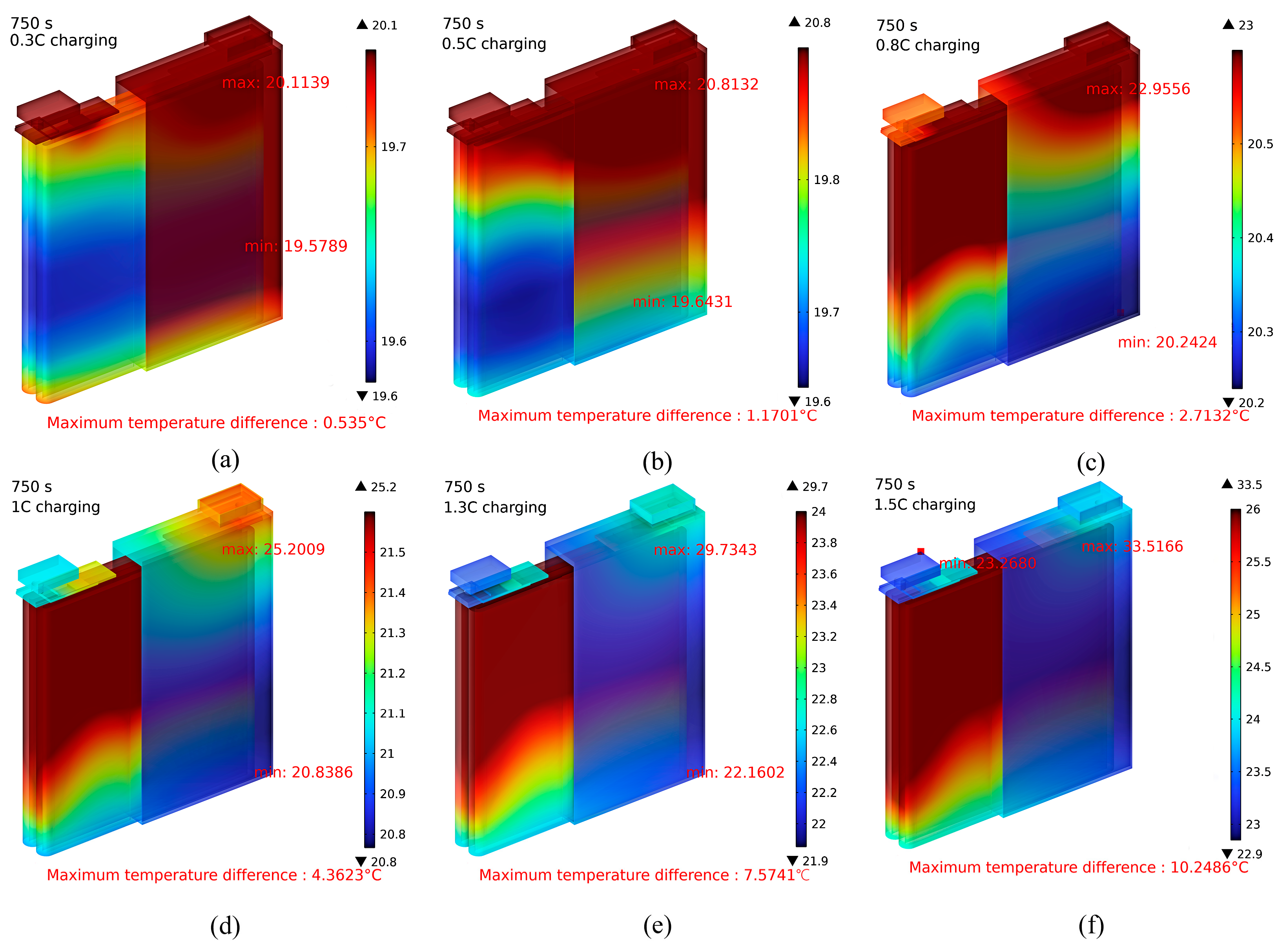
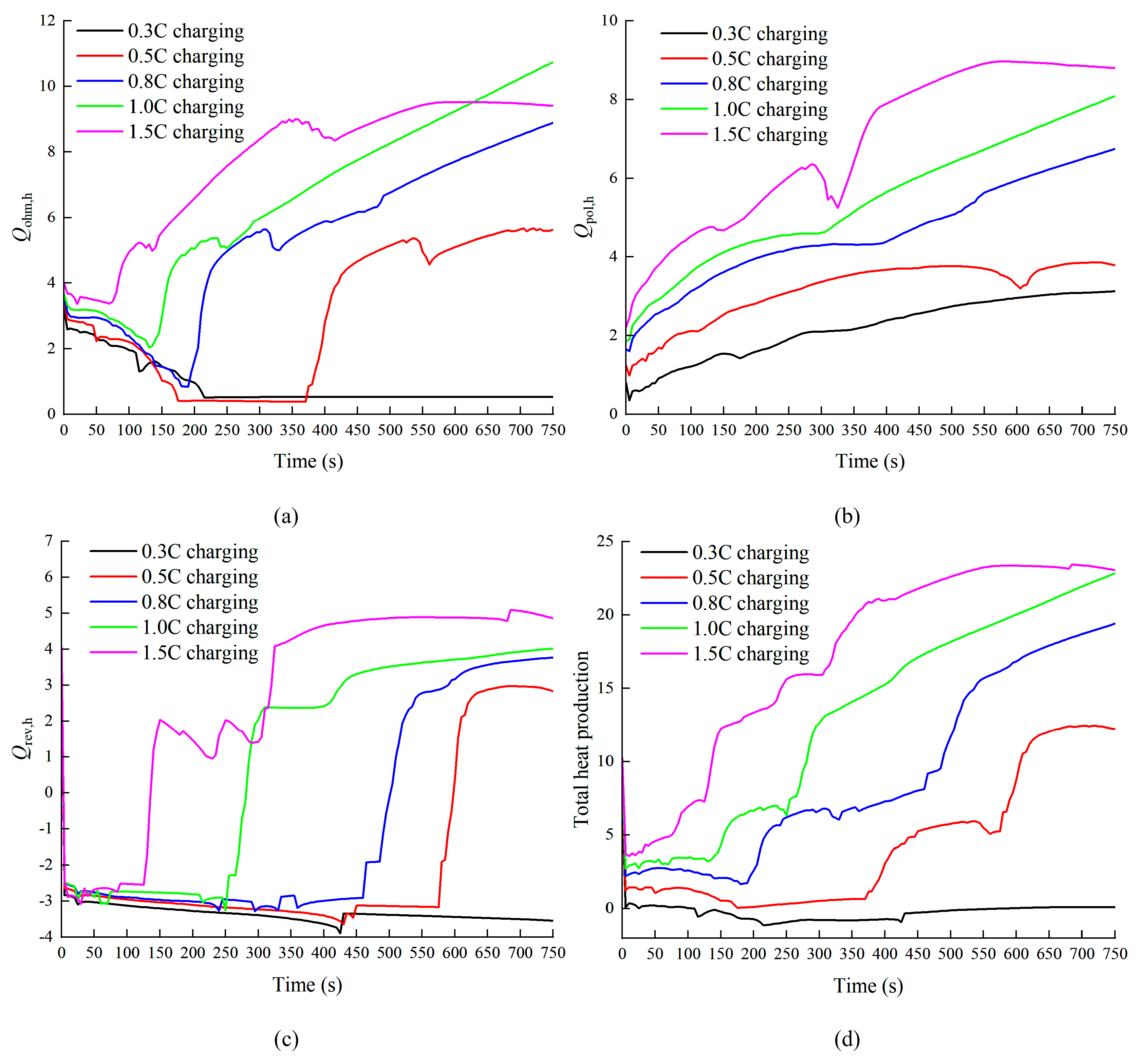
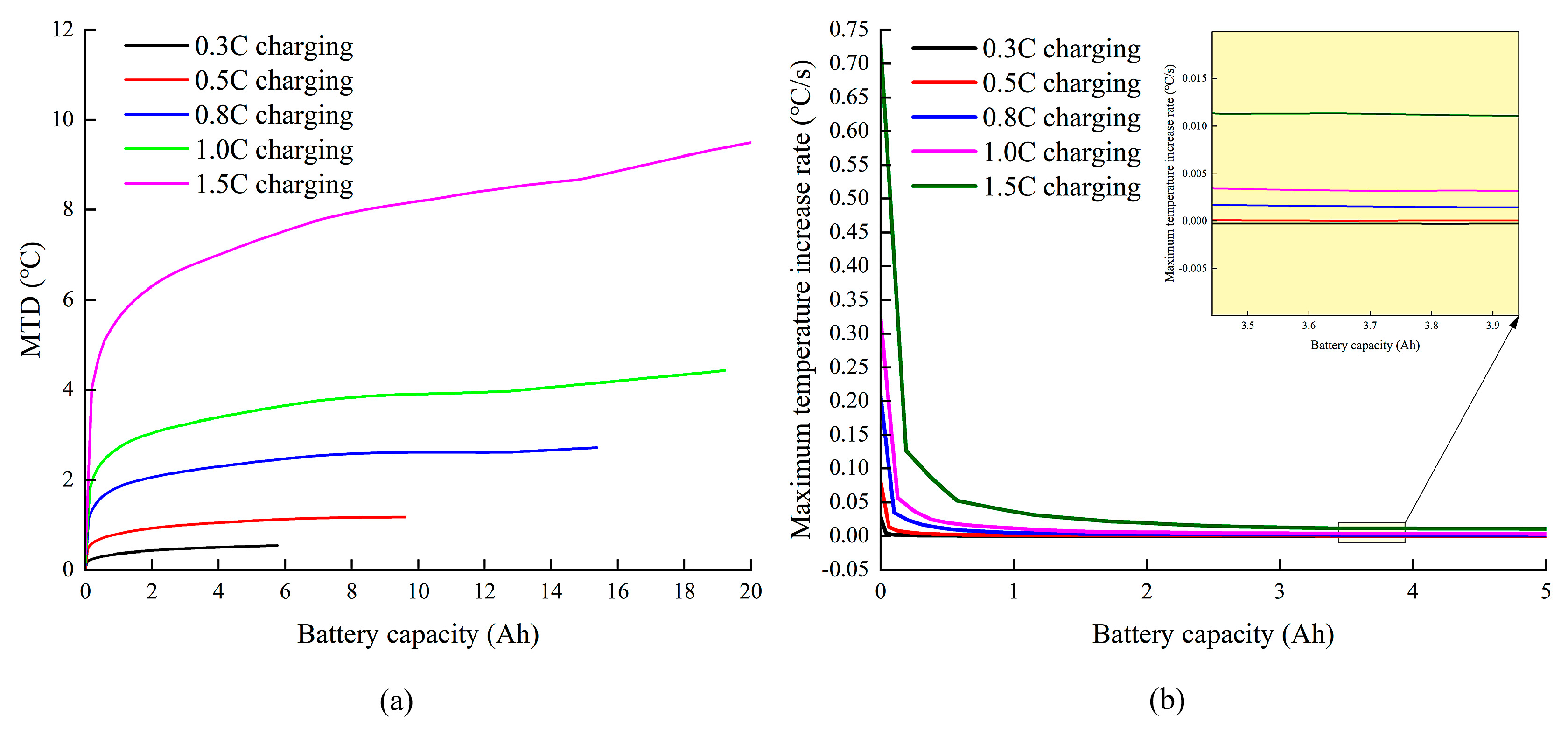
3.1. Effect of Charge and Discharge Rate on Battery Temperature
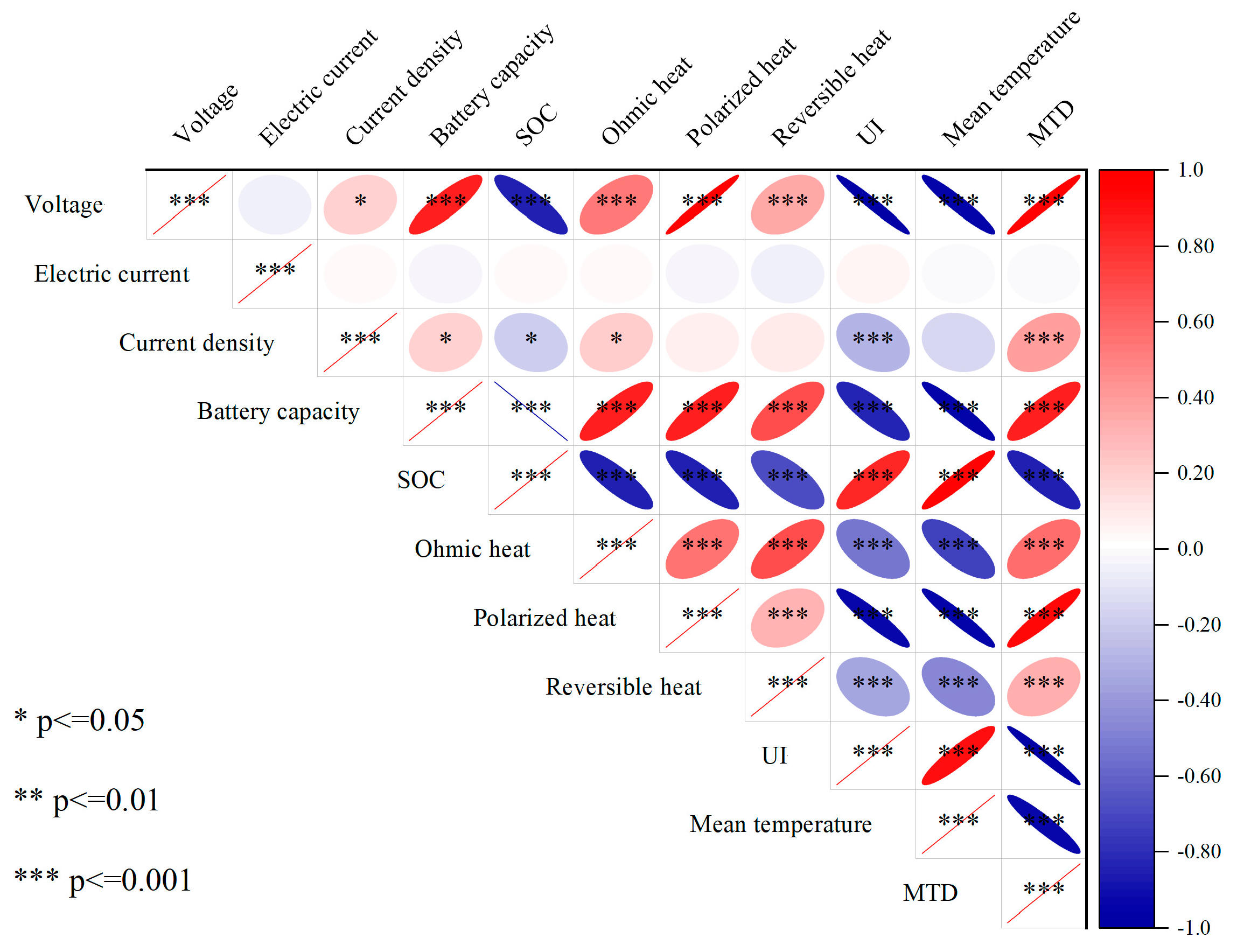
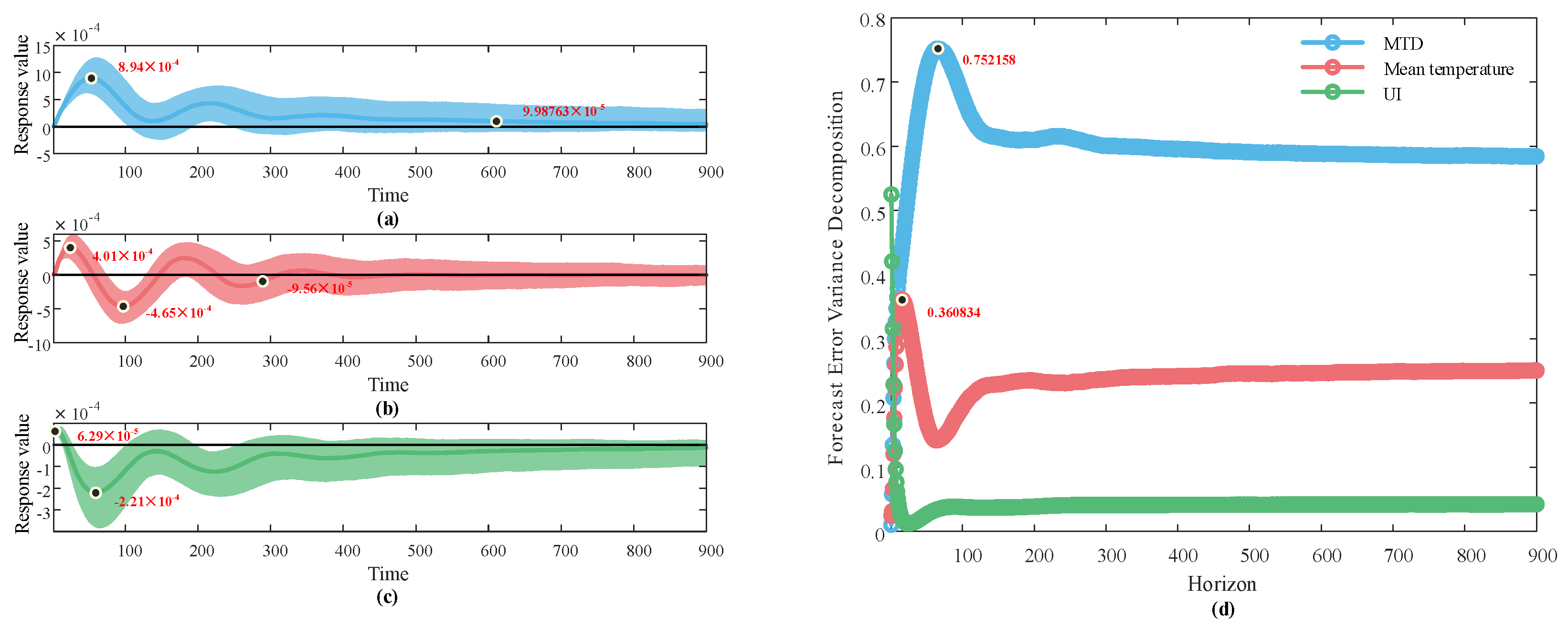
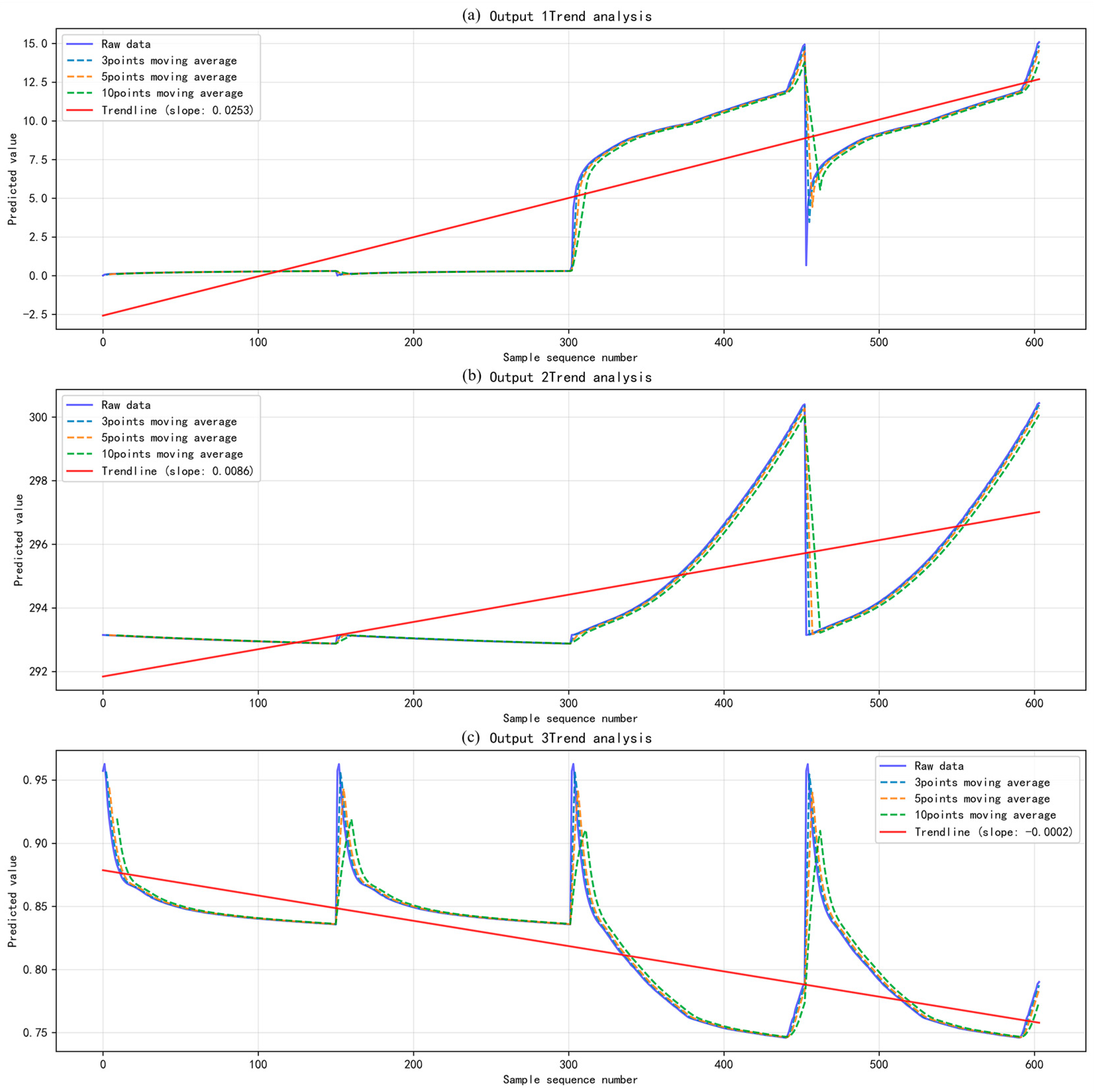
3.2. Dynamic Impact Analysis Results of the Structured Vector Autoregression Model
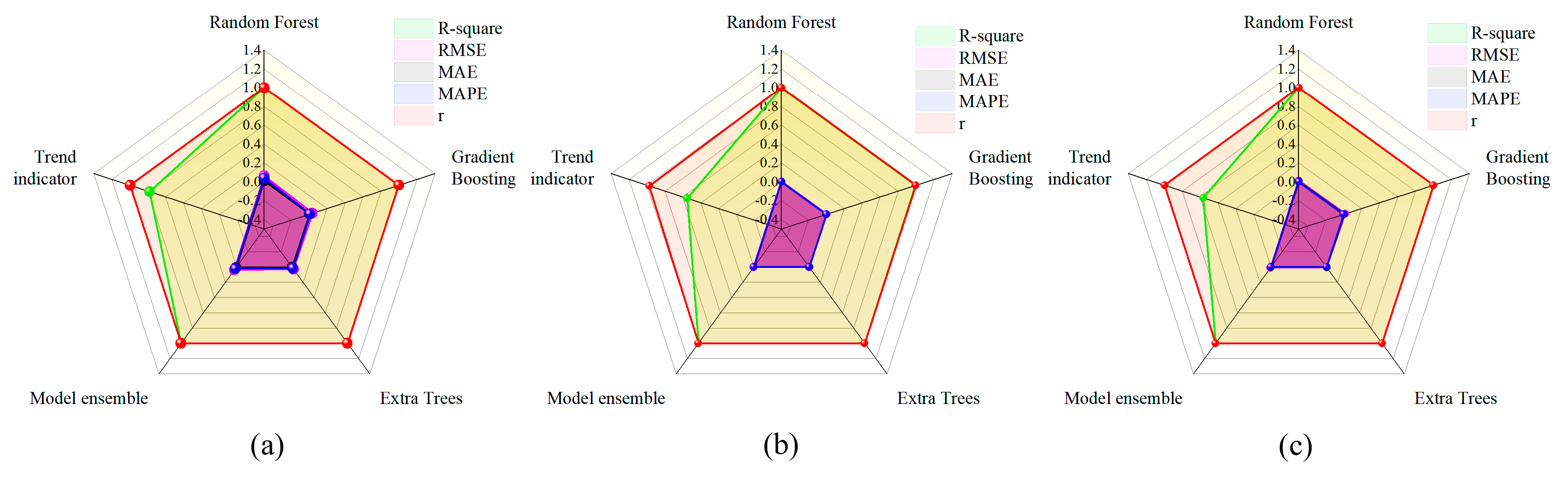
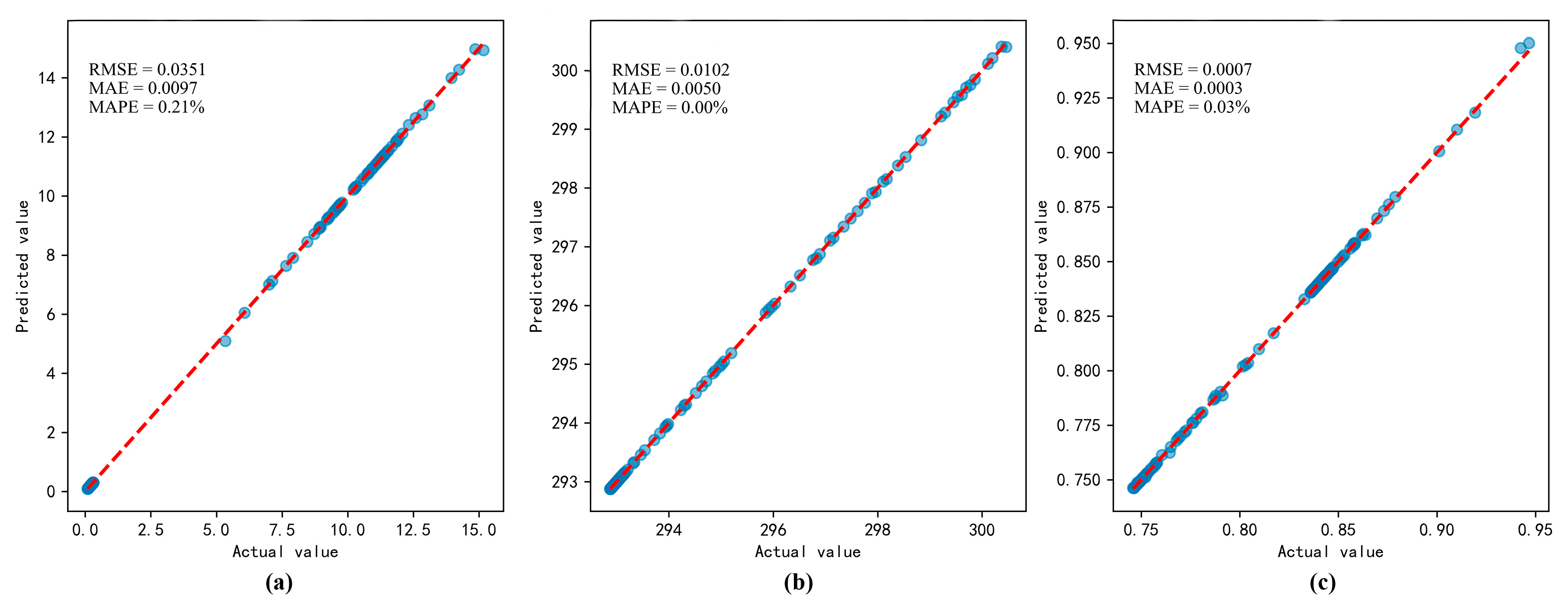
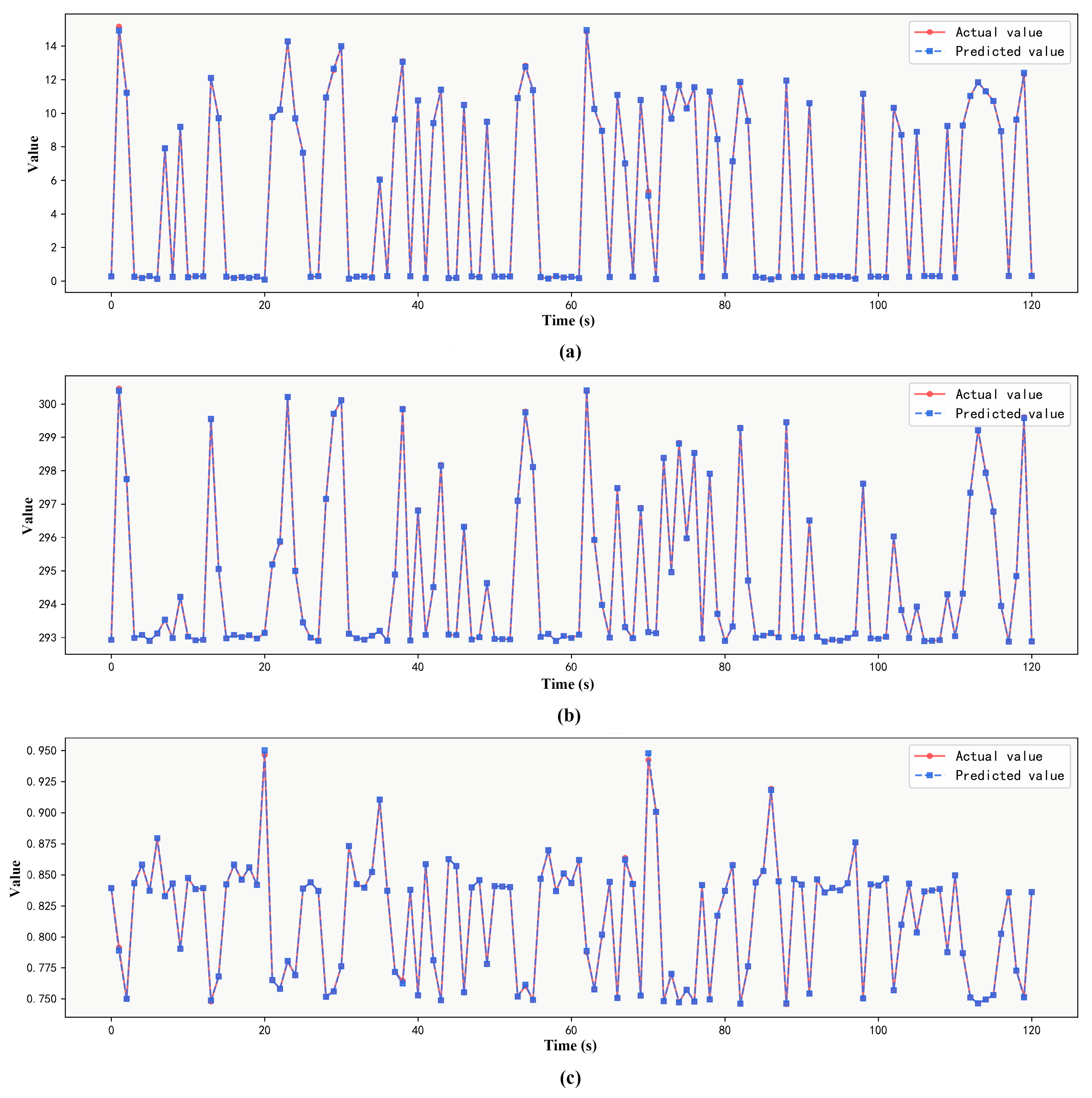
3.3. Prediction Results of the Integrated Learning Regression Prediction System
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | SOC of the positive electrode |
| asap | specific surface area of the spherical active particles |
| A | surface area, m2 |
| A0 | parameter matrix for the current period |
| Al | lag coefficient matrix |
| b | SOC of the negative electrode |
| B | consistency matrix of the coefficients |
| c | concentration, mol/m3 |
| cLi+,e | concentration of Li+ in the electrolyte, mol/m3 |
| CedlL | electric double layer capacitance |
| CLi+,s,max | maximum concentration of Li+ in the spherical active particles, mol/m3 |
| CLi+,s,surf | concentration of Li+ on the surface of the spherical active particles, mol/m3 |
| Cp | heat capacity at constant pressure, J/(kg‧K) |
| d | conforming vector of coefficients |
| D | diffusion coefficient, m2/s |
| DLi+,e | diffusion coefficient of Li+ in the electrolyte, m2/s |
| DLi+,s | diffusion coefficient of Li+ in the spherical active particles in the solid phase, m2/s |
| DLi+,s,i | diffusion coefficient of Li+ at the temperature Ti, m2/s |
| DLi+,s,ref | diffusion coefficient of Li+ at the reference temperature Tref, m2/s |
| diffusion coefficient of Li+ in the electrolyte corrected by the Bruggeman tortuosity exponent, m2/s | |
| et | structural shock vector |
| EaD,i | energy required for the substance to diffuse, J/mol |
| EaR,i | energy required for the substance to react, J/mol |
| f± | mean molar activity coefficient |
| F | Faraday constant, ºC/mol |
| h | convective heat transfer coefficient of the thermal model, W/(m2‧K) |
| i | current, A |
| iadd | externally applied current, A/m2 |
| ie | liquid-phase current, A |
| is | solid-phase current, A |
| J0 | initial exchange current density, A/m2 |
| Jlcd | local current density, A/m2 |
| k0 | reaction temperature rate, m2.5/(mol‧0.5s) |
| k0,i | reaction rate constant of Li+ at the temperature Ti, m2.5/(mol‧0.5s) |
| k0,ref,i | reaction rate constant of Li+ at the reference temperature Tref, m2.5/(mol‧0.5s) |
| LA | distance from the positive E-C boundary to the positive E-S boundary, µm |
| LC | distance from the positive E-S boundary to the negative E-C boundary, µm |
| LS | distance from the positive E-S boundary to the negative E-S boundary, µm |
| n | number of electrons transferred in the battery reaction |
| r | particle radius of the spherical active particles, µm |
| Q | total charge variation, J |
| Qcon,h | convective heat, J |
| Qe | total charge variation in the electrolyte, C |
| Qohm,h | ohmic heat, J |
| Qpol,h | polarization heat, J |
| Qrev,h | reversible heat, J |
| Qs | total charge variation in the solid-phase active material, C |
| R | gas constant, J/(mol‧K) |
| Rs | distance from the center to the surface of the spherical active particle, µm |
| T | battery temperature, K |
| Tamb | ambient temperature, K |
| Ti | temperature, K |
| Tmax | maximum temperature |
| Tmin | minimum temperature |
| Tref | reference temperature, K |
| t | time, s |
| t+ | transference number of Li+ |
| ut | residual matrix |
| U | open-circuit potential of the solid-phase electrode, V |
| Ui | open-circuit potential of Li+ at the temperature Ti, V |
| Uref,i | open-circuit potential of Li+ at the reference temperature Tref, V |
| x | distance from the positive E-C boundary to the negative E-C boundary within a unit computational domain, µm |
| Yt | dependent variable vector at time t |
| gradient operator | |
| ΔS | entropy change in the battery, J/(mol‧K) |
| Greek symbols | |
| αa | anodic charge transfer coefficient |
| αc | cathodic charge transfer coefficient |
| β | consistency vector of the coefficients |
| γ | Bruggeman tortuosity exponent |
| ε | volume fraction |
| εe | volume fraction of the electrolyte |
| volume fraction of the liquid phase corrected by the Bruggeman tortuosity exponent | |
| volume fraction of the solid phase corrected by the Bruggeman tortuosity exponent | |
| ƞ | overpotential, V |
| λ | thermal conductivity, W/(m‧K) |
| ρ | density, kg/m3 |
| σ | electrical conductivity, S/m |
| σcc | electrical conductivity of the current collector, S/m |
| σs | electrical conductivity of the solid phase, S/m |
| the electrical conductivity of Li+ in the liquid phase after correction, S/m | |
| electrical conductivity of Li+ in the solid phase after correction, S/m | |
| φ | potential, V |
| φcc | potential of the current collector, V |
| φe | liquid-phase potential, V |
| φs | solid-phase potential, V |
| Subscripts | |
| cc | current collector correlation coefficient |
| e | liquid-phase correlation coefficient |
| i | value is when i |
| Li+, e | Li+ correlation in the electrolyte |
| Li+, s | Li+ correlation in the solid phase |
| Li+, s, max | maximum value of Li+ in the spherical active particles |
| Li+, s, surf | value of Li+ on the surface of the spherical active particles |
| n | negative electrode |
| p | positive electrode |
| ref | value at the reference temperature Tref |
| s | solid phase correlation coefficient |
| t | at time t |
| Abbreviations | |
| MTD | maximum temperature difference |
| P2D | pseudo-two-dimensional model |
| SD | temperature standard deviation |
| SVAR | structural vector autoregression model |
| UI | temperature uniformity index |
| VAR | vector autoregressive model |
References
- Lei, D.; Wang, Y.; Fu, J.; Zhu, X.; Shi, J.; Wang, Y. Electrochemical-thermal analysis of large-sized lithium-ion batteries: Influence of cell thickness and cooling strategy in charging. Energy 2024, 307, 132629. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, J.; Liu, J. An investigation on the significance of reversible heat to the thermal behavior of lithium ion battery through simulations. J. Power Sources 2014, 266, 422–432. [Google Scholar] [CrossRef]
- Xiong, R.; Zhang, K.; Qu, S.; Tian, J.; Shen, W. A fast pre-heating method for lithium-ion batteries by wireless energy transfer at low temperatures. eTransportation 2023, 16, 100227. [Google Scholar] [CrossRef]
- Ianniciello, L.; Biwolé, P.H.; Achard, P. Electric vehicles batteries thermal management systems employing phase change materials. J. Power Sources 2018, 378, 383–403. [Google Scholar] [CrossRef]
- An, Z.; Jia, L.; Wei, L.; Dang, C.; Peng, Q. Investigation on lithium-ion battery electrochemical and thermal characteristic based on electrochemical-thermal coupled model. Appl. Therm. Eng. 2018, 137, 792–807. [Google Scholar] [CrossRef]
- Liu, T.; Ge, S.; Yang, X.-G.; Wang, C.-Y. Effect of thermal environments on fast charging Li-ion batteries. J. Power Sources 2021, 511, 230466. [Google Scholar] [CrossRef]
- Zhang, X.; Chang, X.; Shen, Y.; Xiang, Y. Electrochemical-electrical-thermal modeling of a pouch-type lithium ion battery: An application to optimize temperature distribution. J. Energy Storage 2017, 11, 249–257. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, S.; Li, L.; Liu, F.; Jiang, L.; Jia, M.; Ai, Y.; Yao, C.; Gu, H. Simulation and parameter identification based on electrochemical- thermal coupling model of power lithium ion-battery. J. Alloys Compd. 2020, 844, 156003. [Google Scholar] [CrossRef]
- Khan, F.M.N.; Rasul, M.G.; Sayem, A.S.M.; Mandal, N.K. A computational analysis of effects of electrode thickness on the energy density of lithium-ion batteries. Energy 2024, 288, 129774. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Mei, W.; Chen, H.; Sun, J.; Wang, Q. The effect of electrode design parameters on battery performance and optimization of electrode thickness based on the electrochemical–thermal coupling model. Sustain. Energy Fuels 2019, 3, 148–165. [Google Scholar] [CrossRef]
- Nie, P.; Zhang, S.-W.; Ran, A.; Yang, C.; Chen, S.; Li, Z.; Zhang, X.; Deng, W.; Liu, T.; Kang, F.; et al. Full-cycle electrochemical-thermal coupling analysis for commercial lithium-ion batteries. Appl. Therm. Eng. 2021, 184, 116258. [Google Scholar] [CrossRef]
- Lin, X.-W.; Jiang, Y.; Yu, H.-T.; Shi, M.-Y.; Liu, B.; Wen, X.-L.; Zhou, Z.-F. A comprehensive investigation on the electrochemical and thermal inconsistencies for 280 Ah energy storage lithium-ion battery. Energy Convers. Manag. 2024, 315, 118750. [Google Scholar] [CrossRef]
- Jiang, F.; Peng, P.; Sun, Y. Thermal analyses of LiFePO4/graphite battery discharge processes. J. Power Sources 2013, 243, 181–194. [Google Scholar] [CrossRef]
- Panchal, S.; Mathew, M.; Fraser, R.; Fowler, M. Electrochemical thermal modeling and experimental measurements of 18650 cylindrical lithium-ion battery during discharge cycle for an EV. Appl. Therm. Eng. 2018, 135, 123–132. [Google Scholar] [CrossRef]
- Jilte, R.; Afzal, A.; Panchal, S. A novel battery thermal management system using nano-enhanced phase change materials. Energy 2021, 219, 119564. [Google Scholar] [CrossRef]
- Mevawalla, A.; Panchal, S.; Tran, M.-K.; Fowler, M.; Fraser, R. Mathematical Heat Transfer Modeling and Experimental Validation of Lithium-Ion Battery Considering: Tab and Surface Temperature, Separator, Electrolyte Resistance, Anode-Cathode Irreversible and Reversible Heat. Batteries 2020, 6, 61. [Google Scholar] [CrossRef]
- Yin, L.; Björneklett, A.; Söderlund, E.; Brandell, D. Analyzing and mitigating battery ageing by self-heating through a coupled thermal-electrochemical model of cylindrical Li-ion cells. J. Energy Storage 2021, 39, 102648. [Google Scholar] [CrossRef]
- Huang, Y.; Lai, X.; Ren, D.; Kong, X.; Han, X.; Lu, L.; Zheng, Y. Thermal and stoichiometry inhomogeneity investigation of large-format lithium-ion batteries via a three-dimensional electrochemical-thermal coupling model. Electrochim. Acta 2023, 468, 143212. [Google Scholar] [CrossRef]
- Bayatinejad, M.A.; Mohammadi, A. Investigating the effects of tabs geometry and current collectors thickness of lithium-ion battery with electrochemical-thermal simulation. J. Energy Storage 2021, 43, 103203. [Google Scholar] [CrossRef]
- Li, H.; Saini, A.; Liu, C.; Yang, J.; Wang, Y.; Yang, T.; Pan, C.; Chen, L.; Jiang, H. Electrochemical and thermal characteristics of prismatic lithium-ion battery based on a three-dimensional electrochemical-thermal coupled model. J. Energy Storage 2021, 42, 102976. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Kong, W. Numerical and experimental study on thermal behavior of prismatic lithium-ion battery for large-capacity energy storage. J. Energy Storage 2024, 83, 110620. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Z.; He, C.; Lin, X.; Li, C.; Huang, J. Research on remaining useful life prediction method for lithium-ion battery based on improved GA-ACO-BPNN optimization algorithm. Sustain. Energy Technol. Assess. 2025, 73, 104142. [Google Scholar] [CrossRef]
- An, Q.; Zhang, X.; Rao, L.; Zhang, M. Novel decomposed genetic algorithm for equivalent circuit model parameter optimization of lithium-ion battery. J. Energy Storage 2025, 108, 115116. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, S.; Fan, Y.; Hai, N.; Huang, Q.; Fernandez, C. An improved dung beetle optimizer- hybrid kernel least square support vector regression algorithm for state of health estimation of lithium-ion batteries based on variational model decomposition. Energy 2024, 306, 132464. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Xie, Y.; Zeng, J.; Fernandez, C. Remaining useful life prediction and state of health diagnosis of lithium-ion batteries with multiscale health features based on optimized CatBoost algorithm. Energy 2024, 300, 131575. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, Y.; Liu, Y.; Xu, R.; Zhu, J.; Wang, J. Structural optimization of serpentine channel water-cooled plate for lithium-ion battery modules based on multi-objective Bayesian optimization algorithm. J. Energy Storage 2024, 91, 112136. [Google Scholar] [CrossRef]
- Yang, H.; Liu, N.; Gu, M.; Gao, Q.; Yang, G. Optimized design of novel serpentine channel liquid cooling plate structure for lithium-ion battery based on discrete continuous variables. Appl. Therm. Eng. 2025, 264, 125502. [Google Scholar] [CrossRef]
- Chen, K.; Li, J.; Liu, K.; Bai, C.; Zhu, J.; Gao, G.; Wu, G.; Laghrouche, S. State of health estimation for lithium-ion battery based on particle swarm optimization algorithm and extreme learning machine. Green Energy Intell. Transp. 2024, 3, 100151. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5. [Google Scholar] [CrossRef]
- Alkhedher, M.; Al Tahhan, A.B.; Yousaf, J.; Ghazal, M.; Shahbazian-Yassar, R.; Ramadan, M. Electrochemical and thermal modeling of lithium-ion batteries: A review of coupled approaches for improved thermal performance and safety lithium-ion batteries. J. Energy Storage 2024, 86, 111172. [Google Scholar] [CrossRef]
- Lin, X.-W.; Zhou, Z.-F.; Zhu, X.-G.; Chen, B.; Zhu, H.; Ben, N.-Y.; Wang, X.-D.; Xu, W.-W. Non-uniform thermal characteristics investigation of three-dimensional electrochemical-thermal coupled model for pouch lithium-ion battery. J. Cleaner Prod. 2023, 417, 137912. [Google Scholar] [CrossRef]
- Dao, T.-S.; Vyasarayani, C.P.; McPhee, J. Simplification and order reduction of lithium-ion battery model based on porous-electrode theory. J. Power Sources 2012, 198, 329–337. [Google Scholar] [CrossRef]
- He, C.X.; Yue, Q.L.; Wu, M.C.; Chen, Q.; Zhao, T.S. A 3D electrochemical-thermal coupled model for electrochemical and thermal analysis of pouch-type lithium-ion batteries. Int. J. Heat Mass Transf. 2021, 181, 121855. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Y.; Ai, L.; Jia, M.; Du, S.; Yin, B.; Woo, S.; Zhang, H. 3D simulation on the internal distributed properties of lithium-ion battery with planar tabbed configuration. J. Power Sources 2015, 293, 993–1005. [Google Scholar] [CrossRef]
- Mei, W.; Chen, H.; Sun, J.; Wang, Q. Numerical study on tab dimension optimization of lithium-ion battery from the thermal safety perspective. Appl. Therm. Eng. 2018, 142, 148–165. [Google Scholar] [CrossRef]
- Dong, T.; Peng, P.; Jiang, F. Numerical modeling and analysis of the thermal behavior of NCM lithium-ion batteries subjected to very high C-rate discharge/charge operations. Int. J. Heat Mass Transf. 2018, 117, 261–272. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, D.; Li, C.; Wang, J.; Zhang, J.; Cheng, Y.; Mei, W.; Cheng, S.; Qin, P.; Duan, Q.; et al. Numerical optimization for a phase change material based lithium-ion battery thermal management system. Appl. Therm. Eng. 2023, 222, 119839. [Google Scholar] [CrossRef]
- Li, L.; Ling, L.; Xie, Y.; Zhou, W.; Wang, T.; Zhang, L.; Bei, S.; Zheng, K.; Xu, Q. Comparative study of thermal management systems with different cooling structures for cylindrical battery modules: Side-cooling vs. terminal-cooling. Energy 2023, 274, 127414. [Google Scholar] [CrossRef]
- Mei, W.; Li, H.; Zhao, C.; Sun, J.; Wang, Q. Numerical study on thermal characteristics comparison between charge and discharge process for lithium ion battery. Int. J. Heat Mass Transf. 2020, 162, 120319. [Google Scholar] [CrossRef]
- Guo, M.; Sikha, G.; White, R.E. Single-Particle Model for a Lithium-Ion Cell: Thermal Behavior. J. Electrochem. Soc. 2011, 158, A122. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Modeling of a Commercial Graphite/LiFePO4 Cell. J. Electrochem. Soc. 2011, 158, A562. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Y.; Jia, M.; Tang, Y.; Lin, Y.; Zhang, Z.; Liu, Y. An electrochemical–thermal model based on dynamic responses for lithium iron phosphate battery. J. Power Sources 2014, 255, 130–143. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Venkatachalapathy, R.; Prakash, J.; Selman, J.R. Entropy Changes Due to Structural Transformation in the Graphite Anode and Phase Change of the LiCoO2 Cathode. J. Electrochem. Soc. 2000, 147, 2432. [Google Scholar] [CrossRef]
- Wu, W.; Xiao, X.; Huang, X. The effect of battery design parameters on heat generation and utilization in a Li-ion cell. Electrochim. Acta 2012, 83, 227–240. [Google Scholar] [CrossRef]
- Han, X.; Huang, Y.; Lai, H. Electrochemical-thermal coupled investigation of lithium iron phosphate cell performances under air-cooled conditions. Appl. Therm. Eng. 2019, 147, 908–916. [Google Scholar] [CrossRef]
- Heidarshenas, B.; Aghaei, A.; Hossein Zamani, A.; Yuan, Y. Comparison of different cooling techniques for a lithium-ion battery at various discharge rates using electrochemical thermal modeling. Appl. Therm. Eng. 2025, 258, 124596. [Google Scholar] [CrossRef]
- Yi, J.; Kim, U.S.; Shin, C.B.; Han, T.; Park, S. Three-Dimensional Thermal Modeling of a Lithium-Ion Battery Considering the Combined Effects of the Electrical and Thermal Contact Resistances between Current Collecting Tab and Lead Wire. J. Electrochem. Soc. 2013, 160, A437. [Google Scholar] [CrossRef]
- Seong Kim, U.; Yi, J.; Shin, C.B.; Han, T.; Park, S. Modeling the Dependence of the Discharge Behavior of a Lithium-Ion Battery on the Environmental Temperature. J. Electrochem. Soc. 2011, 158, A611. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Yang, K.; Liu, J.; Wu, X. Performance and parameter optimization design of microchannel heat sink with different cavity and rib combinations. Case Stud. Therm. Eng. 2024, 53, 103843. [Google Scholar] [CrossRef]
- An, W.; Gao, B.; Liu, J.; Ni, J.; Liu, J. Predicting hourly heating load in residential buildings using a hybrid SSA–CNN–SVM approach. Case Stud. Therm. Eng. 2024, 59, 104516. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, S.; Zhang, J.; Huang, Z.; Han, D. Effects of charging rates on heat and gas generation in lithium-ion battery thermal runaway triggered by high temperature coupled with overcharge. J. Power Sources 2024, 600, 234237. [Google Scholar] [CrossRef]
- Primiceri, G.E. Time Varying Structural Vector Autoregressions and Monetary Policy. Rev. Econ. Stud. 2005, 72, 821–852. [Google Scholar] [CrossRef]





| Parameter | Symbol (Unit) | Positive Electrode | Negative Electrode | Separator |
|---|---|---|---|---|
| Density | ρ (kg/m3) | 3600 | 2300 | 2000 |
| Heat Capacity at Constant Pressure | Cp (J/(kg‧K)) | 881 | 750 | 300 |
| Thermal Conductivity | λ (W/(m‧K)) | 1 | 1 | 10 |
| Radius of Active Particle | r (µm) | 1.2 | 0.3875 | |
| Volume Fraction of Electrolyte | εe | 0.32 | 0.31 | 0.37 |
| Volume Fraction of Solid Phase | εs | 0.633 | 0.655 | |
| Bruggeman Tortuosity Exponent | γ | 1.5 | 1.5 | |
| Electrical Conductivity of Current Collector | σcc (S/m) | 2.326 × 107 | 5.998 × 107 | |
| Initial Exchange Current Density | Jo (A/m2) | 1.5727 | 0.534 | |
| Anodic Charge Transfer Coefficient | αa | 0.5 | 0.5 | |
| Cathodic Charge Transfer Coefficient | αc | 0.5 | 0.5 | |
| Faraday Constant | F (°C/mol) | 96,487 | ||
| Gas Constant | R (J/(mol‧K)) | 8.314 | ||
| Convective Heat Transfer Coefficient | h (W/(m2‧K)) | 5 | ||
| Ambient Temperature | Tamb (K) | 293.15 |
| Parameter | Thermal Conductivity (W/(m‧K)) | Heat Capacity at Constant Pressure (J/(kg‧K)) | Density (kg/m3) | Reference |
|---|---|---|---|---|
| Positive Current Collector | 238 | 900 | 2700 | [49] |
| Negative Current Collector | 400 | 385 | 8960 |
| MTD | Mean Temperature | UI | |
|---|---|---|---|
| Mean Value | 5.0574 K | 294.4292 K | 0.8183 |
| Standard Deviation | 5.0272 | 2.0964 | 0.0482 |
| Coefficient of Variation | 0.9940 | 0.0071 | 0.0589 |
| Maximum Value | 15.0845 K | 300.4394 K | 0.9627 |
| Minimum Value | 0.0103 K | 292.8757 K | 0.7459 |
| Range | 15.0742 K | 7.5638 K | 0.2167 |
| Trend Slope | 0.0253 K/s | 0.0086 K/s | −0.0002 |
| Trend R-square | 0.7726 | 0.5094 | 0.5263 |
| Autocorrelation Coefficient | 0.9922 | 0.9899 | 0.9773 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wang, Y.; Gao, B.; Zhou, S.; Liu, J. Unraveling Electrochemical–Thermal Synergy in Lithium-Ion Batteries: A Predictive Framework Based on 3D Modeling and SVAR. Appl. Sci. 2025, 15, 9129. https://doi.org/10.3390/app15169129
Zhou X, Wang Y, Gao B, Zhou S, Liu J. Unraveling Electrochemical–Thermal Synergy in Lithium-Ion Batteries: A Predictive Framework Based on 3D Modeling and SVAR. Applied Sciences. 2025; 15(16):9129. https://doi.org/10.3390/app15169129
Chicago/Turabian StyleZhou, Xue, Yukun Wang, Bo Gao, Shiyu Zhou, and Jiying Liu. 2025. "Unraveling Electrochemical–Thermal Synergy in Lithium-Ion Batteries: A Predictive Framework Based on 3D Modeling and SVAR" Applied Sciences 15, no. 16: 9129. https://doi.org/10.3390/app15169129
APA StyleZhou, X., Wang, Y., Gao, B., Zhou, S., & Liu, J. (2025). Unraveling Electrochemical–Thermal Synergy in Lithium-Ion Batteries: A Predictive Framework Based on 3D Modeling and SVAR. Applied Sciences, 15(16), 9129. https://doi.org/10.3390/app15169129







