Effect of Pressure Gradient on Flow and Heat Transfer over Surface-Mounted Heated Blocks in a Narrow Channel
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometry and Boundary Conditions
2.2. Numerical Method
2.3. Validation
3. Results
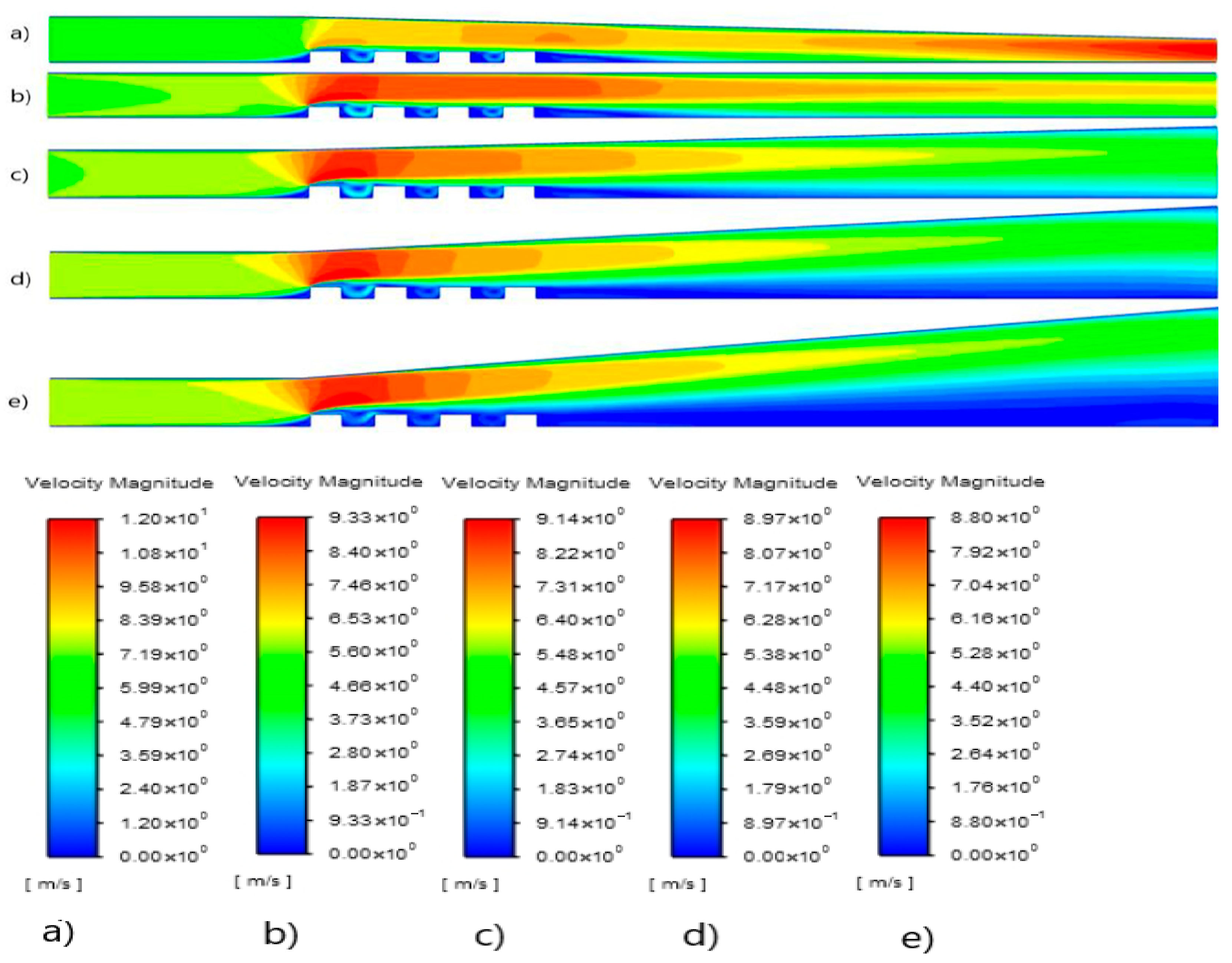
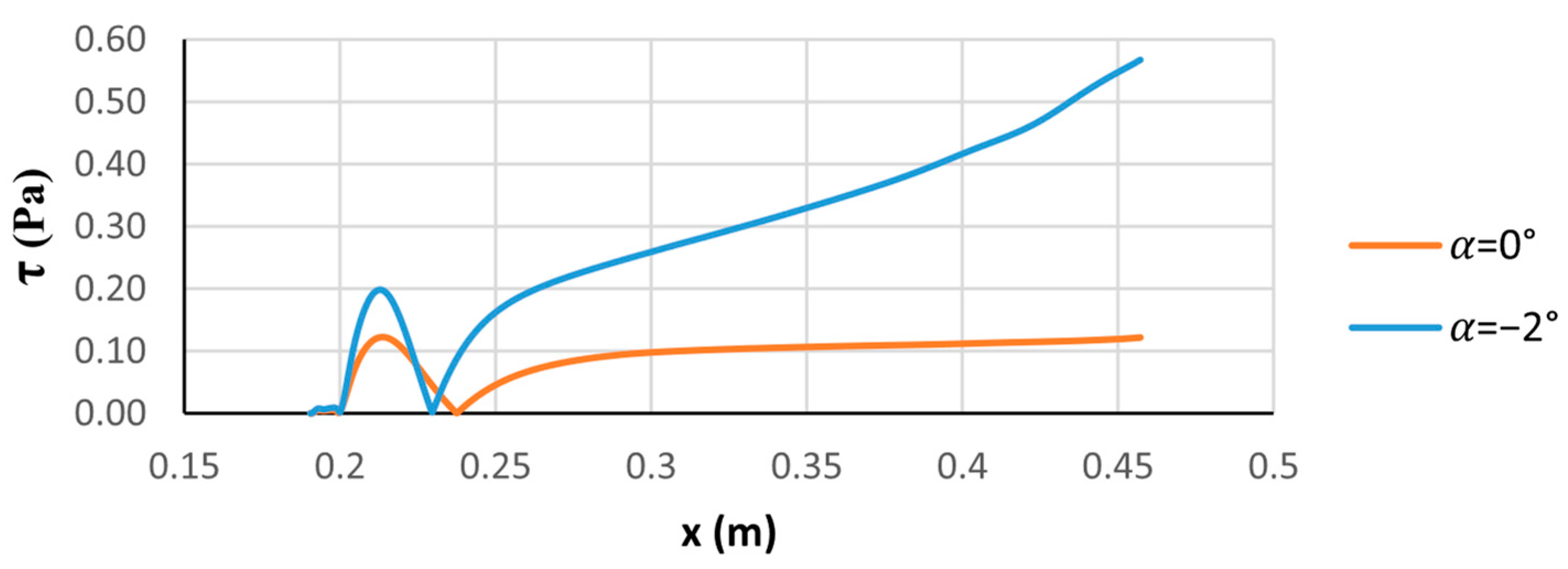
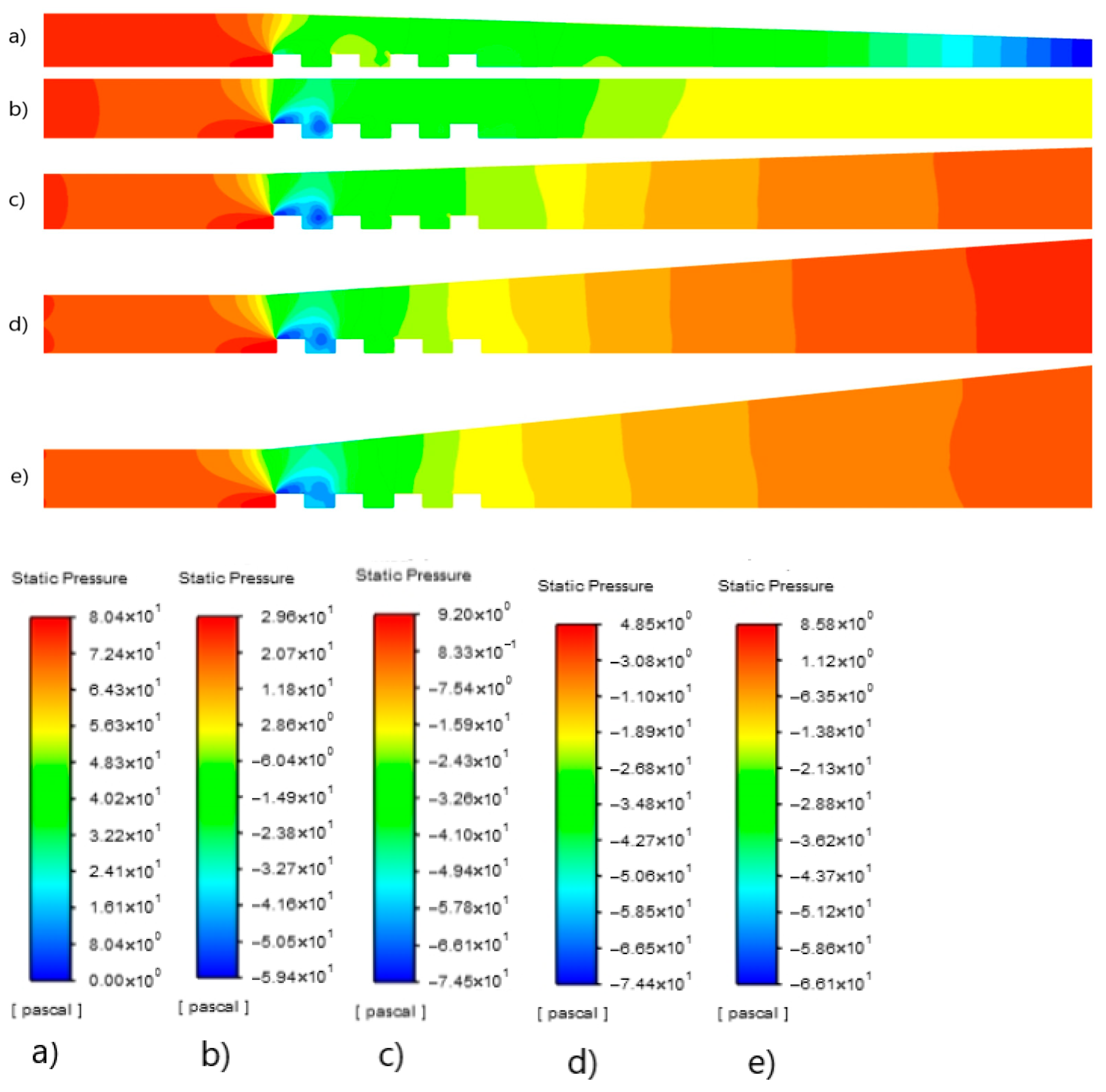
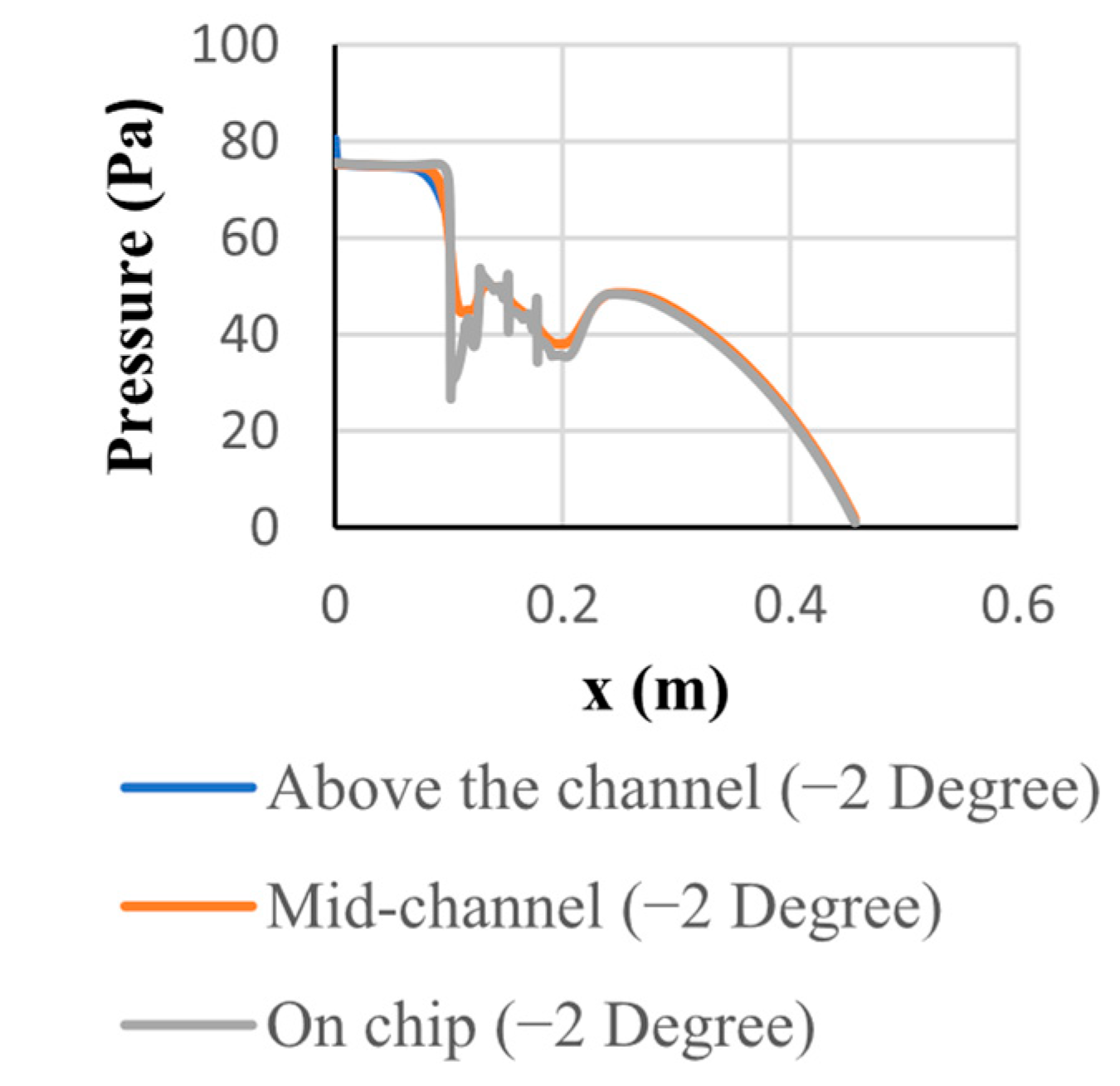
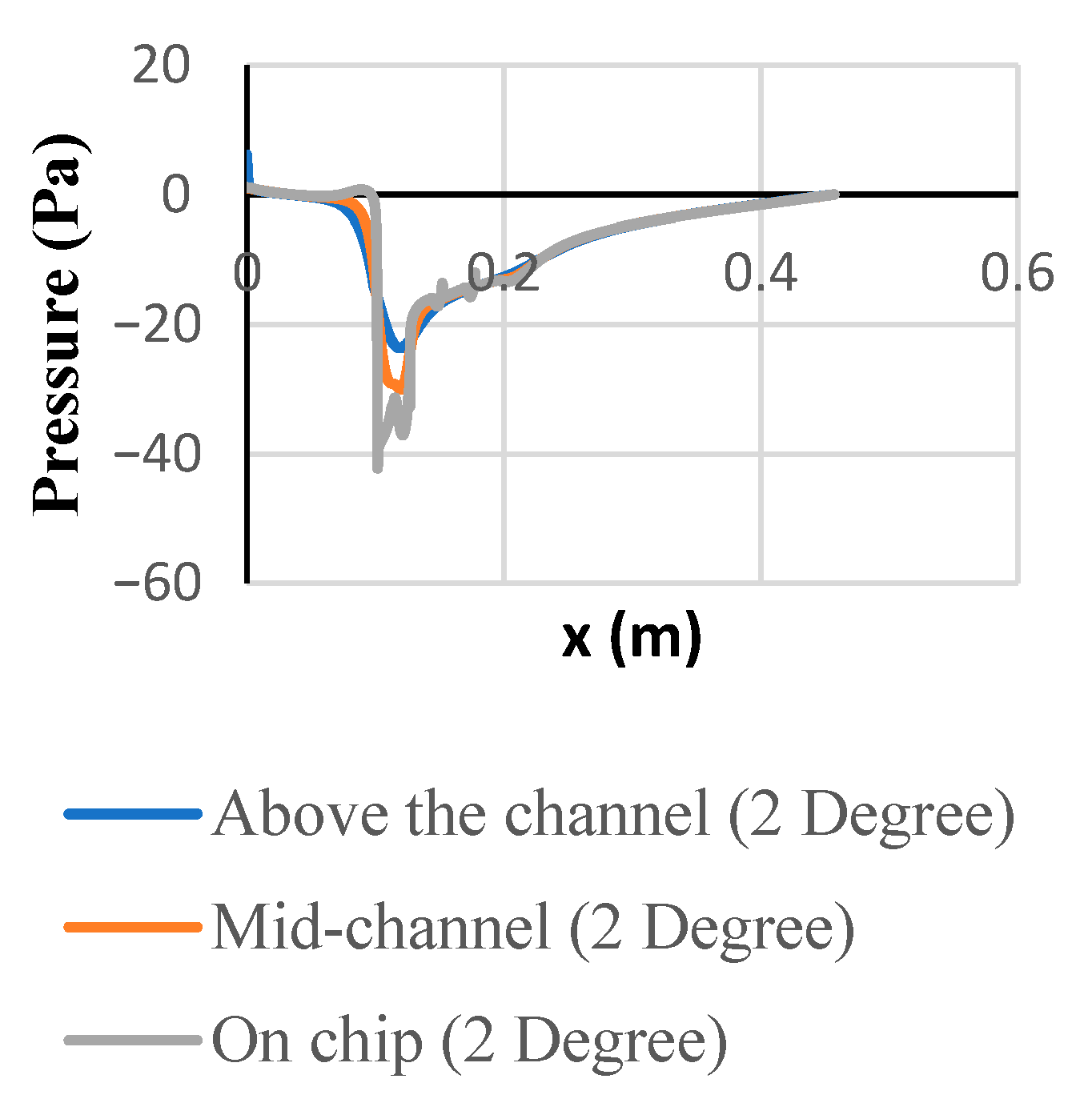
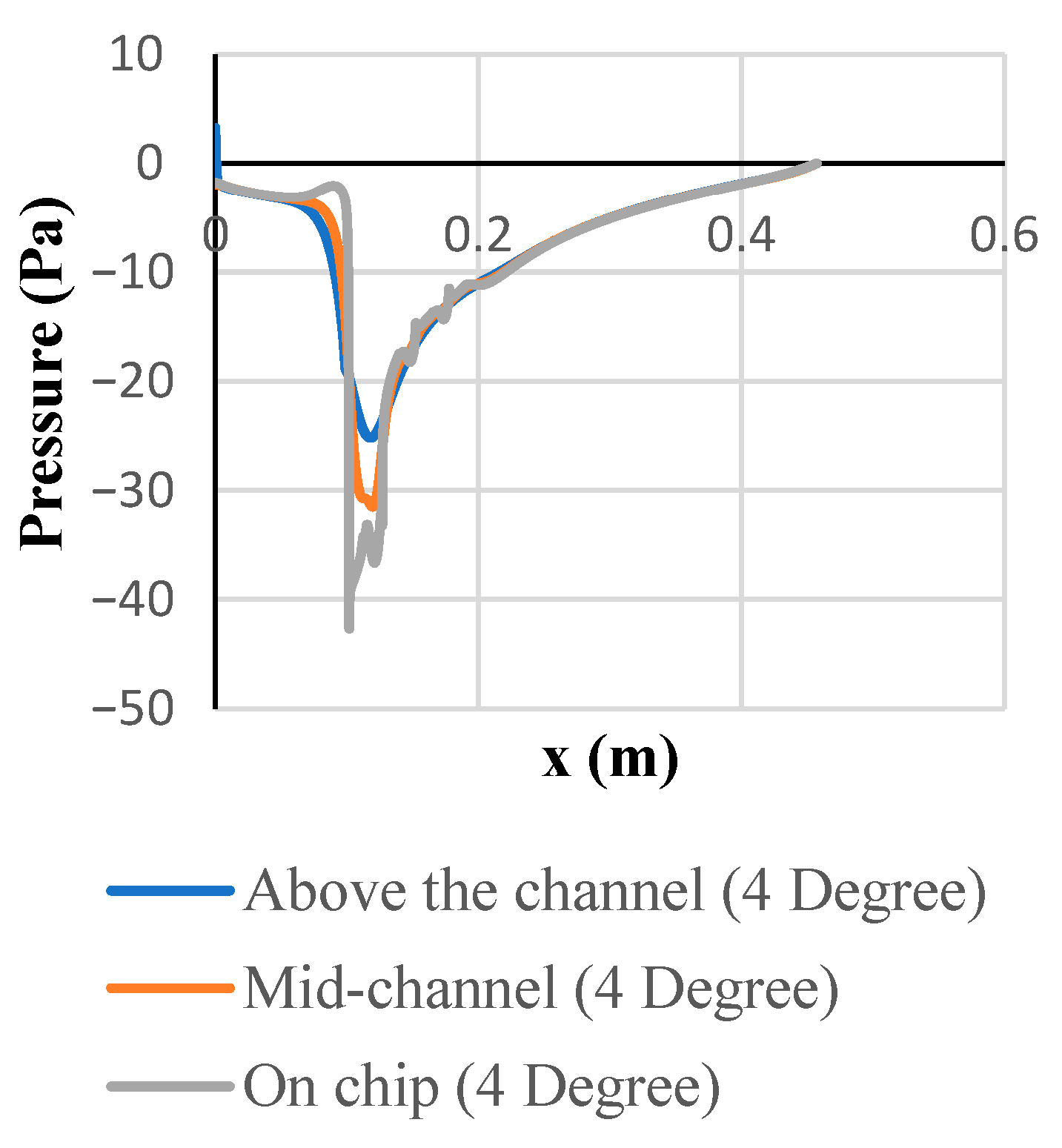
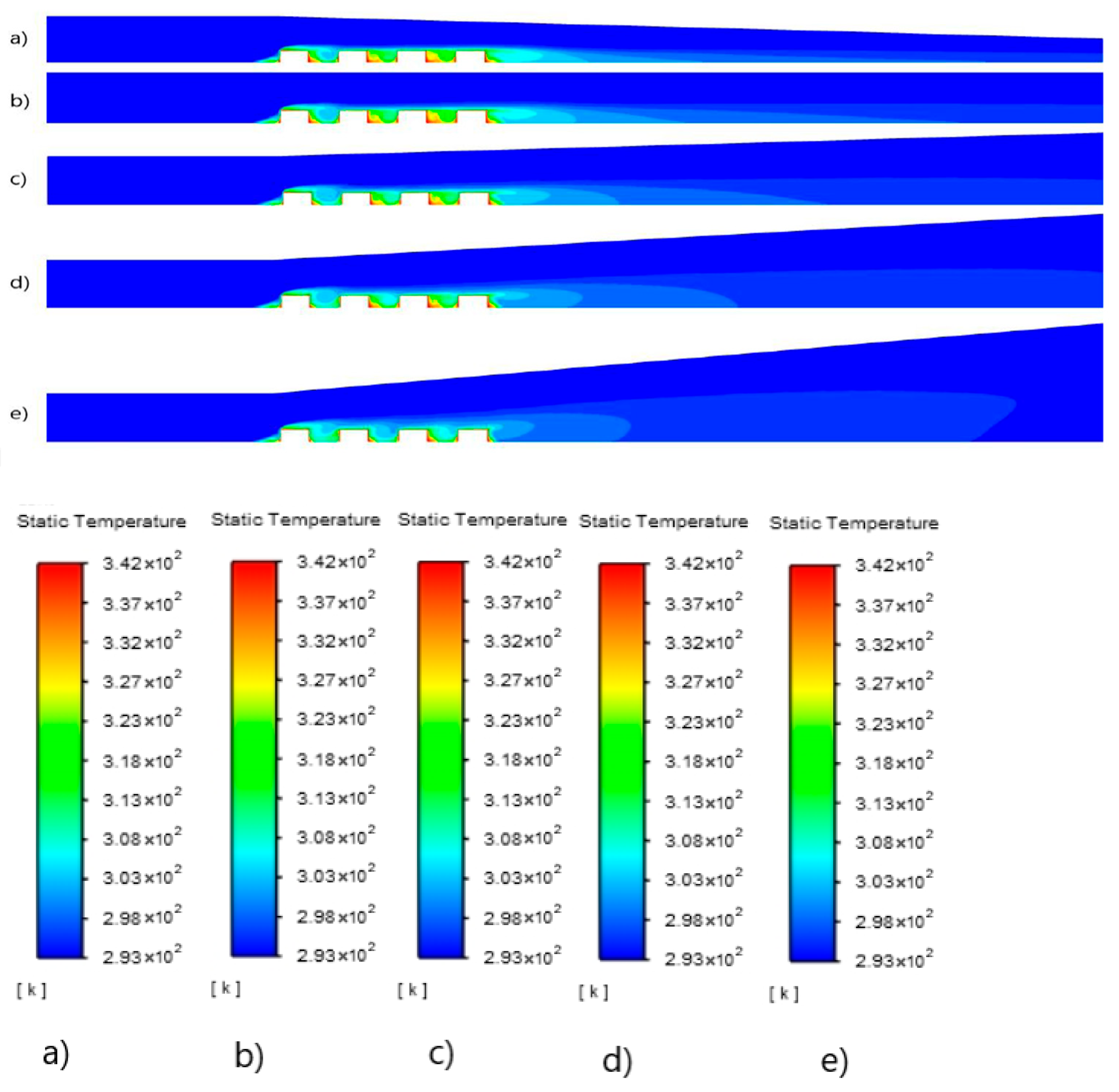
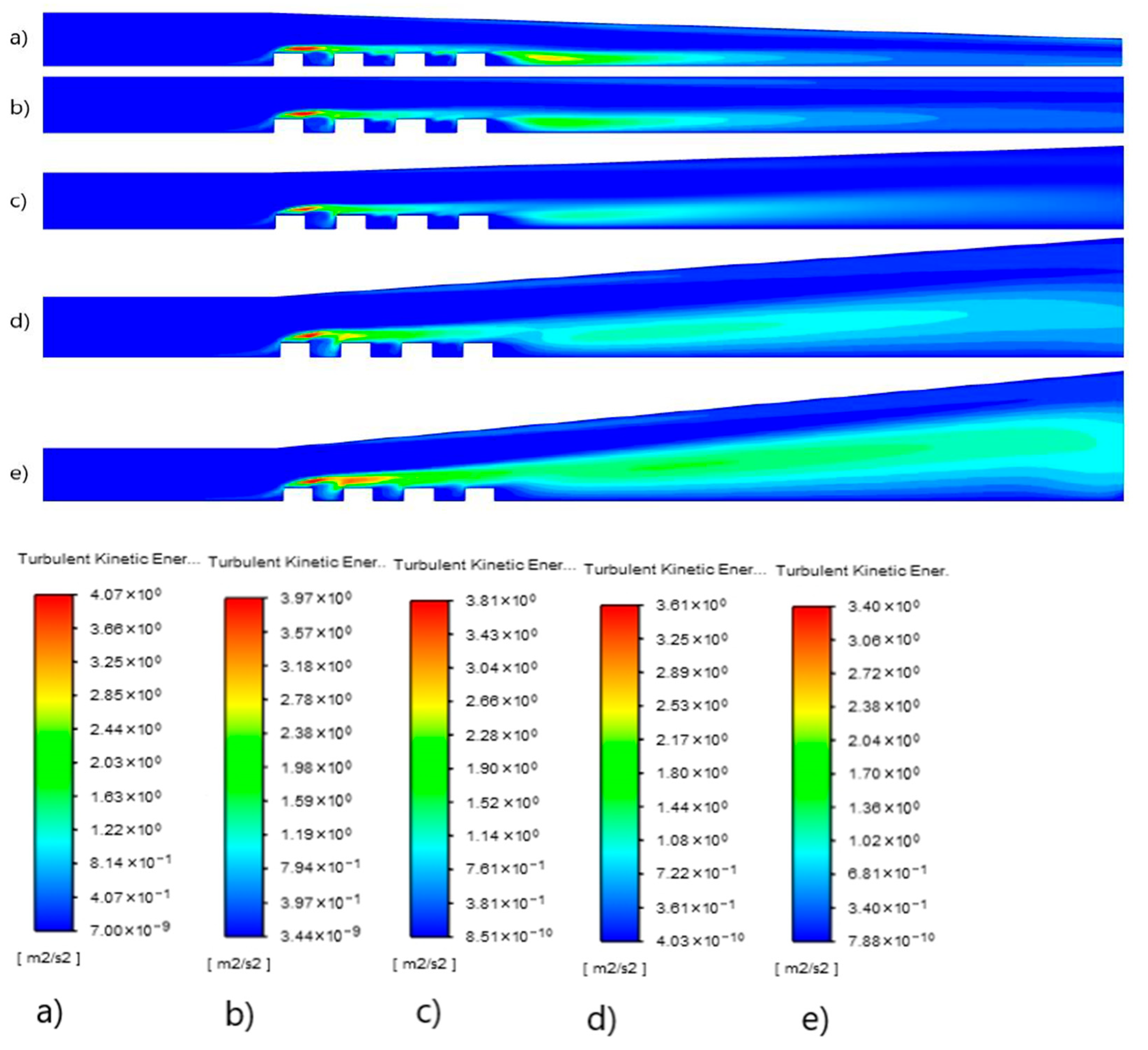
3.1. Velocity, Temperature, Pressure, and Kinetic Energy Distributions
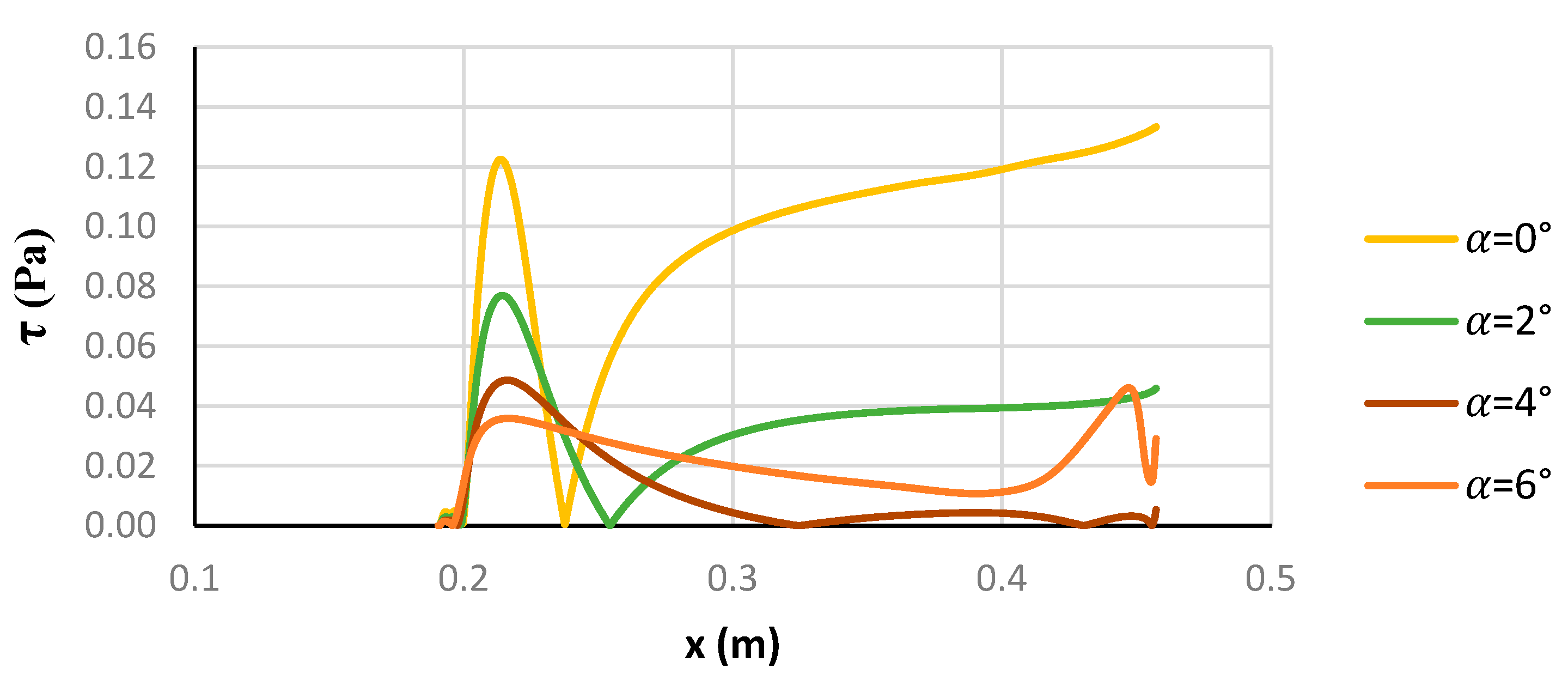
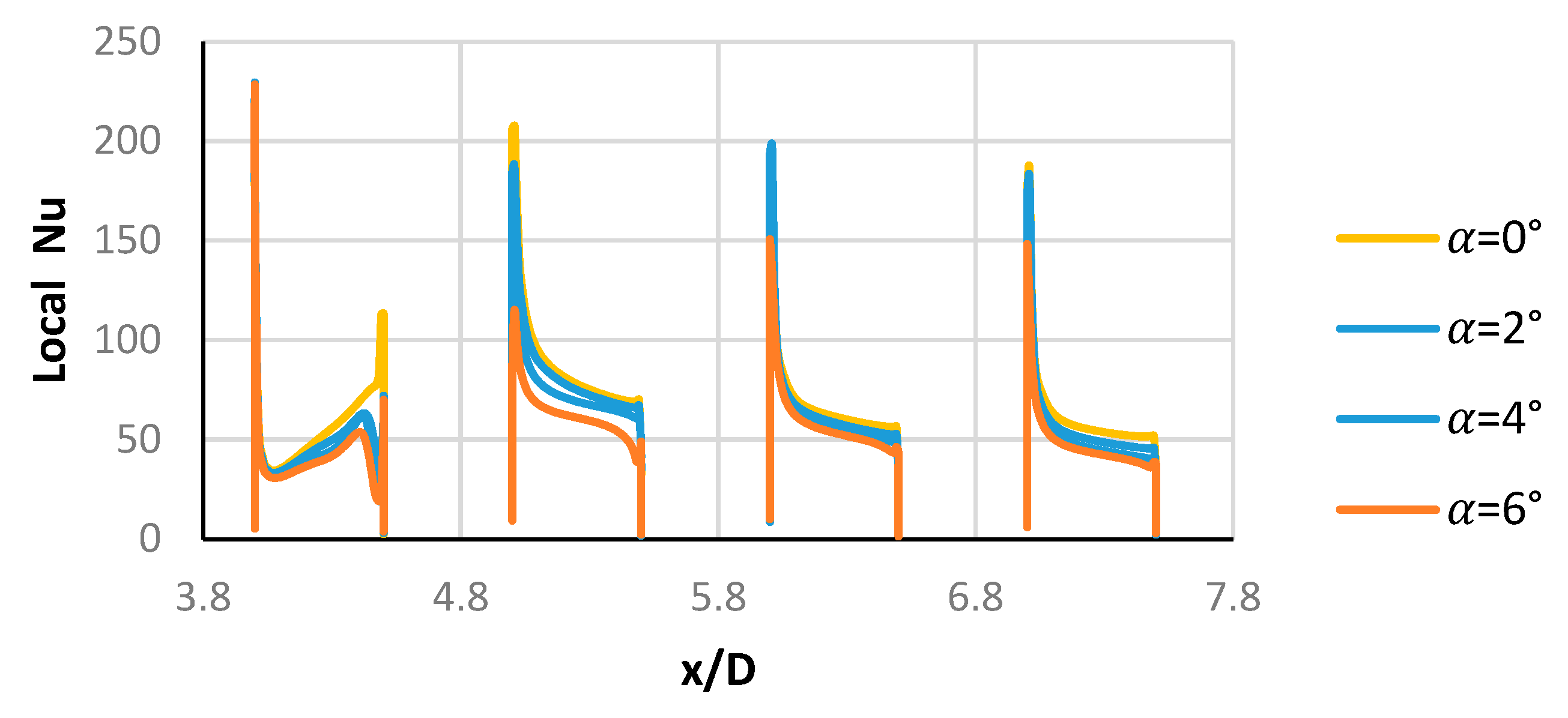
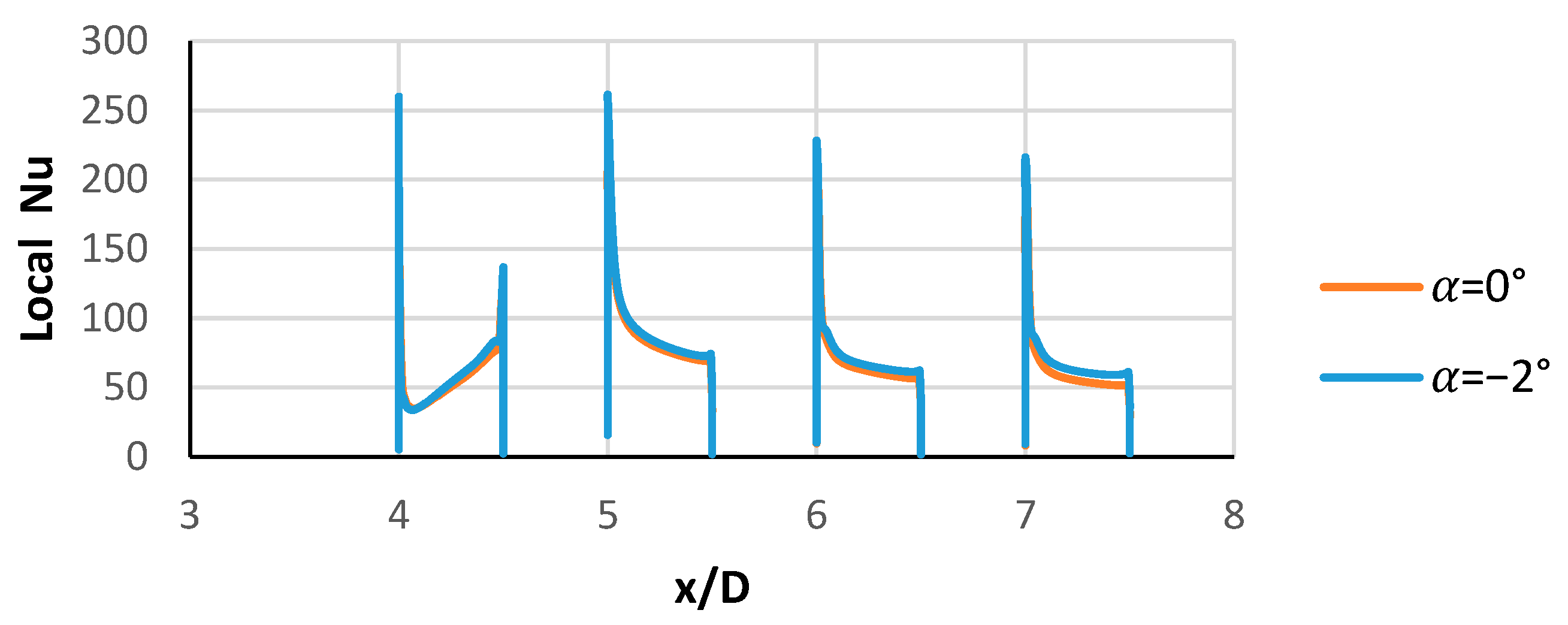
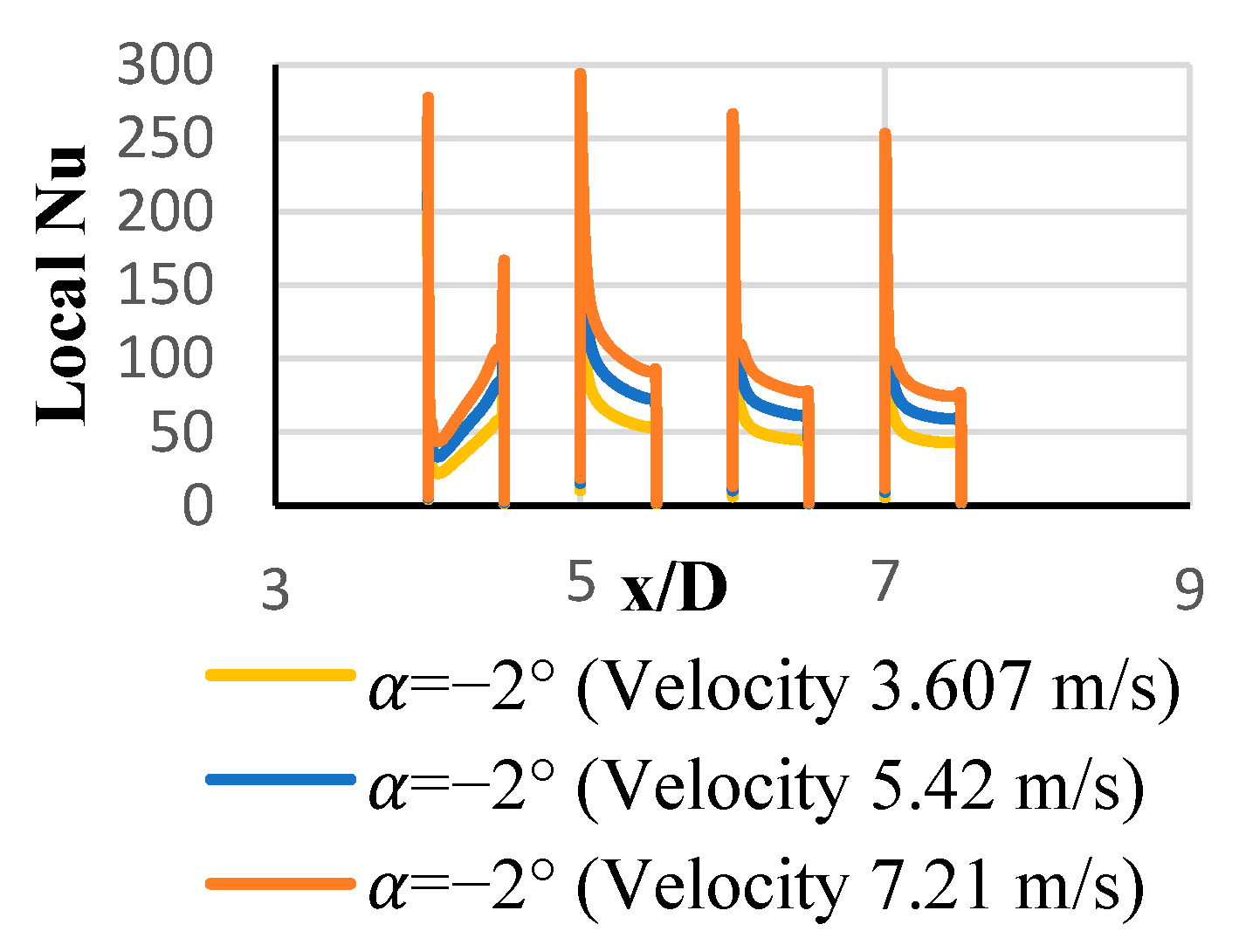
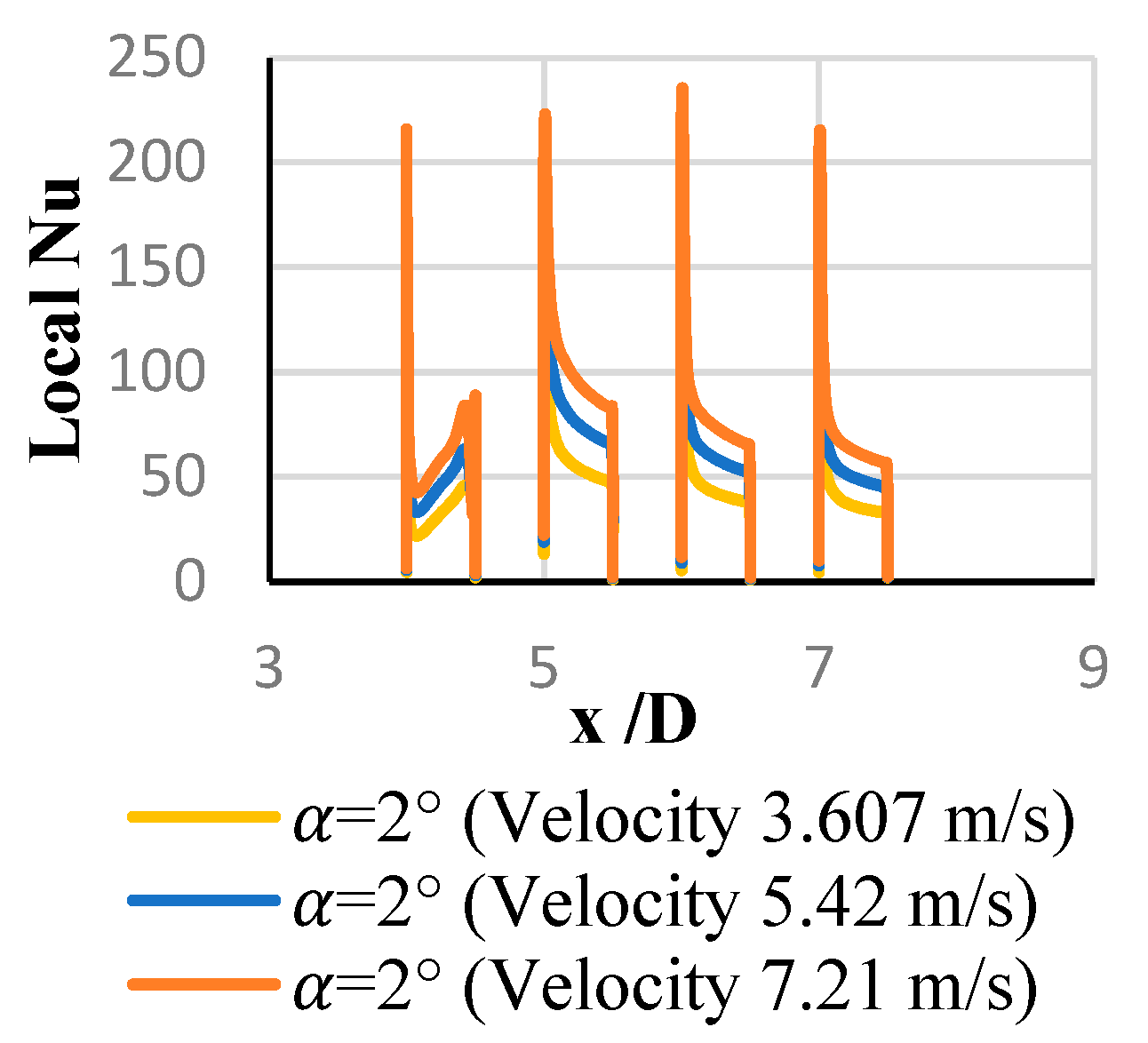
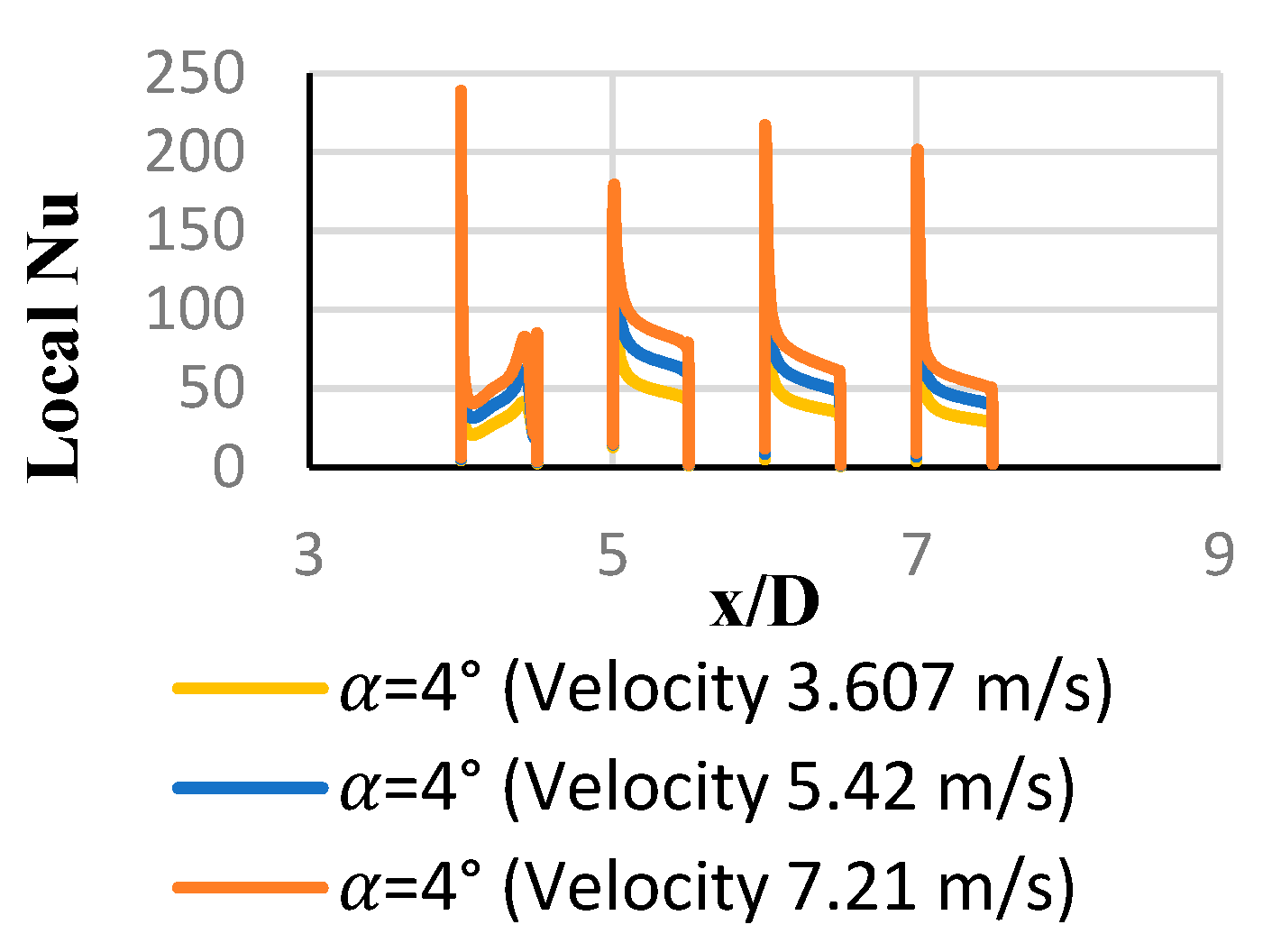
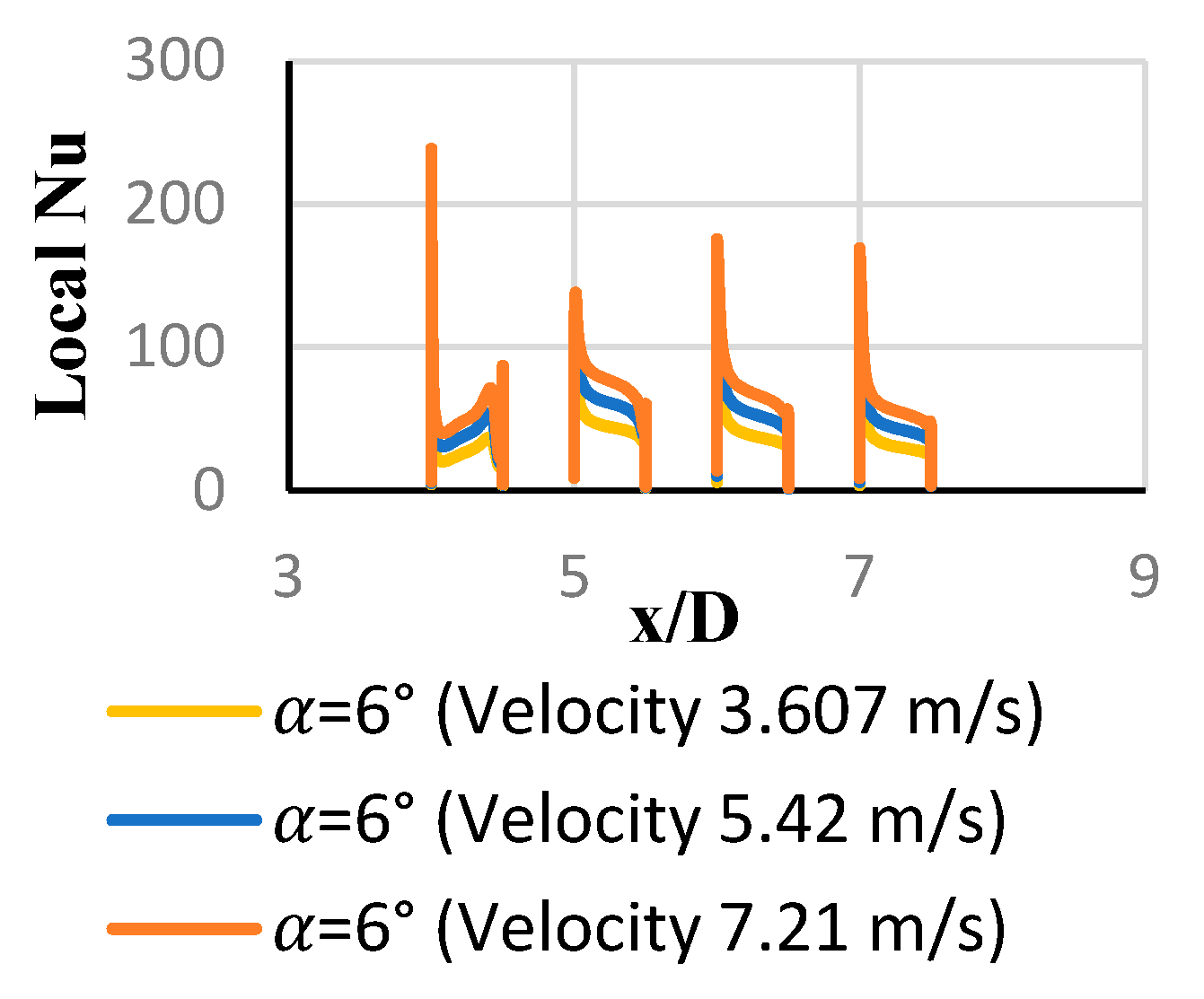
3.2. Local and Average Heat Transfer Coefficients
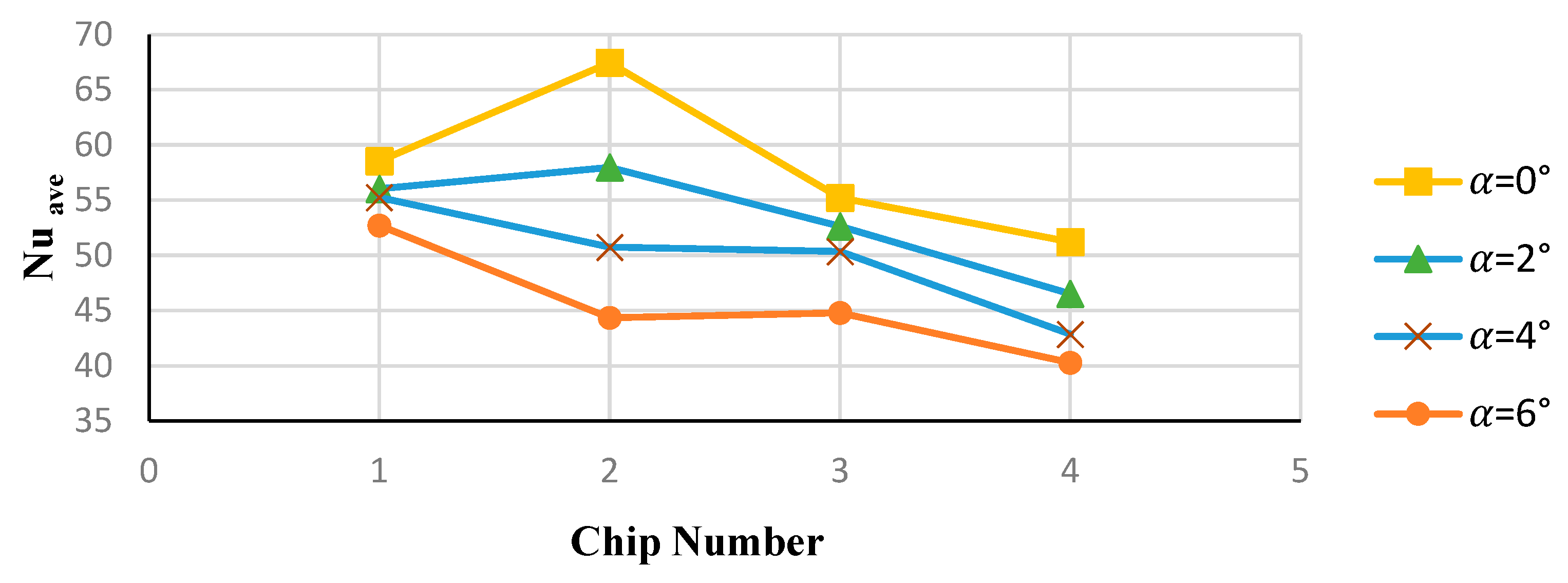
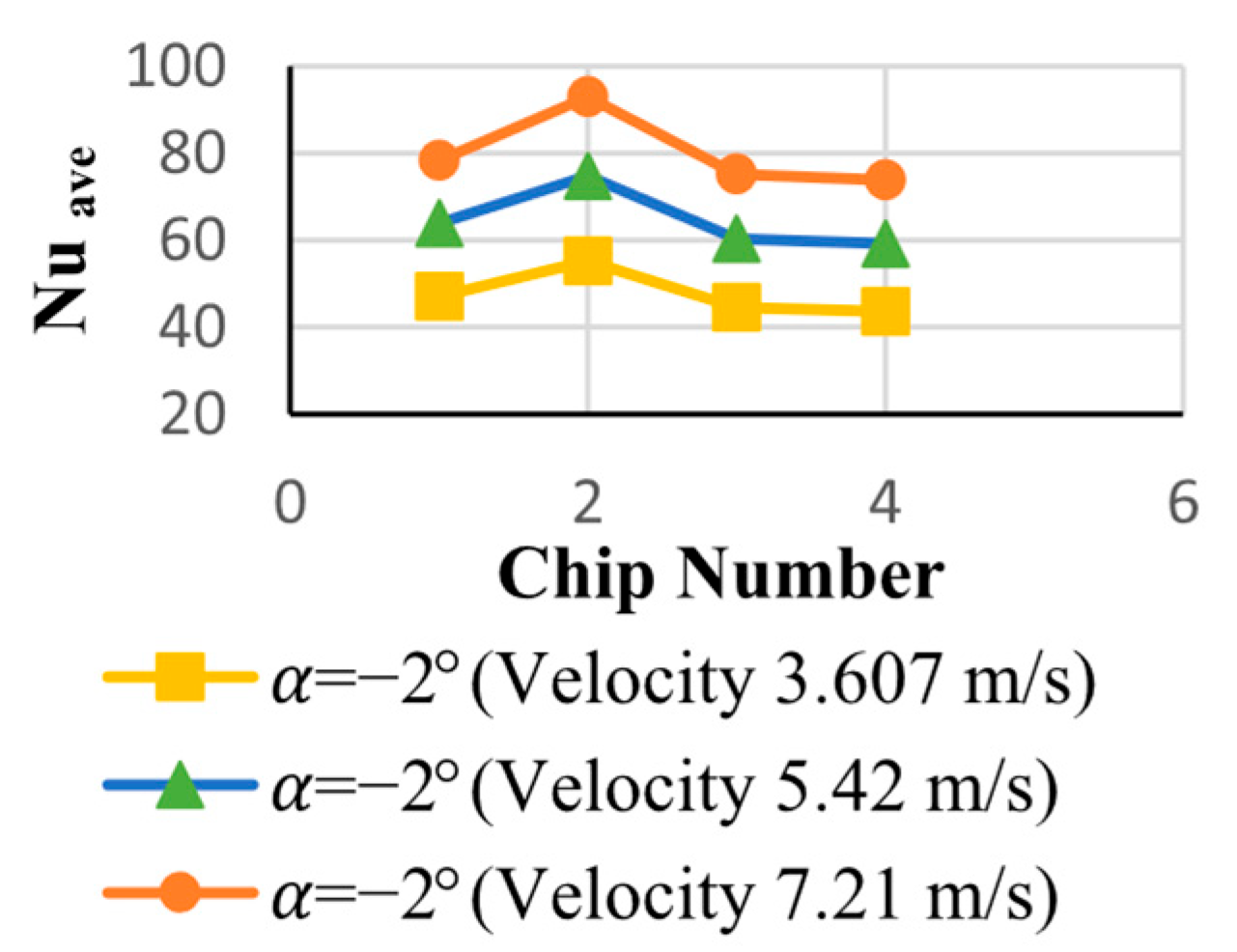
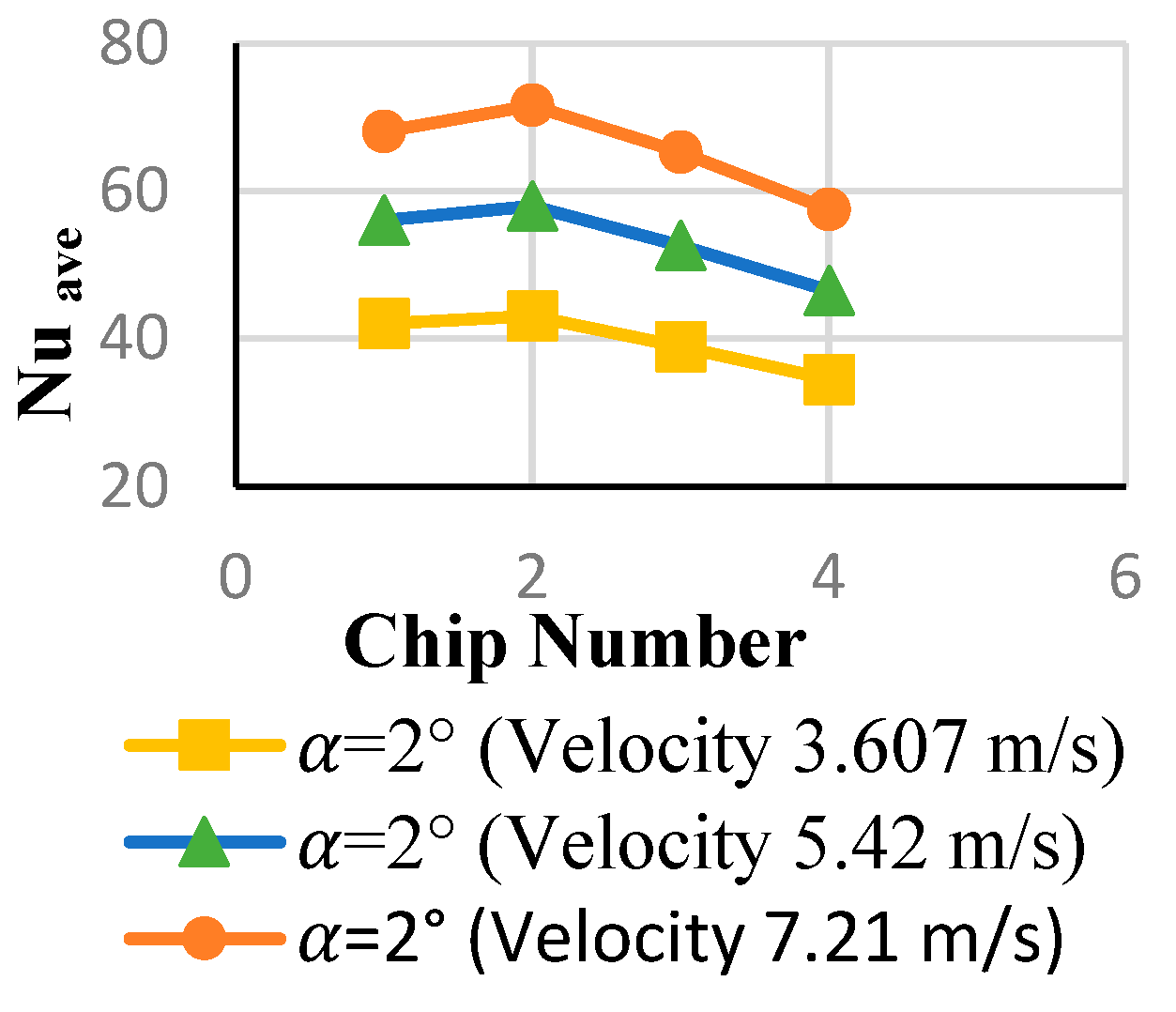
3.3. Heat Transfer over Chips
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| Exp. | Experimental |
| Num. | Numerical |
| RL | Reattachment Length |
| RNG k-ɛ | Renormalization Group k-ɛ Turbulence Model |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
| SIMLEC | Semi-Implicit Method for Pressure-Linked Equations Consistent |
| SST k-ω | Shear Stress Transport k-ω Turbulence Model |
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| Symbols | |
| Avg. | Average |
| h | Chip height [m], local convective heat transfer coefficient [W/m2·K] |
| have | Average heat transfer coefficient [W/m2·K] |
| H | Channel inlet height [m] |
| k | Turbulent kinetic energy [m2/s2], Conductivity [W/mK] |
| L | Chip (Block) length [m] |
| Nu | Local Nusselt number [=hH/k] |
| Nuave | Average Nusselt number [=haveH/k] |
| Re | Reynolds number [=uH/ν] |
| S | Distance between chips [m] |
| T | Channel inlet temperature [K] |
| Ts | Surface temperature [K] |
| U | Uniform channel inlet velocity [m/s] |
| α | Upper plate inclination angle (Divergence angle) [°] |
| ω | Specific dissipation rate [=ε/k] |
| ν | Kinematic viscosity [m2/s] |
References
- Bar-Cohen, A.; Watwe, A.A.; Prasher, R.S. Heat transfer in electronic equipment. In Heat Transfer Handbook, 2nd ed.; Bejan, A., Kraus, A.D., Eds.; Wiley: Hoboken, NJ, USA, 2007; pp. 947–1028. [Google Scholar]
- Barton, I.E. The entrance effect of laminar flow over a backward-facing step geometry. Int. J. Numer. Methods Fluids 1997, 25, 633–644. [Google Scholar] [CrossRef]
- Pulat, E. Simulation of Forced Convection Cooling of Microelectronic Circuit Components. Doctoral Dissertation, Bursa Uludağ University, Bursa, Turkey, 1997. [Google Scholar]
- Meinders, E.R.; Van Der Meer, T.H.; Hanjalić, K. Local convective heat transfer from an array of wall-mounted cubes. Int. J. Heat Mass Transf. 1998, 41, 335–346. [Google Scholar] [CrossRef]
- Xu, G.P.; Tou, K.W.; Tso, C.P. Numerical modelling of turbulent heat transfer from discrete heat sources in a liquid-cooled channel. Int. J. Heat Mass Transf. 1998, 41, 1157–1166. [Google Scholar] [CrossRef]
- Pulat, E.; Öge, A.İ.; Karagöz, İ. Three-dimensional simulation of flow and temperature distribution over a surface-mounted block. In Proceedings of the ULIBTK’99 12th Turkish National Conference on Thermal Sciences and Technologies, Conference Proceeding, Sakarya, Türkiye, 28–29 February 2000; Volume 1. [Google Scholar]
- Etemoğlu, A.B.; İşman, M.K.; Pulat, E.; Can, M. Analysis of cooling of single-chip electronic devices under laminar and turbulent flow. Eng. Mach. 2004, 45, 18–28. [Google Scholar]
- Mathews, R.N.; ve Balaji, C. Numerical simulation of conjugate, turbulent mixed convection heat transfer in a vertical channel with discrete heat sources. Int. Commun. Heat Mass Transf. 2006, 33, 908–916. [Google Scholar] [CrossRef]
- Ratnam, G.S.; Vengadesan, S. Performance of two-equation turbulence models for prediction of flow and heat transfer over a wall-mounted cube. Int. J. Heat Mass Transf. 2008, 51, 2834–2846. [Google Scholar] [CrossRef]
- Gavara, M. Natural convection in a vertical channel with arrays of flush-mounted heaters on opposite conductive walls. Numer. Heat Transf. Part A Appl. 2012, 62, 111–135. [Google Scholar] [CrossRef]
- Aylı, E.; Bayer, O.; Aradağ, S. Experimental investigation and CFD analysis of rectangular profile fins in a square channel for forced convection regimes. Int. J. Therm. Sci. 2016, 109, 279–290. [Google Scholar] [CrossRef]
- Durgam, S.; Venkateshan, S.P.; Sundararajan, T. Experimental and numerical investigations on optimal distribution of heat source array under natural and forced convection in a horizontal channel. Int. J. Therm. Sci. 2017, 115, 125–138. [Google Scholar] [CrossRef]
- Umur, H.; Yemenici, O.; Umur, Y.; Sakin, A. Flow and heat transfer characteristics over rectangular blocked surfaces. Exp. Heat Transf. 2017, 30, 192–204. [Google Scholar] [CrossRef]
- Güngör, M.A. Thermal Analysis of Multi-Chip and Variable Cross-Section Electronic Systems. Master’s Thesis, Bursa Uludağ University, Bursa, Turkey, 2020. [Google Scholar]
- Amghar, K.; Filali, A.; Louhibi, M.A.; Bouali, H.; Salhi, N.; Salhi, M. Numerical study of turbulent heat transfer in a horizontal channel provided with square blocks: Effect of the inter-blocks spacing. J. Therm. Eng. 2021, 7, 650–665. [Google Scholar] [CrossRef]
- Sherry, M.J.; Jacono, D.L.; Sheridan, J. Flow separation characterization of a forward-facing step immersed in a turbulent boundary layer. In Proceedings of the TSFP6 Sixth International Symposium on Turbulence and Shear Flow Phenomena, Seoul, Republic of Korea, 22–24 June 2009. [Google Scholar]
- Meinders, E.R.; Hanjalic, K.; Martunizzi, R.C. Experimental study of the local convection heat transfer from a wall-mounted cube in turbulent channel flow. ASME J. Heat Transf. 1999, 121, 564–573. [Google Scholar] [CrossRef]
- Defraeye, T.; Blocken, B.; Carmeliet, J. CFD analysis of convective heat transfer at the surfaces of a cube immersed in a turbulent boundary layer. Int. J. Heat Mass Transf. 2010, 53, 297–308. [Google Scholar] [CrossRef]
- Shaeri, M.R.; Yaghoubi, M.; Jafarpur, K. Heat transfer analysis of lateral perforated fin heat sinks. Appl. Energy 2009, 86, 2019–2029. [Google Scholar] [CrossRef]
- Davalath, J.; Bayazıtoğlu, Y. Forced convection cooling across rectangular blocks. J. Heat Transf. 1987, 109, 321–328. [Google Scholar] [CrossRef]
- Meinders, E.R.; Van Der Meer, T.H.; Hanjalić, K.; Lasance, C.J.M. Application of infrared thermography to the evaluation of local convective heat transfer on arrays of cubical protrusions. Int. J. Heat Fluid Flow 1997, 18, 152–159. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Changcharoen, W.; Eiamsaard, S. Numerical investigation of turbulent heat transfer in channels with detached rib-arrays. Heat Transf. Asian Res. 2011, 40, 431–447. [Google Scholar] [CrossRef]
- Gupta, S.K.; Rawat, M.K.; Kukreja, N. Analysis of heat transfer enhancement of electronic chip using CFD. Int. J. Sci. Technol. Res. 2019, 8, 1017–1020. [Google Scholar]
- Anwar-ul-Haque, F.A.; Yamada, S.; Chaudhry, S.R. Assessment of turbulence models for turbulent flow over a backward-facing step. In Proceedings of the WCE2007 World Congress on Engineering, London, UK, 2–4 July 2007; Volume II. [Google Scholar]
- Park, T.H.; Choi, H.G.; Yoo, J.Y.; Kim, S.J. Streamline upwind numerical simulation of two-dimensional confined impinging slot jets. Int. J. Heat Mass Transf. 2003, 46, 251–262. [Google Scholar] [CrossRef]
- Jaramillo, J.E.; Pérez-Segarra, C.D.; Oliva, A.; Claramunt, K. Analysis of different RANS models applied to turbulent forced convection. Int. J. Heat Mass Transf. 2007, 50, 3749–3766. [Google Scholar] [CrossRef]
- Lu, B.; Jiang, P.-X. Experimental and numerical investigation of convection heat transfer in a rectangular channel with angled ribs. Exp. Therm. Fluid Sci. 2006, 30, 513–521. [Google Scholar] [CrossRef]
- Bouchenafa, R.; Saim, R.; Abboudi, S. Numerical study of forced convection in a turbulent heat sink made of several rows of blocks of square form. Heat Mass Transf. 2015, 51, 1301–1311. [Google Scholar] [CrossRef]
- Guo, Z.-Y.; Li, D.-Y.; Liang, X.-G. Thermal effects on the recirculation zone in sudden-expansion gas flows. Int. J. Heat Mass Transf. 1996, 39, 2619–2624. [Google Scholar] [CrossRef]
- Driver, D.M.; Seegmiller, H.L. Features of a reattaching turbulent shear layer in divergent channel flow. AIAA J. 1985, 23, 163–171. [Google Scholar] [CrossRef]
- Gürses, D.; Pulat, E. Computational investigation of pressure gradient effects on heat transfer from electronic chips mounted on a surface under turbulent flow. In Proceedings of the ULIBTK’21 23rd Heat Science and Technology Congress, Conference Proceeding, Gaziantep, Türkiye, 8–10 September 2021; Volume 1. [Google Scholar]
- Ateş, M. Effects of External Turbulence and Pressure Gradient on Heat Transfer in Backward-Facing Step Flows. Master’s Thesis, Bursa Uludağ University, Bursa, Turkey, 2015. [Google Scholar]
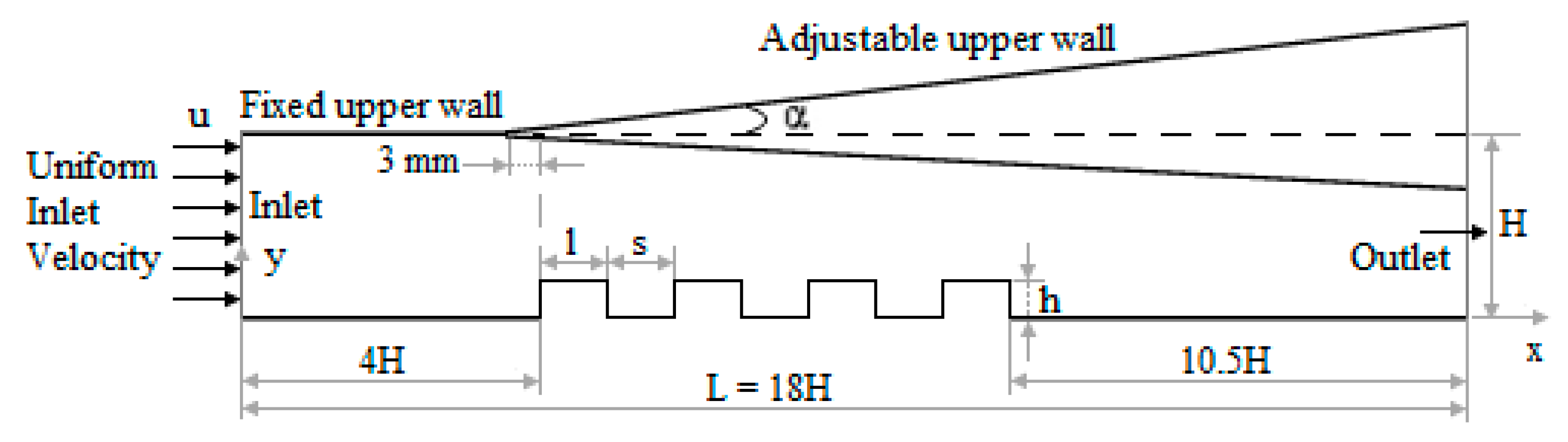



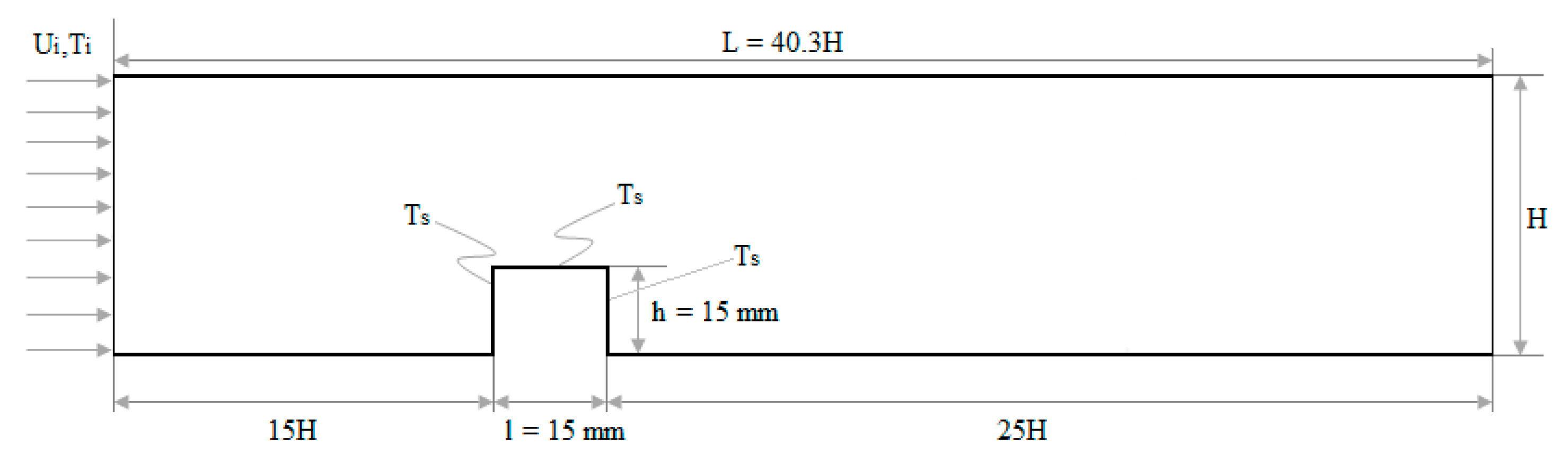







| Inlet | Block Surfaces | Channel Upper Surface | Channel Lower Surface | Outlet | |
|---|---|---|---|---|---|
| Inlet velocity (m/s, uniform profile) | 3.607, 5.42, 7.21 | 0 | 0 | 0 | - |
| Inlet temperature (K, uniform profile) | 293 K | 342 K | Adiabatic | Adiabatic | - |
| Pressure (Pa) | - | - | - | - | 0 |
| H = 4 h (This Study) | H = 3.33 h (Meinders et al., 1998 [4]) | |
|---|---|---|
| Blockage ratio [h/H] | 0.25 | 0.30 |
| Expansion ratio [H/(H − h)] | 1.33 | 1.43 |
| Aspect ratio [l/h] | 2.00 | 1.00 |
| Packaging density [s/l] | 1.00 | 1.00 |
| Mesh Structure | Course | 96,387 |
| Medium | 141,317 | |
| Fine (chosen) | 194,892 |
| Mesh | |||
|---|---|---|---|
| Fine | 1.5225959 | 0.0297 | 4.99845 |
| Medium | 2.704431 | 0.625079 | 6.41723 |
| Coarser | 3.567 | 0.8237 | 7.3537 |
| Angle | Average Nusselt No | ||
|---|---|---|---|
| Re = 6000 | Re = 9015 | Re = 11,993 | |
| α = −2° | 47.6 | 64.57 | 80.07 |
| α = 0° | 43.12 | 58.1 | 71.4 |
| α = 2° | 39.64 | 53.29 | 65.62 |
| α = 4° | 36.8 | 49.8 | 61.66 |
| α = 6° | 33.65 | 45.53 | 56.4 |
| Velocity (m/s) | Inclination Angle (Degree) | RL 1 (cm) | RL 2 (cm) |
|---|---|---|---|
| 3.607 | α = −2° | 0.9477 | 3.9591 |
| α = 0° | 0.8961 | 4.7579 | |
| α = 2° | 0.8136 | 6.5365 | |
| α = 4° | 0.6883 | 14.0766 | |
| α = 6° | 0.5422 | 19.6318 | |
| 5.42 | α = −2° | 0.9477 | 3.9135 |
| α = 0° | 0.9175 | 4.7153 | |
| α = 2° | 0.8345 | 6.3903 | |
| α = 4° | 0.6675 | 13.4918 | |
| α = 6° | 0.5213 | 20.0286 | |
| 7.21 | α = −2° | 0.9477 | 3.8907 |
| α = 0° | 0.9175 | 4.6726 | |
| α = 2° | 0.8554 | 6.2859 | |
| α = 4° | 0.7092 | 12.8443 | |
| α = 6° | 0.5004 | 20.2375 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gürses, D.; Pulat, E. Effect of Pressure Gradient on Flow and Heat Transfer over Surface-Mounted Heated Blocks in a Narrow Channel. Appl. Sci. 2025, 15, 9099. https://doi.org/10.3390/app15169099
Gürses D, Pulat E. Effect of Pressure Gradient on Flow and Heat Transfer over Surface-Mounted Heated Blocks in a Narrow Channel. Applied Sciences. 2025; 15(16):9099. https://doi.org/10.3390/app15169099
Chicago/Turabian StyleGürses, Dildar, and Erhan Pulat. 2025. "Effect of Pressure Gradient on Flow and Heat Transfer over Surface-Mounted Heated Blocks in a Narrow Channel" Applied Sciences 15, no. 16: 9099. https://doi.org/10.3390/app15169099
APA StyleGürses, D., & Pulat, E. (2025). Effect of Pressure Gradient on Flow and Heat Transfer over Surface-Mounted Heated Blocks in a Narrow Channel. Applied Sciences, 15(16), 9099. https://doi.org/10.3390/app15169099







