Research and Verification of the One-Step Resonance and Transport Methods Based on the OpenMOC Code
Abstract
1. Introduction
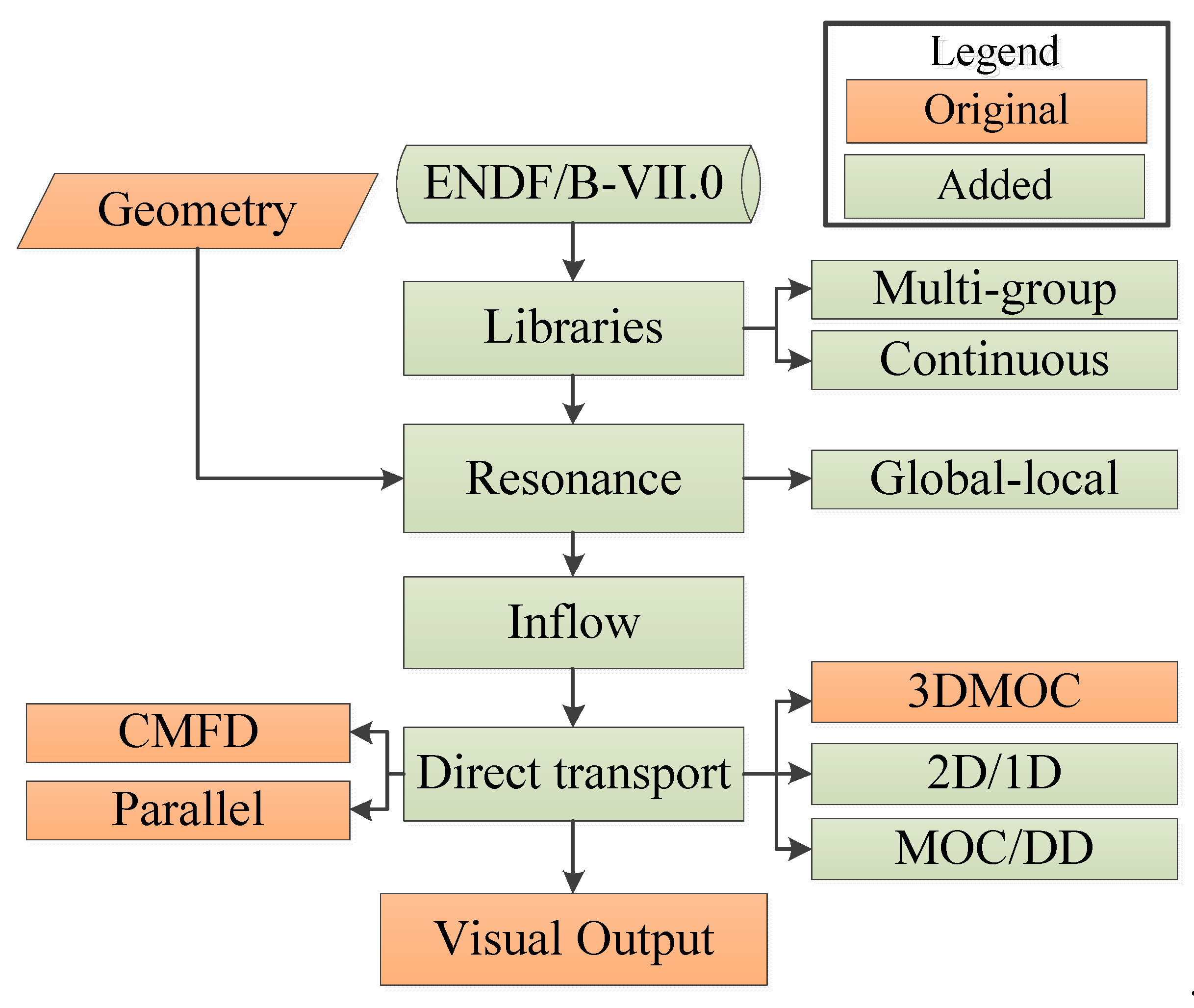
2. Framework of the OpenMOC Code
3. Global–Local Resonance Method
3.1. Library
3.1.1. Multi-Group Library
3.1.2. Ultra-Fine Group Library
3.2. Global Method
3.3. Local Method
4. Direct Transport Method
5. Numerical Results
5.1. Macro C5G7 Benchmark
5.1.1. Sensitivity Analysis of Computational Parameters
5.1.2. Results of the C5G7 Benchmark with Three Direct Transport Methods
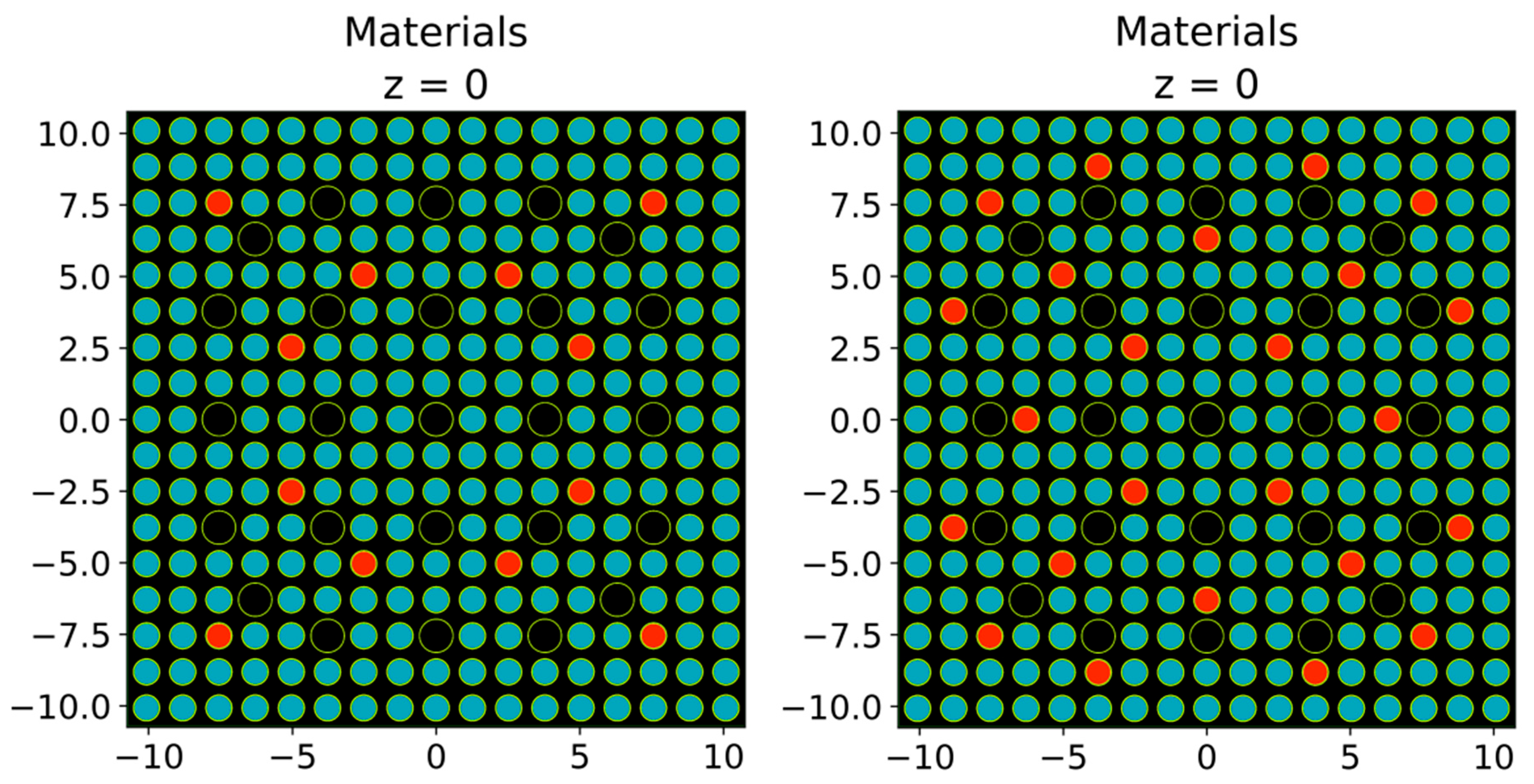
5.2. Micro VERA-1 Benchmark
5.3. Micro VERA-2 Benchmark
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cho, J.Y.; Kim, K.S.; Kim, H.Y.; Lee, C.C.; Zee, S.Q.; Joo, H.G. DeCART v1.2 User’s Manual. KAERI/TR-3438/2007. 2007. Available online: https://inis.iaea.org/records/7kcex-vk911 (accessed on 1 August 2025).
- Park, H.J.; Kim, K.S.; Hong, S.G.; Song, J.S. An improved DeCART library generation procedure with explicit resonance interference using continuous energy Monte Carlo calculation. Ann. Nucl. Energy 2017, 105, 95–105. [Google Scholar] [CrossRef]
- Collins, B.; Kochunas, B.; Jabaay, D.; Downar, T.; Martin, W. Verification of MPACT: Michigan parallel characteristics transport code. Trans. Am. Nucl. Soc. 2013, 108, 795–798. [Google Scholar]
- Choi, N.; Park, H.; Lee, H.; Jae, S.; Jeon, S.; Joo, H.G. Recent Capability and Performance Enhancements of the Whole-core Transport Code nTRACER. In Proceedings of the PHYSOR2020—International Conference on Physics of Reactors: Transition to a Scalable Nuclear Future, Cambridge, UK, 29 March–2 April 2020. [Google Scholar]
- Jung, Y.; Lee, C. Performance Improvement of the Linear System Solver for CMFD Acceleration in PROTEUS-MOC; Transactions of the American Nuclear Society: Minneapolis, MN, USA, 2019. [Google Scholar]
- Boyd, W. Massively Parallel Algorithms for Method of Characteristics Neutral Particle Transport on Shared Memory Computer Architecures; Massachusetts Institute of Technology: Cambridge, MA, USA, 2014. [Google Scholar]
- Gunow, G. Full Core 3D Neutron Transport Simulation Using the Method of Characteristics with Linear Sources; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018. [Google Scholar]
- Schenider, D.; Dolci, F.; Gabriel, F.; Palau, J.-M.; Guillo, M.; Pothet, B. APOLLO3®: CEA/DEN Deterministic Multi-Purpose Code for Reactor Physics Analysis. In Proceedings of the PHYSOR 2016–Unifying Theory and Experiments in the 21st Century, Sun Valley, ID, USA, 1–5 May 2016. [Google Scholar]
- Choi, S.; Choe, J.; Hoang, K.; Lee, W.; Kim, W.; Kim, H. Recent Development Status of Neutron Transport Code STREAM. In Proceedings of the Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Republic of Korea, 23–24 May 2019. [Google Scholar]
- Zhao, C.; Liu, Z.; Liang, L.; Chen, J.; Cao, L.; Wu, H. Improved leakage splitting method for the 2D/1D transport calculation. Prog. Nucl. Energy 2018, 105, 202–210. [Google Scholar] [CrossRef]
- Liu, Z.; He, Q.; Zu, T.; Cao, L.; Wu, H.; Zhang, Q. The pseudo-resonant-nuclide subgroup method based global–local self-shielding calculation scheme. J. Nucl. Sci. Technol. 2018, 55, 217–228. [Google Scholar] [CrossRef]
- Zhang, T.; Xiao, W.; Yin, H.; Sun, Q.; Liu, X. VITAS: A multi-purpose simulation code for the solution of neutron transport problems based on variation nodal methods. Ann. Nucl. Energy 2022, 178, 109335. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, Q.; Liang, L.; Song, P.; Zhao, Q. Investigation on the modeling capability of ALPHA code for fuel rod deformation. Ann. Nucl. Energy 2022, 169, 108892. [Google Scholar] [CrossRef]
- Boyd, W.; Shaner, S.; Li, L.; Forget, B.; Smith, K. The OpenMOC Method of Characteristics Neutral Particle Transport Code. Ann. Nucl. Energy 2014, 68, 43–52. [Google Scholar] [CrossRef]
- Cao, L.; Liu, Z.; Cao, L.; He, Q.; Zhou, X. Implementation and Application of the CSG Method in the NECP-X Code. In Proceedings of the ICONE-27, 27th International Conference on Nuclear Engineering, Ibaraki, Japan, 19–24 May 2019. [Google Scholar]
- Suslov, I. Improvements in the long characteristics method and their efficiency for deep penetration calculations. Prog. Nucl. Energy 2001, 39, 223–242. [Google Scholar] [CrossRef]
- Yamamoto, A. Generalized coarse-mesh rebalance method for acceleration of neutron transport calculations. Nucl. Sci. Eng. 2005, 151, 274–282. [Google Scholar] [CrossRef]
- Choi, N.; Kang, J.; Joo, H. Preliminary Performance Assessment of GPU Acceleration Module in nTRACER. In Proceedings of the Transactions of the Korean Nuclear Society Autumn Meeting, Yeosu, Republic of Korea, 25–26 October 2018. [Google Scholar]
- Gunow, G.; Shanner, S.; Forget, B.; Smith, K. Reducing 3D MOC Storage Requirements with Axial On-the-fly Ray Tracing. In Proceedings of the PHYSOR 2016, Sun Valley, ID, USA, 1–5 May 2016. [Google Scholar]
- Stimpson, S.; Young, M.; Collins, B.; Kelley, B.; Downar, T. Assessment and Improvement of the 2D/1D Method Stability in DeCART. In Proceedings of the M&C 2013, Sun Valley, ID, USA, 5–9 May 2013. [Google Scholar]
- Zheng, Y.; Choi, S.; Lee, D. A new approach to three-dimensional neutron transport solution based on the method of characteristics and linear axial approximation. J. Comput. Phys. 2017, 350, 25–44. [Google Scholar] [CrossRef]
- IAEA. WIMS-D Library Update; IAEA: Vienna, Austria, 2007; ISBN 92–0–105006–2. [Google Scholar]
- Macfarlane, R.; Muir, D.W.; Boicourt, R.M.; Kahler, A.C., III; Conlin, J.L. NJOY2016: Nuclear Data Processing System, Version 2016; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 2018; LA-UR-17-20093. [Google Scholar]
- Liu, Z.; He, Q.; Wen, X.; Zu, T.; Cao, L.; Wu, H. Improvement and optimization of the pseudo-resonant-nuclide subgroup method in NECP-X. Prog. Nucl. Energy 2018, 103, 60–73. [Google Scholar] [CrossRef]
- Sugimura, N.; Yamamoto, A. Evaluation of dancoff factors in complicated geometry using the method of characteristics. J. Nucl. Sci. Technol. 2006, 43, 1182–1187. [Google Scholar] [CrossRef]
- OECD. Calculations Without Spatial Homogenization. MOX Fuel Assembly 3-D Extension Case. Nuclear Science, NEA/NSC/DOC(2005)16.



| Cases | Input Parameters | keff | PinPower Max Diff | PinPower RMS Diff | ||||
|---|---|---|---|---|---|---|---|---|
| Ray Width/cm | Azi/pol Angles | Reflector FSRs | Fuel FSRs | Axial Height/cm | ||||
| 1 | 0.05 | 32/6 | 10 × 10 | 4 × 8 | 3.57 | 1.14297 | 2.96% | 1.01% |
| 2 | 0.03 | 32/6 | 10 × 10 | 4 × 8 | 3.57 | 1.14296 | 2.94% | 1.01% |
| 3 | 0.01 | 32/6 | 10 × 10 | 4 × 8 | 3.57 | 1.14296 | 2.94% | 1.01% |
| 4 | 0.03 | 64/6 | 10 × 10 | 4 × 8 | 3.57 | 1.14318 | 2.96% | 1.03% |
| 5 | 0.03 | 128/6 | 10 × 10 | 4 × 8 | 3.57 | 1.14338 | 2.96% | 1.04% |
| 6 | 0.03 | 64/6 | 8 × 8 | 4 × 8 | 3.57 | 1.14324 | 3.63% | 1.17% |
| 7 | 0.03 | 64/6 | 5 × 5 | 4 × 8 | 3.57 | 1.14331 | 4.30% | 1.36% |
| 8 | 0.03 | 64/6 | 8 × 8 | 4 × 16 | 3.57 | 1.14328 | 3.56% | 1.15% |
| 9 | 0.03 | 64/6 | 8 × 8 | 6 × 16 | 3.57 | 1.14329 | 3.56% | 1.15% |
| 10 | 0.03 | 64/6 | 8 × 8 | 4 × 16 | 7.14 | 1.14366 | 3.28% | 1.08% |
| 11 | 0.03 | 64/6 | 8 × 8 | 4 × 16 | 1.785 | 1.14323 | 3.63% | 1.17% |
| Cases | Input Parameters | keff | PinPower Max Diff | PinPower RMS Diff | |||
|---|---|---|---|---|---|---|---|
| Axial Spacing/cm | Axial Source Region Height /cm | Linear Source | Azi/pol Angles | ||||
| 1 | 1.5 | 0.714 | Yes | 32/6 | 1.14287 | 7.23% | 2.23% |
| 2 | 0.75 | 0.714 | Yes | 32/6 | 1.14277 | 2.57% | 0.91% |
| 3 | 0.25 | 0.714 | Yes | 32/6 | 1.14276 | 2.25% | 0.82% |
| 4 | 0.25 | 1.428 | Yes | 32/6 | 1.14279 | 2.18% | 0.73% |
| 5 | 0.25 | 3.57 | Yes | 32/6 | 1.14309 | 4.02% | 0.98% |
| 6 | 0.25 | 0.714 | No | 32/6 | 1.14287 | 3.64% | 1.24% |
| 7 | 0.75 | 0.714 | Yes | 64/6 | 1.14290 | 2.60% | 0.95% |
| 3DMOC | 2D/1D | MOC/DD | |
|---|---|---|---|
| Unrodded | |||
| Eigenvalue difference | −27 pcm | −32 pcm | −17 pcm |
| Pin power RMS difference | 0.91% | 0.83% | 1.04% |
| Pin power MAX difference | 2.57% | 2.32% | 2.86% |
| Calculation time | 11,323 s | 314 s | 1281 s |
| Outer iteration times | 33 | 85 | 47 |
| RodA | |||
| Eigenvalue difference | −2 pcm | −28 pcm | −19 pcm |
| Pin power RMS difference | 0.80% | 0.78% | 1.02% |
| Pin power MAX difference | 2.14% | 2.14% | 2.79% |
| Calculation time | 11,305 s | 295 s | 1289 s |
| Outer iteration times | 33 | 85 | 47 |
| RodB | |||
| Eigenvalue difference | 40 pcm | −35 pcm | −25 pcm |
| Pin power RMS difference | 0.64% | 0.77% | 0.98% |
| Pin power MAX difference | 1.71% | 2.27% | 2.90% |
| Calculation time | 11,364 s | 284 s | 1323 s |
| Outer iteration times | 34 | 85 | 48 |
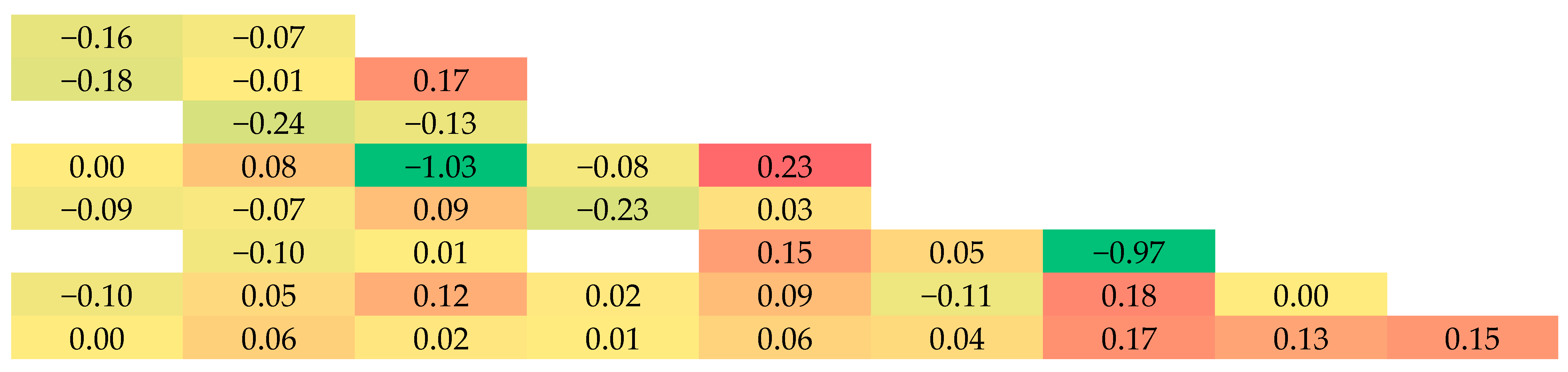
| Cases | Description | keff (KENO-VI) | keff (OpenMOC) | keff Difference/pcm |
|---|---|---|---|---|
| 1A | Fuel, 565 K | 1.18704 ± 5 cpm | 1.18734 | 30 |
| 1B | Fuel, 600 K | 1.18215 ± 7 cpm | 1.18247 | 32 |
| 1C | Fuel, 900 K | 1.17172 ± 7 cpm | 1.17187 | 15 |
| 1D | Fuel, 1200 K | 1.16260 ± 7 cpm | 1.16281 | 21 |
| 1E | IFBA, 600 K | 0.77170 ± 7 cpm | 0.77073 | −97 |
| Cases | Description | keff (KENO-VI) | keff (OpenMOC) | keff Diff /pcm | Pin Power Diff | |
|---|---|---|---|---|---|---|
| Max/% | RMS/% | |||||
| 2A | 565 K | 1.18218 ± 3 cpm | 1.18268 | 50 | 0.20 | 0.07 |
| 2B | 600 K | 1.18336 ± 3 cpm | 1.18392 | 56 | 0.18 | 0.05 |
| 2C | 900 K | 1.17375 ± 3 cpm | 1.17430 | 55 | 0.16 | 0.05 |
| 2D | 1200 K | 1.16559 ± 3 cpm | 1.16604 | 45 | 0.15 | 0.05 |
| 2E | 600 K, 12Pyrex | 1.06963 ± 2 cpm | 1.07051 | 88 | 0.17 | 0.04 |
| 2F | 600 K, 24Pyrex | 0.97602 ± 3 cpm | 0.97692 | 90 | 0.23 | 0.07 |
| 2G | 600 K, 24AIC | 0.84770 ± 3 cpm | 0.84653 | −117 | 0.36 | 0.13 |
| 2H | 600 K, 24B4C | 0.78822 ± 3 cpm | 0.79153 | 331 | 0.54 | 0.14 |
| 2I | Instrument, 600 K | 1.17992 ± 2 cpm | 1.18044 | 52 | 0.19 | 0.05 |
| 2J | Instrument, 900 K, 24Pyrex | 0.97519 ± 3 cpm | 0.97617 | 98 | 0.20 | 0.07 |
| 2K | Zoned, 1200 K, 24Pyrex | 1.02006 ± 3 cpm | 1.02112 | 106 | 0.24 | 0.07 |
| 2L | 80IFBA | 1.01892 ± 2 cpm | 1.01860 | −32 | 0.28 | 0.07 |
| 2M | 128IFBA | 0.93880 ± 3 cpm | 0.93855 | −25 | 0.23 | 0.07 |
| 2N | 104IFBA, 20WABA | 0.86962 ± 3 cpm | 0.86926 | −36 | 0.29 | 0.08 |
| 2O | 12 Gd | 1.04773 ± 2 cpm | 1.04788 | 15 | 1.03 | 0.18 |
| 2P | 24 Gd | 0.92741 ± 2 cpm | 0.92759 | 18 | 1.20 | 0.29 |
| 2Q | Zircaloy Grid | 1.17194 ± 2 cpm | 1.17143 | −51 | 0.57 | 0.14 |
| Average | 44 | 0.37 | 0.10 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Wang, L. Research and Verification of the One-Step Resonance and Transport Methods Based on the OpenMOC Code. Appl. Sci. 2025, 15, 9080. https://doi.org/10.3390/app15169080
Zhao C, Wang L. Research and Verification of the One-Step Resonance and Transport Methods Based on the OpenMOC Code. Applied Sciences. 2025; 15(16):9080. https://doi.org/10.3390/app15169080
Chicago/Turabian StyleZhao, Chen, and Lianjie Wang. 2025. "Research and Verification of the One-Step Resonance and Transport Methods Based on the OpenMOC Code" Applied Sciences 15, no. 16: 9080. https://doi.org/10.3390/app15169080
APA StyleZhao, C., & Wang, L. (2025). Research and Verification of the One-Step Resonance and Transport Methods Based on the OpenMOC Code. Applied Sciences, 15(16), 9080. https://doi.org/10.3390/app15169080




