Single-Objective Surrogate Models for Continuous Metaheuristics: An Overview

Abstract

This paper presents a comprehensive overview of single-objective surrogate models for continuous metaheuristics, addressing computationally expensive optimization problems. Metaheuristics typically require numerous objective function evaluations that become impractical with expensive simulations. Surrogate-assisted metaheuristics address this by substituting costly evaluations with lower-cost approximations. We examine three fundamental approaches: regression models that predict exact objective function values, classification models that categorize solutions, and ranking models focusing on relative ordering. We analyze various surrogate types and discuss their strengths and limitations. We discuss structural approaches from global to local models, sample management strategies, and recent advances in ensemble methods and adaptive sampling techniques.

1. Introduction

In real-world engineering and scientific applications, optimization problems may involve objective functions that are computationally expensive to evaluate. These expensive optimization problems typically require many numerical calculations, complex simulations, or physical experiments to evaluate candidate solutions. For example, in aerospace engineering, evaluating the aerodynamic performance of an aircraft design can require complicated computational fluid dynamics simulations that take hours or even days to complete. Similarly, in structural engineering, finite element analysis to evaluate building performance under various conditions can be very time consuming.

Metaheuristics are a broad family of optimization techniques [1,2] which are applied to approximately solve problems for which it is unacceptably costly to find exact solutions. Typical metaheuristics, e.g., evolutionary algorithms, usually require numerous evaluations of solutions to find nearly optimal ones. Hence, despite their global search capabilities and robustness, the direct application of metaheuristics to computationally expensive optimization problems may become impractical. This limitation has motivated the development of surrogate-assisted metaheuristics which evaluate solutions using a lower-cost approximation to the original optimization problem. In addition to the low simulation cost, it is expected that the use of surrogate models will allow the metaheuristic to yield results of comparable or better quality and at a lower cost than in the case when no surrogate model is used.

Surrogate models, also known as metamodels, are built using a limited number of evaluations of the original optimization problem. The effectiveness of surrogate-assisted metaheuristics depends on several components: the choice and management of surrogate models, the strategy for selecting solutions for evaluation with the original optimization problem formulation, the method to integrate the surrogate model with the metaheuristic, and other problem-specific issues such as high dimensionality and constraints. In recent years, researchers have made significant advances in these areas, developing sophisticated approaches to balance model accuracy, computational efficiency, and optimization performance.

This review is aimed at providing an in-depth analysis of surrogate-assisted metaheuristics for single-objective optimization, focusing on recent developments and current challenges.

The field of surrogate-assisted metaheuristics has been reviewed from several perspectives, each providing a unique lens through which to understand this rapidly growing area.

Early and influential surveys on surrogate-assisted evolutionary algorithms, such as the review by Jin [3], established a classification of model management strategies. This approach, which is referenced in [4], classifies algorithms into individual-based, generation-based, and population-based strategies, focusing on how and when the expensive, real objective function is called alongside the surrogate. While the review [4] acknowledges this framework, it organizes its own review of recent advances around a different primary structure: the distinction between managing a single surrogate and multiple surrogates.

Tong et al. [5] introduce a new taxonomy for surrogate models used in single-objective optimization. Their classification is based on the nature of the prediction the model provides, which they argue is a critical consideration that widely influences the design of the entire algorithm. The authors’ primary division separates models into two main classes. The first class is Absolute Fitness Models, which directly approximate the fitness function values of candidate solutions. The second class consists of Relative Fitness Models, which estimate the relative rank or preference of candidates rather than their exact fitness values. Each of these two categories is further broken down into two subcategories: the absolute category is split into regression-based and similarity-based models, while the relative category is divided into rank-based and classification-based models.

The more recent review by He et al. [6] provides an overview from a different perspective. The authors categorize existing Surrogate-Assisted Evolutionary Algorithms according to the type of objective functions and constraints. This results in a framework covering single-objective unconstrained, single-objective constrained, multi-objective unconstrained, and multi-objective constrained problems. This problem-centric approach shifts the focus from how the model is managed to what kind of problem the algorithm is designed to solve.

The review by Liang et al. [7] organizes its survey around the construction and management of the surrogate models themselves. The authors’ primary division is based on the number of models used, distinguishing between single and multiple surrogate-assisted algorithms. These categories are further broken down by scope into global and local models. The paper also classifies model management based on data handling, differentiating between offline strategies that use only historical data and online strategies that can generate new data during optimization.

This review is structured to guide researchers through a decision-making process rooted in the core components of a surrogate-assisted system. Our organizational principle follows the logical steps of designing such a system: first, we review the fundamental approximation tasks a surrogate can perform—regression, classification, or ranking (Section 3). Second, we catalog the specific model types suited for these tasks, evaluating their characteristics and trade-offs (Section 4). Third, we explore the model’s architectural structure, from simple global models to complex ensembles and hierarchical frameworks (Section 5). Finally, we discuss the dynamic management strategies required for their use, including sampling and forgetting mechanisms (Section 6). This structure is intended to serve as a practical roadmap for understanding and implementing surrogate models.

2. Roles and Benefits of Surrogate Models

2.1. Methods to Express Quality of Points

Metaheuristics are methods designed to traverse the search space $\Omega$ and seek good solutions. Example search spaces include vectors of bits, vectors of real numbers, permutations, or graphs. Each point in the search space is assigned a quality measure. The search aims to find points with the best possible quality value.

A straightforward formalization of the quality measure is to define the objective function $q:\Omega \to \mathcal{R}$ that evaluates the points from the search space. The search is aimed at finding the global minimum of the objective function, i.e., to find points $x^{*}$ that satisfy the condition $\nexists y\in \Omega :q\left(y\right)<q\left(x^{*}\right)$. While a single objective function g(x) provides a direct quality measure, in cases when its computational cost is high, it can be approximated. This approximation can take three fundamental forms—regression, classification, or ranking—as visually summarized in Figure 1.

2.2. Quality-Based Decisions Within the Metaheuristics Framework

Metaheuristics traverse the search space iteratively. In each iteration of a metaheuristic, the algorithm generates a population which contains m points from $\Omega$. In the general context of metaheuristics [1], this step is called diversification, but in evolutionary computation, it is usually referred to as genetic operators. Points generated by the diversification are evaluated and their history is accumulated into the state S of the algorithm by the learning procedure. The state may take various forms: for example, in evolutionary algorithms or in the differential evolution, the state is equivalent to the population. In methods like EDA or CMA-ES, the state contains the parameters of the probability distribution to generate new points during diversification.

If the state contains points from the search space, the diversification procedure takes as input a set P that contains k points from the search space. These points are sampled from the state by the intensification procedure. Examples are the selection process in evolutionary computation and the preparation of points for the mutation in the differential evolution algorithm.

After the diversification is completed, the learning procedure updates the state. In evolutionary computation, the state update is simply the new population, but in CMA-ES, the learning process consists in updating the normal distribution parameters.

The quality of points processed by metaheuristics is used for performing state learning and intensification. For example, selection in evolutionary algorithms reproduces better points with a higher probability. Depending on the particular selection procedure, the selection probability is either proportional to the fitness of individuals (which is usually equal to the objective function) or to the individuals’ ranks (which are assigned after sorting the population). In CMA-ES, ranks of newly generated points are used to update the probability distribution parameters. In differential evolution, the state is updated by comparing the current population with the newly generated offspring.

Hence, when assisted by the surrogate model, the metaheuristic can test more points from the search space within the assumed budget of the true quality evaluations. This increases the chance of achieving higher quality results, thanks to using the surrogate model.

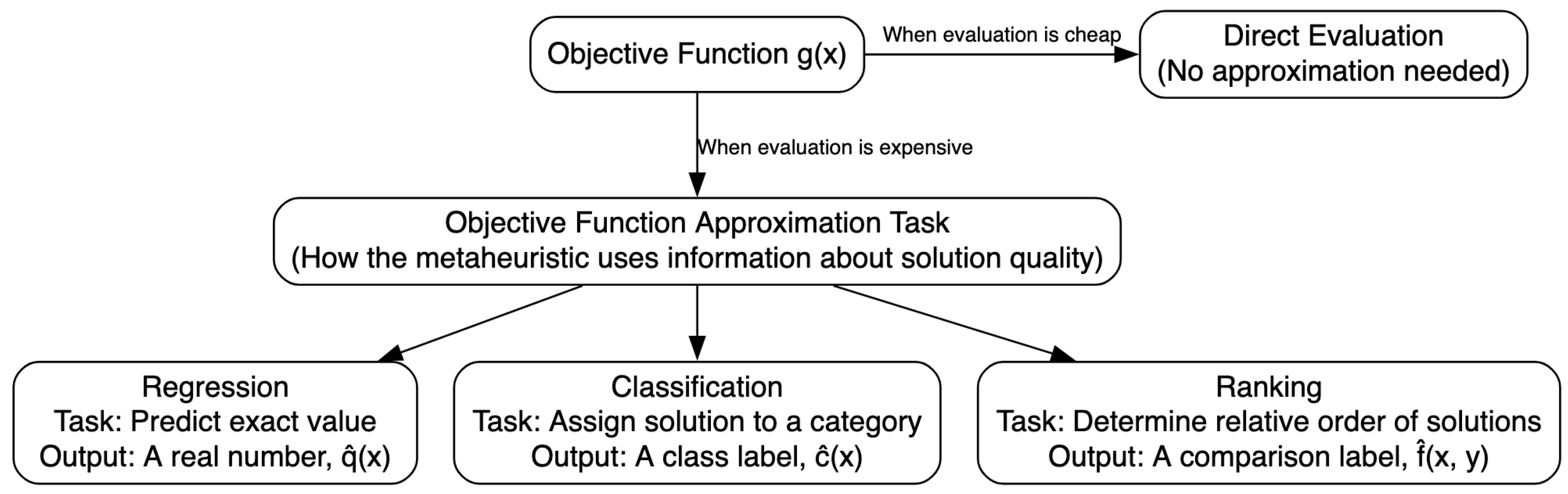
3. Types of Approximation Tasks for Surrogate Models

3.1. Regression Models

Depending on the needs of a particular metaheuristic, the quality of points can be surrogated in several different modes. Perhaps the most natural way of defining a surrogate model is to approximate the objective function

$$q:\Omega \to \mathbb{R}$$

(1)

with the surrogate model $\widehat{q}:\Omega \to \mathbb{R}$.

Regression-based surrogate models approximate the actual objective function values of candidate solutions. They have been widely adopted in single-objective surrogate-assisted evolutionary algorithms [4,7,8,9]. By determining a mapping between the decision variables and their corresponding objective function values, models like these allow quality predictions for new solutions without evaluations of the original objective function [3].

The major advantage of regression-based surrogate models lies in their ability to directly predict the objective function, enabling precise comparisons between candidate solutions [10]. This is particularly valuable when the exact quality values are needed for algorithm operations beyond mere ranking or classification. Moreover, regression models often provide useful information about the landscape’s characteristics, helping to guide the search more effectively [11].

Recent work has shown enhancements that further boost regression model performance in single-objective surrogate-assisted metaheuristics. These include adaptive sampling methods aimed at improving the accuracy of the model in critical regions of the search space [12], ensemble approaches that combine multiple regression models to improve robustness [12], and multi-surrogate frameworks that exploit the strengths of different regression methods [13], where the authors proposed an efficient global optimization algorithm that uses multiple surrogate models to improve prediction reliability and reduce the risk of poor performance from any single model. The importance of surrogate diversity and model selection strategies underlying such frameworks has also been reviewed in earlier surveys [14]. Another example is SAMSO [15], which uses a RBF surrogate combined with a self-improvement filtering rule to reduce evaluations in high-dimensional spaces.

For problems with computationally expensive objective functions, regression models can be particularly beneficial, as they can significantly reduce the number of actual function evaluations needed [16]. However, the accuracy of these models often deteriorates in high-dimensional spaces or when the objective function landscape is highly complex or contains discontinuities [17]. Techniques such as manifold learning and dimensionality reduction have been proposed to address these challenges, allowing regression models to maintain reasonable accuracy even in high-dimensional spaces [18,19]. A notable example is BDDEA-LDG [20], which employs radial basis function surrogates enhanced by localized data generation and a boosting strategy to improve approximation accuracy and robustness under limited data availability.

3.2. Classification Models

The accurate approximation of the objective function value may be too demanding a task to perform using a reasonably small number of points sampled from the search space. Hence, instead of predicting the objective function values, a reasonable solution would be to categorize solutions into classes such as “promising” and “unpromising”, i.e., to define a mapping

$$c:\Omega \to \mathcal{C}$$

(2)

where $\mathcal{C}$ is the finite set of classes, and to approximate c with a surrogate $\widehat{c}:\Omega \to \mathcal{C}$.

Classification-based surrogate models offer an alternative to regression-based models by focusing on the relative quality relationships among candidate solutions rather than predicting exact objective function values, since, in many metaheuristics, the exact objective values are not necessary for the proper operation of the algorithm [5,21]. For instance, Guo et al. [22] propose a classifier-ensemble-based approach that learns to distinguish promising candidates from inferior ones, enabling effective selection without estimating precise objective values.

Classification-based surrogate models can be particularly advantageous when dealing with noisy or imprecise objective functions. They are typically faster to train and apply, making them suitable for large-scale optimization problems where computational efficiency is critical [5]. Additionally, their binary decision structure contributes to robustness against outliers and label noise, which is especially beneficial in real-world classification scenarios involving uncertainty or data imbalance [23]. They also reduce modeling complexity because classification-based surrogates only need to learn decision boundaries rather than detailed functional mappings [5].

Classification-based surrogates can also be combined with regression-based models to balance exploration and exploitation during optimization. Liu et al. [24] demonstrate such a multi-surrogate framework. The authors show how classification and regression can work together to improve search efficiency in single-objective optimization.

Another common approach is to construct a classifier to determine whether a candidate solution is better or worse than a reference point [25]. This binary classification solution is effective in interactive settings where the absolute measurement of quality may be infeasible [26]. Support vector classification has been proposed as a promising approach to guide evolutionary algorithms in computationally expensive optimization, particularly due to its compatibility with the pairwise selection in differential evolution [27]. In addition, fuzzy classification techniques such as Fuzzy-kNN have been shown to improve solution selection in evolutionary algorithms by softening decision boundaries and handling uncertainty, leading to increased robustness in noisy optimization landscapes [28].

Several studies have shown that classification-based surrogates are a good method for handling constraints. These methods guide the search in a more efficient way because of their ability to differentiate feasible from infeasible regions, reducing wasted evaluations while focusing on high-quality solutions. For instance, a classifier can be trained to predict whether a candidate solution is ’feasible’ or ’infeasible’. Before running an expensive evaluation, the metaheuristic can use this cheap classifier to discard candidates predicted to be infeasible, thereby focusing its budget on promising, feasible areas of the search space.

Handoko et al. [29] introduced Feasibility Structure Modeling to estimate feasibility boundaries dynamically, guiding the search efficiently. Pairwise comparison methods enable solutions to be ranked relative to one another without requiring precise objective function predictions. Naharro et al. [30] implemented a classification-based surrogate-assisted evolutionary algorithm using pairwise comparison to improve optimization efficiency, showing that classification-based surrogates can outperform regression-based models in certain scenarios.

Although advantageous, classification-based surrogate models have their own challenges. Imbalanced training data can compromise performance if “better” solutions are far fewer or more difficult to sample. Techniques such as threshold-moving [27] and cost-sensitive learning [31] have been explored to address these challenges, ensuring that classification boundaries remain meaningful, especially in computationally expensive optimization problems [5].

3.3. Ranking Models

If the metaheuristic refers to the relations in quality between points, then, instead of the objective function, it is sufficient to consider the superiority of points:

$$r:X\times X\to \mathcal{C}$$

(3)

where $\mathcal{C}$ is a finite set of class labels. In the single-objective case, the class labels can be defined as

$$r(x,y)=\left\{\begin{array}{cc}-1\hfill & q\left(x\right)<q\left(y\right)\hfill \\ 1\hfill & q\left(y\right)<q\left(x\right)\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(4)

The surrogate model $\widehat{r}:X\times X\to \mathcal{C}$ approximates the classifier without knowing the exact values of the objective function.

The popularity of ranking-based surrogate models has grown in recent years due to their natural alignment with the selection mechanisms of many evolutionary algorithms [32]. Since most selection operators in evolutionary algorithms (such as tournament selection or truncation selection) primarily depend on the rank order of solutions rather than their absolute fitness values, ranking models can directly support these mechanisms without introducing additional modeling errors [5,33,34].

Ranking-based surrogate models, such as the approximate ranking procedure used in [33], reduce the need for precise objective function estimation and are therefore less affected by errors that would hinder regression-based models. Jin [4] shows how ranking-based approaches can provide more reliable guidance for evolutionary algorithms compared to direct fitness approximation in certain scenarios, especially when exact fitness values are difficult to predict precisely. Loshchilov et al. [34] introduce comparison-based surrogate models that learn to predict relative rankings between pairs of solutions, showing that comparison-based optimizers need comparison-based surrogates to achieve good results. Surrogate-assisted evolutionary algorithms frequently employ ranking-based pre-screening mechanisms to reduce the number of expensive fitness evaluations. Blank and Deb [35] introduce a family of surrogate-assisted algorithms where candidate solutions are ranked using surrogate model predictions, and only the top-ranked individuals are selected for evaluation, thereby improving efficiency in high-dimensional search spaces.

Two main ranking-based surrogate approaches have emerged in evolutionary optimization, as outlined by Tong et al. [5]. The Rank on Transformation approach transforms the original objective space into a probability-based or alternative space, where ranking relationships are preserved but become easier to approximate [36]. Gong et al. [36] demonstrate this by approximating a probability density function, allowing cheaper rank-based surrogate models to guide search strategies. The Learn to Rank approach was introduced by Runarsson [37], who applied ordinal regression in evolutionary computation, where models directly predict ranking rather than absolute fitness values. Loshchilov et al. [34] later advanced the method by integrating RankSVM with CMA-ES and demonstrated its effectiveness on computationally expensive optimization problems.

Building on this paradigm, Lu et al. [38] propose the DESSA algorithm, which incorporates RankSVM within a self-adaptive differential evolution framework to pre-select the most promising trial vectors from multiple candidates. This integration significantly reduces expensive fitness evaluations while maintaining competitive optimization performance in computationally expensive problems.

Recent developments in machine learning have led to more sophisticated ranking models that conceptually inspire surrogate modeling strategies in metaheuristics. Techniques such as learning-to-rank approaches offer improved performance in capturing complex ordering relationships among solutions [5,32]. These methods can handle larger sets of candidates simultaneously, as opposed to traditional pairwise comparison methods that scale poorly with the number of solutions.

Another significant advantage of ranking models is their ability to effectively handle multimodal objective functions [5]. By focusing on relative ordering rather than absolute quality values, these models can maintain the distinction between different local optima, facilitating more diverse exploration of the search space. This property makes ranking models particularly suitable for problems where preserving diversity is crucial for finding the global optimum [39].

On the other hand, the accuracy of rank-based models can be sensitive to the distribution of training samples [33]. When training samples are too closely clustered or too widely dispersed, the model’s ability to differentiate between solutions may get worse. Nonetheless, the focus of ranking-based surrogates on preserving solution orderings makes them powerful in situations where precise objective function approximations are either too costly or too unreliable to obtain.

To provide a more practical illustration of these distinct approaches, Figure 2 visualizes the output of a surrogate model performing each of the three tasks on a sample 1D objective function. The figure highlights how regression aims to approximate the function’s curve, classification creates discrete decision regions, and ranking is used to compare specific candidate solutions.

4. Surrogate Models Types

This section reviews the most common families of surrogate models used in metaheuristics. For a comparative overview of their key characteristics, ideal use cases, and main limitations, the reader is referred to

Table 1. A Comparative overview of surrogate model types.

Model Type	Key Characteristics	Ideal Use Case	Main Limitations
Linear Models	Simple, interpretable, linear functional form, required number of samples grows linearly with dimension.	Baseline models; problems that are approximately linear; early-generation guidance.	Cannot capture complex nonlinear relationships.
Quadratic Models	Captures local curvature; foundational to classical Response Surface Methodology, required number of samples grows quadratically with dimension.	Local refinement during later search stages due to their mathematical properties.	Struggles to represent highly nonlinear or multimodal landscapes globally.
Polynomial Regression	Approximates the objective function using low-order polynomials.	Lower-dimensional problems or scenarios where computational resources are constrained.	Prone to unstable behavior with extreme values and poor accuracy in high-dimensional or nonlinear scenarios.
Neural Networks	A broad class of models with diverse architectures. In the surrogate modeling literature, this most often refers to Multi-Layer Perceptrons, which act as universal approximators capable of learning complex nonlinear relationships.	Problems with highly nonlinear and non-smooth response surfaces.	Requires substantial training data and careful tuning; outputs can saturate, creating uninformative “plateau” regions.
Decision Trees	Partition-based models that recursively divide the search space; often used in ensembles.	Problems with discontinuous or piecewise continuous functions, or those with mixed (continuous and categorical) variables.	The performance of a single tree can be unstable; ensembles require careful configuration.
k Nearest Neighbors	An instance-based “lazy learner” that interpolates predictions from the k closest training samples.	Problems where few assumptions can be made about the underlying function; provides exact interpolation at training points (when using distance weighting).	Prediction can be computationally intensive, as the main processing occurs at query time, not during a separate training phase.
Support Vector Machines	Employs the “kernel trick” to efficiently model nonlinear relationships in a high-dimensional feature space.	Noisy or irregular quality landscapes where good generalization is critical to avoid overfitting.	Performance is highly sensitive to the choice of the kernel function and its parameters, which require careful tuning.
Radial Basis Functions	A combination of radially symmetric basis functions, each centered on a training point.	Accurately modeling highly nonlinear problems; widely used in real-world optimization challenges.	Performance can depend on careful parameter tuning; tends to extrapolate poorly by flattening to zero far from training data.
Kriging (Gaussian Process)	A statistical model that uniquely provides an intrinsic estimate of its own prediction uncertainty along with the prediction itself.	Scenarios where the model’s uncertainty is needed to actively guide the sampling strategy, balancing exploration and exploitation.	The computational cost scales cubically with the number of training samples, making it difficult to apply to large datasets.

at the end of this section.

4.1. Linear Models

Linear models offer several advantages in surrogate-assisted optimization. Their simplicity makes them computationally efficient and easily interpretable, providing transparent insights into variable importance and sensitivities [9]. The training process is straightforward, usually employing ordinary least squares or regularized methods like Ridge or LASSO regression when dealing with high-dimensional problems [40].

Despite their simplicity, linear models have been successfully applied to optimization problems with approximately linear or weakly nonlinear objective functions. They can effectively guide the search in early generations, particularly in high-dimensional spaces where more complex models might suffer from overfitting due to limited samples [3,9].

However, linear models have significant limitations in capturing complex nonlinear relationships that are common in many optimization problems. They typically serve as baseline models or components within ensemble approaches rather than standalone surrogates for complex problems [4,10].

4.2. Quadratic Models

Quadratic models form the foundation of classical response surface methodology and have been widely applied in engineering optimization [41]. By capturing local curvature information, quadratic models provide better approximations than linear models for many real-world problems.

Advances in quadratic modeling for surrogate model-assisted metaheuristics include adaptive sampling strategies that efficiently construct and update surrogate models. Shashaani et al. [42] propose a trust-region-based optimization algorithm using fully quadratic surrogate models and adaptive sampling to ensure model fidelity. Their ASTRO-DF framework dynamically adjusts the sampling effort and trust-region size based on local model accuracy, effectively balancing global exploration and local exploitation.

A key advantage of quadratic models is their mathematical properties that guarantee a unique global optimum, making them particularly suitable for local refinement during later stages of metaheuristic search [43]. However, they struggle to accurately represent highly nonlinear or multimodal landscapes, potentially misleading the search in complex optimization scenarios [44].

To address these limitations, researchers have developed hybrid approaches that employ quadratic models within trust-region frameworks. Such methods, exemplified by approaches like BOBYQA [45], restrict the influence of the quadratic approximation to regions where it is expected to be accurate, thus mitigating the risk of poor global approximation.

4.3. Polynomial Regression

Polynomial regression, also referred to as polynomial response surface (PRS) modeling [46], uses low-order polynomials to approximate the objective function. This method is particularly effective for lower-dimensional problems or when computational resources are constrained. However, its approximation accuracy tends to degrade in high-dimensional or highly nonlinear scenarios [47].

PRS models have been widely studied in single-objective engineering optimization. For instance, Wu et al. [48] evaluated PRS models alongside other surrogate models for solving constrained black-box problems. Their results confirmed that while PRS can be computationally efficient for smooth problems, its performance is generally inferior to RBF-based models in capturing nonlinear behavior. Islam et al. [49] demonstrated the practical utility of polynomial surrogates within a surrogate-assisted bilevel optimization framework. Their method adaptively employed first- and second-order polynomial models alongside Kriging, selecting the best-performing surrogate based on validation error. The results showed that even simple polynomial models can significantly reduce the number of function evaluations while maintaining competitive convergence accuracy across a variety of benchmark problems.

Polynomial regression models tend to present unstable behavior with potentially extreme values. These values can create misleading objective function gradients and draw the metaheuristic search towards suboptimal regions or push it away from promising ones [50].

4.4. Neural Networks

Artificial Neural Networks (ANN) have gained increasing attention as surrogate models due to their ability to learn complex nonlinear relationships [51]. However, training ANN requires a substantial amount of data and careful tuning of the network architecture and hyperparameters.

A challenge with neural network-based surrogates is that they often produce saturated outputs at their activation function limits, creating plateau regions that provide little gradient information for selection [52]. This characteristic can potentially affect the efficiency of evolutionary search, particularly in exploration phases.

In regression-based applications, neural networks predict continuous objective function values through complex nonlinear transformations of input features. This approach is particularly effective for problems with highly nonlinear and non-smooth response surfaces. Jin et al. [17] demonstrate the effectiveness of ANN surrogate models in evolutionary optimization frameworks, particularly for approximating expensive fitness functions in complex engineering applications. Their approach notably reduces computational effort, while incorporating mechanisms—such as evolution control and model fidelity estimation—to mitigate the risk of accuracy loss. Jin and Sendhoff [53] further advance this approach by integrating ANN ensembles with clustering techniques to estimate fitness values within population clusters, significantly enhancing surrogate accuracy while minimizing the number of evaluations.

4.5. Decision Trees

Decision trees and their ensemble variants serve as flexible partition-based surrogate models for evolutionary optimization. These models recursively partition the search space into regions with similar objective function characteristics, enabling the efficient approximation of complex quality landscapes [54].

In regression-based applications, decision tree regression models predict continuous objective function values by partitioning the search space into homogeneous regions. This approach is particularly effective for discontinuous or piecewise continuous objective functions. Zheng et al. [55] propose a data-driven single-objective optimization method that employs random forest regression as a surrogate model. Their approach uses random forest to approximate the objective function, enabling efficient optimization with reduced computational cost by leveraging surrogate predictions to guide the search. Liu et al. [24] introduce a multi-surrogate ant colony optimization algorithm (MiSACO) that employs both radial basis function and least-squares boosting tree surrogates to support search in mixed-variable optimization problems. By combining predictions from these models during selection and local search, MiSACO achieves improved optimization performance, especially in problems with both continuous and categorical variables. More recently, Krawczyk and Arabas [56] have evaluated typical regression-based surrogate models, including Random Forest and XGBoost, within the JADE differential evolution framework. Their empirical study on the CEC2013 benchmark suite demonstrates that decision-tree-based models such as Random Forest and XGBoost also yield improvements in optimization efficiency across high-dimensional landscapes.

For classification-based surrogate modeling, decision tree classifiers identify promising regions in the search space. Naharro et al. [57] apply decision tree classifiers to filter unpromising candidates before simulation evaluations.

4.6. k Nearest Neighbors

The k Nearest Neighbors (kNN) model is an example of a whole family of approaches that derive their predictive capabilities from closeness or similarity relationships in the data space. We shall call them instance-based models. Unlike parametric models that estimate the objective function through fixed functional forms, these models adapt their complexity to the available data, which makes them effective for capturing complex, nonlinear relationships with limited assumptions about the underlying function [58].

Instance-based models make predictions directly from the training samples without constructing a compact model representation. Instead, these “lazy learners” initiate processing at query time, when they analyze neighborhood relations to generate predictions [59]. This approach enables highly adaptive modeling capabilities that can capture local dynamics of the objective function.

Instance-based models often provide exact interpolation values at training points, maintaining accuracy for known objective function values [3]. They are flexible and nonparametric, which allows them to adapt to various landscape characteristics without the need for significant domain knowledge [60]. In addition, many types of these models provide uncertainty estimations that are valuable for balancing exploration and exploitation [61].

The kNN model is frequently used as a surrogate model in metaheuristics to estimate the objective function by interpolating from the k nearest samples using distance-based weighting [5,62]. Tian et al. [63] propose a self-adaptive similarity-based surrogate model that dynamically adjusts the neighborhood configuration based on local quality landscape characteristics, demonstrating enhanced performance in evolutionary optimization tasks. Similarly, Miranda-Varela and Mezura-Montes [64] develop a surrogate-assisted approach using a kNN model to approximate both objective values and constraint violations, evaluating its performance under various constraint-handling techniques. Krawczyk and Arabas [65] integrate kNN into the JADE algorithm, using a fixed neighborhood size based on problem dimensionality and an archive of past evaluations. Their method applies a ranking-based update strategy to maintain surrogate consistency and shows improved convergence on the CEC 2013 benchmarks across multiple settings.

For classification-based surrogate modeling, local classifiers such as support vector machines can be trained on subsets of evaluated individuals selected via kNN search. Zhang et al. [28] propose a fuzzy-classification-assisted selection strategy that uses fuzzy kNN to assign soft membership values for solution quality, allowing nuanced prescreening in single-objective evolutionary optimization. Both methods have shown effectiveness in improving convergence speed and reducing computational cost.

4.7. Support Vector Machines

Support vector regression (SVR), especially the kernel version, has also become a popular surrogate modeling technique. These models are effective for noisy or irregular objective functions because of their ability to handle nonlinear relationships through kernel functions and their generalization capabilities [66].

The fundamental premise of kernel SVR is the “kernel trick”, which implicitly maps data points into a high-dimensional feature space where complex relationships become more tractable. This enables the efficient modeling of nonlinear relationships without explicitly computing transformations in the high-dimensional space [67].

Díaz-Manríquez et al. [68] find SVR to offer a balanced trade-off between accuracy and robustness, although it showed limitations in preserving solution rankings. Extending its application, Shi et al. [69] propose a multi-fidelity surrogate model, Co_SVR, which integrates high- and low-fidelity data using SVR and a specialized kernel structure. Their results show that Co_SVR outperforms traditional surrogates in both numerical benchmarks and engineering applications, confirming the strength of SVR in surrogate-assisted optimization. Krawczyk and Arabas [56] observe that integrating SVR as a surrogate within the JADE algorithm, without a careful tuning of the kernel parameter, does not consistently enhance performance. Contrarily, in some cases it even leads to inferior results compared to the baseline JADE, which highlights the importance of careful surrogate model selection and tuning in evolutionary optimization frameworks.

For classification-based surrogate modeling, the support vector machine (SVM) classifier can be used to distinguish between promising and unpromising regions in the search space. Lu et al. [27] propose the Classification-Assisted Differential Evolution approach, where SVMs are trained to compare parent–offspring pairs and identify better solutions. This strategy avoids wasting resources on evaluations of inferior offspring, significantly reducing the number of objective function evaluations while maintaining the optimization performance. Similarly, Bhattacharjee and Ray [70] employ SVM in a dual role within their constraint handling strategy: a binary SVM classifier is used to identify promising offspring solutions, while SVM ranking models estimates the relative quality of candidates based on partial evaluations. This approach enables the selective evaluation of constraints and objective functions, thereby improving efficiency in constrained, expensive optimization problems.

4.8. Radial Basis Functions

Another popular approach is the radial basis function (RBF) model [71,72], which has the ability to handle highly nonlinear problems more accurately than PRS, but often requires careful parameter tuning [73]. Recent developments have focused on adaptive RBF methods that fine-tune their parameters automatically during the optimization process [74]. These models have shown good performance on various scales and are applied in real-world optimization challenges [72].

Li et al. [74] propose a three-layer RBF method for expensive optimization, while Yi et al. [75] develop a variable fidelity surrogate strategy using RBF networks with promising results. Ren et al. [76] introduce BiS-SAHA, a bi-stage surrogate-assisted hybrid algorithm that enhances search robustness by combining RBF surrogate ensembles with an adaptive hybridization of global and local metaheuristics. Su et al. [77] propose HSBCO, a hybrid surrogate-based constrained optimization method that combines Kriging and RBF surrogates in a two-phase strategy to enhance performance. Regis and Shoemaker [78] demonstrate that RBF-assisted surrogate algorithms, such as DYCORS, can reduce the number of expensive function evaluations needed to find high-quality solutions in high-dimensional black-box optimization problems.

A limitation of standard RBF networks is that they typically flatten toward zero outside the influence radius of basis functions, potentially masking promising regions [79]. This characteristic can affect exploration performance in many metaheuristic algorithms.

In regression-based applications, RBF models approximate the objective function by combining radially symmetric basis functions centered at training points. This approach is particularly effective for problems with isotropic response surfaces. An example of RBF application in surrogate-assisted robust optimization is the work by Ong et al. [80], which integrates RBF models with a max–min evolutionary strategy to efficiently address uncertainty in expensive objective functions. Similarly, Müller et al. [81] propose the SO-MI algorithm, which employs RBF surrogates to solve computationally expensive nonlinear mixed-integer black-box problems.

4.9. Kriging

Kriging has emerged as one of the most popular regression-based surrogates for expensive single-objective optimization [5,7,18]. Beyond the prediction of accurate objective function values, Kriging provides estimates of prediction uncertainty, which proves valuable for model management and sample selection strategies [82]. This uncertainty information helps balance exploration and exploitation during the metaheuristic search process.

A key challenge with Kriging models is that their computational cost scales cubically with the number of training samples, making them difficult to apply to very large training sets [83]. However, various model management strategies have been proposed, such as controlled updates of the model, to mitigate this scalability issue [18].

In regression-based applications, Kriging models have gained significant attention in single-objective optimization due to their ability to model complex, expensive-to-evaluate functions with predictive uncertainty. He et al. [84] proposed a dual-Kriging assisted efficient global optimization (EGO) algorithm that introduces a secondary Kriging model to estimate the probability of successful evaluations, thus preventing optimization halts caused by simulation failures and improving robustness in black-box optimization scenarios. Fu et al. [85] address the curse of dimensionality in Kriging modeling by integrating distance correlation into the model construction process, enhancing its performance in high-dimensional design spaces. Akbari et al. [86] develop KASRA, a Kriging-based surrogate model-driven optimization algorithm featuring an adaptive space reduction mechanism, which dynamically narrows the search space around promising regions to accelerate convergence in global optimization. Dong et al. [87] propose SCGOSR, a surrogate-based global optimization strategy that combines hierarchical space reduction with Kriging surrogates, effectively balancing global exploration and local refinement for computationally expensive problems. Collectively, these approaches exemplify the diversity and evolution of Kriging-assisted strategies tailored to improve efficiency, accuracy, and robustness in single-objective optimization. Awad et al. [88] introduce an improved differential evolution algorithm that integrates an adapted Kriging surrogate model, where the correlation parameter is dynamically tuned using covariance and correlation matrices of the evolving population. This adaptation enables the surrogate to more accurately reflect the objective function’s landscape over time, leading to improved convergence and solution quality in numerical optimization tasks.

4.10. Interpolation and Extrapolation Behavior

The performance of surrogate-assisted metaheuristics is related to the ability of surrogate models to correctly approximate the objective function across the search space. This approximation behavior can be categorized into interpolation and extrapolation—both have an important influence on the search dynamics [89].

Interpolation occurs when we predict the function values of points that lie within the convex hull of the training data [9]. Most surrogate models are quite good in interpolation scenarios, which benefits the exploitation phase of evolutionary algorithms. Gaussian process models provide exact interpolation at training points and maintain smooth transitions between them, enabling local refinement during search [90]. Similarly, kNN models with distance-based weighting settings offer exact interpolation at training points because the weight of a point becomes infinite when the distance is zero. This feature ensures that when evaluating a point in the training set, the model returns the exact known objective function value, while smoothly transitioning between known points based on their relative distances, providing good quality estimates in promising regions during search [4].

The quality of interpolation in surrogate-assisted metaheuristics depends on the density and distribution of training samples. Jin et al. [17] demonstrate that as more training samples are gathered—especially in high-performing regions during later generations—the approximation quality of surrogate models improves. This enhancement helps the selection process to more reliably guide the search toward optimal solutions.

On the other hand, extrapolation describes predicting function values for points outside the convex hull of the training data [9], which is very important during the exploration phase. This is a big problem for most surrogate models as noted in [89]. Without prior knowledge about the function’s behavior, models typically default to conservative predictions in extrapolation regions, which can severely limit the algorithm’s ability to discover promising new areas. Polynomial regression models tend to present unstable behavior with potentially extreme values. These values can create misleading gradients in the optimization problem landscape and draw the search towards suboptimal regions of the domain or even drive the search away from promising regions [50]. Gaussian process models generally revert to their prior mean, potentially flattening the quality landscape in unexplored regions [90]. Neural network-based surrogate models often exhibit degraded performance when extrapolating beyond the training distribution, leading to unreliable predictions. Zhu et al. [91] show that this degradation manifests as increased error in regions of higher extrapolation complexity, which may effectively introduce flat or misleading regions in the surrogate landscape that hinder optimization performance. RBF networks typically flatten toward zero outside the influence radius of basis functions, potentially masking promising regions [79].

These extrapolation limitations directly impact the exploration capability of the search, particularly during early generations when the algorithm must explore unknown regions of the search space. As Liu et al. [92] observe, poor extrapolation can mislead the search, resulting in premature convergence or overlooking promising regions. This is especially problematic in multimodal landscapes where global optima may lie outside initially sampled regions.

Several approaches have been developed to address extrapolation limitations in surrogate-assisted metaheuristics. Models like Gaussian processes and neural network ensembles with uncertainty estimation help evolutionary algorithms identify and manage interpolation versus extrapolation regions within the search space, enabling more informed exploration strategies [93]. Uncertainty prediction information works well with the objective function estimation and selection mechanisms. Acquisition criteria such as expected improvement or upper confidence bounds guide the search toward highly uncertain regions, encouraging the exploration of undersampled spaces [94]. Zhou et al. [95] show that using uncertainty metrics in the selection criteria helps global exploration capabilities.

When there is access to domain expertise, using physical constraints or asymptotic behaviors improves extrapolation results in evolutionary optimization [96]. For example, Koziel and Leifsson [97] demonstrate that physics-based response correction methods like space mapping and shape-preserving transformations improve the surrogate model’s global accuracy, enabling evolutionary algorithms to explore viable solutions outside the initial training domain.

Ensemble models with different extrapolation characteristics have proven valuable for improving prediction accuracy outside training set areas, directly improving exploration in evolutionary algorithms [3]. Liaw et al. [98] propose a dynamic ensemble technique that adaptively weights models based on their estimated performance, enabling more accurate objective function approximation across the search domain.

Adaptive sampling strategies have been developed to enhance surrogate-assisted metaheuristics by expanding the interpolation region and improving model accuracy. Iuliano [99] proposes both objective-driven and error-driven sampling methods that are integrated into evolutionary algorithms to refine surrogate predictions during search. Similarly, Liu et al. [100] introduce a hybrid optimization framework combining CMA-ES and BFGS, where a convex hull-based surrogate model is constructed from recent populations to locally approximate the objective function. This method improves the balance between global exploration and local exploitation by guiding local search in regions where the surrogate model demonstrates high local accuracy.

The balance between interpolation and extrapolation behaviors changes as the metaheuristic search progresses. In early generations, when exploration is very important, the algorithms benefit from surrogate models with strong extrapolation capabilities [101]. As populations converge toward promising regions, the sampling density increases, and the interpolation accuracy becomes more important for the fine-tuning of solutions [102].

This dynamic has led to the development of metaheuristics that transit between different surrogate models in the optimization process [103]. Zhou et al. [95] show that ensemble models implemented into evolutionary algorithms, that have complementary interpolation and extrapolation strengths, achieve superior results in various benchmark problems.

5. Structures of Surrogate Models

The majority of metaheuristics maintain populations of points from the search space. Then, each point or group of points can be assigned its own individual model. Another possibility is to maintain a single common model for the whole population, and also to combine individual models and the common model.

Surrogate models can also be classified into global and local ones. Global models approximate the objective function in the entire domain, whereas local models, in subregions of the domain. Usually, global models are the common ones, and local models are individual ones.

5.1. Global Surrogate Models

Global surrogate models, which are trained on uniformly distributed samples across the search space, offer a comprehensive view that supports broader exploration, making them particularly useful in early optimization phases or when avoiding premature convergence is critical [103,104]. They are useful when the underlying function exhibits relatively smooth behavior, without an excessive number of local optima [6,7]. However, fitting a single model to the entire domain can become computationally expensive, especially when the problem has strong nonlinearity or multimodality [103,105]. In such cases, a global model can struggle to capture the complex local dynamics of the objective function without resorting to highly flexible functional forms or substantially increasing the density of the sampled points [5]. At the same time, local models usually allow for better accuracy in specific regions of the search space [4].

5.2. Local Surrogate Models

Local models can be defined for each individual, or for small groups of individuals, in the population. This approach enables highly specialized approximations but requires the management of computational resources [5,6]. A key advantage is that each model can be tailored to capture local characteristics more precisely than a single global or local model. This concept has been useful in selection-based approaches, where surrogate models assist in parent–offspring comparisons by predicting which offspring are more promising for evaluation. Zhang et al. [28] introduce a fuzzy-classification-assisted selection strategy that employs a fuzzy classification model to distinguish promising from unpromising offspring using fitness-based labels, thereby reducing unnecessary evaluations and improving the efficiency of evolutionary optimization.

Various approaches to local surrogate models include locally weighted regression which uses a distance-based weighting scheme that gives higher importance to data points near the solution of interest. This approach can provide accurate local approximations and avoid the difficulties of fitting a single global model across the entire domain. Li et al. [106] develop a distance-based infill strategy combined with local surrogate models that effectively use nearby information for optimization.

Another approach is the trust region methods which iteratively refine a local surrogate within a neighborhood around promising candidate solutions. Ong et al. [107] employ a trust region method that effectively combines precise objective function models with an inexpensive RBF surrogate model for single-objective optimization. The model is updated as new samples are added, and the trust region expands or shrinks based on the surrogate’s performance. This technique has proven particularly beneficial for highly non-convex problems.

Local surrogate models may involve adaptive neighborhood sizing, where the radius (or scope) of the local region is dynamically adjusted based on the surrogate’s predictive error, and strategies using dynamically selected surrogates around current best points have shown promising results. Yu et al. [108] establish local surrogates around the current best points and used the optimal individuals predicted by the local surrogate model to accelerate the convergence of the algorithm. This strategy allows the local model to remain flexible in varying problem landscapes and improves efficiency in single-objective optimization performance. Liu et al. [109] demonstrate how this approach can be particularly effective when combined with uncertainty-based selection strategies.

5.3. Combined Approaches

Surrogate models can be used to approximate the objective function at varying levels of granularity. Jin et al. [17] explore model management strategies in evolutionary optimization, comparing individual-based and generation-based evolution control. Their results indicate that the effectiveness of each strategy depends on problem complexity and computational budget, with local surrogate models being especially useful in ensuring a balance between approximation accuracy and efficiency. This approach is also beneficial for multimodal functions, where different points may be exploring significantly different regions of the domain. Wang et al. [10] successfully apply committee-based active learning for surrogate-assisted particle swarm optimization, showing improved exploration capabilities.

On the other hand, maintaining multiple surrogates can be expensive. Li et al. [74] propose a three-level surrogate modeling approach that balances individual model accuracy with computational cost. Similarly, Chu et al. [110] develop a clustering-assisted framework that groups similar individuals to share surrogate models, balancing model precision with computational efficiency and showed improvements in convergence speed.

A similar principle appears in classification-based surrogate modeling. Lu et al. [27] propose a classification-assisted differential evolution framework, where local SVM classifiers are trained on nearby evaluated individuals (via k nearest neighbors) to decide whether to evaluate offspring. This localized strategy significantly improves computational efficiency by avoiding unnecessary objective function evaluations. Sun et al. [26] extend surrogate-assisted optimization by incorporating weighted semi-supervised learning into interval-based regression surrogates, significantly improving prediction accuracy in interactive settings with limited user evaluations. Nonetheless, these individualized surrogates may introduce additional computational overhead, particularly in high-dimensional problems or large populations [111].

If the optimization method processes a population of points in one iteration, then the surrogate model can be common for the whole population or each point can be assigned its individual surrogate model.

Ensemble surrogate models have become a powerful tool that combines multiple surrogate models to improve prediction accuracy, robustness, and reliability in single-objective optimization problems compared to the use of a single model [5,7,13,14,112,113]. The main idea behind ensemble methods is to combine the strengths of different surrogate models and remove their individual weaknesses. With multiple aggregated prediction sources, ensembles are often more resistant to the specificity of any one model, leading to more accurate and robust approximations of the objective function.

There are many strategies for building ensemble surrogate models. One common approach is to combine different types of base models—such as Kriging, RBF, and polynomial regression—or to use the same type of model with different training parameters or architectures [112]. In addition to combining model types, another effective strategy is to generate a diversity of models through data perturbation and selective model integration [113]. This involves training multiple instances of surrogate models on different subsets of the available data and then using a selection or filtering mechanism to identify the most suitable models to include in the final ensemble.

Once individual surrogate models have been trained, their predictions can be combined in a few ways. The method that is usually used is weighted averaging, where the model weights are determined based on measures of prediction accuracy such as the cross-validation error or the root mean square error [108,112,113]. More complex techniques include the optimal pointwise weighted ensemble, which aims to minimize local prediction errors using a combination of global and local error measures [114]. Studies have shown that these ensemble-based approaches often outperform single-model surrogates in terms of prediction accuracy and robustness, especially in complex optimization landscapes [13,14]. For example, Viana et al. [13] demonstrated that utilizing multiple surrogate models, including RBF and polynomial regression, within the MSEGO algorithm led to improved optimization performance compared to relying on a single surrogate model alone.

Recent research has demonstrated the benefits of adaptively managing ensemble surrogate models during the optimization process. For example, perturbation-based ensemble frameworks can generate and select surrogate models according to the current state of the search, allowing the ensemble to better handle evolving landscape characteristics, even if selection is performed prior to optimization [113]. In addition, advanced strategies, such as selective ensemble techniques, focus on adaptively choosing a diverse subset of surrogate models based on current population characteristics to improve local approximation and guide optimization more effectively [105]. Ren et al. [76] introduce BiS-SAHA, a bi-stage surrogate-assisted hybrid algorithm that leverages an ensemble of RBF surrogate models with different kernel functions during the global search phase. In summary, the flexibility and robustness of the ensemble surrogate methods make them a popular choice for addressing single-objective optimization tasks. The primary limitations of ensemble methods are their increased computational overhead and the complexity of managing multiple models, which can become a significant challenge in itself.

5.4. Hierarchical Approaches

In single-objective optimization, hierarchical surrogate models are an effective tool to manage the trade-off between computational expense and model fidelity [74,115]. These models usually implement a hierarchical structure, where different levels of surrogate models have different purposes during optimization.

Tian et al. [115] propose a two-level surrogate framework for high-dimensional optimization problems. Their framework separates between coarse-grained and fine-grained individuals and utilizes different approximation methods for each group. This concept is further developed in [74] by proposing a three-layer RBF framework that incorporates global exploration, subregion search, and local exploitation. Their results show that this three-layer model achieves better search performance than standard single-level surrogate models.

Ren et al. [76] propose a hierarchical adaptive framework that dynamically changes its complexity at different levels. This approach prevents premature convergence while maintaining computational efficiency by adapting to the optimization’s progress.

Hierarchical approaches can combine different types of surrogate models or modeling strategies at different levels to leverage their complementary strengths and overcome individual limitations [116]. A key advantage of hierarchical surrogate frameworks is their ability to adaptively manage computational resources by using simpler models for initial screening and more sophisticated models for promising regions [117]. For example, Chen et al. [117] develop a surrogate-assisted evolutionary algorithm that uses a hierarchical surrogate technique and an adaptive infill strategy to balance exploration and exploitation during the optimization process.

Many hierarchical approaches combine global and local surrogate models [116,118]. Global models help maintain a broad view of the quality landscape and guide the overall search direction, while local models provide more accurate objective function approximations in promising regions. Tenne et al. [116] propose an algorithm framework using global and local variable surrogate models that demonstrate improved optimization efficiency.

Beyond balancing model complexity, hierarchical surrogate modeling also focuses on utilizing multiple levels of model roles within a surrogate hierarchy [119]. The key idea is to combine computationally cheap low-level models with more selective high-level surrogate selection in a complementary manner. In such frameworks, low-level models are typically used for broad exploration of the search space, while the high-level model is selectively employed to identify promising regions that warrant a more accurate evaluation [119]. Lu et al. [119] demonstrate that this hierarchical structure can significantly reduce the overall computational cost while maintaining optimization quality through strategic model management.

The construction of hierarchical surrogate models requires consideration of the trade-off between model fidelity and computational expense. Lim et al. [118] propose a generalized framework that adaptively determines when to use different fidelity levels based on the current search state and available computational budget. This adaptive solution helps mitigate the “curse of uncertainty” inherent in surrogate-assisted optimization.

One key advantage of hierarchical approaches is their ability to handle different levels of approximation uncertainty [118]. Lower-fidelity models can be used to quickly identify promising regions, while higher-fidelity models help to improve the search in these areas, leading to more robust optimization results [4]. According to Jin [4], this hierarchical structure is especially beneficial for real-world applications where multiple levels of model fidelity are naturally available. However, the main challenges for hierarchical approaches lie in the complexity of their design, the difficulty of managing the transitions between levels, and the potential for significant overhead if not carefully implemented.

6. Strategies of Using and Learning Surrogate Models

A motivation for using a surrogate model is to spare the evaluations of the true quality of points. Yet, the surrogate model would benefit from growing the number of points that have been evaluated using the quality criterion. The surrogate model should be continuously fed with new samples as the metaheuristic generates points traversing the search space since the distribution of generated points is expected to vary over time as the optimization progresses.

An important factor in the effectiveness of any approximation model is the quantity and quality of the training data [104,120]. Larger training sets generally give better approximations, but each additional sample may be expensive to evaluate. Hence, there is a trade-off between collecting more data and maintaining computational efficiency.

Therefore, the quality of the surrogate model relates strongly to two samples management processes that need to be integrated into the surrogate-assisted metaheuristics:

• Sampling strategy: which points should be evaluated using the surrogate model or the true quality criterion;
• Selection and forgetting strategy: to what degree the surrogate model should adapt to newly acquired samples and forget the older ones.

6.1. Sampling Strategy

The most straightforward sampling strategy is to assume a certain percentage of points generated by the metaheuristic to be evaluated using the true quality criterion, and to decide for each point whether it should be surrogated with the probability that equals this percentage. Such a strategy would neglect the context of the optimization problem.

Techniques that are aware of the optimization problem context will usually be based on two factors. The first factor relates to the location of points. Quite often, the approximation of the surrogate model decreases in reliability as distance increases between the evaluated point and the closest sample for which the true objective function is known. Some models, e.g., Gaussian processes, estimate the fidelity of the forecast.

In practice, several approaches have been developed to make more informed sampling decisions. Liu et al. [18] use Lower Confidence Bound prescreening in their GPEME framework, which balances both the predicted objective value and the model’s uncertainty estimate when deciding which points to evaluate exactly. This approach naturally prioritizes regions where the surrogate model predictions are less reliable.

Tong et al. [121] employ leave-one-out cross-validation (LOOCV) error to identify points where the surrogate model shows poor predictive performance. Points with high LOOCV error are selected for exact evaluation, helping to improve the model in regions where it currently provides unreliable approximations.

Another approach is demonstrated by Yu et al. [122], who analyze the local density of available training data through clustering methods. When insufficient training data exists in a region to build a reliable local surrogate model, candidates in that region are evaluated using the exact objective function.

Cai et al. [47] implement a strategy where surrogate-predicted improvements are verified through exact evaluation. If a surrogate model predicts that a solution is better than the current personal best, this prediction is validated using the true objective function.

Also, it can be expected that a higher fidelity result of the surrogate value would be obtained when the point is located inside rather than outside the area covered by the objective function samples. In other words, the surrogate model can be expected to interpolate better than to extrapolate. However, adaptive sampling strategies that use model error estimation to decide when and where to refine the surrogate model have been proposed. For example, Ghassemi et al. [123] introduce a strategy where the number and location of infill samples are dynamically estimated using extrapolated surrogate model error. This allows the model to be updated in regions of high uncertainty, even outside the current sample coverage.

The second factor relates to the influence of surrogate-model values of points on the decisions made within the metaheuristic: points for which the surrogate model estimates good quality will usually be more important for intensification. Therefore, these points should be preferred in sampling the true quality. An example of this strategy is the method introduced by Kern et al. [124] for CMA-ES, which uses an approximate ranking procedure to determine which individuals should be evaluated with the true objective function. Instead of requiring the full population to be evaluated, this adaptive mechanism evaluates only a subset of individuals until the surrogate-based ranking of the top $\mu$ individuals becomes stable. This allows the algorithm to reduce expensive fitness evaluations while still maintaining reliable evolutionary selection based on surrogate predictions.

6.2. Forgetting Strategy

The management of samples is an important part that really changes both the quality of the surrogate model and the overall performance of the optimization process [4,8,17]. The aim of the effective sample management is to balance two competing objectives: minimizing the number of expensive function evaluations and, at the same time, maximizing the information gained from each evaluation [118,125].

As the search progresses, the metaheuristic changes the average location and the distribution of generated points in the search space. For these reasons, the importance of the previously acquired samples of the true quality criterion for the quality of the surrogate model will change.

If the surrogate model is built with an ever-growing archive of past evaluations, the cost of rebuilding the model rises sharply; it is therefore common to cap the archive length and discard samples in a strict first-in–first-out order. This FIFO forgetting rule is found, for instance, in the surrogate-assisted estimation archive of SEA-HHA, whose Recent Data strategy trains on the most recently generated samples [126]. A comparable approach is used in [127], where only the most recent $N_{training}$ points from the archive are used to train the Ranking SVM surrogate model, effectively implementing a temporal forgetting strategy for surrogate construction. Similarly, SW-GP-UCB implements a strict sliding window where the Gaussian process uses only the most recent observations, discarding the earliest datum when the window overflows [128]. Another related example is presented by Zaborski and Mańdziuk, who use a Recursive Least Squares filter for surrogate updates that incorporates a forgetting factor, progressively down-weighting older samples in favor of newer ones [129].

Another method of forgetting is to exclude the samples with the lowest quality. This approach prioritizes maintaining high-quality training data that better represents the quality landscape. Zhou et al. [95] implement this strategy by using only the “top ranking q archived design points of the database as training data” for constructing their global surrogate model, effectively discarding lower-quality samples from the training process. This selective approach ensures that the global surrogate is built using the most promising solutions discovered during the search.

Distance-based forgetting strategies focus on maintaining spatial diversity and avoiding redundant sampling in similar regions of the search space. These distance-based forgetting strategies are more advanced mechanisms designed to actively manage the surrogate’s training archive. These methods focus on maintaining spatial diversity to avoid redundant sampling in similar regions of the search space. By ensuring the training data does not collapse into a single area of interest, the surrogate model is forced to maintain a more global perspective. This is crucial for managing the exploration–exploitation dilemma, as it directly supports continued exploration and reduces the risk of the optimization process converging prematurely based on a narrowly focused model. Sun et al. [101] employ such spatial criteria by maintaining local databases where data samples are selected based on their proximity to the current search region, combining distance thresholds with quality-based criteria. Their approach adds new positions to the database only if they meet specific distance requirements, effectively filtering out spatially redundant samples. Similarly, approaches in derivative-free optimization like ORBIT [130] manage interpolation points based on geometric proximity, where the algorithm maintains well-distributed sample sets by evaluating spatial relationships and selectively constructing interpolation sets from nearby evaluated samples, ensuring adequate coverage of the search space while avoiding clustering of training data. The SOP algorithm [131] implements a bi-objective selection framework where one objective explicitly maximizes the minimum distance to previously evaluated points, promoting exploration in sparsely sampled regions. The algorithm enforces a “Radius Rule” that prevents the selection of points within a specified distance threshold of already selected centers, combined with a tabu mechanism that temporarily excludes underperforming points from the active training set.

7. Concluding Remarks

7.1. Summary

Surrogate-assisted metaheuristics are an attempt to accelerate the optimization process by substituting a fraction of quality evaluations with an approximate quality measure. This simple idea exemplifies the potential of combining machine learning with optimization techniques. When looking at the synergy of benefits, one should bear in mind the limitations. In particular, one should bear in mind No Free Lunch theorems for optimization [132] and for machine learning [133]. Even when dealing with a subclass of optimization problems, when this subclass is sufficiently broad (e.g., multimodal continuous objective functions), it would be virtually impossible to identify the best-performing optimization method. Some indication about the relative quality of methods can be achieved when looking at the results of optimization competitions based on benchmark sets, like CEC [134,135,136] or BBOB [137], but this knowledge is still limited by the small number of example optimization problems that are used to construct the benchmark sets. Similarly with machine learning, although numerous ML datasets—such as the widely used UCI and MNIST datasets [138,139]—have been used for many years to evaluate the performance of popular ML models, there remains an open question: which model should be chosen when approximating a specific function, especially in the absence of any prior knowledge about the function’s class? For the aforementioned reasons, we presented various concepts of incorporating surrogate models into metaheuristics to indicate the directions of development rather than defining ready-to-use recipes.

7.2. A Proposed Decision Framework

To assist researchers in navigating this landscape, we propose a decision-making process rooted in the paper’s structure, which involves the following key steps:

• Identify the Approximation Task: The first and most critical step is to determine the fundamental task the surrogate must perform. This depends entirely on the needs of the chosen metaheuristic—does it require regression (predicting exact values), classification (assigning categories), or ranking (determining relative order)?
• Select the Model Type: Once the task is defined, select a specific model (e.g., RBF, Random Forest, and Kriging) by evaluating trade-offs like the model’s complexity, its training cost, and its ability to handle the problem’s specific characteristics, such as high dimensionality or discontinuities.
• Determine the Model Structure: Consider if the problem requires a more advanced architecture than a single global model. Choices include using multiple local models for specific regions, or more complex ensemble or hierarchical frameworks to improve robustness and manage the fidelity–cost trade-off.
• Define the Management Strategy: Finally, define the dynamic strategies for using the model. This includes the sampling strategy (which points to evaluate with the expensive true function) and the forgetting strategy (which data to keep in the model’s training archive) to align with the computational budget and effectively balance exploration and exploitation.

7.3. Outlook and Future Research

Building upon these general directions, our review points to several specific gaps and pressing challenges in the current literature that offer promising directions for future research.

A significant area is improving the reliability of extrapolation, as it remains a “big problem” for most surrogate models. Models like polynomial regression can become unstable with potentially extreme values, RBF networks tend to flatten toward zero outside the influence of their basis functions, and Gaussian processes generally revert to their prior mean, all of which can mislead the optimization search.

Additionally, while the dynamic management of ensemble and hierarchical models is an active research area, a broader challenge lies in designing truly adaptive model structures that can, for example, autonomously transition from a global to a local model focus as the search progresses from an exploratory to an exploitative phase.

Another critical challenge is enhancing scalability. The accuracy of many regression models is known to deteriorate in high-dimensional spaces, and the computational cost of highly accurate models like Kriging scales cubically with the number of training samples, making them difficult to apply to large datasets. To address this, several advanced techniques are being explored, such as using manifold learning to identify a lower-dimensional embedding of the search space on which a standard surrogate can then operate more effectively. Other approaches focus on localized data generation and adaptive sampling strategies explicitly designed to be more efficient in high-dimensional spaces, reducing the number of samples needed to build a reasonably accurate model.

Furthermore, while the strategic use of prediction uncertainty is a key advantage of models like Kriging, developing robust and efficient methods to estimate and leverage uncertainty from other model types for adaptive sampling remains an important research challenge.

Moreover, there is a need to develop more intelligent forgetting strategies for managing the archive of training data. Current methods often rely on simple rules such as sample age or the solution’s quality, but the field would benefit from adaptive techniques that can dynamically balance a point’s quality against its contribution to spatial diversity to avoid prematurely discarding important information.

Lastly, while this review has focused on unconstrained, static problems, extending these surrogate-assisted frameworks to effectively handle complex constraints and adapt to dynamic environments where the objective function changes over time remain two of the most significant and practical frontiers for future research.

Addressing these open questions will be key in advancing the power and applicability of surrogate-assisted metaheuristics.