An Integrated CNN-BiLSTM-Adaboost Framework for Accurate Pipeline Residual Strength Prediction
Abstract
1. Introduction
2. Methods
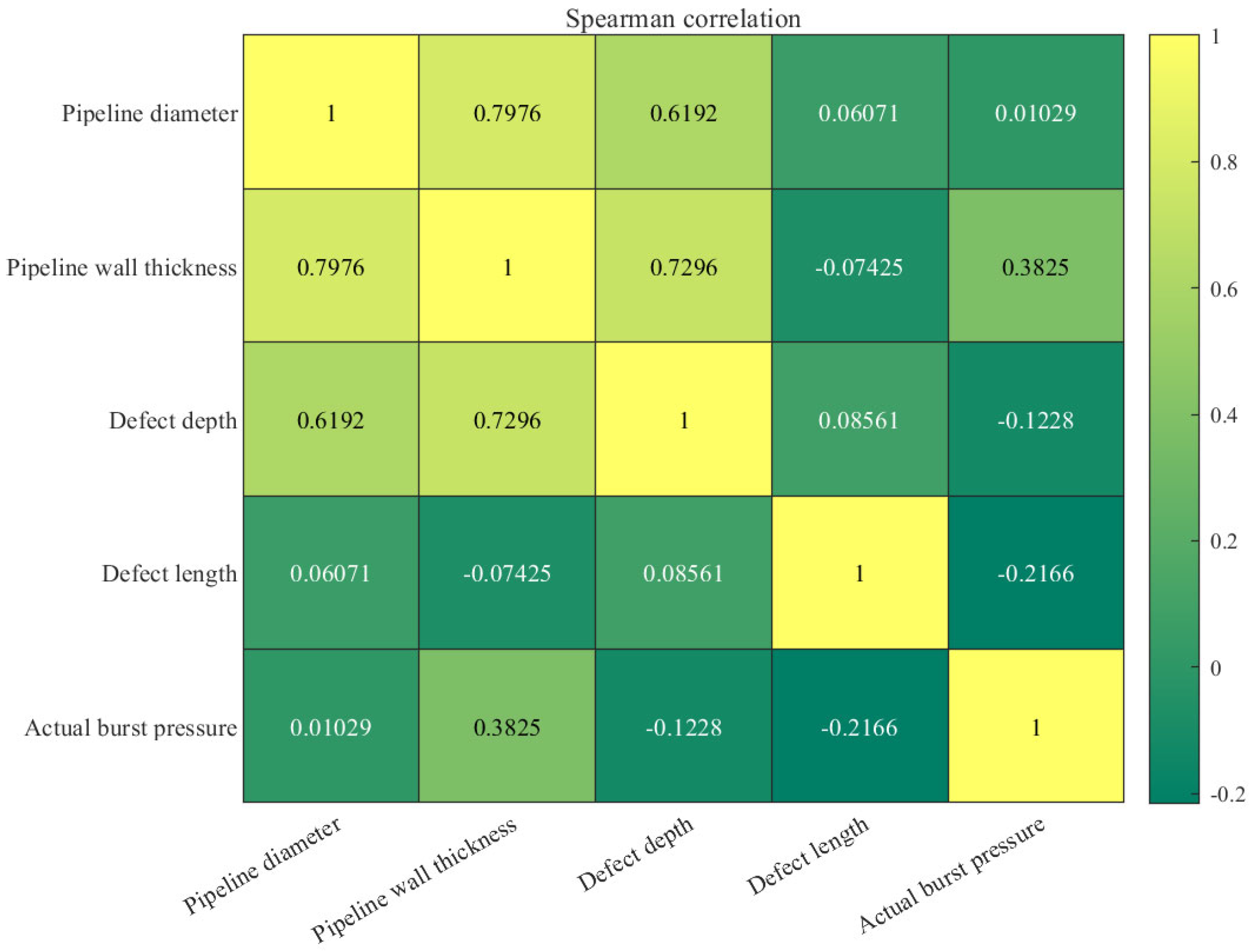
2.1. Residual Strength Prediction Based on Correlation Analysis
2.2. Principle of the CNN-BiLSTM-Adaboost Algorithm and Parameter Setting
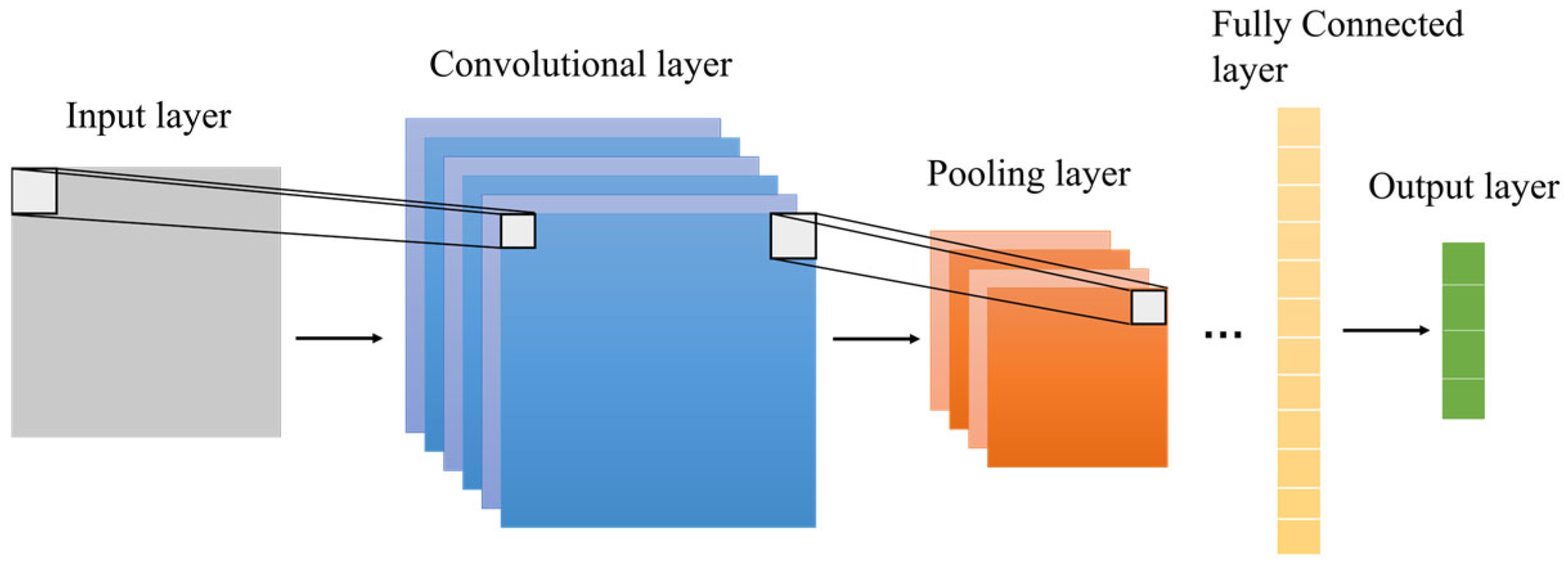
2.2.1. CNN Algorithm
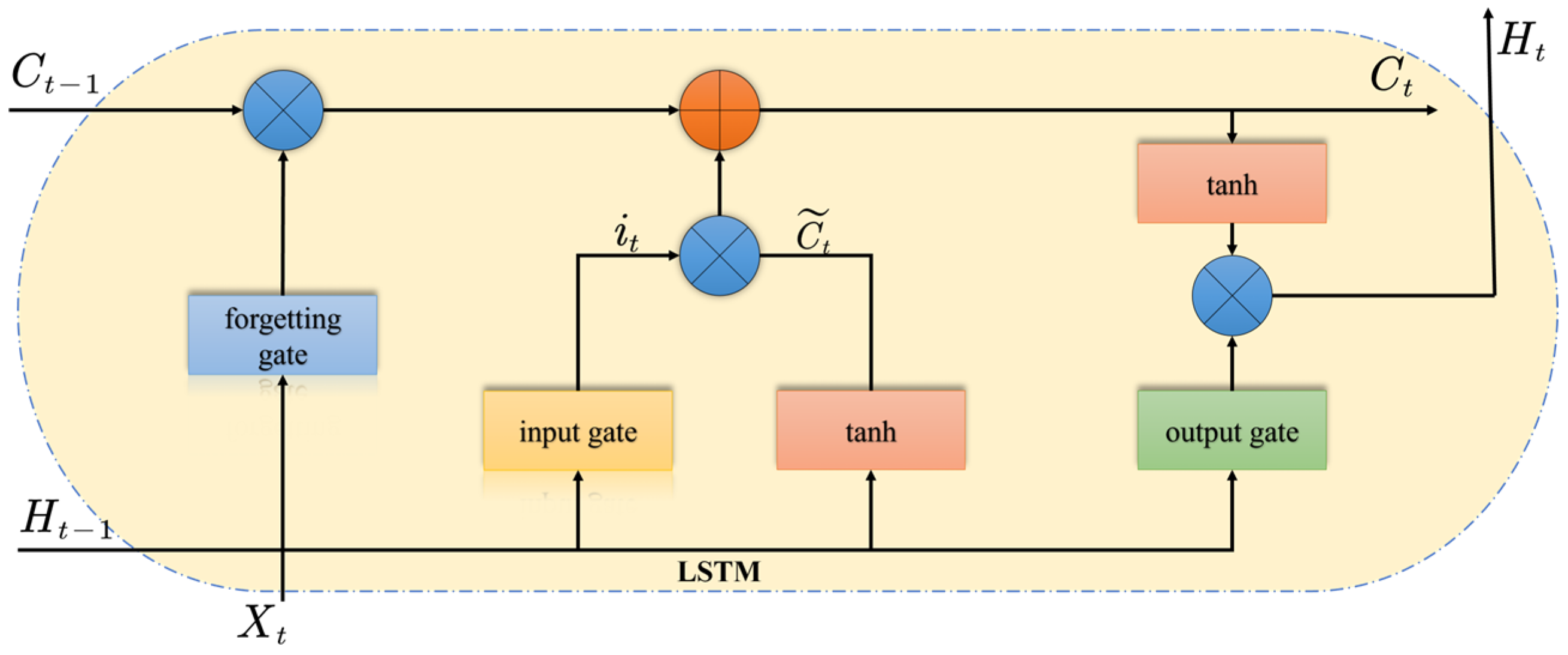
2.2.2. LSTM Algorithm
- 1.
- Input Gate
- 2.
- Forget Gate
- 3.
- Candidate Cell State
- 4.
- Current Cell State
- 5.
- Output Gate
- 6.
- Current Hidden State
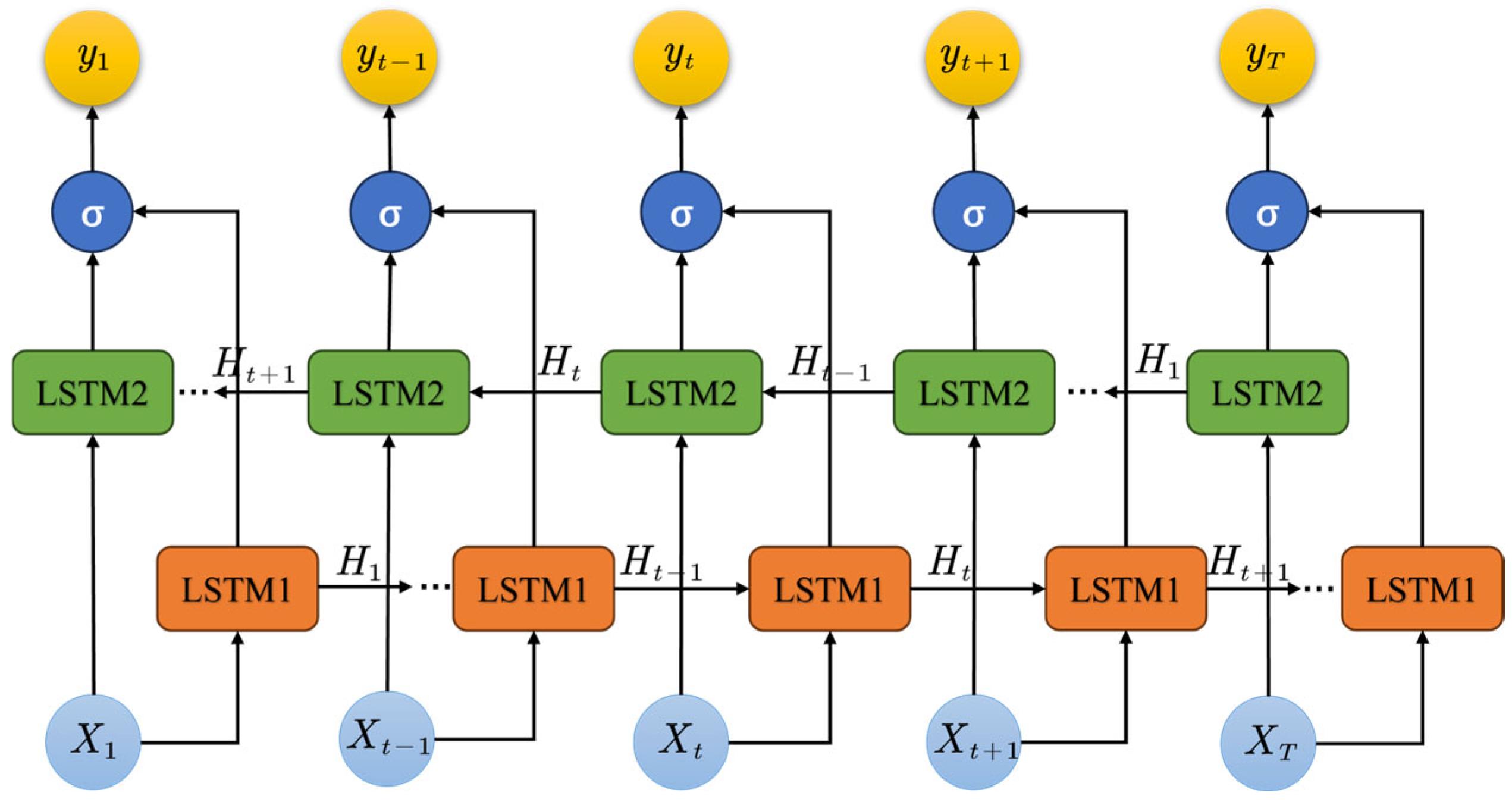
2.2.3. BiLSTM Algorithm
- Forward LSTM
- Backward LSTM
2.2.4. Adaboost Algorithm
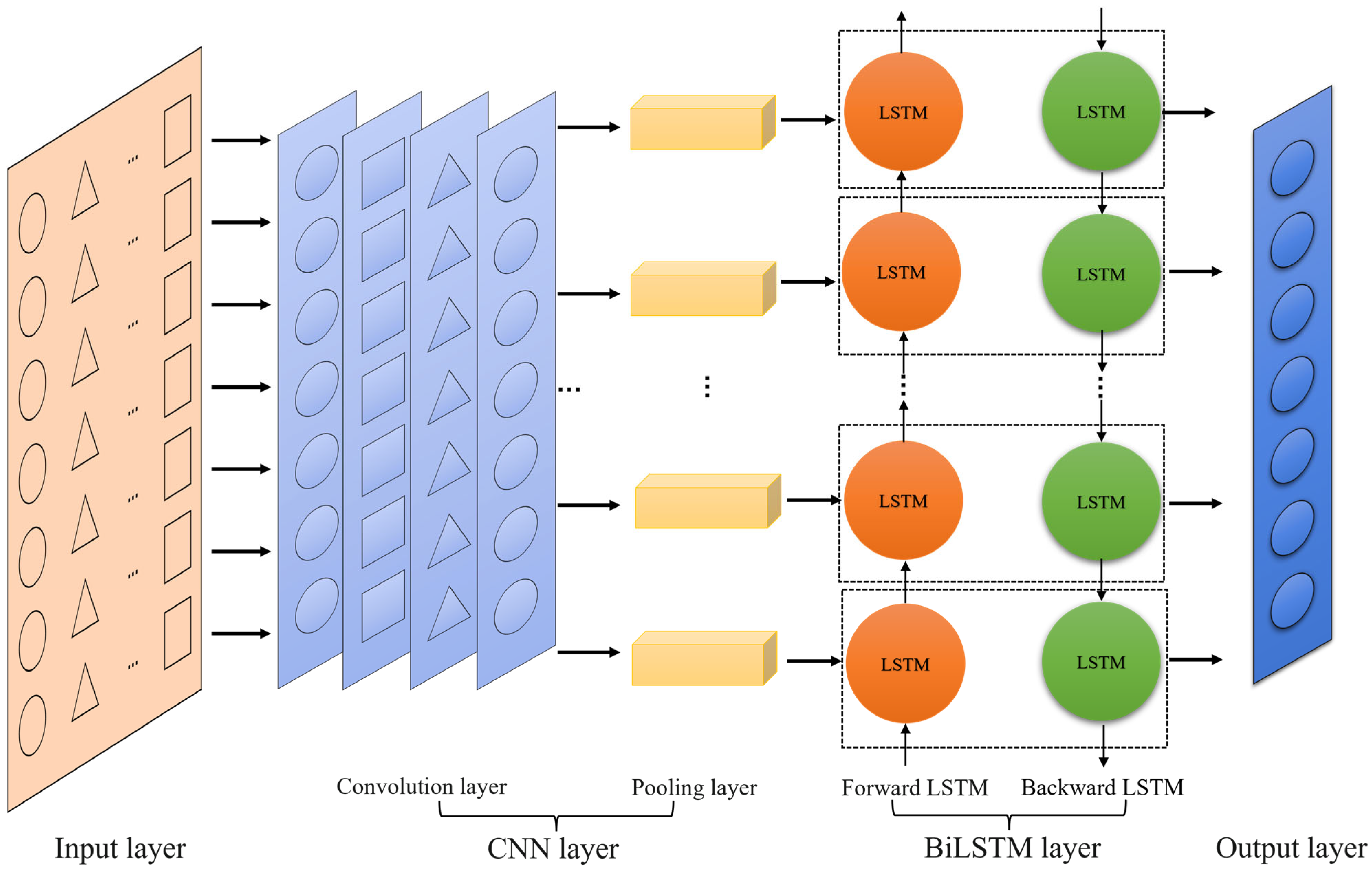
2.2.5. CNN-BiLSTM-Adaboost Algorithm
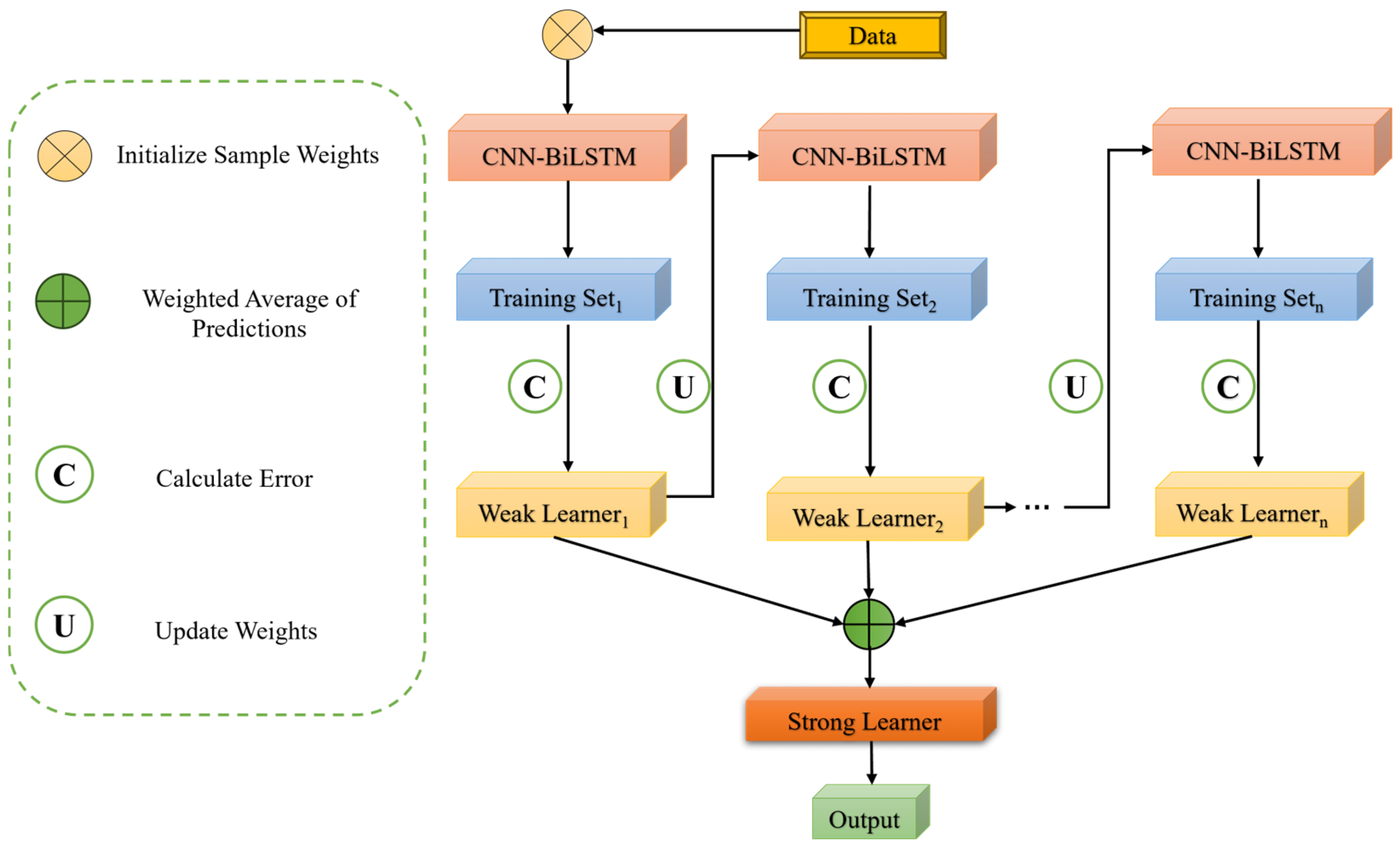
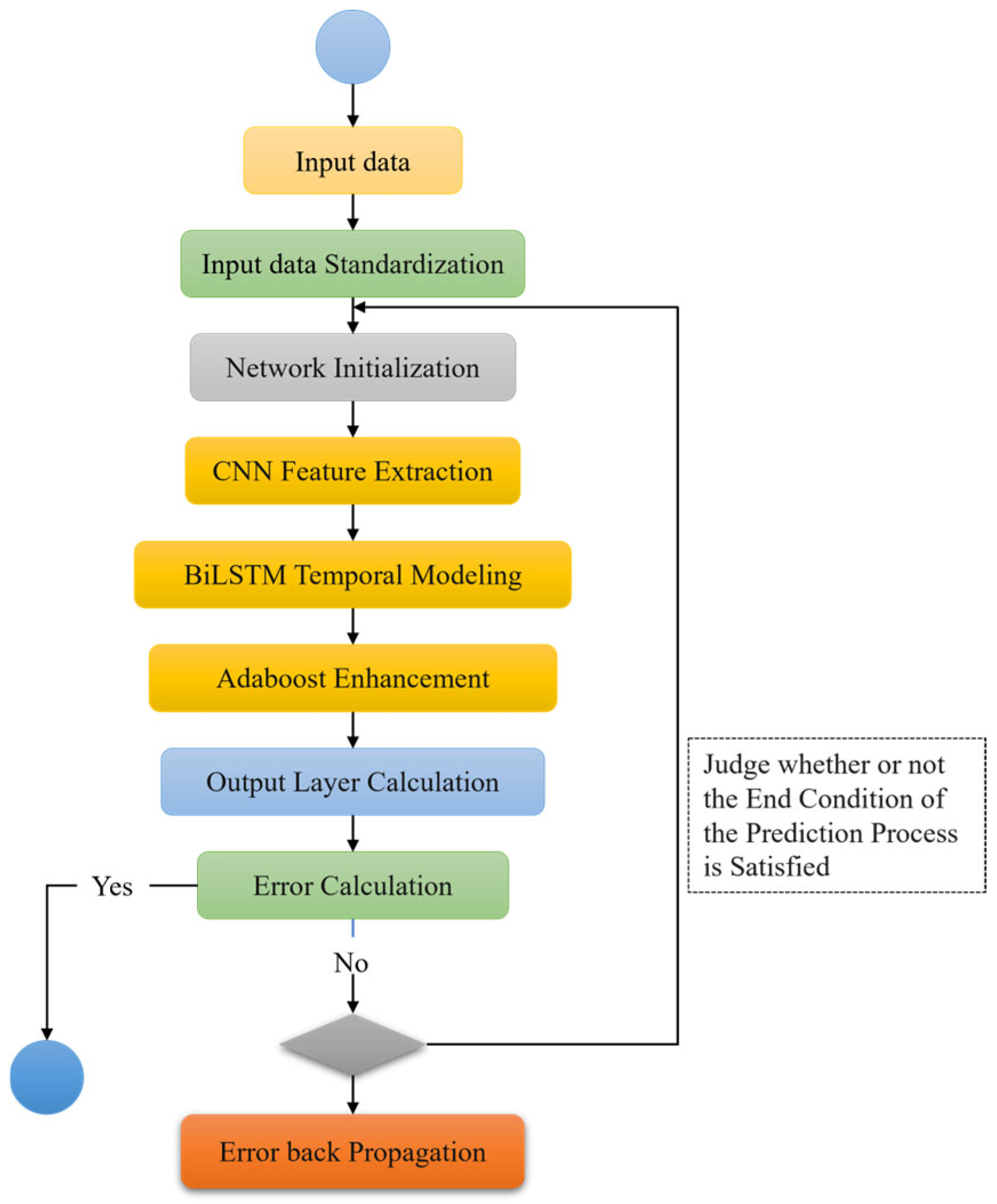
- Workflow of CNN-BiLSTM-Adaboost AlgorithmThe structure of CNN-BiLSTM-Adaboost is shown in Figure 7. The overall workflow of the CNN-BiLSTM-Adaboost algorithm is as follows.
- (a)
- Feature Extraction: CNN is utilized to extract spatial features from the input data, yielding the feature vector .
- (b)
- Sequence Modeling: The feature vector is then input into BiLSTM, which extracts temporal dependency features, resulting in the feature vector .
- (c)
- Classification: Adaboost is employed to classify the feature vector , producing the final prediction .
- 2.
- CNN-BiLSTM-Adaboost Training Process
- (a)
- Input Data: The data required for training the CNN-BiLSTM-Adaboost algorithm is fed into the model.
- (b)
- Data Standardization: As there is a large variance in the input data, z-score standardization is applied to normalize the input data, as shown in Formula (23).
- (c)
- Network Initialization: The weights and biases of each layer of the CNN-BiLSTM-Adaboost model are initialized.
- (d)
- CNN Feature Extraction: The input data is passed through the convolution and pooling layers to extract local spatial features, resulting in a feature vector.
- (e)
- BiLSTM Temporal Modeling: The feature vector output from the CNN layer is passed through the BiLSTM layer, which processes the temporal dependencies in the sequential data via forward and backward LSTM networks, generating an output.
- (f)
- Adaboost Enhancement: The output from the BiLSTM layer is fed into multiple weak regressors, which are combined using the Adaboost algorithm to produce the final output.
- (g)
- Output Layer Calculation: The final output of the model is generated through a fully connected layer and a regression layer, mapping the Adaboost output to the final predicted value.
- (h)
- Error Calculation: The predicted value from the output layer is compared with the actual value for the dataset, and the corresponding prediction error is calculated. The error calculation metrics are the mean absolute percentage error (MAPE) and mean squared error (RMSE):
- (i)
- End Condition Judgment: The training process is evaluated against termination conditions, which include completing a predetermined number of cycles, the weights falling below a certain threshold, or the prediction error rate being below a preset threshold. If any of these conditions are met, training is completed; otherwise, it continues.
- (j)
- Error Back Propagation: The calculated error is propagated backward through the network, updating the weights and biases of each layer. The process then returns to step 4 to continue training.
- 3.
- CNN-BiLSTM-Adaboost Prediction Process
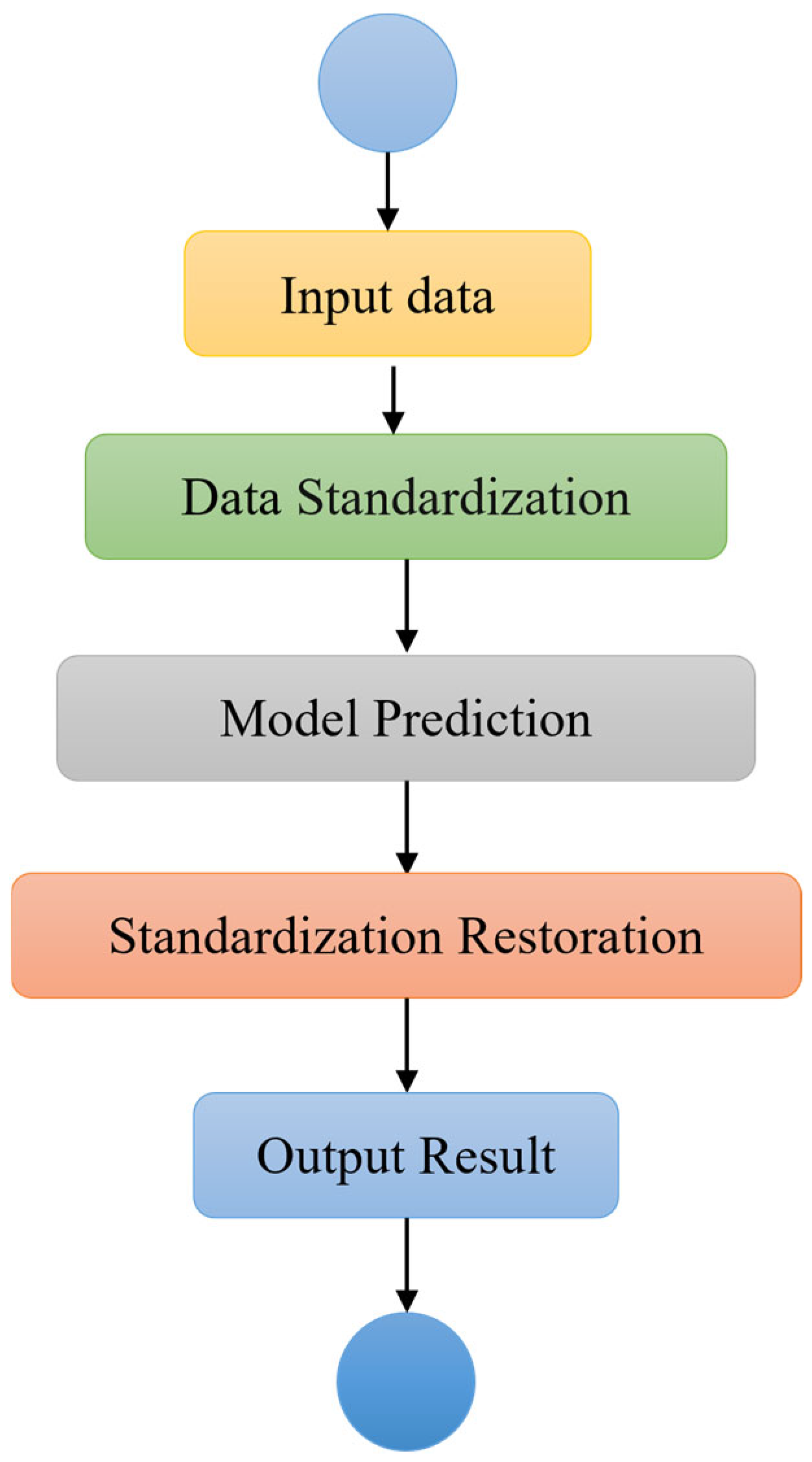
- (a)
- Input Data: The input data required for prediction are fed into the model.
- (b)
- Data Standardization: The input data are standardized using the z-score method to ensure consistency with the data distribution during training.
- (c)
- Model Prediction: The standardized data are then fed into the trained CNN-BiLSTM-Adaboost model to generate the corresponding predicted output value.
- (d)
- Standardization Restoration: The predicted output value from the CNN-BiLSTM-Adaboost model is in a standardized form. It is restored to the original value using the following Formula (26).
- (e)
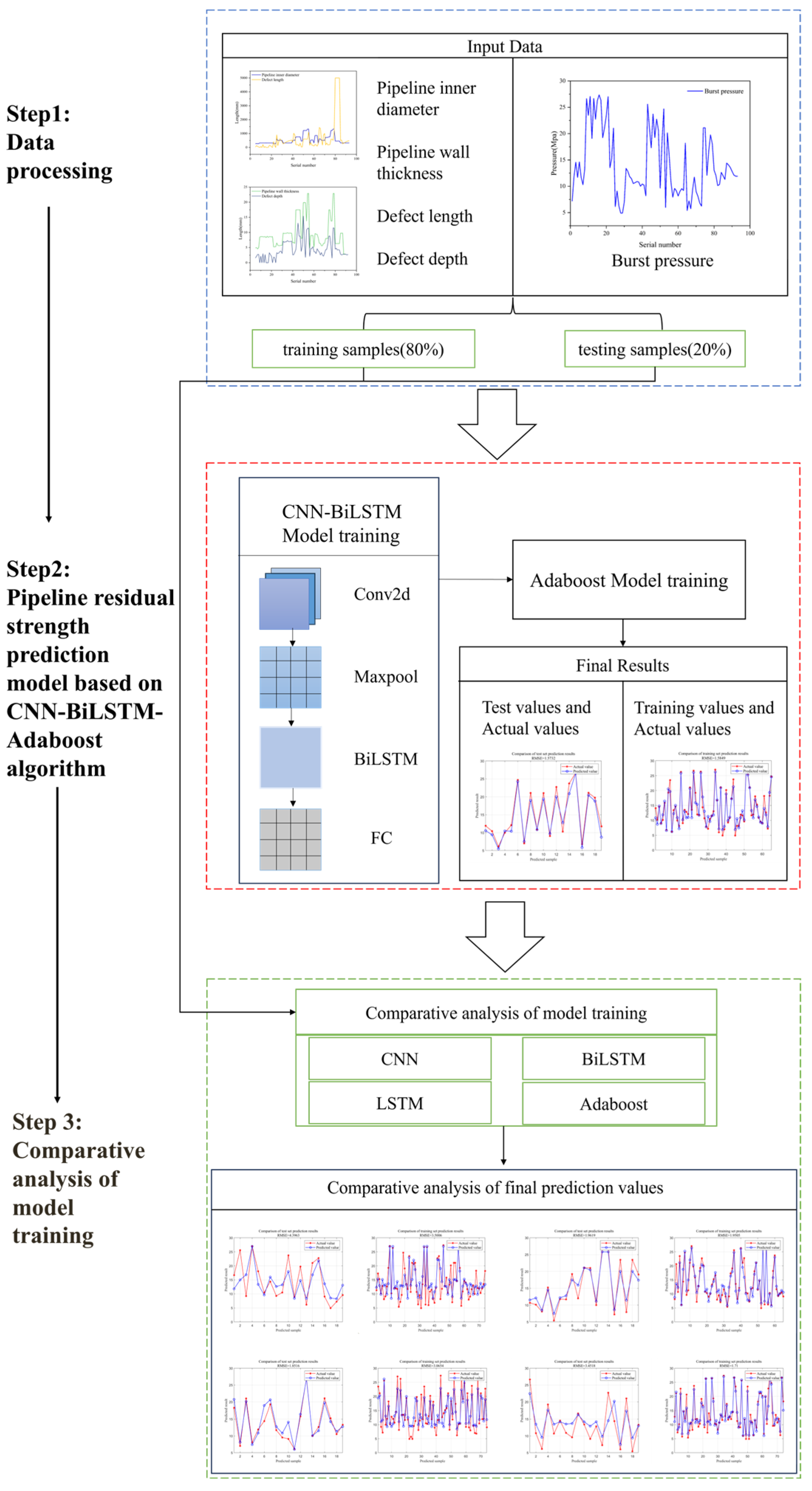
3. Results and Discussion
3.1. CNN Algorithm for Residual Strength Prediction
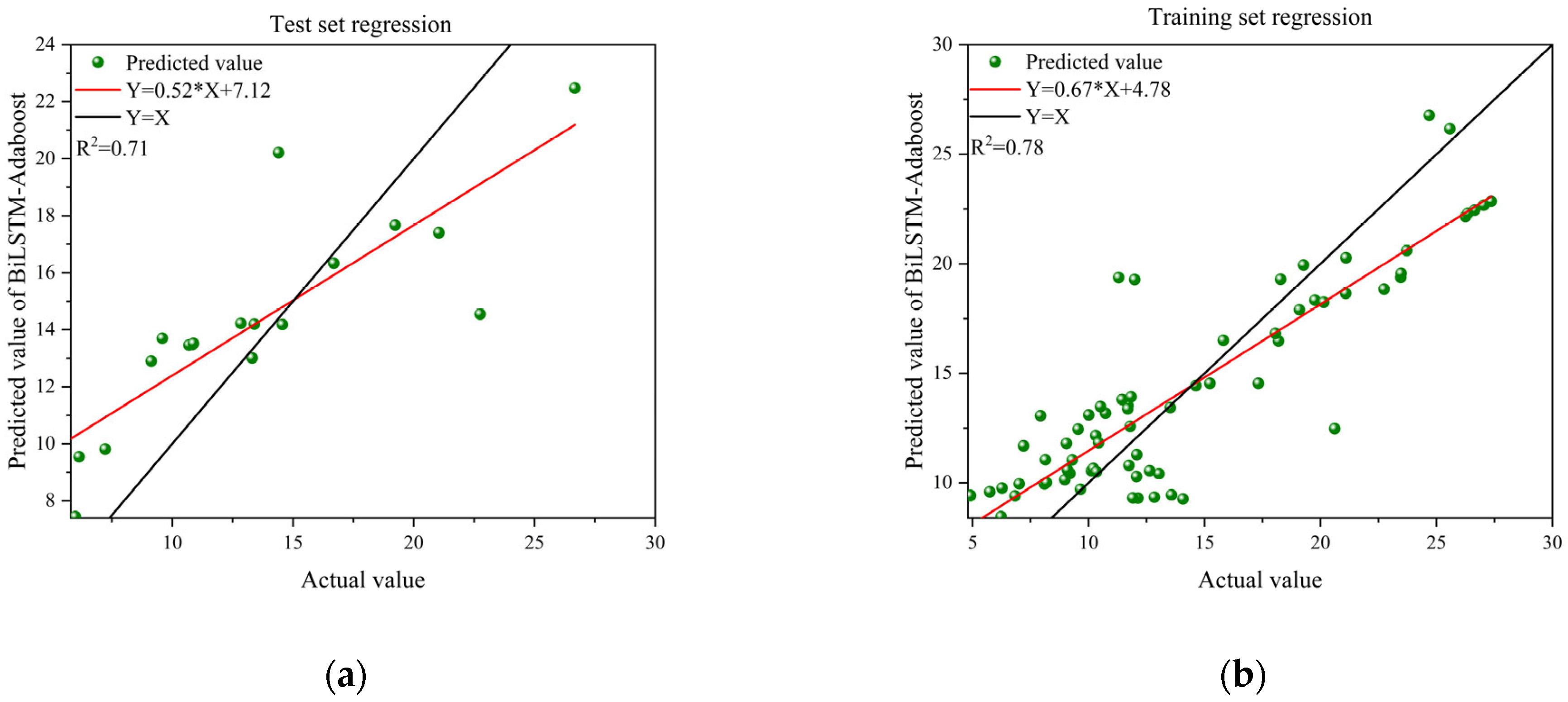
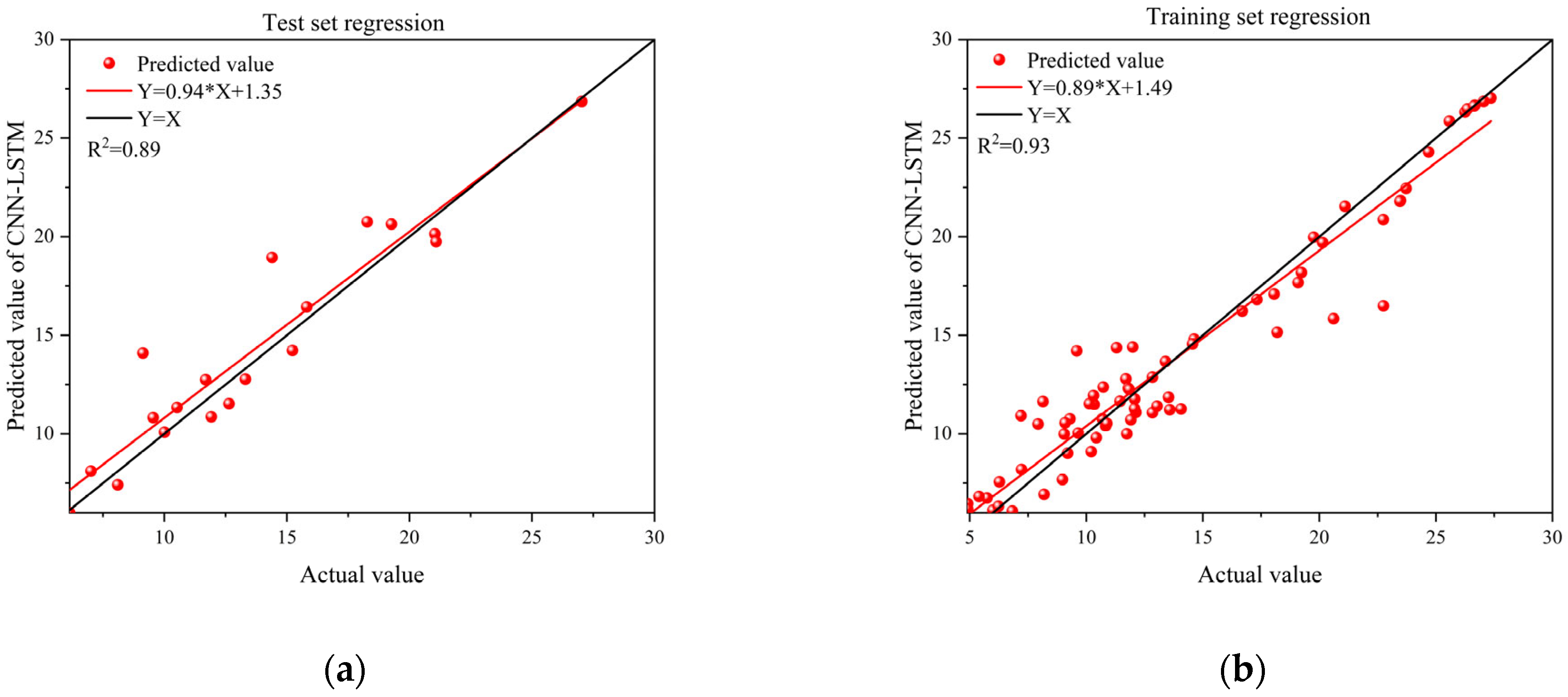
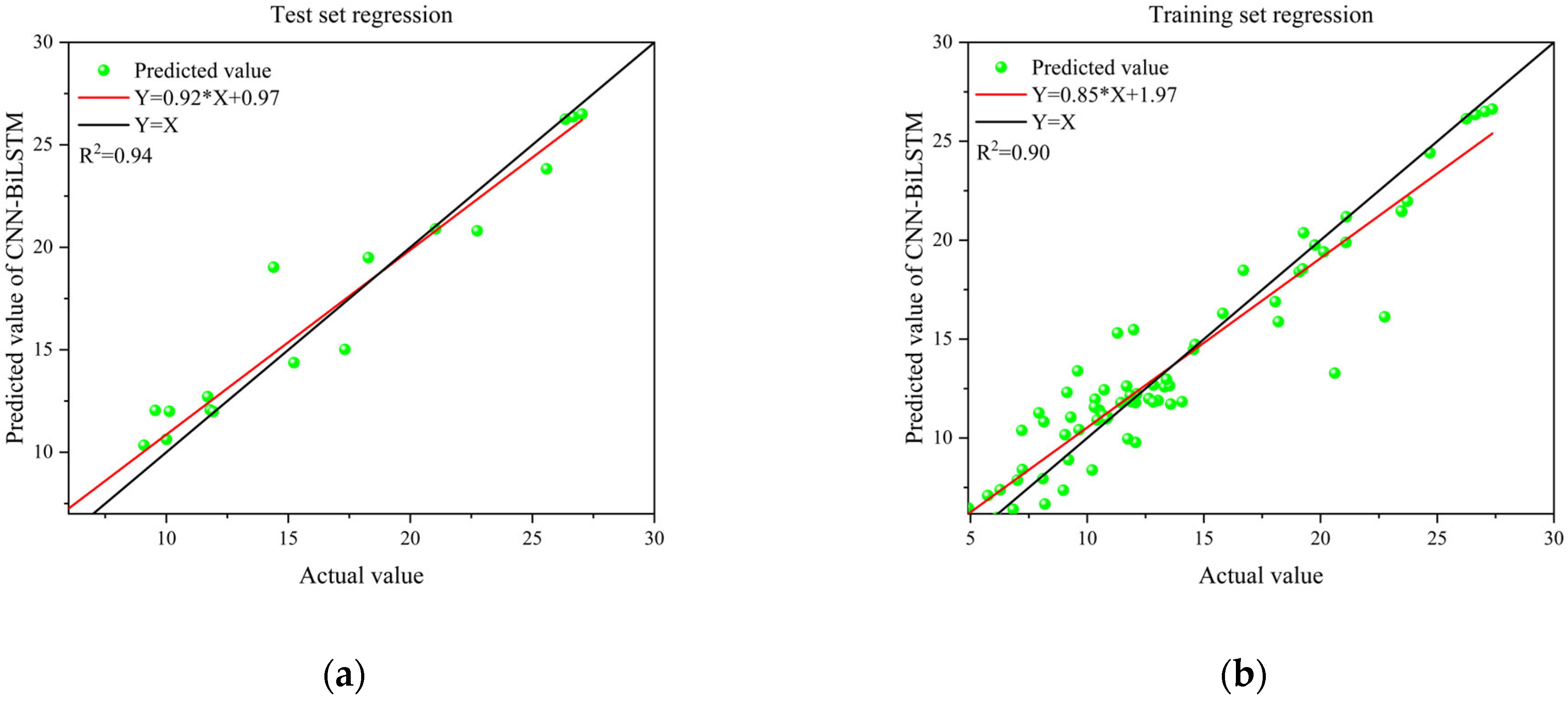
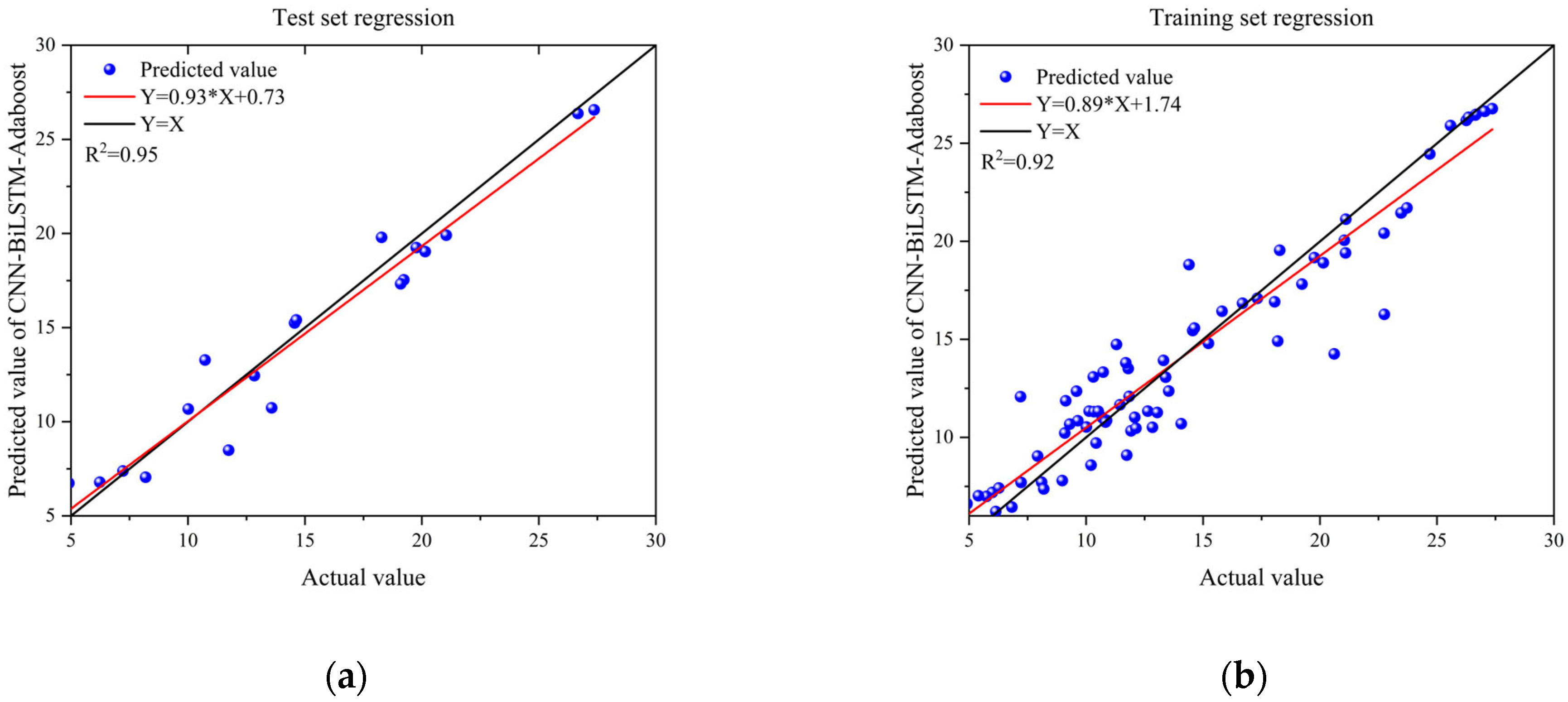
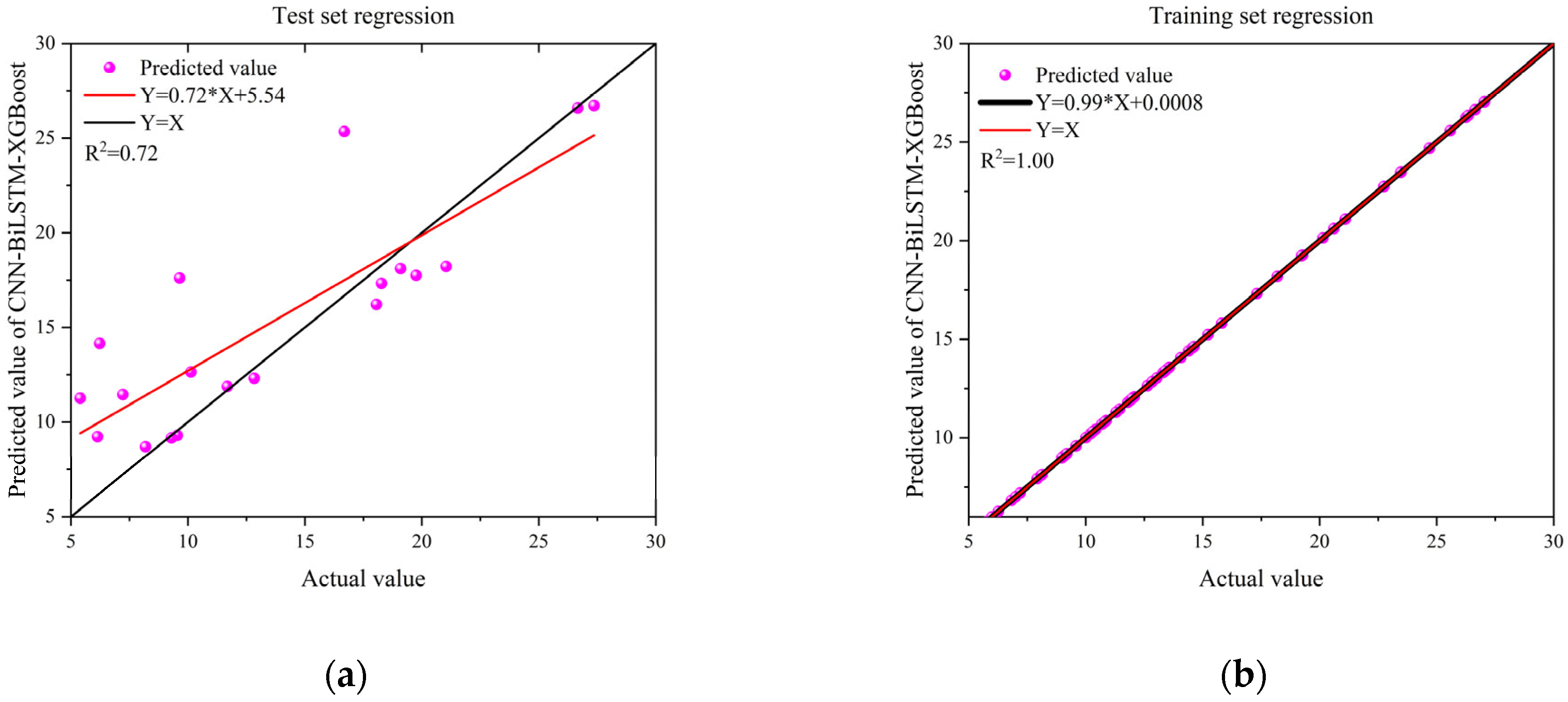
3.2. Comparison of CNN-BiLSTM-Adaboost Algorithm and Standard Methods for Residual Strength Prediction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oh, D.; Race, J.; Oterkus, S.; Koo, B. Burst pressure prediction of API 5L X-grade dented pipelines using deep neural network. J. Mar. Sci. Eng. 2020, 8, 766. [Google Scholar] [CrossRef]
- Lu, H.; Iseley, T.; Matthews, J.; Liao, W.; Azimi, M. An ensemble model based on relevance vector machine and multi-objective SALP swarm algorithm for predicting burst pressure of corroded pipelines. J. Pet. Sci. Eng. 2021, 203, 108585. [Google Scholar] [CrossRef]
- Lu, H.; Xu, Z.D.; Iseley, T.; Matthews, J.C. Novel data-driven framework for predicting residual strength of corroded pipelines. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021045. [Google Scholar] [CrossRef]
- Ma, Y.; Zheng, J.; Liang, Y.; Klemeš, J.J.; Du, J.; Liao, Q.; Lu, H.; Wang, B. Deep pipe: Theory-guided neural network method for predicting burst pressure of corroded pipelines. Process Saf. Environ. Prot. 2022, 162, 595–609. [Google Scholar] [CrossRef]
- Lu, H.; Peng, H.; Xu, Z.D.; Matthews, J.C.; Wang, N.; Iseley, T. A feature selection-based intelligent framework for predicting maximum depth of corroded pipeline defects. J. Perform. Constr. Facil. 2022, 36, 04022044. [Google Scholar] [CrossRef]
- Kong, X.; Wang, Z.; Xiao, F.; Bai, L. Power load forecasting method based on demand response deviation correction. Int. J. Electr. Power Energy Syst. 2023, 148, 109013. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Wang, W.; Li, Y.; Shi, L.; Li, Y. Residual strength prediction of corroded pipelines using multilayer perceptron and modified feed-forward neural network. Reliab. Eng. Syst. Saf. 2023, 231, 108980. [Google Scholar] [CrossRef]
- Sulaiman, S.M.; Jeyanthy, P.A.; Devaraj, D.; Shihabudheen, K.V. A novel hybrid short-term electricity forecasting technique for residential loads using empirical mode decomposition and extreme learning machines. Comput. Electr. Eng. 2022, 98, 107663. [Google Scholar] [CrossRef]
- Yan, S.R.; Tian, M.; Alattas, K.A.; Mohamadzadeh, A.; Sabzalian, M.H.; Mosavi, A.H. An experimental machine learning approach for midterm energy demand forecasting. IEEE Access 2022, 10, 118926–118940. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, T.; Chu, F. Deep convolutional neural network based planet bearing fault classification. Comput. Ind. 2019, 107, 59–66. [Google Scholar] [CrossRef]
- Chuang, W.Y.; Tsai, Y.L.; Wang, L.H. Leak detection in water distribution pipes based on CNN with mel frequency cepstral coefficients. In Proceedings of the 3rd International Conference on Innovative Artificial Intelligence, Suzhou, China, 15–18 March 2019. [Google Scholar]
- Zhou, M.; Yang, Y.; Xu, Y.; Hu, Y.; Cai, Y.; Lin, J.; Pan, H. A pipeline leak detection and localization approach based on ensemble TL1DCNN. IEEE Access 2021, 9, 47565–47578. [Google Scholar] [CrossRef]
- Kang, J.; Park, Y.-J.; Lee, J.; Wang, S.-H.; Eom, D.-S. Novel leakage detection by ensemble CNN-SVM and graph-based localization in water distribution systems. IEEE Trans. Ind. Electron. 2017, 65, 4279–4289. [Google Scholar] [CrossRef]
- Ratinov, L.; Roth, D. Design challenges and misconceptions in named entity recognition. In Proceedings of the 13th Conference on Computational Natural Language Learning, Boulder, CO, USA, 4 June 2009. [Google Scholar]
- Petasis, G.; Petridis, S.; Paliouras, G.; Karkaletsis, V.; Perantonis, S.J.; Spyropoulos, C.D. Symbolic and neural learning for named-entity recognition. In Proceedings of the Symposium on Computational Intelligence and Learning, Chios, Greece, 19–23 June 2000. [Google Scholar]
- Luo, G.; Huang, X.; Lin, C.Y.; Nie, Z.Q. Joint entity recognition and disambiguation. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015. [Google Scholar]
- Cody, R.A.; Tolson, B.A.; Orchard, J. Detecting leaks in water distribution pipes using a deep autoencoder and hydroacoustic spectrograms. J. Comput. Civ. Eng. 2020, 34, 04020001. [Google Scholar] [CrossRef]
- Guo, G.; Yu, X.; Liu, S.; Ma, Z.; Wu, Y.; Xu, X.; Wang, X.; Smith, K.; Wu, X. Leakage detection in water distribution systems based on time-frequency convolutional neural network. J. Water Resour. Plan. Manag. 2021, 147, 04020101. [Google Scholar] [CrossRef]
- Santos, C.; Guimaraes, V.; Niteroi, R.J.; Rio, J. Boosting named entity recognition with neural character embeddings. In Proceedings of the 5th Named Entities Workshop, Beijing, China, 31 July 2015. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Goller, C.; Kuchler, A. Learning task-dependent distributed representations by backpropagation through structure. In Proceedings of the IEEE International Conference on Neural Networks, Washington, DC, USA, 3–6 June 1996. [Google Scholar]
- Labeau, M.; Loser, K.; Allauzen, A. Non-lexical neural architecture for fine-grained POS tagging. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015. [Google Scholar]
- Du, J.; Cheng, Y.; Zhou, Q.; Zhang, J.; Zhang, X. Power load forecasting using BiLSTM-attention. IOP Conf. Ser. Earth Environ. Sci. 2020, 440, 032115. [Google Scholar] [CrossRef]
- Chunsheng, C.; Mengqing, T.; Kejia, Z. Pipeline anomaly data detection method based on Bi-LSTM network. Comput. Technol. Dev. 2023, 33, 215–220. [Google Scholar]
- Li, H.; Wang, S.; Islam, M.; Bobobee, E.D.; Zou, C.; Fernandez, C. A novel state of charge estimation method of lithium-ion batteries based on the IWOA-AdaBoost-Elman algorithm. Int. J. Energy Res. 2021, 46, 5134–5151. [Google Scholar] [CrossRef]
- Fu, Y.; Zheng, Y.; Hao, S.; Miao, Y. Research on comprehensive decision-making of distribution automation equipment testing results based on entropy weight method combined with grey correlation analysis. J. Phys. Conf. Ser. 2021, 2005, 012033. [Google Scholar] [CrossRef]
- Durante, F.; Sempi, C. Principles of Copula Theory; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Zhengshan, L.; Jiaqi, Z.; Jihao, L. Research on failure pressure prediction of corroded pipelines based on integrated algorithm. Comput. Technol. Dev. 2024, 34, 80–86. [Google Scholar]
- Bjornoy, O.H.; Rengard, O.; Fredheim, S. Residual strength of dented pipelines, DNV test results. In Proceedings of the 10th International Offshore and Polar Engineering Conference, Washington, DC, USA, 28 May–2 June 2000. [Google Scholar]
- Freire, J.L.F.; Vieira, R.D.; Castro, J.T.P.; Benjamin, A.C. PART 3: Burst tests of pipeline with extensive longitudinal metal loss. Exp. Tech. 2006, 30, 60–65. [Google Scholar] [CrossRef]
- Wang, S.H.; Fernandes, S.L.; Zhu, Z.; Zhang, Y.D. AVNC: Attention-Based VGG-Style Network for COVID-19 Diagnosis by CBAM. IEEE Sens. J. 2022, 22, 17431–17438. [Google Scholar] [CrossRef] [PubMed]
- Qin, L.; Yu, N.; Zhao, D. Applying the convolutional neural network deep learning technology to behavioural recognition in intelligent video. Teh. Vjesn. Tech. Gaz. 2018, 25, 528–535. [Google Scholar]
- Hao, Y.; Gao, Q. Predicting the trend of stock market index using the hybrid neural network based on multiple time scale feature learning. Appl. Sci. 2020, 10, 3961–3974. [Google Scholar] [CrossRef]
- Kamalov, F. Forecasting significant stock price changes using neural networks. Neural Comput. Appl. 2020, Early Access. [Google Scholar] [CrossRef]
- Fanta, H.; Shao, Z.; Ma, L. ‘Forget’ the Forget Gate: Estimating Anomalies in Videos using Self-contained Long Short-Term Memory Networks. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Geneva, Switzerland, 20–23 October 2020. [Google Scholar]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The Performance of LSTM and BiLSTM in Forecasting Time Series. In Proceedings of the IEEE International Conference on Big Data, Los Angeles, CA, USA, 9–12 December 2019. [Google Scholar]
- Quan, R.; Zhu, L.; Wu, Y.; Yang, Y. Holistic LSTM for Pedestrian Trajectory Prediction. IEEE Trans. Image Process. 2021, 30, 1–12. [Google Scholar] [CrossRef]
- Pu, W. Analysis of ASME B31G residual strength evaluation method. Chem. Des. Commun. 2019, 45, 140–141. [Google Scholar]
- Det Norske Veritas. DNV RP-F101-1999 Recommended Practice for Corroded Pipeline; DNV: Oslo, Norway, 1999. [Google Scholar]
- Xiao, G.; Feng, M.; Zhang, H.; Chen, J.; Wang, F.; Yu, H. Study on failure assessment of X80 high-grade pipeline with defect corrosion. China Saf. Sci. Technol. 2015, 6, 128–133. [Google Scholar]
| Pipeline Steel Grade (mm) | Data Sources |
|---|---|
| X35 | reference literature [28] |
| X42 | reference literature [29,30] |
| X46 | reference literature [28,29,30,31] |
| X52 | reference literature [31,32] |
| X56 | reference literature [32] |
| X60 | reference literature [29,31] |
| X65 | reference literature [28,29,32] |
| X80 | reference literature [32] |
| X100 | reference literature [32] |
| Serial Number | Pipeline Steel Grade | Pipeline Inner Diameter (mm) | Pipeline Wall Thickness (mm) | Defect Depth (mm) | Defect Length (mm) | Burst Pressure (MPa) |
|---|---|---|---|---|---|---|
| 1 | X35 | 508 | 7 | 3.3 | 304.8 | 12 |
| 2 | X42 | 529 | 9 | 4.7 | 160 | 15.7 |
| 3 | X46 | 457.7 | 6.23 | 6.23 | 2750 | 12.06 |
| 4 | X52 | 273.05 | 5.23 | 1.85 | 408.94 | 16.71 |
| 5 | X56 | 506.73 | 5.74 | 3.02 | 132.08 | 10.73 |
| 6 | X60 | 508 | 14.3 | 10.03 | 500 | 13.4 |
| 7 | X65 | 762 | 17.5 | 4.4 | 200 | 24.11 |
| 8 | X80 | 1219 | 19.89 | 1.77 | 607.74 | 23.3 |
| Parameters | Value |
|---|---|
| Convolution layer filters | 64 |
| Convolution layer kernel size | 1 |
| Convolution layer activation function | RELU |
| Convolution layer padding | Same |
| Pooling layer pool size | 1 |
| Pooling layer padding | Same |
| Pooling layer activation function | RELU |
| Number of hidden units in BiLSTM layer | 64 |
| Algorithm | ||||
|---|---|---|---|---|
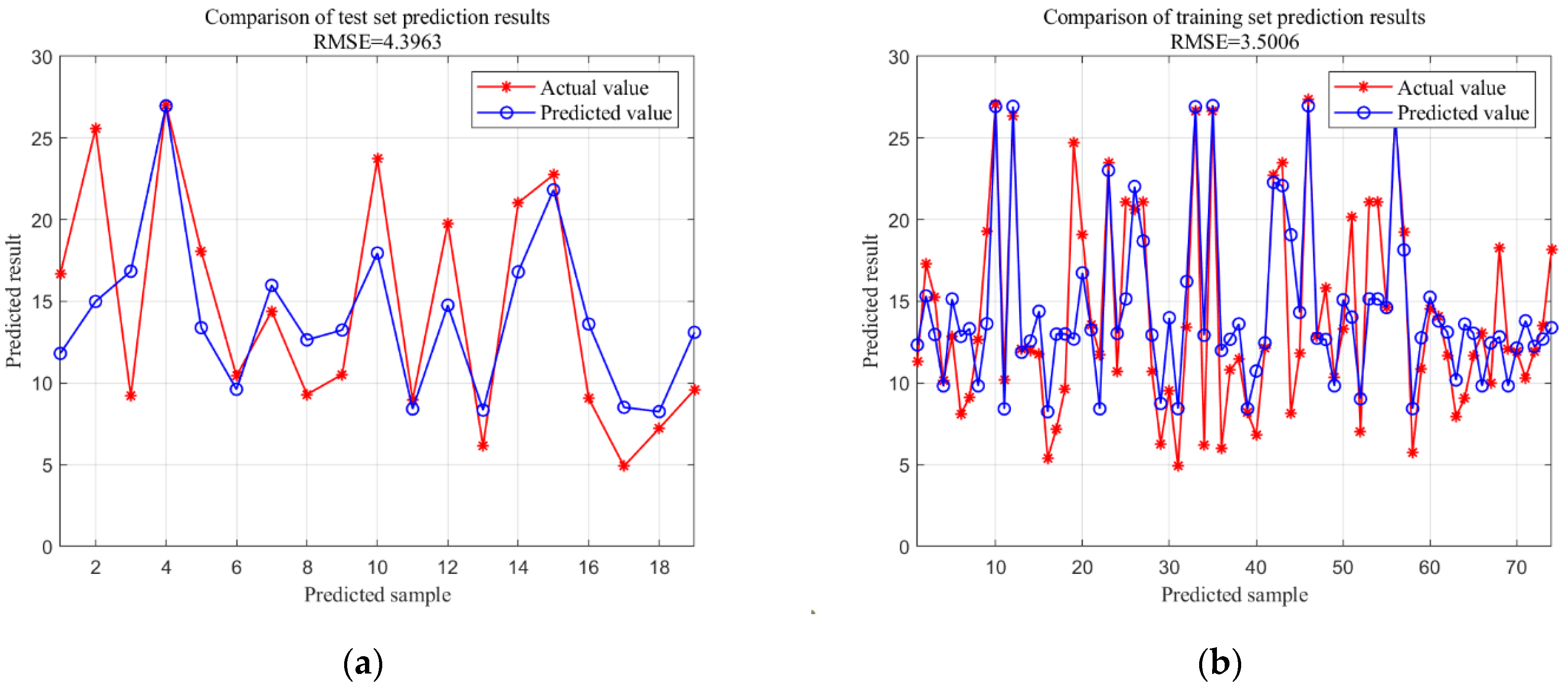
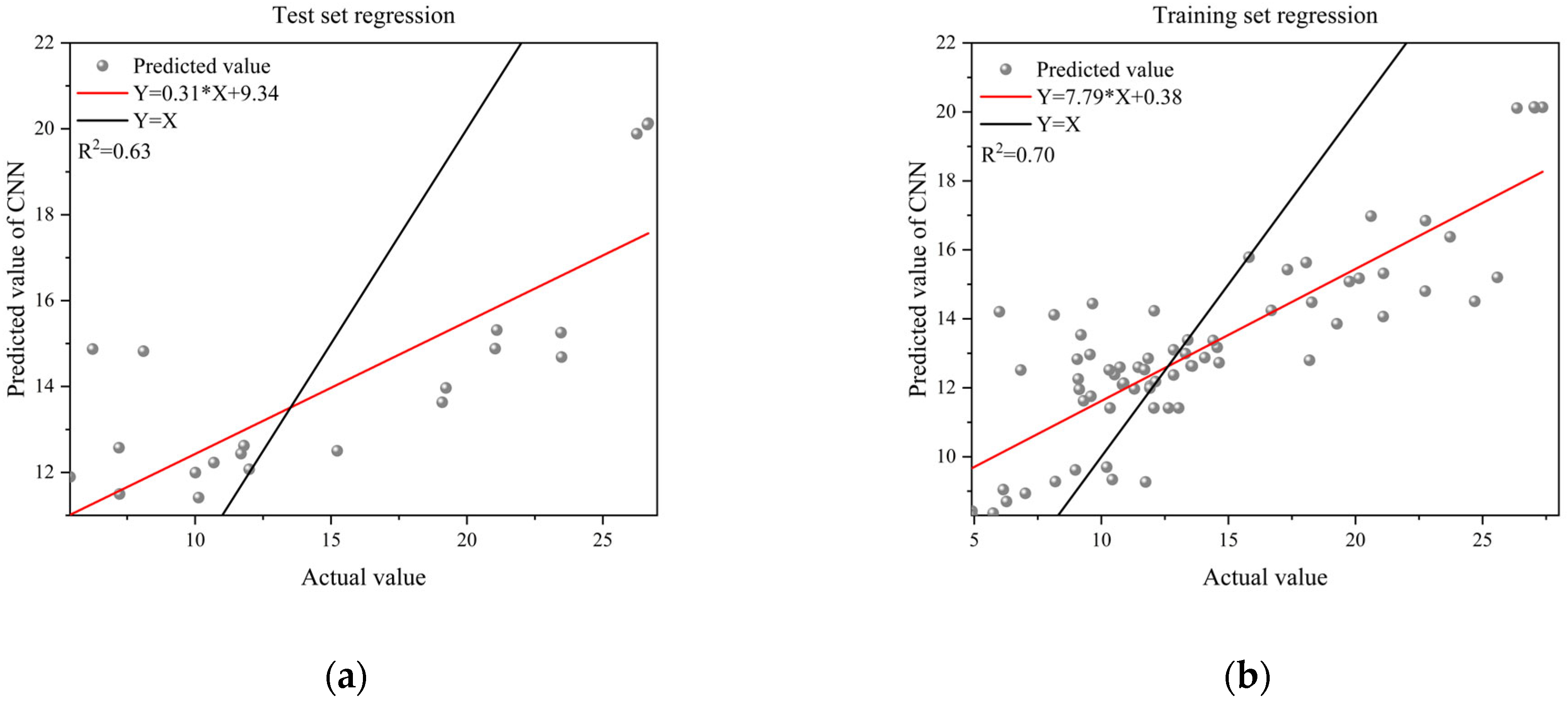
| CNN | 4.3963 | 3.2794 | 28.8084 | 0.6354 |
| LSTM | 8.5470 | 7.147 | 53.7685 | −5.5987 |
| BiLSTM | 6.3117 | 5.5958 | 35.4587 | −2.9485 |
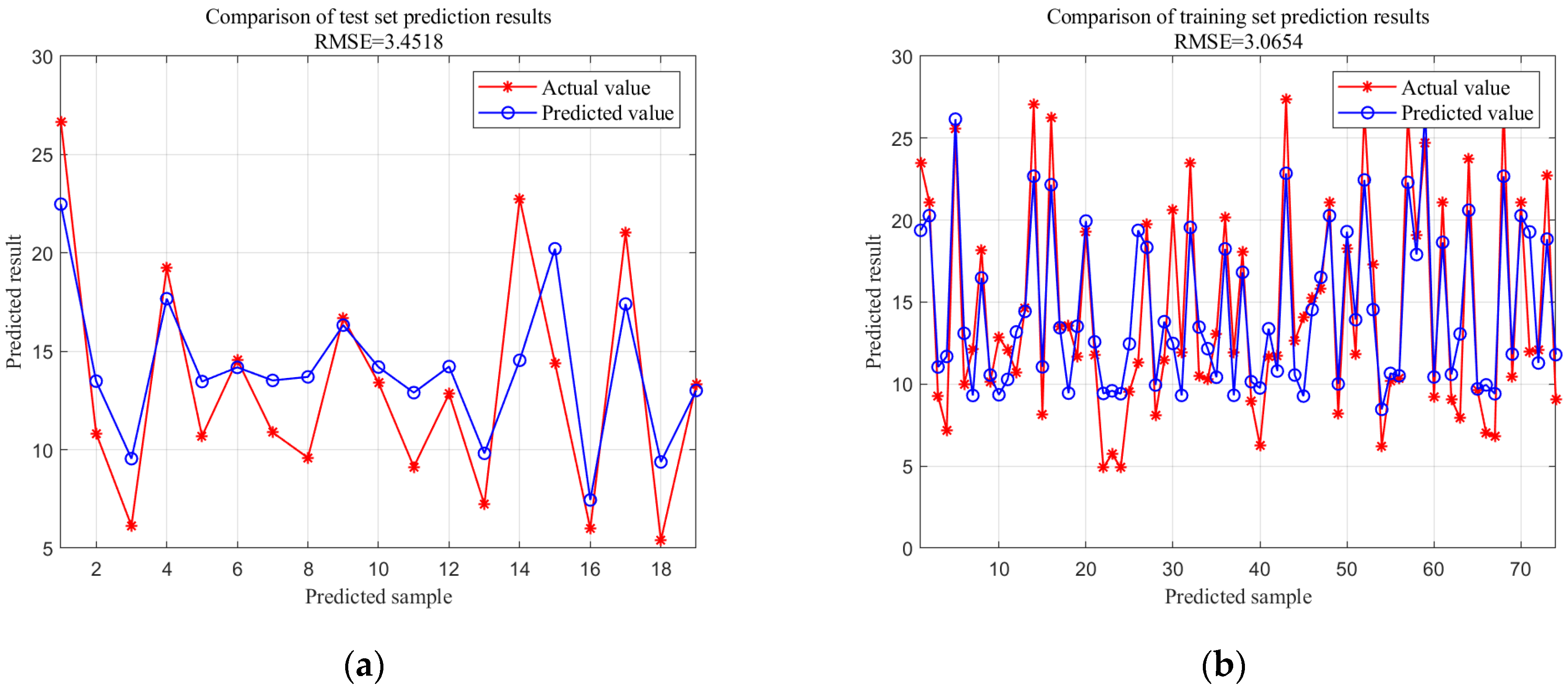
| BiLSTM-Adaboost | 3.0654 | 2.5289 | 15.0926 | 0.7664 |
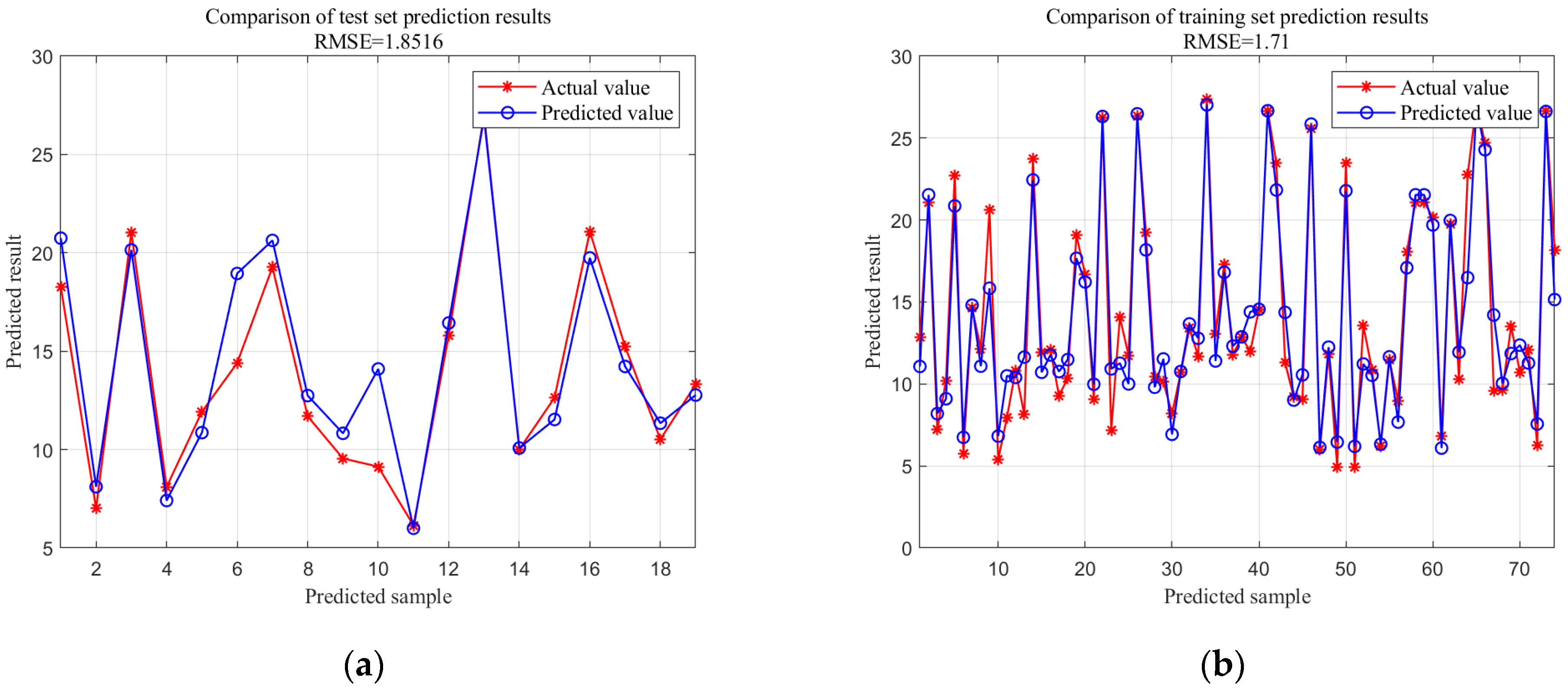
| CNN-LSTM | 1.8516 | 1.3291 | 8.1882 | 0.8828 |
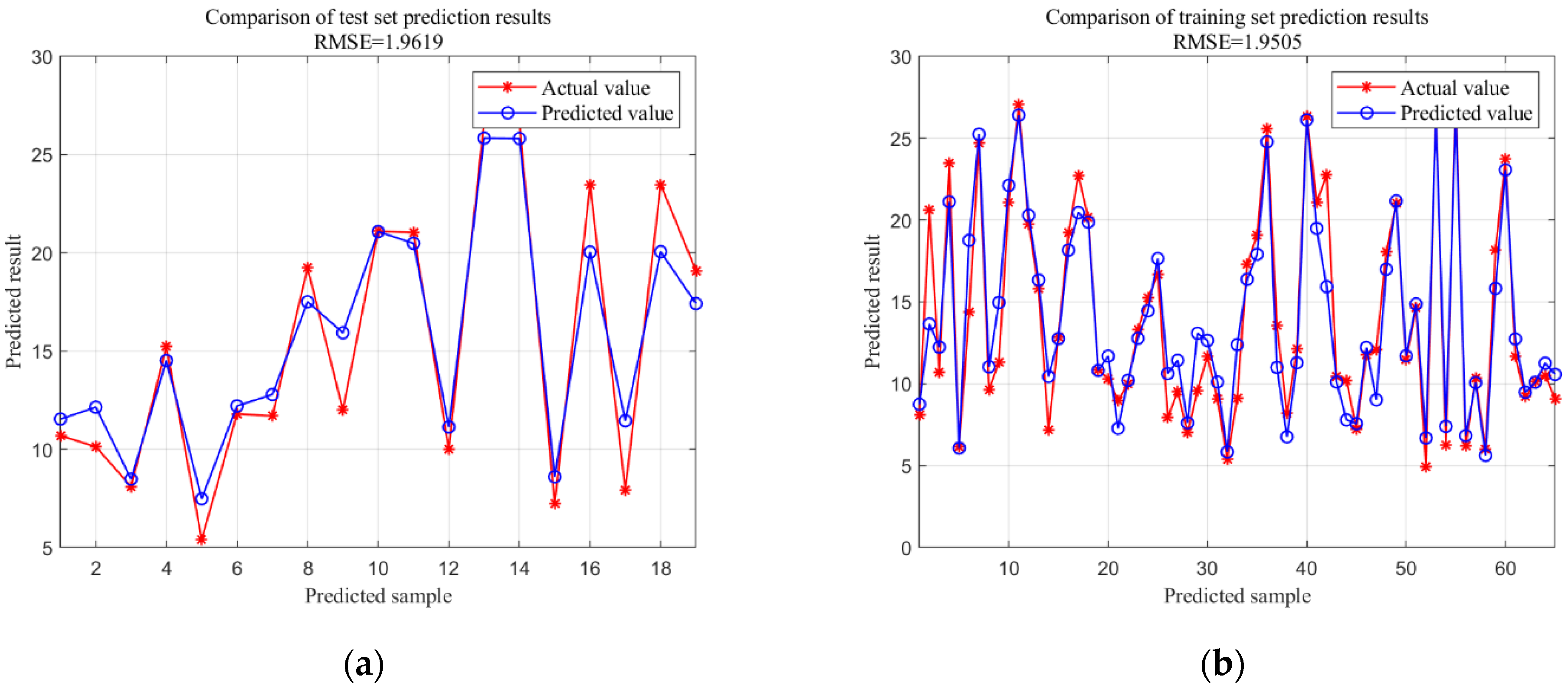
| CNN-BiLSTM | 1.9619 | 1.1757 | 5.9847 | 0.9425 |
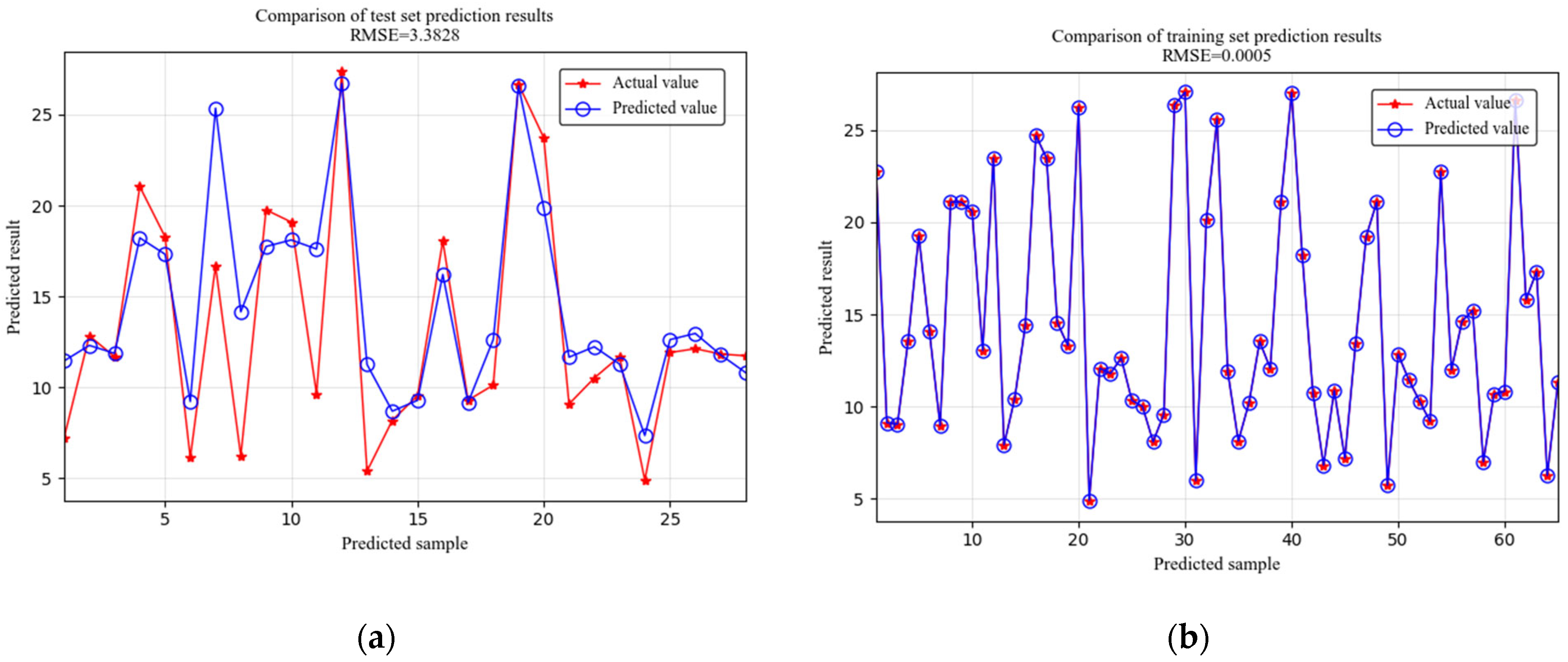
| CNN-BiLSTM-XGBoost | 3.3828 | 2.3119 | 25.0796 | 0.7205 |
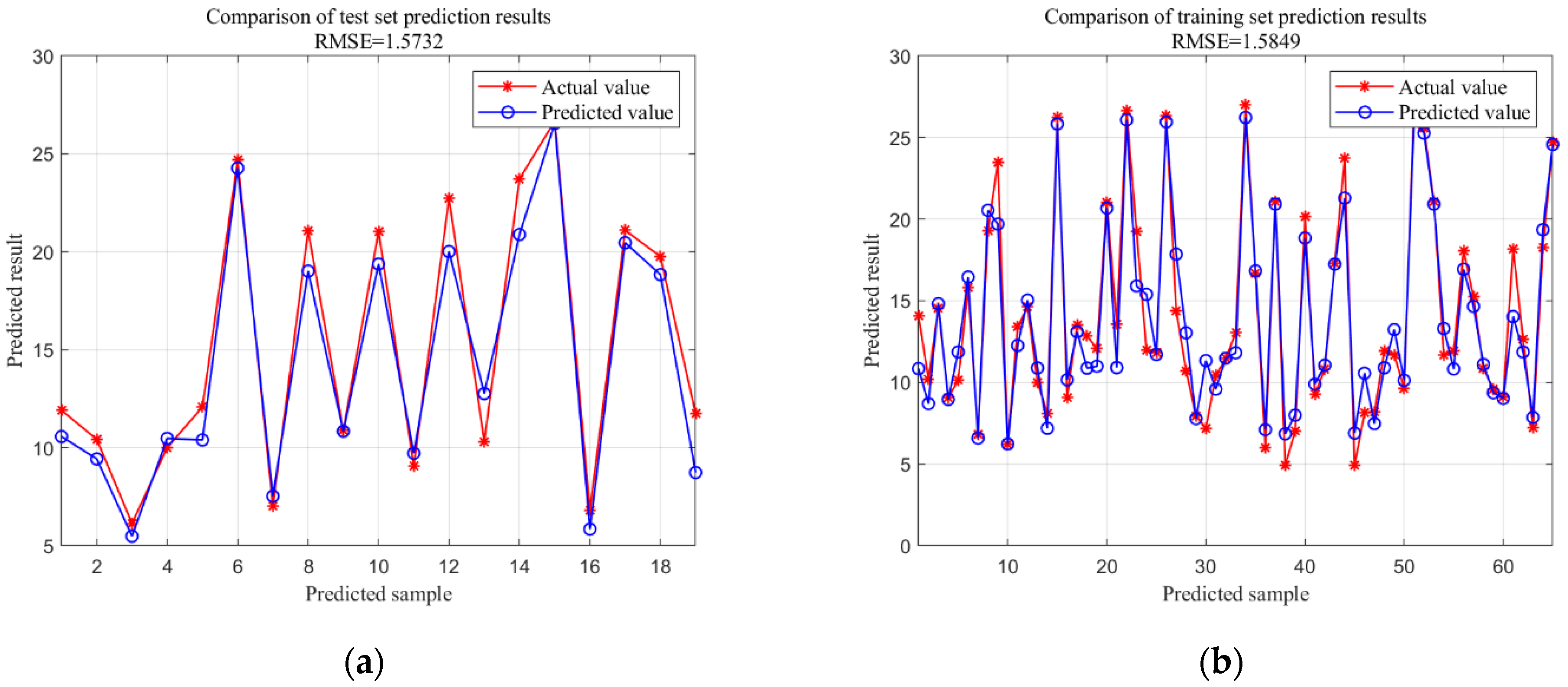
| CNN-BiLSTM-Adaboost | 1.5732 | 1.2463 | 4.6944 | 0.9532 |
| Evaluation Methods | CNN-BiLSTM-Adaboost | ASME B31G | DNV RP-F101 | PCORRC |
|---|---|---|---|---|
| average relative error (%) | 4.694 | 33.595 | 48.085 | 45.447 |
| number of points not meeting conservatism | 1 | 2 | 4 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Wang, Y.; Gu, C.; Guo, Y.; Yang, J.; Xiao, H.; Yang, Z. An Integrated CNN-BiLSTM-Adaboost Framework for Accurate Pipeline Residual Strength Prediction. Appl. Sci. 2025, 15, 9059. https://doi.org/10.3390/app15169059
Lu Q, Wang Y, Gu C, Guo Y, Yang J, Xiao H, Yang Z. An Integrated CNN-BiLSTM-Adaboost Framework for Accurate Pipeline Residual Strength Prediction. Applied Sciences. 2025; 15(16):9059. https://doi.org/10.3390/app15169059
Chicago/Turabian StyleLu, Qian, Yina Wang, Cheng Gu, Yingqing Guo, Jingfei Yang, Hang Xiao, and Zhenfa Yang. 2025. "An Integrated CNN-BiLSTM-Adaboost Framework for Accurate Pipeline Residual Strength Prediction" Applied Sciences 15, no. 16: 9059. https://doi.org/10.3390/app15169059
APA StyleLu, Q., Wang, Y., Gu, C., Guo, Y., Yang, J., Xiao, H., & Yang, Z. (2025). An Integrated CNN-BiLSTM-Adaboost Framework for Accurate Pipeline Residual Strength Prediction. Applied Sciences, 15(16), 9059. https://doi.org/10.3390/app15169059