Abstract
The problem of the numerical estimation of contact strength for parts with stress concentrators, such as non-metallic inclusions, is considered. Using the approaches of mechanics and mathematical modeling, a variational formulation of establishing a relationship between the characteristics of stress concentrators and the strength parameters of the surface layers of parts is presented. In solving the problem, the numerical tools used were the Fenics finite element analysis package and its implementation in Python. The implementation of the developed methodology was carried out on the practical task of determining the strength of railway wheels with subsurface inclusions. The studies have shown a nonlinear dependence of changes in the serviceability of the components’ surface layers on such characteristics of elliptical inclusions as their depth, linear size of the weakened zone, and the ratio of the principal radii. It has been established that the most dangerous in terms of operation are inclusions located at a depth of 3.5 mm from the edge of the contact interaction and having a weakening zone around them.
1. Introduction
The problem of maximizing the service life of parts is considered a key issue in modern engineering. Its solution is inextricably linked to the assessment of the impact of the geometry and material structure of products on their performance parameters. Engineering trends that are typical of the current state of technology development indicate an increase in the use of stress concentrators of various kinds and scales in critical structures. This is due to the requirements of practice for local weight reduction of parts and reduction of their manufacturing cost. Additional factors that contribute to the emergence of stress concentrators are imperfect control over the processing of parts, their maintenance, and intensified operating conditions. This causes a significant change in the stress state not only in certain local areas, but also in the entire product. As a result, its failure often occurs in areas and time intervals other than those expected to be most favorable for failure. Failure of machine and equipment parts during operation is, in most cases, caused by fatigue or loss of strength and is determined by the parameters of the stress state of the object of study [1]. The stress state is a key factor in the operation of products, characterized not only by the value of the stress tensor or its scalar equivalent at each point, but also by the specifics of its distribution [2,3].
Often, even the distribution of the stress–strain state of a structure determined with sufficient accuracy does not guarantee the finding of engineering-based parameters for the long-term serviceability of parts. To solve this problem, it is necessary to know both the local and integral distribution of strength parameters in the product material, and this is also a rather complex task in its own right.
It should be noted that despite a large number of publications on the study of the strength and durability of bodies, the issue of the influence of stress concentrators on the distribution of the stress state, local and integral strength, and the serviceability of parts as a whole is still open and not fully resolved [4,5]. The morphology of geometric and physical stress concentrators can vary considerably [6,7]. They can be circular, elliptical, rectangular, or polygonal in shape with complex configurations. Each of these concentrator shapes has its own characteristics in terms of its effect on the formation of the stress–strain state in structural elements. Thus, the presence of circular inclusions is a source of stress state disturbances, the distribution gradient of which depends on the radius of the stress concentrator and the ratio of the mechanical characteristics of the inclusion and the base metal. That is, a stress state is formed, which is characterized by a one-dimensional directed change around the stress concentrator. Due to this, this type of stress concentrator is the least dangerous during operation. Rectangular and polygonal inclusions are sources of more complex stress states, especially in the vicinity of their vertices. Depending on the angle at the vertex, a stress state is formed, characterized by two-dimensional gradience and significant coordinate heterogeneity. At the same time, stress concentrators in the form of polygons with the most dangerous acute angles are formed quite rarely, which allows this type of concentrator to be classified as having a medium level of danger during product operation. The most dangerous during product operation, especially under friction conditions, are elliptical inclusion concentrators due to the formation of stress state areas with significant gradient parameters in the vicinity of their vertices. It is in these areas that weakening and microcrack propagation processes occur, as confirmed by both theoretical calculations and experimental data [8,9]. Such types of inclusions are most often the cause of accelerated destruction and wear of the surface layers of friction pairs, which is called pitting [9]. The process of surface destruction significantly depends on the ratio of the mechanical characteristics of the base metal and the inclusion, the orientation of the concentrator, and the load regime of the part [10].
However, approaches, both analytical and numerical, that allow the above-described parameters of elliptical-type physical stress concentrators to be taken into account in the performance of products are practically absent in the literature.
In this regard, it can be concluded that research on the development of methods for numerical evaluation of strength parameters of parts containing physical stress concentrators is relevant and in demand.
Historically, the first methods that allowed assessing the influence of stress concentrators on the performance properties of materials were approaches based on the practical application of analytical functions with complex variables. These methods are still used today, and allow for the assessment of the stress–strain state in the vicinity of concentrators for bodies with geometry described by smooth functions. That is why it is possible to analyze the change in stresses and strains for most typical forms of stress concentrators used in classical engineering structures. A thorough summary of the results obtained with the engineering calculations presented is given in [3,4,5].
For example, article [3] compares theoretical methods for assessing stress concentrators with their actual data obtained from experiments, in particular, by the method of photoelasticity. The authors noted that the stresses calculated using analytical methods often differ from the actual values due to the failure to take into account the characteristics of the zones close to the concentrators. It should be noted that in this paper, the parameter of the state of the interface of the zone ‘stress concentrator–base metal’ was not taken into account. This can likely be explained by the peculiarity of the scientific interests of the authors of this article, as well as the complexity of the modeling and experimental plan that arises when additional consideration of the properties of this zone is taken into account.
A comprehensive reference book [4] provides engineering calculation formulas for most cases of geometric stress concentrators that may occur in the manufacturing of parts. This paper points out the limitations of analytical relations, which are the difficulty of simultaneously taking into account the peculiarities of load distribution and the type of concentrators. Due to the engineering orientation of the research, the condition of surfaces and near-surface zones of stress concentrators is not analyzed. As a result, certain limitations are created in the calculation of structures operating under localized loads and containing concentrators, since their simultaneous impact on the reliability of the product is not taken into account.
Paper [5] studies the influence of stress concentrators on the strength and durability of products from the standpoint of fracture mechanics. It is shown that the state of the material of parts at the level of structural components plays a significant role in the processes of its weakening and is practically not taken into account by analytical relations. Since the monograph is a continuation of the classical studies of mechanics for bodies with stress concentrators, the state of the near-surface regions of the material close to these zones was not studied in the paper.
Further development of approaches to assessing the impact of stress concentrators on the performance of parts is associated with the expansion of the concept of a concentrator. Currently, this term is understood not only as a sharp change in the geometry of parts, but also as the presence of inclusions in the material. In the first case, we speak of geometric concentrators, and in the second, of physical ones [11,12,13]. Studies on the influence of physical stress concentrators are presented in [12,13], aimed at establishing the relationship between the stress concentration factor in the body, the nature and shape of inclusions, and the peculiarity of the connections between inclusions and the matrix.
For example, in [12], an analysis of the effect of inclusion placement on the distribution of stresses and strains for a plate in rigid contact with the inclusion and base material was carried out. However, the issue of the peculiarities of the stress state parameters at the interface ‘stress concentrator–base metal’ and its influence on the strength of structures were not considered. The authors of [13] studied the effect of inclusions at the level of structural components on the stress–strain state of the material. The monograph [14] considers the criteria for material failure in the vicinity of stress concentrators, taking into account the physical state of the zone before the crack. Approaches to assessing the stress–strain state of the entire structure containing stress concentrators have been developed, but no determination of its strength characteristics in local boundary zones has been made. This is due to the complexity of forming a reasonable criterion in the transition from studies of the state of local zones to the entire product.
The influence of stress concentrators on such critical parts as machine shafts was studied in [15]. It shows the distribution of stresses caused by local changes in the geometry of products by analytical and numerical methods, taking into account the peculiarities of the state of the surface layers. Paper [16] presents the development of analytical and numerical methods for determining stress and strain fields in the vicinity of soft and hard stress concentrators with different properties. The study of the parameters of the influence of elliptical inclusions in shell systems on the strength of the structure is shown in [17]. The influence of inclusions on the redistribution of the stress–strain state and the change in the maximum stress intensity was established. At the same time, as noted in all of the above studies, the role of the characteristics of stress concentrators in the formation of structural performance is open and not fully explored. The issues of the influence of a set of stress concentrators with different parameters and origins on the operational properties of products are particularly poorly studied.
The analysis of papers [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] allows us to note that there are certain limitations that are common in the study of stress concentrators by analytical methods. They consist of not taking into account the state of the transition zone of the metal–inclusion interface and its impact on the performance of parts.
A special feature of modern analytical approaches to assessing the impact of stress concentrators on the performance of products is that they do not take into account the state of the boundary region ‘base metal—physical stress concentrator’. This is due to both the complexity of the mathematical formulation of this type of problem and the limited use of complex variable approaches. This creates a certain gap in the study of the behavior of real parts with stress concentrators, since the properties of boundary zones often differ from both the base metal and the inclusion. The state of these boundary zones, taking into account the formation of a stress state with significant gradient parameters, leads to weakening and the attainment of a limit state precisely in these local areas. The incompleteness of ideas about the processes of strength loss of structural elements with stress concentrators and the limitations of the mathematical apparatus in the formation of such problems are one of the significant gaps in the study of bodies with inclusions.
The rapid development of computational mathematics and computer mechanics has had a significant impact on the study of bodies with stress concentrators. It has become possible to estimate the change in stresses and strains in the vicinity of stress concentrators of any geometry for parts with sufficient speed and accuracy, which has already been implemented at the level of modern CAD and CAE systems [4].
The current state of materials engineering, processing technologies, and operation of products poses new challenges in the development of calculation schemes for the influence of stress concentrators on the parameters of product properties.
New, often artificially created hierarchically nested compositions of materials are constantly emerging, and their processing technologies and working conditions are becoming more complex [17,18].
This necessitates the introduction of new mathematical modeling technologies that allow establishing links between existing stress concentrators and the heterogeneous stress–strain state at a representative level characteristic of a given material. Such approaches are important for functional gradient, composite materials formed using additive and surface engineering technologies in the analysis of generalized performance parameters of components.
Another little-studied issue is the development of mathematical approaches to assessing the impact of stress concentrators on the service life of products, while taking into account the specifics of the modes and nature of the loads that accompany the operation of parts, components, and structures. This is an urgent problem, since modern technological development leads to the appearance of intense and localized loads in components. Their consideration is based on the formulation of computational mechanics problems that relate the features of load modes and the characteristics of surface stress concentrators [19,20].
As a result of localized loads, a heterogeneous stress–strain state is formed in the bodies, the technological optimization of which allows significant control over the strength and service life of components [20,21].
The development of mathematical approaches for solving these problems is especially in demand for scientific support of surface engineering technologies in the formation of a given structurally heterogeneous state of components and products [21,22].
However, despite the availability of publications related to theoretical and applied studies of the influence of stress concentrators on the performance of structures under distributed and localized loads, there are currently a number of tasks that are not presented in the literature but require a solution. These include the development of numerical methods that allow for assessing the impact of non-metallic inclusions on the distribution of the stress state in the inclusion–base metal interface and, as a result, on the performance of components.
This suggests that it is advisable to conduct research on the development of mathematical modeling methods for assessing the influence of inclusion parameters on the performance characteristics of products operating under localized loads.
When considering any practical problem, it is important to create mathematical models for its solution that clearly demonstrate the influence of the main processes on the behavior of the objects under study. One of the advantages of two-dimensional mechanics problems is the ability to simultaneously display the studied fields of displacement, deformation, and stress throughout the body. This creates convenient conditions for a thorough assessment of the role of inclusions in the performance of the product. In this regard, this article uses a 2-D model of the influence of elliptical inclusions on the contact strength of products.
2. The Aim and Objectives of the Study
The aim of the study is to develop a methodology for numerical evaluation of strength parameters of components with subsurface physical stress concentrators to identify their impact on the performance of structures. This will enable us to establish the distribution of performance properties in local near-surface zones of components, as well as to recommend methods for technological control of these parameters using surface engineering methods.
To achieve this goal, the following tasks were set:
- -
- to build an algorithmic scheme for numerical study of the operational behavior of friction pairs with subsurface defects–non-metallic inclusions of the elliptical type;
- -
- to establish the influence of the presence of this type of defect on the possibility of developing weakening processes in their boundary zones;
- -
- to study the change in the strength of the product as a function of inclusion characteristics such as the depth of their occurrence, the linear size of the weakened zone, and the ratio of principal radii;
- -
- to propose approaches to reduce the impact of inclusions by means of technological modification of the surface layers of products.
The practical application of the strength assessment of parts with subsurface stress concentrators in this work is implemented on parts such as railway wheels. The first task is related to the construction of a mathematical problem of loading a wheel fragment containing a stress concentrator and a numerical (computer) scheme for its solution. Based on the findings of the distribution of the contact strength field in the studied area, the second task helps establish the field of weakening in the body. The third part of the task involves conducting applied research related to the influence of the inclusion parameters and their boundary zone on the performance of wheels. The fourth part is intended to justify technological recommendations for reducing the negative impact of inclusions on the reliability of the surface layers of wheels.
3. Materials and Research Methods
The operational strength parameters of components with stress concentrators serve as the subject of the study.
The main working hypotheses of the study were as follows:
- -
- stress concentrators are additional sources of stress state perturbations that affect the contact strength of surface layers;
- -
- the most pronounced effect of concentrators on the performance of products is manifested in highly loaded structural elements operating under localized loads;
- -
- the peculiarities of material behavior in the ‘inclusion–base metal interface’ are often decisive in the operation of products;
- -
- to assess the operational parameters of the surface layers of components with physical stress concentrators, it is necessary to use reasonable criteria for the material’s limit state.
Railway wheels are one of the types of components that can fully fall under the object of study of this paper, with simultaneous satisfaction of the conditions of all hypotheses. They receive and transfer localized loads from rolling stock to the track. The safety of rolling stock operations depends on their technical condition [23,24]. In the EU countries, standards are used to regulate the strength of wheels as an element of the rolling stock structure [25,26].
These regulatory documents define approaches to assessing the strength of wheels based on stress–strain analysis with subsequent study of their durability, which should be more than 107 load cycles without the appearance of cracks exceeding 1·10−3 m in size.
The main weakness of the calculation methods proposed by these standards is the a priori assumption that the wheel material is characterized by the homogeneity and isotropy of properties.
This assumption is used to simplify the analytical calculation of the stress state of wheels during their long-term operation, but it is not always fulfilled for the following reasons:
(1) many national regulations recommend that the rolling surface be hardened during (or before) operation;
(2) during operation, the structure of the original layer of the wheel surface material changes, also known as tribomutation.
As a result, tribologically transformed layers (TTL) can contain a deformed microstructure, stress concentrators of physical and geometric origin, which are sources of stress state perturbations, and zones with reduced strength parameters [23,24].
For many tribological systems, the contact surfaces of parts consist of several layers: the first surface zone contains organic and inorganic molecules absorbed from the environment; the next zone is the product of chemical interaction between the metal and the environment; the third zone has properties that differ from those of the base metal; the last zone is the base metal. It should be noted that the anisotropy of properties in such layers is a rare phenomenon, but the heterogeneity of properties is the most common characteristic of these zones.
The structure of the surface layers of wheels formed as a result of targeted technological and operational influences is characterized by gradient properties, and it is not advisable to use mathematical models of homogeneous media to describe it adequately.
In this regard, the following author’s model of a continuous non-homogeneous isotropic medium is proposed, taking into account both the possibility of coordinating changes in the basic elastic properties and the spatial distribution of damageability [27]:
where is the displacement vector; is the unit tensor; is Hamilton’s differential operator; is bulk compression modulus; is shear modulus; is the tensor product symbol; is the scalar product symbol; is damageability; . In expression (1), is the area occupied by the body under study and is the surface of the body under study. Damage is understood as a certain continuum assessment of structural degradation, which can be carried out using the scalar function . We will interpret as the classical studies in the mechanics of damaged media, when it is assumed that the material is completely intact at and the material is destroyed at [28].
In general, damageability is understood as a decrease in the elastic response of a material due to a reduction in the effective area that transfers force from one part of the body to another, which in turn is caused by the appearance of a scattered field of microdefects of various origins (microcracks, dislocations, micropores, etc.) [29]. The practical significance of introducing this value lies in the continuous consideration of all structural imperfections that are difficult to assess individually at a discrete level. At the same time, the limitation for this value is most often represented by model assumptions, according to which this parameter is introduced into mathematical relations. Damage in the body can be measured as a change in the body’s response to various external influences. According to the authors of this work, the best technology for measuring damage is by scattering microhardness or hardness values, which is called the LM hardness method [30].
For most functioning structures, varies in the range of . Additionally, it is assumed that in the area under study, there are N stress concentrators Ki (), each characterized by a vector Yi with M parameters , where is a concentrator number. The coordinates of the concentrators can serve as parameters , their sizes (or radii for elliptical or circular concentrators), angles at the vertices (for concentrators in the form of polygons), the state of roughness of the concentrators’ internal surfaces, etc.
The surface is represented as the following set of domains:
where is the surface area where the load is set; is the area of the surface where the displacement is set (in particular, the conditions for fixing the component); is the unloaded surface area.
As a result of force loads, a stress state is formed in the body, which is characterized by a tensor at each point .
Since the stress state does not unambiguously determine the performance parameters of a component, the following expression will be used to analyze the strength of a body in a local zone:
where is the coefficient of safety margin; is the scalar equivalent of the stress tensor; is the scalar strength equivalent of the material.
When analyzing the relationship (3), one can see that satisfies the condition . Let us assume that the criterion of optimal functioning of the component corresponds to the largest ‘average integral’ value of the expression :
The advantage of relations (3)–(4) is the possibility of their use both for optimizing the stress state of structures and for technological processes of surface strengthening of parts, which allows increasing the operational reliability of products.
They have been tested on a wide range of surface engineering applications, and the results are partially presented in [21,22].
It should be noted that from the standpoint of applied research, there are practically no numerical values for relations (3)–(4). From the standpoint of theoretical concepts of mechanics problems, the presence of second-order discontinuities in the function σ*(x) and the exit of the deformed state from the zone of model concepts of elasticity theory can act as constraints.
The functional (4), characterizing the contact strength, depends on the distribution of damage in the body , boundary conditions, material properties , , and stress concentrators, which are characterized by a collection of sets Yi ():
This problem statement is generalized.
Let us focus on the problem of analyzing the stress state and the level of contact strength of railway wheels in the possible presence of a subsurface stress concentrator of physical origin (inclusion) of elliptical shape at a certain depth d from the surface, with a zone of weakened material around the inclusion with a level of damage ω.
To study the stress–strain state in the zone of the physical stress concentrator of the wheel, we consider this problem as a contact problem in a 2-D formulation under force loading of a part fragment that is directly close to the edge of the contact interaction (Figure 1).
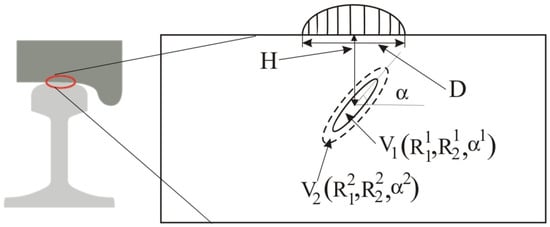
Figure 1.
Contact problem for a body with a stress concentrator: V1 is physical stress concentrator, V2 is area around the stress concentrator with an increased damage value, main radii of the areas V1 and V2, αj is a rotation angle of areas V1 and V2 relative to the normal to the load plane, D is size of the contact zone, H is depth of the physical stress concentrator, .
Area V1 is the area containing inclusions, V2 is the area of the ‘inclusion–base metal’ interface. The properties of area V2 differ from both the base metal and the inclusion.
The value of the initial power load in the contact zone is set to 12.5∙104 H, the friction coefficient is 0.25, and α1 = α2 = 60°. Assume that the center of the elliptical stress concentrator is 2 mm deep from the center of the contact area. The dimensional parameters of the elliptical concentrator are taken to be equal to mm, mm. Parameters of domain V2 are (). Damage level ω is 0.8.
The values of force loads and friction coefficient were selected based on literature sources [21,31]. The depth of occurrence and the dimensional parameters of the defect were adopted based on [32]. When selecting the parameters of the boundary zone ‘inclusion—base metal’, we relied on the thorough work [33], choosing those at which the phenomenon of loss of working capacity may occur with less than 105 load cycles. This number of cycles was chosen because it is less than the inter-repair mileage of the rolling stock.
Suppose that the inclusions are of the SiO2 type with the following mechanical characteristics: E = 0.7·1011 Pa, σ0 = 330 MPa. The main material is wheel steel with E = 2.1·1011 Pa, σ0 = 1100 MPa. Here, E is the modulus of material elasticity and σ* is material tensile strength. The initial data presented above are based on the analysis of scientific and regulatory literature on the reliability of railway wheels with operational or technological defects [32,34,35].
4. Distribution of Stress State and Contact Strength of Components with SiO2 Inclusion
4.1. Algorithmic Scheme for Numerical Study of the Operational Behaviour of Friction Pairs with Non-Metallic Inclusions of Elliptical Type
To solve the problem described in paragraph 2, we will use computational mechanics approaches, namely the Fenics finite element analysis package and its implementation in Python [36]. This toolkit provides ample opportunities due to the use of various mathematical models of the material continuum, scalability, and the absence of any commercial and educational restrictions. The main developers of the Fenics package are universities in the USA and Sweden. Post-processing of the results of finite element analysis was performed using the free package MatPlotLib for Python [37]. The material continuum model (1) was used as the basic model.
The problem was solved by the finite element method (FEM) using the method of weighted nonunions (weak formulation of the FEM) [36,37], where the weighting function is the vector :
is the area of integration, is the stress tensor, which according to model (1) is equal to:
The essence of the weak FEM formulation is to select a function distribution that allows us to ensure the basic condition (6) in a given functional space as accurately as possible.
Weak formulation is one of the ways to help solve FEM mechanics problems by passing from the continuum description of mathematical models to systems of linear algebraic equations. Since the solutions of these equations are a discrete distribution of the desired value. In the case of Equation (1), these are displacements that are converted into stresses according to Hooke’s law, and then, according to Equation (3), into the coefficient of safety of the structure.
After integrating by parts of expression (6), one can obtain the following result:
Taking into account the ratio , where is the surface vector, one can get.
Equation (9) is the basic one for solving the problem of finding the operational parameters of structures operating under power loads.
The number of finite elements in each numerical experiment was equal to 25,218; the type of finite elements was a triangle with quadratic basis functions of the Continuous Galerkin (CG) type [36]. The average size of a finite element is 0.1797 mm.
The integral Mises criterion [33,34] was used as a strength criterion in the following form:
where , .
The advantage of this criterion is that its reliability has been confirmed by a sufficiently large number of experiments in the analysis of the strength of a wide class of both ductile and quasi-brittle materials.
4.2. Determination of the Inclusions’ Influence on the Weakening Processes in the Boundary Zone
As a result of the calculations, we obtained the following distribution of the field of displacements, deformations, and stresses (Figure 2).


Figure 2.
Formed fields in the studied object as a result of force loads: (a) shows displacements; (b) shows stresses in the Mises form (109 Pa).
The stress distribution in the Mises shape at the inclusion–base metal interface is shown in more detail in Figure 3.

Figure 3.
Stress distribution in the Mises shape in a fragment of the studied object around the inclusion.
The analysis of the results (Figure 2 and Figure 3) showed that the displacement field of a body with an inclusion in the considered problem is practically not distorted (Figure 2a). At the same time, the stress field in the contact interaction zone (Figure 2b) has zones of growth directly in the loading zone and a sharp change in the stress state at the metal–inclusion interface (Figure 3).
4.3. Study of the Change in the Strength of Near-Surface Layers Depending on the Depth of Inclusion, the Linear Size of the Weakened Zone, and the Ratio of the Main Radii of the Physical Stress Concentrator
The next changes for the functional (4), depending on the following parameters, were studied:
- (1)
- the depth of the inclusion L(d), where d is the distance of the inclusion from the contact surface (Figure 4);
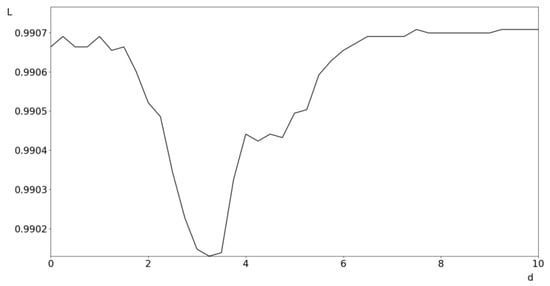 Figure 4. Dependence of the level of contact strength for the wheel (L) on the location of the inclusion (d, mm) relative to the contact surface.
Figure 4. Dependence of the level of contact strength for the wheel (L) on the location of the inclusion (d, mm) relative to the contact surface. - (2)
- the linear size z of the weakened zone around the concentrator L(z), (Figure 5);
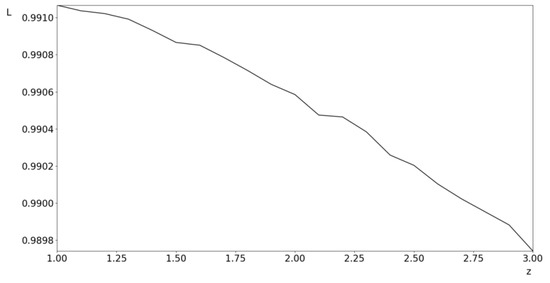 Figure 5. Dependence of the change in the level of contact strength (L) of a structural element on the size of the weakened zone around the inclusion z.
Figure 5. Dependence of the change in the level of contact strength (L) of a structural element on the size of the weakened zone around the inclusion z. - (3)
- the ratio of the main radii of the concentrator L(n), where , (Figure 6).
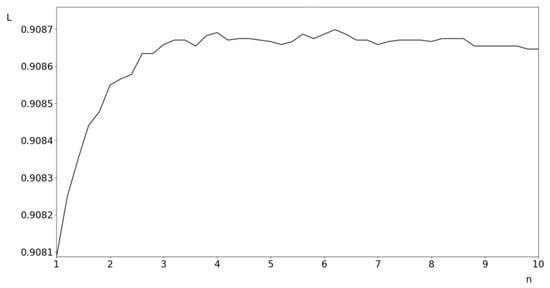 Figure 6. Dependence of the change in the level of contact strength of a structural element (L) on the ratio of the main inclusion radii (n).
Figure 6. Dependence of the change in the level of contact strength of a structural element (L) on the ratio of the main inclusion radii (n).
For the first numerical experiment, the parameter d was changed from 0 to 10 mm in steps of 0.25 mm (40 numerical experiments were performed in total).
As can be seen from Figure 4, the dependence of the value of the contact strength on the location of the inclusion is as follows: at first, the contact strength decreases, reaching a minimum value at a depth of 3–3.5 mm, then begins to increase, and at a depth of the defect of more than 7 mm remains almost constant.
For the second experiment, it is assumed that the value of () (Figure 1), where changes from 1 to 3 with step 0.1 (that is, 20 numerical experiments were conducted). As a result, the following distribution of the functional L on the parameter z was obtained (Figure 5).
As can be seen, as the weakened zone around the inclusion increases, the contact strength decreases, as shown in Figure 5.
When studying the change in contact strength as a function of the ratio of the principal radii of the physical stress concentrator L(n), where , parameter n was changed from 1 to 10 with step 0.2 (that is, 47 numerical experiments were conducted).
As a result, we obtained the following distribution of the functional L of n (Figure 6).
The results obtained suggest that with an increase in the parameter n, the contact strength of a structural element increases. At the same time, there is a value of n (greater than or equal to 3) after it is attained, and the contact strength remains constant.
4.4. Proposed Approaches to Technological Modification of Surface Layers to Reduce the Impact of Inclusions
Traditional mechanical approaches to increasing the strength and durability of structures by introducing new materials and solutions based on them have now reached a certain limit. Therefore, a new trend has already emerged in modern engineering: the development of new technologically modified layers that restore and protect critical parts of machinery and equipment.
It should be noted that controlling the distribution of both material properties and the stress–strain state in a component is one of the principles of creating products with controlled performance parameters. From the standpoint of technological mechanics, this problem itself consists of three independent, though interrelated, subtasks:
(1) establishing the performance of modified surface layers;
(2) determination of the impact of the performance of modified surface layers on the strength properties of the component (product);
(3) assessment of the bearing capacity of the system ‘modified layer–base metal’.
The advantage of the numerical methodology proposed in this paper is its sufficient versatility, determining the optimal parameters of layers via different methods of technological modification and formation of the operational properties of products on the basis of the same principles.
Currently, two approaches are being developed in the formation of coatings:
(1) the creation of multilayer coatings that provide a smooth transition from the base to the surface;
(2) the formation of coatings with variable composition in depth.
The main disadvantage of the first approach is its complexity, as multilayer coatings require a variety of equipment combined into a single process cycle. The second option is more attractive and economically feasible.
Therefore, it is proposed to form coatings using ‘mono-technological’ solutions according to the scheme of plasma hardening or electro-erosion alloying, which is given in [19,20,21,22,38]. The main requirement for such coatings (modified near-surface layers) should be the formation of gradient structures with increased and decreased local strength parameters.
This reduces the negative impact of stress state disturbances caused by stress concentrators and, as a result, increases the performance of products.
Using the approaches developed by the authors, the possibility of increasing the contact durability of 12Kh17T (AISI 430) steel by 3.7 times was demonstrated and experimentally confirmed by optimizing the laser alloying modes [39]. The rational thickness of the plasma-hardened layer of locomotive wheel tires was also established depending on the operating parameters [40].
5. Discussion
The research is a further development of the studies on assessing the impact of stress concentrators on the performance properties of products in the direction of taking into account the peculiarities of the stress state distribution in the zone ‘stress concentrator–base metal’. It has been shown that the presence of subsurface inclusions in a body significantly changes its stress–strain state, transforming it from homogeneous to heterogeneous with the presence of a spatial gradient under localized loads.
The fact (Figure 3) of a sharp change in the stress state at the metal–inclusion interface was established. This may indicate the possibility of crack formation (structural weakening) not by the mechanism of tearing or shearing, but due to zones with lower strength parameters, in particular, with increased damage. A sharp distortion of the stress field leads to the development of negative phenomena such as corrosion, diffusion saturation of this zone with impurity elements, etc.
Due to the methodology proposed in this paper and the research conducted, the dependence of the change in the strength of the product on characteristics of inclusions, such as their depth, linear size of the weakened zone, and the ratio of the principal radii, was established for the first time.
The results obtained for the first time showed the following:
1. The most ‘dangerous’ inclusions are those located at a depth of 3–3.5 mm from the surface of the contact interface, since at this value of the defect depth, the level of contact strength decreases significantly. At a distance of more than 7 mm from the edge of the contact interaction, its effect on the contact strength is almost constant.
2. It has been established that with an increase in the weakened zone around the inclusion, the contact strength decreases, which negatively affects the level of serviceability of parts. Therefore, it is necessary to technologically achieve the minimum value of the size of the weakened zone around the inclusion.
3. The contact strength of a structural element increases with an increase in the ratio of the principal radii of the elliptical inclusion. At the same time, there is a value of n (greater than or equal to 3) after which the contact strength remains constant. The geometric shape of an inclusion has less effect on the contact strength of components than its size.
4. The proposed methodology is universal for the numerical evaluation of the strength parameters of components with inclusions of various types. Its use enables the determination of the influence of the parameters of stress concentrators and their boundary regions on the strength of products under localized loads, with adjustable accuracy.
Experimental validation of the developed methodology on other classes of materials and with a different problem formulation is presented in [39,40]. A good correlation between numerical estimates and data obtained from research on wear of parts under loads close to those specified in the regulations was established. At the same time, the limitations of the authors’ proposal are the a priori assumption of media isotropy and the lack of consideration at the model level of material viscosity and diffusion processes typical, in particular, for the functioning of structural elements under impulse loads in chemically active environments.
The results also have disadvantages. In the course of research, it becomes necessary to conduct a large number of numerical experiments, requiring a significant amount of computing time. One of the ways to reduce the use of machine time is to use surrogate mathematical models in the study of systems with stress concentrators.
The practical significance of the results obtained can be divided into regulatory and technological directions. The first area is related to the introduction of requirements for the limit parameters of non-metallic inclusions in their surface layers in regulatory documents governing the production or operation of rolling stock wheels. The second is aimed at developing and maintaining a technological modification of the wheel material that reduces the negative impact of these concentrates.
It should be noted that the distortion of the stress field in the presence of physical stress concentrators is one of the factors that negatively affect the performance of components. Therefore, to reduce the distortion, we can recommend a technological modification of the surface layers according to the scheme given in [21,22,38].
Many questions about the influence of geometric and mechanical parameters of inclusions on the performance of components remain open. Practically unexplored is the influence of properties of the internal surfaces of inclusions–the base metal and the areas around them on the strength and durability of structures [38,41].
The development of approaches to managing this condition allows us to form ‘mosaic zones’ in the areas of contact interaction of bodies with increased or decreased strength parameters, corresponding to the classical approaches (principles) of Charpy. The development of this principle for friction units allows us to significantly control the efficiency of their work and ensure the reliability of operation.
6. Conclusions
- The paper presents a methodology for numerical study of the behavior of friction pair components with subsurface defects such as non-metallic elliptical inclusions. This methodology allows us to determine the distribution of displacement, stress, and deformation fields in the local near-surface zones of parts, as well as to recommend methods for technological control of these parameters.
- On the basis of the developed methodology, the stress–strain state of railway wheels with the presence of an elliptical inclusion of SiO2 technological origin was evaluated. It was established that there is a sudden change in the stress state at the metal–inclusion interface and the weakening of the structure in this zone at the main radii of the physical elliptical concentrator equal to mm, mm. It is shown that the contact strength of products significantly depends on the dimensional parameters of this zone, and that it decreases with increasing size of the boundary zone.
- The results of the estimation of changes in the components’ strength showed a nonlinear dependence of the serviceability components in the surface layers on characteristics of inclusions, such as their depth, linear size of the weakened zone, and the ratio of principal radii. It is shown that the most dangerous in terms of operation are inclusions located at a depth of 3.5 mm from the edge of the contact interaction and having a significantly weakened zone around them. At the same time, local weakening of parts with inclusions occurs not by the mechanism of tearing or shearing, but due to the formation of zones with lower strength parameters and increased damage. So, it is necessary to avoid the appearance of inclusions at this depth when manufacturing or operating rolling stock wheels.
- The conducted research suggests that the elimination of the negative impact of the inhomogeneous stress distribution around the inclusion can be achieved by controlled modification of the surface layers of components. To do this, it is necessary to ensure the formation of functional gradient structures with high strength parameters and resistance to the formation of scattered and localized damage in the contact zone. This will reduce the negative impact of stress state disturbances caused by stress concentrators and, as a result, increase the performance of products.
- Further development of the research presented in this article is possible in the direction of improving the mathematical model (1), taking into account the anisotropy of media, thermal and diffusion processes typical for contact interaction of bodies in the presence of chemically active media. Another important direction for expanding the approaches proposed in this paper is to consider the combined effect of multiple stress concentrators on the performance of friction pair components. This will enable the development of computer modelling technologies for the functioning of tribosystems with a virtually complete consideration of all the main processes occurring in tribo-couplings.
Author Contributions
Conceptualization, P.P., O.K. and M.K.; methodology, O.K. and M.V.; software, M.K.; validation, M.V.; investigation, P.P., M.K. and O.K.; writing—original draft preparation, P.P., O.K., M.K. and M.V.; writing—review and editing, P.P., O.K., M.K. and M.V.; visualization, M.V. and M.K.; project administration, P.P. and M.V.; funding acquisition, P.P. and M.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Maiti, S.K. Fracture Mechanics: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Kuna, M. Introduction. In Finite Elements in Fracture Mechanics. Solid Mechanics and Its Applications; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef][Green Version]
- Sivak, P.; Delyova, I.; Bocko, J. Comparison of Stress Concentration. Factors Obtained by Different Methods. Appl. Sci. 2023, 13, 13328. [Google Scholar] [CrossRef]
- Pilkey, W.D.; Pilkey, D.F.; Bi, Z. Peterson’s Stress Concentration Factors, 4th ed.; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Gross, D.; Seeling, T. Fracture Mechanics with an Introduction to Micromechanics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Zhu, C.; Yang, L.; Zhao, L.; Ma, Y.; Wang, Y.; Shen, X.; Wang, H. Research and Application of the Original Position Statistical Distribution Analysis Method for Non-Metallic Inclusions in P91 Steel. Metals 2023, 13, 793. [Google Scholar] [CrossRef]
- Nikolic, K.; De Wispelaere, J.; Ravi, G.; Hertelé, S.; Depover, T.; Verbeken, K.; Petrov, R.H. Confirming Debonding of Non-Metallic Inclusions as an Important Factor in Damage Initiation in Bearing Steel. Metals 2023, 13, 1113. [Google Scholar] [CrossRef]
- Oreavbiere, A.; Khan, M. Muhammad Khan Mathematical Complexities in Modelling Damage in Spur Gears. Machines 2024, 12, 346. [Google Scholar] [CrossRef]
- Velázquez, J.C.; Hernández-Huerta, J.J.; Diaz-Cruz, M.; Hernández-Sánchez, E.; Cervantes-Tobón, A.; Cabrera-Sierra, R.; Cabrera-Sierra, R. Study on the Influence of Non-Metallic Inclusions on the Pitting Corrosion of API 5L X60 Steell. Coatings 2023, 13, 1040. [Google Scholar] [CrossRef]
- Zhao, Y.; Ren, G.; Chen, L.; Gu, G.; Zhu, J.; Zhao, A. Influence of Non-Metallic Inclusions on Very High-Cycle Fatigue Performance of High-Strength Steels and Interpretation via Crystal Plasticity Finite Element Method. Metals 2024, 14, 948. [Google Scholar] [CrossRef]
- Murakami, Y. Theory of Elasticity and Stress Concentration; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Zhao, K.; Wany, T.-Y. Influence of Inclusion’s Position of Stress Distribution of Inclusion-matrix Interface. ICTETS 2019, 688, 033054. [Google Scholar] [CrossRef]
- Horton, E.W.; Demir, E.; Agius, D.; Kareer, A.; Collins, D.M.; Mostafavi, M.; Knowles, D. The inclusion and role of micro mechanical residual stress on deformation of stainless steel type 316L at grain level. Mater. Sci. Eng. A 2023, 145096, 145096. [Google Scholar] [CrossRef]
- Savruk, M.; Kazberuk, A. Stress Concentration at Notches; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Murat, T.O.; Fulya, E. Determination of stress concentration factors for shafts under tension. Mater. Test. 2020, 62, 413–421. [Google Scholar] [CrossRef]
- Rana, A.K.; Paul, S.K.; Dey, P.P. Stress field in an isotropic elastic solid containing a circular hard or soft inclusion under uniaxial tensile stress. Mater. Today Proc. 2019, 11, 657–666. [Google Scholar] [CrossRef]
- Hudramovich, V.S.; Hart, E.L.; Marchenko, O.A. Reinforcing Inclusion Effect on the Stress Concentration within the Spherical Shell Having an Elliptical Opening Under Uniform Internal Pressure. Strength Mater. 2020, 52, 832–842. [Google Scholar] [CrossRef]
- Iqbal, M.; Karuppanan, S.; Perumal, V.; Ovinis, M.; Iqbal, M. A systematic review of stress concentration factors (SCFs) in composite reinforced circular hollow section (CHS) joints. Compos. Part C Open Access 2024, 15, 100515. [Google Scholar] [CrossRef]
- Menezes, P.L.; Nosonovsky, M.; Ingole, S.P.; Kailas, S.V.; Lovell, M.R. (Eds.) Tribology for Scientists and Engineers: From Basics to Advanced Concepts; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Pruncu, C.I.; Aherwar, A.; Gorb, S. (Eds.) Tribology and Surface Engineering for Industrial Applications; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Stotsko, Z.A.; Kuzin, O.A.; Kuzin, M.O.; Mechnik, V.A. Estimation of strength properties of functionally graded structures with elliptical stress concentrators. Arch. Mater. Sci. Eng. 2022, 113, 35–41. [Google Scholar] [CrossRef]
- Luchko, Y.Y.; Kuzin, O.A.; Kopylov, V.I.; Kuzin, M.O. Assessment Approaches to Optimum Surface Hardening Parameters of Stress Concentrator-Bearing Structures. Strength Mater. 2023, 55, 720–726. [Google Scholar] [CrossRef]
- Harmon, M.; Lewis, R. Review of top of rail friction modifier tribology. Tribol. Mater. Surf. Interfaces 2016, 10, 150–162. [Google Scholar] [CrossRef]
- Lewis, R.; Olofsson, U. (Eds.) Wheel-Rail Interface Handbook; CRC Press: Boca Raton, FL, USA, 2019; 924p. [Google Scholar]
- EN 13979-1:2022; Railway Applications-Wheelsets and Bogies-Monobloc Wheels-Technical Approval Procedure-Part 1: Forged and Rolled Wheels. CEN: Brussels, Belgium, 2003.
- EN 13262:2022; Railway Applications-Wheelsets and Bogies-Wheels-Product Requirements. CEN: Brussels, Belgium, 2004.
- Kuzin, N. A mathematical model describing the variation in material properties. Int. Appl. Mech. 2015, 51, 474–479. [Google Scholar] [CrossRef]
- Arthur, J.; Evily, M. Metal Failures: Mechanics, Analysis, Prevention; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Kuna, M. Theory–Numeric–Applications. In Meinhard Kuna Finite Elements in Fracture Mechanics; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Lebedev, A.A.; Shvets, V.P. Assessment of damage in structural steels by the parameters of scatter of hardness characteristics in loaded and unloaded states. Strength Mater. 2008, 40, 302–307. [Google Scholar] [CrossRef]
- International Heavy Haul Association. Guidelines to Best Practices for Heavy Haul Railway Operations: Wheel and Rail Interface Issues; IHHA: Virginia Beach, VA, USA, 2001. [Google Scholar]
- Vakulenko, I.O.; Anofriyev, V.H.; Hryshchenko, M.A.; Perkov, O.M. Defects of Railway Wheels; Makovetskyi Public: Dnipropetrovsk, Ukraine, 2009; 112p. (In Ukrainian) [Google Scholar]
- Troshchenko, V.T. The Strength of Materials and Structures; Akademperiodika: Kyiv, Ukraine, 2005; 1008p. (In Russian) [Google Scholar]
- Aspund, M.; Palo, M.; Famurewa, S.; Pantatalo, M. A study of railway wheel profile parameters used as indicators of an increased risk of wheel defects. J. Rail Rapid Transit 2014, 230, 323–334. [Google Scholar] [CrossRef]
- Pukach, P.Y.; Medynskyi, I.P.; Demkiv, I.I.; Kuzin, O.A.; Kuzin, M.O.; Bilushchak, H.I. Optimization of the Stress-Strain State of Functional Gradient Structures with Stress Raisers. Strength Mater. 2024, 56, 559–567. [Google Scholar] [CrossRef]
- Langtangen, H.P.; Logg, A. Solving PDEs in Python: The FEniCS Tutorial I; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Johansson, R. Numerical Python: Scientific Computing and Data Science Applications with Numpy, SciPy and Matplotlib; Apress: New York, NY, USA, 2019. [Google Scholar]
- Al-Quraan, T.M.A.; Tokaruk, V.V.; Mikosianchyk, O.A.; Mnatsakanov, R.G.; Kichata, N.M.; Kuzin, N.O. Influence of Continuity of Electric Spark Coatings on Wear Resistance of Aluminum Alloy. Tribol. Ind. 2021, 43, 603–614. [Google Scholar] [CrossRef]
- Duryahina, Z.A.; Kuzin, O.A.; Kuzin, M.O.; Shcherbovs’kykh, N.V. Influence of the modes of laser alloying on the parameters of wear resistance of 12Kh17T Steel. Mater. Sci. 2011, 47, 327–333. [Google Scholar] [CrossRef]
- Kopylov, V.; Kuzin, O.; Kuzin, N. Application of computational mechanics approaches for increasing of tribosystem operational parameters by using plasma hardening method. J. Appl. Math. Comput. Mech. 2021, 20, 61–70. [Google Scholar] [CrossRef]
- Gubenko, S.I. Nonmetallic Inclusions and Strength of Steels; Palmarium Academic Press: Geisenheim, Germany, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).