Advances in Evaluation Methods for Artificial Fracture Networks in Shale Gas Horizontal Wells
Abstract
1. Introduction
2. Direct Monitoring
- Geophysical Field Responses: By capturing field signals induced by hydraulic fracturing, such as seismic waves (microseismic monitoring) and electromagnetic anomalies (wide-field electromagnetic methods), the spatial distribution of fractures can be inferred;
- Chemical Tracer Migration: The transport behavior of radioactive or non-radioactive tracers within the fracture network is utilized to analyze fracture connectivity and proppant distribution;
- Fiber-Optic Sensing Responses: Distributed fiber-optic systems detect disturbances in temperature or acoustic signals to enable in situ monitoring of fracture initiation, propagation, and closure.
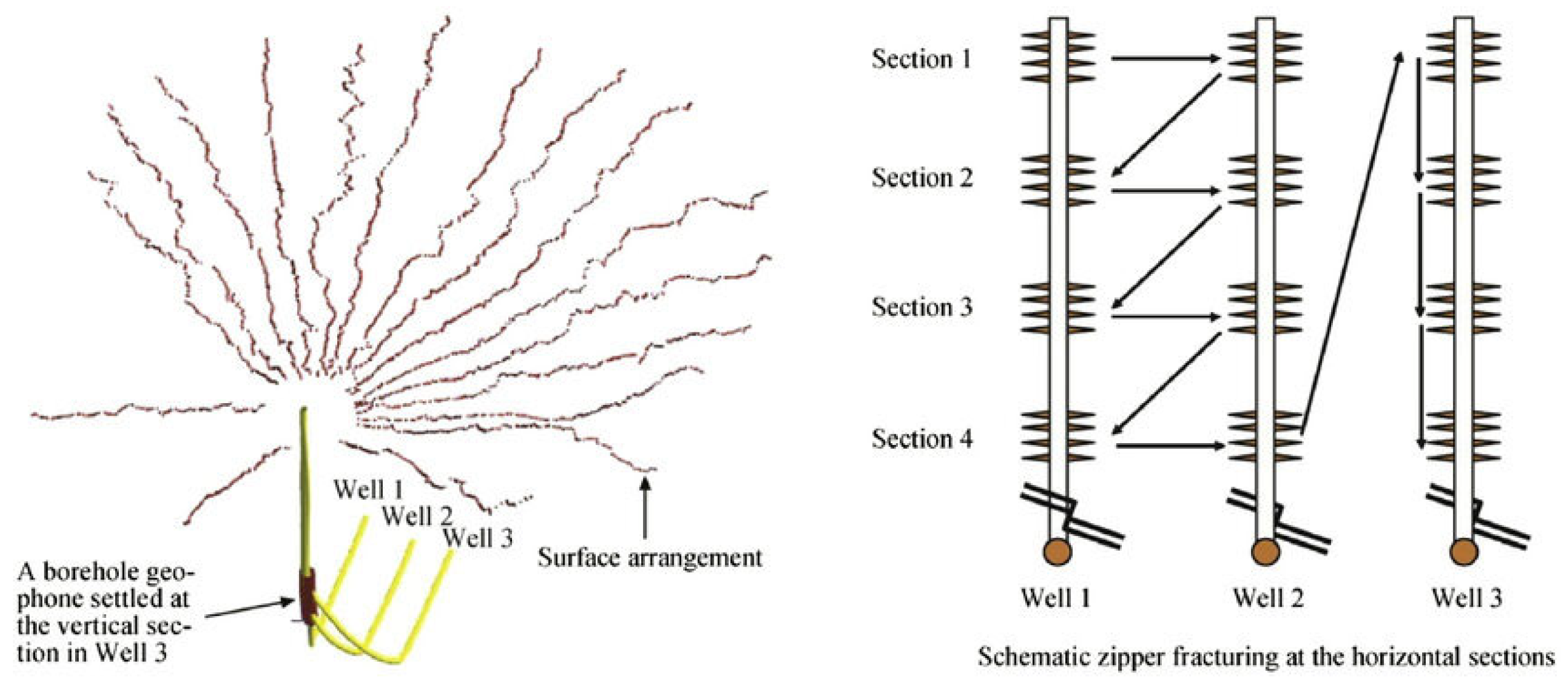
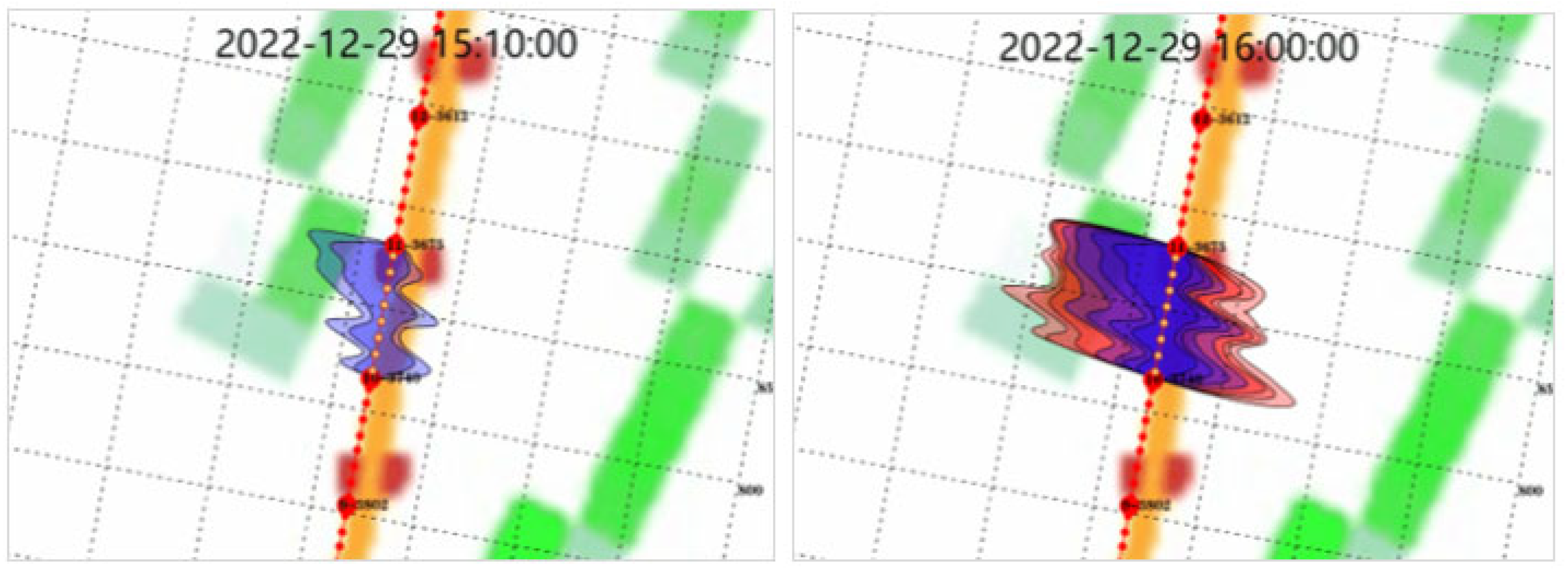
2.1. Microseismic Monitoring
- The cost of large-scale array deployment increases exponentially. A 3000-channel geophone system can exceed USD 2 million;
- Simplified P-wave velocity models limit vertical resolution (tons of meters);
- Industrial noise sources (e.g., pumping units >90 dB, rig vibrations 10–50 Hz) overlap with the microseismic frequency band (100–1000 Hz), requiring advanced adaptive filtering and deep learning denoising algorithms to improve signal-to-noise ratio [21].
- Lack of standardized magnitude calibration [25]: Accurate magnitude estimation is crucial for calculating stimulated rock volume and guiding fracturing operations [26]. However, traditional magnitude formulas were developed for larger-scale seismic events, leading to discrepancies in event magnitudes when extrapolated to microseismic scales;
- High-frequency signal attenuation at depth: In deep shale formations (>3500 m) such as those in the Sichuan Basin, more than 70% of microseismic events cannot be detected by surface arrays due to severe signal attenuation [27];
- Uncertainty in fracture parameter inversion: Microseismic monitoring essentially captures acoustic emissions, identifying rupture points rather than full fracture geometries. Parameters like fracture length and conductivity are influenced by monitoring geometry and inversion models, requiring integration with geomechanical simulations and facing issues of non-uniqueness [28].
2.2. Tracer Monitoring
- Spatial distribution of proppant;
- Supplementary fracture characterization;
- Contribution of individual fracturing stages;
- Inter-well interference intensity.
- Emulsified Tracers: Composed of water/oil dual-phase soluble tracers, they are co-injected with the fracturing fluid through an emulsification process. Their phase-selective solubility enables multi-phase flow dynamic monitoring within the matrix-fracture system.
- Perforation Tracers: Made of high-temperature-resistant metal-based composite tracer materials (e.g., tungsten-rare earth oxides), which are embedded into the cemented multi-stage fracturing system using perforation charge integration. These tracers are released upon activation by high temperatures (>800 °C) during the perforation phase, and are mainly applied in cement plug and perforation fracturing operations.
- Controlled-Release Tracers: Polymer-based tracer compounds placed on the exterior of production casing that gradually release tracers upon contact with formation fluids.
- Solubility and co-migration with the carrier fluid at matching velocities;
- Chemical stability (excluding radioactive tracers) without adsorption or degradation;
- Low natural background concentration in the target formation for high signal-to-noise detection;
- Detectable in trace quantities with high-sensitivity analytical methods;
- Cost-effectiveness, considering synthesis, injection, and detection costs;
- Safety and environmental compliance throughout injection and production stages;
2.2.1. Qualitative Analysis
2.2.2. Analytical (Semi-Analytical) Modeling
2.2.3. Numerical Modeling
- Radiotracer attenuation: Radioactive tracers experience significant attenuation when passing through casing, cement sheaths, and surrounding rock. Additionally, isotopes with short half-lives are often unsuitable for long-term monitoring (e.g., >30 days after fracturing) [57].
- Limited resolution in far-field fracture detection: Due to the constraints of tracer diffusion coefficients, current techniques primarily characterize proppant distribution near the wellbore.
- Limited spatial resolution and diagnostic independence: Tracer data often lack the resolution required to map fine-scale fracture geometries. As such, their diagnostic capabilities should be viewed as complementary, rather than standalone.
2.3. Wide-Field Electromagnetic Monitoring (WFEM)
- Economic Constraints: The cost of a single 3D monitoring campaign is significantly high—approximately 2 to 3 times that of microseismic monitoring. This limits its widespread deployment in commercial field operations.
- Inversion Non-Uniqueness: Different inversion algorithms (e.g., Occam or Marquardt) can yield resistivity results with 15–25% variability, leading to fracture length estimation deviations of up to ±20%. The inherent ill-posed nature of electromagnetic inversion makes it sensitive to initial conditions and algorithm selection.
- Geological Adaptability: In areas with low-resistivity overburden, the attenuation rate can reach 0.8 dB/m, which severely reduces detection resolution for deep fractures (>3 km)—vertical resolution can decline to ±50–100 m at such depths.
- Environmental Electromagnetic Interference: During field acquisition, WFEM is highly susceptible to electromagnetic interference from surface infrastructure, such as power lines, metal pipelines, and other electromagnetic noise sources. These interferences degrade data quality and increase inversion instability. Special precautions must be taken during deployment in such environments.
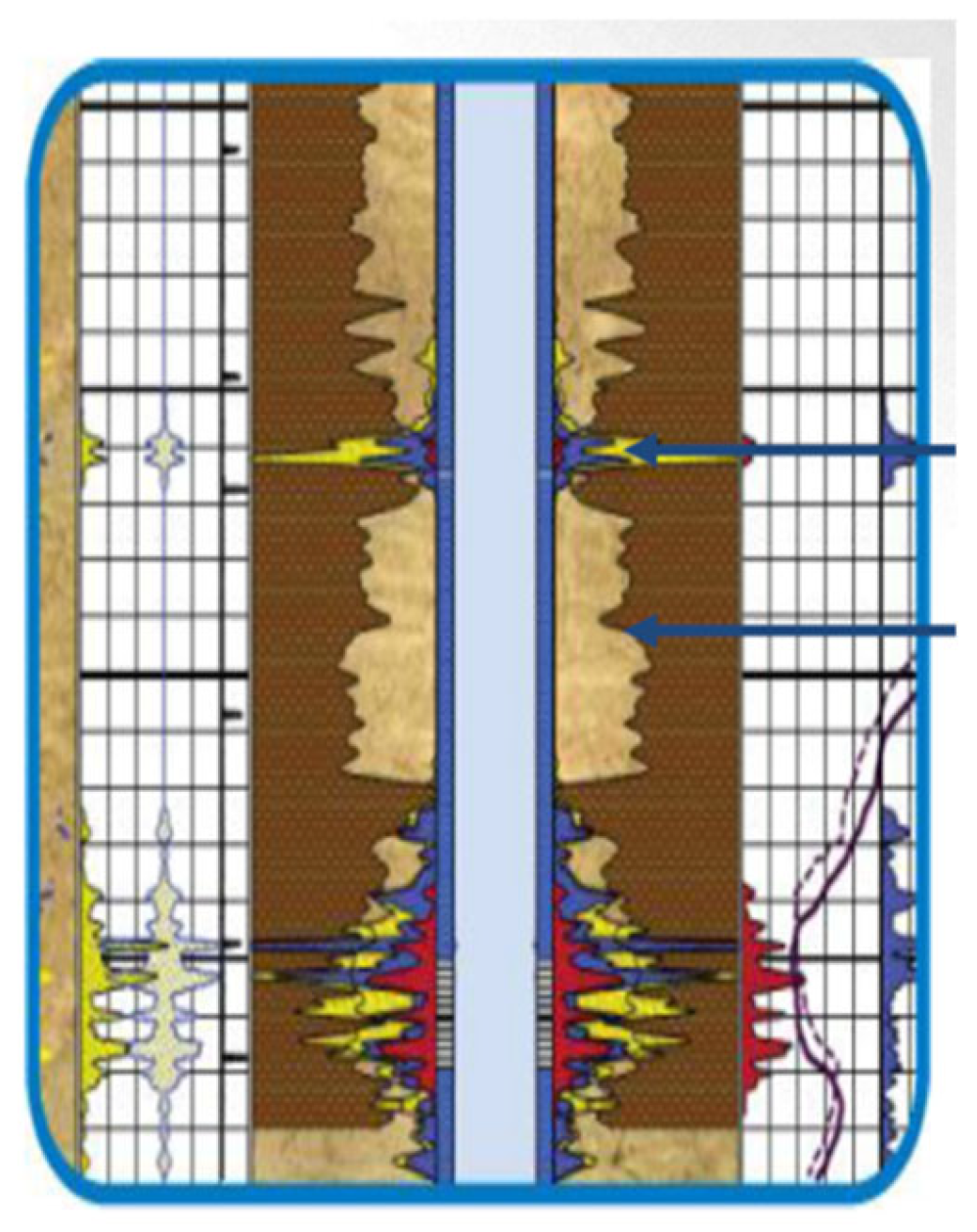
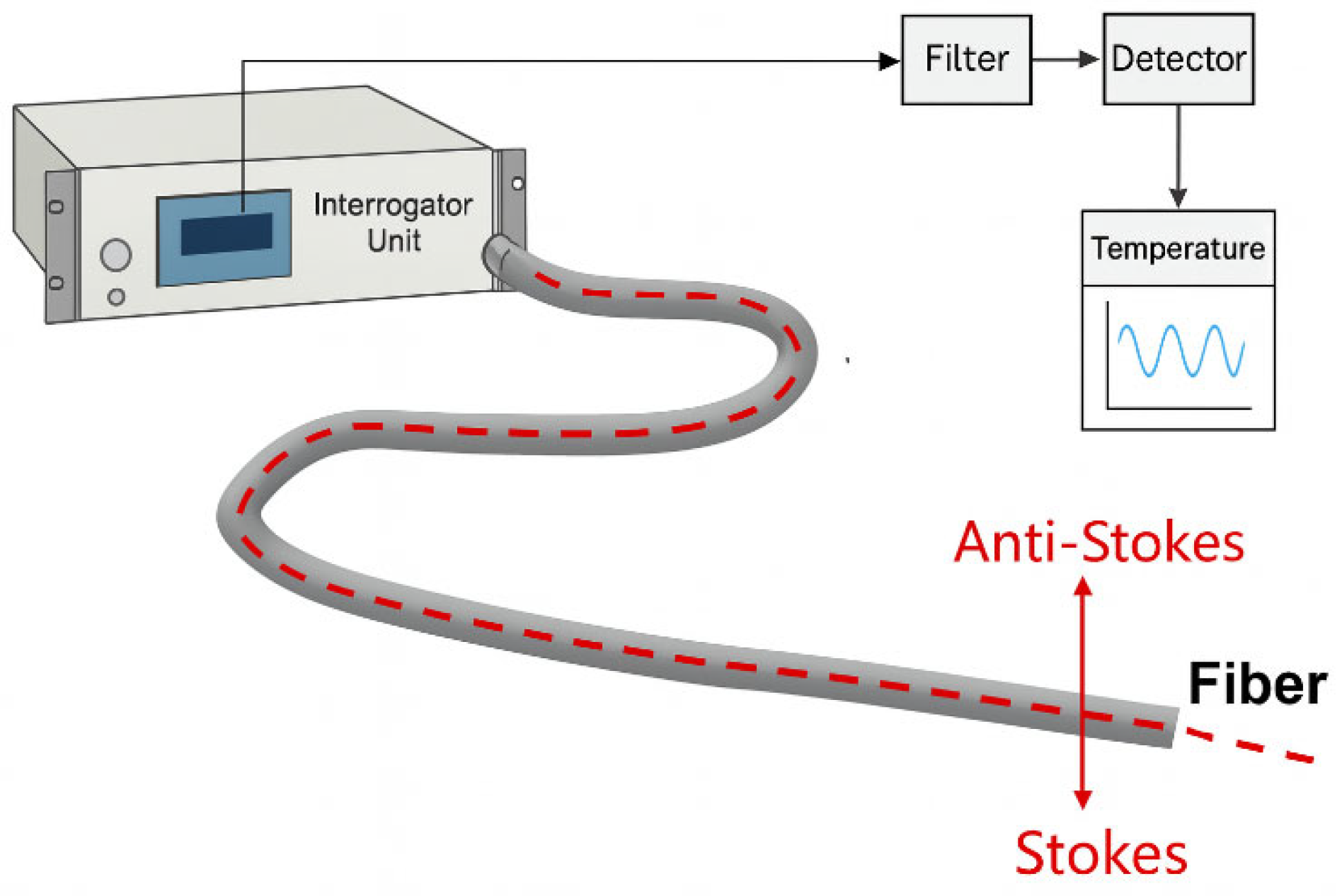
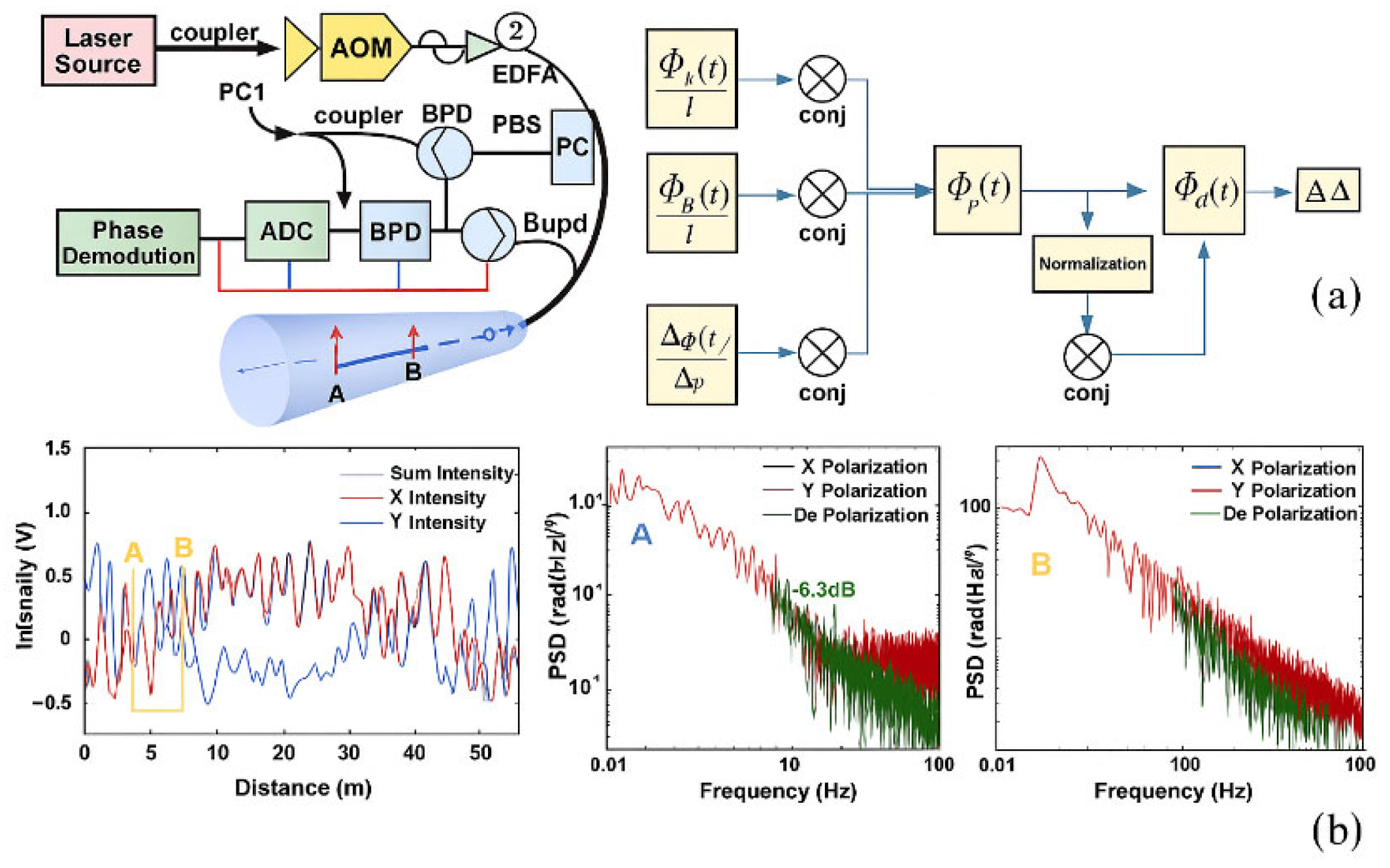
2.4. Distributed Fiber-Optic Monitoring (DTS, DAS)
- High cost of sensors and deployment: the installation and maintenance of distributed optical fibers are capital-intensive. Specialized hardware, fiber-optic cables, and permanent downhole installations drive up overall operational costs.
- Massive data generation and management challenges: continuous monitoring produces vast quantities of data. Challenges arise in data storage, processing, visualization, and security, especially in large-scale multi-well applications [93].
- Risk of fiber damage during fracturing operations: the high-pressure injection of fracturing fluids and proppants may damage optical fibers—especially when placed inside the wellbore—compromising long-term data acquisition.
- Immature data interpretation models and tools: current software platforms and theoretical models for interpreting DTS/DAS signals are still under development. Effective analysis requires interdisciplinary knowledge of optics, mechanics, geophysics, well logging, and hydraulic fracturing [94].
2.5. Field Experiments and Core Analysis
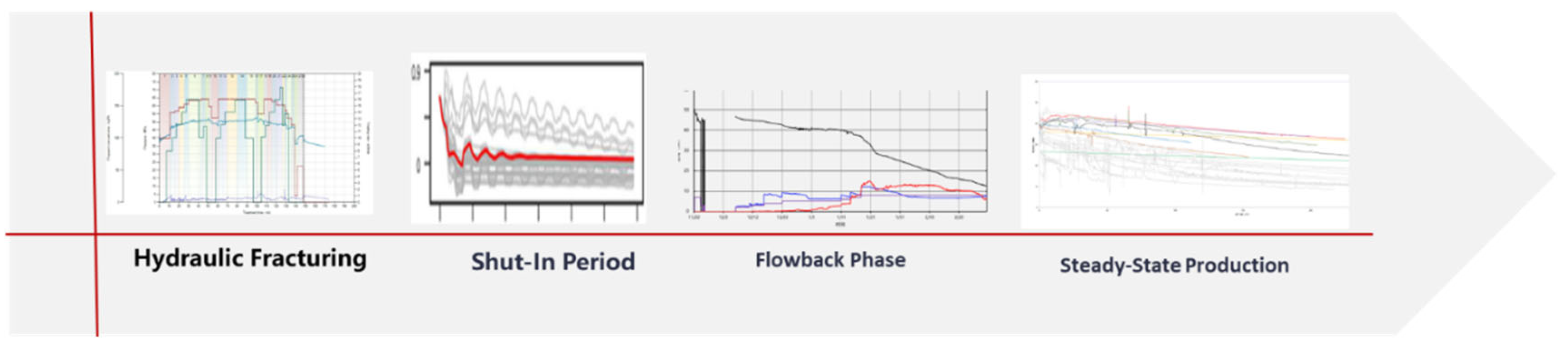
3. Dynamic Inversion
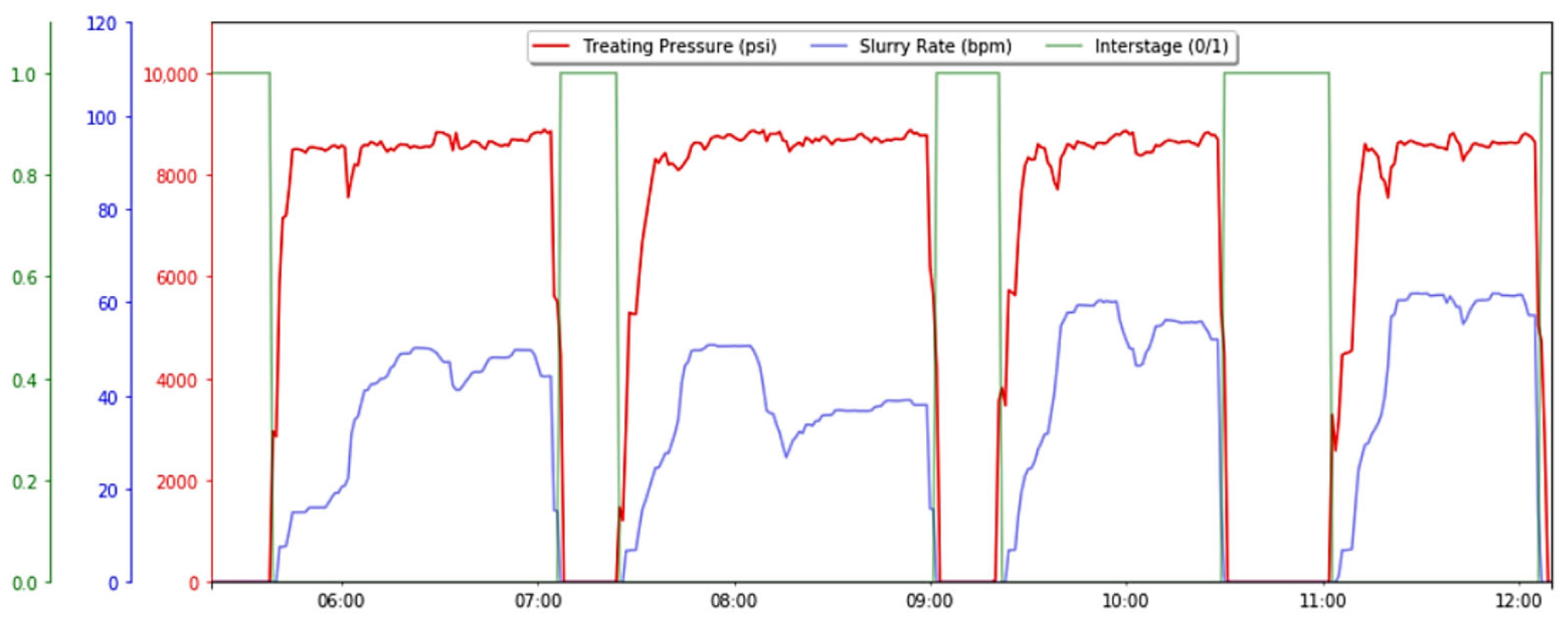
3.1. Fracture Evaluation Based on Fracturing Stage Treatment Curves
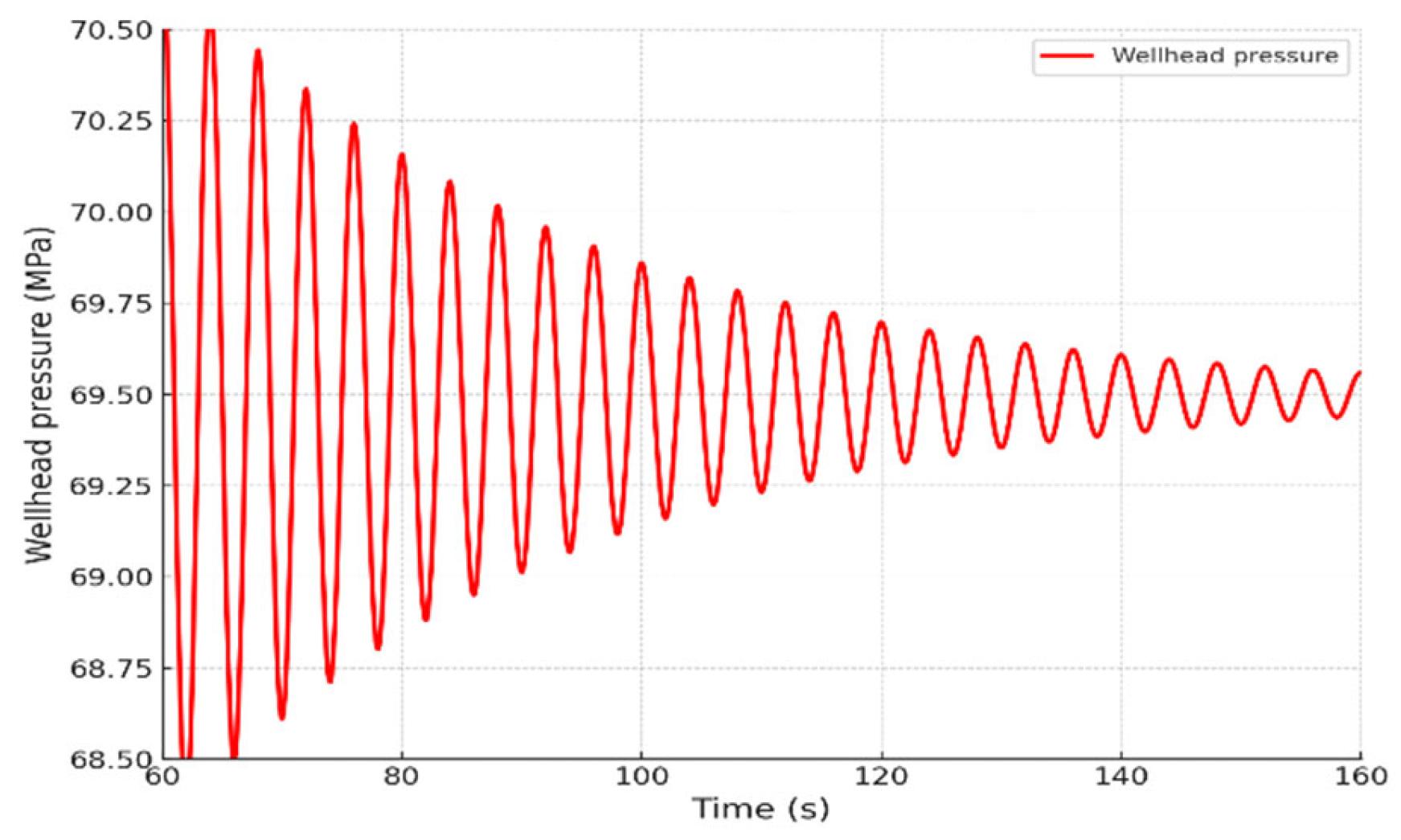
3.2. Fracture Evaluation Based on Shut-In Water Hammer Curve
3.3. Fracture Network Inversion Based on Flowback and Stable Production Data
4. Summary of Current Fracture Evaluation Methods and Future Development Trends
- Multi-Source Data Fusion: Integrate direct monitoring (e.g., microseismic, fiber optics) and dynamic inversion (e.g., flowback curves, production simulations) to build a “geology-engineering-production” unified evaluation framework.
- AI-Driven Optimization: Leverage machine/deep learning (e.g., CNN-based microseismic signal classification, reinforcement learning for parameter adjustment) to enhance inversion efficiency.
- High-Resolution Real-Time Monitoring: Develop low-cost distributed fiber sensors and wide-field electromagnetic arrays for minute-level fracture imaging, enabling real-time fracturing optimization.
- Digital Twin Integration: Combine real-time monitoring with predictive simulations to create virtual replicas of fracturing processes for scenario testing and decision support.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Q.; Chen, X.; Jha, A.N.; Rogers, H. Natural gas from shale formation-the evolution, evidences and challenges of shale gas revolution in United States. Renew. Sustain. Energy Rev. 2014, 30, 1–28. [Google Scholar] [CrossRef]
- Hao, F.; Zou, H.; Lu, Y. Mechanisms of shale gas storage: Implications for shale gas exploration in China. AAPG Bull. 2013, 97, 1325–1346. [Google Scholar] [CrossRef]
- Tang, Y.; Tang, X.; Wang, G.Y.; Zhang, Q. Summary of hydraulic fracturing technology in shale gas development. Geol. Bull. China 2011, 30, 393–399. [Google Scholar]
- Liu, Z.; Wang, T.; Gao, Y.; Zeng, Q.; Zhuang, Z.; Huang, K.C. The key mechanical problems on hydraulic fracture in shale. Guti Lixue Xuebao/Acta Mech. Solida Sin. 2016, 37, 34–49. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, H.; Zhang, Q.; Xiong, D. Properties of a shale bedding plane and its influence on the geometric parameters of fracture propagation in volume fracturing. Eng. Fract. Mech. 2022, 266, 108413. [Google Scholar] [CrossRef]
- Wright, C.A.; Weijers, L.; Davis, E.J.; Mayerhofer, M. Understanding hydraulic fracture growth: Tricky but not hopeless. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999; p. SPE-56724. [Google Scholar] [CrossRef]
- Ren, L.; Su, Y.; Zhan, S.; Meng, F. Progress of the research on productivity prediction methods for stimulated reservoir volume (SRV)-fractured horizontal wells in unconventional hydrocarbon reservoirs. Arab. J. Geosci. 2019, 12, 184. [Google Scholar] [CrossRef]
- King, G.E. Hydraulic fracturing 101: What every representative, environmentalist, regulator, reporter, investor, university researcher, neighbor and engineer should know about estimating frac risk and improving frac performance in unconventional gas and oil wells. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 6–8 February 2012; p. SPE-152596. [Google Scholar] [CrossRef]
- Mueller, M. Meeting the challenge of uncertainty in surface microseismic monitoring. First Break 2013, 31. [Google Scholar] [CrossRef]
- Cipolla, C.; Maxwell, S.; Mack, M. Engineering guide to the application of microseismic interpretations. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 6–8 February 2012; p. SPE-152165. [Google Scholar] [CrossRef]
- Shu, H.; Dawod, A.Y. Microseismic Monitoring Signal Waveform Recognition and Classification: Review of Contemporary Techniques. Appl. Sci. 2023, 13, 12739. [Google Scholar] [CrossRef]
- Van Der Baan, M.; Eaton, D.; Dusseault, M. Microseismic monitoring developments in hydraulic fracture stimulation. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20 May 2013; p. ISRM-ICHF. [Google Scholar] [CrossRef]
- Maxwell, S.C.; Rutledge, J.; Jones, R.; Fehler, M. Petroleum reservoir characterization using downhole microseismic monitoring. Geophysics 2010, 75, A129–A175. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Aguilera, R.; Pedersen, P.K.; Spencer, R.J. Shale gas, part 8: Shale gas development optimization. CSPG Reserv. 2011, 38, 25–31. [Google Scholar]
- Maxwell, S.C.; Raymer, D.; Williams, M.; Primiero, P. Tracking microseismic signals from the reservoir to surface. Lead. Edge 2012, 31, 1300–1308. [Google Scholar] [CrossRef]
- Furong, W.; Yan, Y.; Yin, C. Real-time microseismic monitoring technology for hydraulic fracturing in shale gas reservoirs: A case study from the Southern Sichuan Basin. Nat. Gas Ind. B 2017, 4, 68–71. [Google Scholar] [CrossRef]
- Li, L.; Tan, J.; Wood, D.A.; Zhao, Z.; Becker, D.; Lyu, Q.; Chen, H. A review of the current status of induced seismicity monitoring for hydraulic fracturing in unconventional tight oil and gas reservoirs. Fuel 2019, 242, 195–210. [Google Scholar] [CrossRef]
- Duncan, P.M. Microseismic monitoring: Technology state of play. In Proceedings of the SPE Unconventional Resources Conference/Gas Technology Symposium, Pittsburgh, PA, USA, 23–25 February 2010; p. SPE-131777. [Google Scholar] [CrossRef]
- Eisner, L.; Duncan, P.M.; Heigl, W.M.; Keller, W.R. Uncertainties passive seismic monitoring. Lead. Edge 2009, 28, 648–655. [Google Scholar] [CrossRef]
- Peyret, O.; Drew, J.; Mack, M.; Brook, K.; Maxwell, S.; Cipolla, C. Subsurface to surface microseismic monitoring for hydraulic fracturing. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012; p. SPE-159670. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Wolhart, S. A validation assessment of microseismic monitoring. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 9–11 February 2016; p. D021S004R001. [Google Scholar] [CrossRef]
- Maxwell, S. Microseismic: Growth born from success. Lead. Edge 2010, 29, 338–343. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Du, J.; Zimmer, U. Measurements of hydraulic-fracture-induced seismicity in gas shales. SPE Prod. Oper. 2012, 27, 240–252. [Google Scholar] [CrossRef]
- Zhao, J.; Ren, L.; Lin, C.; Lin, R.; Hu, D.; Wu, J.; Jiang, H. A review of deep and ultra-deep shale gas fracturing in China: Status and directions. Renew. Sustain. Energy Rev. 2025, 209, 11511. [Google Scholar] [CrossRef]
- Shemeta, J.; Anderson, P. It’s a matter of size: Magnitude and moment estimates for microseismic data. Lead. Edge 2010, 29, 296–302. [Google Scholar] [CrossRef]
- Maxwell, S.; Zimmer, U.; Warpinski, N.; Waltman, C. Quality control/assurance reporting of passive microseismic data. In Proceedings of the SEG International Exposition and Annual Meeting, New Orleans, LA, USA, 1–6 October 2006; p. SEG-2006. [Google Scholar] [CrossRef]
- Dwan, F.; Qiu, J.; Zhou, M.; Yuan, R.S.; Zhang, Z. Sichuan shale gas microseismic monitoring: Acquisition, processing, and integrated analyses. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013; p. IPTC-16571. [Google Scholar] [CrossRef]
- Mahmoud, A.; Gowida, A.; Aljawad, M.S.; Al-Ramadan, M.; Ibrahim, A.F. Advancement of hydraulic fracture diagnostics in unconventional formations. Geofluids 2021, 2021, 4223858. [Google Scholar] [CrossRef]
- Webster, P.; Cox, B.; Molenaar, M. Developments in diagnostic tools for hydraulic fracture geometry analysis. In Proceedings of the Unconvenional Resources Technology Conference, Denver, CO, USA, 12–14 August 2013; pp. 218–224. [Google Scholar] [CrossRef]
- Sani, A.M.; Podhoretz, S.B.; Chambers, B.D. The use of completion diagnostics in Haynesville shale horizontal wells to monitor fracture propagation, well communication, and production impact. In SPE Canada Unconventional Resources Conference; SPE: Richardson, TX, USA, 2015; p. D021S006R002. [Google Scholar]
- Palisch, T.; Al-Tailji, W.; Bartel, L.; Cannan, C.; Czapski, M.; Lynch, K. Recent advancements in far-field proppant detection. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 9–11 February 2016; p. D021S006R007. [Google Scholar] [CrossRef]
- Zhang, J.; Smith, H.; Palisch, T.; Reynaud, L. A Novel Technology for Locating and Evaluating Hydraulic Fractures in Horizontal Wells-Modeling and Field Results. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018; p. D011S004R003. [Google Scholar] [CrossRef]
- Dugstad, O. Well to Well Tracer Tests, Chapter 6, Reservoir Engineering and Petrophysics. Pet. Eng. Handb. 2007, 651. [Google Scholar] [CrossRef]
- Salman, A.; Kurtoglu, B.; Kazemi, H. Analysis of Chemical Tracer Flowback in Unconventional Reservoirs. In Proceedings of the SPE/CSUR Unconventional Resources Conference, Calgary, AB, Canada, 30 September–2 October 2014. [Google Scholar] [CrossRef]
- Li, G. Oilfield Tracer Analysis and Application for Hydraulic Fracture Diagnostics. Ph.D. Dissertation, Texas A&M University, San Antonio, TX, USA, May 2021. [Google Scholar]
- Du, Y.; Guan, L. Interwell tracer tests: Lessons learned from past field studies. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 5–7 April 2005; p. SPE-93140. [Google Scholar] [CrossRef]
- Aparecida de Melo, M.; de Holleben, C.R.; Almeida, A.R. Using tracers to characterize petroleum reservoirs: Application to Carmopolis Field, Brazil. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 25 March 2001; p. SPE-69474. [Google Scholar] [CrossRef]
- Mercado, M.; Perez, C.E.; Asadi, M.; Casas, D.R. Gas flood-flow pattern evaluation: A successful interwell field study. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Port of Spain, Trinidad and Tobago, 27 April 2003; p. SPE-81005. [Google Scholar] [CrossRef]
- Kumar, A.; Seth, P.; Shrivastava, K.; Manchanda, R.; Sharma, M.M. Integrated analysis of tracer and pressure-interference tests to identify well interference. SPE J. 2020, 25, 1623–1635. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z.; Li, Y.; Luo, H.; Cui, X.; Nie, S.; Ye, K. Evaluation of the release mechanism of sustained-release tracers and its application in horizontal well inflow profile monitoring. ACS Omega 2021, 6, 19269–19280. [Google Scholar] [CrossRef] [PubMed]
- Katashov, A.; Belova, A.; Husein, N.; Drobot, A.; Upadhye, V.; Stepanova, M.; Vasechkin, D. Tracer-Based Technology for Evaluation the Productivity of Frac Ports and the Contribution of Near and Far Zones of Fractures During Hydraulic Stimulation. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2022; p. D031S039R006. [Google Scholar] [CrossRef]
- Roshan, H.; Sarmadivaleh, M.; Iglauer, S. Shale fracture surface area measured by tracking exchangeable cations. J. Pet. Sci. Eng. 2016, 138, 97–103. [Google Scholar] [CrossRef]
- Lal, M.K.; Singh, A.K.; Ezernack, J.; Spencer, J. Advanced reservoir characterization in antelope shale using chemical tracer technology. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 24 January 2017; p. D011S001R007. [Google Scholar] [CrossRef]
- Brigham, W.E.; Smith, D.H., Jr. Prediction of tracer behavior in five-spot flow. In Proceedings of the SPE Conference on Production Research and Engineering, Tulsa, OK, USA, 3 May 1965; p. SPE-1130. [Google Scholar] [CrossRef]
- Abbaszadeh-Dehghani, M.; Brigham, W.E. Analysis of well-to-well tracer flow to determine reservoir layering. J. Pet. Technol. 1984, 36, 1753–1762. [Google Scholar] [CrossRef]
- Jensen, C.L.; Horne, R.N. Matrix Diffusion and Its Effect on the Modeling of Tracer Returns from the Fractured Geothermal Reservoir at Wairakei, New Zealand (No. SGP-TR-74-43); Stanford University: Palo Alto, CA, USA, 1983. [Google Scholar]
- Rivera, J.R.; Ramirez, J.S.; Rodriguez, F.G. Parallel Fractures Model for Tracer Flow Through Geothermal Reservoirs-Preliminary Results; Stanford University: Stanford, CA, USA, 20–22 January 1987. [Google Scholar]
- Tian, W.; Wu, X.; Shen, T.; Kalra, S. Estimation of hydraulic fracture volume utilizing partitioning chemical tracer in shale gas formation. J. Nat. Gas Sci. Eng. 2016, 33, 1069–1077. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, M.M. Diagnosing hydraulic fracture geometry, complexity, and fracture wellbore connectivity using chemical tracer flowback. Energies 2020, 13, 5644. [Google Scholar] [CrossRef]
- Holditch, S.A.; Holcomb, D.L.; Rahim, Z. Using tracers to evaluate propped fracture width. In Proceedings of the SPE Eastern Regional Meeting, Pittsburgh, PA, USA, 2 November 1993; p. SPE-26922. [Google Scholar] [CrossRef]
- Lange, A.; Bouzian, J.; Bourbiaux, B. Tracer-test simulation on discrete fracture network models for the characterization of fractured reservoirs. In Proceedings of the SPE Europec featured at EAGE Conference and Exhibition, Madrid, Spain, 13 June 2005; p. SPE-94344. [Google Scholar] [CrossRef]
- Ghods, P.; Zhang, D. Automatic estimation of fracture properties in multi-stage fractured shale gas horizontal wells for reservoir modeling. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 19–23 March 2012; p. SPE-153913. [Google Scholar] [CrossRef]
- Elahi, S.H.; Jafarpour, B. Characterization of fracture length and conductivity from tracer test and production data with Ensemble Kalman filter. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 20–22 July 2015; pp. 1192–1200. [Google Scholar] [CrossRef]
- Elahi, S.H.; Jafarpour, B. Dynamic fracture characterization from tracer-test and flow-rate data with ensemble Kalman filter. SPE J. 2018, 23, 449–466. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, L.; Liu, T.; Yang, D. Modeling tracer flowback behaviour for a multifractured horizontal well in a tight oil reservoir using the embedded discrete fracture model. J. Pet. Sci. Eng. 2022, 212, 110347. [Google Scholar] [CrossRef]
- Bhatnagar, A. Overcoming challenges in fracture stimulation through advanced fracture diagnostics. In Proceedings of the SPE Asia Pacific Hydraulic Fracturing Conference, Beijing, China, 24 August 2016; p. D021S004R005. [Google Scholar] [CrossRef]
- Bartuska, J.E.; Pechiney, J.J.; Leonard, R.S.; Woodroof, R.A. Optimizing completion designs for horizontal shale gas wells using completion diagnostics. In Proceedings of the SPE Unconventional Resources Conference/Gas Technology Symposium, Pittsburgh, PA, USA, 5 June 2012; p. SPE-155759. [Google Scholar] [CrossRef]
- Warpinski, N.R. Hydraulic fracture diagnostics. J. Pet. Technol. 1996, 48, 907–910. [Google Scholar] [CrossRef]
- Lichtenberger, G.J. Field applications of interwell tracers for reservoir characterization of enhanced oil recovery pilot areas. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium, Oklahoma, OK, USA, 7 April 1991; p. SPE-21652. [Google Scholar] [CrossRef]
- He, J.-S. Wide field electromagnetic method and pseudo random signal method. J. Cent. South Univ. Sci. Technol. 2010, 41, 1065–1072. [Google Scholar]
- He, J.-S.; Yang, Y.; Li, D.-Q.; Weng, J.-B. Wide field electromagnetic sounding methods. In Proceedings of the Symposium on the Application of Geophysics to Engineering and Environmental Problems, Austin, TX, USA, 22–26 March 2015; pp. 325–329. [Google Scholar] [CrossRef]
- He, J.-S. Combined application of wide-field electromagnetic method and flow field fitting method for high-resolution exploration: A case study of the Anjialing No. 1 Coal Mine. Engineering 2018, 4, 667–675. [Google Scholar] [CrossRef]
- Liu, R.; Liu, J.; Liu, C.; Guo, R.; Wang, H.; Liu, Z. A feasibility study of the wide-field electromagnetic method for hidden ore deposits prospecting. J. Appl. Geophys. 2020, 179, 104121. [Google Scholar] [CrossRef]
- Yuan, B.; Li, D.; Bayless, R.C. Wide field electromagnetic method for shale gas exploration in southern China: A case study. J. Environ. Eng. Geophys. 2017, 22, 279–289. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, B.; Peng, C.S.; Yang, Y. Application of a wide-field electromagnetic method to shale gas exploration in South China. Appl. Geophys. 2017, 14, 441–448. [Google Scholar] [CrossRef]
- Xie, W.B.; Jiang, Q.Y.; Li, D.Q.; Zhang, Q.X.; Pei, J. Interpolation analysis of electromagnetic real-time monitoring data for hydraulic fracturing based on random forest. China Sci. Technol. Inf. 2020, 12, 88–89. [Google Scholar]
- Yang, J.; Liu, Y. Application of wide-field electromagnetic method in fracturing monitoring of deep shale horizontal wells in Huang 202 well area. China Pet. Chem. Stand. Qual. 2023, 4, 130–132. [Google Scholar]
- Ye, Z.Q.; Fan, Q.H.; Xu, Y.J.; Lu, F.B.; Xiao, W.L. Application of wide-field electromagnetic method in shale gas fracturing monitoring in southern Sichuan. In Proceedings of the 33rd National Natural Gas Academic Annual Conference (2023) V: New Energy and Energy Conservation, Guangxi, China, 1–2 June 2023; pp. 108–113. [Google Scholar]
- Hu, Z.F.; Luo, W.F.; Wang, S.J.; Kang, H.X.; Zhou, H.; Zhang, Y.X.; Zhan, S.Q. Application of wide-field electromagnetic method in fracturing monitoring of well Anye-2. Geophys. Geochem. Explor. 2023, 47, 718–725. [Google Scholar] [CrossRef]
- Tie, J.; Zhang, Y.; Cheng, X. Application effectiveness of wide-field electromagnetic method fracturing monitoring technology in Xinjiang region. In Proceedings of the 2024 International Conference on Oil and Gas Field Exploration and Development, Volume I, Shanxi, China, 12–14 September 2024; pp. 1054–1064. [Google Scholar] [CrossRef]
- He, J.-S. New advances in the theory and applications of wide-field electromagnetic method. Geophys. Geochem. Explor. 2020, 44, 985–990. [Google Scholar]
- Karaman, O.S.; Kutlik, R.L.; Kluth, E.L. A field trial to test fiber optic sensors for downhole temperature and pressure measurements, West Coalinga Field, California. In Proceedings of the SPE Western Regional Meeting, Anchorage, AK, USA, 22 May 1996; p. SPE-35685. [Google Scholar] [CrossRef]
- Nath, D.K.; Finley, D.B.; Kaura, J.D.; Krismartopo, B.; Yudhiarto, W. Real-time fiber-optic distributed temperature sensing (DTS)—New applications in the oil field. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24 September 2006; p. SPE-103069. [Google Scholar] [CrossRef]
- Nath, F.; Hoque, S.S.; Mahmood, M.N. Recent advances and new insights of fiber optic techniques in fracture diagnostics used for unconventional reservoirs. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 13–15 June 2023; pp. 2276–2295. [Google Scholar] [CrossRef]
- Rogers, A. Distributed optical-fibre sensing. Meas. Sci. Technol. 1999, 10, R75. [Google Scholar] [CrossRef]
- Hartog, A.H. An Introduction to Distributed Optical Fibre Sensors; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Li, H.; Luo, H.; Xiang, Y.; Li, Y.; Jiang, B.; Cui, X.; Gao, S.; Zou, S.; Xin, Y. DTS based hydraulic fracture identification and production profile interpretation method for horizontal shale gas wells. Nat. Gas Ind. B 2021, 8, 494–504. [Google Scholar] [CrossRef]
- Holley, E.H.; Kalia, N. Fiber-optic monitoring: Stimulation results from unconventional reservoirs. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 20–22 July 2015; pp. 300–315. [Google Scholar] [CrossRef]
- Hartog, A. A distributed temperature sensor based on liquid-core optical fibers. J. Light. Technol. 1983, 1, 498–509. [Google Scholar] [CrossRef]
- Tabatabaei, M.; Zhu, D. Fracture-stimulation diagnostics in horizontal wells through use of distributed-temperature-sensing technology. SPE Prod. Oper. 2012, 27, 356–362. [Google Scholar] [CrossRef]
- Tarrahi, M.; Gildin, E.; Moreno, J.; Gonzales, S. Dynamic integration of DTS data for hydraulically fractured reservoir characterization with the ensemble Kalman filter. In Proceedings of the SPE Trinidad and Tobago Section Energy Resources Conference, Port of Spain, Trinidad and Tobago, 9 June 2014; p. D031S018R003. [Google Scholar] [CrossRef]
- Yoshida, N.; Zhu, D.; Hill, A.D. Temperature-prediction model for a horizontal well with multiple fractures in a shale reservoir. SPE Prod. Oper. 2014, 29, 261–273. [Google Scholar] [CrossRef]
- Kalia, N.; Gorgi, S.; Holley, E.; Cullick, A.S.; Jones, T. Wellbore Monitoring in Unconventional Reservoirs: Value of Accurate DTS Interpretation and Risks Involved. In Proceedings of the SPE Unconventional Resources Conference/Gas Technology Symposium, Woodlands, TX, USA, 1 April 2014; p. D031S007R003. [Google Scholar] [CrossRef]
- Cui, J.; Zhu, D.; Jin, M. Diagnosis of production performance after multistage fracture stimulation in horizontal wells by downhole temperature measurements. SPE Prod. Oper. 2016, 31, 280–288. [Google Scholar] [CrossRef]
- Sun, H.; Yu, W.; Sepehrnoori, K. A new comprehensive numerical model for fracture diagnosis with distributed temperature sensing DTS. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; p. D011S002R002. [Google Scholar] [CrossRef]
- Ashry, I.; Mao, Y.; Wang, B.; Hveding, F.; Bukhamsin, A.Y.; Ng, T.K.; Ooi, B.S. A review of distributed fiber-optic sensing in the oil and gas industry. J. Light. Technol. 2022, 40, 1407–1431. [Google Scholar] [CrossRef]
- Jin, G.; Roy, B. Hydraulic-fracture geometry characterization using low-frequency DAS signal. Lead. Edge 2017, 36, 975–980. [Google Scholar] [CrossRef]
- Sherman, C.S.; Mellors, R.J.; Morris, J.P. Subsurface monitoring via physics-informed deep neural network analysis of das. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019; p. ARMA-2019. [Google Scholar]
- Titov, A.; Binder, G.; Jin, G.; Tura, A.; Aaron, P.; Yates, M.; Gunnell, A. Analysis of scattered waves observed in inter-stage DAS VSP data from zipper-fracturing operations. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2020; pp. 3793–3797. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Grubert, M.; Laing, C.; Chavarria, A.; Cole, S.; Oukaci, Y. Distributed acoustic and temperature sensing applications for hydraulic fracture diagnostics. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 4–6 February 2020; p. D021S004R003. [Google Scholar] [CrossRef]
- Shang, Y.; Sun, M.; Wang, C.; Yang, J.; Du, Y.; Yi, J.; Ni, J. Research progress in distributed acoustic sensing techniques. Sensors 2020, 22, 6060. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Z.; Wang, F. Research progress of applying distributed fiber optic measurement technology in hydraulic fracturing and production monitoring. Energies 2020, 15, 7519. [Google Scholar] [CrossRef]
- Richards, J.; Bartlett, R.; Onen, D.; Crowther, G.; Molenaar, M.M.; Reynolds, A.; Berlang, W. Cloud-Based Solution for Permanent Fiber-Optic DAS Flow Monitoring. In Proceedings of the SPE Digital Energy Conference and Exhibition, The Woodlands, TX, USA, 3–5 March 2015; p. D031S018R001. [Google Scholar] [CrossRef]
- Sui, W.; Liu, R.; Cui, K. Application and research progress of distributed optical fiber acoustic sensing monitoring for hydraulic fracturing. Sci. Sin. Technol. 2021, 51, 371–387. [Google Scholar] [CrossRef]
- Courtier, J.; Chandler, K.; Gray, D.; Martin, S.; Thomas, R.; Wicker, J.; Ciezobka, J. Best practices in designing and executing a comprehensive hydraulic fracturing test site in the Permian Basin. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017; p. URTEC-2697483. [Google Scholar] [CrossRef]
- Curth, P.J.; Courtier, J.R.; Smallwood, G.B.; Mauro, R.; Evans, S. Earth model assists Permian asset valuation. Oil Gas J. 2015, 113, 64–69. [Google Scholar]
- Courtier, J.; Wicker, J.; Jeffers, T. Optimizing the development of a stacked continuous resource play in the Midland basin. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016; p. URTEC-2461811. [Google Scholar] [CrossRef]
- Heidbach, O.; Rajabi, M.; Cui, X.; Fuchs, K.; Müller, B.; Reinecker, J.; Reiter, K.; Tingay, M.; Wenzel, F.; Xie, F.; et al. World stress map database release 2016. Tectonophysics 2016, 744, 484–498. [Google Scholar] [CrossRef]
- Trowbridge, S.; Wicker, J.; Courtier, J.; Fairfield, R.; Campbell, T. Application of microseismic to assess hydraulic fracture behavior in relation to completion design and landing zone. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017; p. URTEC-2674376. [Google Scholar] [CrossRef]
- Gale, J.F.; Elliott, S.J.; Laubach, S.E. Hydraulic fractures in core from stimulated reservoirs: Core fracture description of HFTS slant core, Midland Basin, West Texas. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018; pp. 1340–1357. [Google Scholar] [CrossRef]
- Maity, D.; Ciezobka, J. An interpretation of proppant transport within the stimulated rock volume at the hydraulic-fracturing test site in the Permian Basin. SPE Reserv. Eval. Eng. 2019, 22, 477–491. [Google Scholar] [CrossRef]
- Li, T.; Chu, W.; Leonard, P.A. Analysis and interpretations of pressure data from the hydraulic fracturing test site (HFTS). In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019; pp. 2923–2938. [Google Scholar] [CrossRef]
- Maity, D.; Ciezobka, J. A data analytics framework for cored fracture imaging and novel characterization workflow-application on samples from Hydraulic Fracturing Test Site HFTS in the Midland Basin. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020; p. D011S001R005. [Google Scholar] [CrossRef]
- Salahshoor, S.; Maity, D.; Ciezobka, J. Stage-level data integration to evaluate the fracturing behavior of horizontal wells at the Hydraulic Fracturing Test Site (HFTS): An insight into the production performance. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Virtual, 20–22 July 2020; p. D033S074R003. [Google Scholar] [CrossRef]
- Salahshoor, S. Analysis and Interpretation of Multi-Source Data at the Hydraulic Fracturing Test Site: A Data-Driven Approach to Improve Well Performance Evaluation in Heterogeneous Formations. In Proceedings of the Latin America Unconventional Resources Technology Conference, Virtual, 16–18 November 2020; pp. 252–262. [Google Scholar] [CrossRef]
- Ciezobka, J.; Reeves, S. Overview of hydraulic fracturing test sites (HFTS) in the Permian Basin and summary of selected results (HFTS-I in Midland and HFTS-II in Delaware). In Proceedings of the Latin America Unconventional Resources Technology Conference, Virtual, 16–18 November 2020; pp. 93–102. [Google Scholar] [CrossRef]
- Ciezobka, J. Overview of hydraulic fracturing test site 2 in the Permian Delaware Basin (HFTS-2). In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021; pp. 259–278. [Google Scholar] [CrossRef]
- Gale, J.F.W.; Elliott, S.J.; Rysak, B.G.; Ginn, C.L.; Zhang, N.; Myers, R.D.; Laubach, S.E. Fracture description of the HFTS-2 slant core, Delaware Basin, West Texas. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021; pp. 1122–1133. [Google Scholar] [CrossRef]
- Zhishuai, Z.; James, D.; Bevc Dimitri, N.; Tan, I.L.C.; Swafford, Y.; Laura Craven, M.; Vissotski, A. Hydraulic Fracture Characterization by Integrating Multidisciplinary Data from the Hydraulic Fracturing Test Site 2 (HFTS-2). In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021. [Google Scholar] [CrossRef]
- Bessa, F.; Jerath, K.; Ginn, C.; Johnston, P.; Zhao, Y.; Brown, T.; Sahni, V. Subsurface characterization of hydraulic fracture test site-2 (HFTS-2), Delaware basin. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021; pp. 241–258. [Google Scholar] [CrossRef]
- Pudugramam, V.S.; Zhao, Y.; Bessa, F.; Li, J.; Zakhour, N.; Brown, T.; Sahni, V. Analysis and Integration of the Hydraulic Fracturing Test Site-2 (HFTS-2) Comprehensive Dataset. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021; pp. 1562–1578. [Google Scholar] [CrossRef]
- Liu, X.; Tan, Y.; Singh, A.; Waddle, R.; Hilarides, K.; Forand, D.; Rijken, M. Learnings on fracture and geomechanical modeling from the hydraulic fracturing test site in the Midland Basin, West Texas. In Proceedings of the Asia Pacific Unconventional Resources Technology Conference, Virtual, 16–18 November 2021; pp. 416–442. [Google Scholar] [CrossRef]
- Cao, M.; Zheng, S.; Elliott, B.; Sharma, M. Impact of complex fracture networks on well productivity: A case study of the hydraulic fracturing test site# 2. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 1–3 February 2022; p. D011S001R002. [Google Scholar] [CrossRef]
- Nolte, K.G.; Smith, M.B. Interpretation of fracturing pressures. J. Pet. Technol. 1981, 33, 1767–1775. [Google Scholar] [CrossRef]
- Nolte, K.G. Determination of fracture parameters from fracturing pressure decline. In Proceedings of the SPE Annual Technical Conference and Exhibition, Las Vegas, NV, USA, 23–26 September 1979; p. SPE-8341. [Google Scholar] [CrossRef]
- Pirayesh, E.; Soliman, M.Y.; Rafiee, M. Make Decision on the Fly: A New Method to Interpret Pressure-Time Data During Fracturing-Application to Frac Pack. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September 2013. [Google Scholar] [CrossRef]
- Al-Husain, H.M.; Soliman, M.Y.; Stegent, N.A. Application of moving reference point MRP method to cotton valley and travis peak sand fracturing treatments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017; p. D021S005R006. [Google Scholar] [CrossRef]
- Surjaatmadja, J.B.; Stephenson, S.; Bhaumik, C.; Thompson, S.; Cheng, A. Analysis of generated and reflected pressure waves during fracturing reveals fracture behavior. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September 2002; p. SPE-77598. [Google Scholar] [CrossRef]
- Zhao, J.; Ren, L.; Jiang, T.; Hu, D.; Wu, L.; Wu, J.; Du, L. Ten years of gas shale fracturing in China: Review and prospect. Nat. Gas Ind. B 2022, 9, 158–175. [Google Scholar] [CrossRef]
- Zhao, J.; Ren, L.; Lin, R.; Li, K.; Li, Y. Automatic Diagnosis Method for Wellhead Pressure Curve of Hydraulic Fracturing in Shale Gas Horizontal Well. U.S. Patent No. 10,689,972, 23 June 2020. [Google Scholar]
- Martinez, A.D.; Wright, C.A.; Wright, T.B. Field Application of Real-Time Hydraulic Fracturing Analysis. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 26–28 April 1993; p. SPE-25916. [Google Scholar] [CrossRef]
- Crockett, A.R.; Okusu, N.M.; Cleary, M.P. A complete integrated model for design and real-time analysis of hydraulic fracturing operations. In Proceedings of the SPE Western Regional Meeting, Oakland, CA, USA, 2–4 April 1986; p. SPE-15069. [Google Scholar] [CrossRef]
- Crockett, A.R.; Willis, R.M., Jr.; Cleary, M.P. Improvement of hydraulic fracture predictions by real-time history matching on observed pressures. SPE Prod. Eng. 1989, 4, 408–416. [Google Scholar] [CrossRef]
- Westwood, R.F.; Toon, S.M.; Cassidy, N.J. A sensitivity analysis of the effect of pumping parameters on hydraulic fracture networks and local stresses during shale gas operations. Fuel 2017, 203, 843–852. [Google Scholar] [CrossRef]
- Jenkins, A.; Fathi, E.; Belyadi, F. Stress field behavior induced by hydraulic fracture in shale reservoirs: A practical view on cluster spacing. J. Nat. Gas Sci. Eng. 2017, 48, 186–196. [Google Scholar] [CrossRef]
- Hoda, S.; Iriarte, J. Robust Event Recognition in Real-Time Hydraulic Fracturing Data for Live Reporting and Analysis. In Proceedings of the Unconventional Resources Technology Conference, Virtual, 20–22 July 2020; pp. 3398–3415. [Google Scholar] [CrossRef]
- Zhukova, K.; Antonic, M.; Soleša, M.; Camber, D. Data-Driven Model for Measuring Hydraulic Fracturing Efficiency by Utilizing the Real-Time Treatment Data. In Proceedings of the International Petroleum Technology Conference, Riyadh, Saudi Arabia, 21–23 February 2022; p. D031S107R002. [Google Scholar] [CrossRef]
- Blauer, R.E.; Holcomb, D.L. Using 3D fracture simulation alone may result in incorrect fracture-geometry determination and unreliable real-time fracture analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996; p. SPE-36674. [Google Scholar] [CrossRef]
- Dung, N.; David, C.; Tom, D.; Jon, S.; Nico, R.; Annie, O. Practical applications of water hammer analysis from hydraulic fracturing treatments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Virtual, 4–6 May 2021; p. D011S002R009. [Google Scholar] [CrossRef]
- Carey, M.A.; Mondal, S.; Sharma, M.M. Analysis of water hammer signatures for fracture diagnostics. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015; p. D031S034R003. [Google Scholar] [CrossRef]
- Holzhausen, G.; Gooch, R. Impedance of hydraulic fractures: Its measurement and use for estimating fracture closure pressure and dimensions: Presented at the SPE. In Proceedings of the DOE Low Permeability Gas Reservoirs Symposium, Denver, CO, USA, 19–22 May 1985. [Google Scholar] [CrossRef]
- Paige, R.W.; Murray, L.R.; Roberts, J.D.M. Field application of hydraulic impedance testing for fracture measurement. SPE Prod. Facil. 1995, 10, 7–12. [Google Scholar] [CrossRef]
- Yew, C.H.; Ashour, A.A.I.S. A Study of the Fracture Impedance Method. In Proceedings of the Annual Technical Meeting, Calgary, AB, Canada, 9–11 June 1996. [Google Scholar] [CrossRef]
- Patzek, T.W.; De, A. Lossy transmission line model of hydrofractured well dynamics. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 10–13 May 1998; p. SPE-46195. [Google Scholar] [CrossRef]
- Mondal, S. Pressure Transients In Wellbores: Water Hammer Effects And Implications For Fracture Diagnostics Diagnostics. Master’s Thesis, The University of Texas at Austin, Austin, TX, USA, December 2010. [Google Scholar]
- Carey, M.A.; Mondal, S.; Sharma, M.M.; Hebert, D.B. Correlating water hammer signatures with production log and microseismic data in fractured horizontal wells. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 9–11 February 2016; p. D021S004R006. [Google Scholar] [CrossRef]
- Iriarte, J.; Merritt, J.; Kreyche, B. Using water hammer characteristics as a fracture treatment diagnostic. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium, Oklahoma City, OK, USA, 27–31 March 2017; p. D031S007R004. [Google Scholar] [CrossRef]
- Shen, J.; He, H.; Li, Y.; Zou, L.; Wang, Y.; Zhu, Z.; Fu, S. An investigation of data analysis method for hydraulic fracturing based on the water hammer effect. Unconv. Resour. 2023, 3, 284–290. [Google Scholar] [CrossRef]
- Hu, X.; Luo, Y.; Zhou, F.; Qiu, Y.; Li, Z.; Li, Y. Evaluation of multi-fractures geometry based on water hammer signals: A new comprehensive model and field application. J. Hydrol. 2022, 612, 128240. [Google Scholar] [CrossRef]
- Jia, K.; Wang, X.; Lu, D. Comprehensive model for multi-fracture localization based on water hammer signals: Evaluation and field application. Phys. Fluids 2024, 36, 123612. [Google Scholar] [CrossRef]
- Castillo, J.L. Modified fracture pressure decline analysis including pressure-dependent leak off. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 18–19 May 1987; p. SPE-16417. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, Y.; Liu, J.; Peng, F.; Teng, Q.; Xiao, Y.; Han, X. A method of quickly evaluating the fracture complexity of network fracturing. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 14–16 November 2016; p. D011S011R006. [Google Scholar] [CrossRef]
- Tu, Z.; Hu, X.; Zhou, F.; Huang, G.; Han, S.; Zhou, Q. A new multi-fracture geometry inversion model based on hydraulic-fracture treatment pressure falloff data. J. Pet. Sci. Eng. 2022, 215, 110724. [Google Scholar] [CrossRef]
- Jatykov, T.; Bimuratkyzy, K. Case study: An approach for hydraulic fracturing minifrac G-function analysis in relation to facies distribution in multilayered clastic reservoirs. SPE Prod. Oper. 2022, 37, 99–106. [Google Scholar] [CrossRef]
- Kolle, J.J.; Theimer, A.R.; Fraser, A.W.; Fletcher, S. Predicting the extended reach capabilities of a water-hammer tool with variable bypass control. In Proceedings of the SPE/ICoTA Well Intervention Conference and Exhibition, Houston, TX, USA, 22–23 March 2016; p. D021S008R004. [Google Scholar] [CrossRef]
- Ma, X.; Zhou, F.; Ortega Andrade, J.A.; Gosavi, S.; Burch, D. Evaluation of water hammer analysis as diagnostic tool for hydraulic fracturing. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019; p. D023S030R007. [Google Scholar] [CrossRef]
- Bakar, R.; Ozkan, E.; Kazemi, H. Modeling and analysis of diagnostic fracture injection tests DFITs. In Proceedings of the SPE Europec featured at EAGE Conference and Exhibition, Amsterdam, The Netherlands, 18–21 October 2021; p. D031S006R001. [Google Scholar] [CrossRef]
- Wenchao, L.; Chengcheng, Q.; Ping, W.; Wensong, H.; Yuewu, L.; Wei, D.; Yuping, S. Study on fracture characteristics difference between fracturing fluid flowback and gas production stages of shale gas wells. Chin. J. Theor. Appl. Mech. 2023, 55, 1382–1393. [Google Scholar] [CrossRef]
- Song, B.; Ehlig-Economides, C.; Economides, M.J. Design of multiple transverse fracture horizontal wells in shale gas reservoirs. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2011; p. SPE-140555. [Google Scholar] [CrossRef]
- Taghavinejad, A.; Sharifi, M.; Heidaryan, E.; Liu, K.; Ostadhassan, M. Flow modeling in shale gas reservoirs: A comprehensive review. J. Nat. Gas Sci. Eng. 2020, 83, 103535. [Google Scholar] [CrossRef]
- Crafton, J.W. Well evaluation using early time post-stimulation flowback data. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 27–30 September 1998; p. SPE-49223. [Google Scholar] [CrossRef]
- Crafton, J.W.; Gunderson, D. Use of extremely high time-resolution production data to characterize hydraulic fracture properties. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006; p. SPE-103591. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Williams-Kovacs, J.D. Modeling two-phase flowback of multifractured horizontal wells completed in shale. Spe J. 2013, 18, 795–812. [Google Scholar] [CrossRef]
- Xu, Y.; Adefidipe, O.A.; Dehghanpour, H. Estimating fracture volume using flowback data from the Horn River Basin: A material balance approach. J. Nat. Gas Sci. Eng. 2015, 25, 253–270. [Google Scholar] [CrossRef]
- Williams-Kovacs, J.D.; Clarkson, C.R. A modified approach for modeling two-phase flowback from multi-fractured horizontal shale gas wells. J. Nat. Gas Sci. Eng. 2016, 30, 127–147. [Google Scholar] [CrossRef]
- Wang, F.; Pan, Z.; Zhang, S. Impact of chemical osmosis on water leak off and flowback behavior from hydraulically fractured gas shale. J. Pet. Sci. Eng. 2017, 151, 264–274. [Google Scholar] [CrossRef]
- Xu, Y.; Dehghanpour, H.; Ezulike, O.; Virues, C. Effectiveness and time variation of induced fracture volume: Lessons from water flowback analysis. Fuel 2017, 210, 844–858. [Google Scholar] [CrossRef]
- Yang, T.; Wu, X. Water flowback analysis and hydraulic fracture characterization in Marcellus unconventional reservoir. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium, Oklahoma City, OK, USA, 27–31 March 2017; p. D031S009R002. [Google Scholar] [CrossRef]
- Zhang, F.; Emami-Meybodi, H. A semianalytical method for two-phase flowback rate-transient analysis in shale gas reservoirs. SPE J. 2020, 25, 1599–1622. [Google Scholar] [CrossRef]
- Zhang, F.; Emami-Meybodi, H. A type-curve method for two-phase flowback analysis in hydraulically fractured hydrocarbon reservoirs. J. Pet. Sci. Eng. 2022, 209, 109912. [Google Scholar] [CrossRef]
- Lee, S.T.; Brockenbrough, J.R. A new approximate analytic solution for finite-conductivity vertical fractures. SPE Form. Eval. 1986, 1, 75–88. [Google Scholar] [CrossRef]
- Brown, M.L.; Ozkan, E.; Raghavan, R.S.; Kazemi, H. Practical Solutions for Pressure-Transient Responses of Fractured Horizontal Wells in Unconventional Shale Reservoirs. SPE Reserv. Eval. Eng. 2009, 14, 663–676. [Google Scholar] [CrossRef]
- Stalgorova, E.; Mattar, L. Practical analytical model to simulate production of horizontal wells with branch fractures. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October 2012. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Zhao, J.; Luo, J.-X.; Zhang, B.-N. “Triple porosity” modeling of transient well test and rate decline analysis for multi-fractured horizontal well in shale gas reservoirs. J. Pet. Sci. Eng. 2013, 110, 253–262. [Google Scholar] [CrossRef]
- Qiu, K.; Li, H. A new analytical solution of the triple-porosity model for history matching and performance forecasting in unconventional oil reservoirs. SPE J. 2018, 23, 2060–2079. [Google Scholar] [CrossRef]
- Meng, M.; Chen, Z.; Liao, X.; Wang, J.; Shi, L. A well-testing method for parameter evaluation of multiple fractured horizontal wells with non-uniform fractures in shale oil reservoirs. Adv. Geo-Energy Res. 2020, 4, 187–198. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Hu, X.; Dai, C.; Fang, S. Fracture network types revealed by well test curves for shale reservoirs in the Sichuan Basin, China. Energy Geosci. 2024, 5, 100135. [Google Scholar] [CrossRef]
- Ezulike, D.O.; Dehghanpour, H. A model for simultaneous matrix depletion into natural and hydraulic fracture networks. J. Nat. Gas Sci. Eng. 2014, 16, 57–69. [Google Scholar] [CrossRef]
- Stalgorova, K.; Mattar, L. Analytical model for unconventional multifractured composite systems. SPE Reserv. Eval. Eng. 2013, 16, 246–256. [Google Scholar] [CrossRef]
- Deng, Q.; Nie, R.S.; Jia, Y.L.; Huang, X.-Y.; Li, J.-M.; Li, H.-K. A new analytical model for non-uniformly distributed multi-fractured system in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2015, 27, 719–737. [Google Scholar] [CrossRef]
- Zeng, J.; Wang, X.; Guo, J.; Zeng, F. Composite linear flow model for multi-fractured horizontal wells in heterogeneous shale reservoir. J. Nat. Gas Sci. Eng. 2017, 38, 527–548. [Google Scholar] [CrossRef]
- Wu, Y.H.; Fang, S.D.; Wang, S.R.; Huang, S.J.; Ma, L.Q.; Fu, G.Q. A novel production data analysis method for multi-fractured horizontal wells with infill well-caused fracture interference. Pet. Sci. 2023, 20, 2967–2980. [Google Scholar] [CrossRef]
- Cheng, L.-S.; Cao, C.; Pan, Q.-Y.; Jia, P.; Cao, R.-Y.; Wang, Z.-K.; Shi, J.-J. A semi-analytical pressure and rate transient analysis model for inner boundary and propped fractures exhibiting dynamic behavior under long-term production conditions. Pet. Sci. 2024, 21, 2520–2535. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, X.; Zhao, X.; Dou, X.; Zhu, L. Performance of horizontal wells with fracture networks in shale gas formation. J. Pet. Sci. Eng. 2015, 133, 646–664. [Google Scholar] [CrossRef]
- Li, Z.; Wu, X.; Han, G.; Zhang, L.; Zhao, R.; Shi, S. A semi-analytical pressure model of horizontal well with complex networks in heterogeneous reservoirs. J. Pet. Sci. Eng. 2021, 202, 108511. [Google Scholar] [CrossRef]
- Cui, G.; Tan, Y.; Chen, T.; Feng, X.-T.; Elsworth, D.; Pan, Z.; Wang, C. Multidomain two-phase flow model to study the impacts of hydraulic fracturing on shale gas production. Energy Fuels 2020, 34, 4273–4288. [Google Scholar] [CrossRef]
- Deng, J.; He, J.; Song, H. An improved mathematical model of gas-water two-phase flows in fractured horizontal wells accounting for physical contact behaviors of fractures with total factor characteristics. Phys. Fluids 2024, 36, 8. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Haghshenas, B.; Ghanizadeh, A.; Qanbari, F.; Williams-Kovacs, J.D.; Riazi, N.; Deglint, H.J. Nanopores to megafractures: Current challenges and methods for shale gas reservoir and hydraulic fracture characterization. J. Nat. Gas Sci. Eng. 2016, 31, 612–657. [Google Scholar] [CrossRef]
- Alfarge, D.; Wei, M.; Bai, B. Evaluating the performance of hydraulic-fractures in unconventional reservoirs using production data: Comprehensive review. J. Nat. Gas Sci. Eng. 2019, 61, 133–141. [Google Scholar] [CrossRef]
- Barree, R.D.; Fisher, M.K.; Woodroof, R.A. A practical guide to hydraulic fracture diagnostic technologies. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September 2002; p. SPE-77442. [Google Scholar] [CrossRef]
- Cipolla, C.L.; Wright, C.A. State-of-the-art in hydraulic fracture diagnostics. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 16–18 October 2000; p. SPE-64434. [Google Scholar] [CrossRef]
- Wright, C.A.; Cipolla, C.C. Diagnostic Techniques to Understand Hydraulic Fracturing: What? Why? and How? In Proceedings of the SPE/CERI Gas Technology Symposium, Calgary, AB, Canada, 3–5 April 2000; p. SPE-59735-MS. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Beierle, J.J. Integration of microseismic and other post-fracture surveillance with production analysis: A tight gas study. J. Nat. Gas Sci. Eng. 2011, 3, 382–401. [Google Scholar] [CrossRef]
- Holley, E.H.; Zimmer, U.; Mayerhofer, M.J.; Samson, E. Integrated analysis combining microseismic mapping and fiber-optic distributed temperature sensing (DTS). In Proceedings of the SPE Canada Unconventional Resources Conference, Calgary, AB, Canada, 19–21 October 2010; p. SPE-136565. [Google Scholar] [CrossRef]
| Evaluation Method | Parameters Acquired | Parameters Acquired | Limitations |
|---|---|---|---|
| Microseismic | Fracture half-length, height, azimuth, dip | Non-invasive, real-time fracture evolution tracking | Signal interference susceptibility, geological sensitivity |
| Tracers | Fracture height, width, length | Intuitive results, multi-medium applicability | Environmental risks, geological/rock property constraints |
| Wide-Field Electromagnetics | Fracture length, height, cluster efficiency | Non-invasive, deep reservoir applicability | High cost, inversion ambiguity |
| Distributed Fiber Optics | Fracture volume, length, formation pressure | High sensitivity, multiparameter measurement | High equipment costs, environmental sensitivity |
| Field Experiments | Fracture width, proppant distribution, conductivity | Detailed parameter insights | Limited scalability, high cost/time |
| Evaluation Method | Parameters Acquired | Parameters Acquired | Limitations |
|---|---|---|---|
| Fracturing | SRV, fracture area, half-length, conductivity | High-resolution pumping data | Solution non-uniqueness |
| Shut-in | Closure pressure, fracture complexity | Stage-specific parameter evaluation | Short monitoring duration |
| Flowback | Fracture volume, half-length, pressure | Single-phase flow simplicity | Underdeveloped mechanistic models |
| Production | EUR, permeability, fracture parameters | Production history matching | Parameter averaging, flow regime limitations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Sun, Y.; Xiong, W.; Niu, W.; Tang, Z.; Li, Y. Advances in Evaluation Methods for Artificial Fracture Networks in Shale Gas Horizontal Wells. Appl. Sci. 2025, 15, 9008. https://doi.org/10.3390/app15169008
Yuan H, Sun Y, Xiong W, Niu W, Tang Z, Li Y. Advances in Evaluation Methods for Artificial Fracture Networks in Shale Gas Horizontal Wells. Applied Sciences. 2025; 15(16):9008. https://doi.org/10.3390/app15169008
Chicago/Turabian StyleYuan, Hang, Yuping Sun, Wei Xiong, Wente Niu, Zejun Tang, and Yong Li. 2025. "Advances in Evaluation Methods for Artificial Fracture Networks in Shale Gas Horizontal Wells" Applied Sciences 15, no. 16: 9008. https://doi.org/10.3390/app15169008
APA StyleYuan, H., Sun, Y., Xiong, W., Niu, W., Tang, Z., & Li, Y. (2025). Advances in Evaluation Methods for Artificial Fracture Networks in Shale Gas Horizontal Wells. Applied Sciences, 15(16), 9008. https://doi.org/10.3390/app15169008






