Voxel-Based Multi-Person Multi-View 3D Pose Estimation in Operating Room
Abstract
1. Introduction
- We are the first to apply a voxel-based 3D multi-person pose estimation framework to real-world operating room scenarios, achieving a favorable balance between accuracy and computational efficiency, which is critical for clinical applications.
- We propose a Fine-Grained Depth-Wise Projection Decay (FDPD) strategy that directly incorporates high-resolution depth maps into voxel space reconstruction. This approach effectively reduces depth ambiguity and significantly improves pose estimation accuracy, especially under limited camera views.
- We design an attention-enhanced encoder–decoder architecture that integrates positional encoding and a gating mechanism. This enables the model to capture both local features and global context, enhancing robustness to occlusions and complex spatial configurations commonly found in surgical environments.
2. Related Works
2.1. Multi-Person Multi-View 3D Pose Estimation
2.2. 3D HPE in Operating Room (OR)
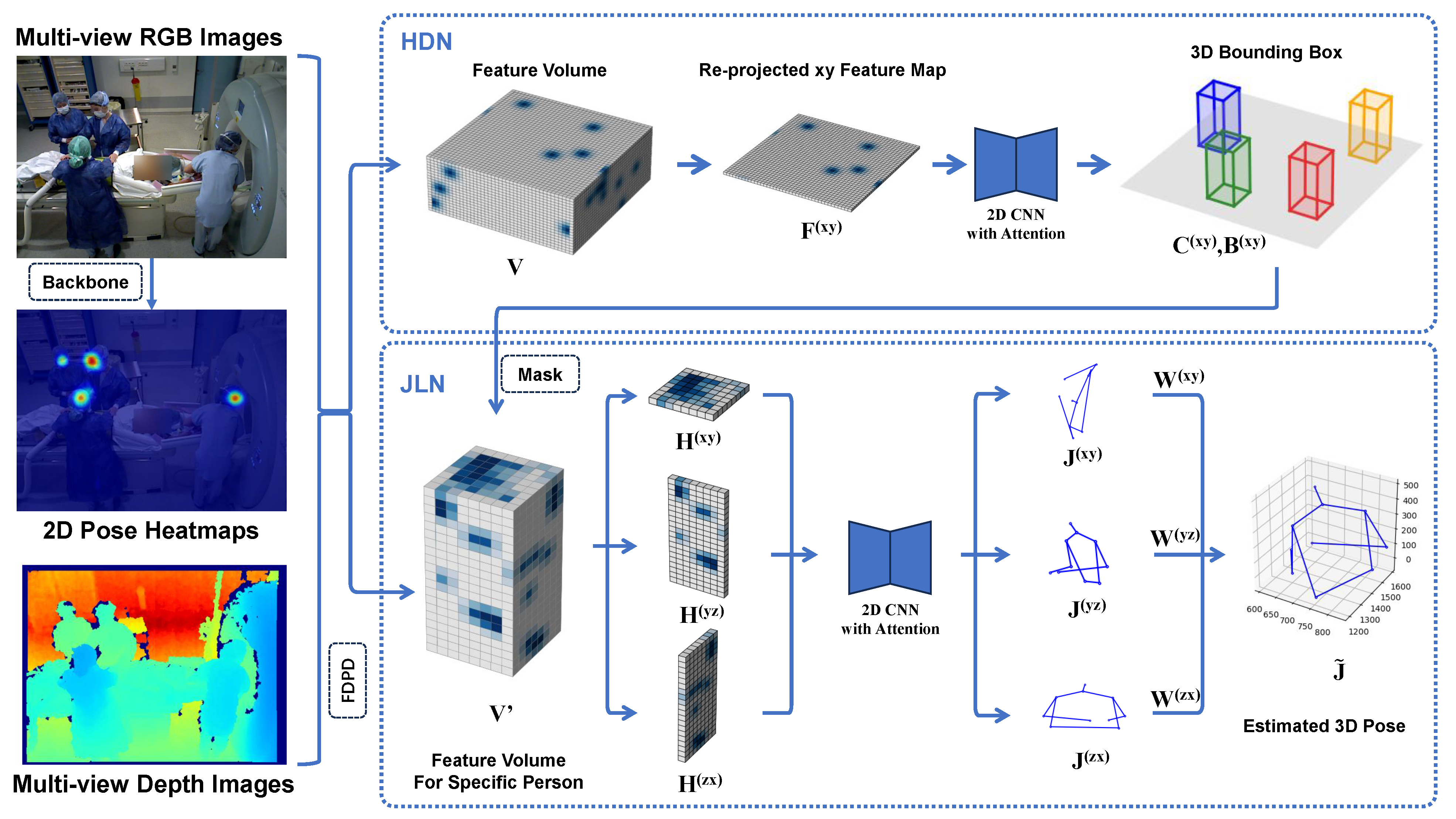
3. Methods
3.1. Overview
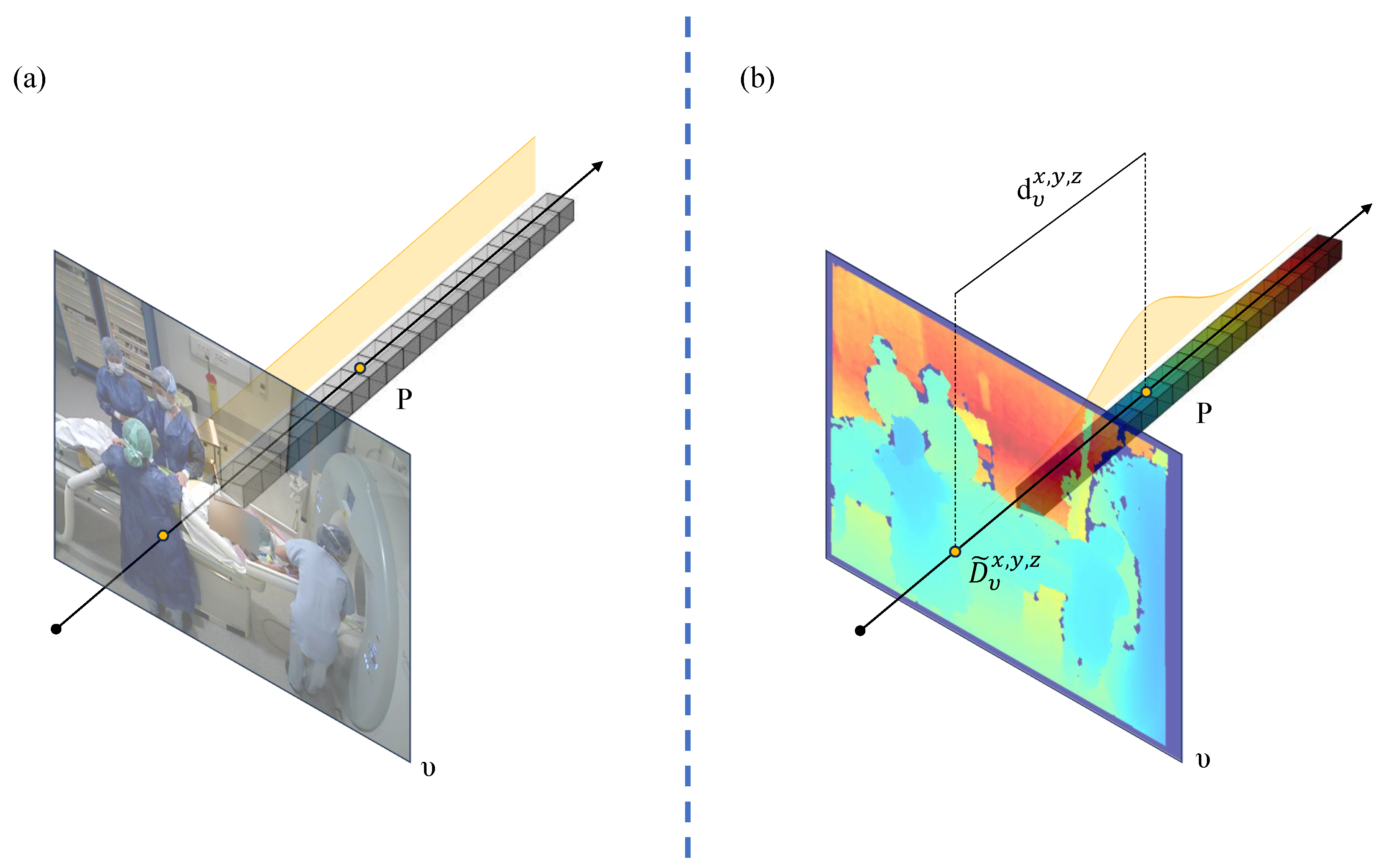
3.2. The Fine-Grained Depth-Wise Projection Decay (FDPD)
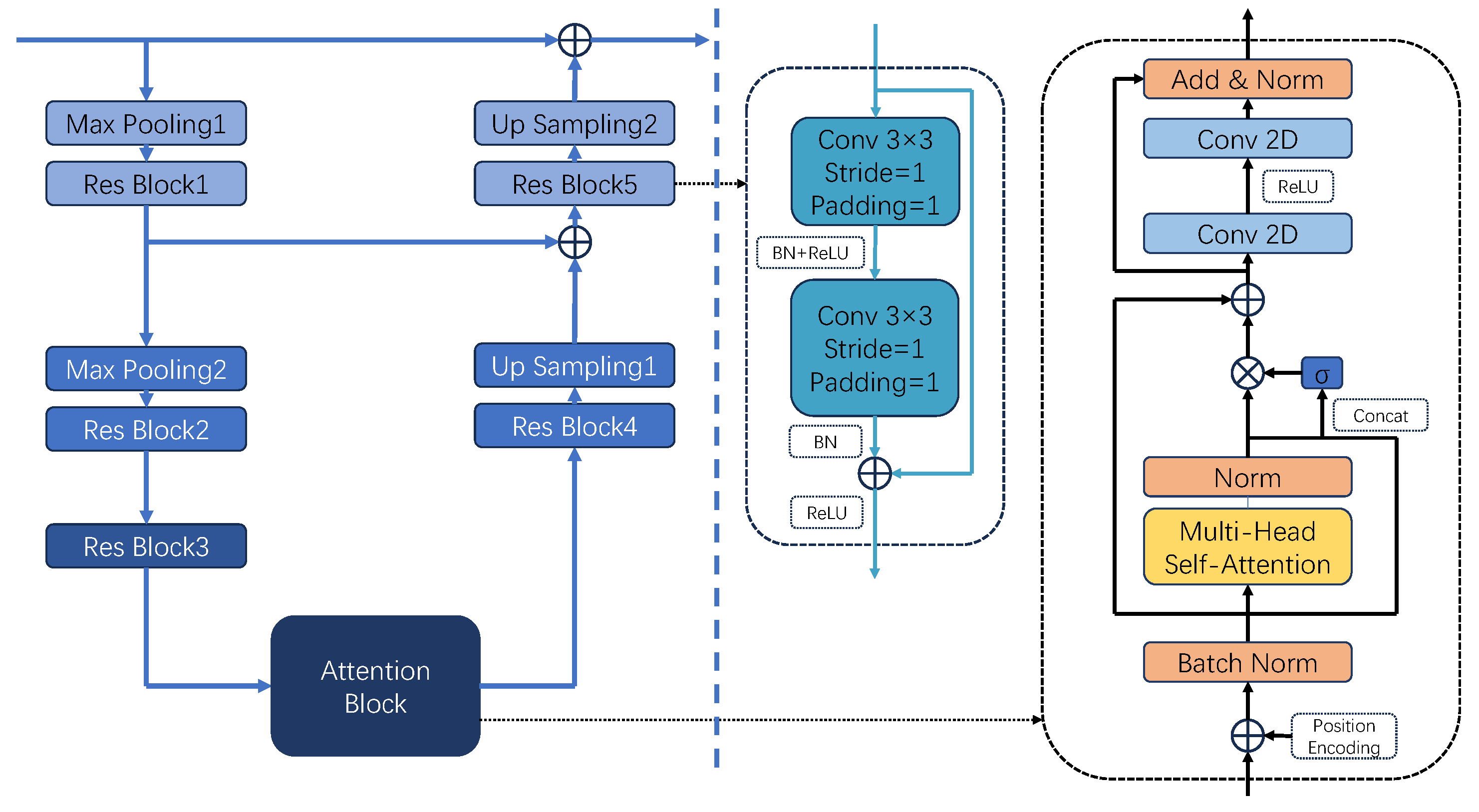
3.3. Encoder–Decoder Structure with Attention Mechanism
3.4. Human Detection Network
3.5. The Joint Localization Network
4. Experiments
4.1. Datasets
4.2. Metrics
4.3. Implementation Details
4.4. Comparison with SOTA
4.5. Ablation Study
4.5.1. Evaluation of FDPD
4.5.2. Evaluation of Attention Mechanism
4.6. Qualitative Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mascagni, P.; Padoy, N. OR black box and surgical control tower: Recording and streaming data and analytics to improve surgical care. J. Visc. Surg. 2021, 158, S18–S25. [Google Scholar] [CrossRef]
- Özsoy, E.; Pellegrini, C.; Czempiel, T.; Tristram, F.; Yuan, K.; Bani-Harouni, D.; Eck, U.; Busam, B.; Keicher, M.; Navab, N. Mm-or: A large multimodal operating room dataset for semantic understanding of high-intensity surgical environments. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 19378–19389. [Google Scholar]
- Profetto, L.; Gherardelli, M.; Iadanza, E. Radio Frequency Identification (RFID) in health care: Where are we? A scoping review. Health Technol. 2022, 12, 879–891. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Wang, C.; Wang, J.; Wang, N.; Zeng, W. Cross view fusion for 3D human pose estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 4342–4351. [Google Scholar]
- Iskakov, K.; Burkov, E.; Lempitsky, V.; Malkov, Y. Learnable triangulation of human pose. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 7718–7727. [Google Scholar]
- Ye, H.; Zhu, W.; Wang, C.; Wu, R.; Wang, Y. Faster voxelpose: Real-time 3D human pose estimation by orthographic projection. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 142–159. [Google Scholar]
- Zhuang, Z.; Zhou, Y. FasterVoxelPose+: Fast and accurate voxel-based 3D human pose estimation by depth-wise projection decay. In Proceedings of the Asian Conference on Machine Learning, Hanoi, Vietnam, 5–8 December 2024; pp. 1763–1778. [Google Scholar]
- Srivastav, V.; Issenhuth, T.; Kadkhodamohammadi, A.; de Mathelin, M.; Gangi, A.; Padoy, N. MVOR: A multi-view RGB-D operating room dataset for 2D and 3D human pose estimation. arXiv 2018, arXiv:1808.08180. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Lupión, M.; Polo-Rodríguez, A.; Medina-Quero, J.; Sanjuan, J.F.; Ortigosa, P.M. 3D human pose estimation from multi-view thermal vision sensors. Inf. Fusion 2024, 104, 102154. [Google Scholar] [CrossRef]
- Boldo, M.; De Marchi, M.; Martini, E.; Aldegheri, S.; Quaglia, D.; Fummi, F.; Bombieri, N. Real-time multi-camera 3D human pose estimation at the edge for industrial applications. Expert Syst. Appl. 2024, 252, 124089. [Google Scholar] [CrossRef]
- Zhu, X.; Ye, X. GAN-BodyPose: Real-time 3D human body pose data key point detection and quality assessment assisted by generative adversarial network. Image Vis. Comput. 2024, 149, 105144. [Google Scholar] [CrossRef]
- Srivastav, V.; Chen, K.; Padoy, N. Selfpose3d: Self-supervised multi-person multi-view 3D pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 2502–2512. [Google Scholar]
- Li, Y.J.; Xu, Y.; Khirodkar, R.; Park, J.; Kitani, K. Multi-person 3D pose estimation from multi-view uncalibrated depth cameras. arXiv 2024, arXiv:2401.15616. [Google Scholar]
- Niu, Z.; Lu, K.; Xue, J.; Wang, J. Skeleton Cluster Tracking for robust multi-view multi-person 3D human pose estimation. Comput. Vis. Image Underst. 2024, 246, 104059. [Google Scholar] [CrossRef]
- Amara, K.; Guerroudji, M.A.; Zenati, N.; Kerdjidj, O.; Atalla, S.; Mansoor, W.; Ramzan, N. Augmented Reality localisation using 6 DoF phantom head Pose Estimation-based generalisable Deep Learning model. In Proceedings of the 2024 8th International Conference on Image and Signal Processing and their Applications (ISPA), Biskra, Algeria, 21–22 April 2024; pp. 1–6. [Google Scholar]
- Xu, M.; Shu, Q.; Huang, Z.; Chen, G.; Poslad, S. ARLO: Augmented Reality Localization Optimization for Real-Time Pose Estimation and Human–Computer Interaction. Electronics 2025, 14, 1478. [Google Scholar] [CrossRef]
- Zhu, Y.; Xiao, M.; Xie, Y.; Xiao, Z.; Jin, G.; Shuai, L. In-bed human pose estimation using multi-source information fusion for health monitoring in real-world scenarios. Inf. Fusion 2024, 105, 102209. [Google Scholar] [CrossRef]
- Tsoy, A.; Liu, Z.; Zhang, H.; Zhou, M.; Yang, W.; Geng, H.; Jiang, K.; Yuan, X.; Geng, Z. Image-free single-pixel keypoint detection for privacy preserving human pose estimation. Opt. Lett. 2024, 49, 546–549. [Google Scholar] [CrossRef] [PubMed]
- Salehin, S.; Kearney, S.; Gurbuz, Z. Kinematic Cycle Consistency Using Wearables and RF Data for Improved Human Skeleton Estimation. In Proceedings of the 2024 58th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 27–30 October 2024; pp. 1215–1219. [Google Scholar]
- Joo, H.; Liu, H.; Tan, L.; Gui, L.; Nabbe, B.; Matthews, I.; Kanade, T.; Nobuhara, S.; Sheikh, Y. Panoptic studio: A massively multiview system for social motion capture. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3334–3342. [Google Scholar]
- Belagiannis, V.; Amin, S.; Andriluka, M.; Schiele, B.; Navab, N.; Ilic, S. 3D pictorial structures for multiple human pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1669–1676. [Google Scholar]
- Guo, Y.; Li, Z.; Li, Z.; Du, X.; Quan, S.; Xu, Y. PoP-Net: Pose Over Parts Network for Multi-Person 3D Pose Estimation From a Depth Image. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 1240–1249. [Google Scholar]
- Jiang, T.; Billingham, J.; Müksch, S.; Zarate, J.; Evans, N.; Oswald, M.; Pollefeys, M.; Hilliges, O.; Kaufmann, M.; Song, J. WorldPose: A World Cup Dataset for Global 3D Human Pose Estimation. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Tu, H.; Wang, C.; Zeng, W. Voxelpose: Towards multi-camera 3D human pose estimation in wild environment. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part I 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 197–212. [Google Scholar]
- Zheng, C.; Zhu, S.; Mendieta, M.; Yang, T.; Chen, C.; Ding, Z. 3D human pose estimation with spatial and temporal transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 11656–11665. [Google Scholar]
- Zhang, J.; Cai, Y.; Yan, S.; Feng, J. Direct multi-view multi-person 3D pose estimation. Adv. Neural Inf. Process. Syst. 2021, 34, 13153–13164. [Google Scholar]
- Zhang, W.; Liu, M.; Liu, H.; Li, W. SVTformer: Spatial-View-Temporal Transformer for Multi-View 3D Human Pose Estimation. Proc. Aaai Conf. Artif. Intell. 2025, 39, 10148–10156. [Google Scholar] [CrossRef]
- Chen, L.; Ai, H.; Chen, R.; Zhuang, Z.; Liu, S. Cross-view tracking for multi-human 3D pose estimation at over 100 fps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3279–3288. [Google Scholar]
- Maier-Hein, L.; Eisenmann, M.; Sarikaya, D.; März, K.; Collins, T.; Malpani, A.; Fallert, J.; Feussner, H.; Giannarou, S.; Mascagni, P.; et al. Surgical data science–from concepts toward clinical translation. Med. Image Anal. 2022, 76, 102306. [Google Scholar] [CrossRef]
- Özsoy, E.; Czempiel, T.; Örnek, E.P.; Eck, U.; Tombari, F.; Navab, N. Holistic or domain modeling: A semantic scene graph approach. Int. J. Comput. Assist. Radiol. Surg. 2024, 19, 791–799. [Google Scholar] [CrossRef] [PubMed]
- Belagiannis, V.; Wang, X.; Shitrit, H.B.B.; Hashimoto, K.; Stauder, R.; Aoki, Y.; Kranzfelder, M.; Schneider, A.; Fua, P.; Ilic, S.; et al. Parsing human skeletons in an operating room. Mach. Vis. Appl. 2016, 27, 1035–1046. [Google Scholar] [CrossRef]
- Özsoy, E.; Örnek, E.P.; Eck, U.; Czempiel, T.; Tombari, F.; Navab, N. 4d-or: Semantic scene graphs for or domain modeling. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Singapore, 18–22 September 2022; pp. 475–485. [Google Scholar]
- Hansen, L.; Siebert, M.; Diesel, J.; Heinrich, M.P. Fusing information from multiple 2D depth cameras for 3D human pose estimation in the operating room. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1871–1879. [Google Scholar] [CrossRef]
- Kadkhodamohammadi, A.; Padoy, N. A generalizable approach for multi-view 3D human pose regression. Mach. Vis. Appl. 2021, 32, 6. [Google Scholar] [CrossRef]
- Srivastav, V.; Gangi, A.; Padoy, N. Unsupervised domain adaptation for clinician pose estimation and instance segmentation in the operating room. Med. Image Anal. 2022, 80, 102525. [Google Scholar] [CrossRef]
- Gerats, B.G.; Wolterink, J.M.; Broeders, I.A. 3D human pose estimation in multi-view operating room videos using differentiable camera projections. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2023, 11, 1197–1205. [Google Scholar] [CrossRef]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5693–5703. [Google Scholar]

| Method | View | MPJPE (cm) | ||||
|---|---|---|---|---|---|---|
| Shoulder | Hip | Elbow | Wrist | Average | ||
| MV3DReg | 3 | 4.9 | 9.9 | 10.5 | 14.3 | 9.9 |
| Gerats et al. | 5.6 (±0.7) | 10.1 (±1.5) | 8.8 (±1.4) | 11.9 (±1.4) | 9.1 (±1.2) | |
| Faster VoxelPose | 7.8 (±1.2) | 10.9 (±1.6) | 9.0 (±1.0) | 12.5 (±1.6) | 10.0 (±1.3) | |
| Ours | 5.6 (±0.4) | 8.6 (±0.5) | 7.8 (±0.7) | 9.7 (±1.3) | 7.9 (±0.7) | |
| MV3DReg | 2 | 8.1 | 16.0 | 19.4 | 29.8 | 18.3 |
| Gerats et al. | 9.2 (±1.5) | 13.2 (±1.5) | 15.0 (±2.4) | 17.4 (±0.7) | 13.7 (±1.1) | |
| Faster VoxelPose | 9.4 (±1.4) | 13.3 (±1.7) | 11.4 (±1.1) | 15.6 (±1.9) | 12.4 (±1.5) | |
| Ours | 7.3 (±0.9) | 10.6 (±1.2) | 10.0 (±1.3) | 12.1 (±1.5) | 10.0 (±1.0) | |
| MV3DReg | 1 | 14.4 | 29.9 | 27.3 | 36.1 | 26.9 |
| Gerats et al. | 13.6 (±6.2) | 19.6 (±6.4) | 18.2 (±7.2) | 22.6 (±9.3) | 18.5 (±6.6) | |
| Faster VoxelPose | 12.5 (±4.4) | 15.2 (±5.1) | 15.2 (±5.3) | 18.9 (±6.4) | 15.5 (±5.5) | |
| Ours | 11.3 (±4.1) | 13.4 (±5.3) | 12.8 (±5.7) | 17.0 (±6.3) | 13.6 (±5.2) | |
| (mm) | MPJPE (cm) | |||
|---|---|---|---|---|
| 200 | 40.05 | 53.83 | 55.84 | 11.2 |
| 1000 | 58.06 | 69.17 | 75.96 | 9.0 |
| 2000 | 68.93 | 77.51 | 83.15 | 7.2 |
| 3000 | 54.32 | 62.73 | 63.61 | 9.1 |
| Method | Attention | Position Encoding | Gating Mechanism | MPJPE (cm) | ||
|---|---|---|---|---|---|---|
| (a) | × | × | × | 52.67 | 67.32 | 9.8 |
| (b) | √ | × | × | 57.35 | 71.43 | 9.4 |
| (c) | √ | √ | × | 60.31 | 75.10 | 8.3 |
| (d) | √ | × | √ | 57.95 | 74.19 | 8.7 |
| (e) Ours | √ | √ | √ | 68.93 | 83.15 | 7.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Xie, S.; Quan, T.; Ren, X.; Miao, Y. Voxel-Based Multi-Person Multi-View 3D Pose Estimation in Operating Room. Appl. Sci. 2025, 15, 9007. https://doi.org/10.3390/app15169007
Luo J, Xie S, Quan T, Ren X, Miao Y. Voxel-Based Multi-Person Multi-View 3D Pose Estimation in Operating Room. Applied Sciences. 2025; 15(16):9007. https://doi.org/10.3390/app15169007
Chicago/Turabian StyleLuo, Junjie, Shuxin Xie, Tianrui Quan, Xuesong Ren, and Yubin Miao. 2025. "Voxel-Based Multi-Person Multi-View 3D Pose Estimation in Operating Room" Applied Sciences 15, no. 16: 9007. https://doi.org/10.3390/app15169007
APA StyleLuo, J., Xie, S., Quan, T., Ren, X., & Miao, Y. (2025). Voxel-Based Multi-Person Multi-View 3D Pose Estimation in Operating Room. Applied Sciences, 15(16), 9007. https://doi.org/10.3390/app15169007






