Uncertainty-Aware Design of High-Entropy Alloys via Ensemble Thermodynamic Modeling and Search Space Pruning

Abstract

The discovery and design of high-entropy alloys (HEAs) faces significant challenges due to the vast combinatorial design space and uncertainties in thermodynamic data. This work presents a modular, uncertainty-aware computational framework with the primary objective of accelerating the discovery of solid-solution HEA candidates. The proposed pipeline integrates ensemble thermodynamic modeling, Monte Carlo-based estimation, and a structured three-phase pruning algorithm for efficient search space reduction. Key quantitative results are achieved in two main areas. First, for binary alloy thermodynamics, a Bayesian Neural Network (BNN) ensemble trained on domain-informed features predicts mixing enthalpies with high accuracy, yielding a mean absolute error (MAE) of 0.48 kJ/mol—substantially outperforming the classical Miedema model (MAE = 4.27 kJ/mol). These probabilistic predictions are propagated through Monte Carlo sampling to estimate multi-component thermodynamic descriptors, including $\Delta H_{\mathrm{mix}}$ and the $\mathrm{\Omega }$ parameter, while capturing predictive uncertainty. Second, in a case study on the Al-Cu-Fe-Ni-Ti system, the framework reduces a 2.4 million (2.4 M) candidate pool to just 91 high-confidence compositions. Final selection is guided by an uncertainty-aware viability metric, $P\left(\mathrm{HEA}\right)$, and supported by interpretable radar plot visualizations for multi-objective assessment. The results demonstrate the framework’s ability to combine physical priors, probabilistic modeling, and design heuristics into a data-efficient and interpretable pipeline for materials discovery. This establishes a foundation for future HEA optimization, dataset refinement, and adaptive experimental design under uncertainty.

1. Introduction

High-entropy alloys (HEAs), characterized by their multi-element compositions and high configurational entropy, have emerged as a transformative class of materials with exceptional mechanical, thermal, and chemical properties. This configurational entropy—often maximized through equimolar or near-equimolar combinations of five or more elements—plays a central role in stabilizing single-phase structures and enabling superior performance. HEAs hold great promise in advanced applications requiring high strength, corrosion resistance, and thermal stability, as discussed in Section 2.

However, the design of HEAs poses a substantial challenge due to the immense combinatorial nature of their composition space, which grows rapidly with the number of constituent elements. Traditional experimental and trial-and-error approaches are inefficient and cost-prohibitive given the millions of possible combinations. Furthermore, predictive modeling is hindered by the scarcity and inconsistency of available thermodynamic data. The complex interplay of entropy, enthalpy, and atomic interaction complicates phase stability predictions, and recent studies have emphasized that configurational entropy alone is not always a sufficient criterion for HEA formation.

To effectively navigate this vast design space and manage modeling uncertainty, machine learning (ML) has emerged as a powerful tool. It enables fast, scalable, and (sometimes) interpretable predictions even in high-dimensional, data-scarce regimes. In particular, uncertainty-aware models—such as Bayesian neural networks and Monte Carlo dropout techniques—are crucial for quantifying predictive confidence, especially when screening candidate alloys in underexplored or extrapolative regions.

Despite these advances, many existing approaches still rely on deterministic criteria, which can lead to misleading conclusions in the presence of uncertainty. There is a growing need for design pipelines that seamlessly integrate thermodynamic principles, data-driven modeling, uncertainty quantification, and efficient compositional pruning.

To address these challenges, we propose a physically grounded, uncertainty-aware computational framework for HEA discovery. Our pipeline combines ensemble thermodynamic modeling, Monte Carlo-based enthalpy estimation, Bayesian deep learning, and hierarchical search space reduction.

• Our key contributions are as follows:

1.

Domain-informed ensemble modeling of binary alloy thermodynamics: We construct an ensemble of two Bayesian neural networks (BNN1 and BNN2), which incorporate symmetry-aware data augmentation and predict Redlich–Kister polynomial coefficients. This architecture supports enthalpy of mixing predictions with uncertainty estimates, enhancing generalizability across alloy systems and improving interpretability (Section 3.1).

2.

Monte Carlo-based HEA enthalpy estimation: We use a Monte Carlo approach [1] to propagate binary mixing enthalpy distributions into multi-component HEAs, resulting in probabilistic and physically consistent estimates (Section 3.2).

3.

Three-phase pruning algorithm for HEA discovery: A structured, multi-phase algorithm filters candidate compositions using configurational entropy, atomic size mismatch, electronegativity difference, and thermodynamic criteria (including the $\mathrm{\Omega }$ parameter), all while accounting for model uncertainty (Section 3.3).

4.

Uncertainty-aware visualization for decision support: We introduce radar plot-based visualizations for interpretable, multi-objective evaluation of HEA candidates. These visual tools facilitate human-in-the-loop design with clear assessments of prediction confidence (Section 3.5).

The remainder of this paper is organized as follows: Section 2 reviews prior work on HEA modeling and uncertainty quantification. Section 3 details the proposed framework, including model architecture, training, and hierarchical pruning. Section 4 presents experimental results and analysis. Finally, Section 5 concludes the paper and outlines directions for future research.

2. Related Work

The field of High-Entropy Alloys (HEAs) has received significant attention due to their exceptional properties and vast compositional design space [2,3]. This section provides an overview of HEA design, highlighting challenges in compositional exploration, thermodynamic modeling, the growing role of machine learning (ML), and current strategies for reducing the search space.

2.1. High-Entropy Alloy Design: Opportunities and Challenges

HEAs are defined by their multi-element compositions and elevated configurational entropy, which can stabilize solid-solution phases and impart outstanding mechanical, thermal, and chemical properties [2]. This stabilization often arises from equimolar or near-equimolar combinations of several elements [4]. However, the definition of HEAs remains debated. In many studies, entropy is not the dominant factor influencing phase stability, making the broader term multi-principal element alloys more appropriate [4]. Overreliance on entropy-based criteria may bias research toward single-phase solid solutions, which are not always optimal for targeted applications [4].

A key challenge in HEA development lies in navigating their vast compositional space, which grows combinatorially with the number of constituent elements [2,3]. Traditional experimental approaches are often inefficient and costly, particularly when small compositional changes can result in millions of potential alloy combinations. Furthermore, predictive modeling is hindered by limited and inconsistent thermodynamic data [3].

HEAs hold promise in several advanced applications:

• Biomedical Load-Bearing Materials: Ti-Zr-Nb-Hf-Ta HEAs, designed using d-electron alloy theory, first-principles calculations, and CALPHAD [5], have demonstrated low Young’s modulus, high yield strength, and excellent ductility without the need for complex post-processing [6,7]. These alloys frequently form metastable $\beta$-phase structures with nanoscale inhomogeneities, enhancing mechanical performance.
• Biodegradable Magnesium (Mg) Alloys: Balancing strength and corrosion resistance in Mg alloys is particularly challenging. Bayesian optimization and explainable ML methods have been used to perform high-dimensional multi-objective optimization [8]. Thermodynamic modeling of Mg-containing HEAs remains difficult, as conventional descriptors often fail to predict solid-solution formation reliably [9].
• Nuclear Engineering: Cobalt-free refractory HEAs (RHEAs) are of interest due to the radioactivity concerns associated with cobalt under irradiation [10,11]. Alloys such as FeNiMnCr have shown excellent radiation resistance, including reduced void formation and irradiation-induced hardening [12]. Zr-Si-based high-entropy coatings incorporating Nb, Cr, Al, and Fe have also demonstrated exceptional oxidation resistance at 1000–1200 °C due to multilayer oxide formation and diffusion-resistant interfaces [13].
• Hydrogen Storage: HEAs are being explored as tunable solid-state hydrogen storage materials [14]. ML models predict hydrogen-to-metal (H/M) ratios and valence electron configurations (VEC), while neural-network-based approaches incorporate descriptors such as mixing entropy ($\Delta S_{\mathrm{m}}$), atomic size mismatch ($\delta r$), and bulk modulus (k) [15].

2.2. Thermodynamic Modeling of Binary Alloys

Reliable modeling of binary alloy mixing enthalpies is essential for understanding and predicting the thermodynamics of more complex systems such as HEAs [16,17]. Two classical approaches dominate this area: the Miedema model and the CALPHAD method, which commonly employs the Redlich–Kister polynomial for enthalpy representation.

• Miedema Model: This semi-empirical model estimates the mixing enthalpy of binary alloys based on macroscopic properties of pure elements [18,19,20,21,22,23]. It attributes energy contributions to chemical potential differences and electron density discontinuities. Despite its simplicity, it is consistent across many systems and valuable when experimental data are scarce [24]. The model has been refined over time, including adaptations for Mg-based and transition metal systems [22]. Its physically interpretable parameters are also frequently used as features in ML workflows [17].
• Redlich–Kister Polynomial: Widely used in CALPHAD, this algebraic form represents the excess Gibbs free energy as a polynomial expansion [25,26]. The coefficients are typically derived from experimental or simulated mixing enthalpies in the liquid phase [16]. While not a physical model, it serves as a flexible fitting tool for thermodynamic assessments.

Most models treat the mixing enthalpy as temperature-independent, particularly in the solid solution regime. However, recent HEA applications—notably in nuclear materials—underscore the importance of temperature-dependent stability and oxidation resistance [13]. Future modeling should aim to incorporate temperature effects more explicitly, especially for high-temperature coatings and structural applications.

Both the Miedema and CALPHAD-based approaches are constrained by the incomplete and inconsistent nature of thermodynamic datasets [3]. As a result, first-principles methods (e.g., density functional theory, DFT) are increasingly employed to supplement or generate reliable data [26,27].

2.3. Machine Learning in Alloy Design

Machine learning is transforming alloy design by enabling fast, scalable predictions in high-dimensional and data-scarce environments [2,3,28]. Techniques such as LightGBM, Support Vector Regression (SVR), k-Nearest Neighbors (KNN), Random Forests (RF), and Artificial Neural Networks (ANN) have been successfully used to predict enthalpy of mixing, hydrogen storage capacity, and mechanical properties [8,15].

Several studies have highlighted the value of embedding domain knowledge into ML pipelines. For example, ref. [17] introduced a CALPHAD-guided ML model for predicting binary mixing enthalpies using Miedema parameters and elemental properties as features. Their model achieved strong accuracy, and feature attribution via SHAP (Shapley Additive Explanations) revealed alignment between model-extracted and physically meaningful descriptors.

A comprehensive review [2] emphasized the importance of transparency, multi-objective optimization, and integration of materials knowledge in ML models for HEA design. The authors noted that while uncertainty quantification and inverse design are crucial for practical deployment, they are still emerging and not yet widely adopted.

While classical thermodynamic models are often used to derive features or training targets, more integrative approaches are still rare. Future work may benefit from strategies such as pretraining neural networks on physically motivated outputs or using probabilistic ML frameworks, which remain largely unexplored in the context of alloy design.

2.4. Search Space Reduction in HEA Design

Given the immense compositional space of HEAs, search space reduction is critical. Traditional methods rely on empirical heuristics and thermodynamic descriptors—such as mixing entropy ($\Delta S_{\mathrm{mix}}$), mixing enthalpy ($\Delta H_{\mathrm{mix}}$), atomic size mismatch ($\delta r$), valence electron concentration (VEC), and the $\mathrm{\Omega }$ parameter. Several works [29,30,31] have cataloged commonly used empirical criteria, often applying threshold-based filters for properties like $\Delta H_{\mathrm{mix}}$ and $\delta r$. In parallel, CALPHAD-based thermodynamic assessments continue to play a central role in evaluating phase stability [26,27].

However, most traditional approaches are deterministic and do not account for uncertainty in experimental data, model assumptions, or extrapolations. This limitation can lead to both false positives and overlooked candidates. While some recent efforts have begun incorporating probabilistic and hierarchical filtering strategies, uncertainty quantification remains underdeveloped in practice. As noted by [2], future research is expected to focus on frameworks that integrate uncertainty-aware filtering with thermodynamic, structural, and electronic criteria. Such pipelines can significantly narrow down millions of compositions to a small, experimentally viable subset while maintaining transparency and robustness.

In summary, advancing HEA discovery will require deeper integration of physically informed machine learning models with rigorous uncertainty quantification. While significant progress has been made in leveraging classical descriptors, thermodynamic databases, and ML for property prediction and compositional filtering, systematic inclusion of physical priors, probabilistic reasoning, and interpretability mechanisms remains a key opportunity. Addressing these gaps is essential for building robust, generalizable, and transparent predictive tools for next-generation alloy design.

3. Methods

Our HEA design framework is centered on uncertainty-aware estimation of the enthalpy of mixing ($\Delta H_{\mathrm{mix}}$) for multi-component alloys. This is achieved through a combination of data-driven binary predictions extended to higher-order systems via a Monte Carlo sampling approach. The estimated thermodynamic properties are then used in a hierarchical pruning pipeline, followed by visualization for final candidate selection. This section outlines the key methodological components.

3.1. Domain-Informed Ensemble Modeling for Binary Alloy Mixing Enthalpy

We construct an ensemble of two domain-informed Bayesian neural networks (BNN1 and BNN2) to estimate the enthalpy of mixing in binary alloys, $\Delta H_{\mathrm{mix}}^{\left(\mathrm{bin}\right)}$. These predictions form the basis for computing the thermodynamic properties of multi-component alloys.

Each BNN is pretrained using data generated from a physically motivated thermodynamic model and subsequently fine-tuned on experimental measurements from the Entall database (see Section 3.6 and [32] for the dataset details):

• BNN1 is pretrained on Miedema model (MM) outputs;
• BNN2 is pretrained on values computed from Redlich–Kister (RK) polynomials.

To generate RK-based pretraining data, we use coefficients provided by Deffrennes et al. [16], adopting a truncated form of the Redlich–Kister polynomial:

$$\Delta H_{\mathrm{mix}}\left(x\right)=(1-x)x\sum _{k=0}^3{a}_k{(1-2x)}^k,$$

(1)

where x is the concentration of the second component. In line with common practice in the HEA literature, we evaluate this expression at $x=0.5$ to obtain a representative value for each binary pair.

Rather than predicting a single scalar enthalpy value, both BNNs are trained to output three geometric descriptors that compactly encode the Redlich–Kister polynomial:

$$\left\{\begin{array}{c}d{f}_0=\Delta H_{\mathrm{mix}}^{\prime }\left(0\right),\hfill \\ d{f}_1=\Delta H_{\mathrm{mix}}^{\prime }\left(1\right),\hfill \\ f_{05}=\Delta H_{\mathrm{mix}}\left(0.5\right),\hfill \end{array}\right.$$

(2)

from which the polynomial coefficients $\left\{a_k\right\}$ can be analytically reconstructed. This reparameterization improves model stability and interpretability, particularly in sparse data regimes [33].

To enforce permutation invariance (i.e., that A–B and B–A yield the same enthalpy) and capture relevant elemental relationships, we use symmetry-aware data augmentation and construct input features from mat2vec [34] embeddings. For each binary alloy A–B, the embeddings of the two elements are concatenated to a 400-dimensional feature vector, which is compressed via an autoencoder to a 32-dimensional latent vector serving as input to the BNNs [33].

We adopt variational inference to model uncertainty in network weights and use dropout-based sampling at inference time to obtain predictive distributions. Training is supervised by minimizing the RMSE between the predicted Redlich–Kister curve and experimental measurements at available composition points.

Remark 1. 

Earlier iterations of this work explored a broader ensemble of four models, including the MM and RK models directly. However, experimental results showed that these deterministic models significantly underperformed compared to the BNNs. Since their information is already captured during pretraining, we exclude them from the final ensemble. This simplification improves performance while retaining domain knowledge and enabling principled uncertainty estimation. While BNN1 + BNN2 shows only marginal improvement in mean error over BNN1, it consistently achieves better overall performance across different systems and exhibits a narrower error distribution. The ensemble benefits from the complementary strengths of the two models, improving robustness without added complexity.

3.2. Monte Carlo-Based Estimation of HEA Enthalpy

To extend binary enthalpy predictions to high-entropy alloys (HEAs), we employ a Monte Carlo sampling strategy that propagates uncertainty from binary systems to multi-component alloys. This probabilistic procedure enables estimation of not only the expected enthalpy of mixing but also its distribution, which is critical for uncertainty-aware design and filtering.

For each binary alloy, we use the ensemble of Bayesian models (BNN1 and BNN2) to obtain a distribution over the mixing enthalpy at equiatomic composition ($x=0.5$). The distributions are approximated by repeatedly sampling from the posterior of each BNN, using dropout-based inference. These samples are combined and summarized by computing their empirical mean and standard deviation. The results are stored in a lookup table, which maps each binary pair $(i,j)$ to a normal distribution parameterized by $({\mu }_{ij},{\sigma }_{ij})$.

This procedure is described in Algorithm 1, which produces the lookup table used for HEA-level enthalpy estimation.

To compute the enthalpy of mixing for an n-component HEA, we use the standard pairwise approximation:

$$\Delta H_{\mathrm{mix}}^{\left(\mathrm{HEA}\right)}=4\sum _{i=1}^{n-1}\sum _{j=i+1}^n{c}_i{c}_j\Delta H_{\mathrm{mix}}^{\left(ij\right)}\left(0.5\right),$$

(3)

where $c_i$ and $c_j$ are the atomic fractions of elements i and j, and $\Delta H_{\mathrm{mix}}^{\left(ij\right)}\left(0.5\right)$ is sampled from the normal distribution $\mathcal{N}({\mu }_{ij},{\sigma }_{ij})$ stored in the lookup table.

We perform multiple Monte Carlo draws over all pairwise interactions to propagate uncertainty from the binary to HEA level. Each sample yields a full $\Delta H_{\mathrm{mix}}^{\left(\mathrm{HEA}\right)}$ estimate, forming an empirical distribution over the HEA enthalpy. From this, we derive the mean, standard deviation, and confidence intervals used in downstream pruning and ranking stages.

This approach allows us to incorporate both model-based uncertainty and compositional variability into thermodynamic evaluation, which is especially valuable in data-scarce regimes and for novel alloy compositions where extrapolation risks are high.

Algorithm 1: Construction of Binary Alloy Lookup Table for $f_{05}$ via Monte Carlo Sampling.

3.3. Three-Phase Pruning Algorithm for HEA Discovery

The pruning algorithm is a core component of our HEA design pipeline, aimed at systematically reducing the immense compositional space of multi-element alloys. This hierarchical process efficiently filters out unpromising candidates based on physical, chemical, and thermodynamic criteria—significantly narrowing the number of compositions requiring downstream analysis.

The algorithm proceeds in three phases, each applying progressively more stringent constraints:

1.

Phase 1: Composition Generation with Baseline Constraints

This phase constructs a broad pool of candidate compositions while applying essential, universal constraints:

• Normalization constraint (${\sum }_{i=1}^N{X}_i=1$): Ensures atomic fractions sum to one.
• Entropy threshold ($\Delta S_{\mathrm{con}}\ge 1.35R$): Retains only compositions with sufficiently high configurational entropy—a defining trait of HEAs.

Remark 2. 

The total number of n-element compositions with a discretization step s is given by the following:

$$C_{n,s}=\left({\displaystyle \genfrac{}{}{0pt}{}{\lfloor 100/s\rfloor -1}{n-1}}\right)$$

(4)

highlighting the need for efficient filtering in spaces that often contain millions of candidate alloys.

2.

Phase 2: Geometric and Chemical Property Filters

This phase eliminates compositions likely to form intermetallics or structurally incompatible phases, based on established empirical rules [29,30,31]:

• Atomic size mismatch ($\delta r$): Candidates must satisfy $\delta r<6.6\%$ to ensure structural compatibility.
• Electronegativity difference ($\delta \chi$): Only alloys with $\delta \chi <10\%$ are retained, reducing the likelihood of phase separation or complex compounds.
• Refined entropy filter: Configurational entropy is recomputed using the exact composition. For near-equiatomic candidates, a stricter threshold of $\Delta S_{\mathrm{con}}\ge 1.6R$ is applied. For non-equiatomic cases, the original threshold of $1.35R$ is retained.

3.

Phase 3: Probabilistic Thermodynamic Filtering

The final phase assesses the thermodynamic viability of remaining candidates using uncertainty-aware ensemble predictions of enthalpy of mixing ($\Delta H_{\mathrm{mix}}$) combined with the $\mathrm{\Omega }$ parameter.

Instead of applying hard cutoffs to single-point estimates, we compute a probabilistic success rate via Monte Carlo sampling. For each candidate:

• 1000 samples are drawn from the distribution of $\Delta H_{\mathrm{mix}}$ (assumed to be normal), using precomputed means and standard deviations from the lookup table described in Algorithm 1.
• For each sample, the corresponding $\mathrm{\Omega }$ value is computed based on the current composition and sampled $\Delta H_{\mathrm{mix}}$.
• A trial is considered a success if the following two conditions are met:

  $$-15\le \Delta H_{\mathrm{mix}}\le +5\mathrm{and}\mathrm{\Omega }\ge 1.1$$

  (5)
• The probability of satisfying HEA criteria is estimated as follows:

  $$P_{hea}={\displaystyle \frac{\# \mathrm{successful} \mathrm{samples}}{\# \mathrm{total} \mathrm{samples}}}$$

  (6)

This probabilistic evaluation avoids premature exclusion of borderline cases and integrates model uncertainty into the decision process. Additional details are provided in Section 3.4, which formalizes this uncertainty quantification and thresholding strategy.

Remark 3. 

This three-phase pruning framework effectively reduces the search space by several orders of magnitude while retaining compositions most likely to form stable, single-phase HEAs. Its integration of empirical rules, thermodynamic principles, and predictive uncertainty makes it well suited for high-throughput alloy design in underexplored composition spaces.

3.4. Integrated Uncertainty Quantification and Probabilistic Filtering

Our framework is fundamentally uncertainty-aware, with probabilistic reasoning integrated at every stage of the HEA discovery pipeline. From binary alloy modeling to final candidate selection, predictive uncertainty informs both intermediate representations and final decisions.

Ensemble-based Bayesian neural networks (BNN1, BNN2) generate distributions over binary enthalpy values at equiatomic compositions, summarized as means and standard deviations in a precomputed lookup table. These uncertainty-aware binary values are propagated through a Monte Carlo estimation procedure to evaluate HEA-level enthalpies.

Thermodynamic feasibility is assessed probabilistically in the pruning phase, where the joint probability of satisfying both enthalpy and $\mathrm{\Omega }$ constraints is estimated via repeated sampling. The resulting metric, $P\left(\mathrm{HEA}\right)$, reflects the likelihood that a candidate meets the required criteria under uncertainty, and serves as a final decision threshold.

This consistent treatment of uncertainty across modeling, estimation, and filtering enables more reliable predictions—especially important in compositional regions where experimental data is sparse or absent.

3.5. Uncertainty-Aware Visualization for Multi-Objective Evaluation

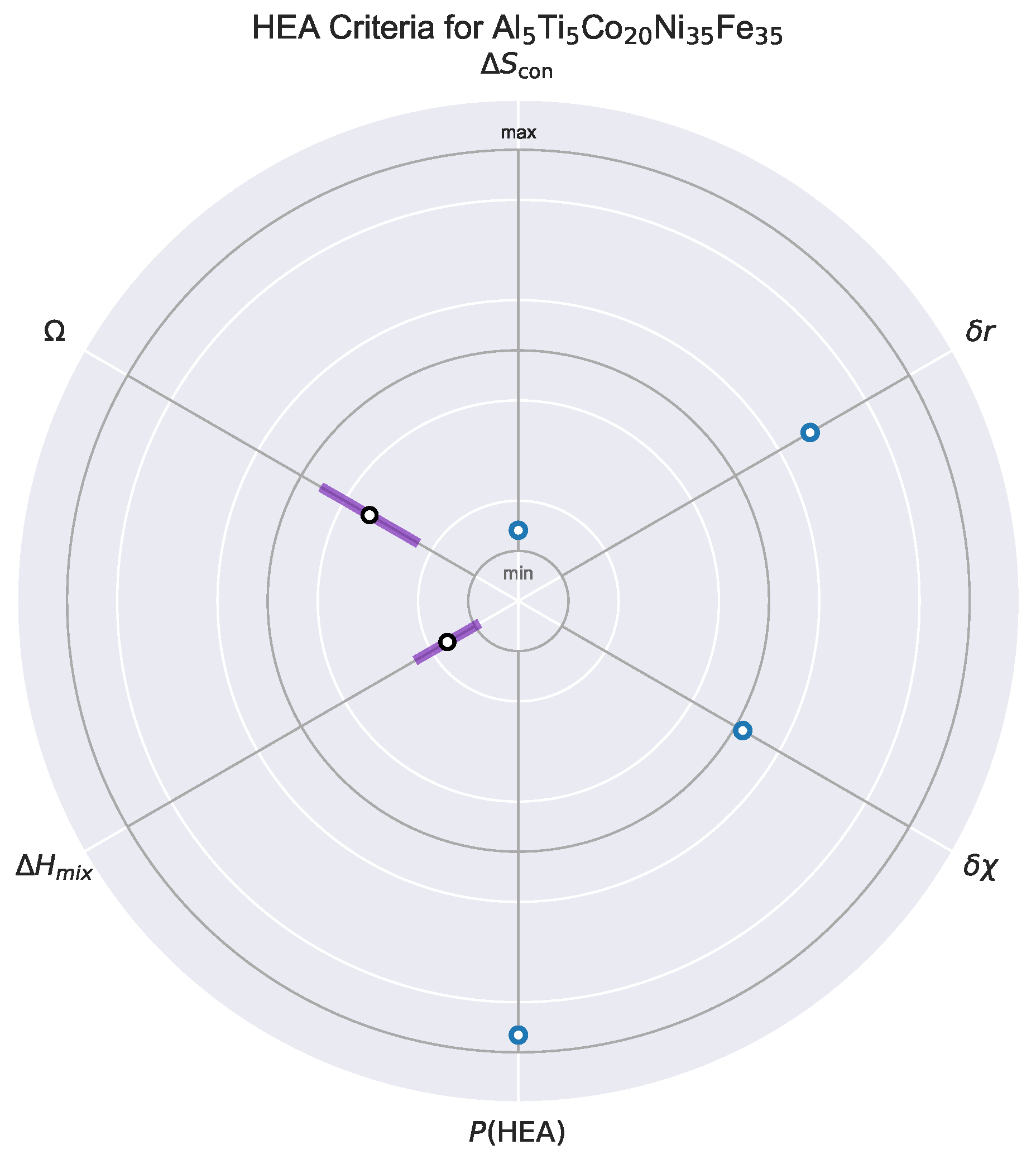
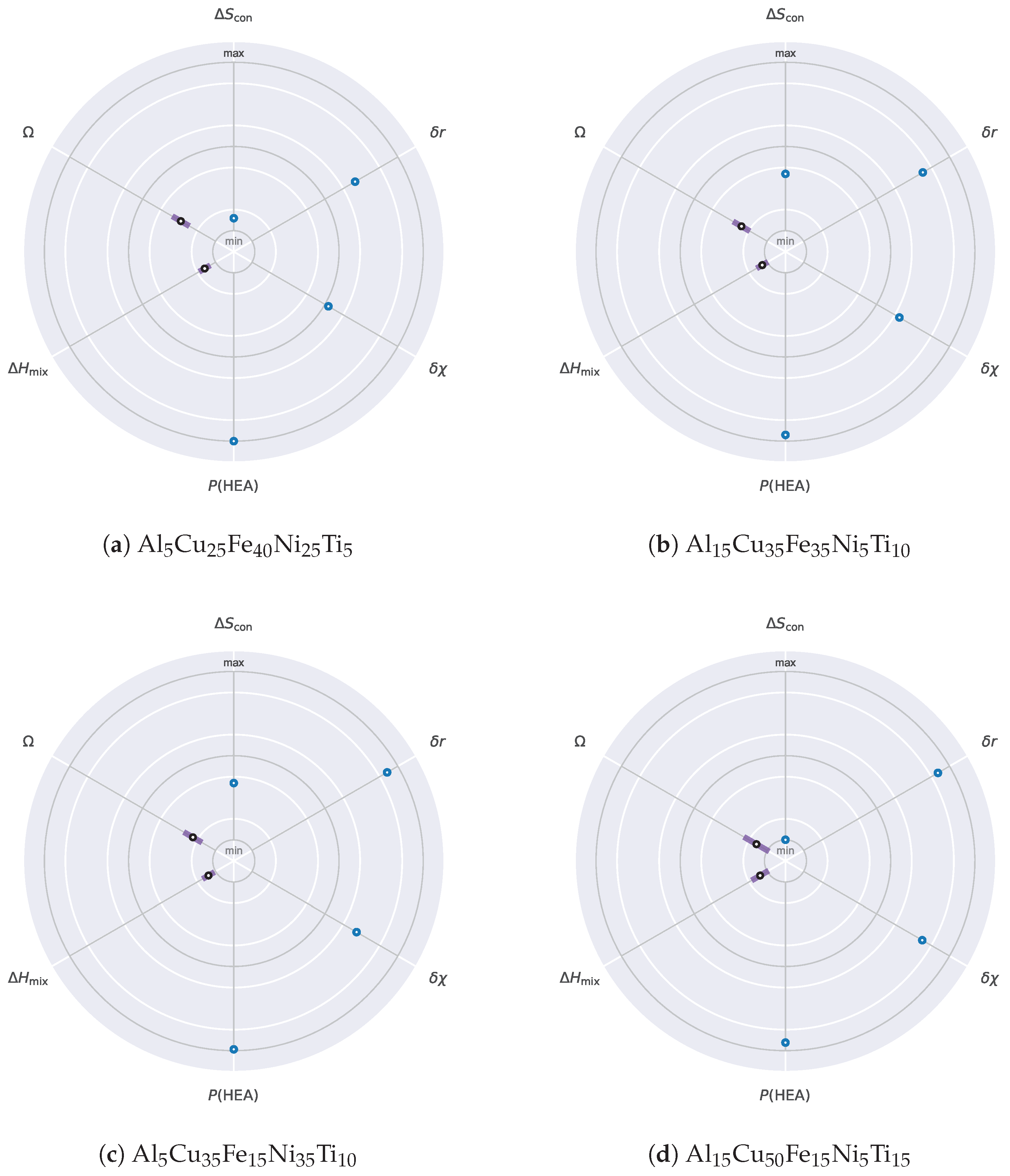
We introduce a radar plot-based visualization method to support rapid, multi-criteria evaluation of high-entropy alloy (HEA) candidates, offering an interpretable, uncertainty-aware summary of each composition’s performance across six key metrics. This tool is crucial for human-in-the-loop decision-making in the final design stage, visualizing trade-offs and providing a compact, intuitive snapshot of thermodynamic and physical properties for selecting top-ranked candidates after automated filtering (see Figure 1).

3.5.1. Criteria Displayed

Each axis of the radar plot corresponds to a normalized design criterion used throughout the pruning process. The displayed metrics and their definitions are as follows:

• Configurational Entropy:

  $$\Delta S_{\mathrm{con}}=-R\sum _{i=1}^n{c}_{i}ln{c}_i$$

  (7)
• Atomic Size Mismatch:

  $$\delta r=\sqrt{\sum _{i=1}^n{c}_i{\left(1-{\displaystyle \frac{r_i}{\overline{r}}}\right)}^2},\overline{r}=\sum _{i=1}^n{c}_i{r}_i$$

  (8)
• Electronegativity Difference:

  $$\delta \chi =\sqrt{\sum _{i=1}^n{c}_i{\left({\chi }_i-\overline{\chi }\right)}^2},\overline{\chi }=\sum _{i=1}^n{c}_i{\chi }_i$$

  (9)
• Enthalpy of Mixing (Mean and Uncertainty):

  $$\Delta H_{\mathrm{mix}}^{\left(\mathrm{HEA}\right)}=4\sum _{i<j}{c}_i{c}_j\Delta H_{\mathrm{mix}}^{\left(ij\right)}\left(0.5\right)$$

  (10)
  Estimated via Monte Carlo sampling of binary enthalpies from BNN ensembles.
• Thermodynamic Stability Parameter:

  $$\mathrm{\Omega }={\displaystyle \frac{T_m·\Delta S_{\mathrm{con}}}{|\Delta H_{\mathrm{mix}}|}},T_m=\sum _{i=1}^n{c}_i{T}_{m,i}$$

  (11)

  where $T_m$ is the composition-weighted average melting temperature of the alloy.
• Probability of HEA Formation:

  $$P\left(\mathrm{HEA}\right)={\displaystyle \frac{1}{N}}\sum _{k=1}^N\mathbb{1}\left(-15\le \Delta H_{\mathrm{mix}}^{\left(k\right)}\le +5\wedge {\mathrm{\Omega }}^{\left(k\right)}\ge 1.1\right)$$

  (12)

  where each sample k corresponds to a draw from the Monte Carlo-based uncertainty propagation. This metric reflects the likelihood that a candidate satisfies both core thermodynamic criteria and serves as the final pruning criterion.

3.5.2. Uncertainty-Aware Representation and Interpretation

The radar plot distinguishes between deterministic metrics ($\Delta S_{\mathrm{con}}$, $\delta r$, $\delta \chi$, and $P\left(\mathrm{HEA}\right)$)—shown as solid blue points—and probabilistic metrics ($\Delta H_{\mathrm{mix}}$, $\mathrm{\Omega }$), visualized as vertical purple bars representing the $\pm 2\sigma$ range with white mean markers. Each axis is normalized relative to its acceptable physical range, and inner/outer rings denote key thresholds or extrema. This enables rapid assessment of whether a candidate’s properties fall within desirable regions or exceed critical thresholds, helping identify strengths and weaknesses across objectives.

For instance:

• For atomic size mismatch ($\delta r$) and electronegativity difference ($\delta \chi$), lower values (closer to the center) are preferred to promote structural compatibility.
• For configurational entropy ($\Delta S_{\mathrm{con}}$) and the $\mathrm{\Omega }$ parameter, higher values (towards the outer ring) favor solid-solution formation.
• For $\Delta H_{\mathrm{mix}}$, the optimal region lies within the acceptable range (e.g., −15 to +5 kJ/mol).
• For $P\left(\mathrm{HEA}\right)$, higher probabilities (towards the outer ring) indicate greater predicted viability.

This approach improves transparency, embeds model uncertainty directly into the design space, and avoids over-reliance on scalar ranking metrics. It also supports comparison between predicted and known HEAs, guiding expert selection and highlighting candidates where additional investigation may be warranted.

3.6. Dataset Characteristics and Limitations

The training data used in this work is sourced from the Entall database [32], a curated collection of experimentally measured thermodynamic properties of binary alloys. Specifically, the dataset comprises 3951 enthalpy of mixing ($\Delta H_{\mathrm{mix}}$) records across 89 binary systems, with measurements collected at various compositions.

Most entries are derived from calorimetric experiments, ensuring physical accuracy. However, the dataset exhibits typical limitations of experimental thermodynamics: (i) uneven coverage across composition space and alloy systems, (ii) missing data for many binary pairs, and (iii) discrepancies due to differing experimental setups and reporting standards.

To partially mitigate these issues, we employ a physically motivated data augmentation strategy [33]. Each binary alloy $(A,B,x)$ is augmented with its symmetric counterpart $(B,A,1-x)$, embedding elemental permutation and compositional reflection into the dataset. This symmetry-based augmentation improves generalization and helps encode fundamental thermodynamic invariances. Additionally, these embeddings are compressed using an autoencoder to reduce dimensionality and limit overfitting, especially in low-data regimes.

Our Bayesian ensemble of neural networks further quantifies epistemic uncertainty arising from data gaps and inconsistencies (see Section 3.1), making model predictions more robust to the underlying data limitations.

Remark 4. 

The reliability of the framework ultimately depends on the quality and diversity of the underlying data. While the data forms the foundation, it is the model—through ensemble learning and uncertainty quantification—that mediates how these inputs are translated into predictions.

4. Results and Discussion

We evaluate the proposed framework from two complementary angles: (i) predictive performance for binary alloy thermodynamics, and (ii) its utility in guiding multi-component alloy discovery. In addition to reporting results, we weave in discussion to contextualize the implications for the materials design.

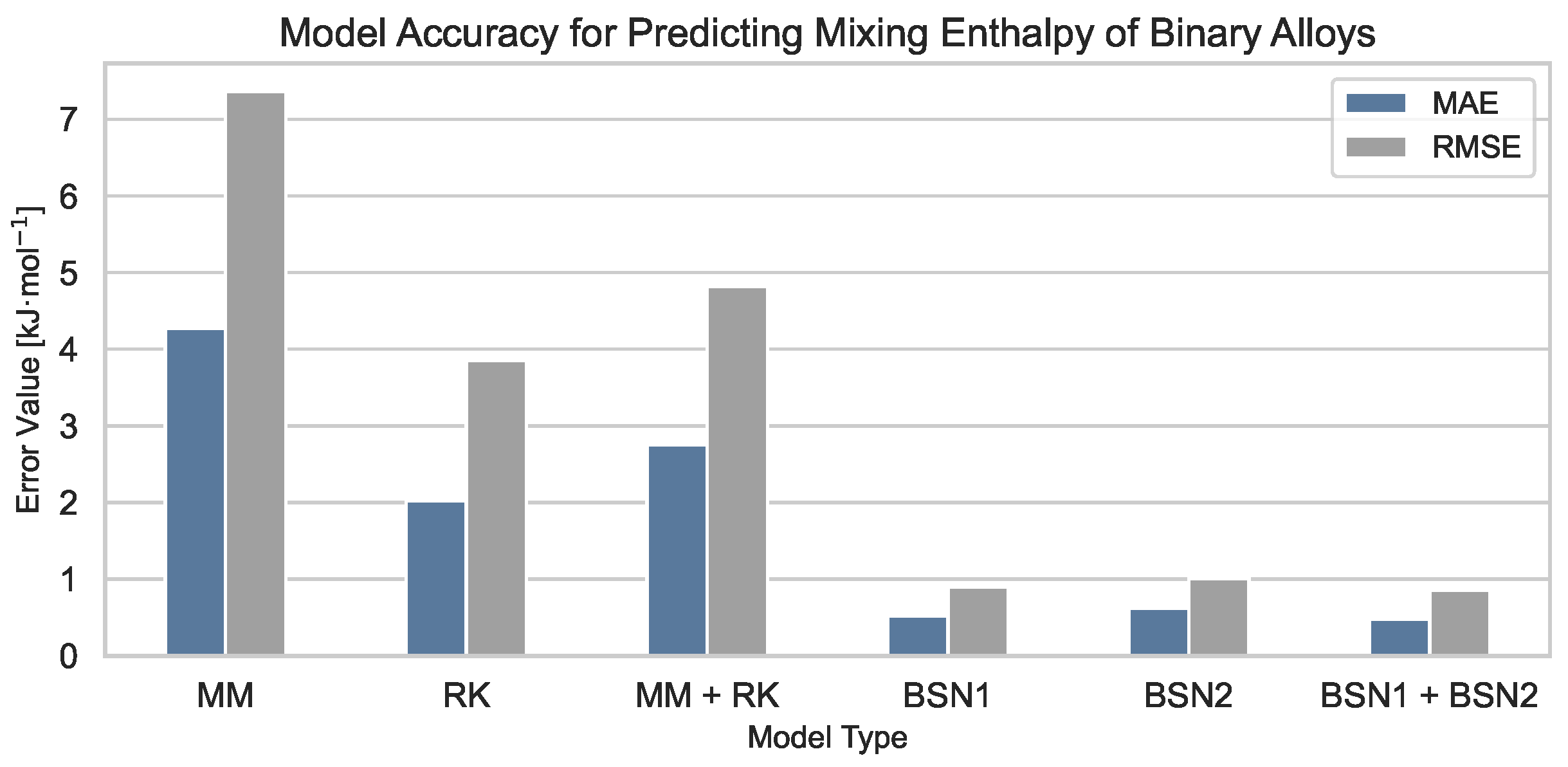
4.1. Benchmarking Model Performance for Binary Systems

To assess predictive accuracy, we evaluated six modeling strategies for binary alloy enthalpy of mixing ($\Delta H_{\mathrm{mix}}$) using 89 systems from Entall database [32].

Table 1. Prediction accuracy for binary alloy enthalpies of mixing using classical, hybrid, and Bayesian models. Evaluated on 89 systems from Entall database [32].

Model	MAE (kJ/mol)	RMSE (kJ/mol)
Miedema Model (MM)	4.27	7.36
Redlich–Kister (RK)	2.02	3.85
MM + RK Ensemble	2.75	4.82
Bayesian Neural Network 1 (BNN1)	0.52	0.90
Bayesian Neural Network 2 (BNN2)	0.62	1.01
BNN1 + BNN2 Ensemble	0.48	0.86

presents error metrics (MAE and RMSE), and Figure 2 visually compares model performance.

Discussion. BNN-based models significantly outperform classical approaches, achieving over 75% error reduction compared to MM and RK. Notably, the BNN1 + BNN2 ensemble yields the best results, despite only marginal gains over BNN1 alone. Experiments with more complex ensembles (e.g., MM + RK + BNNs) did not yield further improvements. This suggests that the BNNs—partially pretrained on MM and RK outputs—have already internalized the strengths of these classical models. As such, they do not function as “weak learners”, unlike typical ensemble scenarios, and a minimal BNN-only ensemble is both sufficient and computationally efficient.

4.2. Model Calibration and Uncertainty-Aware Predictions

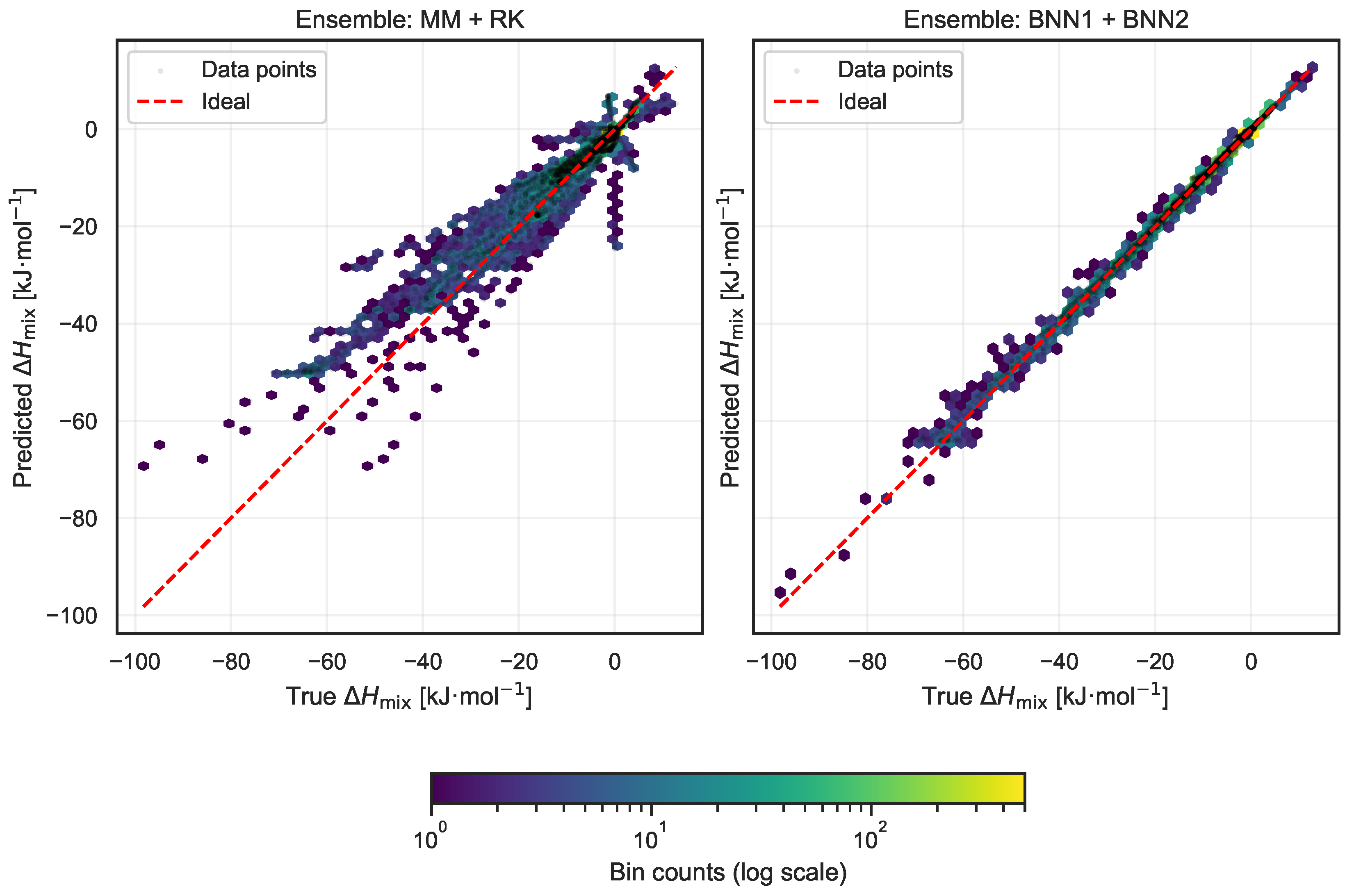
Figure 3 compares predicted versus experimental $\Delta H_{\mathrm{mix}}$ values using the MM + RK and BNN1 + BNN2 ensembles. The BNN ensemble shows tighter clustering around the identity line ($y=x$), confirming higher fidelity.

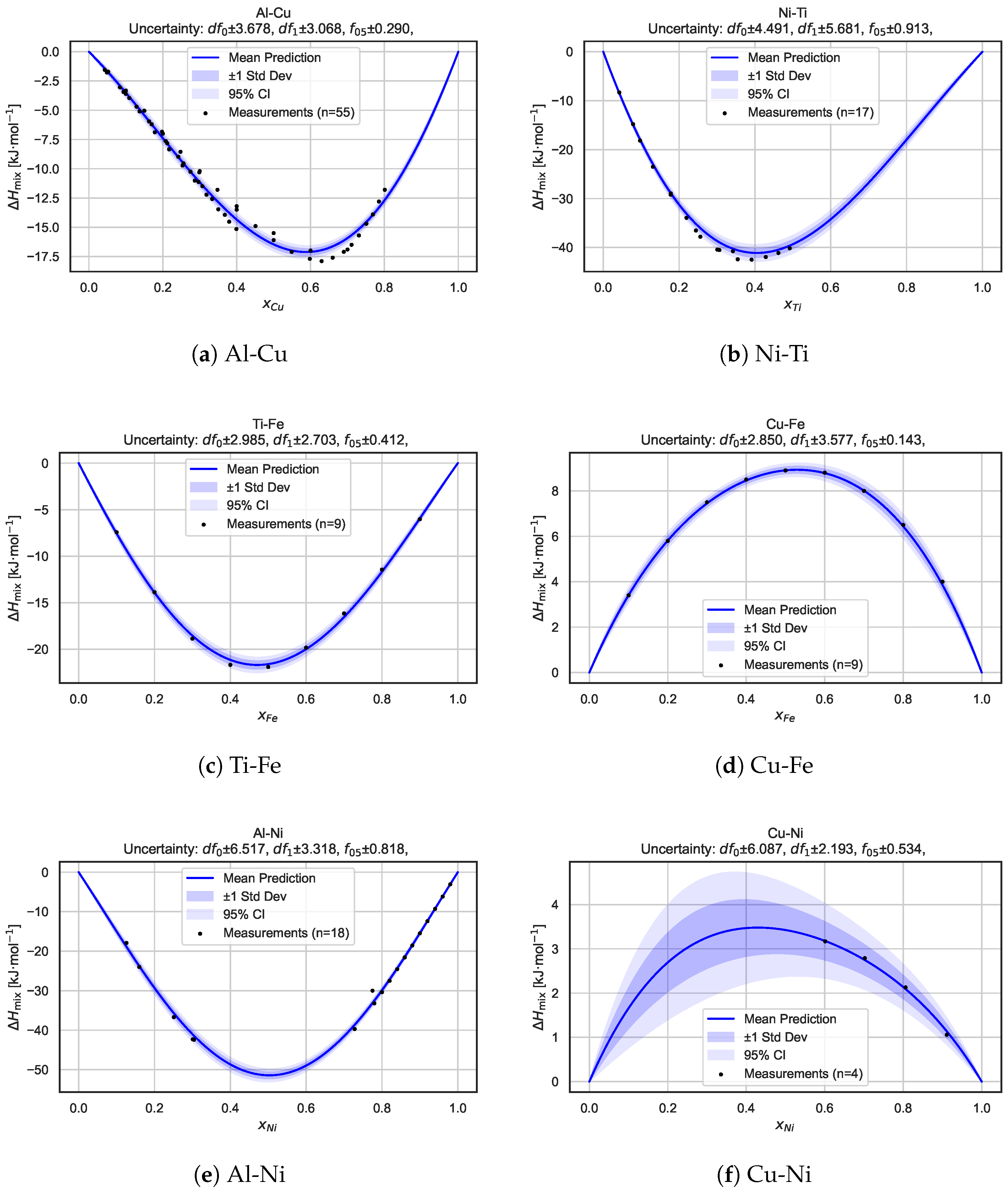
To demonstrate the quality of uncertainty estimates, Figure 4 shows predicted $\Delta H_{\mathrm{mix}}$ curves and associated uncertainty bands for six selected binary systems. The BNN ensemble not only provides accurate predictions but also calibrates confidence intervals, facilitating risk-aware downstream use.

Discussion. The model’s ability to express uncertainty is essential in materials design, where experimental validation is expensive. Confidence intervals help avoid false positives and identify composition regions warranting further exploration. The observed alignment between predicted intervals and ground truth suggests well-calibrated epistemic uncertainty.

4.3. Hierarchical Screening of Multi-Component HEA Candidates

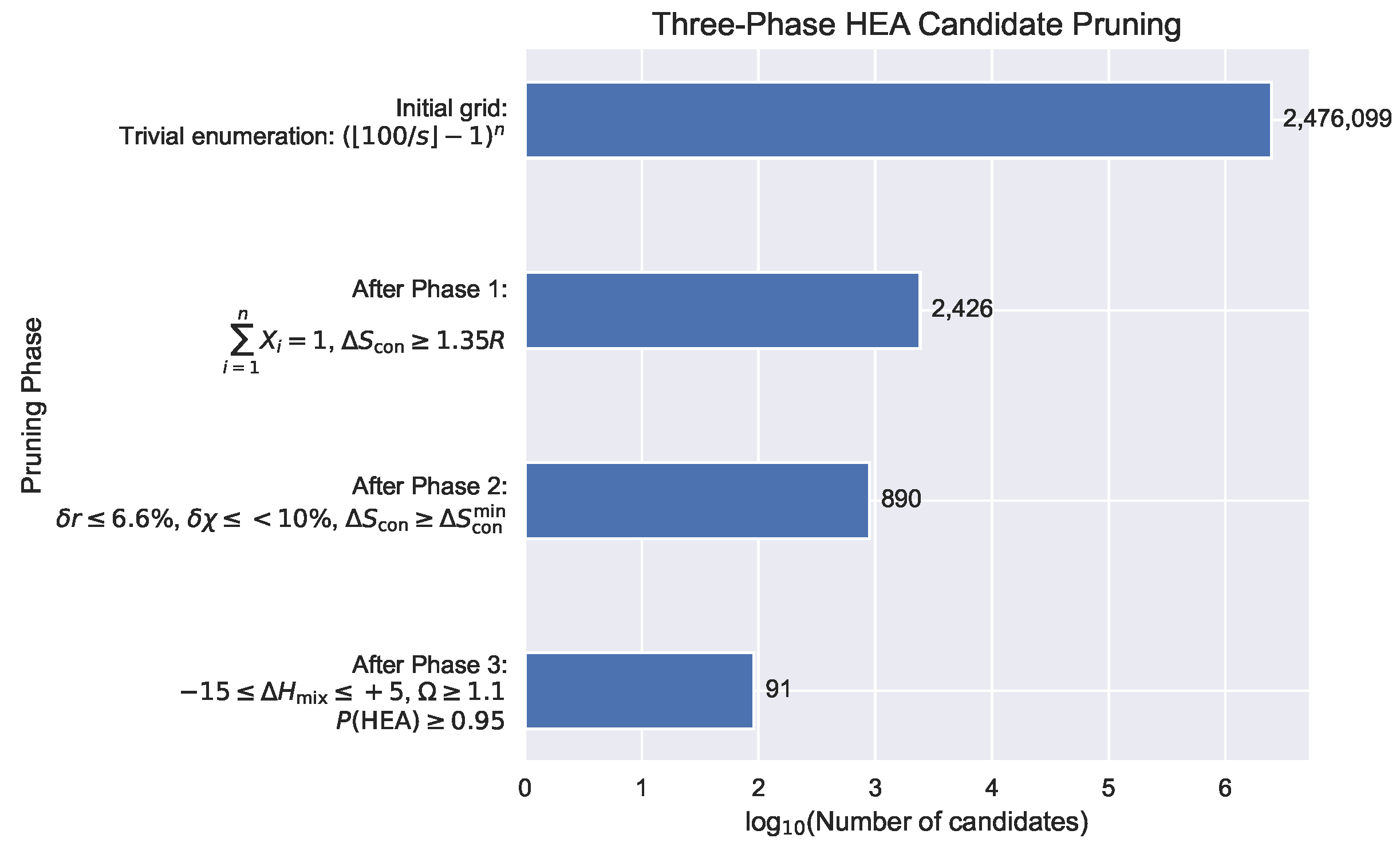
We demonstrate the framework’s utility in guiding discovery by applying it to the Al-Cu-Fe-Ni-Ti HEA system. Figure 5 visualizes the pruning process across three stages.

Discussion. Despite starting from a massive 2.4 M composition space (using 5% resolution), the pipeline reduces the set to 91 high-confidence candidates. Each phase enforces progressively stricter criteria, culminating in uncertainty-aware thermodynamic thresholds. The framework enables practical candidate enumeration without exhaustive enumeration or black-box filtering.

4.4. Case Study: Structural Tendencies in the Al-Cu-Fe-Ni-Ti System

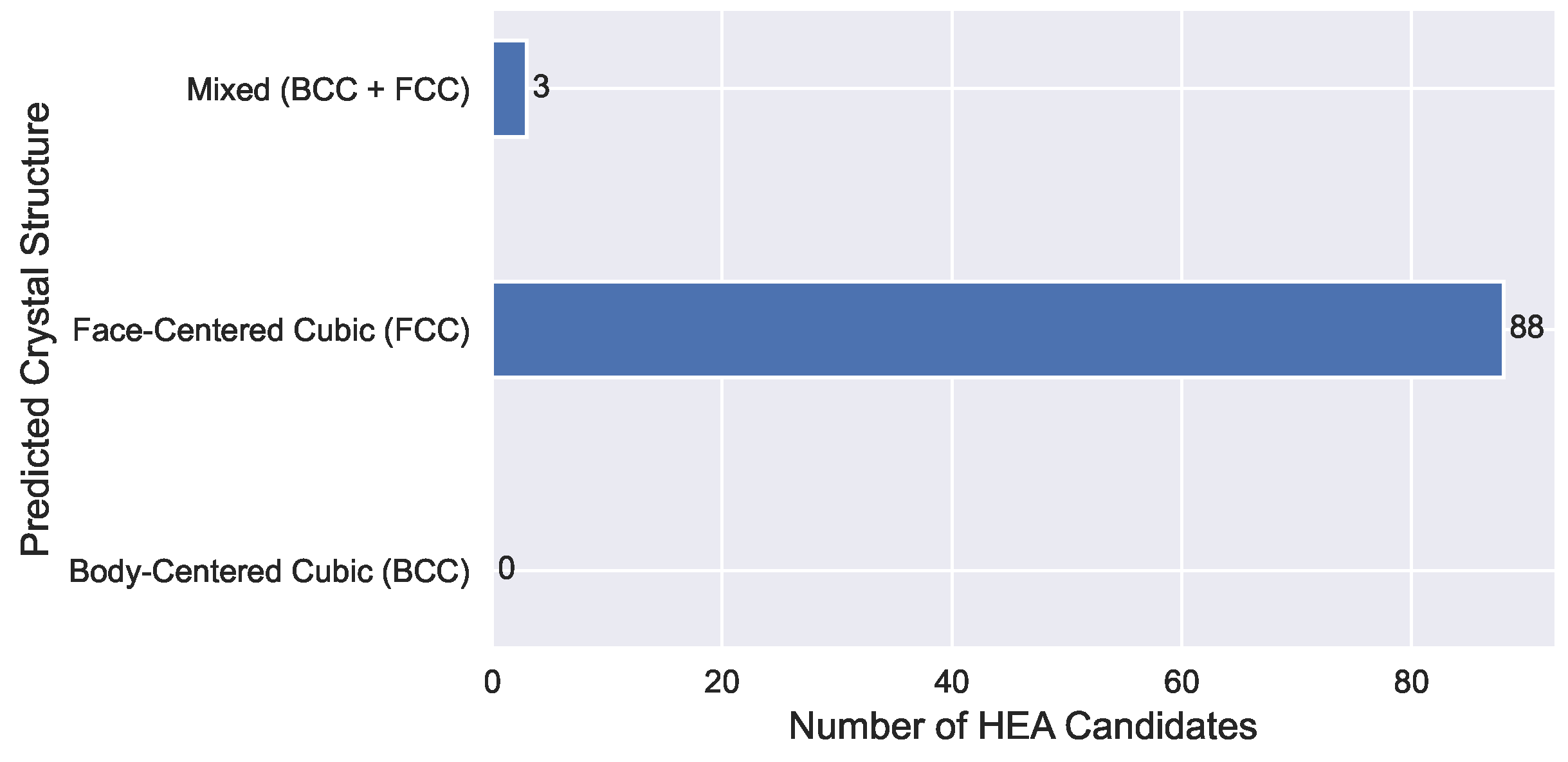
As an illustrative downstream application, we further analyzed the 91 filtered candidates by predicting their likely crystal structures to demonstrate how the output of the framework can support subsequent materials characterization. As shown in Figure 6, nearly all are predicted to form FCC phases.

We also visualized four representative compositions using radar plots (Figure 7) to highlight how individual candidates score across all key criteria, including uncertainty estimates.

Discussion. This case study exemplifies a downstream use of the framework. The structural trends align with known alloy phase behavior and provide actionable leads. More broadly, this illustrates how the framework supports intuitive filtering, interpretable decision metrics, and extensibility to other compositional spaces or design targets (e.g., elastic moduli, corrosion resistance).

4.5. Interpretability and Role of Uncertainty

Uncertainty-aware modeling supports not only robust filtering but also meaningful human interaction with predictions. Three advantages stand out:

• Risk-aware design: Confidence bounds help avoid overfitting to uncertain predictions.
• Transparent decision-making: Visual tools like radar plots clarify trade-offs.
• Modularity: The probabilistic outputs can be used as inputs to subsequent Bayesian optimization or experimental planning pipelines.

Discussion. Our framework transforms alloy thermodynamic modeling into a robust, interpretable, and extensible decision support system. It balances fidelity and uncertainty, generalizes across alloy types, and integrates seamlessly into materials design workflows.

5. Conclusions

We have presented a modular, uncertainty-aware framework for high-entropy alloy (HEA) discovery that tightly integrates physics-informed Bayesian neural networks with classical thermodynamic knowledge and a multi-phase compositional pruning pipeline. This combination enables rapid identification of solid-solution HEA candidates from vast composition spaces with improved confidence and interpretability.

Key outcomes:

• A lightweight ensemble of two Bayesian neural networks (BNNs) significantly outperformed classical models in predicting binary alloy enthalpies of mixing, achieving an MAE of 0.48 kJ/mol on benchmark data from the Entall dataset.
• All predictions were accompanied by uncertainty estimates, enabling risk-aware propagation of enthalpy distributions into multi-component Monte Carlo simulations.
• The hierarchical screening process—combining configurational entropy filters, geometric/electrochemical constraints, and uncertainty-aware thermodynamic criteria—efficiently reduced a 2.4 M candidate pool (Al-Cu-Fe-Ni-Ti) to 91 high-confidence HEA compositions.
• A final probabilistic viability score, $P\left(\mathrm{HEA}\right)$, aggregates uncertainty across key descriptors and offers a clear decision-making criterion for human or automated selection.

These outcomes demonstrate the framework’s direct utility in accelerating the discovery of novel HEAs by significantly reducing the vast compositional search space from millions to a manageable number of high-confidence candidates. This computational efficiency translates into substantial savings in time and experimental resources, enabling materials scientists to focus efforts on the most promising compositions for further synthesis and characterization.

Limitations and caveats. The presented framework depends on the quality of the data used to train the thermodynamic models, particularly binary mixing enthalpies. No matter how sophisticated the model is, poor-quality or inconsistent training data can lead to incorrect filtering, potentially eliminating viable candidates—a classic “garbage in, garbage out” scenario. Although our Bayesian modeling and Monte Carlo sampling approach allows for explicit quantification of uncertainty, predictions in underexplored composition spaces—such as systems involving rare elements or sparse binary data—still carry elevated risk and must be interpreted with caution. Continued efforts in dataset curation, validation, and error correction are essential to ensure trustworthy results.

Moreover, the thermodynamic criteria currently used—such as the accepted range for $\Delta H_{\mathrm{mix}}$ (e.g., [$-15$, $+5$] kJ/mol) and the threshold for $\mathrm{\Omega }$—reflect current conventions in HEA design. However, these thresholds are not universally accepted and remain the subject of active debate. Therefore, the effectiveness of our pipeline is partially constrained by the underlying criteria and their empirical nature. Refinement of these design rules is a critical direction for the field.

While the framework is applicable to general n-component systems and arbitrary compositions, its performance ultimately depends on the accuracy of the underlying binary thermodynamic models. In compositionally extreme or highly imbalanced regions, limitations in available binary data may propagate to higher-order predictions. Finally, although our symmetry-augmented embeddings are constructed from mat2vec-based elemental descriptors and further refined via autoencoding to capture domain-specific binary interactions [33], they may still inherit corpus-related biases that reduce transferability to poorly represented systems (alloys).

Future work. The presented framework provides a robust foundation for advancing HEA design, with several promising directions to expand its practical utility and scope. First, its uncertainty-aware outputs naturally support adaptive experimental design: regions with high predictive uncertainty (indicated by wide confidence intervals) can be prioritized for validation, with resulting data used to refine the models. Second, the framework can be extended to incorporate additional descriptors—such as mechanical strength, elastic moduli, corrosion resistance, or phase stability predictions from CALPHAD or DFT—broadening its applicability. Finally, it lays the groundwork for inverse design strategies, where optimal compositions are identified based on target properties under uncertainty.

Final remarks. Overall, our approach provides a reliable and interpretable decision-support system for HEA discovery. By systematically quantifying uncertainty, enforcing physical constraints, and providing clear metrics for human-in-the-loop filtering, the framework addresses a major bottleneck in computational materials design: making trustworthy predictions in the face of limited data and uncertainty arising from measurement errors.