CAESAR: A Unified Framework for Foundation and Generative Models for Efficient Compression of Scientific Data
Abstract
1. Introduction
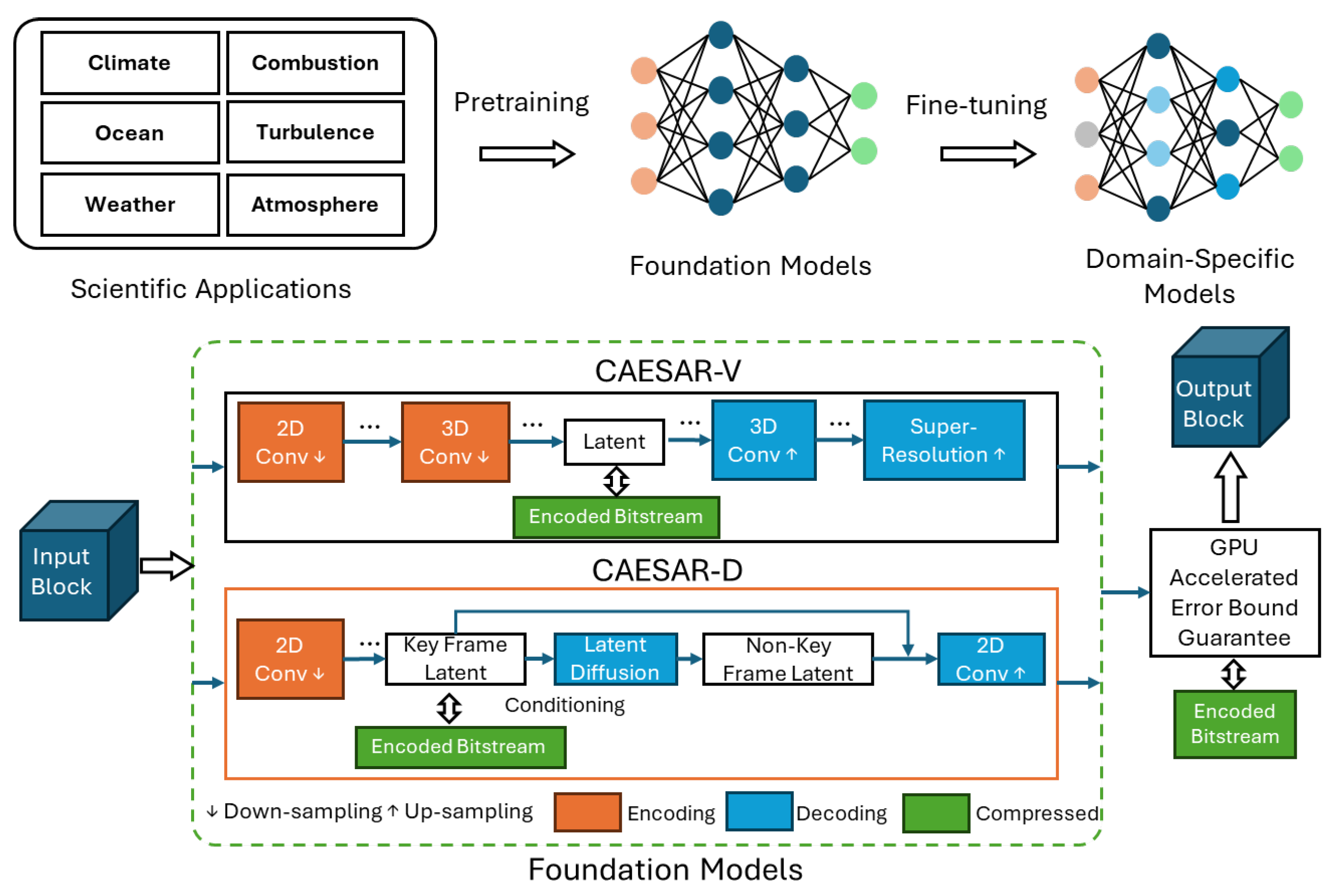
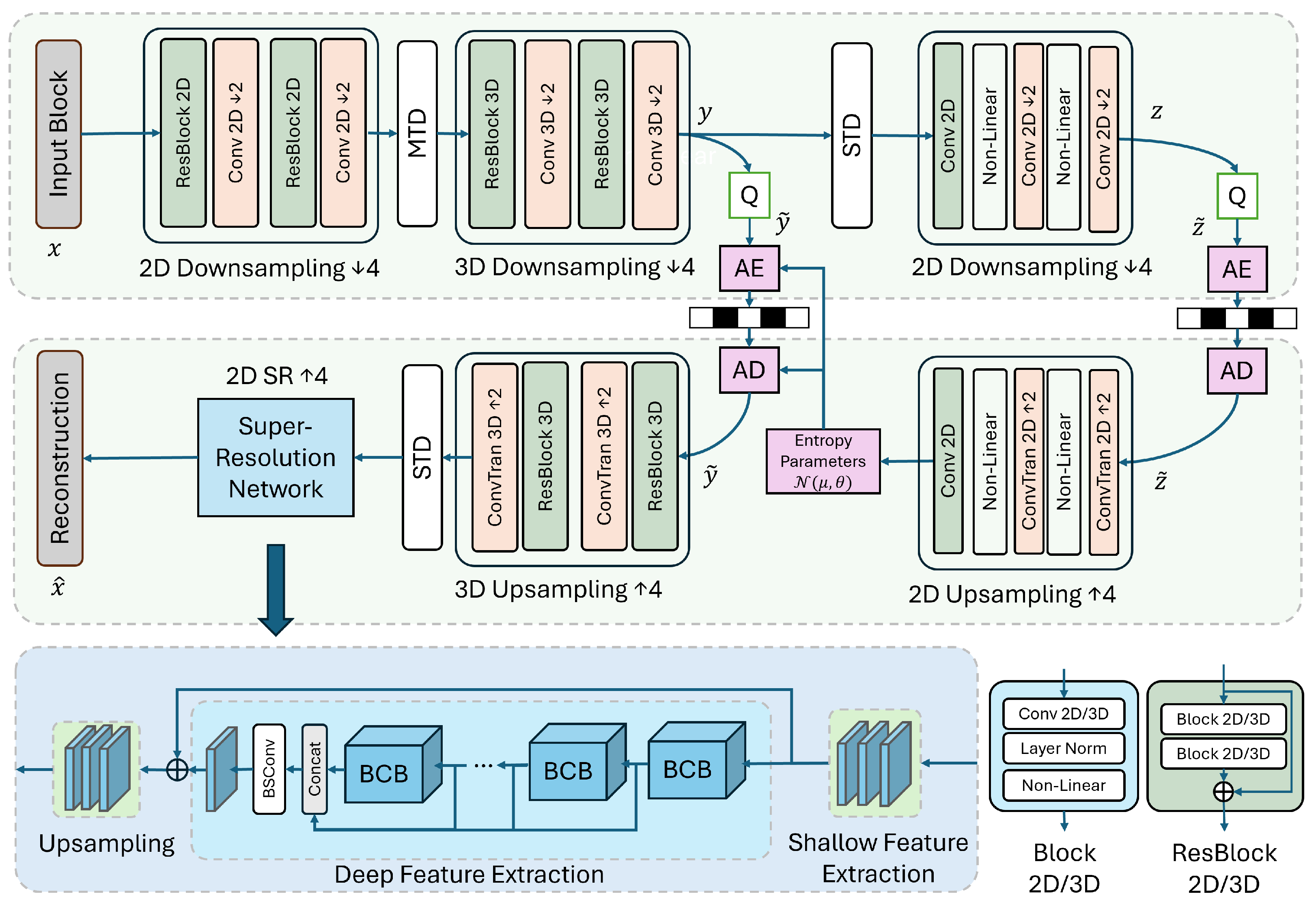
- A transform-based foundation model, combining a variational autoencoder (VAE) with hyper-prior structures and an integrated super-resolution (SR) module, referred to as CAESAR-V. The VAE captures latent space dependencies for efficient transform-based compression, while the SR module enhances reconstruction quality by refining low-resolution outputs. Alternating between 2D and 3D convolutions allows the model to efficiently capture spatiotemporal correlations at low computational cost.
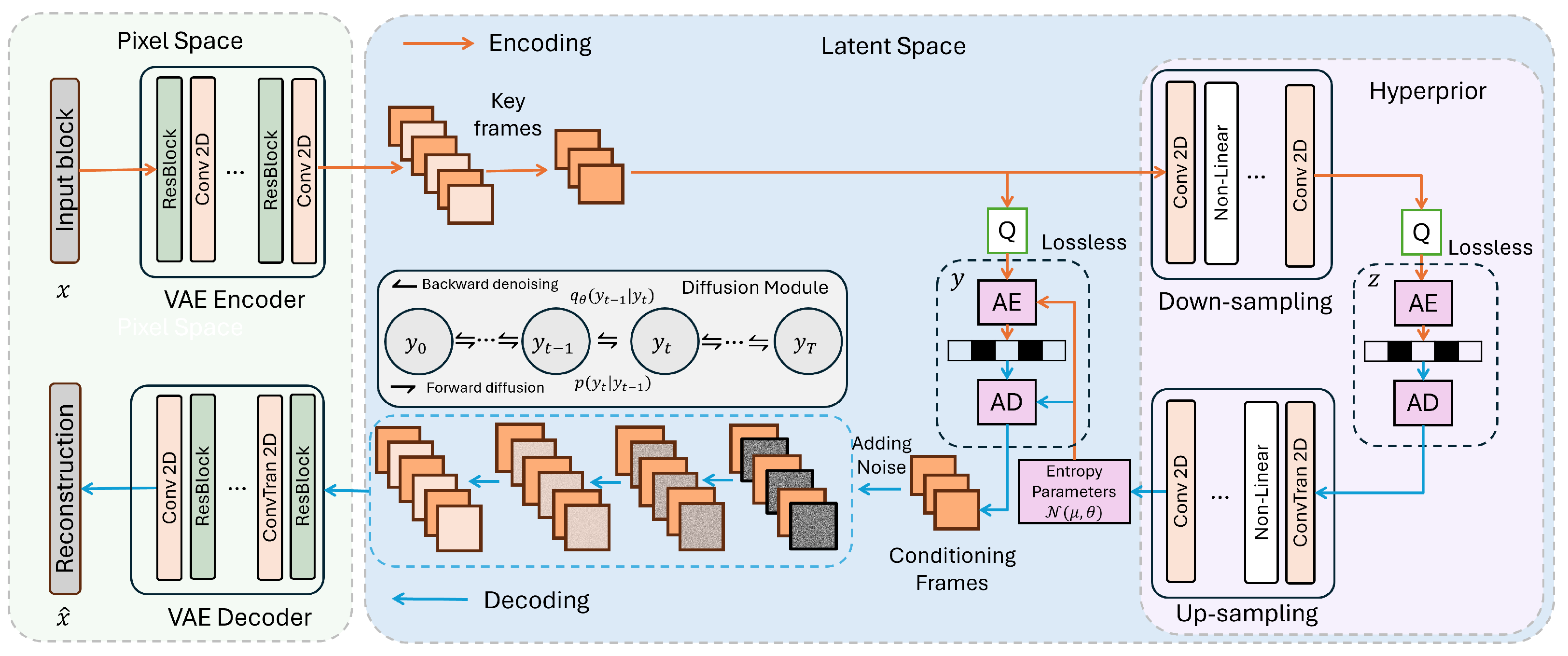
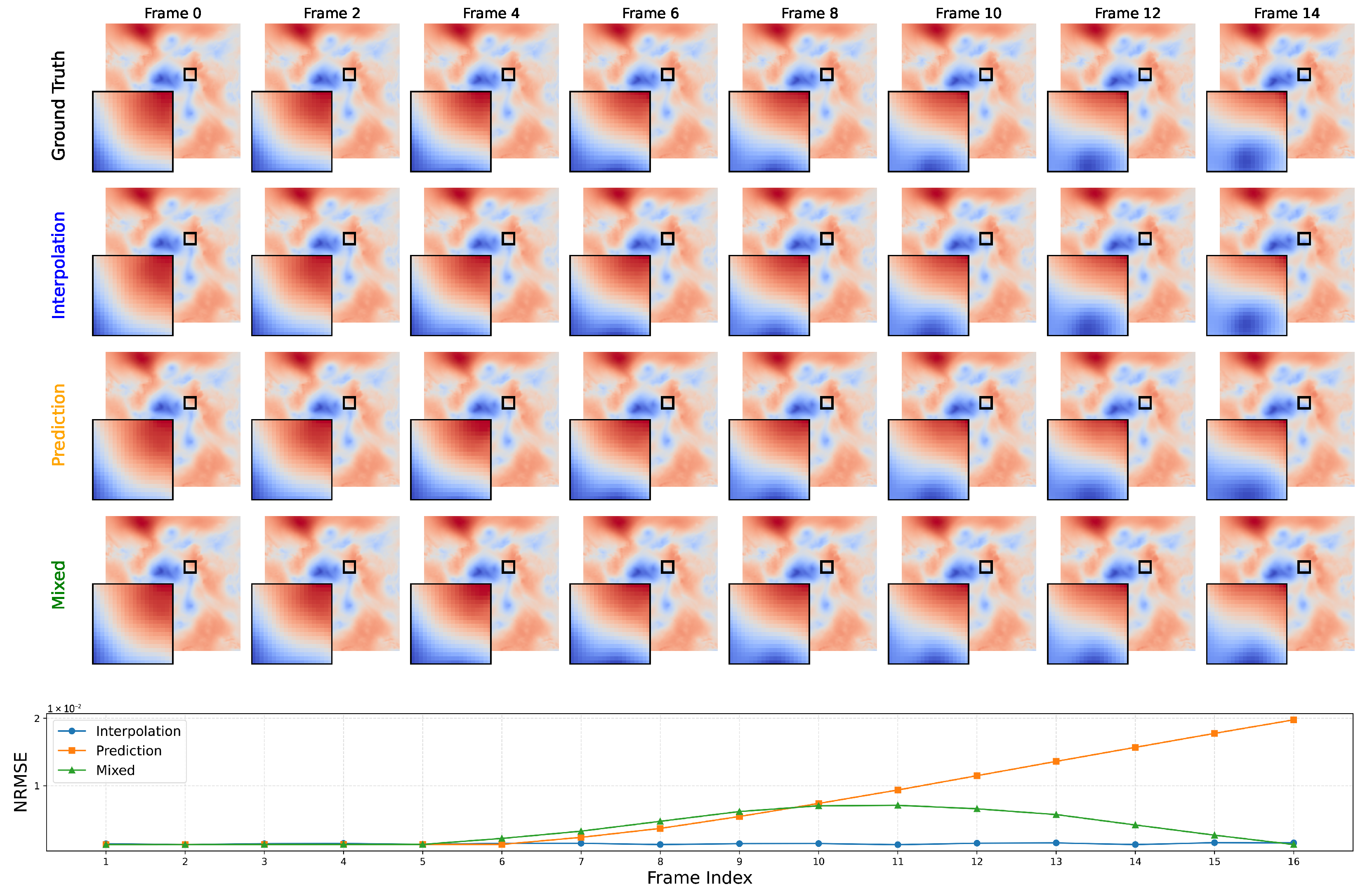
- A generative foundation model, named CAESAR-D, that integrates transform-based compression for keyframes with generative diffusion-driven temporal interpolation across data blocks. Our method employs a variational autoencoder (VAE) paired with a hyperprior to compress selected keyframes into compact latent representations. These latent codes are not only used to reconstruct the corresponding keyframes but also to condition a conditional diffusion (CD) model tasked with generating the missing intermediate blocks. The CD model begins from noisy inputs for non-keyframe positions and iteratively denoises them, using the latent embeddings of neighboring keyframes as auxiliary context. This framework achieves high compression efficiency while preserving strict reconstruction accuracy by statistically inferring intermediate frames in a data-consistent, generative manner.
- We propose two complementary foundation frameworks for scientific data compression: (i) a transform-based model combining a variational autoencoder (VAE) with hyperprior structures and a super-resolution (SR) module, and (ii) a generative model based on conditional latent diffusion for learned spatiotemporal interpolation across data blocks.
- We incorporate a GPU-parallelized post-processing module that enforces user-specified error-bound guarantees on the reconstructed primary data, achieving throughput of 0.4 GB/s to 1.1 GB/s, thereby supporting scientific applications demanding quantifiable accuracy.
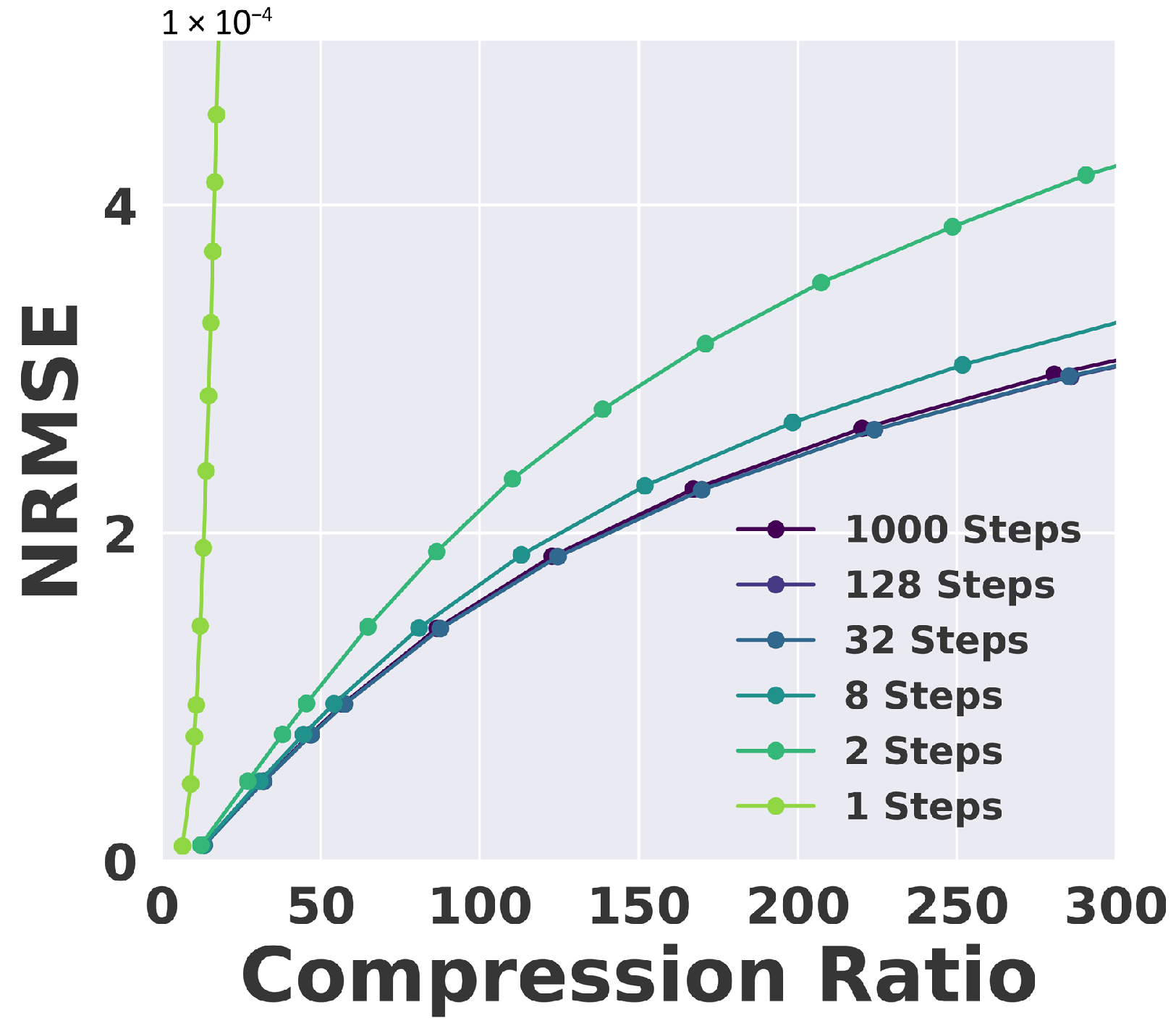
- To improve the efficiency and scalability of the generative model, we fine-tune the diffusion process to operate with significantly fewer denoising steps, ensuring its applicability to large-scale and real-time scientific workflows.
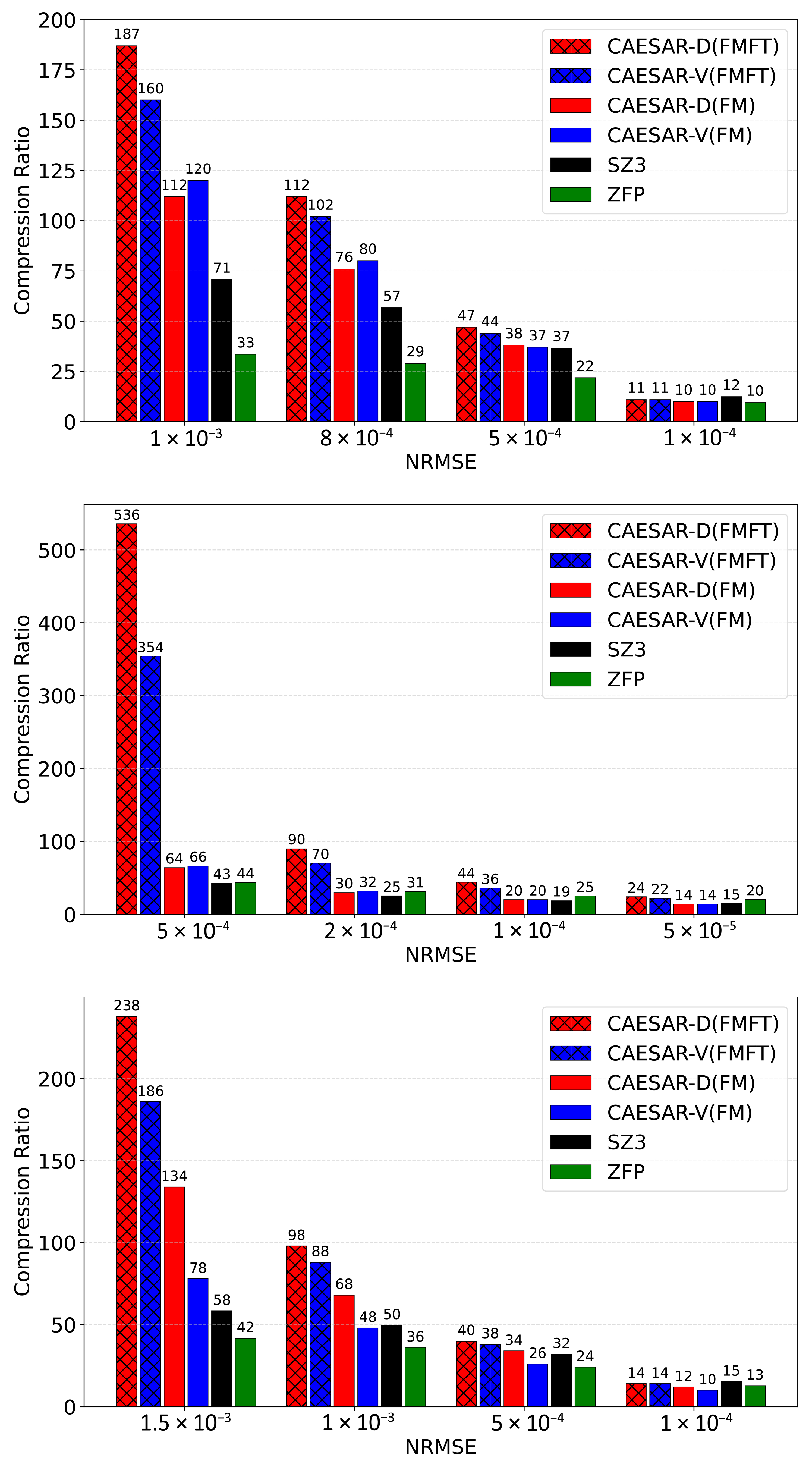
- Both foundation models are pretrained on diverse multi-domain scientific datasets, achieving more than 2× higher compression ratios than state-of-the-art rule-based compressors without domain-specific tuning. Further fine-tuning on target datasets yields an additional 1.5–5× improvement in compression ratio while preserving strict reconstruction error guarantees.
2. Related Work
3. Methodology
3.1. Preliminaries
3.1.1. Error Bounded Data Compression
3.1.2. VAE with Hyperprior
3.2. CAESAR-V Foundation Model
3.2.1. Variational 3D Autoencoder
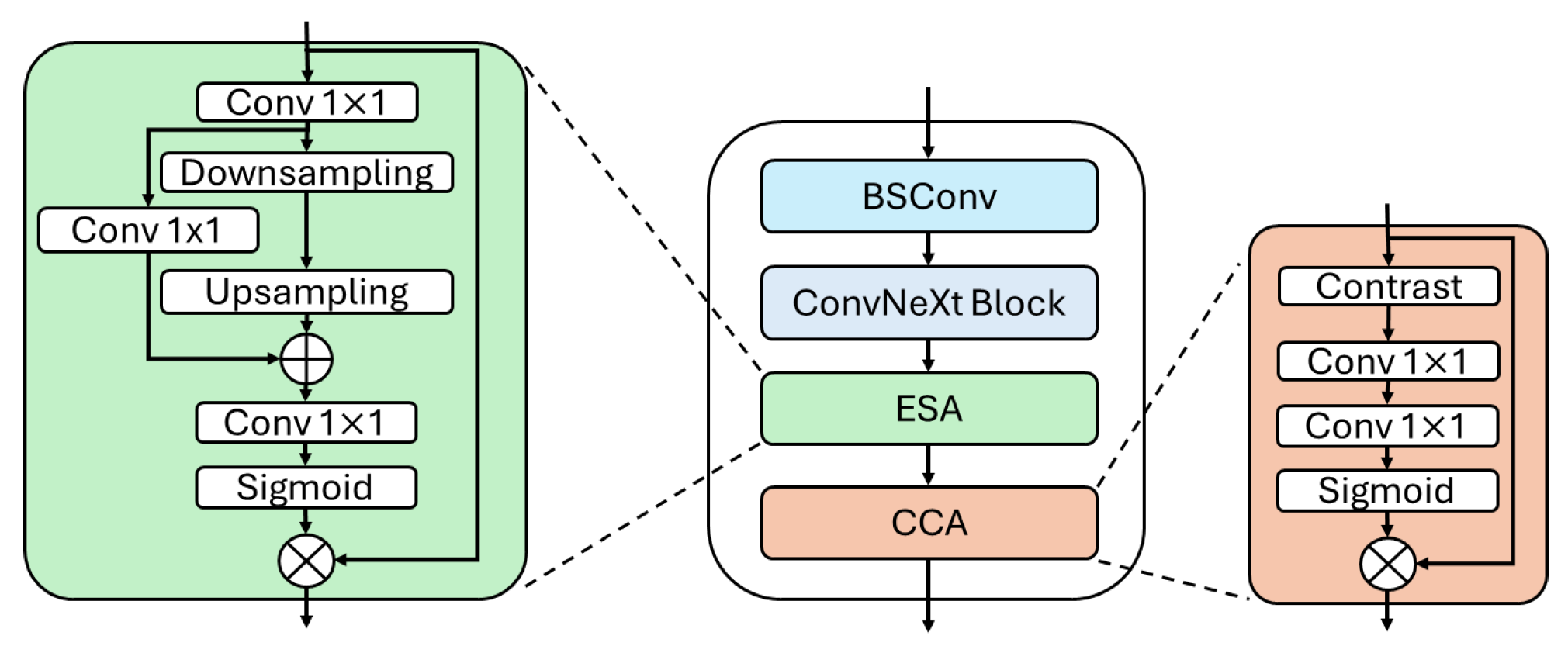
3.2.2. SR Module
3.2.3. Compression and Decompression Procedure
3.3. CAESAR-D Foundation Model
3.3.1. Latent Diffusion Models
3.3.2. Keyframe Conditioning
3.3.3. Compression and Decompression Procedure
3.4. Model Training
3.5. Error Bound Guarantees and GPU Acceleration
3.5.1. PCA-Based Error Bound Guarantee
3.5.2. Quantization Bin Upper Bound
3.5.3. GPU Acceleration
4. Experiments
4.1. Evaluation Metrics and Datasets
- E3SM Dataset
- S3D Dataset
- JHTDB Dataset
- ERA5 Dataset
- Hurricane Dataset
- TUM-TF Dataset
- HYCOM Dataset
- PDEBench Dataset
- OpenFOAM Dataset
| Application | Domain | Dimensions | Total Size |
|---|---|---|---|
| E3SM | Climate | 61 GB | |
| S3D | Combustion | 8.9 GB | |
| JHTDB | Fluid Dynamics | 45 GB | |
| ERA5 | Atmospheric Reanalysis | 21 GB | |
| Hurricane | Weather | 4.3 GB | |
| TUM-TF | Turbulence | 19 GB | |
| HYCOM | Oceanology | 3.6 GB | |
| PDEBench | Physics | 5.6 GB | |
| OpenFOAM | CFD | 15 GB |
4.2. Implementation Details
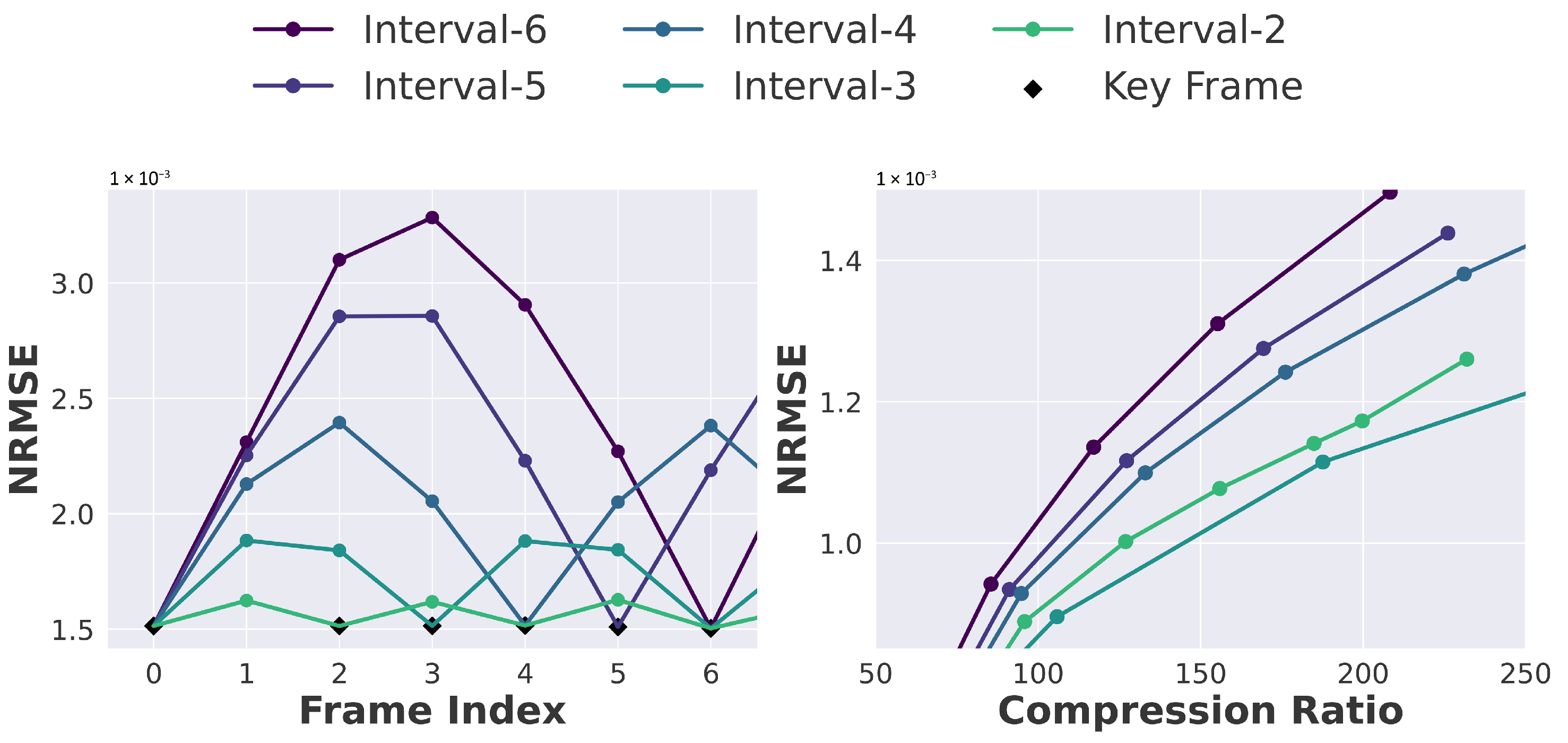
4.3. Keyframe Selection
4.4. Impact of Keyframe Interval and Denoising Steps
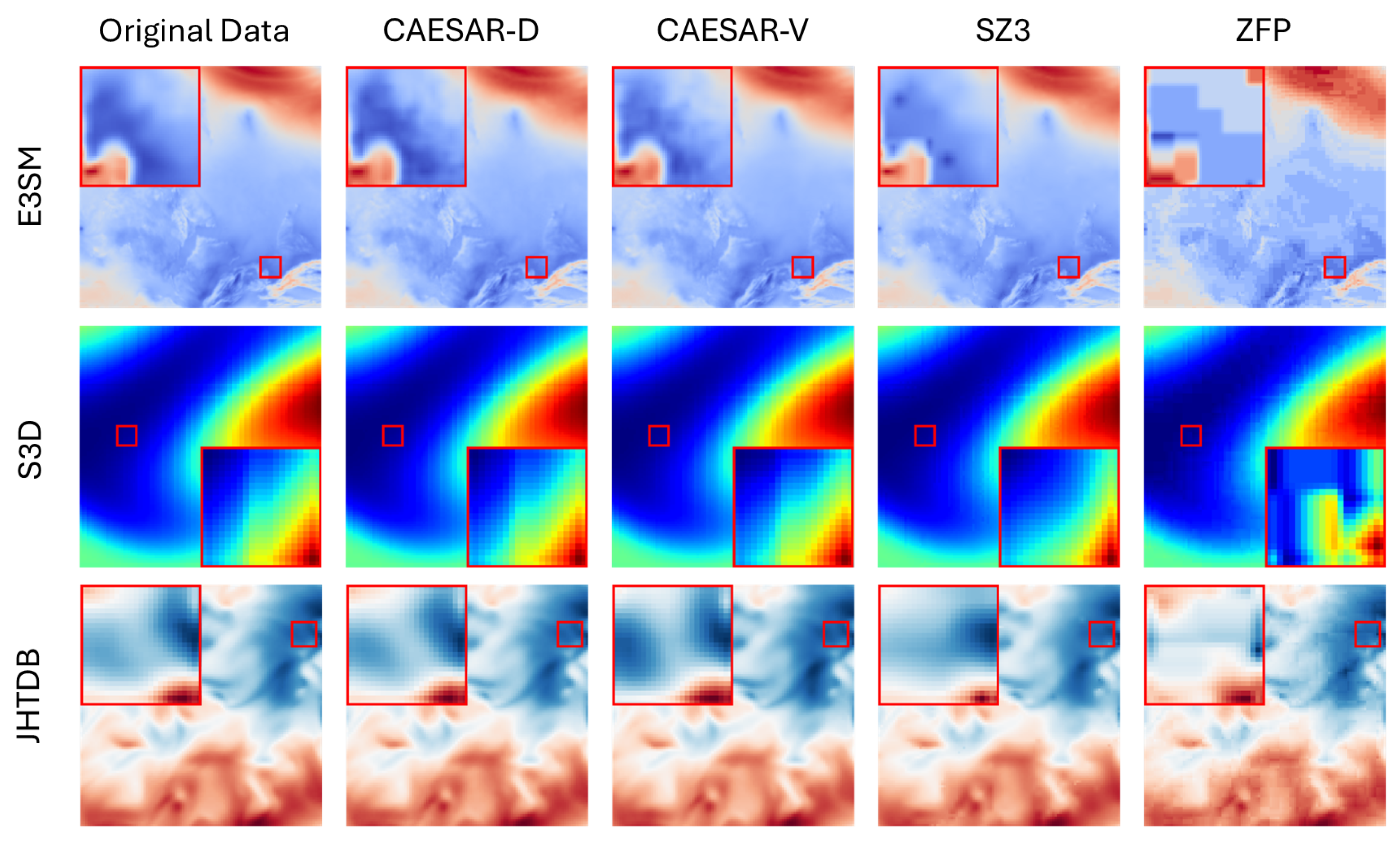
4.5. Comparison with Other Methods
4.6. Model Inference Speed
4.7. Post-Processing Speed on GPU
5. Limitations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 4015–4026. [Google Scholar] [CrossRef]
- Ainsworth, M.; Tugluk, O.; Whitney, B.; Klasky, S. Multilevel techniques for compression and reduction of scientific data-the univariate case. Comput. Vis. Sci. 2018, 19, 65–76. [Google Scholar] [CrossRef]
- Li, X.; Gong, Q.; Lee, J.; Klasky, S.; Rangarajan, A.; Ranka, S. Machine Learning Techniques for Data Reduction of Climate Applications. arXiv 2024, arXiv:2405.00879. [Google Scholar] [CrossRef]
- Li, X.; Lee, J.; Rangarajan, A.; Ranka, S. Attention based machine learning methods for data reduction with guaranteed error bounds. In Proceedings of the 2024 IEEE International Conference on Big Data (BigData), Washington DC, USA, 15–18 December 2024; IEEE: New York, NY, USA, 2024; pp. 1039–1048. [Google Scholar] [CrossRef]
- Liang, X.; Zhao, K.; Di, S.; Li, S.; Underwood, R.; Gok, A.M.; Tian, J.; Deng, J.; Calhoun, J.C.; Tao, D.; et al. SZ3: A modular framework for composing prediction-based error-bounded lossy compressors. IEEE Trans. Big Data 2022, 9, 485–498. [Google Scholar] [CrossRef]
- Li, X.; Zhu, L.; Rangarajan, A.; Ranka, S. Generative Latent Diffusion for Efficient Spatiotemporal Data Reduction. arXiv 2025, arXiv:2507.02129. [Google Scholar] [CrossRef]
- Golaz, J.C.; Caldwell, P.M.; Van Roekel, L.P.; Petersen, M.R.; Tang, Q.; Wolfe, J.D.; Abeshu, G.; Anantharaj, V.; Asay-Davis, X.S.; Bader, D.C.; et al. The DOE E3SM coupled model version 1: Overview and evaluation at standard resolution. J. Adv. Model. Earth Syst. 2019, 11, 2089–2129. [Google Scholar] [CrossRef]
- Yoo, C.S.; Lu, T.; Chen, J.H.; Law, C.K. Direct numerical simulations of ignition of a lean n-heptane/air mixture with temperature inhomogeneities at constant volume: Parametric study. Combust. Flame 2011, 158, 1727–1741. [Google Scholar] [CrossRef]
- Wan, M.; Chen, S.; Eyink, G.; Meneveau, C.; Perlman, E.; Burns, R.; Li, Y.; Szalay, A.; Hamilton, S. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 2008, 9, N31. [Google Scholar] [CrossRef]
- Fox, A.; Diffenderfer, J.; Hittinger, J.; Sanders, G.; Lindstrom, P. Stability analysis of inline ZFP compression for floating-point data in iterative methods. SIAM J. Sci. Comput. 2020, 42, A2701–A2730. [Google Scholar] [CrossRef]
- Ballester-Ripoll, R.; Lindstrom, P.; Pajarola, R. TTHRESH: Tensor compression for multidimensional visual data. IEEE Trans. Vis. Comput. Graph. 2019, 26, 2891–2903. [Google Scholar] [CrossRef]
- Ainsworth, M.; Tugluk, O.; Whitney, B.; Klasky, S. Multilevel techniques for compression and reduction of scientific data—The multivariate case. SIAM J. Sci. Comput. 2019, 41, A1278–A1303. [Google Scholar] [CrossRef]
- Gong, Q.; Chen, J.; Whitney, B.; Liang, X.; Reshniak, V.; Banerjee, T.; Lee, J.; Rangarajan, A.; Wan, L.; Vidal, N.; et al. MGARD: A multigrid framework for high-performance, error-controlled data compression and refactoring. SoftwareX 2023, 24, 101590. [Google Scholar] [CrossRef]
- Mun, S.; Fowler, J.E. DPCM for quantized block-based compressed sensing of images. In Proceedings of the 2012 Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; IEEE: New York, NY, USA, 2012; pp. 1424–1428. [Google Scholar] [CrossRef]
- Boyce, J.M.; Doré, R.; Dziembowski, A.; Fleureau, J.; Jung, J.; Kroon, B.; Salahieh, B.; Vadakital, V.K.M.; Yu, L. MPEG immersive video coding standard. Proc. IEEE 2021, 109, 1521–1536. [Google Scholar] [CrossRef]
- Liang, X.; Di, S.; Tao, D.; Li, S.; Li, S.; Guo, H.; Chen, Z.; Cappello, F. Error-controlled lossy compression optimized for high compression ratios of scientific datasets. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 438–447. [Google Scholar] [CrossRef]
- Liu, J.; Di, S.; Zhao, K.; Liang, X.; Chen, Z.; Cappello, F. FAZ: A flexible auto-tuned modular error-bounded compression framework for scientific data. In Proceedings of the 37th International Conference on Supercomputing, Orlando, FL, USA, 21–23 June 2023; pp. 1–13. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar] [CrossRef]
- Minnen, D.; Ballé, J.; Toderici, G.D. Joint autoregressive and hierarchical priors for learned image compression. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar] [CrossRef]
- Li, X.; Lee, J.; Rangarajan, A.; Ranka, S. Foundation Model for Lossy Compression of Spatiotemporal Scientific Data. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 June 2025; Springer: Berlin/Heidelberg, Germany, 2025; pp. 368–380. [Google Scholar] [CrossRef]
- Croitoru, F.A.; Hondru, V.; Ionescu, R.T.; Shah, M. Diffusion models in vision: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10850–10869. [Google Scholar] [CrossRef]
- He, C.; Shen, Y.; Fang, C.; Xiao, F.; Tang, L.; Zhang, Y.; Zuo, W.; Guo, Z.; Li, X. Diffusion models in low-level vision: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2025. [Google Scholar] [CrossRef] [PubMed]
- Voleti, V.; Jolicoeur-Martineau, A.; Pal, C. MCVD: Masked Conditional Video Diffusion for Prediction, Generation, and Interpolation. arXiv 2022. arXiv:2205.09853. [Google Scholar] [CrossRef]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. In Proceedings of the the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 2256–2265. [Google Scholar] [CrossRef]
- Song, Y.; Ermon, S. Generative modeling by estimating gradients of the data distribution. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Volume 33, pp. 6840–6851. [Google Scholar] [CrossRef]
- Song, J.; Meng, C.; Ermon, S. Denoising Diffusion Implicit Models. In Proceedings of the International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar] [CrossRef]
- Yang, R.; Mandt, S. Lossy image compression with conditional diffusion models. In Proceedings of the Advances in Neural Information Processing Systems, Orleans, LA, USA, 10–16 December 2023; Volume 36, pp. 64971–64995. [Google Scholar] [CrossRef]
- Ballé, J.; Minnen, D.; Singh, S.; Hwang, S.J.; Johnston, N. Variational image compression with a scale hyperprior. arXiv 2018, arXiv:1802.01436. [Google Scholar] [CrossRef]
- Bai, H.; Liang, X. A very lightweight image super-resolution network. Sci. Rep. 2024, 14, 13850. [Google Scholar] [CrossRef] [PubMed]
- Haase, D.; Amthor, M. Rethinking depthwise separable convolutions: How intra-kernel correlations lead to improved mobilenets. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 14600–14609. [Google Scholar] [CrossRef]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar] [CrossRef]
- Hui, Z.; Gao, X.; Yang, Y.; Wang, X. Lightweight image super-resolution with information multi-distillation network. In Proceedings of the the 27th ACM International Conference on Multimedia, Nice, France, 21 October 2019; pp. 2024–2032. [Google Scholar] [CrossRef]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar] [CrossRef]
- Blattmann, A.; Rombach, R.; Ling, H.; Dockhorn, T.; Kim, S.W.; Fidler, S.; Kreis, K. Align your latents: High-resolution video synthesis with latent diffusion models. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 22563–22575. [Google Scholar] [CrossRef]
- Ho, J.; Salimans, T.; Gritsenko, A.; Chan, W.; Norouzi, M.; Fleet, D.J. Video diffusion models. arXiv 2022, arXiv:2204.03458. [Google Scholar] [CrossRef]
- Blattmann, A.; Dockhorn, T.; Kulal, S.; Mendelevitch, D.; Kilian, M.; Lorenz, D.; Levi, Y.; English, Z.; Voleti, V.; Letts, A.; et al. Stable video diffusion: Scaling latent video diffusion models to large datasets. arXiv 2023, arXiv:2311.15127. [Google Scholar] [CrossRef]
- Van den Oord, A.; Kalchbrenner, N.; Espeholt, L.; Vinyals, O.; Graves, A. Conditional image generation with pixelcnn decoders. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar] [CrossRef]
- Lee, J.; Gong, Q.; Choi, J.; Banerjee, T.; Klasky, S.; Ranka, S.; Rangarajan, A. Error-Bounded Learned Scientific Data Compression with Preservation of Derived Quantities. Appl. Sci. 2022, 12, 6718. [Google Scholar] [CrossRef]
- Lee, J.; Rangarajan, A.; Ranka, S. Nonlinear-by-Linear: Guaranteeing Error Bounds in Compressive Autoencoders. In Proceedings of the 2023 Fifteenth International Conference on Contemporary Computing, IC3-2023, Noida, India, 3–5 August 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 552–561. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S). ERA5 Hourly Data on Pressure Levels from 1940 to Present. 2018. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-pressure-levels?tab=overview (accessed on 9 June 2025).
- National Center for Atmospheric Research (NCAR). 2004. Available online: http://vis.computer.org/vis2004contest/data.html (accessed on 10 August 2025).
- Lienen, M.; Lüdke, D.; Hansen-Palmus, J.; Günnemann, S. 3D Turbulent Flow Simulations around Various Shapes. Dataset. TUM University Library, Munich, Germany, 2024. Available online: https://mediatum.ub.tum.de/1737748 (accessed on 12 August 2025).
- HYCOM: Hybrid Coordinate Ocean Model. 2024. Available online: https://www.hycom.org/dataserver (accessed on 9 June 2025).
- Takamoto, M.; Praditia, T.; Leiteritz, R.; MacKinlay, D.; Alesiani, F.; Pflüger, D.; Niepert, M. PDEBench Datasets; DaRUS, University of Stuttgart: Stuttgart, Germany, 2022. [Google Scholar] [CrossRef]
- OpenFOAM Foundation. OpenFOAM: The Open Source CFD Toolbox. 2024. Available online: https://openfoam.org (accessed on 10 August 2025).
- Lindstrom, P. Fixed-Rate Compressed Floating-Point Arrays. IEEE Trans. Vis. Comput. Graph. 2014, 20, 2674–2683. [Google Scholar] [CrossRef] [PubMed]


| Devices | Methods | Encoder (MB/s) | Decoder (MB/s) |
|---|---|---|---|
| A100 80 GB | CAESAR-V | 943 | 652 |
| CAESAR-D-128 Steps | 1942 | 16 | |
| CAESAR-D-32 Steps | 1942 | 61 | |
| CAESAR-D-8 Steps | 1942 | 203 | |
| RTX 2080 24 GB | CAESAR-V | 336 | 251 |
| CAESAR-D-128 Steps | 825 | 6 | |
| CAESAR-D-32 Steps | 825 | 25 | |
| CAESAR-D-8 Steps | 825 | 93 |
| Error Bound | A100 GPU (MB/s) | RTX 2080 GPU (MB/s) | CPU (MB/s) |
|---|---|---|---|
| 1 × 10 | 1181 | 636 | 52 |
| 1 × 10 | 855 | 514 | 12 |
| 1 × 10 | 556 | 291 | 6 |
| 1 × 10 | 474 | 226 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhu, L.; Lee, J.; Sengupta, R.; Klasky, S.; Ranka, S.; Rangarajan, A. CAESAR: A Unified Framework for Foundation and Generative Models for Efficient Compression of Scientific Data. Appl. Sci. 2025, 15, 8977. https://doi.org/10.3390/app15168977
Li X, Zhu L, Lee J, Sengupta R, Klasky S, Ranka S, Rangarajan A. CAESAR: A Unified Framework for Foundation and Generative Models for Efficient Compression of Scientific Data. Applied Sciences. 2025; 15(16):8977. https://doi.org/10.3390/app15168977
Chicago/Turabian StyleLi, Xiao, Liangji Zhu, Jaemoon Lee, Rahul Sengupta, Scott Klasky, Sanjay Ranka, and Anand Rangarajan. 2025. "CAESAR: A Unified Framework for Foundation and Generative Models for Efficient Compression of Scientific Data" Applied Sciences 15, no. 16: 8977. https://doi.org/10.3390/app15168977
APA StyleLi, X., Zhu, L., Lee, J., Sengupta, R., Klasky, S., Ranka, S., & Rangarajan, A. (2025). CAESAR: A Unified Framework for Foundation and Generative Models for Efficient Compression of Scientific Data. Applied Sciences, 15(16), 8977. https://doi.org/10.3390/app15168977








