Beam Finite Element Model Modification Considering Shear Stiffness: Octet-Truss Unit Cell with Springs
Abstract
1. Introduction
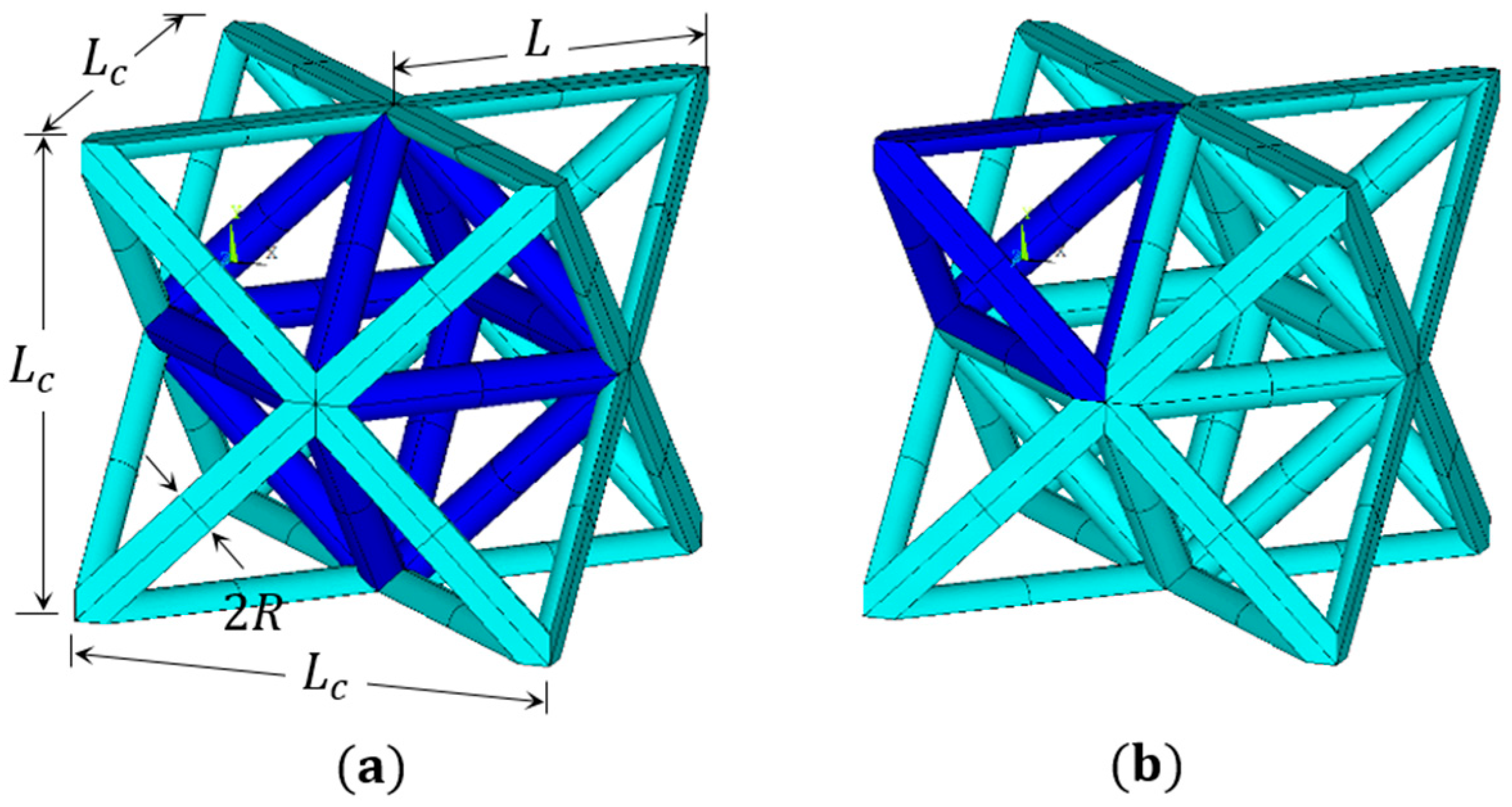
2. Properties of Octet-Truss Unit Cell Lattice Material
3. Finite Element Simulations of Octet-Truss UC for Homogenization
3.1. Solid UC Model
3.2. Unmodified Beam UC Model
3.3. Comparison of Solid UC and Unmodified Beam UC Models
3.4. Investigation of the Modified Beam UC Model Found in the Literature
3.5. A Novel Beam UC Model Modification Using Spring Elements
4. Octet-Truss Lattice Structure Examples
4.1. Example 1: Compressed Lattice Structure
4.2. Example 2: Laterally Loaded Lattice Structure
5. Conclusions
- The average stress homogenization method commonly applied to composite materials in the literature was modified and used for lattice materials.
- The homogenized material constants of octet-truss cells are presented with respect to both the strut aspect ratio and the relative density in the range of = 0.01–0.5.
- The results of the octet-truss solid model and the unmodified beam model are compared; here, it is observed that the difference between the solid model and the beam model is less than 12% for low values of relative density, < 0.09, but for higher values, the results of the beam model underestimate the results of the solid model. These differences reach up to approximately 40% and 30% for the elastic and shear moduli, respectively, for = 0.5.
- Closed expressions for the moduli of the octet-truss lattice material are presented in terms of the aspect ratio by curve-fitting on the results of the solid model for = 0.1–0.5. The moduli with respect to those of bulk material and unmodified beam model are presented by Equations (6a,b) and (7a,b), respectively. As a practical alternative method to be used at this level, the error will remain under 12% if these equations are used for > 0.09.
- Beam model modification, achieved by increasing the stiffness of the struts at the joint region, is investigated in detail. It is concluded that both of the modulus values cannot be exactly fitted to the solid model results with this type of modification.
- A new modification method for the beam model is proposed by including seven spring elements, with two different spring constants, k1 and k2, with which not only the elastic but also the shear modulus can be captured. The required spring constants for various relative densities of the octet-truss lattice unit cell are presented. This proposed modified beam model provides a straightforward procedure to calculate the parameters.
- The closed expressions of the spring constants, k1 and k2, in terms of aspect ratio, are presented for relative density range of = 0.1–0.5.
- In this model, the springs are attached to the joints at both the face centers and the corners of the octet-truss unit cell. The same spring arrangement can also be applied to unit cells that lack joints at both of the locations by using multiple unit cells within the RVE.
- An alternative method for obtaining the spring constants is presented with closed expressions in terms of the differences between the moduli of the solid model versus those of the unmodified beam model, in addition to the differences in the unit cell side lengths, which are very practical for linear elastic materials. The spring system can be mounted to any beam model of lattice cell for calibration, and the constants can be calculated easily using Equation (11a,b).
- The performance of the UC models forming the basis of lattice structures is evaluated through two example problems with increasing numbers of unit cells. The first example involves the compression of the lattice structure, at which the elastic modulus is dominant in mechanical behavior. It is observed that the results of all the models converged to a constant value when the number of unit cells is n = 6.
- In the second example, where the shear modulus is primarily dominant in governing the behavior of the lattice structure, the beam model with springs gave results that were closest to those of the solid model. The proposed beam model with springs for the octet-truss lattice is suitable for large-scale structures where shear modulus is dominant in dictating mechanical behavior.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, C.; Han, Y.; Lu, J. Design and optimization of lattice structures: A review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]
- ISO/ASTM 52900:2021; Additive Manufacturing—General Principles—Fundamentals and Vocabulary. ASTM International: West Conshohocken, PA, USA, 2021.
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Alomar, Z.; Concli, F. A review of the selective laser melting lattice structures and their numerical models. Adv. Eng. Mater. 2020, 22, 2000611. [Google Scholar] [CrossRef]
- Ling, C.; Cernicchi, A.; Gilchrist, M.D.; Cardiff, P. Mechanical behavior of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading. Mater. Des. 2019, 162, 106–118. [Google Scholar] [CrossRef]
- Dejean, T.T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical behaviors of SLM additive manufactured octet-truss and truncated-octahedron lattice structures with uniform and taper beams. Int. J. Mechanical Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Somnic, J.; Jo, B.W. Review: Status and challenges in homogenization methods for lattice materials. Materials 2022, 15, 605. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. London A Math. Phys. Sci. 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, W. Energy-based homogenization method for lattice structures with generalized periodicity. Comput. Struct. 2024, 302, 107478. [Google Scholar] [CrossRef]
- Dong, Z.; Quan, W.; Ma, X.; Li, X.; Zhou, J. Asymptotic homogenization of effective thermal-elastic properties of concrete considering its three-dimensional mesostructure. Comput. Struct. 2023, 279, 106970. [Google Scholar] [CrossRef]
- Hedayati, R.; Shokrnia, M.; Alavi, M.; Sadighi, M.; Aghdam, M.M. Viscoelastic Behavior of Cellular Biomaterials Based on Octet-Truss and Tetrahedron Topologies. Materials 2024, 17, 5865. [Google Scholar] [CrossRef]
- Feyel, F.; Chaboche, J.L. FE2 multiscale approach for modelling the elastoviscoplastic behaviour of long fibre SiC/Ti composite materials. Comput. Methods Appl. Mech. Eng. 2000, 183, 309–330. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Linear multiscale analysis and finite element validation of stretching and bending dominated lattice materials. Mech. Mater. 2012, 46, 57–68. [Google Scholar] [CrossRef]
- Zeman, J.; Vondřejc, J.; Novák, J.; Marek, I. Accelerating a FFT-based solver for numerical homogenization of periodic media by conjugate gradients. J. Comput. Phys. 2010, 229, 8065–8071. [Google Scholar] [CrossRef]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using Abaqus; CRC Press: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Labeas, G.N.; Sunaric, M.M. Investigation on the static response and failure process of metallic open lattice cellular structures. Strain 2010, 46, 195–204. [Google Scholar] [CrossRef]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Finite element modeling concepts and linear analysis of 3D regular open cell structures. J. Mater. Sci. 2005, 40, 5859–5866. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.J.; Mines, R.A.W.; Tsopanos, S.; Smith, M. An investigation into the compressive properties of stainless-steel micro-lattice structures. J. Sandw. Struct. Mater. 2010, 13, 303–329. [Google Scholar] [CrossRef]
- Ptochos, E.; Labeas, G. Elastic modulus and Poisson’s ratio determination of micro-lattice cellular structures by analytical, numerical and homogenization methods. J. Sandw. Struct. Mater. 2012, 14, 597–626. [Google Scholar] [CrossRef]
- Ptochos, E.; Labeas, G. Shear modulus determination of cuboid metallic open-lattice cellular structures by analytical, numerical and homogenization methods. Strain 2012, 48, 415–429. [Google Scholar] [CrossRef]
- Smith, M.; Guan, Z.; Cantwell, W.J. Finite element modelling of the compressive response of lattice structures manufactured using the selective laser melting technique. Int. J. Mech. Sci. 2013, 67, 28–41. [Google Scholar] [CrossRef]
- Karttunen, A.T.; Reddy, J.N. Hierarchy of beam models for lattice core sandwich structures. Int. J. Solids Struct. 2020, 204–205, 172–186. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Zhang, D.Z.; Zhai, W. Geometry effect on mechanical properties and elastic isotropy optimization of bamboo-inspired lattice structures. Addit. Manuf. 2023, 64, 103438. [Google Scholar] [CrossRef]
- Zhong, H.Z.; Song, T.; Li Das, C.W.; Gu, J.F.; Qian, M. Understanding the superior mechanical properties of hollow-strut metal lattice materials. Scr. Mater. 2023, 115341. [Google Scholar] [CrossRef]
- Inan, M. Strength of Materials; Sami, S., Translator; ITU Vakfi Yayinlari: Istanbul, Turkey, 2019; ISBN 9786059581158. [Google Scholar]
- ANSYS. Mechanical Enterprise Academic Research; Release 2025 R1, Mechanical APDL; Ansys Inc.: Canonsburg, PA, USA, 2025. [Google Scholar]
- Gholibeygi, S.; Ergün, H.; Ayhan, B. Investigation of beam finite element models of octet-truss unit cell using homogenization. In Proceedings of the Fifteenth International Conference on Computational Structures Technology, CST 2024; Ivanyi, P., Kruis, J., Topping, B.H.V., Eds.; Faculty of Civil Engineering, Czech Technical University: Praha, Czech Republic, 4–6 September 2024. [Google Scholar] [CrossRef]



















| Finite Element Type | |||
|---|---|---|---|
| Surface Name | Solid UC Model (SOLID185) | Beam UC Models (BEAM188) | |
| tensile test | Top, Bottom | ||
| Front, Back | |||
| Left | |||
| Right | |||
| shear test | Left, Right | ||
| Front, Back | nodes are coupled | nodes are coupled | |
| Bottom | |||
| Top | |||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 |
| Solid UC Model | Deshpande et al. (2001) [4] | Unmodified Beam UC Model | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1000 | |||
| Model: | Solid Structure | Homogenized Bulk Structure | Beam Structure with Stiff Joints | Beam Structure with Springs |
|---|---|---|---|---|
| Finite element: | SOLID185 | SOLID185 | BEAM188 | BEAM188 |
| Material type: | Linear/isotropic | Linear/Anisotropic (cubic symmetric) | Linear/isotropic | Linear/isotropic |
| Material data: | Stiffness matrix data: |
| Solid Structure Models (Solid, Homogenized Bulk) | Beam Structure Models (with Stiff Joints, with Springs) | |
|---|---|---|
| Left | X-sym | X-sym |
| Bottom | Y-sym | Y-sym |
| Back | Z-sym | Z-sym |
| Top |
| Solid Structure Models (Solid, Homogenized Bulk) | Beam Structure Models (with Stiff Joints, with Springs) | |
|---|---|---|
| Left | ||
| Back | Z-sym | Z-sym |
| Right |
| Example 1: Compression (1/8 of 10 Cell Structure) | Example 2: Laterally Loaded (Half of 9 Cell Structure) | |||||
|---|---|---|---|---|---|---|
| UC Model | Time (Sec) | Elements | Nodes | Time (Sec) | Elements | Nodes |
| Solid | ||||||
| Homogenized bulk | ||||||
| Beam—stiff joint | ||||||
| Beam—spring | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholibeygi, S.; Ergün, H.; Ayhan, B. Beam Finite Element Model Modification Considering Shear Stiffness: Octet-Truss Unit Cell with Springs. Appl. Sci. 2025, 15, 8969. https://doi.org/10.3390/app15168969
Gholibeygi S, Ergün H, Ayhan B. Beam Finite Element Model Modification Considering Shear Stiffness: Octet-Truss Unit Cell with Springs. Applied Sciences. 2025; 15(16):8969. https://doi.org/10.3390/app15168969
Chicago/Turabian StyleGholibeygi, Soheil, Hale Ergün, and Bahar Ayhan. 2025. "Beam Finite Element Model Modification Considering Shear Stiffness: Octet-Truss Unit Cell with Springs" Applied Sciences 15, no. 16: 8969. https://doi.org/10.3390/app15168969
APA StyleGholibeygi, S., Ergün, H., & Ayhan, B. (2025). Beam Finite Element Model Modification Considering Shear Stiffness: Octet-Truss Unit Cell with Springs. Applied Sciences, 15(16), 8969. https://doi.org/10.3390/app15168969







