An Improved Soft Actor–Critic Framework for Cooperative Energy Management in the Building Cluster
Abstract
1. Introduction
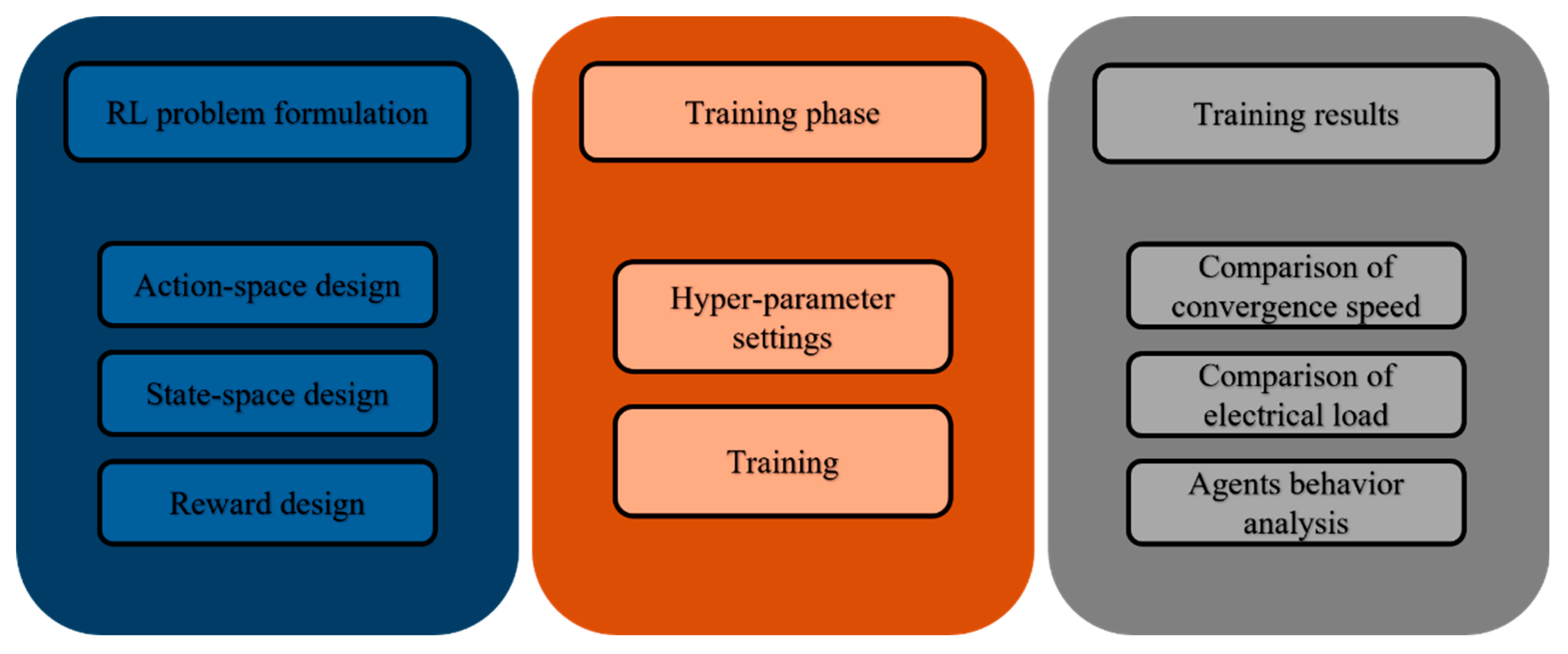
2. Materials and Methods
2.1. Framework
2.2. Model of ORAR-SAC Control Algorithm
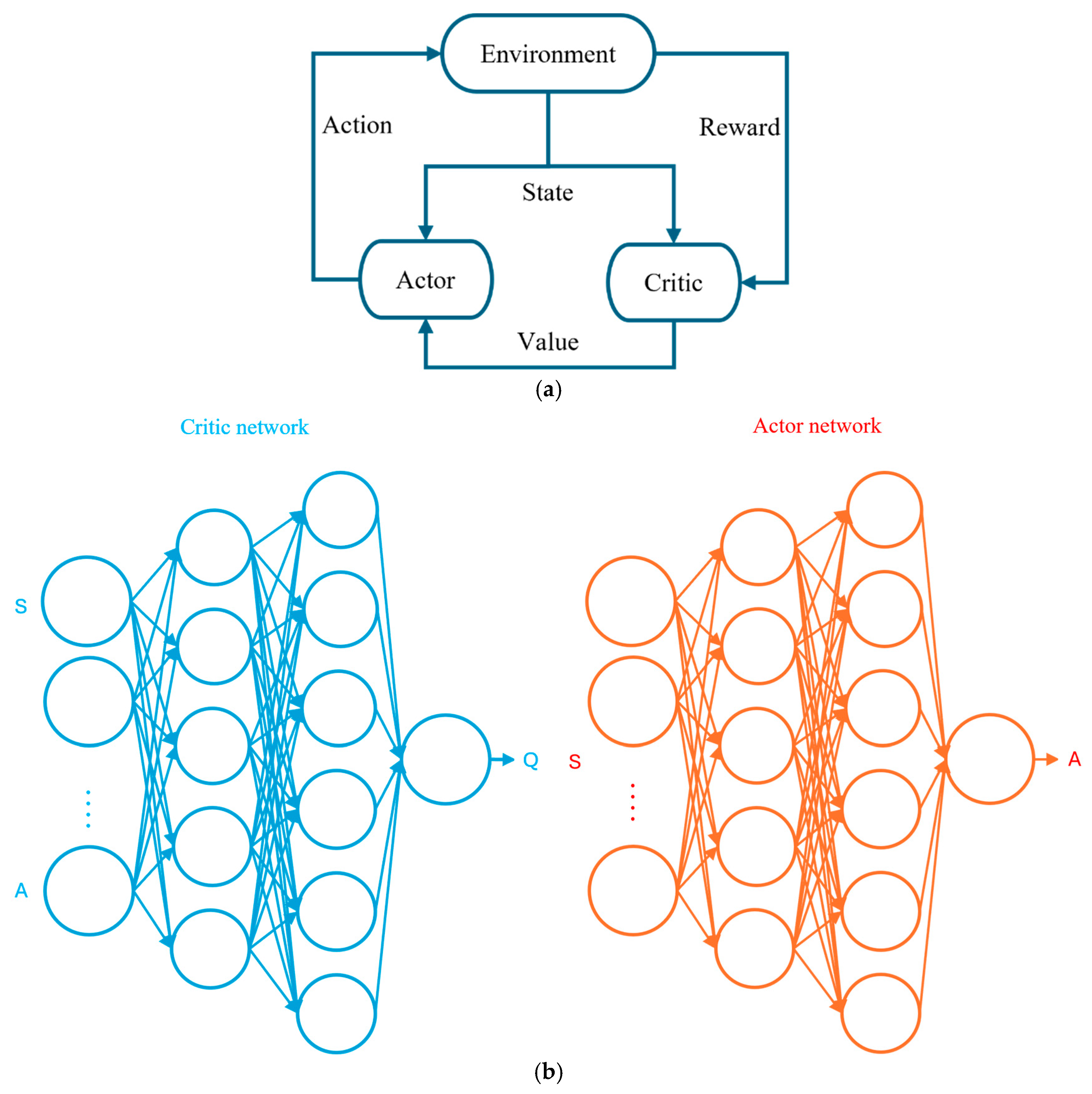
2.2.1. Reinforcement Learning
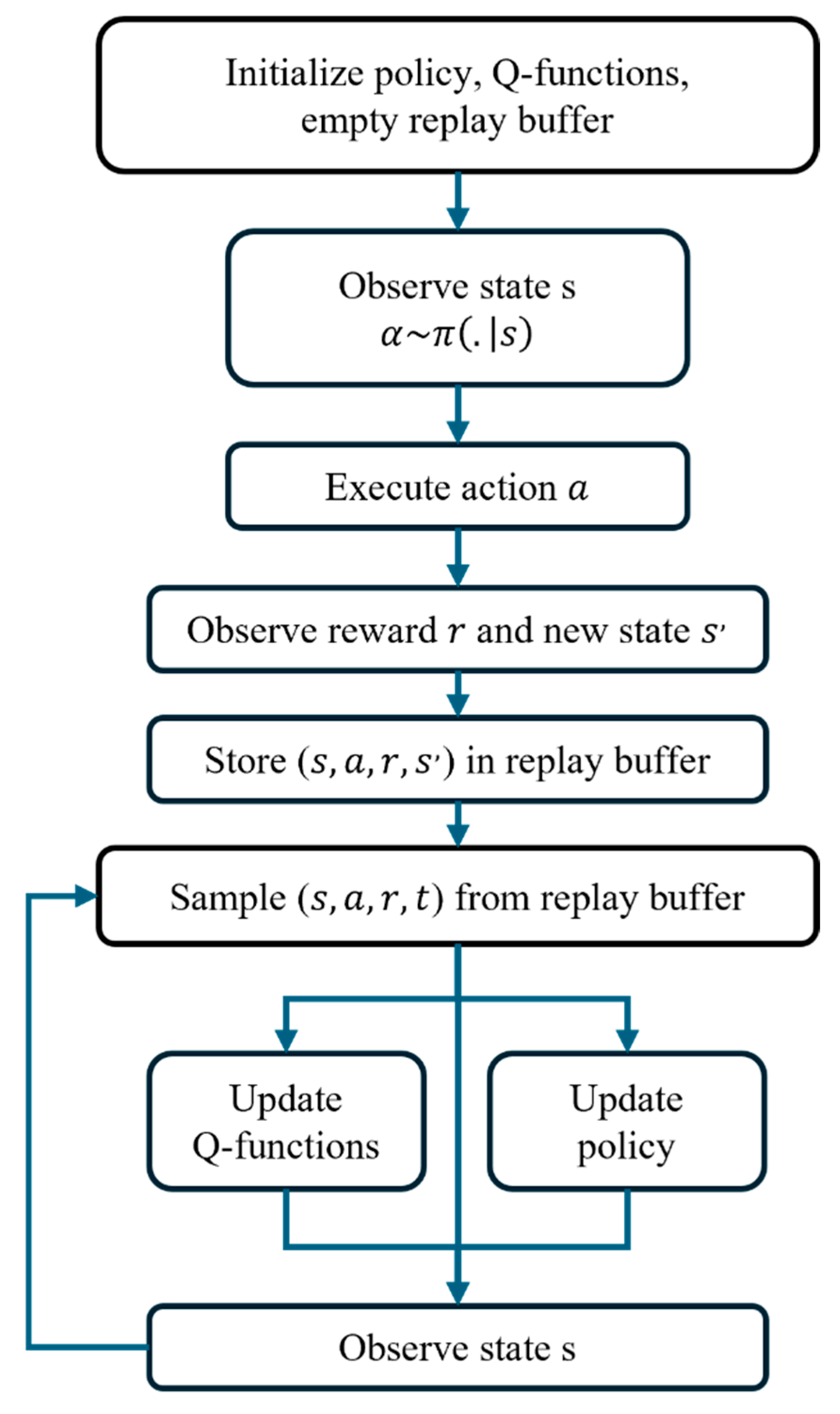
2.2.2. Soft Actor–Critic
2.2.3. Ordered Replay Buffer
2.2.4. Alpha Regularization Strategy
2.3. Design of DRL Framework and Controller
2.3.1. Baseline Rule-Based Control
2.3.2. Action Space Design
2.3.3. State Space Design
2.3.4. Reward Design
2.3.5. Hyperparameter Design
2.4. CityLearn Simulation Environment
3. Results
3.1. Study Site
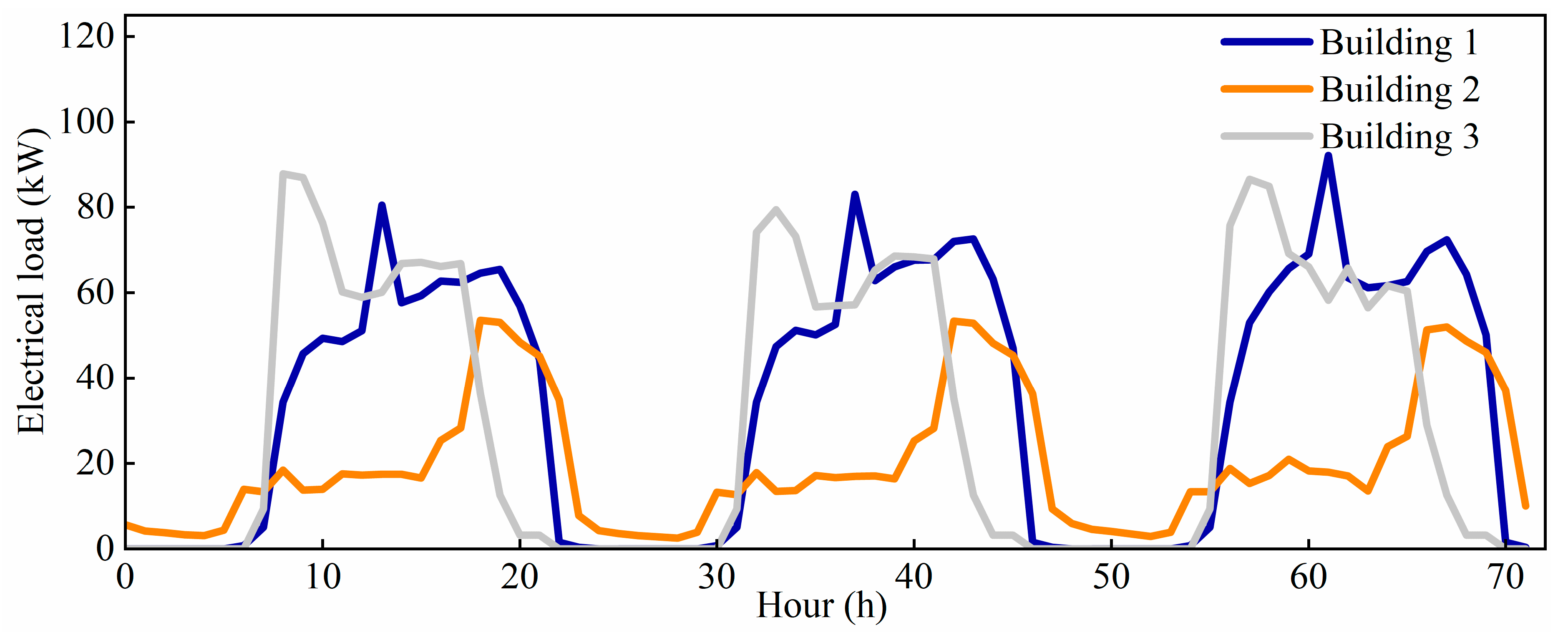
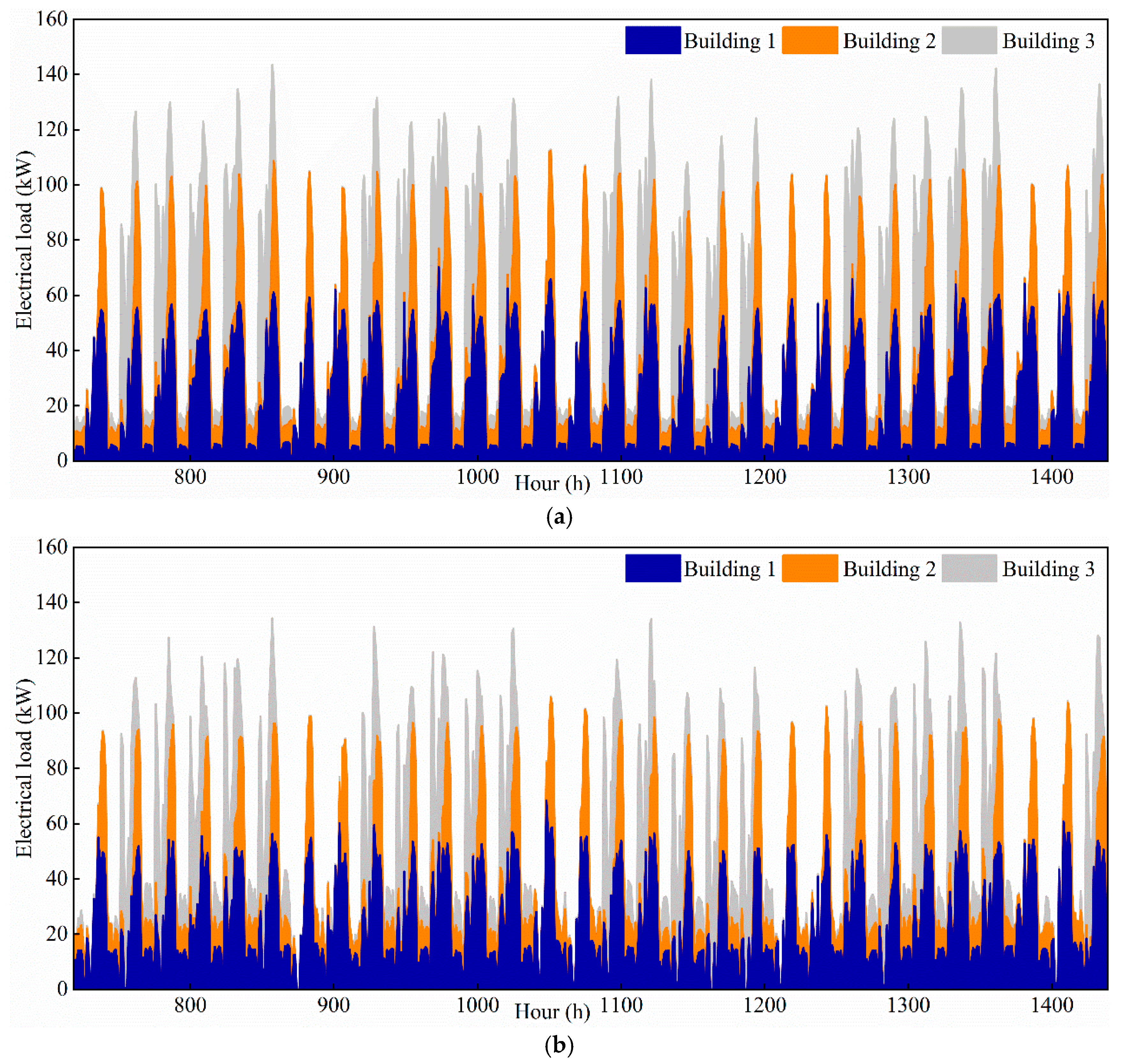
3.2. Characteristics of Building Load and Operating Modes
3.3. Analysis of Results
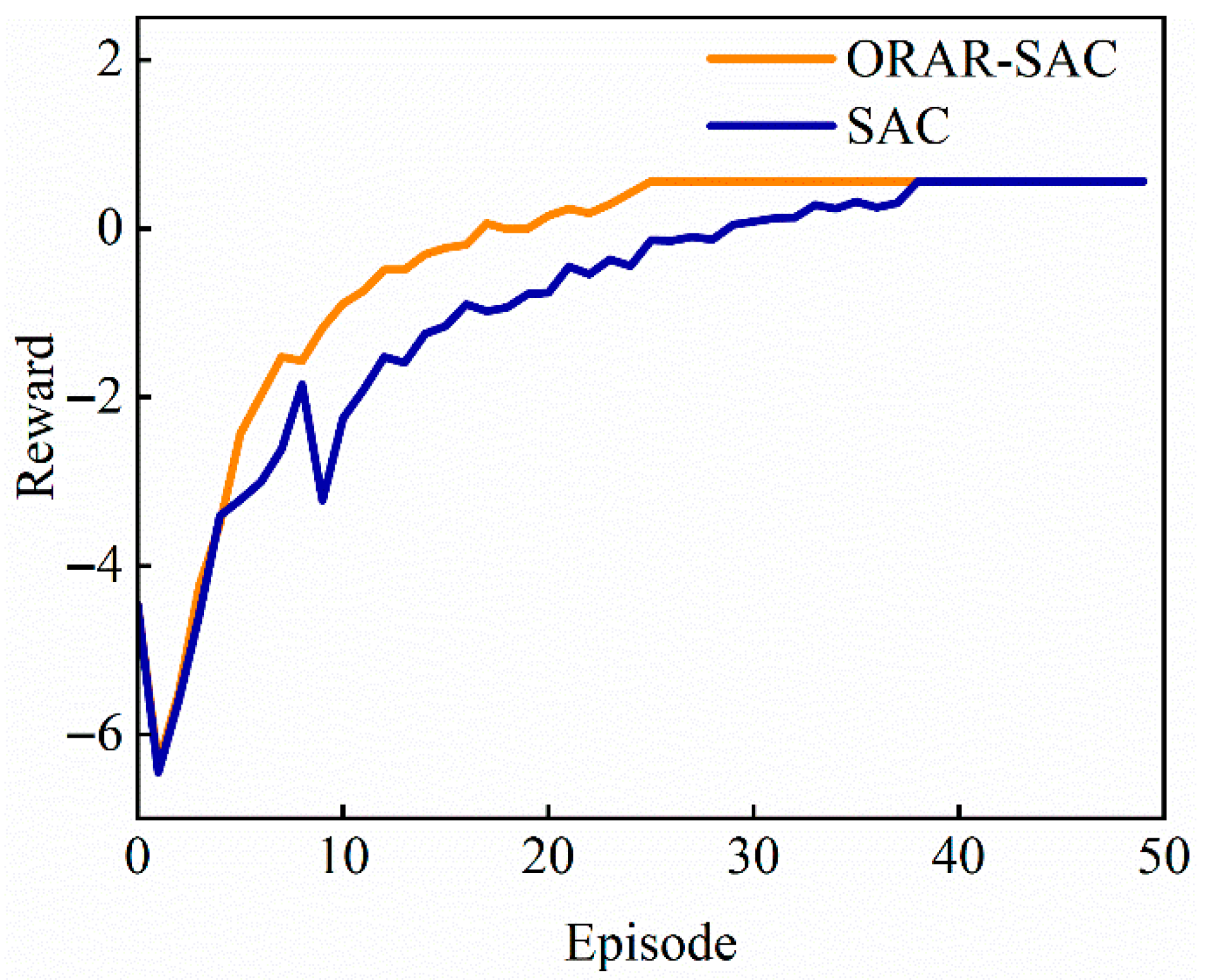
3.3.1. Comparative Analysis of Algorithm Convergence
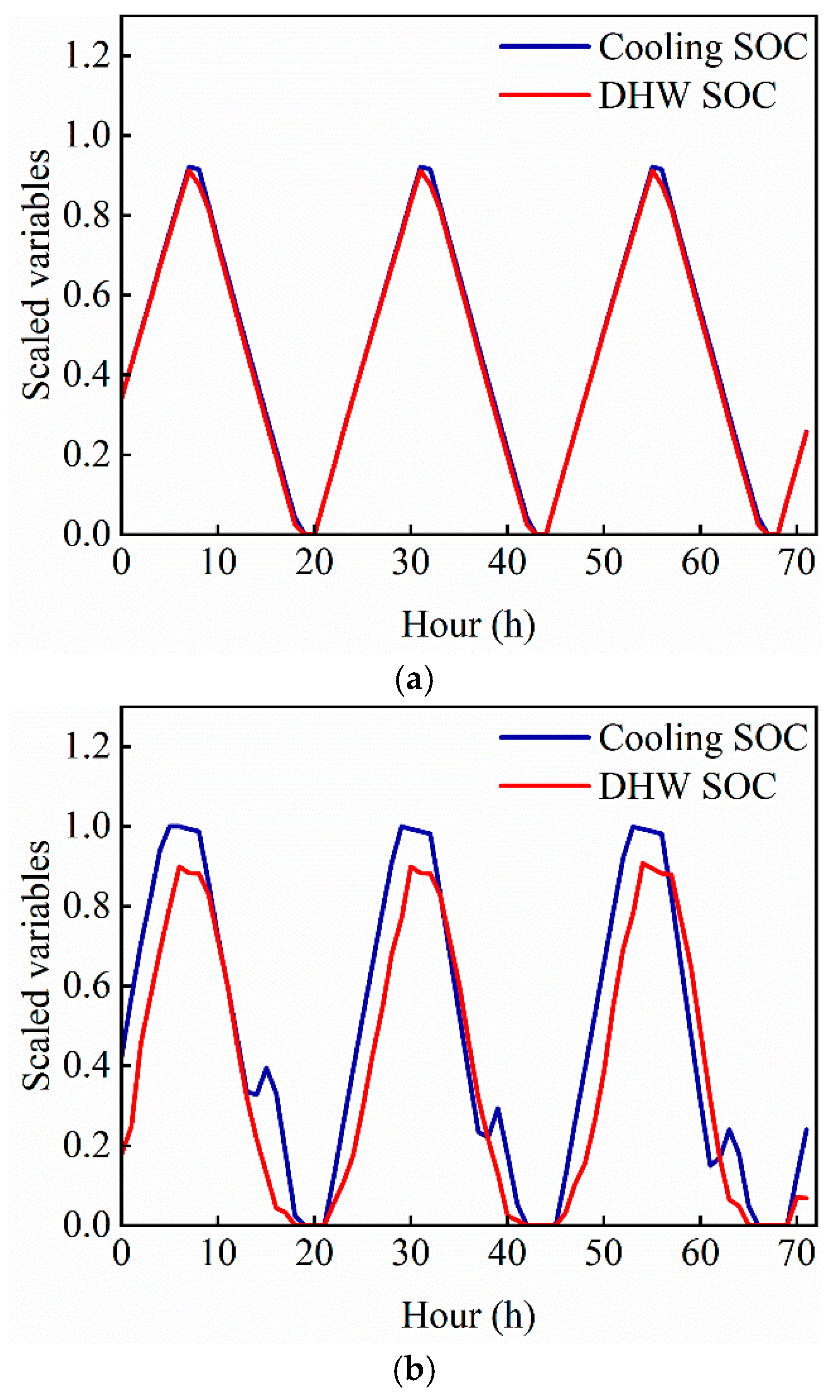
3.3.2. Comparison of Operating Behaviors of Energy Storage Systems
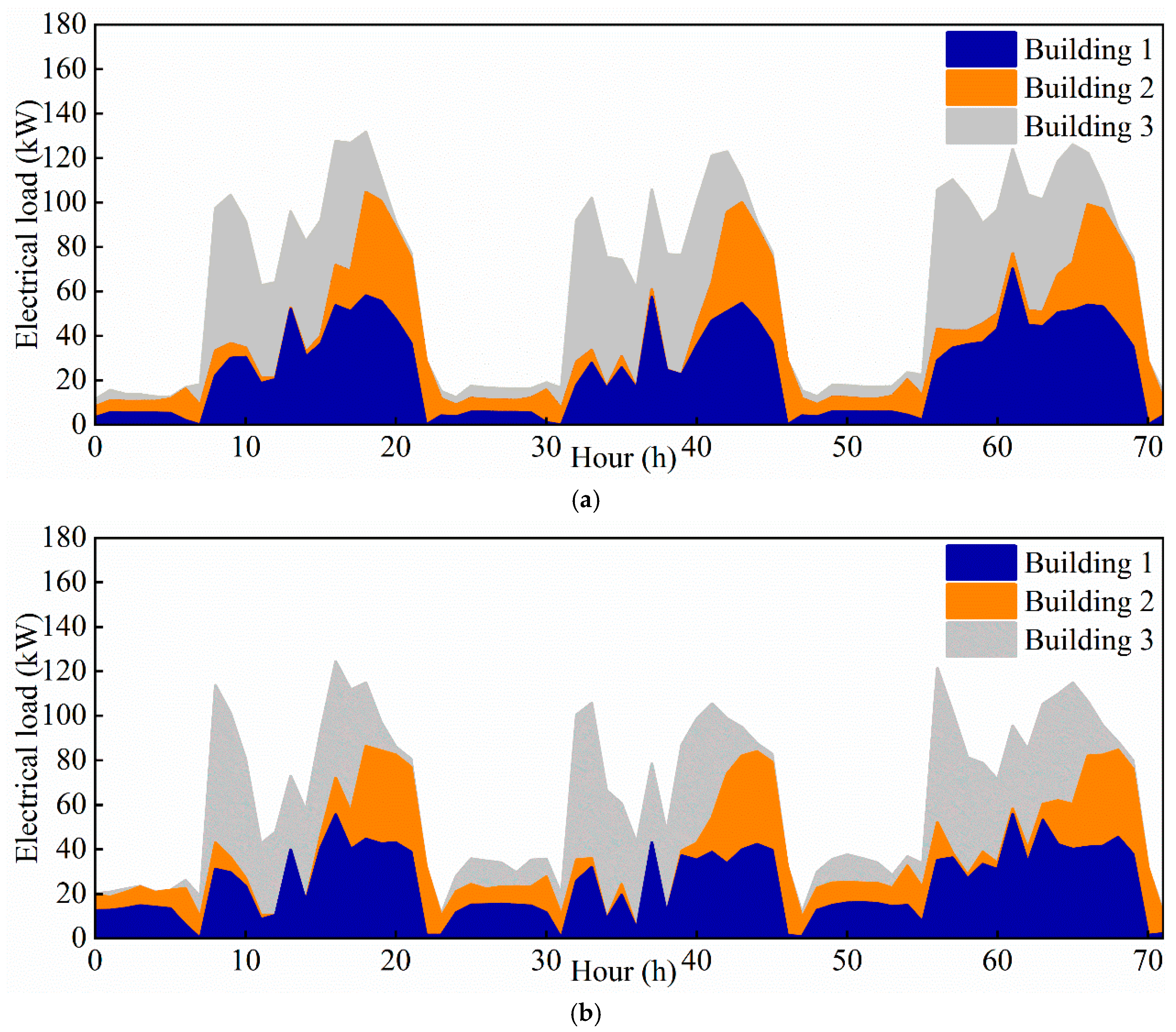
3.3.3. Comparative Analysis of Building Electrical Load
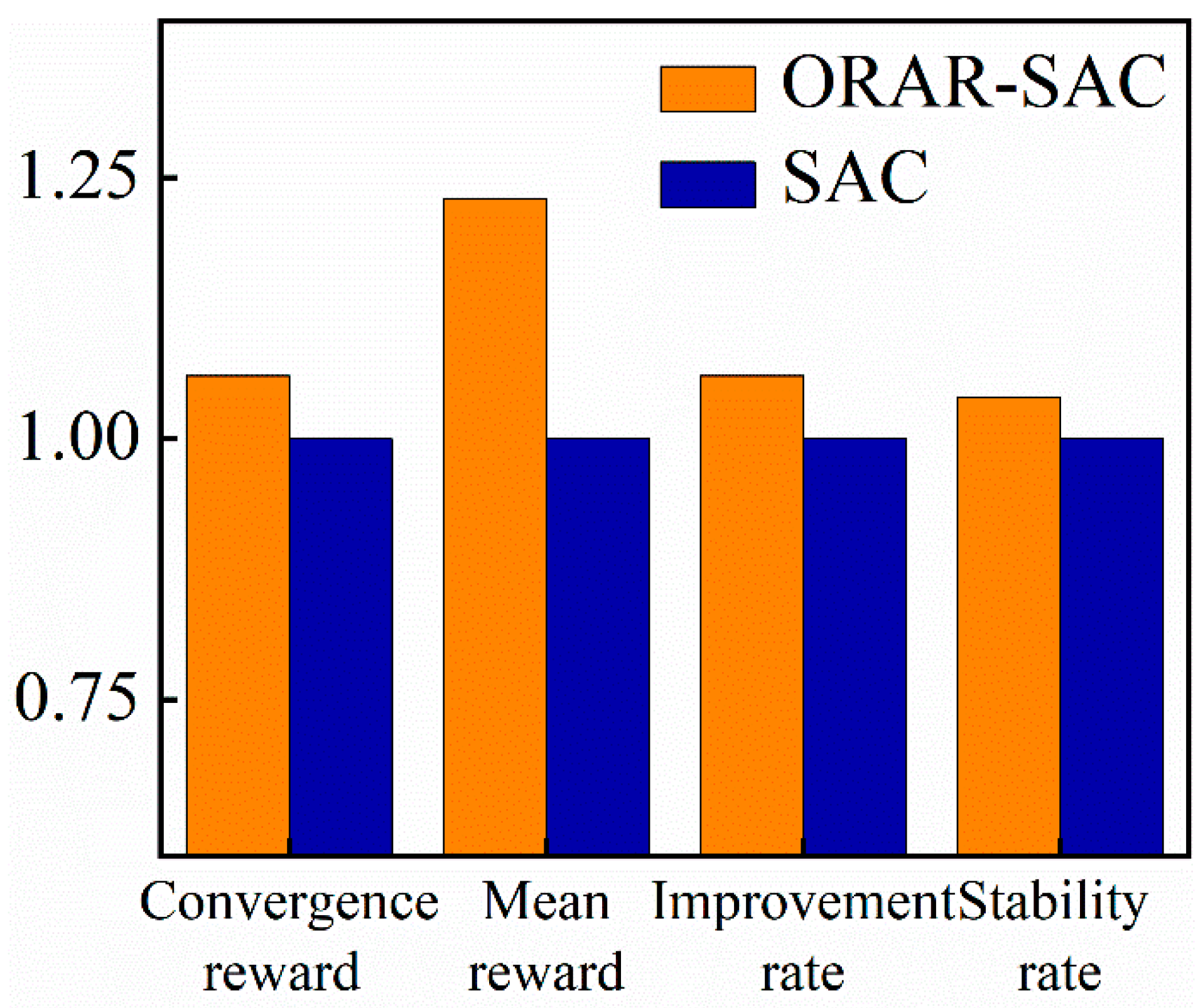
3.3.4. Quantitative Comparison of Key Performance Indicators (KPIs)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAC | Soft Actor–Critic |
| ORAR-SAC | Ordered replay and Alpha regularization Soft Actor–Critic |
| AC | Air conditioning |
| RBC | Rule-Based Control |
| MPC | Model Predictive Control |
| RL | Reinforcement learning |
| PV | Photovoltaic |
| MDP | Markov Decision Process |
| DRL | Deep Reinforcement Learning |
| DHW | Demand heating water |
| KPI | Key performance indicator |
References
- Gupta, V.; Deb, C. Envelope design for low-energy buildings in the tropics: A review. Renew. Sustain. Energy Rev. 2023, 186, 113650. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Wang, M.; Peng, J.; He, Y. Optimization study of photovoltaic direct-driven air conditioning system based on occupants’ behavior and thermal comfort. Renew. Energy 2025, 251, 123389. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, Y.; Yang, J.; Chen, Y.; Guo, B.H.W. Development of urban building energy models for Wellington city in New Zealand with detailed survey data on envelope thermal characteristics. Energy Build. 2024, 321, 114647. [Google Scholar] [CrossRef]
- Blad, C.; Bøgh, S.; Kallesøe, C. A Multi-Agent Reinforcement Learning Approach to Price and Comfort Optimization in HVAC-Systems. Energies 2021, 14, 7491. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, Z.; Lin, X.; Wang, C.; Sun, Z.; Chen, Y. Designing and Optimizing Heat Storage of a Solar-Assisted Ground Source Heat Pump System in China. Int. J. Photoenergy 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Battaglia, M.; Haberl, R.; Bamberger, E.; Haller, M. Increased self-consumption and grid flexibility of PV and heat pump systems with thermal and electrical storage. Energy Procedia 2017, 135, 358–366. [Google Scholar] [CrossRef]
- Sun, L.; Li, J.; Chen, L.; Xi, J.; Li, B. Energy storage capacity configuration of building integrated photovoltaic-phase change material system considering demand response. IET Energy Syst. Integr. 2021, 3, 263–272. [Google Scholar] [CrossRef]
- Nematirad, R.; Pahwa, A.; Natarajan, B.; Wu, H. Optimal sizing of photovoltaic-battery system for peak demand reduction using statistical models. Front. Energy Res. 2023, 11, 1297356. [Google Scholar] [CrossRef]
- Rashid, M.M.U.; Granelli, F.; Hossain, M.A.; Alam, M.S.; Al-Ismail, F.S.; Shah, R. Development of Cluster-Based Energy Management Scheme for Residential Usages in the Smart Grid Community. Electronics 2020, 9, 1462. [Google Scholar] [CrossRef]
- Gonzato, S.; Chimento, J.; O’Dwyer, E.; Bustos-Turu, G.; Acha, S.; Shah, N. Hierarchical price coordination of heat pumps in a building network controlled using model predictive control. Energy Build. 2019, 202, 109421. [Google Scholar] [CrossRef]
- Manrique Delgado, B.; Ruusu, R.; Hasan, A.; Kilpeläinen, S.; Cao, S.; Sirén, K. Energetic, Cost, and Comfort Performance of a Nearly-Zero Energy Building Including Rule-Based Control of Four Sources of Energy Flexibility. Buildings 2018, 8, 172. [Google Scholar] [CrossRef]
- Zou, B.; Peng, J.; Li, S.; Li, Y.; Yan, J.; Yang, H. Comparative study of the dynamic programming-based and rule-based operation strategies for grid-connected PV-battery systems of office buildings. Appl. Energy 2022, 305, 117875. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- El Makroum, R.; Khallaayoun, A.; Lghoul, R.; Mehta, K.; Zörner, W. Home Energy Management System Based on Genetic Algorithm for Load Scheduling: A Case Study Based on Real Life Consumption Data. Energies 2023, 16, 2698. [Google Scholar] [CrossRef]
- Malik, S.; Kim, D. Prediction-Learning Algorithm for Efficient Energy Consumption in Smart Buildings Based on Particle Regeneration and Velocity Boost in Particle Swarm Optimization Neural Networks. Energies 2018, 11, 1289. [Google Scholar] [CrossRef]
- Rajwar, K.; Deep, K.; Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges. Artif. Intell. Rev. 2023, 56, 13187–13257. [Google Scholar] [CrossRef]
- Manjavacas, A.; Campoy-Nieves, A.; Jiménez-Raboso, J.; Molina-Solana, M.; Gómez-Romero, J. An experimental evaluation of deep reinforcement learning algorithms for HVAC control. Artif. Intell. Rev. 2024, 57, 173. [Google Scholar] [CrossRef]
- Wei, T.; Wang, Y.; Zhu, Q. Deep Reinforcement Learning for Building HVAC Control. In Proceedings of the 54th Annual Design Automation Conference, Austin, TX, USA, 18–22 June 2017; ACM: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Brandi, S.; Piscitelli, M.S.; Martellacci, M.; Capozzoli, A. Deep reinforcement learning to optimise indoor temperature control and heating energy consumption in buildings. Energy Build. 2020, 224, 110225. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T. Reinforcement learning for building controls: The opportunities and challenges. Appl. Energy 2020, 269, 115036. [Google Scholar] [CrossRef]
- Ruelens, F.; Claessens, B.J.; Vandael, S.; De Schutter, B.; Babuska, R.; Belmans, R. Residential Demand Response of Thermostatically Controlled Loads Using Batch Reinforcement Learning. IEEE Trans. Smart Grid 2017, 8, 2149–2159. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H. Incentive-based demand response for smart grid with reinforcement learning and deep neural network. Appl. Energy 2019, 236, 937–949. [Google Scholar] [CrossRef]
- Kazmi, H.; Mehmood, F.; Lodeweyckx, S.; Driesen, J. Gigawatt-hour scale savings on a budget of zero: Deep reinforcement learning based optimal control of hot water systems. Energy 2018, 144, 159–168. [Google Scholar] [CrossRef]
- Fang, P.; Wang, M.; Li, J.; Zhao, Q.; Zheng, X.; Gao, H. A Distributed Intelligent Lighting Control System Based on Deep Reinforcement Learning. Appl. Sci. 2023, 13, 9057. [Google Scholar] [CrossRef]
- Avila, L.; De Paula, M.; Trimboli, M.; Carlucho, I. Deep reinforcement learning approach for MPPT control of partially shaded PV systems in Smart Grids. Appl. Soft Comput. 2020, 97, 106711. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y.-C.; Lin, C.E. A Deep Reinforcement Learning-Based MPPT Control for PV Systems under Partial Shading Condition. Sensors 2020, 20, 3039. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Ren, Z.; Wei, S.; Huang, L.; Li, F.; Liu, Y. Dynamic Optimal Power Flow Method Based on Reinforcement Learning for Offshore Wind Farms Considering Multiple Points of Common Coupling. J. Mod. Power Syst. Clean Energy 2024, 12, 1749–1759. [Google Scholar] [CrossRef]
- Darbandi, A.; Brockmann, G.; Ni, S.; Kriegel, M. Energy scheduling strategy for energy hubs using reinforcement learning approach. J. Build. Eng. 2024, 98, 111030. [Google Scholar] [CrossRef]
- Sun, H.; Hu, Y.; Luo, J.; Guo, Q.; Zhao, J. Enhancing HVAC Control Systems Using a Steady Soft Actor–Critic Deep Reinforcement Learning Approach. Buildings 2025, 15, 644. [Google Scholar] [CrossRef]
- Park, Y.; Jun, W.; Lee, S. A Comparative Study of Deep Reinforcement Learning Algorithms for Urban Autonomous Driving: Addressing the Geographic and Regulatory Challenges in CARLA. Appl. Sci. 2025, 15, 6838. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, F.; Yang, Z. Soft Actor-Critic-Based Energy Management Strategy for Hybrid Energy Storage System in Urban Rail Transit Dc Traction Power Supply System. Elsevier BV 2025. [Google Scholar] [CrossRef]
- Li, H.; Qian, X.; Song, W. Prioritized experience replay based on dynamics priority. Sci. Rep. 2024, 14, 6014. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, H.; Yang, J.; Lin, Y. Deep reinforcement learning for path planning of autonomous mobile robots in complicated environments. Complex Intell. Syst. 2025, 11, 277. [Google Scholar] [CrossRef]
- Kaspar, K.; Nweye, K.; Buscemi, G.; Capozzoli, A.; Nagy, Z.; Pinto, G.; Eicker, U.; Ouf, M.M. Effects of occupant thermostat preferences and override behavior on residential demand response in CityLearn. Energy Build. 2024, 324, 114830. [Google Scholar] [CrossRef]
- Yan, D.; Zhou, X.; An, J.; Kang, X.; Bu, F.; Chen, Y.; Pan, Y.; Gao, Y.; Zhang, Q.; Zhou, H.; et al. DeST 3.0: A new-generation building performance simulation platform. Build. Simul. 2022, 15, 1849–1868. Available online: https://link.springer.com/article/10.1007/s12273-022-0909-9 (accessed on 2 July 2025). [CrossRef]
- Yatawatta, S. Reinforcement learning. Astron. Comput. 2024, 48, 100833. [Google Scholar] [CrossRef]
- Han, M.; May, R.; Zhang, X.; Wang, X.; Pan, S.; Yan, D.; Jin, Y.; Xu, L. A review of reinforcement learning methodologies for controlling occupant comfort in buildings. Sustain. Cities Soc. 2019, 51, 101748. [Google Scholar] [CrossRef]





| Variable Group | Variable | Unit |
|---|---|---|
| Weather | Temperature | °C |
| Temperature forecast (6 h) | °C | |
| Direct solar radiation | W/m2 | |
| Direct solar radiation forecast (6 h) | W/m2 | |
| District | Total load | kW |
| Electricity price | CNY/kWh | |
| Hour of day | H | |
| Building | Non-shiftable load | kW |
| Solar generation | W/m2 | |
| Cooling storage SOC | [—] | |
| DHW SOC | [—] |
| Weight Value | Average Reward | Relative Performance |
|---|---|---|
| 0.05 | −2702.58 | 0.00% |
| 0.08 | −2698.08 | 0.00% |
| 0.1 | −2695.08 | 0.00% |
| 0.12 | −2698.08 | −0.11% |
| 0.15 | −2702.58 | −0.28% |
| 0.2 | −2710.08 | −0.55% |
| 0.3 | −2725.08 | −1.10% |
| Variable | Value | |
|---|---|---|
| 1 | DNN architecture | 2 Layers |
| 2 | Neurons per hidden layer | 256 |
| 3 | DNN optimizer | Adam |
| 4 | Batch size | 512 |
| 5 | Learning rate l | 0.001 |
| 6 | Decay rate | 0.005 |
| 7 | Temperature α | 1.2 |
| 8 | Target model update | 2 |
| 9 | Episode length | 92 * 24 Control steps |
| 10 | Training episodes | 50 |
| Building Parameters | |||
|---|---|---|---|
| Location | Beijing | ||
| Building type | Mall | Hotel | office |
| Number of floors | 2 | 3 | 3 |
| Building area (m2) | 4327 | 2160 | 4385 |
| External wall heat transfer coefficient/[W·(m2·K)−1] | 0.25 | 0.18 | 0.15 |
| External window heat transfer coefficient/[W·(m2·K)−1] | 1.2 | 1.2 | 1.2 |
| Roof heat transfer coefficient /[W·(m2·K)−1] | 0.3 | 0.3 | 0.3 |
| Building Type | Air Conditioning Area (m2) | Cold Storage Capacity (kWh) | Electric Heater Capacity (kW) | Hot Storage Capacity (kWh) | PV Capacity (kW) | |
|---|---|---|---|---|---|---|
| Building1 | Mall | 3727 | 195 | 15 | 45 | 47.75 |
| Building2 | Hotel | 1719 | 70 | 10 | 30 | 19.5 |
| Building3 | Office | 3127 | 180 | 15 | 45 | 0 |
| Energy Consumption/kWh | Electricity Cost/CNY | Carbon Emissions/ kg CO2 | Peak Load/kW | Average Daily Peak Load/kW | |
|---|---|---|---|---|---|
| ORAR-SAC | 113,103 | 106,833 | 63,111 | 148 | 105 |
| RBC | 117,155 | 120,298 | 65,372 | 159 | 117 |
| Energy Consumption/kWh | p-Value | Electricity Cost/CNY | p-Value | Peak Load/kW | p-Value | |
|---|---|---|---|---|---|---|
| ORAR-SAC | 113,133 326 | 106,982 | 146 4 | |||
| RBC | 117,203 | 120,348 | 160 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Gao, Y.; Sun, Z.; Mao, Q. An Improved Soft Actor–Critic Framework for Cooperative Energy Management in the Building Cluster. Appl. Sci. 2025, 15, 8966. https://doi.org/10.3390/app15168966
Lu W, Gao Y, Sun Z, Mao Q. An Improved Soft Actor–Critic Framework for Cooperative Energy Management in the Building Cluster. Applied Sciences. 2025; 15(16):8966. https://doi.org/10.3390/app15168966
Chicago/Turabian StyleLu, Wencheng, Yan Gao, Zhi Sun, and Qianning Mao. 2025. "An Improved Soft Actor–Critic Framework for Cooperative Energy Management in the Building Cluster" Applied Sciences 15, no. 16: 8966. https://doi.org/10.3390/app15168966
APA StyleLu, W., Gao, Y., Sun, Z., & Mao, Q. (2025). An Improved Soft Actor–Critic Framework for Cooperative Energy Management in the Building Cluster. Applied Sciences, 15(16), 8966. https://doi.org/10.3390/app15168966






