Research on Direct Spread Spectrum Signal Monitoring Technology Based on Combined Partitioned Matched Filter–Fast Fourier Transform and Partitioned Matched Filter–Fractional Fourier Transform Algorithms

Abstract

To address the challenge of monitoring BeiDou RDSS signals under low signal-to-noise ratio (SNR) and high-dynamic conditions, this paper introduces a hierarchical joint processing algorithm combining PMF-FFT and PMF-FRFT. The method counters the energy dispersion issue in conventional FFT-based techniques by employing a two-stage “coarse–fine” strategy. A computationally efficient PMF-FFT performs a rapid coarse search, followed by an intelligent trigger, based on a correlation peak morphology, that initiates a localized PMF-FRFT fine search for high-dynamic signals, to precisely estimate the code phase, center frequency, and Doppler rate. Experimental results demonstrated that the algorithm’s acquisition performance was comparable to a global PMF-FRFT search and superior to the conventional PMF-FFT, achieving a 4.91% correlation peak improvement at −10 dB SNR and a gain of nearly 30% in extreme conditions (−20 dB SNR, 1000 Hz offset). Crucially, its average processing time (∼0.088 s) was on the same order of magnitude as PMF-FFT (∼0.0568 s) and significantly faster than global PMF-FRFT (∼0.3317 s). The proposed algorithm effectively balances detection performance with computational efficiency, offering a viable solution for the real-time monitoring of high-dynamic DSSS signals.

1. Introduction

The BeiDou Navigation Satellite System (BDS), a critical component of the Global Navigation Satellite System (GNSS), not only provides global Positioning, Navigation, and Timing (PNT) services, but also features a unique Radio Determination Satellite Service (RDSS) [1]. This service enables short message communication, playing an indispensable role in sectors such as emergency rescue, fishery management, and transportation. The Beidou RDSS signal is essentially a direct spread spectrum signal (DSSS signal). The RDSS system facilitates location requests and short message transmissions via uplink signals sent from user terminals to satellites. The L-band uplink, in particular, serves as the crucial channel for information exchange between the user and the system. Effective monitoring of these RDSS uplink signals is a core technical imperative for ensuring system quality of service, managing spectrum resources, detecting and locating potential interference sources, and verifying overall system integrity. However, RDSS uplink signals are inherently weak and, upon arrival at a monitoring receiver, are often submerged far below the background noise floor. This makes the detection and acquisition of these signals a technical challenge of paramount importance [1,2].

Signal acquisition is the first and most computationally intensive and time-consuming stage in the receiver processing chain. Its objective is to search for and lock onto the presence of a signal within a two-dimensional uncertainty space defined by code phase and Doppler frequency shift. In low signal-to-noise ratio (SNR) environments, extensive free-space path loss severely attenuates the RDSS uplink signal, resulting in an extremely low carrier-to-noise-density ratio ($C/N_0$), where the signal energy is completely overwhelmed by noise [3,4].

Conventional acquisition algorithms based on the Fast Fourier Transform (FFT) operate on the fundamental assumption that the carrier frequency remains constant throughout the coherent integration interval [5]. The presence of a Doppler rate violates this assumption, causing the signal’s energy to “smear” across multiple frequency bins in the FFT domain. This prevents the formation of a sharp correlation peak, thereby degrading the peak’s magnitude, drastically reducing the probability of detection, and potentially leading to complete acquisition failure. To address the challenge of rapid DSSS signal acquisition, researchers have proposed various algorithms. The traditional serial search method, which exhaustively tests every possible code phase and frequency combination, is simple in principle but prohibitively time-consuming for real-time applications. The Parallel Code-Phase Search (PCS) technique, which leverages a convolution theorem to transform time-domain correlation into frequency-domain multiplication, dramatically enhances the search efficiency in the code phase dimension and has become the mainstream approach in modern receivers. The Partitioned Matched Filter-FFT (PMF-FFT) algorithm, an evolution of this technique, partitions a long code into segments, effectively reducing the demands on FFT size and memory. This strikes a favorable balance between computational efficiency and resource consumption, with the principle behind it illustrated in Figure 1.

Nevertheless, all FFT-based algorithms share a common bottleneck. Their performance deteriorates significantly in low-SNR, high-dynamic scenarios due to the energy smearing problem caused by the Doppler rate. Furthermore, data bit transitions within a coherent integration period violate the periodicity assumption required for FFT-based circular correlation, leading to a split or collapsed correlation peak and subsequent acquisition failure. To contend with non-stationary signals, the Fractional Fourier Transform (FRFT), a generalization of the Fourier transform, has garnered considerable attention in the signal processing community. The FRFT can be interpreted as a rotation of the signal in the time–frequency plane, providing a “fractional domain” that interpolates between the time and frequency domains. One of the most important properties of the FRFT is its exceptional energy-focusing capability for Linear Frequency Modulated (LFM) signals [6]. By selecting an optimal transform order, an LFM signal’s energy can be compressed into a sharp impulse in the fractional domain, a property that has led to its successful application in radar signal processing and communication parameter estimation [7,8]. However, the FRFT introduces a substantial increase in computational complexity, placing significant demands on hardware resources for real-time signal processing.

To address the challenge of monitoring RDSS uplink signals in low-SNR environments, this paper introduces a novel hierarchical joint PMF-FFT and PMF-FRFT algorithm. The core idea of this algorithm is to solve the problem in a phased, hierarchical manner [9,10].

Coarse Acquisition Stage: We employ the computationally efficient PMF-FFT algorithm to perform a rapid, broad search across the wide two-dimensional code phase-frequency space. This allows for a swift reduction of the uncertainty range at a low computational cost. Fine Acquisition Stage: We implement an intelligent trigger mechanism that analyzes the morphological features of the correlation surface from the coarse acquisition stage, to determine if the target is in a high-dynamic state. If high dynamics are detected, the PMF-FRFT algorithm is activated to perform a precise three-dimensional search (code phase, center frequency, and frequency rate) within a small region localized around the coarse acquisition result.

This hierarchical architecture strategically combines the speed of PMF-FFT with the precision of PMF-FRFT, aiming to achieve robust and rapid acquisition of high-dynamic, low-SNR BPSK-DSSS signals at a manageable computational cost. The framework proposed herein not only provides an effective monitoring tool for the BeiDou RDSS system but also presents a principle that can be generalized to other DSSS communication and navigation systems operating in high-dynamic environments.

2. Signal Model and Characteristic Analysis

2.1. BeiDou RDSS Uplink Signal Model

According to the public Interface Control Document (ICD), the L-band uplink signal of the BeiDou RDSS system is a Direct-Sequence Spread Spectrum (DSSS) signal modulated with Binary Phase-Shift Keying (BPSK) [1,2]. Based on the principles of DSSS communication systems, the mathematical expression for the received BPSK signal at the RF front-end can be modeled in continuous time as

$$\begin{array}{c}\hfill s\left(t\right)=\sqrt{2P}·d\left(t\right)·c\left(t\right)·cos(2\pi f_{c}t+{\varphi }_0)\end{array}$$

(1)

where P is the signal power; $d\left(t\right)$ is the low-rate navigation or communication data bit stream taking values from $\{+1,-1\}$; $c\left(t\right)$ is the high-rate pseudo-random noise (PN) spreading code sequence, also taking values from $\{+1,-1\}$; $f_c$ is the carrier center frequency; and ${\varphi }_0$ is the initial carrier phase.

For analysis and processing, this is typically converted to its equivalent complex baseband form:

$$\begin{array}{c}\hfill s_b\left(t\right)=A·d\left(t\right)·c\left(t\right)·e^{j{\varphi }_0}\end{array}$$

(2)

where $A=\sqrt{P}$ is the signal amplitude.

2.2. Signal Characteristics in a High-Dynamic Environment

When an RDSS user terminal is in a high-dynamic state, the signal received at the monitoring station is significantly affected by the Doppler effect. The complex baseband model of the received signal, $r\left(t\right)$, then becomes [11]

$$\begin{array}{c}\hfill r\left(t\right)=A·d(t-\tau )·c(t-\tau )·e^{j(2\pi {\int }_0^t{f}_d\left(\xi \right)d\xi +\varphi \left(t\right))}+n\left(t\right)\end{array}$$

(3)

where $\tau$ is the unknown code phase delay, $f_d\left(t\right)$ is the time-varying instantaneous Doppler frequency shift, $\varphi \left(t\right)$ includes the initial phase and phase noise, and $n\left(t\right)$ is Additive White Gaussian Noise (AWGN).

For a platform moving with constant acceleration, the relative radial velocity with respect to the monitoring station changes linearly, which in turn causes the Doppler frequency shift to vary linearly with time. Over a short coherent integration interval, we can approximate $f_d\left(t\right)$ with a first-order linear model:

$$\begin{array}{c}\hfill f_d\left(t\right)=f_0+f_{r}t\end{array}$$

(4)

where $f_0$ is the constant Doppler shift caused by the initial radial velocity, and $f_r$ is the Doppler rate caused by the radial acceleration.

At the receiver, the signal is first mixed with a local carrier $e^{-j2\pi f_{\mathrm{local}}t}$ to remove the bulk of the carrier frequency. The resulting signal is

$$\begin{array}{cc}\hfill r_{\mathrm{if}}\left(t\right)& =A·d(t-\tau )·c(t-\tau )·e^{j(2\pi {\int }_0^t(f_0+f_r\xi -f_{\mathrm{local}})d\xi +\varphi \left(t\right))}+n^{\prime }\left(t\right)\hfill \\ \hfill & =A·d(t-\tau )·c(t-\tau )·e^{j(2\pi (f_0-f_{\mathrm{local}})t+\pi f_r{t}^2+\varphi \left(t\right))}+n^{\prime }\left(t\right)\hfill \end{array}$$

(5)

Next, this signal is correlated with a locally generated PN code replica $c(t-\tau )$ that is aligned in code phase (i.e., $\widehat{\tau }=\tau$). Assuming no data bit transitions (i.e., $d\left(t\right)$ is constant within one coherent integration period), the signal component $y\left(t\right)$ at the correlator output is where $A^{\prime }$ is the post-correlation signal amplitude and $\Delta f=f_0-f_{\mathrm{local}}$ is the residual center frequency offset.

This equation clearly reveals that due to the Doppler rate $f_r$, a quadratic phase term, $\pi f_r{t}^2$, appears in the correlator output. This is the defining characteristic of a Linear Frequency Modulated (LFM) signal, also known as a “chirp” signal. This finding is critical, as it reveals a fundamental physical transformation: the high dynamics of the channel convert the originally stationary BPSK-modulated signal into a non-stationary LFM signal after despreading. Therefore, any algorithm chosen to solve the high-dynamic acquisition problem must be capable of efficiently detecting and estimating the parameters of LFM signals. This provides a solid theoretical foundation for introducing the Fractional Fourier Transform (FRFT), which is arguably the most powerful mathematical tool for processing LFM signals [6,7].

3. Fundamental Algorithms for Rapid Signal Acquisition

3.1. Partitioned PMF-FFT Rapid Signal Acquisition Algorithm

3.1.1. Principle and Derivation of FFT-Based Parallel Code-Phase Search (PCS)

FFT-based Parallel Code-Phase Search (PCS) is the standard technique for modern DSSS signal acquisition. Its core principle is the use of the convolution theorem to equate time-domain circular correlation with frequency-domain multiplication, thereby enabling parallel processing of the code phase dimension and dramatically improving search efficiency [12].

For a discrete received signal $r\left[n\right]$ and a local PN code replica $c\left[n\right]$, both of length N, their discrete circular correlation $R_{\mathrm{circ}}\left[m\right]$ is defined as

$$\begin{array}{c}\hfill R_{circ}\left[m\right]=\sum _{k=0}^{N-1}r\left[k\right]·c^{\ast }\left[(k-m)(modN)\right]\end{array}$$

(6)

where m represents the code phase offset, $m=0,1,\dots ,N-1$, and $\ast$ denotes the complex conjugate. Direct computation would require $O\left(N^2\right)$ multiplications and additions, which is computationally prohibitive for real-time systems.

According to the circular convolution theorem, the circular correlation of two sequences in the time domain is equivalent to the product of their respective Discrete Fourier Transforms (DFTs) in the frequency domain. Specifically,

$$\begin{array}{c}\hfill \mathrm{DFT}\left\{R_{\mathrm{circ}}\left[m\right]\right\}=\mathrm{DFT}\left\{r\left[n\right]\right\}·\mathrm{DFT}\left\{c^{\ast }\left[(-n)(modN)\right]\right\}\end{array}$$

(7)

Using the properties of the DFT, we know that $\mathrm{DFT}\left\{c^{\ast }\left[(-n)(modN)\right]\right\}={\left(\mathrm{DFT}\left\{c\left[n\right]\right\}\right)}^{\ast }$. Let $R\left(k\right)=\mathrm{DFT}\left\{r\right[n\left]\right\}$ and $C\left(k\right)=\mathrm{DFT}\left\{c\right[n\left]\right\}$. The equation can then be written as

$$\begin{array}{c}\hfill \mathrm{DFT}\left\{R_{\mathrm{circ}}\left[m\right]\right\}=R\left(k\right)·C^{\ast }\left(k\right)\end{array}$$

(8)

To return from the frequency domain to the time-domain correlation values, we apply the Inverse Discrete Fourier Transform (IDFT):

$$\begin{array}{c}\hfill R_{\mathrm{circ}}\left[m\right]=\mathrm{IDFT}\{R\left(k\right)·C^{\ast }\left(k\right)\}\end{array}$$

(9)

By using the Fast Fourier Transform (FFT) and its inverse (IFFT) algorithms, this operation can be computed with high efficiency. The entire process can be summarized as

$$\begin{array}{c}\hfill R_{\mathrm{circ}}\left[m\right]=\mathrm{IFFT}\{\mathrm{FFT}\left\{r\left[n\right]\right\}·{\left(\mathrm{FFT}\left\{c\left[n\right]\right\}\right)}^{\ast }\}\end{array}$$

(10)

This equation demonstrates that all N correlation values for every code phase offset can be computed simultaneously with one FFT, one frequency-domain complex multiplication, and one IFFT. This drastically reduces the computational complexity from $O\left(N^2\right)$ to $O\left(N{log}_{2}N\right)$.

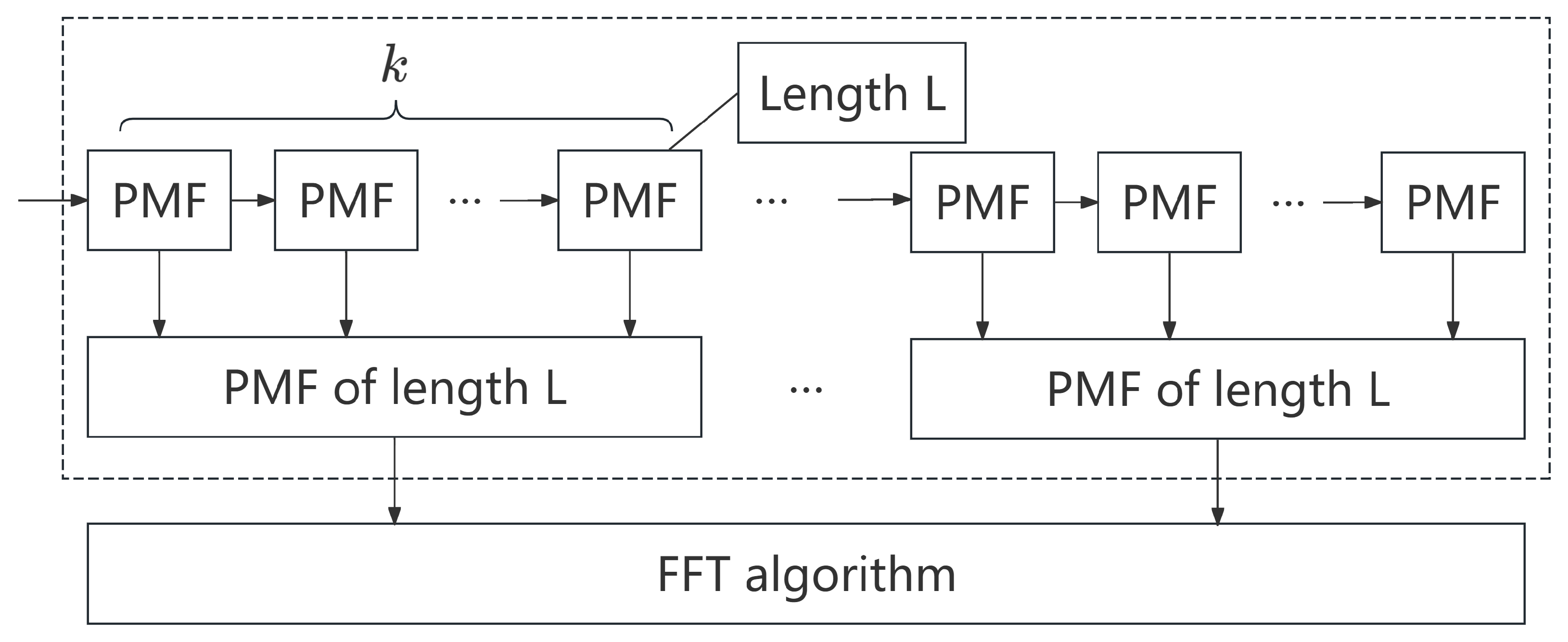
3.1.2. Introduction of Partitioned Matched Filtering (PMF)

When the spreading code is very long (e.g., well over 1 ms), performing a single FFT on the entire sequence can be prohibitive in terms of computation and memory. The Partitioned Matched Filter (PMF) technique addresses this by dividing a full coherent integration period (corresponding to one or more code periods) into several shorter data segments. The specific principle is shown in Figure 2.

Assume the total integration data length is $M_{\mathrm{total}}$, which is divided into K segments, each of length X ($M_{\mathrm{total}}=K·X$). FFT-based correlation is performed on each data segment individually, and the results from each segment are then coherently or non-coherently accumulated. The PMF-FFT algorithm proceeds as follows:

1. The received signal $r\left[n\right]$ is divided into K data segments $r_i\left[n\right]$ of length X, for $i=0,1,\dots ,K-1$.

2. For each data segment $r_i\left[n\right]$, an FFT-based circular correlation is performed with the corresponding local code segment $c_{\mathrm{seg}}\left[n\right]$:

$$\begin{array}{c}\hfill Y_i\left[m\right]=\mathrm{IFFT}\left\{\mathrm{FFT}\left\{r_i\left[n\right]\right\}·{\left(\mathrm{FFT}\left\{c_{\mathrm{seg}}\left[n\right]\right\}\right)}^{\ast }\right\}\end{array}$$

(11)

3. The K partial correlation results are accumulated. Non-coherent accumulation (summing the squared magnitudes) is more commonly used, as it is robust to data bit transitions:

$$\begin{array}{c}\hfill R_{\mathrm{final}}\left[m\right]=\sum _{i=0}^{K-1}{\left|Y_i\left[m\right]\right|}^2\end{array}$$

(12)

The PMF-FFT algorithm significantly reduces the required FFT size and computational complexity, while retaining the efficiency of parallel search, making it a practical solution for rapid acquisition [13,14].

3.1.3. Limitation Analysis

Although PMF-FFT performs excellently in static or low-dynamic scenarios, its performance bottleneck in high-dynamic environments is pronounced.

Sensitivity to Doppler Rate: Each frequency bin of an FFT corresponds to an ideal single-frequency sinusoid. When the received signal exhibits LFM characteristics due to a Doppler rate $f_r$, its energy traces a slanted line in the time–frequency plane, not a horizontal one. This causes the signal’s energy to be smeared across multiple adjacent frequency bins in the FFT spectrum, preventing the formation of a sharp, high-SNR peak. This “energy smearing” effect severely attenuates the correlation peak height and degrades the probability of detection [15].

Data Bit Transitions: The RDSS uplink signal carries data, meaning the data bits (typically +1 or −1) will transition. If a data bit transition occurs within a coherent integration period $T_{\mathrm{coh}}$ (e.g., a change from +1 to −1), the signal’s phase flips by ${180}^{\circ }$. This abrupt change destroys the signal’s periodicity, which is a fundamental prerequisite for FFT-based circular correlation. The consequence is a splitting, distortion, or even complete cancellation of the peak in the Cross-Ambiguity Function (CAF), leading to acquisition failure.

3.2. PMF-FRFT Algorithm for High-Dynamic Environments

The Fractional Fourier Transform (FRFT) offers a new avenue for solving the aforementioned problems. The FRFT is a generalization of the conventional Fourier transform and can be intuitively understood as a rotation of the signal’s coordinates in the time–frequency domain [6,9].

3.2.1. Mathematical Definition of FRFT

The p-th order FRFT of a signal $x\left(t\right)$ (corresponding to a rotation angle $\alpha =p\pi /2$) is defined as [6,8,16]

$$\begin{array}{c}\hfill X_p\left(u\right)={\mathcal{F}}^p\left[x\left(t\right)\right]\left(u\right)={\int }_{-\infty }^{\infty }{K}_p(t,u)x\left(t\right)dt\end{array}$$

(13)

where $K_p(t,u)$ is the transform kernel, one common form of which is

$$\begin{array}{c}\hfill K_p(t,u)=\left\{\begin{array}{cc}\sqrt{{\displaystyle \frac{1-jcot\alpha }{2\pi }}}{e}^{j({\displaystyle \frac{t^2+u^2}{2}}cot\alpha -utcsc\alpha )},\hfill & \alpha \ne k\pi \hfill \\ \delta (t-u),\hfill & \alpha =2k\pi \hfill \\ \delta (t+u),\hfill & \alpha =(2k+1)\pi \hfill \end{array}\right.\end{array}$$

(14)

When $p=1$ (i.e., $\alpha =\pi /2$), the FRFT reduces to the standard Fourier transform; when $p=0$ (i.e., $\alpha =0$), it is equivalent to the identity transform [6].

3.2.2. Energy-Focusing Property and Theoretical Derivation

The most compelling property of the FRFT is its “energy-focusing” effect on LFM signals [6,7]. As established in Section 2.2, the despread signal in a high-dynamic environment is an LFM signal, whose complex envelope can be expressed as

$$\begin{array}{c}\hfill y\left(t\right)=A^{\prime }·e^{j(2\pi f_{0}t+\pi f_r{t}^2)}\end{array}$$

(15)

The instantaneous frequency of this signal is $f_i\left(t\right)=f_0+f_{r}t$, which corresponds to a line with slope $f_r$ in the time–frequency (Wigner–Ville) distribution.

The FRFT operation can be interpreted as rotating the time–frequency coordinate system by an angle $-\alpha$. If the chosen rotation angle ${\alpha }_{\mathrm{opt}}$ is perfectly complementary to the tilt angle of the LFM signal in the time–frequency plane, i.e., $cot\left({\alpha }_{\mathrm{opt}}\right)=-f_r$, then in this new fractional domain coordinate system, the slanted energy distribution becomes a vertical line. This means all the signal’s energy is perfectly focused onto a single fractional frequency point $u_{\mathrm{opt}}$, and its FRFT result manifests as a sharp impulse [6,7].

$$\begin{array}{c}\hfill |X_{p_{\mathrm{opt}}}\left(u\right)|\propto |\delta (u-u_{\mathrm{opt}})|\end{array}$$

(16)

Here, the optimal transform order $p_{\mathrm{opt}}$ has a one-to-one correspondence with the Doppler rate $f_r$, while the peak location $u_{\mathrm{opt}}$ is directly related to the center frequency offset $f_0$.

This property effectively makes the FRFT a generalized matched filter bank. The conventional FFT is a matched filter bank optimized for detecting signals with a known, constant frequency. The FRFT, in contrast, can be viewed as a matched filter bank optimized for detecting LFM signals with a known “chirp rate” (i.e., Doppler rate). By performing the FRFT across different orders p, we are essentially matching the input signal against a series of LFM basis functions with different chirp rates. Therefore, a two-dimensional search (for the optimal order p and peak location u) can simultaneously estimate both the Doppler rate $f_r$ and the center frequency offset $f_0,$ providing a fundamental tool to directly address the high-dynamic problem [7].

4. Hierarchical Joint PMF-FFT and PMF-FRFT Algorithm

Simply using PMF-FRFT for a global three-dimensional search (code phase, frequency, and frequency rate) is computationally prohibitive and fails to meet real-time monitoring requirements. To this end, we have designed a hierarchical joint algorithm that fuses the speed of PMF-FFT with the precision of PMF-FRFT, achieving a balance between performance and efficiency.

4.1. Overall Algorithm Framework Design

The algorithm employs a two-stage “coarse–fine” acquisition strategy, with the overall framework depicted in Figure 3.

• Stage 1: Coarse Acquisition and Decision
  • The receiver samples and partitions the incoming IF signal.
  • The PMF-FFT algorithm is used to perform a two-dimensional parallel search over code phase and Doppler frequency. The Doppler frequency search step is kept large (e.g., equal to the inverse of the coherent integration time, $1/T_{\mathrm{coh}}$) to reduce the computational load.
  • A two-dimensional correlation magnitude matrix (code phase vs. frequency bin) is generated.
  • A Constant False Alarm Rate (CFAR) detector is applied to the correlation matrix to identify potential signal peaks.
  • If a signal peak is detected, an intelligent decision mechanism is initiated to analyze the morphology of the energy distribution in the region surrounding the peak. If the energy is concentrated in a sharp, single peak, the signal is classified as low-dynamic, and the coarse acquisition result is output directly. If the energy is smeared, presenting as a broad or multi-peaked structure, the signal is classified as high-dynamic, triggering the second stage.
• Stage 2: Fine Acquisition and Parameter Estimation
  • This stage is only triggered when Stage 1 classifies the signal as high-dynamic.
  • A small, three-dimensional uncertainty space is defined, centered on the coarse code phase and frequency estimates from Stage 1.
  • Within this confined space, the PMF-FRFT algorithm is employed to conduct a fine search. The search dimensions include code phase, center frequency (fractional domain location u), and Doppler rate (FRFT order p).
  • The point of maximum energy in the 3D search space is located. Its corresponding coordinates, $(\widehat{\tau },\widehat{f_0},\widehat{f_r})$, constitute the final, fine acquisition result.

4.2. Coarse Acquisition and Decision Threshold

In the coarse acquisition stage, signal detection is fundamentally a binary hypothesis testing problem:

• $H_0$: The received signal contains only noise.
• $H_1$: The received signal contains the target signal plus noise.

According to the Neyman–Pearson criterion, the optimal decision rule that maximizes the probability of detection $P_d$ for a given probability of false alarm $P_{fa}$ is the Likelihood Ratio Test (LRT). The decision rule is

$$\begin{array}{c}\hfill \Lambda \left(r\right)={\displaystyle \frac{p\left(r\right|H_1)}{p\left(r\right|H_0)}}\underset{H_0}{\stackrel{H_1}{\gtrless }}\gamma \end{array}$$

(17)

where $p\left(r\right|H_i)$ is the probability density function of observing the data r given that hypothesis $H_i$ is true, and $\gamma$ is the decision threshold determined by $P_{fa}$.

In practical applications, the noise power is unknown and potentially variable. Using a fixed threshold $\gamma$ would lead to an unstable false alarm rate. Therefore, Constant False Alarm Rate (CFAR) processing is necessary. Cell-Averaging CFAR (CA-CFAR) is a common method that estimates the local noise level by averaging the power of noise samples in a reference window surrounding the Cell Under Test (CUT). This estimate is then used to dynamically adjust the decision threshold, ensuring that the probability of false alarm $P_{fa}$ remains constant across different noise backgrounds.

4.3. Fine Acquisition and Parameter Estimation

The transition from coarse to fine acquisition is a critical design element of this algorithm. A simple trigger based on whether a peak exceeds the CFAR threshold is insufficient. In high-dynamic situations, energy smearing may cause the peak to fall below the threshold even when a signal is present, or the peak may exceed the threshold, but with a significant positional error.

This paper proposes an intelligent trigger mechanism based on the morphological analysis of the correlation surface. The physical basis for this is that a low-dynamic signal, after FFT processing, exhibits highly concentrated energy and a sharp correlation peak. In contrast, a high-dynamic signal’s energy is smeared, causing the correlation peak to become short, wide, and even split [5]. We can quantify this morphological difference to make a decision.

• In the coarse acquisition correlation matrix, find the maximum peak cell that exceeds the CFAR threshold.
• Define a small window (e.g., $3\times 3$ or $5\times 5$ cells) centered on this peak.
• Calculate the variance or standard deviation of all correlation magnitude values within this window.
• Compare the calculated variance against a preset morphological threshold ${\gamma }_{\mathrm{variance}}$:
  • If the variance is less than or equal to ${\gamma }_{\mathrm{variance}}$, this indicates that the energy is concentrated and the peak has a good shape. This suggests the signal is likely in a low-dynamic or static state, and the coarse acquisition result is sufficiently accurate. The acquisition process can be terminated or proceed to a simple peak refinement.
  • If the variance is greater than ${\gamma }_{\mathrm{variance}}$, this indicates significant energy smearing and poor peak morphology. This strongly implies the presence of high dynamics, necessitating the activation of the PMF-FRFT fine acquisition stage to accurately estimate the Doppler rate.

Once fine acquisition has been triggered, the PMF-FRFT search space is strictly confined to a small neighborhood around the coarse acquisition result $({\widehat{\tau }}_{\mathrm{coarse}},{\widehat{f}}_{\mathrm{coarse}})$. For instance, the code phase search range might be limited to just a few chips, the frequency search range to a few coarse frequency bins, and the FRFT order p (corresponding to $f_r$) search conducted within a typical range predetermined by the platform’s maximum expected acceleration. This focused search strategy is key to ensuring the computational efficiency of the entire algorithm.

4.4. Algorithm Complexity Analysis

The computational complexity of the algorithm is primarily determined by the number of real multiplications and additions. Let the coherent integration data length be N, the number of PMF segments be M (each of length $N/M$), the number of FFT/FRFT points be L (where $L\ge N/M$), the number of coarse frequency search bins be $N_{d,\mathrm{coarse}}$, the number of fine FRFT order search points be $N_p$, and the number of fine frequency search bins be $N_{d,\mathrm{fine}}$.

• PMF-FFT (Coarse Acquisition): The main overhead comes from performing M FFTs of length L, frequency-domain multiplications, and one IFFT of length L, repeated for each frequency search bin. The total complexity is approximately $O(N_{d,\mathrm{coarse}}·(M·L{log}_{2}L))$.
• PMF-FRFT (Fine Acquisition): The main overhead comes from performing PMF-FRFT calculations over the $N_p \times N_{d,\mathrm{fine}}$ grid. If a fast FRFT algorithm is used, its single-instance complexity is comparable to that of an FFT, at $O\left(L{log}_{2}L\right)$. The total complexity is approximately $O(N_p·N_{d,\mathrm{fine}}·(M·L{log}_{2}L))$.

Because the fine acquisition search space ($N_p,N_{d,\mathrm{fine}}$) is much smaller than a global search, and this stage is only triggered when necessary, the total average computational load of this hierarchical algorithm is far lower than that of a global three-dimensional brute-force search.

Table 1. Order-of-magnitude comparison of computational complexity for different acquisition algorithms.

Algorithm	Complexity Order (Multiplications)
Global Fine-Grid PMF-FFT	$O(N_{d,\mathrm{full}}·N{log}_{2}L)$
Global 2D PMF-FRFT	$O(N_{d,\mathrm{full}}·N_p·N{log}_{2}L)$
Proposed Hierarchical Alg.	$O(N_{d,\mathrm{coarse}}·N{log}_{2}L+P_{\mathrm{trigger}}·N_{d,\mathrm{fine}}·N_p·N{log}_{2}L)$

P_trigger is the probability of triggering fine acquisition. In most low-dynamic scenarios, P_trigger is small, and the algorithm’s complexity approaches that of a conventional PMF-FFT.

provides an order-of-magnitude comparison of the computational complexity of different algorithms.

5. Analysis of Experimental Results

This study evaluated the performance of a novel hierarchical architecture, which combines a segmented Parallel Matched Filter (PMF) using the Fast Fourier Transform (FFT) with a localized search using the Fractional Fourier Transform (FRFT), for the acquisition of Non-Periodically Spread Long Code–Direct Sequence Spread Spectrum (NPLC-DSSS) signals. To validate its advantages, the performance of the proposed algorithm was benchmarked against the conventional PMF-FFT method by monitoring NPLC-DSSS signals under various conditions, including different code and segment lengths.

The acquisition process for the proposed hierarchical method consists of two stages.

• Stage 1: Rapid Coarse Search via FFT. A 262,144-point FFT, identical to that used in the baseline FFT method, performs a rapid scan across the entire search space. The top three candidate signals, ranked by their correlation peak values, are identified, and their respective peak values, code phases, and frequencies are recorded.
• Stage 2: Localized Fine Search via FRFT and Global Optimization. The algorithm then iterates through these three candidate regions. Within a small neighborhood of each candidate, a computationally moderate 16,384-point FRFT conducts a precise search. Upon completion, the results from all coarse and fine searches are globally compared, and the signal with the highest overall correlation peak is selected as the final output.

5.1. Analysis of Acquisition Correlation Performance

Figure 4 illustrates the simulated frequency offset detection performance. The vertical axis represents the normalized correlation value; a higher value indicates a smaller phase difference between the received and local signals, corresponding to more accurate phase acquisition. Across all tested frequency offsets, the performance curves of the PMF-FRFT and the proposed hierarchical algorithm are nearly identical and are demonstrably superior to the conventional PMF-FFT algorithm. The performance of the PMF-FFT algorithm degraded slightly as the frequency offset increased, a manifestation of the “picket-fence effect”. In contrast, the two FRFT-based algorithms exhibited superior robustness to frequency deviations, maintaining high correlation peaks, even at an offset of 2000 Hz.

Figure 5 displays the average maximum correlation value as a function of the signal-to-noise ratio (SNR), averaged over all frequency offsets. As expected, the performance of all algorithms improved with increasing SNR. Again, the PMF-FRFT and the hierarchical algorithm showed congruent performance and slightly outperformed the PMF-FFT method. The performance enhancement from the FRFT-based methods was most pronounced at a low SNR of −10 dB, where they achieved a 4.91% improvement in correlation peak value.

Figure 6 provides a heatmap that visualizes the percentage performance improvement of PMF-FRFT relative to PMF-FFT across a range of SNRs and frequency offsets. The improvement was calculated by dividing the maximum correlation value obtained by the FRFT method by that of the FFT method for each specified condition. The warmer tones on the heatmap indicate regions where the FRFT’s advantage was most significant. It is observable that in low-SNR scenarios with frequency desynchronization, the FRFT provided more robust detection capabilities.

As shown in Figure 6, when considering the combined effects of frequency offset and SNR, the FRFT-based methods consistently outperformed the FFT-based approach. For instance, at a frequency offset of 1000 Hz and an SNR of −20 dB, the FRFT method achieved a performance gain (in terms of frequency accuracy) of nearly 30% over the FFT method. This substantial difference can be attributed to the FFT’s frequency resolution limitations, which can cause significant spectral leakage and thus poor performance at specific frequency points. Overall, the analysis confirms that the performance advantage of the FRFT-based methods was most evident at lower SNRs. Across all static frequency offset tests, the PMF-FRFT and hierarchical algorithms achieved an average correlation peak gain of 2.53% over the conventional PMF-FFT.

5.2. Analysis of Acquisition Time

Acquisition time is a critical metric for evaluating the real-time feasibility of an acquisition algorithm. Figure 7 compares the acquisition times for the three algorithms. The conventional PMF-FFT algorithm, serving as the baseline, exhibited the shortest average processing time, at approximately 0.0568 s. The two-dimensional PMF-FRFT algorithm, which must perform an exhaustive search across both code phases and multiple fractional orders, was computationally intensive. Its average processing time was 0.3317 s, approximately 5.8-times longer than the PMF-FFT baseline, posing a significant challenge to real-time implementation.

In contrast, the proposed hierarchical algorithm demonstrated a remarkable balance of performance and efficiency. With an average processing time of 0.088 s, its computational cost was on the same order of magnitude as the baseline PMF-FFT method (0.0568 s) and was substantially faster than the full two-dimensional PMF-FRFT search (0.3317 s). This efficiency highlights its significant potential as a practical engineering solution.

In summary, the analysis demonstrates that the proposed hierarchical joint algorithm strikes an optimal balance between detection performance and computational efficiency. It achieves the superior detection robustness of the PMF-FRFT method, with only a marginal increase in computational cost compared to the PMF-FFT, while simultaneously avoiding the prohibitive computational complexity of a full two-dimensional PMF-FRFT search. Therefore, this algorithm presents a high-performance and pragmatically viable solution for the real-time, reliable monitoring of DSSS signals.

6. Summary

To address the challenge of monitoring BeiDou RDSS signals (a DSSS signal) in low signal-to-noise ratio (SNR) and high-dynamic environments, this paper introduces a hierarchical joint processing algorithm. The proposed method overcomes the performance degradation of conventional FFT-based acquisition techniques, which suffer from energy dispersion in the presence of high Doppler frequency rates. The algorithm employs a two-stage “coarse–fine” acquisition strategy. First, a computationally efficient segmented matched-filter FFT (PMF-FFT) performs a rapid two-dimensional coarse search to quickly narrow the uncertainty range of code phase and frequency. Subsequently, a decision-making mechanism based on correlation peak morphology analysis identifies whether the signal is in a high-dynamic state. If a high-dynamic state is detected, a segmented matched-filter fractional Fourier transform (PMF-FRFT) is initiated for a three-dimensional fine search within a localized region around the coarse acquisition results. This stage precisely estimates the code phase, center frequency, and Doppler frequency rate. Experimental results demonstrated that the acquisition performance of the hierarchical algorithm was comparable to that of a global PMF-FRFT search and superior to the conventional PMF-FFT method. Crucially, its average processing time was significantly lower than that of the global PMF-FRFT, remaining on the same order of magnitude as the PMF-FFT. This approach achieves an effective balance between detection performance and computational efficiency, offering a feasible technical solution for the real-time monitoring of high-dynamic DSSS signals.

7. Experiments and Data Analysis

For the monitoring of non-periodic long-code direct spreading signals (NPLC-DSSS) under low signal-to-noise ratios (SNR $< -20$ dB), the joint processing algorithm of hierarchical PMF-FFT and PMF-FRFT proposed in this paper realizes a theoretical breakthrough and engineering practicability enhancement through a triple innovative mechanism: through parallel frequency–domain searching of segmented PMF-FFT and fractional-order focus of FRFT, the time–frequency coupling effect is decoupled, and the two-dimensional searching space of traditional PMF-FRFT is compressed to one dimension, to significantly suppress the code phase nonlinear offset problem under high dynamic scenarios. By decoupling the time–frequency coupling effect through the segmented PMF-FFT and the fractional-order focusing of FRFT, the two-dimensional search space of the traditional PMF-FRFT is compressed into one dimension, which significantly suppresses the nonlinear shift of the code phase in high-dynamic scenarios. Based on the overlapping segmentation and fractional order adaptive strategy, the average correlation peak of the joint algorithm in the FRFT domain is improved by many orders of magnitude compared with the traditional PMF-FFT, which effectively solves the energy dispersion problem of the non-periodic pseudo-code. Through a hierarchical segmentation architecture (optimal segmentation length = 256), the computational complexity of PMF-FRFT is reduced from $O\left(N^2\right)$ to $O(NlogN+MlogM)$, which shortens the processing time and realizes real-time capture capability for long-code direct-expansion signals.

The experimental results show that the algorithm surpassed the traditional methods in the core indexes of detection sensitivity, dynamic adaptability, and computational efficiency, and it provides a new theoretical framework and engineering realization path for highly dynamic weak signal monitoring in non-cooperative scenarios. Future research will further explore the fast estimation of fractional order and hardware parallelization acceleration to meet the real-time processing requirements of higher bit rate signals [17,18].