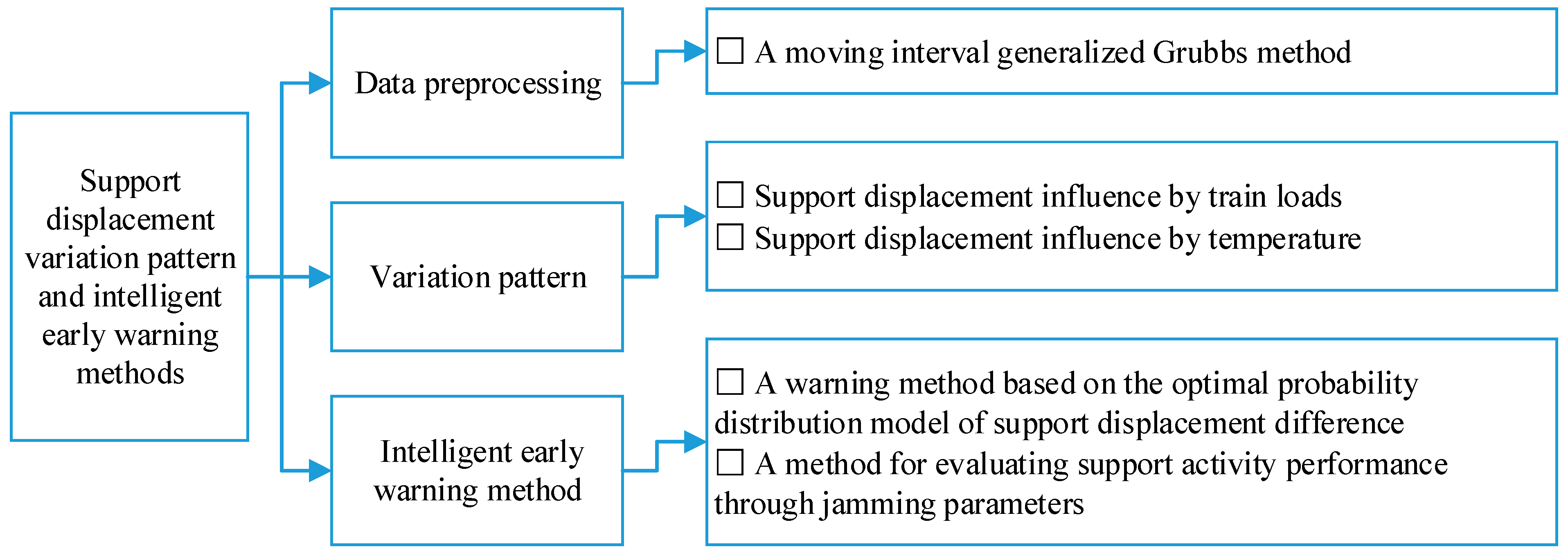
Study on the Support Displacement Variation Pattern and Intelligent Early-Warning Methods for Kilometer-Level Railway Bridges
Abstract
1. Introduction
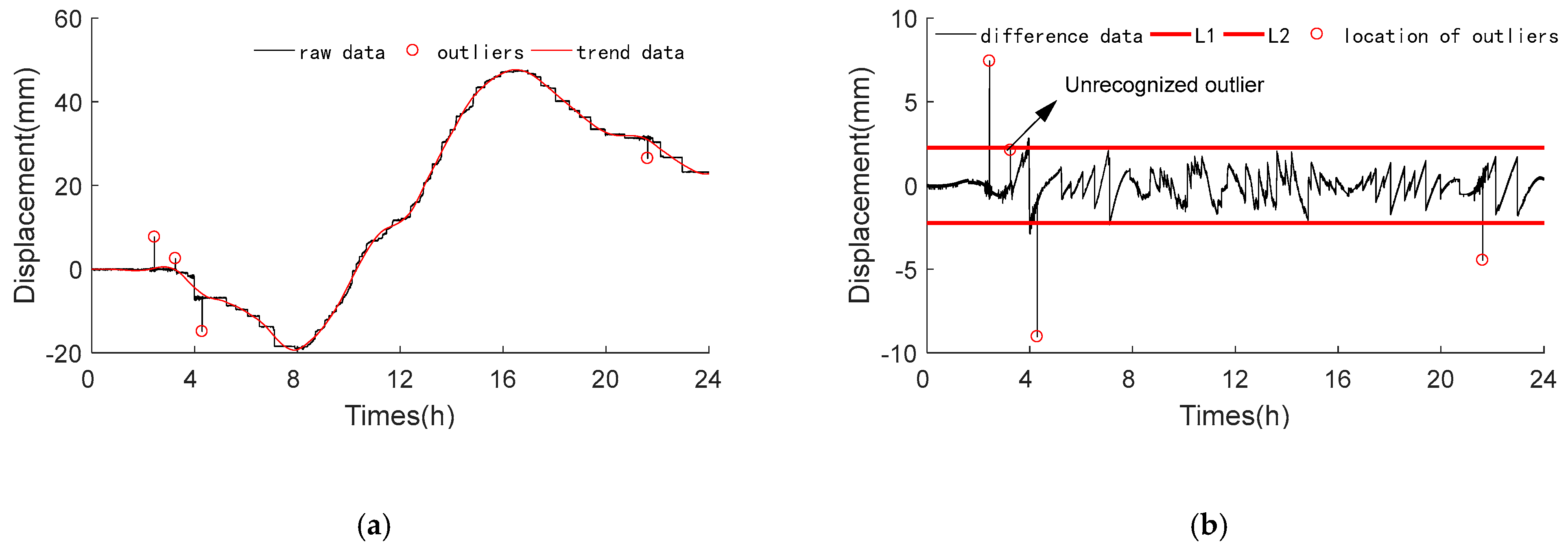
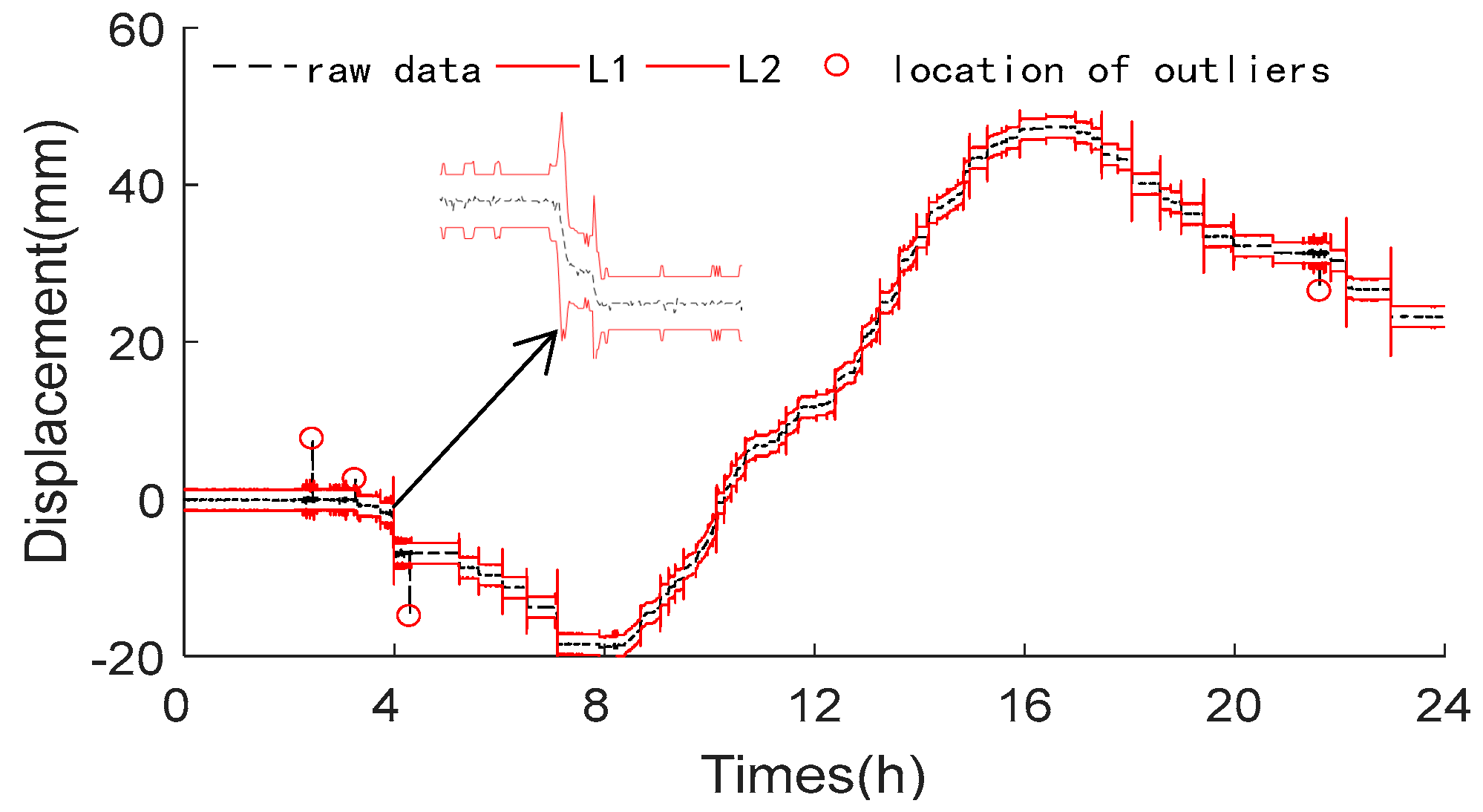
2. Data Preprocessing Method
3. Support Displacement Analysis
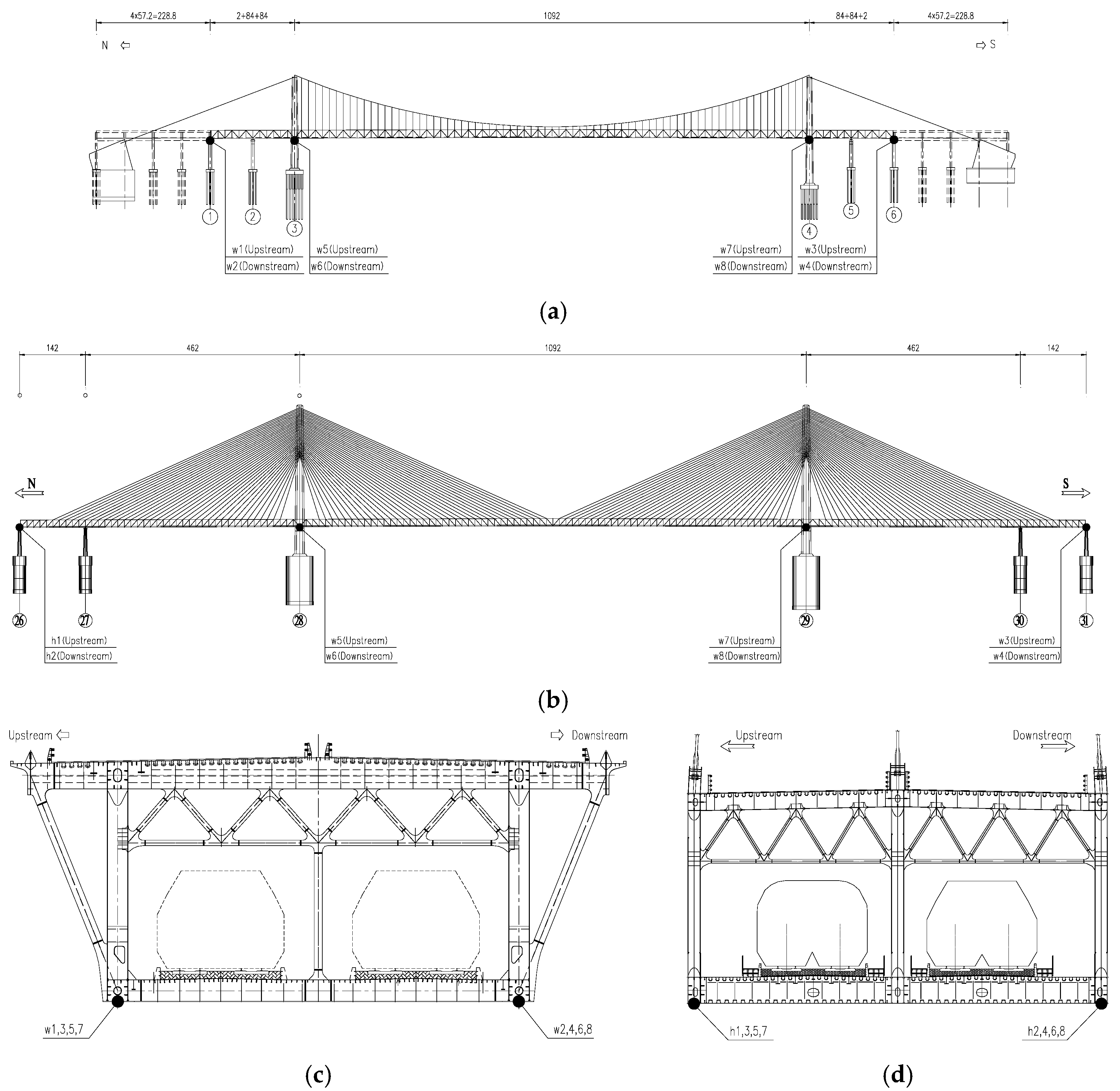
3.1. Bridge Description
3.2. Monitoring Results Analysis
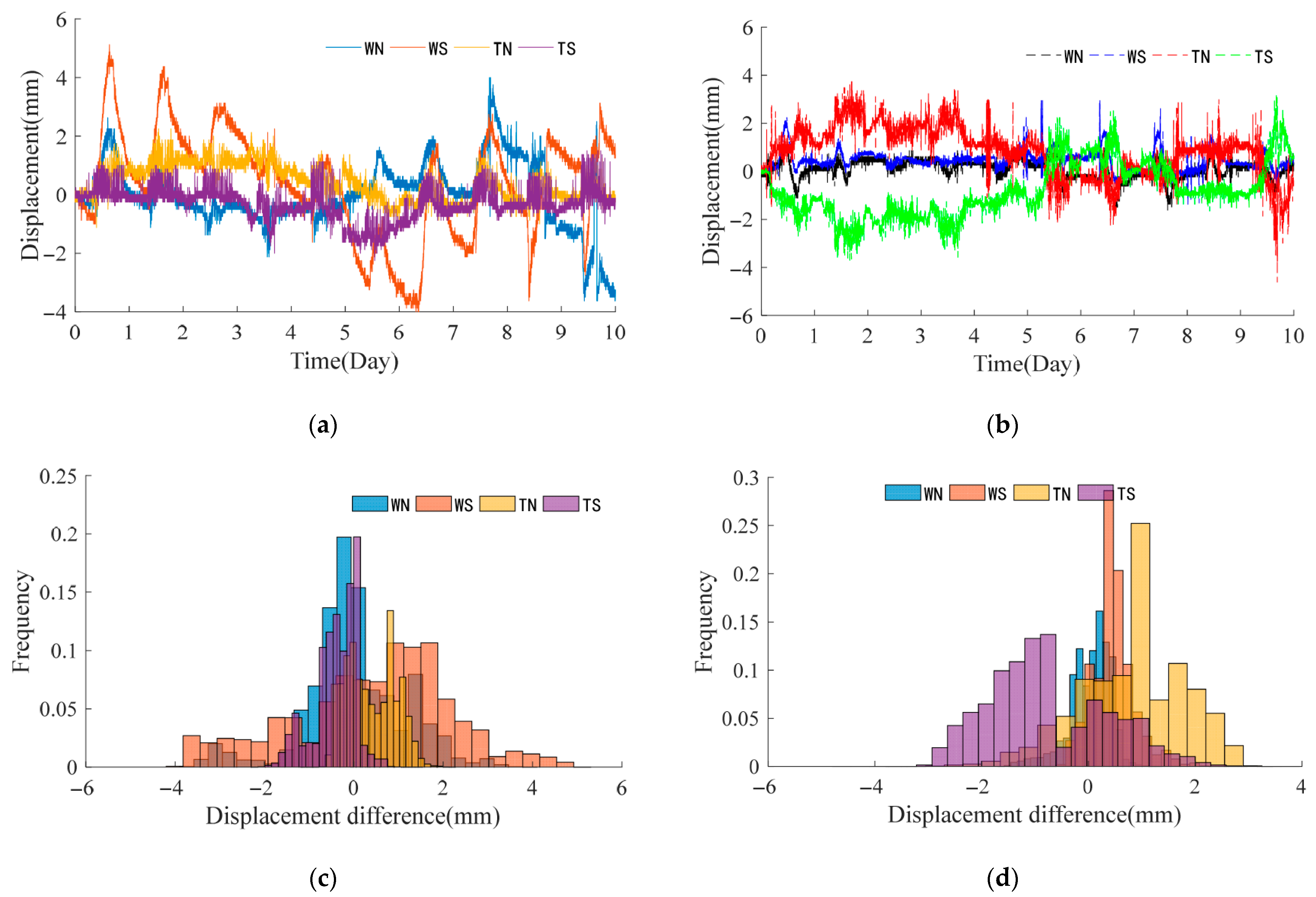
3.3. Support Displacement Influenced by Train Loads
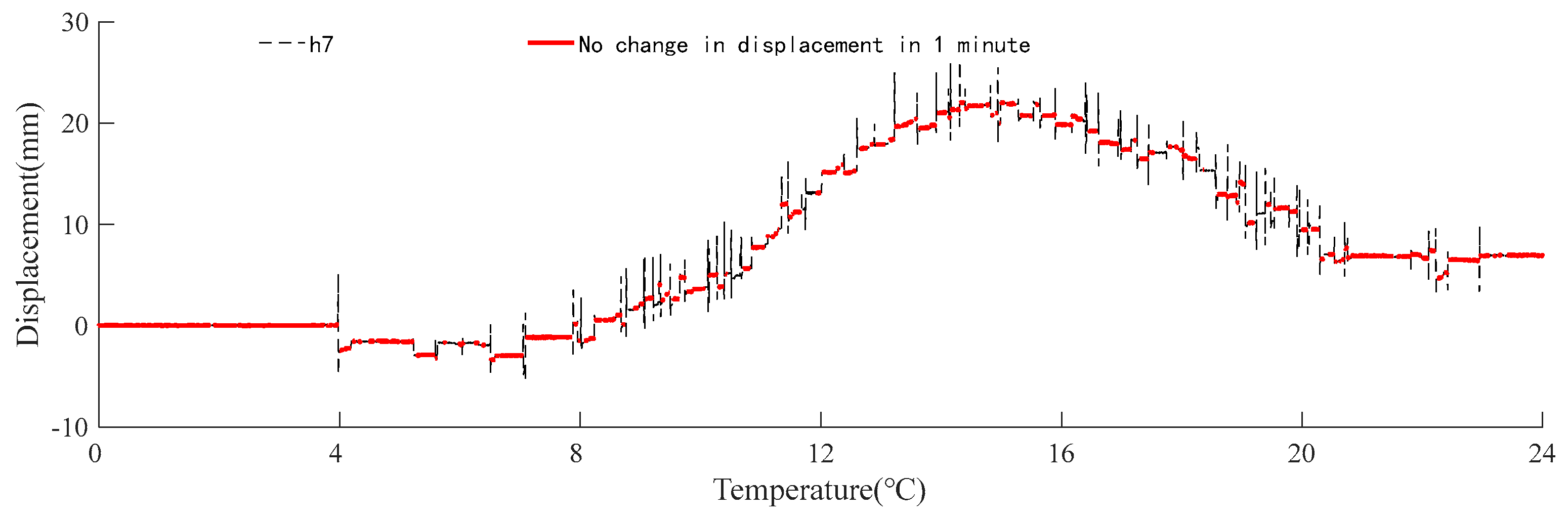
3.4. Support Displacement Influenced by Temperature
4. Intelligent Early Warning Method of Support Displacement
4.1. Establishment and Verification of Early-Warning Model
- (1)
- Record the absolute value of the displacement difference as , which is the data location.
- (2)
- Initialize the distribution function, select the Gaussian distribution function, and calculate the distribution characteristics and distribution function expression of .
- (3)
- Divide the monitoring data into m intervals; calculate the frequency value of the displacement difference of the j-th (j = 1, 2, 3, …, m) interval, as well as the integral value of the distribution function.
- (4)
- Based on the principle of least squares, calculate the residuals between the frequency values and the distribution function integral values in each segment . Use the sum of the squares of the 2-norm of the vector to measure the degree of fitting model, denoted as . A smaller a indicates that the distribution function is closer to the optimal probability distribution.
- (5)
- Iterate through all distribution functions in the MATLAB (2016b) toolbox, with the criterion of being the smallest; calculate the optimal probability distribution function ; and obtain the statistical characteristics of the distribution function.
- (6)
- Calculate the quantile value of the optimal probability distribution function at a 97.5% confidence level as the early-warning threshold for the displacement difference of the support.
4.2. Evaluation of Support Wear and Jamming
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yanez-Borjas, J.J.; Valtierra-Rodriguez, M.; Camarena-Martinez, D.; Amezquita-Sanchez, J.P. Statistical time features for global corrosion assessment in a truss bridge from vibration signals. Measurement 2020, 160, 107858. [Google Scholar] [CrossRef]
- Deng, L.; Yan, W.; Nie, L. A simple corrosion fatigue design method for bridges considering the coupled corrosion-overloading effect. Eng. Struct. 2019, 178, 309–317. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Y.; Zhao, W.; Wu, T. A visual measurement method of vibration displacement of railway bridge bearings based on phase correlation. Measurement 2025, 240, 115600. [Google Scholar] [CrossRef]
- Wu, G.M.; Yi, T.H.; Yang, D.H.; Li, H.N. Damage detection of tension pendulums in cable-stayed bridges using structural frequency variance. J. Perform. Constr. Facil. 2021, 35, 4020126. [Google Scholar] [CrossRef]
- Freire, L.M.R.; De Brito, J.; Correia, J.R. Management system for road bridge structural bearings. Struct. Infrastruct. Eng. 2014, 10, 1068–1086. [Google Scholar] [CrossRef]
- Freire, L.M.R.; De Brito, J.; Correia, J.R. Inspection survey of support bearings in road bridges. J. Perform. Constr. Facil. 2015, 29, 4014098. [Google Scholar] [CrossRef]
- Yarnold, M.T.; Moon, F.L. Temperature-based structural health monitoring baseline for long-span bridges. Eng. Struct. 2015, 86, 157–167. [Google Scholar] [CrossRef]
- Xia, Q.; Xia, Y.; Wan, H.P.; Zhang, J.; Ren, W. Condition analysis of expansion joints of a long-span suspension bridge through metamodel-based model updating considering thermal effect. Struct. Control. Health Monit. 2020, 27, e2521. [Google Scholar] [CrossRef]
- Sun, B.; Zheng, G.; Zhang, X. Application of contact laser interferometry in precise displacement measurement. Measurement 2021, 174, 108959. [Google Scholar] [CrossRef]
- Ribeiro, D.; Santos, R.; Cabral, R.; Saramago, G.; Montenegro, P.; Carvalho, H.; Correia, J.; Calçada, R. Non-contact structural displacement measurement using unmanned aerial vehicles and video-based systems. Mech. Syst. Signal Process. 2021, 160, 107869. [Google Scholar] [CrossRef]
- Hui, L.X.; Lei, G.; Yan, W.; Haoran, S.; Yong, H. Micro-displacement amplifier of giant magnetostrictive actuator using flexure hinges. J. Magn. Magn. Mater. 2022, 556, 169415. [Google Scholar] [CrossRef]
- Chu, X.; Zhou, Z.; Zhu, W.; Duan, X. Multi-point displacement synchronous monitoring method for bridges based on computer vision. Appl. Sci. 2023, 13, 6544. [Google Scholar] [CrossRef]
- Bhandari, P.; Jang, S.; Malla, R.B.; Han, S. ANN-based bridge support fixity quantifica-tion using thermal response data from real-time wireless sensing. Sensors 2024, 24, 5350. [Google Scholar] [CrossRef]
- Wu, G.M.; Yi, T.H.; Yang, D.H.; Li, H.N.; Liu, H. Early warning method for bearing displacement of long-span bridges using a proposed time-varying temperature-displacement model. J. Bridge Eng. 2021, 26, 04021068. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, B.; Huang, K.; Wang, L. Probabilistic prediction and early warning for bridge bearing displacement using sparse variational gaussian process regression. Struct. Saf. 2025, 114, 102564. [Google Scholar] [CrossRef]
- Cui, M.; Wu, G.; Dang, J.; Chen, Z.; Zhou, M. Deep learning-based condition assessment for bridge elastomeric bearings. J. Civ. Struct. Health Monit. 2022, 12, 245–261. [Google Scholar] [CrossRef]
- Kollar, D.; Kovesdi, B.; Volgyi, I.; Biro, I. Assessment of deformation in bridge bearing areas using measurements and welding simulation. J. Constr. Steel Res. 2022, 194, 107305. [Google Scholar] [CrossRef]
- Zhou, G.D.; Yi, T.H.; Chen, B.; Zhang, H. Analysis of three-dimensional thermal gradients for arch bridge girders using long-term monitoring data. Smart Struct. Syst. 2015, 15, 469–488. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, L.; Ding, J.; Qin, Y.; Zhong, Y.; Lu, B. Study on peculiar beam-rail interaction on road-cum-rail bridges with thousand-meter-scale main span. J. China Railw. Soc. 2023, 45, 80–87. [Google Scholar]
- Ni, Y.Q.; Hua, X.G.; Wong, K.Y.; Ko, J.M. Assessment of bridge expansion joints using long-term displacement and temperature measurement. J. Perform. Constr. Facil. 2007, 21, 143–151. [Google Scholar] [CrossRef]
- Huang, H.B.; Yi, T.H.; Li, H.N.; Liu, H. New representative temperature for performance alarming of bridge expansion joints through temperature-displacement relationship. J. Bridge Eng. 2018, 23. [Google Scholar] [CrossRef]
- McCarthy, E.; Wright, T.; Padgett, J.E.; DesRoches, R.; Bradford, P. Development of an experimentally validated analytical model for modular bridge expansion joint behavior. J. Bridge Eng. 2014, 19, 235–244. [Google Scholar] [CrossRef]
- Deng, Y.; Li, A.; Liu, Y.; Chen, S. Investigation of temperature actions on flat steel box girders of long-span bridges with temperature monitoring data. Adv. Struct. Eng. 2018, 21, 2099–2113. [Google Scholar] [CrossRef]
- Asad, A.T.; Kim, B.; Cho, S.; Sim, S.-H.; Jankowski, Ł. Prediction model for long-term bridge bearing displacement using artificial neu-ral network and bayesian optimization. Struct. Control. Health Monit. 2023, 2023, 6664981. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.; Liu, D.; Liu, Z. Performance Influence of Train Driving on Shanghai-Nantong Yangtze River Bridge Considering Additional Deformation. J. Railw. Eng. Soc. 2016, 33, 63–68. [Google Scholar]
- Wang, G.X.; Ding, Y.L.; Song, Y.S.; Wu, L.-Y.; Yue, Q.; Mao, G.-H. Detection and location of the degraded bearings based on monitoring the longitudinal expansion performance of the main girder of the dashengguan yangtze bridge. J. Perform. Constr. Facil. 2016, 30, 4015074. [Google Scholar] [CrossRef]
- Gao, W.; Li, G.; Su, Q.; Han, W. Impact of rigid central clamps on longitudinal deformation of long-span suspension bridges under vehicle excitations. Struct. Infrastruct. Eng. 2022, 18, 760–774. [Google Scholar] [CrossRef]
- Zhang, B.; Ren, Y.; He, S.; Gao, Z.; Li, B.; Song, J. A review of methods and applications in structural health monitoring (SHM) for bridges. Measurement 2025, 245, 116575. [Google Scholar] [CrossRef]
- Lee, T.; Jin, S.S.; Kim, S.T.; Min, J. Online anomaly detection for long-term structural health monitoring of caisson quay walls. Eng. Struct. 2025, 323, 119197. [Google Scholar] [CrossRef]
- Khan, S.M.; Atamturktur, S.; Chowdhury, M.; Rahman, M. Integration of structural health monitoring and intelligent transportation systems for bridge condition assessment: Current status and future direction. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2107–2122. [Google Scholar] [CrossRef]
- Deng, Y.; Zhao, Y.; Ju, H.; Yi, T.-H.; Li, A. Abnormal data detection for structural health monitoring: State-of-the-art review. Dev. Built Environ. 2024, 17, 100337. [Google Scholar] [CrossRef]
- Xie, G.; Chen, W.; Liu, X.; Zheng, K.; Zou, B.; Sun, H. Research and application of verification error data processing of electricity meter based on grubbs criterion. In Proceedings of the 2019 International Conference on Smart Grid and Electrical Automation (ICSGEA), Xiangtan, China, 10–11 August 2019. [Google Scholar]
- Liu, X.; Sun, Z.; Guo, T. Deflection Prediction of a Rail-Cum-Road Suspension Bridge Under Multiple Operational Loads With Improved GPR and FSF. Struct. Control Health Monit. 2024, 2024, 8880157. [Google Scholar] [CrossRef]
- Gao, Z.; Xu, W.; Mei, X.; Zhang, Y.; Huo, X. Key construction technology of HuSuTong yangtze river bridge. Struct. Eng. Int. 2023, 33, 84–88. [Google Scholar] [CrossRef]
- Peng, L.L. Technical scheme and application of track-bridge integrated inspection and monitoring system for long-span bridges. Railw. Eng. 2023, 63, 33–37. [Google Scholar]
- Qin, S.; Gao, Z. Developments and prospects of long-span high-speed railway bridge technologies in China. Engineering 2017, 3, 787–794. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, Y.; Li, X.; Zhang, J. Effect of temperature changes on bearing motion of long-span steel truss continuous girder bridge. Constr. Build. Mater. 2024, 430, 136440. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Jiang, L.; Zhang, N. Long-term field test of temperature gradients on the composite girder of a long-span cable-stayed bridge. Adv. Struct. Eng. 2019, 22, 2785–2798. [Google Scholar] [CrossRef]
- Miao, C.Q.; Deng, Y.; Ding, Y.L.; Li, A.Q. Damage alarming for bridge expansion joints using novelty detection technique based on long-term monitoring data. J. Cent. South Univ. 2013, 20, 226–235. [Google Scholar] [CrossRef]
- Zhu, R.; Guo, T.; Xie, L.; Song, L.; Yang, K.; Tesfamariam, S. Seismic risk assessment of self-centering prestressed concrete frames with sliding and masonry infill walls: Experimental and numerical models. Bull. Earthq. Eng. 2024, 22, 4115–4141. [Google Scholar] [CrossRef]

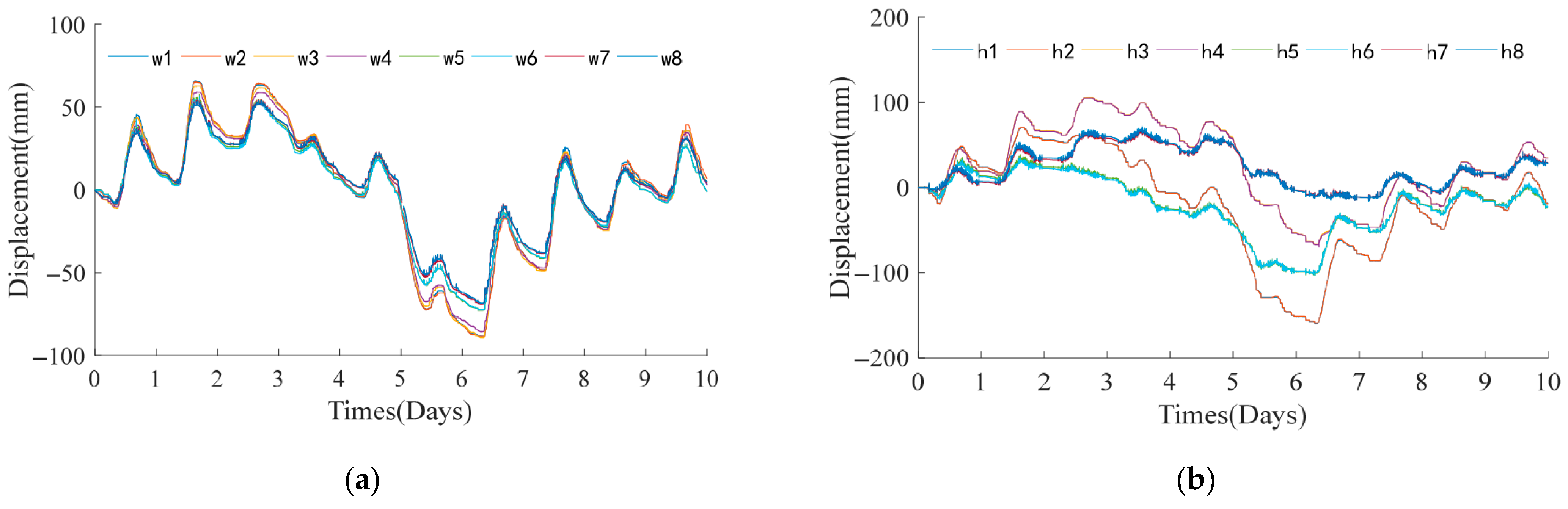

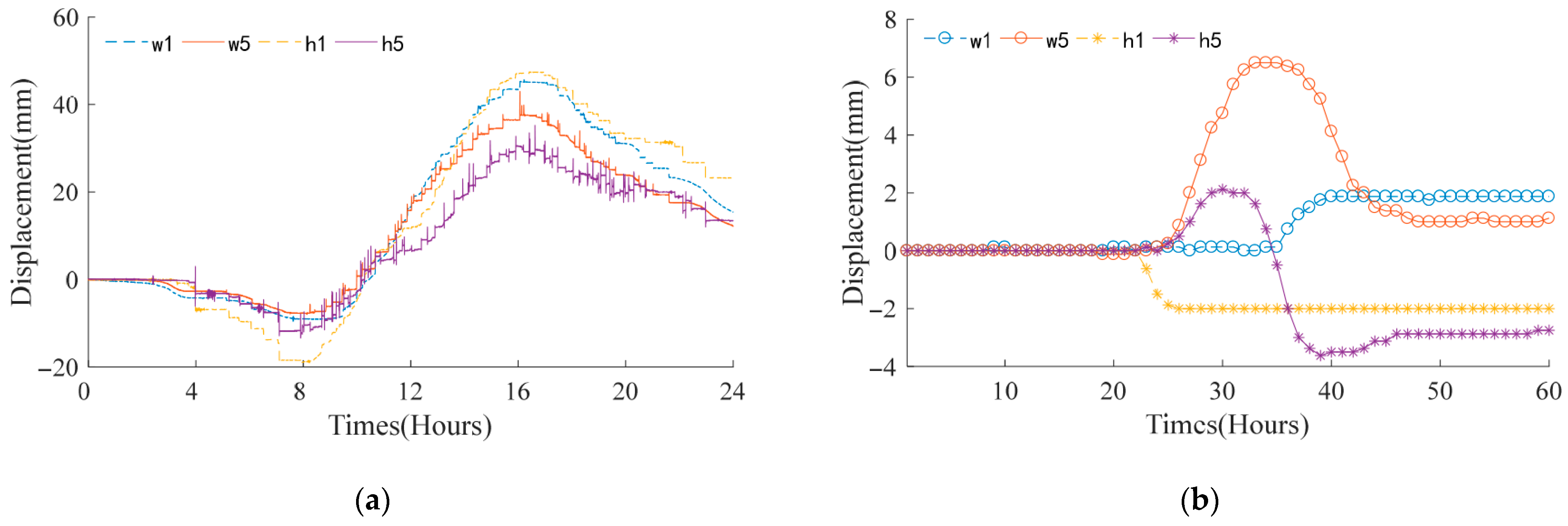
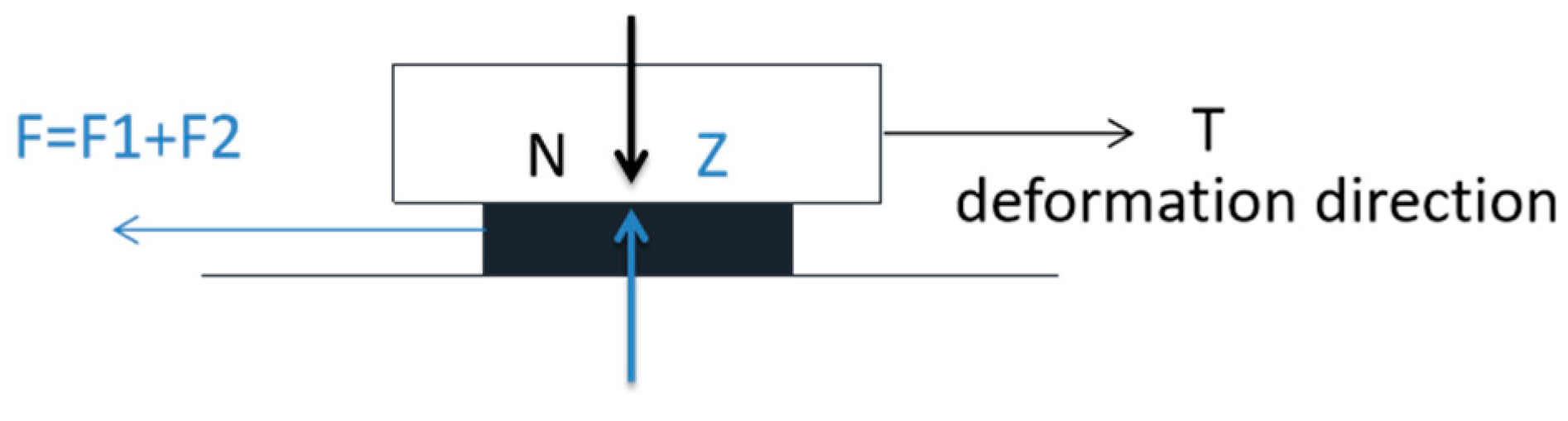
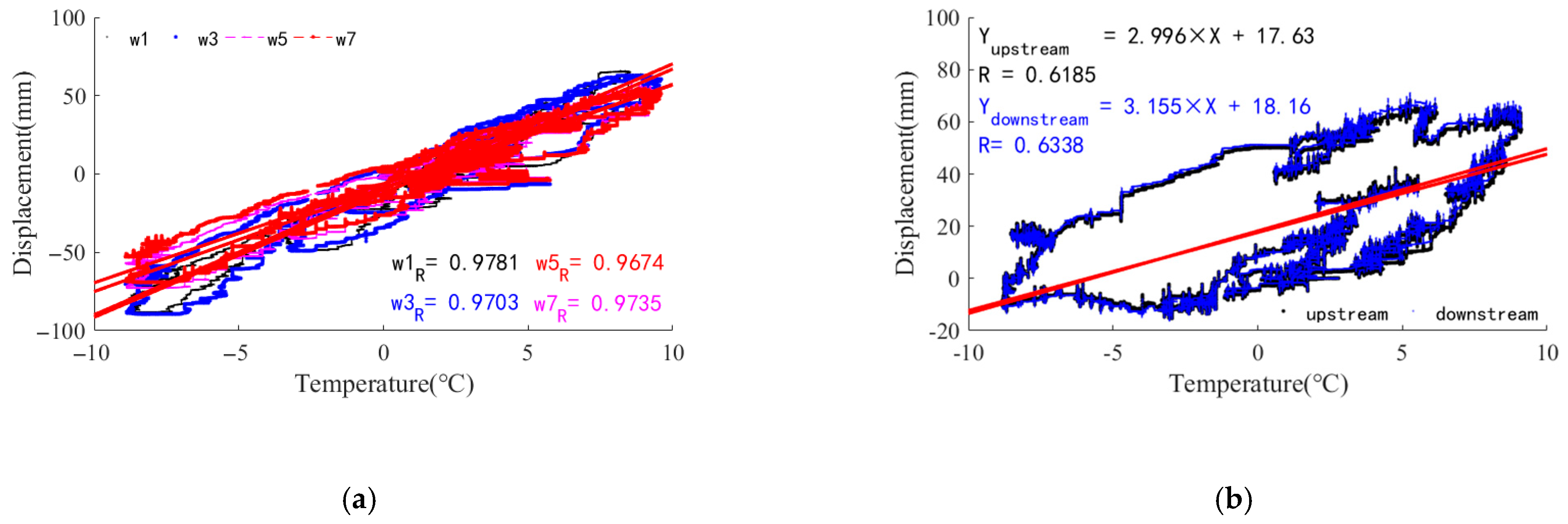


| No. | Support Displacement of W Bridge/mm | Support Displacement of H Bridge/mm | ||||||
|---|---|---|---|---|---|---|---|---|
| Max | Min | Mean | Range | Max | Min | Mean | Range | |
| w1/h1 | 65.88 | −88.25 | 0.13 | 154.13 | 70.00 | −160.13 | −17.88 | 230.12 |
| w2/h2 | 65.38 | −88.62 | 0.15 | 154.00 | 70.13 | −159.62 | −17.95 | 229.75 |
| w3/h3 | 63.00 | −89.50 | 0.09 | 152.50 | 105.17 | −68.25 | 25.87 | 173.42 |
| w4/h4 | 59.25 | −85.87 | −0.30 | 145.12 | 104.58 | −69.75 | 25.42 | 174.33 |
| w5/h5 | 57.50 | −72.75 | −0.71 | 130.25 | 38.13 | −103.75 | −19.57 | 141.88 |
| w6/h6 | 56.50 | −72.38 | −1.10 | 128.88 | 35.00 | −103.25 | −20.39 | 138.25 |
| w7/h7 | 54.75 | −69.25 | 1.55 | 124.00 | 68.29 | −15.38 | 22.30 | 83.67 |
| w8/h8 | 54.00 | −68.50 | 1.94 | 122.50 | 71.04 | −16.25 | 23.08 | 87.29 |
| Measuring Point | W Bridge | H Bridge | ||||
|---|---|---|---|---|---|---|
| k | R | d | k | R | d | |
| Upstream of the north girder end (w1/h1) | 8.14 | 0.9735 | 17.59 | 12.41 | 0.9838 | 19.93 |
| Downstream of the north girder end (w2/h2) | 8.20 | 0.9732 | 15.83 | 12.39 | 0.984 | 15.88 |
| Upstream of the south girder end (w3/h3) | 8.01 | 0.9703 | 12.51 | 8.35 | 0.8418 | 52.05 |
| Downstream of the south girder end (w4/h4) | 7.68 | 0.9708 | 13.60 | 8.35 | 0.8427 | 54.78 |
| Upstream of the north tower (w5/h5) | 6.62 | 0.9735 | 14.85 | 7.10 | 0.9598 | 9.27 |
| Downstream of the north tower (w6/h6) | 6.54 | 0.974 | 21.27 | 6.97 | 0.9588 | 8.69 |
| Upstream of the south tower (w7/h7) | 6.32 | 0.9674 | 14.81 | 3.00 | 0.6185 | 45.81 |
| Downstream of the south tower (w8/h8) | 6.25 | 0.9649 | 13.81 | 3.15 | 0.6338 | 18.16 |
| Eigenvalue | W Bridge | H Bridge | ||||||
|---|---|---|---|---|---|---|---|---|
| WN | WS | TN | TS | HN | HS | TN | TS | |
| Max | 4.00 | 5.12 | 2.25 | 1.50 | 1.37 | 2.96 | 3.75 | 3.21 |
| Min | −3.63 | −4.00 | −1.13 | −2.25 | −1.63 | −1.46 | −4.62 | −3.71 |
| Mean | −0.02 | 0.39 | 0.39 | −0.39 | 0.07 | 0.45 | 0.82 | −0.78 |
| Range | 7.63 | 9.12 | 3.38 | 3.75 | 3.00 | 4.42 | 8.38 | 6.92 |
| Bridge | w1/h1 | w2/h2 | w3/h3 | w4/h4 | w5/h5 | w6/h6 | w7/h7 | w8/h8 |
|---|---|---|---|---|---|---|---|---|
| W | 17.59 | 15.83 | 12.51 | 13.60 | 14.85 | 21.27 | 14.81 | 13.81 |
| H | 19.93 | 15.88 | 52.05 | 54.78 | 9.27 | 8.69 | 45.81 | 49.09 |
| X | h1 | h2 | h3 | h4 | h5 | h6 | h7 | h8 |
|---|---|---|---|---|---|---|---|---|
| 0.06 | 19.93 | 15.88 | 32.60 | 35.01 | 9.27 | 8.69 | 28.94 | 32.10 |
| 0.07 | 19.93 | 15.88 | 32.60 | 35.01 | 9.27 | 8.69 | 28.94 | 32.10 |
| 0.08 | 19.93 | 15.88 | 32.60 | 35.01 | 9.27 | 8.69 | 28.94 | 32.10 |
| 0.09 | 19.93 | 15.88 | 52.05 | 54.78 | 9.27 | 8.69 | 45.81 | 49.09 |
| 0.10 | 19.93 | 15.88 | 52.05 | 54.78 | 9.27 | 8.69 | 45.81 | 49.09 |
| 0.11 | 19.93 | 15.88 | 52.05 | 54.78 | 9.27 | 8.69 | 45.81 | 49.09 |
| 0.12 | 19.93 | 15.88 | 52.05 | 54.78 | 9.27 | 8.69 | 45.81 | 49.09 |
| 0.13 | 86.28 | 85.74 | 83.21 | 81.75 | 69.26 | 71.44 | 78.38 | 78.47 |
| 0.14 | 86.28 | 85.74 | 83.21 | 81.75 | 69.26 | 71.44 | 78.38 | 78.47 |
| M | h1 | h2 | h3 | h4 | h5 | h6 | h7 | h8 |
|---|---|---|---|---|---|---|---|---|
| 20 | 36.88 | 33.43 | 73.93 | 75.85 | 25.94 | 25.83 | 71.65 | 72.74 |
| 40 | 25.77 | 21.89 | 59.67 | 62.18 | 14.19 | 13.85 | 55.57 | 58.07 |
| 60 | 19.93 | 15.88 | 52.05 | 54.78 | 9.27 | 8.69 | 45.81 | 49.09 |
| 80 | 16.00 | 12.17 | 46.89 | 49.28 | 6.06 | 5.84 | 38.24 | 41.92 |
| 100 | 13.50 | 9.57 | 43.02 | 45.58 | 4.38 | 4.06 | 33.08 | 36.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Guo, T.; Chen, Z.; Zhao, H. Study on the Support Displacement Variation Pattern and Intelligent Early-Warning Methods for Kilometer-Level Railway Bridges. Appl. Sci. 2025, 15, 8931. https://doi.org/10.3390/app15168931
Liu X, Guo T, Chen Z, Zhao H. Study on the Support Displacement Variation Pattern and Intelligent Early-Warning Methods for Kilometer-Level Railway Bridges. Applied Sciences. 2025; 15(16):8931. https://doi.org/10.3390/app15168931
Chicago/Turabian StyleLiu, Xingwang, Tong Guo, Zheheng Chen, and Hanwei Zhao. 2025. "Study on the Support Displacement Variation Pattern and Intelligent Early-Warning Methods for Kilometer-Level Railway Bridges" Applied Sciences 15, no. 16: 8931. https://doi.org/10.3390/app15168931
APA StyleLiu, X., Guo, T., Chen, Z., & Zhao, H. (2025). Study on the Support Displacement Variation Pattern and Intelligent Early-Warning Methods for Kilometer-Level Railway Bridges. Applied Sciences, 15(16), 8931. https://doi.org/10.3390/app15168931








