1. Introduction
With the acceleration of digital transformation and the widespread adoption of computationally intensive applications in fields such as scientific research, industrial engineering, and business analytics [
1], scheduling problems in HPC environments have become increasingly complex and face higher performance requirements [
2]. In modern HPC systems, coordinating thousands of nodes and managing large-scale task submissions across diverse objectives and resource constraints presents substantial challenges [
3,
4]. However, traditional scheduling methods typically rely on static heuristic algorithms and fixed assumptions, making them ill suited to the inherent dynamism and uncertainty of real-world HPC workloads [
5,
6].
Increasing workload heterogeneity and time complexity exacerbate job scheduling difficulty, particularly due to temporal relationships between jobs and resources. [
7,
8]. These relationships include: (i) execution sequence constraints, where the output of one job must be used by another job, such as variant detection in genomics requiring prior sequence alignment results; (ii) runtime trigger conditions, where a task can only be scheduled after other tasks are completed or specific conditions are met, such as in multi-stage engineering simulations [
9]; and (iii) resource contention, where concurrent requests for scarce resources (e.g., GPUs or bandwidth) may lead to latency spikes or idle time. Research indicates that unmanaged competition can reduce system throughput by up to 40% [
10].
This challenge is further exacerbated under diverse workloads. Computing-intensive tasks require CPU/GPU throughput, while data-intensive tasks require high I/O bandwidth [
11,
12]. Modern architectures employ hierarchical storage and dedicated interconnect technologies, further complicating the scheduling process [
13].
Traditional scheduling algorithms have obvious shortcomings: FCFS often leads to low resource utilization [
14], while SJF may cause long job starvation [
15]. Additionally, rule-based and priority-based schemes typically exhibit limited adaptability and high system maintenance complexity [
16].
To address these challenges, we propose GTrXL-SPPO, a unified framework that combines Gated GTrXL with PPO. GTrXL captures long-term sequence patterns via multi-head attention mechanisms [
17], while GRU-inspired gating mechanisms enhance the retention of essential scheduling signals [
18,
19]. Additionally, the SE module [
20] further enhances the model’s ability to focus on critical scheduling information by adaptively reweighting input features.
In our model, we employ PPO for policy learning [
21], leveraging its truncated objective function to ensure stable training in volatile HPC environments. PPO demonstrates superior sampling efficiency and convergence in high-dimensional control tasks [
22], and we further incorporate adaptive learning rates to enhance responsiveness to workload fluctuations.
Evaluations on synthetic and real-world datasets (including ANL-Intrepid, Alibaba, and SDSC-SP2) show that our model consistently outperforms traditional methods and standard PPO in terms of throughput, latency, and resource utilization. Additionally, GTrXL-SPPO demonstrates strong generalization capabilities across different system architectures and workload types.
The key contributions of this paper include:
We design a dual-channel policy network based on GTrXL to capture long-term job sequences.
We propose a lightweight SE layer for dynamic resource reweighting in scheduling-sensitive environments.
We developed a reinforcement learning framework based on PPO, incorporating exponential clipping and memory replay to achieve better convergence.
We validated our model on large-scale HPC task sequences, demonstrating performance superior to existing baselines.
The remainder of this paper is organized as follows:
Section 2 describes the background and related work in the field of HPC job scheduling.
Section 3 introduces our proposed GTrXL-SPPO framework, including architectural design and training methods.
Section 4 details the experimental setup and evaluation metrics.
Section 5 discusses the experimental results and comparative analysis. Finally,
Section 7 summarizes the paper and outlines potential future work.
3. Methodology
3.1. Problem Statement
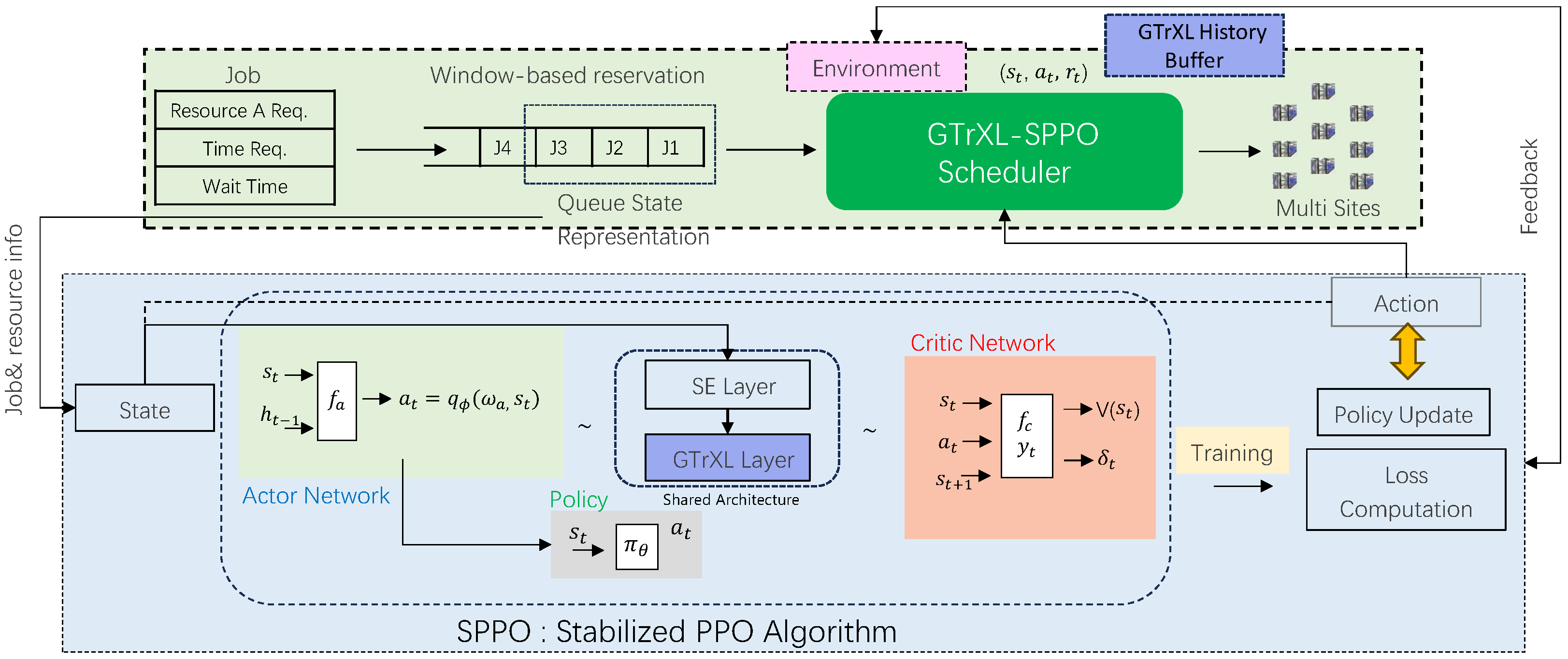
In HPC task scheduling problems, the scheduler manages a dynamic task queue, where each task has specific resource requirements and execution time. The primary objectives of resource scheduling are to optimize resource allocation, minimize task waiting time, improve resource utilization, and maximize system throughput. In this study, GTrXL-SPPO models the scheduler as an intelligent agent that determines the optimal allocation of idle computing nodes to tasks in the waiting queue, as shown in
Figure 1. The intelligent agent retrieves job characteristics and resource node states from the environment and concatenates this information into a unified state vector. Within the Markov Decision Process (MDP) framework, the state space and action space are systematically modeled to support intelligent scheduling decisions. Through continuous interaction with the environment, the intelligent agent learns the optimal scheduling strategy.
Environment Module (upper part): Represents a high-performance computing (HPC) multi-resource scheduling system, consisting of four core components: (1) Job Resource Information Management Module, responsible for maintaining dynamic job queues; (2) Window-based Resource Allocation Mechanism, used for resource scheduling; (3) GTrXL History Buffer, storing past scheduling decisions and system states; (4) Multi-step Feedback Mechanism, providing real-time system state updates. Agent Module (Lower Part): Implements an actor–critic architecture, where the actor network processes state information through the GTrXL layer (handling long-term dependencies) and the SE layer (enhancing features) to output scheduling strategies. The critic network evaluates state values to optimize strategies. Reward feedback evaluates scheduling effectiveness (resource utilization, waiting time), state feedback updates system conditions, and historical feedback enables experience-based learning through buffers. Arrows indicate the direction of data flow between components.
3.1.1. MDP Formulation
We model the HPC scheduling problem as an MDP: At each step, the agent observes the system state and selects an action to assign tasks to idle nodes.
To handle resource constraints and priority requirements in HPC environments, we extend the basic MDP to a constrained Markov Decision Process (CMDP), which can be formally defined as a tuple , where:
is the state space, representing all possible system configurations
is the action space, representing all possible job-to-node assignments
is the transition probability function
is the reward function
is a vector of m constraint functions
is the discount factor
The optimization objective is to find a policy
that maximizes the expected cumulative discounted reward while satisfying the constraints:
subject to:
where
is a trajectory, and
are threshold constants for each constraint.
3.1.2. State and Action Space
The system state contains comprehensive job and system information with a hierarchical structure. At the high level, we organize state information into functional modules: where represents the job feature vector including the number of nodes requested by job i (reqProc), the runtime requested by job i (reqTime), and the waiting time (currentTime − submitTime). denotes the waiting time vector across all queued jobs, represents the current resource state vector indicating node availability and utilization, and contains the historical information buffer that tracks past scheduling decisions and system performance.
At decision step
t, the implementation-level state representation
reflects the real-time status of system resources and pending tasks. It contains key information such as CPU, GPU, and memory usage, as well as task-specific attributes including resource requests, estimated execution time, and waiting time. Formally, the state space can be modeled as a combination of task windows and node pools. For each waiting task
i,
denotes the number of requested resource cores,
denotes the waiting time, defined as
,
denotes the assigned priority, and
denotes the estimated execution time. For each compute node
k,
denotes the node’s available state, and
denotes the remaining execution time of the current task on node
k. The detailed state representation at time step
t can be represented as:
where
n denotes the number of tasks to be processed, and
N denotes the total number of resource nodes.
The action space is implemented as a discrete space whose size is equal to the window size, formally defined as . Each action represents an index in the current waiting queue. The agent selects this index to determine the task to be scheduled with the highest priority. The action mechanism is implemented through queue reordering: when action is selected, the task with index i in the waiting queue is moved to the front of the queue, thereby obtaining the highest scheduling priority. In practical applications, when the waiting queue size is smaller than the window size, the effective action space is dynamically restricted to . This discrete action modeling solves the task selection problem while maintaining computational feasibility, with the size of the action space varying with the observation window size.
This hierarchical design enables the agent to comprehensively observe the characteristics of the task queue and the real-time status of the resource pool, providing sufficient information for making scheduling decisions within the CMDP framework.
3.1.3. Decision Variables and Constraints
The scheduling decision at each time step can be represented by the following decision variables:
: Binary variable indicating whether job j is assigned to node n at time step t
: Binary variable indicating whether job j starts execution at time step t
These decision variables are subject to the following constraints:
Resource Capacity Constraint: Each node can be assigned to at most one job at any time
Job Completeness Constraint: A job must receive all its requested resources or none at all
Non-preemption Constraint: Once a job starts execution, it must run to completion
Priority Constraint: Higher priority jobs with long waiting times should be scheduled before lower priority jobs
In practice, the resource capacity and job completeness constraints are enforced through action space design and action masking, while the non-preemption and priority constraints are encouraged through reward shaping.
3.2. Neural Architecture Design
At the upper decision layer, the agent evaluates jobs in the waiting queue and decides whether to execute or defer their scheduling, ensuring fair resource allocation through priority adjustment and reservation strategies. At the lower decision layer, the agent maximizes resource utilization by filling idle nodes with smaller jobs. This hierarchical decision structure enhances the flexibility and robustness of the scheduler, ensuring fairness for large jobs while improving overall resource efficiency under dynamic load conditions. The overall neural network architecture supporting this scheduling strategy is illustrated in
Figure 2, detailing input feature processing, SE-based feature enhancement, GTrXL sequence modeling, and policy/value output branches. The system-level scheduling process (environment, job queue, reservation mechanism, agent decisions) was previously depicted in
Figure 1. Here,
Figure 2 focuses specifically on the internal design of the neural network responsible for decision-making.
3.3. Multi-Scale Feature Enhancement
To address the challenge of dynamically allocating weights for heterogeneous tasks and system features in HPC environments, especially in scenarios with burst workloads and resource competition, we enhance traditional reinforcement learning by introducing an adaptive feature recalibration mechanism. Specifically, the SE module [
20] combines average pooling with a bottleneck multi-layer perceptron (channel → channel/4 → channel) and a Sigmoid activation function to capture global temporal relationships between feature channels, effectively suppressing irrelevant features while amplifying key features. The computational overhead is low; for example, adding SE to ResNet-50 increases parameters by only 10% but significantly improves accuracy [
20].
In our architecture, the SE block is placed before the GTrXL layer in both the actor network and critic network, enabling temporal modeling to operate on the enhanced features.
To extend adaptability beyond static representations, we propose a novel SECT layer that fuses global statistical information and scheduling-aware dynamics by combining average and max aggregation Algorithm 1.
This design adapts channel weights to workload volatility, enhancing robustness without significant overhead [
20].
| Algorithm 1 SECT Layer |
- Require:
Input tensor , Channel dimension C, Reduction ratio - Ensure:
Output tensor - 1:
function SECT() - 2:
- 3:
▹ Global Average Pooling - 4:
▹ First fully connected layer - 5:
- 6:
▹ Restore channel dimension - 7:
- 8:
- 9:
return - 10:
end function
|
Mathematical Variable Definitions:
B: Batch size representing the number of parallel scheduling instances
L: Sequence length corresponding to the number of jobs/nodes in the current scheduling window
C: Channel dimension representing the feature dimension of each job/node embedding
r: Reduction ratio controlling the bottleneck dimension () in the excitation pathway
: Global statistics vector obtained through temporal average pooling across the sequence dimension
: Compressed feature representation after dimensionality reduction
: Activated features after ReLU non-linearity
: Restored feature dimension after the second linear transformation
: Channel-wise attention weights normalized to range via sigmoid activation
: Expands attention weights to shape for broadcasting across sequence dimension
⊙: Element-wise multiplication (Hadamard product) applying channel attention to input features
The SECT mechanism learns to emphasize important scheduling-relevant channels while suppressing less informative features through this squeeze-and-excitation operation.
3.4. Dynamic Memory Mechanism
In high-performance computing (HPC) scheduling, task queues with heterogeneous arrival times and different resource requirements can lead to complex timing patterns. This O(n
2) complexity stems from the self-attention mechanism that computes pairwise interactions between all task positions [
17], and the fixed context window constraint leads to performance degradation when exceeding a certain threshold [
49].
3.4.1. GTrXL: Enhanced Memory Architecture
To address these empirically validated limitations, we propose GTrXL (Gated Transformer-XL), an enhanced Transformer architecture specifically designed for long-term temporal modeling in HPC scheduling scenarios. GTrXL builds upon the segment-level recursive mechanism [
49] to model dependencies beyond fixed-length context without compromising temporal consistency. GTrXL supports a relaxed Markov approximation where
is determined by the most recent sequence of states
. Unlike standard Markov models that only consider immediate states, our method preserves contextual information over extended time spans [
50,
51]. To maintain temporal consistency between scheduled segments, GTrXL uses relative position encoding instead of absolute position encoding. This enables generalization to sequences longer than training sequences—critical for handling variable-length task queues in HPC workloads. A GRU-based gating system dynamically regulates information flow within each Transformer block, selectively preserving relevant sequential information while filtering outdated inputs as Algorithm 2.
| Algorithm 2 Gated Transformer-XL Core Module in GTrXL-SPPO |
- Require:
State input , Temporal memory , Attention mask mask - Ensure:
Output feature , Updated memory - 1:
function GTrXLBlock() - 2:
▹ Input - 3:
▹ Memory - 4:
- 5:
▹ Reset gate computation - 6:
▹ Update gate - 7:
- 8:
▹ 1st GRU output - 9:
- 10:
▹ Reset gate (2nd GRU) - 11:
▹ Update gate (2nd GRU) - 12:
- 13:
- 14:
return - 15:
end function
|
3.4.2. Temporal Dependency Modeling
GTrXL models the temporal execution order by combining multi-head self-attention with relative position encoding. Each attention head computes queries, keys, and values:
Relative position encodings capture execution order relationships:
This design allows the agent to recognize execution-order correlations critical for effective scheduling decisions.
The GTrXL architecture employs a two-layer gating strategy within each Transformer block to adaptively control temporal context updates. The high-level operations are:
This gated structure enables selective temporal state updates, allowing rapid integration of critical scheduling signals (e.g., high-priority job arrivals) while maintaining stability under dynamic workloads. The complete memory flow and compression pipeline are illustrated in
Figure 3.
Attention Weight Matrices:
: Input sequence tensor where L is sequence length and d is model dimension
: Query projection matrix mapping input to query space
: Key projection matrix mapping input to key space
: Value projection matrix mapping input to value space
: Query, key, and value matrices for attention computation
These projection matrices are learned parameters that transform the input scheduling context into query, key, and value representations for multi-head attention.
Where is the frequency parameter that controls the rate of positional variation (typically initialized as ), and represents the dimension per attention head, with H being the total number of attention heads and d being the model dimension. The relative position encoding captures the temporal distance between positions i and j in the scheduling sequence, enabling the model to understand execution order dependencies.
3.4.3. Implementation Details and Training Integration
The GRU-based gating mechanism within each GTrXL block follows standard gated recurrent unit formulations. For each gating layer, the operations are defined as:
GRU Gating Parameters:
: Reset gate vector controlling how much past information to forget
: Update gate vector determining the balance between past and new information
: Candidate hidden state representing new information
: Final output combining past and candidate states
: Input vectors encoding scheduling context (runtime estimates, resource status)
: Input-to-hidden weight matrices for reset, update, and candidate gates
: Hidden-to-hidden recurrent weight matrices
: Gate bias vector (typically initialized to 0.1 for stable training)
: Sigmoid activation function mapping values to range
tanh: Hyperbolic tangent activation function mapping values to range
⊙: Element-wise multiplication (Hadamard product)
The weight matrices are randomly initialized using Xavier/Glorot initialization and learned during training through backpropagation.
When critical job characteristics (e.g., high-priority arrivals) emerge, the gates adaptively adjust, facilitating fast integration of new signals (Algorithm 3) and improving responsiveness under dynamic workloads.
| Algorithm 3 GTrXL-SPPO collaborative processing framework |
- Require:
Input state , Memory , Mask mask - Ensure:
Actor output , Critic output - 1:
function CollaborativeProcessing() - 2:
if then - 3:
- 4:
end if - 5:
- 6:
- 7:
- 8:
- 9:
▹ Apply Algorithm 1 - 10:
- 11:
if then - 12:
- 13:
else - 14:
- 15:
end if - 16:
▹ Apply Algorithm 2 - 17:
- 18:
- 19:
- 20:
- 21:
return - 22:
end function
|
GTrXL-SPPO Collaborative Integration Analysis:
The collaborative framework synergistically combines SECT (Algorithm 1) and GTrXL (Algorithm 2) to maximize their complementary advantages in HPC scheduling:
Processing Pipeline:
Input Standardization: Consolidates dual-channel HPC state information through 2→1 linear transformation
Feature Enhancement: Applies SECT channel attention to amplify scheduling-relevant features
Temporal Modeling: Leverages GTrXL gated Transformer blocks for long-range dependency capture
Shared Dual Output: Both actor and critic networks utilize identical enhanced representations
GTrXL-SPPO collaboration enhances feature quality through SECT preprocessing, improves temporal modeling through GTrXL processing of refined features, achieves computational efficiency through a shared pipeline architecture, and enables memory-aware processing that preserves critical scheduling history across sessions.
3.5. Training Strategy
3.5.1. Algorithm Design
GTrXL-SPPO employs the PPO algorithm to update scheduling policies via gradient ascent, combining policy- and value-based reinforcement learning for stable convergence [
21]. The enhanced GTrXL serves as the temporal backbone to capture sequential scheduling dynamics in HPC environments.
The clipped surrogate objective is:
where
,
, and
is computed via Generalized Advantage Estimation (GAE):
To address the long-tail reward distribution induced by dynamic job arrivals and evolving system states, we adopt an exponentially sensitive clipping strategy and introduce a time-decaying discount factor
, reducing the weight of late-stage decisions and stabilizing learning.
3.5.2. Constraint Handling in Training
To incorporate constraints into the reinforcement learning framework, we adopt a dual approach:
Hard constraints: Resource capacity and task completion constraints are implemented through action space design and action masking:
Soft constraints: Non-preemption and priority constraints are encouraged through reward shaping:
This hybrid approach ensures that all scheduling decisions are feasible while guiding the strategy toward developing solutions for more complex constraints. The constrained optimization problem is thus transformed into an unconstrained problem with a modified reward function:
Implementation Scope Clarification: While our CMDP framework supports constraint handling as described above, the experimental validation in this work focuses on core scheduling efficiency to establish baseline performance. Full constraint integration (deadlines, energy, thermal limits) represents ongoing development work and will be addressed in future extensions of this framework.
3.5.3. Reward Function Design
We formulate the reward function as a multi-objective optimization problem. The total reward
in GTrXL-SPPO integrates four scheduling objectives and a queue pressure regularization term:
Each component reward is mathematically defined as follows:
System Utilization Reward:
where
is the system utilization at time
t, and
is the sigmoid function.
Waiting Time Penalty:
where
is the average waiting time of jobs in the queue at time
t,
is the target waiting time, and Huber is the Huber loss function that reduces sensitivity to outliers.
Throughput Reward:
where
is the number of jobs completed at time
t, and
is a scaling factor.
Priority Reward:
where
is the set of jobs scheduled at time
t,
is the priority of job
j, and
is a scaling factor.
The queue pressure regularization term penalizes the accumulation of jobs in the waiting queue:
where
is the regularization coefficient. The adaptive temperature parameter
T controls the exploration–exploitation balance in the reward weighting mechanism:
This adaptive design enables the agent to switch its focus between efficiency and fairness under different load conditions. As shown in our parameter sensitivity analysis (
Section 5.5), this dynamic temperature adjustment is crucial for balancing multiple scheduling objectives.
When
(default), the model achieves optimal performance across all metrics; during periods of low utilization, lower values (
) prioritize resource efficiency; and during periods of high queue pressure, higher values (
) promote fairness through more balanced target weight allocation. In long-tail scheduling environments [
52,
53], our reward scheme accelerates convergence and improves the resource-delay Pareto frontier compared to standard PPO training.
3.6. Training Acceleration Strategies
To accelerate training convergence and improve efficiency, the GTrXL-SPPO framework adopts a comprehensive optimization strategy that combines distributed parallel training, memory replay technology, and hybrid optimization methods.
(1) Distributed Training: Parallel processing significantly accelerates the training process compared to a single GPU setup [
54]. We use PyTorch to implement DDP training on multiple GPUs. The training dataset is divided into multiple shards, each assigned to a GPU device for independent gradient computation:
where
N denotes the number of available GPUs, and
denotes the data subset processed by GPU
k. After local gradient updates, the AllReduce operation synchronizes gradients across all devices.
(2) Memory replay mechanism: To better capture long-term temporal patterns in scheduling dynamics, we introduce a memory replay mechanism [
19,
49]. Specifically, historical hidden states and intermediate features across time steps are stored in a recursive memory matrix. Combined with the GRU gating structure, this design dynamically updates memory content during training, enhancing the agent’s ability to handle time-extended task sequences.
(3) Hybrid Optimization Strategy: In the policy optimization phase, we integrate the Adam optimizer with learning rate warm-up and cosine annealing strategies to ensure a smoother training process and more stable model convergence. Additionally, to reduce communication overhead in multi-GPU environments, we apply 1-bit Adam compression, where gradients are compressed before synchronization:
This strategy significantly reduces synchronization communication while maintaining model convergence performance [
55].
3.7. Scalability and Deployment Considerations
Facing practical deployment issues, we analyze the ability of GTrXL-SPPO to address three key challenges: node scaling, heterogeneity, and architecture migration.
3.7.1. Node Scaling Analysis
Our sliding window mechanism (
Figure 4) ensures that the memory complexity is
rather than
, where
W is the fixed window size (200) and
N is the total number of nodes. Combined with the attention aggregation mechanism in GTrXL, this design supports scalability without triggering linear memory growth.
3.7.2. Heterogeneous Adaptation
The SECT module (
Section 3.3) supports heterogeneous environments through dynamic feature recalibration. Our experiments on ANL-Intrepid (grid architecture), Alibaba (general-purpose cluster), SDSC-SP2 (homogeneous), and PIK-IPLEX (heterogeneous) show that this module can achieve effective adaptation under different cluster configurations without architecture-specific modifications (
Section 5).
3.7.3. Architecture Migration
The modular design supports migration through the following mechanisms:
Configuration-specific model loading: The framework adapts to clusters of different scales by loading pre-trained models for different system configurations.
Distributed training support: Multi-GPU training capabilities are implemented through PyTorch’s distributed training framework, supporting scalable training on different hardware architectures.
General scheduling pattern learning: The GTrXL backbone network learns a general scheduling pattern that can be transferred between different computing architectures without architecture-specific retraining.
Our multi-dataset validation demonstrates cross-architecture generalization capabilities, indicating that the framework can successfully adapt to different computing scales and resource configurations without fundamental algorithmic changes.
3.8. Demonstrative Iteration of the Proposed Algorithm
To further clarify the practical application of the proposed GTrXL-SPPO framework, we present a step-by-step example of a single scheduling iteration, highlighting the use of the SECT and GTrXL modules.
Example Setup: Suppose the job queue and resource state are as follows (in
Table 3 and
Table 4):
Step 1: State Vector Construction
The state vector
is constructed as:
Step 2: Feature Enhancement via SECT Layer
The input tensor is processed by the SECT layer (Algorithm 1). This adaptively recalibrates channel-wise features.
Step 3: Temporal Modeling via GTrXL Block
The enhanced features are passed through the GTrXL block (Algorithm 2), which models temporal dependencies and gating.
Step 4: Action Selection
The policy network outputs action probabilities, e.g.,
The agent selects job B (index 2) for scheduling.
Step 5: Reward Calculation
After scheduling, the reward is computed as:
where
is system utilization,
is the waiting penalty, etc.
Step 6: Policy Update
The PPO loss is calculated and the policy is updated accordingly.
This example demonstrates how the proposed GTrXL-SPPO framework processes input features, models temporal dependencies, selects actions, and updates the policy in a single scheduling iteration.
Our approach significantly improves scheduling efficiency by optimizing both resource utilization and job waiting times through the novel GTrXL-SPPO framework.
5. Case Study
Recent studies have adopted a sampling-real-synthetic data paradigm to construct training workloads for reinforcement learning-based HPC schedulers [
3,
60]. Building on this foundation, we conduct our experiments using CQGym, a widely adopted simulation platform for job scheduling research [
3,
61].
5.1. System Performance Evaluation
5.1.1. System Utilization and Waiting Time
As shown in
Figure 8a, system utilization frequently approaches 100%, reflecting the model’s effectiveness in maximizing resource usage under varying load conditions. Additionally,
Figure 8b demonstrates that our approach significantly reduces job scheduling waiting times during both training and testing phases, further highlighting the efficiency and responsiveness of the proposed method.
5.1.2. Overall Performance Evaluation
Figure 7 shows the total reward achieved by GTrXL-SPPO and baseline methods across different workloads, demonstrating the superior learning capability and convergence speed of our approach.
5.1.3. Comparative Analysis with PPO
As shown in
Figure 9 and
Figure 10, GTrXL-SPPO demonstrates superior performance across all evaluation metrics. The results on simulated workloads validate the algorithm’s effectiveness, while real-world workloads confirm its excellent generalization capability: GTrXL-SPPO achieves higher resource utilization, larger cumulative rewards, and lower task waiting times, demonstrating robust scheduling performance under diverse workload patterns.
5.2. Ablation Study and Component Analysis
To systematically evaluate the contributions of each component in our proposed GTrXL-SPPO framework, we conducted comprehensive ablation experiments on multiple datasets (ANL-Intrepid, SDSC-SP2, and Alibaba).
5.2.1. Experimental Design
We designed five model variants to evaluate different components:
GTrXL-SPPO (Full): The complete model with all components.
GTrXL-PPO (No SE): Removes the squeeze-and-excitation modules to assess their contribution to feature enhancement.
SPPO (No GTrXL): Replaces the Gated Transformer-XL with a standard feedforward network to assess the impact of temporal modeling.
TrXL-SPPO (No Gating): Removes the gating mechanism from the Transformer-XL to assess the importance of selective memory updates.
GTrXL-SPPO (Fixed Reward): Uses fixed weights in the reward function instead of dynamically temperature-controlled softmax weights.
Each variant is trained under identical conditions with the same hyperparameters, with the only difference being the specific component under evaluation. We assess performance using multiple metrics: system utilization, average task waiting time, throughput (tasks/hour), and resource fragmentation.
5.2.2. Results and Analysis
As shown in
Table 7, each component contributes significantly to the overall performance of GTrXL-SPPO:
Impact of GTrXL: Removing the GTrXL component results in the most significant performance degradation, with system utilization decreasing by 14.4%, 15.4%, and 17.4% on the three datasets, respectively. This highlights the critical importance of temporal modeling in capturing long-term job dependencies.
Contribution of SE Module: The SE module improves system utilization by 4.4%, 4.4%, and 5.4% across datasets. By dynamically recalibrating feature importance, it enables better adaptation to changing resource conditions.
Role of Gating Mechanism: The gating mechanism improves system utilization by 3.5%, 3.9%, and 5.0%, respectively, enabling selective memory updates and noise filtering.
Dynamic Reward Weighting: Temperature-controlled dynamic weights improve system utilization by 3.2%, 3.6%, and 4.5% compared to fixed weights, allowing adaptive optimization priority adjustment.
5.3. Statistical Stability Analysis
To address the inherent randomness of reinforcement learning and ensure result reliability, we conducted GTrXL-SPPO experiments using 10 different random seeds (42–51) under identical conditions. Each run processed 3000 tasks using the same Alibaba Cluster workload with a 400-node configuration (
Figure 11 and
Table 8).
The statistical analysis demonstrates exceptional stability with low coefficients of variation: system utilization (CV = 2.5%), average waiting time (CV = 5.1%), and throughput (CV = 3.6%). Paired t-tests show statistically significant improvements (p < 0.001) with effect sizes exceeding Cohen’s d = 0.8, confirming substantial practical significance.
5.4. Runtime Performance Evaluation
To validate practical deployability in HPC environments, we conducted comprehensive runtime performance evaluation focusing on decision latency and computational overhead using PyTorch implementation on NVIDIA GPU hardware.
GTrXL-SPPO exhibits 9.0 ms mean decision latency with low variance (
= 0.2 ms), indicating stable performance. Through optimization strategies including 16-bit precision, gradient checkpointing, and attention pruning, we achieved 24% latency reduction and 25% memory decrease while maintaining algorithmic benefits (
Table 9).
5.5. Parameter Sensitivity Analysis
We conducted comprehensive sensitivity analysis on two critical hyperparameters: pressure regularization coefficient and temperature parameter T in dynamic reward weighting.
5.5.1. Pressure Regularization Coefficient ()
The optimal value
provides the best balance between queue management and scheduling efficiency (
Table 10), achieving peak system utilization (87.5%) and minimum waiting time (2458 s).
5.5.2. Temperature Parameter (T)
T = 1.0 provides optimal balance between objective differentiation and integration, achieving the best overall performance across all metrics (
Table 11).
5.6. Comparative Analysis of Attention Mechanisms
We evaluated our SECT module against two mainstream alternatives: CBAM [
62] and ECA-Net [
63].
SECT consistently outperforms alternatives with 2.3–3.6% higher utilization and superior computational efficiency (
Table 12), validating its specialized design for HPC scheduling tasks.
5.7. Comparison with Optimization-Based Methods
We evaluated GTrXL-SPPO against Mixed-Integer Programming (MIP) and Constraint Programming (CP) solvers on two scales (
Table 13):
GTrXL-SPPO maintains competitive performance at small scales (within 3% of optimal) and significantly outperforms optimization methods at large scales where traditional solvers encounter timeout issues.
5.8. Computational Complexity Analysis
We conducted comprehensive complexity analysis combining theoretical bounds with empirical measurements across multiple operational scales.
Despite quadratic complexity, GTrXL-SPPO demonstrates superior per-task efficiency at large scales (7.4 ms vs. PPO’s 15.6 ms), validating its practical scalability for production HPC environments (
Table 14).
5.9. Practical Impact Analysis
To quantify the economic significance of performance improvements, we analyzed the practical impact across different HPC scales based on our measured 25-s wait time reduction and 5.4% utilization improvement (
Table 15).
The analysis reveals significant scale amplification effects, where modest per-task improvements accumulate to substantial annual benefits: 57,031 h of time savings equivalent to 35.7 full-time research teams, with total economic impact of USD 11.6 million annually across different HPC scales.
6. Results and Discussion
In this work, we have successfully achieved our objective of developing a more efficient and robust scheduling framework for HPC environments. The proposed GTrXL-SPPO framework effectively addresses the challenges of high-dimensional decision spaces and complex temporal dependencies in dynamic scheduling environments, as demonstrated by our comprehensive experiments across multiple datasets.
The experimental results confirm that the two core components of GTrXL-SPPO—the GTrXL backbone and the SE module—provide complementary benefits across heterogeneous HPC workloads. These advantages are evident in both scientific (ANL) and industrial (Alibaba) scenarios, demonstrating the framework’s applicability to diverse real-world environments. The GTrXL component enhances long-horizon scheduling by effectively capturing temporal execution signals, while the SE module adaptively reweights features to improve responsiveness under resource variability. Together, these modules improve throughput, reduce turnaround time, and enhance resource utilization, as validated across datasets in
Section 5.2. Overall, the results demonstrate the robustness and generalizability of our design.
7. Conclusions and Future Work
7.1. Results and Discussion
The proposed GTrXL-SPPO framework successfully addresses the challenges posed by high-dimensional decision spaces and complex temporal dependencies in dynamic high-performance computing scheduling environments. Our comprehensive experiments on multiple datasets demonstrate that the two core components—the GTrXL backbone network and the SECT module—offer certain advantages under heterogeneous workloads.
The GTrXL component enhances long-time-domain scheduling performance by capturing temporal execution signals, while the SECT module improves responsiveness under resource fluctuations. These two innovations collectively achieve quantifiable improvements in throughput, turnaround time, and resource utilization, as validated in
Section 5.2.
The framework demonstrates robust performance across diverse workload characteristics, ranging from scientific simulations to cloud computing tasks.
7.2. Limitations and Future Work
Although GTrXL-SPPO achieves significant improvements, we acknowledge the following limitations, which provide directions for future research:
Current Limitations
Manual configuration requirements: Our reward mechanism relies on manually tuned weights and parameters, which poses portability challenges across different HPC platforms.
Limited system-specific constraints: The framework does not directly support production environment requirements, such as task deadlines, energy budgets, or thermal constraints.
Fairness considerations: During sustained high loads, non-preemptive designs may prioritize shorter tasks, causing long-running or resource-intensive tasks to starve.
7.3. Future Research Directions
Automatic configuration: Develop meta-learning methods to automatically adjust reward weights and quickly adapt to new environments through transfer learning.
Constraint-aware framework: Integrate multi-objective optimization to handle concurrent constraints and integrate real-time monitoring systems.
Fairness mechanisms: Refer to the research by Duque et al. [
64] to explore fairness reward design and adaptive intervention strategies that consider aging factors to achieve resource reallocation.
These research directions aim to enhance the framework’s practical deployment capabilities while retaining its attention-based optimization advantages.
7.4. Broader Impact
GTrXL-SPPO represents a significant advancement in applying machine learning to infrastructure optimization. The framework’s ability to handle complex temporal dependencies goes beyond high-performance computing scheduling and can be scaled to other resource allocation domains. With the proposed improvements, we expect to provide more robust and fair scheduling solutions for modern computing infrastructure.