1. Introduction
The Solidity programming language, designed by Gavin Wood under the Ethereum Foundation, was created to facilitate the implementation of smart contracts on the Ethereum Virtual Machine (EVM) using an object-oriented paradigm [
1]. Initially, Solidity’s code was compiled directly into EVM’s bytecode by the Solidity compiler. This bytecode was then deployed onto the blockchain and executed on demand. However, the importance of compiler-level code optimization is a well-established principle in software engineering, and Solidity is no exception to this rule. Direct compilation from Solidity to the EVM bytecode posed certain limitations on optimization, prompting the Solidity compiler team to design an intermediate language called Yul. Yul acts as a bridge between Solidity and EVM bytecode, where most of the optimizations are applied [
2]. As of today, the Solidity compiler incorporates manually hardcoded sequences of optimization steps.
One of the key challenges associated with compiler optimization is determining the optimal order of optimization steps. This issue, known as the phase-ordering problem, is well-known in the domain of compilers and is inherently complex, as the solution space is vast and the problem is classified as NP-complete [
3]. Various strategies have been proposed to address this challenge across different programming languages. A common approach involves relying on expert-designed sequences of optimization steps, typically created by the compiler developers or language designers. While this method may not always yield the most efficient solutions, it remains widely used. Notably, the Solidity compiler employs a predefined sequence of optimization steps, as specified by its development team (the default optimization steps settled by Solidity team can be found at
https://github.com/ethereum/solidity/blob/develop/libsolidity/interface/OptimiserSettings.h#L42 (accessed on 20 May 2025).
An early algorithmic approach to addressing this problem involves the use of genetic algorithms [
4,
5,
6,
7]. These algorithms evolve random sequences of optimization steps into better-performing chains through iterative refinement. However, genetic algorithms have significant drawbacks. The process of searching for an optimal solution is computationally expensive, and due to the nature of these algorithms, there is no clear separation between the learning phase and the prediction phase. Consequently, this approach often results in a single, static chain of optimization steps. Given the vast diversity of programs, it is virtually impossible to find one universal chain of steps that performs equally well across all use cases. While some programs may benefit from such optimizations, others may experience degraded performance. It is worth noting that in 2020, the Solidity compiler team conducted research to explore the use of genetic algorithms for identifying better optimization sequences (reports from this research can be found at
https://github.com/ethereum/solidity/issues/7806, accessed on 7 August 2025). Despite this effort, they ultimately opted to retain a manually curated optimization sequence.
The introduction of neural networks marked a significant milestone in the quest to find solutions for compiler optimization with distinct learning and prediction phases. In [
8], the authors proposed NEAT, an approach that combines genetic algorithms and neural networks to predict dynamic program-specific optimization steps. Unlike static optimization sequences, NEAT enables the generation of tailored steps for individual programs and even specific functions. This method was implemented and tested on a Java compiler, yielding promising results. With the advent of greater computational power and advancements in deep neural network techniques, researchers began exploring reinforcement learning (RL) as a natural and elegant solution to the problem of determining optimization steps.
Reinforcement learning has since become a focal point of research in this domain. For example, in [
9,
10], RL-based approaches were proposed to address the phase-ordering problem in LLVM. These studies compared RL-based solutions to the standard LLVM compiler optimization level (-O3), demonstrating the potential for RL to outperform conventional methods. The authors of these works suggest that future advancements in this field may involve hybrid solutions combining reinforcement learning and transformer models, which are seen as a promising direction for solving optimization challenges more effectively.
However, applying neural networks to this problem introduces a significant challenge: The program’s code must be represented in the form of constant-sized vectors. This requires the development of methods to vectorize program code or its components (e.g., functions). While several studies have proposed solutions for vectorizing LLVM’s intermediate representation (IR), such as [
11,
12], no equivalent solution currently exists for Yul, the intermediate language used in the Solidity compiler. Addressing this gap is the primary focus of this paper.
The lack of a publicly available dataset of Yul code compounds the difficulty of this task. While datasets for Solidity code are available, the optimization improvements discussed earlier require embeddings specifically derived from Yul code. To address this, the author first created a comprehensive dataset of approximately 350,000 Yul scripts [
13]. Drawing inspiration from [
12], the author generated triplets for knowledge graph embedding, which served as embedding seeds for Yul elements. Finally, a solution was developed to calculate vector representations for Yul-based programs. This method computes the final vector representation of a Yul program by summing the vectors of all components within the program’s Abstract Syntax Tree (AST).
One of the key challenges the author encountered was validating the results, which arises for two main reasons. First, as previously noted, to the best of the author’s knowledge, there are no prior attempts to vectorize Yul’s code. This lack of prior work means there are no existing results or benchmarks for direct comparison. Second, evaluating the quality of the obtained vector representations is inherently complex. How can one definitively judge whether the generated vectors accurately represent the structure and relationships of Yul programs?
Manually assessing the similarity between thousands of Yul codes to validate the vector distribution is not feasible. Human judgment alone cannot reliably determine how “close” certain programs are to one another in terms of their structural or functional characteristics. To address this, the author made a best-effort attempt by categorizing contracts into meaningful groups and analyzing whether the resulting vector distributions aligned with these categories. While not definitive, this approach provides some evidence of the method’s effectiveness. Additionally, the distribution of embedding seeds was analyzed, and their alignment with expectations further supports the plausibility of the generated vectors.
However, the most rigorous way to validate the proposed vectorization method would be to integrate it into a practical application—such as combining it with a neural network-based phase-ordering solution like reinforcement learning. The success of such an approach would provide a more concrete and objective measure of the vectorization method’s effectiveness. This step, however, is beyond the scope of the current work and is left as a topic for future research.
The structure of this paper is as follows.
Section 2 reviews related work, focusing on prior attempts to address similar problems for different programming languages and compilers. Additionally, it examines foundational research that underpins the proposed solution, including studies on graph embeddings.
Section 3 provides a deeper theoretical background to knowledge graph embeddings, and it also introduces the grammar and structure of the Yul intermediate language and other relevant concepts.
Section 4 outlines the proposed solution for vectorizing the Yul code. It describes the methodology, implementation details, and techniques used to generate vector representations for Yul-based programs. The results achieved through the implementation of this approach are presented and analyzed in
Section 5, highlighting its effectiveness and key observations. Finally,
Section 6 concludes this paper by summarizing contributions and discussing potential applications and future directions for research in this area.
2. Related Works
The representation of a source code for machine learning applications has evolved significantly in recent years. Traditional compiler-based methods—such as representing programs as lexical tokens, Program Dependence Graphs (PDGs), or Abstract Syntax Trees (ASTs) [
14,
15,
16,
17]—are well suited for parsing, compilation, and static analysis. However, these symbolic representations are generally incompatible with modern AI techniques, which rely on dense, continuous vector inputs to train deep neural networks. To address this limitation, researchers have adopted code embeddings inspired by word embedding techniques in natural language processing, such as Word2Vec by Mikolov et al. [
18] and GloVe by Pennington et al. [
19]. Code embeddings aim to encode both the semantic and syntactic properties of programs into high-dimensional vectors, facilitating similarity comparisons and supporting downstream tasks such as code classification, summarization, and repair.
Early efforts to vectorize source code leveraged structured representations such as ASTs. For example, code2vec by Alon et al. [
11] introduced a neural architecture that learns embeddings for Java code by aggregating paths in the AST, capturing both syntactic and semantic relationships to support tasks like method name prediction and code summarization. This approach was later extended by code2seq [
20], which generates vector sequences to improve interpretability. Although AST-based methods excel at encoding hierarchical code features, they often struggle to scale effectively for large code bases and to capture complex dependencies. Kanade et al. developed CuBERT [
21], a BERT-based model pre-trained on the Python source code that leverages contextual embeddings to capture language-specific semantics. Similarly, Mou et al. [
22] proposed a tree-based convolutional neural network (CNN) to classify C++ programs by embedding ASTs, while Gupta et al. [
23] introduced a token-based sequence-to-sequence model to diagnose and repair common errors in student-written C programs. These approaches highlight the importance of domain-specific adaptations but are typically limited in their generalizability across different programming languages.
Another notable study proposes a generic triplet-based embedding framework [
12]. Unlike the previously mentioned approaches, which are language-specific, this method is designed to be language-agnostic. In this framework, code elements are decomposed into structural “triplets” (entity–relation–entity) and subsequently encoded using a Knowledge Graph Embedding method [
24,
25]. However, while the embedding technique itself is language-independent, generating the triplets requires language-specific preprocessing. The authors demonstrated this approach using LLVM intermediate representation (IR), a stack-based low-level language (similar to assembly) that simplifies triplet extraction due to its linear structure. Their method also includes a process for generating a complete vector representation of a program from the IR embeddings.
Building on these insights and the aforementioned triplet-based framework, this study proposes a novel method to embed Yul, an intermediate language used in Ethereum smart contracts. Unlike lower-level languages, Yul is a higher-level language that incorporates constructs such as if-statements, switch statements, continue statements, functions, and other control structures, and its structure can be represented as an AST. Thus, the tree structure must be analyzed to generate the required triplets for obtaining embeddings of Yul operations. In a subsequent phase of AST analysis, these embeddings are aggregated into a holistic vector representation of the entire program. This complete method is referred to as yul2vec.
3. Background
3.1. Ethereum and Solidity
The emergence of the Ethereum blockchain in 2014 marked a significant advancement in the field of cryptocurrencies, representing the most substantial innovation since the deployment of Bitcoin.
Bitcoin’s core concept revolves around a decentralized, distributed ledger secured through cryptographic techniques, which enables the tracking of transactions between parties without reliance on a central authority. Ethereum extended this fundamental idea by introducing the capability to not only track asset flows but also maintain the state of applications within its ledger. This enhancement enables applications to utilize a globally distributed storage system where data is immutable and cannot be altered or corrupted by third parties.
This breakthrough paved the way for a new and expansive market for so-called smart contracts—decentralized, distributed applications that leverage Ethereum’s global storage. To facilitate the development of smart contracts on the Ethereum Virtual Machine (EVM), the Ethereum Foundation introduced Solidity, a high-level programming language designed specifically for this purpose [
26]. Solidity shares some structural similarities with JavaScript, making it accessible to developers familiar with web-based scripting languages.
Contracts written in Solidity are compiled into EVM bytecode, which is then deployed onto the Ethereum blockchain. The cost of deploying a smart contract depends on the amount of bytecode stored in the blockchain, as measured by its byte size. Additionally, executing any smart contract function that modifies the blockchain state incurs an extitgas fee.
3.2. Yul Intermediate Layer
As with many programming languages, Solidity employs various optimizations to enhance the efficiency of compiled codes. However, unlike conventional compilers that primarily optimize for specific CPU architectures or execution speed, Solidity optimizations serve a dual purpose. The first objective is to minimize the size of the deployed bytecode, particularly the initialization code, which is functionally similar to constructors in object-oriented programming languages. The second objective is to optimize gas consumption, thereby reducing the cost of smart contract execution.
Directly optimizing Solidity’s code into EVM’s bytecode proved to be a challenging and inefficient task. To address this issue and enhance the effectiveness of bytecode optimizations, the Solidity team introduced an intermediate representation language known as Yul in 2018. Over several years of development, Yul matured and was officially recognized as a standard, production-ready, and intermediate Solidity compilation step by 2022.
Yul operates at the level of EVM opcodes while also maintaining features reminiscent of high-level programming languages. It includes control structures such as loops, switch-case statements, and functions, distinguishing it from low-level assembly languages or intermediate representations like LLVM IR. Despite its expressive syntax, Yul maintains a relatively simple grammar. Listing 1 provides a syntax specification, which serves as the foundation for extracting code features and vectorizing Yul code for further analysis. A formal grammar specification for Yul can be found in the official documentation [
27]. A distinctive characteristic of Yul is its strict adherence to a single data type—the 256-bit integer—aligning with the native word size of the EVM. This constraint simplifies the language while ensuring compatibility with the underlying EVM infrastructure.
It is also important to elaborate on the structure of Yul programs, which actually consist of two distinct components. When Solidity code is compiled, it produces a Yul representation in the form of an Abstract Syntax Tree (AST). This AST contains two subcomponents: the initialization code and the runtime code. The first component—the initialization code—is executed at the time the smart contract is deployed. Its purpose is to set up the necessary storage variables and initialize them with default or specified values. This initialization logic can be non-trivial and is somewhat analogous to the constructor of an object in object-oriented programming languages. The second component—the runtime code—represents the core logic of the smart contract. This code is stored on the blockchain and is what actually handles interactions after deployment.
Figure 1 illustrates an overview of the Yul architecture.
| Listing 1. Yul specification schema. |
| Block = ‘{’ Statement* ‘}’ |
| Statement = |
| Block | |
| FunctionDefinition | |
| VariableDeclaration | |
| Assignment | |
| If | |
| Expression | |
| Switch | |
| ForLoop | |
| BreakContinue | |
| Leave |
| FunctionDefinition = |
| ‘function’ Identifier ‘(’ TypedIdentifierList? ‘)’ |
| ( ‘->’ TypedIdentifierList )? Block |
| VariableDeclaration = |
| ‘let’ TypedIdentifierList ( ‘:=’ Expression )? |
| Assignment = |
| IdentifierList ‘:=’ Expression |
| Expression = |
| FunctionCall | Identifier | Literal |
| If = |
| ‘if’ Expression Block |
| Switch = |
| ‘switch’ Expression ( Case+ Default? | Default ) |
| Case = |
| ‘case’ Literal Block |
| Default = |
| ‘default’ Block |
| ForLoop = |
| ‘for’ Block Expression Block Block |
| BreakContinue = |
| ‘break’ | ‘continue’ |
| Leave = ‘leave’ |
| FunctionCall = |
| Identifier ‘(’ ( Expression ( ‘,’ Expression )* )? ‘)’ |
| Identifier = [a-zA-Z_$] [a-zA-Z_$0-9.]* |
| IdentifierList = Identifier ( ‘,’ Identifier)* |
| TypeName = Identifier |
| TypedIdentifierList = Identifier ( ‘:’ TypeName )? ( ‘,’ Identifier ( ‘:’ TypeName )? )* |
| Literal = |
| (NumberLiteral | StringLiteral | TrueLiteral | FalseLiteral) ( ‘:’ TypeName )? |
| NumberLiteral = HexNumber | DecimalNumber |
| StringLiteral = ‘‘‘‘ ([^"\r\n\\] | ‘\\’ .)* ’’’’ |
| TrueLiteral = ‘true’ |
| FalseLiteral = ‘false’ |
| HexNumber = ‘0x’ [0-9a-fA-F]+ |
| DecimalNumber = [0-9]+ |
3.3. Importance of Yul Optimization
Compiler optimizations are important for enhancing the efficiency and performance of applications, particularly because automated techniques applied at different levels (closer to binary code, at the intermediate language level, etc.) can often outperform manual optimizations. In the case of Yul, the primary objective of optimization is to reduce the cost of Ethereum transactions.
Transactions on the Ethereum blockchain can take various forms. Similarly to Bitcoin, transactions may involve direct cryptocurrency transfers. However, Ethereum also supports transactions that invoke smart contract functions, modifying their internal state. The sender bears the cost of these transactions in the form of gas fees, making cost-effectiveness a critical factor in the adoption and usability of decentralized applications.
In contrast to Bitcoin’s non-Turing-complete scripting language—where execution costs are directly proportional to script size—Ethereum’s Turing-complete smart contracts introduce additional complexity. Due to the presence of loops and dynamic computations, execution costs cannot be determined in advance. To address this, Ethereum employs a gas model, in which each EVM opcode has a predefined gas cost. The total execution cost of a smart contract function is calculated as the sum of the gas costs of the executed opcodes.
Given the direct correlation between bytecode efficiency and transaction costs, optimizing the Yul code has a significant impact on reducing gas fees. Efficient bytecode minimizes computational overhead, making decentralized applications more affordable and accessible to users. The bytecode size is also important, as it directly affects the initial deployment cost of the contract (i.e., the cost of storing the script on the blockchain). However, this deployment cost is a one-time expense, making it less critical compared to the recurring costs associated with contract execution.
Table 1 provides an overview of various EVM opcodes and their corresponding gas costs, highlighting the importance of compiler-driven optimizations in reducing transaction expenses.
3.4. Representation Learning
As previously explained, the objective of this paper is to obtain vector representations of Yul programs to serve as suitable inputs for various machine learning tasks. To develop a method for vectorizing entire programs, it is necessary to establish a structural representation of the atomic components of the Yul language, particularly individual instructions.
To achieve meaningful representations of individual instructions, machine learning techniques are employed. Given the absence of labeled data for supervised learning—since generating such data is the very task at hand—unsupervised learning emerges as the natural choice. An unsupervised method must autonomously learn to represent individual instructions by capturing their relationships, similarities, and distinctive features. One promising approach for this is the use of context-window-based embeddings, as seen in models like Word2Vec. These embeddings capture semantic similarities by analyzing the local context of words or tokens within a fixed window. While effective in identifying local syntactic patterns, such embeddings may fall short in capturing the broader structural relationships inherent in programming languages.
A more suitable alternative is Knowledge Graph Embeddings (KGEs), which model relationships between entities and their interactions. In this approach, knowledge is represented as a collection of triplets in the form
, where
h (head) and
t (tail) are entities, and
r represents the relation between them. The goal is to learn vector representations of these components, where relationships are modeled as translations in a high-dimensional space.
Figure 2 illustrates how such translations can be represented in two-dimensional space. This translational property forms the foundation of many KGE methods, which operate under the assumption that, given any two elements of a triplet, it should be possible to infer the third. Various methods accomplish this in different ways.
In this paper, I employ the TransE method [
28], a well-known KGE approach. TransE learns representations by modeling relationships in the form of
for a given triplet
. It achieves this by being trained on a series of valid triplets while minimizing a margin-based ranking loss
, which ensures that the distances of the vector representation of a valid triplet
between the vector of the invalid triplet
are at least separated by a margin
m. The loss function is given by the following:
where
denotes the hinge loss.
The TransE method is computationally efficient, requiring relatively few parameters, and it has been shown to be both effective and scalable [
29].
4. Yul Code Vectorization
In this section, I present the proposed method for vectorizing the Yul code. First, I discuss the process of learning embeddings for atomic entities, followed by embeddings for entire Yul contracts, which are obtained through an analysis of the abstract syntax tree (AST) of the Yul code.
I believe this work will initiate research on applying AI to Yul code and the Solidity compiler.
4.1. Vectorizing Atomic Yul Entities
The first step involves learning embeddings for the atomic components of Yul code—namely, the entities used in representation learning, as described in
Section 3.4. As previously mentioned, this work is based on the framework presented in [
12], where the authors extracted entities and learned embeddings using the Knowledge Graph Embedding (KGE) method for the LLVM-IR language. In this study, the initial task was to define entities specific to the Yul language.
According to the framework, three categories of entities are required: operations (opcodes), types of operations, and argument variations. As mentioned in
Section 3.2, Yul includes built-in opcodes that correspond to EVM opcodes, which naturally fall into the first category. Additionally, developers can define custom functions. In this work, all such function calls are represented by a single custom opcode named functioncall. Furthermore, unlike simple stack-based languages, Yul provides a basic high-level structure with elements commonly found in Java, JavaScript, C++, and other high-level languages, such as for loops and switch statements. These keyword-based statements are also considered separate opcodes.
The second category, types of operations, presents a challenge because Yul is based on a single data type, a 256-bit value. To introduce differentiation among opcode types and improve vector distribution, an artificial classification was proposed. For example, Boolean instructions that return only 0 or 1 (as a 256-bit value) are categorized as the Boolean type. Similarly, operations that handle address-like data (such as blockchain addresses) are classified under the address type.
The third category pertains to variations in opcode arguments. An argument may be a literal, a variable, or a function call.
Table 2 lists the extracted entities used for embedding learning (EVM opcodes are omitted, as they were discussed in previous sections and tables). The relationships between entities include Type (type of entity), Next (next instruction), and
Arg0…ArgN (
n-th argument).
Figure 3 illustrates the example triplets extracted from several lines of code.
With a defined schema for entities, the next step is to process Yul code to collect entities for the KGE learning process. As previously mentioned, Yul is not a stack-based language, meaning that entity extraction is not as straightforward as iterating through the code line by line. Instead, we must obtain the Abstract Syntax Tree (AST) representation of the program. The Solidity compiler (solc) provides an option to generate an AST in JSON format from Yul code. Using this representation, I apply graph processing with a depth-first search (DFS) approach, adapting the traversal method to the specific node types defined by Yul’s syntax.
For example, a for-loop in Yul consists of multiple components: a pre-condition (where the loop variable may be defined), a condition (e.g., x < 10), a post-condition (where the loop variable can be modified), and the loop body (which contains the instructions executed in each iteration). Extracting triplets from a for-loop requires processing each of these components separately. The loop body itself may contain a sequence of statements, each of which might introduce additional structures requiring deeper traversal.
Listing 2 presents a pseudo-code implementation for extracting triplets from Yul’s code.
| Listing 2. Triplet extraction from Yul code. |
| function extract_arguments(ast): |
| arguments = [] |
| for arg in ast: |
| if arg[“nodeType”] eq “YulFunctionCall”: |
| arguments += “function” |
| else if arg[“nodeType”] eq “YulIdentifier”: |
| arguments += “variable” |
| else if arg[“nodeType”] eq “YulLiteral”: |
| arguments += “constant” |
| else: |
| arguments += “unknown” |
| return arguments |
| |
| function extract_function_call(ast): |
| opcode_name = ast[“functionName”][“name”] |
| opcode_type = EVM_OPCODES[ast[“functionName”][“name”]] |
| if opcode_type is null: |
| opcode_type = “unknownTy” |
| opcode_name = “functioncall” |
| |
| append_triplet(opcode_name, opcode_type, extract_arguments(ast[’arguments’])) |
| |
| function extract_triplets(ast): |
| nodeType = ast[“nodeType”] |
| |
| match nodeType: |
| case “YulObject”: |
| extract_triplets(ast[“code”]) |
| case “YulCode”: |
| extract_triplets(ast[“block”]) |
| case “YulBlock”: |
| for statement in ast[“statements”]: |
| extract_triplets(statement) |
| case “YulFunctionCall”: |
| extract_function_call(ast) |
| case “YulExpressionStatement”: |
| extract_triplets(ast[“expression”]) |
| case “YulVariableDeclaration” | “YulAssignment”: |
| extract_triplets(ast[“value”]) |
| case “YulFunctionDefinition”: |
| extract_triplets(ast[“body”]) |
| case “YulIf”: |
| append_triplet(“if”, “booleanTy”, extract_arguments([ast[’condition’]])) |
| extract_triplets(ast[“body”]) |
| case “YulForLoop”: |
| append_triplet(“forloop”, “voidTy”) |
| extract_triplets(ast[“pre”]) |
| extract_triplets(ast[“condition”]) |
| extract_triplets(ast[“post”]) |
| extract_triplets(ast[“body”]) |
| case “YulSwitch”: |
| append_triplet(“switch”, “voidTy”, extract_arguments([ast[’expression’]])) |
| for switch_case in ast[“cases”]: |
| extract_triplets(switch_case[“body”]) |
| case “YulBreak”: |
| append_triplet(“break”, “voidTy”) |
| case “YulContinue”: |
| append_triplet(“continue”, “voidTy”) |
| case “YulLeave”: |
| append_triplet(“leave”, “voidTy”) |
| case “YulIdentifier” | “YulLiteral”: |
| # do nothing |
| |
| for yul_code in yul_dataset: |
| ast = parse_ast(yul_code) |
| extract_triplets(ast) |
4.2. Vectorizing Entire YUL Contracts
Although Yul is a high-level language constructed and represented in an Abstract Syntax Tree (AST) form, at the lowest level of the representation, the fundamental unit that undergoes vectorization is a single expression. According to the Yul specification, such an expression can be categorized as a function call, an identifier (i.e., a variable name), or a literal (e.g., a constant value such as 10).
The vectorization process relies on previously categorized embeddings, which include EVM opcodes, custom opcodes, return types, and argument types. The formal definition for vectorizing a single expression is given as follows:
where
V denotes the vectorization function, and
represents an expression indexed by
n. The terms
and
correspond to the opcode and return type vectors of the given expression, which are obtained from previously trained embeddings. The term
represents the argument vectors, which are computed in a context-aware manner and will be described in detail in the following section. The individual components are weighted by the factors
,
, and
.
Notably, some opcodes or custom functions do not have associated arguments. In such cases, the last term in Equation (
1) becomes a zero vector. For example, Yul keywords that are mapped directly to opcodes, such as break and leave, are treated as simple opcodes with an associated return type of voidTy:
On the other hand, conditional expressions within control flow statements, such as if and for-loop, are treated as arguments. Specifically, the condition expression in an if statement is vectorized as follows:
This approach ensures that expressions within control flow statements maintain structural consistency during the vectorization process. In particular, the weighting factors (, , and ) play a crucial role in capturing the relative importance of opcodes, return types, and arguments, respectively. The subsequent section provides a deeper discussion on the context-aware computation of argument vectors, which further refines the expressiveness of the vectorized representations.
4.3. Context Awareness
The notion of context awareness in the vectorization of Yul code can be understood through two key approaches.
The first approach involves handling non-EVM built-in functions. Whenever a custom function (i.e., a function that is not part of the learned embeddings) is invoked, its opcode vector is not directly assigned. Instead, the vector representation of the function is first computed based on its definition. This ensures that custom functions are evaluated dynamically at runtime rather than relying on a generic functioncall vector. As a result, vectorized expressions are more precise and are tailored to the specific execution context of the program.
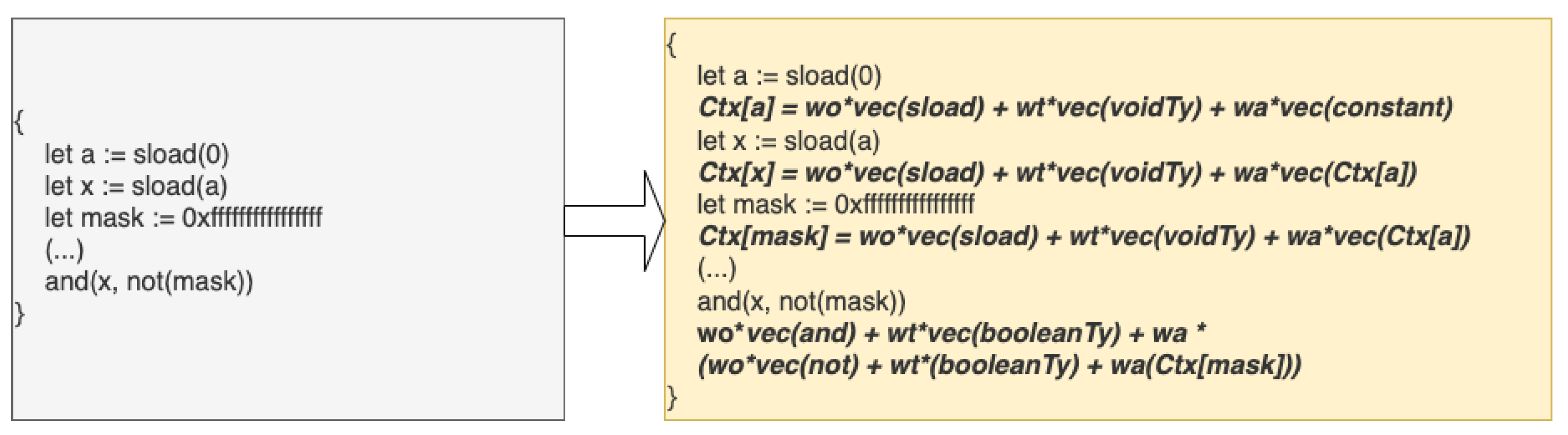
The second crucial aspect of context awareness is variable tracking. A variable definition (i.e., a declaration without an immediate assignment) is represented as a zero vector since it does not yet hold any meaningful computational value. However, once an assignment occurs, the computed vector of the assigned expression is stored. Whenever the variable is subsequently used as an argument in another expression, its stored vector value is substituted accordingly. This mechanism ensures that variables retain contextual information across expressions, improving the fidelity of the vectorized representation.
An illustration of this variable tracking mechanism is presented in
Figure 4, which demonstrates how assigned values propagate through vectorized expressions while preserving contextual dependencies.
4.4. Aggregated Yul Code Vectorization
The final vector representation of a given Yul program is obtained by summing the vectors of all statements within the main block of the code. The vector representation of each statement, in turn, is computed as the sum of the vectors of the expressions contained within it. In other words, to derive the final program vector, I traverse the Abstract Syntax Tree (AST) of the Yul code in a depth-first search (DFS) manner, aggregating the vectors of each expression encountered. Since statements can either be single expressions or combinations of multiple expressions (e.g., a for-loop statement consisting of multiple expressions, including loop conditions and nested expressions inside the loop body), the traversal ensures that all relevant expressions are considered.
However, certain expressions yield a zero vector as their direct result. This occurs in cases such as the following:
Variable Definitions: A variable declaration without an assigned value does not contribute to the aggregated vector.
Assignments: As described in the previous subsection, assignments do not produce a direct vectorized representation. Instead, the vector of the assigned expression is computed and stored in memory (referred to as the context map) for future use, but the assignment operation itself results in a zero vector.
Function Definitions: Defining a function does not contribute directly to the final aggregated vector, as function definitions return a zero vector. However, the function’s vector representation is computed and stored in the context map, ensuring that whenever the function is invoked, its computed vector is retrieved and incorporated into subsequent expressions.
The depth-first aggregation approach ensures that nested expressions are fully evaluated before their parent expressions, maintaining a structured and context-aware vectorization process. The AST traversal must be performed twice: the first pass collects all function definitions into the context map, while the second pass carries out the actual evaluation to compute the final vector.
A pseudo-code implementation of the final Yul code vectorization process is presented in Listing 3, illustrating how expressions and statements are recursively processed to construct the final vector representation.
| Listing 3. Vectorizing Yul code with use of previously learned embeddings and tracking the context (for variables). It is worth mentioning that vectorizing should happen twice for each Yul contract: once to collect all functions in the context, calculating them, and the second one to obtain the final vector. |
| function vectorize_arguments(ast): |
| final_vector = [] |
| for arg in ast: |
| if arg[“nodeType”] eq “YulFunctionCall”: |
| final_vector += vectorize_function_call(arg) |
| else if arg[“nodeType”] eq “YulIdentifier”: |
| final_vector += context[arg[“name”]] || embeddings[“variable”] |
| else if arg[“nodeType”] eq “YulLiteral”: |
| final_vector += embeddings[“constant”] |
| return final_vector |
| |
| function vectorize_function_call(ast): |
| op_code = ast[“functionName”][“name”] |
| if op_code in EVM_OPCODES[op_code]: |
| op_code_type = EVM_OPCODES[op_code] |
| op_code_vec = embeddings[op_code] || embeddings[“functioncall”] |
| else: |
| op_code_type = ‘unknownTy’ |
| if op_code not in context[“functions”]: |
| op_code_vec = embeddings[“functioncall”] |
| else: |
| if context[“functions”][op_code][“calculated”]: |
| op_code_vec = context[“functions”][op_code][“vector”] |
| else: |
| op_code_vec = vectorize_ast(context[“functions”][op_code][“code”]) |
| context[“functions”][op_code][“calculated”] = true |
| context[“functions”][op_code][“vector”] = op_code_vec |
| |
| return op_code_vec * ow + embeddings[op_code_type] * tw + vectorize_arguments(ast[‘arguments’]) * aw |
| |
| def vectorize_ast(ast, ctx): |
| nodeType = ast[“nodeType”] |
| |
| match nodeType: |
| case “YulObject”: |
| return vectorize_ast(ast[“code”]) |
| case “YulCode”: |
| return vectorize_ast(ast[“block”]) |
| case “YulBlock”: |
| final_vector = [] |
| for statement in ast[“statements”]: |
| final_vector += vectorize_ast(statement) |
| return final_vector |
| case “YulFunctionCall”: |
| return vectorize_function_call(ast) |
| case “YulExpressionStatement”: |
| return vectorize_ast(ast[“expression”]) |
| case “YulVariableDeclaration” | “YulAssignment”: |
| var_vector = vectorize_ast(ast[“value”]) |
| for var in ast[“variableNames”]: |
| context[var[“name”]] = var_vector |
| return [] |
| case “YulFunctionDefinition”: |
| if ast[“name”] not in context[“functions”]: |
| context[“functions”][ast[“name”]] = {“calculated”: False, “vector”: [], “code”: ast[“body”]} |
| return [] |
| case “YulIf”: |
| return embeddings[“if”] * ow + embeddings[“booleanTy”] * tw + vectorize_ast(ast[‘condition’]) * aw + vectorize_ast(ast[’body’]) |
| case “YulForLoop”: |
| final_vector = [] |
| final_vector += embeddings[“forloop’)] * ow |
| final_vector += embeddings[“voidTy”] * tw |
| final_vector += vectorize_ast(ast[“pre”]) |
| final_vector += vectorize_ast(ast[“condition”]) * aw |
| final_vector += vectorize_ast(ast[“post”]) |
| final_vector += vectorize_ast(ast[“body”]) |
| return final_vector |
| case “YulSwitch”: |
| final_vector = [] |
| final_vector += embeddings[“switch”] * ow |
| final_vector += embeddings[“voidTy”] * tw |
| final_vector += vectorize_ast(ast[“expression”]) * aw |
| for switch_case in ast[“cases”]: |
| final_vector += vectorize_ast(switch_case[“body”]) |
| return final_vector |
| case “YulBreak”: |
| return embeddings[“break”] * ow + embeddings[“voidTy”] * tw |
| case “YulContinue”: |
| return embeddings[“continue”] * ow + embeddings[“voidTy”] * tw |
| case “YulLeave”: |
| return embeddings[“leave”] * ow + embeddings[“voidTy”] * tw |
| case “YulIdentifier”: |
| return context[ast[“name”]] || embeddings[“variable”] |
| case “YulLiteral”: |
| return embeddings[“constant”] |
| |
| for yul_code in yul_dataset: |
| ast = parse_ast(yul_code) |
| vectorize_ast(ast) |
| vectorize_ast(ast) |
5. Experimental Results
To validate the proposed approach, experiments were conducted on a dataset [
13] comprising over 340,000 Yul files. All evaluations were performed on a machine equipped with a 10-core Apple M2 CPU and 32 GB of RAM. The evaluation process is divided into two main categories: (1) embeddings of fundamental Yul entities, which serve as the foundation for subsequent processing tasks, and (2) holistic vectorization of complete Yul contracts.
To the best of the author’s knowledge, the vectorization of Yul contracts has not been explored in the previous literature. As a result, there are no established benchmarks or directly comparable methods available for evaluation. While this limits the ability to perform standard comparative analysis, it also highlights the novelty and pioneering nature of the proposed approach. In light of this, a thorough internal evaluation was conducted to assess both performance and representational quality. The results aim to provide an initial baseline for future research in this area.
5.1. Yul Entities Embeddings
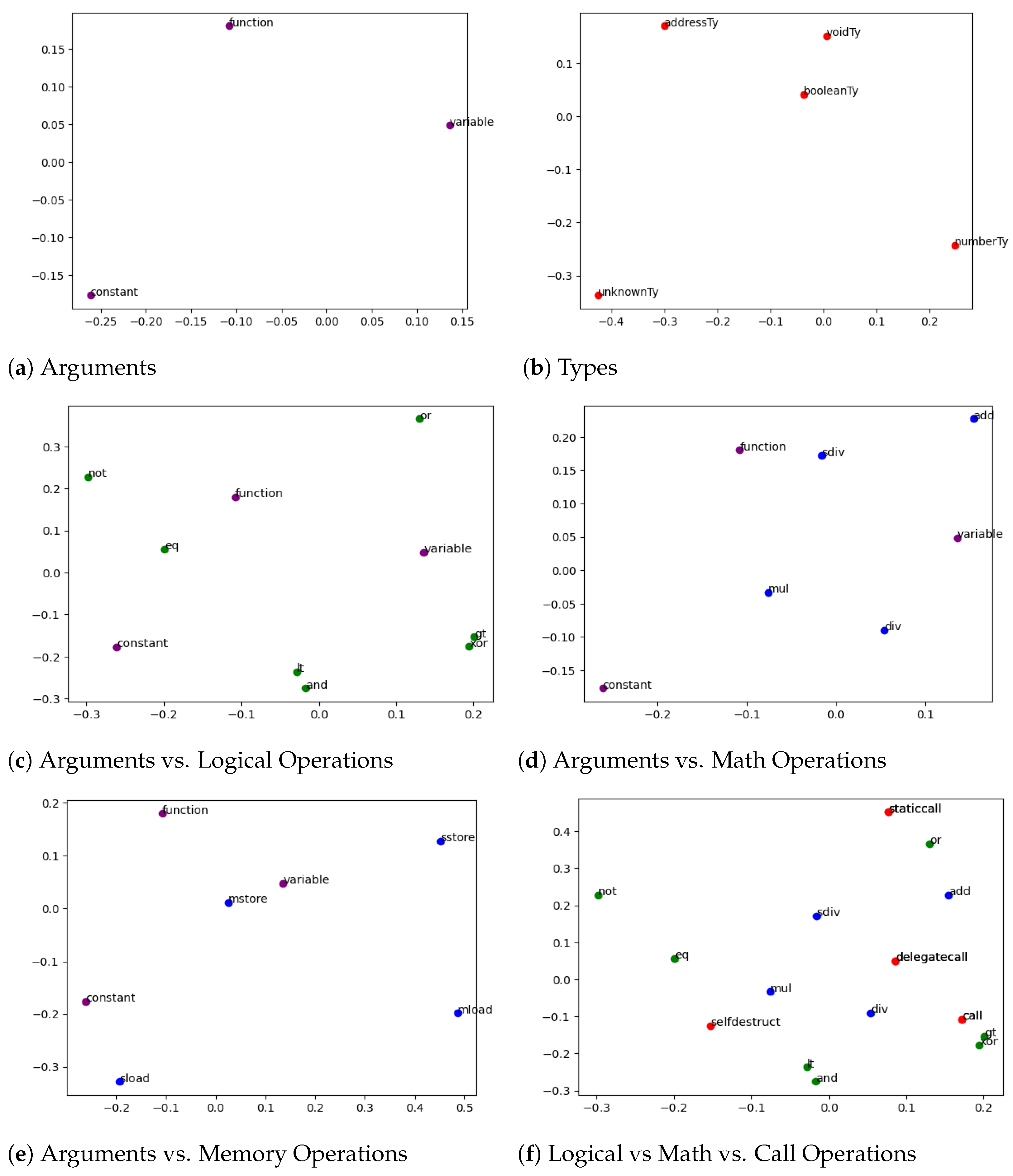
Basic embeddings of Yul elements were analyzed to demonstrate that the relationships between entities are effectively captured and that the proposed method is capable of identifying the semantic characteristics of Yul instructions and their arguments. To facilitate the interpretation of results, entities were categorized into several functional groups: function arguments, data types, logical operations, arithmetic operations, memory/storage operations (for reading and writing data to memory or blockchain storage), and call operations (used to invoke functions from external contracts).
To visualize the relationships and distances between these entities, the 300-dimensional embedding vectors were projected into a two-dimensional space using Principal Component Analysis (PCA). The results of this dimensionality reduction are shown in
Figure 5.
In
Figure 5a, we observe that the three representative function argument types are clearly separated and equidistant from one another, indicating that the model distinguishes them well.
Figure 5b presents a similar scenario, particularly highlighting a significant distance between numberTy and unknownTy. The latter appears frequently in cases where the type is ambiguous or undefined—such as outputs from user-defined functions—explaining its divergence from the more precisely defined types.
In
Figure 5c, a clear distinction between logical operations and argument types is evident. The logical operations are roughly evenly distributed around the argument types, suggesting that these operations interact with various types uniformly, reflecting the generality of logical constructs in the Yul language.
Figure 5d reveals a pronounced separation between argument types and arithmetic operations, as well as noticeable clustering among the operations themselves. A stronger association is observed between arithmetic operations and variable-/function-related argument types, as opposed to constants. This aligns with common developer practices, where variables and function results are more frequently involved in arithmetic computations than constant values.
In
Figure 5e, the store operations are evenly and distinctly distributed, indicating that the model recognizes their individual semantics. Notably, the proximity of the mstore operation to the variable argument type supports the intuitive understanding that memory storage is commonly used to hold variable values during execution.
Lastly,
Figure 5f compares logical, arithmetic, and call operations. Although distinct clusters for each category are not strongly pronounced, entities within the same category tend to be positioned relatively closer to one another. Moreover, the overall separation between different categories suggests that the embedding space reflects their functional distinctions to a reasonable extent.
5.2. Yul Vector Distribution
This subsection presents a key contribution of this paper—the distribution of vectors generated from entire Yul programs using the method described in
Section 4.4. The previously mentioned dataset, containing approximately 350,000 samples, was used. For the sake of clarity in presentation, a representative subset of these samples was selected.
A central goal of this method is to automatically capture similarities between contracts without human supervision. Paradoxically, this also makes it difficult to evaluate or interpret the quality of the resulting vector distributions using human judgment alone, as there is no clearly defined notion of an “ideal” distribution.
To address this challenge, three evaluation tests were conducted:
Parameter Evaluation on 14 Simple Scripts: Embeddings were computed for 14 simple Yul scripts sourced from the Solidity repository’s Yul optimizer tests.Samples of Yul scripts used for unit-testing the Yul optimizer in the Solidity project:
https://github.com/ethereum/solidity/tree/develop/test/libyul/yulOptimizerTests/fullSuite (accessed on 7 August 2025). These minimal examples are particularly useful for quick checks and parameter tuning, as they are small and typically involve only limited syntactic constructs. Their simplicity also makes it feasible for humans to intuitively assess semantic similarity.
Automated Categorization of 2000 Samples: Embeddings were generated for the first 2000 entries in the dataset and automatically assigned to one of five categories:
Initial Code (Red)—Yul code generated as part of the constructor section during Solidity compilation, usually containing boilerplate logic for deploying contract bytecode.
Libraries (blue)—Common utility libraries, such as Strings or Base64.
ERC-20 Contracts (Green)—Implementations of the ERC-20 token standard.
ERC-721 Contracts (Yellow)—Implementations of the ERC-721 non-fungible token standard.
Other (Purple)—Contracts that do not fit any of the above categories.
Classification into the first two categories is highly reliable: Initial code files typically include the “initial” suffix in their filenames, while library files often use the library name as a prefix. For ERC-20 and ERC-721 contracts, classification was based on the presence of indicative keywords (e.g., ERC20, ERC721) in the code. While this heuristic is not perfect, it is adequate for identifying broad trends in the embedding space.
Manual Evaluation on Selected Contracts: A small subset of contracts with known categories was manually selected to qualitatively validate the clustering behavior of the embeddings.
Despite the limitations inherent in automated and heuristic-based classification, this three-pronged evaluation approach offers valuable insights into the representational capabilities of the proposed vectorization method. As previously noted, the primary goal is not for humans to directly label or interpret Yul programs but to enable models to learn and capture latent semantic similarities. In future work, these embeddings could serve as robust inputs to downstream tasks, such as solving compiler optimization problems like phase ordering.
The results of Test 1 are presented in
Figure 6. The figure shows four visualizations of the vectorized Yul scripts using different weighting schemes for operations, types, and arguments. The specific weight configurations are as follows:
, , and .
, , and .
, , and .
, , and .
Domain knowledge of smart contract behavior is helpful for interpreting these results. In particular, the scripts storage.yul and unusedFunctionParameterPruner_loop.yul are noteworthy. Both scripts primarily consist of three sstore operations—an important observation, as storage operations are among the most gas-intensive in Ethereum. Although unusedFunctionParameterPruner_loop.yul is longer a result of its custom function implementation, the essential functionality of both scripts is the same: performing three storage operations. The key difference is that storage.yul stores a constant value, whereas the latter stores a value returned by a function. Despite apparent syntactic differences, their semantic similarity should be captured by a well-designed embedding.
Indeed, we observe that these two scripts are placed closely together—yet distant from the others—in
Figure 6a,d, which suggests that the embeddings in those settings successfully capture this similarity. A somewhat less precise but still reasonable grouping is seen in
Figure 6c. By contrast, the other settings result in more tightly clustered embeddings with less meaningful separation, leading me to conclude that the weighting schemes used in
Figure 6a,d are most promising for further exploration.
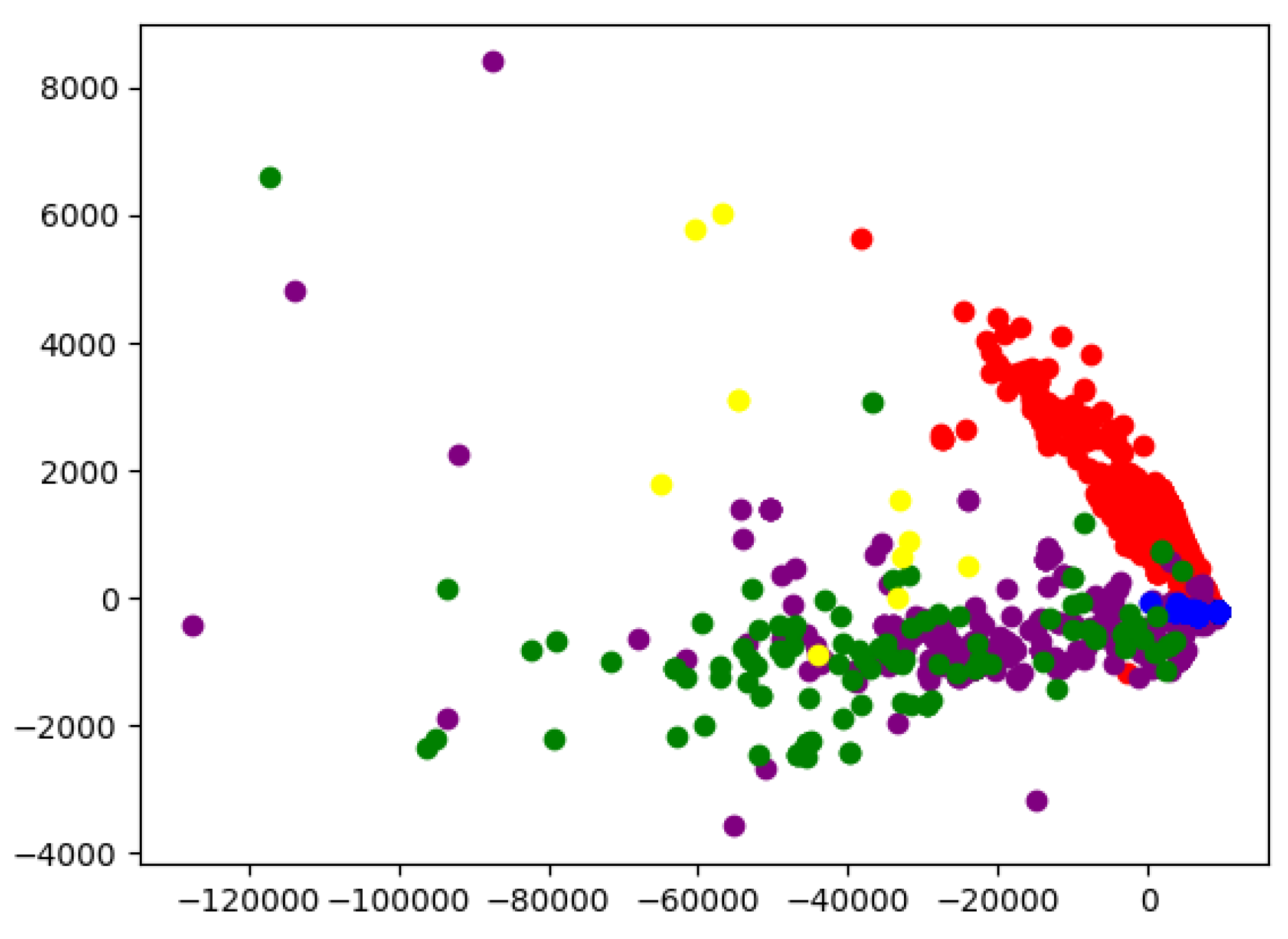
The results of Test 2 are presented in
Figure 7. Clear clusters are observed for both initial code and library contracts, which are located near each other yet distinctly separated from other categories. ERC-20 contracts, though more widely dispersed along the X-axis, tend to concentrate along the lower region of the Y-axis. In contrast, ERC-721 contracts are mostly positioned above ERC-20 samples. The “Other” category does not form a well-defined cluster, which may be attributed to the limitations of automatic categorization. However, it is also reasonable to assume that contracts outside the predefined categories could still share similar characteristics with them.
Additionally, for this test, the performance in terms of execution time required to generate an embedding vector per script was measured, including its relation to script length. The results are summarized in
Table 3. These measurements show that the vector computation time is negligible, making it feasible to perform repeatedly in downstream applications—for example, recalculating embeddings at each optimization step during compilation.
Figure 8 presents the results of Test 3, which further evaluates the two most promising weight configurations identified in the earlier analysis—configurations 1 and 4. Specifically,
Figure 8a corresponds to configuration 1, while
Figure 8b corresponds to configuration 4.
This comparison clearly identifies configuration 1 (, , ) as the most effective. This weighting scheme emphasizes operations as the most significant factor, assigns half that importance to types, and considers argument values as the least critical for capturing the semantic characteristics of Yul’s code.
Figure 8a reveals trends consistent with those observed in Test 2. For instance, ERC-20 contracts are concentrated in the bottom-left region, while ERC-721 contracts cluster near the center-top area. Contracts categorized as “Other” are grouped around the mid-left region, mirroring patterns seen previously. Initial code samples are tightly clustered in a distinct region, with library contracts positioned nearby but slightly offset. In some cases, red and blue points overlap—these correspond to initial code segments that originate from library contracts.
6. Summary and Future Work
Although the results are challenging to evaluate due to the absence of established benchmarks—and given the inherently abstract goal of enabling machines to capture latent semantic characteristics that are not easily interpretable by humans—they nevertheless appear promising. Despite these challenges, the experiments demonstrate that the vector representations are meaningfully clustered according to basic contract categories. This indicates that the proposed method is capable of capturing non-trivial patterns in Yul code, far beyond what would be expected from a random or purely syntactic representation.
These findings offer a promising outlook for the future application of this approach. In particular, the generated vectors demonstrate potential as high-quality input features for downstream neural network models. One especially compelling direction is the use of these embeddings in compiler optimization tasks, such as addressing the phase-ordering problem in the Solidity compiler. As mentioned in the
Section 1, Deep Reinforcement Learning (DRL) presents a strong candidate for solving the phase-ordering problem by iteratively performing the following steps:
Receive an input representing Yul script.
Select the most appropriate optimization step using a technique such as Deep Q-Networks (DQNs).
Apply the selected optimization step to the current Yul script.
Generate a new input from the modified script.
Repeat the process until a termination condition is met.
However, to explore this approach for any programming language, the input representing code must first be vectorized into a fixed-size representation that is suitable for neural network processing. Addressing this challenge was, in fact, one of the key motivations behind this work and represents an essential first step toward enabling such applications.
By integrating these learned representations into optimization pipelines, it may become possible to automate and improve performance-tuning processes that currently rely heavily on expert heuristics.
Future work will focus on evaluating the embeddings in practical downstream tasks, exploring alternative aggregation strategies for program-level vectorization, and benchmarking against emerging methods as this area of research evolves.