An Efficient Distributed Identity Selective Disclosure Algorithm
Abstract
Featured Application
Abstract
1. Introduction
- We propose a secure and efficient hash-based selective disclosure algorithm, MECQV, which introduces implicit certificates as a verifiable method for credential issuance and verification.
- We combine Merkle trees and zero-knowledge proof algorithms to hide the Merkle tree verification path, resisting man-in-the-middle attacks.
- We evaluate MECQV both theoretically and experimentally. We compare the performance of MECQV with FlexDID. Our results show that all the operations of MECQV can be completed within 10 ms on a Linux Ubuntu 22.04 LTS machine. MECQV not only enhance the security of the hash-based selective disclosure method, ensuring unforgeability, but it also perform 80% faster than anonymous credential schemes.
2. Related Work
3. Preliminaries
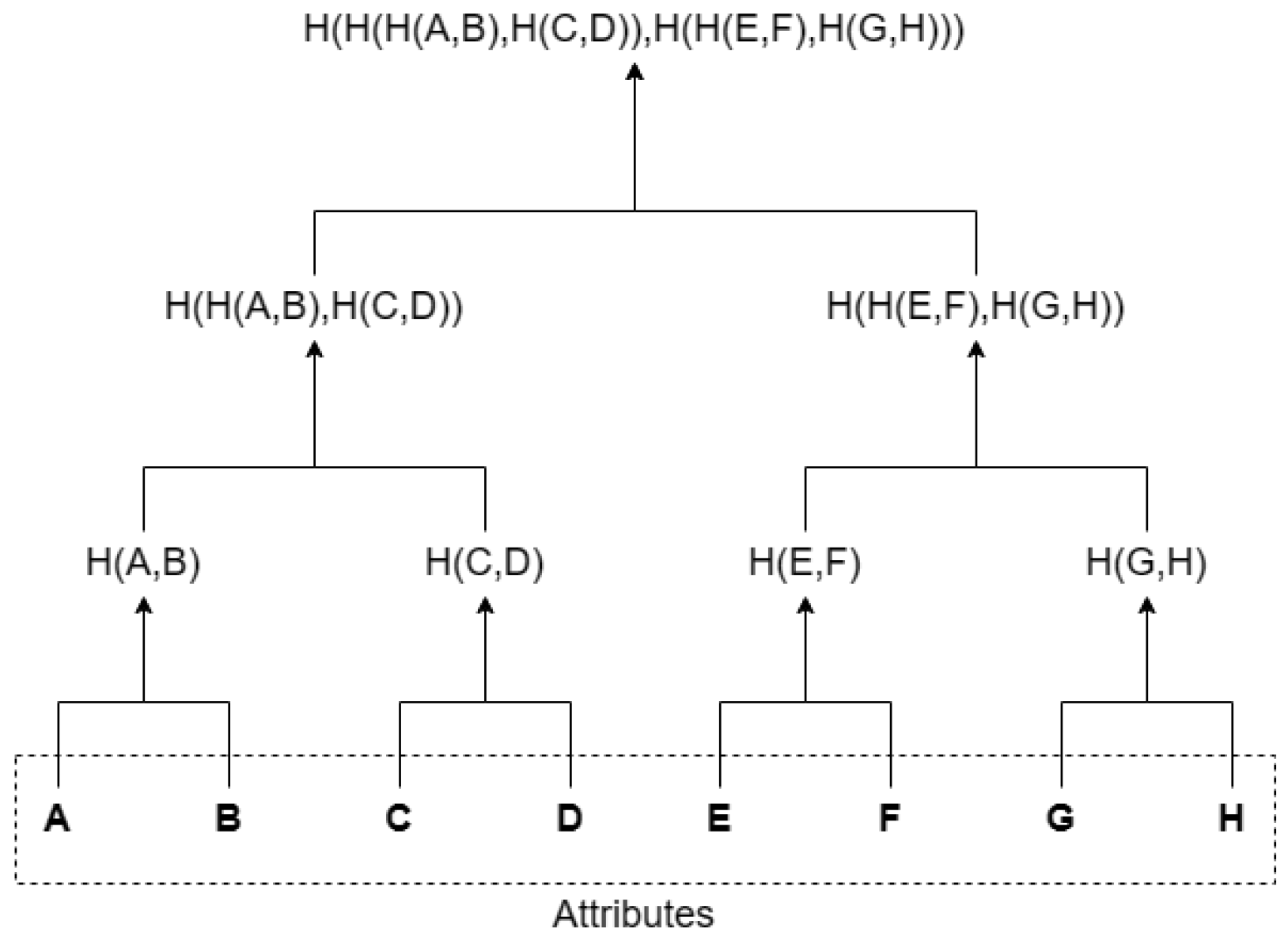
3.1. Merkle Tree
3.2. Implicit Certificate
- ECQV Setup In this step, the CA establishes the elliptic curve domain parameters, hash functions, and certificate encoding formats, and each entity selects a random number generator. The CA generates key pairs, and each entity must keep a true copy of the CA’s public key and domain parameters.
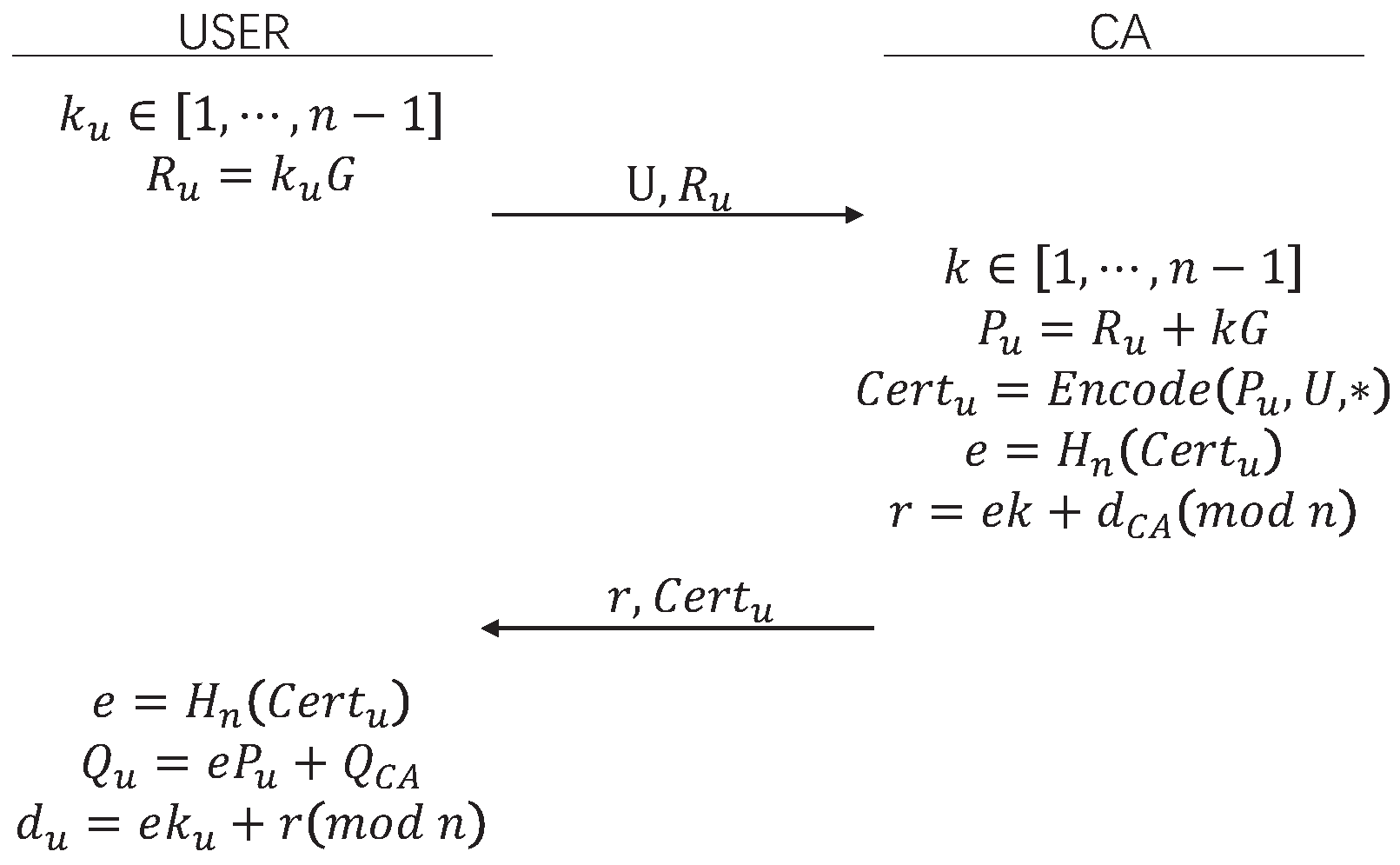
- Cert Request The requester, U, must generate a certificate request, which is sent to the CA. The encryption component of this request is a public key, generated in the same way as the CA’s public key during the ECQV Setup.
- Cert Generate Upon receiving the certificate request from U, the CA first confirms U’s identity and then creates an implicit certificate. The CA then sends a response to U.
- Cert PK Extraction Given U’s implicit certificate, domain parameters, the CA’s public key, and a public key extraction algorithm, U’s public key is calculated.
- Cert Reception Upon receiving the certificate response, U must verify the validity of the implicit certificate key pair.
4. Selective Disclosure Algorithm Based on Implicit Certificates (MECQV)
4.1. Algorithm Definition
- : This algorithm is used to generate the system’s public security parameters. is the system’s security parameter, and the input is . The output is the system’s public parameters .
- : This algorithm is executed by the data owner (U). The input includes the public parameters and the set of attributes . The output is a credential request that U sends to the certificate authority (A). We present an algorithm as shown in Algorithm 1.
- : The credential generation involves the following two algorithms:
- -
- : This algorithm generates a Merkle tree and verifies the root node.
- -
- : This algorithm takes the Merkle tree root node and the user’s public key as input to validate U’s attributes. The output includes the public key reconstruction value , the private key reconstruction value , and the main credential . We present an algorithm as shown in Algorithm 2.
- : This algorithm is executed by U, who takes the public key reconstruction value and private key reconstruction value as input. It outputs the credential’s public key and private key . We present an algorithm as shown in Algorithm 3.
- : This algorithm is executed by U. It takes the disclosed attribute set S, the Merkle tree root node , and the proof path from the leaf nodes to the root node as inputs. The output is the sub-credential . We present an algorithm as shown in Algorithm 4.
- -
- : This algorithm generates a zero-knowledge proof for the Merkle tree leaf node verification path.
- -
- : This algorithm signs the proof generated by the previous algorithm.
- : The verifier (V) executes this algorithm, which takes the main credential and the sub-credential as input. It outputs either 1 (valid) or 0 (invalid). We present an algorithm as shown in Algorithm 5.
| Algorithm 1 Credential request |
|
| Algorithm 2 Credential generation |
|
| Algorithm 3 Credential extraction |
|
| Algorithm 4 Credential presentation |
|
| Algorithm 5 Credential verification |
|
4.2. Algorithm Description
- Initialization stage: Given the security parameter k, generate a k-bit prime number p and an elliptic curve , where the curve is defined over the finite field with a base point G and order n. Assume the existence of a collision-resistant hash function .
- Credential request stage: U randomly selects an n-bit number as the private key and computes the public key . U generates the credential request and sends to certificate authority (A).
- Credential generation stage: This stage consists of the following two algorithms:
- : This algorithm takes the attribute set and treats them as the leaf nodes of a Merkle tree. It uses a hash function to generate the root node .
- : A randomly selects a number , computes , and generates the credential . The certificate hash is computed as , and the private key reconstruction value is calculated as , where is A’s private key.
- Credential acceptance stage: U computes , the credential public key , and the credential private key . Here, is the certificate authority’s public key. The verification step is .
- Credential presentation stage: Credential presentation involves the following two algorithms:
- : This algorithm generates a zero-knowledge proof for the leaf node verification path in the Merkle tree.
- : A random number k is chosen, and the point is calculated. The signature parameter is . If , a new random number is chosen. The value is computed, and the signature is obtained. If , a new random number is selected. The signature is generated, and the sub-credential is output.
- Credential verification stage: V first extracts the public key reconstruction value from the credential and computes . V verifies that the signature satisfies the conditions and . The value is computed, and . The values , compute . If the point , the output is 0. Otherwise, check whether . Finally, verify the validity of the proof .
4.3. Security Model
- The adversary can observe Bob’s credential request to the certificate authority, denoted as .
- After observing Bob’s request, the adversary can send to the certificate authority and receive the response , where is the private key reconstruction value generated by the certificate authority, and is the Merkle tree root.
5. System Model
System Flow
- Initialization phaseIn the key generation phase, the patient, hospital, and doctor each register their own DID identities, and the identity registration process is the process of generating their respective keys. Taking the patient’s DID identity registration as an example, the steps are as follows:
- (a)
- The patient randomly selects and calculates , where is the patient’s private key and is the patient’s public key.
- (b)
- The patient generates a DID identifier, .
- (c)
- The patient generates a DID document, which includes the patient’s identifier, public key, signature, and other information. The patient sends a registration request to the blockchain node, .
- (d)
- After receiving the request, the blockchain node verifies the validity of the DID identifier and document, and it then packages them into a block for on-chain storage.
- Credential request phaseIn the credential request phase, the patient sends their attributes to the hospital and applies for a credential related to those attributes.
- (a)
- The patient generates a temporary key pair according to the steps in the above algorithm.
- (b)
- The patient uses the DID identifier registered on the blockchain to send a credential request to the hospital as follows: .
- Credential generation phaseIn the credential generation phase, the hospital issues a credential for the patient based on the received attributes. The hospital must first determine whether the patient’s identity attributes are valid. Then, the hospital uses the algorithm to generate the patient’s credential, attaching the DID identifier to anchor the relationship between the patient’s identity and the credential. After generating the credential, the hospital uploads it to the blockchain network.
- (a)
- Upon receiving the request, the hospital first queries the patient’s DID identity from the blockchain network and retrieves the patient’s public key information from the DID document. Then, the hospital verifies whether the attributes submitted by the patient are valid.
- (b)
- The issuing institution generates the public and private key reconstruction values and the credential based on the credential generation algorithm from step three.
- (c)
- The issuing institution returns the credential and the private key reconstruction value to the patient.
- (d)
- After receiving the credential and private key reconstruction value, the patient calculates the credential public and private keys using the algorithm in the credential acceptance phase.
- Credential presentation phaseIn the credential presentation phase, the doctor initiates an identity verification request. After receiving the request, the patient runs the and algorithms to generate proof of the attributes. The patient then sends the proof and the credential to the doctor.
- (a)
- The doctor initiates an identity verification request to the patient.
- (b)
- The patient selects the attributes (e.g., age) to disclose and generates a zero-knowledge proof for that attribute. The purpose of this proof is to hide the Merkle tree verification path.
- (c)
- The patient signs the zero-knowledge proof of the verification path using the credential’s private key, , and sends the signature and credential to the doctor.
- Credential verification phaseUpon receiving the proof and credential from the patient, the doctor first queries the blockchain to verify the patient’s DID identity. Then, the doctor calculates the credential public key from the parameters in the credential to verify the signature in the proof. After the signature is verified, the doctor verifies the zero-knowledge proof by comparing the root node obtained from the zero-knowledge proof calculation with the root node contained in the credential to validate the attribute disclosed by the patient.
- (a)
- The doctor verifies the credential by first checking the correctness of the signature, then verifying the validity of the credential, and finally verifying the validity of the proof .
- (b)
- In verifying the signature, the doctor can both verify whether the patient owns the private key corresponding to the credential and whether the credential was issued by the hospital. Ultimately, the doctor verifies whether the root node of the Merkle tree in the credential is valid based on the zero-knowledge proof.
6. Performance and Security Analysis
6.1. Performance Analysis
- Credential request phase: In the request phase, the user does not need to perform complex calculations, and the number of attributes has very little impact on this phase.
- Credential generation phase: Due to the use of implicit certificate generation, the computational complexity is low, and the number of attributes has a minimal impact on this phase.
- Credential presentation phase: This phase is the most time-consuming due to the complexity of the zero-knowledge proof computation.
- Credential verification phase: The verification phase has a relatively short time consumption, and there is no significant increase in time as the number of attributes increases.
6.2. Security Analysis
- (i) An integer , such that ;
- (ii) A pair , where , meaning that is the signature for the message m.
- (i) is a certificate created by based on Bob’s request; or
- (ii) is not a certificate issued by the issuer.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pointcheval, D.; Sanders, O. Short randomizable signatures. In Proceedings of the Topics in Cryptology-CT-RSA 2016: The Cryptographers’ Track at the RSA Conference 2016, San Francisco, CA, USA, 29 February–4 March 2016; Proceedings. Springer: Berlin/Heidelberg, Germany, 2016; pp. 111–126. [Google Scholar]
- Boneh, D.; Gentry, C.; Lynn, B.; Shacham, H. Aggregate and verifiably encrypted signatures from bilinear maps. In Proceedings of the Advances in Cryptology—EUROCRYPT 2003: International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 4–8 May 2003; Proceedings 22. Springer: Berlin/Heidelberg, Germany, 2003; pp. 416–432. [Google Scholar]
- Maram, D.; Malvai, H.; Zhang, F.; Jean-Louis, N.; Frolov, A.; Kell, T.; Lobban, T.; Moy, C.; Juels, A.; Miller, A. Candid: Can-do decentralized identity with legacy compatibility, sybil-resistance, and accountability. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 1348–1366. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 20 August 2023).
- Zyskind, G.; Nathan, O.; Pentland, A. Decentralizing Privacy: Using Blockchain to Protect Personal Data. In Proceedings of the Proc. IEEE Symposium on Security and Privacy (S&P), San Jose, CA, USA,, 21–22 May 2015; pp. 461–475. [Google Scholar]
- International Data Corporation (IDC). Blockchain Adoption Trends Report; Technical Report IDC_TR-2023-BC01; IDC: Needham, MA, USA, 2023. [Google Scholar]
- Hyperledger Foundation. Hyperledger Fabric: A Distributed Operating System for Permissioned Blockchains; Version 2.4 Documentation; Hyperledger Foundation: San Francisco, CA, USA, 2022. [Google Scholar]
- Tobin, A.; Reed, D. The inevitable rise of self-sovereign identity. Sovrin Found. 2016, 29, 18. [Google Scholar]
- Androulaki, E.; Barger, A.; Bortnikov, V.; Cachin, C.; Christidis, K.; Caro, A.D.; Enyeart, D.; Ferris, C.; Laventman, G.; Manevich, Y.; et al. Hyperledger Fabric Performance Characterization and Optimization. In Proceedings of the IEEE International Conference on Blockchain (ICBC), Toronto, ON, Canada, 2–6 May 2020; pp. 1–10. [Google Scholar]
- W3C. Decentralized Identifiers (DIDs) v1.0; W3C Recommendation; W3C: Cambridge, MA, USA, 2022. [Google Scholar]
- Sovrin Foundation. Sovrin: A Protocol and Token for Self-Sovereign Identity; White Paper; Sovrin Foundation: Provo, UT, USA, 2021. [Google Scholar]
- Camenisch, J.; Dubovitskaya, M.; Lehmann, A.; Neven, G.; Paquin, C.; Preiss, F.S. An Architecture for Privacy-Enhancing Credential Systems. In Proceedings of the ACM Conference on Computer and Communications Security (CCS), Virtual, 9–13 November 2020; pp. 477–494. [Google Scholar]
- Microsoft Security Response Center. Entra ID Vulnerability Analysis Report; Technical Report; Microsoft: Redmond, WA, USA, 2023. [Google Scholar]
- Soltani, R.; Nguyen, U.T.; An, A.; Galdi, C. A Survey of Self-Sovereign Identity Ecosystem. Secur. Commun. Netw. 2021, 2021, 8873429. [Google Scholar] [CrossRef]
- Waters, B. Efficient identity-based encryption without random oracles. In Proceedings of the Advances in Cryptology–EUROCRYPT 2005: 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; Proceedings 24. Springer: Berlin/Heidelberg, Germany, 2005; pp. 114–127. [Google Scholar]
- Sonnino, A.; Al-Bassam, M.; Bano, S.; Meiklejohn, S.; Danezis, G. Coconut: Threshold issuance selective disclosure credentials with applications to distributed ledgers. arXiv 2018, arXiv:1802.07344. [Google Scholar]
- Bian, Y.; Wang, X.; Jin, J.; Jiao, Z.; Duan, S. Flexible and Scalable Decentralized Identity Management for Industrial Internet of Things. IEEE Internet Things J. 2024, 11, 27058–27072. [Google Scholar] [CrossRef]
- Saito, K.; Watanabe, S. Lightweight selective disclosure for verifiable documents on blockchain. ICT Express 2021, 7, 290–294. [Google Scholar] [CrossRef]
- Chaum, D. Security without identification: Transaction systems to make big brother obsolete. Commun. ACM 1985, 28, 1030–1044. [Google Scholar] [CrossRef]
- Lysyanskaya, A.; Rivest, R.L.; Sahai, A.; Wolf, S. Pseudonym systems. In Proceedings of the Selected Areas in Cryptography: 6th Annual International Workshop, SAC’99 Kingston, Kingston, ON, Canada, 9–10 August 1999; Proceedings 6. Springer: Berlin/Heidelberg, Germany, 2000; pp. 184–199. [Google Scholar]
- Camenisch, J.; Lysyanskaya, A. An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In Proceedings of the Advances in Cryptology—EUROCRYPT 2001: International Conference on the Theory and Application of Cryptographic Techniques Innsbruck, Innsbruck, Austria, 6–10 May 2001; Proceedings 20. Springer: Berlin/Heidelberg, Germany, 2001; pp. 93–118. [Google Scholar]
- Blanton, M. Online subscriptions with anonymous access. In Proceedings of the 2008 ACM Symposium on Information, Computer and Communications Security, Tokyo, Japan, 18–20 March 2008; pp. 217–227. [Google Scholar]
- Camenisch, J.; Lysyanskaya, A. Signature schemes and anonymous credentials from bilinear maps. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 56–72. [Google Scholar]
- De Salve, A.; Lisi, A.; Mori, P.; Ricci, L. Selective disclosure in self-sovereign identity based on hashed values. In Proceedings of the 2022 IEEE Symposium on Computers and Communications (ISCC), Rhodes, Greece, 30 June–3 July 2022; pp. 1–8. [Google Scholar]
- Merkle, R.C. Secrecy, Authentication, and Public Key Systems; Stanford University: Stanford, CA, USA, 1979. [Google Scholar]
- Campagna, M. SEC 4: Elliptic Curve Qu-Vanstone Implicit Certificate Scheme (ECQV); Standards for Efficient Cryptography, Version 1.0; SEC: Redwood City, CA, USA, 2013.


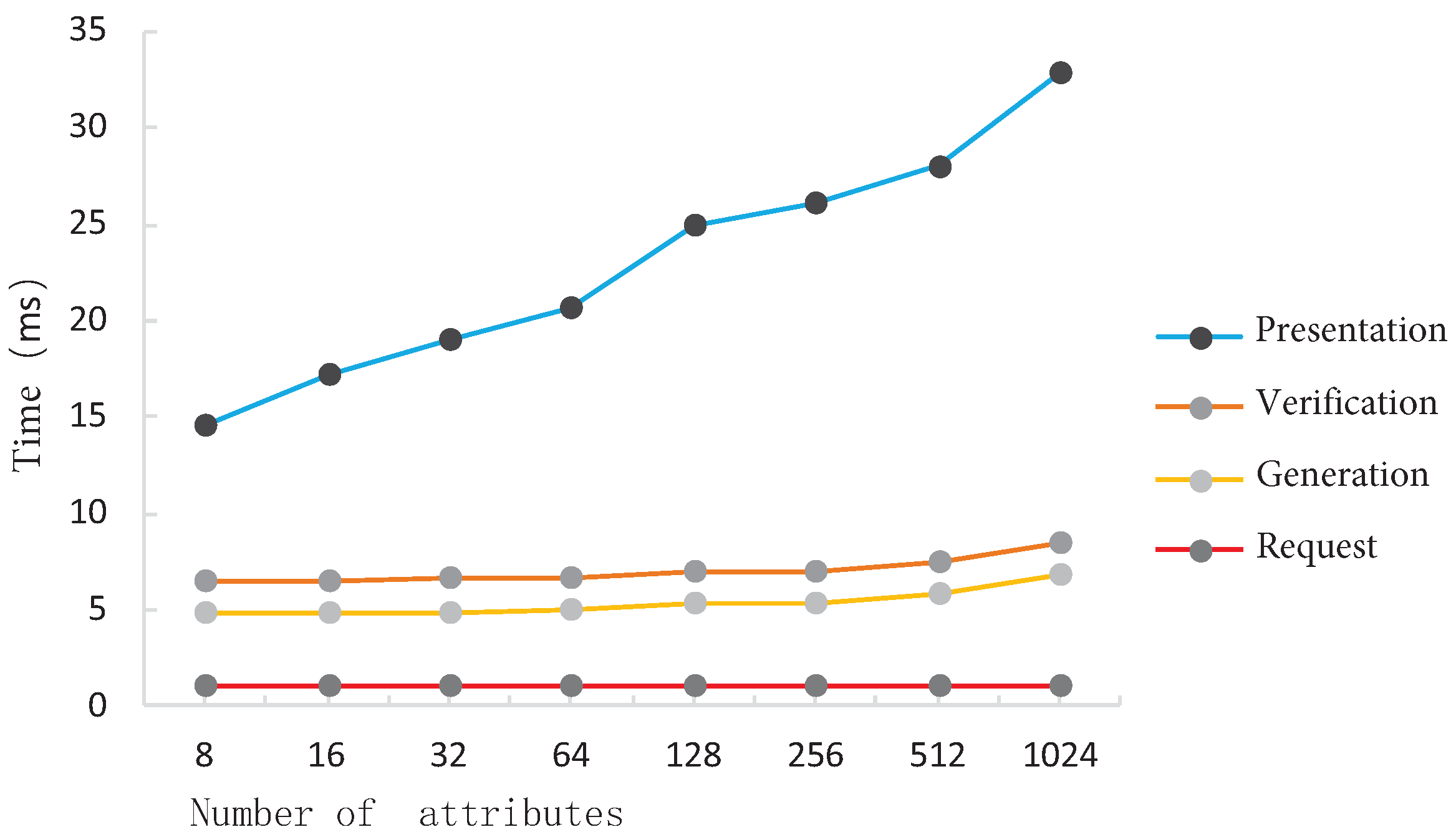
| Phase | Metrics | MECQV | FlexDID |
|---|---|---|---|
| Credential Generation | Execution time | 2.1 ms () | 12.5 ms () |
| Computational complexity | |||
| Resource consumption | 58 KB | 210 KB | |
| Credential Presentation | Execution time | 8.3 ms | 22.7 ms |
| Computational complexity | |||
| Resource consumption | 320 Bytes | 850 Bytes | |
| Credential Verification | Execution time | 1.7 ms | 9.8 ms |
| Computational complexity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Zhang, G. An Efficient Distributed Identity Selective Disclosure Algorithm. Appl. Sci. 2025, 15, 8834. https://doi.org/10.3390/app15168834
Wang G, Zhang G. An Efficient Distributed Identity Selective Disclosure Algorithm. Applied Sciences. 2025; 15(16):8834. https://doi.org/10.3390/app15168834
Chicago/Turabian StyleWang, Guanzheng, and Guoyan Zhang. 2025. "An Efficient Distributed Identity Selective Disclosure Algorithm" Applied Sciences 15, no. 16: 8834. https://doi.org/10.3390/app15168834
APA StyleWang, G., & Zhang, G. (2025). An Efficient Distributed Identity Selective Disclosure Algorithm. Applied Sciences, 15(16), 8834. https://doi.org/10.3390/app15168834






