Water Vapor Transmission Properties of Autoclaved Aerated Concrete of Four Density Classes—Experimental Determination in Stationary Processes

Abstract

Moisture in porous building materials significantly affects all their technical parameters. For this reason, it is important to accurately determine coefficients that describe moisture transport inside these materials. The main parameters concerning the hygroscopic range are as follows: water vapor permeability δ, water vapor resistance factor μ, and water vapor diffusion coefficient D. Autoclaved aerated concrete (AAC), one of the most popular materials used for the construction of external walls, was tested. The study focused on the four density classes: 400, 500, 600, and 700. Using a modified cup method, measurements of the corresponding coefficients δ, μ, D were carried out in six ranges of relative air humidity: 11–30, 30–54, 54–60, 60–75, 75–85, 85–98%. The results prove that not only the level of humidity tested, but also the structure within the same material group has a significant impact on all parameters, strongly differentiating their values. In this regard, precise numerical simulations concerning moisture transport processes in autoclaved aerated concrete must take into account both its density class and the moisture range in which these processes occur.

1. Introduction

This paper discusses the problem of non-linearity relating to the transport of water in a porous building material in the range of hygroscopic moisture, whereby a group of autoclaved aerated concretes was selected as the research material. The experiments were conducted on the most common density classes: 400, 500, 600, and 700 kg/m³, which differ only in their pore structures. To eliminate the uncontrollable influence of other factors, it was ensured that all concretes came from the same manufacturer, while guaranteeing that the same raw materials were used in the production of each class and that the same technological parameters were maintained.

Autoclaved aerated concrete is the most commonly used material in external building partitions, exposed to variable environmental conditions, especially those subjected to low temperatures. The main advantage of this type of concrete is its low thermal conductivity, which guarantees high thermal insulation of these partitions. Unfortunately, as a result of the occurrence of moisture, both thermal insulation and most technical properties of this material, such as strength, frost resistance, and durability, deteriorate.

For this reason, it is very important to ensure the possibility to assess the drying rate of the partitions from technological moisture, as well as to diagnose the course of mass exchange processes during the operation of the external partitions exposed to varying humidity conditions. A prerequisite for correctly conducting this type of simulation is knowledge of the moisture transport coefficients of the material built into the partition.

For the hygroscopic range, which is the subject of this paper, researchers use two different concepts for determining the transport coefficient, based on stationary and non-stationary mass exchange between the porous medium and its environment.

Tests conducted under non-stationary conditions are described, for example, in [1], where an attempt was made to evaluate non-linearity by measuring desorption diffusivity in narrow ranges of relative humidity φ: 30→12%, 50→30%, 75→50%, 85→75%, 97→85%. Three calculation procedures were used: root t-type, logarithmic, and half-time methods. Cement mortars with different water/cement ratios were chosen as a model medium to test the suitability of these procedures. A high compatibility of the first two procedures was obtained and a significant dependence of diffusivity on the relative air humidity φ was proven.

In paper [2], very long-term measurements in desiccators were described, and evaluation of the diffusion coefficient using an advanced optimization algorithm. All measurements were conducted in three temperatures and cement mortars with different water-cement ratios were used as the subject of the study. At each temperature, five ranges of relative humidity Δφ were tested. Measurements in each interval Δφ were carried out until the state of moisture equilibrium was achieved in all tested samples. Desorption studies at one temperature extended over a period of about 18 months. The authors presented a description of tested moisture transport processes by applying linear and non-linear diffusion theories for comparison. It was found that the moisture transfer in hygroscopic porous materials for wide ranges of the air humidity changes should be modeled by the non-linear diffusion theory, with the diffusion coefficient being a function of moisture content.

Paper [3] is a continuation in this regard. The aim was to present a description of moisture transport in building materials by applying a non-linear diffusion model, in which the effective diffusion coefficient, being a function of moisture content, is implemented. In summary of the obtained results, it was concluded that the theory of non-linear diffusion allows for a more precise description of the moisture transport processes in hygroscopic porous materials, such as cement mortar.

The problem of non-linearity is also discussed in [4]. The effective diffusion coefficients were estimated for cement mortars tested at five moisture levels. The diffusion coefficients were determined by way of adjustment of the theoretical and experimental drying curves. Theoretical drying curves were determined from numerical solutions of linear diffusion equations with an average diffusion coefficient assigned to each of the narrow humidity ranges. The theoretical drying curves were correlated with those corresponding experimentally using the Levenberg–Marquardt modified iterative algorithm. The Gauss–Newton numerical method was used for a minimization problem by fitting the drying curves, and in this way the values of diffusion coefficients for the tested mortars were determined.

On the other hand, research on autoclaved aerated concretes of four density classes (400, 500, 600, 700) was presented in paper [5], in which the non-linearity was evaluated using non-stationary mass transfer processes. Paper [5] evaluates the usefulness of the new calculation technique to determine the relationship between effective diffusivity and the concentration of moisture. The drying curves and the moisture distribution for AAC samples that had different drying times were determined experimentally. The results obtained were then used in a numerical procedure to estimate the value of the diffusion coefficient. The dependence of the coefficient on moisture concentration was approximated by a polygonal chain. An entirely satisfactory correlation with experimental data was obtained by the application of an eight-segment polygonal chain.

Continuing this topic, this article presents an experiment concerning the same four classes of autoclaved aerated concretes (400, 500, 600, 700), which aimed to evaluate the possibility of using stationary measurement techniques to determine their moisture transport coefficients and to assess the variability of these parameters in the entire range of hygroscopic humidity.

In contrast to the various non-stationary methods described in the literature, stationary methods are standardized, and the course of determining the transport coefficients of building materials is described in detail in standards, e.g., Refs. [6,7,8,9,10].

These standards distinguish three main coefficients: water vapor permeability δ, water vapor resistance factor μ, water vapor diffusion coefficient D. To determine their values, the following measurement techniques are proposed: the dry-cup method, the wet-cup method, and the inverted wet-cup method.

These methods are employed to determine the transport coefficients of various materials. In paper [11], specific problems encountered when using the cup method to determine water vapor permeability in porous membranes are discussed. It highlights the necessity of considering air layer resistance when testing this type of coating material.

Paper [12] discusses the use of both the dry-cup and wet-cup methods to evaluate the water vapor permeability of nine different building materials, such as wood fiber insulation, gypsum board, two samples of AAC, two samples of OSB/3, hollow concrete blocks, rainscreen membrane, and hemp concrete. All the materials exhibit a wide range of permeability. For the dry-cup tests, the three following desiccants were examined: silica gel, calcium chloride CaCl₂ powder, and saturated solution of potassium hydroxide KOH, while a saturated solution of potassium nitrate KNO₃ was used for a wet-cup test. In all the experiments, wireless sensors were used to measure the relative humidity within the air layer in the cup. It was found that the humidity inside the cups varied during the measurements, making it necessary to adjust the results obtained. Differences between dry- and wet-cup experiments were analyzed.

Paper [13] evaluates the influence of pre-conditioning on the vapor permeability determined by cup tests. Autoclaved aerated concrete (AAC) and ceramic brick (CB) were chosen as the materials to be tested. It was found that for the weak hygroscopic materials such as CB, pre-conditioning methods do not significantly affect the results. However, for strongly hygroscopic materials such as AAC, the manner in which pre-conditioning is conducted can have an impact on the results obtained, particularly in wet-cup tests.

Analyses carried out as part of work [14] revealed differences in the results from measurements carried out in different laboratories under different conditions. These differences may relate to temperature and relative humidity control, cup design, sample sizing measuring, weighing, pre-conditioning and sealing method, as well as data processing. The same materials used in the EC HAMSTAD project were selected for the testing studies as follows: autoclaved aerated concrete, calcium silicate board, and ceramic brick. The experimental results obtained were then analyzed in comparison with the EC HAMSTAD report to calculate various errors. The authors concluded, based on the analyses conducted, that errors related to material heterogeneity vary depending on different tests and conditions. Repeatability errors are generally insignificant for tests regarding hygroscopic properties; however, at the same time, reproducibility errors are significant, which require more detailed regulations.

Hence, proper preparation of the study using the cup technique and its correct implementation is important. In Section 2.1.1, the different methods—dry cup, wet cup, and inverted wet cup—are discussed in greater detail, referencing the appropriate standards [6,7,8,9,10].

In addition, Section 2.1.1 describes the results of dry and wet-cup tests for autoclaved aerated concretes [15,16,17], as well as for other mineral building materials, such as high performance concretes with and without the addition of metakaolin [18], high performance concretes with and without the addition of microsilica [19], self-compacting concretes with lime and fly ash [20]. Section 2.1.1 also discusses the results obtained from inverted-cup measurements for different concretes [21] and mortars [22,23].

The analysis of these three standard test methods (dry-cup method, wet-cup method, and inverted wet-cup method) and the results obtained with their help indicates that they have their limitations and determine the values of transport coefficients (δ, μ, D), but only within broad relative humidity ranges, without the possibility of reconstructing their variability with humidity in the entire range of hygroscopic moisture.

For example, the simultaneous use of both measurement techniques, dry-cup method and wet-cup method, allows to determine the parameters δ, μ, D with the division of the entire hygroscopic humidity range into two main sub-ranges φ < 50% (dry cup) and φ > 50% (wet cup). These data are not detailed enough to carry out precise simulations relating to the different levels of hygroscopic moisture in which a given building material may be found in real conditions.

The analysis of the test results described in [22,24,25,26,27] indicated such possibilities, but with stationary measurements carried out using the modified cup method that was presented in Section 2. The results obtained by this technique allowed reproduction of the variation in diffusion coefficients over almost the entire range of relative humidity.

This modified cup method was used in our own measurements, described in the following sections of the article. These studies were one of the component blocks of an extensive experiment carried out as part of the [28] thesis, in which various methods of measuring moisture transport parameters were tested.

The novelty of the article is that it presents the experimental determination of three basic parameters (δ, μ, D) using a modified cup method, in which the entire range of hygroscopic humidity is divided into narrow research intervals, which makes it possible to reconstruct for all classes the variability of each of the properties with the change in the relative air humidity φ. The authors decided to undertake this type of research because moisture in porous building materials significantly affects all their technical parameters. For this reason, it is important to accurately determine coefficients that describe moisture transport inside these materials, especially when they are used in external envelopes exposed to varying weather conditions.

2. Experimental Setup

2.1. Cup Methods

2.1.1. Standard Cup Methods

The cup method is the most widely used measurement technique for determining moisture transport coefficients in the hygroscopic range. Using this method, parameters such as water vapor permeability δ, water vapor diffusion coefficient D, and water vapor resistance factor μ are determined.

The principle of the cup method is to place a parallel-walled sample of the tested material under specific thermal and humidity conditions that are maintained throughout the measurement so that there is a different relative humidity on each side of the sample, while keeping the temperature constant.

In the dry-cup method, to keep the relative humidity inside the test vessel at about 0%, calcium chloride (CaCl₂, particle size < 3 mm) is most often recommended. The standards also provide other desiccants, such as magnesium perchlorate, Mg(ClO₄)₂, phosphorus pentoxide, P₂O₅, and silica gel. An aqueous saturated solution of LiCl·H₂O is also proposed to maintain the relative humidity at the level of approx. 12%.

In the wet-cup method, distilled water is used to achieve an internal humidity of approximately 100%. In addition to water, saturated aqueous solutions of certain salts are also proposed in the standards, e.g., ammonium dihydrogen phosphate, NH₄H₂PO₄ (93%) or potassium nitrate, KNO₃ (94%).

There are also proposals for using other saturated aqueous salt solutions to achieve intermediate moisture ranges, e.g., sodium dichromate, Na₂Cr₂O₇·2H₂O (52%), magnesium nitrate, Mg(NO₃)₂ (53%), or potassium chloride, KCl (85%).

Figure 1 shows the three basic standard cup methods: dry cup, wet cup, and inverted wet cup.

Below is presented a more detailed description of selected research works and the results obtained in them with regard to the basic parameters of water vapor transport, which were determined in measurements carried out with the use of standard cup methods.

This type of research on autoclaved aerated concretes has been carried out by Jerman and his team. Papers [15,16,17] present the results of tests on concrete classes 300, 350, 400, and 500 kg/m³. The measurements were carried out using a dry cup with CaCl₂ or silica gel and a wet cup with water. A 2 cm-thick sample was tested in two directions: along the block wall and across the block.

The material was shown to have isotropic properties with respect to water vapor transport. Analyzing the results presented in the works [15,16,17], there is no clear dependence of the water vapor diffusion coefficient on the class of aerated concrete.

Paper [18] dealt with the study of high-performance concretes with and without metakaolin. The water vapor diffusion coefficient was determined, and it was found that the cement-based concrete had a higher diffusion coefficient than the metakaolin concrete in both the dry-cup and wet-cup methods.

High performance concretes were also studied in [19]. C90/105 concrete with the addition of microsilica and C60/75 concrete without the addition of microsilica were tested. The water vapor diffusion coefficients for both materials showed similar values.

In [20], self-compacting concrete modified with the addition of lime and fly ash was investigated. Samples were isolated with epoxy resin, placed in cups, and sealed with technical plasticine. In the dry-cup method, CaCl₂ was used, while in the wet-cup method, an aqueous saturated solution of K₂SO₄ was used. Calculations of the water vapor diffusion coefficient were carried out. In the low relative humidity range, the same water vapor diffusion coefficient was obtained for both materials. In the range of higher relative humidity, the coefficient reached a higher value for the concrete with fly ash addition.

The inverted wet-cup method is used much less frequently than the dry- and wet-cup methods. It was used in [21], where tests were performed on 20 concrete mixtures varying in binder, additives, and the water to binder ratio. The test consisted of fixing the 1.8 cm thick specimens in glass vessels containing water and sealing the joints, then turning the vessels upside down and placing them in a climatic chamber. In the first year of the test, the chamber was set at 20 °C and 85% relative humidity, and in the following year at 20 °C and 65%. Paper [21] did not present test results from the 100–85% relative humidity range because stationary conditions were not achieved in the first year. However, the results obtained under relative humidity conditions of 100–65% are presented. It was found that the lower the water/binder ratio, the lower the diffusion coefficient, and that the diffusion coefficient is less dependent on the degree of moisture for high-performance concrete than for ordinary concrete.

The inverted wet-cup method was also used in [22,23]. Monograph [22] presents test results for three cement mortars with water/cement ratios w/c = 0.50, 0.65, 0.80. Measurements were made on 0.6 cm-thick specimens at 20 °C, 35 °C, and 50 °C with relative humidity in the chamber maintained at 75%. The method was compared with the wet-cup method. The relations of the coefficients determined by the inverse-wet-cup method to those determined by the wet-cup method reached different values depending on the microstructure of each mortar and on the temperature level.

2.1.2. Modified Cup Methods

The dry- and wet-cup methods have some limitations. Namely, they describe moisture transport coefficients only for certain conditions. Tests using a dry vessel provide information on the properties of materials at low humidities, while tests using a wet vessel refer to high humidities. Unfortunately, the results obtained from the dry-cup and wet-cup methods are insufficient for conducting detailed thermal and moisture analyses. Modifications to the cup method have been proposed to ensure that water vapor transmission properties can be assessed in the entire moisture range.

One of the modifications is the combination of the dry- and wet-cup method. This type of modification was proposed in [29]. In general, the method involves placing a round, parallel-walled sample in a vessel between two containers, the lower one containing water and the upper containing desiccant (e.g., CaCl₂). The desiccant is separated from the sample by a thin layer of highly permeable coating, such as polyolefin. The test kit assumes an average relative humidity of approximately 50%. However, during the course of the test, this humidity may vary slightly depending on the type of sample being tested and the moisture content of the desiccant. The entire test system (supported by two interconnected aluminum plates) is placed in a chamber with a constant temperature. At regular intervals, the entire set is removed from the chamber, the sample, water container, and desiccant container are separated, and each of them is weighed independently. Figure 2 shows a schematic concept of this type of research setup.

The advantage of the modified combined dry–wet method is that it provides data on the moisture accumulated in the sample during vapor transport. In contrast, the other methods only provide data on the water vapor transport through the sample of the tested material.

Another modification is to place saturated aqueous solutions of certain salts in the cups to obtain different relative humidities inside them. Testing of such prepared measuring systems is carried out in a climatic chamber at different humidity levels. Such an arrangement makes it possible to conduct tests in various humidity ranges [22,24,25,26,27].

This modified method was used in our own research, described in Section 2.3. Figure 3 schematically presents the concept of this type of research setup.

2.2. Materials

It was decided to perform experiments on the most common density classes: 400, 500, 600, 700 kg/m³, differing only in the structure of porosity. To eliminate the uncontrolled influence of raw materials and technological factors, care was taken to ensure that all the test concretes came from the same manufacturer, while also guaranteeing the invariability of the raw materials used in the production of concretes of all classes. To produce AAC, the following raw materials have been used: sand, ground quicklime, cement, gypsum, alumina powder, and water. The lower the density, the higher the strength class of aerated concrete, and vice versa. Strength class means the average compressive strength in N/mm². The manufacturer assigns the following average compressive strengths to the density classes of 400, 500, 600, and 700 kg/m³: 2.0, 2.5, 3.0, and 4.0 N/mm².

The compatibility of the starting raw materials was tested in control tests by determining the percentage phase contribution in aerated concretes of four density classes. Bruker’s D8 X-ray diffractometer was used for tests, allowing, among other things, the analysis of the phase composition of all samples and texture analysis. The mineral composition of the samples was determined using X-ray diffraction with the Debye–Sherrer method. The following parameters were used: CuKa radiation, reflective graphite monochromator, lamp voltage 45 kV, step recording: step = 0.050 2Q, counting time per step = 1 s.

The percentage phase contribution obtained for all tested classes are shown in Figure 4. The analysis was performed semi-quantitatively using the XRAYAN software (version 4.0.1). While this approach does not provide full Rietveld refinement, it enables an approximate estimation of the phase proportions in the analyzed samples.

The results of the tests showed that the phase composition of all tested autoclaved aerated concretes is comparable. In all concrete types, the dominant phases are quartz (52.54–58.97%) and tobermorite (28.35–35.42%).

The purpose of the XRD analysis was to confirm the constancy of the raw materials used in the production of concrete of all classes, in order to eliminate the uncontrolled influence of other material and technological factors; thus, it considers only the effect of the variation in microstructural parameters in the analysis (see

Table 1. Results of porosimetry measurements for autoclaved aerated concretes of density classes 400, 500, 600, and 700.

Material	Pc [%]	S [m2/g]	ε [-]	Φ [μm]
AAC 400	83.59	33.1331	1.5415	16.85
AAC 500	80.22	38.9507	1.6694	46.13
AAC 600	76.85	39.4442	1.7167	36.66
AAC 700	72.52	44.4741	1.7607	0.51

).

In order to obtain data on the porosity structure of the considered concretes, porosimetry tests were carried out. The tests were conducted using a PoreMaster porosimeter from Quantachrome Instruments, which allows the determination of the volume and surface area of macropores and mesopores, as well as the determination of the size distribution of these pores. The results of tests conducted for four density classes (400, 500, 600, and 700) are presented in [5], in the form of a summary of individual differential curves of pore volume distribution with respect to their diameter.

Analysis of the differential curves determined the value of the effective radius for which each curve has an extreme.

Class 400 aerated concrete has dominant pore sizes that are in the macropore range (dominant diameter of about 30 μm). On the other hand, aerated concretes of classes 500 and 600 have a dominant pore diameter of about 100 μm, which also falls into the macropore group. In the case of aerated concrete of class 700, a clear multi-modal pore size distribution is evident with dominant effective diameters of about 15 μm, 20 μm, and 30 μm belonging to the macropore group.

Table 1 collects the resultant values from porosimetry tests for total porosity P, specific pore surface area S, tortuosity of the pores ε, and average pore diameter Φ (by volume).

Analyzing the average values of total porosity determined for each class, as presented in Table 1, reveals a uniform tendency: a gradual decrease in total porosity with increasing density class, from P ≈ 84% (for AAC 400) to P ≈ 73% (for AAC 700). At the same time, there is a uniform inverse trend in the case of specific surface area and pore tortuosity—an increase in both parameters was observed with increasing density class—in the range from S ≈ 33 m²/g (AAC 400) to S ≈ 44 m²/g (AAC 700) and in the range from ε ≈ 1.54 (AAC 400) to ε ≈ 1.76 (AAC 700). This indicates an increase in the number of fine pores in higher classes of concrete and their more complicated geometrical course. An analysis of the Φ values summarized in the last column of Table 1 shows that the smallest average pore diameter is found in the concrete of class 700, larger in the concrete of class 400, and the largest Φ values are seen in the concrete classes 500 and 600.

2.3. Measurements

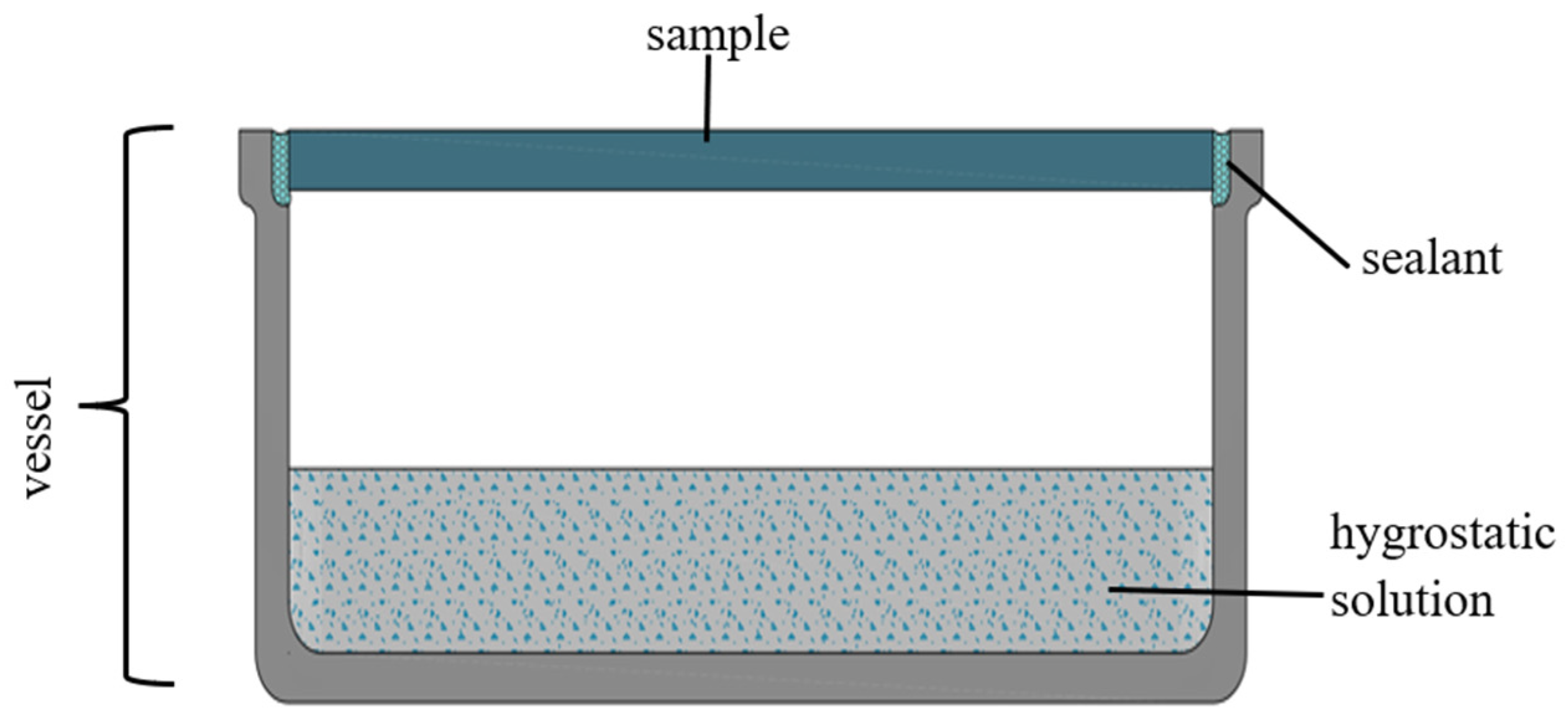
The research using the modified cup method began with testing and preparatory work. First, suitable test vessels were prepared (see Figure 5), and then the appropriate sealant was evaluated and selected as part of the tests. Suggestions for the selection of sealants can be found, for example, in [30]. In the experiment, a sealant based on mixtures of bituminous resins and polystyrene in organic solvents was used. Subsequently, tight joints were made between the components of all the test cups, and saturated hygrostatic solutions were prepared for subsequent stabilization of the humidity inside these vessels. Based on standards [31,32], the following salts were selected: LiCl, MgCl₂, Mg(NO₃)₂, NaNO₂, NaCl, KCl, and K₂SO₄, to ensure that relative air humidity above the saturated solutions is maintained at the levels of 11, 33, 54, 65, 75, 85, 98%, respectively (at T = 20 °C). In preparing the experiment, care was taken to ensure constant measuring conditions, as even slight fluctuations in temperature, humidity, or even gas pressure can negatively affect the accuracy of the determined parameters [12,33,34,35,36].

In the next step, disk samples with a thickness of 0.9 cm and a diameter of 17 cm were prepared. The disks were cut in a direction in which moisture would migrate through them and across the envelope. Edge disks were discarded, and only samples from inside the blocks were selected for testing. Prior to the main experiment, all samples were inventoried in terms of initial mass and geometric dimensions, while the initial volumetric density was determined. Then, after permanent designation, the samples were conditioned under conditions corresponding to the subsequent climates to be stabilized in the climate chamber. Conditioning was carried out in order to reduce baseline measurement time by relatively stabilizing the initial moisture content of the samples at an appropriate level.

Once the preparatory work was completed, the main experiment began, which consisted of three investigation blocks.

The first stage of investigation consisted of the preparation of 12 vessels containing an aqueous saturated solution of lithium chloride LiCl→φ = 11% (3 for each class of blocks), 12 vessels with an aqueous saturated solution of magnesium nitrate Mg(NO₃)₂→φ = 54% (3 each for each class of blocks), and 4 test vessels containing an aqueous saturated solution of magnesium chloride MgCl₂ →φ = 33% (1 for each class of blocks). Disks of the four density classes were mounted in the vessels so prepared, and the edges of the contact between each sample and the vessel were sealed (Figure 5).

The test sets were placed in a climate chamber (Figure 6), in which a constant relative humidity of 30% with an accuracy of ±3% and a temperature of 20 °C with an accuracy of ±0.2 °C were maintained.

The second stage of the study involved the preparation of 12 vessels containing an aqueous saturated solution of magnesium nitrate Mg(NO₃)₂→φ = 54% (3 for each class of blocks), 12 vessels containing an aqueous saturated solution of sodium chloride NaCl→φ = 75% (3 each for each class of blocks), and 4 test vessels containing an aqueous saturated solution of sodium nitrite NaNO₂→φ = 65% (1 for each class of blocks). Disks of the four density classes were mounted in the vessels so prepared, and the edges of the contact between each sample and each vessel were sealed. The test cups were then placed in a climate chamber, where a constant relative humidity of 60% and a temperature of 20 °C were maintained.

The third stage of investigation consisted of the preparation of 12 vessels containing an aqueous saturated solution of sodium chloride NaCl→ φ = 75% (3 for each class of blocks), 12 vessels containing an aqueous saturated solution of potassium sulfate K₂SO₄ → φ = 98% (3 for each class of blocks), and 4 test vessels containing an aqueous saturated solution of potassium chloride KCl→φ = 85% (1 for each class of blocks). Disks of the four density classes were mounted in the vessels so prepared, and the edges of the contact between any sample and a vessel were sealed. All test cups were placed in a climate chamber with a constant relative humidity of 85% and a temperature of 20 °C.

3. Results and Discussion

Water vapor permeance P_wv (kg/(Pa·m²·s)) was calculated according to the formula [9]:

$$P_{wv}={\displaystyle \frac{1}{\left(\frac{A∆p}{\frac{∆G}{∆t}}\right)-\frac{d_a}{{\delta }_a}}}$$

(1)

Here A (m²) denotes the sample surface, p (Pa) is the pressure, ΔG/Δt (kg/s) is the water vapor flow rate, d_a (m) is the air layer thickness, and δ_a (kg/(m·s·Pa)) denotes the water vapor permeability in the air.

The Schirmer equation [8] was used to calculate the water vapor permeability of air δ_a:

$${\delta }_a=\left({\displaystyle \frac{0.086·p_0}{R_v·T·p}}\right)·({{\displaystyle \frac{T}{273}})}^{1.81}$$

(2)

where p₀ (Pa) is the standard atmospheric pressure, and R_v (J/(kg·K)) is the gas constant of water vapor.

In the next step, the water vapor permeability δ (kg/(m·s·Pa)) of the tested materials were calculated using the formula [8]:

δ = P_wv·d

(3)

The average values of δ coefficients obtained for each class of aerated concrete are summarized in Figure 7.

Water vapor diffusion resistance factors μ (-) were calculated according to the formula [7]:

$$\mu ={\displaystyle \frac{{\delta }_a}{\delta }}$$

(4)

The resultant values of the diffusion resistance μ of aerated concrete of each class for the six tested moisture ranges Δφ are summarized in Figure 8.

Next, the water vapor diffusion coefficients D were determined. The following formula was used:

$$D={\displaystyle \frac{∆Gd}{A∆t(c_2-c_1)}}$$

(5)

where c (g/m³) is the concentration of water vapor in the air.

Average values of diffusion coefficients D for the four tested density classes and the six ranges Δφ, are summarized in Figure 9.

The values of all parameters (δ, μ, D) presented in Figure 7, Figure 8 and Figure 9 are in each case the arithmetic means of the three component results. The figures illustrate the variability of parameters δ, μ, and D determined for four classes of concrete, tested in six ranges of Δφ. These summaries illustrate the change in the value of each of the three parameters over almost the entire range of air relative humidity, i.e., from φ = 11% to φ = 98%.

These comparisons presented in Figure 7, Figure 8 and Figure 9 prove the strongly marked and highly complex influence on all parameters (δ, μ, D) of the levels of the tested humidity Δφ, within which various mechanisms of moisture transport appear.

At the same time, Figure 7, Figure 8 and Figure 9 illustrate the influence of the microstructure (its variation within the studied classes 400–700) on the tested water transport parameters δ, μ, D.

The data presented in Figure 7 indicate that the water vapor permeability coefficients δ of the concretes of each class in most Δφ intervals satisfy the relationship δ (700) < δ (600) < δ (500) < δ (400). A slight deviation from this rule occurs in the lowest of the tested humidity ranges Δφ = 11–30%, where the relationship δ (700) < δ (600) < δ (500) ≈ δ (400) holds. Relationships are different in the range of the highest humidities of 85–98%, where δ (700) < δ (400) < δ (500) < δ (600). The interrelationships for the two extreme classes in the following ranges of Δφ reach the following values of δ (400)/δ (700): 1.84, 3.33, 2.52, 3.09, 2.84, 1.10.

Analyzing the data for the parameter μ given in Figure 8, we find the opposite trend to that occurring in the case of parameter δ. This is obvious from the relationship between these parameters expressed in Equation (4). In most intervals of Δφ, relationships μ (400) < μ (500) < μ (600) < μ (700) apply. It is slightly different in the lowest humidity range tested, Δφ = 11–30%, where the relationship μ (400) ≈ μ (500) < μ (600) < μ (700) holds. In the range of the highest humidity of 85–98%, the concrete of class 700 still has the highest resistance μ, but the interrelationships are as follows: μ (700) > μ (400) > μ (500) > μ(600). The identified ratios of water vapor resistance factors μ of the two extreme classes (400 and 700) in the subsequent tested ranges Δφ reach the following values μ (700)/μ (400): 1.84, 3.33, 2.52, 3.09, 2.84, 1.10. For obvious reasons, the values μ (700)/μ (400) are identical to those determined for δ (400)/δ (700).

The data presented in Figure 9 indicate that the D coefficients of the tested aerated concretes generally meet the relationship D (700) < D (600) < D (500) < D (400). There is a slight deviation from this rule appearing in the lowest of the tested humidity ranges 11–30%, where the relationship D (700) < D (600) < D (500) = D (400) holds. However, the relationships are definitely different in the range of the highest humidity 85–98%, where D (700) < D (400) < D (500) < D (600). The interrelationships for the diffusion coefficients of the two extreme classes in the subsequent ranges Δφ were as follows: D (400)/D (700) = 1.66, 1.87, 1.88, 1.92, 1.52, 1.07.

If we compare the determined variability of the diffusion coefficients D of the tested concretes of class 400–700 with the literature data, it should be noted that there is a high qualitative similarity to the variability of the diffusion coefficients reproduced in [26] for two types of concretes. Both of these concretes showed gradual decreases and increases in the values of D as the relative humidity φ increased. For the BO-SN concrete, the lowest values of D were obtained in the highest humidity range φ ≈ 90%.

Also, stepwise increases and decreases in D value with the increase in the tested humidity φ can be observed for the mortars presented in [22], as well as in [27] in the case of mortar with w/c = 0.38.

The data collected in the experiment, presented in Figure 7, Figure 8 and Figure 9, show that the influence of the specific microstructure of individual classes on the determined values of all parameters is revealed in different ways.

The results of porosimetric tests showed that the aerated concrete of class 700 has the lowest total porosity (72.52%), while the aerated concrete of class 400 has the highest total porosity (83.59%). Therefore, in the aerated concrete of class 400, there will be more favorable conditions for the transport of water vapor and thus the highest moisture diffusion coefficient in the range of relative air humidity up to 85%.

In the range of the highest humidity φ = 85–98%, the mechanisms of moisture transport change, capillary flow begins to dominate, and molecular flow loses its intensity. Pores with different diameters than at lower humidity levels will be involved. This also highlights the dominants on the differential curves of the pore size distribution (cf. Ref. [5]).

While for pore diameters below 3 μm the curves are not very different, in the range above 3 μm, the differences between each of the classes are very significant. In this case, the highest proportion of the thickest pores is observed in classes 500 and 600, finer pores of the order of 30 μm in class 400, and the absence of a clear extreme for class 700 concrete, characterized by the lowest proportion of pores in this range.

This variation is also reflected in the data contained in Table 1 concerning the average diameter Φ (by volume). Concrete class 700 has the lowest Φ value (Φ ≈ 0.5 μm), concrete class 400 has a higher value (Φ ≈ 17 μm), and the highest Φ values occur in classes 500 and 600 (Φ ≈ 40 μm).

Consequently, in terms of the highest humidity, class 700 shows the lowest value of δ and D coefficients, slightly higher class 400, and the highest δ and D coefficients are found in the case of classes 500 and 600. The transport processes are obviously influenced not only by the transverse dimensions of the pores, but also by their shape and specific surface area. The observed trends in the case of these two parameters are unambiguous (cf. Table 1)—with the increase in the density class, there is an increase in the tortuosity of the pores ε and their specific surface area S.

The data obtained provide clear evidence that within the same material group (made on identical initial raw materials), a strong diversity of parameters describing the diffusion flow, assigned to the same range Δφ, should be expected. This regularity occurred in all six ranges Δφ studied. Mutual relationships in the case of diffusion coefficients D, e.g., of two extreme classes (400 and 700) in individual Δφ ranges, were at the level of D (400)/D (700): 1.66 (Δφ = 11–30%), 1.87 (Δφ = 30–54%), 1.88 (Δφ = 54–60%), 1.92 (Δφ = 60–75%), 1.52 (Δφ = 75–85%), 1.07 (Δφ = 85–98%).

In the case of δ coefficients, a much stronger differentiation in the relation of δ (400)/δ (700) was observed: 1.84 (Δφ = 11–30%), 3.33 (Δφ = 30–54%), 2.52 (Δφ = 54–60%), 3.09 (Δφ = 60–75%), 2.84 (Δφ = 75–85%), 1.10 (Δφ = 85–98%). The relationship μ (700)/μ (400) was at the same level.

The variation in the moisture parameters δ, μ, D is particularly strong in the humidity ranges φ < 85%. In the range of highest humidity Δφ = 85–98%, the variation across the classes is relatively small—for D (400)/D (700) it is 7%, and for δ (400)/δ (700) and μ (400)/μ (700) it is 10%.

Quantitatively summarizing the results obtained, it should be stated that within a given density class, as the relative humidity φ changes, there are very significant differences in the values of D, δ, and μ coefficients determined in the six Δφ intervals tested. For each class, the highest values of coefficients D and δ were found in the range Δφ = 75–85%, and the lowest values of D and δ were found in the range Δφ = 11–30%.

The interrelationships D_max/D_min were at the level of 3.0 (class 400), 2.9 (class 500), 3.2 (class 600), and 3.3 (class 700), i.e., they differed on average 3 times. However, the δ_max/δ_min relationships were even more pronounced, amounting to 8.2 (class 400), 7.7 (class 500), 6.2 (class 600), and 5.3 (class 700). The relationships μ_max/μ_min were at the same level as the ratios δ_max/δ_min; however, for each class, the values μ_max were in the range Δφ = 11–30%, and the μ_min values were in the range Δφ = 75–85%.

4. Conclusions

The modified cup method proved to be an effective research technique for unambiguously determining the variability of transport coefficients (δ, μ, D) over the entire range of relative humidity and for each concrete class tested. These coefficients for all autoclaved aerated concretes were strongly non-linear functions of relative air humidity with a very complex course.

In the case of each concrete class 400–700:

-

The highest values of coefficients D and δ, and consequently the lowest values of parameter μ, were recorded in the range Δφ = 75–85%;

-

The lowest values of coefficients D and δ, and consequently the highest values of parameter μ, were noted in the range Δφ = 12–35%.

The mutual relations D_max/D_min (2.9–3.3), as well as δ_max/δ_min and μ_max/μ_min (5.3–8.2), are discussed in detail in Section 3.

In summary of the obtained results, it should be stated that the scale of their differentiation is significant enough to prove the necessity of taking into account the variability of each parameter along with humidity. At different levels of humidity, the values of the parameters describing the occurring mass transfer processes will be different.

The analysis of data collected in the experiment, summarized in Figure 7, Figure 8 and Figure 9, makes it clear that not only the level of humidity tested, but also the structure of the porous material has a significant impact on all parameters (δ, μ, D), strongly differentiating their values.

In a wide range, covering four intermediate humidity intervals Δφ (30–54%; 54–60%; 60–75%; 75–85%), the following uniform trends were recorded:

-

D (700) < D (600) < D (500) < D (400);

-

δ (700) < δ (600) < δ (500) < δ (400);

-

μ (700) > μ (600) > μ (500) > μ (400).

The differences between the parameters determined in these four intervals are as follows: D (400)/D (700) = 1.52–1.92, δ (400)/δ (700) = 2.52–3.33, μ (400)/μ (700) = 2.52–3.33.

The results obtained in all intervals Δφ, as well as their mutual relationships, are discussed in detail in Section 3.

In summary, it should be stated that the scale of differentiation of all three parameters (D, δ, and μ) within the classes of 400–700 is significant and ranges from several dozen percent (in the case of the coefficient D) to several hundred percent (in the case of the parameters δ and μ).

The results obtained in an extensive, multi-stage experiment show that in performing precise moisture calculations, it is necessary to take into account the variability of the D, δ, and μ parameters, which strongly depend on both the specific microstructure (even within the same material group) and the level of moisture at which the processes occur. Otherwise, the simulations carried out will not provide a correct description of the phenomena analyzed, for example, in building partitions exposed to environmental factors that often change strongly both in daily and seasonal cycles. The authors plan to carry out such comparative simulations using complete data on the moisture variability of parameters (δ, μ, D), determined by a modified cup method in the range of φ = 11–98%, as well as using data determined by the dry-cup method for φ < 50% and the wet-cup method for φ > 50%.