Modification of Typical Headland Manoeuvres Using Transition Curves

Abstract

During headland manoeuvres of agricultural tractors, self-propelled machines, and autonomous agricultural vehicles, it is crucial not only to achieve the required working width but also to minimise the number of turns, path length, and time to reach the next field pass. The shortest trajectories can be obtained using Dubins curves or Reeds–Shepp paths. However, traversing such paths at constant velocity is only theoretically feasible. At the junctions between path segments, either the vehicle must stop or the steering angle must change at an infinite rate. These points exhibit abrupt changes in acceleration components, resulting in infinite jerk. This study presents the use of transition curves for executing U-turns and Ω-turns during headland manoeuvres. Implementing curves with gradually varying curvature ensures smooth transitions between trajectory segments, reducing sudden direction changes and improving motion dynamics. The curvature and tangent angle are defined using trigonometric functions. For the designed trajectory, kinematic parameters, including wheel steering angles, were determined for two models of agricultural tractors. The results provide a solid foundation for future research on refining transition curve models and integrating the proposed solutions with agricultural vehicle control systems.

1. Introduction

Efficient trajectory planning—particularly the execution of smooth, time-saving headland manoeuvres—has become a cornerstone of modern field automation. As arable holdings expand and labour shortages intensify, farmers rely on agricultural tractors, self-propelled machines, and autonomous vehicles to execute precise and dynamically smooth turns, minimise soil compaction, and shorten or eliminate non-productive travel. Over the past two decades, a substantial body of research has emerged to address these needs, progressing from rule-based patterns towards optimisation frameworks and, more recently, learning-driven strategies.

Early studies focused on generating reference trajectories that onboard controllers could reliably follow. Pioneering work in this area produced sub-optimal yet implementable paths for robot tractors and combined feed-forward with feedback tracking schemes [1]. In parallel, algorithms for full-field traversal sequences began to tackle overall logistics, reducing non-working distance through judicious ordering of passes [2,3]. Once GPS guidance matured, sensor feedback was integrated into automatic tractor–trailer control [4]. Around the same time, researchers proposed the Spiral Connection Method (SCM), an extension of Dubins paths that inserts steering-rate-limited spiral segments, making the trajectory kinematically feasible, and shortening headland-turning time [5].

As interest grew, the community turned to planning tailored to human behaviour and environmental context. Researchers developed a reverse-manoeuvre planner with steering and speed controllers for autonomous vehicles, proposed GNSS-based algorithms to recognise combine-harvester operation modes automatically, and devised mowing-tractor paths derived from human driving patterns [6,7,8].

Geometry-centred approaches flourished in parallel. Clothoid-based path-shaping techniques refined both Dubins and Reeds–Shepp solutions. Researchers also examined transition curves with linear, polynomial, and trigonometric curvature, and developed headland algorithms that respect steering- and acceleration constraints. As a result, inspection and maintenance robots began to use clothoid paths that satisfy dynamic limits [9,10,11,12,13].

Cost-oriented optimisation soon followed. Researchers developed route planners that balance fuel, time, and headland width. Leader–follower teams of autonomous tractors demonstrated coordinated turns. Other studies optimised travel paths to eliminate unnecessary manoeuvres, shorten headland-turn duration, and smooth trajectories in irregular fields by using circular, generalised elementary, and bi-elementary segments [14,15,16,17,18].

Mechanical constraints and precise navigation technologies have likewise shaped algorithmic progress. These developments led researchers to examine fifth-wheel tractor dynamics, asymmetric tractor–mower agility, and the use of RTK-GNSS and IMU sensors in control systems [19,20,21,22,23]. Numerical optimisation bridged theoretical models with hardware limits, yielding direct solutions for switch-back manoeuvres and multi-trailer headland turns that minimise crop damage and inter-segment collisions. Complementary work unified path-length, time, and curvature constraints when determining headland width for T-turns and similar patterns on irregular fields [24,25,26].

Building on that equipment-specific perspective, researchers modelled a tracked combine harvester and showed that its header and track geometry favour a semicircular turn for the shortest, fastest headland path [27]. Related efforts refined asymmetric switch-back plans by coupling them with automatic shuttle-shifting on tractor–implement pairs, while integrated arc-linear and cubic-curve schemes addressed turning, obstacle avoidance, and track merging in a single sweep [28,29,30].

Recent trends have shifted beyond deterministic templates towards real-time and data-driven planning. Convex-polytope representations paired with numerical refinements now yield collision-free headland paths under explicit geometric constraints [31]. Improved Hybrid-A* and Reeds–Shepp hybrids provide smoother solutions across varied operational scenarios [32]. Optimised Bézier curves enable obstacle avoidance without sacrificing arable area, and unified steering–hydrostatic controllers consistently achieve sub-decimetre tracking accuracy in diverse vehicles [33,34]. Recent work shows that model-free reinforcement learning can successfully learn tractor–trailer headland-turn policies directly through interaction, pointing toward plug-and-play adaptability [35]. Finally, holistic coverage planners embed curvature- or energy-based metrics, generating routes that respect motion limits and minimise overall resource consumption [36,37].

The aim of this study is to present and analytically develop new variants of U- and Ω-turns in which the traditional Dubins or Reeds–Shepp arcs are replaced by transition curves whose smoothly varying curvature is defined by trigonometric functions. First, relations describing the curvature and tangent angle are derived; integrating these relations yields the trajectory coordinates together with the profiles of velocity, acceleration, and jerk. Next, the obtained equations are implemented in the kinematic models of two representative tractors, allowing the required wheel-steering angles to be calculated. Finally, to verify the proposed trajectory model, a numerical simulation is carried out in the Mathcad environment, combining symbolic and numerical calculations to compare the continuity of acceleration and the resulting jerk with those of classical manoeuvre geometries.

The remainder of the paper is organised as follows. Section 2 presents typical headland manoeuvres, the mathematical description of the trigonometric transition curve, and the proposed strategy for generating smooth U-turn and Ω-turn trajectories based on this approach. It also introduces the kinematic models of steering configurations for two models of wheeled working machines. Section 3 describes the results of simulation studies conducted using the Mathcad environment. It presents time profiles of curvature and tangent angle along the trajectory, time profiles of kinematic parameters, and the variation in the steering angle for both tractor models. Section 4 presents a comparative analysis using the classical Ω-turn as reference. Finally, Section 5 summarises the main findings of the study, outlining the advantages of the proposed approach and indicating implementation opportunities for precision agriculture.

2. Materials and Methods

2.1. Object of Analysis

During the manoeuvring of agricultural machines on headlands, in addition to the requirement to achieve the desired working width W_set, it is also crucial to minimise the number of turns, the total path length, and the time required to reach the next field pass [24]. Figure 1 presents the typical turning patterns in the manoeuvring areas: semicircular turn, U-turn, Ω-turn, and fishtail turn [27,28]. The shortest paths are obtained using the Dubins curves or Reeds–Shepp paths, which apply the minimum turning radius R_min [38,39]. However, considering limited steering speed and acceleration, the application of the trajectories shown in Figure 1 under the constant velocity conditions is only theoretically feasible. At the junction points between individual path segments, the vehicle would either have to stop or the wheel steering would have to occur with an infinitely large speed. During transitions from the straight segments to arcs (or vice versa) as well as at the tangency points between arcs, abrupt changes in acceleration occur. This results in infinite jerk values (i.e., the time derivative of acceleration).

Two of the most universal paths were selected for modification: the U-turn (Figure 1b) and the Ω-turn (Figure 1c). These paths allow the required working width W_set to be achieved for both W_set > 2R_min and W_set < 2R_min, and do not require a stop due to a change in the direction of movement.

2.2. Transition Curves

Figure 2 shows the planar curve with marked geometric parameters.

The curvature of the planar curve is defined as follows:

$$\kappa (\mathrm{l})=\underset{\Delta \mathrm{l}\to 0}{\lim }{\displaystyle \frac{\Delta \theta }{\Delta \mathrm{l}}}={\displaystyle \frac{\mathrm{d}\theta }{\mathrm{d}\mathrm{l}}},$$

(1)

where Δθ–the angle between the tangents to the curve at the endpoints of the arc, Δl–the arc length.

Therefore, the function θ(l) is defined by the following relationship:

$$\theta (\mathrm{l})={\displaystyle \int \kappa (\mathrm{l})\mathrm{d}\mathrm{l}},$$

(2)

In engineering applications requiring real-time trajectory generation, the use of trigonometric transition curves offers several practical advantages over classical clothoids. While clothoids require the numerical evaluation of Fresnel integrals, which increases computational complexity, trigonometric curves allow for closed-form expressions of curvature, tangent angle, and trajectory coordinates. This significantly simplifies implementation, especially in embedded systems and autonomous machine control. Specifically, in the case of a trigonometric transition curve, the relationship for curvature as a function of arc length l is given by

$$\kappa (\mathrm{l})={\displaystyle \frac{1}{2}}({\kappa }_1+{\kappa }_2)-{\displaystyle \frac{1}{2}}({\kappa }_2-{\kappa }_1)\cos {\displaystyle \frac{\pi \mathrm{l}}{\mathrm{L}}},$$

(3)

where κ₁—the curvature at the starting point, κ₂—the curvature at the endpoint, L—the arc length of the curve.

The form of the function θ(l) defined using Equation (2), for the curve whose curvature is given by Equation (3), is as follows:

$$\theta (\mathrm{l})={\displaystyle \frac{1}{2}}({\kappa }_1+{\kappa }_2)\mathrm{l}-{\displaystyle \frac{1}{2}}({\kappa }_2-{\kappa }_1){\displaystyle \frac{\mathrm{L}}{\pi }}\sin {\displaystyle \frac{\pi \mathrm{l}}{\mathrm{L}}},$$

(4)

In the case of transition curves, where the minimum curvature κ = 0 and the maximum curvature κ = 1/R_min, Equation (3) can be written in a simplified form:

$$\kappa (\mathrm{l})={\displaystyle \frac{\kappa }{2}}\left(1\pm \cos {\displaystyle \frac{\pi \mathrm{l}}{\mathrm{L}}}\right),$$

(5)

The “+” sign should be used when κ₁ = κ and κ₂ = 0, whereas the “–” sign should be used when κ₁ = 0 and κ₂ = κ.

Taking into account the initial tangent angle to the curve θ₀, as well as the sign determined by the direction of change in the tangent angle along the curve (“+” when the angle increases and “–” when it decreases), Equation (4) can be written in the following form:

$$\theta (\mathrm{l})={\theta }_0\pm {\displaystyle \frac{\kappa }{2}}\left[\mathrm{l}\pm {\displaystyle \frac{\mathrm{L}}{\pi }}\sin {\displaystyle \frac{\pi \mathrm{l}}{\mathrm{L}}}\right],$$

(6)

The coordinates of an arbitrary point on the transition curve are calculated using the following relationships:

$$\mathrm{x}(\mathrm{l})={\mathrm{x}}_{\mathrm{B}}+{\displaystyle \int \cos \theta (\mathrm{l})\mathrm{d}\mathrm{l}}$$

(7)

$$\mathrm{y}(\mathrm{l})={\mathrm{y}}_{\mathrm{B}}+{\displaystyle \int \sin \theta (\mathrm{l})\mathrm{d}\mathrm{l}}$$

(8)

where x_B, y_B—coordinates of the starting point of the curve.

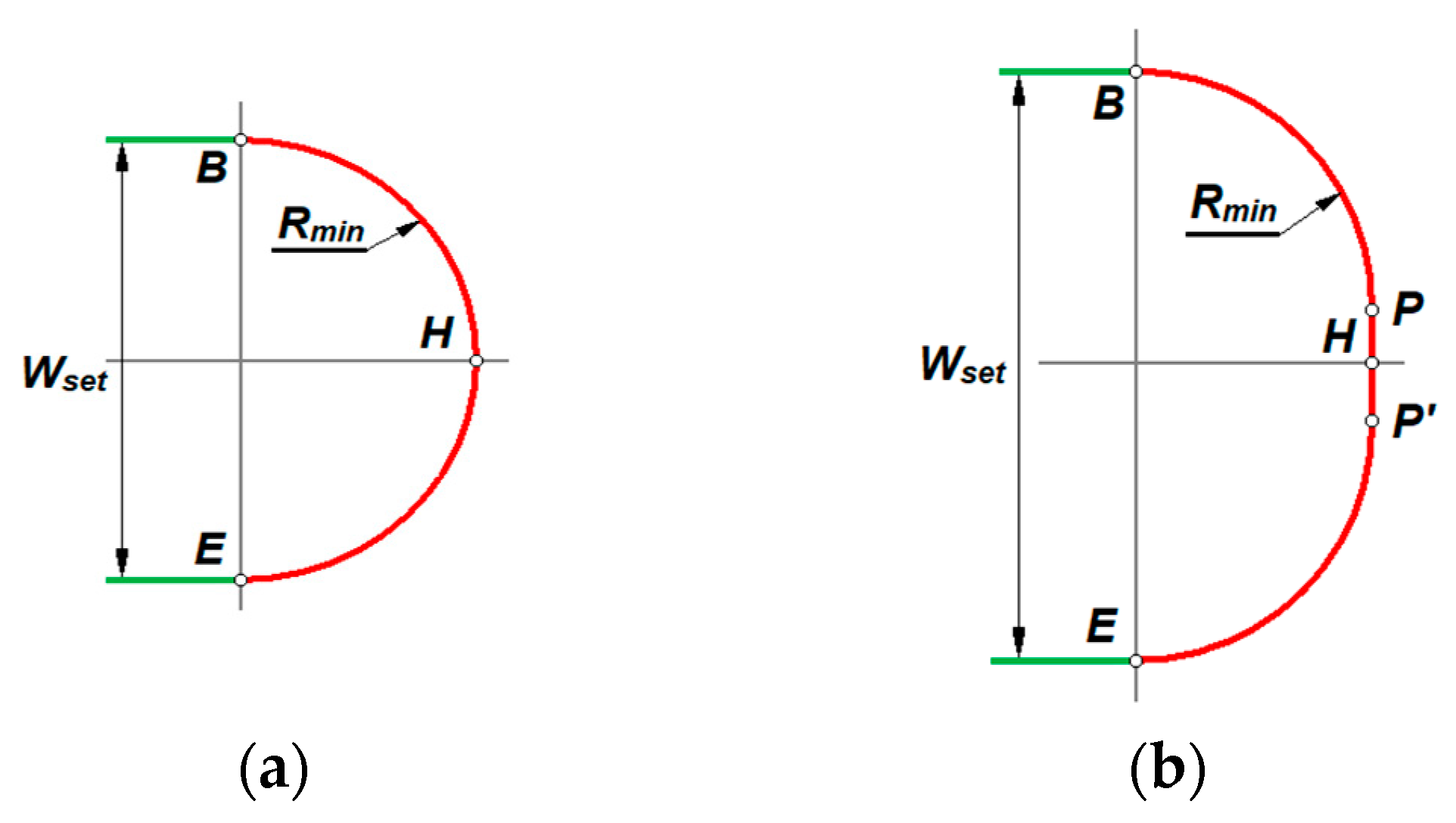
2.3. U-Turn Modification

Figure 3 presents the modified U-turn that incorporates transition curves. These curves gradually change the curvature, minimising sudden changes in direction and improving the motion dynamics. Without loss of generality, the analysis will focus only on one half of the path, as the trajectory is symmetrical. This half of the path consists of two transition curves and a straight-line segment:

• The first transition curve (segment P0-P1) introduces a gradual increase in the curvature from 0 to 1/R_min, reaching a tangent angle of π/4 at point P1;
• The second transition curve (segment P1-P2) decreases the curvature from 1/R_min to 0, while simultaneously increasing the tangent angle at point P2 to π/2;
• Straight-line segment (segment P2-H).

Table 1. Curvature—κ and tangent angle—θ at characteristic points of the modified U-turn.

Points of the Path	Curvature κ	Tangent Angle θ
P0	0	0
P1	1/Rmin	π/4
P2	0	π/2
H	0	π/2

summarises the curvatures and tangent angles to the curve at the characteristic points of the modified U-turn.

The relationships describing the path curvature (5), the tangent angle to the curve (6), and the coordinates of the path points (7) and (8) can be expressed as functions of time. To achieve this, the following steps should be performed:

• Based on the minimum turning radius R_min and the range of change in angle θ, calculate the length of the transition curves:

$${\mathrm{L}}_1={\mathrm{L}}_2=2\theta {\mathrm{R}}_{\min },$$

(9)

• Taking into account the required length of the straight-line segment P2 to H is equal to L₃, determine the motion times for each path segment:

$${\mathrm{t}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{L}}_{\mathrm{i}}}{\mathrm{v}}}\hspace{1em}\mathrm{for}\hspace{1em}\mathrm{i}=1,2,3,$$

(10)

• Assuming that the initial time T₀ = 0, calculate the total motion time T_n for the successive segments:

$${\mathrm{T}}_{\mathrm{n}}={\mathrm{T}}_0+{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{t}}_{\mathrm{i}}}\hspace{1em}\mathrm{for}\hspace{1em}\mathrm{n}=1,2,3,$$

(11)

Assuming a constant motion velocity—v and introducing the substitutions l = vt and dl = vdt, express the following as functions of time within the defined intervals [T_i−1, T_i] for i = 1, 2, 3:

-

The curvature;

-

The tangent angle to the curve;

-

The displacements (coordinates of the path points).

Velocities, accelerations, and jerks should be determined as successive derivatives with respect to time of the displacement functions (coordinates of the path points).

2.4. Ω-Turn Modification

Figure 4 presents the modified Ω-turn, in which transition curves have been implemented.

Similarly to the modified U-turn case, the path was designed to ensure smooth transitions between individual trajectory segments. Half of the path consists of three transition curves and a circular arc:

• The first transition curve (segment P0-P1) introduces a gradual increase in the curvature from 0 to 1/R_min reaching a tangent angle of θ at point P1;
• The second transition curve (segment P1-P2) decreases the curvature from 1/R_min to 0, while simultaneously increasing the tangent angle at point P2 to 2θ;
• The third transition curve (segment P2-P3) again increases the curvature to 1/R_min while gradually reducing the tangent angle to 0 at point P3;
• The circular arc (segment P3-H) corresponds to a quarter of a circle and is characterised by a constant curvature of 1/R_min.

Table 2. Curvature—κ and tangent angle—θ at characteristic points of the modified Ω-turn.

Points of the Path	Curvature κ	Tangent Angle θ
P0	0	0
P1	1/Rmin	θ
P2	0	2θ
P3	1/Rmin	0
H	1/Rmin	−π/2

summarises the curvature values and tangent angles of the curve at the characteristic points of the modified Ω-turn.

Similarly to the modified U-turn path, in order to determine the relationships describing the curvature, the tangent angle to the curve, and the coordinates of the path points as functions of time, the following steps should be performed:

• Based on the minimum turning radius R_min and the required change in angle θ, calculate the length of the transition curves and the length of the circular arc:

$${\mathrm{L}}_1={\mathrm{L}}_2=2\theta {\mathrm{R}}_{\min }$$

(12)

$${\mathrm{L}}_3=4\theta {\mathrm{R}}_{\min }$$

(13)

$${\mathrm{L}}_4={\displaystyle \frac{\pi {\mathrm{R}}_{\min }}{2}}$$

(14)

• Calculate the motion times for the successive path segments and the cumulative times using Equations (10) and (11), for i = 1, 2, 3, 4;
• Express the curvature, the tangent angle to the curve, and the displacements as functions of time within the defined intervals [T_i−1, T_i] for i = 1, 2, 3, 4.

Velocities, accelerations, and jerks, similarly to the modified U-turn path, should be determined as successive derivatives with respect to time of the displacement functions.

2.5. Kinematic Models of Steering Configurations

Figure 5 presents two models of a wheeled working machine moving along a curved path. In model I (Figure 5a), it is assumed that only the front axle wheels can steer. In model II (Figure 5b), it is assumed that the steering angle can be adjusted individually for each wheel. There were introduced the following notation: O—the instantaneous centre of rotation of the working machine, O_T—the centre of mass of the machine or another reference point, R—the turning radius of the tractor, δ_FL—the steering angle of the front-left wheel, δ_FR—the steering angle of the front-right wheel, δ_RL—the steering angle of the rear-left wheel, δ_RR—the steering angle of the rear-right wheel, B_TF—the front axle track width, B_TR—the rear axle track width, L_TF—the position of the front axle, L_TR—the position of the rear axle.

For both model I and model II, the steering angle of the front axle wheels can be calculated using the following equation:

$${\delta }_{\mathrm{F}\mathrm{L}}=\arctan ({\displaystyle \frac{{\mathrm{L}}_{\mathrm{T}\mathrm{F}}}{\mathrm{R}-\frac{{\mathrm{B}}_{\mathrm{T}\mathrm{F}}}{2}}}),$$

(15)

$${\delta }_{\mathrm{F}\mathrm{R}}=\arctan ({\displaystyle \frac{{\mathrm{L}}_{\mathrm{T}\mathrm{F}}}{\mathrm{R}+\frac{{\mathrm{B}}_{\mathrm{T}\mathrm{F}}}{2}}}).$$

(16)

whereas for model II, the steering angles of the rear axle wheels can be calculated as follows:

$${\delta }_{\mathrm{R}\mathrm{L}}=\arctan ({\displaystyle \frac{-{\mathrm{L}}_{\mathrm{T}\mathrm{R}}}{\mathrm{R}-\frac{{\mathrm{B}}_{\mathrm{T}\mathrm{R}}}{2}}}),$$

(17)

$${\delta }_{\mathrm{R}\mathrm{R}}=\arctan ({\displaystyle \frac{-{\mathrm{L}}_{\mathrm{T}\mathrm{R}}}{\mathrm{R}+\frac{{\mathrm{B}}_{\mathrm{T}\mathrm{R}}}{2}}}).$$

(18)

In the case of straight-line motion, where the turning radius R tends to infinity, the steering angles of all wheels tend to zero. Therefore, for such segments, the steering angles can be directly set to zero without evaluating the arctangent function.

3. Results

To verify the proposed trajectory model, a numerical simulation was conducted in the Mathcad environment based on symbolic and numerical calculations. The simulation was performed for the following data: R_min = 3.25 m, v = 2π/3 ms^–1, L_TF = 0.65 m, L_TR = 0.8 m, B_TF = 1.65 m, B_TR = 0.8 m.

In the previous section, the values of L₃ and θ were assumed as given for the modified U-turn and Ω-turn. However, in the simulation, these values were calculated in order to obtain the desired working width W_set.

For the modified U-turn, the following procedure was applied to determine L₃:

• Calculate the segment lengths L_i and motion times t_i for the first two path segments, assuming θ = π/4;
• Calculate the cumulative times T_n for n = 1 and n = 2;
• Calculate the y-coordinate of point P2;
• Calculate the working width based on the following equation:

$${\mathrm{L}}_3={\displaystyle \frac{1}{2}}{\mathrm{W}}_{\mathrm{set}}-{\mathrm{y}}_{\mathrm{P}2}.$$

(19)

For the given working width W_set = 16 m, the length of the straight-line segment is L₃ = 2.033 m.

Figure 6 presents the time profiles of curvature κ(t) and tangent angle θ(t) for the modified U-turn.

Figure 7 presents the time profiles of displacement (Figure 7a), velocity (Figure 7b), acceleration (Figure 7c), and jerk (Figure 7d) components along the x and y axes for the modified U-turn manoeuvre.

Figure 8 presents the time profiles of wheel steering angles for the modified U-turn in model I (Figure 8a) and model II (Figure 8b). The turning radius R used in Equations (15)–(18) was calculated as the inverse of the signed curvature, which accounts for the steering direction.

In the case of the modified Ω-turn, for a given working width W_set, the procedure to determine the required angle θ can be outlined in the following steps:

• Assume the initial angle value θ_init and the angle increment Δθ;
• Calculate the angles θ_i, lengths L_i, and motion times t_i for the first three segments of the path;
• Calculate the cumulative times T_n for n = 1, n = 2, n = 3;
• Calculate the y-coordinate of point P3;
• Calculate the working width based on the following formula:

$$\mathrm{W}=2({\mathrm{R}}_{\min }-{\mathrm{y}}_{\mathrm{P}3})$$

(20)

The algorithm should be repeated by increasing the angle θ by Δθ until the calculated working width W becomes less than the given working width W_set. Algorithm 1 presents the pseudocode of this algorithm.

Algorithm 1. Exemplary pseudocode of the algorithm for calculating the angle θ with a precision of Δθ.

function θ (θinit, ∆θ, Rmin, v, Wset) θ←θinit κ←1/Rmin            // Define curvature as the inverse of the minimum turning radius        repeat         θ←θ+∆θ         // Define angles for each segment         θ[1]←θ         θ[2]←θ         θ[3]←2*θ         // Calculate lengths and travel times for each segment               for i from 1 to 3 do                    L[i] ←2*Rmin*θ[i]                    t[i]←L[i]/v               end for         // Compute cumulative times                 T0←0                 T1←t[1]                 T2←T1+t[2]                 T3←T2+t[3]         // Compute y-coordinates at characteristic points                  y_P1 ← v*∫ from T0 to T1 of sin(κ/2*(v*t-L[1]/π*sin(π*v*t/L[1])))dt                  y_P2 ← y_P1+v*∫ from T1 to T2 of sin(θ+κ/2*(v*(t-T1)+L[2]/π*sin(π*v*(t-T1)/L[2])))dt                  y_P3 ← y_P2+v*∫ from T2 to T3 of sin(2*θ-κ/2*(v*(t-T2)-L[3]/π*sin(π*v*(t-T2)/L[3])))dt              // Compute the working width based on the y-coordinate of point P3                  W←2*(Rmin-y_P3)        until (W <= Wset) return θ end function

The presented algorithm was used to calculate the angle θ for W_set = 2 m. To obtain an initial estimate of θ, the values θ_init = 9° and Δθ = 1° were assumed. The algorithm performed seven loop iterations and returned the value θ = 16°, for which the working width was W = 1.803 m, thus satisfying the condition W ≤ W_set. To increase the accuracy, the calculation was repeated with θ_init = 15.5° and Δθ = 0.025°. The algorithm executed six loop iterations and returned the value θ = 15.650°, for which the working width was W = 1.999 m, again meeting the condition W ≤ W_set. The calculated angle θ = 15.650° was then used in the simulation.

Figure 9 presents the time profiles of curvature κ(t) and tangent angle θ(t) for the modified Ω-turn.

Figure 10 presents the time profiles of displacement (Figure 10a), velocity (Figure 10b), acceleration (Figure 10c), and jerk (Figure 10d) components along the x and y axes for the modified Ω-turn manoeuvre.

Figure 11 presents the time profiles of wheel steering angles for the modified Ω-turn in model I (Figure 11a) and model II (Figure 11b). Similarly to the modified U-turn case, the turning radius R was calculated as the inverse of the signed curvature, which accounts for the steering direction.

4. Discussion

For the comparative analysis, the classical Ω-turn was selected (Figure 1c), in which tangency points occur both between the straight-line segment and the circular arc, as well as between two circular arcs.

The displacement profiles x(t) and y(t) belong to class C¹, which ensures the continuity of the motion path (Figure 12a). However, at times t_B and t_P1, abrupt changes in the tangent angle to the trajectory occur, corresponding to changes in the direction of the velocity vector without continuity of derivatives (Figure 12b). The functions v_x(t) and v_y(t) remain continuous, but their derivatives are not, which excludes C¹ continuity. In the acceleration profiles a_x(t) and a_y(t), discontinuities appear at t_B and t_P1, indicating a lack of C⁰ continuity. The underlying cause of such behaviour is as follows. At the moment when circular motion begins—t_B—a normal acceleration component appears, and at t_P1, its direction changes abruptly, resulting in discontinuities in both a_x(t) and a_y(t) components (Figure 12c). Consequently, the path is not of class C² and requires smoothing, for example, by applying appropriate transition curves, in order to enable its physical realisation.

When analysing the steering angle profiles (Figure 13), discontinuities in their changes can also be observed. Executing such a path would require the instant transitions of the wheels from the straight-ahead position to the maximum left steering angle at time t_B. This change in steering angle would have to occur in a negligibly short time. An even more demanding transition occurs at time t_P1, where the wheels would have to be instantaneously switched from one extreme steering position to the opposite one, again in nearly zero time. In practice, performing such a manoeuvre is infeasible due to mechanical limitations of the steering system and the dynamic constraints of the vehicle [5,9].

To address these issues, researchers have proposed various solutions. Backman et al. introduced the Spiral Connection Method (SCM) as a modification of the commonly used Dubins curve, making the resulting trajectory feasible for agricultural machinery [5,12]. Cariou et al. used clothoids to design feasible manoeuvres for the vehicles performing headland turns [6,13]. Similarly, Sabelhaus et al. presented a path shaping method based on clothoids. The authors modified the Dubins and Reeds–Shepp curves for seven different agricultural headland manoeuvres [9,10]. Graf Plessen and Bemporad focused on trajectory smoothing for fields with irregular boundaries using three methods for generating smooth reference paths: circular segments, generalised elementary paths, and bi-elementary paths [17].

5. Conclusions

The conducted analyses demonstrated that the use of transition curves during U-turn and Ω-turn manoeuvres significantly improves the continuity of machine motion trajectories. The introduction of smooth curvature variation eliminates discontinuities in the acceleration and jerk components, which are characteristic of classical solutions based on circular arcs and straight-line segments. The simulation performed for two steering system models (with a steerable axle and with individual steering of all wheels) confirmed the feasibility of implementing modified paths. The obtained kinematic parameter profiles, including displacement, velocity, acceleration, and jerk, indicate significantly better motion dynamics compared to classical paths. The introduced modifications not only enhance the comfort and safety of manoeuvres but also pave the way for full integration of smoothed paths with automatic machine control systems.

The results obtained in this study provide a robust foundation for future research aimed at enhancing transition curve models and ensuring their seamless integration with advanced agricultural machinery control systems. This approach can significantly improve precision and operational efficiency, enabling more effective and autonomous operations in the agricultural sector.