Predicting Dike Piping Hazards Using Critical Slowing Down Theory on Electrical Signals
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Study
2.1.1. Design of Experimental Model
2.1.2. Materials
2.2. Denoising Method
2.2.1. EEMD
- (1)
- Add a noise sequence with an amplitude of α to the original data sequence of various signals, resulting in a new sequence , as shown in Equation (1).
- (2)
- Apply Empirical Mode Decomposition (EMD) to in order to extract several intrinsic mode function (IMF) components at different time scales, along with a residual sequence .
- (3)
- Repeat steps (1) and (2) N times, adding a distinct white noise sequence each time. This process generates N sets of IMF components and residual sequences, where the jth-order IMF of the ith set is denoted as IMFij, and the residual sequence of the ith set is denoted as , where i ≤ N.
- (4)
- Independently compute the average of the N sets of corresponding IMF components and residual sequences to derive the final EEMD decomposition result, as presented in Equation (2).
2.2.2. Grouping Calculation of IMF Components
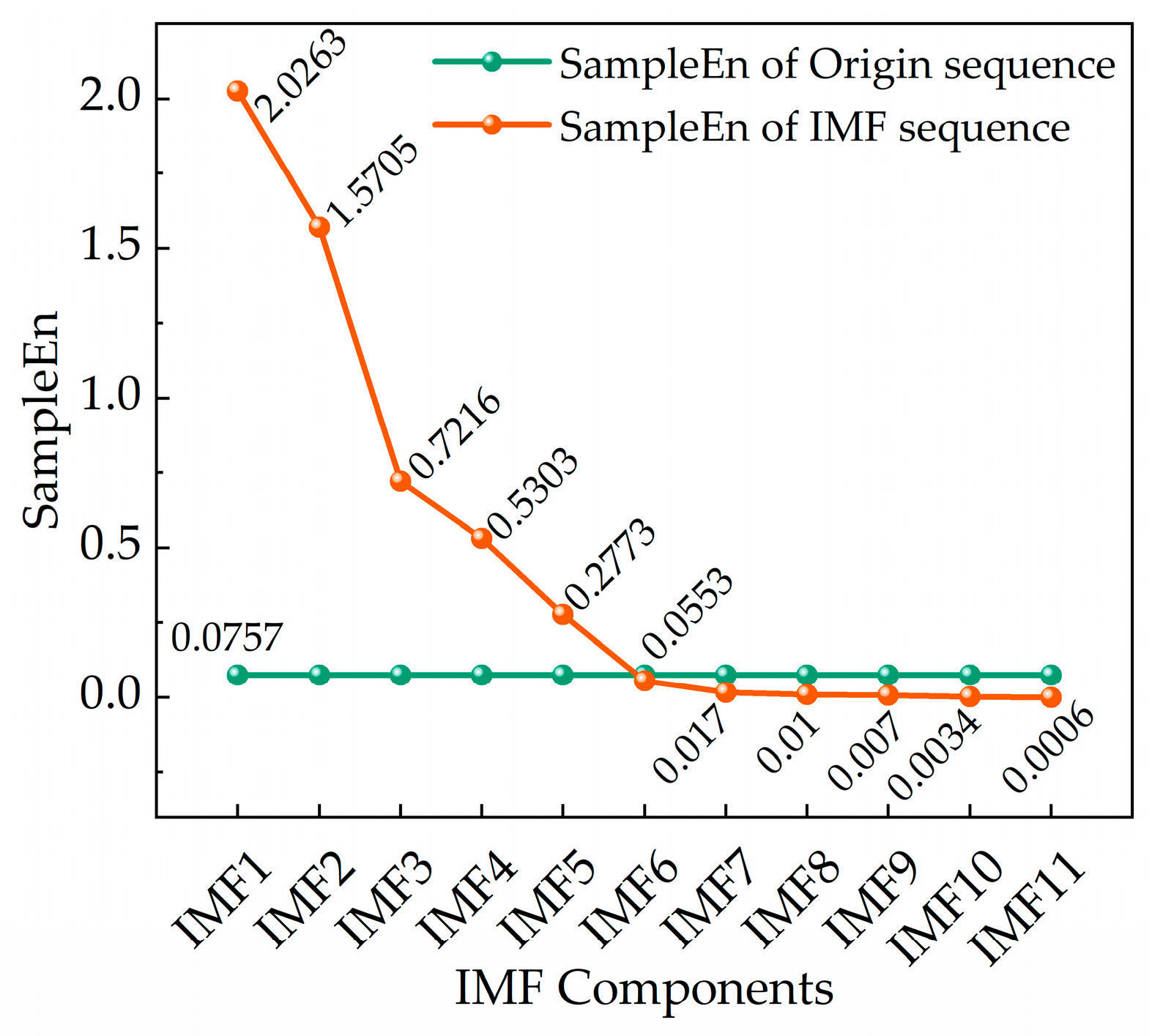
2.2.3. Sample Entropy
2.2.4. Wavelet Denoising
2.3. Critical Slowing Down Theory
3. Results
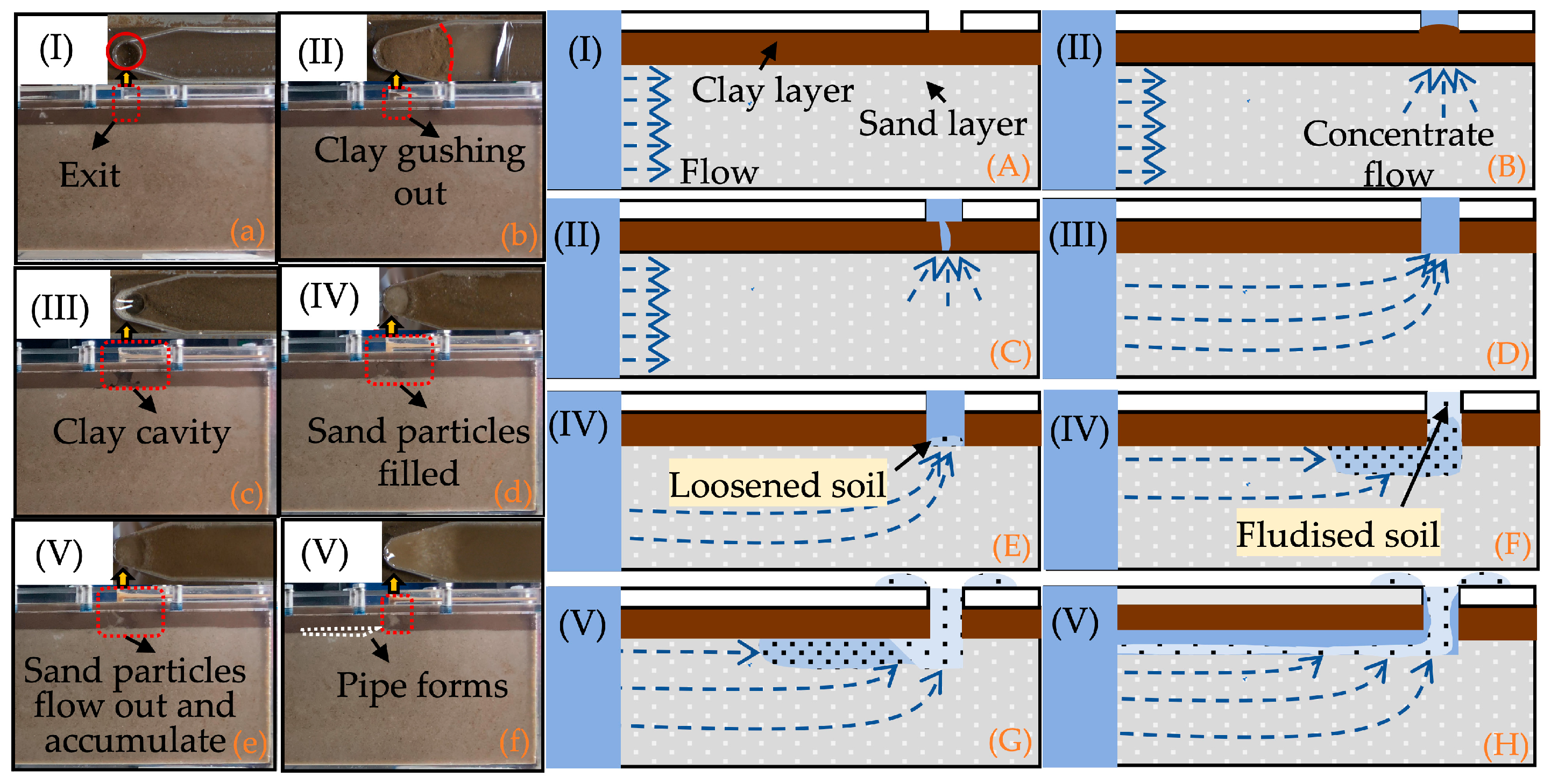
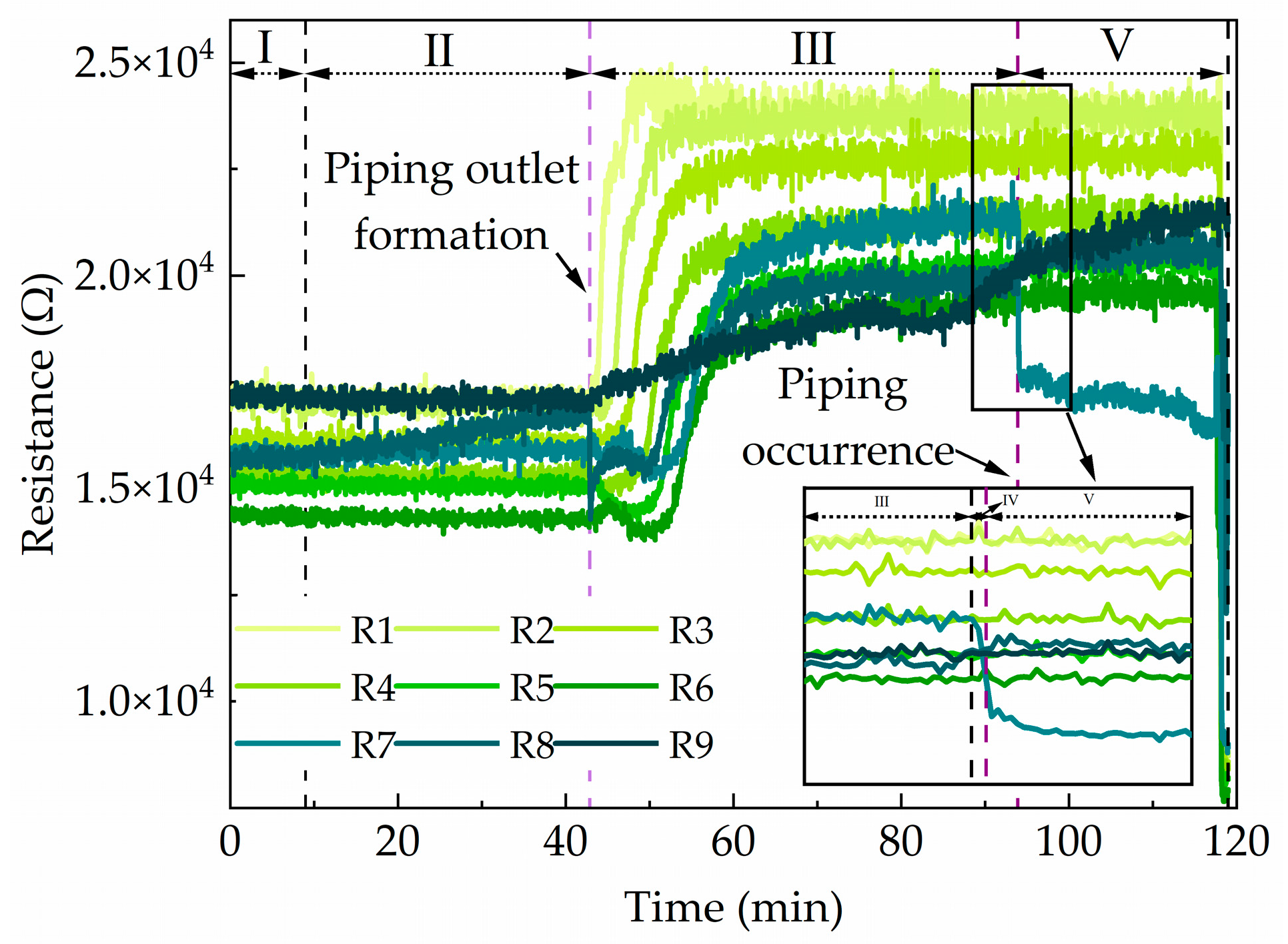
3.1. Analysis of Experimental Data for Piping
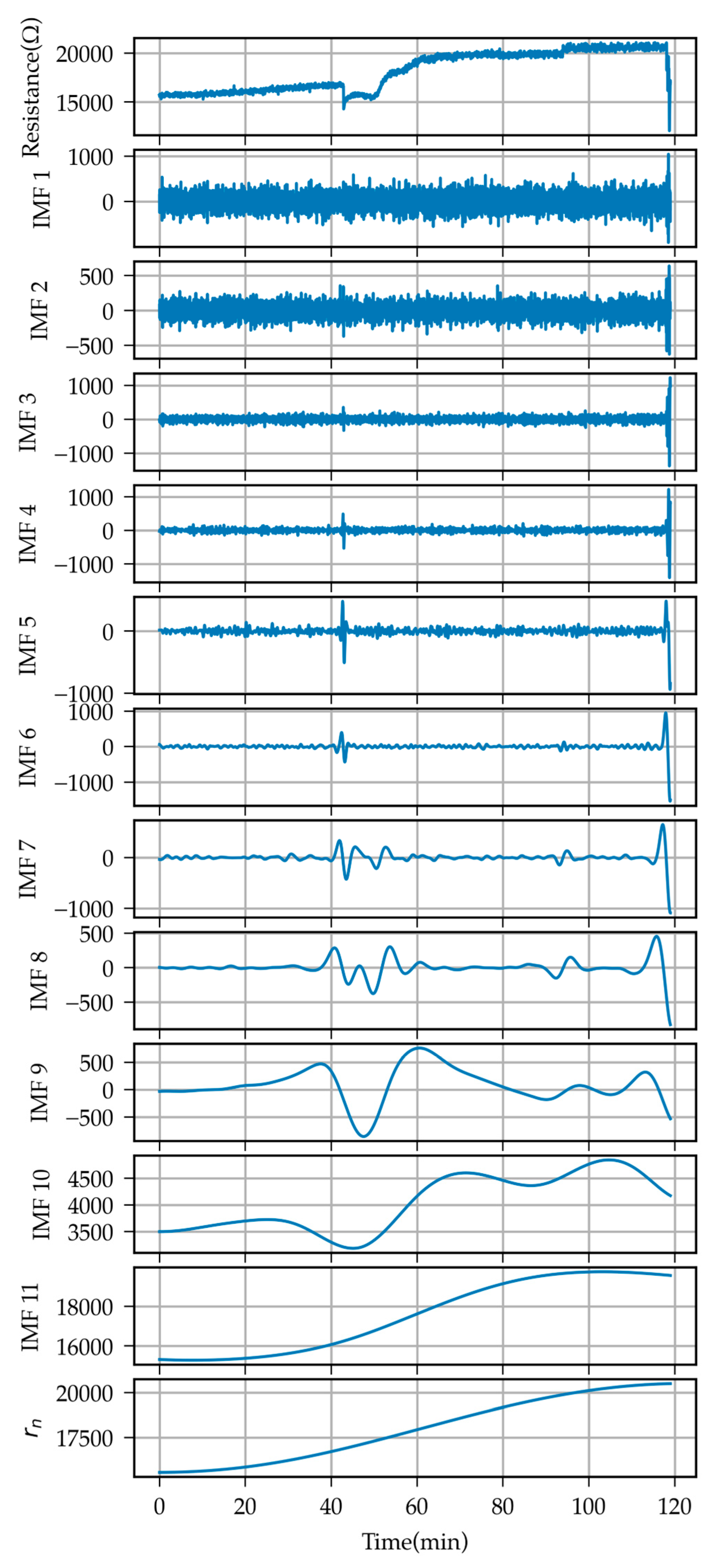
3.2. Decomposition and Reconstruction of Electrical Signal Sequences for Piping Processes
4. Discussion
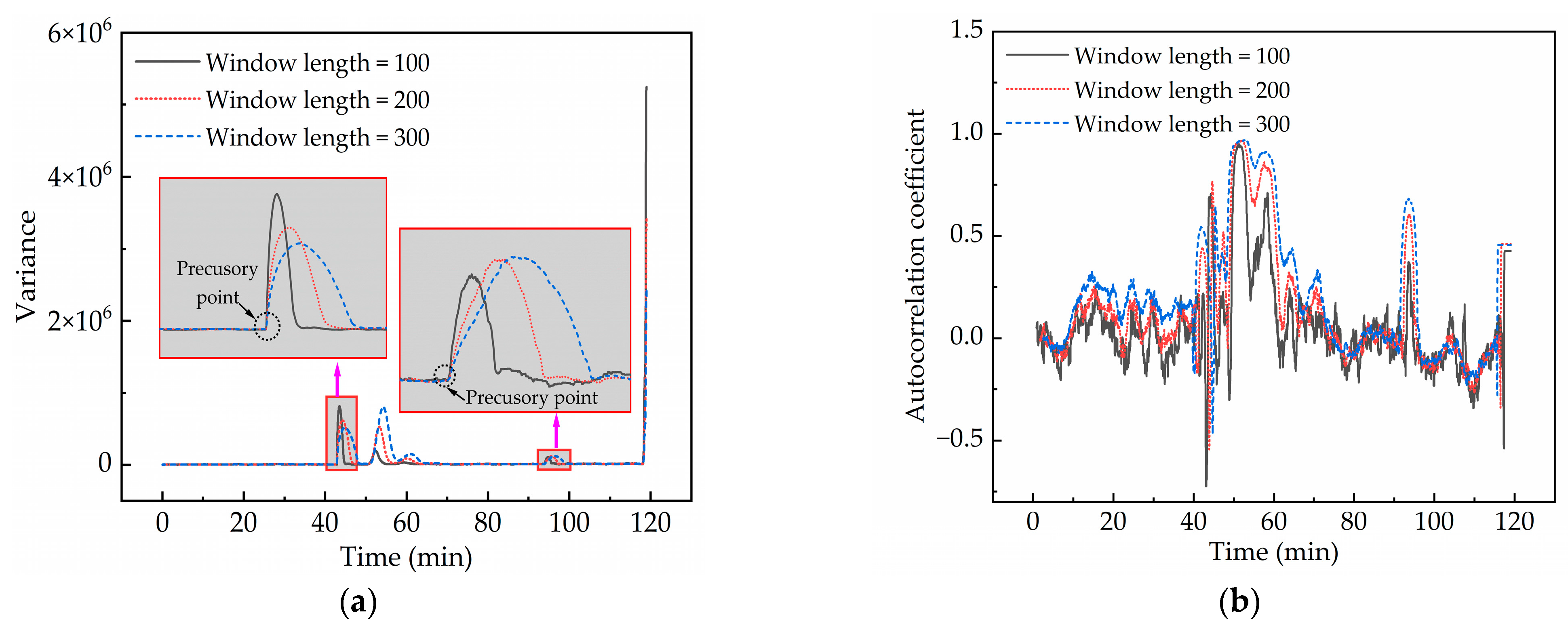
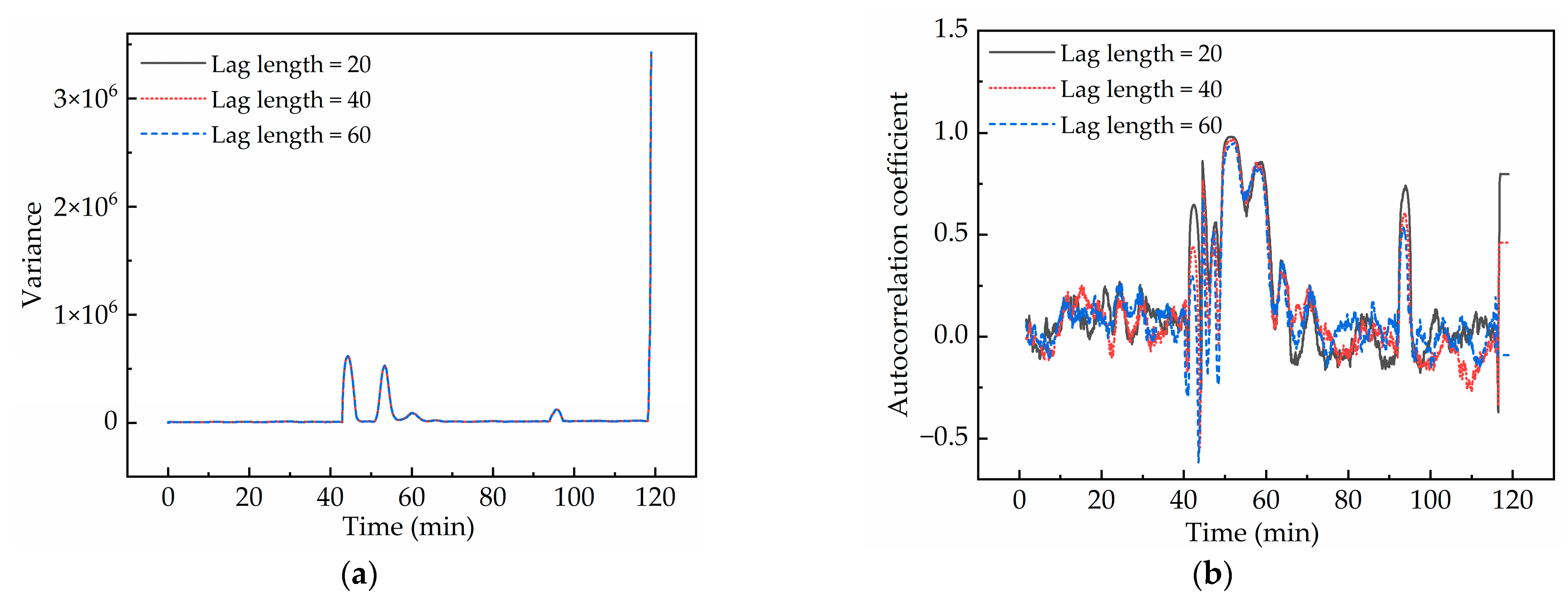
4.1. Determination of Window Length and Lag Length
4.2. Effective Precursory Characteristics of the Piping Process
5. Conclusions
- (1)
- The evolution of the piping process exhibited distinct phase characteristics. At the moments of piping outlet formation and piping occurrence, the electrical signals showed critical transition features, further validating the universality of the critical slowing down phenomenon.
- (2)
- The time-series characteristics of the electrical signals were analyzed using Ensemble Empirical Mode Decomposition (EEMD), which decomposed the signals into low- and high-frequency components. The low-frequency component reflects the staged characteristics of the piping process, while the high-frequency component captures the abrupt variations. Together, these components offer a multi-scale perspective on the evolution of piping.
- (3)
- The original sequences of the electrical signals displayed a sharp increase in critical slowing down indicators (variance and autocorrelation coefficient) at the critical transition points of the piping process, with the variance curve providing a more intuitive depiction of abrupt variations.
- (4)
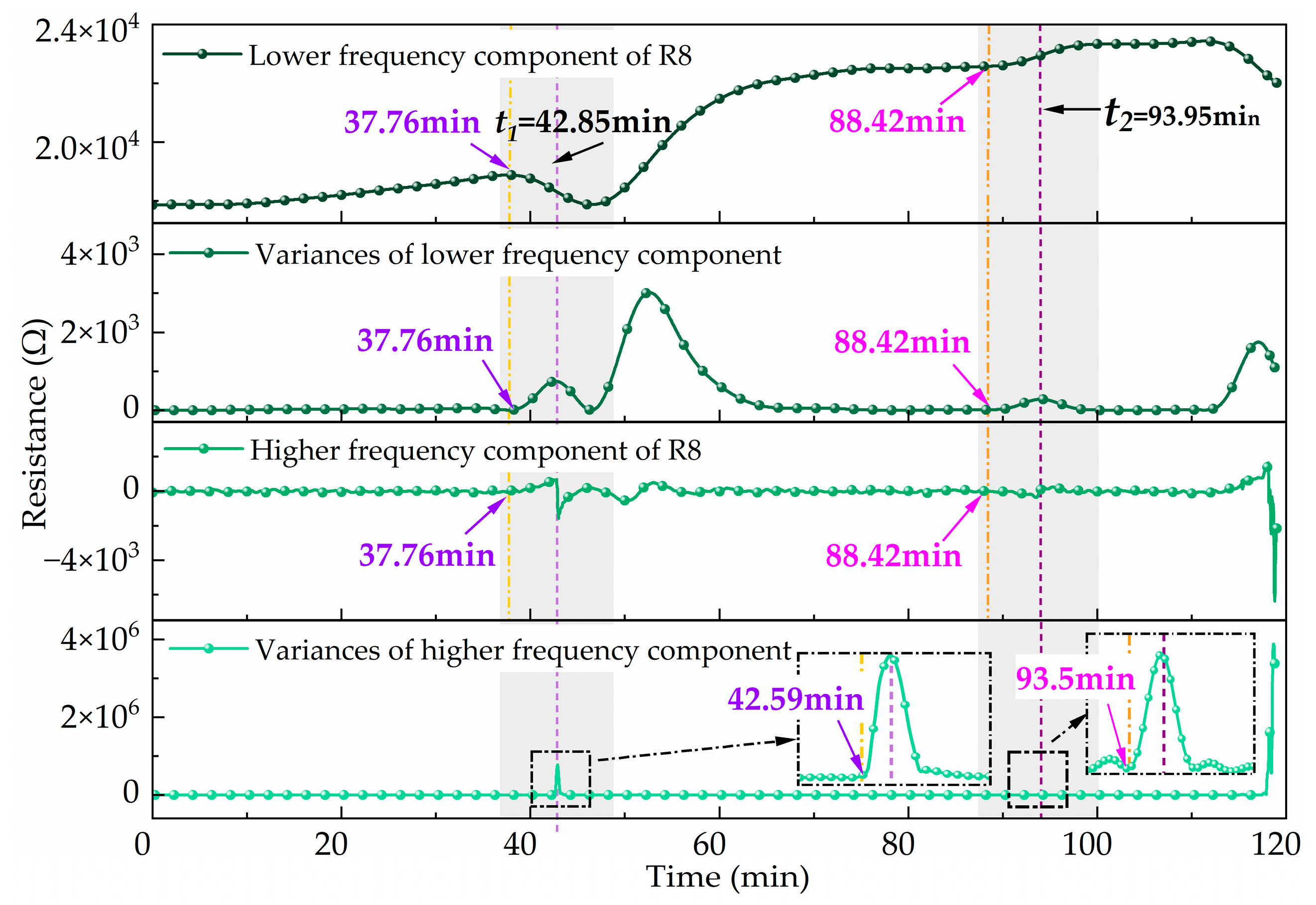
- The reconstructed components of the electrical signals exhibited CSD characteristics. At the moment of piping outlet formation and piping occurrence, the sharp increase in the variance of the reconstructed low- and high-frequency components of electrical signals served as effective precursory characteristics. Quantitatively, the variance of the low-frequency component increased sharply 5.09 min before the formation of the piping outlet and 5.53 min before piping occurrence. In contrast, the variance of the high-frequency component increased 0.26 min and 0.45 min earlier, respectively. The precursory point of low-frequency variance appears earlier than that of high-frequency variance. The low-frequency variance provides an early warning for piping hazards, while the high-frequency variance offers a short-term warning.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beck, K.K.; Fletcher, M.; Gadd, P.S.; Heijnis, H.; Saunders, K.M.; Simpson, G.L.; Zawadzki, A. Variance and Rate-of-change as Early Warning Signals for a Critical Transition in an Aquatic Ecosystem State: A Test Case from Tasmania, Australia. J. Geophys. Res. Biogeosciences 2018, 123, 495–508. [Google Scholar] [CrossRef]
- Hao, W.; Wei, H.; Peng-Cheng, Y. Using the Principle of Critical Slowing down to Discuss the Abrupt Climate Change. Acta Phys. Sin. 2013, 62, 039206. [Google Scholar] [CrossRef]
- Yan, R.; Jiang, C.-S.; Zhang, L.-P. Study on Critical Slowing down Phenomenon of Radon Concentrations in Water before the Wenchuan MS8. 0 Earthquake. Chin. J. Geophys. 2011, 54, 1817–1826. [Google Scholar]
- Lenton, T.M.; Held, H.; Kriegler, E.; Hall, J.W.; Lucht, W.; Rahmstorf, S.; Schellnhuber, H.J. Tipping Elements in the Earth’s Climate System. Proc. Natl. Acad. Sci. USA 2008, 105, 1786–1793. [Google Scholar] [CrossRef]
- Tian, H.; Li, Z.; Shen, X.; Zang, Z.; Song, J.; Zhang, Q. Identification Method of Infrared Radiation Precursor Information of Coal Sample Failure and Instability under Uniaxial Compression. Infrared Phys. Technol. 2021, 119, 103957. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Niu, Y.; Cheng, F.; Ali, M.; Bacha, S. An Experimental Study on the Precursory Characteristics of EP before Sandstone Failure Based on Critical Slowing Down. J. Appl. Geophys. 2019, 170, 103818. [Google Scholar] [CrossRef]
- Liang, P.; Li, Z.; Li, Q.; Yu, G.; Wang, S.; Han, Q.; Huang, X. The Critical Slowing-down Characteristics of Multi-Physical Field Monitoring Information about the Brittle Failure of Rock under Three-Point Bending. Nondestruct. Test. Eval. 2024, 39, 701–723. [Google Scholar] [CrossRef]
- Kanning, W.; Bocovich, C.; Schweckendiek, T.; Mooney, M.A. Incorporating Observations to Update the Piping Reliability Estimate of the Francis Levee. In Geotechnical Safety and Risk V; IOS Press: Amsterdam, The Netherlands, 2015; pp. 861–866. [Google Scholar]
- Foster, M.; Fell, R.; Spannagle, M. The Statistics of Embankment Dam Failures and Accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Cho, I.; Ha, I.; Kim, K.; Ahn, H.; Lee, S.; Kang, H. 3D Effects on 2D Resistivity Monitoring in Earth-fill Dams. Near Surf. Geophys. 2014, 12, 73–81. [Google Scholar] [CrossRef]
- Richards, K.S.; Reddy, K.R. Critical Appraisal of Piping Phenomena in Earth Dams. Bull. Eng. Geol. Environ. 2007, 66, 381–402. [Google Scholar] [CrossRef]
- Mooney, M.A.; Parekh, M.L.; Lowry, B.; Rittgers, J.; Grasmick, J.; Koelewijn, A.R.; Revil, A.; Zhou, W. Design and Implementation of Geophysical Monitoring and Remote Sensing during a Full-Scale Embankment Internal Erosion Test. In Geo-Congress 2014: Geo-Characterization and Modeling for Sustainability; ASCE Library: Reston, VA, USA, 2014; pp. 202–211. [Google Scholar]
- Ahmed, A.S.; Revil, A.; Bolève, A.; Steck, B.; Vergniault, C.; Courivaud, J.; Jougnot, D.; Abbas, M. Determination of the Permeability of Seepage Flow Paths in Dams from Self-Potential Measurements. Eng. Geol. 2020, 268, 105514. [Google Scholar] [CrossRef]
- Lee, B.; Oh, S.; Yi, M.-J. Mapping of Leakage Paths in Damaged Embankment Using Modified Resistivity Array Method. Eng. Geol. 2020, 266, 105469. [Google Scholar] [CrossRef]
- Masi, M.; Ferdos, F.; Losito, G.; Solari, L. Monitoring of Internal Erosion Processes by Time-Lapse Electrical Resistivity Tomography. J. Hydrol. 2020, 589, 125340. [Google Scholar] [CrossRef]
- Shin, S.; Park, S.; Kim, J.-H. Time-Lapse Electrical Resistivity Tomography Characterization for Piping Detection in Earthen Dam Model of a Sandbox. J. Appl. Geophys. 2019, 170, 103834. [Google Scholar] [CrossRef]
- Moffat, R. A Laboratory Study of Particle Migration in Cohesionless Soils. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, August 2002. [Google Scholar]
- Xiao, Y.; Pan, H.; Luo, G. Modelling of Flow in Backward Erosion Pipes. Geomech. Energy Environ. 2023, 35, 100476. [Google Scholar] [CrossRef]
- Alasadi, S.A.; Bhaya, W.S. Review of Data Preprocessing Techniques in Data Mining. J. Eng. Appl. Sci. 2017, 12, 4102–4107. [Google Scholar]
- Golyandina, N.; Korobeynikov, A.; Zhigljavsky, A. Singular Spectrum Analysis with R; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 3-662-57380-6. [Google Scholar]
- Zhang, J.; Jiang, Q.; Ma, B.; Zhao, Y.; Zhu, L. Signal De-Noising Method for Vibration Signal of Flood Discharge Structure Based on Combined Wavelet and EMD. J. Vib. Control 2017, 23, 2401–2417. [Google Scholar] [CrossRef]
- Lu, S.; Wang, J.; Xue, Y. Study on Multi-Fractal Fault Diagnosis Based on EMD Fusion in Hydraulic Engineering. Appl. Therm. Eng. 2016, 103, 798–806. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Çelik, A.; Mandev, M.B. Hourly Significant Wave Height Prediction via Singular Spectrum Analysis and Wavelet Transform Based Models. Ocean Eng. 2023, 281, 114771. [Google Scholar] [CrossRef]
- Ghanbarzadeh, M.; Aminghafari, M. A New Hybrid-Multiscale SSA Prediction of Non-Stationary Time Series. Fluct. Noise Lett. 2016, 15, 1650005. [Google Scholar] [CrossRef]
- Barbosh, M.; Singh, P.; Sadhu, A. Empirical Mode Decomposition and Its Variants: A Review with Applications in Structural Health Monitoring. Smart Mater. Struct. 2020, 29, 093001. [Google Scholar] [CrossRef]
- Van Beek, V.; VandenBoer, K.; Bezuijen, A. Influence of Sand Type on Pipe Development in Small-and Medium-Scale Experiments. In Proceedings of the 7th International Conference on Scour and Erosion, Perth, Australia, 2–5 December 2014; Volume 1, pp. 111–120. [Google Scholar]
- Xiao, Y.; Cao, H.; Pan, H.; Luo, G.; Zhu, D. Incipient Motion of Sands near the Pipe Tip. Acta Geotech. 2024, 19, 4107–4119. [Google Scholar] [CrossRef]
- Dubey, R.; Kumar, M.; Upadhyay, A.; Pachori, R.B. Automated Diagnosis of Muscle Diseases from EMG Signals Using Empirical Mode Decomposition Based Method. Biomed. Signal Process. Control. 2022, 71, 103098. [Google Scholar] [CrossRef]
- Kim, T.K. T Test as a Parametric Statistic. Korean J. Anesthesiol. 2015, 68, 540–546. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Qarib, H.; Adeli, H. A Comparative Study of Signal Processing Methods for Structural Health Monitoring. J. Vibroengineering 2016, 18, 2186–2204. [Google Scholar] [CrossRef]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; Van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-Warning Signals for Critical Transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef]
- Guttal, V.; Jayaprakash, C. Changing Skewness: An Early Warning Signal of Regime Shifts in Ecosystems. Ecol. Lett. 2008, 11, 450–460. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zhang, Z.; Gu, C.; Li, Y.; Zhang, K.; Xie, M. A Coupled Model for Dam Foundation Seepage Behavior Monitoring and Forecasting Based on Variational Mode Decomposition and Improved Temporal Convolutional Network. Struct. Control Health Monit. 2023, 2023, 3879096. [Google Scholar] [CrossRef]
- Beale, C.; Niezrecki, C.; Inalpolat, M. An Adaptive Wavelet Packet Denoising Algorithm for Enhanced Active Acoustic Damage Detection from Wind Turbine Blades. Mech. Syst. Signal Process. 2020, 142, 106754. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L.; Wu, X.; Zhang, K.; Skibniewski, M.J. Structural Health Monitoring and Assessment Using Wavelet Packet Energy Spectrum. Saf. Sci. 2019, 120, 652–665. [Google Scholar] [CrossRef]
- Archie, G.E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Hu, L.; Tang, C.; Zheng, H. Predicting Rock Failure with the Critical Slowing down Theory. Eng. Geol. 2021, 280, 105960. [Google Scholar] [CrossRef]
- Xu, C.; Xue, L.; Cui, Y.; Zhai, M.; Bu, F. Critical Slowing down Phenomenon for Predicting the Failure of Solid Rocks and Cement Mortar Materials: Insight from Acoustic Emission Multiparameters. Constr. Build. Mater. 2023, 399, 132523. [Google Scholar] [CrossRef]
- Fell, R.; Fry, J.-J. Internal Erosion of Dams and Their Foundations: Selected and Reviewed Papers from the Workshop on Internal Erosion and Piping of Dams and Their Foundations, Aussois, France; Crc Press: Boca Raton, FL, USA, 2005; ISBN 1-4822-6614-8. [Google Scholar]
- Chen, J.; Cheng, F.; Xiong, F.; Ge, Q.; Zhang, S. An Experimental Study: Fiber Bragg Grating–Hydrothermal Cycling Integration System for Seepage Monitoring of Rockfill Dams. Struct. Health Monit. 2017, 16, 50–61. [Google Scholar] [CrossRef]
- Kanning, W.; Baars, S.V.; Vrijling, J. The Stability of Flood Defenses on Permeable Soils: The London Avenue Canal Failures in New Orleans. In Proceedings of the 6th Conference of the International Conference on Case Histories in Geotechnical Engineering, Arlington, VA, USA, 14 August 2008. [Google Scholar]
- An, Q.; Steinberg, A.M.; Jella, S.; Bourque, G.; Füri, M. Early Warning Signs of Imminent Thermoacoustic Oscillations through Critical Slowing Down. J. Eng. Gas Turbines Power 2019, 141, 054501. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, Z.; Lai, J.; Qiu, J.; Cheng, Y.; Zhang, J. Critical Slowing down Precursor Information for the Acoustic Emission Response Characteristics of Defective Tuffs. Theor. Appl. Fract. Mech. 2024, 129, 104220. [Google Scholar] [CrossRef]
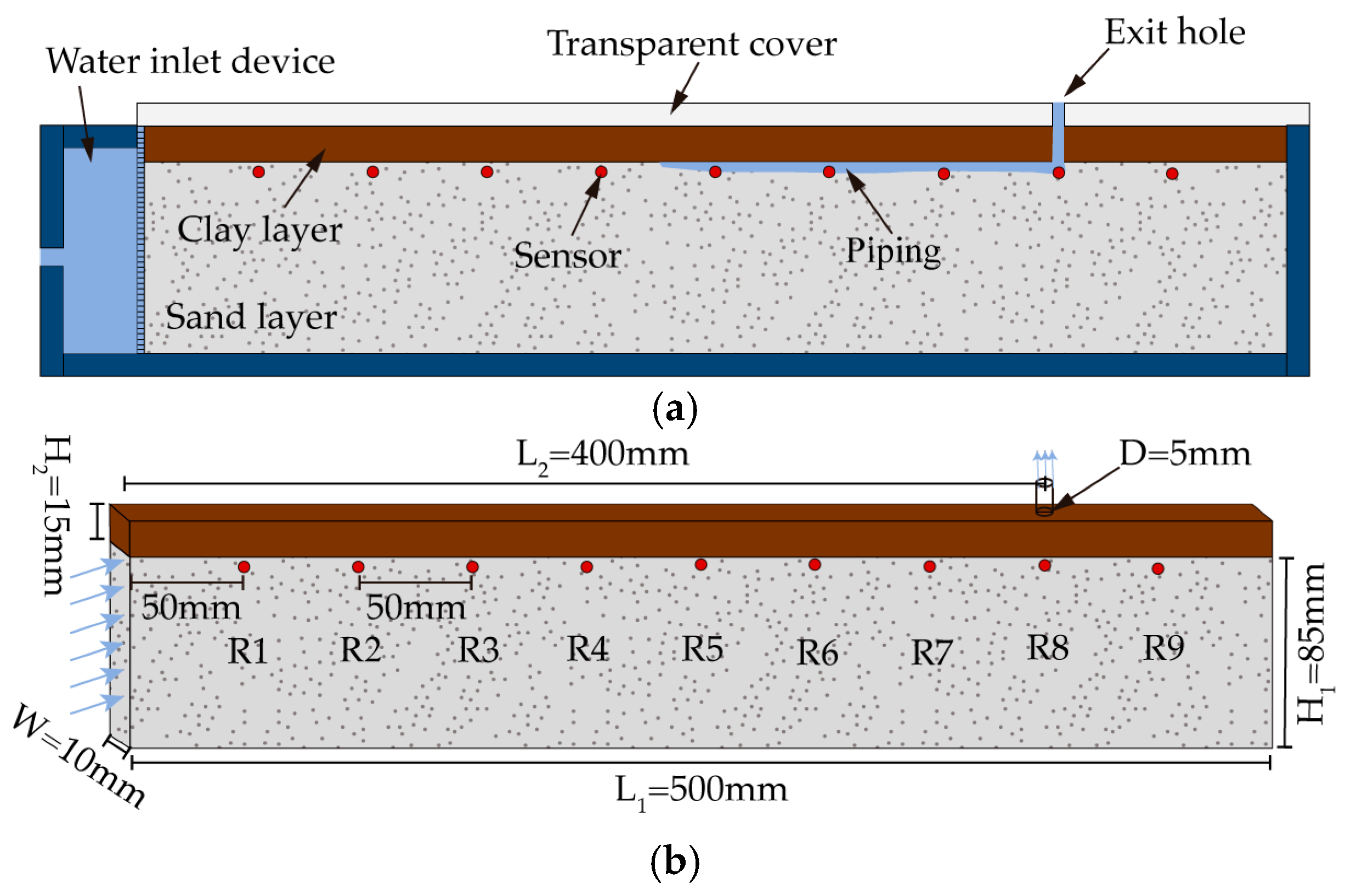
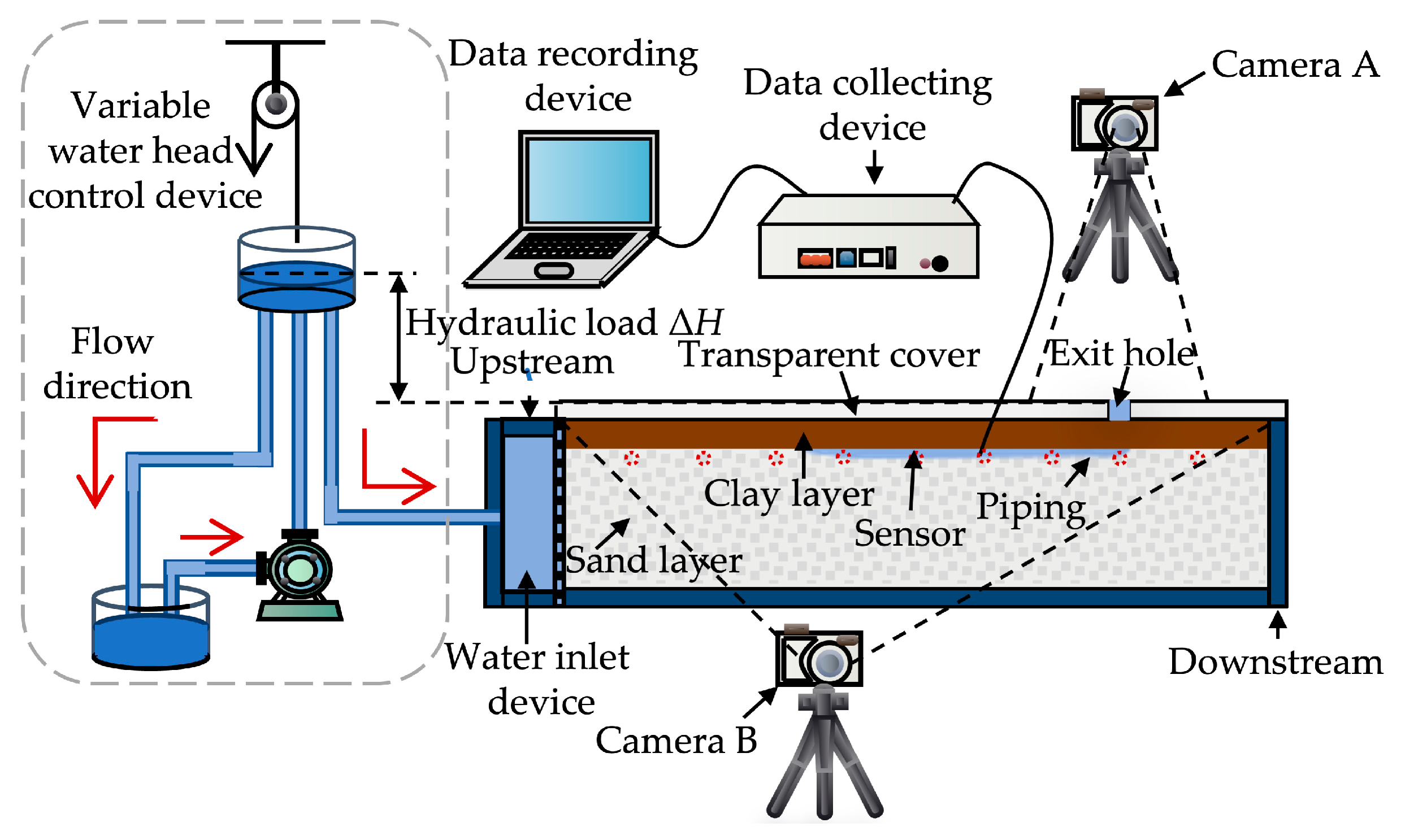


| Grain Composition Characteristics | Dry Density/g·cm−3 | Relative Density | Porosity | Permeability Coefficient /cm·s−1 | ||
|---|---|---|---|---|---|---|
| Grain Size Range/mm | Percentage | 30 d50/mm | ||||
| 0.075–0.25 | 25% | 15 | 1.52 | 2.62 | 0.32 | 0.04 |
| 0.25–0.5 | 25% | |||||
| 0.5–1 | 50% | |||||
| Index | Calculation Results |
|---|---|
| IMF 1 | 0.7677 |
| IMF 2 | 0.8854 |
| IMF 3 | 0.9298 |
| IMF 4 | 0.9859 |
| IMF 5 | 0.6247 |
| IMF 6 | 0.5158 |
| IMF 7 | 0.7925 |
| IMF 8 | 0.7332 |
| IMF 9 | 0 |
| IMF 10 | 0 |
| IMF 11 | 0 |
| IMF 12 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Wang, Y.; Ren, J. Predicting Dike Piping Hazards Using Critical Slowing Down Theory on Electrical Signals. Appl. Sci. 2025, 15, 8814. https://doi.org/10.3390/app15168814
Wang T, Wang Y, Ren J. Predicting Dike Piping Hazards Using Critical Slowing Down Theory on Electrical Signals. Applied Sciences. 2025; 15(16):8814. https://doi.org/10.3390/app15168814
Chicago/Turabian StyleWang, Tongtong, Yuan Wang, and Jie Ren. 2025. "Predicting Dike Piping Hazards Using Critical Slowing Down Theory on Electrical Signals" Applied Sciences 15, no. 16: 8814. https://doi.org/10.3390/app15168814
APA StyleWang, T., Wang, Y., & Ren, J. (2025). Predicting Dike Piping Hazards Using Critical Slowing Down Theory on Electrical Signals. Applied Sciences, 15(16), 8814. https://doi.org/10.3390/app15168814






