Analysis of Penetration Performance Between a Hollow Penetrator and Seabed Clay by Coupled Eulerian–Lagrangian Method
Abstract
1. Introduction
2. Finite Element Model
2.1. Model Description
2.2. FE Model Using the CEL Method
2.3. Soil Constitutive Model and Mean Pressure
- (1)
- The clay was modelled as an undrained elastic–perfectly plastic material during the penetration process, which was described by the Tresca yield criterion with an associated flow rule;
- (2)
- The strain rate of the soil was not considered in this study;
- (3)
- The penetration process was conducted using a displacement-controlled method.
2.4. Validation of the Method
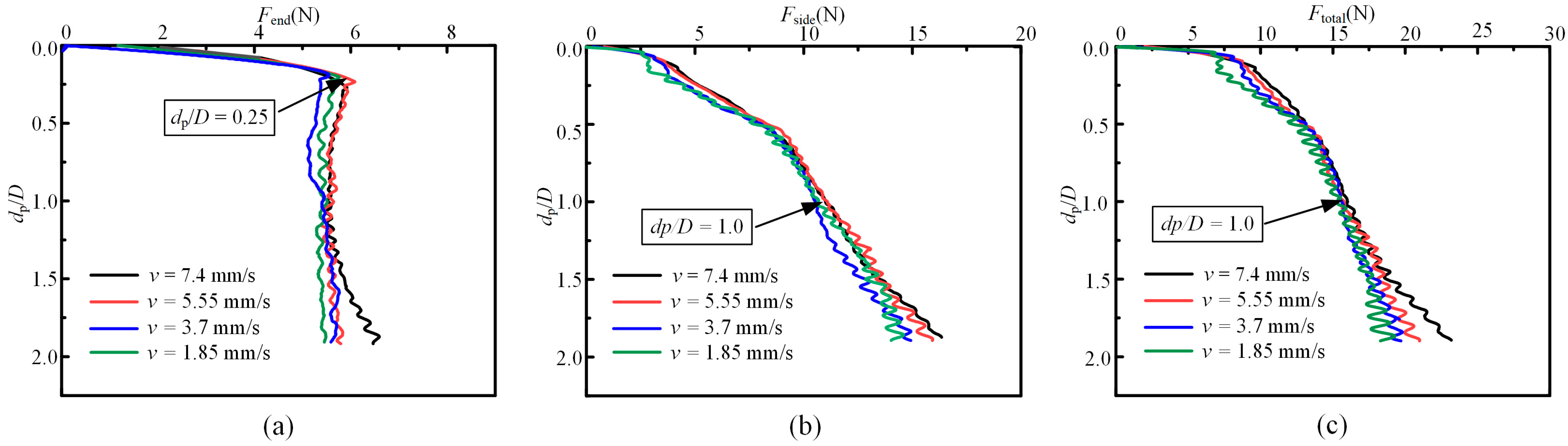
3. Sensitivity Analysis of Penetration Velocity
4. Parametric Study of Penetrator Structure on the Penetration Performance
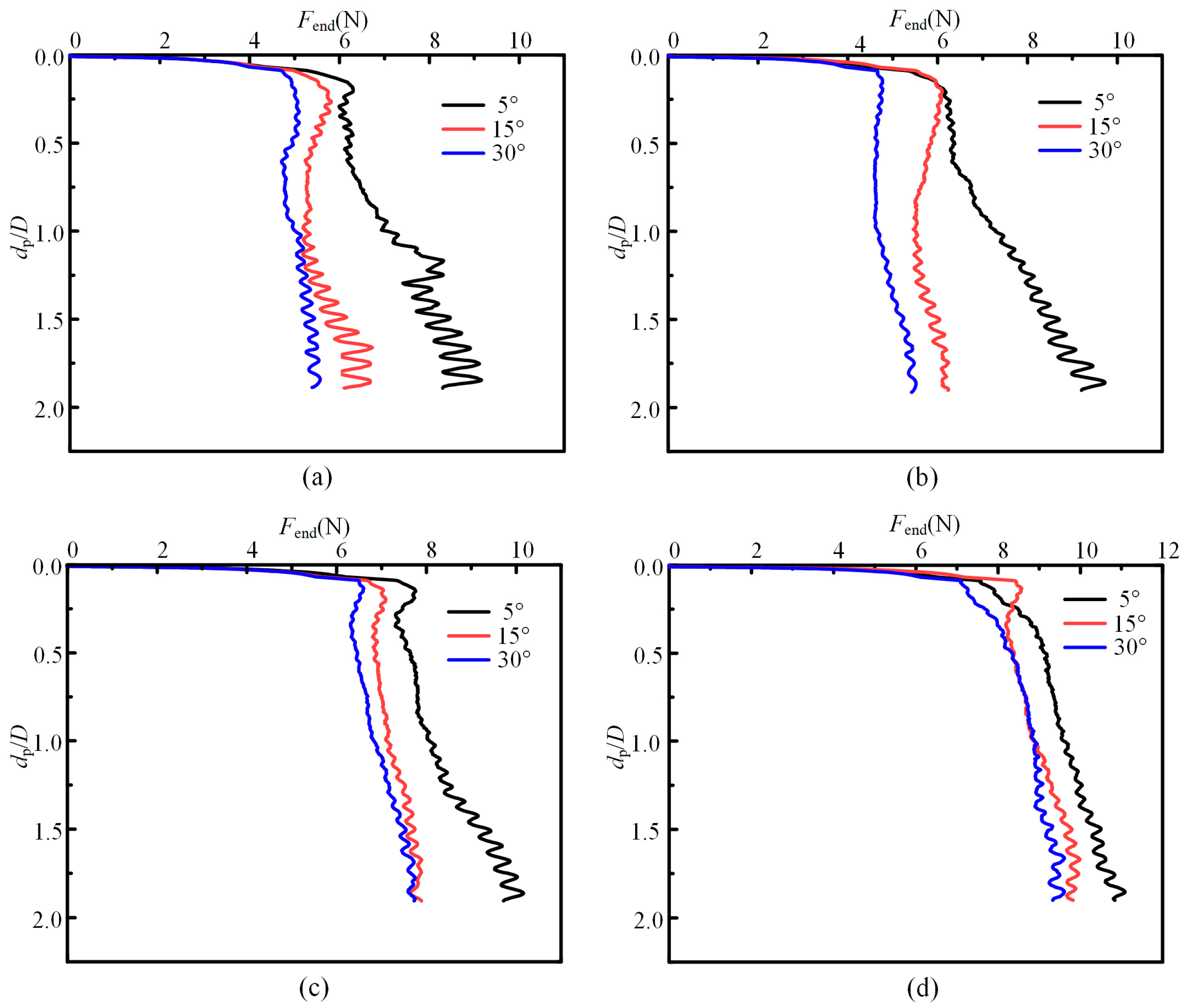
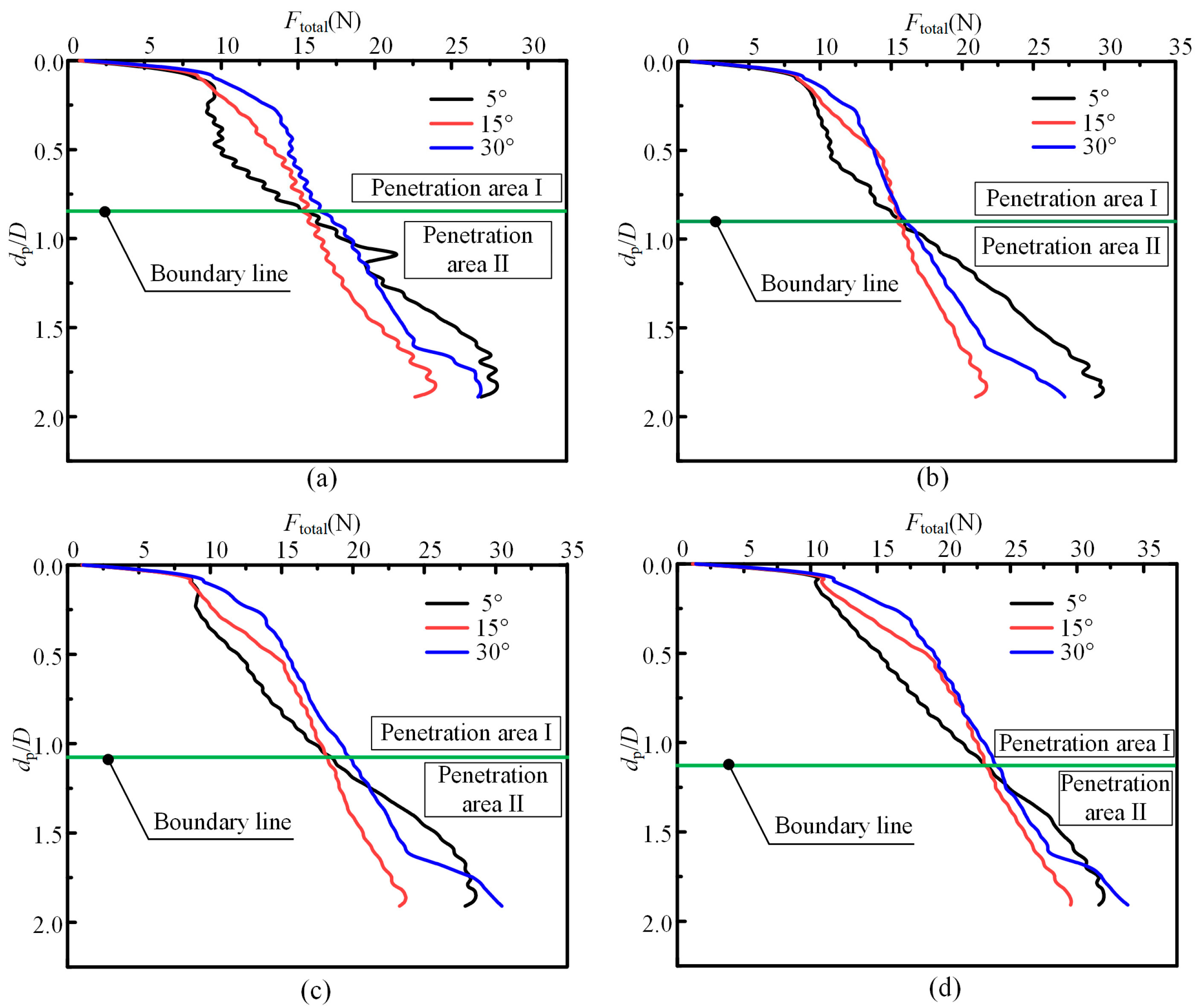
4.1. Effect of the Parameter of the Penetrating Head
4.2. Effect of Width of the End Face on the Penetrating Head Under Higher Su Condition
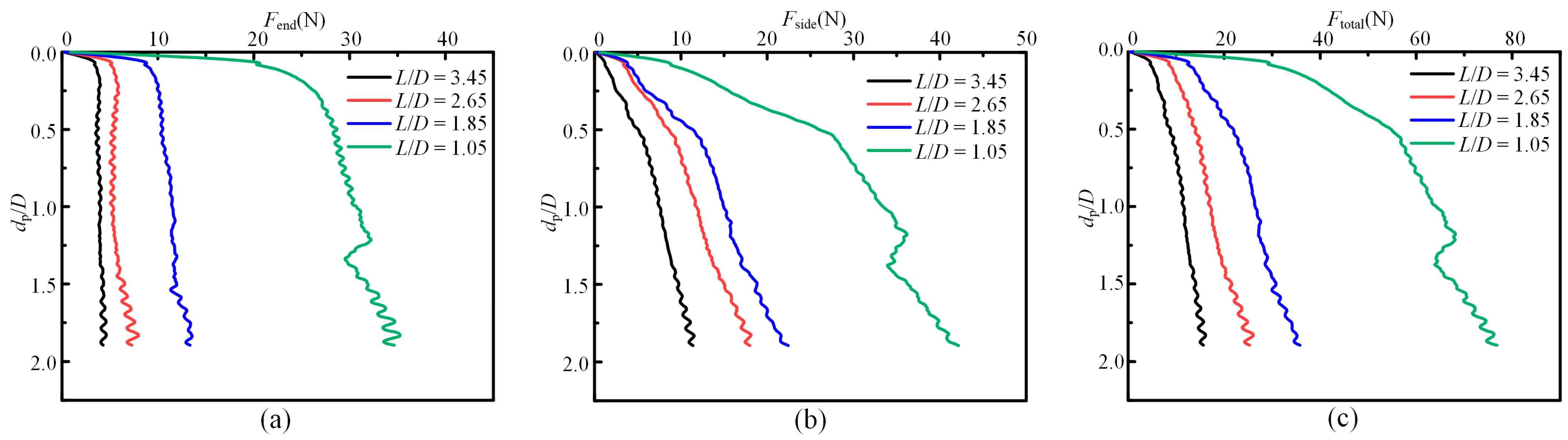
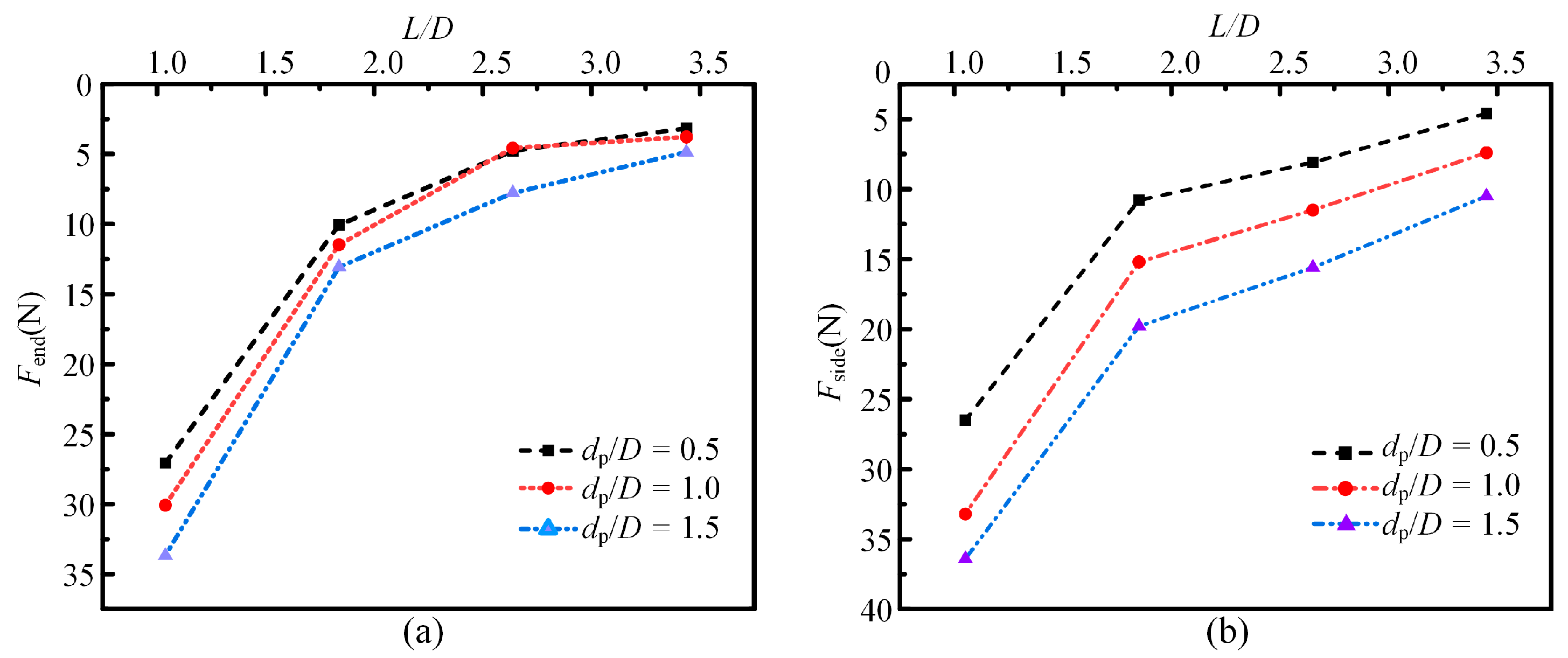
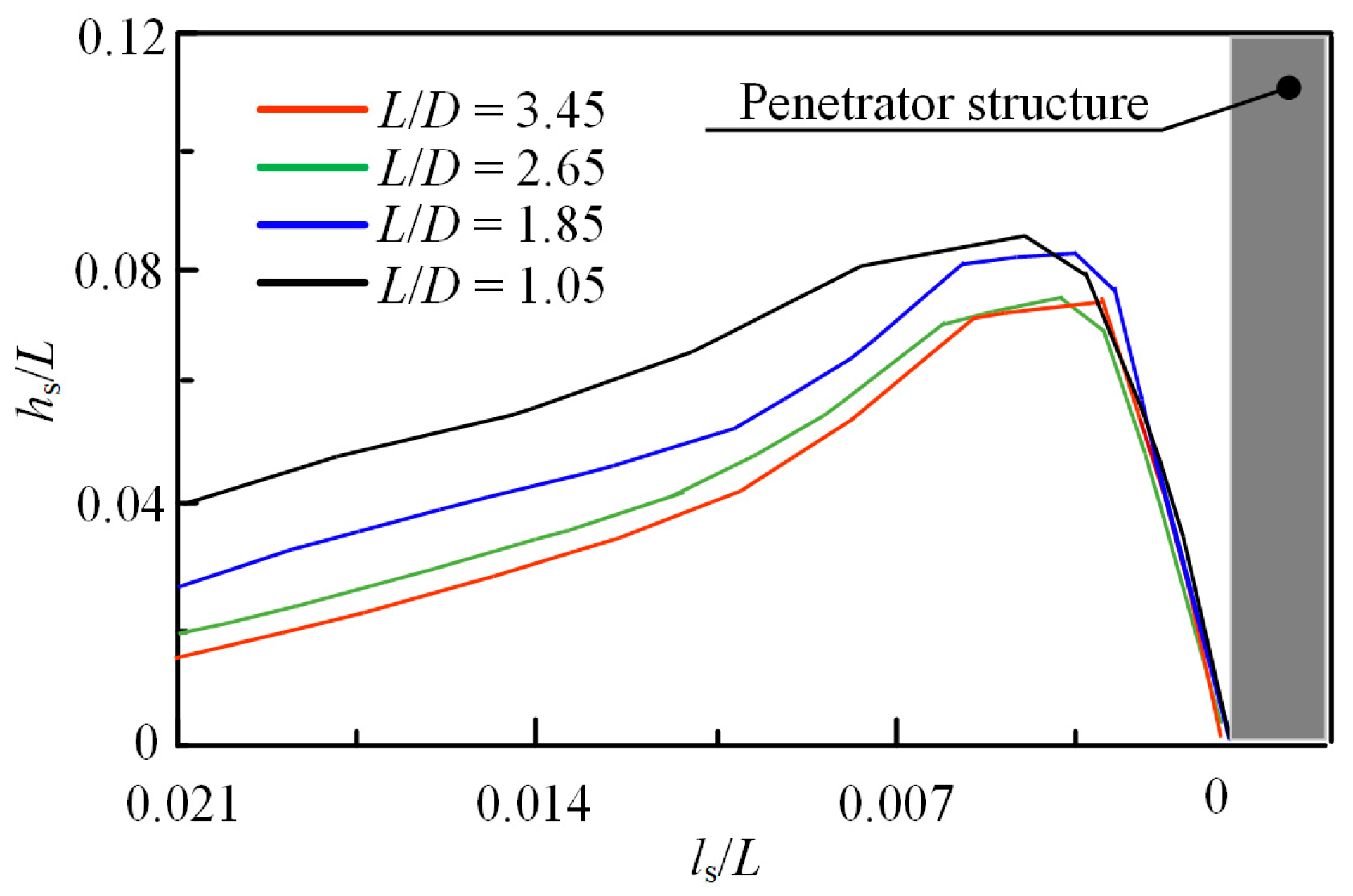
4.3. Effect of the Length/Diameter Ratio of the Penetrator Structure
5. Conclusions
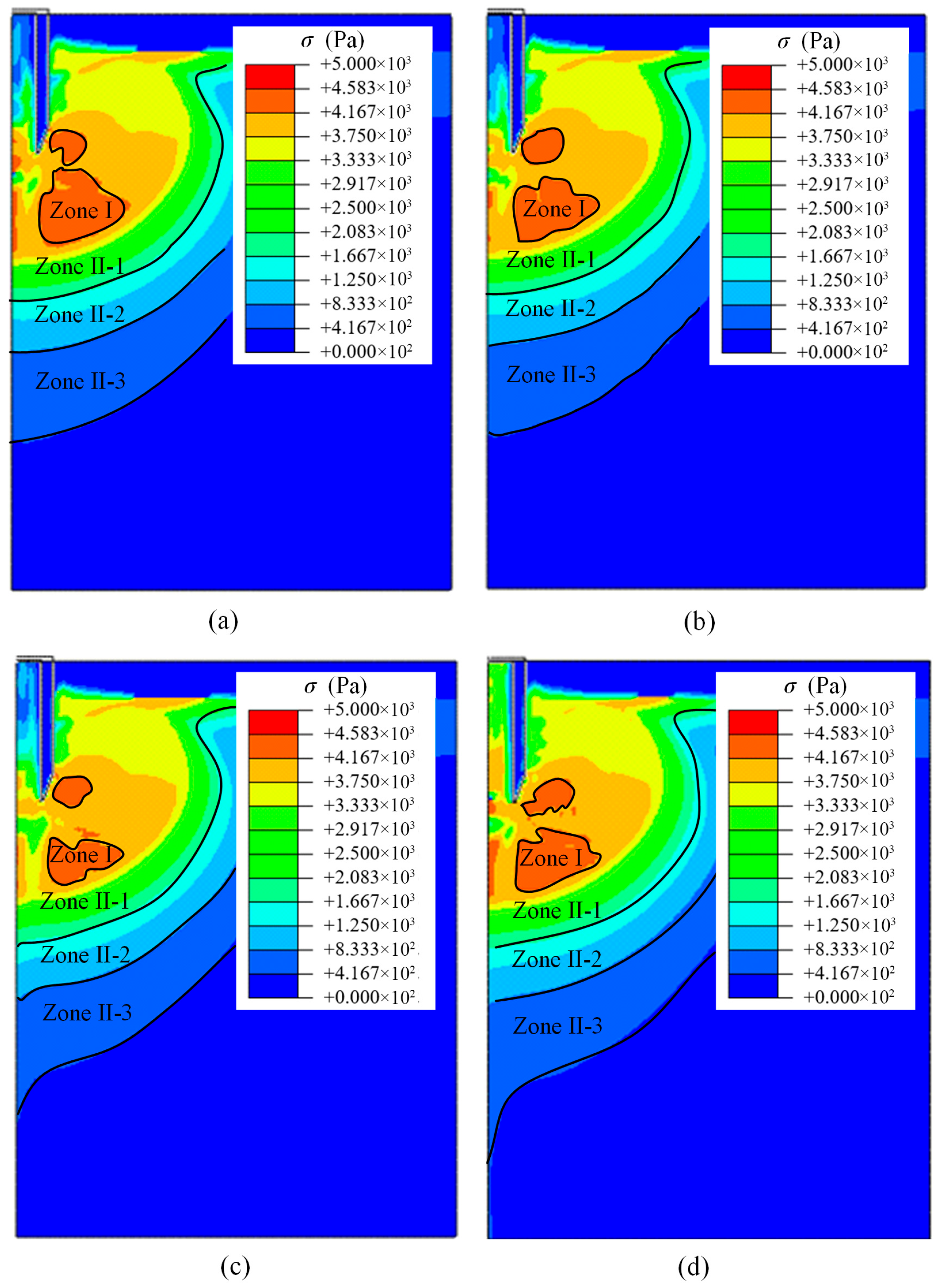
- The CEL large deformation method effectively simulated the penetration processes, with the resistance of the side of the penetrator structure increasing synchronously with depth, while the resistance of the end face of the penetrator structure converged marginally.
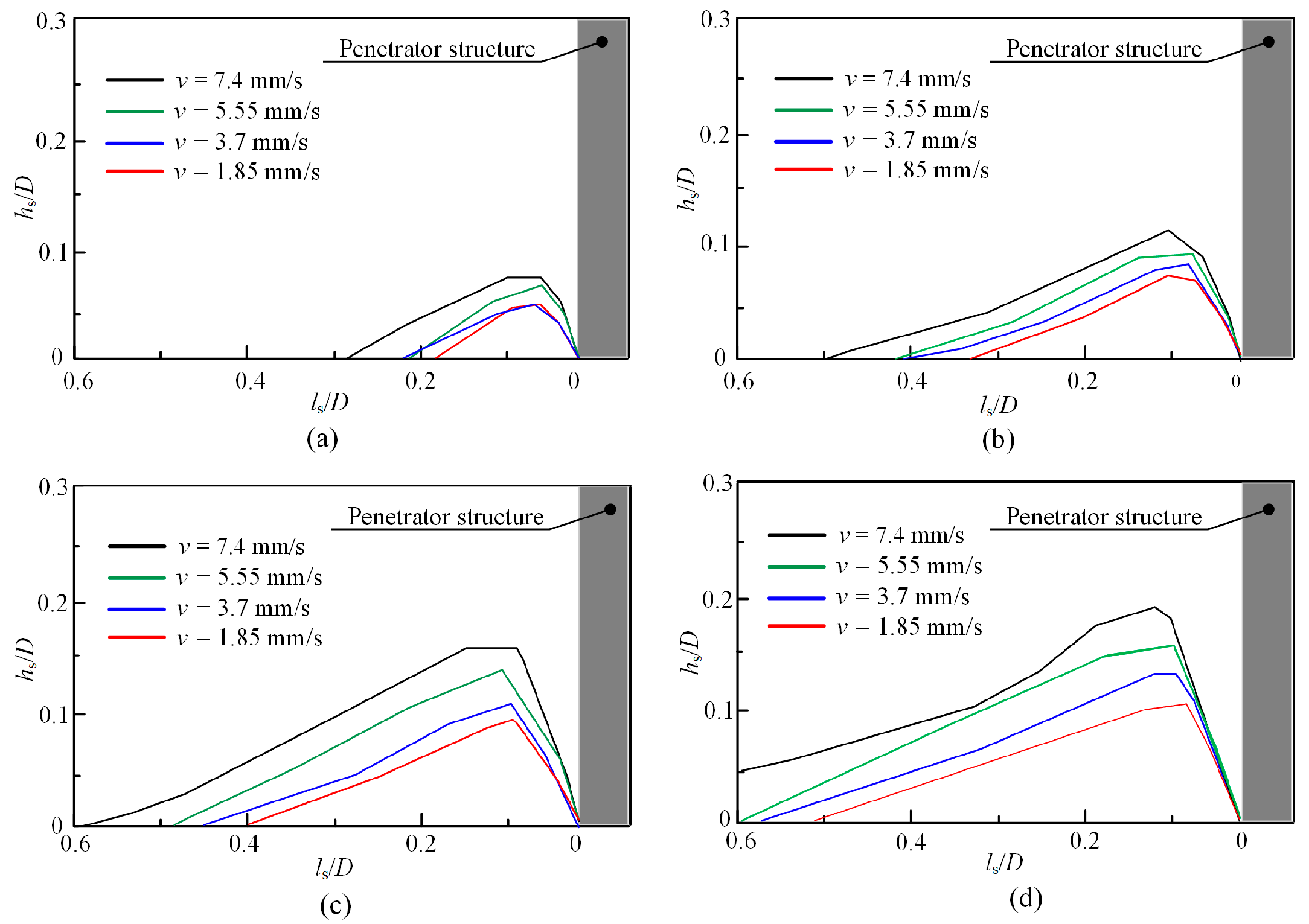
- The kinetic energy of the penetrator structure critically influenced soil flow, while penetration resistance and mean pressure remained almost constant under different velocity conditions. Balancing computational efficiency with simulation accuracy for penetration performance, the penetration velocity was set at 7.4 mm/s.
- The penetrator structure with a 15° head angle achieved the minimal penetration resistance as depth increased progressively. This angle can be considered the optimal choice for developing a low-disturbance penetrator structure in the deep-sea environment.
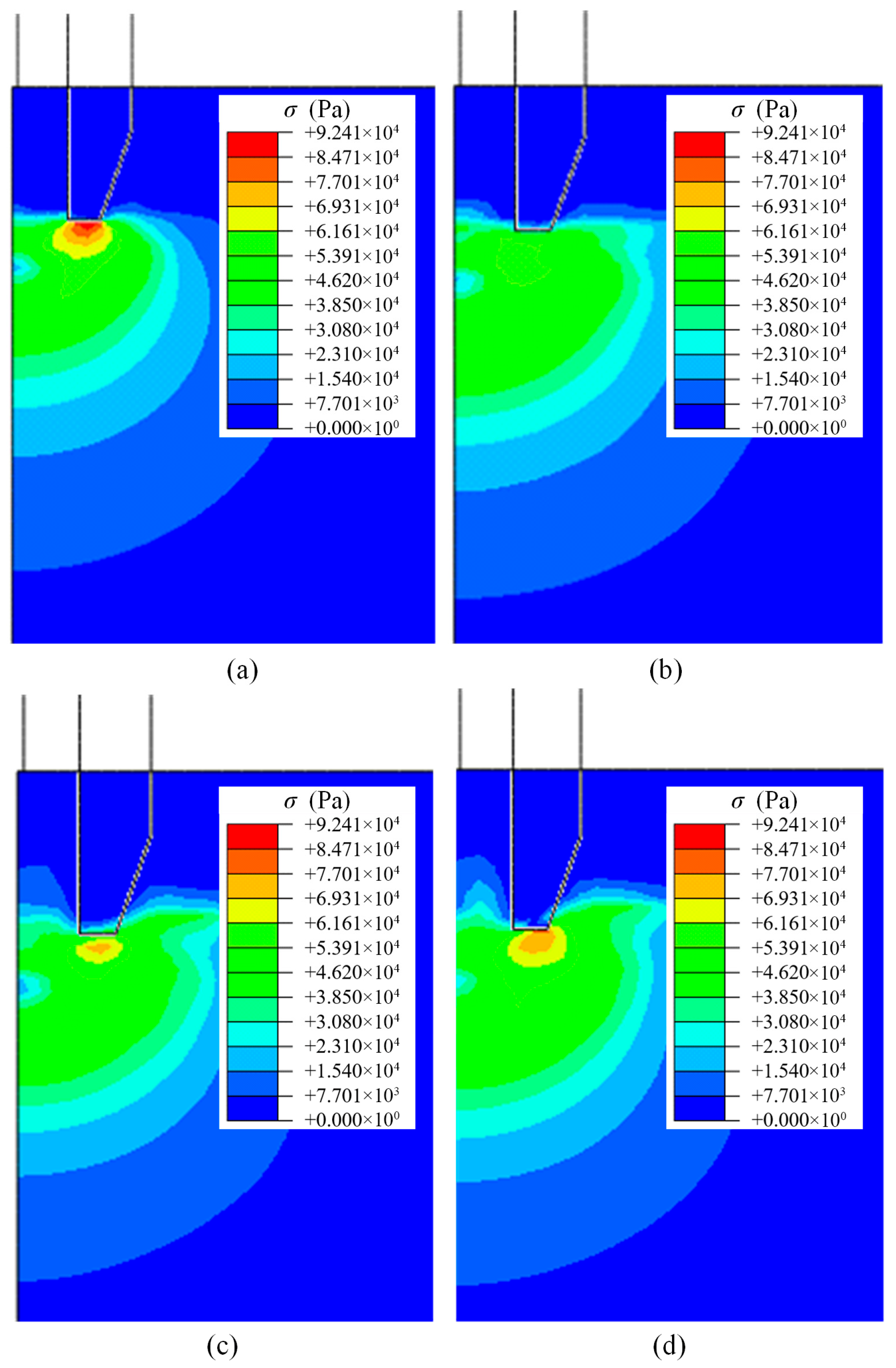
- Plastic deformation of the in situ soil primarily occurred at the end face on the penetrating head. The width of the end face on the penetrating head (b/D) was the key parameter governing the area of the interaction region. When Sum was small, b/D had little effect on Fend; however, at 10 times Sum, Fend showed a positive correlation with b/D.
- The decrease in L/D ratios proportionally amplified both the penetration resistance and the soil heave characteristics. The selection of the penetrator structure diameter depends not only on the penetration performance described in this study but also on the requirements for soil sample collection in mineral resource exploration missions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, D.; Chen, L.; Zhou, Z.; Wang, D.; Zhang, Y.; Yang, X.; Fang, X.; Wang, X.; Lu, H.; Dai, L.; et al. Development of a Pressure Coring System for the Investigation of Deep Underground Exploration. Int. J. Min. Sci. Technol. 2023, 33, 1351–1364. [Google Scholar] [CrossRef]
- Xie, H.; Gao, M.; Zhang, R.; Zhou, H.; Gao, F.; Chen, L.; Peng, X.; Li, X.; Ju, Y. Application Prospects of Deep In-Situ Condition-Preserved Coring and Testing Systems. Adv. Geo-Energy Res. 2024, 14, 12–24. [Google Scholar] [CrossRef]
- Peterson, M.N.A. Design and Operation of a Wireline Pressure Core Barrel; Scripps Institution of Oceanography: La Jolla, CA, USA, 1984. [Google Scholar] [CrossRef]
- Dickens, G.R.; Wallace, P.J.; Paull, C.K.; Borowski, W.S. Detection of Methane Gas Hydrate in the Pressure Core Sampler (PCS): Volume-Pressure-Time Relations during Controlled Degassing Experiments. In Proceedings of the Ocean Drilling Program: Scientific Results; Texas A&M University: College Station, TX, USA, 2000; Volume 164, pp. 113–126. [Google Scholar] [CrossRef]
- Abid, K.; Spagnoli, G.; Teodoriu, C.; Falcone, G. Review of Pressure Coring Systems for Offshore Gas Hydrates Research. Underw. Technol. 2015, 33, 19–30. [Google Scholar] [CrossRef]
- Burger, J.; Gupta, D.; Jacobs, P.; Shillinglaw, J. Overview on Hydrate Coring, Handling and Analysis; Westport Technology Center: Houston, TX, USA, 2006; p. 126. [Google Scholar]
- Schultheiss, P.; Holland, M.; Humphrey, G. Wireline Coring and Analysis under Pressure: Recent Use and Future Developments of the HYACINTH System. Sci. Drill. 2009, 7, 44–50. [Google Scholar] [CrossRef]
- Schultheiss, P.J.; Francis, T.J.G.; Holland, M.; Roberts, J.A.; Amann, H.; Parkes, R.J.; Martin, D.; Rothfuss, M.; Tyunder, F.; Jackson, P.D. Pressure Coring, Logging and Subsampling with the HYACINTH System. Geol. Soc. Lond. Spec. Publ. 2006, 267, 151–163. [Google Scholar] [CrossRef]
- Mazzeo, A.; Aguzzi, J.; Calisti, M.; Canese, S.; Vecchi, F.; Stefanni, S.; Controzzi, M. Marine Robotics for Deep-Sea Specimen Collection: A Systematic Review of Underwater Grippers. Sensors 2022, 22, 648. [Google Scholar] [CrossRef]
- Agarwala, N. Using Robotics to Achieve Ocean Sustainability During the Exploration Phase of Deep Seabed Mining. Mar. Technol. Soc. J. 2023, 57, 130–150. [Google Scholar] [CrossRef]
- Ragni, R.; Bienen, B.; O’Loughlin, C.D.; Stanier, S.A.; Cassidy, M.J.; Morgan, N. Observations of the Effects of a Clay Layer on Suction Bucket Installation in Sand. J. Geotech. Geoenviron. Eng. 2020, 146, 04020020. [Google Scholar] [CrossRef]
- Zou, X.; Jiang, Y.; Wang, Y. Failure Mechanism of Single Pile-Friction Footing Hybrid Foundation under Combined V–H–M Loadings by PIV Experiments and FE Method. Ocean Eng. 2023, 280, 114461. [Google Scholar] [CrossRef]
- Wang, X.; Yang, X.; Zeng, X. Centrifuge Modeling of Lateral Bearing Behavior of Offshore Wind Turbine with Suction Bucket Foundation in Sand. Ocean Eng. 2017, 139, 140–151. [Google Scholar] [CrossRef]
- Ma, P.; Liu, R.; Lian, J.; Zhu, B. An Investigation into the Lateral Loading Response of Shallow Bucket Foundations for Offshore Wind Turbines through Centrifuge Modeling in Sand. Appl. Ocean Res. 2019, 87, 192–203. [Google Scholar] [CrossRef]
- Hossain, M.S.; Hu, Y.; Randolph, M.F.; White, D.J. Limiting Cavity Depth for Spudcan Foundations Penetrating Clay. Geotechnique 2005, 55, 679–690. [Google Scholar] [CrossRef]
- Teh, K.L.; Leung, C.F.; Chow, Y.K.; Cassidy, M.J. Centrifuge Model Study of Spudcan Penetration in Sand Overlying Clay. Geotechnique 2010, 60, 825–842. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, X.; Zhou, M.; Tian, Y. Investigation on the Behavior of Stiffened Caisson Installation in Uniform Clay from Large Deformation Modeling. Int. J. Geomech. 2020, 20, 04020149. [Google Scholar] [CrossRef]
- Hu, P.; Wang, D.; Cassidy, M.J.; Stanier, S.A. Predicting the Resistance Profile of a Spudcan Penetrating Sand Overlying Clay. Can. Geotech. J. 2014, 51, 1151–1164. [Google Scholar] [CrossRef]
- Wang, T.; Wu, R.; Liu, W.; Bao, X. Simulation of T-Bar Penetration in Soft Clay with Adhesive Contact. Mar. Georesour. Geotechnol. 2020, 38, 154–163. [Google Scholar] [CrossRef]
- Tu, W.; He, Y.; El Naggar, M.H.; Liu, L.; Gu, X.; Cheng, X. Analysis of Bucket Foundation Installation in Clay Considering Soil Large Deformation. Ocean Eng. 2023, 287, 115754. [Google Scholar] [CrossRef]
- Bae, J.; Kim, Y.; Hossain, M.S. Developing an optimal shape for dynamically installed anchor. In Proceedings of the ASME 2023 42nd International Conference on Ocean, Offshore and Arctic Engineering, Melbourne, Australia, 11–16 June 2023; Volume 9, pp. 1–10. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Kong, D.; Lou, X.; Zhu, B. Development of an Adaptive Meshing Upper Bound Limit Analysis Method for Large Deformation Axisymmetric Geotechnical Problems. Sci. Rep. 2025, 15, 5771. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Liu, Z.; Shi, D.; Wang, F. Investigation on Perforation Drilling to Mitigate Punch-through Potential in Sand Overlying Soft Clay. Appl. Ocean Res. 2022, 119, 103026. [Google Scholar] [CrossRef]
- Ullah, S.N.; Hu, Y.; Stanier, S.; White, D. Lateral Boundary Effects in Centrifuge Foundation Tests. Int. J. Phys. Model. Geotech. 2017, 17, 144–160. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, J.; Tong, L.; Sun, K.; Guo, Y.; Wei, C. Experimental Study of Soil Responses around a Pipeline in a Sandy Seabed under Wave-Current Load. Appl. Ocean Res. 2023, 130, 103409. [Google Scholar] [CrossRef]
- Tu, Y.; Tu, W.; Gu, X.; Xiao, K.; Zheng, M.; Shen, K. Influence of the Installation on the Bearing Performance of the Bucket Foundation under Combined Loading. Mar. Georesour. Geotechnol. 2025, 1–16. [Google Scholar] [CrossRef]
- Huang, M.; Tu, W.; Gu, X. Time Domain Nonlinear Lateral Response of Dynamically Loaded Composite Caisson-Piles Foundations in Layered Cohesive Soils. Soil Dyn. Earthq. Eng. 2018, 106, 113–130. [Google Scholar] [CrossRef]
- Chen, W.; Randolph, M.F. External Radial Stress Changes and Axial Capacity for Suction Caissons in Soft Clay. Geotechnique 2007, 57, 499–511. [Google Scholar] [CrossRef]
- Chen, C.; Long, J.; Li, G. Experimental study on mechanical properties of seafloor sediments of deep South China Sea. Ocean Eng. 2015, 33, 1–7. [Google Scholar] [CrossRef]
- Vulpe, C.; Gourvenec, S.; Power, M. A Generalised Failure Envelope for Undrained Capacity of Circular Shallow Foundations under General Loading. Geotech. Lett. 2014, 4, 187–196. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, H.; Yuan, J.; Chu, J. Numerical Simulation of XCC Pile Penetration in Undrained Clay. Comput. Geotech. 2019, 106, 18–41. [Google Scholar] [CrossRef]
- Dingle, H.R.C.; White, D.J.; Gaudin, C. Mechanisms of Pipe Embedment and Lateral Breakout on Soft Clay. Can. Geotech. J. 2008, 45, 636–652. [Google Scholar] [CrossRef]
- Chatterjee, S.; Randolph, M.F.; White, D.J.; Wang, D. Large Deformation Finite Element Analysis of Vertical Penetration of Pipelines in Seabed. Front. Offshore Geotech. II 2010, 785–790. [Google Scholar] [CrossRef]
- Wang, D.; Bienen, B.; Nazem, M.; Tian, Y.; Zheng, J.; Pucker, T.; Randolph, M.F. Large Deformation Finite Element Analyses in Geotechnical Engineering. Comput. Geotech. 2015, 65, 104–114. [Google Scholar] [CrossRef]
- Shen, Y. Research on the Impact Type Penetrator and Its Mechanical Properties During Penetrating Lunar Regolith Pro-File. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, October 2017. [Google Scholar]
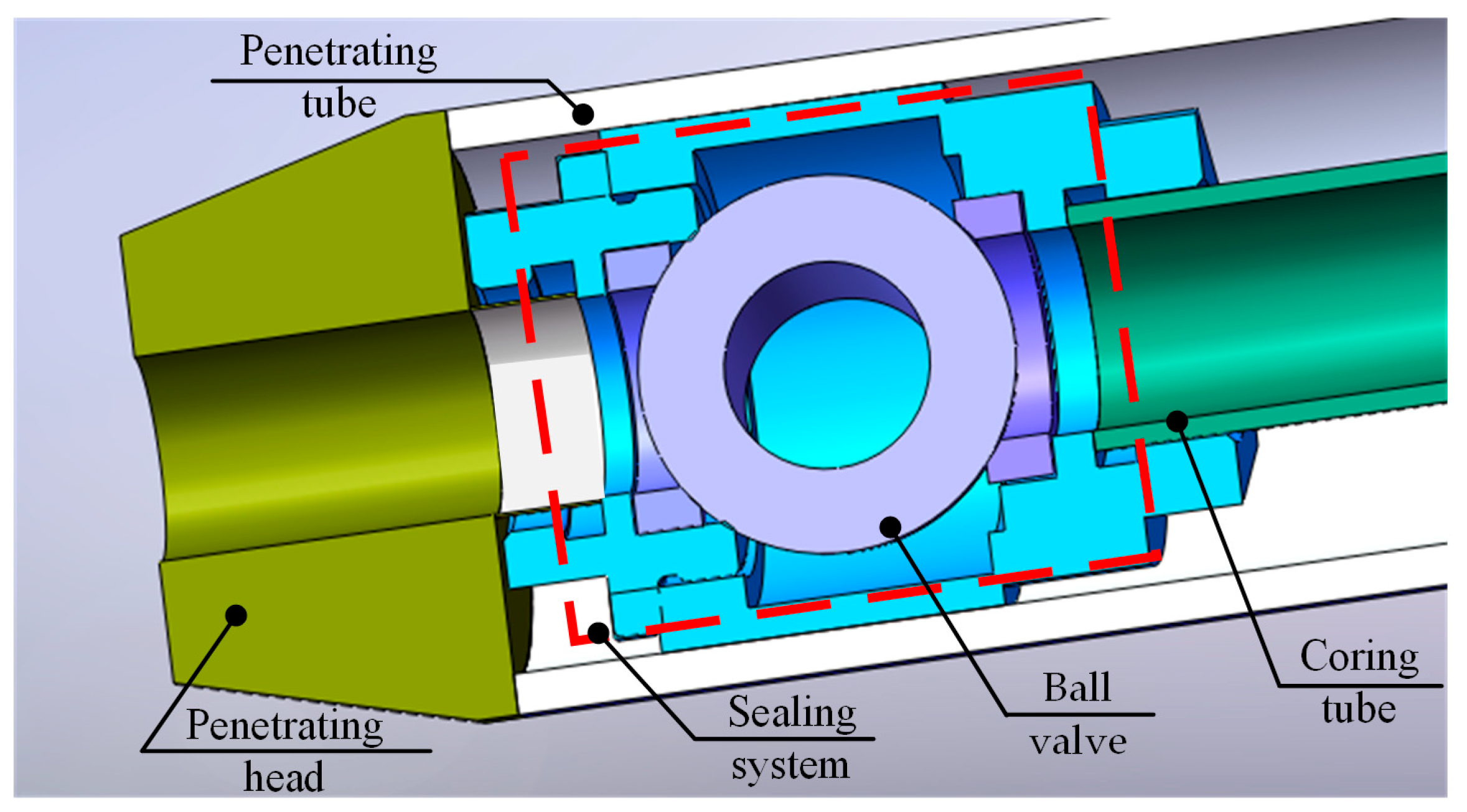
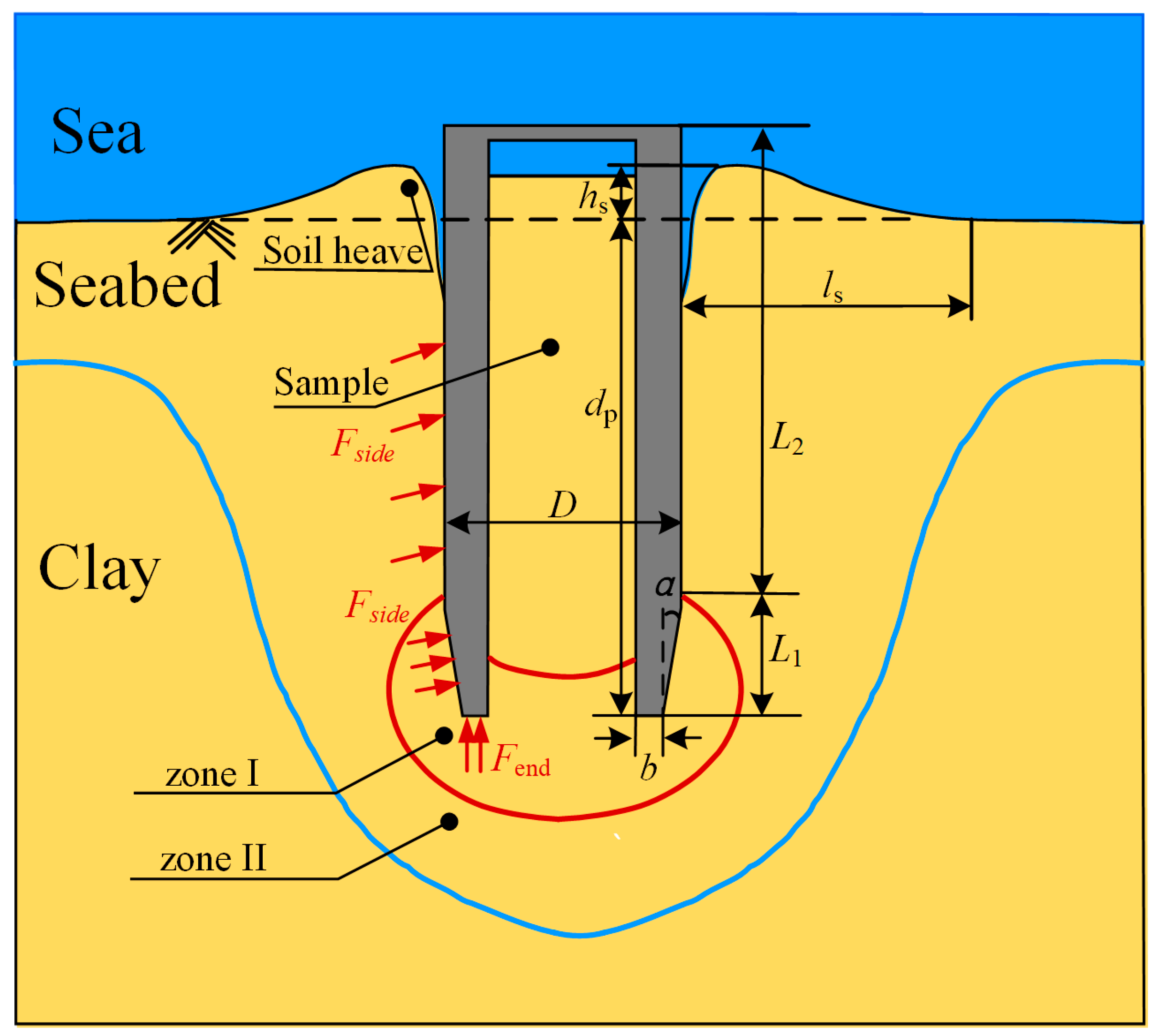
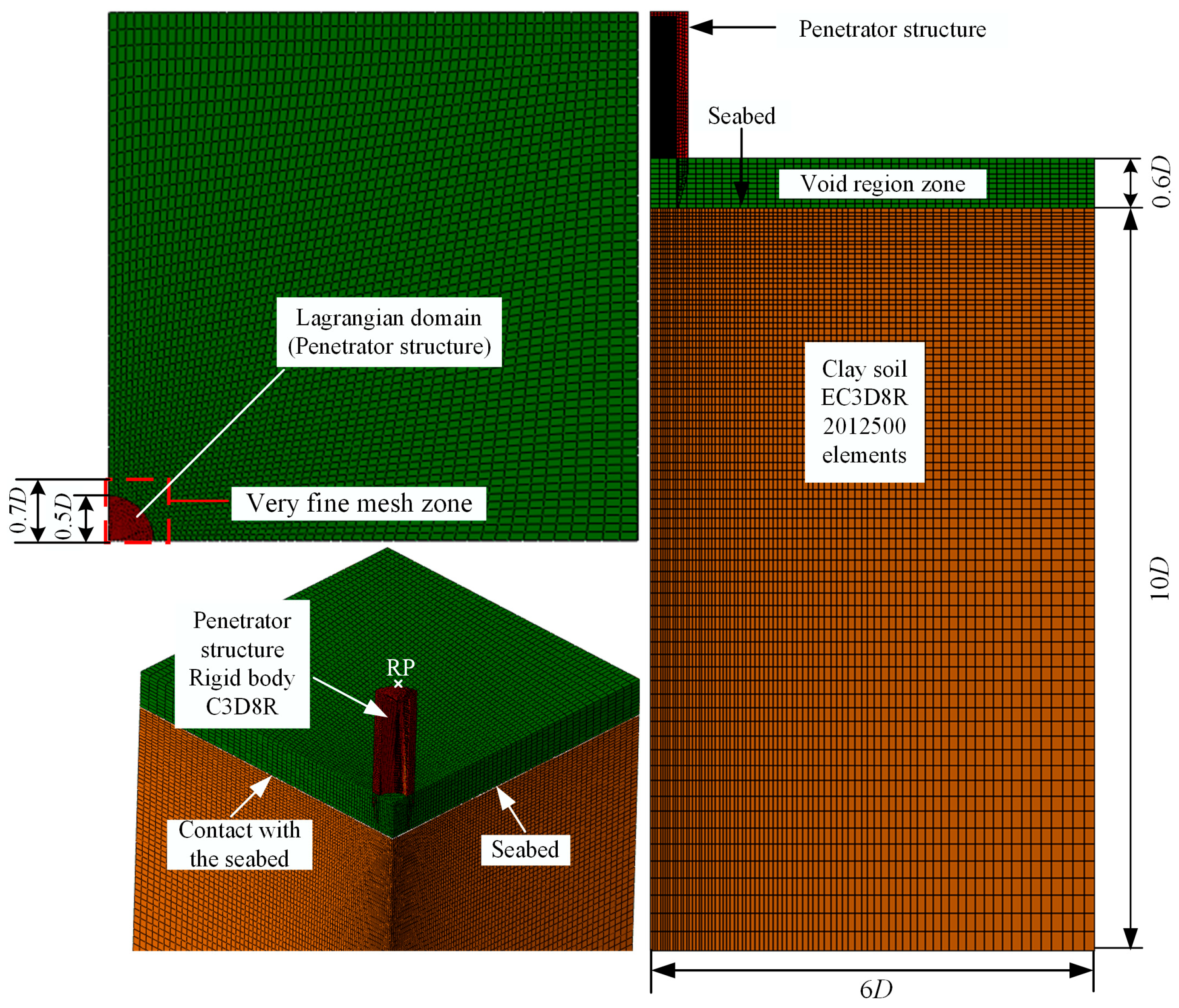




| Parameter | Description | Value or Normalization |
|---|---|---|
| D | Diameter of the penetrator structure | D = 74 mm |
| L1 | Height of the penetrating head | |
| L2 | Height of the penetrating tube | / |
| L | Height of the penetrator structure, which is equal to the sum of L1 and L2 | L/D |
| b | Width of the end face on the penetrating head | b/D |
| α | Angle of the penetrating head | / |
| dp | Depth of the penetration process | dp/D |
| hs | Height of the soil heave | hs/D |
| ls | Distance from the penetrator structure to the margin of soil heave | ls/D |
| Fend | Resistance of the end face of the penetrator structure | / |
| Fside | Resistance of the side of the penetrator structure | / |
| Ftotal | Combination of Fend and Fside | / |
| Parameter | Value | Normalized Value |
|---|---|---|
| α | 5°, 15°, 30° | / |
| b | 2 mm, 4 mm, 6 mm, 10 mm | 0.027, 0.054, 0.081, 0.135 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Zhen, Z.; Hou, H.; Zhang, J. Analysis of Penetration Performance Between a Hollow Penetrator and Seabed Clay by Coupled Eulerian–Lagrangian Method. Appl. Sci. 2025, 15, 8778. https://doi.org/10.3390/app15168778
Liang J, Zhen Z, Hou H, Zhang J. Analysis of Penetration Performance Between a Hollow Penetrator and Seabed Clay by Coupled Eulerian–Lagrangian Method. Applied Sciences. 2025; 15(16):8778. https://doi.org/10.3390/app15168778
Chicago/Turabian StyleLiang, Jieneng, Zhiwen Zhen, Heying Hou, and Jian Zhang. 2025. "Analysis of Penetration Performance Between a Hollow Penetrator and Seabed Clay by Coupled Eulerian–Lagrangian Method" Applied Sciences 15, no. 16: 8778. https://doi.org/10.3390/app15168778
APA StyleLiang, J., Zhen, Z., Hou, H., & Zhang, J. (2025). Analysis of Penetration Performance Between a Hollow Penetrator and Seabed Clay by Coupled Eulerian–Lagrangian Method. Applied Sciences, 15(16), 8778. https://doi.org/10.3390/app15168778







