Research on Intelligent Predictions of Surrounding Rock Ahead of the Tunnel Face Based on Neural Network and Longitudinal Deformation Curve
Abstract
1. Introduction
2. Fundamental Theory of Tunnel Surrounding Rock Response
2.1. Hoek–Brown Criterion
2.2. Longitudinal Deformation Profile of Surrounding Rock
3. Numerical Modeling and Validation
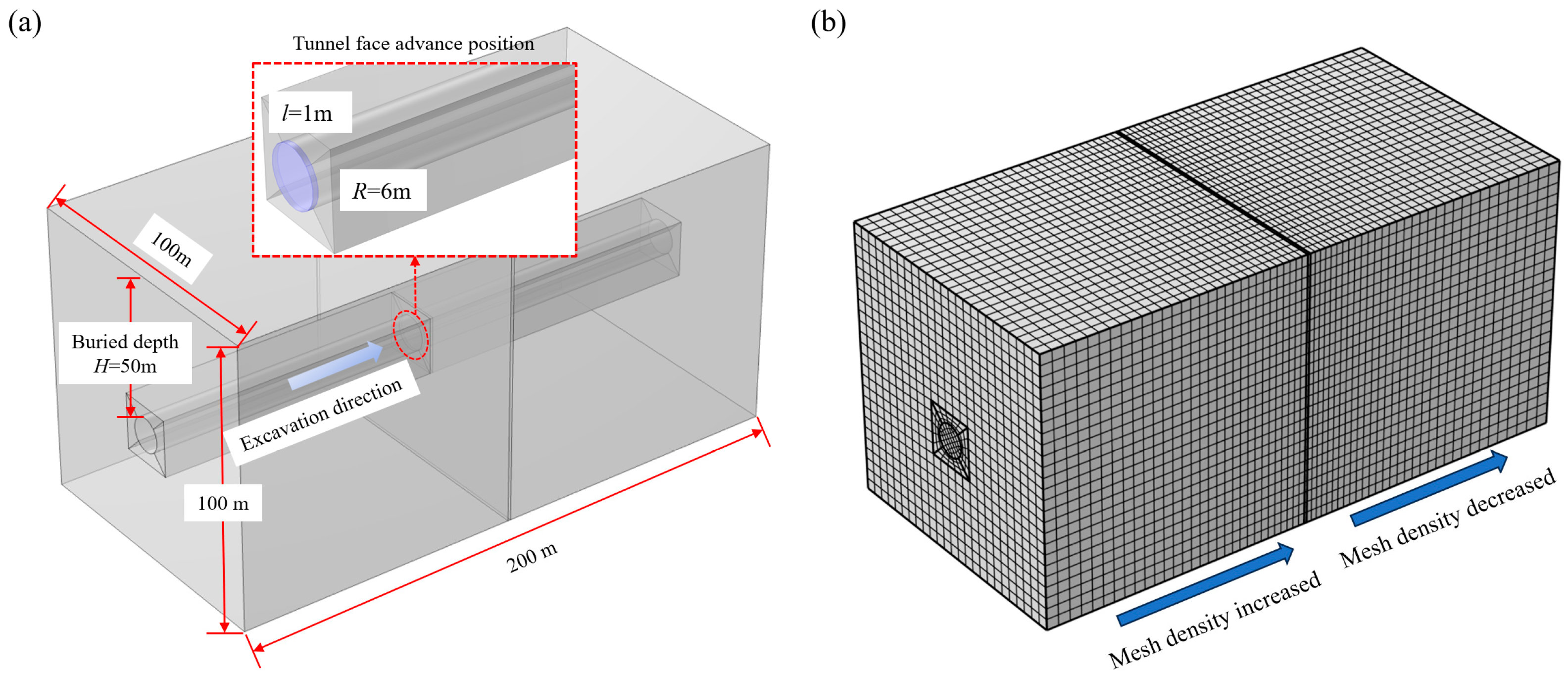
3.1. Numerical Model Development
3.1.1. Fundamental Model Settings
3.1.2. Parameter Determination for Numerical Modeling
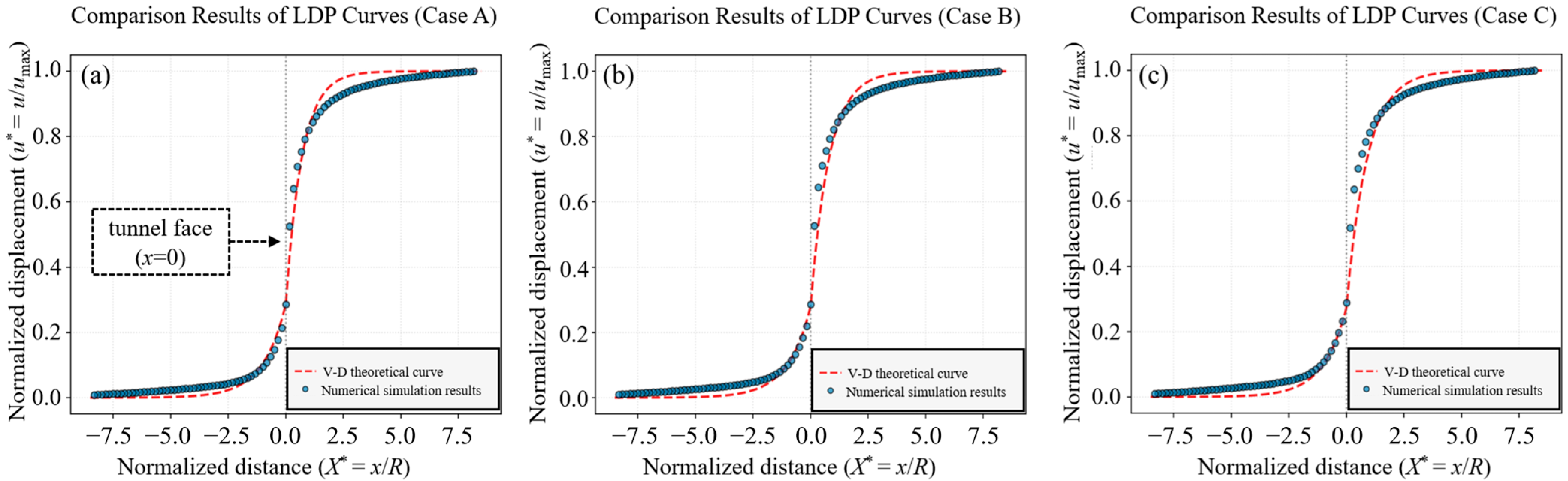
3.2. Numerical Model Validation
4. Analysis of LDP Characteristics Under Different Stratigraphic Parameters
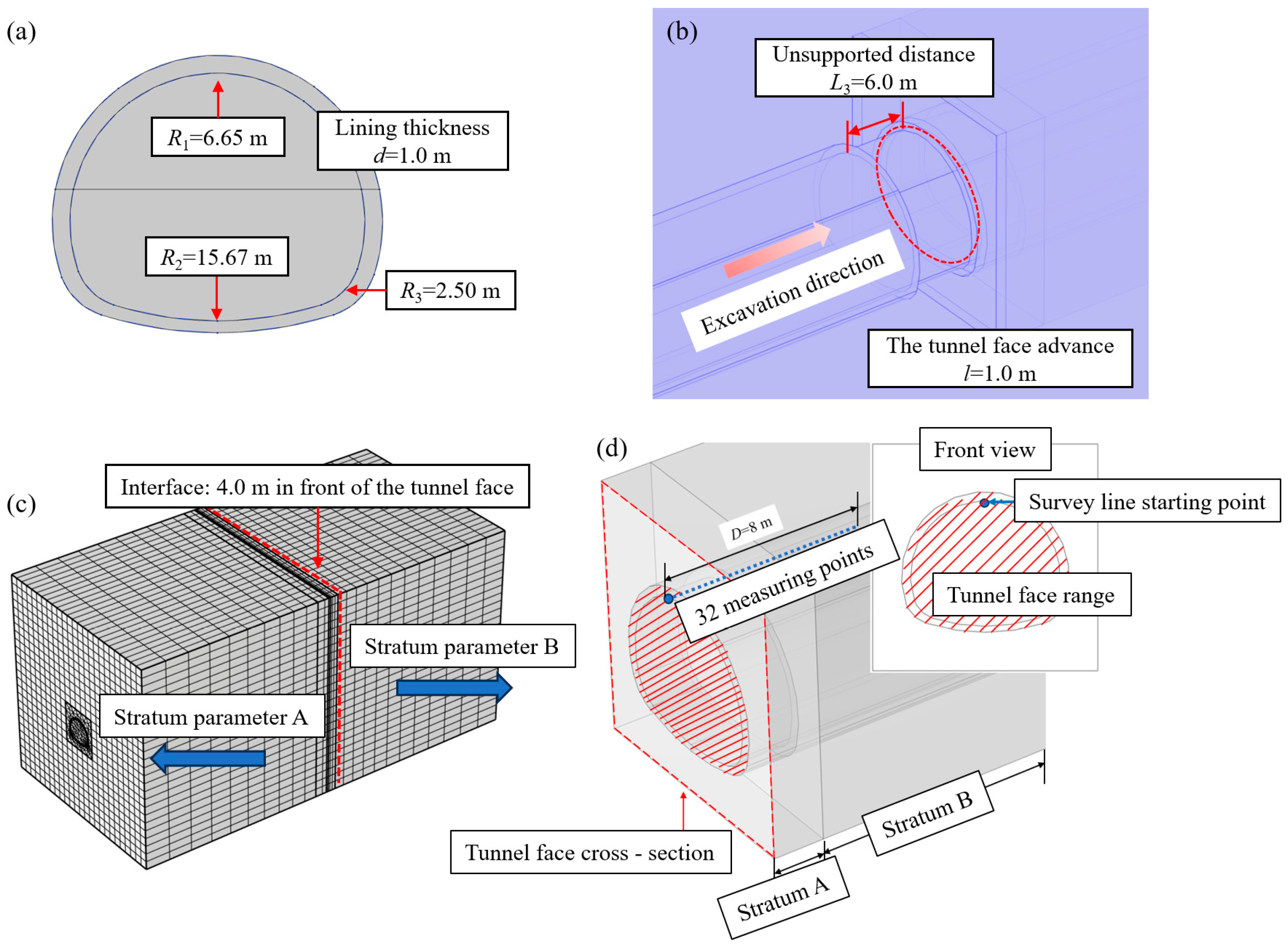
4.1. Numerical Modeling Framework
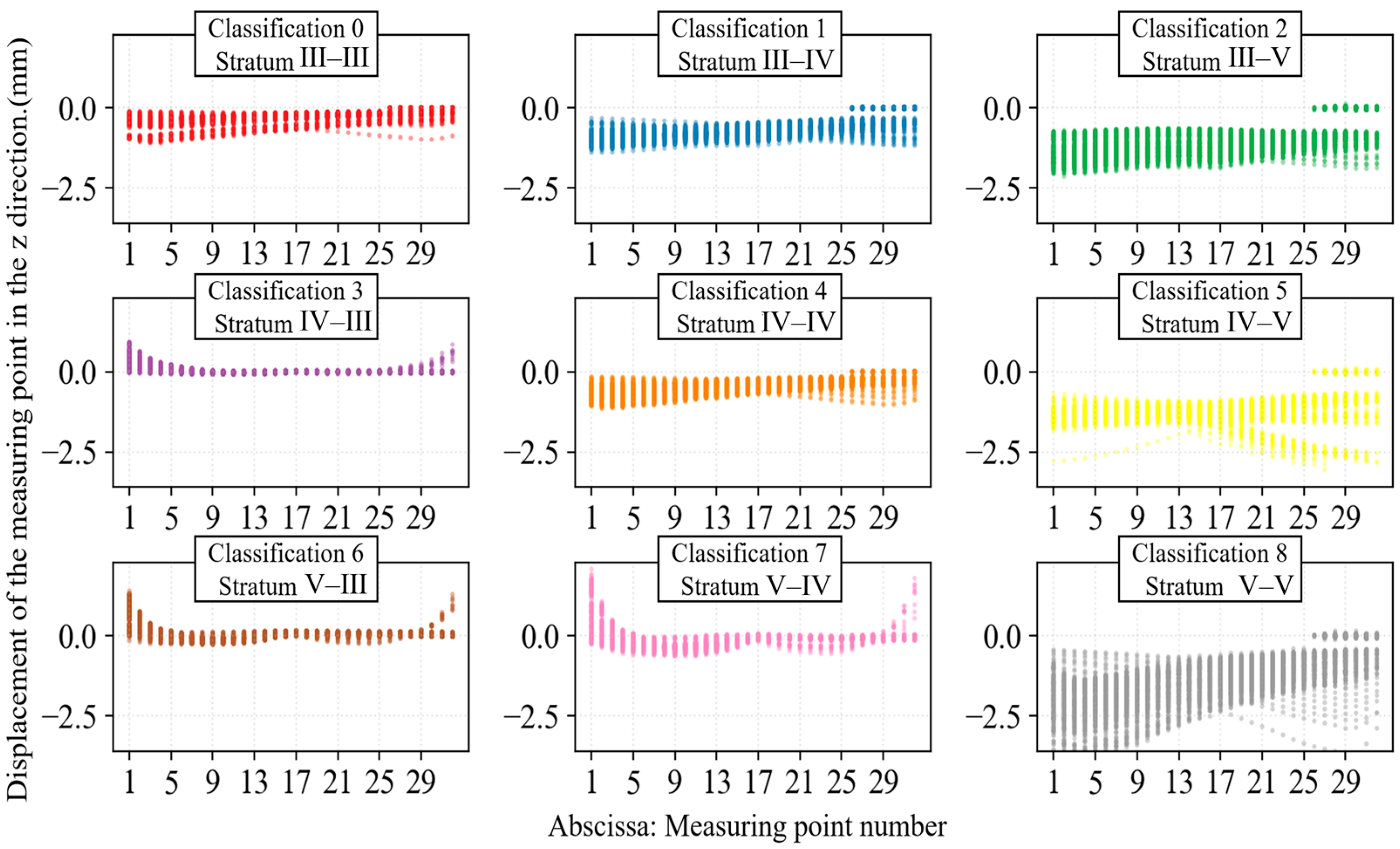
4.2. Characteristic Analysis of Surrounding Rock Longitudinal Deformation Profile
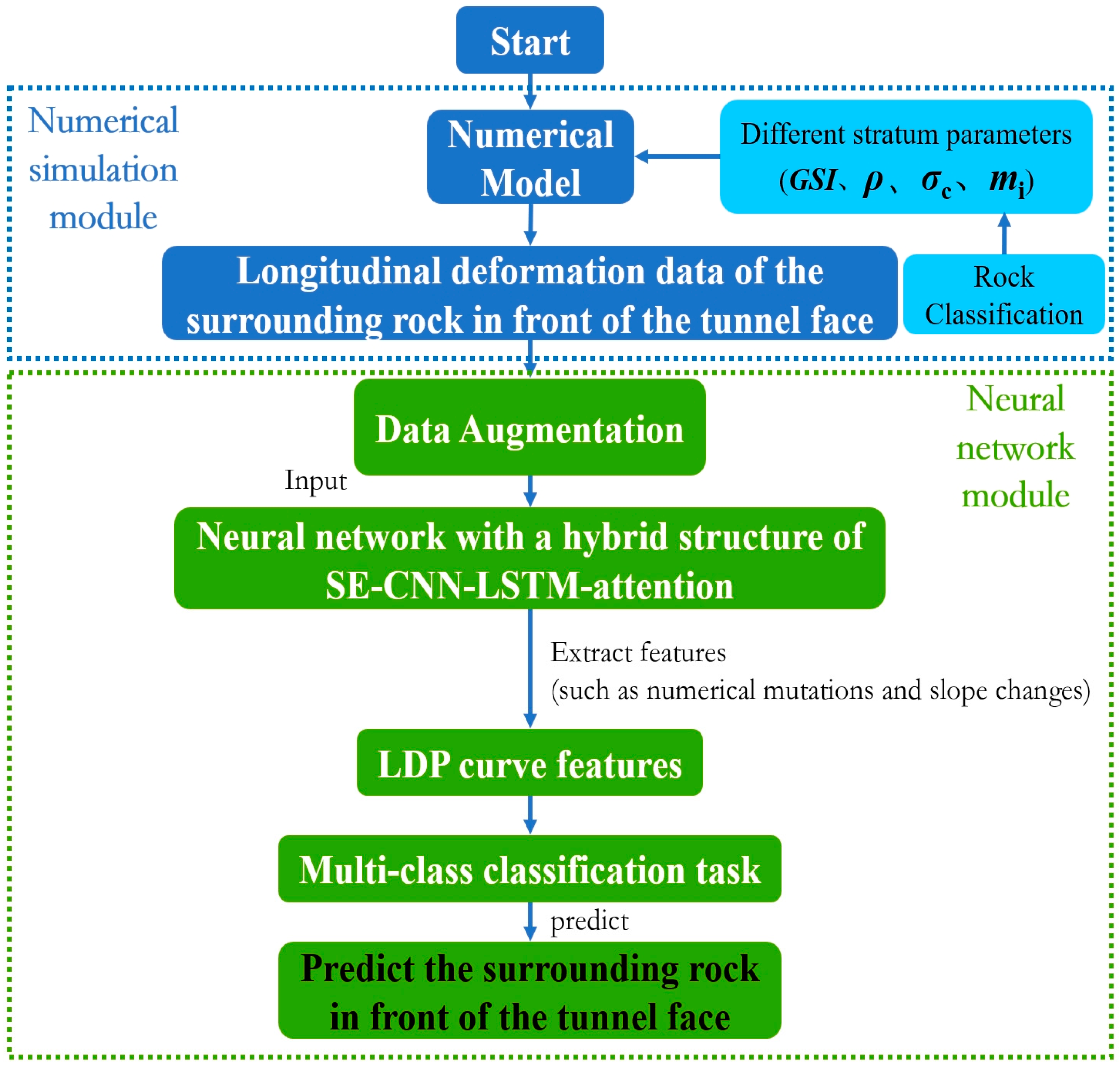
5. A Prediction Model for Rock Mass Classification Ahead of the Driving Face
5.1. Intelligent Prediction Fundamentals for Rock Mass Classification
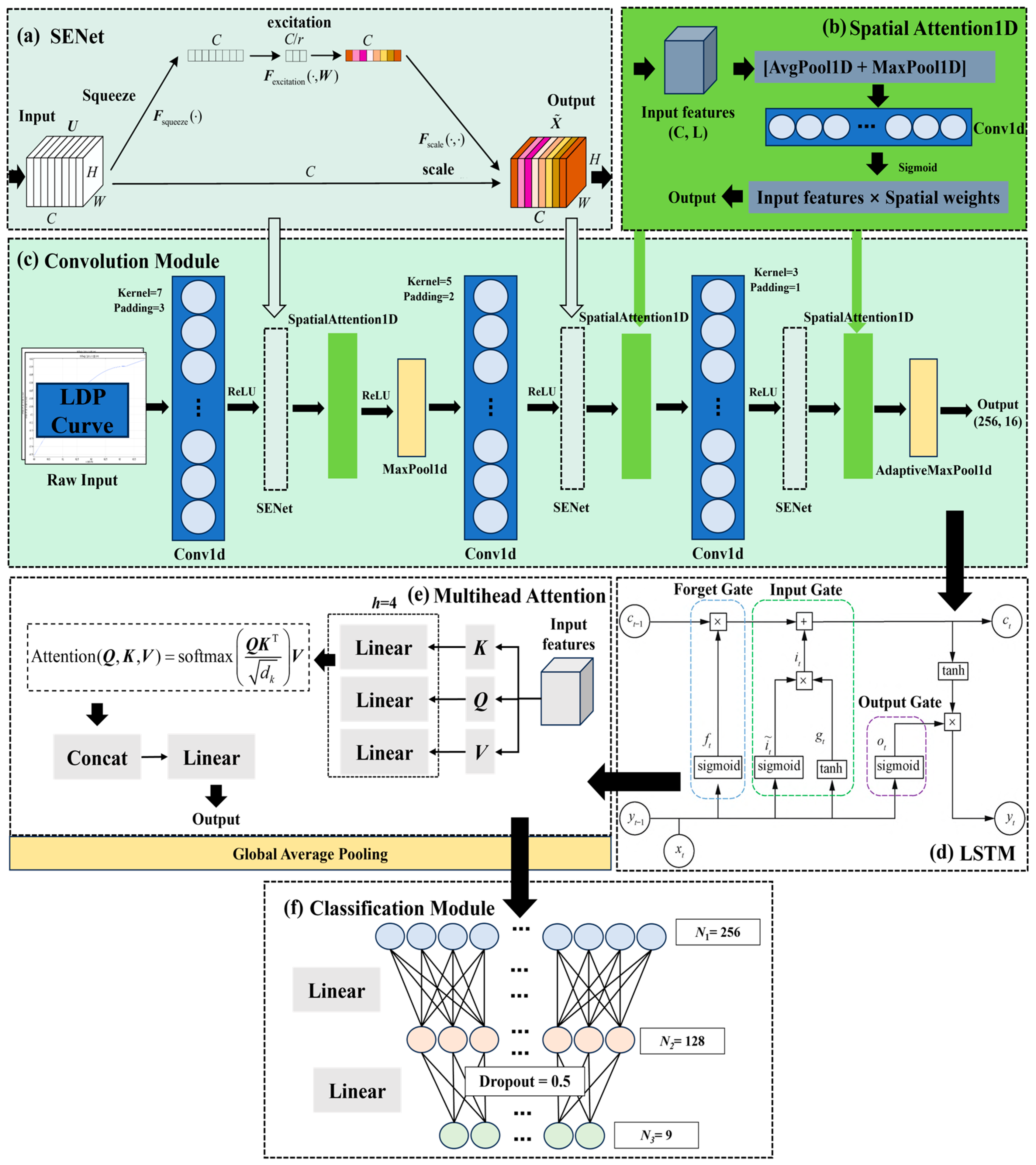
5.1.1. SE-CNN Architecture
5.1.2. Long Short-Term Memory (LSTM)
5.1.3. Attention Mechanism
5.2. SE-CNN-LSTM-Attention Hybrid Architecture Development
5.2.1. Architectural Configuration
5.2.2. Loss Function and Optimizer
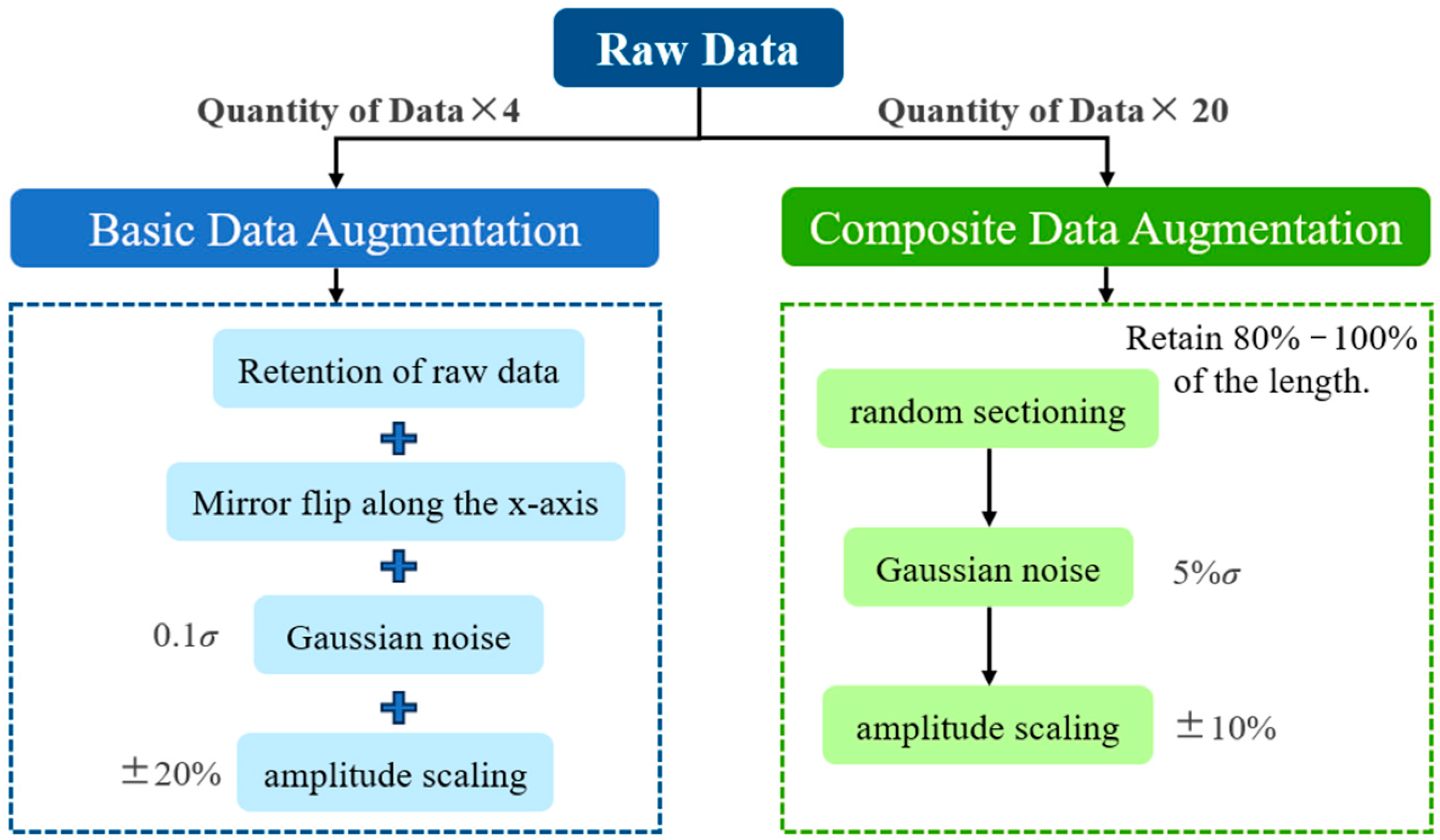
5.3. Model Parameter Determination
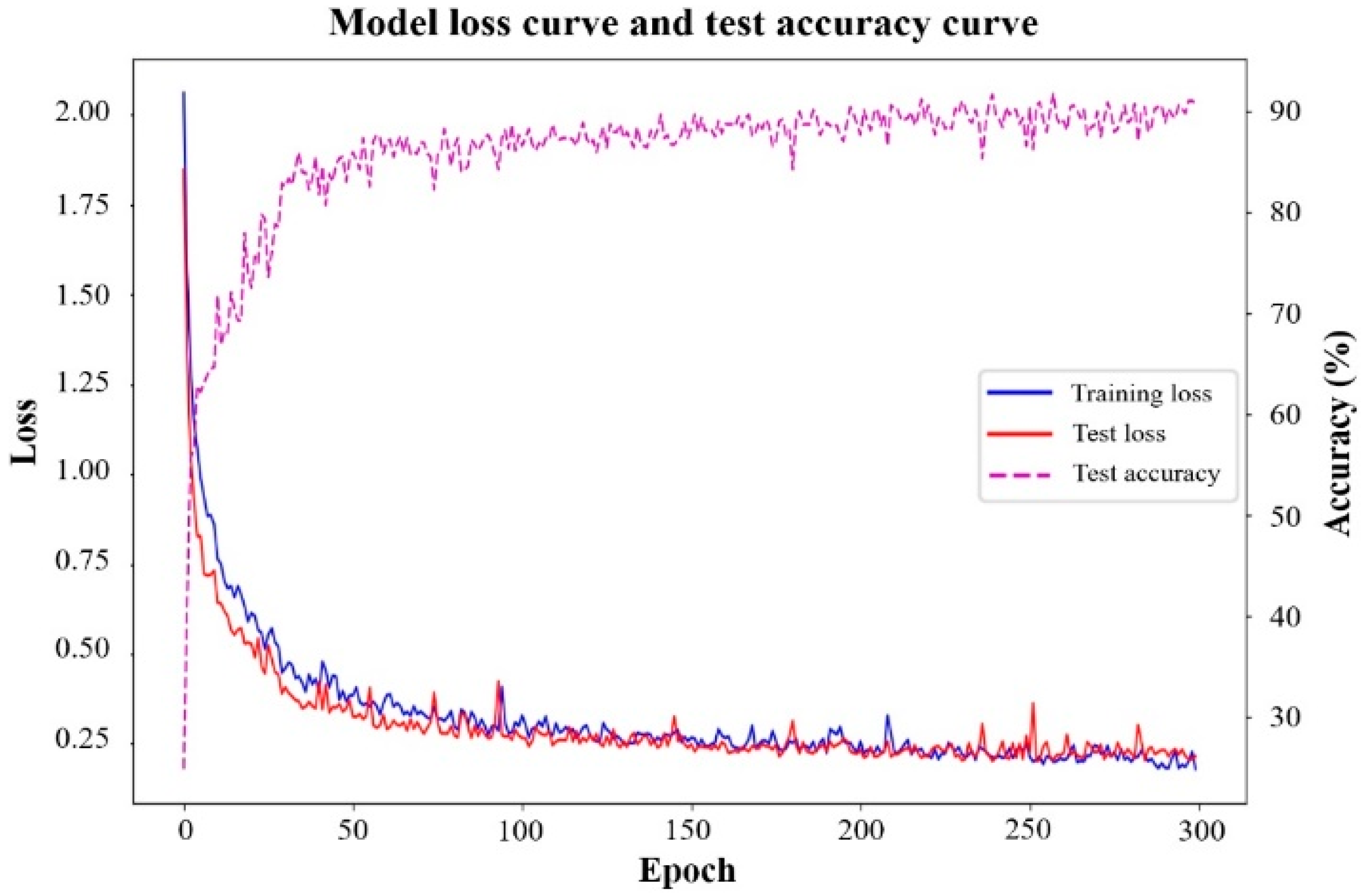
5.4. Results and Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gaurav, T.; Bhardwaj, P.; Madhavi, L.G.; Babu, G.L.S. Analysis of Tunnel Support Requirements Using Deterministic and Probabilistic Approaches in Average Quality Rock Mass. Int. J. Geomech. 2018, 18, 04018017. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zhang, D.L.; Hou, Y.J.; Li, A. Whole-process Deformation Laws and Determination of Stability Criterion of Surrounding Rock of Tunnels Based on Statistics of Field Measured Data. Chin. J. Geotech. Eng. 2021, 43, 1261–1270. (In Chinese) [Google Scholar] [CrossRef]
- Li, H.; Tan, Y.; Zeng, D.; Su, D.; Qiao, S. Attitude-Predictive Control of Large-Diameter Shield Tunneling: PCA-SVR Machine Learning Algorithm Application in a Case Study of the Zhuhai Xingye Express Tunnel. Appl. Sci. 2025, 15, 1880. [Google Scholar] [CrossRef]
- Liu, H.; Ma, T.; Lin, Y.; Peng, K.; Hu, X.; Xie, S.; Luo, K. Deep Learning in Rockburst Intensity Level Prediction: Performance Evaluation and Comparison of the NGO-CNN-BiGRU-Attention Model. Appl. Sci. 2024, 14, 5719. [Google Scholar] [CrossRef]
- Yang, T.; Wen, T.; Huang, X.; Liu, B.; Shi, H.; Liu, S.; Peng, X.; Sheng, G. Predicting Model of Dual-Mode Shield Tunneling Parameters in Complex Ground Using Recurrent Neural Networks and Multiple Optimization Algorithms. Appl. Sci. 2024, 14, 581. [Google Scholar] [CrossRef]
- Dung, C.V.; Anh, L.D. Autonomous Concrete Crack Detection Using Deep Fully Convolutional Neural Network. Autom. Constr. 2019, 99, 52–58. [Google Scholar] [CrossRef]
- Song, R.J. Numerical Simulation Study on Optimization of Freezing Pipe Position under Seepage Conditions Based on Simulated Annealing Algorithm. KSCE J. Civ. Eng. 2024, 28, 5441–5451. [Google Scholar] [CrossRef]
- Chen, F.; Tong, T.; Hua, J.; Cui, C. Crack Identification for Bridge Condition Monitoring Combining Graph Attention Networks and Convolutional Neural Networks. Appl. Sci. 2025, 15, 5452. [Google Scholar] [CrossRef]
- Liu, X.; Yin, C. 3D Reconstruction of Asphalt Pavement Macro-Texture Based on Convolutional Neural Network and Monocular Image Depth Estimation. Appl. Sci. 2025, 15, 4684. [Google Scholar] [CrossRef]
- Zhang, C.; Li, N.; Dong, X.; Liu, B.; Liu, M. Machine Learning-Based 3D Soil Layer Reconstruction in Foundation Pit Engineering. Appl. Sci. 2025, 15, 4078. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Wang, H.; Wang, Z.B. Ore Image Classification Based on Improved CNN. Comput. Electr. Eng. 2022, 99, 107800. [Google Scholar] [CrossRef]
- Gong, L.; Qi, Y.D.; Wang, J.; He, S.L. Application of PCA-PNN Model in Safety Prediction and Evaluation of Surrounding Rock of Railway Tunnel. J. Railw. Sci. Eng. 2020, 17, 940–946. (In Chinese) [Google Scholar] [CrossRef]
- Lei, M.F.; Zhang, Y.B.; Wang, W.D.; Lei, N.J.; Zeng, C.; Xiao, Y.Z.; Huang, J.; Gong, C.J. Investigation and Application on Lithology Intelligent Recognition Method Based on Mask R-CNN. J. Railw. Sci. Eng. 2022, 19, 3372–3382. (In Chinese) [Google Scholar] [CrossRef]
- Li, S.C.; Liu, H.L.; Li, L.P.; Shi, S.S.; Zhang, Q.Q.; Sun, S.Q.; Hu, J. A Quantitative Method for Rock Structure at Working Faces of Tunnels Based on Digital Images and Its Application. Chin. J. Rock Mech. Eng. 2017, 36, 1–9. (In Chinese) [Google Scholar] [CrossRef]
- Reid, T.R.; Harrison, J.P. A Semi-Automated Methodology for Discontinuity Tracing. Rock Mech. Rock Eng. 2000, 33, 271–294. [Google Scholar] [CrossRef]
- Lemy, F.; Hadjigeorgiou, J. Discontinuity Trace Map Construction Using Photographs of Rock Exposures. Int. J. Rock Mech. Min. Sci. 2003, 40, 903–917. [Google Scholar] [CrossRef]
- Jiao, Y.Y.; Ou, G.Z.; Wang, H. Prediction of tunnel squeezing based on evidence theory. J. Basic Sci. Eng. 2021, 29, 1156–1170. (In Chinese) [Google Scholar] [CrossRef]
- Sun, Y.; Feng, X.; Yang, L. Predicting Tunnel Squeezing Using Multiclass Support Vector Machines. Adv. Civ. Eng. 2018, 2018, 4543984. [Google Scholar] [CrossRef]
- Chen, Y.; Li, T.; Zeng, P. Dynamic and Probabilistic Multi-class Prediction of Tunnel Squeezing Intensity. Rock Mech. Rock Eng. 2020, 53, 3521–3542. [Google Scholar] [CrossRef]
- Dwivedi, R.D.; Singh, M.; Viladkar, M.N. Prediction of Tunnel Deformation in Squeezing Grounds. Eng. Geol. 2013, 161, 55–64. [Google Scholar] [CrossRef]
- Aydan, T.; Akagi, T.; Kawamoto, T. The squeezing potential of rocks around tunnels:theory and prediction. Rock Mech. Rock Eng. 1993, 26, 137–163. [Google Scholar] [CrossRef]
- Singh, M.; Singh, B.; Choudhari, J. Critical Strain and Squeezing of Rock Mass in Tunnels. Tunn. Undergr. Space Technol. 2007, 22, 343–350. [Google Scholar] [CrossRef]
- Yu, J.; Ma, Q.F.; Tu, B.X.; Liu, S.Y.; Zhou, J.F.; Cai, Y.Y. A New Approach of Coupling Between LDP and GRC For Quantitative Evaluation of Time-dependent Self-carrying Capacity of Surrounding Rock. J. Beijing Jiaotong Univ. 2018, 42, 9–18. [Google Scholar] [CrossRef]
- Song, F.; Rodriguez-Dono, A.; Olivella, S.; Zhong, Z. Analysis and Modelling of Longitudinal Deformation Profiles of Tunnels Excavated in Strain-softening Time-dependent Rock Masses. Comput. Geotech. 2020, 125, 104589. [Google Scholar] [CrossRef]
- Wang, Z.L.; Wang, M.N.; Li, D.G. Analysis and Modeling of Longitudinal Deformation Profiles Considering the Reinforcement Effect of Tunnel Face in Weak Rocks. KSCE J. Civ. Eng. 2022, 26, 5372–5383. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek-Brown Failure Criterion and GSI 2018 Edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown Failure Criterion-2002 Edition. In Proceedings of the North American Rock Mechanics Society NARMS-TAC 2002, Toronto, ON, Canada, 7–10 July 2002; University of Toronto Press: Toronto, ON, Canada, 2002; pp. 267–273. [Google Scholar]
- Wu, S.C. Rock Mechanics; Higher Education Press: Beijing, China, 2021; p. 151. (In Chinese) [Google Scholar]
- Hoek, E.; Diederichs, M.S. Empirical Estimation of Rock Mass Modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Vásárhelyi, B. A Possible Method for Estimating The Poisson’s Rate Values of The Rock Masses. Acta Geod. Geophys. Hung. 2009, 44, 313–322. [Google Scholar] [CrossRef]
- Panet, M. Le Calcul des Tunnels Par La Méthode De Convergence-Confinement; Press de l’école Nationale des Ponts Chaussées: Paris, France, 1995; p. 178. [Google Scholar]
- Unlu, T.; Gercek, H. Effect of Poisson’s Ratio on The Normalized Radial Displacements Occurring Around the Face of A Circular Tunnel. Tunn. Undergr. Space Technol. 2003, 18, 547–553. [Google Scholar] [CrossRef]
- Vlachopoulos, N.; Diederichs, M.S. Improved Longitudinal Displacement Profiles for Convergence Confinement Analysis of Deep Tunnels. Rock Mech. Rock Eng. 2009, 42, 131–146. [Google Scholar] [CrossRef]
- Tang, X.J. Theoretical Research and Application of Tunnel Convergence-Confinement Method. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2009. (In Chinese). [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: New York, NY, USA, 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef]
- Dong, X.Q.; Jing, L.T.; Tian, R.; Dong, X.Y. Prediction Method of Transformer Top Oil Temperature Based on LSTM Model. J. Electr. Power 2023, 38, 38–45. (In Chinese) [Google Scholar] [CrossRef]
- Wang, X.G.; Hu, B.; Wang, J.D.; Jia, P.F.; Jiao, W. Quantitative Research on Hoek-Brown Strength Criterion Based on GSI. Chin. J. Rock Mech. Eng. 2015, 34, 3805–3812. (In Chinese) [Google Scholar] [CrossRef]
- GB/T 50218-2014; Standard for Engineering Rock Mass Classification: 2014. China Planning Press: Beijing, China, 2014.

| Categories of Geological Parameters | Ρ (kg/m3) | σci (MPa) | GSI | mi |
|---|---|---|---|---|
| Condition A | 2.5 × 103 | 35 | 50 | 20 |
| Condition B | 2.3 × 103 | 15 | 30 | 20 |
| Condition C | 2.1 × 103 | 5 | 15 | 20 |
| Condition | Description of Rock Mass Characteristics | The Recommended Value of D |
|---|---|---|
| 1 | Tunnel boring machines cause minimal disturbance to the surrounding rock during excavation or blasting based on excellent quality control | 0 |
| 2 | Mechanical or manual (non-blasting) excavation of poor-quality rock masses causes minimal disturbance to the surrounding rock | 0 |
| 3 | The squeezing leads to the uplift of the tunnel bottom and requires the installation of an invert | 0.5 (when there is no invert) |
| 4 | Poor-quality blasting results in severe local damage of 2 to 3 m in the surrounding rock of hard rock tunnels | 0.8 |
| Categories of Geological Parameters | RMSE | R2 |
|---|---|---|
| Condition A | 0.027 | 0.996 |
| Condition B | 0.030 | 0.996 |
| Condition C | 0.033 | 0.995 |
| Combination Scheme Number | Parameters of the Surrounding Rock in the Initial Excavation | Parameters of the Surrounding Rock in Front of the Tunnel Face |
|---|---|---|
| 1 | A | A |
| 2 | A | B |
| 3 | A | C |
| 4 | B | A |
| 5 | B | B |
| 6 | B | C |
| 7 | C | A |
| 8 | C | B |
| 9 | C | C |
| Scheme Number | Parameters of the Surrounding Rock | Characterization of the LDP Curve |
|---|---|---|
| 1 | A-A | The deformation amount increases slightly and then decreases slowly, and the overall deformation amount is very small |
| 2 | A-B | The deformation amount increases slightly and then decreases slowly. After passing through the stratum interface, the deformation amount decreases rapidly, and the overall deformation amount is relatively small |
| 3 | A-C | The deformation amount increases slightly and then decreases slowly. After passing through the stratum interface, it increases rapidly, and the overall deformation amount is moderate |
| 4 | B-A | Before reaching the stratum interface, the deformation amount first increases and then decreases. After passing through the interface, it remains basically unchanged, and the overall deformation amount is relatively small |
| 5 | B-B | The deformation amount first increases and then decreases slowly, and the overall deformation amount is relatively small |
| 6 | B-C | Before reaching the stratum interface, the deformation amount first increases and then decreases. After passing through the interface, it decreases rapidly, and the overall deformation amount is relatively large |
| 7 | C-A | Before reaching the stratum interface, the deformation amount first increases and then decreases, and the overall deformation amount is relatively small |
| 8 | C-B | Before reaching the stratum interface, the deformation amount first increases and then decreases, and the overall deformation amount is relatively small |
| 9 | C-C | The deformation amount first increases and then decreases, and the overall deformation amount is relatively large |
| Module Name | Module Level | Component Name | Input Dimension | Output Dimension | Function Description |
|---|---|---|---|---|---|
| Input | 1 | Raw Input | 32 | (1, 32) | Input of original features |
| Convolution module | 2 | Conv1d | (1, 32) | (64, 32) | Extract local features through convolution |
| 3 | BatchNorm1d | (64, 32) | (64, 32) | Standardize channel features to accelerate training | |
| 4 | ReLU | (64, 32) | (64, 32) | Nonlinear activation | |
| 5 | SEBlock | (64, 32) | (64, 32) | Channel attention | |
| 6 | SpatialAttention1D | (64, 32) | (64, 32) | Spatial attention | |
| 7 | MaxPool1d (2) | (64, 32) | (64, 16) | Down-sampling to reduce the computational load | |
| 8 | Conv1d | (64, 16) | (128, 16) | Further extract features through convolution | |
| 9 | ReLU | (128, 16) | (128, 16) | Nonlinear activation | |
| 10 | SEBlock | (128, 16) | (128, 16) | Secondary fine-tuning of channel attention | |
| 11 | SpatialAttention1D | (128, 16) | (128, 16) | Secondary fine-tuning of spatial attention | |
| 12 | Conv1d | (128, 16) | (256, 16) | Increase in the number of convolution channels | |
| 13 | ReLU | (128, 16) | (128, 16) | Nonlinear activation | |
| 14 | SEBlock | (256, 16) | (256, 16) | Final fine-tuning of channel attention | |
| 15 | SpatialAttention1D | (256, 16) | (256, 16) | Final fine-tuning of spatial attention | |
| 16 | AdaptiveMaxPool1d | (256, 16) | (256, 16) | Adaptively fix the output length | |
| LSTM module | 17 | LSTM | (16, 256) | (16, 256) | Treat positions as time steps to capture sequence dependencies |
| Multi-head attention module | 18 | MultiheadAttention | (16, 256) | (16, 256) | Focus on different features to enhance the extraction of key information |
| Classification module | 19 | Global Average Pooling | (16, 256) | 256 | Perform dimensional Average Pooling to generate a global feature vector |
| 20 | Linear | 256 | 128 | Reduce the dimension through a fully connected layer | |
| 21 | Dropout | 128 | 128 | Randomly mask 50% of neurons to prevent overfitting | |
| 22 | Linear | 128 | 9 | Output classification results |
| Grade of Surrounding Rock | BQ | ρ (kg/m3) | Rc (MPa) | GSI | Kv | mi | |
|---|---|---|---|---|---|---|---|
| Grade III | maximum value | 420 | 2.6 × 103 | 40 | 70 | 0.8 | 20 |
| minimum value | 390 | 2.5 × 103 | 30 | 50 | |||
| Grade IV | maximum value | 310 | 2.4 × 103 | 20 | 50 | 0.6 | 20 |
| minimum value | 295 | 2.3 × 103 | 15 | 30 | |||
| Grade V | maximum value | 230 | 2.2 × 103 | 10 | 30 | 0.4 | 20 |
| minimum value | 215 | 2.1 × 103 | 5 | 15 | |||
| Classification Number | Surrounding Rock Grade at the Initial Excavation | Surrounding Rock Grade in Front of the Tunnel Face |
|---|---|---|
| 0 | III | III |
| 1 | III | IV |
| 2 | III | V |
| 3 | IV | III |
| 4 | IV | IV |
| 5 | IV | V |
| 6 | V | III |
| 7 | V | IV |
| 8 | V | V |
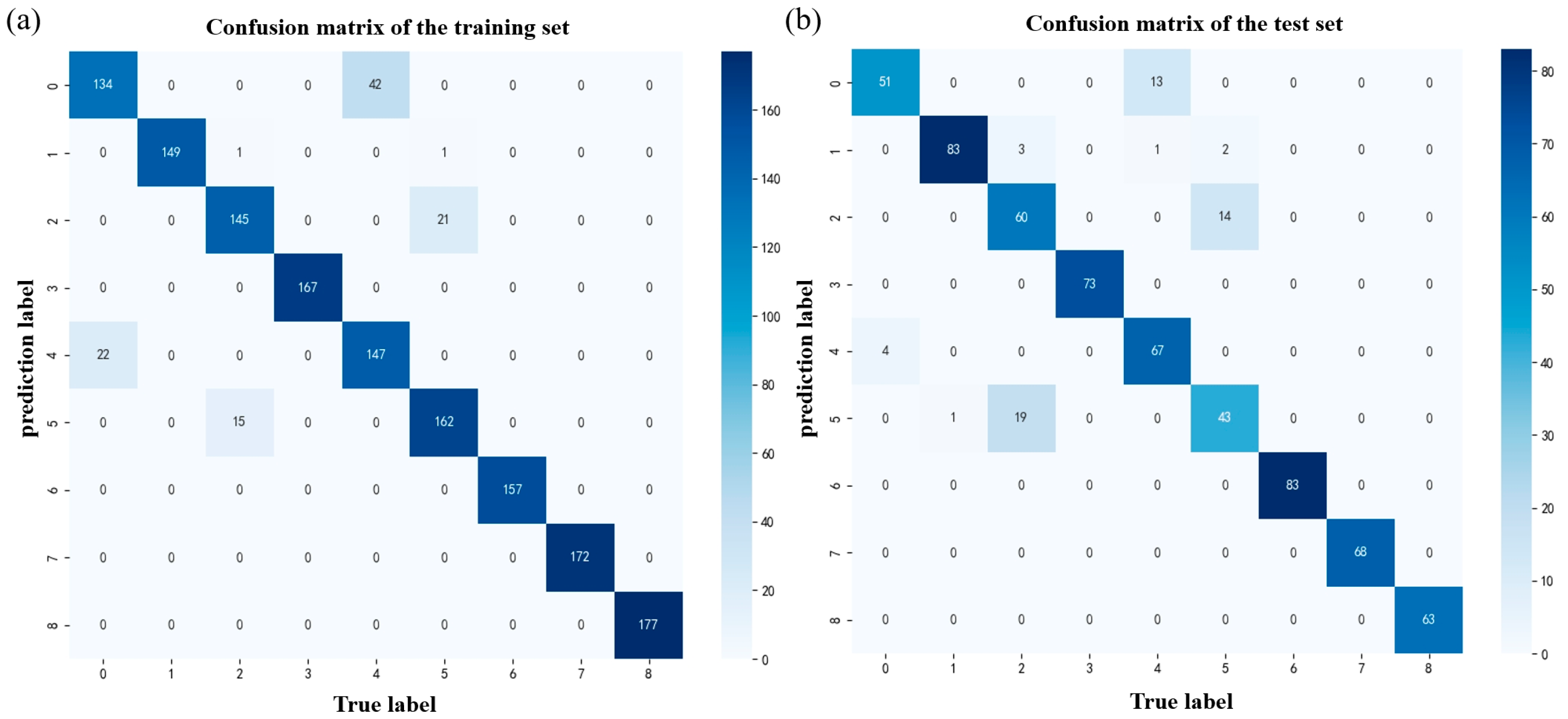
| Formation Classification | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| 0 | 0.8590 | 0.7614 | 0.8072 | 176 |
| 1 | 1.0000 | 0.9868 | 0.9933 | 151 |
| 2 | 0.9006 | 0.8735 | 0.8869 | 166 |
| 3 | 1.0000 | 1.0000 | 1.0000 | 167 |
| 4 | 0.7778 | 0.8698 | 0.8212 | 169 |
| 5 | 0.8804 | 0.9153 | 0.8975 | 177 |
| 6 | 1.0000 | 1.0000 | 1.0000 | 157 |
| 7 | 1.0000 | 1.0000 | 1.0000 | 172 |
| 8 | 1.0000 | 1.0000 | 1.0000 | 177 |
| Macro avg | 0.9353 | 0.9341 | 0.9340 | 1512 |
| Weighted avg | 0.9338 | 0.9325 | 0.9325 | 1512 |
| Accuracy | 0.9325 | 1512 | ||
| Formation Classification | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| 0 | 0.9273 | 0.7969 | 0.8571 | 64 |
| 1 | 0.9881 | 0.9326 | 0.9565 | 89 |
| 2 | 0.7317 | 0.8108 | 0.7962 | 74 |
| 3 | 1.0000 | 1.0000 | 1.0000 | 73 |
| 4 | 0.8272 | 0.9437 | 0.8816 | 71 |
| 5 | 0.7288 | 0.6825 | 0.7049 | 63 |
| 6 | 1.0000 | 1.0000 | 1.0000 | 83 |
| 7 | 1.0000 | 1.0000 | 1.0000 | 68 |
| 8 | 1.0000 | 1.0000 | 1.0000 | 63 |
| Macro avg | 0.9114 | 0.9074 | 0.9080 | 648 |
| Weighted avg | 0.9152 | 0.9120 | 0.9123 | 648 |
| Accuracy | 0.9120 | 648 | ||
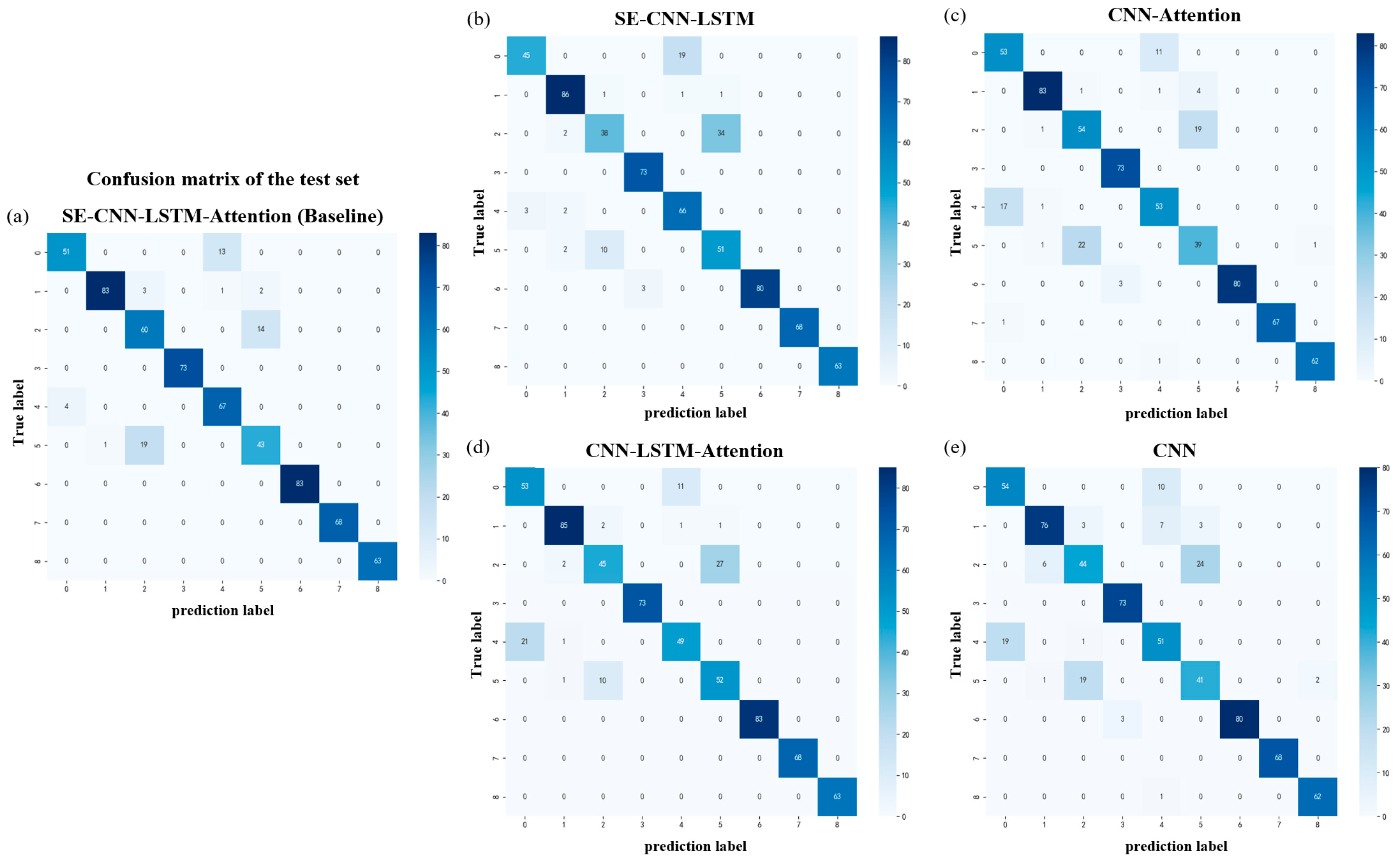
| Model Name | Composition of the Core Module | Description of Differences (in Comparison with the Model in this Paper) | Key Parameter Configuration |
|---|---|---|---|
| SE-CNN-LSTM-Attention (Baseline) | SE + SA + CNN3 + LSTM + Attn | none | Conv1d (k = 7, 5, 3), SE (reduction = 16), SA (k = 5, 5, 3), LSTM (h = 256), MultiheadAttn (4 head) |
| SE-CNN-LSTM | SE + CNN3 + LSTM | -SA, -Attn | Conv1d (k = 7, 5, 3), SE (reduction = 16), LSTM (h = 256) |
| CNN-LSTM-Attention | CNN3 + LSTM + Attn | -SE, -SA | Conv1d (k = 7, 5, 3), LSTM (h = 256), MultiheadAttn (4 head) |
| CNN-Attention | CNN3 + Attn | -SE, -SA, -LSTM | Conv1d (k = 7, 5, 3), MultiheadAttn (4 head) |
| CNN | CNN3 | -SE, -SA, -LSTM, -Attn | Conv1d (k = 7, 5, 3) |
| Model Name | Accuracy | Precision | Recall | F1-Score | |||
|---|---|---|---|---|---|---|---|
| Macro Avg | Weighted Avg | Macro Avg | Weighted Avg | Macro Avg | Weighted Avg | ||
| SE-CNN-LSTM-Attention (Baseline) | 91.20% | 0.9114 | 0.9152 | 0.9074 | 0.9120 | 0.9080 | 0.9123 |
| SE-CNN-LSTM | 87.96% | 0.8854 | 0.8897 | 0.8762 | 0.8796 | 0.8732 | 0.8774 |
| CNN-LSTM-Attention | 88.12% | 0.8793 | 0.8862 | 0.8785 | 0.8812 | 0.8755 | 0.8804 |
| CNN-Attention | 87.04% | 0.8655 | 0.8724 | 0.8655 | 0.8704 | 0.8650 | 0.8709 |
| CNN | 84.72% | 0.8426 | 0.8488 | 0.8455 | 0.8472 | 0.8472 | 0.8432 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, S.; Song, R.; Wu, Y.; Zhang, Z.; Fu, H.; Peng, Y.; Li, Z.; Liu, Y. Research on Intelligent Predictions of Surrounding Rock Ahead of the Tunnel Face Based on Neural Network and Longitudinal Deformation Curve. Appl. Sci. 2025, 15, 8771. https://doi.org/10.3390/app15168771
Shao S, Song R, Wu Y, Zhang Z, Fu H, Peng Y, Li Z, Liu Y. Research on Intelligent Predictions of Surrounding Rock Ahead of the Tunnel Face Based on Neural Network and Longitudinal Deformation Curve. Applied Sciences. 2025; 15(16):8771. https://doi.org/10.3390/app15168771
Chicago/Turabian StyleShao, Shuai, Renjie Song, Yimin Wu, Zhicheng Zhang, Helin Fu, Yichen Peng, Zelong Li, and Yao Liu. 2025. "Research on Intelligent Predictions of Surrounding Rock Ahead of the Tunnel Face Based on Neural Network and Longitudinal Deformation Curve" Applied Sciences 15, no. 16: 8771. https://doi.org/10.3390/app15168771
APA StyleShao, S., Song, R., Wu, Y., Zhang, Z., Fu, H., Peng, Y., Li, Z., & Liu, Y. (2025). Research on Intelligent Predictions of Surrounding Rock Ahead of the Tunnel Face Based on Neural Network and Longitudinal Deformation Curve. Applied Sciences, 15(16), 8771. https://doi.org/10.3390/app15168771





