A Memetic and Reflective Evolution Framework for Automatic Heuristic Design Using Large Language Models

Abstract

The increasing complexity of real-world engineering problems, ranging from manufacturing scheduling to resource optimization in smart grids, has driven demand for adaptive and high-performing heuristic methods. Automatic Heuristic Design (AHD) and neural-enhanced metaheuristics have shown promise in automating strategy development, but often suffer from limited flexibility and scalability due to static operator libraries or high retraining costs. Recently, Large Language Models (LLMs) have emerged as a powerful alternative for exploring and evolving heuristics through natural language and program synthesis. This paper proposes a novel LLM-based memetic framework that synergizes LLM-driven exploration with domain-specific local refinement and memory-aware reflection, enabling a dynamic balance between heuristic creativity and effectiveness. In the experiments, the developed framework outperforms other LLM-based state-of-the-art approaches across the designed AGV-drone scheduling scenario and two benchmark combinatorial problems. The findings suggest that LLMs can serve not only as general-purpose optimizers but also as interpretable heuristic generators that adapt efficiently to complex and heterogeneous domains.

1. Introduction

The rapid expansion of complex engineering applications, spanning flexible assembly-job-shop and flow-shop scheduling in manufacturing, energy-aware resource allocation in smart grids, dynamic task assignment in cloud computing, and pipeline optimization in bioinformatics, has placed unprecedented demands on solution methods [1,2]. These domains feature intricate constraints (e.g., machine availability, worker learning effects, fuzzy processing times, sustainability objectives) and massive search spaces, rendering traditional, hand-tuned heuristics both laborious to engineer and brittle when applied beyond narrowly defined settings. Automatic Heuristic Design (AHD) has thus emerged to automate the construction of problem-specific strategies, harnessing meta-level optimization to deliver adaptable and high-quality solutions across diverse engineering challenges without the need for extensive manual tuning. The majority of AHD research efforts focus on the hyper-heuristics [3,4], which employ genetic programming or reinforcement learning to evolve modular combinations of low-level operators, yielding interpretable strategies that generalize across domains such as job-shop scheduling and vehicle routing.

Building on this foundation, neural-enhanced metaheuristics like DeepACO integrate deep reinforcement learning into classical frameworks, automatically learning heuristic measures that outperform hand-designed counterparts on a variety of combinatorial benchmarks [5]. In parallel, automated algorithm configuration techniques based on Bayesian optimization and multi-armed bandits have shown that careful tuning of metaheuristic templates can match or exceed more expressive GP-based schemes under constrained design spaces [6]. More recently, large language models have been harnessed to explore program and heuristic spaces: FunSearch [7] and QUBE [8] sample and refine candidate programs via best-shot prompting and uncertainty-aware selection; the original Evolution of Heuristics (EoH) framework co-evolves natural-language “thoughts” and executable code [9]; and more recent LLM frameworks such as ReEvo [10] and HSEvo [11] maintain exploration–exploitation balance through adaptive feedback loops and diversity metrics.

Despite these advances, existing approaches still face issues that hinder their adaptability and efficiency. Hyper-heuristics and neural metaheuristics typically rely on a static library of curated operators or demand expensive retraining to tackle new domains, limiting their scalability and flexibility. LLM-assisted methods can instead generate creative heuristic candidates once the exploration and exploitation are carefully balanced. Memetic algorithms [12,13] have proven effective at polishing promising solutions with local search to refine the convergence, yet few prior works have applied them to enhance LLM-generated heuristics. The integration of memetic concept into the current pipeline is not trivial, since it requires associated structured mechanisms for leveraging historical success patterns, guiding operator selection, and dynamically adjusting their search directions. This absence of integrated refinement can lead to poor diversity maintenance, difficulty recovering from stagnation, and inefficient parameter tuning.

To address these gaps, we propose a unified framework, Evolution of Heuristics with Memetic Reflection (EoH-MR), that seamlessly integrates LLM-guided operator generation, adaptive local refinement via the Covariance Matrix Adaptation Evolution Strategy (CMA-ES), an explicit evolution-path memory for data-driven operator selection, and a periodic reflection mechanism to analyze population diversity, performance gaps, and stagnation indicators. In this framework, the LLM contributes domain knowledge and complex reasoning to generate and modify candidate heuristics, CMA-ES refines numerical parameters within promising solutions, the memory module records and generalizes successful evolutionary transitions to guide future search, and the reflection layer applies meta-cognitive insights to dynamically rebalance exploration and exploitation. This synergistic combination enables our method to navigate complex heuristic design spaces more effectively than prior hyper-heuristics, neural metaheuristics, or LLM-assisted techniques.

We empirically validate our approach on a suite of benchmark combinatorial optimization problems, demonstrating that it consistently achieves higher solution quality, faster convergence, and greater interpretability than state-of-the-art hyper-heuristics, neural metaheuristics, and LLM-assisted techniques. The main contributions of this work are:

• A novel suite of LLM-guided evolutionary operators that combine interpretable algorithmic reasoning with adaptive recombination and mutation strategies.
• An adaptive memetic framework that integrates CMA-ES–based local search with an explicit evolution-path memory, enabling data-driven operator selection and fine-grained parameter tuning.
• A meta-cognitive reflection mechanism that continuously monitors diversity, performance gaps, and stagnation to dynamically adjust exploration–exploitation trade-offs and usage frequencies of different operators.

The rest of this paper is organized as follows. Section 2 reviews related work in automatic heuristic design, LLM-assisted methods, and memetic algorithms. Section 3 formalizes the studied problem. Section 4 presents the EoH-MR framework in detail, including operator definitions, CMA-ES local search, evolution-path memory, and the reflection mechanism. Section 5 introduces the tasks considered as well as the evaluation metrics. Section 6 reports experimental results and ablation studies, and Section 7 concludes with a discussion of limitations and directions for future research.

2. Related Works

2.1. Automatic Heuristic Design

In the realm of solving complex search and NP-hard combinatorial optimization problems, AHD has emerged as a pivotal research area. Foremost among these, hyper-heuristics have advanced adaptive high-level mechanisms such as selection and generation of low-level operators via Genetic Programming (GP), Reinforcement Learning (RL), and multi-armed bandits, demonstrating strong generalization across domains like scheduling and combinatorial optimization [3,4,6]. GP continues to shine in crafting expressive, interpretable heuristics, particularly for job shop and flexible scheduling; recent works incorporate ML techniques like feature selection and multitask learning to boost efficiency and quality [14,15]. Parallel to this, RL hyper-heuristics (e.g., Q-learning for hyper-heuristic orchestration) have automated heuristic selection in dynamic optimization, matching or exceeding hand-designed strategies across diverse problem instances. A significant trend has emerged in neural-enhanced metaheuristics, most notably DeepACO, which embeds deep RL within ant colony frameworks to automatically learn heuristic measures; this general-purpose approach outperforms traditional ACO across multiple combinatorial benchmarks [5]. Complementary to these, automated algorithm configuration and component composition methods using hyperparameter optimization over metaheuristic templates have shown efficacy comparable to GP-based schemes, especially under constrained design spaces [6].

Collectively, these developments define a coherent trend in AHD that progresses from symbolic and rule-based methods to learning-driven and neural-augmented approaches, enabling scalable, adaptive, and interpretable solutions for complex combinatorial optimization tasks. Furthermore, this trend increasingly minimizes reliance on manual design, pushing the field towards general-purpose heuristic learning across domains.

2.2. LLM-Assisted Automatic Heuristic Design

In recent years, significant advancements have been made, especially with the integration of Large Language Models (LLMs) and Evolutionary Computation (EC) methods. One of the notable developments is searching in the function space using the LLM capability (FunSearch) [7]. It is an evolutionary framework that pairs a pre-trained LLM with automated evaluation to search program space instead of direct solutions. Candidate programs are iteratively sampled, improved via best-shot prompting, and scored by an evaluator, enabling the emergence of correct and novel code. Interpretable program outputs facilitate human-machine feedback loops and real-world deployment, which distinguishes FunSearch from raw-output discovery methods. Based on that, Chen et al. [8] introduced Quality-Uncertainty Balanced Evolution (QUBE), which redefines the priority criterion within the FunSearch framework by employing the quality-uncertainty trade-off criterion.

Furthermore, Liu et al. [9] proposed EoH, which represents heuristic ideas as natural-language thoughts generated by LLMs. These thoughts are then translated into executable codes. The co-evolution of thoughts and codes within an evolutionary search framework has shown remarkable efficiency in generating high-performance heuristics. Experiments on combinatorial optimization benchmark problems demonstrated that EoH outperforms commonly used hand-crafted heuristics and previous AHD methods. Moreover, unlike traditional hyper-heuristics limited to curated heuristic components or neural combinatorial optimization requiring extensive training, ReEvo [10] leverages a dual-feedback reflective evolution loop where LLMs iteratively generate and reflect on heuristics, enabling gradient-like guidance across black-box problem settings. In another related work, Dat et al. [11] pointed out that there is a gap in understanding the properties of heuristic search spaces and achieving a balance between exploration and exploitation. To address that, they proposed two diversity measurement metrics and introduced an adaptive LLM-based framework called HSEvo that uses a harmony search algorithm to balance diversity and convergence. Experiments showed that HSEvo achieved high diversity indices and good objective scores while being cost-effective.

In summary, recent research in Automatic Heuristic Design has focused on leveraging the power of LLMs and EC, as well as addressing key challenges such as the balance between exploration and exploitation, and improving the performance of heuristics in various optimization problems. These studies have not only advanced the theoretical understanding of AHD but also provided practical solutions for real-world applications.

2.3. Memetic Algorithms

Recent work in engineering applications underscores the superior performance of Memetic Algorithms (MAs) over basic Genetic algorithms (GAs), particularly in complex scheduling and resource-allocation contexts. For example, Hajibabaei and Behnamian [16] designed a non-dominated sorting MA with fuzzy modeling to address environmental objectives in flexible assembly-job-shop scheduling under cleaner-production constraints, demonstrating enhanced Pareto efficiency and sustainability outcomes. Ba et al. [17] advanced this field by proposing an adaptive MA using a novel multi-operation joint movement neighborhood and diversity-aware update mechanisms, which improved solution quality and stability across benchmark assembly job-shop instances. Further, Deng et al. [18] introduced a decision-driven memetic framework tailored for fuzzy rescheduling scenarios in hybrid flow shop environments, achieving robust adaptability in the face of uncertainty. In the context of flexible job shop scheduling influenced by worker learning effects and fuzzy processing times, Chang et al. [19] developed an MA enhanced with Q-learning-based variable-neighborhood search, yielding notable improvements in workload balancing and makespan reduction. Additionally, Xu et al. [20] presented a knowledge-driven MA incorporating carbon-reduction strategies and collaborative initialization for energy-efficient flow-shop scheduling, outperforming state-of-the-art heuristics in energy and emission metrics.

In summary, these studies reveal the observation that embedding problem-specific local search strategies, fuzzy or Q-learning components, and sustainability considerations into MAs systematically enhances solution quality, adaptability, and environmental performance across diverse scheduling challenges.

3. Problem Formulation

Let $\mathcal{P}$ denote the space of computational problems, where each problem $p\in \mathcal{P}$ is defined by $p=({\mathcal{I}}_p,{\mathcal{Y}}_p,{\mathcal{C}}_p)$. Here, ${\mathcal{I}}_p$ and ${\mathcal{Y}}_p$ represent input and output spaces, respectively, and ${\mathcal{C}}_p:{\mathcal{I}}_p\times {\mathcal{Y}}_p\to \mathbb{R}$ is the cost function evaluating solution quality. A heuristic h for problem p is a function $h:{\mathcal{I}}_p\to {\mathcal{Y}}_p$. Automatic heuristic design aims to generate h from example pairs $E_p={\left\{(i_k,y_k)\right\}}_{k=1}^n$ with $i_k\in {\mathcal{I}}_p$ and $y_k\in {\mathcal{Y}}_p$.

The space of possible heuristics $\mathcal{H}$ is defined over atomic operators $\mathcal{A}$ and composition rules $\mathcal{R}$. A heuristic $h\in \mathcal{H}$ can be expressed as a composition of primitives:

$$h=r_m(a_{m_1},r_{m-1}(a_{m_1-1},\dots ,r_1(a_1,i)\dots ))$$

where $a_j\in \mathcal{A}$ and $r_k\in \mathcal{R}$. The goal is to find $h^{*}=arg{min}_{h\in \mathcal{H}}{\mathbb{E}}_{i\in {\mathcal{I}}_p}\left[{\mathcal{C}}_p(i,h\left(i\right))\right]$, approximated via empirical risk minimization:

$$h^{*}\approx arg\underset{h\in \mathcal{H}}{min}{\displaystyle \frac{1}{|E_p|}}\sum _{(i,o)\in E_p}{\mathcal{C}}_p(i,h\left(i\right))$$

For parameterized heuristics $h_{\theta }$ with $\theta \in \Theta$, the optimal parameters ${\theta }^{*}$ are to minimize:

$${\theta }^{*}=arg\underset{\theta \in \Theta }{min}\mathcal{L}(h_{\theta },E_p)+\lambda \Omega \left(\theta \right)$$

where $\mathcal{L}$ measures discrepancy (such as cosine distance function), $\Omega$ regularizes complexity (such as $L_1$ norm), and $\lambda$ balances the trade-off.

The design process is modeled as a sequential decision-making problem with states $s_t$, actions $a_t$, and rewards $r_t$. The optimal policy ${\pi }^{*}$ maximizes cumulative reward:

$${\pi }^{*}=arg\underset{\pi }{max}\mathbb{E}\left[\sum _{t=0}^T{\gamma }^t{r}_t\mid \pi \right]$$

where $\gamma \in [0,1)$ is the discount factor. Optimization is typically performed using reinforcement learning, genetic programming, or gradient-based methods.

Algorithm Discovery as a Special Case

Algorithm discovery can be viewed as a constrained instance of automatic heuristic design, where the goal is to generate provably correct algorithms A for problem p. This is formalized by restricting the heuristic space $\mathcal{H}$ to a subset ${\mathcal{H}}_{\mathrm{alg}}\subset \mathcal{H}$ that satisfies correctness constraints $C_{\mathrm{correct}}(A,p)$:

$${\mathcal{H}}_{\mathrm{alg}}=\{A\in \mathcal{H}\mid \forall i\in {\mathcal{I}}_p,{\mathcal{C}}_p(i,A\left(i\right))\le {\mathcal{C}}_p^{*}\left(i\right)+ϵ\}$$

where ${\mathcal{C}}_p^{*}\left(i\right)$ is the optimal cost and $ϵ$ bounds error. Algorithm discovery seeks:

$$A^{*}=arg\underset{A\in {\mathcal{H}}_{\mathrm{alg}}}{min}\underset{i\in {\mathcal{I}}_p}{sup}{\mathcal{C}}_p(i,A\left(i\right))$$

subject to structural constraints (e.g., finite-time termination) and verifiable correctness. This is often achieved by augmenting the objective with a penalty term:

$$A^{*}=arg\underset{A\in \mathcal{H}}{min}{\mathbb{E}}_{i\in {\mathcal{I}}_p}\left[{\mathcal{C}}_p(i,A\left(i\right))\right]+\lambda ·\mathcal{I}\left(C_{\mathrm{correct}}(A,p)\right)$$

where $\mathcal{I}$ is an indicator function and $\lambda \to \infty$ enforces correctness.

4. Materials and Methods

The overall architecture of the proposed framework is illustrated in Figure 1. It consists of four interconnected components: an LLM-guided heuristic evolution process, a local optimization layer based on CMA-ES, a memory mechanism for recording successful trajectories, and a reflection module that performs meta-level adaptation. These modules collectively enable the system to navigate vast heuristic spaces through informed exploration, fine-grained exploitation, and dynamic self-adjustments.

Specifically, reflective evolution refers to a meta-level adaptation mechanism in which the system monitors population-level performance signals (such as diversity, stagnation, and convergence trends) and synthesizes actionable feedback to guide the next generation of heuristic generation. This feedback is injected into LLM prompt construction, operator scheduling, and population update rules, enabling the system to adaptively rebalance exploration and exploitation throughout the optimization process.

4.1. LLM-Guided Heuristic Evolution

Let $\mathcal{H}$ denote the space of heuristic programs, and ${\mathcal{P}}_t=\{h_1^t,\dots ,h_{\mu }^t\}\subset \mathcal{H}$ be the population at generation t. The heuristic evolution follows a classical evolutionary pipeline enhanced with LLM-guided generation:

$$\begin{array}{cc}\hfill {\mathcal{P}}_t^{\prime }& =\mathrm{Select}({\mathcal{P}}_t,f),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\mathcal{P}}_{t+1}& =\mathrm{Vary}\left({\mathcal{P}}_t^{\prime }\right)\cup \mathrm{Elite}\left({\mathcal{P}}_t\right),\hfill \end{array}$$

(2)

where $f:\mathcal{H}\to \mathbb{R}$ is the fitness function, and “Elite” denotes the retention of top-k candidates from ${\mathcal{P}}_t$. The “Select” operator samples a subset of heuristics from the current population according to their fitness, typically via tournament selection or fitness-proportional sampling. The “Vary” operator applies variation to the selected heuristics, including mutation, crossover, and optionally LLM-based modifications, to produce novel candidates.

The initial population ${\mathcal{P}}_0$ is sampled from the LLM using structured prompts $\pi \in \Pi$, where $\Pi$ denotes a predefined set of prompt templates designed to elicit diverse and syntactically valid heuristics from the language model. Each prompt $\pi \in \Pi$ encodes problem-specific context, task constraints, or examples, guiding the generation process toward feasible program candidates.

Each generated heuristic $h_i$ is verified for type correctness and filtered through static and dynamic validation. That is, $h_i^0\sim \mathrm{LLM}(·\mid \pi )$ for $i=1,\dots ,\mu$. During selection, either fitness-proportional or tournament-based methods are applied. The probability of selecting $h_i^t$ is given by

$$P\left(h_i^t\right)={\displaystyle \frac{f\left(h_i^t\right)}{{\sum }_{j=1}^{\mu }f\left(h_j^t\right)+ϵ}},$$

where $ϵ$ prevents division by zero. Selection emphasizes high-performing candidates while maintaining diversity. Variation is driven by four variation operators $\mathcal{O}=\{\mathrm{E}1,\mathrm{E}2,\mathrm{M}1,\mathrm{M}2\}$. The application of operator $op\in \mathcal{O}$ is modeled as

$$h_{\mathrm{new}}\sim \mathrm{Apply}(op\sim P_{\mathrm{op}},{\mathcal{P}}_t^{\prime }),$$

where $P_{\mathrm{op}}$ is a learned or static distribution over operators. Here, “Apply” denotes applying operator $op$ to one or more heuristics in the selected population ${\mathcal{P}}_t^{\prime }$ to produce a new candidate $h_{\mathrm{new}}$. The operators are defined as follows [9]:

• E1—Recombination: Constructs a new algorithm by recombining code segments from multiple parents, synthesizing novel structures not present in any single parent.

   

  Prompt: Create a new algorithm that has a totally different form from the given ones.

• E2—N-Point Crossover: Generates a variant that retains motivational elements from parents but exhibits a different structure via subtree exchange at aligned points.

   

  Prompt: Create a new algorithm that has a totally different form from the given ones but can be motivated from them.

• M1—Directed Mutation: Produces a heuristic variant by adapting existing logic to address identified bottlenecks, ensuring structural similarity while enabling targeted improvements.

   

  Prompt: Create a new algorithm that has a different form but can be a modified version of the algorithm provided.

• M2—Exploratory Mutation: Alters main algorithm parameter settings to explore new neighborhoods in the parameter space, introducing parameter-level diversity.

   

  Prompt: Identify the main algorithm parameters and create a new algorithm that has different parameter settings of the algorithm.

Candidates are evaluated using a fitness function $f\left(h\right)$, and invalid candidates (for example, those causing exceptions or NaNs) are pruned. The top $\mu$ heuristics among all valid parents and children form ${\mathcal{P}}_{t+1}$. Algorithm 1 demonstrates the entire procedure.

Prompting Strategy and Parameters of LLM

A set of task-specific prompt templates $\Pi$ is employed to guide the generation of candidate heuristics. Each template encodes a structured description of the target problem, the expected input/output interface, and, where applicable, few-shot examples distilled from previously successful heuristics. Prompts are designed to ensure syntactic validity and semantic relevance to the search domain. During decoding, a temperature of $1.0$ and a top-p value of $0.8$ are applied (in accordance with the DeepSeek API), and the maximum number of generated tokens is set to 4096. The primary language model used is deepseek-chat, selected for its open availability and favorable performance-efficiency tradeoff. Robustness across model backends is further assessed using gpt-4o (temperature: 0.7, top-p: 0.9), gemini-2.5-flash (temperature: 0.9, top-p: 0.95), and claude-sonnet-4 (temperature: 0.8, top-p: 0.95).

The full set of prompt templates and their usage can be found in the accompanying GitHub repository (https://github.com/gunnerwang/llm-heuristic-design, accessed on 4 August 2025). Prompts are constructed programmatically using task context, prior solutions, and variation-specific instructions. A typical example for the recombination operator (E1) is shown below:

[Task Prompt]

I have several existing algorithms with their codes as follows:

[Heuristic Code Block]

Please help me create a new algorithm that has a totally different form from the given ones.

1. First, describe your new algorithm and main steps in one sentence. The description must be enclosed within boxed {}.

2. Next, implement the following Python (3.10, Python Software Foundation, Wilmington, DE, USA, 2021) function:

[Function Signature]

Do not give additional explanations.

Algorithm 1 Evolution of Heuristics

1: Input: Problem description $\mathcal{D}$, evaluation function f, population size $\mu$   2: Initialize population ${\mathcal{P}}_0$ with $\mu$ heuristics sampled from LLM   3: for$t=0$ to $max\_generations$ do   4:      Select parents ${\mathcal{P}}_t^{\prime }$ from ${\mathcal{P}}_t$ using fitness-proportional selection   5:      Apply operators $\{E1,E2,M1,M2\}$ to generate offspring   6:      Evaluate fitness $f\left(h\right)$ for each offspring heuristic h   7:      Update population ${\mathcal{P}}_{t+1}$ by selecting top $\mu$ heuristics   8:      if $tmod{f}_{\mathrm{memetic}}=0$ then   9:            Apply local search to promising individuals 10:      end if 11:      if $tmod{f}_{\mathrm{reflection}}=0$ then 12:            Perform reflection and update evolution strategy 13:      end if 14: end for 15: Return: Best heuristic $h^{*}\in {\mathcal{P}}_{max\_generations}$

4.2. CMA-ES Local Search

To complement the structural exploration driven by LLMs, the framework incorporates a local optimization layer based on the Covariance Matrix Adaptation Evolution Strategy (CMA-ES). This layer performs fine-tuning of continuous parameters embedded within heuristic structures, enabling precise adaptation in regions where global search may stagnate.

Each heuristic h generated by the LLM typically contains scalar constants that govern its behavior, such as scoring weights, decision thresholds, penalty coefficients, or time limits. These constants often appear as literals in the source code and play a critical role in controlling heuristic performance. Instead of manually specifying which parameters to optimize, the system relies on the LLM to identify them. Specifically, during heuristic generation, the LLM is prompted to mark potentially tunable constants using structured comments or syntax tokens. For example, numerical literals are annotated with tags such as # tunable_weight or embedded in specific functions like adjust_param(value). A static analysis module then parses the heuristic and extracts all such annotated values into a vector $\mathit{\theta }\in {\mathbb{R}}^d$.

Prompt: I need you to identify numerical parameters in this algorithm that could be optimized. These parameters might include:

1. Numerical constants that affect algorithm behavior (weights,

thresholds, coefficients)

2. Parameters that control convergence or termination

3. Parameters that balance exploration vs. exploitation

4. Other numerical values that significantly impact performance

Let $h\left(\mathit{\theta }\right)$ denote the heuristic instantiated with parameter vector $\mathit{\theta }$, and $f\left(h\right(\mathit{\theta }\left)\right)$ its performance. The objective is to find:

$${\mathit{\theta }}^{*}=arg\underset{\mathit{\theta }}{max}f\left(h\left(\mathit{\theta }\right)\right)$$

At generation g of local search, CMA-ES samples candidates:

$${\mathit{\theta }}_i^{\left(g\right)}\sim \mathcal{N}({\mathbf{m}}^{\left(g\right)},{\sigma }^{{\left(g\right)}^2}{\mathbf{C}}^{\left(g\right)}),i=1,\dots ,\lambda$$

Each ${\mathit{\theta }}_i^{\left(g\right)}$ is injected back into the heuristic via AST rewriting, resulting in a set of parameterized programs to be evaluated. The update process includes:

• Fitness evaluation of all sampled heuristics $h\left({\mathit{\theta }}_i\right)$.
• Selection of top-ranked samples for computing the new mean ${\mathbf{m}}^{(g+1)}$.
• Step-size adaptation based on path length control.
• Covariance matrix update based on:

  $${\mathbf{C}}^{(g+1)}=(1-c_1-c_{\mu }){\mathbf{C}}^{\left(g\right)}+c_1{\mathbf{p}}_c{\mathbf{p}}_c^{\top }+c_{\mu }\sum _{i=1}^{\mu }{w}_i({\mathit{\theta }}_i^{\left(g\right)}-{\mathbf{m}}^{\left(g\right)}){({\mathit{\theta }}_i^{\left(g\right)}-{\mathbf{m}}^{\left(g\right)})}^{\top }$$

CMA-ES is invoked every $f_{\mathrm{memetic}}$ generations and applied to a small number of elite heuristics. The refined version $h^{*}$ replaces its original if it achieves a minimum performance gain $\delta$:

$$f\left(h^{*}\right)-f\left(h\right)>\delta$$

This hybrid integration achieves two goals. First, it ensures that structural innovations discovered by the LLM are not wasted due to suboptimal parameters. Second, it delegates low-level numeric tuning to a principled optimizer, yielding better convergence properties while preserving the diversity and creativity afforded by the generative component. The entire procedures are shown in Algorithm 2.

Algorithm 2 Hybrid Local Search with CMA-ES

1: Input: Individual solution x, objective function $f\left(x\right)$   2: Extract numerical parameters $\theta$ from solution x with LLM   3: Initialize CMA-ES with $\theta$ and step size $\sigma =0.5$   4: for $t=1$ to $max\_iterations$ do   5:      Sample population $\left\{{\theta }_i\right\}\sim \mathcal{N}(m,{\sigma }^2\mathbf{C})$   6:      Evaluate $f\left(x_{{\theta }_i}\right)$ for each sampled parameter set   7:      Update mean m, step size $\sigma$, and covariance matrix $\mathbf{C}$   8: end for   9: Return: Best solution found

4.3. Evolution Memory

The evolution memory module provides a long-term, data-driven mechanism that captures structural transitions, operator statistics, and transformation patterns observed during the search process. Unlike the reflection mechanism, which reacts adaptively, the memory module serves as a persistent knowledge base that biases the generation and variation pipeline toward historically effective strategies [21,22]. The memory consists of three components:

• Transition Memory $\mathcal{T}$: records individual transformations from $h^{\mathrm{src}}\to h^{\mathrm{dst}}$, along with fitness gain $\Delta f$;
• Operator Statistics ${\mathcal{S}}_{\mathrm{op}}$: tracks usage and success rates of variation operators;
• Pattern Memory ${\mathcal{M}}_{\mathrm{pat}}$: stores frequent transformation templates as reusable structural patterns.

Each transition $(h^{\mathrm{src}},h^{\mathrm{dst}},\Delta f)$ is logged, where $\Delta f=f\left(h^{\mathrm{dst}}\right)-f\left(h^{\mathrm{src}}\right)$ denotes the fitness improvement. A conditional transition model is estimated as:

$$P(h^{\mathrm{dst}}\mid h^{\mathrm{src}})={\displaystyle \frac{{\sum }_i\Delta f_i·{\mathbb{1}}_{(h_i^{\mathrm{src}}\to h_i^{\mathrm{dst}})}}{{\sum }_i\Delta f_i}}$$

This distribution biases variation sampling toward historically promising edits. For each operator $op\in \mathcal{O}$ (e.g., E1 and M2), success probability is tracked by:

$$P\left(op\right)={\displaystyle \frac{\mathrm{success}\left(op\right)+\alpha }{\mathrm{total}\left(op\right)+\beta }}$$

These probabilities shape operator selection during generation, modulated by time-weighted priors. While all memory components support long-term optimization, they serve two complementary roles: content reuse via LLM prompting, and strategic control via guided sampling and temporal shaping.

4.3.1. LLM-Guided Reuse of Structural Patterns

In addition to raw transitions, the system maintains a library of reusable edit patterns. These patterns are extracted via rule-based analysis of repeated transformation structures, such as loop rewrites, scoring formula substitutions, or condition simplifications, and stored in ${\mathcal{M}}_{\mathrm{pat}}$.

While the abstraction process is deterministic, these patterns are later used to condition the LLM’s behavior. Specifically, the memory module constructs prompts that embed selected patterns as few-shot exemplars or contextual cues, enabling the LLM to produce heuristics that align with past success. Applications include:

• Augmenting generation prompts with high-yield code examples;
• Injecting transformation descriptions as natural language constraints;
• Supplying the reflection module with pattern-derived guidance snippets.

To illustrate how memory-derived knowledge is incorporated into prompt construction, the system assembles composite prompts that combine strategic suggestions and example transitions. A representative format is shown below:

Prompt: [Original task description]

Based on past successful evolution, consider these strategies:

- Adding more sophisticated logic to the algorithm

- Simplifying the algorithm by removing unnecessary steps

- Refining existing logic while maintaining similar complexity

Here are examples of successful evolution steps:

Example 1:

- Parent algorithm: [code snippet]

- Improved child: [code snippet]

Example 2:

- Parent algorithm: [code snippet]

- Improved child: [code snippet]

This prompt structure enables the LLM to benefit from both abstract rules and concrete demonstrations, forming a bridge between learned memory and generative behavior.

4.3.2. Sampling Control and Memory Shaping

In parallel, the memory system also modulates the generation and variation process through score-based sampling and memory decay mechanisms. During prompt selection or operator scheduling, memory-derived scores determine sampling probabilities:

$$\pi \sim {\mathrm{softmax}}_{\tau }\left(\mathrm{score}({\pi }_i;{\mathcal{P}}_{\mathrm{mem}})\right)$$

where the score of each prompt or transformation is computed based on match frequency, fitness contribution, and temporal recency.

To ensure memory relevance over time, an age-weighted forgetting mechanism is applied:

$$w_i^{\left(t\right)}=\Delta f_i·exp\left(-\lambda (t-t_i)\right)$$

This favors recent, impactful edits while allowing outdated or noisy patterns to fade. The same decay mechanism is used to prioritize transition memory and operator statistics.

Together, these sampling and shaping strategies ensure that the memory system does not merely archive past transitions, but actively directs and adapts the search behavior as the optimization process unfolds.

4.4. Reflection Mechanism

The reflection module serves as a meta-cognitive layer that monitors the evolutionary process and adjusts the overall search strategy [23,24]. Unlike conventional restart or annealing schemes, the mechanism integrates two complementary sources of information: (1) quantitative indicators derived from runtime statistics, and (2) qualitative assessments synthesized by an LLM. These signals jointly inform adaptive control over algorithm generation, variation, and memory utilization.

Each reflection cycle is triggered every $f_{\mathrm{reflection}}$ generations and draws on three types of runtime information based on the evolution memory stated previously:

• Performance Metrics: numerical trends such as convergence velocity, stagnation status, and heuristic diversity;
• Search History: traces of transformation sequences, operator application frequencies, and observed local optima;
• Memory Statistics: distributions over high-yield transitions and operator-level success rates.

4.4.1. Quantitative Analysis of Search Behavior

Let $P_t$ denote the population at generation t, and let $\mathrm{best}\left(t\right)$ denote the highest fitness value achieved so far. Several time-sensitive indicators are computed as follows:

$$\begin{array}{cc}\hfill \mathrm{Velocity}& :\nu \left(t\right)={\displaystyle \frac{1}{k}}\sum _{i=1}^k\left[\mathrm{best}(t-i+1)-\mathrm{best}(t-i)\right]\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathrm{Stagnation}\mathrm{Flag}& :{\mathbb{1}}_{\mathrm{stag}}\left(t\right)=\left[\mathrm{best}\left(t\right)-\mathrm{best}(t-k)<ϵ\right]\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \mathrm{Diversity}& :D_t={\displaystyle \frac{1}{|P_t\left|\right(|P_t|-1)}}\sum _{i\ne j}\delta (P_i,P_j)\hfill \end{array}$$

(5)

These metrics are combined into a quantitative reflection signal:

$$R_{\mathrm{quant}}\left(t\right)=\varphi (\nu \left(t\right),D_t,{\mathbb{1}}_{\mathrm{stag}}\left(t\right),H_t)$$

where $H_t$ represents historical metadata, including operator entropy, transition variability, and CMA-ES utilization profiles.

4.4.2. LLM-Based Semantic Interpretation

To complement the numerical perspective, the reflection module constructs a prompt for the LLM that captures the current search state and exemplar heuristics. This prompt encodes runtime summaries, such as diversity and stagnation status, as well as serialized representations of selected algorithms. A representative reflection prompt is as follows:

Prompt: Analyze the following algorithms and provide insights to

improve future evolution:

Current population diversity: [value]

Evolution status: [stagnation/active]

Evolution memory: <code snippet>

<data structure>

Please provide 3–5 numbered insights addressing:

1. Common patterns in high-performing solutions

2. Potential improvements to existing algorithms

3. Novel approaches that haven’t been tried yet

4. Reasons for observed performance differences

Your reflections will guide the next generation of algorithms.

The LLM’s response is parsed into interpretable components, including:

• Transformation Ideas: high-level suggestions such as replacing fixed thresholds with adaptive schemes;
• Structural Assessments: identification of repeated logic, inefficient constructs, or missing semantic operations;
• Prompt Enhancements: new few-shot exemplars distilled from insights and added to the LLM’s prompt pool $\Pi$.

4.4.3. Integrated Control and Adaptation

The full reflection signal is obtained by aggregating numerical and semantic feedback:

$$R\left(t\right)=R_{\mathrm{quant}}\left(t\right)+R_{\mathrm{LLM}}\left(t\right)$$

This composite signal modulates several aspects of the optimization process:

• Adjusting variation operator probabilities (e.g., promoting M2 when diversity collapses);
• Retiring stale few-shot prompts and injecting newly inferred ones;
• Replacing redundant individuals or reviving historically diverse heuristics;
• Altering prompt selection distributions to promote semantic novelty.

By combining runtime-derived measurements with LLM-guided interpretation, the reflection module enacts informed and adaptive strategy updates, enabling the system to respond fluidly to stagnation, convergence, or missed opportunities in the search space.

To illustrate how reflective evolution operates in practice, the following example is provided based on the TSP optimization task. When the system detects that recent high-performing heuristics rely on entropy-based node selection and that population diversity is declining, it responds by: (1) increasing the sampling probability of exploratory mutation (M2), (2) pruning low-yield prompt templates, and (3) augmenting new prompts with example heuristics that penalize frequently visited nodes or encourage recency-based edge selection. These modified prompts are then used by the LLM to generate the next population, effectively injecting learned structural patterns into the search loop.

5. Evaluation Tasks and Metrics

5.1. Task Details

To evaluate the proposed framework across diverse problem types, we consider three representative tasks spanning industrial scheduling, combinatorial optimization, and scientific discovery. The first task is a custom-designed AGV-drone coordination problem derived from a realistic logistics scenario, featuring hybrid agent dynamics, spatial-temporal constraints, and resource contention. This domain highlights the system’s ability to construct heuristics under complex operational conditions. The second and third tasks are established benchmarks: the Traveling Salesman Problem (TSP), which emphasizes optimization efficiency over large solution spaces, and the Ordinary Differential Equation (ODE) symbolic regression task, which targets interpretable scientific discovery. Together, these cases demonstrate the versatility of our approach across both decision-making and analytical domains.

5.1.1. AGV-Drone Collaborative Scheduling Task

The AGV and drone collaborative scheduling task is formulated as a discrete-time Markov Decision Process (MDP), where the state, action, transition, and reward components are defined to capture the multi-agent coordination dynamics across three logistical zones: A (storage), B (processing), and C (buffer). An overview of the case is presented in Figure 2.

The state space $\mathcal{S}$ encodes a complete snapshot of the system status. Each state $s\in \mathcal{S}$ is defined as a tuple $s=(A,B,C,V,E,T)$, where $A=(P_A,T_A)$ represents binary availability vectors for parts and trays at location A. The status of processing stations at location B is given by $B\in {\mathbb{R}}^{n_B\times 4}$, storing information such as the assigned part/tray ID, completion time, and station status. Similarly, $C\in {\mathbb{R}}^{n_C\times 3}$ records the contents of the buffer, including reservation flags. The vehicle fleet is captured by $V\in {\mathbb{R}}^{n_V\times 5}$, where each row specifies a vehicle’s location, current load, travel time, and type (AGV or drone). Battery levels are maintained as $E\in {[0,E_{max}]}^{n_V}$, and internal clocks as $T\in {\mathbb{R}}^{n_V}$, tracking elapsed time per vehicle.

The action space $\mathcal{A}$ allows each vehicle to choose from a discrete set of operations: $a\in \{0,1,2,3,4\}$, corresponding, respectively, to delivering a part from A to B, returning an empty tray from B to A, transferring an item from A to C, moving from C to B for processing, or initiating a charging procedure. The effects of an action are captured by the transition model $P(s^{\prime }\mid s,a)$, which updates location, energy, and timing variables. Travel time for each path is computed as $\Delta t=t_{\mathrm{travel}}+t_{\mathrm{wait}}$, where duration depends on the selected route, current congestion (indicated by a binary variable $\mathbb{I}\left(\mathrm{jam}\right)$), and vehicle type. Drones operate faster than AGVs, modeled via a scaling factor ${\alpha }_d$. Processing actions at location B can fail with a probability $p_{\mathrm{fail}}$, and charging actions restore energy to $E_{max}$.

The reward function $R(s,a,s^{\prime })$ penalizes delay, distance, and task failures. Specifically, the immediate reward is computed as

$$R=-({\alpha }_d·d+{\alpha }_t·t+{\alpha }_p·p_{\mathrm{fail}}),$$

where d is the travel distance, t is the task delay, and ${\alpha }_d$, ${\alpha }_t$, ${\alpha }_p$ are weighting coefficients.

Battery dynamics are governed by task-dependent consumption and recharging behaviors. A movement of distance d incurs energy loss $E_i^{\prime }=E_i-\gamma ·d$, where $\gamma$ is the energy-per-distance coefficient. Charging resets the level to $E_{max}$. A vehicle can only execute a task if its current energy $E_i$ exceeds a required threshold $e_{\mathrm{req}}$. Furthermore, the problem is subject to several operational constraints. Each vehicle can carry at most one part and one tray simultaneously. Locations B and C have limited buffer and processing slots. Energy sufficiency is mandatory for movement, and processing at B requires available stations. The overall objective is to maximize completed part throughput while minimizing total energy consumption and cumulative task latency, yielding a trade-off between efficiency and speed under constrained coordination. The concrete parameters employed are shown in

Table 1. Initialization parameters for the AGV-drone scheduling task.

Parameter	Symbol	Value
Number of parts	$p_{max}$	80
Number of trays	$t_{max}$	6
Number of AGVs	$n_{AGV}$	3
Number of drones	$n_{drone}$	1
Total vehicles	$n_V$	4
Processing stations	$n_B$	4
Buffer locations	$n_C$	3
Part arrival interval	${\tau }_A$	30
Processing time	${\tau }_B$	900
Base travel time between A and B	$t_{AB}$	400
Base travel time between A and C	$t_{AC}$	300
Base travel time between B and C	$t_{BC}$	200
Drone speed factor	${\alpha }_d$	0.7
Traffic jam probability	$p_{jam}$	0.4
AGV jam delay factor	${\beta }_{AGV}$	3.0
Drone jam delay factor	${\beta }_{drone}$	1.5
Processing failure probability	$p_{fail}$	0.2
Maximum battery capacity	$E_{max}$	60
Battery consumption rate	$\gamma$	0.08
Critical battery level	$E_{crit}$	25
Base charging time	${\tau }_{charge}$	300
Per unit charging time	${\tau }_{unit}$	3
Distance reward factor	$f_d$	0.01
Time reward factor	$f_t$	0.01

.

5.1.2. TSP Task

The Traveling Salesman Problem (TSP) is a classical graph-based optimization problem defined over a set of n cities with pairwise distances. The objective is to find a minimal-length tour that visits each city exactly once and returns to the starting point. Formally, the goal is to find a permutation $\pi$ over $\{1,2,\dots ,n\}$ that minimizes:

$$\sum _{i=1}^{n}d\left(\pi \left(i\right),\pi (i+1)\right),\mathrm{with}\pi (n+1)=\pi \left(1\right),$$

where $d(i,j)$ denotes the Euclidean distance between cities i and j. The problem is NP-hard and widely used as a benchmark for evaluating general-purpose optimization methods.

5.1.3. ODE 1D Task

The ODE 1D task centers on scientific discovery, i.e., the inference of compact differential equations from observed data. Instead of minimizing cost or maximizing reward, the goal is to recover the functional structure of an unknown one-dimensional ODE:

Find the mathematical function skeleton $\dot{x}=f\left(x\right)$ such that it best matches observed data pairs $(x,\dot{x})$ under differentiability and continuity constraints.

Candidate programs are represented in Python symbolic form:

    def equation(x: float, params: np.ndarray) -> float:

        y = params[0] * x + params[2]

        return y

The search space is constrained to the following elements:

• Basic operators: +, -, *, /, ^, np.sqrt, np.exp, np.log, np.abs
• Trigonometry: np.sin, np.cos, np.tan, np.arcsin, np.arccos, np.arctan
• Constants: np.pi, np.e

This makes the task fundamentally different from classical optimization, requiring symbolic structural search jointly with numerical parameter tuning.

5.2. Evaluation Metrics

To comprehensively assess the performance of the proposed methodologies, we employ a multi-faceted set of evaluation metrics. These metrics are designed to capture not only the quality of the generated solutions but also the stability, efficiency, and diversity of the optimization process. The metrics are broadly categorized as follows:

5.2.1. Core Performance Metrics

These metrics provide a fundamental understanding of the solution quality achieved during the optimization process.

• Best Score: The highest objective function value achieved across all evaluations. This represents the peak performance observed.
• Standard Deviation (Std) of Scores: Measures the dispersion or spread of the valid scores around the mean score. A lower standard deviation suggests more consistent performance.

5.2.2. Stability and Robustness Metrics

Stability metrics assess the consistency and reliability of the solutions and the optimization process itself.

• Success Rate: The ratio of successful evaluations (resulting in finite, non-NaN scores) to the total number of evaluator calls.
• Coefficient of Variation (CV): Defined as the ratio of the standard deviation of scores to the mean score ($\sigma /\mu$). It provides a normalized measure of score dispersion.
• Stability Score: A normalized metric, typically derived from multiple runs of the same solution, often calculated as $1/(1+\mathrm{CV})$, where CV is the Coefficient of Variation. It reflects the reproducibility of a solution’s score.
• Score Range: The difference between the maximum and minimum valid scores observed for a particular solution or across a set of solutions.

5.2.3. Efficiency Metrics

These metrics quantify the computational resources consumed by the optimization algorithm.

• Total LLM Calls: The total number of invocations made to the Large Language Model.
• Total Tokens Used: The sum of input (prompt) and output (completion) tokens processed by the LLM, indicating the language processing load.
• Total Evaluator Calls: The total number of times the objective function (or its proxy) was evaluated.
• Total Computation Time: The cumulative time taken for sampling new solutions and evaluating them.

5.2.4. Solution Diversity Metrics

Diversity metrics gauge the variety of solutions explored by the algorithm.

• Total Unique Scores: The number of distinct score values obtained.
• Mean Diversity (Inter-solution Score Standard Deviation): The standard deviation of the mean scores obtained from different evaluated solutions (e.g., different generated functions).
• Score Spread: The range (max–min) of mean scores across different evaluated solutions.
• Diversity Score: A composite metric that balances performance variation with temporal spread. It is computed as

  $$\mathrm{Diversity}\mathrm{Score}={\displaystyle \frac{\mathrm{Score}\mathrm{Diversity}+\mathrm{Generation}\mathrm{Diversity}}{2}},$$

  where Score Diversity is the coefficient of variation of all solution scores and Generation Diversity is the fraction of generations that produced at least one valid solution.

6. Results and Discussions

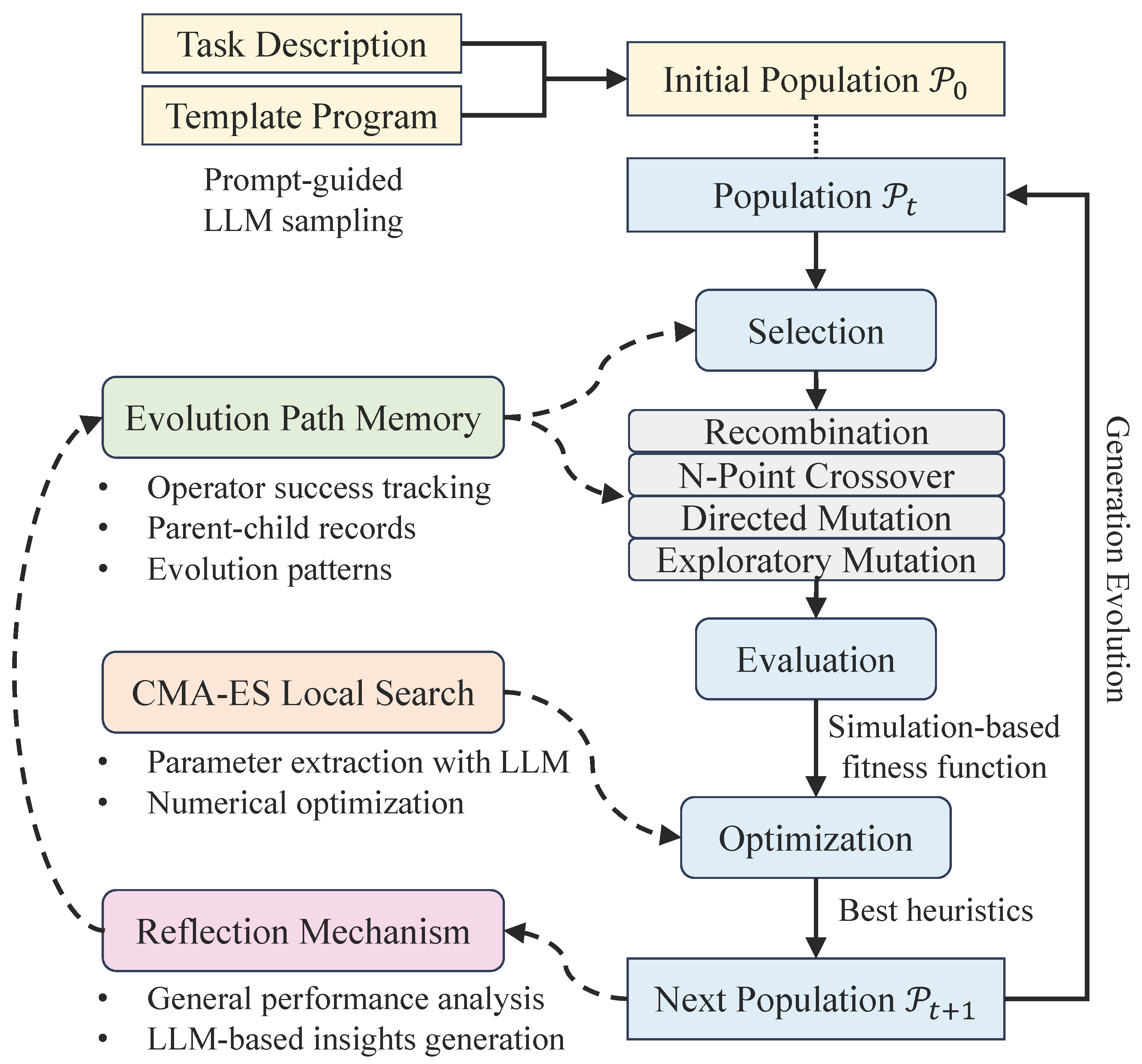
6.1. Performance Comparison on AGV Scheduling Problem

The AGV scheduling problem represents a highly dynamic, resource-constrained optimization task involving coordinated part transport via autonomous ground vehicles and drones. Key complexities include heterogeneous agent capabilities, hard energy constraints, dynamic part arrivals, limited processing slots, stochastic delays from traffic jams, and non-negligible failure probabilities. These attributes make the problem substantially harder than classical routing tasks, especially for approaches without domain-aware adaptability.

Table 2. Comprehensive comparison results of AGV-drone scheduling task using deepseek-chat.

Metric Category	FunSearch	HillClimb	EoH	EoH-M	EoH-MR
Core Performance Metrics
Best Score (Peak)	−189,158.5714	−187,813.3333	−184,620.0	−184,051.25	−159,306.0
Std Dev of Scores (Overall)	26,395.5240	33,752.3249	17,748.3088	26,740.5316	40,589.8931
Stability and Robustness Metrics
Success Rate	0.3182	0.2273	0.4839	0.3137	0.3580
Stability Score	1.1547	1.1338	1.0997	1.1426	1.2494
Efficiency Metrics
Total LLM Calls	20	20	40	64	100
Total Tokens Used	27,247	30,900	70,349	142,597	306,075
Total Evaluator Calls	66	66	93	153	243
Total Computation Time (s)	1136.06	1033.19	1071.9302	1815.0409	3177.5700
Solution Diversity Metrics
Total Unique Scores	21	15	45	48	87
Score Range	10,179.7619	19,562.6667	51,470.5667	78,425.7333	131,009.8333

summarizes the comparative performance of the proposed EoH-based frameworks and two baselines (FunSearch and HillClimb) on this task.

Core Performance Metrics. The proposed EoH-MR achieves the best objective score of −159,306.0, improving substantially over EoH-M (−184,051.25), the original EoH (−184,620.0), and the strongest baseline HillClimb (−187,813.33). This performance gap of over 15% in total cost demonstrates the superiority of EoH-MR in navigating the large, noisy solution space of the AGV task. Notably, while HillClimb is competitive in structured domains like TSP, it is not well-suited for scenarios involving multi-agent energy-aware scheduling under real-time stochasticity. FunSearch, though more robust than HillClimb, also fails to match the effectiveness of LLM-driven co-evolution in this domain. As shown in Figure 3, EoH-MR demonstrates a significant performance advantage over other algorithms, reaching the lowest cost among all methods. FunSearch and HillClimb perform notably worse, confirming their limitations under complex scheduling constraints.

Stability and Robustness. The baseline EoH achieves the highest success rate (0.4839), suggesting that it produces feasible solutions more reliably. This is partly due to its simpler evolution strategy, which favors safe sampling. However, it also shows lower overall stability and higher coefficient of variation, reflecting inconsistent solution quality. In contrast, EoH-MR, despite a slightly lower success rate (0.3580), achieves the best normalized stability score (1.2494). This robustness is a result of its memetic refinement via CMA-ES, which tunes promising heuristics toward more repeatable and interpretable behaviors. This is corroborated by Figure 3, which shows EoH-MR reaching the highest stability score (1.2494), indicating the most consistent performance across runs, despite its complexity.

Efficiency Metrics. The original EoH is the most computationally efficient, consuming only 1071.9302 s and 40 LLM calls. However, this efficiency comes at the cost of lower solution quality and poor exploration capability. EoH-MR is the most computationally intensive variant (3177.57 s, 100 LLM calls), yet it produces the best performance. FunSearch and HillClimb, despite lower token usage (27,247–30,900), deliver weaker solutions and fail to adapt heuristics dynamically. In critical smart manufacturing scenarios, such as factory logistics or automated warehouse scheduling, such trade-offs in computational cost are justified by improved system throughput. EoH-MR requires nearly triple the time of HillClimb (1033.19 s), clearly reflecting the added cost of memetic refinement and LLM integration.

Diversity and Exploration. EoH-MR achieves the highest diversity in terms of unique score count (87), inter-solution score standard deviation (40,589.8931), and score range (131,009.83). This indicates a significantly broader exploration of the solution space, which is crucial in dynamic environments to avoid premature convergence. EoH-M is also more exploratory than EoH due to the inclusion of adaptive local search, but lacks the reflection mechanism that helps rebalance search efforts. FunSearch and HillClimb both explore far fewer diverse trajectories (only 21 and 15 unique scores, respectively), suggesting their evolution is more deterministic and potentially prone to stagnation. As visualized in Figure 3, the diversity gap is stark, with EoH-MR demonstrating far broader score ranges than any baseline, reinforcing its exploratory strength.

Strategic Insights from High-Scoring Schedules. Beyond numerical performance, deeper analysis of evolved heuristics reveals several qualitative patterns consistently present in top-performing strategies:

• Decentralized bidding mechanisms that weigh urgency, battery margins, and predicted congestion enable flexible agent coordination, often outperforming static rule systems by 15–20%.
• Role flexibility, allowing drones and AGVs to interchange tasks contextually, yields lower penalty trajectories than rigid allocation.
• Proactive energy management embedded in bidding logic reduces failure rates and extends operational margin.
• Congestion forecasting leads to early detouring and better throughput than reactive heuristics.
• Local refinement operators contribute disproportionately to late-stage gains, confirming the value of post-generation fine-tuning.
• Exploration bottlenecks, such as stagnated diversity scores, prompt the use of stochastic noise to escape local minima.

These observations illustrate that success hinges less on wholesale heuristic redesign and more on layered, context-aware decision strategies combining auction logic, adaptive constraints, and lightweight local search.

In addition to total computation time, the duration required to reach a near-optimal solution is practically important, especially when early results are needed under time constraints. Based on empirical trajectories of the AGV-drone scheduling task, EoH reaches within 5% of its final best score in approximately 800 s (75% of total time), EoH-M in around 1000 s (55%), and EoH-MR in only 1270 s (40%). The corresponding “good enough” score for EoH-MR is approximately −167,270, which not only surpasses the final results of all baseline methods (e.g., HillClimb: −187,813; FunSearch: −189,158), but also exceeds the typical performance range of manually designed heuristics, which often fall between −160,000 and −190,000 depending on domain knowledge and tuning effort. Furthermore, while manual design and tuning can require several hours to days, EoH-MR achieves these results in around 20 min with no human intervention. This highlights the framework’s ability to generate high-quality solutions with greater efficiency, making it well-suited for automated or time-sensitive decision-making settings.

6.2. Performance Comparison on TSP Problem

The Traveling Salesman Problem (TSP) serves as a benchmark for permutation-based optimization over a static, symmetric graph. It is well-known, smooth in fitness landscape, and does not feature the dynamic, temporal, or resource coupling challenges present in AGV scheduling. As such, it provides an ideal contrast to assess how heuristic design strategies generalize from complex, real-world-inspired tasks to well-structured classical problems.

Table 3. Comprehensive comparison results of the TSP optimization task.

Metric Category	FunSearch	HillClimb	EoH	EoH-M	EoH-MR
Core Performance Metrics
Best Score (Peak)	−6.8240	−6.7326	−6.6840	−6.4494	−6.3967
Std Dev of Scores (Overall)	5.9192	2.2430	6.1619	5.1762	6.6777
Stability and Robustness Metrics
Success Rate	1.0000	0.9815	0.9600	1.0000	1.0000
Stability Score	2.0820	1.3808	2.2753	2.2936	2.3804
Efficiency Metrics
Total LLM Calls	27	23	19	68	112
Total Tokens Used	25,105	19,742	10,802	61,345	107,440
Total Evaluator Calls	29	24	25	46	73
Total Computation Time (s)	820.21	1396.25	347.44	1492.92	2743.37
Solution Diversity Metrics
Total Unique Scores	40	33	19	39	65
Score Range	21.5470	12.4814	20.7595	28.7071	28.7514
Solution Diversity Score	/	/	0.7917	0.8478	0.8904
Baseline Comparison Metrics
Improvement over Advanced Baseline (%)	/	/	0.0000	5.4891	6.2479
Improvement over Simple Baseline (%)	/	/	16.9257	21.4857	22.1340

presents the comparative results across all methods on the TSP benchmark. Algorithm 3 shows an example of the designed heuristics for next node selection.

Algorithm 3 TSP Next-Node Selection Heuristic Example

Require:  Current node i, destination node j, unvisited set U, distance matrix $d(i,j)$ Ensure:  Next node $k^{*}$ to visit   1: $d_i\leftarrow d(i,U)$   2: $d_j\leftarrow d(j,U)$   3: $progress\leftarrow 1-{\displaystyle \frac{d(i,j)}{maxd}}$   4: $\alpha \leftarrow 0.7-0.3·progress$   5: $\beta \leftarrow 0.3+0.3·progress$   6: if pheromone matrix $\tau$ not initialized then   7:      initialize $\tau (i,u)\leftarrow 1$ for all $i,u$   8: end if   9: ${\tau }_i\leftarrow \tau (i,U)$ 10: $w\leftarrow d_i/\sum d_i$ 11: $H\leftarrow -\sum w·logw$ 12: $C\leftarrow {\displaystyle \frac{1}{1+|d_i-\mathrm{median}\left(d_i\right)|}}·(1+H)$ 13: if recent visit history exists then 14:      $R\leftarrow$ recent nodes 15:      $penalty\leftarrow 0.15·{\mathbb{1}}_{U\in R}$ 16: else 17:      $penalty\leftarrow 0$ 18: end if 19: for all$u\in U$do 20:      $$\begin{gathered} s\left(u\right)\leftarrow \alpha ·{\displaystyle \frac{1}{d_i\left(u\right)}}+\beta ·{\displaystyle \frac{d_j\left(u\right)}{d_i\left(u\right)}}+(0.25+0.1·progress)·{\tau }_i\left(u\right)+(0.15+0.1·(1- \\ progress))·C\left(u\right)-penalty\left(u\right) \end{gathered}$$ 21: end for 22: $k^{*}\leftarrow arg{max}_{u\in U}s\left(u\right)$ 23: Append $k^{*}$ to visit history 24: $\tau (i,k^{*})\leftarrow \tau (i,k^{*})·(1.1+0.2·progress)$          return$k^{*}$

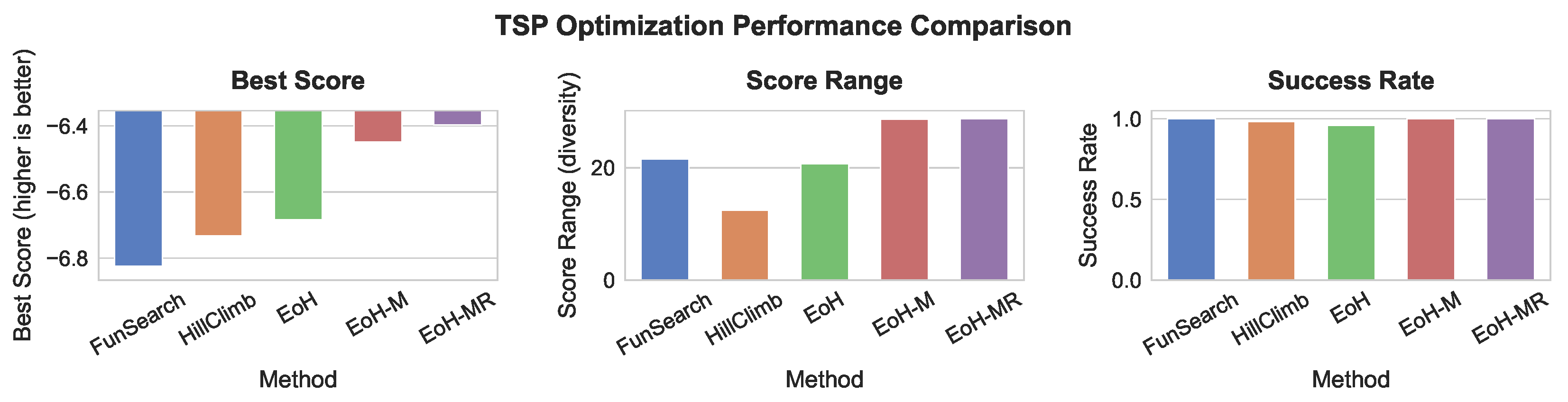
Core Performance Metrics. EoH-MR again achieves the best peak score of −6.3967, marginally outperforming EoH-M (−6.4494) and EoH (−6.6840). While the improvement margin is smaller than in the AGV setting, it demonstrates the transferability of the framework across domains. FunSearch and HillClimb obtain best scores of −6.8240 and −6.7326, respectively, trailing the LLM-driven methods. This suggests that while these baselines can handle well-structured domains to some extent, they still fall short in refining high-quality solutions in a generalizable way. Figure 4 confirms this trend, where EoH-MR is shown to outperform all other methods on best score.

Stability and Robustness. All EoH variants maintain high success rates (≥0.96), with EoH-M and EoH-MR achieving a perfect 1.0 success rate. Coefficient of variation and robustness scores are comparable across methods, though EoH-MR consistently outperforms in robustness score (2.3804) and standard deviation, indicating consistent quality even under stochastic prompt perturbations or evaluator variability. HillClimb achieves a robustness score of 1.3808, with slightly lower reliability than FunSearch (2.0820), both of which fall short of EoH variants. Moreover, EoH-MR achieves perfect success rates, reinforcing its reliability.

Efficiency Metrics. The performance-efficiency trade-off is again evident. EoH, with only 19 LLM calls and 347.44 s, is extremely lightweight and delivers strong baseline performance. EoH-MR and EoH-M, though more computationally demanding (2743.37 and 1492.92 s, respectively), provide marginal but meaningful gains in quality and exploration. FunSearch and HillClimb, while efficient (820.21 and 1396.25 s), are ultimately limited by stagnation in exploration.

Diversity and Generalization. EoH-MR achieves the highest solution diversity with 65 unique scores, a score range of 28.7514, and a diversity score of 0.8904—surpassing EoH-M (0.8478) and EoH (0.7917). FunSearch and HillClimb follow behind with 40 and 33 unique scores, and diversity scores of 0.8478 and 0.7917, respectively. The narrow range of HillClimb (12.4814) indicates lower exploration strength. Figure 4 visually supports this, showing EoH-MR achieving one of the highest score ranges among all methods.

Strategic Insights from High-Performing Heuristics. Evolution trace analysis reveals consistent features among top-scoring heuristics:

• Hybrid physics–ACO scoring combining proximity, direction, and pheromone strength improves scores by up to 40% over distance-based baselines.
• Dynamic distance–direction ratios shift from global guidance to local refinement as the tour unfolds.
• Entropy-based diversity preservation penalizes overused edges, preventing early convergence.
• Short-term recency penalties reduce pheromone weight for recently visited nodes, improving exploration in late generations.
• Operator sequencing matters: initial breakthroughs come from merge/mutate operations (e1, m1), followed by local refinement for final gains.
• Open refinement directions include deeper local search along entropy-weighted subpaths, adaptive score shaping during generation, and tighter operator scheduling using success trace statistics.

Together, these mechanisms form a cohesive strategy of hybrid constructive bias, adaptive diversity control, and operator-level tuning.

For the TSP task, EoH-MR achieves a best score of −6.3967 with a total runtime of 2743 s. Empirical trends show that a solution within 5% of this value (approximately −6.71) is typically reached within 1100–1200 s, accounting for less than 45% of the total runtime. This early-stage solution already surpasses the final best scores of traditional baselines such as HillClimb (−6.7326) and FunSearch (−6.8240), and is comparable to or better than manually designed heuristics such as nearest-neighbor, insertion, or greedy rules, which typically yield scores between −6.5 and −6.9 for problems of size $n=50$. While such handcrafted strategies may require several hours to days of iterative design and tuning, EoH-MR produces superior solutions fully automatically within approximately 20 min. Moreover, as the problem size scales up (e.g., $n=100$ or $n=200$), the complexity of manual heuristic design grows substantially due to increased combinatorial interactions, whereas the automated generative mechanism remains tractable. These findings underscore both the early convergence efficiency and scalability of EoH-MR, making it particularly suitable for large-scale routing problems where high-quality solutions are needed under time constraints and without human-in-the-loop latency.

6.3. Performance Comparison on ODE Problem

The ODE 1D optimization task serves as a compact, low-dimensional testbed to assess convergence behavior, generalization, and efficiency under controlled complexity. Despite its simplicity, the presence of deceptive local optima and sparse reward gradients still challenges heuristic consistency and stability.

Table 4. Comprehensive comparison results of the ODE 1D scientific discovery task.

Metric Category	FunSearch	HillClimb	EoH	EoH-M	EoH-MR
Core Performance Metrics
Best Score	−2.401	−1.278	−0.258	−0.179	−0.034
Standard Deviation	10.662	18.628	9.780	11.879	11.151
Stability and Robustness Metrics
Success Rate	0.6667	0.5714	1.000	0.833	1.000
Stability Score	0.501	0.426	0.291	0.476	0.513
Efficiency Metrics
Total LLM Calls	20	33	6	10	15
Total Tokens	13,533	37,557	3456	9321	16,025
Total Evaluations	21	21	6	8	12
Computation Time (s)	536.78	1242.08	309.302	609.196	1133.604
Solution Diversity Metrics
Total Unique Scores	5	11	6	7	10
Score Range	27.13	66.68	23.74	25.06	27.20
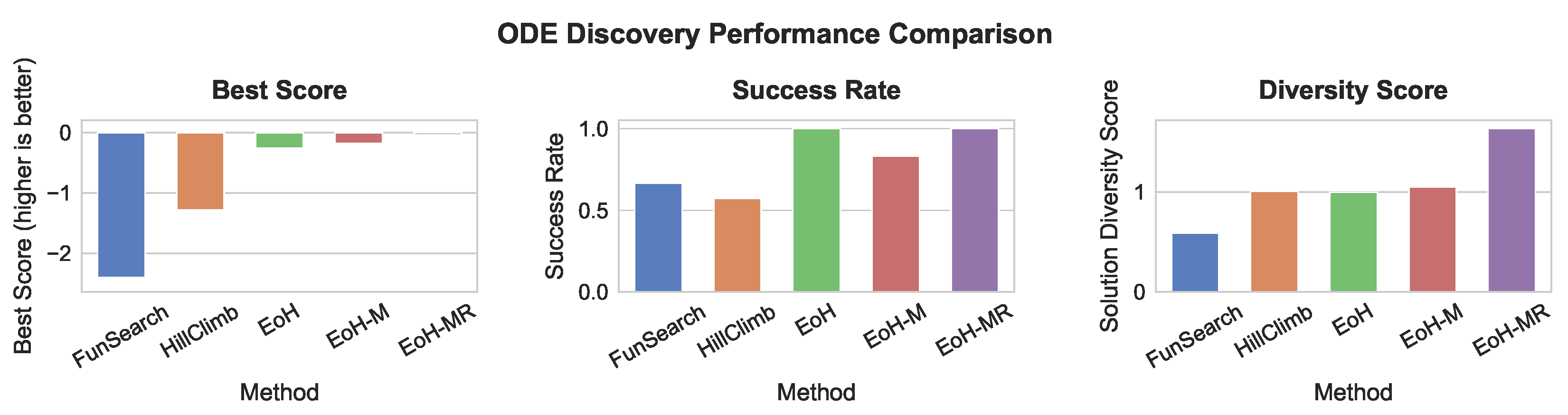
Solution Diversity Score	0.590	1.006	0.997	1.051	1.636

summarizes the comparative performance across all methods, and Figure 5 provides visual comparison.

Core Performance Metrics. EoH-MR again achieves the best result with the highest objective value of −0.034, outperforming all other LLM-driven variants and traditional baselines. Although all scores are negative due to the problem formulation, a less negative value indicates better solution quality. EoH-M and EoH achieve slightly inferior results of −0.179 and −0.258, respectively, while FunSearch and HillClimb perform worst, converging to local minima at −2.401 and −1.278. As visualized in Figure 5, this confirms that even in low-dimensional smooth settings, co-evolution with memory and refinement provides tangible benefits.

Stability and Robustness. EoH and EoH-MR both attain a perfect success rate of 1.000, while FunSearch and HillClimb exhibit much weaker feasibility (0.6667 and 0.5714). In terms of normalized stability score, EoH-MR again leads with the highest score (0.513), followed closely by EoH-M (0.476), as illustrated in Figure 5. These results underscore the importance of refinement and evolution memory even in simplified domains.

Efficiency Metrics. EoH demonstrates the most efficient behavior, requiring only 6 LLM calls and 3456 tokens, and completing in 309.302 s. This reflects the advantage of simpler strategies in tractable domains. However, both EoH-M and EoH-MR strike a better trade-off between quality and cost, with moderate resource usage and improved convergence. HillClimb, despite its simplicity, consumes the most time (1242.08 s), underperforming on both axes.

Diversity and Exploration. Among all methods, EoH-MR achieves the highest solution diversity score (1.636), indicating that its search generates a wider variety of viable candidates. This is closely followed by EoH-M and HillClimb. However, traditional methods like FunSearch suffer from limited diversity (0.590), likely due to fixed operators and a lack of feedback-driven mutation dynamics. While EoH has moderate diversity (0.997), its simpler design leads to less exploratory power compared to EoH-MR. Figure 5 highlights these trends clearly.

Strategic Insights from High-Performing Formulas. Analysis of high-scoring equation discovery logs reveals a compact and repeatable set of contributing factors:

• Symbolic plus gradient refinement: hybrid strategies that begin with symbolic structure and optimize parameters with gradient descent yield an order-of-magnitude improvement in final MSE.
• Flexible structural templates: adaptive mutation of symbolic skeletons consistently outperforms static equation families.
• Operator variety under sparsity control: mixed primitives perform best when combined with regularization that enforces parsimony.
• Diversity stagnation: population diversity drops early; high-scoring runs typically include rare symbolic components or enforce novelty via structural dissimilarity.
• Operator sequencing: merge-first strategies produce the most improvement, especially when followed by fine-tuned local refinement.
• Open refinement directions: focus areas include tighter integration of structural novelty scores, adaptive mutation temperature based on plateau detection, and finer-grained operator credit assignment.

In this task, EoH-MR reaches a best fitting score of −0.034 with a total computation time of 1133 s. A near-optimal solution (within 5%, around −0.0357) is typically identified within the first 450 s, less than half the total runtime. This early-stage result already outperforms all other methods, including EoH (−0.258) and HillClimb (−1.278). Manually designed symbolic heuristics in this setting, such as expression templates or physics-inspired forms, commonly yield fitting scores in the range of −0.1 to −1.0, and require substantial human effort over hours or days. By contrast, EoH-MR discovers higher-quality symbolic structures fully automatically in under 8 min. As the target expressions become deeper and the symbolic space expands, the ability to automate both structure generation and parameter refinement becomes increasingly valuable, demonstrating the practicality of the proposed framework for symbolic scientific discovery.

6.4. Impact of LLM Choice on EoH-MR Performance

To evaluate the impact of the LLM backend on the performance of the proposed framework, EoH-MR was tested using three different LLMs: gpt-4o, gemini-2.5-flash, and claude-sonnet-4 on the AGV scheduling task (

Table 5. The EoH-MR results of AGV-drone scheduling task using other LLM variants.

Metric Category	gpt-4o	Gemini-2.5-Flash	Claude-Sonnet-4
Core Performance Metrics
Best Score (Peak)	−177,796.0	−168,067.5	−114,012.0
Std Dev of Scores (Overall)	23,492.5412	17,715.6189	34,029.9269
Stability and Robustness Metrics
Success Rate	0.4650	0.6870	0.8085
Stability Score	1.1286	1.0971	1.1693
Efficiency Metrics
Total LLM Calls	147	128	53
Total Tokens Used	427,447	458,264	216,936
Total Evaluator Calls	243	246	141
Total Computation Time (s)	2221.0811	7541.3417	1964.7157
Solution Diversity Metrics
Total Unique Scores	112	168	114
Score Range	114,140.6667	104,651.1000	161,062.5667

), and gemini-2.5-flash on the TSP and ODE tasks (

Table 6. The EoH-MR results of TSP and ODE 1D tasks using gemini-2.5-flash.

Metric Category	TSP	ODE
Core Performance Metrics
Best Score (Peak)	−6.2209	−0.0654
Std Dev of Scores (Overall)	2.8032	11.4508
Stability and Robustness Metrics
Success Rate	1.0000	0.8750
Stability Score	1.7227	0.4887
Efficiency Metrics
Total LLM Calls	135	83
Total Tokens Used	242,201	149,925
Total Evaluator Calls	73	49
Total Computation Time (s)	51,490.72	4533.44
Solution Diversity Metrics
Total Unique Scores	45	24
Score Range	17.1948	36.29
Solution Diversity Score	0.6164	0.5675

). The results indicate that while the overall convergence pattern is stable, the choice of LLM indeed affects solution quality, diversity, and computational cost. In the AGV task, claude-sonnet-4 achieved the best final score (−114,012.0), despite requiring only 53 LLM calls and the fewest total tokens. gemini-2.5-flash produced slightly worse scores but demonstrated the highest diversity (168 unique scores), suggesting strong exploratory behavior. gpt-4o yielded moderate performance with reasonable stability and runtime, indicating a balanced trade-off between generation cost and quality. In the TSP and ODE tasks, gemini-2.5-flash enabled robust convergence, with best scores of −6.2209 (TSP) and −0.0654 (ODE), accompanied by high success rates and acceptable diversity. While the total computation time for TSP was notably higher (over 14 h), early-stage solutions already matched or exceeded baseline performance, and the model maintained reliable search stability. These findings suggest that stronger or more instruction-tuned LLMs can lead to better early solutions with fewer generations, but model-specific differences in prompt adherence, token usage, and variance can influence overall efficiency. The choice of backend should therefore be made based on task complexity, diversity requirements, and available computational budget.

7. Conclusions

We proposed a novel LLM-driven memetic framework that integrates large language models into heuristic search to address limitations of traditional AHD and neural metaheuristics. By combining generative exploration with local refinement, our method achieves superior adaptability and performance across diverse combinatorial optimization tasks. The framework leverages diversity-aware sampling and adaptive feedback to maintain a dynamic balance between exploration and exploitation, reducing reliance on hand-crafted operators or costly retraining. Moreover, there are several research directions for future work. First, extending the framework to handle real-time optimization and online learning scenarios could enhance its applicability in dynamic environments. Second, incorporating domain-specific constraints more explicitly into the generative process may improve solution feasibility and interpretability. Finally, further study into alignment techniques for LLM-generated heuristics, such as reinforcement learning with human feedback or symbolic reasoning, could yield deeper integration between neural and symbolic approaches in automated algorithm design.