Multi-Probe Measurement Method for Error Motion of Precision Rotary Stage Based on Reference Plate

Abstract

The error motion of the precision rotary stage, particularly the tilt error motion, significantly influences the accuracy of machining and measuring equipment. Nonetheless, reliable and effective in situ measurement methods for tilt error motion are still limited. Based on the analysis of the conventional three-probe measurement method, this paper proposes a multi-probe measurement method using an ultra-precision reference plate with high-resolution displacement sensors. This method employs principles and methods to avoid harmonic suppression issues through optimal probe designs, enabling simultaneous quantification of tilt and axial error motions via error separation. Error separation techniques can effectively decouple motion errors from artifact form error, making them widely applicable in precision measurement data processing. Experimental validation confirmed that the synchronous measurement error is not greater than 4.69%, consequently affirming the metrological efficacy and reliability of the method. This study provides an effective method for real-time error characterization of rotary stages.

1. Introduction

The precision rotary stage is a mechanical device engineered for highly accurate rotational positioning and motion control, enabling controlled angular displacements with minimal errors for tasks demanding ultra-fine adjustments. It typically consists of components such as a rotor and stator and is extensively utilized in the semiconductor industry and the domain of precise measurement. The error motion of its axis refers to the undesired deviation in the position or orientation of a moving component from its ideal path during rotary displacement. The error motion, especially the tilt error motion, can significantly affect the machining and measuring accuracy of products. Even minimal tilt error motion can, through amplification, diminish the motion accuracy of the rotary stage in both axial and radial directions. Therefore, in order to evaluate and improve the performance of the precision rotary stage, it is particularly important to measure the error motion [1,2].

Typically, the measurement method for the error motion of a rotary stage is similar to that of a machine tool spindle, achieved by affixing a standard artifact (such as a standard sphere or cylinder) to the spindle [3]. The sensor measurement data include both the spindle error motion and the form error of the standard artifact. By utilizing suitable error separation methods, these two components can be efficiently separated. The most commonly employed error separation techniques may be classified into three main categories based on various separation principles: the reversal method [4,5], the multi-step method [6,7], and the multi-probe method [8,9]. Each category may be further subdivided based on certain application contexts. Recent scholarly focus has increasingly centered on in situ measurement of machine tool spindles [10] and the application of measurement methodologies in ultra-precision machining. By integrating error motion measurement with error compensation techniques, researchers have developed feasible solutions for rapid calibration in ultra-precision machining processes [11,12]. Nevertheless, the majority of the aforementioned measuring techniques primarily concentrate on radial and axial error motion, while investigation into the measurement of tilt error motion is comparatively limited. The spindle error analyzer (SEA) developed by Lion Precision Company is extensively utilized to measure error motion in precision spindles. It employs capacitance sensors to assess the double-ball standard rod. It integrates with dedicated data acquisition and processing software to execute the measurement of the 5 degrees-of-freedom (DOF) error motion of the spindle [13]. Lee devised a spindle error motion measurement system and ascertained the radial and tilt error motions of the spindle by evaluating data gathered from various cross-sections [14]. In another study, Salsbury performed trials employing the Estler reversal method to separate tilt and face error motions from the form error of the typical artifact [15]. Additionally, Kim employed the reverse method to quantify the radial, axial, and tilt error motions of a rotary stage and developed a specialized sensor fixture to improve the efficiency and convenience of the measuring process [1]. The aforementioned measurements of tilt error motion are predominantly derived from the reverse method. Throughout the measurement procedure, both the standard artifact and the sensor must be precisely rotated by 180°. This process may introduce errors due to reverse installation. Moreover, due to the necessity of the reversal process, in situ measurement is not feasible [16]. These disadvantages have constrained the widespread implementation of the reverse method in measuring tilt error motion.

In recent years, laser interferometry-based measurement systems have seen increasing application in spindle error measurement [17,18,19,20,21,22]. These systems provide the substantial benefit of concurrently assessing multi-degree-of-freedom spindle error motions in a single measurement. Nonetheless, they exhibit certain practical constraints: the optical path is exceedingly vulnerable to environmental disturbances, and the systems have intricate installation and calibration processes, eventually leading to diminished measurement efficiency.

In summary, the development of a reliable and effective in situ measurement method for tilt error motion is highly significant. Building upon the analysis of the conventional three-probe error separation principle, this study introduces an innovative multi-probe measurement method for the error motion of a precision rotary stage utilizing a reference plate. Experimental validation accurately quantified both tilt and axial error motions. The synchronous measurement error does not exceed 4.69%, indicating the reliability and practical applicability of the method for industrial precision measurement applications. The proposed multi-probe measurement method significantly enhances the feasibility of in situ error motion measurement while establishing a novel research paradigm for precision motion metrology. Its capability to simultaneously deliver laboratory-grade accuracy and high-repeatability performance markedly extends the evaluation limits for precision rotary stage technologies.

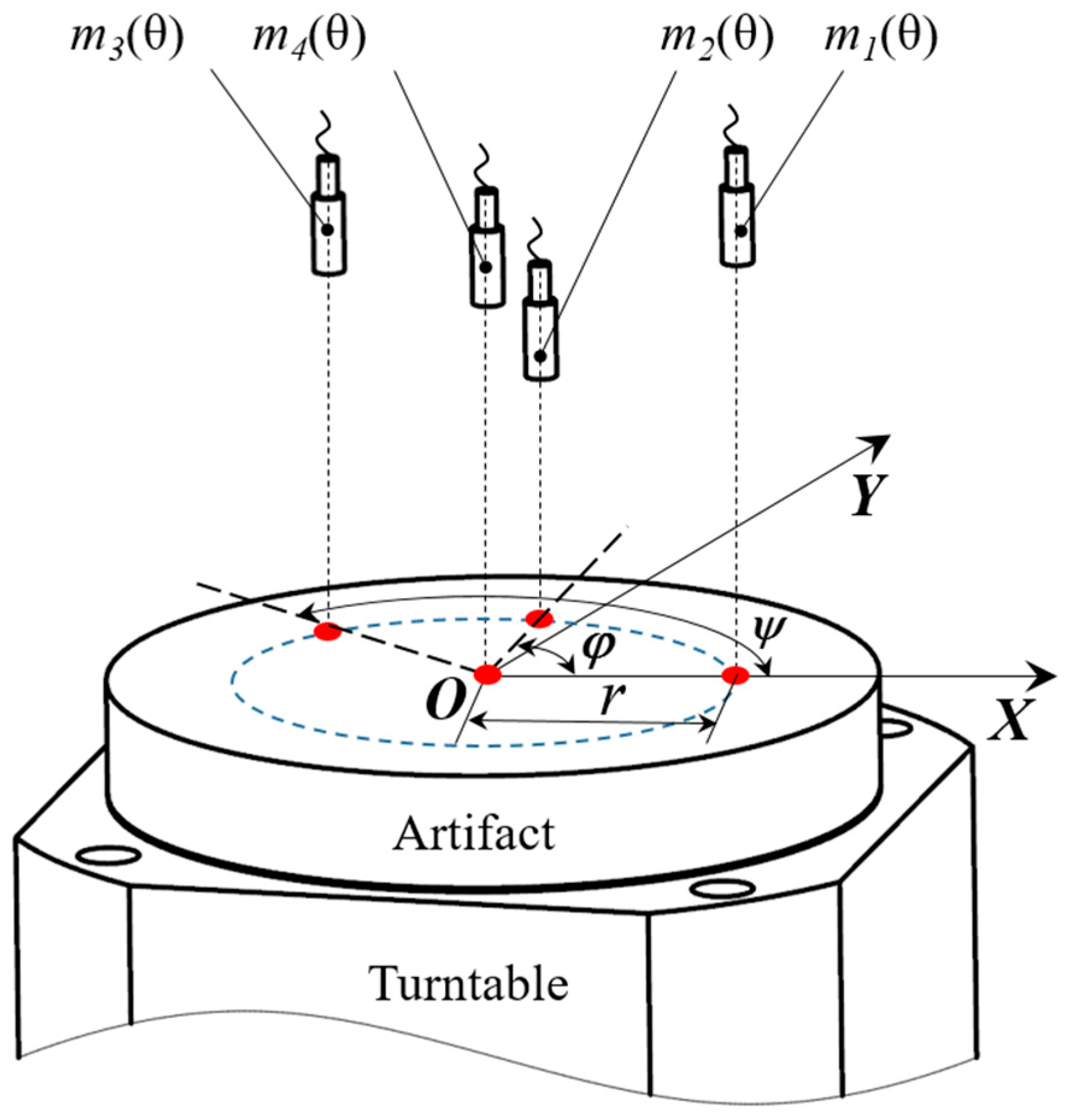
2. Multi-Probe Measurement Method for Error Motion Based on Reference Plate

2.1. Analysis of Conventional Three-Probe Measurement Method

This section presents a concise analysis of the conventional three-probe measurement method and elucidates the correlation between the tilt error motions of the rotary stage corresponding to different probe installation angles. These findings lay the theoretical foundation for developing a multi-probe measurement method based on a reference plate.

The conventional three-probe measurement method is primarily employed for assessing the radial error motion of the rotational axis. As illustrated in Figure 1, the measurement configuration comprises a spherical or cylindrical reference artifact concentrically affixed to the rotary stage alongside three displacement sensors arranged at varying installation angles $\phi$ and $\psi$ within the identical measurement plane. The measurements recorded by the three displacement sensors are a summation of the artifact’s roundness $R(\theta )$, including a phase shift due to sensor location, and the $D_x(\theta )$ and $D_y(\theta )$ components of the rotary stage error motion [3,23]. Here, $\theta$ denotes the rotation angle of the rotary stage and serves as the independent variable for the function of error motion and form error. The roundness error of the artifact can be separated from sensor measurements through error separation, enabling the quantification of the rotary stage radial error motion.

When the standard artifact exhibits an ideal spherical or cylindrical geometry (i.e., the roundness error $R(\theta )=0$), the sensor measurements exclusively reflect the superposition of the rotary stage radial error motions along the X and Y axes, denoted as $D_x(\theta )$ and $D_y(\theta )$, respectively, as mathematically expressed in Equations (1)–(3). The subscripts x and y denote the directions of the X and Y axes, respectively.

$$m_A(\theta )=D_x(\theta )$$

(1)

$$m_B(\theta )=D_x(\theta )\cos \phi +D_y(\theta )\sin \phi$$

(2)

$$m_C(\theta )=D_x(\theta )\cos \psi +D_y(\theta )\sin \psi$$

(3)

Actually, the measured radial error motion of the rotary stage in any measurement plane arises from the superposition of two distinct components: translational motion and axis tilting motion. Let $T(\theta )$ signify the tilt error motion of the rotary stage axis and H represent the axial distance between the sensor measurement plane and the center of tilt motion. The radial error component generated by tilt is then expressed as the product $T(\theta )\times H$. Consequently, the comprehensive radial error motion measurement $m_B(\theta )$ at any given angular position, along with the X and Y directional radial error motion, can be described as follows [24]:

$$m_B(\theta )=d(\theta )+T(\theta )H$$

(4)

$$D_x(\theta )=d_x(\theta )+T_x(\theta )H$$

(5)

$$D_y(\theta )=d_y(\theta )+T_y(\theta )H$$

(6)

where $d(\theta )$ denotes the radial error motion component arising from the translational motion of the rotary stage axis. Substituting Equations (4)–(6) into Equation (2) and integrating Equation (7) yields Equation (8).

$$d(\theta )=d_x(\theta )\cos \phi +d_y(\theta )\sin \phi$$

(7)

$$T(\theta )=T_x(\theta )\cos \phi +T_y(\theta )\sin \phi$$

(8)

Equation (8) demonstrates that at arbitrary probe installation angle $\phi$ or $\psi$, the tilt error motion $T(\theta )$ of the rotary stage axis can be represented as a function of the orthogonal tilt error components $T_x(\theta )$ and $T_y(\theta )$ along the rotary stage X and Y axes. This analytical paradigm is also applicable to Equation (3), yielding identical functional relationships.

2.2. Multi-Probe Measurement Method Based on Reference Plate

Similar to radial error motion, the measured face error motion of a rotary stage arises from translational and tilting motions of its axis. Specifically, the face error motion component $F(r,\theta )$ induced by the tilting motion at radius r is expressed as [15].

$$F(r,\theta )=T(\theta )r$$

(9)

Multiplying both sides of Equation (8) by radius r and substituting the result into Equation (9) yields the following expression:

$$F(r,\theta )=F_x(r,\theta )\cos \phi +F_y(r,\theta )\sin \phi .$$

(10)

Equation (10) demonstrates that the face error motion $F(r,\theta )$, associated with any probe installation angle ($\phi$ or $\psi$), can be represented as a function of the face error motions $F_x(r,\theta )$ and $F_y(r,\theta )$ along the X and Y axes at a certain radius r. The subscripts x and y denote the X and Y axes, respectively.

Building upon these findings, the tilt error motion of the rotary stage axis can be quantitatively assessed through appropriate error separation techniques, provided that the face error motion of the rotary stage is accurately measured. Figure 2 illustrates the principle of our proposed multi-probe measurement system employing a reference standard artifact. The measurement setup consists of (1) a precision reference plate affixed to the rotary stage being tested and (2) an array of four displacement sensors positioned above the reference plate. The measurement configuration comprises three probes arranged along the circumference of radius r: one aligned with the X axis of the measurement plane and the other two positioned at angular offsets $\phi$ and $\psi$ relative to the X axis. The fourth probe is precisely aligned with the rotational axis of the rotary stage, serving as an essential reference for detecting axial motion.

Using an analysis similar to that presented in [4,15], we define the following:

$Z(\theta )$:	axial error motion of the axis of rotation, coaxial to the axis;
$Z_{fs}(\theta )$:	fundamental synchronous axial error motion of the axis of rotation;
$Z_{rs}(\theta )$:	residual synchronous axial error motion of the axis of rotation;
$Z_a(\theta )$:	asynchronous axial error motion of the axis of rotation;
$P(r,\theta )$:	form error of the reference plate as a function of the radial (r) and angular (θ) positions;
$P_f(r,\theta )$:	fundamental form error of the reference plate;
$P_r(r,\theta )$:	residual form error of the reference plate.

Their interrelationship is as follows:

$$Z(\theta )=Z_{fs}(\theta )+Z_{rs}(\theta )+Z_a(\theta )$$

(11)

$$P(r,\theta )=P_f(r,\theta )+P_r(r,\theta ).$$

(12)

For the sake of notation, we assume that r is an arbitrarily chosen value. Accordingly, $P(r,\theta )$, $P_f(r,\theta )$, and $P_r(r,\theta )$ are abbreviated as $P(\theta )$, $P_f(\theta )$, and $P_r(\theta )$, respectively, while $F(r,\theta )$, $F_x(r,\theta )$, and $F_y(r,\theta )$ are shortened as $F(\theta )$, $F_x(\theta )$, and $F_y(\theta )$, respectively.

The experimental data acquired by the four displacement sensors can be represented by Equations (13)–(16):

$$m_1(\theta )=P(\theta )+Z(\theta )+F_x(\theta )+V_1(\theta )$$

(13)

$$m_2(\theta )=P(\theta -\phi )+Z(\theta )+F_x(\theta )\cos \phi +F_y(\theta )\sin \phi +V_2(\theta )$$

(14)

$$m_3(\theta )=P(\theta -\psi )+Z(\theta )+F_x(\theta )\cos \psi +F_y(\theta )\sin \psi +V_3(\theta )$$

(15)

$$m_4(\theta )=Z(\theta )$$

(16)

where $V_1(\theta )$ to $V_3(\theta )$ represent the deficiency of squareness in mounting the reference plate relative to the axis of rotation. We remove the first-order harmonic components from the measurement data to rectify inaccuracies generated by misalignment. Subsequently, we substitute Equations (11) and (12) and subtract Equation (16) from Equations (13)–(15), resulting in the following:

$${m^{\prime }}_1(\theta )=P_r(\theta )+F_x(\theta )$$

(17)

$${m^{\prime }}_2(\theta )=P_r(\theta -\phi )+F_x(\theta )\cos \phi +F_y(\theta )\sin \phi$$

(18)

$${m^{\prime }}_3(\theta )=P_r(\theta -\psi )+F_x(\theta )\cos \psi +F_y(\theta )\sin \psi .$$

(19)

To separate $P_r(\theta )$ from $F_x(\theta )$ and $F_y(\theta )$, a weighted function $M(\theta )$ for the three measurements is constructed as follows:

$$\begin{array}{ll}M(\theta )& ={m^{\prime }}_1(\theta )+a{m^{\prime }}_2(\theta )+b{m^{\prime }}_3(\theta )\\ & =P_r(\theta )+a{P}_r(\theta -\phi )+b{P}_r(\theta -\psi )\end{array}.$$

(20)

Thus, the function $M(\theta )$ can be expressed as a weighted linear combination of the reference plate’s residual form error $P_r(\theta )$, including a phase shift due to probe location. The weighted coefficients a and b are derived by solving Equations (17)–(20), yielding the following:

$$\left\{\begin{array}{l}a={\displaystyle \frac{-\sin \psi }{\sin \left(\psi -\phi \right)}}\\ b={\displaystyle \frac{\sin \phi }{\sin \left(\psi -\phi \right)}}\end{array}\right..$$

(21)

By using Fourier transformation, $P_r(\theta )$ and $M(\theta )$ can be decomposed as follows:

$$P_r(\theta )={\displaystyle \sum _{k=2}^{\infty }{A}_k\cos k\theta +B_k\sin k\theta }$$

(22)

$$M(\theta )={\displaystyle \sum _{k=2}^{\infty }{F}_k\cos k\theta +G_k\sin k\theta }.$$

(23)

The substitution of Equations (22) and (23) into Equation (20), followed by simplification, leads to the following:

$${\displaystyle \sum _{k=1}^{\infty }{F}_k\cos k\theta +G_k\sin k\theta }={\displaystyle \sum _{k=1}^{\infty }\left(A_k{\alpha }_k-B_k{\beta }_k\right)\cos k\theta +\left(A_k{\beta }_k+B_k{\alpha }_k\right)\sin k\theta }$$

(24)

where

$$\left\{\begin{array}{l}{\alpha }_k=1+a\cos k\phi +b\cos k\psi \\ {\beta }_k=a\sin k\phi +b\sin k\psi \end{array}\right..$$

(25)

Equation (24) can be reformulated in the following matrix format:

$$\left[\begin{array}{cc}{\alpha }_k& -{\beta }_k\\ {\beta }_k& {\alpha }_k\end{array}\right]\left[\begin{array}{c}{A}_k\\ B_k\end{array}\right]=\left[\begin{array}{c}{F}_k\\ G_k\end{array}\right].$$

(26)

According to Equations (23) and (25), once the probe installation angles $\phi$ and $\psi$ are determined, the respective $F_k$, $G_k$, ${\alpha }_k$, and ${\beta }_k$ may be calculated for each integer k. The matrix Equation (26) establishes the correlation between the unknown variables ($A_k$, $B_k$) and the known quantities ($F_k$, $G_k$). Solving this matrix equation allows us to determine $A_k$ and $B_k$, which subsequently enables the calculation of $P_r(\theta )$ through Equation (22). Then we may obtain $F_x(\theta )$ and $F_y(\theta )$ using Equations (17) and (18), ultimately yielding the final solutions $T_x(\theta )$ and $T_y(\theta )$.

The measured signals $Z(\theta )$, $T_x(\theta )$, and $T_y(\theta )$ encompass both synchronous and asynchronous error components. The synchronous error components, which occur at integer multiples of the rotational frequency, can be derived by averaging multiple revolutions of the probe signals:

$$\left\{\begin{array}{l}{Z}_s(\theta )={\displaystyle \frac{1}{l}}{\displaystyle \sum _{i=0}^{l-1}{Z}_i(\theta +2\pi i)}\\ T_{xs}(\theta )={\displaystyle \frac{1}{l}}{\displaystyle \sum _{i=0}^{l-1}{T}_{xi}(\theta +2\pi i)}\\ T_{ys}(\theta )={\displaystyle \frac{1}{l}}{\displaystyle \sum _{i=0}^{l-1}{T}_{yi}(\theta +2\pi i)}\end{array}\right.$$

(27)

where l represents the number of consecutive revolutions recorded. The asynchronous error components occur at non-integer multiples of the rotational frequency. The asynchronous error in a given single revolution can be determined by subtracting the synchronous error components from the measurement results:

$$\left\{\begin{array}{l}{Z}_a(\theta )=Z_i(\theta )-Z_s(\theta )\\ T_{xa}(\theta )={T_x}_i(\theta )-T_{xs}(\theta )\\ T_{ya}(\theta )={T_y}_i(\theta )-T_{ys}(\theta )\end{array}\right..$$

(28)

Reference [16] indicates that when the parameter k equals $n(2\pi /\Delta )\pm 1$, both ${\alpha }_k$ and ${\beta }_k$ will be zero. This condition renders the coefficient matrix in Equation (26) singular, leading to an unsolvable problem: a phenomenon known as harmonic suppression. Here, $\Delta$ represents the greatest common divisor (GCD) of $\phi$, $\psi$, and $2\pi$. Harmonic suppression engenders considerable measurement inaccuracies. To avoid or reduce these errors, meticulous selection of the probe placement angle is crucial so as to either minimize $\Delta$ or eliminate it entirely. Figure 3 illustrates the behavior of determinant $W_k$ for the coefficient matrix in Equation (26) when $\phi ={40}^{\circ }$ and $\psi ={160}^{\circ }$.

Since $\Delta ={40}^{\circ }$ at this point, Figure 3 distinctly demonstrates the following two key observations: Firstly, when k takes values of $9n\pm 1$ (where n is an integer), the determinant $W_k$ consistently equals zero, confirming the prior mathematical conclusions. Secondly, the figure reveals that in instances when $k=9n$, ${\beta }_k$ becomes zero while ${\alpha }_k$ remains non-zero, hence $W_k$ retaining a non-zero value in these cases.

3. Experimental Setup

The experimental setup for the reference plate-based multi-probe measurement method is illustrated in Figure 4. The configuration comprises several essential components: the test rotary stage (an externally pressurized air-static bearing rotary stage developed by Chang Guang Satellite Technology Co., Ltd., Changchun, China, R200), leveling fixture, precision reference plate, capacitive displacement sensors, and data acquisition apparatus. The reference plate is affixed to the rotary stage surface, with its alignment meticulously adjusted using the leveling fixture. This alignment process ensures that the end face of the reference plate remains as perpendicular as possible to the rotational axis of the rotary stage, thus effectively minimizing first-order harmonic error in the acquired measurement data.

The reference plate is an aluminum alloy component, 100 mm in diameter, machined using single-point diamond turning. The surface profile measurement findings were acquired using an interferometer (ZYGO 4 inch, 6 nm PV precision, Middlefield, CT, USA) over an annular region (75 mm diameter, 10 mm width) of the plate. The processed surface exhibits a peak-to-valley (PV) form accuracy of 58.2 nm. The high precision of the reference plate renders it especially appropriate for error separation in rotary stage error motion measurements.

Four high-precision capacitance sensors are affixed above the reference plate, utilizing a universal fixture. The fixture has accurately machined mounting holes arranged in a specific geometric configuration: three sensor probes are positioned along a circumference with a 75 mm diameter, while the fourth probe is located at the exact center of this circle. By precisely adjusting the fixture, the fourth probe is aligned to be coaxial with the rotational axis of the rotary stage. To avoid or reduce measurement inaccuracies induced by harmonic suppression, the probe mounting holes are deliberately located at prime-numbered angular intervals around the circumference. This configuration ensures that when either angle $\phi$ or angle $\psi$ is a prime number, the greatest common divisor (GCD) of $\phi$, $\psi$, and $2\pi$ equals 1 ($\Delta =1$). Consequently, the determinant $W_k$ is zero exclusively when k fulfills the condition $k=360n\pm 1$. In practical testing circumstances, the value of k typically does not exceed 100. Therefore, this prime-based angular distribution strategy successfully eliminates harmonic suppression effects. Figure 5 demonstrates that the non-zero behavior of $W_k$ at $\phi ={37}^{\circ }$ and $\psi ={313}^{\circ }$ (two meticulously chosen prime angles) effectively validates the method’s capability to avoid harmonic suppression.

The experiment was performed in an environmentally controlled laboratory (±0.1 °C, VC-D vibration grade). The measurement system employed four Micro-Epsilon CSH02 high-precision capacitive displacement sensors featuring a ±100 μm measurement range with an exceptional 0.4 nm resolution. The sensors were connected to a dedicated Micro-Epsilon NCDT6530 data acquisition device functioning at a sampling frequency of 62.5 Hz. The precision rotary stage was driven at a constant speed of 10 rpm, achieving an angular sampling density of approximately one data point per degree. Data acquisition began following rotational stabilization, with the system performing continuous multi-revolution data capture cycles to provide an adequate dataset for subsequent signal processing and analysis.

4. Experimental Results and Discussion

The error motion experiment was conducted according to the configurations outlined in Section 3 and the error separation algorithm established in Section 2, based on the analytical results presented in Figure 5 at the angular locations $\phi ={37}^{\circ }$ and $\psi ={313}^{\circ }$. Figure 6 illustrates the measured error motion curves of the rotary stage, with the first column displaying the comprehensive error motion along with the synchronous component (shown by the red curve) and the second column depicting the asynchronous error components. The first two rows represent the tilt error motions along the X and Y axes ($T_x(\theta )$ and $T_y(\theta )$, respectively), while the third row exhibits the axial error motion $Z(\theta )$. Notably, the synchronous error motion features distinct third-order harmonic characteristics, as indicated by three periodic peaks per entire revolution.

The error motion measurement curves acquired at $\phi ={240}^{\circ }$ and $\psi ={313}^{\circ }$ are presented in Figure 7, and the synchronous error motion demonstrates identical third-order harmonic characteristics to those observed in Figure 6. The extensive experimental data compiled in

Table 1. Results of measured error motion.

Components	Tx(θ).Sync /μrad	Tx(θ).Async /μrad	Ty(θ).Sync /μrad	Ty(θ).Async /μrad	Z(θ).Sync /nm	Z(θ).Async /nm
[0°,37°,313°]	4.04	0.65	3.57	0.8	67.1	7.2
[0°,90°,313°]	3.74	0.44	3.62	0.52	68.1	5.1
[0°,120°,163°]	3.89	0.48	3.92	0.47	70.3	6.3
[0°,120°,211°]	4.02	0.49	3.62	0.68	70.1	4.9
[0°,120°,313°]	3.93	0.63	3.80	0.77	71.4	8.4
[0°,163°,313°]	3.98	0.72	3.89	0.63	68.5	7.8
[0°,240°,313°]	3.74	0.67	3.79	0.72	70.3	6.7
Average	3.91	0.58	3.74	0.66	69.4	6.6
Max absolute error to average	0.17	0.14	0.18	0.19	2.3	1.8
Max relative error to average (%)	4.24	24.51	4.69	28.32	3.31	26.72

includes (1) comparative results from these two measurement sets, (2) supplementary measurements obtained at varying probe installation angles, and (3) the ensemble average of all measurements. Statistical analysis reveals significant uniformity across all datasets, with the maximum relative deviation of synchronous errors not exceeding 4.69% in relation to the mean value. The repeatability of the synchronous error during the error separation procedure reflects the stability of the measuring method and necessitates careful consideration [3]. The experimental evidence conclusively demonstrates that the reference plate-based multi-probe methodology attains significant measurement stability, enabling precise measuring of both tilt error motions and axial error motion in precision rotary stages.

Theoretically, the measurement results of rotary stage error motion should remain consistent regardless of variations in probe installation angles. The observed discrepancies in Table 1 primarily stem from the following factors: asynchronous rotating axis inaccuracy, probe mounting precision, and variances in sensor performance.

Figure 8b illustrates the curve of the residual form error $P_r(\theta )$ of the reference plate derived from the error separation method detailed in Section 2. The measured curve exhibits a peak-to-valley (PV) value of 54.9 nm, indicating a 5.67% relative deviation from the direct measurements acquired with the interferometer shown in Figure 8a. Notably, both profiles display remarkably similar variation tendencies throughout the circumference, characterized by an alternating pattern of two raised and two depressed regions. The discrepancy in the observed PV value arises due to the exclusion of the first-order form error component (fundamental form error $P_f(\theta )$) from the multi-probe measurement. These findings collectively confirm that the multi-probe error separation method successfully separates the reference plate form error from the rotary stage error motion, hence further demonstrating the accuracy of the multi-probe measurement method.

Table 2. Comparison between multi-probe method and existing approaches.

Items	Reversal	SEA	Interferometry	Multi-Probe
Setup simplicity	Yes	No	No	Yes
Measurement accuracy	Yes	Yes	Yes	Yes
Measurement repeatability	Yes	Yes	Yes	Yes
Low cost	No	No	No	Yes

systematically compares several measurement methods across critical dimensions such as setup complexity and measurement accuracy, demonstrating that the proposed method surpasses alternatives in terms of setup simplicity and cost effectiveness.

While the multi-probe method provides a reliable metrological performance, its implementation requires strict axial alignment of the fourth sensor with the rotary stage to ensure that both the axial error motion measurement and the subsequent tilt error motion calculation are accurate. Furthermore, the methodology’s inability to account for radial error motions limits its applicability in scenarios requiring comprehensive error analysis.

5. Conclusions

This paper investigates a novel measurement method for the error motion of the precision rotary stage. Firstly, the conventional three-probe measurement method is examined, establishing that the face error motion, corresponding to the arbitrary probe installation angle, can be expressed as a function of the face error motions along the X and Y axes at the radius r of the rotary stage. Subsequently, a multi-probe measurement method based on a standard reference plate is proposed, along with principles and methodologies to address harmonic suppression issues during error separation. Finally, an experimental setup is established to verify the proposed error motion measurement method. The results indicate that the multi-probe error separation method successfully separates the form error of the reference plate from the rotary stage error motion, achieving synchronous measurement accuracy within 4.69%. Consequently, this method can precisely measure the tilt and axial error motion of the rotary stage. The main conclusions of this study can be summarized as follows:

1.

Face error motion can be mathematically modeled as a function of its X-axis and Y-axis components.

2.

Probe distribution with prime-numbered angular intervals demonstrates optimal efficacy in eliminating harmonic suppression issues.

3.

The reference plate-based multi-probe measurement method enables in situ measurement of tilt and axial error motions, though its inability to simultaneously measure radial error motions presents a limitation.

The multi-probe measurement method for error motion based on a reference plate demonstrates significant applicability for in situ measurement of precision rotary stages in both machining and metrology equipment. This method introduces a novel paradigm for measuring the error motion of precision rotary stages, effectively advancing precision motion metrology through the following three primary contributions: (1) facilitating real-time decoupling of intrinsic error components, (2) improving metrological traceability, and (3) overcoming the harmonic suppression limitations present in conventional methods.