Hypergraph-Driven High-Order Knowledge Tracing with a Dual-Gated Dynamic Mechanism

Abstract

Knowledge tracing (KT), a core educational data mining task, models students’ evolving knowledge states to predict future learning. In online education systems, the exercises are numerous, but they are typically associated with only a few concepts. However, existing models rarely integrate exercise information with high-order exercise–concept correlations, focusing solely on optimizing models’ final predictive performance. To address these limitations, we propose the Hypergraph-Driven High-Order Knowledge Tracing with a Dual-Gated Dynamic Mechanism (HGKT), a novel framework that (1) captures correlations between exercises and concepts through a two-layer hypergraph convolution; (2) integrates hypergraph-driven exercise embedding and temporal features (answer time and interval time) to characterize learning behavioral dynamics; and (3) designs a learning layer and a forgetting layer, with the dual-gating mechanism dynamically balancing their impacts on the knowledge state. Experiments on three public datasets demonstrate that the proposed HGKT model achieves superior predictive performance compared to all baselines. On the longest interaction sequence dataset, ASSISChall, HGKT improves prediction AUC by least 1.8%. On the biggest interaction records dataset, EdNet-KT1, it maintains a state-of-the-art AUC of 0.78372. Visualization analyses confirm its interpretability in tracing knowledge state evolution. These results validate HGKT’s effectiveness in modeling high-order exercise–concept correlations while ensuring practical adaptability in real-world online education platforms.

1. Introduction

With the rapid developments in artificial intelligence technology and online education systems, knowledge tracing (KT) [1], as the core technology of educational artificial intelligence, has attracted increasing attention from researchers. Through the assessment of students’ knowledge states derived from their learning interactions, KT can improve learning efficiency and facilitate a better understanding of the learning process for students. Nevertheless, most existing KT methods [2,3,4] assess the students knowledge state without considering the high-order relations between the exercises and knowledge concepts. In actuality, the relations between the exercises and concepts have a profound impact on learning progression and significantly influence future performance predictions.

Research on knowledge tracing (KT) began in the 1990s, with Corbett and Anderson’s [5] foundational work, which is widely regarded as the first major contribution to the field and the origin of the KT concept. Advances in deep learning subsequently spurred the rapid development of numerous KT models. For instance, deep knowledge tracing [2] pioneered the use of deep learning for KT, while memory-augmented KT models were introduced by Zhang et al. (2017) [3]. More innovations include attention enhanced KT frameworks proposed in several studies [6,7,8] as well as graph neural network (GNN)-based approaches [9,10,11] that model relational structures, such as knowledge component (KC) similarities, dependencies, and question-KC mappings, to enhance performance. Beyond diverse neural architectures, KT research progresses using two main types of models. The first models leverage educational data features, including exercise content [12], difficulty levels [13], relationships between exercises and concepts [14], and cold start [15]. The second models incorporate psychological studies on student learning and forgetting behavior [16,17,18,19], considering additional factors that influence knowledge state tracing, such as the time interval between a student’s interactions and the number of times that the knowledge concepts have been practiced. The rise of large language models (LLMs) has spurred the emergence of knowledge tracing frameworks [20,21] that integrate LLM capabilities with sequential interaction modeling. This integration addresses the intricate exercise–knowledge component relationships that are prevalent in real-world educational scenarios. While GNN-based methods like GKT [10] capture skill dependencies through pairwise graphs, they fail to model high-order exercise–concept correlations. In contrast, HGKT’s hypergraph convolution explicitly resolves multi-hop correlations, overcoming limitations in graph-based KT. Similarly, LLM-enhanced frameworks (e.g., LLM-KT [21]) treat exercise IDs as mere numerical tokens, failing to interpret sequential interactions that reflect knowledge states. This fragmented tokenization obscures behavioral semantics. HGKT achieves higher interpretability in knowledge state evolution.

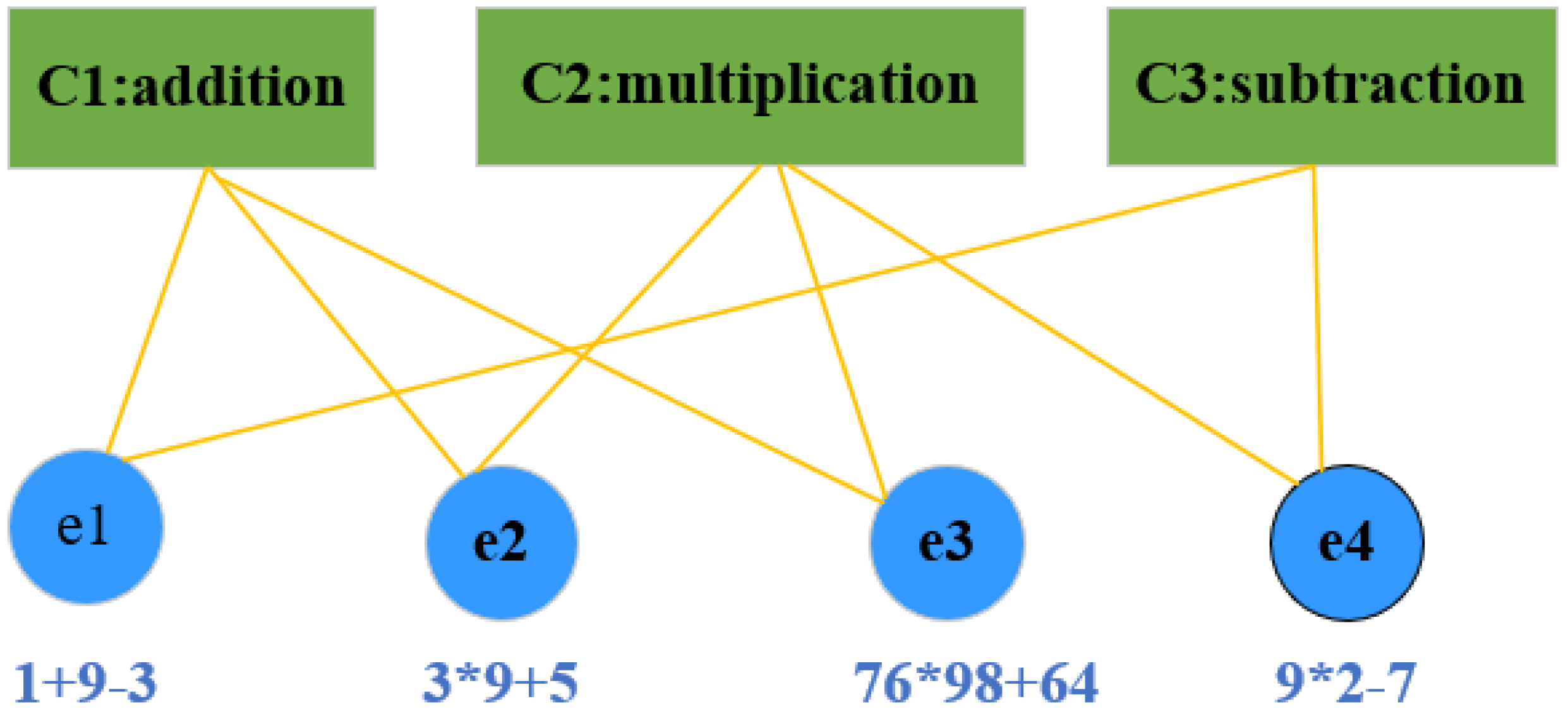
Existing KT approaches [3,4] typically construct predictive models based on knowledge concepts rather than target questions. In KT, it is common to encounter scenarios with several concepts and numerous exercises, where one concept may be associated with many exercises, and a single exercise may correspond to multiple concepts. However, these knowledge tracing (KT) approaches treat knowledge concepts as independent entities, neglecting their inherent hierarchical and composite relationships, which can result in degraded performance. For example, in Figure 1, there are four exercises that are associated with more than one concept. Despite the fact that exercises e2 and e3 assess identical concepts, different difficulty levels may yield different correct response probabilities. Therefore, it is important to research the high-order correlations between the exercises and concepts.

In this paper, we study how to capture latent high-order exercise–concept correlations. Motivated by the hypergraph neural network (HGNN)’s proven superiority in modeling many-to-many complex relationships within data mining, we employ a two-layer hypergraph convolutional network to capture the latent correlations between exercises and concepts. This work makes the following contributions.

(1)

This work proposes a novel Hypergraph-Driven High-Order Knowledge Tracing with a Dual-Gated Dynamic Mechanism (HGKT) model to capture correlations between exercises and concepts through a two-layer hypergraph convolution. The proposed HGKT provides superior adaptability and performance for online education learning assessment.

(2)

This work designs a learning layer and a forgetting layer, where knowledge acquisition follows learning gain dynamics while memory decay adheres to Ebbinghaus forgetting principles [22]. This model effectively captures the dynamics of human learning.

(3)

The proposed HGKT model is evaluated on three public education datasets, including ASSIST2012, ASSISTChall and EdNet-KT1. HGKT achieves superior predictive performance across different datasets.

This paper is structured into the following sections. Section 2 reviews prior research on knowledge tracing models and recent hypergraph neural network (HGNN) applications in educational data mining. Section 3 formally defines and mathematically formulates the knowledge tracing problem. The architecture of the proposed HGKT model is detailed in Section 4, with specific elaboration on the implementation and functionality of its layers. Section 5 elaborates the experimental framework, encompassing dataset specifications, evaluation metrics, benchmark configurations, and comparative results analysis. Section 6 synthesizes the core contributions of this work, discusses theoretical and practical implications, and suggests actionable directions for future knowledge tracing research.

2. Related Work

2.1. Knowledge Tracing

Knowledge tracing (KT) approaches can be categorized into two paradigms: (1) Traditional methods like Bayesian knowledge tracing (BKT) and factor analysis models [23]. BKT [5] is a classic hidden Markov model which represents knowledge states with binary variables. While item response theory (IRT) [22,24], a foundational factor analysis model, analyzes performance through learner ability and item difficulty. (2) Deep learning-based approaches: deep knowledge tracing (DKT) [2] and DKT+ [25] pioneers the use of RNN/LSTM for temporal dependency modeling. Dynamic key–value memory networks (DKVMN) [3] incorporate memory-augmented neural networks into knowledge tracing, utilizing a static key matrix to store latent concepts and a dynamic value matrix to track and update mastery levels. Self-attentive knowledge tracing (SAKT) [26] introduces attention mechanisms to KT. Context-aware AKT [6] integrates cognitive theory with contextualized representations, GKT [10] builds a skill relation graph and learns their relation explicitly. CKT [27] designs hierarchical convolutional layers to extract individualized learning rates based on continuous learning interactions of students. Learning process-consistent knowledge tracing (LPKT) [19] integrated forgetting curves and learning gains to enhance temporal consistency. LPKT relies on a static Q matrix which is a binary mapping of exercises to knowledge concepts. LPKT’s extension LPKT-S [28] emphasizes time interval effects and individual progress variance.

2.2. Hypergraph Neural Networks

Traditional knowledge tracing methods (e.g., BKT, IRT) and existing deep learning models (e.g., DKT, SAKT) typically rely on graph structures or sequential modeling to capture knowledge concept correlations. However, constrained by the binary relationship representation capability of ordinary graphs, they struggle to explicitly model high-order correlations and hierarchical dependencies between exercises and knowledge concepts. Recently, hypergraph neural networks (HGNN) [29,30,31] have gradually been introduced into educational data mining due to their superiority in modeling many-to-many complex relationships. Unlike conventional graphs, hypergraphs utilize hyperedges to connect multiple nodes simultaneously, making them inherently suitable for capturing multidimensional collaborative effects among knowledge concepts. For instance, in knowledge tracing scenarios, a single exercise may involve multiple knowledge concepts (forming a hyperedge), while different exercises can establish high-order correlations through shared subsets of knowledge concepts. Although existing studies have applied GNN [9] to KT tasks (e.g., the GKT model [10]), they remain limited to low-order neighborhood information aggregation and fail to capture multi-hop collaborative influences across exercises. The proposed HGKT model innovatively employs a dual-layer hypergraph convolutional architecture: the first layer models exercise–knowledge concept membership relationships, while the second layer discovers high-order exercise correlations based on shared knowledge concepts, thereby explicitly deconstructing the collaborative evolution mechanism of knowledge states. This approach transcends the pairwise relationship constraints of traditional graph models, providing finer-grained interpretable representations for knowledge tracing.

3. Problem and Definition

Knowledge tracing formalizes the learning domain through a set of students $\mathbf{S}=\left\{s_1,s_2,\dots ,s_i,\dots ,s_I\right\}$, a set of exercises $\mathbf{E}=\left\{e_1,e_2,\dots ,e_j,\dots ,e_J\right\}$, and a set of knowledge concepts $\mathbf{C}=\left\{c_1,c_2,\dots ,c_m,\dots ,c_M\right\}$, where each exercise is related to specific knowledge concepts. Exercise–concept associations are encoded in a binary mapping matrix $\mathbf{Q}\in {[0,1]}^{J\times M}$, which elements satisfy $Q_{jm}=1$ represents that the knowledge concept $c_m$ is required for exercise $e_j$, otherwise, $Q_{jm}=0$. The Q-matrix constitutes the foundational relational schema between assessment items and latent competencies.

Given a student’s temporal interaction sequence $H_t=\left\{(e_1,a_1),(e_2,a_2),...,(e_t,a_t)\right\}$, the KT problem constitutes two interdependent objectives: (1) knowledge state diagnosis—estimate a latent knowledge state vector ${\mathbf{h}}_t\in [0,1]$ that characterizes the student’s mastery—and (2) performance prediction—modeling the conditional response probability $P(a_{t+1}=1\mid e_{t+1},H_t)$ for any subsequent exercise $e_{t+1}$ at $t+1$.

4. Methodology

4.1. The HGKT Model

As illustrated in Figure 2, the proposed model architecture comprises four core components: (1) a hypergraph-enhanced exercise–knowledge concept embedding representation, (2) a learning module (modeling knowledge gain), (3) a forgetting module (modeling knowledge decay), and (4) a prediction module. The hypergraph neural network explicitly constructs heterogeneous correlations between exercises and knowledge concepts through hyperedge connections, employing a dual-layer hypergraph convolution mechanism to capture high-order exercise interaction patterns. Both the learning and forgetting modules incorporate temporal features to dynamically regulate knowledge gain and decay, ensuring adaptive alignment with learners’ evolving cognitive states.

4.1.1. Hypergraph-Enhanced Embedding Layer

Define a hypergraph $\mathcal{G}=(\mathcal{V},\epsilon )$, where $\mathcal{V}$ represents a set of vertices, and $\epsilon$ represents a set of hyperedges. In the hypergraph $\mathcal{G}$, an exercise $e_t$ corresponds to a vertex, and a knowledge concept c corresponds to a hyperedge. 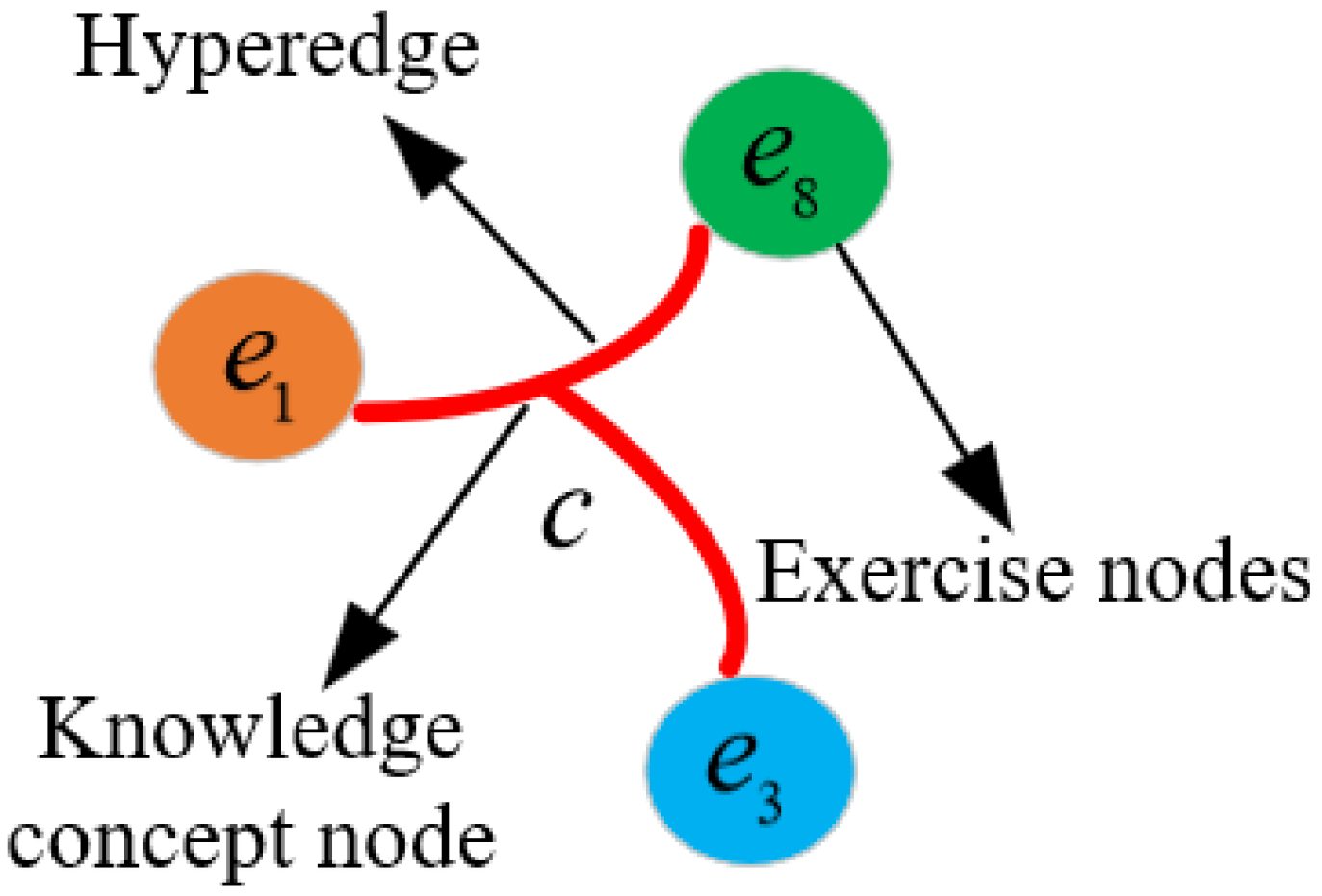The incidence matrix $\mathcal{H}\in {\mathbb{R}}^{\left|\mathcal{V}\right|\times \left|\epsilon \right|}$ is based on the $\mathit{Q}$ matrix, an exercise–knowledge concept association matrix that represents node–hyperedge relationships. In a hypergraph, a hyperedge denotes a group relationship connecting multiple vertices simultaneously, as illustrated in Figure 3. Here, C represents knowledge concepts, $e_t$ represents exercises, and each exercise forms a hyperedge with its associated knowledge concepts. Exercise–knowledge concepts incidence matrix $\mathcal{H}$ each entry is defined as follows:

$$\mathcal{H}({\mathcal{V}}_i,{\epsilon }_j)=\left\{\begin{array}{c}1,if{\mathcal{V}}_i\in {\epsilon }_j\hfill \\ 0,if{\mathcal{V}}_i\notin {\epsilon }_j\hfill \end{array}\right.$$

(1)

where if a vertex belongs to a hyperedge, then $\mathcal{H}({\mathcal{V}}_i,{\epsilon }_j)=1$; otherwise, $\mathcal{H}({\mathcal{V}}_i,{\epsilon }_j)=0$.

By constructing the hypergraph using the exercise–knowledge concepts incidence matrix $\mathcal{H}$, each exercise and its associated knowledge concepts form hyperedges. A hypergraph neural network is employed to explicitly model the complex relationships between exercises and knowledge concepts, capturing high-order exercise correlations which latent dependencies formed when multiple exercises nonlinearly interact through shared knowledge concepts through a two-layer hypergraph convolution.

Hypergraph convolution employs a message propagation mechanism, enabling exercise embeddings to aggregate features from related knowledge concepts and form enhanced representations that incorporate knowledge structure information. The generation of enhanced exercise embeddings involves two convolutional layers:

First convolution layer: Uses a non-linear transformation with ReLU activation to fuse exercise features with their associated knowledge concepts features into embedding using incidence matrix $\mathcal{H}$.

$${\mathit{X}}^{\left(\mathbf{1}\right)}=ReLU({\mathit{W}}_1·\mathcal{H}·{\mathit{e}}_t+{\mathit{b}}_1)$$

(2)

where ${\mathit{W}}_1$ is the weight matrix, and ${\mathit{b}}_1$ is the bias term. ReLU is a non-linear activation function.

Second Convolution Layer: Propagates features across concept-sharing exercises through incidence matrix operations, where hyperedges dynamically cluster exercises with overlapping concepts—mathematically formalizing high-order relationships as multi-hop paths exercise-concept-exercise in hypergraph topology. This further refines the feature representation, producing the final enhanced embedding ${\mathit{E}}_t$ with a dimensionality of $d_k$.

$${\mathit{E}}_t={\mathit{W}}_2·\mathcal{H}·{\mathit{X}}^{\left(\mathbf{1}\right)}+{\mathit{b}}_2$$

(3)

where ${\mathit{W}}_2$ is the weight matrix, and ${\mathit{b}}_2$ is the bias term.

The enhanced embeddings not only retain the semantic information of the exercises themselves but also encode the association patterns among knowledge concepts, allowing for a more precise characterization of an exercise’s position within the knowledge space.

During each forward propagation, the hypergraph structure is dynamically reconstructed, enabling the convolution operations to adapt to varying knowledge point association patterns across different exercises.

Therefore, the representation of the basic learning unit $(E_t,a{t}_t,a_t)$ is constructed by concatenating $E_t$, $a{t}_t$, and $a_t$, which are then fused through a multilayer perceptron (MLP) to integrate the enhanced exercise representation ${\mathit{E}}_t$, answer time representation ${\mathit{at}}_t$, and answer representation ${\mathit{a}}_t$. The embedding layer can be formulated as

$${\mathit{l}}_t={\mathit{W}}_3^T({\mathit{E}}_t\oplus {\mathit{at}}_t\oplus {\mathit{a}}_t)+{\mathit{b}}_3$$

(4)

where ⊕ is operation of concatenating, ${\mathit{W}}_3$ is the weight matrix, and ${\mathit{b}}_3$ is the bias term.

4.1.2. Learning Gain

Learning knowledge gain refers to the knowledge advancement a learner achieves through consecutive learning interactions (e.g., $l_{t-1}$ and $l_t$), driven by learning activities. Its core lies in quantifying short-term progress through performance differences and integrating dynamic features of the learning process. Specifically, learning gain is benchmarked by the difference in performance between adjacent learning units, a difference that reflects positive changes in the learner’s knowledge state. Simultaneously, the time interval $i{t}_t$ between interactions directly impacts the gain effect—shorter intervals typically imply a more compact learning process, which may lead to higher knowledge gains. Additionally, the learner’s prior knowledge state $h_{t-1}$ moderates the gain: learners with lower initial knowledge levels often exhibit greater potential for improvement, resulting in more significant latent progress. Thus, knowledge gain comprehensively captures the dynamics and diversity of knowledge acquisition during learning by integrating three dimensions: performance differences, learning continuity (time intervals), and individual capability disparities (knowledge mastery). Therefore, the learner’s initial learning gain ${\mathit{lg}}_t$ can be modeled as

$${\mathit{lg}}_t=tanh({\mathit{W}}_4^T[{\mathit{l}}_t\oplus {\mathit{it}}_t\oplus {\mathit{l}}_{t-1}\oplus {\mathit{h}}_{t-1}]+{\mathit{b}}_4)$$

(5)

where tanh is a non-linear activation function.

Since not all knowledge learned by a learner is fully absorbed, a learning gate ${\mathbf{\Gamma }}_t$ is introduced to control the learner’s knowledge absorption capacity. Specifically, the concatenation of the representation vectors from two consecutive learning interactions, the time interval, and the learner’s prior knowledge state is processed through a sigmoid function to compute the absorption capacity:

$${\mathbf{\Gamma }}_t=\sigma ({\mathit{W}}_5^T[{\mathit{l}}_t\oplus {\mathit{it}}_t\oplus {\mathit{l}}_{t-1}\oplus {\mathit{h}}_{t-1}]+{\mathit{b}}_5)$$

(6)

Here, ⊕ denotes vector concatenation. $\sigma (·)$ is a non-linear sigmoid activation function. The learner’s actual learning gain ${\mathit{LG}}_t$ is then obtained by multiplying the learning gate with the normalized initial learning gain:

$${\mathit{LG}}_t={\mathbf{\Gamma }}_t·(({\mathit{lg}}_t+1)/2)$$

(7)

To derive the exercise-specific learning gain associated with the knowledge concepts of exercise $e_t$, the actual gain is further multiplied by the knowledge concept vector ${\mathit{q}}_{e_t}$ of the current exercise:

$${\mathit{RLG}}_t={\mathit{q}}_{e_t}·{\mathit{LG}}_t$$

(8)

4.1.3. Forgetting Layer

Within the forgetting layer, the forgetting erasure vector ${\mathit{Fe}}_t$ is computed via a sigmoid gating mechanism that integrates three inputs: (1) the previous knowledge state ${\mathit{h}}_{t-1}$, (2) the actual learning gain vector ${\mathit{LG}}_t$ and (3) the time interval vector ${\mathit{it}}_t$. The sigmoid — based erasure gate operationalizes Ebbinghaus’s exponential forgetting law, where memory strength will diminish predictably over time without reinforcement. This is formally expressed as

$${\mathit{Fe}}_t=\sigma ({\mathit{W}}_6^T[{\mathit{h}}_{t-1}\oplus {\mathit{LG}}_t\oplus {\mathit{it}}_t]+{\mathit{b}}_6)$$

(9)

The forgetting update vector uses the tanh function to model the non-linear strengthening of knowledge through deliberate practice. This aligns with cognitive load theory’s focus on effortful encoding.

$${\mathit{Fa}}_t=tanh({\mathit{W}}_7^T[{\mathit{h}}_{t-1}\oplus {\mathit{LG}}_t\oplus {\mathit{it}}_t]+{\mathit{b}}_7)$$

(10)

By combining the forgetting erasure vector and the forgetting update vector, the forgetting vector ${\mathit{F}}_t$ can be obtained. The erasure vector continuously attenuates prior knowledge states, while the update vector selectively amplifies retrieval-reinforced concepts. This is a biology-inspired balance where forgetting pressures counteract with practice-driven potentiation.

$${\mathit{F}}_t=(1-{\mathit{Fe}}_t)(1+{\mathit{Fa}}_t)$$

(11)

Therefore, based on the forgetting vector ${\mathit{F}}_t$ and the related learning gain ${\mathit{RLG}}_t$, the updated knowledge state matrix ${\mathit{h}}_t$ is

$${\mathit{h}}_t={\mathit{RLG}}_t+{\mathit{F}}_t·{\mathit{h}}_{t-1}$$

(12)

4.1.4. Predicting Layer

Our model dynamically tracks learners’ knowledge states by integrating learning gains (knowledge improvement from interactions) and forgetting effects (time-dependent decay). This dual mechanism allows the model to simulate how knowledge is both acquired and eroded, providing a realistic representation of cognitive processes.

When predicting a learner’s performance on an upcoming exercise $e_{t+1}$, the model combines the exercise’s embedding with the current knowledge state ${\mathit{h}}_t$. This fused representation is processed through a fully connected layer with a sigmoid activation function, generating a probability of correct response. Formally,

$$p_{t+1}=\sigma ({\mathit{W}}_8^T[{\mathit{e}}_{t+1}\oplus {\mathit{h}}_t]+{\mathit{b}}_8)$$

(13)

The prediction layer outputs $p_{t+1}$, representing the probability of a student correctly answering exercise $e_{t+1}$, with $p_{t+1}\in (0,1)$. A threshold of 0.5 is applied. If $p_{t+1}>0.5$, the model predicts a correct answer; otherwise, the prediction is incorrect.

4.1.5. Object Function

The goal of knowledge tracing is to predict the likelihood of a student answering a question correctly. To achieve this, the objective function minimizes the negative log-likelihood between the predicted probabilities $p_t$ and the ground-truth responses $a_t$, while incorporating $L2$ regularization to prevent overfitting:

$$\mathcal{L}\left(\theta \right)=-\sum _{t-1}^T[a_{t}log{p}_t+(1-a_t)log(1-p_t)]+{\lambda }_{\theta }{∥\theta ∥}_2^2$$

(14)

where $\theta$ is all the parameters in HGKT, and ${\lambda }_{\theta }$ is a regularized hyperparameter.

5. Experiments

In this section, we present a comprehensive overview of the datasets used for evaluation, baseline models adopted for comparative analysis, and specifics of the training process.

5.1. Datasets

In our experiments, we evaluated our method on three public datasets: ASSIST2012, ASSISTChall, and EdNet-KT1. All datasets are derived from real-world sequences of student exercise–answer interactions. A detailed description of each dataset is summarized in

Table 1. Statistics of all datasets.

Statistics	Datasets
	ASSIST2012	ASSISTChall	EdNet-KT1
Students	29,018	1709	784,309
Exercises	53,091	3162	12,372
Concepts	265	102	141
Questions Per Concepts	200.34	31	87.74
Answer Time	26,747	1326	9292
Interval Time	29,748	2839	41,830
Avg. Length	93.45	551.68	125.45

. The detailed introduction of the datasets is as follows.

ASSIST2012 (https://drive.google.com/file/d/1cU6Ft4R3hLqA7G1rIGArVfelSZvc6RxY/view?usp=sharing (accessed on 31 July 2025)): This dataset was collected through the ASSISTments online education platform during the period spanning September 2012 to October 2013. It comprises learning interaction logs generated during practice sessions, the dataset captures learner engagement through similar exercise sequences designed for skill consolidation. Each record includes multidimensional educational metadata such as exercises, knowledge concepts, answer time and student’s answer. To optimize knowledge tracing model performance, records lacking associated knowledge concept annotations were systematically filtered during dataset preprocessing.

ASSISTChall (https://sites.google.com/view/assistmentsdatamining/dataset?authuser=0 (accessed on 31 July 2025)): Released in 2017 through a data mining competition, the comprehensive ASSISTment Challenge dataset offers the richest metadata among ASSISTments repositories. It encompasses 3162 unique questions answered by 1709 students across 102 knowledge concepts, generating 942,816 interactions. On average, this dataset exhibits substantially longer learning sequences compared to ASSIST2012.

EdNet-KT1 (https://github.com/riiid/ednet (accessed on accessed on 31 July 2025)): EdNet dataset represents the largest publicly released intelligent tutoring system (ITS) collection to date. EdNet-KT1, a subsample derived from the EdNet, originates from Santa—an AI-powered multi-platform tutoring system. There are 784,309 students which contain 131,441,538 interactions in EdNet-KT1. Due to computational constraints, we extracted interaction records from a randomly selected 10% of students as experimental data.

5.2. Baseline Methods

In order to evaluate the performance of our proposed model, we use the following models as our baselines:

DKT [2]: DKT pioneered the use of deep neural networks for knowledge tracing. Utilizing recurrent neural networks (RNNs), it effectively models the complex temporal dynamics of student interactions and learning progressions. This enables more accurate predictions of student performance and mastery, significantly advancing educational analytics and personalized learning.

DKT+ [25]: DKT+ represents an architectural refinement of the original deep knowledge tracing (DKT) framework, specifically designed to mitigate two critical limitations: input reconstruction deficiency, where the base model exhibits inadequate auto-regressive fidelity in reproducing observed interaction sequences and temporal prediction instability, characterized by inconsistent mastery trajectory projections for knowledge components across successive time steps.

DKVMN [3]: leveraging memory-augmented neural architectures, the dynamic key–value memory network (DKVMN) model advances knowledge tracing capabilities. Its core framework deploys a static key matrix for persistent concept embedding and a dynamic value matrix capturing temporal mastery evolution. This dual-memory mechanism substantially enhances neural inference fidelity for latent knowledge state estimation. The innovative integration of associative memory modules yields superior accuracy and computational efficiency in learning progression modeling, ultimately enabling adaptive instructional optimization and measurable pedagogical outcomes enhancement.

AKT [6]: AKT is a context-sensitive knowledge tracing framework that incorporates dual self-attention mechanisms to separately model exercise characteristics and learner responses. Its core innovation lies in a knowledge retriever module that leverages attention mechanisms to dynamically retrieve historical knowledge states pertinent to the target exercise, enabling contextualized prediction of learner proficiency.

SAKT [26]: SAKT model predicts student mastery by identifying the most relevant past knowledge components (KCs) for a given target KC. It leverages attention mechanisms to focus on a select subset of a student’s previous activities for each prediction. This targeted approach, relying on fewer KCs than RNN-based models, significantly mitigates the data sparsity problem common in knowledge tracing.

LPKT [19]: The learning process-consistent knowledge tracing (LPKT) framework operationalizes knowledge state monitoring by explicitly simulating cognitive learning dynamics. This approach synergistically incorporates temporal features—response latency and inter-practice intervals—to quantify incremental learning gains and memory decay across successive learning events. Mnemonic reinforcement is achieved through empirically validated forgetting curve integration, ensuring longitudinal prediction stability. Foundationally, LPKT employs a static Q-matrix to establish binary exercise–concept mappings, preserving essential assessment-skill relational semantics.

5.3. Experimental Setting

The statistical details of the three datasets are summarized in

Table 2. Results of comparison of models on student performance prediction.

Models	ASSIST2012		ASSISTChall		EdNet-KT1
	AUC	ACC	AUC	ACC	AUC	ACC
DKT	0.72430	0.71265	0.72185	0.71963	0.68632	0.68903
DKT+	0.72510	0.71312	0.72210	0.71352	0.64254	0.67352
DKVMN	0.71488	0.72415	0.70630	0.70198	0.67086	0.68231
SAKT	0.72213	0.72750	0.78743	0.74150	0.68041	0.68652
AKT	0.77814	0.75352	0.75621	0.71063	0.75827	0.71024
LPKT	0.77189	0.75936	0.79837	0.73774	0.77324	0.72026
HGKT	0.78812	0.76087	0.81305	0.74533	0.78372	0.72074

. To balance computational efficiency and sequence context, the maximum length of student response history was capped at 200 entries. The data was split into 80% for training and validation (with an 80 – 20 split between training and validation subsets) and 20% for testing.

We ordered student learning records based on answer timestamps and standardized all input sequences to fixed lengths. Sequence lengths are fixed at 100 for the ASSIST2012 and EdNet-KT1 datasets, and 500 for the ASSISTChall dataset. Sequences exceeding the threshold length were segmented into multiple independent fixed-length subsequences. Shorter sequences were padded with zero vectors to reach the target length. A standard 5-fold cross-validation protocol was employed. In each fold, 80% of students data were split as training set (80%), and validation set (20%). The remaining 20% used as the test set. Parameters were randomly initialized using a uniform distribution. All hyperparameters were learned via the training set, with optimal models selected based on validation performance. A dropout layer (rate = 0.2) was integrated into the HGKT module to mitigate overfitting. Dimension parameters $d_k$ and $d_e$ are set to 128, $d_a=50$. Q-matrix small positive value $\gamma =0.03$ and learning rate is $3\times {10}^{-3}$. Batch size is 128. To ensure repeatability and fairness, all experiments were conducted on a Windows server equipped with NVIDIA Quadro RTX 6000 GPUs.

5.4. Experiment Results

5.4.1. The Prediction Performance

Given the inherent difficulty in quantifying latent knowledge states, we operationalize model evaluation through response prediction accuracy—a well-established proxy metric for knowledge estimation fidelity in KT literature. To validate HGKT’s efficacy, comprehensive benchmarking against state-of-the-art baselines was conducted, with comparative performance on learner outcome forecasting detailed in Table 2. All experiments employ standardized evaluation protocols using the receiver operating characteristic’s area under the curve (AUC) and accuracy (ACC), both bounded in [0, 1]. Elevated metric values correspond to enhanced diagnostic capability, signifying superior model performance.

From Table 2, experimental results across three benchmark datasets (ASSIST2012, ASSISTChall, and EdNet-KT1) demonstrate the consistent superiority of the proposed HGKT model over all baseline methods, achieving state-of-the-art performance in both AUC and ACC. Specifically, HGKT improves the AUC by 1.8% compared to the previous best model, LPKT. Its effectiveness is particularly notable on the ASSISTChall dataset, characterized by the longest learning sequences, indicating enhanced adaptability to extended learning contexts. Furthermore, from Figure 4, HGKT achieves superior AUC and ACC performance on the largest dataset, EdNet-KT1, highlighting its robustness in complex learning scenarios. The model significantly outperforms traditional LSTM-based approaches (e.g., yielding an average AUC gain of 11.879% over DKT). These results collectively affirm HGKT’s effectiveness and adaptability for diverse knowledge tracing tasks.

5.4.2. Ablation Study

To validate the capability of hypergraph neural networks in capturing high-order relationships among knowledge concepts and examine the limitations of traditional binary Q-matrices(defining exercise–knowledge concept relationships), this study compares the performance between knowledge tracing models using hypergraph-enhanced embedding methods and those relying on static Q-matrix. Across three datasets, we evaluate the HGKT model and its two constructed variants against the LPKT baseline.

• HGKT: Uses Q-matrix only for related learning gain;
• HGKT-LG: Replaces related learning gain with direct learning gain (no Q-matrix usage;)
• HGKT-Q: Entirely eliminates Q-matrix dependency;
• LPKT: Uses Q-matrix for related learning gain and knowledge states update.

As revealed in Figure 5, the HGKT-Q framework’s implementation of hypergraph neural networks achieves significantly better performance than traditional Q-matrix-driven approaches LPKT, demonstrating the effectiveness of high-order relationship modeling in educational data analytics. However, the performance superiority of HGKT over HGKT-LG and HGKT-Q indicates the Q-matrix serves as a static knowledge concept-exercise mapping, its synergistic combination with learning gain through related computation enables precise exercise-specific knowledge enhancement quantification. The performance superiority of HGKT-LG over HGKT-Q indicates Q-matrix’s implicit structural benefits even without explicit multiplicative operations, whereas HGKT’s optimal performance stems from its Q-matrix-constrained explicit operations that focus learning gains on exercise-relevant concepts. These findings collectively highlight the necessity of integrating static Q-matrix with hypergraph neural networks for effective knowledge tracing.

5.4.3. Visualization of the Student Knowledge State

This study of visually demonstrates the dynamic tracing performance of the HGKT model in monitoring students’ evolving knowledge states. Figure 6 shows using 15 exercises (e1–e15) from the ASSISTChall dataset, covering three concepts: C1 (addition), C2 (ordering numbers), and C3 (subtraction). The horizontal axis represents the exercise sequence, while colored markers above indicate ✓ (correct) or × (incorrect) responses for concept-specific exercises, the following conclusions are drawn:

(1) When students answered incorrectly in e11, their mastery of related knowledge concepts still shows an upward trend, indicating that the HGKT model can effectively identify the implicit dependency relationships among related knowledge concepts and verifying the model’s ability to capture higher-order knowledge structures. While students make mistakes in exercises e8 and e13, the model detects a significant decrease in the mastery, indicating that the model can correct the assessment results of the knowledge state in real time and provide targeted feedback for knowledge gaps.

(2) During the initial learning stage, the learning gain of new knowledge concept is significant. For example, after completing exercise e6, the mastery of knowledge concept C3 increases by 27%. However, with the repeated practice of the same knowledge concept and the continuous practice of the same knowledge concept five times (exercises e7 – e11), the mastery degree of C2 only increased by 3%, indicating that there is a phenomenon of diminishing returns from repeated training. It corresponds to the marginal utility theory in cognitive psychology, suggesting that systems should prioritize recommending understudied concepts to optimize learning efficiency.

(3) The HGKT model captures the knowledge decline caused by the forgetting mechanism. After the practice of exercise e5, the mastery degree of knowledge concept C1 continuously declined from a peak of 90% to 62% because it was not covered in eight consecutive questions. The model successfully captured this typical forgetting curve. It is suggested that when the attenuation rate of knowledge point mastery is greater than a certain threshold, the review reminder mechanism should be triggered to strengthen memory retention through interval repetition.

6. Conclusions

In this work, we proposed the Hypergraph-driven Knowledge Tracing (HGKT) framework. Extensive experiments on three diverse public datasets (ASSIST2012, ASSISChall, and Ednet-KT) demonstrate HGKT’s state-of-the-art predictive performance. HGKT achieved significant improvements over baseline models, with average AUC gains of 6.71%, 8.82%, and 12.15% on ASSIST2012, ASSISChall, and Ednet-KT, respectively, alongside corresponding accuracy increases of 4.0%, 3.44%, and 3.96%. These results validate HGKT’s efficacy in predicting student knowledge state.

The key advancements stem from HGKT’s novel two-layer convolutional architecture employing hypergraph neural networks. This design effectively captures intricate high-order correlations among exercises and knowledge concepts–a critical limitation in prior models. HGKT successfully integrates rich hypergraph-derived exercise representations with essential temporal features (answer time and interval time). Furthermore, our cognitively inspired dual-gating strategy dynamically balances learning and forgetting mechanisms, enabling realistic modeling of evolving knowledge states. Visualization analyses confirm the model’s interpretability in tracing this evolution. The consistent performance gains across datasets with varying characteristics underscore HGKT’s strong practical potential for real-world educational platforms.

Future work will focus on employing knowledge distillation to develop lightweight HGKT variants, significantly reducing model complexity and inference latency to enable real-time deployment on large-scale platforms. Concurrently, we will explore integration with large foundation models (LLMs) to enable multimodal knowledge tracing, incorporating textual content, images, or audio prompts for richer contextual understanding. Building on this, further refinement of knowledge concept representation and interaction modeling will enhance generalizability across diverse educational domains and curricula. These combined enhancements aim to broaden HGKT’s applicability and solidify its role within next-generation intelligent tutoring systems.