Correlation Measures in Metagenomic Data: The Blessing of Dimensionality

Abstract

Microbiome analysis has revolutionized our understanding of various biological processes, spanning human health and epidemiology (including antimicrobial resistance and horizontal gene transfer), as well as environmental and agricultural studies. At the heart of microbiome analysis lies the characterization of microbial communities through the quantification of microbial taxa and their dynamics. In the study of bacterial abundances, it is becoming more relevant to consider their relationship, to embed these data in the framework of network theory, allowing characterization of features like node relevance, pathways, and community structure. In this study, we address the primary biases encountered in reconstructing networks through correlation measures, particularly in light of the compositional nature of the data, within-sample diversity, and the presence of a high number of unobserved species. These factors can lead to inaccurate correlation estimates. To tackle these challenges, we employ simulated data to demonstrate how many of these issues can be mitigated by applying typical transformations designed for compositional data. These transformations enable the use of straightforward measures like Pearson’s correlation to correctly identify positive and negative relationships among relative abundances, especially in high-dimensional data, without having any need for further corrections. However, some challenges persist, such as addressing data sparsity, as neglecting this aspect can result in an underestimation of negative correlations.

1. Introduction

Techniques based on next-generation sequencing (NGS) can elucidate the complex functioning of natural microbial communities directly in their natural environment. New branches of research have been created, such as the study of human microbiota, which shows heterogeneity between different anatomical sites and individual variability [1,2], or the ability to characterize and monitor the presence of antimicrobial resistance worldwide [3]. Complementing the analyses conducted directly on the abundance of microbiota samples, it can be greatly beneficial to explore a second layer of information represented by the relationships among the observed species. Network theory provides many essential tools to characterize collective properties of the ecology of a natural environment by defining central elements or communities in the system and allowing visualization of these results by exploiting network structural properties [4]. Consequently, the initial step in reconstructing any network involves the identification and quantification of relationships between species, often achieved by assessing correlations or conditional dependencies among each pairwise combination of variables.

In this study, we specifically focus on marginal correlations rather than partial correlations. Although partial correlations are a powerful tool for network reconstruction, by explicitly removing indirect associations, they complicate the direct assessment and interpretation of the biases introduced by compositionality and sparsity. Marginal correlations, being simpler and more straightforward, allow a clearer analysis of these biases, which are expected to similarly affect partial correlations.

Independent from the NGS techniques used like RNA-seq, 16s, or whole-genome shotgun, the underlying data are similar, composed of counts of sequencing reads mapped to a large number of references (taxa), and the unifying theoretical framework is their compositional nature [5,6].

Taxa abundance is determined by the number of read counts, which is affected by sequencing depth and varies from sample to sample. Typically, a sum constraint is imposed over all the samples (1 for probability, 100 for percentage, or $10^6$ for part per million) called L1 normalization, to remove the effect of sample depth.

In this way, data are described as proportions and referred to as compositional data [7]. However, as noted by Pearson at the end of the 19th century, compositional data can generate spurious correlations between measurements [8]. From a mathematical point of view, the data lie on a simplex [9]; thus, it can be extremely dangerous to use Euclidean metrics for proximity and correlation estimations in a non-Euclidean context.

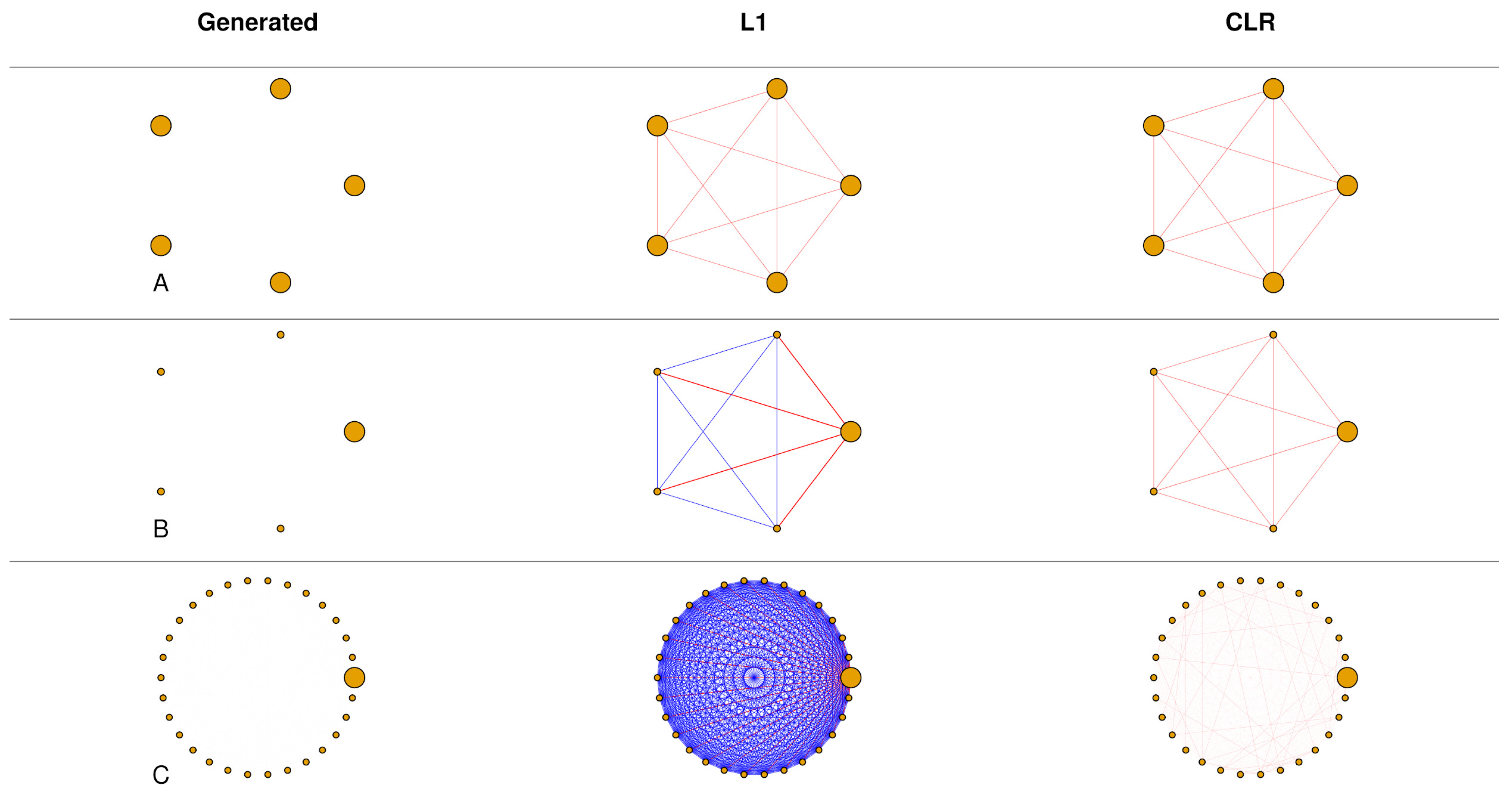
These biases on correlation between relative abundances can be significant in some datasets but mild in others [Figure 1], and the diversity within each sample, called $\alpha$-diversity, concurs to enforce this bias [10]. Correlation biases become more pronounced when counts are concentrated in a few taxa. Conversely, when counts are distributed more evenly across samples, these biases tend to decrease. In this study, we compute the dataset within-sample diversity as the average Pielou index across samples, obtained by normalizing the Shannon entropy with respect to the number of taxa in each sample. This measure reflects how evenly taxa are distributed within individual profiles (referred to as $\underset{\_}{P}$, see Section 2).

Hence, it is imperative to take into account these compositional effects when reconstructing networks from metagenomic data. Failing to do so may lead to entirely incorrect conclusions, endangering the accuracy and reliability of inferred ecological interactions [11].

To improve correlation estimates on relative abundances, methods such as sparse correlations for compositional data (SparCC) [10]), proportionality for compositional data (Rho), and many others [12,13,14,15,16,17,18,19,20,21,22] have been developed, almost all making extensive use of the compositional theory introduced by Aitchison [9].

Aitchison provided a family of transformations to handle these types of data, known as log-ratio transformations. The counts of each sample are expressed relative to a reference to enable comparisons, followed by the application of a logarithm. One common choice is the centered log-ratio transformation (CLR), where each element is divided by the geometric mean of the sample in a logarithmic scale. This operation is both isomorphic and isometric, preserving distances. However, like L1 normalization, CLR also introduces a sum constraint, where the sample sum is fixed to 0. This constraint is equivalent to mapping the counts on a Cartesian hyperplane instead of a simplex, and it also introduces spurious dependencies between variables.

Our work shows that, unlike L1 normalization, the bias introduced by the sum constraint in CLR strongly depends on the dataset dimensionality D, or more explicitly it is related to the number of taxa or references [Figure 1]. In our study, we not only demonstrate but also quantify these biases, which diminish as the dimensionality increases. In metagenomic contexts, where dimensionality can extend to hundreds or more, the impact of spurious correlations introduced by CLR becomes negligible, making any subsequent step for correlation estimation less critical.

Furthermore, there are additional typical sources of error in the estimation of correlations in metagenomic datasets. Often a large part of taxa in the NGS experiments are under the detection limits of the sequencing techniques, producing very sparse abundance matrices. It is really common to find datasets where more than 70–80% of species are undetected; typically, they are assigned a value of 0. The unobserved species are not to be interpreted as the absence of that species but rather as a missing value in which we have no further information. Moreover, non-zero counts exhibit strongly non-normal distributions in non-transformed data, with heavy tails that invalidate the assumptions of Pearson’s correlation. The distribution that better describes the real NGS data is still a debated discussion, but in different contexts the zero-inflated negative binomial distribution (ZINB) is employed [12,23,24]. The ZINB distribution can effectively capture the excess of zeros and the dispersion in the data, making it a suitable choice for representing counts in metagenomic datasets, particularly given its discrete nature similar to the counts.

Another factor that could introduce biases in CLR-transformed data is the magnitude of correlation among variables. Distortions can arise in densely connected networks due to the CLR transformation’s fixed zero-sum constraint. As an example, in scenarios where all variables are positively correlated, the zero-sum constraint might distort the underlying relationships by artificially inflating or deflating values to meet the zero-sum requirement. While this issue is significant in networks with dense connections, it is typically less relevant in metagenomic contexts, characterized by sparsely correlated species, aligning with the usual structure observed in biological datasets [25,26,27] (see Supplementary Section S1).

The aim of this manuscript is to explore the biases affecting correlation estimates, particularly in the context of compositionality and zero-excess issues commonly encountered in metagenomic datasets. In the absence of ground truth, we create synthetic datasets across a wide range of conditions, varying dimensionality, diversity, data distribution, and sparsity to characterize the biases in correlation estimation. To achieve this, we have developed a model focused on the “Normal to Anything” approach that allows the generation of random variables with arbitrary marginal distributions starting from multivariate normal variables with a desired correlation structure.

This work is structured to address three main considerations. The first is the examination of the biases introduced by L1 and CLR transformations in relation to dimensionality and within diversity. This involves a thorough analysis of how these transformations impact data interpretation across various compositional contexts. Importantly, we acknowledge that, while CLR is extensively used in metagenomics as a crucial analytical tool, its application is often not accompanied by a deep understanding of its limitations and advantages.

The second consideration corroborates our findings regarding compositional biases arising from L1 and CLR transformations. For this, we compare various recently developed methods on real metagenomic data with the simplest approach of using Pearson correlation on CLR-transformed abundances (Pearson + CLR). Our analysis reveals an almost complete overlap in the final results, emphasizing the significance of the CLR transformation.

The third aspect of our research evaluates the role of zero measurements in estimating correlation after minimizing compositional biases through optimal transformation. This involves assessing how zero counts affect the accuracy of correlation measures, thereby providing insights into the appropriate handling of sparse data in metagenomic studies.

2. Materials and Methods

2.1. Within-Dataset Diversity $\underset{\_}{P}$

The within-dataset diversity $\underset{\_}{P}$ is defined as the mean value over all the samples of the Pielou index [28], which is the Shannon entropy normalized to 1 with respect to the dimension. Given a dataset $\chi$ composed of N distinct samples $x$ of dimension D, the following is obtained:

$$P(x) = {\displaystyle \frac{H\left(x\right)}{ln\left(D\right)}} = -{\displaystyle \frac{{\sum }_{i=1}^D{p}_i \cdot ln\left(p_i\right)}{ln\left(D\right)}}$$

where $H\left(x\right)$ is the Shannon entropy, and $p_i$ corresponds to the i-th taxa relative abundance in the sample. Finally, the diversity of a dataset $\underset{\_}{P}$ is calculated as follows:

$$\underset{\_}{P}(\chi ) = {\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{P}_i\left(x\right)$$

2.2. Generation of Gaussian Data for Characterization of L1 and CLR Correlation Biases

Our examination of the biases introduced by L1 and CLR transformations began with the creation of synthetic datasets modeled on Gaussian distributions. This methodology was specifically crafted to underscore the compositional biases inherent in metagenomic datasets, with a concentrated focus on dimensionality ($D$) and within-sample diversity ($\underset{\_}{P}$)—elements that are fundamentally tied to the compositional nature of the data. Our objective was to isolate and examine biases arising specifically from these compositional attributes, recognizing their direct impact on correlation analysis. While we acknowledge that sparsity and non-Gaussian distribution patterns also affect correlation metrics, these elements are secondary in the context of compositional data analysis. They were thus delineated outside of this study’s primary scope and are addressed in a subsequent section.

Utilizing the mvtnorm (v1.3) R package [29], we constructed a matrix of variables following a multivariate Gaussian distribution. In this matrix, the dimension D corresponds to the variables (or taxa), and N signifies the number of observations or samples, all governed by a predefined correlation matrix. To enable the calculation of the Pielou index without modifying the correlation structure, all generated values were shifted to be positive.

To tune the within-dataset diversity of the generated Gaussian data, a simple but functional strategy was employed: applying a multiplicative factor to one selected variable from the Gaussian-generated dataset. This deliberate manipulation skewed the distribution towards this variable, thus altering the dataset’s diversity ($\underset{\_}{P}$) without distorting the established correlation structure.

Following this adjustment for within-dataset diversity, both L1 and CLR transformations were applied to the synthetic datasets. We then extracted the correlation matrices from these transformed datasets to analyze the biases each normalization method introduced.

2.3. Realistic Synthetic Data Generation for Sparsity Biases Characterization on Correlation Measurement

To generate realistic artificial data with specified characteristics such as dimensionality (D), correlation structure (R), and sparsity ($\varphi$), we extensively used the “Normal to Anything” (NorTA) paradigm. This framework is capable of producing an arbitrary multivariate distribution that conforms to a pre-established correlation structure R, drawing upon the principles of the copula functions theory [30]. Essentially, the NorTA method allows for the transformation of normally distributed data into any desired distribution while preserving the original correlation structure. The core principle of the NorTA approach involves two main steps: Firstly, generating a multivariate normal dataset with the desired correlation structure, and secondly, transforming this dataset to have the targeted distribution while maintaining the predetermined correlations. The transformation is mathematically represented as follows:

$$U_{Gen}= F^{-1}\left(CDF\right(U\left)\right)$$

In this equation, U represents the multivariate normal data, CDF is the cumulative distribution function of the normal distribution, $F^{-1}$ is the inverse CDF (quantile function) of the target distribution, and $U_{Gen}$ is the transformed data with the desired distribution and correlation structure.

We have already defined key parameters of the generated dataset; indeed, the dimensionality (D) and the correlation structure (R) are trivially integrated within the NorTA framework. However, the delineation of dataset sparsity ($\varphi$) is a less obvious aspect, and it is determined by the selection of the marginal distribution $\rho$. To introduce sparsity, we had to appeal to the zero-inflated or the hurdle versions of conventional distributions. These modified distributions include an additional parameter, commonly denoted as $\varphi$, which regulates the proportion of zero-valued data. Thus, the level of sparsity within the final dataset $\varphi$ depends on the ${\varphi }_i$ parameters designated for each marginal distribution.

Finally, we performed L1 and CLR transformations on the tuned dataset $U_{Gen}$, yielding $U_{L1}$ and $U_{CLR}$, respectively, each with their corresponding correlation matrices $R_{L1}$ and $R_{CLR}$. The central goal of our model is to assess how these transformations impact the correlation matrices in comparison to the original matrix $R$, not to respect the empirical matrix from $U_{Gen}$. Specifically, we aimed also to evaluate the CLR transformation’s efficacy in addressing the skewness and normalizing data with heavy-tailed distributions through logarithmic scaling.

Since the CLR transformation is not defined for zero values, we replaced them with a value corresponding to the $65\%$ of the sample detection limit, in order to minimize the distortion in the covariance structure [31].

Zero counts in NGS data do not necessarily indicate true absence but may result from limited sequencing depth or detection sensitivity. They are better interpreted as a combination of biological and technical zeros, rather than classical missing data. To evaluate the impact of zero replacement, we used several zero-replacement methods from the zCompositions [32] package and compared the resulting correlations after CLR transformation. The results are shown in Supplementary Section S3 and indicate that the differences introduced by the replacement strategy were generally limited.

2.4. HMP2 16S Human Gut Data

We utilized the Human Microbiome Project’s second iteration (HMP2) dataset, which encompasses operational taxonomic unit (OTU) counts and taxonomic classifications from a longitudinal study on the microbiomes of healthy and prediabetic individuals over a period of up to four years [33]. The complete dataset includes 1122 samples encompassing 1953 OTUs derived from 96 subjects. Each sample is accompanied by metadata indicating the health status of the corresponding subject. To enhance the homogeneity of the dataset for our analysis, we narrowed the focus to a single subject coded as 69-001, who is classified as healthy and has contributed 51 samples. To refine the dataset further, we applied a filtering process based on OTU prevalence and median values of the abundances. Specifically, we retained OTUs with non-zero values in ≥33% of the samples and a median value of non-zero counts ≥5. This stringent selection criterion was designed to eliminate the rarest OTUs and focus on those with a consistent presence across the samples, thereby facilitating a more robust subsequent analysis.

2.5. Data and Code Availability

For free access to all the code and data utilized, please visit the following URL: https://github.com/Fuschi/Correlation-Biases-on-Metagenomics-Data, accessed on 15 May 2025—GitHub Repository. This repository contains comprehensive resources for replicating the analyses based on R base, VGAM, mvtnorm, and igraph [34,35].

3. Results

3.1. Compositional Biases Become Negligible with High Dimensionality

To comprehend and quantify the compositional biases inherent in Pearson correlation, we conducted a comprehensive comparative analysis. We compared the known correlation structure initially provided as input to the model with the correlation structures obtained after applying L1 and CLR normalizations, while systematically varying the dimensionality $D$ and the within-dataset diversity $\underset{\_}{P}$ (see the Section 4). In total, we generated 1560 distinct datasets by systematically varying two parameters: the dimensionality $D$, which ranged from 5 to 200 in steps of 5 (i.e., 40 values), and the within-dataset diversity $\underset{\_}{P}$, which ranged from 0.025 to 0.975 in steps of 0.025 (i.e., 39 values). For each of the 1560 combinations of D and $\underset{\_}{P}$, we created a dataset where the relative abundance vectors were sampled to match the target diversity within a tolerance of ±0.005. To isolate the effects of the L1 and CLR transformations, we made deliberate efforts to minimize any known sources of error and chose the simplest experimental conditions to ensure the robustness of our findings. In line with these principles, we consistently conducted the analysis with an uncorrelated covariance structure, and we chose to work with normally distributed variables to avoid potential errors in the Pearson correlations that may result from non-normally distributed data. Furthermore, to minimize random correlations and sampling errors, we used a large number of samples in our simulations. The goal was not to reproduce realistic conditions but to create a controlled setting where the effect of compositionality could be isolated. Since the dimensionality in our simulations ranges from 5 to 200 variables, we chose N = 10,000 to ensure that even in the highest-dimensional case (D = 200), spurious correlations due to finite sample effects would be negligible. By simulating data with a fully sparse correlation structure (i.e., all true correlations set to zero), we could directly assess how different transformations—such as CLR or L1—introduce spurious associations purely due to the compositional constraint. Realistic scenarios are addressed in the following section using real 16S data from HMP2, which confirm the qualitative trends observed in this idealized setting.

Finally, we quantified the biases by calculating the mean absolute error (MAE) on all values of the matrix obtained by subtracting L1- and CLR-normalized correlation matrices, denoted as $R^{L1}$ and $R^{CLR}$, to the original correlation matrix R, as follow:

$$MA{E}_{D,\underset{\_}{P}}(K) = {\displaystyle \frac{{\sum }_{i=1}^D\left|R_i^K- R_i\right|}{D^2}} \mathrm{with}\mathrm{K}=\mathrm{L}1\mathrm{or}\mathrm{CLR}$$

MAE values theoretically range from 0 (perfect agreement with the ideal correlation) to 2 (maximum possible distortion, achieved only when $R_i= \pm 1$ and the estimated correlation is exactly opposite).

The distinct behaviors of the two normalizations are evident, as they introduce different biases on correlation (see Figure 2). Specifically, L1 correlations are primarily influenced by within-dataset diversity, with the biases becoming more pronounced as the values within a sample become more heterogeneously distributed. On the other hand, CLR data exhibit biases that are independent of dataset diversity, and these distortions diminish rapidly with increasing dimensionality. Building upon the premise of complete independence of the CLR biases on correlation from dataset diversity, we can estimate this effect by calculating an average overall diversity value $\underset{\_}{P}$. We observe that the error decreases to less than 0.01 for dimensionality values greater than or equal to $100$. Thus, we posit that in typical metagenomic scenarios, where the dimensionality often extends into the hundreds, the effects of compositionality are negligible. Furthermore, in Supplementary Section S1 we evaluate the MAE across different correlation densities, demonstrating that in metagenomic networks characterized by sparse correlations, these biases do not present a significant issue.

3.2. Comparison Between Correlation-Based Methods on Real Data

In order to assess whether the conclusions drawn from our simulations are consistent with real data, we compared different correlation-based methods on a subset of 51 samples from the HMP2 dataset, selecting the subject 69-001 in healthy condition. Correlations were computed both at the OTU level (171 variables after filtering) and at the phylum level (7 aggregated taxa). We considered Pearson correlation after L1 normalization (Pearson + L1), proportionality (Rho), and SparCC, using Pearson correlation on CLR-transformed data (Pearson + CLR) as a reference. Rho is based on the concept of proportionality and offers a scale-invariant alternative to correlation, aiming to mitigate the impact of the constant-sum constraint in compositional data. SparCC, instead, estimates correlations from log-ratio transformed data under the assumption of sparsity in the underlying structure and is the only method among those considered that explicitly models and corrects compositional effects.

At the OTU level, both Rho and SparCC showed near-perfect agreement with Pearson + CLR (R = 0.99, Figure 3B,C), confirming the consistency among these methods in high-dimensional settings. In contrast, Pearson + L1 displayed a more dispersed pattern (R = 0.81, Figure 3A). This divergence is likely driven by uneven taxa-wise heterogeneity, with an average within-sample diversity $\underset{\_}{P}$ of 0.68, consistent with the patterns observed in the simulation results (Figure 2A) where L1-based correlations are strongly affected by sample diversity.

At the phylum level, the differences among methods become more pronounced. Rho remains closely aligned with Pearson + CLR (R = 0.98, Figure 3E), while Pearson + L1 fails to reconstruct any meaningful pattern (R = 0.15, Figure 3D). This failure is likely due to the combination of low dimensionality and reduced within-sample diversity, which averages around 0.5 across phyla. SparCC also diverges more markedly from Pearson + CLR (R = 0.38, Figure 3F), as it actively applies corrections for compositionality that become more relevant in such low-dimensional settings. These results are coherent with our simulation findings, which demonstrated that compositional biases are amplified at low dimensionality, where transformations alone are insufficient to fully mitigate distortion. Conversely, at higher dimensionality (e.g., the OTU-level case), the impact of such corrections is minimal, explaining the near-complete overlap among methods.

Overall, these results validate our simulation findings: marginal correlations, combined with appropriate transformations such as CLR, yield stable and interpretable estimates in high-dimensional microbiome data. Additionally, they clearly illustrate how compositional and sparsity-induced biases gain significance specifically at lower dimensionalities.

3.3. Data Sparsity Remains a Limitation

In this section, we focus on the error on estimating correlation as a function of the ratio of zero values in the samples, similar to real-world scenarios. To achieve this, we have implemented zero-inflated negative binomial distribution as the target distribution within our modeling framework based on the NorTA approach (see Section 2). This distribution was selected to accurately capture the frequent occurrence of zero counts and the asymmetrical distributions seen in real data.

In the preceding section, we discussed measures taken to minimize the impact of spurious correlations introduced by the CLR transformation. To achieve this, we standardized the dimensionality (D) of all generated datasets to 200, a choice informed by its effectiveness in ensuring that correlation errors remain consistently below the threshold of 0.01. In this analysis as well, we fixed the number of observations N to $10^4$ to reduce errors within the estimated correlation matrix. Furthermore, we only took the CLR into consideration for the analysis given that L1 in real situations, with more heterogeneously distributed data, is impractical, as seen in the previous section.

We generate data that closely resemble real-world observations deriving the parameters munb, size, and $\varphi$ of the zero-inflated negative binomial distribution from the actual distributions of the OTUs of subject 69-001 in the HMP2 dataset, using the fitdist function from the R package SpiecEasi [36]. Each taxon was then generated using random parameters falling within the range of the first and ninth deciles of the previously fitted ZINB parameters, distributed according to their empirical distribution using the quantile function of base R.

To quantify the error, we consider the absolute difference between the initial data correlation matrix R and the correlation on the same data transformed through the NorTA approach and CLR, $R_{CLR}$ with non-zero correlation only being between two taxa labelled I and J.

We build the correlation matrix specifically by varying only the value between I and J, labelled as r, from −0.9 to 0.9 in steps of 0.05, leaving all the other 198 taxa uncorrelated. In practice, all the other taxa other than I and J only contribute to reducing the biases introduced by the CLR transformation. Moreover, we varied the ratio of zero counts (${\varphi }_I$ and ${\varphi }_J$) of their respective marginal distributions from 0 to 0.95 in increments of 0.025. This process enables us to track the correlation error between taxa I and J across different levels of sparsity and correlation.

This process was repeated 100 times for every combination of $\varphi$ and r, and MAE was calculated as follows (see Figure 4A):

$$MA{E}_{r,\varphi }={\displaystyle \frac{{\sum }_{i=1}^{100}\left|R^i(r,\varphi ) - R_{CLR}^i(r,\varphi )\right|}{100}}$$

An important aspect to emphasize in our methodology is the deliberate decision to randomly generate parameters for each ZINB distribution. This approach was intended to observe the correlation phenomenon in a manner that is as independent as possible from any specific data distribution, ensuring that our findings are not biased by particular distributional characteristics of the data. The pseudo-code below summarizes our methodology:

This approach was intended to observe the correlation phenomenon in a manner that is as independent as possible from any specific data distribution, ensuring that our findings are not biased by particular distributional characteristics of the data. The pseudo-code that summarizes our methodology can be found in Supplementary Section S2.

MAE significantly differs between positive and negative correlations, as clearly illustrated in Figure 4A. While the error generally grows with an increasing number of zeros, this effect is particularly marked for taxa with negative correlations, as observed in the upper left section of the figure. Additionally, it is noteworthy that when variables are uncorrelated, the presence of zeros does not significantly impact the results.

An important aspect in the application of the CLR transformation is the number of zero counts, which requires the introduction of pseudo-counts to avoid logarithm divergence. This is illustrated in Figure 4B, using data from the HMP2 dataset, where we consider two pairs of OTUs with a high percentage of zeros and opposite signs of the correlation values.

When examining negatively correlated variables in metagenomic studies, most of the non-zero values of one variable are matched with the pseudo-counts of the other.

Such a pattern leads to flattening on the x- and y- axes of the two OTU scatter plots, producing a hyperbolic-like pattern (Figure 4B) that tends to underestimate the value of negative correlation.

We show that CLR significantly increases the negative correlation value mitigating this phenomenon, also in the case of positively correlated OTUs (Figure 4D,E).

4. Discussion

The network analysis framework is a robust tool for enhancing our comprehension of metagenomic studies, enabling us to unravel the intricate dynamics of microbial ecosystems. Although network reconstruction from second-order statistics such as correlation offers a straightforward methodology, the compositional nature of metagenomic data presents unique analytical challenges that require specialized techniques. Our study conducts a detailed investigation into the potential biases that affect the accuracy of correlation measures, considering factors such as dimensionality, diversity, and sparsity of datasets, characteristics commonly associated with metagenomics data of any type.

Our analysis is focused on the effect of the centered log-ratio (CLR) transformation when applied to compositional data.

We initially used synthetic datasets to isolate and systematically study the influence of key parameters such as dimensionality (D), within-sample diversity (Pielou’s index), and sparsity (zero counts). These controlled experiments allowed us to disentangle their individual and combined effects on correlation distortions.

We then confirmed the main findings on real-world data from Human Microbiome Project 2 (HMP2), showing that the same patterns of spurious correlation behavior observed in synthetic settings persist in practical scenarios.

Specifically, we found that the spurious correlations introduced by the CLR transformation decrease as a function of sample dimensionality. This contrasts with the L1 transformation, where spurious correlations are mainly influenced by the diversity within the dataset and do not decrease with sample dimensionality.

Given the high dimensionality that characterizes metagenomic datasets—in the order of hundreds or more OTUs or taxa—the spurious correlations associated with CLR thus become negligible, in general, when the commonly adopted assumption of a sparse correlation network is maintained.

The CLR transformation is also adequate to remove the effect of diversity for sufficiently high-dimensionality data (in the order of hundreds) without additional adjustments, at difference with L1 transformation for which high diversity remains an issue.

To validate the role of the CLR transformation in compositional data analysis, we conducted a comparative study using various algorithms specifically designed to estimate associations in metagenomic datasets.

Our findings indicate a striking convergence of SparCC and Rho with Pearson correlation on CLR-transformed data, particularly in high-dimensional settings. This agreement supports the idea that CLR, despite its simplicity, is sufficient to recover robust correlation patterns when dimensionality is high, with more complex corrections (such as those implemented in SparCC) becoming relevant only in low-dimensional contexts.

This convergence suggests that the log-ratio transformation is the critical normalizing step across all methods, effectively neutralizing the compositional bias inherent to the data.

However, we must also acknowledge the substantial impact of dataset sparsity (i.e., the presence of many species with zero counts in many samples) on correlation measures: the large number of zero counts associated with low-abundance taxa can significantly distort correlations, more severely affecting negative correlations.

While CLR mitigates these distortions, the proportion of zero counts is the crucial parameter: the larger the zero count ratio, the larger the distortion. It is thus impossible to entirely eliminate the bias introduced by zero counts, unless we eliminate any information about very rare species.

A compromise must thus be found between minimizing correlation distortions and retaining low-abundance species in the analysis. This trade-off is fundamental for ensuring the accuracy and comprehensiveness of metagenomic data interpretation as a function of the study design.