Physics-Based Data Augmentation Enables Accurate Machine Learning Prediction of Melt Pool Geometry
Abstract
Featured Application
Abstract
1. Introduction
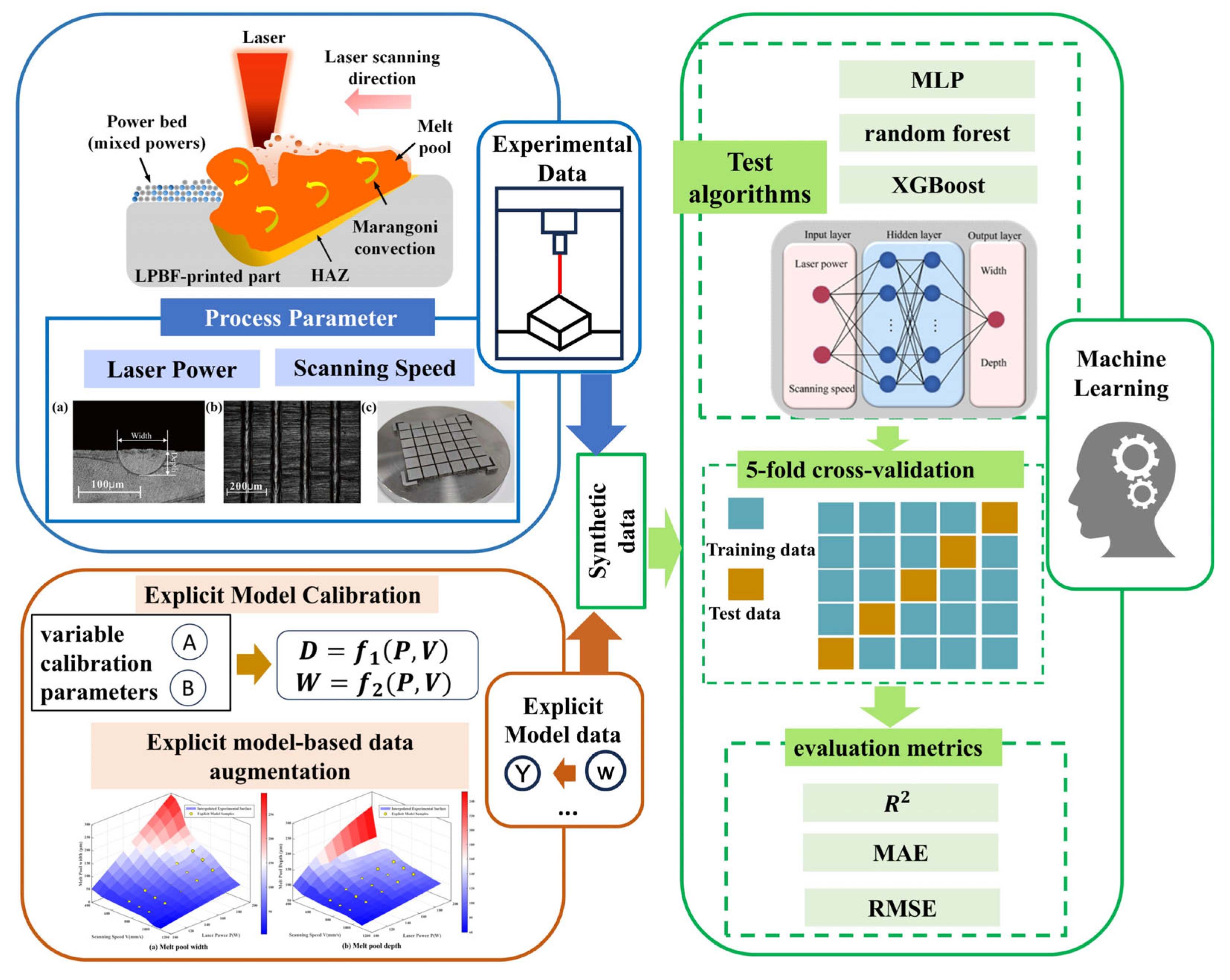
2. Materials and Methods
2.1. Experimental Materials and Design
2.2. Explicit Model-Based Data Augmentation
2.3. Framework Overview and Motivation
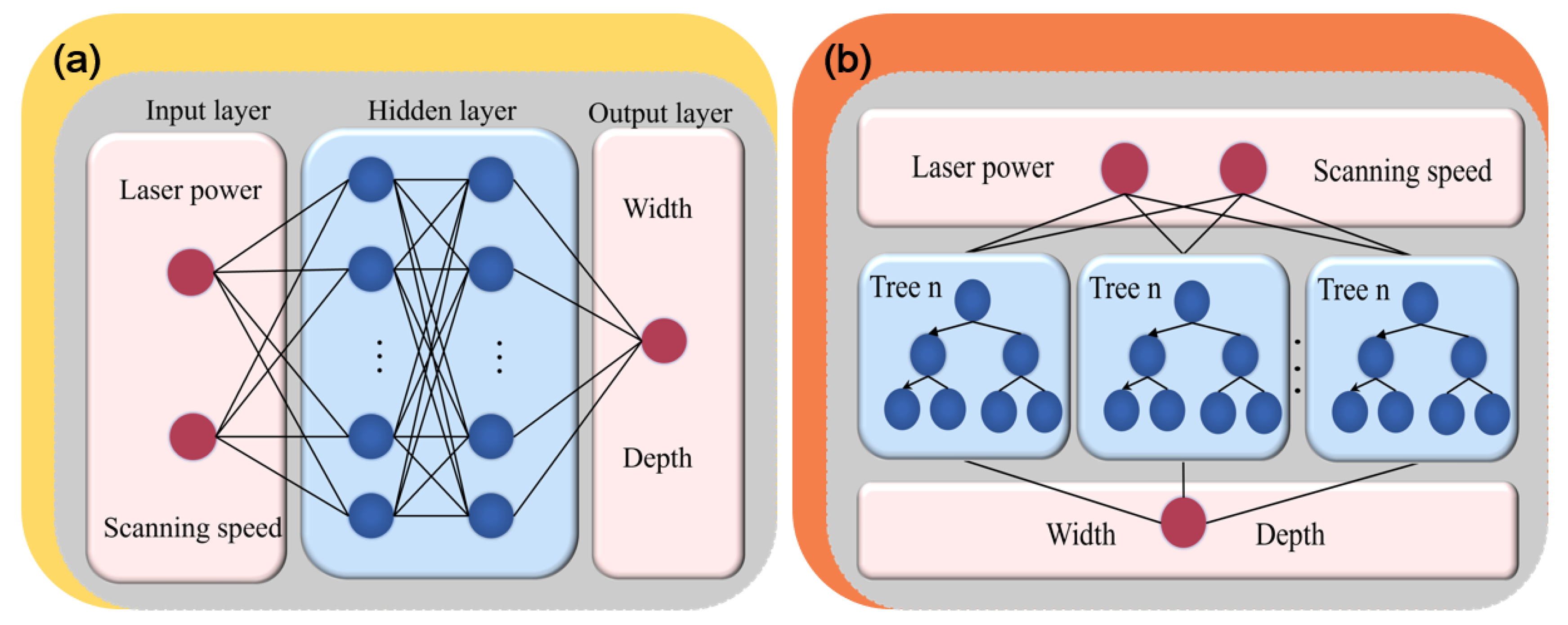
2.4. Machine Learning Modeling and Optimization
- (coefficient of determination): measures how well predictions approximate actual values.
- MAE (mean absolute error): evaluates average absolute deviation.
- RMSE (root mean squared error): penalizes larger errors more severely.
3. Results and Discussion
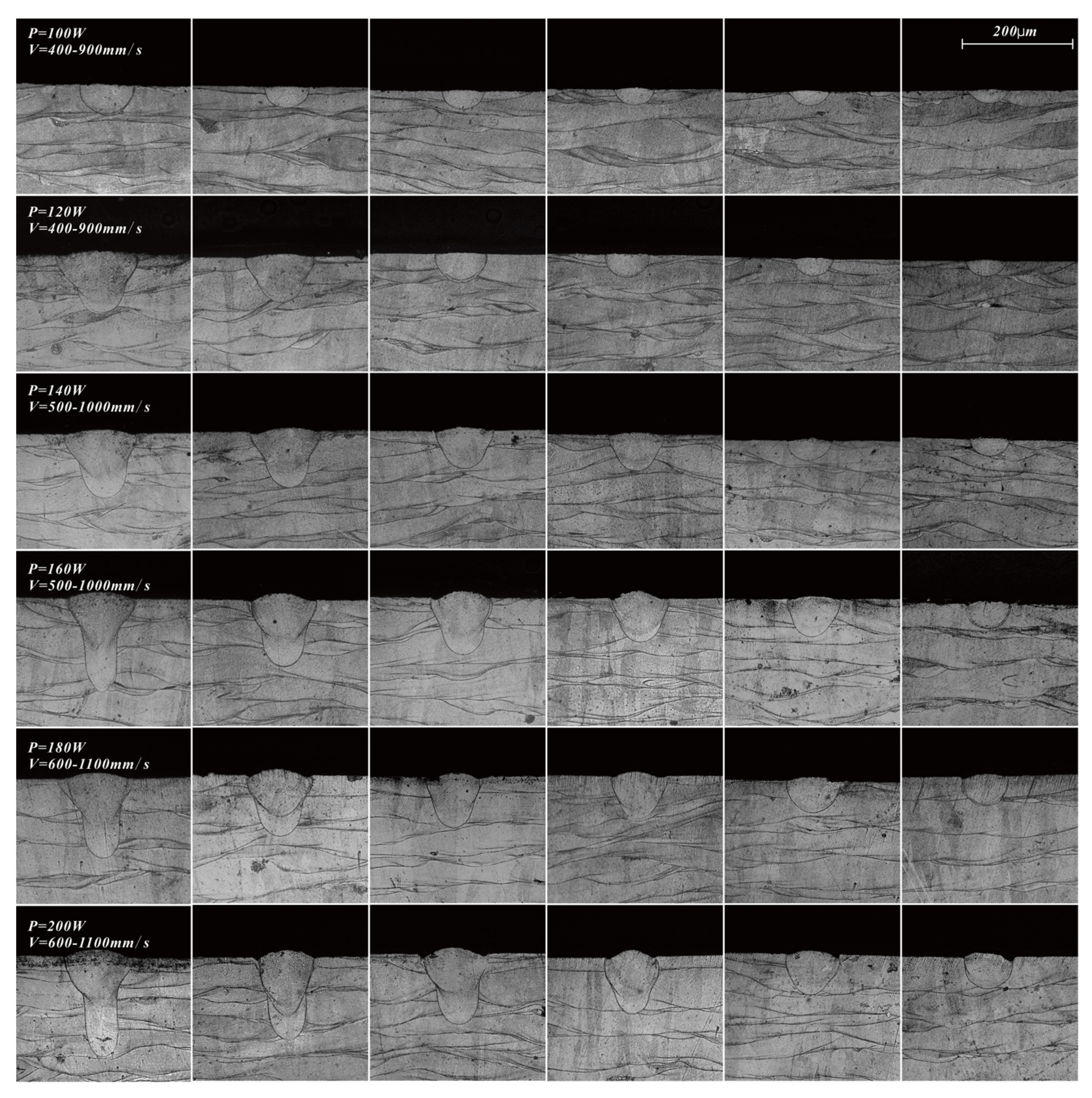
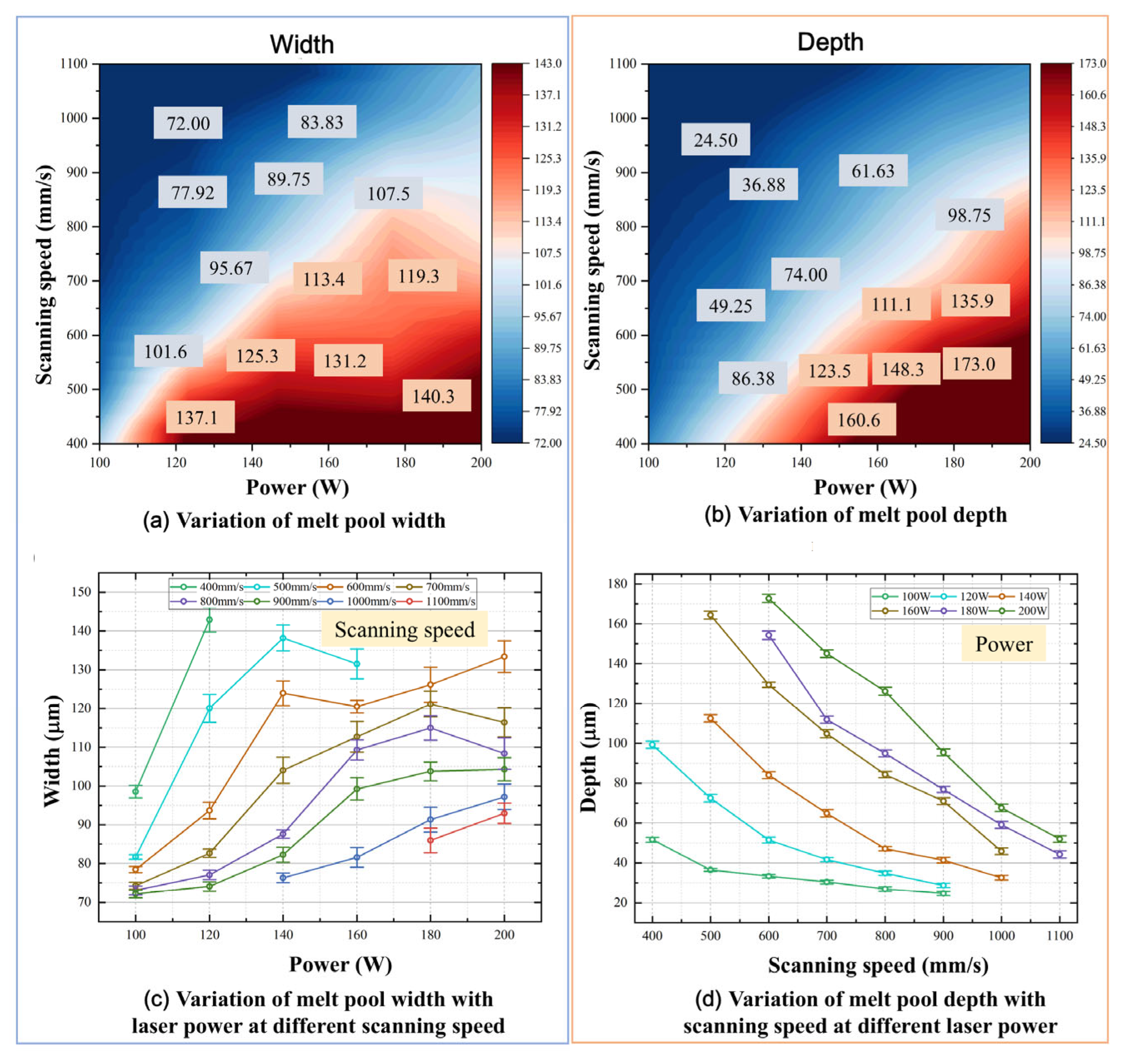
3.1. Analysis of Experimental Data
3.2. Calibration of the Explicit Model
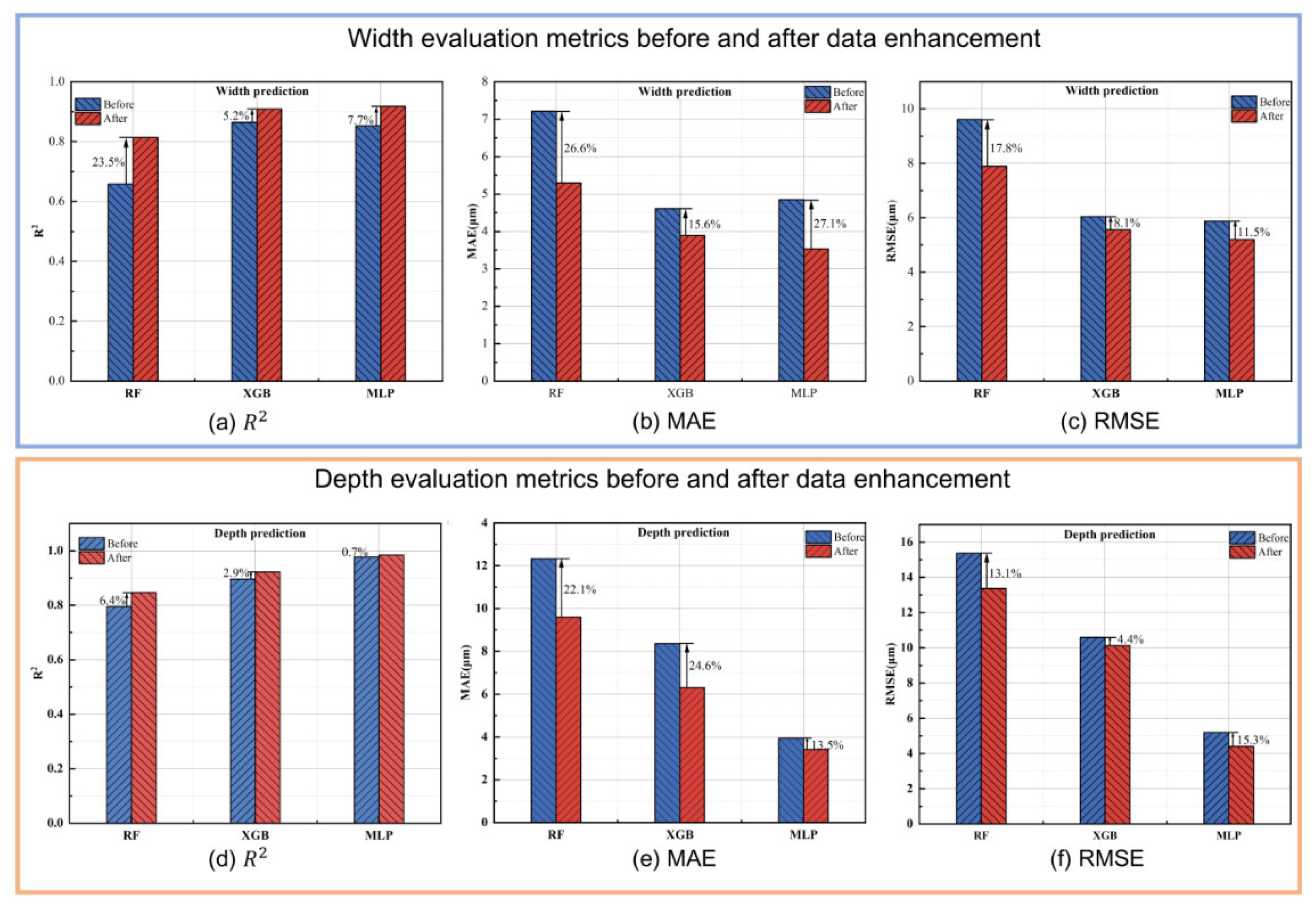
3.3. Model Training Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ASTM52900-15; Standard Terminology for Additive Manufacturing—General Principles—Terminology. ASTM International: West Conshohocken, PA, USA, 2015.
- Guo, C.; Xu, Z.; Li, G.; Wang, J.; Hu, X.; Li, Y.; Lu, J. Printability, microstructures, and mechanical properties of a novel Co-based superalloy fabricated via laser powder bed fusion. J. Mater. Sci. Technol. 2024, 189, 96–109. [Google Scholar] [CrossRef]
- Araya, M.; Jaskari, M.; Rautio, T.; Guillén, T.; Järvenpää, A. Assessing the compressive and tensile properties of TPMS-Gyroid and stochastic Ti64 lattice structures: A study on laser powder bed fusion manufacturing for biomedical implants. J. Sci. Adv. Mater. Devices 2024, 9, 100663. [Google Scholar] [CrossRef]
- Rosenthal, S.; Bechler, N.; Hahn, M.; Tekkaya, A.E. Large sandwich sheets enabled by joining rolled sheets and additively manufactured core structures. Manuf. Lett. 2023, 35, 249–257. [Google Scholar] [CrossRef]
- Coldsnow, K.; Yan, D.; Paul, G.E.; Torbati-Sarraf, H.; Poorganji, B.; Ertorer, O.; Isgor, O.B. Electrochemical behavior of alloy 22 processed by L-PBF. Electrochim. Acta 2022, 421, 140519. [Google Scholar] [CrossRef]
- Lanzutti, A.; Sordetti, F.; Montanari, R.; Varone, A.; Marin, E.; Andreatta, F.; Fedrizzi, L. Effect of powder recycling on inclusion content in AISI 316L produced by L-PBF. J. Mater. Res. Technol. 2023, 23, 3638–3650. [Google Scholar] [CrossRef]
- Ramirez-Cedillo, E.; Uddin, M.J.; Sandoval-Robles, J.A.; Mirshams, R.A.; Ruiz-Huerta, L.; Rodriguez, C.A.; Siller, H.R. Process planning of L-PBF of AISI 316L for improving surface quality and relating part integrity with microstructural characteristics. Surf. Coat. Technol. 2020, 396, 125956. [Google Scholar] [CrossRef]
- Tusher, M.M.H.; Ince, A. Exploring VHCF response in L-PBF AlSi7Mg alloy: Influence of T6 heat treatment on microstructural characteristics and defect distribution. Int. J. Fatigue 2024, 185, 108471. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, R.; Liu, Y.; Zhang, L. Understanding melt pool characteristics in laser powder bed fusion: An overview of single- and multi-track melt pools for process optimization. Adv. Powder Mater. 2023, 2, 100137. [Google Scholar] [CrossRef]
- Chouhan, A.; Aggarwal, A.; Kumar, A. Role of melt flow dynamics on track surface morphology in the L-PBF additive manufacturing process. Int. J. Heat Mass Transf. 2021, 178, 121602. [Google Scholar] [CrossRef]
- Cacace, S.; Semeraro, Q. On the lack of fusion porosity in L-PBF processes. Proc. CIRP 2022, 112, 352–357. [Google Scholar] [CrossRef]
- Galbusera, F.; Caprio, L.; Previtali, B.; Demir, A.G. The influence of novel beam shapes on melt pool shape and mechanical properties of L-PBF produced Al-alloy. J. Manuf. Process. 2023, 85, 1024–1036. [Google Scholar] [CrossRef]
- Kusuma, C.; Ahmed, S.H.; Mian, A.; Srinivasan, R. Effect of laser power and scan speed on melt pool characteristics of commercially pure titanium (CP-Ti). J. Mater. Eng. Perform. 2017, 26, 3560–3568. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, Y.; Strayer, S.; Zhao, Y.; Aoyagi, K.; Koizumi, Y.; To, A.C. Elucidating the effect of preheating temperature on melt pool morphology variation in Inconel 718 laser powder bed fusion via simulation and experiment. Addit. Manuf. 2021, 37, 101642. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y.; Li, X.; Zhong, Y.; Lin, K.; Liao, B.; Zhang, S. Single-track investigation of additively manufactured mold steel with larger layer thickness processing: Track morphology, melt pool characteristics and defects. Opt. Laser Technol. 2024, 171, 110378. [Google Scholar] [CrossRef]
- Qi, X.; Liang, X.; Wang, J.; Zhang, H.; Wang, X.; Liu, Z. Microstructure tailoring in laser powder bed fusion (L-PBF): Strategies, challenges, and future outlooks. J. Alloys Compd. 2024, 970, 172564. [Google Scholar] [CrossRef]
- Trageser, J.E.; Mitchell, J.A.; Johnson, K.L.; Rodgers, T.M. A Bézier curve fit to melt pool geometry for modeling additive manufacturing microstructures. Comput. Methods Appl. Mech. Eng. 2023, 415, 116208. [Google Scholar] [CrossRef]
- Kazemi, Z.; Soleimani, M.; Rokhgireh, H.; Nayebi, A. Melting pool simulation of 316L samples manufactured by selective laser melting method, comparison with experimental results. Int. J. Therm. Sci. 2022, 176, 107538. [Google Scholar] [CrossRef]
- Lüthi, C.; Afrasiabi, M.; Bambach, M. An adaptive smoothed particle hydrodynamics (SPH) scheme for efficient melt pool simulations in additive manufacturing. Comput. Math. Appl. 2023, 139, 7–27. [Google Scholar] [CrossRef]
- De Leon, E.; Riensche, A.; Bevans, B.D.; Billings, C. A review of modeling, simulation, and process qualification of additively manufactured metal components via the laser powder bed fusion method. J. Manuf. Mater. Process. 2025, 9, 22. [Google Scholar] [CrossRef]
- Wang, C.; Tan, X.P.; Tor, S.B.; Lim, C.S. Machine learning in additive manufacturing: State-of-the-art and perspectives. Addit. Manuf. 2020, 36, 101538. [Google Scholar] [CrossRef]
- Wu, C.; Luo, J.; Zhong, J.; Xu, Y.; Wan, B.; Huang, W.; Li, Q. Topology optimisation for design and additive manufacturing of functionally graded lattice structures using derivative-aware machine learning algorithms. Addit. Manuf. 2023, 78, 103833. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.; Pan, Z.; Zhou, W. Recent progress of sensing and machine learning technologies for process monitoring and defects detection in wire arc additive manufacturing. J. Manuf. Process. 2024, 125, 489–511. [Google Scholar] [CrossRef]
- Maleki, E.; Shamsaei, N. A comprehensive study on the effects of surface post-processing on fatigue performance of additively manufactured AlSi10Mg: An augmented machine learning perspective on experimental observations. Addit. Manuf. 2024, 86, 104179. [Google Scholar] [CrossRef]
- Fan, F.; Jalui, S.; Shahed, K.; Mullany, B.; Manogharan, G. Mass finishing for additive manufacturing postprocessing: Tribological analysis, surface topology, image processing, predictive model, and processing recommendations. Tribol. Int. 2024, 204, 110486. [Google Scholar] [CrossRef]
- Karkaria, V.; Goeckner, A.; Zha, R.; Chen, J.; Zhang, J.; Zhu, Q.; Chen, W. Towards a digital twin framework in additive manufacturing: Machine learning and Bayesian optimization for time series process optimization. J. Manuf. Syst. 2024, 75, 322–332. [Google Scholar] [CrossRef]
- Roy, A.; Swope, A.; Devanathan, R.; Van Rooyen, I.J. Chemical composition based machine learning model to predict defect formation in additive manufacturing. Materialia 2024, 33, 102041. [Google Scholar] [CrossRef]
- Mohammed, A.S.; Almutahhar, M.; Sattar, K.; Alhajeri, A.; Nazir, A.; Ali, U. Deep learning based porosity prediction for additively manufactured laser powder-bed fusion parts. J. Mater. Res. Technol. 2023, 27, 7330–7335. [Google Scholar] [CrossRef]
- Akbari, P.; Ogoke, F.; Kao, N.Y.; Meidani, K.; Yeh, C.Y.; Lee, W.; Farimani, A.B. MeltpoolNet: Melt pool characteristic prediction in metal additive manufacturing using machine learning. Addit. Manuf. 2022, 55, 102817. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Le-Hong, T.; Lin, P.C.; Chen, J.Z.; Pham, T.D.Q.; Van Tran, X. Data-driven models for predictions of geometric characteristics of bead fabricated by selective laser melting. J. Intell. Manuf. 2023, 34, 1241–1257. [Google Scholar] [CrossRef]
- Inayathullah, S.; Buddala, R. Review of machine learning applications in additive manufacturing. Results Eng. 2024, 25, 103676. [Google Scholar] [CrossRef]
- Mundra, P.; Debnath, D.; Garg, A. A Supervised Machine Learning Model for Regression to Predict Melt Pool Formation and Morphology in Laser Powder Bed Fusion. Appl. Sci. 2023, 13, 3720. [Google Scholar] [CrossRef]
- Guo, S.; Agarwal, M.; Cooper, C.; Tian, Q.; Gao, R.X.; Grace, W.G.; Guo, Y.B. Machine learning for metal additive manufacturing: Towards a physics-informed data-driven paradigm. J. Manuf. Syst. 2022, 62, 145–163. [Google Scholar] [CrossRef]
- Mondal, S.; Gwynn, D.; Ray, A.; Basak, A. Investigation of Melt Pool Geometry Control in Additive Manufacturing Using Hybrid Modeling. Metals 2020, 10, 683. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, Z.; Yan, J. Machine learning for metal additive manufacturing: Predicting temperature and melt pool fluid dynamics using physics-informed neural networks. Comput. Mech. 2021, 68, 1061–1076. [Google Scholar] [CrossRef]
- Sharma, R.; Raissi, M.; Guo, Y. Physics-informed deep learning of gas flow–melt pool multi-physical dynamics during powder bed fusion. CIRP Ann. 2023, 72, 161–164. [Google Scholar] [CrossRef]
- Ritto, T.G.; Rochinha, F.A. Digital twin, physics-based model, and machine learning applied to damage detection in structures. Mech. Syst. Signal Process. 2021, 155, 107614. [Google Scholar] [CrossRef]
- Ren, K.; Chew, Y.; Zhang, Y.F.; Fuh, J.Y.H.; Bi, G.J. Thermal field prediction for laser scanning paths in laser aided additive manufacturing by physics-based machine learning. Comput. Methods Appl. Mech. Eng. 2020, 362, 112734. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Hong, J.K.; Kang, N.; Choi, Y.S. Calibration of laser penetration depth and absorptivity in finite element method based modeling of powder bed fusion melt pools. Met. Mater. Int. 2020, 26, 891–902. [Google Scholar] [CrossRef]
- Guo, M.; Gu, D.; Xi, L.; Du, L.; Zhang, H.; Zhang, J. Formation of scanning tracks during selective laser melting (SLM) of pure tungsten powder: Morphology, geometric features and forming mechanisms. Int. J. Refract. Met. Hard Mater. 2019, 79, 37–46. [Google Scholar] [CrossRef]
- Dilip, J.J.S.; Zhang, S.; Teng, C.; Zeng, K.; Robinson, C.; Pal, D.; Stucker, B. Influence of processing parameters on the evolution of melt pool, porosity, and microstructures in Ti-6Al-4V alloy parts fabricated by selective laser melting. Prog. Addit. Manuf. 2017, 2, 157–167. [Google Scholar] [CrossRef]
- ASTM E8/E8M-15; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2015.
- Huang, Y.; Fleming, T.G.; Clark, S.J.; Marussi, S.; Withers, P.J. Keyhole fluctuation and pore formation mechanisms during laser powder bed fusion additive manufacturing. Nat. Commun. 2022, 13, 1079. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Parab, N.D.; Li, X.; Fezzaa, K.; Tan, W.; Rollett, A.D. Critical instability at moving keyhole tip generates porosity in laser melting. Science 2020, 370, 1080–1086. [Google Scholar] [CrossRef] [PubMed]

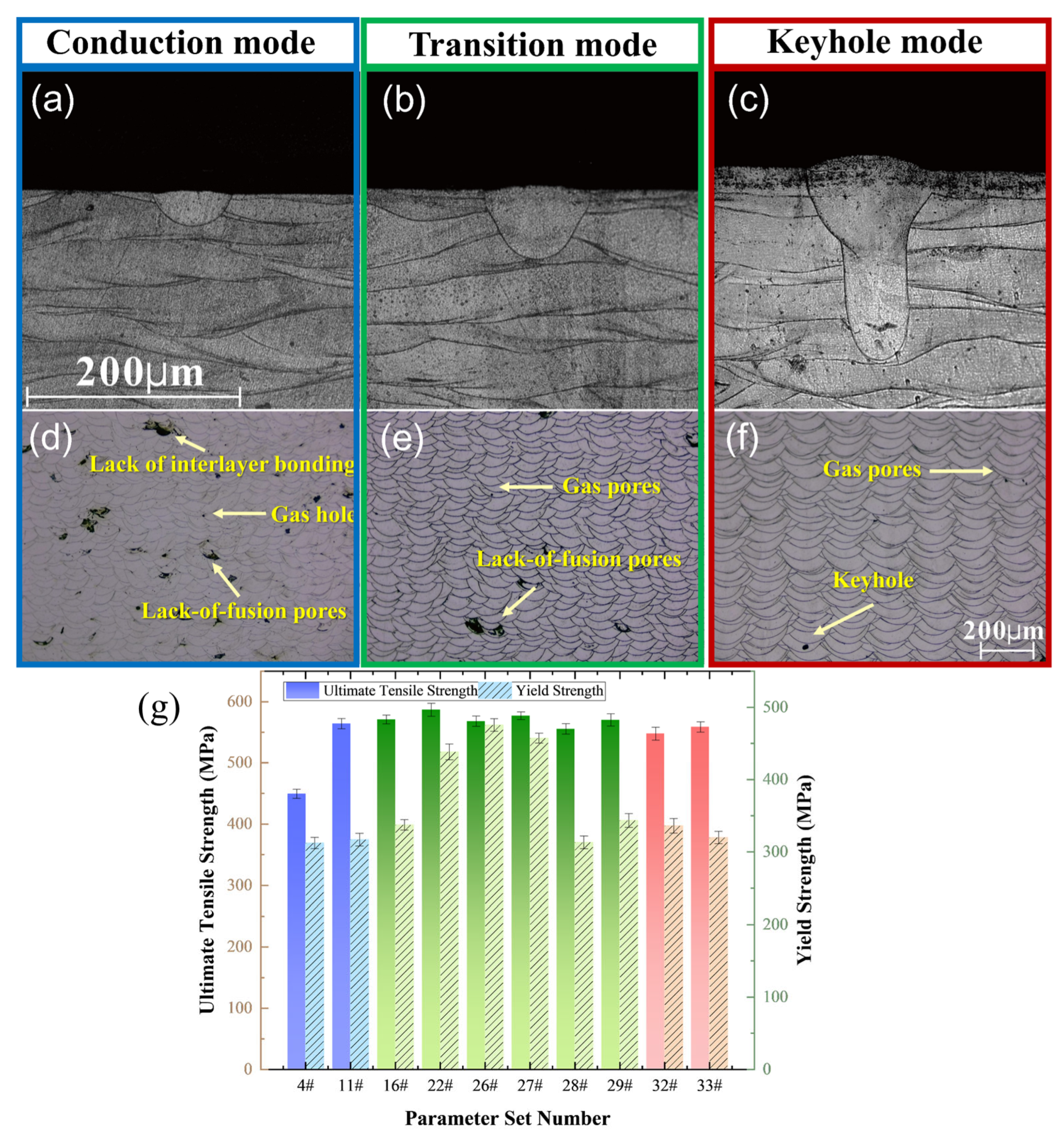
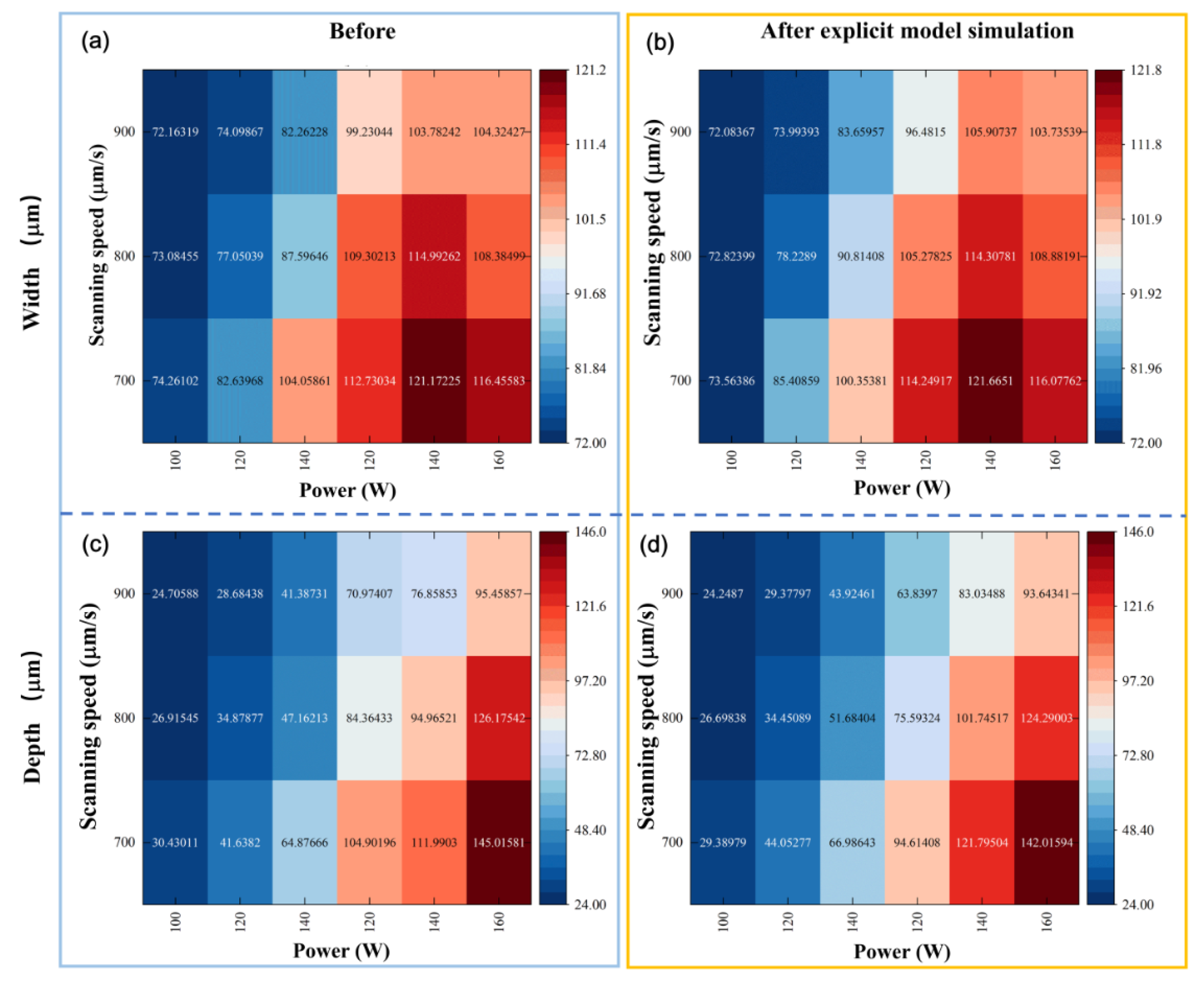
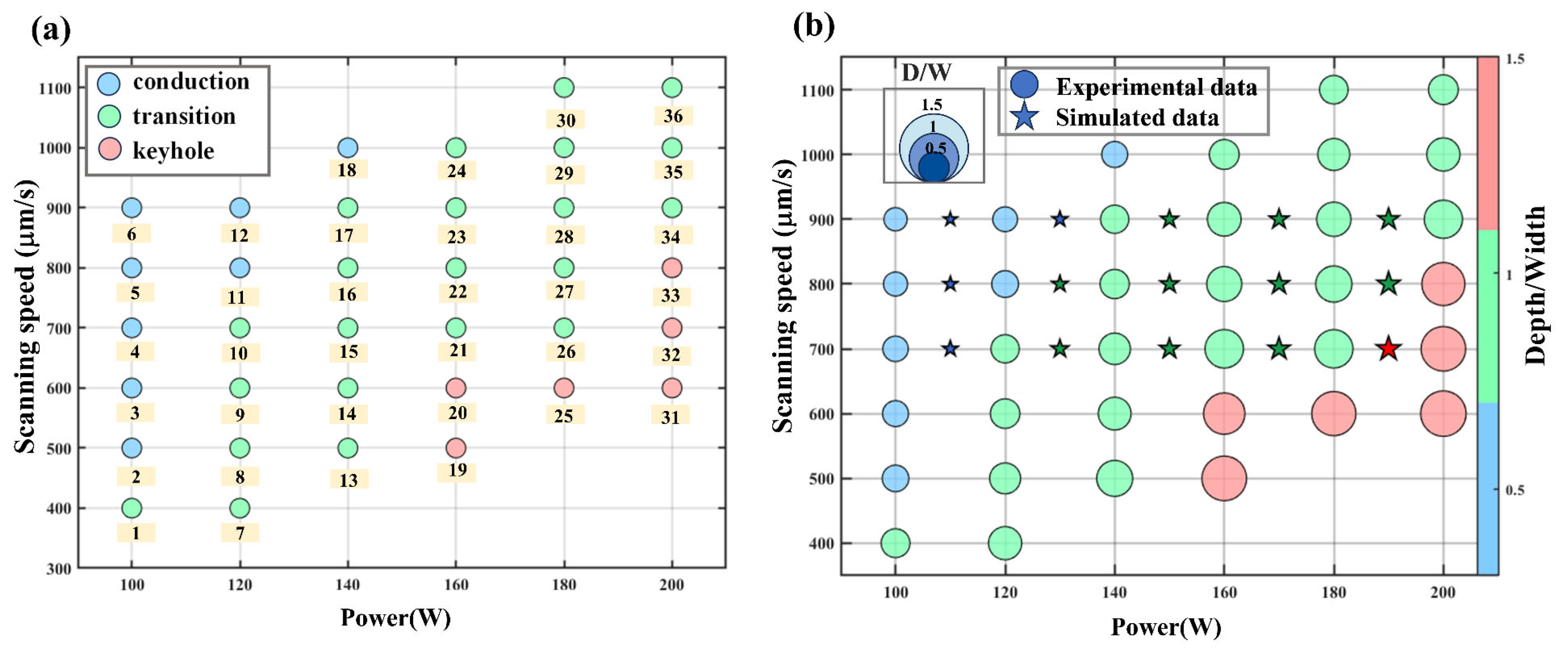
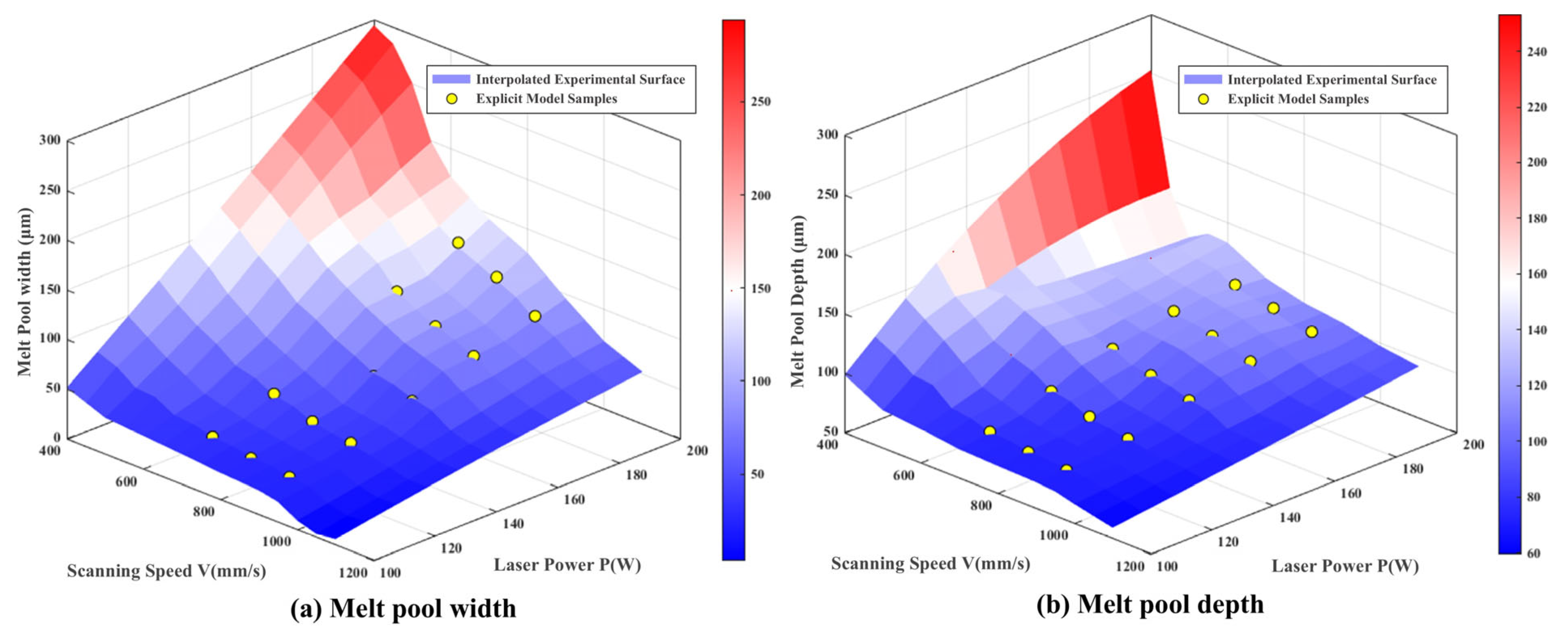


| Elements | Fe | C | Cr | Ni | Mo | Mn | Si |
|---|---|---|---|---|---|---|---|
| 316 L | 67.98 | 0.0086 | 17.11 | 11.01 | 2.42 | 0.81 | 0.66 |
| Process Parameters (Symbol, Unit) | Values |
|---|---|
| Laser power (P, W) | 100, 120, 140, 160, 180, 200 |
| Scan speed (V, mm/s) | 400, 500, 600, 700, 800, 900, 1000, 1100 |
| Laser spot diameter (, mm) | 0.06 |
| Hatch spacing (d, mm) | 0.5 |
| Layer thickness (H, mm) | 0.03 |
| Task (Label) | Equation |
|---|---|
| Depth | |
| Width |
| Model Number | The Number of Neurons in the Hidden Layer | ||||
|---|---|---|---|---|---|
| First Layer | Second Layer | Third Layer | Forth Layer | Fifth Layer | |
| Model 1 | 48 | 32 | - | - | - |
| Model 2 | 48 | 32 | 16 | - | - |
| Model 3 | 64 | 48 | 32 | 16 | - |
| Model 4 | 64 | 48 | 32 | 16 | 8 |
| Model | Hyperparameters | Before Data Enhancement | Data Enhancement |
|---|---|---|---|
| RF | n_estimators | 372 | 148 |
| max_depth | 6 | 191 | |
| min_samples_split | 2 | 2 | |
| min_samples_leaf | 1 | 1 | |
| XGBoost | n_estimators | 1213 | 1066 |
| learning_rate | 0.1 | 0.3 | |
| max_depth | 4 | 3 | |
| min_child_weight | 1 | 1 | |
| Subsample | 0.8 | 0.8 |
| Scanning Speed (mm/s) | Laser Power (W) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | |
| 400 | S0 | - | S9 | - | - | - | - | - | - | - | - |
| 500 | S1 | - | S10 | - | S18 | - | S27 | - | - | - | - |
| 600 | S2 | - | S11 | - | S19 | - | S28 | - | S36 | - | S45 |
| 700 | S3 | S6 * | S12 | S15 * | S20 | S24 * | S29 | S33 * | S37 | S42 * | S46 |
| 800 | S4 | S7 * | S13 | S16 * | S21 | S25 * | S30 | S34 * | S38 | S43 * | S47 |
| 900 | S5 | S8 * | S14 | S17 * | S22 | S26 * | S31 | S35 * | S39 | S44 * | S48 |
| 1000 | - | - | - | - | S23 | - | S32 | - | S40 | - | S49 |
| 1100 | - | - | - | - | - | - | - | - | S41 | - | S50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Li, R.; Zhou, J.; Dai, C.; Yu, J.; Zhang, Q. Physics-Based Data Augmentation Enables Accurate Machine Learning Prediction of Melt Pool Geometry. Appl. Sci. 2025, 15, 8587. https://doi.org/10.3390/app15158587
Liu S, Li R, Zhou J, Dai C, Yu J, Zhang Q. Physics-Based Data Augmentation Enables Accurate Machine Learning Prediction of Melt Pool Geometry. Applied Sciences. 2025; 15(15):8587. https://doi.org/10.3390/app15158587
Chicago/Turabian StyleLiu, Siqi, Ruina Li, Jiayi Zhou, Chaoyuan Dai, Jingui Yu, and Qiaoxin Zhang. 2025. "Physics-Based Data Augmentation Enables Accurate Machine Learning Prediction of Melt Pool Geometry" Applied Sciences 15, no. 15: 8587. https://doi.org/10.3390/app15158587
APA StyleLiu, S., Li, R., Zhou, J., Dai, C., Yu, J., & Zhang, Q. (2025). Physics-Based Data Augmentation Enables Accurate Machine Learning Prediction of Melt Pool Geometry. Applied Sciences, 15(15), 8587. https://doi.org/10.3390/app15158587






