Research on the Cross-Efficiency Model of the Innovation Dynamic Network in China’s High-Tech Manufacturing Industry
Abstract
1. Introduction
2. Research Methods
2.1. Cross-Efficiency Model
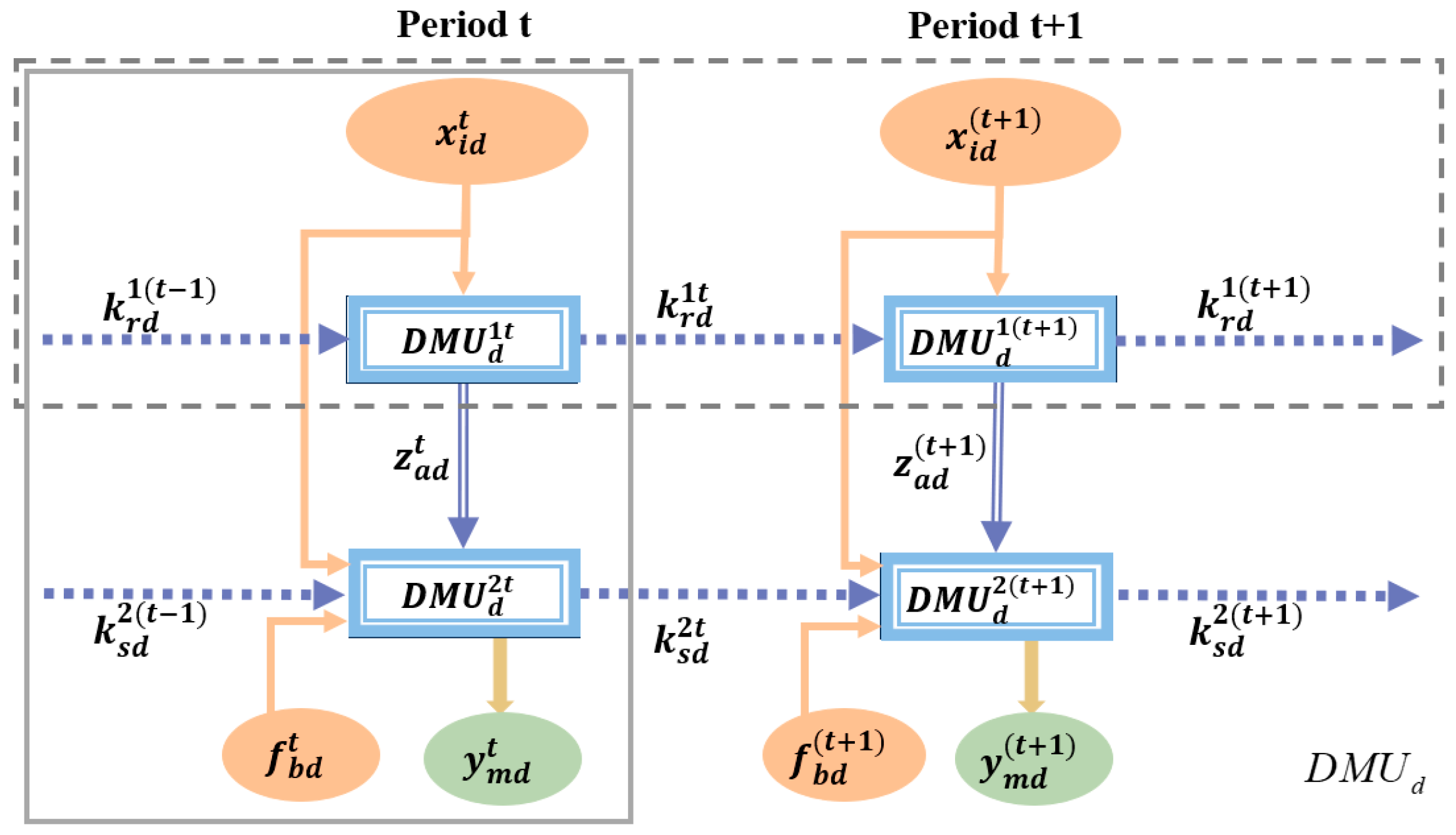
2.2. Two-Stage Dynamic Network Model
2.3. Two-Stage Dynamic Network Cross-Efficiency Model
3. Empirical Research
3.1. Selection of the Indicator System
3.2. Data Sources and Processing
3.2.1. Data Sources
3.2.2. Calculation of the Stock of Funds
3.3. Analysis of Results
3.3.1. Analysis of Cross-Efficiency Modeling Results
3.3.2. Analysis of the Results of the Two-Stage Dynamic Network Model
3.3.3. Analysis of the Results of the Two-Stage Dynamic Network Cross-Efficiency Model
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.Y.; Zheng, X.R.; Li, S.Q.; Wei, A.L. Measurement of the Development Level of China’s Provincial High-Tech Industries from 2019 to 2021. Stat. Appl. 2024, 13, 202–219. [Google Scholar]
- Han, C.; Thomas, S.R.; Yang, M.; Ieromonachou, P.; Zhang, H.R. Evaluating R&D investment efficiency in China’s high-tech industry. J. High Technol. Manag. Res. 2017, 28, 93–109. [Google Scholar]
- Ding, S. A novel discrete grey multivariable model and its application in forecasting the output value of China’s high-tech industries. Comput. Ind. Eng. 2019, 127, 749–760. [Google Scholar] [CrossRef]
- Li, J.; Feng, H.Y. The Economic Growth Effect of the High-tech Manufacturing Industry and High-Tech Service Industry Co-Agglomeration. Sci. Technol. Prog. Policy 2020, 37, 54–62. [Google Scholar]
- Yu, K.; Gong, R.; Hu, S.; Luo, Y. Based on Analytic Hierarchy Process to Discuss Key Factors in High-tech Industrial Ecology Development. Ekoloji Derg. 2018, 106, 449. [Google Scholar]
- Meng, L.; Sun, L.Y. The Influencing Factors of Technological Innovation Efficiency in High-tech Industry: An Analysis from the Perspective of Industry. J. Nanchang Norm. Univ. 2019, 40, 20–22. [Google Scholar]
- Gui, J.Y. Measurement and Improvement Strategy of China’s Provincial High-tech Industry Development Level. Econ. Rev. J. 2018, 7, 83–92. [Google Scholar]
- Chen, X.X.; Shi, D.H. An Analysis of the Comprehensive Evaluation of High-Quality Development of High-tech Industry in China. J. Nanjing Univ. Financ. Econ. 2019, 5, 34–44. [Google Scholar]
- Wang, Z.X.; Wang, Y.Y. Evaluation of the provincial competitiveness of the Chinese high-tech industry using an improved TOPSIS method. Expert Syst. Appl. 2014, 41, 2824–2831. [Google Scholar] [CrossRef]
- Wang, R.D.; Zhang, J.J. Research on the measurement of the level of global industrial chain of China’s provincial high tech industry. Times Econ. Trade 2020, 29, 6–10. [Google Scholar]
- Liu, C.Y.; Gao, X.Y.; Ma, W.L.; Chen, X.T. Research on regional differences and influencing factors of green technology innovation efficiency of China’s high-tech industry. J. Comput. Appl. Math. 2020, 369, 112597. [Google Scholar] [CrossRef]
- Yang, X.Q.; Peng, J.X.; Wang, J. Research on the Transformation Efficiency of Scientific and Technological Achievements of High-tech Industry in China Based on DEA Model. Inn. Mong. Sci. Technol. Econ. 2023, 12, 25–27. [Google Scholar]
- Zhang, B.; Luo, Y.; Chiu, Y.H. Efficiency evaluation of China’s high-tech industry with a multi-activity network data envelopment analysis approach. Socio-Econ. Plan. Sci. 2019, 66, 2–9. [Google Scholar] [CrossRef]
- Yu, Y.; Liao, J.Q.; Wang, X.M.; Zhu, W.W. Identifying the drivers of new product development performance change in China’s high-tech industry: A two-stage production-theoretical decomposition analysis. Expert Syst. Appl. 2024, 261, 125513. [Google Scholar] [CrossRef]
- Yang, J.W.; Wang, M.Q.; Li, D. Research on R&D Innovation Efficiency Evaluation of China’s Provincial High-tech Industry Based on Two-stage DEA Model with Shared Inputs. Sci. Technol. Manag. Res. 2017, 37, 84–90. [Google Scholar]
- Wang, Y.; Pan, J.F.; Pei, R.M.; Yi, B.W.; Yang, G.L. Assessing the technological innovation efficiency of China’s high-tech industries with a two-stage network DEA approach. Socio-Econ. Plan. Sci. 2020, 71, 100810. [Google Scholar] [CrossRef]
- Chen, Y.W.; Wang, M.Q.; Chen, Y.Y.; Geng, J.G. Research on the Efficiency of China’s High-tech Industry R&D Innovation Based on the Improved Two-stage DEA. Soft Sci. 2018, 32, 14–18. [Google Scholar]
- Lin, S.F.; Lin, R.Y.; Sun, J.; Wang, F.; Wu, W.X. Dynamically evaluating technological innovation efficiency of high-tech industry in China: Provincial, regional and industrial perspective. Socio-Econ. Plan. Sci. 2021, 74, 100939. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, C.X.; Li, C.Y.; Feng, Z.J. Innovation Efficiency Evaluation of New and High Technology Industries Based on DEA-Malmquist Index. Sci. Technol. Manag. Res. 2017, 37, 79–84. [Google Scholar] [CrossRef]
- Wang, S.T.; Lin, X. Research on innovation efficiency evaluation of high-tech enterprises based on DEA-Malmquist index model. Hebei Enterp. 2024, 9, 21–25. [Google Scholar]
- He, Y.B.; Zhang, S.; Lin, T. Research on efficiency measurement of China’s high-tech industry innovation ecosystem and its improvement path. Syst. Eng.—Theory Pract. 2024, 44, 546–562. [Google Scholar]
- Wang, Q.J.; Wang, Q.; Zhou, X. Research on Efficiency Evaluation and Influencing Factors of High-Tech Industry R&D Activities. Sci. Technol. Prog. Policy 2018, 35, 59–65. [Google Scholar]
- Sexton, T.R.; Silkman, R.H.; Hogan, A.J. Data envelopment analysis: Critique and extensions. New Dir. Program Eval. 1986, 32, 73–105. [Google Scholar] [CrossRef]
- Doyle, J.; Green, R. Efficiency and cross efficiency in DEA: Derivations meanings and the uses. J. Oper. Res. Soc. 1994, 45, 567–578. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chin, K.S. A neutral DEA model for cross—Efficiency evaluation and its extension. Expert Syst. Appl. 2010, 37, 3666–3675. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Management, Model and Industrial Applications of Linear Programming; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Chen, Y.; Du, J.; Sherman, H.D.; Zhu, J. DEA model with shared resources and efficiency decomposition. Eur. J. Oper. Res. 2010, 207, 339–349. [Google Scholar] [CrossRef]
- Liu, Z.H.; Xi, C.J.; Yang, Y. The Measurement Method of Regional Scientific and Technological Innovation Efficiency Based on Dynamic Network SBM Model. Inf. Sci. 2022, 40, 145–153. [Google Scholar]
- Hollanders, H.J.; Celikel-Esser, F. Measuring Innovation Efficiency; INNO Metrics Thematic Paper; European Commission: Brussels, Belgium, 2007. [Google Scholar]
- Deng, J. The R&D Capital Stock and Output Efficiency of the Hi-tech Industry in China. South China J. Econ. 2007, 8, 56–64. [Google Scholar]
- Wen, J.Q. Research on the measurement of enterprise R&D capital stock under the perspective of SNA. China Collect. Econ. 2022, 31, 91–93. [Google Scholar]
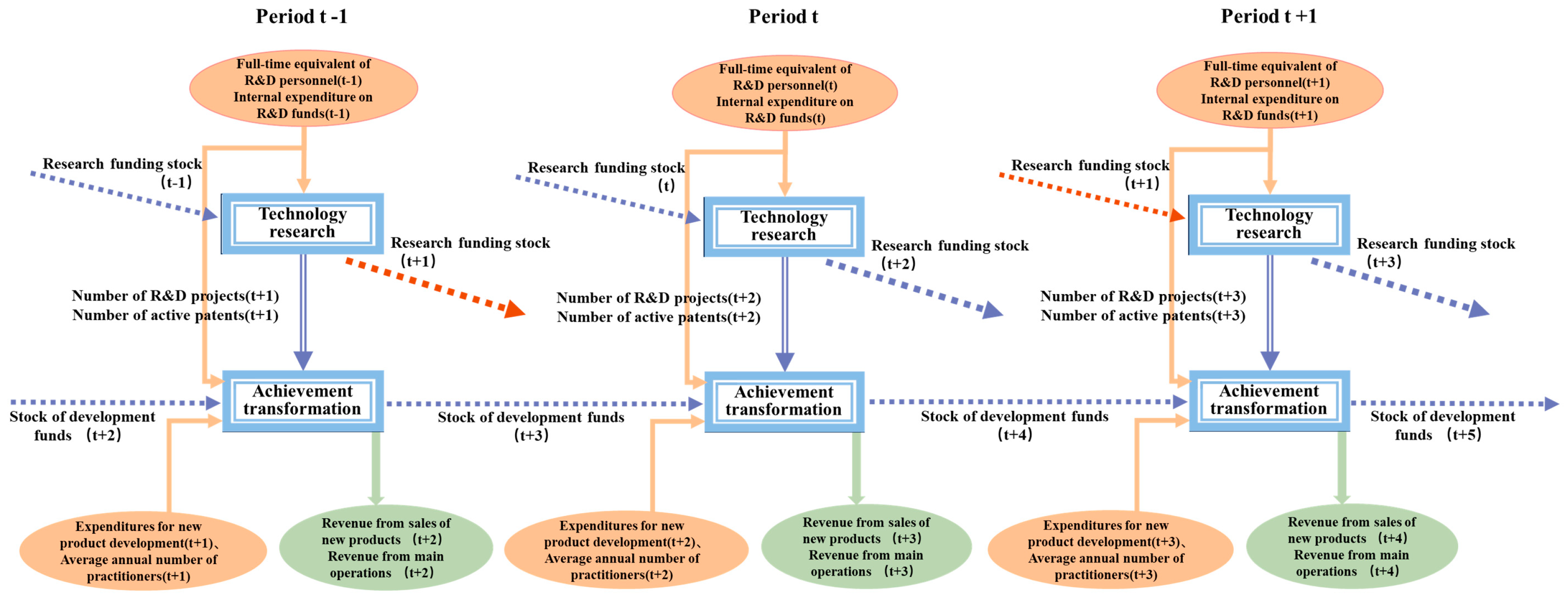



| Segmentation by Stage | Form | Indicator |
|---|---|---|
| Technology research stage | Shared input indicator | Full-time equivalent of R&D personnel (t) |
| Internal expenditure on R&D funds (t) | ||
| Link output indicator | Number of R&D projects (t + 2) | |
| Number of active patents (t + 2) | ||
| Carry-over output indicator | Research funding stock (t + 2) | |
| Achievement transformation stage | Independent input indicator | Expenditures for new product development (t + 2) |
| Average annual number of practitioners (t + 2) | ||
| Carry-over output indicator | Stock of development funds (t + 3) | |
| Final output indicator | Revenue from sales of new products (t + 3) | |
| Revenue from main operations (t + 3) |
| Particular Year | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|---|---|---|---|---|---|---|---|
| Expenditure price index | 101.03 | 101.91 | 107.44 | 106.28 | 103.27 | 101.13 | 109.48 | 105.20 |
| Serial Number | DMU | 2016 | 2017 | 2018 | 2019 | Average Efficiency |
|---|---|---|---|---|---|---|
| 1 | Shanghai | 0.522 | 0.481 | 0.352 | 0.230 | 0.396 |
| 2 | Yunnan | 0.675 | 1 | 0.557 | 0.466 | 0.675 |
| 3 | Neimenggu | 0.602 | 0.346 | 0.623 | 1 | 0.643 |
| 4 | Beijing | 1 | 1 | 1 | 0.569 | 0.892 |
| 5 | Jilin | 0.396 | 0.342 | 0.418 | 0.761 | 0.479 |
| 6 | Sichuan | 0.571 | 0.477 | 0.479 | 0.311 | 0.459 |
| 7 | Tianjin | 0.626 | 0.681 | 0.689 | 0.461 | 0.614 |
| 8 | Ningxia | 1 | 1 | 0.904 | 1 | 0.976 |
| 9 | Anhui | 0.927 | 1 | 0.790 | 0.545 | 0.816 |
| 10 | Shandong | 0.463 | 0.564 | 0.695 | 0.555 | 0.569 |
| 11 | Shanxi | 0.669 | 0.631 | 0.803 | 0.732 | 0.709 |
| 12 | Guangdong | 0.948 | 0.865 | 0.533 | 0.347 | 0.673 |
| 13 | Guangxi | 1 | 0.645 | 1 | 0.565 | 0.802 |
| 14 | Xinjiang | 1 | 0.208 | 1 | 1 | 0.802 |
| 15 | Jiangsu | 0.673 | 0.814 | 0.615 | 0.472 | 0.644 |
| 16 | Jiangxi | 1 | 1 | 0.995 | 0.610 | 0.901 |
| 17 | Hebei | 0.541 | 0.573 | 0.522 | 0.422 | 0.514 |
| 18 | Henan | 1 | 1 | 1 | 1 | 1 |
| 19 | Zhejiang | 0.840 | 0.903 | 0.696 | 0.540 | 0.745 |
| 20 | Hainan | 0.131 | 0.119 | 0.182 | 0.909 | 0.335 |
| 21 | Hubei | 0.796 | 0.728 | 0.427 | 0.374 | 0.581 |
| 22 | Hunan | 0.533 | 0.568 | 0.599 | 0.445 | 0.536 |
| 23 | Gansu | 1 | 0.413 | 0.626 | 0.348 | 0.597 |
| 24 | Fujian | 0.756 | 0.627 | 0.633 | 0.335 | 0.588 |
| 25 | Guizhou | 0.325 | 0.305 | 0.329 | 0.266 | 0.306 |
| 26 | Liaoning | 0.372 | 0.351 | 0.404 | 0.313 | 0.360 |
| 27 | Chongqing | 0.979 | 0.897 | 0.826 | 0.447 | 0.787 |
| 28 | Shaanxi | 0.346 | 0.255 | 0.316 | 0.268 | 0.296 |
| 29 | Qinghai | 0.705 | 1 | 0.949 | 1 | 0.913 |
| 30 | Heilongjiang | 0.765 | 0.492 | 1 | 0.337 | 0.648 |
| Serial Number | DMU | 2016 | 2017 | 2018 | 2019 | Average Efficiency |
|---|---|---|---|---|---|---|
| 1 | Shanghai | 0.461 | 0.424 | 0.327 | 0.192 | 0.351 |
| 2 | Yunnan | 0.413 | 0.993 | 0.469 | 0.406 | 0.570 |
| 3 | Neimenggu | 0.246 | 0.245 | 0.497 | 0.723 | 0.428 |
| 4 | Beijing | 0.857 | 0.890 | 1.000 | 0.382 | 0.782 |
| 5 | Jilin | 0.348 | 0.323 | 0.374 | 0.391 | 0.359 |
| 6 | Sichuan | 0.486 | 0.455 | 0.450 | 0.276 | 0.417 |
| 7 | Tianjin | 0.508 | 0.559 | 0.577 | 0.410 | 0.514 |
| 8 | Ningxia | 0.967 | 0.933 | 0.833 | 0.923 | 0.914 |
| 9 | Anhui | 0.827 | 0.919 | 0.773 | 0.462 | 0.745 |
| 10 | Shandong | 0.391 | 0.448 | 0.543 | 0.495 | 0.469 |
| 11 | Shanxi | 0.438 | 0.387 | 0.690 | 0.503 | 0.505 |
| 12 | Guangdong | 0.787 | 0.766 | 0.485 | 0.290 | 0.582 |
| 13 | Guangxi | 0.428 | 0.318 | 0.851 | 0.265 | 0.466 |
| 14 | Xinjiang | 0.374 | 0.109 | 0.826 | 0.227 | 0.384 |
| 15 | Jiangsu | 0.614 | 0.759 | 0.609 | 0.413 | 0.599 |
| 16 | Jiangxi | 0.901 | 0.838 | 0.876 | 0.544 | 0.790 |
| 17 | Hebei | 0.446 | 0.472 | 0.505 | 0.313 | 0.434 |
| 18 | Henan | 0.831 | 0.802 | 0.997 | 0.644 | 0.819 |
| 19 | Zhejiang | 0.703 | 0.770 | 0.656 | 0.457 | 0.647 |
| 20 | Hainan | 0.063 | 0.106 | 0.175 | 0.222 | 0.142 |
| 21 | Hubei | 0.686 | 0.647 | 0.398 | 0.325 | 0.514 |
| 22 | Hunan | 0.489 | 0.497 | 0.589 | 0.393 | 0.492 |
| 23 | Gansu | 0.458 | 0.384 | 0.532 | 0.294 | 0.417 |
| 24 | Fujian | 0.682 | 0.582 | 0.544 | 0.296 | 0.526 |
| 25 | Guizhou | 0.282 | 0.294 | 0.300 | 0.222 | 0.275 |
| 26 | Liaoning | 0.334 | 0.327 | 0.377 | 0.270 | 0.327 |
| 27 | Chongqing | 0.834 | 0.821 | 0.787 | 0.365 | 0.702 |
| 28 | Shaanxi | 0.297 | 0.229 | 0.309 | 0.230 | 0.266 |
| 29 | Qinghai | 0.552 | 0.786 | 0.701 | 0.933 | 0.743 |
| 30 | Heilongjiang | 0.413 | 0.324 | 0.717 | 0.289 | 0.436 |
| Serial Number | DMU | 2016 | 2017 | 2018 | 2019 | Average Efficiency |
|---|---|---|---|---|---|---|
| 1 | Shanghai | 0.396 | 0.375 | 0.297 | 0.168 | 0.309 |
| 2 | Yunnan | 0.408 | 0.924 | 0.409 | 0.360 | 0.525 |
| 3 | Neimenggu | 0.269 | 0.225 | 0.448 | 0.739 | 0.420 |
| 4 | Beijing | 0.742 | 0.798 | 0.927 | 0.333 | 0.700 |
| 5 | Jilin | 0.304 | 0.297 | 0.334 | 0.412 | 0.337 |
| 6 | Sichuan | 0.408 | 0.413 | 0.414 | 0.250 | 0.371 |
| 7 | Tianjin | 0.455 | 0.522 | 0.540 | 0.360 | 0.469 |
| 8 | Ningxia | 0.886 | 0.860 | 0.763 | 0.833 | 0.836 |
| 9 | Anhui | 0.715 | 0.832 | 0.703 | 0.400 | 0.663 |
| 10 | Shandong | 0.345 | 0.418 | 0.510 | 0.434 | 0.427 |
| 11 | Shanxi | 0.396 | 0.383 | 0.640 | 0.475 | 0.474 |
| 12 | Guangdong | 0.663 | 0.673 | 0.439 | 0.251 | 0.506 |
| 13 | Guangxi | 0.424 | 0.309 | 0.788 | 0.277 | 0.450 |
| 14 | Xinjiang | 0.468 | 0.109 | 0.656 | 0.330 | 0.391 |
| 15 | Jiangsu | 0.532 | 0.686 | 0.556 | 0.361 | 0.534 |
| 16 | Jiangxi | 0.780 | 0.759 | 0.785 | 0.487 | 0.703 |
| 17 | Hebei | 0.400 | 0.453 | 0.462 | 0.294 | 0.402 |
| 18 | Henan | 0.747 | 0.762 | 0.916 | 0.599 | 0.756 |
| 19 | Zhejiang | 0.628 | 0.708 | 0.595 | 0.393 | 0.581 |
| 20 | Hainan | 0.068 | 0.097 | 0.157 | 0.268 | 0.148 |
| 21 | Hubei | 0.587 | 0.574 | 0.369 | 0.286 | 0.454 |
| 22 | Hunan | 0.434 | 0.460 | 0.538 | 0.350 | 0.446 |
| 23 | Gansu | 0.517 | 0.343 | 0.481 | 0.264 | 0.401 |
| 24 | Fujian | 0.594 | 0.529 | 0.505 | 0.259 | 0.471 |
| 25 | Guizhou | 0.249 | 0.270 | 0.267 | 0.197 | 0.246 |
| 26 | Liaoning | 0.289 | 0.299 | 0.345 | 0.237 | 0.293 |
| 27 | Chongqing | 0.719 | 0.748 | 0.722 | 0.327 | 0.629 |
| 28 | Shaanxi | 0.265 | 0.211 | 0.280 | 0.200 | 0.239 |
| 29 | Qinghai | 0.467 | 0.813 | 0.687 | 0.873 | 0.710 |
| 30 | Heilongjiang | 0.400 | 0.327 | 0.636 | 0.255 | 0.404 |
| Serial Number | DMU | 2016 | 2017 | 2018 | 2019 | Average Efficiency |
|---|---|---|---|---|---|---|
| 1 | Shanghai | 0.419 | 0.399 | 0.309 | 0.173 | 0.325 |
| 2 | Yunnan | 0.401 | 0.935 | 0.429 | 0.368 | 0.533 |
| 3 | Neimenggu | 0.281 | 0.238 | 0.480 | 0.714 | 0.428 |
| 4 | Beijing | 0.801 | 0.848 | 0.968 | 0.351 | 0.742 |
| 5 | Jilin | 0.314 | 0.306 | 0.345 | 0.394 | 0.340 |
| 6 | Sichuan | 0.432 | 0.428 | 0.428 | 0.257 | 0.387 |
| 7 | Tianjin | 0.474 | 0.536 | 0.562 | 0.376 | 0.487 |
| 8 | Ningxia | 0.915 | 0.899 | 0.799 | 0.868 | 0.870 |
| 9 | Anhui | 0.745 | 0.865 | 0.732 | 0.416 | 0.689 |
| 10 | Shandong | 0.361 | 0.433 | 0.533 | 0.454 | 0.445 |
| 11 | Shanxi | 0.390 | 0.366 | 0.637 | 0.475 | 0.467 |
| 12 | Guangdong | 0.704 | 0.715 | 0.457 | 0.261 | 0.534 |
| 13 | Guangxi | 0.398 | 0.305 | 0.764 | 0.252 | 0.430 |
| 14 | Xinjiang | 0.442 | 0.110 | 0.737 | 0.274 | 0.391 |
| 15 | Jiangsu | 0.551 | 0.712 | 0.577 | 0.376 | 0.554 |
| 16 | Jiangxi | 0.792 | 0.785 | 0.808 | 0.499 | 0.721 |
| 17 | Hebei | 0.409 | 0.457 | 0.479 | 0.299 | 0.411 |
| 18 | Henan | 0.745 | 0.762 | 0.932 | 0.615 | 0.763 |
| 19 | Zhejiang | 0.650 | 0.729 | 0.622 | 0.412 | 0.603 |
| 20 | Hainan | 0.069 | 0.102 | 0.164 | 0.262 | 0.149 |
| 21 | Hubei | 0.624 | 0.610 | 0.383 | 0.298 | 0.479 |
| 22 | Hunan | 0.447 | 0.468 | 0.556 | 0.358 | 0.457 |
| 23 | Gansu | 0.512 | 0.358 | 0.514 | 0.270 | 0.413 |
| 24 | Fujian | 0.624 | 0.551 | 0.527 | 0.271 | 0.493 |
| 25 | Guizhou | 0.256 | 0.277 | 0.279 | 0.205 | 0.255 |
| 26 | Liaoning | 0.304 | 0.307 | 0.360 | 0.245 | 0.304 |
| 27 | Chongqing | 0.743 | 0.773 | 0.738 | 0.336 | 0.647 |
| 28 | Shaanxi | 0.278 | 0.220 | 0.293 | 0.209 | 0.250 |
| 29 | Qinghai | 0.484 | 0.837 | 0.694 | 0.861 | 0.719 |
| 30 | Heilongjiang | 0.399 | 0.333 | 0.654 | 0.263 | 0.412 |
| Serial Number | DMU | Overall Efficiency Value | Stage 1 Efficiency Value | Stage 2 Efficiency Value |
|---|---|---|---|---|
| 1 | Shanghai | 0.774405 | 0.443462 | 0.146154 |
| 2 | Yunnan | 0.947053 | 0.332505 | 0.448106 |
| 3 | Neimenggu | 0.863417 | 0.495243 | 0.325395 |
| 4 | Beijing | 1 | 0.590699 | 0.612533 |
| 5 | Jilin | 0.758956 | 0.446096 | 0.200793 |
| 6 | Sichuan | 0.802218 | 0.486668 | 0.279002 |
| 7 | Tianjin | 0.928797 | 0.302415 | 0.429519 |
| 8 | Ningxia | 1 | 0.318312 | 0.753214 |
| 9 | Anhui | 0.990402 | 0.604228 | 0.487683 |
| 10 | Shandong | 0.921920 | 0.364952 | 0.418672 |
| 11 | Shanxi | 1 | 0.168742 | 0.548059 |
| 12 | Guangdong | 0.856469 | 0.570199 | 0.053439 |
| 13 | Guangxi | 0.975229 | 0.606961 | 0.467347 |
| 14 | Xinjiang | 0.764179 | 0.510609 | 0.146037 |
| 15 | Jiangsu | 0.931260 | 0.393364 | 0.422927 |
| 16 | Jiangxi | 1 | 0.441619 | 0.547284 |
| 17 | Hebei | 0.866948 | 0.308851 | 0.366886 |
| 18 | Henan | 1 | 0.274016 | 0.910339 |
| 19 | Zhejiang | 0.959041 | 0.383756 | 0.456063 |
| 20 | Hainan | 0.682115 | 0.438424 | 0.048969 |
| 21 | Hubei | 0.847507 | 0.581689 | 0.204838 |
| 22 | Hunan | 0.878838 | 0.360040 | 0.377812 |
| 23 | Gansu | 0.783275 | 0.281361 | 0.283223 |
| 24 | Fujian | 0.875199 | 0.384368 | 0.372973 |
| 25 | Guizhou | 0.728923 | 0.405509 | 0.161186 |
| 26 | Liaoning | 0.747690 | 0.406133 | 0.230784 |
| 27 | Chongqing | 1.000000 | 0.420755 | 0.537713 |
| 28 | Shaanxi | 0.696487 | 0.233117 | 0.193475 |
| 29 | Qinghai | 1 | 0.628615 | 0.728512 |
| 30 | Heilongjiang | 0.845018 | 0.243439 | 0.345608 |
| Hebei | Overall Efficiency Value | Stage 1 Efficiency Value | Stage 2 Efficiency Value |
|---|---|---|---|
| Full cycle | 0.866948 | 0.308851 | 0.366886 |
| 2016 | 0.334131 | 0.155995 | 0.337072 |
| 2017 | 0.433745 | 0.315810 | 0.435771 |
| 2018 | 0.373970 | 0.369668 | 0.374011 |
| 2019 | 0.334313 | 0.450185 | 0.333258 |
| Serial Number | DMU | Overall Efficiency Value | Stage 1 Efficiency Value | Stage 2 Efficiency Value |
|---|---|---|---|---|
| 1 | Shanghai | 0.813357 | 0.249872 | 0.824476 |
| 2 | Yunnan | 0.810733 | 0.253328 | 0.820066 |
| 3 | Neimenggu | 0.811440 | 0.234682 | 0.823061 |
| 4 | Beijing | 0.801637 | 0.548428 | 0.812584 |
| 5 | Jilin | 0.813297 | 0.409206 | 0.816844 |
| 6 | Sichuan | 0.812225 | 0.253072 | 0.821677 |
| 7 | Tianjin | 0.808339 | 0.268955 | 0.816890 |
| 8 | Ningxia | 0.796537 | 0.219304 | 0.807736 |
| 9 | Anhui | 0.799821 | 0.235918 | 0.809517 |
| 10 | Shandong | 0.808562 | 0.270846 | 0.817088 |
| 11 | Shanxi | 0.813070 | 0.235249 | 0.822682 |
| 12 | Guangdong | 0.807938 | 0.251826 | 0.819104 |
| 13 | Guangxi | 0.816251 | 0.243628 | 0.826848 |
| 14 | Xinjiang | 0.821312 | 0.330308 | 0.821530 |
| 15 | Jiangsu | 0.808527 | 0.254284 | 0.818083 |
| 16 | Jiangxi | 0.809149 | 0.229838 | 0.820081 |
| 17 | Hebei | 0.807175 | 0.263308 | 0.808980 |
| 18 | Henan | 0.805053 | 0.225447 | 0.808061 |
| 19 | Zhejiang | 0.799889 | 0.241973 | 0.809114 |
| 20 | Hainan | 0.834021 | 0.324571 | 0.842910 |
| 21 | Hubei | 0.808363 | 0.251950 | 0.819425 |
| 22 | Hunan | 0.810506 | 0.255088 | 0.819720 |
| 23 | Gansu | 0.810213 | 0.250349 | 0.819847 |
| 24 | Fujian | 0.808588 | 0.254699 | 0.817627 |
| 25 | Guizhou | 0.816073 | 0.426705 | 0.817243 |
| 26 | Liaoning | 0.813300 | 0.255949 | 0.822585 |
| 27 | Chongqing | 0.809759 | 0.228837 | 0.819621 |
| 28 | Shaanxi | 0.812482 | 0.278667 | 0.820348 |
| 29 | Qinghai | 0.806722 | 0.225267 | 0.815790 |
| 30 | Heilongjiang | 0.806412 | 0.288813 | 0.806941 |
| Hebei | Overall Efficiency Value | Stage 1 Efficiency Value | Stage 2 Efficiency Value |
|---|---|---|---|
| Full cycle | 0.807175 | 0.263308 | 0.808980 |
| 2016 | 0.602637 | 0.213525 | 0.603283 |
| 2017 | 0.723661 | 0.460353 | 0.724044 |
| 2018 | 0.724006 | 0.445400 | 0.724327 |
| 2019 | 0.620914 | 0.396470 | 0.621245 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Ma, J.; Liu, Z. Research on the Cross-Efficiency Model of the Innovation Dynamic Network in China’s High-Tech Manufacturing Industry. Appl. Sci. 2025, 15, 8552. https://doi.org/10.3390/app15158552
Wang D, Ma J, Liu Z. Research on the Cross-Efficiency Model of the Innovation Dynamic Network in China’s High-Tech Manufacturing Industry. Applied Sciences. 2025; 15(15):8552. https://doi.org/10.3390/app15158552
Chicago/Turabian StyleWang, Danping, Jian Ma, and Zhiying Liu. 2025. "Research on the Cross-Efficiency Model of the Innovation Dynamic Network in China’s High-Tech Manufacturing Industry" Applied Sciences 15, no. 15: 8552. https://doi.org/10.3390/app15158552
APA StyleWang, D., Ma, J., & Liu, Z. (2025). Research on the Cross-Efficiency Model of the Innovation Dynamic Network in China’s High-Tech Manufacturing Industry. Applied Sciences, 15(15), 8552. https://doi.org/10.3390/app15158552




