A Stress Analysis of a Thin-Walled, Open-Section, Beam Structure: The Combined Flexural Shear, Bending and Torsion of a Cantilever Channel Beam
Abstract
1. Introduction
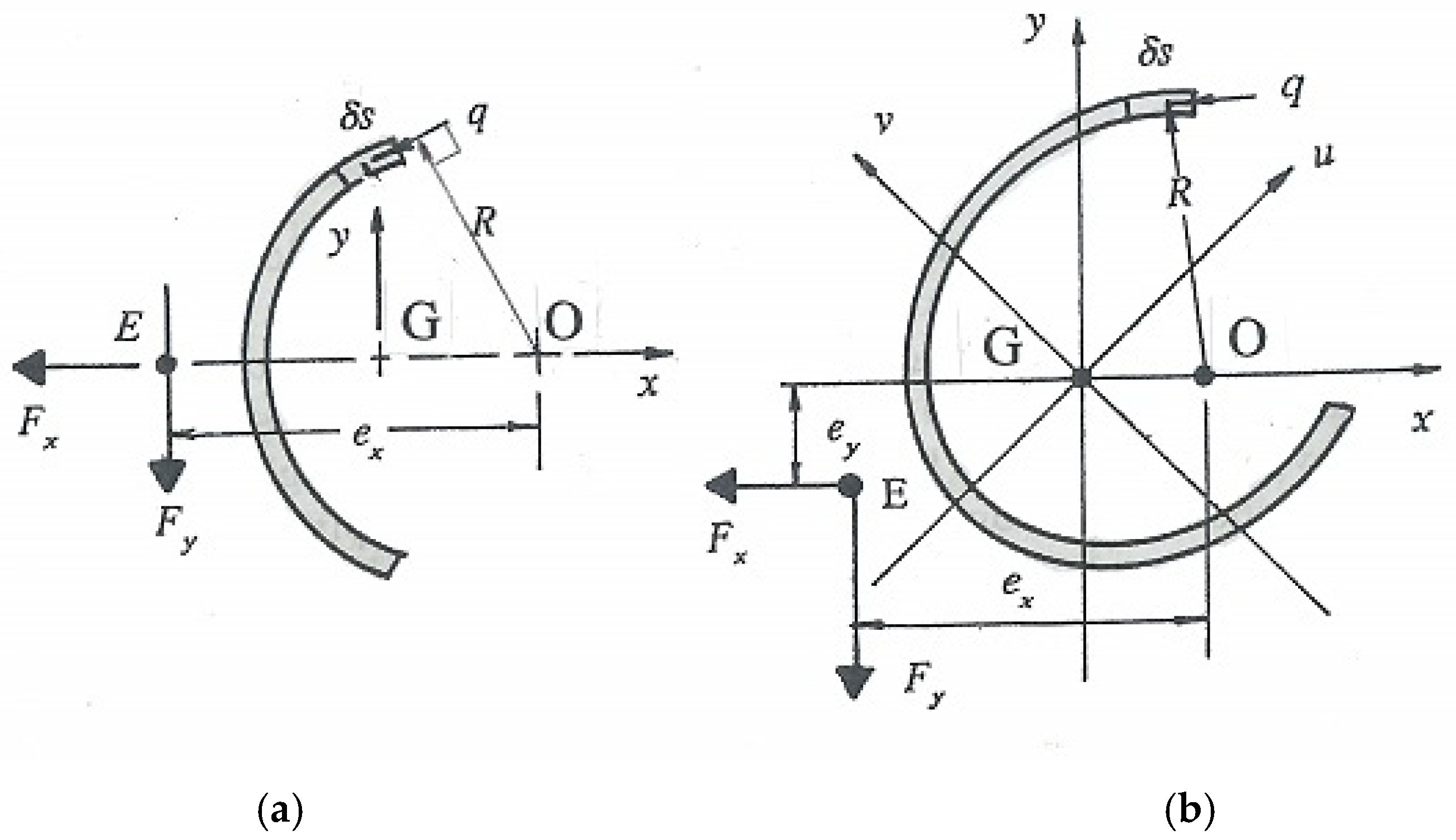
Thin-Walled Elasticity Theory
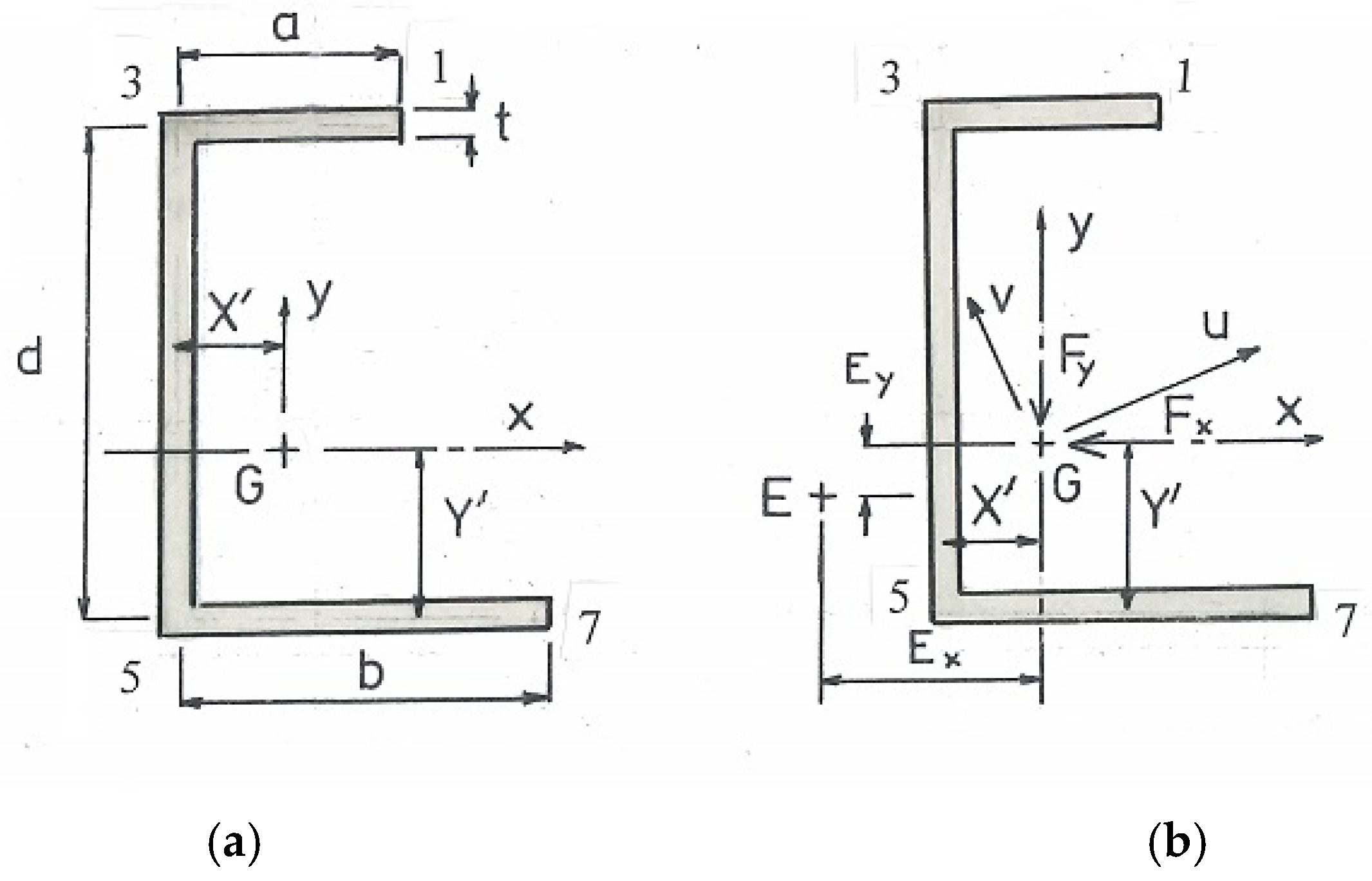
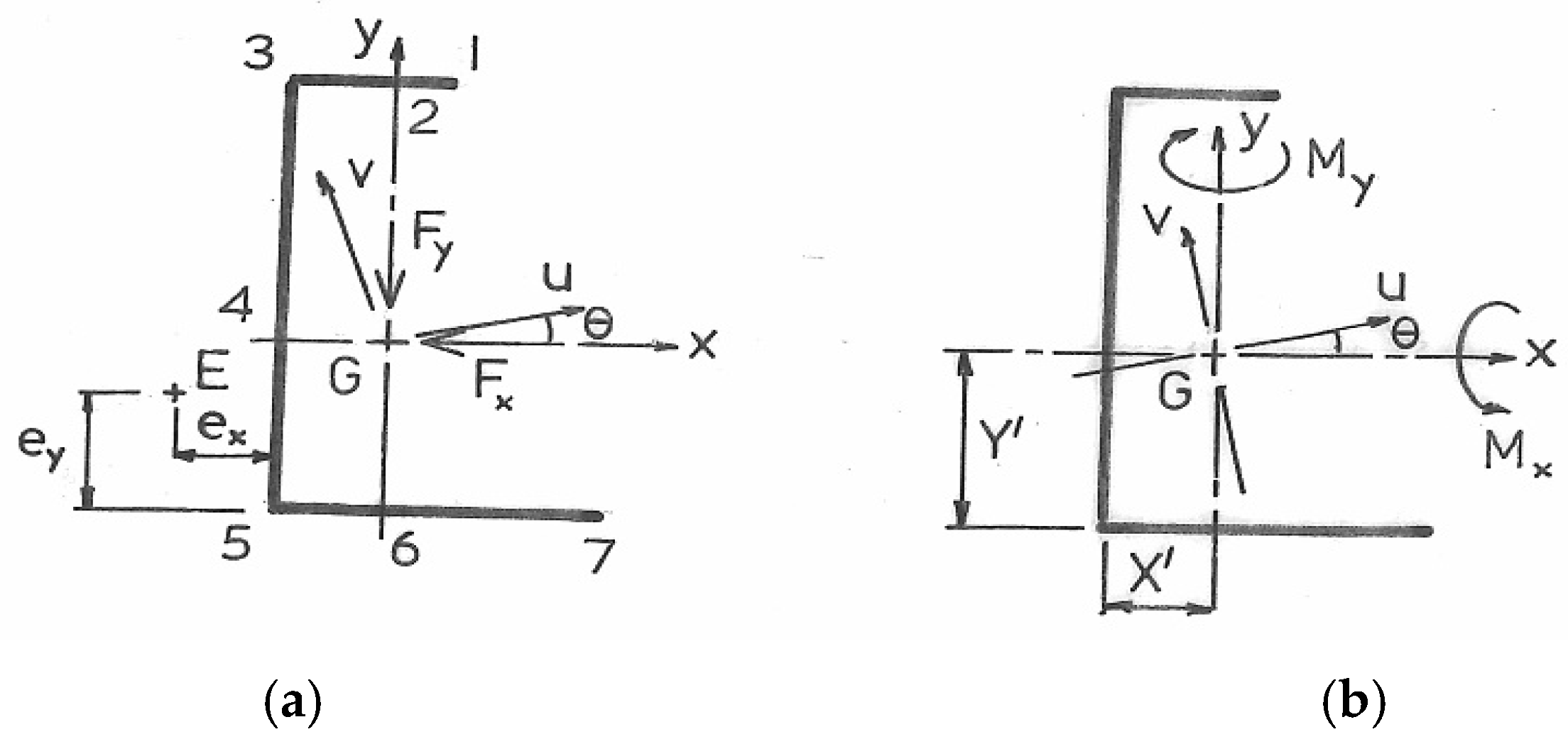
2. Non-Symmetric Cross-Section
2.1. Bending
2.2. Shear
2.3. Axial Stress Superposition
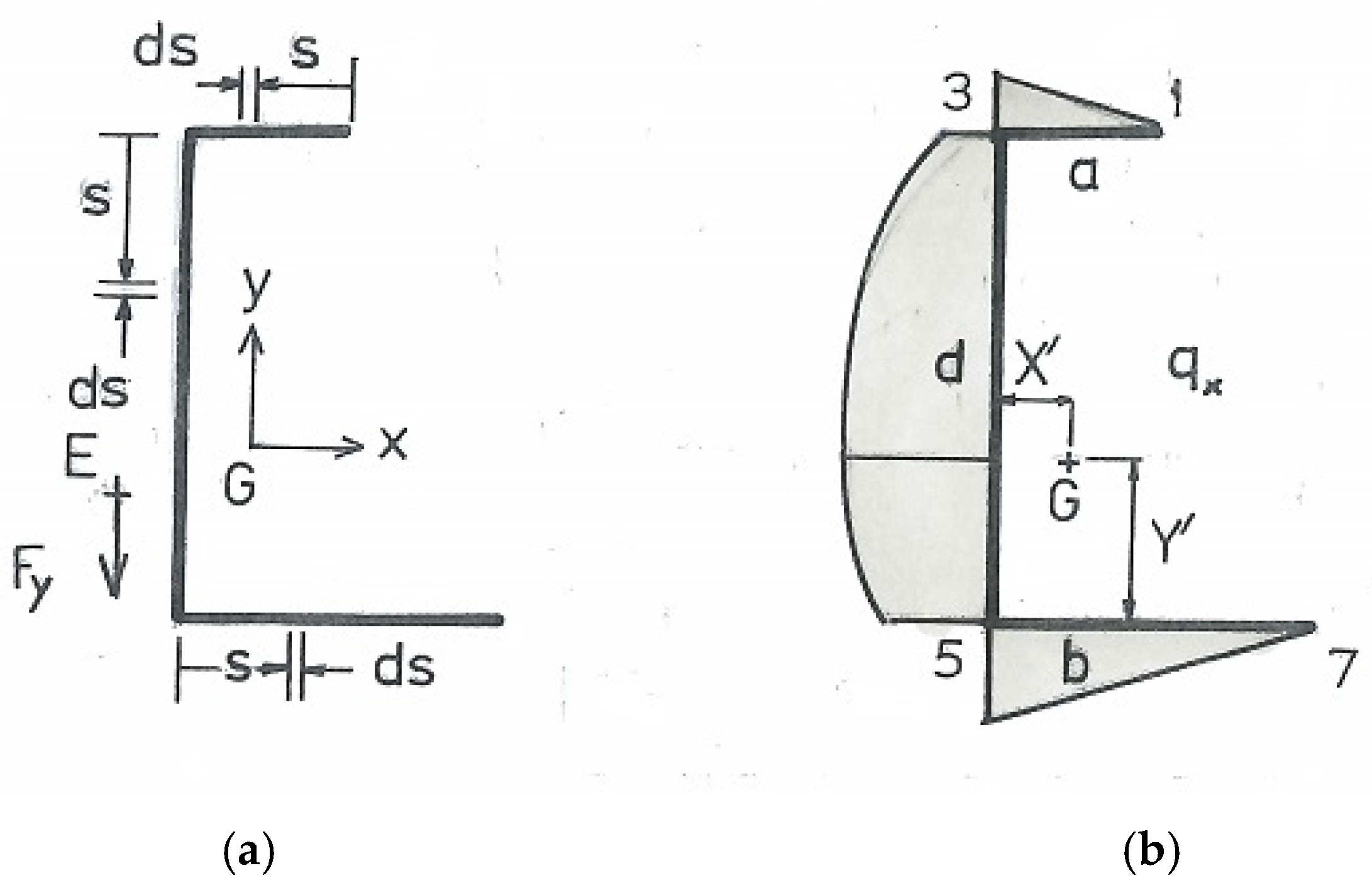
2.4. Net Shear Stress
2.5. Symmetrical Channel
- Note (1): For a cantilever, the bending moments at a given position, z, along the length are given as Mx = Fy(L − z) and My = Fx(L − z). The moments show their maxima at the fixing where z = 0.
- Note (2): The shear flow terms are independent of length z when transverse shear forces Fx and Fy are applied at the free end of a cantilever beam. Equilibrium requires that every cross-section along the length is subjected to the same shear forces. However, the third term in Equation (7) is dependent upon z from Equation (6c).
- Note (3): The net shear stress (Equation (7)) has a linear distribution through the thickness. The flexural shear flow, qF, provides the mean shear stress at mid thickness. With qF, the shear flow due to axial torsion qT is superimposed to give a linear thickness variation in qnet between the free edges.
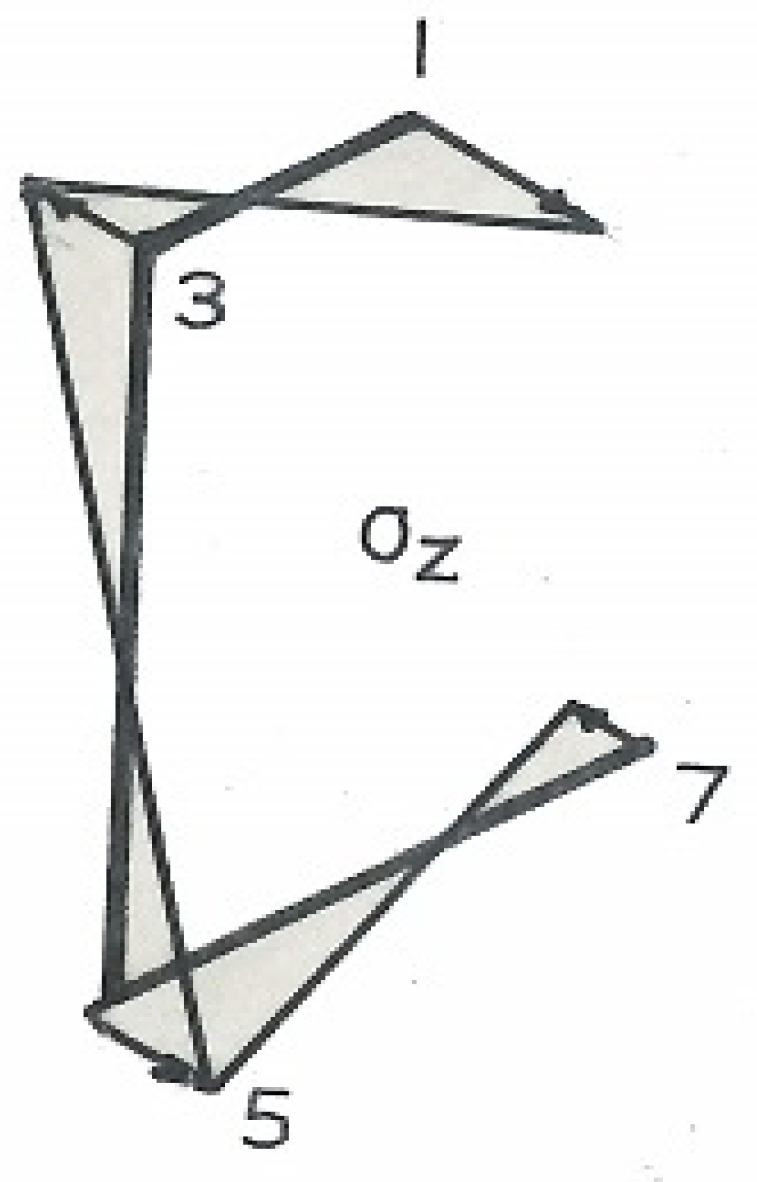
3. Torsional Shear Flow Calculations
| 1–3: 0 ≤ s ≤ a; ꞷ = ds/2; Q1–3 = ∫s (ds/2 − ϖ)ds = ds2/4 − ϖs |
| Q1 = 0, Q3 = da2/4 − ϖa; | Q3/a3 = (1/4)(d/a) − ϖ/a2 |
| 3–4: a ≤ s ≤ a + d/2; ꞷ = es + (ad/2 − ea); Q3–4 = ∫s [es + (ad/2 − ea) − ϖ] ds |
| Q4/a3 = (1/2)(e/a)[1 + (1/2)(d/a)]2 + (ko/a2 − ϖ/a2)[1 + (1/2)(d/a)] + k1/a3 |
| 4–5: a + d/2 ≤ s ≤ a + d; y = −se + (ad/2 + ed + ea); Q4–5 = ∫s [−se + (ad/2 + ed + ea) − ϖ]ds |
| = ∫s (k3 −se − ϖ) ds |
| Q5/a3 = −(1/2)(e/a)(1 + d/a)2 − (ϖ/a2 − k3/a2)(1 + d/a) + k4/a3 |
| 5–7: a + d ≤ s ≤ 2a + d; ꞷ = −ds/2 + d(a + d/2); Q5–7 = ∫s [−ds/2 + d(a + d/2) − ϖ]ds |
| = ∫s (k5 −sd/2 − ϖ) ds |
| Q7/a3 = −(1/4)(d/a)(2 + d/a)2 − (2 + d/a)(ϖ/a2 − k5/a2) + k6/a3 |
| ko/a2 = (1/2)(d/a) − (e/a) |
| k1/a3 = −(1/4)(d/a) + (1/2)(e/a) |
| k3/a2 = (e/a)(d/a) + e/a +(1/2)(d/a) |
| k4/a3 = (e/a)[1 + (1/2)(d/a)]2 + [1 + (1/2)(d/a)](ko/a2 − k3/a2) + k1/a3 |
| k5/a2 = (d/a)[1 + (1/2)(d/a)] |
| k6/a3 = (1 + d/a)2[(1/4)(d/a) − (e/a)] + (1 + d/a)(k3/a2 − k5/a2) + k4/a3 |
| ∃/a2 = (1/4)(d/a)[2(1 + d/a) +(e/a)(d/a)]/(2 + d/a) |
| e/a = 3(a/d)/[1 + 6(a/d)] |
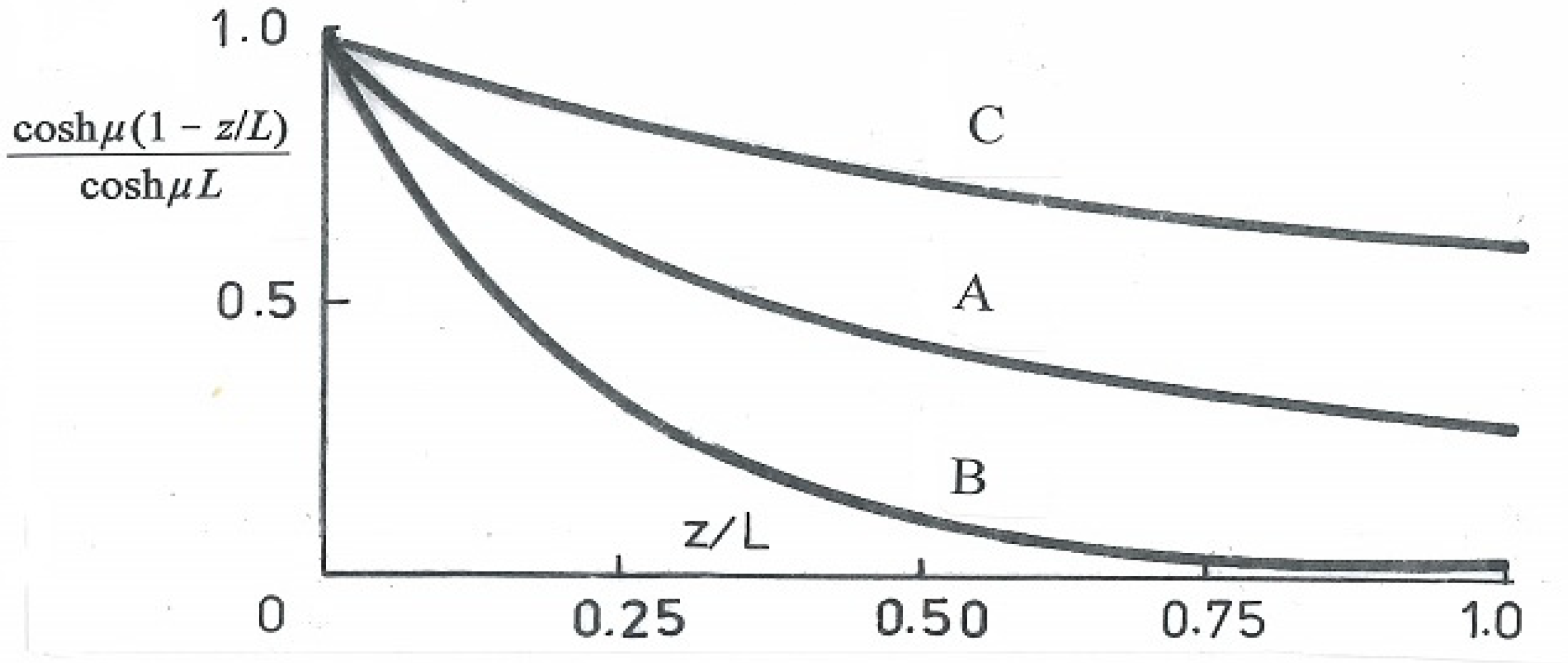
- A: J = 67.74 mm4, µ = √(GJ/EΓ1) = 6.562 × 10−3 mm−1, µL = 6.562 × 10−3 × 300 = 1.9685;
- B: J = 1016.8 mm4, µ = √(GJ/EΓ1) = 4.55 × 10−3 mm−1, µL = 4.55 × 10−3 × 103 = 4.55;
- C: J = 44.656 mm4, µ = √(GJ/EΓ1) = 2.73 × 10−3 mm−1, µL = 2.73 × 10−3 × 340 = 0.936.
| qi = Et (d3θ/dz3)Qi = Et × (− 0.2656 × 10−6)T/G × Qi |
| = 3 × (1/16 × 25.4) × (− 0.2656 × 10−6) × (1 × 103) × Qi |
| = −(1.265 × 10−3) Qi |
| q1 = q4 = q7 = 0 ∴ q3 = −q5 = −(1.265 × 10−3) × (−11/32)(1/2 × 25.4)3 = 0.891 N/mm |
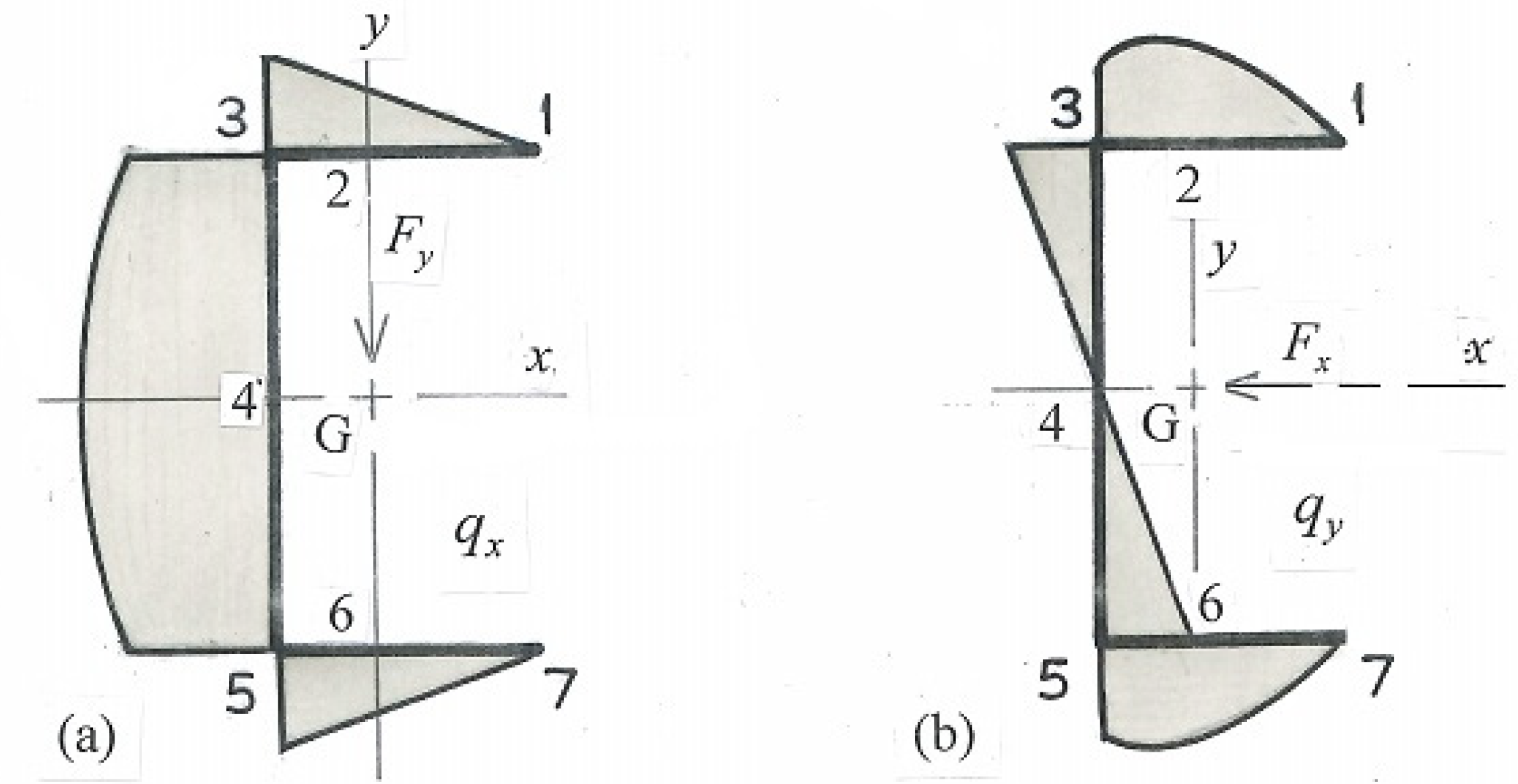
4. Flexural Shear Flow
| X′/a = (a/d)/[1 + 2(a/d)] Ix = 2[at(d/2)2 + at3/12] + td3/12 = atd2/2 + at3/6 + td3/12 Ix/d4 = (1/2)(a/t)(t/d) + (1/6)(a/d)(t/d)3 + (1/12)(t/d) Iy = dt3/12 + dtX′2 + 2[ta3/12 + at (a/2 − X′)2] Iy/d4 = (1/12)(t/d)3 + (t/d)(X′/d)2 + 2{(1/12)(t/d)(a/d)3 + (a/d)(t/d)[(1/2)(a/d) − (X′/d)]2} |
| 1–3: Dx = t ∫s y ds = tds/2 + Dx1 at 1, s = 0, Dx1 = 0 (free edge) at 2, (y–axis), s = a −X′, Dx2 = td (a −X′)/2 at 3. s = a, Dx3 = tda/2 3–5, Dx = t ∫s (d/2 − s) ds = t(ds/2 − s2/2) + Dx3 at 3, s = 0, Dx3 = tda/2 at 4, (x-axis) s = d/2, Dx4 = t(d2/4 −d2/8) + tda/2 = td2/8 + tda/2 ✓ (NA, web centre) at 5, s = d, Dx5 = Dx3 = tda/2 5–7 Dx = −t ∫s (d/2) ds + Dx5 = −tds/2 + Dx5 at 5, s = 0, Dx = Dx5 = tda/2 at 6, (y-axis), s = X′, Dx6 = −tdX′/2 + tda/2 = Dx2 at 7, s = a, Dx7 = −tda/2 + tda/2 = 0 ✓ (at the free edge) |
| 1–3: Dy = t ∫s[a − (s + X′)] ds = (a −X′)s − s2/2 + Dy1 at 1, s = 0, Dy1 = 0 at 2 (y–axis, NA), s = a − X′, Dy2 = t [(a − X′)2 − (a − X′)2/2] = (t/2)(a − X′)2 at 3, s = a, Dy3 = t [(a − X′)a − a2/2] = at(a/2 − X′) 3–5: Dy = −t ∫s X′ ds + Dy3 = −t X′ s + Dy3 at 3, s = 0, Dy3 = at(a/2 − X′) at 4 (x-axis), s = d/2, Dy4 = a2t/2 − X′ t (a + d/2) at 5, s = d, Dy5 = −t X′ d + at (a/2 − X′) = a2t/2 − X′ t (a + d) 5−7: Dy = −t ∫s(s −X′) ds + Dy5 = ts (s/2 − X′) + Dy5 at 5: s = 0, Dy5 = a2t/2 − X′ t (a + d) at 6 (y–axis, NA): s = X′, Dy6 = X′ t (X′/2 −X′) + a2t/2 −X′ t (a + d) Dy6 = (a2t/2) −X′ t (X′/2 + d + a) at 7, s = a, Dy7 = ta (a/2 − X′) + a2t/2 −X′ t (a + d) = a2t −X′ t (2a + d) |
| Dy1 = 0 Dy2 = (at2/2)[(a + d)/(2a + d)]2 (y-axis, NA) Dy3 = (at2/2)d/(2a + d) Dy4 = a2t/2 − X′ t (a + d/2) = 0 (x-axis) Dy5 = (at2/2)[1 − 2(a + d)/(2a + d)] = Dy3 Dy6 = (a2t/2) −X′ t (X′/2 + d + a) = (a2t/2)[1 − a2/(2a + d)2 − 2(a + d)/(2a + d)] = Dy2 Dy7 = a2t − a2t(2a + d)/(2a + d) = 0 ✓ |
5. Net Flexural Shear Flow
| X′/a = (a/d)∕[1 + 2(a/d)] ex/a = 3(a/d)∕[1 + 6(a/d)] ϖ/a2 = (1/4)(d/a)[2(1 + d/a) + (e/a)(d/a)]∕(2 + d/a) Ix = 2[at(d/2)2 + at3/12] + td3/12 = atd2/2 + at3/6 + td3/12 Ix/d4 = (1/2)(a/d)(t/d) + (1/6)(a/d)(t/d)3 + (1/12)(t/d) Iy = dt3/12 + dtX′2 + 2[ta3/12 + at(a/2 − X′)2] Iy/d4 = (1/12)(t/d)3 + (t/d)(X′/d)2 + 2{(1/12)(t/d)(a/d)3 + (a/d)(t/d)[(1/2)(a/d) − (X′/d)]2} |
| (Iy/Fx)qnet = Dy + (Fy/Fx)(Iy/Ix)Dx = [a2t/2 − X′ t (a + d/2)] + (1 × 0.1571)(td2/8 + tda/2) = [(1/2)(a/d)2(t/d) − (X′/d)(t/d)(a/d + 1/2)]d3 + 0.1571[(1/8)(t/d) + (1/2)(t/d)(a/d)]d3 = [(1/2)(1/2)2(1/16) −(1/8)(1/16)(1/2 + 1/2)]d3 + 0.1571[(1/8)(1/16) + (1/2)(1/16)(1/2)]d3 = 0 + (3.682 × 10−3) d3 |
| qnet = 1.1226 × 100/25.4 = 4.42 N/mm ∴ τ = qnet/t = 16 × 4.42 = 70.7 MPa |
6. Net Shear Flow
7. Net Axial Stress
7.1. Net Bending Stress
| (d4/a)(σz1/FL) = 1/(2 × 0.02085)(2) + (1 − 1/4)/0.003276 = 276.9, |σz1 = 2534.6 × 10−3F (d4/a)(σz2/FL) = 1/0.02085 = 47.96, |σz2 = 439 × 10−3F (d4/a)(σz3/FL) = 1/0.02085 − 0.25/0.003276 = −28.35, |σz3 = −259.5 × 10−3F (d4/a)(σz4/FL) = −0.25/0.003276 = −76.31, |σz4 = −698.5 × 10−3F (d4/a)(σz5/FL) = −1/0.02085 − 0.25/0.003276 = −124.27, σz5 = −1137.5 × 10−3F (d4/a)(σz6/FL) = −1/0.02085 = −47.96, |σz6 = −439 × 10−3F (d4/a)(σz7/FL) = −1/0.02085 + 0.75/0.003276 = 180.97, |σz7 = 1656.5 × 10−3F |
| (d4/a)(σz1/FL) = (1/0.026395 × 7/8) + (1/0.0053615 × 11/15) = 169.9, |σz1 = 1105.65 × 10−3F (d4/a)(σz2/FL) = (1/0.026395 × 7/8) = 33.1502, |σz2 = 215.69 × 10−3F (d4/a)(σz3/FL) = (1/0.026395 × 7/8) − (1/0.0053615 × 4/15) = 16.587, |σz3 = −107.92 × 10−3F (d4/a)(σz4/FL) = −(1/0.0053615 × 4/15) = −49.74, |σz4 = −323.6 × 10−3F (d4/a)(σz5/FL) = −(1/0.026395 × 7/8) − (1/0.0053615 × 4/15) = −82.888 |σz5 = −539.31 × 10−3F (d4/a)(σz6/FL) = −(1/0.026395 × 7/8) = −33.105, |σz6 = −215.69 × 10−3F (d4/a)(σz7/FL) = −(1/0.026395 × 7/8) + (1/0.0053615 × 11/15) = 103.63, |σz7 = 674.27 × 10−3F |
| (d4/a)(σz1/FL) = (1/0.006251 × 3/2) + (1/0.0004334 × 4/5) = 2085.83, |σz1 = 2188.4 × 10−3F (d4/a)(σz2/FL) = (1/0.006251 × 3/2) = 239.96, |σz2 = 251.76 × 10−3F (d4/a)(σz3/FL) = (1/0.006251 × 3/2) − (1/0.0004343 × 1/5) = −221.51, |σz3 = −232.4 × 10−3F (d4/a)(σz4/FL) = −(1/0.0004343 × 1/5) = −461.47, |σz4 = −484.16 × 10−3F (d4/a)(σz5/FL) = −(1/0.006251 × 3/2) − (1/0.0004343 × 1/5) = −701.43, |σz5 = −735.92 × 10−3F (d4/a)(σz6/FL) = −(1/0.006251 × 3/2) = −239.96, |σz6 = −251.76 × 10−3F (d4/a)(σz7/FL) = −(1/0.006251 × 3/2) + (1/0.0004334 × 4/5) = 1605.91, |σz7 = 1684.9 × 10−3F |
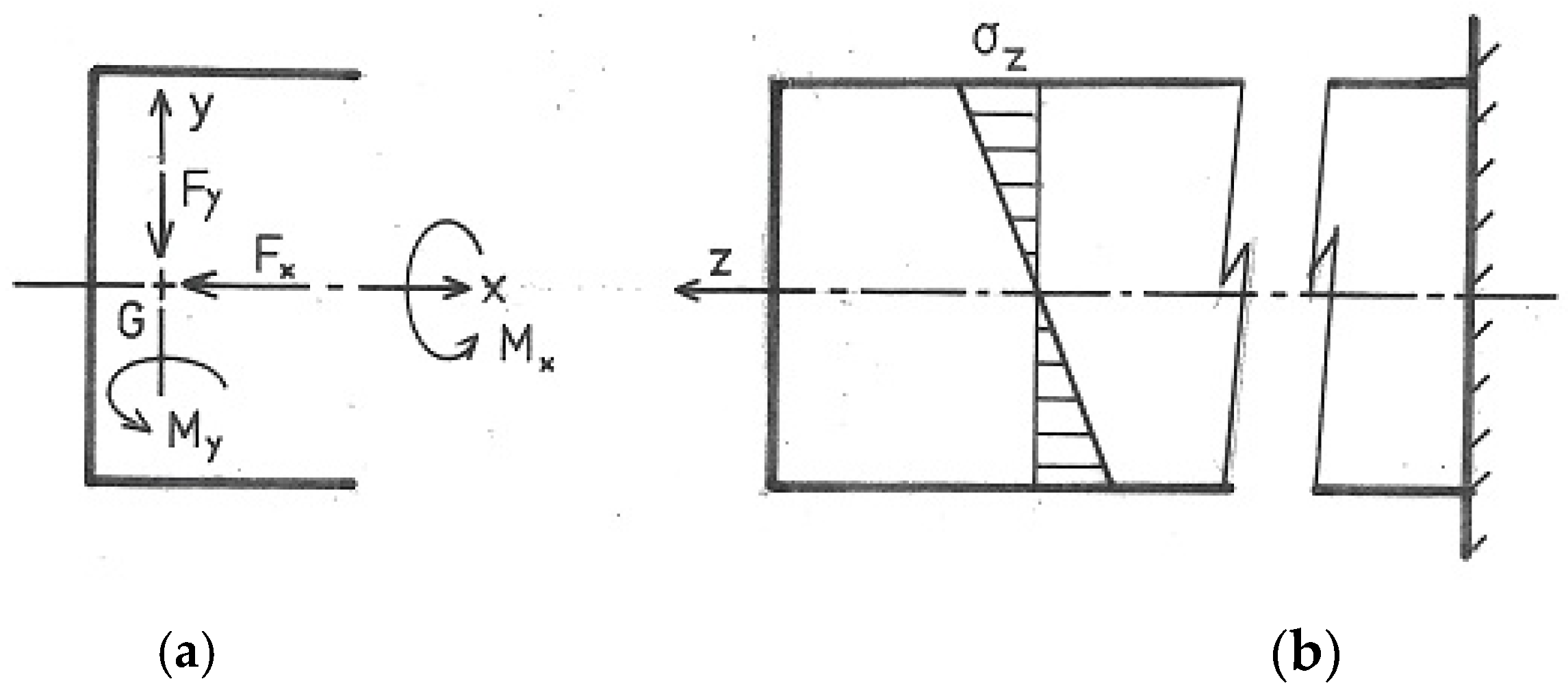
7.2. Constrained Axial Stress Distribution
| d/a = 2, ex/a = 3/8, L = 300 mm, a = 12.7 mm, t = 1.5875 mm, Γ1/a5t = 0.66275, ϖ/a2 = 0.8438, X′/a = 1/4, μ = 0.8189t/a2, μL = 0.8189(t/a)(L/a) = 2.418, (1 − e−2μL)/(1 + e−2μL) = 0.9842 |
| at 1 ꞷ1 = 0, ∴ (at2/T)σz1 = 1.8135(0.8438 − 0) = 1.5303 at 3, ꞷ3 = ad/2, ∴ (at2/T)σz3 = 1.8135[0.8438 − (1/2)(d/a)] = −0.2834 at 4, ꞷ4 = (a + e)d/2, ∴ (at2/T)σz4 = 1.8135[0.8438 − (1/2)(d/a)(1 + e/a)] = −0.9633 |
| σz1 = 1.5303 (T/at2) = 1.5303 × 62.5/1.58752 = 37.95 MPa σz3 = 0.2834 (T/at2) = −0.2834 × 62.5/1.58752 = −7.04 MPa σz4 = −0.9633 (T/at2) = −0.9633 × 62.5/1.58752 = −23.89 MPa |
| d/a = 7/4, ex/a = 12/31, L = 1000 mm, a = 25.4 mm, t = 3.175 mm, Γ1/a5t = 0.448, ϖ/a2 = 0.7206, X′/a = 4/15, μ = 0.924t/a2, μL = 0.924(t/a)(L/a) = 4.5474, (1 − e−2μL)/(1 + e−2μL) = 0.99978. |
| at 1, ꞷ1 = 0, ∴ (at2/T)σz1 = 2.2172(0.7206 − 0) = 1.5977 at 3, ꞷ3 = ad/2, ∴ (at2/T)σz3 = 2.2172[0.7206 − (1/2)(d/a)] = −0.3423 at 4, ꞷ4 = (a + e)d/2, ∴ (at2/T)σz4 = 2.2172[0.7206 − (1/2)(d/a)(1 + e/a)] = −1.0933 |
| σz1 = 1.5977 (T/at2) = 1.5977 × 65.38/3.1752 = 10.36 MPa σz3 = 0.2834 (T/at2) = −0.3423 × 65.38/3.1752 = −2.22 MPa σz4 = −1.0933 (T/at2) = −1.0933 × 65.38/3.1752 = −7.09 MPa |
| d/a = 3, ex/a = 1/3, L = 340 mm, a = 15.875 mm, t = 1.19063 mm, Γ1/a5t = 1.6375, ϖ/a2 = 1.35, X′/a = 1/5, μ = 0.5825t/a2, μL = 0.5825(t/a)(L/a) = 0.9356, (1 − e−2μL)/(1 + e−2μL) = 0.7332. |
|
at 1 ꞷ1 = 0, ∴ (at2/T)σz1 = 0.7687 (1.35 − 0) = 1.0377 at 3, ꞷ3 = ad/2, ∴ (at2/T)σz3 = 0.7687 [1.35 − (1/2)(d/a)] = −0.1153 at 4, ꞷ4 = (a + e)d/2, ∴ (at2/T)σz4 = 0.7687 [1.35 − (1/2)(d/a)(1 + e/a)] = −0.4996 |
| σz1 = 1.5977 (T/at2) = 1.0377 × 53.33/1.190632 = 39.04 MPa σz3 = 0.2834 (T/at2) = −0.1153 × 53.33/1.190632 = −4.34 MPa σz4 = −1.0933 (T/at2) = −0.49966 × 53.33/1.190632 = −18.80 MPa |
7.3. Net Axial Stress Distribution
8. Yield Criteria
9. Non-Symmetric Section
9.1. Centroid Position and Moments of Area
| Ix/d3t = (a/d)(b/d)(a/d + b/d) + (1/4)(a/d)(1 + a/d) + (1/4)(b/d)(1 + b/d) | (17a) |
| + (3/2)(a/d)(b/d)]∕(1 + a/d + b/d)2 | |
| Iy = at(a/2 − X′)2 + dtX′2 + bt(b/2 −X′)2 |
| Iy/d3t = (a/d)[(a/d)(1 + b/d) − (b/d)2]2 + [(a/d)2 + (b/d)2]2 | (17b) |
| + (b/a)[(b/d)(1 + a/d) − (a/d)2]∕4(a/d + b/d +1)2 | |
| Ixy = + at(d − Y′)(a/2 − X′) − dtX′(d/2 − Y′) − btY′(b/2 − X′) |
| Ixy/d3t = (a/d)(1 − Y′/d)[(1/2)(a/d) − (X′/d)] − (X′/d)(1/2 − Y′/d) | (17c) |
| − (b/d)(Y′/d)[(1/2)(b/d) − (X′/d)] |
9.2. Shear Flow Under Fy′ and Fx′
| at 1: s = 0, Dx1 = 0 at 2 (y–axis) s = a − X′; Dx2 = t(d − Y′)(a − X′) at 3: s = a, Dx3 = t(d − Y′)a 3–5: Dx = t ∫s y ds = t ∫s (d − Y′ − s)ds = t[(d − Y′)s − s2/2] + Dx3 at 3: s = 0, Dx = Dx3 = t(d − Y′)a at 4: (x-axis) s = d − Y′; Dx4 = t(d − Y′)2/2 + t(d − Y′)a at 5: s = d, Dx5 = t[(d − Y′)d − d2/2] + t(d − Y′)a 5–7: Dx = t ∫s y ds = −tY′s + Dx5 at 5: s = 0, Dx = Dx5 at 6: s = X′, (y-axis); Dx6 = −tY′X′ + Dx5 at 7: s = b, Dx7 = −tY′b + Dx5 = 0 ✓ |
| 1–3: Dy = t ∫s x ds = t∫0s (a − X′ − s) ds = t[(a − X′)s − s2/2] at 1: s = 0, Dy1 = 0 at 2 (y–axis) s = a − X′; Dy2 = t(a − X′)2/2 at 3: s = a, Dy3 = t[(a − X′)a − a2/2] = ta(a/2 − X′) 3–5: Dy = t ∫s x ds = −tX′s + Dy3 at 3: s = 0, Dy = Dy3 = ta(a/2 − X′) at 4: (x-axis) s = d − Y′; Dy4 = −tX′(d − Y′) + ta(a/2 − X′) at 5: s = d, Dy5 = −tX′d + Dy3 = −tX′d + ta(a/2 − X′) 5–7: Dy = t ∫s x ds = t∫s (s − X′) ds + Dy5 = t(s2/2 − X′s) − tX′d + ta(a/2 − X′) at 5: s = 0, Dy = Dy5 = −tX′d + ta(a/2 − X′) at 6: (y–axis) s = X′; Dy6 = −tX′2/2 − tX′d + ta(a/2 − X′) at 7: s = b, Dy7 = t(b2/2 − X′b) − tX′d + ta(a/2 − X′) = 0 ✓ |
- Note 1: The conversion from Dx and Dy, given in Table 10, to net shear flow in Equation (18) follows from the multiplication involving equivalent forces and second moments of area in Equation (2a,b).
- Note 2: The assumption is made in Table 10 that shear flow calculated from transverse forces Fx and Fy applied at G is the same as when those forces are transferred to E. It is the torque accompanying that transfer, as required for static equivalence, that serves to modify the flexural shear flow.
9.3. Shear Centre
| = (tda2)(d − Y′)∕(2Ix) |
| = (tda2)(2a − 3X′)/(6Iy) |
9.4. Shear Flow Under Combined Loading
| Fx′ = [Fx − (Ixy/Ix) Fy]∕(1 − Ixy2/Ix Iy) | (20a) |
| = 1.5216Fx + 0.3927Fy |
| Fy′ = [Fy − (Ixy/Iy)Fx]∕(1 − Ixy 2/Ix Iy) | (20b) |
| = 1.5216Fy + 2.0458Fx |
| q = (6.445Fy + 8.6646Fx)Dx/d3t + (34.0Fx + 8.775Fy)Dy/d3t | (20c) |
| = (6.445Fy + 8.6646Fx)Dx/d3t + (34.0Fx + 8.775Fy)Dy/d3t |
| Dx1/d3 = 0 Dx2/d3 = (t/d)(1 − Y′/d)(a/d −X′/d) = (1/40)(7/12)(1/3 − 5/36) = 0.002836 Dx3/d3 = (t/d)(1 − Y′/d)(a/d) = (1/40)(1 − 5/12)(1/3) = 0.004861 Dx4/d3 = (1/2)(t/d)(1 − Y′/d)2 + (t/d)(1 − Y′/d)(a/d) = (1/2)(1/40)(7/12)2 + (1/40)(7/12)(1/3) = 0.009115 Dx5/d3 = (t/d)(1 − Y′/d − 1/2) + (t/d)(1 − Y′/d)(a/d) = (1/40)(7/12 − 1/2) + (1/40)(7/12)(1/3) = 0.006944 Dx6/d3 = −(t/d)(Y′/d)(X′/d) + Dx5/d3 = −(1/40)(5/12)(5/36) + 0.006944 = 0.005498 Dx7/d3 = −(t/d)(Y′/d)(b/d) + Dx5/d3 = −(1/40)(5/12)(2/3) + 0.006944 = 0 (check) |
| Dy1/d3 = 0 Dy2/d3 = (1/2)(t/d)[(a/d) − X′/d]2 = (1/2)(1/40)(1/3 − 5/36)2 = 0.0004726 Dy3/d3 = (t/d)(a/d)[(1/2)(a/d) − X′/d] = (1/40)(1/3)(1/6 − 5/36) = 0.0002313 Dy4/d3 = −(t/d)(X′/d)(1 − Y′/d) + (t/d)(a/d)[(1/2)(a/d) − X′/d] =−(1/40)(5/36)(7/12) + (1/40)(1/3)(1/6 − 5/36) = −0.001794 Dy5/d3 = −(t/d)(X′/d) + (t/d)(a/d)[(1/2)(a/d) − X′/d] =−(1/40)(5/36) + (1/40)(1/3)(1/6 − 5/36) = −0.003241 Dy6/d3 = −(1/2)(t/d)(X′/d)2 − (t/d)(X′/d) + (t/d)(a/d)[(1/2)(a/d) − X′/d] =−(1/2)(1/40)(5/36)2 − (1/40)(5/36) + (1/40)(1/3)(1/6 − 5/36) = −0.00348 Dy7/d3 = (t/d)[(1/2)(t/d)2− (X′/d)(b/d)] − (t/d)(X′/d) + (t/d)(a/d)[(1/2)(a/d) − X′/d] = (1/40)[(1/2)(4/9) − (5/36)(2/3)] − (1/40)(5/36) + (1/40)(1/3)(1/6 − 5/36) = 0 (check) |
9.5. Centroid Forces Fx and Fy
| (1) Fx/Fy = 0, (Fx = 0, Fy = F) |
| qt/F = 6.444(Dx/d3) + 8.775(Dy/d3) |
| q2t/F = 0 q2t/F = (6.444 × 0.002836) + (8.775 × 0.0004726) = 0.02242 q3t/F = (6.444 × 0.004861) + (8.775 × 0.0002315) = 0.03336 q4t/F = (6.444 × 0.009115) − (8.775 × 0.001794) = 0.042995 q5t/F = (6.444 × 0.006944) − (8.775 × 0.003241) = 0.01631 q6t/F = (6.444 × 0.005498) − (8.775 × 0.00348) = 0.004892 q7t/F = 0 (2) Fx/Fy = ∞, (Fx = F, Fy = 0) qt/F = 8.6646(Dx/d3) + 34.0(Dy/d3) |
| q2t/F = 0 q2t/F = (8.6646 × 0.002836) + (34.0 × 0.0004726) = 0.04064 q3t/F = (8.6646 × 0.004861) + (34.0 × 0.0002315) = 0.12083 q4t/F = (8.6646 × 0.009115) − (34.0 × 0.001794) = 0.01798 q5t/F = (8.6646 × 0.006944) − (34.0 × 0.003241) = −0.05003 q6t/F = (8.6646 × 0.005498) − (34.0 × 0.00348) = −0.07068 q7t/F = 0 (3a) Fx/Fy = 1, (Fx = Fy = F) qt/F = 15.109(Dx/d3) + 42.775(Dy/d3) |
| q1t/F = 0 q2t/F = (15.109 × 0.002836) + (42.775 × 0.0004726) = 0.2450 q3t/F = (15.109 × 0.004861) + (42.775 × 0.0002315) = 0.08335 q4t/F = (15.109 × 0.009115) − (42.775 × 0.001794) = 0.06098 q5t/F = (15.109 × 0.006944) − (42.775 × 0.003241) = −0.0337 q6t/F = (15.109 × 0.005498) − (42.775 × 0.00348) = −0.06578 (3b) Fx/Fy = + 1, (Fx = Fy = −F) |
| (4a) Fx/Fy = −1, (Fx = −F, Fy = F) qt/F = (6.494 − 8.6646)(Dx/d3) + (−34.0 + 8.775)(Dy/d3) = −2.2206(Dx/d3) − (25.225(Dy/d3) |
| q1t/F = 0 q2t/F = −(2.2206 × 0.002836) − (25.225 × 0.0004726) = −0.01822 q3t/F = −(2.2206 × 0.004861) − (25.225 × 0.0002315) = −0.01663 q4t/F = −(2.2206 × 0.009115) + (25.225 × 0.001794) = −0.0250 q5t/F = −(2.2206 × 0.006944) + (25.225 × 0.003241) = 0.06633 q6t/F = −(2.2206 × 0.005498) + (25.225 × 0.00348) = 0.07557 (4b) Fx/Fy = −1, (Fx = F, Fy = −F) |
| (5) Fx/Fy = 2, (Fx = 2F, Fy = F) qt/F = (6.444 + 2 × 8.6646)(Dx/d3) + (34.0 × 2 + 8.775)(Dy/d3) = 23.7732(Dx/d3) + 76.775(Dy/d3) |
| q1t/F = 0 q2t/F = (23.7732 × 0.002836) + (76.775 × 0.0004726) = 0.1037 q3t/F = (23.7732 × 0.004861) + (76.775 × 0.0002315) = 0.1333 q4t/F = (23.7732 × 0.009115) − (76.775 × 0.001794) = 0.07896 q5t/F = (23.7732 × 0.006944) − (76.775 × 0.003241) = −0.08375 q6t/F = (23.7732 × 0.005498) − (76.775 × 0.00348) = −0.13647 (6) Fx/Fy = 1/2, (Fx = F, Fy = 2F) qt/F = (2 × 6.444 + 8.6646)(Dx/d3) + (34.0 + 2 × 8.775)(Dy/d3) = 21.5526(Dx/d3) + 31.55(Dy/d3) |
| q1t/F = 0 q2t/F = (21.5526 × 0.002836) + (51.55 × 0.0004726) = 0.08548 q3t/F = (21.5526 × 0.004861) + (51.55 × 0.0002315) = 0.11673 q4t/F = (21.5526 × 0.009115) − (51.55 × 0.001794) = 0.10397 q5t/F = (21.5526 × 0.006944) − (51.55 × 0.003241) = −0.01741 q6t/F = (21.5526 × 0.005498) − (51.55 × 0.00348) = −0.0609 |
| = 0.4483d(d/3)2 + ∣0.3447d2s − 0.06865ds2∣d/34d/3 + ∣0.0236d2s + 0.05175ds2∣4d/32d = 0.04981 + [(0.4596 − 0.1220) − (0.1149 − 0.00763)] +[(0.0472 + 0.2070) − (0.03247 + 0.092)] = 0.04981 + 0.23033 + 0.12973 = 0.40987d3 ϖ = 0.2049d2 |
| ꞷ1 = 0, (GJ/T)w1 = 0.2049d2 ꞷ2 = 0.1743d2, (GJ/T)w2 = 0.2049d2 − 0.1743d2 = 0.0306d2 ꞷ3 = 0.2988d2, (GJ/T)w3 = 0.2049d2 − 0.2988d2 = −0.0939d2 ꞷ4 = 0.21884d2, (GJ/T)w3 = 0.2049d2 − 0.2188d2 = −0.0139d2 ꞷ5 = 0.1616d2, (GJ/T)w3 = 0.2049d2 − 0.1616d2 = 0.0433d2 ꞷ6 = 0.1760d2, (GJ/T)w3 = 0.2049d2 − 0.1760d2 = 0.0289d2 ꞷ7 = 0.2306d2, (GJ/T)w3 = 0.2049d2 − 0.2306d2 = −0.0257d2 |
| Γ1 = (0.009925d5t + 0.05398d5t + 0.025904d5t) − (0.2049d2)2t(2d) = (0.089809 − 0.083968) d5t = 0.00584d5t |
| (d3t2/T)σz = 24.536 (ϖ − ꞷ) | (23b) |
| = 24.536 (0.2049d2 − ꞷ) |
| ꞷ1 = 0, (d3t2/T)σz1 = 5.027d2 ꞷ2 = 0.1743d2, (d3t2/T)σz2 = 24.536(0.2049d2 − 0.1743d2) = 0.751d2 ꞷ3 = 0.2988d2, (d3t2/T)σz3 = 24.536(0.2049d2 − 0.2988d2) = −2.304d2 ꞷ4 = 0.2188d2, (d3t2/T)σz4 = 24.536(0.2049d2 − 0.2188d2) = −0.341d2 ꞷ5 = 0.1616d2, (d3t2/T)σz5 = 24.536(0.2049d2 − 0.1616d2) = 1.062d2 ꞷ6 = 0.1760d2, (d3t2/T)σz3 = 24.536(0.2049d2 − 0.1760d2) = 0.709d2 ꞷ7 = 0.2306d2, (d3t2/T)σz7 = 24.536(0.2049d2 − 0.2306d2) = −0.631d2 |
9.6. Torsional Shear Flow
| d3θ/dz3 = −(μ2T/JG) = −T/EΓ1 ∴ q = −Tt/Γ1 × Q = (−Tt/0.00584d5t) × (−0.0185d3) = 3.1678T/d2 = (3.1678 × 1000)/(1.875 × 25.4)2 = 1.398 N/mm |
| θ = (T/GJ) [z + sinhμ(L − z)∕μcoshμL] − (T/GJ)(sinhμL)∕(μcoshμL) | (25a) |
| = (T/GJ){z + [sinhμ(L − z) − sinhμL]∕μcoshμL} |
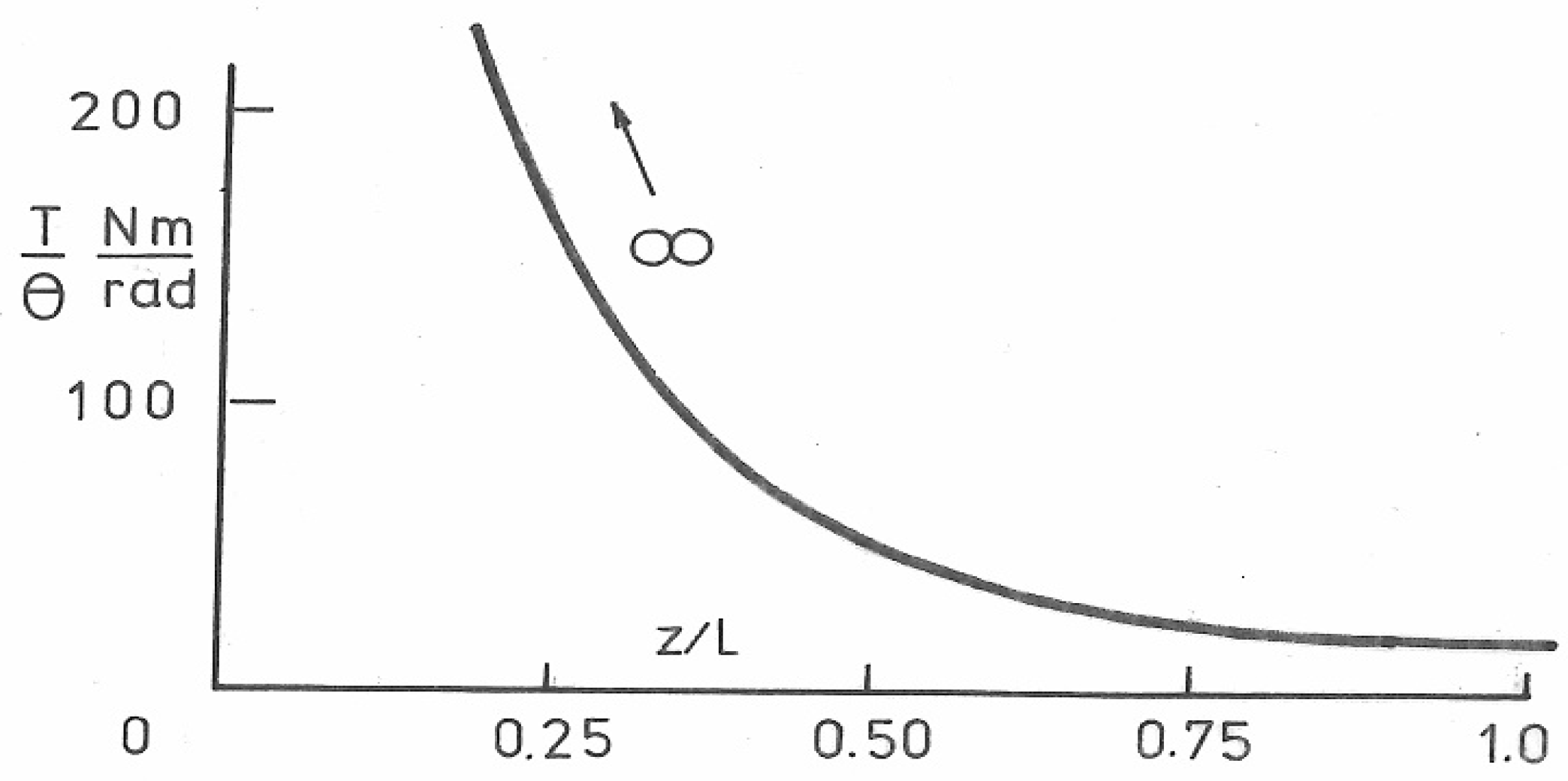
| T/θ = GJ∕{L/4 + [sinh(3 μL/4) − sinhμL]∕μcoshμL} = (70 × 103 × 53.588)∕[125 + (1.675 − 2.695)∕(0.003434 × 2.874] = 173.27 × 103 N mm/c = 173.27 N m/c |
| T/θ = GJ∕{L/2 + [sinh(μL/2) − sinhμL]∕μcoshμL} = (70 × 103 × 53.588)∕[250 + (0.968 − 2.695)∕(0.003434 × 2.874)] = 50 × 103 N mm/c = 50 N m/c |
| T/θ = GJ∕{3L/4 + [sinh(μL/4) − sinhμL]∕μcoshμL} = (70 × 103 × 53.588)∕[375 + (0.4426 − 2.695)∕(0.003434 × 2.874)] = 25.56 × 103 N mm/c = 25.56 N m/c |
| T/θ = GJ∕{L + [sinh(0) − sinhμL]∕μcoshμL} = (70 × 103 × 53.588)∕[500 + (0 − 2.695)∕(0.003434 × 2.874)] = 25.56 × 103 N mm/c = 16.53 N m/c |
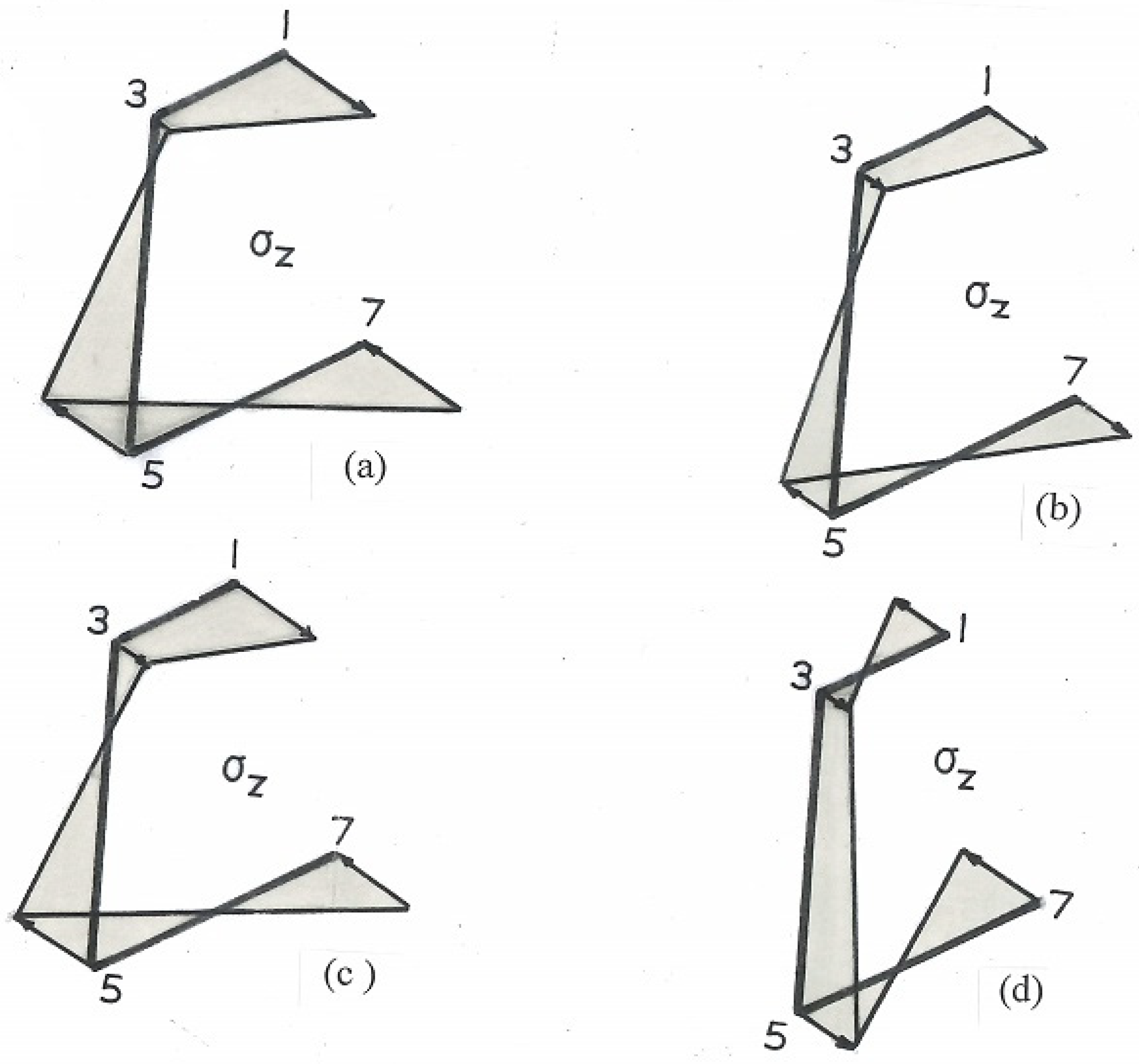
9.7. Bending Stress Distribution
9.8. Trans-Moments
| X′ = 5d/36, Y′ = 5d/12, ex = 21d/153, ey = 9d/87, Ix = 17d3t/72, Iy = 87d3t/1944 and Ixy = −39d3t/648. |
| σz = [Fy (500 − z)1.522 + Fx (500 − z)2.046] y∕0.2361d3t + [Fx (500 − z)1.522 + Fy (500− z)0.3879] x∕0.04475d3t | (31a) |
| σz = (761 Fy + 1023 Fx)(y/d)∕0.2361d3t + (761 Fx + 193.95 Fy)(x/d)∕0.04475d3t σz d2t/103 = (3.223Fy + 4.333Fx)(y/d) + (17.005Fx + 4.334Fy)(x/d) | (31b) |
- (1)
- Fx = F; Fy = 0, |σz d2t/103 = 4.333(y/d) + 17.005(x/d);
- (2)
- Fy = F; Fx = 0, |σz d2t/103 = 3.223(y/d) + 4.334(x/d);
- (3)
- Fx = Fy = F, |σz d2t/103 = 7.556(y/d) + 21.339(x/d);
- (4)
- Fx = −F; Fy = F, |σz d2t/103 = −1.11(y/d) − 12.671(x/d).
| σz = (Mx Ey)/IEx + (My Ex)/IEy = (Fy L)Ey/IEx + (Fx L)Ex/IEy | (33a) |
| σz = FyL(0.3132d)∕(0.4323d3t) + FxL(0.2761d)∕(0.1972d3t) = (0.7245Fy + 1.40Fx)L/(d3t) | (33b) |
9.9. Axial Symmetry
| IEy = (3.28 × 10−3)d4 + (2dt)(5a/8)2 IEy/d4 = (3.28 × 10−3) + 2(t/d)(5/8)2(a/d)2 = (3.28 × 10−3) + 2(1/16)(5/8)2(1/2)2 = 0.01548 ∴ IEy = 0.01548d4 = 6446.2 mm4 |
| σz1 = σz7 = (a − X′)σz∕(ex + X′) = (a − a/4)σz∕(3a/8 + a/4) = 6σz/5 = 6 × 36.9/5 = + 44.28 MPa σz2 = σz6 = 0 σz3 = σz4 = σz5 = −X′ σz∕(ex + X′) = −(a/4)σz∕(3a/8 + a/4) = −2σz/5 = −14.76 MPa |
| σz1 = σz7 = 100 × (300 + 5a/8)(a − a/4)/6446.2 = 100 × 307.94 × 9.525/6446.2 = +45.5 MPa σz2 = σz6 = 0 σz3 = σz4 = σz5 = 100 × (300 + 5a/8)(−a/4)/6446.2 = 100 × 307.94 × (−3.175)/6446.2 = −15.17 MPa |
10. Conclusions
- (1)
- Establish the flexural shear flow distribution with equivalent forces for the principal axes transferred to the shear centre.
- (2)
- Calculate the unconstrained warping displacements for the resultant St. Venant torque, arising from the transfer in (1), applied to the shear centre.
- (3)
- Calculate the axial stress produced by the Wagner torque arising from constraining warping by fixing one end.
- (4)
- Calculate the torsional shear flow arising from the Wagner torque in (3).
- (5)
- Assess the increased torsional stiffness at length positions arising from (3).
- (6)
- Find the net shear flow (stress) distribution from the addition of (1) and (4). Note the stress gradient across the thickness with (1) providing the mean stress and (4) the superimposed linear distribution due to torsion.
- (7)
- Find the bending stress distribution from equivalent moments referred to the principal axes with end forces applied at the centroid.
- (8)
- Find the net axial stress distribution from the addition of (3) and (7).
- (9)
Funding
Data Availability Statement
Conflicts of Interest
References
- Rees, D.W.A.; Al-Sheikh, A.M.S. Theory of flexural shear, bending and torsion for a thin-walled beam of open section longitudinal axis of loading thin-walled beams of open section. World J. Mech. 2024, 14, 23–53. [Google Scholar] [CrossRef]
- ESDU 78020; Local Buckling and Crippling of I, Z and Channel Section Struts. National Technical Reports Library: Alexandria, VA, USA, 1978.
- Nix, W.D. Mechanical properties of thin films. Metall. Trans. A 1989, 20, 2217–2245. [Google Scholar] [CrossRef]
- Zou, M.; Ma, Y.; Yuan, X.; Hu, Y.; Liu, J.; Jin, Z. Flexible devices: From materials, architectures to applications. J. Semicond. 2018, 39, 011010. [Google Scholar] [CrossRef]
- Papangelis, J. On the stresses in thin-walled channels under torsion. Buildings 2024, 14, 3533. [Google Scholar] [CrossRef]
- Yu, Y.; Wei, H.; Zheng, B.; Tian, D.; He, I. Integrated dynamic analysis of thin-walled beams coupled bi-directional loading, torsion and axial vibration under axial loads. Appl. Sci. 2024, 14, 11390. [Google Scholar] [CrossRef]
- Vlasov, V.Z. Thin-Walled Elastic Beams; Oldbourne Press: London, UK, 1961. [Google Scholar]
- Baigent, A.H.; Hancock, G.J. Structural analysis of assemblages of thin-walled members. Eng. Struct. 1982, 4, 207–216. [Google Scholar] [CrossRef]
- Boresi, A.P.; Schmidt, R.J.; Sidebottom, O.M. Advanced Mechanics of Materials, 2nd ed.; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Wagner, H. Torsion and Buckling of Open Sections; No. NACA-TM-807; NTRS-NASA: Washington, DC, USA, 1936. [Google Scholar]
- Oden, J.T.; Ripperger, E.A. Mechanics of Elastic Structures, 2nd ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Cook, R.D.; Young, W.C. Advanced Mechanics of Materials, 2nd ed.; Prentice-Hall: Hoboken, NJ, USA, 1998. [Google Scholar]
- Gao, Z.H. A unified theory of thin-walled structures. J. Struct. Mech. 1981, 9, 179–197. [Google Scholar]
- Vetyuko, Y. Direct Approach to Elastic Deformation and Stability of Rods of Open Profile; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gjelsvik, A. Theory of Thin-Walled Beams; John Wiley and Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Bleich, F.; Bleich, H.H. Buckling Strength of Metal Structures; McGraw-Hill: New York, NY, USA, 1952. [Google Scholar]
- Hoff, N.J. The effect of the edge conditions on the buckling of thin-walled circular cylindrical shells in axial compression. In Applied Mechanics; Görtler, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar] [CrossRef]
- Drillenberg, M. Torsion and Shear Stresses Due to Shear Centre Eccentricity; SCIA 2017; Delft University of Technology: Delft, The Netherlands, 2017. [Google Scholar]
- Wen, Y.L.; Kuo, M.H. General expression for the torsional warping of a thin-walled open section beam. Int. J. Mech. Sci. 2003, 43, 830–849. [Google Scholar]
- Wang, G. Restrained torsion of open thin-walled beams including shear deformation effects. J. Zhejiang Univ. Sci. 2012, A13, 260–273. [Google Scholar] [CrossRef]



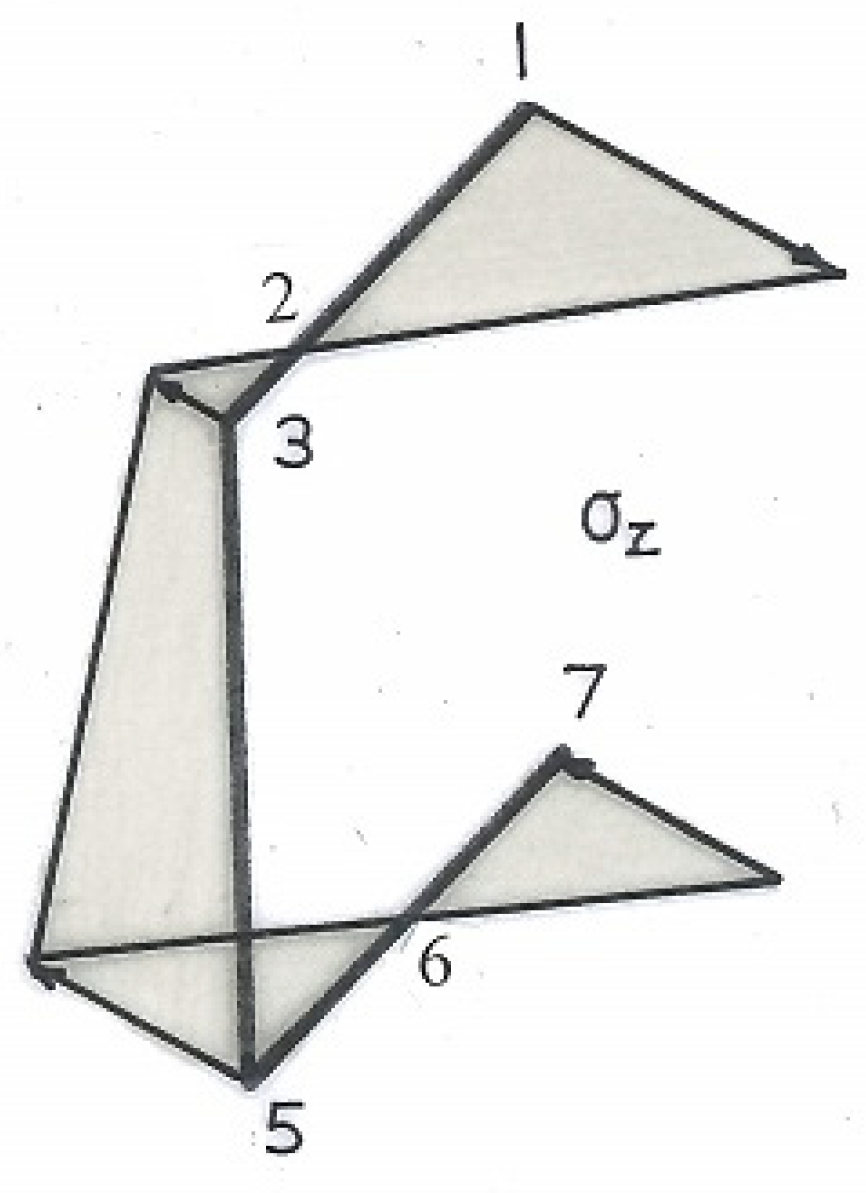
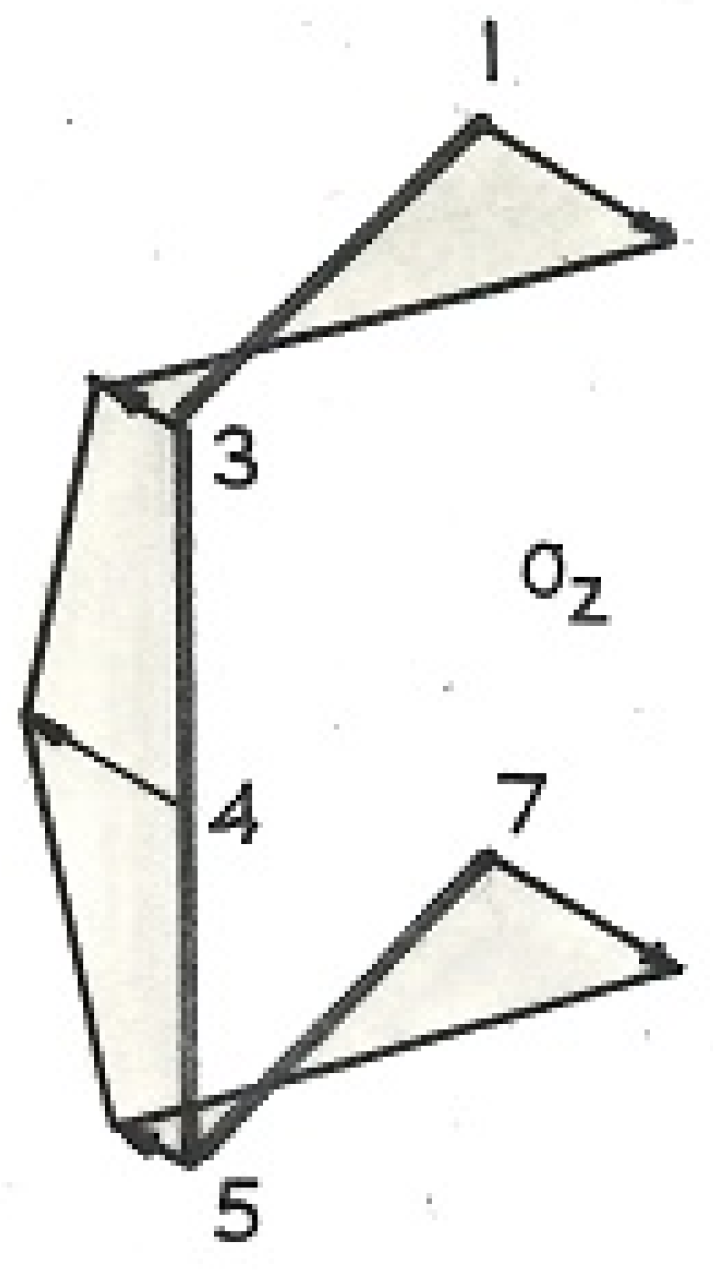




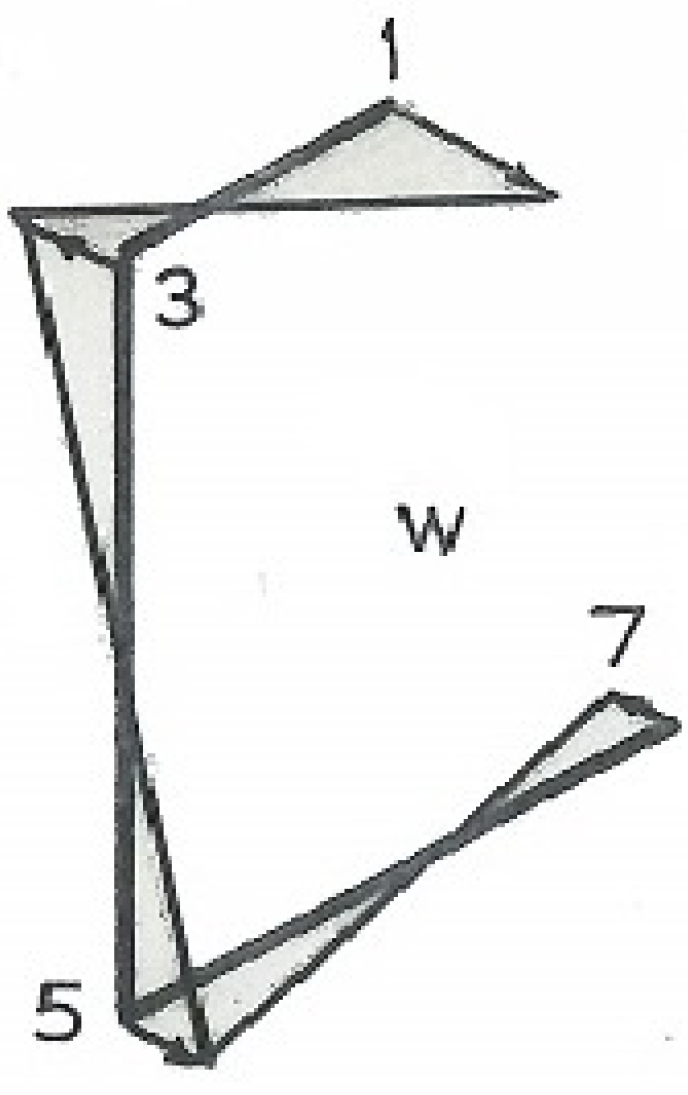
| Section A: a = ½″, d = 1″, t = 1/16″, d/a = 2, ex/a = 3/8, ϖ/a2 = 27/32 ko/a2 = 1 − 3/8 = 5/8 k1/a3 = −(1/4) × 2 + (1/2)(3/8) = −5/16 k3/a2 = 3/4 + 3/8 + 1 = 17/8 k4/a3 = (3/8) × 4 + 2(5/8 − 17/8) − 5/16 = −29/16 k5/a2 = 2(1 + 1) = 4 k6/a3 = (3)2(1/2 − 3/16) + 3(17/8 − 4) − 29/16 = −74/16 Q1 = 0 Q3/a3 = (1/4) × 2 − 27/32 = −11/32 Q4/a3 = (3/16)(1 + 1)2 +(5/8 − 27/32) × 2 − 5/16 = 0 (check) Q5/a3 = −(3/16) × 32 − (27/32 − 17/8) × 3 − 29/16 = 11/32 Q7/a3 = −(1/2) × 16 − 4(27/32 − 4) − 74/16 = 0 (check) |
| Section B: a = 1″, d = 1¾″, t = ⅛″, d/a = 7/4, ex/a = 12/31, ϖ/a2 = 0.7207 ko/a2 = 7/8 − 12/31 = 0.488 k1/a3 = (1/4)(7/4 − 24/31) − 0.488 = −0.244 k3/a2 = (12/31 × 7/4) + 12/31 + (1/2)(7/4) = 1.9375 k4/a3 = (12/31)(1 + 7/8)2 + (1 + 7/8)(0.488 − 1.9375) − 0.244 = −1.6047 k5/a2 = (7/4)(1 + 7/8) = 3.2813 k6/a3 = (11/4)2(7/16 − 12/62) + (11/4)(1.9375 − 3.2813) − 1.6037 = −3.4498 Q1 = 0 Q3/a3 = (1/4)(7/4) − 0.7207 = −0.2832 Q4/a3 = (12/62)(1 + 7/8)2 + (0.488 −0.7207)(1 + 7/8) − 0.244 = 0 (check) Q5/a3 = −(12/62)(11/4)2 − (0.7207 − 1.9395)(11/4) −1.6047 = 0.2832 Q7/a3 = −(7/16)(2 + 7/4)2 − (2 + 7/4)(0.7207 −3.2813) − 3.4498 = 0 (check) |
| Section C: a = ⅝″, d = 1⅞″, t = 3/64″, d/a = 3, ex/a = 1/3, ϖ/a2 = 27/20 ko/a2 = 3/2 − 1/3 = 7/6 k1/a3 = (1/4)(3 −2/3) − 7/6 = −7/12 k3/a2 = 3/2 + 1 + 1/3 = 17/6 k4/a3 = (1/3)(1 + 3/2)2 + (1 + 3/2)(7/6 − 17/6) − 7/12 = −8/3 k5/a2 = 3(1 + 3/2) = 15/2 k6/a3 = 16(3/4 −1/6) + 4(17/6 − 15/2) − 8/3 = −12 Q1 = 0 Q3/a3 = 3/4 −27/20 = −3/5 Q4/a3 = 1/6(1 + 3/2)2 + (7/6 −27/20)(1 + 3/2) − 7/12 = 0 (check) Q5/a3 = −(1/6)(16) − (27/20 −17/6)4 − 8/3 = 3/5 Q7/a3 = −3/4(25) − 5(27/20 −15/2) − 12 = 0 (check) |
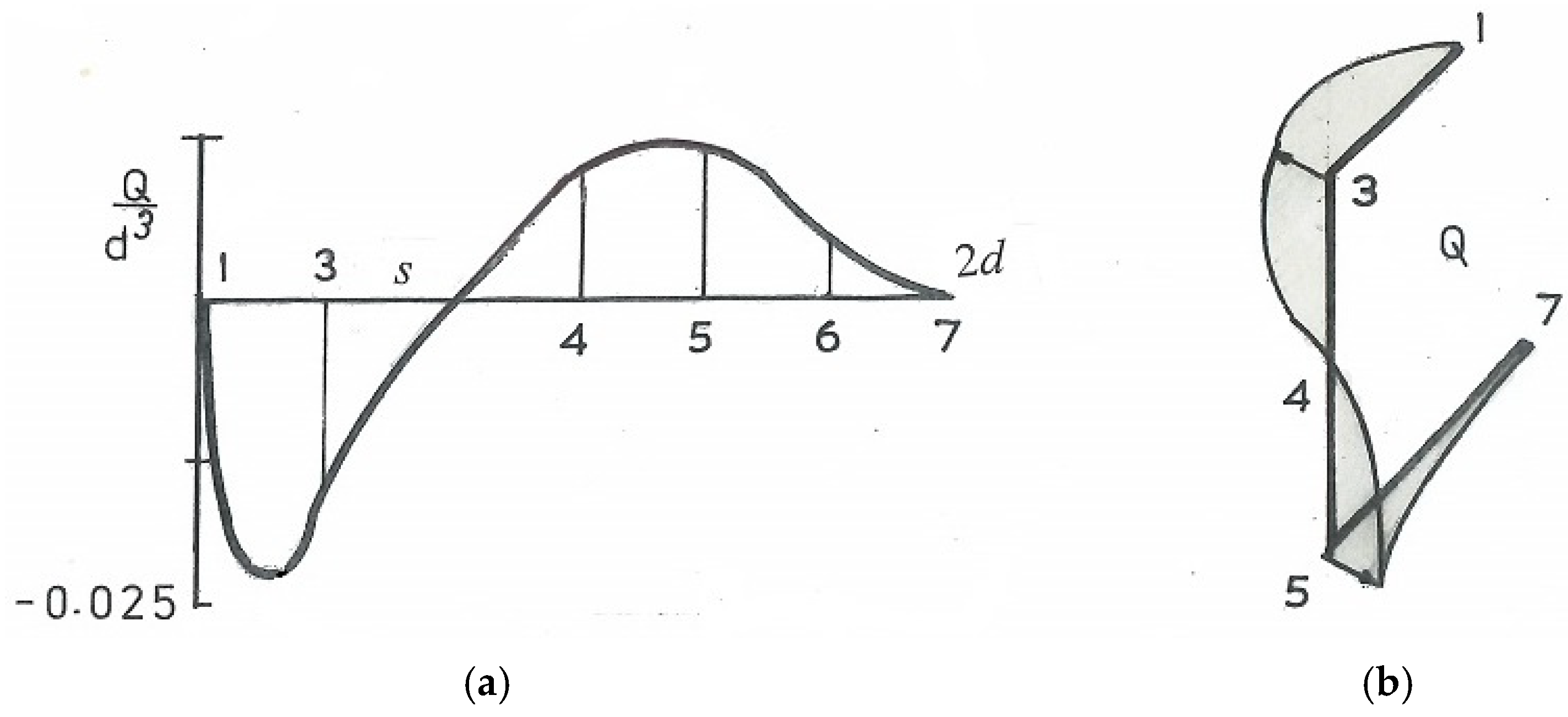
| Successive Normalised Length Ratios | |||||
| z/L | 0 | 1/4 | 1/2 | 3/4 | 1 |
| 1 − z/L | 1 | 3/4 | 1/2 | 1.4 | 0 |
| (A) μL(1 − z/L) | 1.9685 | 1.4764 | 0.9843 | 0.4921 | 0 |
| coshμL(1 − z/L) | 3.65 | 2.303 | 1.5248 | 1.1236 | 1 |
| coshμL(1 − z/L) | 1 | 0.631 | 0.4178 | 0.3078 | 0.274 |
| coshμL | |||||
| (G/T) d3θ/dz3 × 106 | −0.6357 | −0.4011 | −0.2656 | −0.1957 | −0.1742 |
| (B) μL(1 − z/L) | 4.55 | 3.4125 | 2.275 | 1.1375 | 0 |
| coshμL(1 − z/L) | 47.32 | 15.187 | 4.9154 | 1.7198 | 1 |
| coshμL(1 − z/L) | 1 | 0.3209 | 0.1039 | 0.03634 | 0.02113 |
| coshμL | |||||
| (G/T) d3θ/dz3 × 109 | −20.4 | −6.533 | −2.1155 | 0.7399 | −0.4302 |
| (C) μL(1 − z/L) | 0.936 | 0.702 | 0.468 | 0.234 | 0 |
| coshμL(1 − z/L) | 1.471 | 1.2567 | 1.1115 | 1.0275 | 1 |
| coshμL(1 − z/L) | 1 | 0.8543 | 0.7556 | 0.6985 | 0.6798 |
| coshμL | |||||
| (G/T) d3θ/dz3 × 106 | −0.167 | 0.1426 | −0.1261 | −0.1166 | −0.1135 |
| Section A: a = 1/2″, d = 1″, t = 1/16″, L = 300 mm (11.81″) a/d = ½, a/t = 8, t/d = 1/16, X′/a = 1/4, X′/d = 1/8, ex/a = 3/8 Ix = 0.02055d4; Iy = 0.00328d4, Iy/Ix = 0.1571, ϖ/a2 = 27/32 |
| Section B: a = 1″, d = 1¾″, t = ⅛″, L = 1 m (39.37″) a/d = 4/7, a/t = 8, t/d = 1/14, X′/a = 4/15, X′/d = 16/105, ex/a = 12/31 Ix = 0.026375d4; Iy = 0.0053615d4, Iy/Ix = 0.20315, ϖ/a2 = 0.7207 |
| Section C: a = 5/8″, d = 1⅞″, t = 3/64″, L = 340 mm (13.39″) a/d = 1/3, a/t = 40/3, t/d = 1/40, X′/a = 1/5, X′/d = 1/15, ex/a = 1/3 Ix = 0.006251d4; Iy = 0.0004334d4, Iy/Ix = 0.06934, ϖ/a2 = 27/20 |
| Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Dy/d3 | 0 | 1/227.55 | 1/256 | 0 | −1/256 | −1/227.55 | 0 |
| Dx/d3 | 0 | 3/256 | 1/64 | 3/128 | 1/64 | 3/256 | 0✓ |
| × Iy/Ix | 0 | 1/543.18 | 1/407.38 | 1/271.59 | 1/407.38 | 1/543.18 | 0 |
| ∑D/d3 | 0 | 1/160.37 | 1/157.21 | 1/271.59 | −1/688.92 | −1/391.6 | 0 |
| qx + qy | 0 | 7.485 | 7.636 | 4.420 | −1.742 | −3.065 | 0 |
| qT | 0 | 1.731 | 1.692 | 0 | −1.692 | −1.731 | 0✓ |
| ∑q | 0 | 9.216 | 9.328 | 4.420 | −3.434 | −4.796 | 0 |
| τ =∑q/t | 0 | 5.805 | 5.876 | 2.784 | −2.163 | −3.021 | 0 |
| Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Dy/d3 | 0 | 6.27 × 10−3 | 5.42 × 10−3 | 0 | −5.42 × 10−3 | −6.27 × 10−3 | 0 |
| Dx/d3 | 0 | 14.97 × 10−3 | 20.41 × 10−3 | 29.34 × 10−3 | 20.41 × 10−3 | 14.97 × 10−3 | 0 (check) |
| ×Iy/Ix | 0 | 3.337 × 10−3 | 4.146 × 10−3 | 5.96 × 10−3 | 4.146 × 10−3 | 3.337 × 10−3 | 0 |
| ∑D/d3 | 0 | 9.607 × 10−3 | 9.566 × 10−3 | 5.96 × 10−3 | −1.274 × 10−3 | 2.933 × 10−3 | 0 |
| qx + qy | 0 | 4.0312 | 4.0139 | 2.5009 | −0.5345 | −1.2307 | 0 |
| qT | 0 | 1.550 | 1.497 | 0 | −1.497 | −1.550 | 0 (check) |
| ∑q | 0 | 5.5812 | 5.5109 | 2.5009 | −2.0315 | −2.7807 | 0 |
| τ = ∑q/t | 0 | 1.758 | 1.736 | 0.7877 | −0.64 | −0.8758 | 0 |
| Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Dy/d3 | 0 | 8.88 × 10−4 | 8.333 × 10−4 | 0 | −8.333 × 10−3 | −8.88 × 10−4 | 0 |
| Dx/d3 | 0 | 33.33 × 10−4 | 41.7 × 10−4 | 72.92 × 10−4 | 41.7 × 10−4 | 33.33 × 10−4 | 0 (check) |
| ×Iy/Ix | 0 | 2.311 × 10−4 | 2.892 × 10−4 | 5.056 × 10−4 | 2.892 × 10−4 | 2.311 × 10−4 | 0 |
| ∑D/d3 | 0 | 11.191 × 10−4 | 11.225 × 10−4 | 5.056 × 10−4 | −5.441 × 10−4 | −6.569 × 10−4 | 0 |
| qx + qy | 0 | 5.4218 | 5.4383 | 2.4495 | −2.6361 | −3.1826 | 0 |
| qT | 0 | 1.23 | 1.23 | 0 | −1.23 | −1.23 | 0 (check) |
| ∑q | 0 | 6.652 | 6.668 | 2.450 | −3.866 | −4.413 | 0 |
| τ = ∑q/t | 0 | 5.587 | 5.60 | 2.458 | −3.247 | −2.707 | 0 |
| Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| x | a − X′ | 0 | −X′ | −X′ | −X′ | 0 | a − X′ |
| y | d /2 | d /2 | d /2 | 0 | −d/2 | −d/2 | −d/2 |
| Channel A | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1st term, MPa | 37.95 | 4.12 | −7.04 | −23.89 | −7.04 | 4.12 | 37.95 |
| 2nd term, MPa | 253.46 | 43.9 | −25.93 | −69.85 | −113.75 | −43.9 | 165.65 |
| ∑σz, MPa | 291.4 | 48.02 | −32.97 | −93.74 | −120.79 | −39.78 | 203.60 |
| ∑τ, MPa | 0 | 5.805 | 5.876 | 2.784 | −2.163 | −3.021 | 0 |
| ST | 0.859 | 5.06 | 7.144 | 2.662 | 2.068 | 6.213 | 1.23 |
| SV | 0.859 | 5.096 | 7.24 | 2.663 | 2.069 | 6.231 | 1.23 |
| Channel B | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1st term, MPa | 10.36 | 1.14 | −2.22 | −7.09 | −2.22 | 1.14 | 10.36 |
| 2nd term, MPa | 110.4 | 21.57 | −10.79 | −32.36 | −53.93 | −21.57 | 67.43 |
| ∑σz, MPa | 120.76 | 22.71 | −13.0 | −39.45 | −56.15 | −20.44 | 77.8 |
| ∑τ, MPa | 0 | 1.758 | 1.736 | 0.7877 | −0.64 | −0.8758 | 0 |
| ST | 2.07 | 10.88 | 18.58 | 6.332 | 4.451 | 12.165 | 3.213 |
| SV | 2.07 | 10.91 | 18.736 | 6.329 | 4.452 | 12.197 | 3.213 |
| Channel C | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1st term, MPa | 39.04 | 4.34 | −4.34 | −18.8 | −4.34 | 4.34 | 39.04 |
| 2nd term, MPa | 218.8 | 25.18 | −23.24 | −48.42 | −73.59 | −25.18 | 168.5 |
| ∑σz, MPa | 257.8 | 29.52 | −27.58 | −67.22 | −77.93 | −20.84 | 207.54 |
| ∑τ, MPa | 0 | 5.587 | 5.60 | 2.058 | −3.247 | −3.767 | 0 |
| ST | 0.97 | 7.92 | 8.40 | 3.712 | 3.196 | 11.30 | 1.205 |
| SV | 0.97 | 8.05 | 8.55 | 3.714 | 3.20 | 11.46 | 1.205 |
| Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Channel A | 37.95 | 4.12 | −7.04 | −23.89 | −7.04 | 4.12 | 37.95 |
| Channel B | 10.36 | 1.14 | −2.22 | −7.09 | −2.22 | 1.14 | 10.36 |
| Channel C | 39.04 | 4.34 | −4.34 | −18.80 | −4.34 | 4.34 | 39.04 |
| Point | Dxi/d3 (Fy at E) | Dyi/d3 (Fx at E) |
|---|---|---|
| 1 | 0 | 0 |
| 2 | (t/d)(1 − Y′/d)(a/d − X′/d) | (1/2)(t/d)(a/d − X′/d)2 |
| 3 | (t/d)(1 − Y′/d)(a/d) | (t/d)(a/d)[(1/2)(a/d) − X′/d] |
| 4 | (1/2)(t/d)(1 − Y′/d)2 + (t/d)(1−Y′/d)(a/d) | −(t/d)(X′/d)(1 − Y′/d) + (t/d)(a/d)[(1/2)(a/d − X′/d] |
| 5 | (t/d)(1/2 − Y′/d) + (t/d)(1 − Y′/d)(a/d) | −(t/d)(X′/d) + (t/d)(a/d)[(1/2)(a/d)− X′/d] |
| 6 | −(t/d)(Y′/d)(X′/d) + Dx5 | −(1/2)(t/d)(X′/d)2 − (t/d)(X′/d) + (t/d)(a/d)[(1/2)(a/d) −X′/d] |
| 7 | 0 | 0 |
| Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| x/d | 7/36 | 0 | −5/36 | −5/36 | −5/36 | 0 | 19/36 |
| y/d | 7/12 | 7/12 | 7/12 | 0 | −5/12 | −5/12 | −5/12 |
| Equation (1) | 5.834 | 2.528 | 0.166 | −2.362 | −4.167 | −1.805 | 7.169 |
| σz/MPa | 216.05 | 93.61 | 6.15 | −87.47 | −154. | −66.84 | 265.5 |
| Equation (2) | 2.723 | 1.88 | 1.278 | −0.6019 | −1.95 | −1.343 | 0.9445 |
| σz/MPa | 100.83 | 69.62 | 47.32 | −22.29 | −72.02 | −49.73 | 34.97 |
| Equation (3) | 8.557 | 4.408 | 1.444 | −2.964 | −6.112 | −3.148 | 8.114 |
| σz/MPa | 316.9 | 163.2 | 53.5 | −109.8 | −226.3 | −116.6 | 300.5 |
| Equation (4) | −3.111 | −2.464 | 1.112 | 1.76 | 2.222 | 0.4625 | −6.225 |
| σz/MPa | −115.2 | −91.2 | 43.2 | 65.2 | 82.3 | 17.1 | −230.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rees, D.W.A. A Stress Analysis of a Thin-Walled, Open-Section, Beam Structure: The Combined Flexural Shear, Bending and Torsion of a Cantilever Channel Beam. Appl. Sci. 2025, 15, 8470. https://doi.org/10.3390/app15158470
Rees DWA. A Stress Analysis of a Thin-Walled, Open-Section, Beam Structure: The Combined Flexural Shear, Bending and Torsion of a Cantilever Channel Beam. Applied Sciences. 2025; 15(15):8470. https://doi.org/10.3390/app15158470
Chicago/Turabian StyleRees, David W. A. 2025. "A Stress Analysis of a Thin-Walled, Open-Section, Beam Structure: The Combined Flexural Shear, Bending and Torsion of a Cantilever Channel Beam" Applied Sciences 15, no. 15: 8470. https://doi.org/10.3390/app15158470
APA StyleRees, D. W. A. (2025). A Stress Analysis of a Thin-Walled, Open-Section, Beam Structure: The Combined Flexural Shear, Bending and Torsion of a Cantilever Channel Beam. Applied Sciences, 15(15), 8470. https://doi.org/10.3390/app15158470






