Modeling of Dynamics of Nonideal Mixer at Oscillation and Aperiodic Damped Mode of Driving Member Motion

Abstract

The dynamics of the vibrational mode of motion of the driving member of a nonideal system, a mixing–whipping device based on a simple slide-crank mechanism, was studied. The highly nonlinear differential equations of motion were solved numerically by the Runge–Kutta method. The interaction of the mixing–whipping device with the nonideal excitation source causes the rotational speed of the engine shaft and the rotation angle of the driving member to fluctuate, accomplishing a damped process. The parameters of the device and the nonideal energy source have an effect on the kinematic, vibrational and energy characteristics of the system. An increase in the engine’s torque, crank length, number and radius of piston holes, and piston mass, as well as a decrease in the fluid’s density, leads to a reduction in the oscillation range of the crank angle, amplitude and period of angular velocity oscillations of the engine shaft and the mixing–whipping force power. The effects of a nonideal energy source may be used in designing a mixing–whipping device based on a slider-crank mechanism to select effective system parameters and an energy-saving motor in accordance with the requirements of technological processes and products.

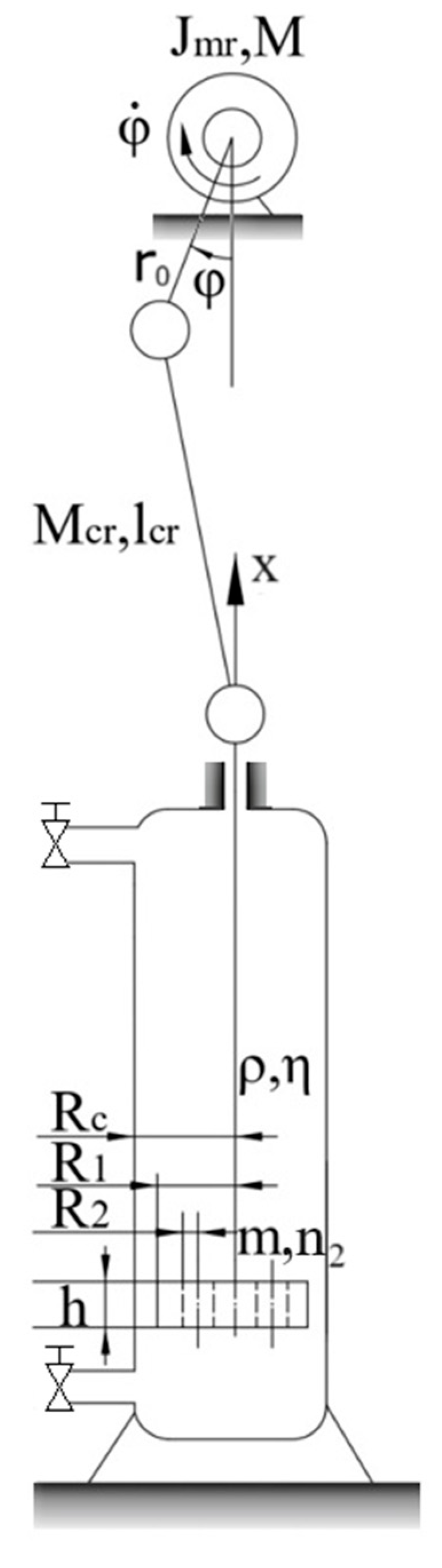
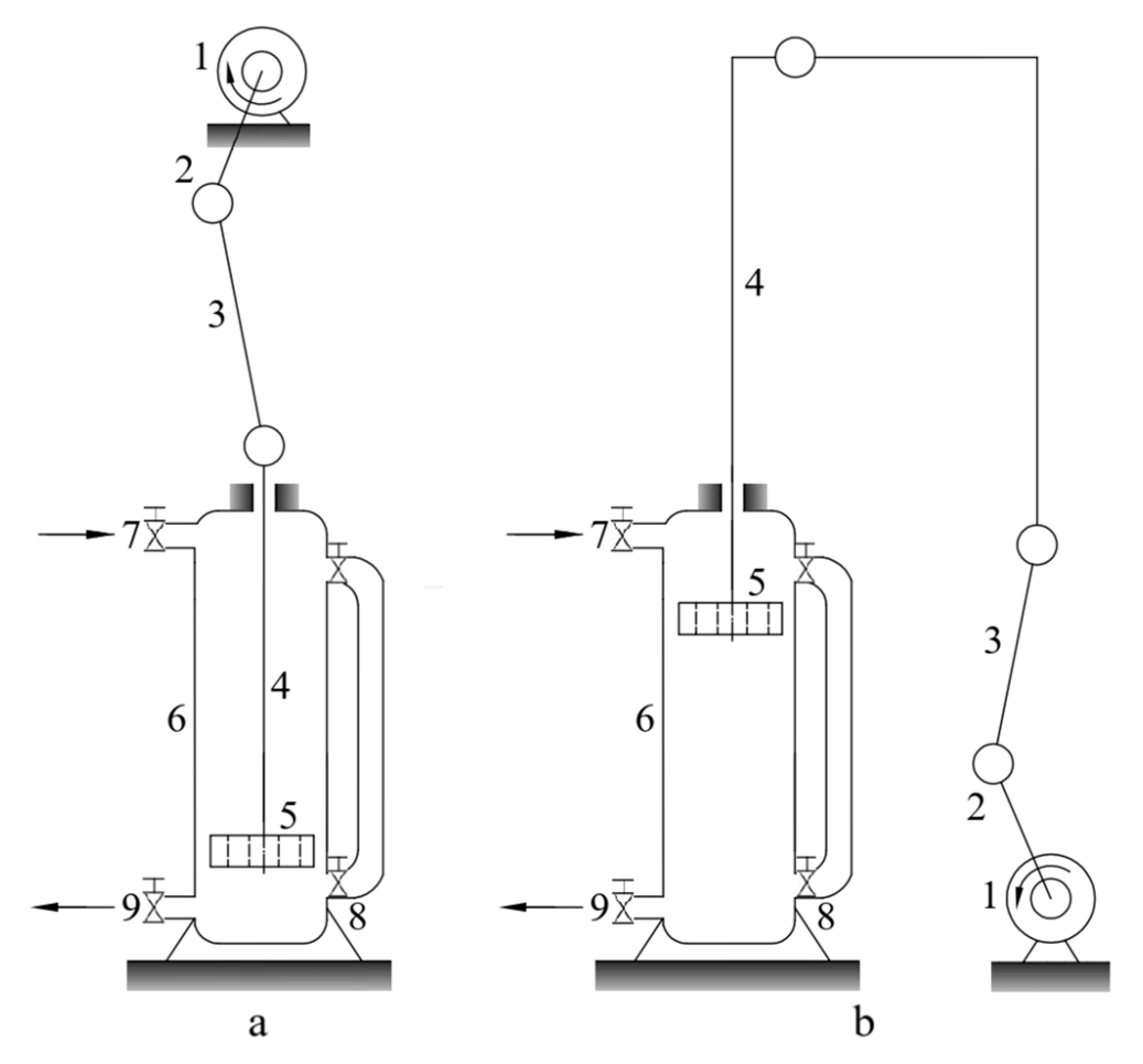
1. Introduction

Studying nonideal oscillating systems wherein the excitation source is affected by the dynamic behavior of the subordinate nonlinear system is considered a challenging task in theoretical and practical research in engineering sciences. When this behavior has no effect on excitation, such systems are known as ideal systems or ideal-powered systems. The behavior of ideal systems is very well known in the modern literature, but there are fewer findings on nonideal systems. Reviews of nonideal problems have been published in the papers [1,2,3,4]. The theory of nonideal mechanical system (NIS) was developed in [5,6]. For this kind of nonideal dynamic system, it is necessary to add a member (equation) describing the interaction between the power supply and the subordinate system. Compared to an ideal system, the differential equations of a nonideal system are significantly nonlinear.

The nonideal source effect is known to be manifested in actual machines and mechanisms. Let us consider the response of the dynamics of nonideal vibrating systems based on some lever mechanisms.

More generalized dynamic and mathematical models of the nonideal flat lever orthogonal vibration table mechanism were created in the article [7]. In the paper [8], the responses of rotational motion dynamics and oscillatory damped motion of the mechanism were studied. As a result of the influence of the lever mechanism on the excitation source during stable modes of the motor shaft rotation, it was shown that its rotational speed fluctuates relative to its average value. The frequency of variation in rotational speed was equal to its mean value, and its amplitude was inversely proportional to this value. This means that the smaller the rotational speed of the motor, the larger the amplitude and smaller the frequency of variation in the rotational speed of the driving member. The actuated rotational speed depends on the length of the crank and the engine torque. The conditions imposed on the amplitude of oscillations, regularities of change in the amplitude of the damped oscillatory motion of the crank, as well as the dependence of the frequency of the oscillatory motion on its amplitude and the parameters of the energy source and mechanism are established. Stability conditions of rotational motion and oscillatory damped motion are found. The studies in [9] focused on the oscillatory motion of the mechanism at slow engine speeds. The characteristics of the change in the amplitude of the motor rotational speed depending on the length of the driving member and on the mass of the load on the operating member were determined. In the papers [7,10], the influence of friction in kinematic pairs on the dynamics of the orthogonal vibration table mechanism with a low-speed engine at a constant stationary load in the operating member was studied.

One of the simplest lever mechanisms is the crank-slider mechanism, which converts the rotational movement of the driving element into translational movement, and therefore it is the base for many devices. This mechanism has been extensively analyzed and applied in internal combustion and Stirling engines, compressors [11,12,13,14,15,16], robotics and mechatronic devices [17,18,19,20,21], excavation, tunneling, and construction machinery [22,23,24], power equipment [25,26,27], forging and stamping machines [28,29], and various other applications [30,31,32]. There is a significant amount of research carried out on the simple crank-driven mechanism, since it is the main element of the devices. Most of the studies relate to rigid member mechanisms with the crank (crankshaft) being rigidly supported and rotating at a constant rotational speed. Most of these studies are either analytical or numerical and examine various mechanical aspects of the dynamic response and stability of crank-driven mechanism of devices [33].

By connecting two crank-slider mechanisms, it is possible to obtain a corresponding device that also converts the rotational motion of the driving member into translational motion of the slider connected to the mixing piston. The idea of combining two crank-slider mechanisms is not new. Crank-slider mechanisms with dual sliders and combined systems are already used in instruments, devices, machines, and robots for various purposes [34,35,36,37,38]. In papers [33,39], the problem is extended by incorporating a nonideal force and flexible support for the crank (crankshaft). These two factors in combination with the nonlinearity of the kinematics give rise to a model that closely resembles the actual mechanism. The slide-crank mechanism, due to its simplicity, is adopted as the basic mechanism for the cutting device. In the paper [40], a more realistic system is considered: the mechanism is mounted on an elastic support and the effect of nonideal force on the system and the cutting process is analyzed. In the paper [6], different designs of mechanisms are compared: simple, eccentric and slide-crank mechanism. Kinematic and dynamic analysis of ideal and nonideal force systems resting on rigid and spring supports is given. The advantages and disadvantages of the systems are outlined.

In articles [41,42], a new model of the effect of the movement of a single-action crank-driven pump on the modes of a nonideal energy source, i.e., a damless hydraulic turbine, and vice versa, was developed and studied. Consequently, the rotation of the hydraulic turbine becomes nonuniform, and the coefficient of nonuniformity of motion depends on the parameters of the piston pump and the hydraulic turbine itself. The average value of the hydraulic turbine angular velocity depends only on the parameters of the nonideal force source and the velocity of the watercourse flow.

To date, although there are patents and hand-made unsophisticated slide-crank mixing mechanisms (see, for example, [43,44,45,46]), there has been no mathematical modeling of the dynamics of these mechanisms, taking into account the technological processes carried out by different modes of motion of the driving member, the interaction with the source of energy. For this reason, this paper aims to study the dynamics of the oscillation-damped mode of the driving member motion, focusing on the application of slide-crank mechanism for mixing–whipping and shaking the slurry with appropriate technological characteristics, thus making a significant contribution to the theory of nonideal mechanical systems.

2. Materials and Methods

Equations of Motion and Their Solutions

The schematic diagram of the device for slurry mixing, whipping and shaking, based on the slide-crank mechanism, is shown in Figure 1.

For numerical calculations of the piston-type crank-slider mechanism shown in Figure 1, the dimensions of the links, engine parameters, and fluid characteristics used are listed in

Table 1. Parameters of mechanism links, engine, and fluid.

Parameter	Name	Value
r0	crank length	0.10 m
lcr	connecting rod length	0.60 m
Mcr	connecting rod mass	1 kg
m	piston mass	20 kg
Rc	cylinder radius	0.10 m
R1	piston radius	0.08 m
R2	hole radius	0.002 m
n2	number of holes	2
h	piston height	5 × 10−3 m
ρ	density of fluid	1038 kg⋅m−3
η	dynamic viscosity of fluid	1.75 × 10−3 Pa⋅s (20 °C)
a	motor torque	43 N⋅m
b	motor rotor drag force torque	42.879 N⋅m⋅s−1
Jmr	motor rotor moment of inertia	60.75 × 10−3 kg⋅m2

.

We accept the following assumptions, simplifications and hypotheses. The density of the liquid in the working volume is considered unchangeable (the density of the process fluid, koumiss and shubat, are close to the density of water). When the liquid passes through the holes of the piston, in the thin applied layer, the flow is assumed to be laminar (Re = (47.5 ÷ 71.2) < Re_cr), the edge effects are neglected, and the flow in the gap between the cylinder and the piston is assumed to be laminar (Re = (23.8 ÷ 35.6) < Re_cr) under the conditions of smallness of the radius of the holes and the size of the gap between the piston and the cylinder compared to the radius of the piston. To simplify the equation of motion of the device, we assume the length of the crank is many times less than the length of the connecting rod, and the mass of the engine rotor is many times greater than the mass of the piston. The crank, connecting rod, slider, and piston are considered stiff and perfectly aligned in the absence of motion, with their centers located along a vertical line. The slider is constrained on both sides by guides, ensuring strictly vertical movement. The piston holes are located at the vertices of a regular polygon, with their centers coinciding with the connection point to the slider. The piston’s center of mass coincides with its geometric center. The position of the piston holes does not affect the mass center coordinate. At low crankshaft rotation speeds, dynamic balancing of centrifugal forces acting on the crank and connecting rod is not necessarily due to the relatively smallness of these forces.

The focus is on the dynamics of technological processes carried out by the piston with the mixing–whipping force in the operating volume, and therefore, compared to the mixing–whipping force, the friction forces in kinematic pairs and in guides of vertical motion of a slide can be neglected, due to their insignificance.

Using the Lagrangian method, the differential equations of motion of the mixing and churning device were constructed based on a simple piston crank-slider mechanism for cases of upward and downward movement of the piston (Figure 1). The position of the nonideal system’s motor mechanism is determined by the generalized coordinate: the angular coordinate φ of the drive element due to its rotation. Then, the differential equation of Lagrange motion has the following form:

$$\begin{array}{l}{\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial T}{\partial \dot{\phi }}}-{\displaystyle \frac{\partial T}{\partial \phi }}=Q_{\phi u},\\ {\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial T}{\partial \dot{\phi }}}-{\displaystyle \frac{\partial T}{\partial \phi }}=Q_{\phi d},\end{array}$$

(1)

where T is the kinetic energy of the system, and Q_φu and Q_φd are the generalized forces in cases of upward and downward movement of the piston, respectively. To do this, it is necessary to make expressions of the kinetic energy of the system: the device motor.

The kinetic energy of the system consists of two components: the kinetic energy of the rotary motion of the engine rotor and the kinetic energies of the translational energy of the piston with the slide at r << lcr:

$$T={\displaystyle \frac{1}{2}}{J}_{mr}{\dot{\phi }}^2+{\displaystyle \frac{1}{2}}m{\dot{v}}^2,$$

(2)

where $J_{mr}={\displaystyle \frac{1}{2}}{M}_{mr}{R}^2$ is the inertia moment of the engine rotor, and v is the speed of the piston with the slide. To determine the velocity v, it is necessary to take into account some geometric properties of the device.

If the influence of the final length of the connecting rod is neglected, the path traveled by the piston can be related to the angle φ of rotation of the crank by the following relation:

$$x=r_0\left(1-\cos \phi \right).$$

(3)

Piston and slide speed are as follows:

$$v={\displaystyle \frac{dx}{dt}}=r_0\sin \phi \dot{\phi }.$$

(4)

Substituting this expression in (2), we obtain the kinetic energy of the system in the form

$$T={\displaystyle \frac{1}{2}}\left(J_{mr}+m{r}_0^2{\sin }^2\phi \right){\dot{\phi }}^2.$$

(5)

Considering that M_mr >> m,

$$T={\displaystyle \frac{1}{2}}{J}_{mr}{\dot{\phi }}^2.$$

(6)

The crank of the mechanism is driven by the dynamic torque of the motor M and, as a result of the translational movement of the slide, creates the resulting F of the pressure forces F₁, friction F₂ and F₃ acting on the piston. For the proposed mechanism, the DC motor with rectilinear characteristic has a dynamic torque as follows:

$$M=a-b\dot{\phi },$$

(7)

There are relatively few studies dedicated to the calculation of viscous fluid flow through plate holes. For example, articles [47,48] study the flow of a viscous compressible medium through drilled (porous) plate holes, including the influence of the entrance effect. The mass flow rate through the holes depends on the pressure difference on the plate, depending on the relevant parameters such as the diameter of the hole, the thickness of the plate, and the properties of the medium.

The force of interaction between the piston and the fluid, F, includes the pressure force, buoyant force, and gravitational force F₁, the friction force acting on the outer lateral surface of the piston F₂, and the friction force acting on the surfaces of the piston’s holes F₃.

We determine the projection of the pressure force, buoyant force, and gravity force acting on the piston. For this purpose, let us consider a flow tube with two cross-sections: the first coincides with the cross-section of the cylinder and the lower boundary of the piston, and the second coincides with the cross-sections of the holes and the clearance between the piston and the cylinder, as well as the upper boundary of the piston. Assuming the fluid is incompressible and has low viscosity, we apply the continuity equation and Bernoulli’s equation to these sections. By solving the resulting system of equations simultaneously, we find the pressure difference of the fluid between the upper and lower surfaces of the piston:

$$\Delta p=p_2-p_1=-{\displaystyle \frac{\rho }{2}}\left[{\displaystyle \frac{1}{n_2^2}}{\left({\displaystyle \frac{R_c}{R_2}}\right)}^4-1\right]v^2+\rho g_{x}h+{\displaystyle \frac{m{g}_x}{\pi \left(R_1^2-n{R}_2^2\right)}}.$$

(8)

Here, g_x is the projection of gravitational acceleration onto the direction of fluid flow through the piston holes and the gaps between the piston and cylinder: g_x = −g when the fluid moves downward, and g_x = g when the fluid moves upward. A detailed derivation of Formula (8) is provided in Appendix A.

Now, the projections of the pressure force, buoyant force, and gravitational force acting on the piston can be readily determined, taking into account the value v from (4):

$$F_{1s}=\left\{-{\displaystyle \frac{\rho }{2}}\left[{\displaystyle \frac{1}{n_2^2}}{\left({\displaystyle \frac{R_c}{R_2}}\right)}^2-1\right]{\left(r_0\sin \phi \dot{\phi }\right)}^2+\rho g_{x}h+{\displaystyle \frac{m{g}_x}{\pi \left(R_1^2-n_2{R}_2^2\right)}}\right\}\pi \left(R_1^2-n_2{R}_2^2\right),$$

(9)

To determine the friction force between the piston and the fluid, consider axisymmetric, straight-line fluid flows in a cylindrical coordinate system (r, θ, x), where r is the radial coordinate, θ is the polar angular coordinate, and the axis $x$ coincides with the flow symmetry axis. Applying the axisymmetry condition ([49], Section 6.2, Formula 6.37) to the continuity equation and subsequently to the viscous fluid motion equation for steady flow u_x = u_x(r), we obtain an ordinary differential equation ([49], Section 6.2, Formula 6.40):

$$-{\displaystyle \frac{\partial p}{\partial x}}+\eta {\displaystyle \frac{1}{r}}{\displaystyle \frac{d}{dr}}\left(r{\displaystyle \frac{\partial u_x}{\partial r}}\right)+\rho g_x=0,$$

(10)

When the pressure gradient $\partial p/\partial x$ is constant, the general solution of Equation (10) ([49], Section 6.2, Formula 6.43) is as follows:

$$u_x={\displaystyle \frac{1}{4\eta }}\left({\displaystyle \frac{\partial p}{\partial x}}-\rho g_x\right)r^2+c_1\ln r+c_2.$$

(11)

The constants $c_1$ and $c_2$ are determined from the flow boundary conditions.

Next, we find the projection of the friction force exerted on the lateral surface of the piston.

Using the boundary conditions on the lateral surface of the piston and the inner surface of the cylinder as follows:

$$\begin{array}{l}r=R_1:u_x=v;\\ r=R_c:u_x=0\end{array}$$

(12)

Equation (11) may be rewritten as follows:

$$u_x={\displaystyle \frac{1}{4\eta }}\left({\displaystyle \frac{\partial p}{\partial x}}-\rho g_x\right)\left(r^2-R_c^2\right)+\left[v+{\displaystyle \frac{1}{4\eta }}\left({\displaystyle \frac{\partial p}{\partial x}}-\rho g_x\right)\left(R_c^2-R_1^2\right)\right]{\displaystyle \frac{\ln \frac{r}{R_c}}{\ln \left(R_1/R_c\right)}}.$$

(13)

Under the conditions $R_c-R_1$ << $R_1$ and $h$, neglecting edge effects, the flow of the fluid between the piston and cylinder can be considered laminar. By substituting the gradient $\partial p/\partial x$ with $\Delta p/h$ and taking into account Expression (8) for ΔP and Expression (4) for $v$, and substituting (13) into Newton’s law, we find the friction force acting on the lateral surface of the piston as follows:

$$\begin{array}{l}{F}_{2s}\approx -\left\{-{\displaystyle \frac{\rho }{2}}\left[{\displaystyle \frac{1}{n_2^2}}{\left({\displaystyle \frac{R_c}{R_2}}\right)}^2-1\right]{\left(r_0\sin \phi \dot{\phi }\right)}^2+{\displaystyle \frac{m{g}_s}{\pi \left(R_1^2-n_2{R}_2^2\right)}}\right\}\left[\pi R_1^2+{\displaystyle \frac{\pi \left(R_c^2-R_1^2\right)}{2\ln \left(R_1/R_c\right)}}\right]\\ -{\displaystyle \frac{2\pi \eta h}{\ln \left(R_1/R_c\right)}}{r}_0\sin \phi \dot{\phi },\end{array}$$

(14)

Now, we find the projections of the friction forces acting on the surfaces of the cylindrical holes under conditions of steady laminar flow at low engine shaft speeds, assuming the following relation holds: $R_2$ << $h$. Edge effects are neglected.

In Equation (11), to determine the constants $c_1$ and $c_2$ we use the following boundary conditions of the flow (see example 6.2.4, Figure 6.13 in [49]):

$$\begin{array}{l}r=R_2:u_x=v;\\ r=k{R}_2:u_x=0.\end{array}$$

(15)

Then, taking into account $k\to 0:{\displaystyle \frac{\ln \left[r/\left(k{R}_2\right)\right]}{\ln \left(1/k\right)}}\to 1$, Equation (11) will take the form of

$$u_x=v+{\displaystyle \frac{1}{4\eta }}\left({\displaystyle \frac{\partial p}{\partial x}}-\rho g_x\right)\left(r^2-R_2^2\right).$$

(16)

In Expression (16), we replace the value $v$ with its expression from (4), substitute the gradient $\partial p/\partial x$ with $\Delta p/h$, and then replace the value ΔP with its expression from (8). By substituting the resulting laminar flow velocity in the piston hole into Newton’s law, we obtain the projections of the friction forces between the fluid and the surfaces of the holes:

$$F_{3s}\approx -n_2\left\{-{\displaystyle \frac{\rho }{2}}\left[{\displaystyle \frac{1}{n_2^2}}{\left({\displaystyle \frac{R_c}{R_2}}\right)}^2-1\right]{\left(r_0\sin \phi \dot{\phi }\right)}^2+{\displaystyle \frac{m{g}_x}{\pi \left(R_1^2-n_2{R}_2^2\right)}}\right\}\pi R_2^2,$$

(17)

The expression for the virtual work of the projection of the resultant force $F_x={\displaystyle \sum _{i=1}^3{F}_{ix}}$, exerted by the fluid on the piston and the engine torque M is given by the following form:

$$\delta A=M\delta \phi +F\delta x,$$

(18)

where $\delta x=r_0\sin \phi \delta \phi$ is the change in the coordinate x_, and substituting this value in (18), the following is derived:

$$\delta A=Q_{\phi }\delta \phi =\left(M+F_x{r}_0\sin \phi \right)\delta \phi .$$

(19)

Generalized forces of the system, according to (19), are as follows:

$$Q_{\phi }=M+F_x{r}_0\sin \phi ,$$

(20)

where

$$\begin{array}{l}{F}_x=-{\displaystyle \frac{2\pi \eta h}{\ln \left(R_1/R_c\right)}}{r}_0\sin \phi \dot{\phi }+{\displaystyle \frac{\rho }{2}}\left[{\displaystyle \frac{1}{n_2^2}}{\left({\displaystyle \frac{R_c}{R_2}}\right)}^2-1\right]\left[2\pi n_2{R}_2^2+{\displaystyle \frac{\pi \left(R_c^2-R_1^2\right)}{2\ln \left(R_1/R_c\right)}}\right]r_0^2{\sin }^2\phi {\dot{\phi }}^2+\\ \left\{\rho g_{x}h\pi \left(R_1^2-n_2{R}_2^2\right)-{\displaystyle \frac{m{g}_x}{\pi \left(R_1^2-n_2{R}_2^2\right)}}\left[2\pi n_2{R}_2^2+{\displaystyle \frac{\pi \left(R_c^2-R_1^2\right)}{2\ln \left(R_1/R_c\right)}}\right]\right\}.\end{array}$$

(21)

Here, $F_x=F_u$ or $F_d$ depending on the value $g_x$ or direction of the piston’s movement (i.e., the direction of fluid flow through the piston holes and the gaps between the piston and cylinder).

Substituting (6), (21) into (1), taking into account (13), (8)–(10), we obtain the following equations:

For the upward movement of the piston:

$$\ddot{\phi }+\left(f_1{\sin }^2\phi +b/J_{mr}\right)\dot{\phi }+f_2{\sin }^3\phi {\dot{\phi }}^2+{\omega }_{0u}^2\sin \phi =M/J_{mr},$$

(22)

and for downward movement of the piston:

$$\ddot{\phi }+\left(f_1{\sin }^2\phi +b/J_{mr}\right)\dot{\phi }+f_2{\sin }^3\phi {\dot{\phi }}^2+{\omega }_{0d}^2\sin \phi =M/J_{mr},$$

(23)

where

$$\begin{array}{l}{\mu }_1={\displaystyle \frac{1}{J_{mr}}}{\displaystyle \frac{2\pi \eta h}{\ln \left(R_1/R_c\right)}}{r}_0^2,{\mu }_2={\displaystyle \frac{1}{J_{mr}}}\left\{-{\displaystyle \frac{\rho }{2}}\left[{\displaystyle \frac{1}{n_2^2}}{\left({\displaystyle \frac{R_c}{R_2}}\right)}^2-1\right]\left[2\pi n_2{R}_2^2+{\displaystyle \frac{\pi \left(R_c^2-R_1^2\right)}{2\ln \left(R_1/R_c\right)}}\right]r_0^3\right\},\\ {\omega }_{0u}^2={\displaystyle \frac{1}{J_{mr}}}\left\{-{\displaystyle \frac{mg}{\pi \left(R_1^2-n_2{R}_2^2\right)}}\left[2\pi n_2{R}_2^2+{\displaystyle \frac{\pi \left(R_c^2-R_1^2\right)}{2\ln \left(R_1/R_c\right)}}\right]+\rho gh\pi \left(R_1^2-n_2{R}_2^2\right)\right\}{r}_0,\\ {\omega }_{0d}^2={\displaystyle \frac{1}{J_{mr}}}\left\{{\displaystyle \frac{mg}{\pi \left(R_1^2-n_2{R}_2^2\right)}}\left[2\pi n_2{R}_2^2+{\displaystyle \frac{\pi \left(R_c^2-R_1^2\right)}{2\ln \left(R_1/R_c\right)}}\right]-\rho gh\pi \left(R_1^2-n_2{R}_2^2\right)\right\}{r}_0\end{array}$$

(24)

Replacing the mechanical characteristic of the motor with Expression (7), introducing dimensionless time $\tau ={\omega }_{0u}t,\tau ={\omega }_{0d}t$ and after small transformations, we obtain the equation of motion of the device in the following form:

For the piston lifting time,

$${\phi }^{″}+{\displaystyle \frac{1}{{\omega }_{0u}}}\left({\mu }_1{\sin }^2\phi +{\displaystyle \frac{b}{J_{mr}}}\right){\phi }^{\prime }+{\mu }_2{\sin }^3{{\phi }^{\prime }}^2+\sin \phi ={\displaystyle \frac{a}{J_{mr}{\omega }_{0u}^2}},$$

(25)

where $\phi \subseteq \left[0,\pi \right]\cup \left[2\pi ,3\pi \right]\cup \left[4\pi ,5\pi \right]\dots \left[2n\pi ,\left(2n+1\right)\pi \right],n=0,1,2,\dots ,$ and for the piston lowering time:

$${\phi }^{″}+{\displaystyle \frac{1}{{\omega }_{0d}}}\left({\mu }_1{\sin }^2\phi +{\displaystyle \frac{b}{J_{mr}}}\right){\phi }^{\prime }+{\mu }_2{\sin }^3\phi {{\phi }^{\prime }}^2+\sin \phi ={\displaystyle \frac{a}{J_{mr}{\omega }_{0d}^2}},$$

(26)

where $\phi \subseteq \left[\pi ,2\pi \right]\cup \left[3\pi ,4\pi \right]\cup \left[5\pi ,6\pi \right]\dots \left[\left(2n-1\right)\pi ,2n\pi \right],n=1,2,3,\dots$

Equations (25) and (26), the dash sign denotes the dimensionless time derivative $\tau$. The differential Equations (25) and (18) differ from each other by coefficients ${\omega }_{0u}^2$ and ${\omega }_{0d}^2$, but have the same form; therefore, it is sufficient to solve one of them. Equations (25) and (26) are significantly nonlinear since the nonlinear term enters the equations without a small parameter. The essentially nonlinear model of the differential equations of motion (25) and (26) allows for an in-depth study of the dynamics of the mixing–whipping device in both rotational and oscillatory or aperiodically damped modes of the driving member’s motion. In contrast, vibrational systems with nonideal power sources and flexible supports (which are mostly weakly nonlinear) lack this capability and are generally limited to analyzing dynamics only in the rotational mode of the driving element. A comprehensive study of the influence of system parameters on the device’s dynamics is possible only within essentially nonlinear systems. At $a/\left(J_{mr}{\omega }_0^2\right)$ > 1, there is a rotational mode, and at $a/\left(J_{mr}{\omega }_0^2\right)$ < 1, there are oscillatory and aperiodically damped crank motion modes. Depending on the value $b/\left({\omega }_0{J}_{mr}\right)$, the crank movement is divided into oscillatory-damping and aperiodic-damping modes.

The mixing and whipping processes are carried out mainly under the influence of the piston pressure force, and therefore the mixing and whipping force and its power are determined by the expressions

$$F={\displaystyle \frac{1}{2}}\rho \pi \left(R_1^2-n_2{R}_2^2\right)\left[{\displaystyle \frac{1}{n_2^2}}{\left({\displaystyle \frac{R_c}{R_2}}\right)}^2-1\right]r_0^2{\sin }^2\phi {\dot{\phi }}^2,P={\displaystyle \frac{1}{2}}\rho \pi \left(R_1^2-n_2{R}_2^2\right)\left[{\displaystyle \frac{1}{n_2^2}}{\left({\displaystyle \frac{R_c}{R_2}}\right)}^2-1\right]r_0^3{\sin }^3\phi {\dot{\phi }}^3.$$

(27)

The equations of motion of the device (25) and (26) are solved using the MATLAB R2023b software package (https://www.mathworks.com/products/new_products/release2023b.html (accessed on 22 June 2025)) using the fourth-order Runge–Kutta method for oscillating and aperiodic damped modes of motion of the crank. This resulted in graphical dependences of the rotation angle and rotational speed of the actuating engine shaft on time, mixing and whipping force power from the angle of rotation and rotational speed of the excitation source shaft, and the parameters of the nonideal mechanical system. The obtained graphical dependences of the engine shaft rotation speed on time indicate the superiority of the main harmonic of the solutions of the equations of motion in them and, consequently, the inherent oscillatory characteristics for them.

3. Results and Discussion

The results of solving the equations of motion (25) and (26) and calculating the mixing and whipping force power (27), as graphs of dependencies φ = φ(t), $\dot{\phi }=\dot{\phi }(t)$, $P=P(\phi )$ and $P=P(\dot{\phi })$ at different parameters of the system, are shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25.

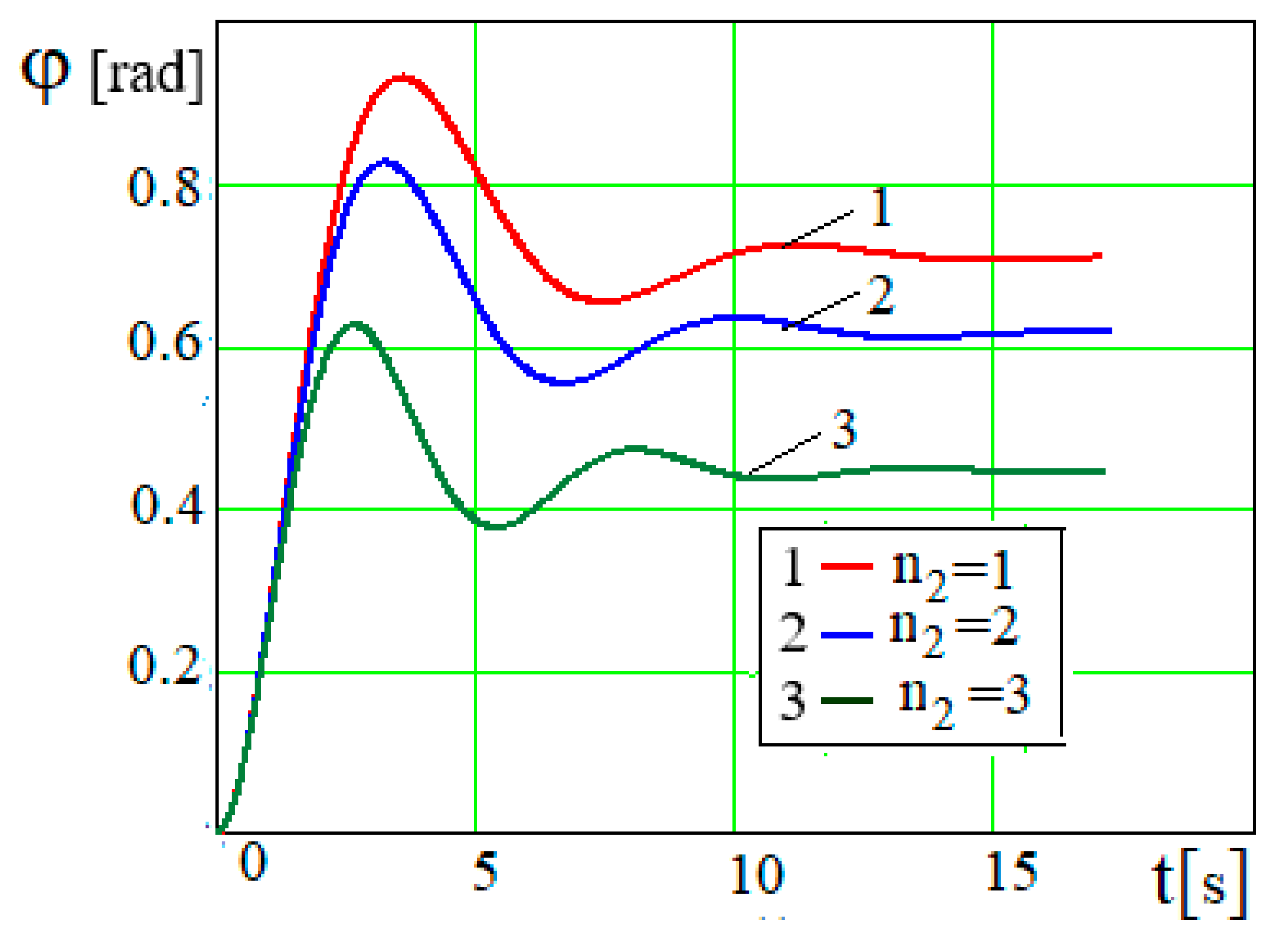
If the engine power (torque a) is insufficient for the rotary motion of the crank, then the crank will perform a damped oscillation process. The crank, under the action of torque a, initially rotates upwards by some angle and then falls downwards, before reaching the neutral equilibrium position under the action of torque; it rises again, etc., until the oscillations are completely damped out.

The greater the engine torque a, the greater the initial maximum crank angle (Figure 2). The crank deflection angle φ tends to a limit of constant value φ₁ as time elapses after completing the oscillating process. The greater the engine torque a, the greater the value of the crank angle ${\phi }_l$. This means that the crank makes damped oscillations not around the neutral equilibrium position, but around a certain value ${\phi }_l$ of angle φ. This is caused by the fact that, at the rotational speed of the crank $\dot{\phi }\to 0$, its angle of rotation is $\phi \to \arcsin \left[a/\left(J_{mr}{\omega }_0^2\right)\right]$. With constant magnitude of $J_{mr}$ and coefficient ${\omega }_0^2$ the limiting angle of rotation of the crank ${\phi }_l$~$\arcsin k_{1}a$ (where $k_1=1/\left(J_{mr}{\omega }_0^2\right)$). Considering that the maximum crank angle is 1.57 rad, the larger the engine torque a, the larger the limiting crank angle φ_l and the oscillation period.

Figure 2. Dependence φ = φ(t) for different values of a.

Figure 2. Dependence φ = φ(t) for different values of a.

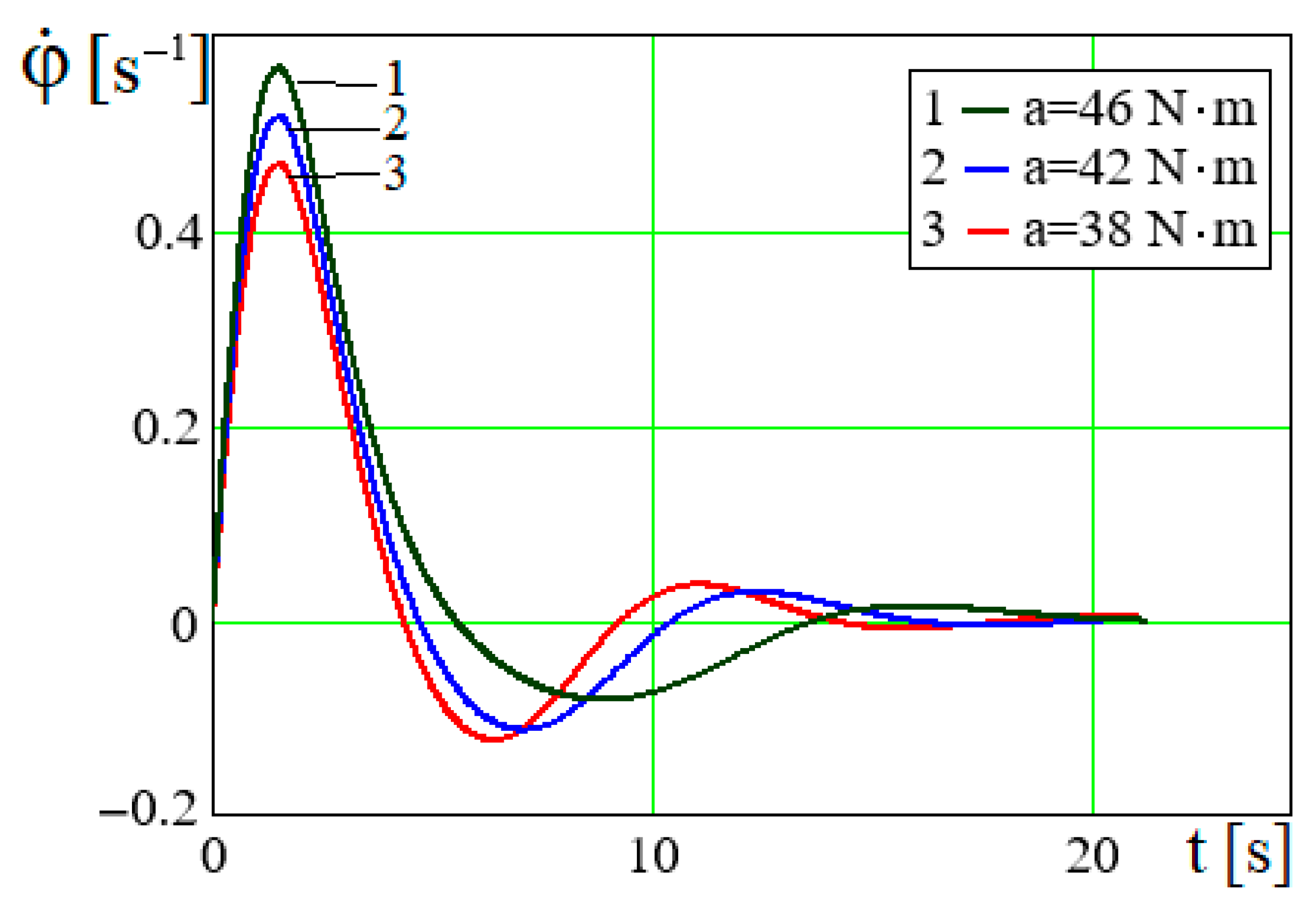
The rotational speed of the crank $\dot{\phi }$ also makes damped oscillations around the zero value with initial and subsequent amplitudes; the less the rotational speed, the less the corresponding torque value with decreased period (Figure 3).

Dependency graphs P = P(φ) and $P=P(\dot{\phi })$ in Figure 4 and Figure 5 show that during the upward rotation of the crank, the pressure force on the piston from above increases, and, accordingly, the power of the mixing–whipping force decreases and the value of P reaches its maximum in further increasing the crank angle (Figure 4). In this case, the rate of increase in the rotational speed of the excitation source shaft will be greatly attenuated and the motor shaft rotational speed will decrease by the end of the cycle (Figure 5). From the relations (27), $P$~${\dot{\phi }}^3{\sin }^3\phi$. The general character of dependence P = P(φ) (Figure 4) is determined by the relation $P$~${\sin }^3\phi$, but the amplitude and periodicity of the function ${\sin }^3\phi$ are influenced by the value $\dot{\phi }$, to be more precise, by the value a. Since $\phi =\phi \left(\dot{\phi }\right)$ and $\dot{\phi }=\dot{\phi }\left(a\right)$ (Figure 3), $\phi =\phi \left(a\right)$ (Figure 2). The smaller the value of the a engine torque, the smaller is the amplitude and period of oscillation of the mixing–whipping force power P depending on the angle of rotation φ of the crank according to the graphical relationships φ = φ(t) and $\dot{\phi }=\dot{\phi }(t)$ in Figure 2 and Figure 3. Maximum magnitudes of the values φ and $\dot{\phi }$ in the graphical dependencies φ(t) and $\dot{\phi }(t)$ (Figure 2 and Figure 3) determine the right boundaries of the dependencies P = P(φ) and $P=P(\dot{\phi })$ (Figure 4 and Figure 5); the minimum values φ_l and $\dot{\phi }$ ($\dot{\phi }\prec 0$) (Figure 2 and Figure 3) determine the left boundaries of the power graphical dependencies.

Thus, the graphs in Figure 2, Figure 3, Figure 4 and Figure 5 show the results of the action of the power parameters of the excitation source on the kinematic parameters of the driving member of the device and on the energy characteristic of the dynamics of the operating member.

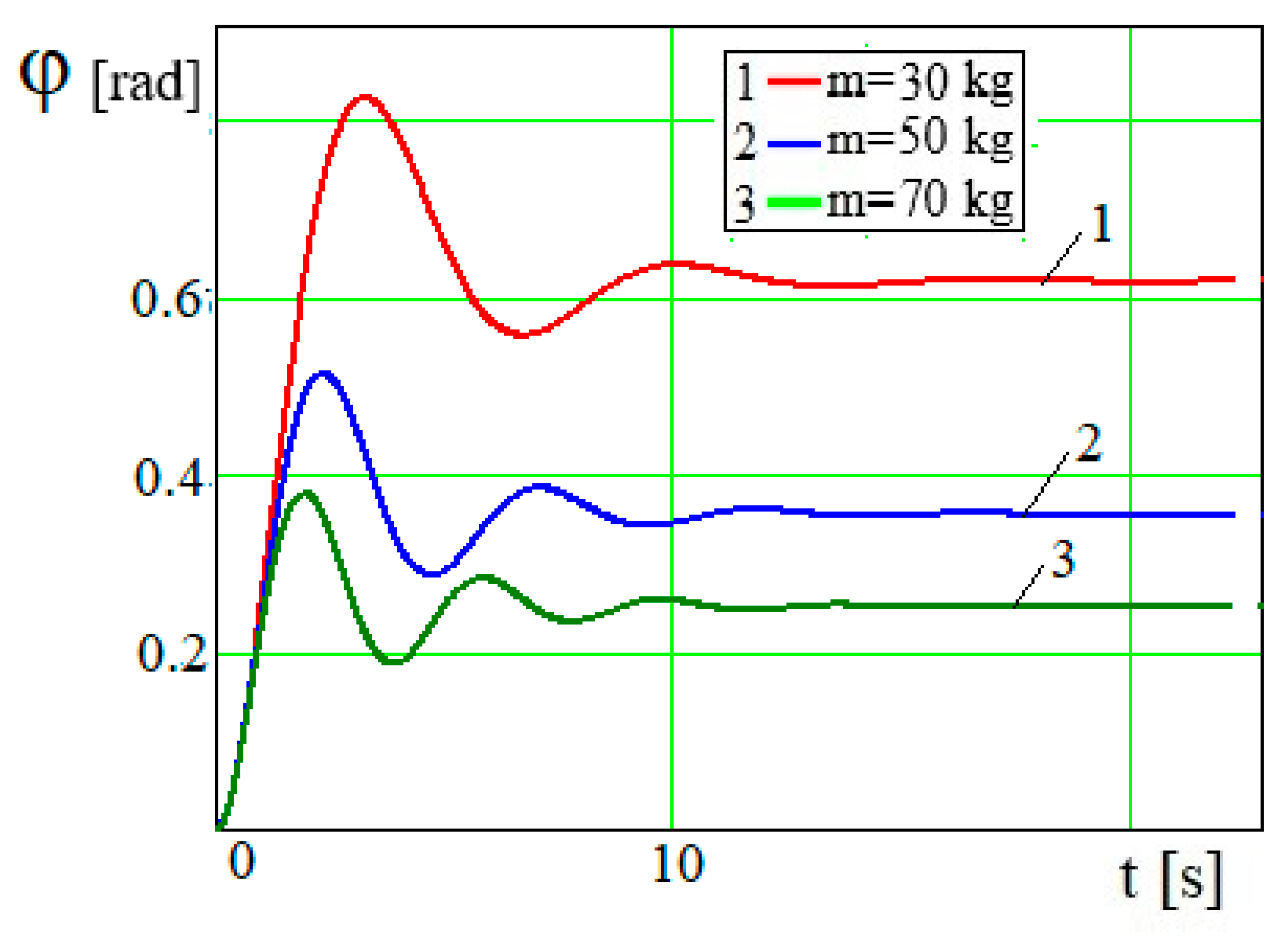
In Figure 6 and Figure 7, lines 1, 2 and 3, which are oscillatory characteristics of the vibrational mode of engine shaft motion, depend on the piston mass. The values of the mass of the piston m are taken in relation to the rotating torque of the motor a for the effect of an oscillatorily and aperiodically damped mode of crank movement. As the piston mass increases, the amplitude of oscillations of the angle $\phi$ and the period of its damped oscillations decrease. After a lapse of time, the lines practically straighten out, and the angle of rotation $\phi$ tends to the limit values. The limiting value of the rotation angle ${\phi }_l$~$\arcsin \left(k_2/{\omega }_0^2\right)$ (where $k_2={a/J}_{mr}$); in turn, ${\omega }_0^2$~$m$. As the mass of the piston increases, the value ${\phi }_l$ of the angle φ decreases (Figure 6).

Figure 3. Dependence $\dot{\phi }=\dot{\phi }(t)$ for different values of a.

Figure 3. Dependence $\dot{\phi }=\dot{\phi }(t)$ for different values of a.

Figure 4. Dependence P = P(φ) for different values of a.

Figure 4. Dependence P = P(φ) for different values of a.

Figure 5. Dependence $P=P(\dot{\phi })$ for different values of a.

Figure 5. Dependence $P=P(\dot{\phi })$ for different values of a.

Figure 6. Dependence φ = φ(t) for different values of m.

Figure 6. Dependence φ = φ(t) for different values of m.

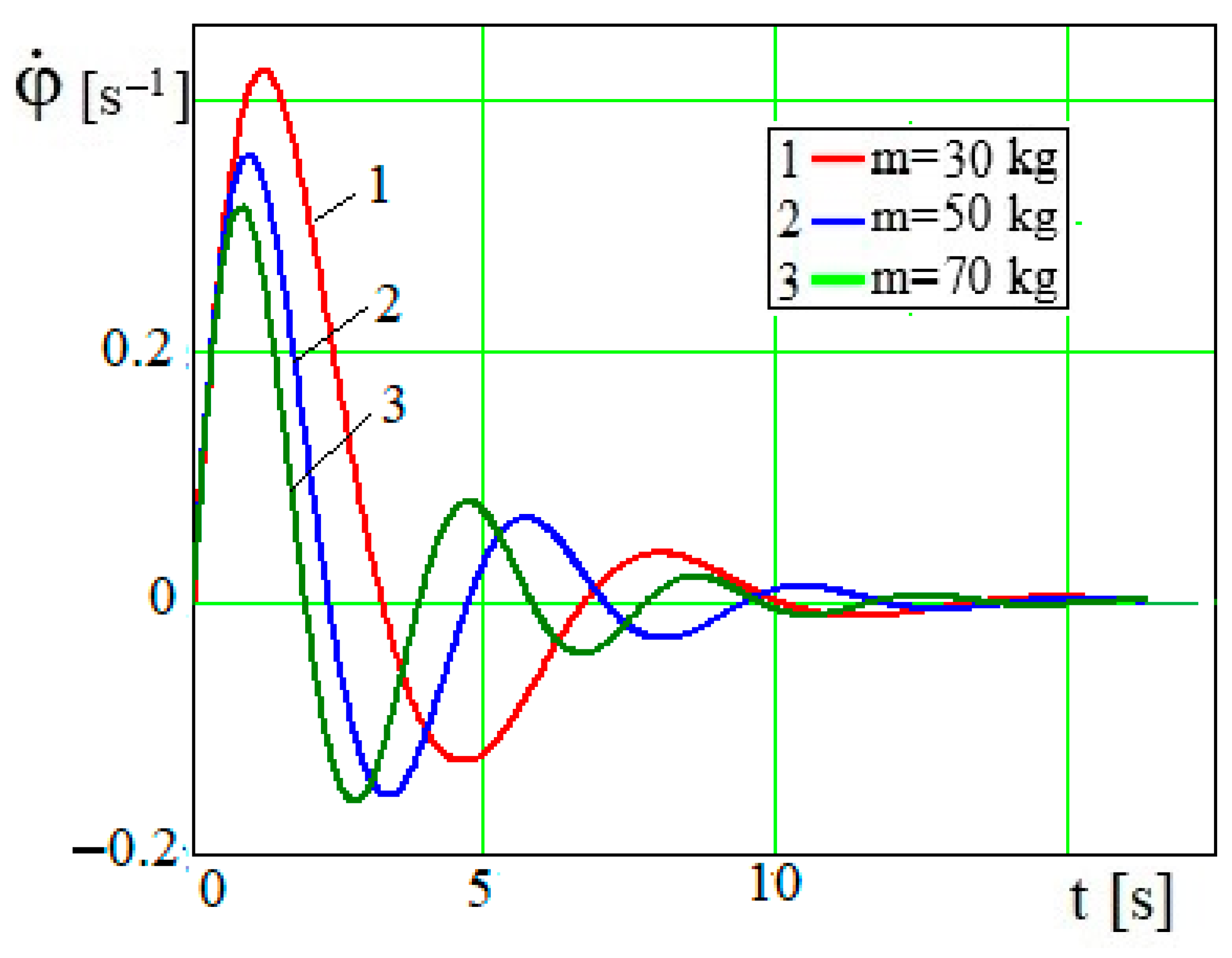
Figure 7. Dependence $\dot{\phi }=\dot{\phi }(t)$ for different values of m.

Figure 7. Dependence $\dot{\phi }=\dot{\phi }(t)$ for different values of m.

The vibrational characteristics of the motor shaft rotation depend on the parameters of the device members. At relatively small piston masses, the engine shaft performs a rotational motion. In Figure 7, at sufficiently large piston masses, the shaft of the force source makes a damped oscillation of the engine shaft speed $\dot{\phi }$. As the piston mass increases, the initial and subsequent amplitudes and period of oscillation $\dot{\phi }$ decrease, and the line around which the oscillation process occurs is defined by the zero magnitude value $\dot{\phi }$. The greater the magnitude of the force moment resulting from the piston gravity (or piston mass) directed opposite to the a engine torque, the smaller the maximum magnitudes of the oscillations $\phi$ and $\dot{\phi }$, and the smaller the repeatability of their oscillations.

It follows from Formula (27) that the power of the mixing and whipping force is $P$~${\dot{\phi }}^3{\sin }^3\phi$.

Then, in turn, the limit value of the excitation source shaft rotation angle based on Equation (25) or (26) is as follows: ${\phi }_l$~$\arcsin \left[1/\left(J_{mr}{\omega }_0^2\right)\right]$. At $\dot{\phi }\to {\dot{\phi }}_l=0$ (${\dot{\phi }}_l$—engine shaft rotational speed limit value) limit, the magnitude value is $P_l$~${\displaystyle \frac{1}{m^3}}{\dot{\phi }}_l^3$, taking into account ${\omega }_0^2$~$m$. 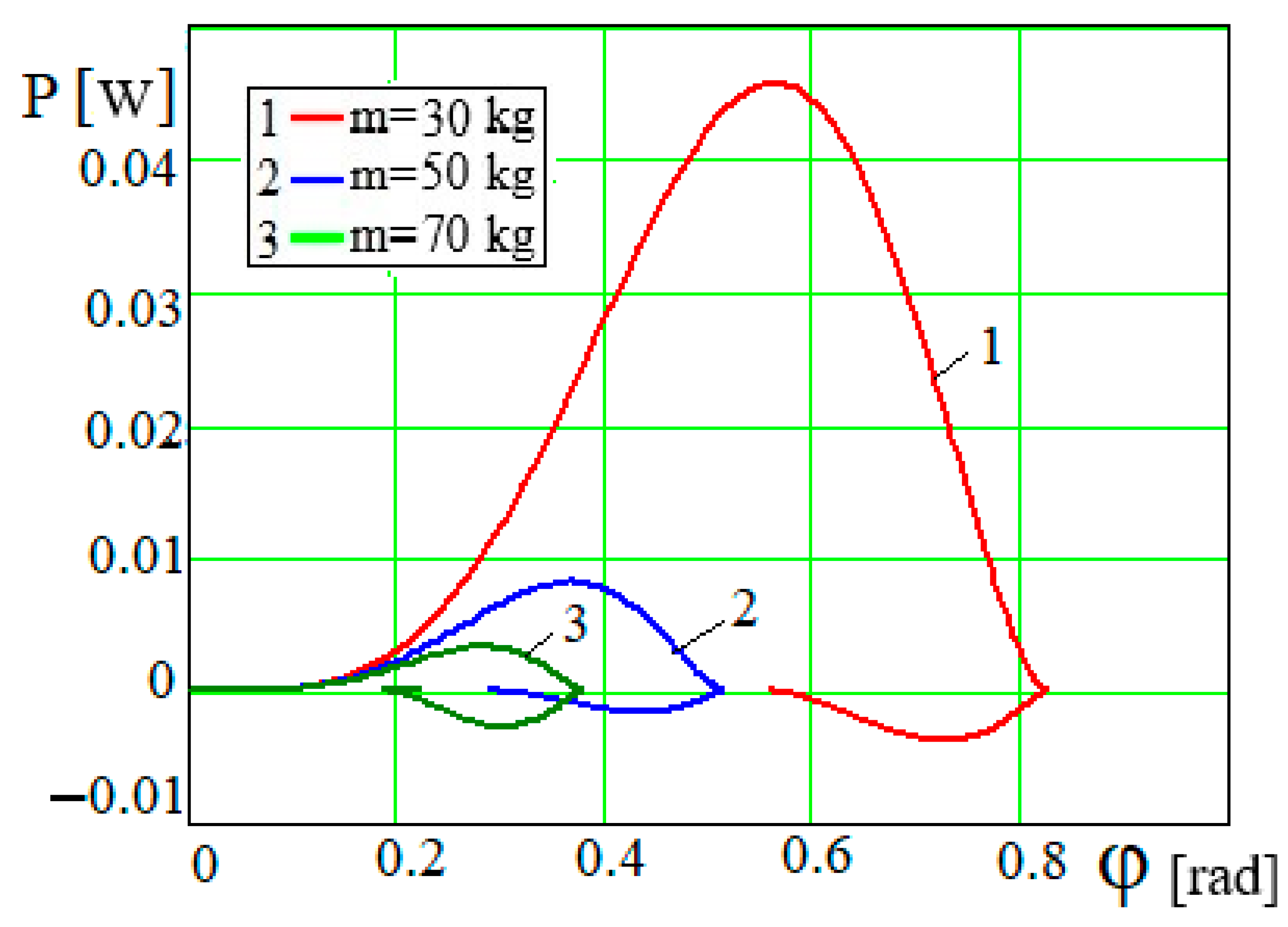The limit values of the rotation angle corresponding to the power value $P=P_l$ coincide with the values of this angle in the dependencies φ = φ(t) in Figure 6. Dependency graphs $P=P(\dot{\phi })$ and $P=P(\dot{\phi })$ in Figure 8 and Figure 9 show that the larger the mass of the piston, the smaller the maximum power values of the mixing and whipping forces $P$. The decrease in the maximum value of P with increasing mass m is accompanied by a shift in the corresponding magnitudes of the values $\phi$ and $\dot{\phi }$ to the beginning of the abscissa. The graphs in Figure 9 show that, when approaching the end of the oscillating damping process, the technological process of whipping intensifies, which is demonstrated by a sharp increase in the force of mixing and whipping and its power and at some of their values and a sharp drop in their values. At $\dot{\phi }\to 0$, $P\to 0$ (Figure 9). The rightmost limits of the graphs P = P(φ) and $P=P(\dot{\phi })$ are limited by the maximum values of φ and $\dot{\phi }$. The leftmost limits of the graphs P = P(φ) and $P=P(\dot{\phi })$ are defined by the minimum values of φ and $\dot{\phi }$.

Figure 8. Dependence P = P(φ) for different values of m.

Figure 8. Dependence P = P(φ) for different values of m.

Figure 9. Dependence $P=P(\dot{\phi })$ for different values of m.

Figure 9. Dependence $P=P(\dot{\phi })$ for different values of m.

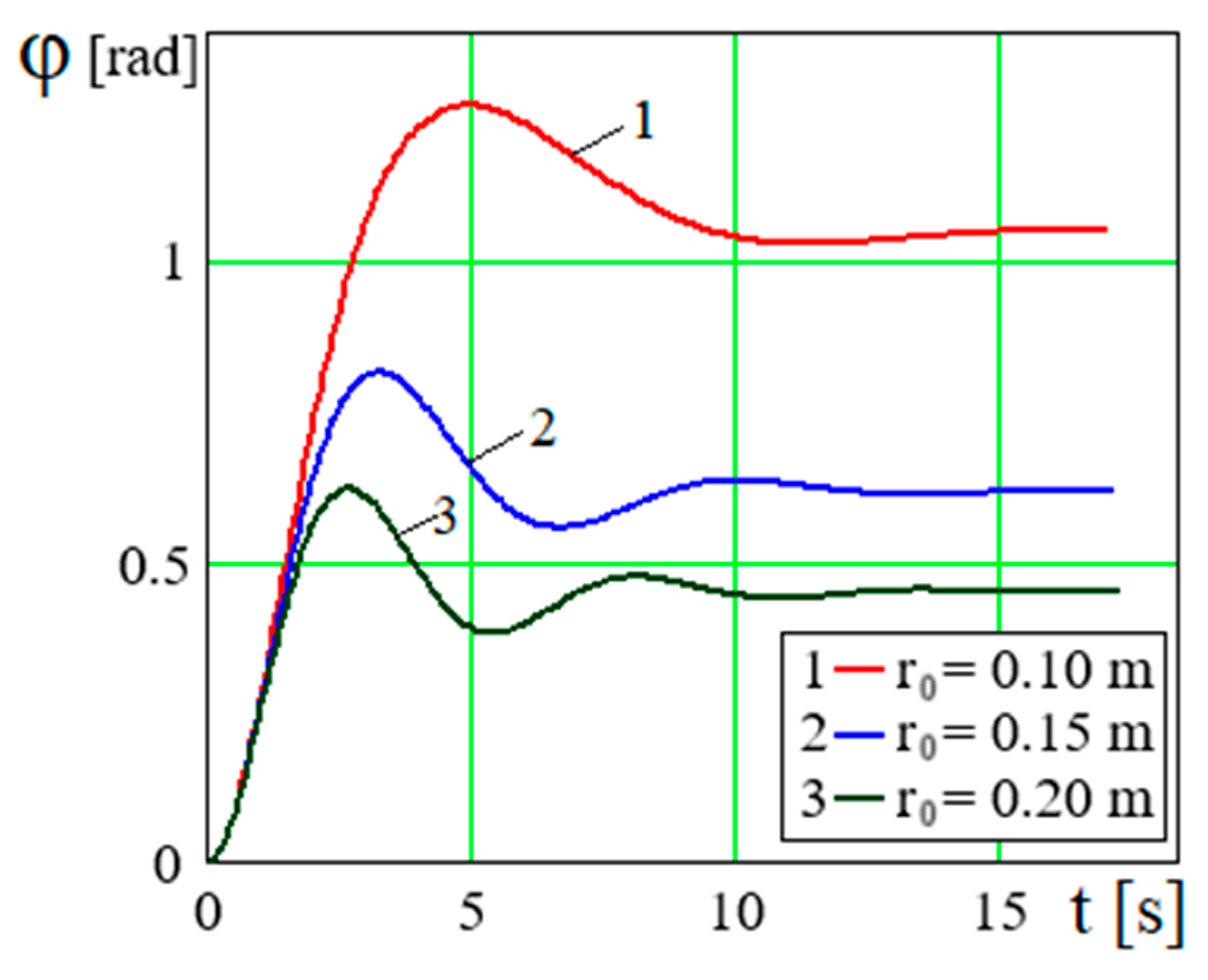
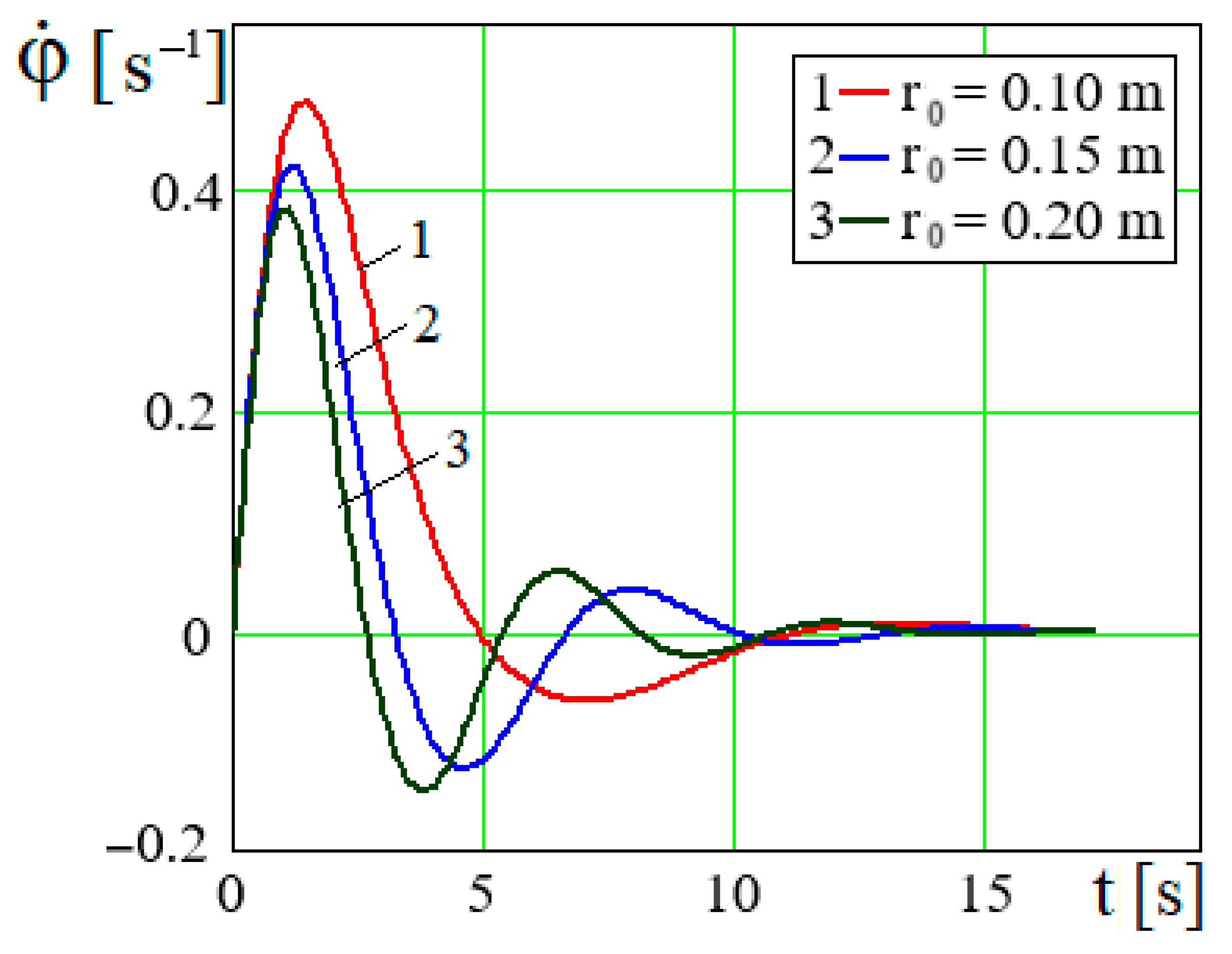
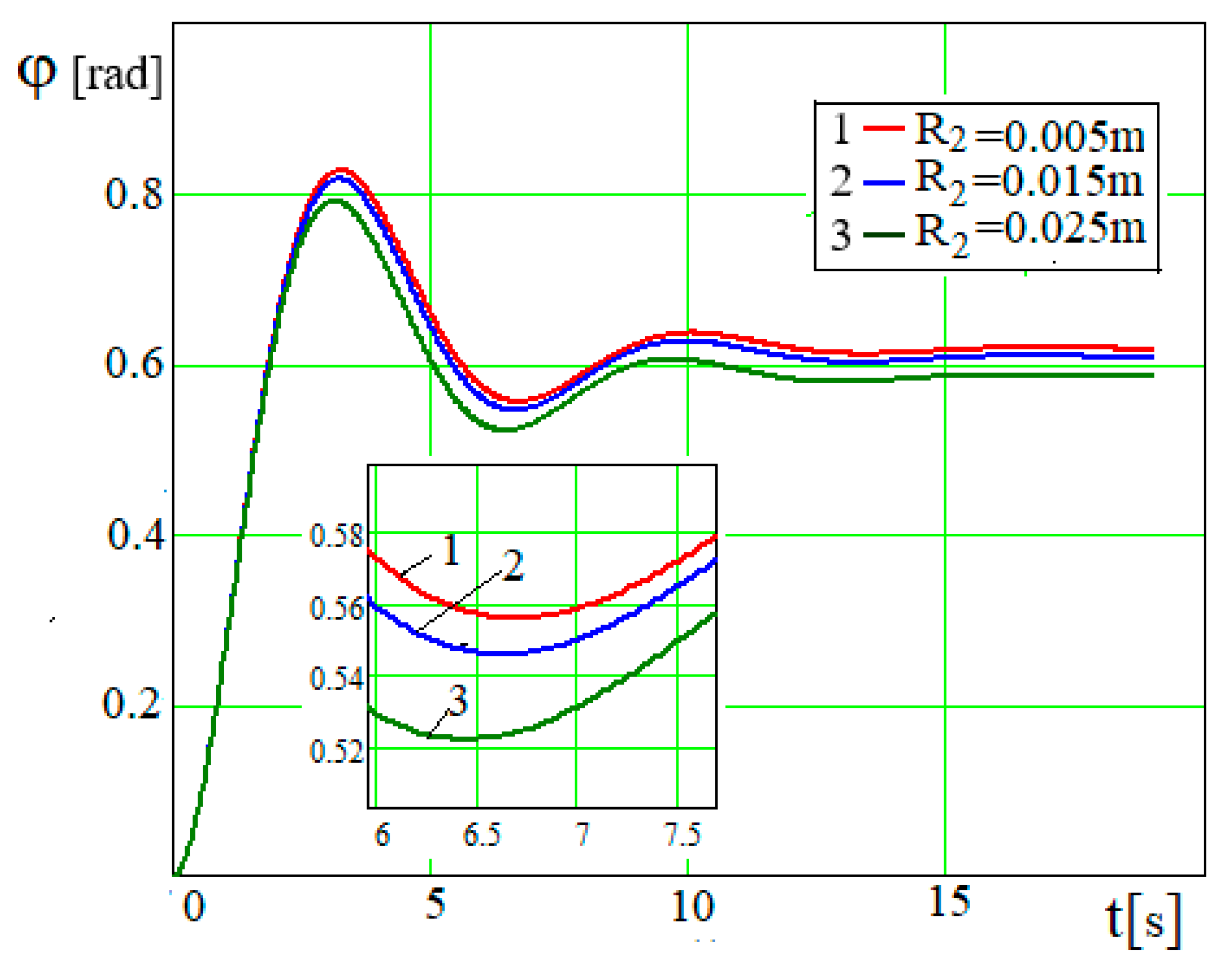
The device parameters, including the crank length, influence the kinematic oscillation parameters of the engine shaft motion (Figure 10 and Figure 11). After a lapse of time, the rotation angle of the driven engine shaft oscillates around the values to which it tends to oscillate, with an amplitude and period of oscillation smaller the longer the length of the driving member, as it is known that the limiting value of the rotation angle φ: ${\phi }_l$~$\arcsin \left(k_2/{\omega }_0^2\right),$ while ${\omega }_0^2$~$r$.

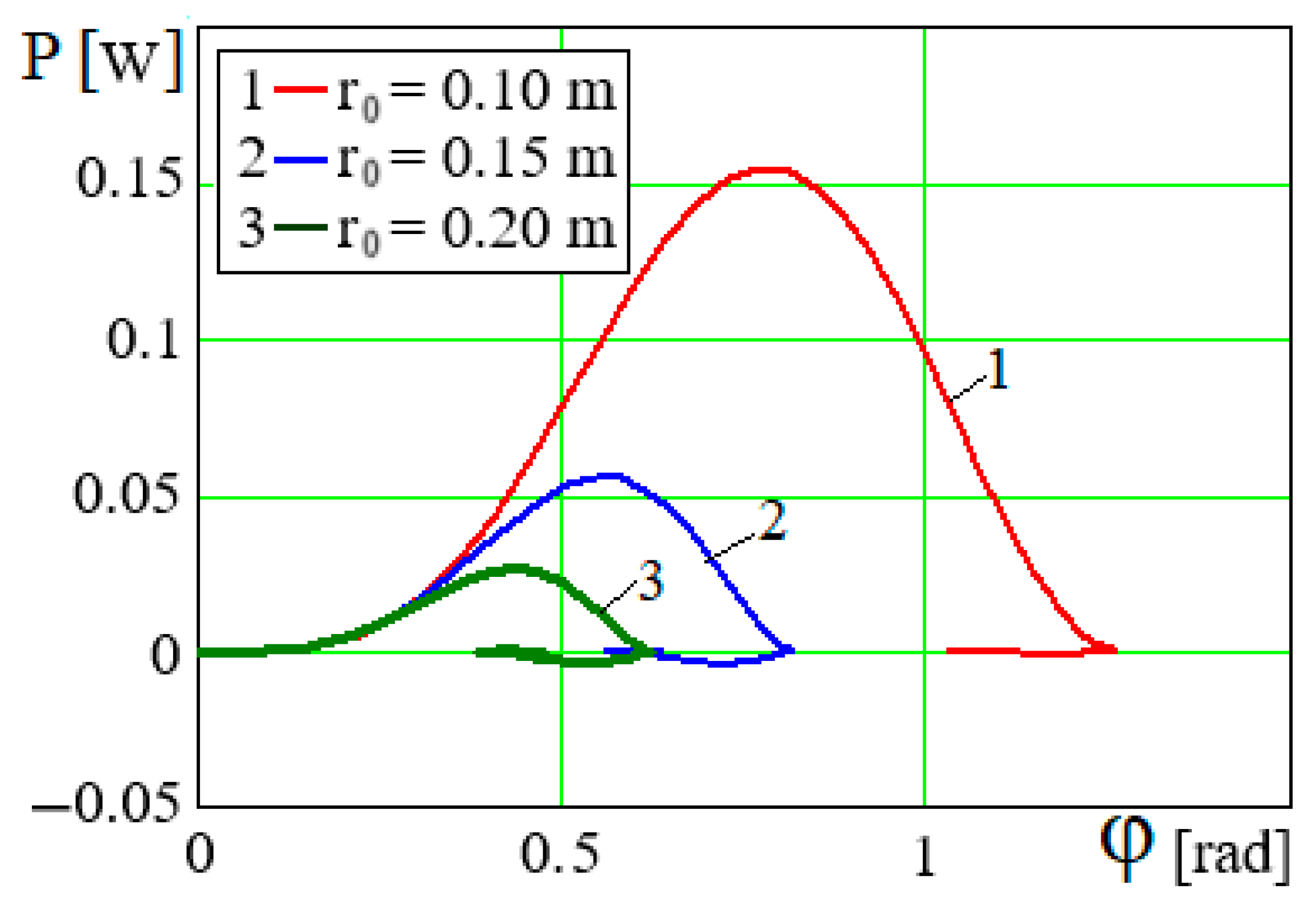
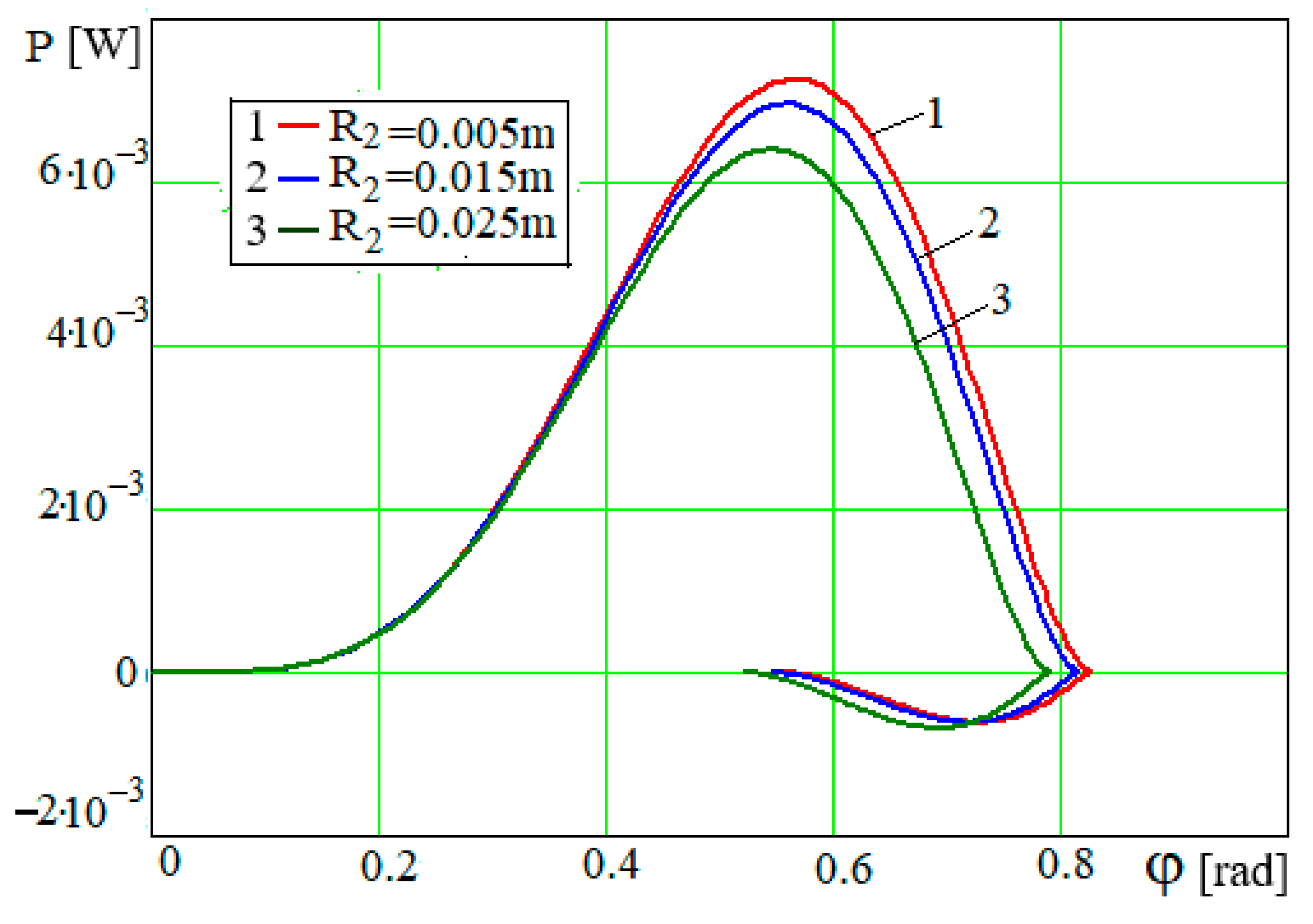
From Formula (27), we obtain $P$~$r^3{\dot{\phi }}^3{\sin }^3\phi$. From this dependence, the first thing to note is the proportionality $P$~$r^3$. Despite this dependence, based on the graphical relationships in Figure 12 and Figure 13, the predominant relationship is $P$~${\sin }^3\phi {\dot{\phi }}^3$, i.e., the value ${\sin }^3\phi$ is proportional to the minus n-th degree of $r$, the value ${\dot{\phi }}^3$ is proportional to the minus m-th degree of $r$, and the total should be n + m > 3.

Figure 10. Dependence φ = φ(t) for different values of r.

Figure 10. Dependence φ = φ(t) for different values of r.

Figure 11. Dependence $\dot{\phi }=\dot{\phi }(t)$ for different values of r.

Figure 11. Dependence $\dot{\phi }=\dot{\phi }(t)$ for different values of r.

Figure 12. Dependence P = P(φ) at a = 23 N·m, m = 20 kg and various values of r.

Figure 12. Dependence P = P(φ) at a = 23 N·m, m = 20 kg and various values of r.

Figure 13. Dependence $P=P(\dot{\phi })$ for different values of r.

Figure 13. Dependence $P=P(\dot{\phi })$ for different values of r.

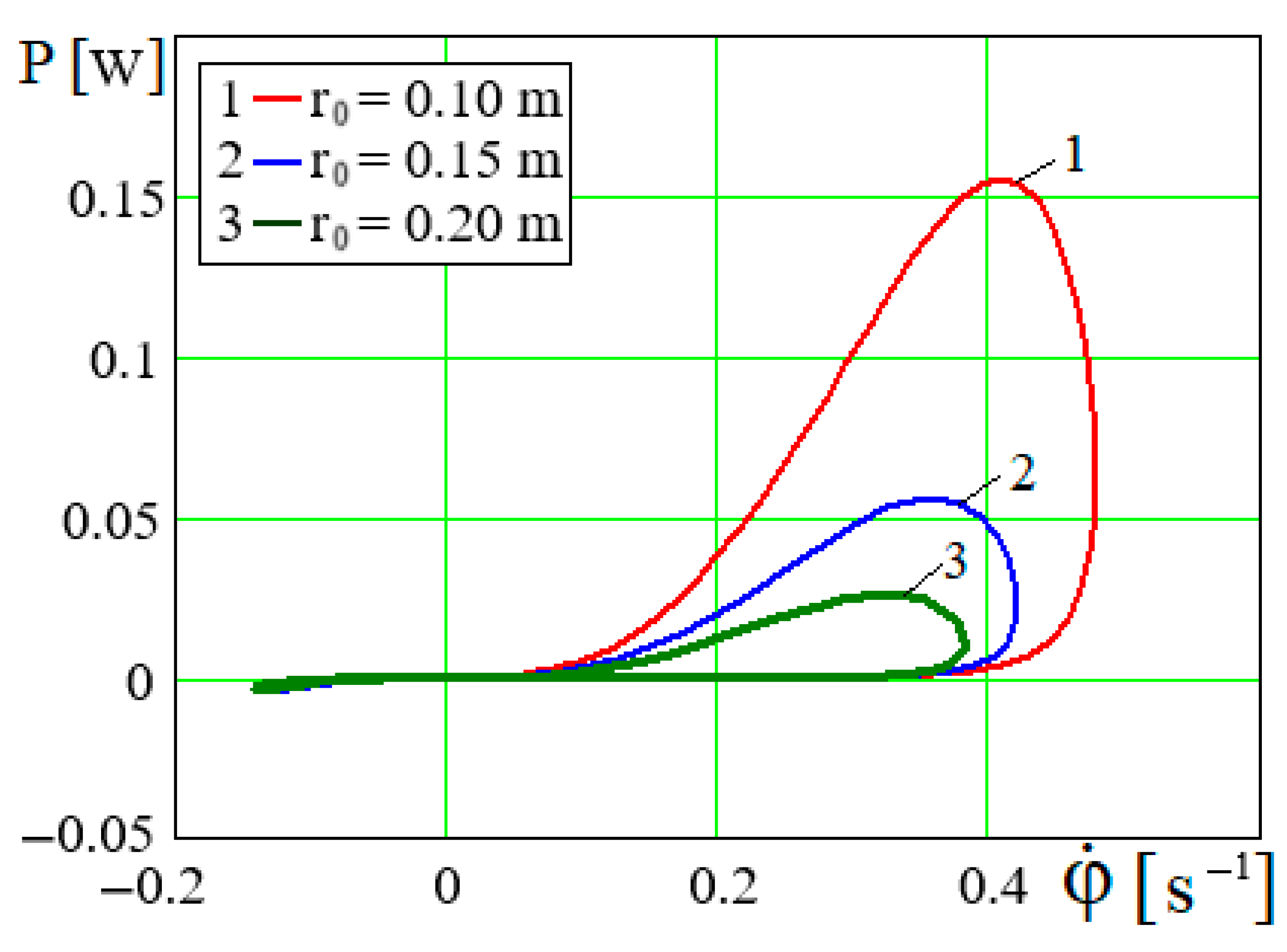
On the other hand, the limit values of the excitation source shaft angle ${\phi }_l$~$\arcsin \left(k_2/r\right)$ for different values of r, to which the value of φ at the end of the oscillating damping process will tend, are the same in Figure 10 and Figure 12. The rightmost limits of the curves P = P(φ) along the axis φ at various values of r in Figure 12 are determined by the maximum values of φ in the graphical patterns φ = φ(t) in Figure 10. The curves P = P(φ) end at those points that correspond to the limit values ${\phi }_l$~$\arcsin \left(k_2/r\right)$ of the rotation angle $\phi$. Likewise, the right borders of the curves $P=P(\dot{\phi })$ in Figure 13 are determined by the maximum values of rotational speed $\dot{\phi }$, and the left borders by the minimum values ${\dot{\phi }}_l\prec 0$ in Figure 11. The sections P = P(φ) in Figure 12, where there is a “decrease” of φ along the abscissa axis, correspond to the sections of the dependences φ = φ(t) in Figure 10 after the maximum values of φ_max.

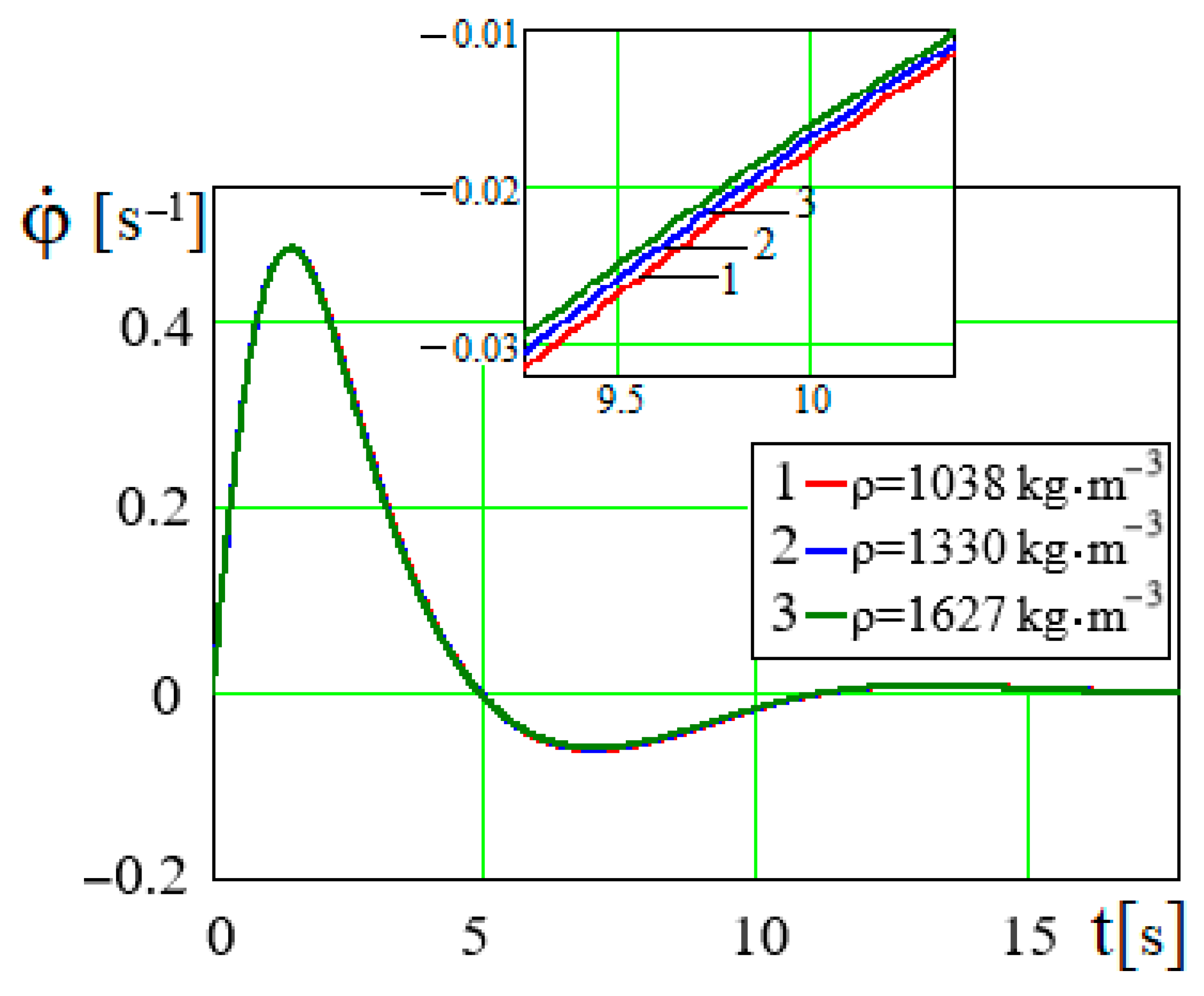
The limit value of the shaft angle of a nonideal engine is ${\phi }_l$~$\arcsin \left(k_2/\rho \right)$. The value is $1/\rho$~$0.6\cdot {10}^{-3}÷{10}^{-3}$. Therefore, the lines φ(t) that correspond to the values of ρ are positioned so densely (Figure 14), that, at the end of the oscillating and aperiodic damped oscillation, they merge into a single line and $\dot{\phi }\to 0$. Dense placement of lines of dependence of $\dot{\phi }=\dot{\phi }(t)$ at various values of fluid density ρ is also observed in Figure 15. It follows from Formula (27) that $P$~$\rho {\dot{\phi }}^3{\sin }^3\phi$. The general character of the dependence P = P(φ) in Figure 16 is determined by the graph of the periodic function ${\sin }^3\phi$, and its amplitude is affected by $\rho {\dot{\phi }}^3$. Regardless of the fact that there are dependencies $\phi =\phi \left(\dot{\phi }\right)$ and $\dot{\phi }=\dot{\phi }\left(\rho \right)$, the density of the fluid ρ slightly affects the oscillation period of P = P(φ). This effect has been well observed in the graphical relationships φ = φ(t) and $\dot{\phi }=\dot{\phi }(t)$ in Figure 14 and Figure 15.

Figure 14. Dependence φ = φ(t) for different values of ρ.

Figure 14. Dependence φ = φ(t) for different values of ρ.

Figure 15. Dependence $\dot{\phi }=\dot{\phi }(t)$ for different values of ρ.

Figure 15. Dependence $\dot{\phi }=\dot{\phi }(t)$ for different values of ρ.

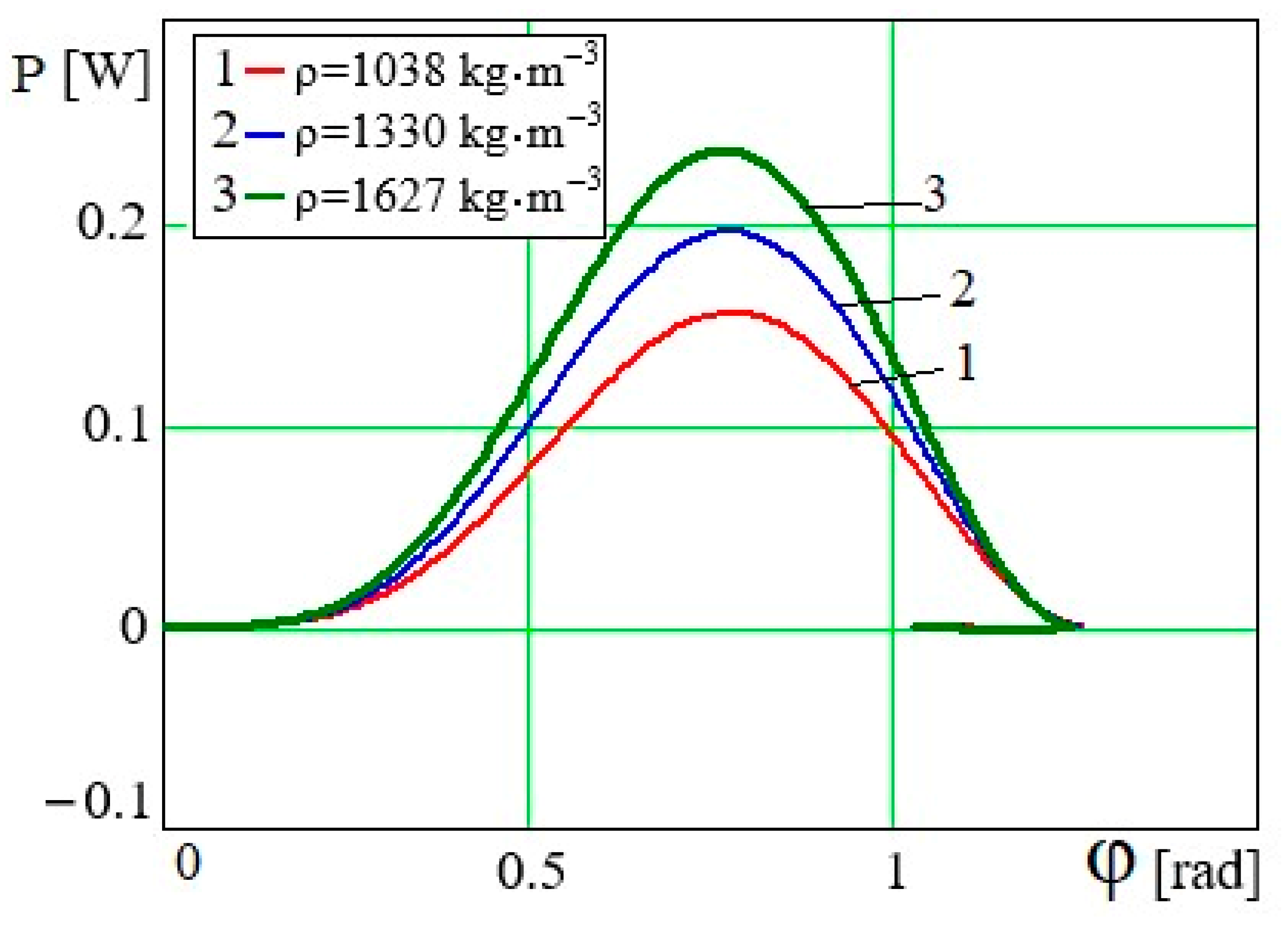
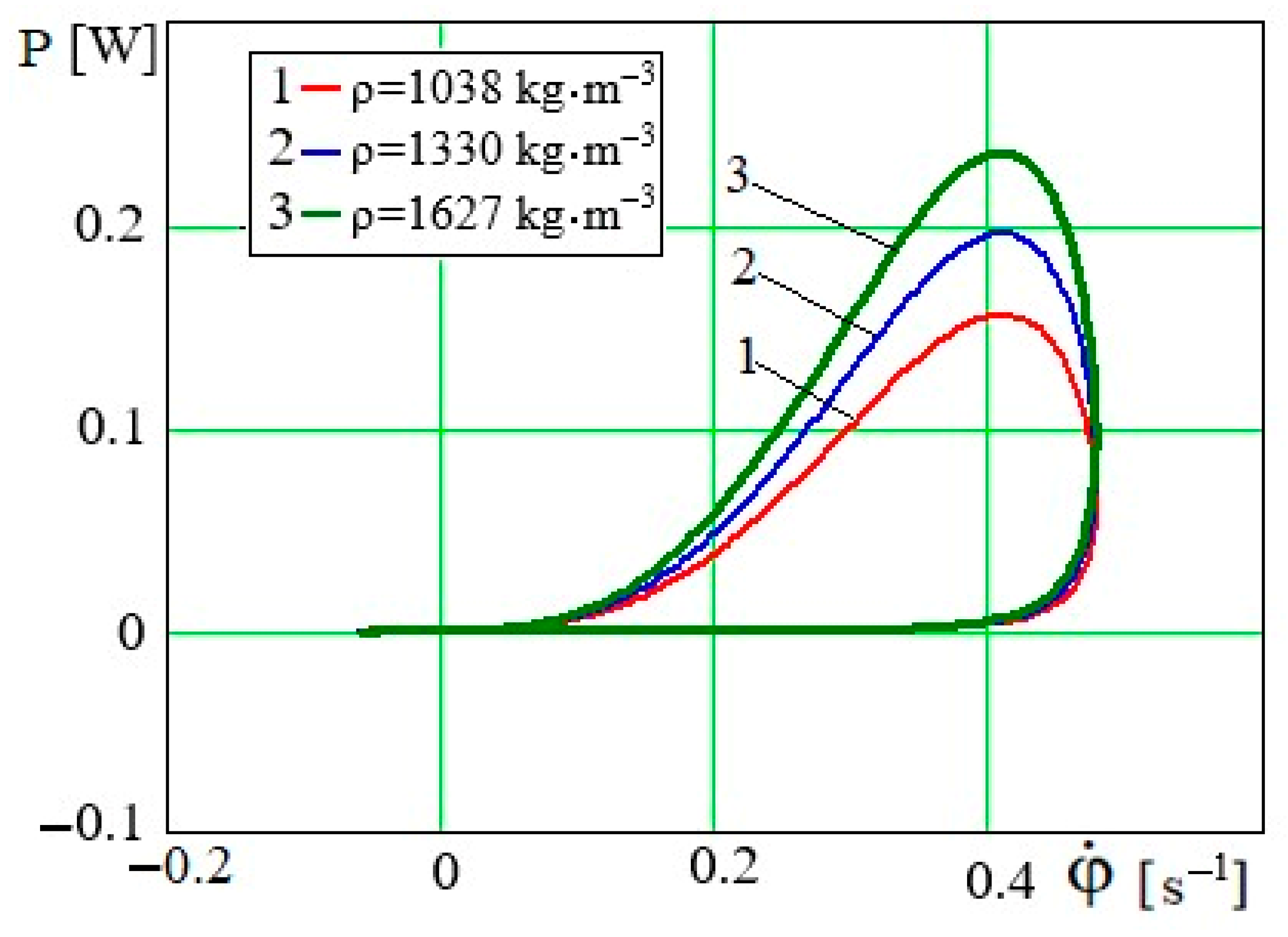
It is obvious from graphical dependences P = P(φ) and $P=P(\dot{\phi })$ in Figure 16 and Figure 17, that the more the density of fluid, the more force and power will be required for the implementation of technological processes of mixing and whipping. In contrast to similar graphical dependences P = P(φ) and $P=P(\dot{\phi })$, the values of abscissas φ and $\dot{\phi }$, corresponding to the maximum values of power, with increasing density of fluid remain almost unchanged. This is approximately the same for all curves φ = φ(t) and $\dot{\phi }=\dot{\phi }(t)$ at various values of density of fluid in Figure 14 and Figure 15. The maximum values φ_max = 1.25 rad and ${\dot{\phi }}_{\max }=0.48$ ${\mathrm{s}}^{-1}$ determine the rightmost limits of graphical dependences P = P(φ) and $P=P(\dot{\phi })$ in Figure 16 and Figure 17, and the limit value of ${\phi }_l\approx 1.045$ rad and value $\dot{\phi }\approx -0.08$ ${\mathrm{s}}^{-1}$ (Figure 14 and Figure 15) for the endpoint graphs.

Figure 16. Dependence P = P(φ) for different values of ρ.

Figure 16. Dependence P = P(φ) for different values of ρ.

Figure 17. Dependence $P=P(\dot{\phi })$ for different values of ρ.

Figure 17. Dependence $P=P(\dot{\phi })$ for different values of ρ.

The effect of the number of $n_2$ piston holes on $\phi =\phi \left(t\right)$ and the dependencies $\dot{\phi }=\dot{\phi }\left(t\right)$ is graphically presented in Figure 18 and Figure 19. The greater the number of holes $n_2$, the less the resistance to the movement of the piston and, accordingly, the less the stirring–beating force (27.1) and the initial maximum angle of deflection of the motor shaft. At the rotational speed of the crank $\dot{\phi }\to 0$, its angle of rotation $\phi \to \arcsin \left(k_2/{\omega }_0^2\right)$ (where $k_2={a/J}_{mr}$), and, in turn, the value ${\omega }_0^2$ depends on $n_2$ according to Formula (24.2) or (24.3). The limit values of ${\phi }_l$, to which the angle φ tends during the damped oscillatory process, are different from zero (Figure 18).

At the force source shaft angle of $\phi \to {\phi }_l$, the engine shaft rotational speed is $\dot{\phi }\to {\dot{\phi }}_l$.

Figure 18. Dependence φ = φ(t) at m = 25 kg and various values of $n_2$.

Figure 18. Dependence φ = φ(t) at m = 25 kg and various values of $n_2$.

Figure 19. Dependence $\dot{\phi }=\dot{\phi }(t)$ at m = 25 kg and various values of $n_2$.

Figure 19. Dependence $\dot{\phi }=\dot{\phi }(t)$ at m = 25 kg and various values of $n_2$.

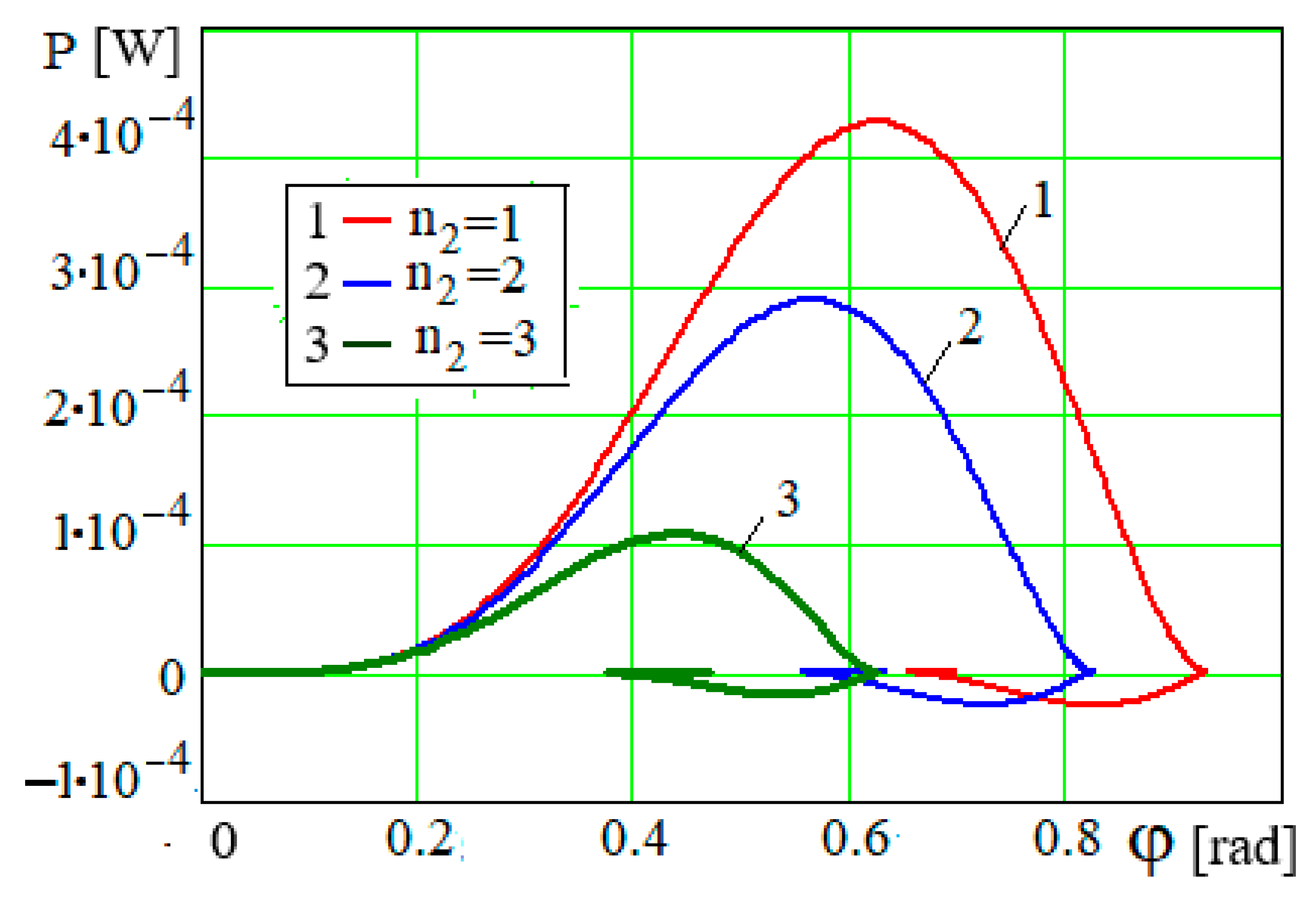
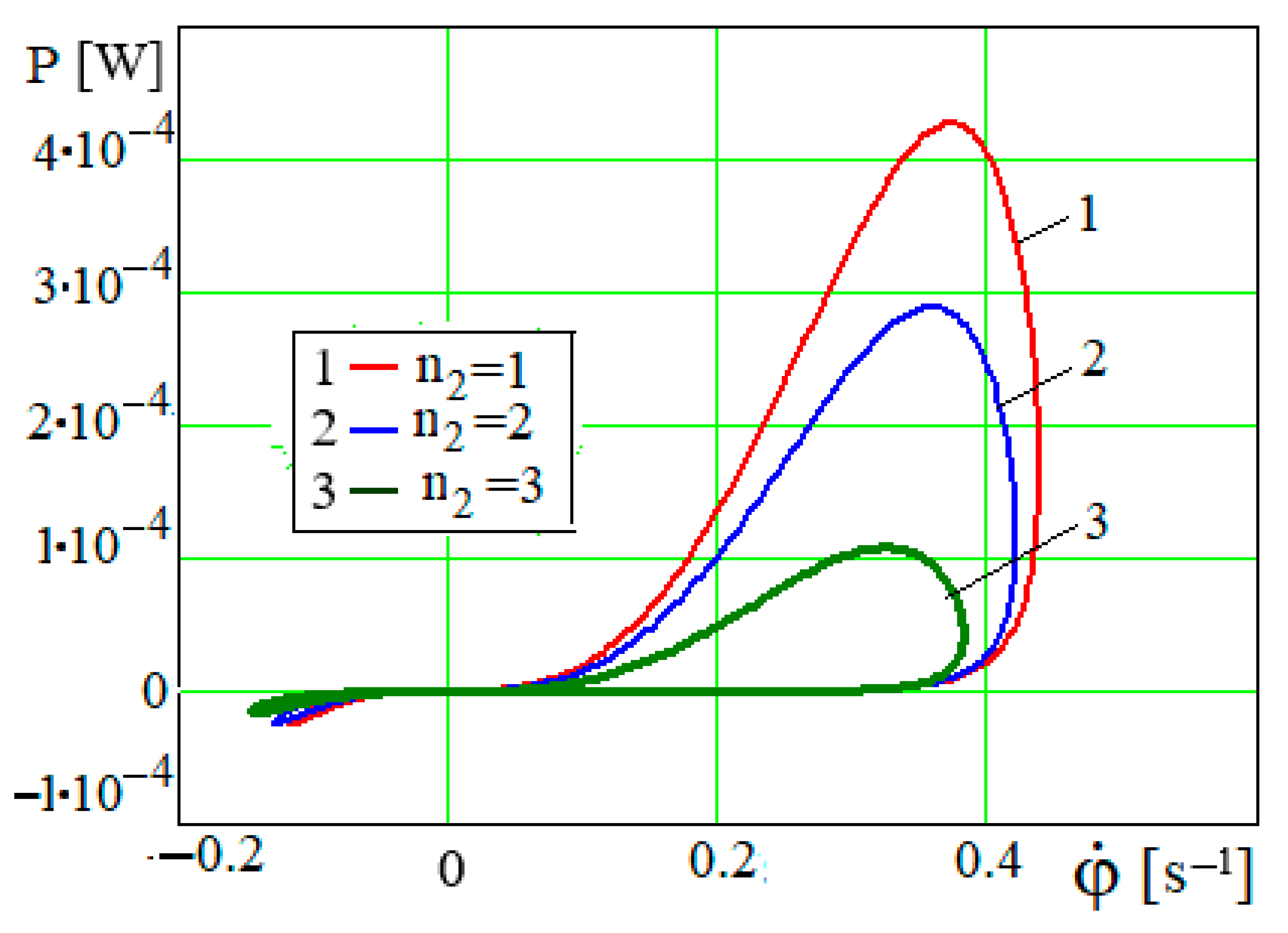
As seen in Figure 20, the greater the number of holes $n_2$, the less the maximum power of the upward lifting force of the piston required. This is obvious from the dependence of the power of the stirring–beating force on the number of holes n₂ of the piston (27.2). The maximum deflection angles of φ in Figure 18 define the right limits of the dependence P = P(φ) at various values of $n_2$, and the limit values of ${\phi }_l$ the left end limits. The value $n_2$ affects the rotation angle φ in the relation of $P$~${\sin }^3\phi$, since $\phi =\phi \left(\dot{\phi }\right)$ and $\dot{\phi }=\dot{\phi }\left(n_2\right)$ (Figure 19), and therefore the periodicity of the function is ${\sin }^3\phi$. The larger the $n_2$, the larger is the period of the function ${\sin }^3\phi$ (Figure 20).

Figure 20. Dependence P = P(φ) at m = 25 kg and various values of $n_2$.

Figure 20. Dependence P = P(φ) at m = 25 kg and various values of $n_2$.

Figure 21. Dependence $P=P(\dot{\phi })$ at m = 25 kg and various values of $n_2$.

Figure 21. Dependence $P=P(\dot{\phi })$ at m = 25 kg and various values of $n_2$.

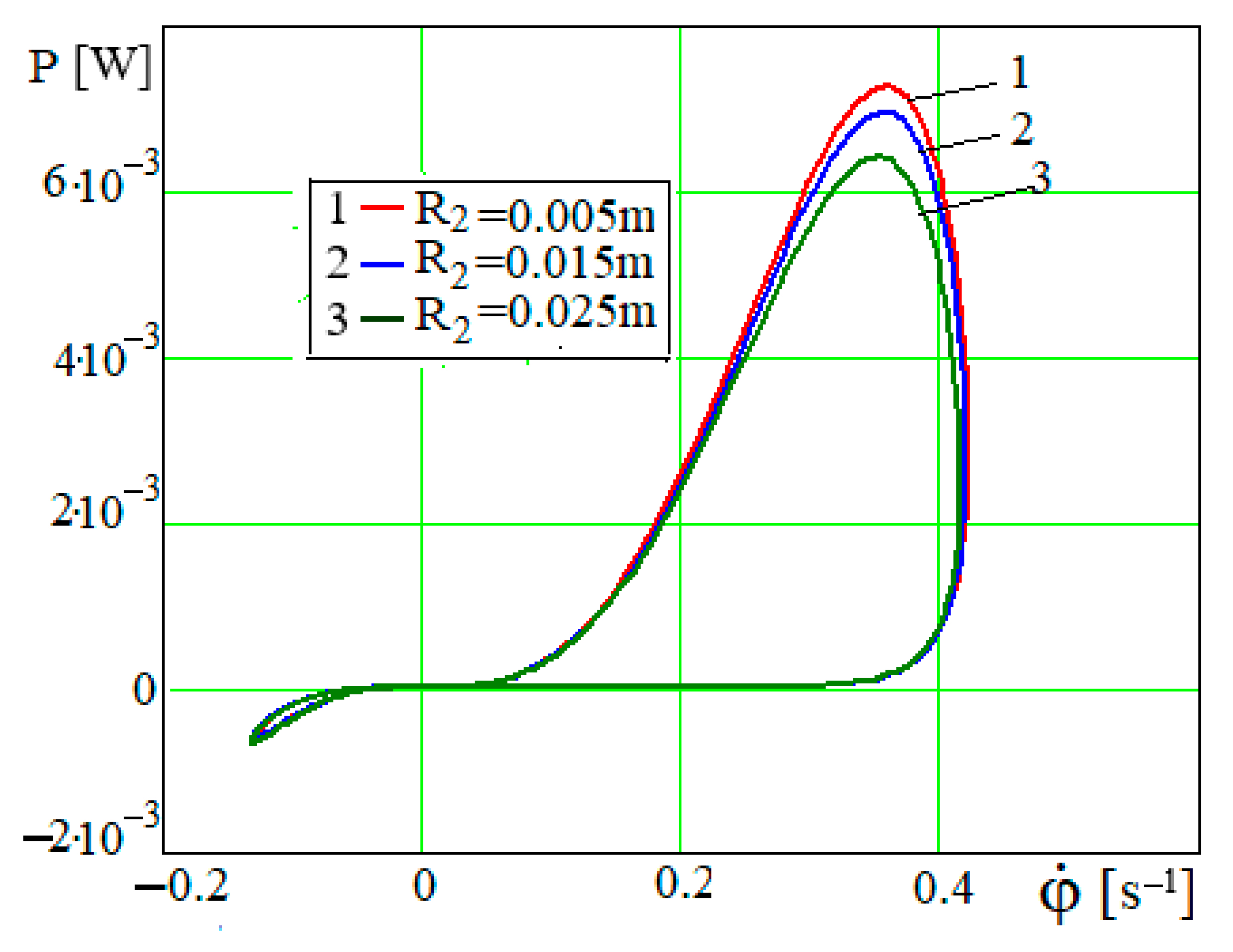
The radius of the holes on the piston $R_2$ has little effect on the dependences φ = φ(t) and $\dot{\phi }=\dot{\phi }\left(t\right)$ (Figure 22 and Figure 23). Therefore, the $R_2$ values are taken to obtain more visual graphs. These graphical dependences have almost the same period of oscillation, but the initial and subsequent amplitudes are larger. The angle of rotation φ over time tends to the limits, which are determined by the relation $\phi \to {\phi }_l=\arcsin \left(k_2/{\omega }_0^2\right)$, where ${\omega }_0^2={\omega }_0^2\left(R_2\right)$. Obviously, $\phi \to {\phi }_l$ at $\dot{\phi }\to {\dot{\phi }}_l=0$ (Figure 23).

Figure 22. Dependence φ = φ(t) at m = 30 kg and various values of $R_2$.

Figure 22. Dependence φ = φ(t) at m = 30 kg and various values of $R_2$.

Figure 23. Dependence $\dot{\phi }=\dot{\phi }(t)$ at m = 30 kg and various values of $R_2$.

Figure 23. Dependence $\dot{\phi }=\dot{\phi }(t)$ at m = 30 kg and various values of $R_2$.

When the piston hole expands, less power of the mixing–whipping force is utilized, because the resistance of the fluid to the piston motion will be reduced (Figure 24 and Figure 25). The higher the amplitudes of oscillations of $\phi$ (Figure 22), the wider the right boundary and larger the left final boundary of the dependence P = P(φ) and larger the period of oscillations (Figure 24). The appearance of the negative parts of the dependence P = P(φ) and $P=P(\dot{\phi })$ is associated with a decrease in the value of $\phi$ after the initial maximum (Figure 22) and the negative part of the dependence $\dot{\phi }=\dot{\phi }\left(t\right)$ (Figure 23). Obviously, the right boundary of the dependence $P=P(\dot{\phi })$ (Figure 25) is determined by the maximum value of $\dot{\phi }$ (Figure 23).

Figure 24. Dependence P = P(φ) at m = 30 kg and various values of $R_2$.

Figure 24. Dependence P = P(φ) at m = 30 kg and various values of $R_2$.

Figure 25. Dependence $P=P(\dot{\phi })$ at m = 30 kg and various values of $R_2$.

Figure 25. Dependence $P=P(\dot{\phi })$ at m = 30 kg and various values of $R_2$.

Summarizing all dependencies φ = φ(t = τ/ω₀), an assessment can be made regarding the applicability of the Runge–Kutta method quartic for the numerical solution of the equation of motion Equation (25) or (26). When solving the equation of motion Equation (25), the mesh step was selected in such a way as to ensure the required calculation accuracy. If numerical solutions are available on two meshes y(τ, h) and y(τ, rh), where r > 1, then the error of the solution on the mesh with the smaller step is given by

Δφ(τ, h) = [ φ(τ, h) − φ(τ, rh]/(r^p − 1),

where p is the order of the Runge–Kutta scheme, r is the ratio of the steps, and h is the increment step of the variable τ.

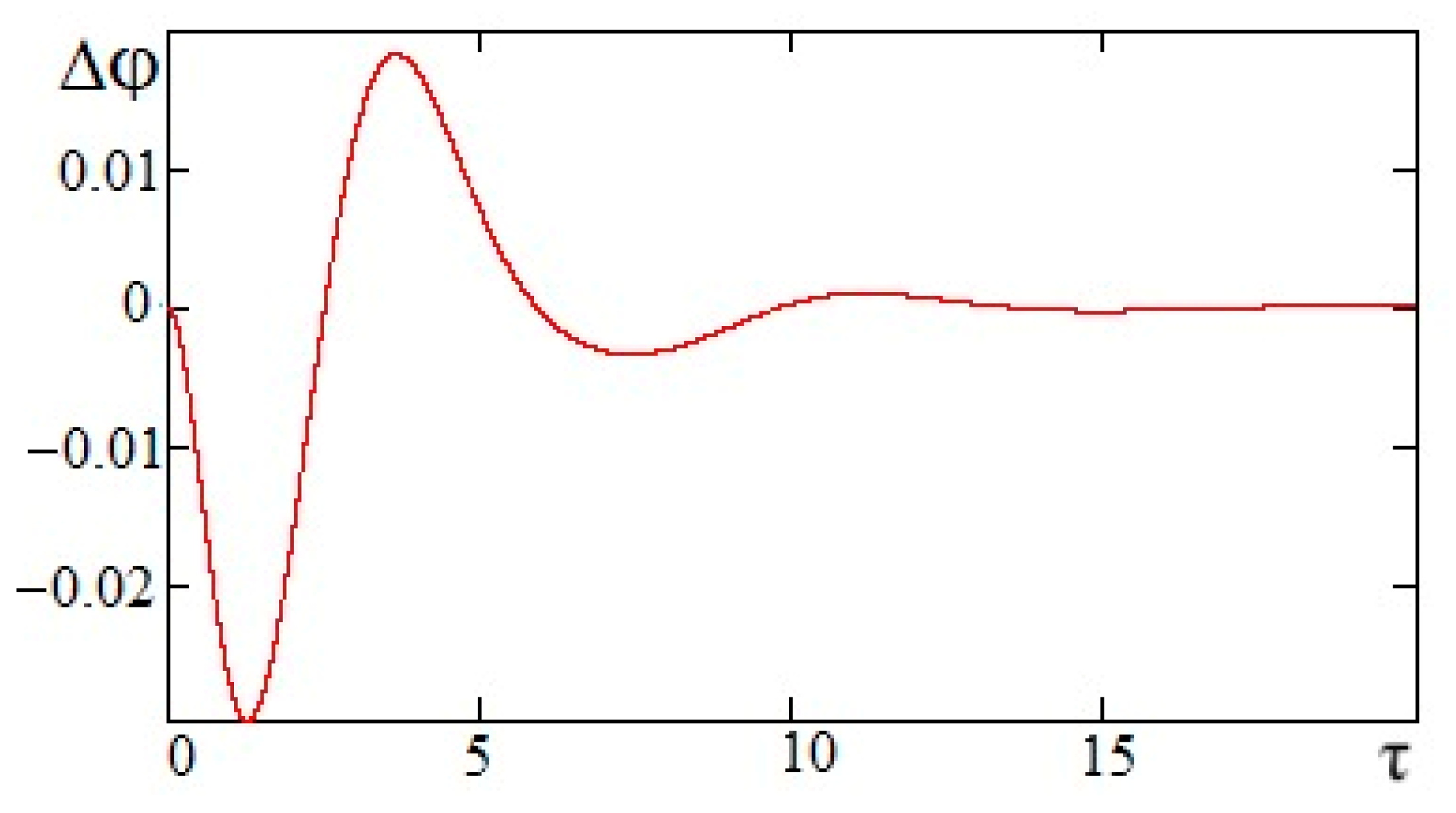
The dependence of the solution error of Equation (25) on the dimensionless time at r = 2, h = 2 × 10⁻³, p = 4 is shown in Figure 26.

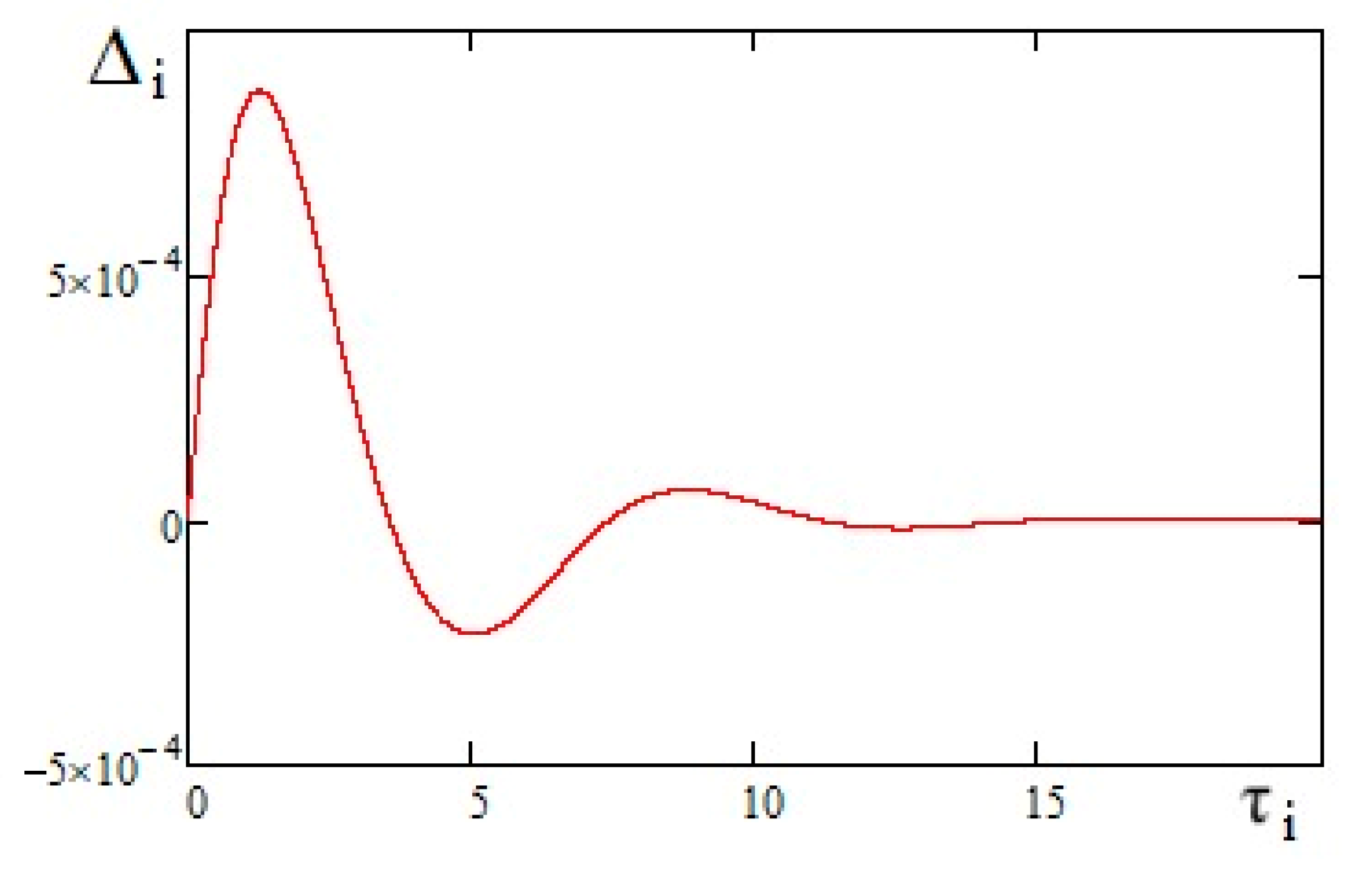
The dependence of the solution increment Δ_i = φ _i+1 − φ_i (i = 1, 2, 3, n) of Equation (25) on dimensionless time is shown in Figure 27. The graph in Figure 27 shows that the increment between values of the solution of Equation (25) tends to zero as time increases. Therefore, the solution of Equation (25) is convergent.

As is known, the results of solving the equations of motion Equations (25) and (26) are presented in Figure 2, Figure 6, Figure 10, Figure 14, Figure 18, and Figure 22 as graphical dependencies φ = φ(t), for various system parameters. The solution curves of Equation (25) shown in these figures vary slowly and do not exhibit a rapid “transient phase.” When developing the mathematical model of the mixing and whipping system for low-viscosity suspensions (for example, kumys viscosity averages η = 1.75·10⁻³ Pa·s), it was assumed that the whipping effect is negligible. The very soft, small-sized particles of the suspension, in the form of protein flakes, easily break apart under low forces. Therefore, the resulting equations of motion do not include terms describing the whipping effect. These equations are easily solved numerically using the Runge–Kutta method quartic with a moderate integration step that ensures the required accuracy. Therefore, the equations of motion (25) and (26) are non-stiff. No signs related to stiffness were observed while solving Equation (25).

The phase trajectories of the vibrational motion of the driving member are represented as twisted spirals [8,50,51]. These spirals become more pronounced with increasing crank length, number and radius of piston holes, and piston mass, and decrease with higher fluid density. As the system transitions to rotational motion [7,8,9,10,41,42], the spirals straighten out and transform into curves with periodically varying amplitude $\dot{\phi }=\dot{\phi }\left(\phi \right)$ around lines defined by the driven angular velocity of the engine shaft [7,8,9,10,50].

4. Principles of Operation and Creation of a Mixing and Churning Device Based on a Crank-Slider Mechanism

The device based on the slide-crank mechanism of the second class operates as follows (Figure 28). From the engine 1 through the drive (gearbox and clutch) rotating crank 2, the motion is transmitted through the connecting rod 3 to the slide 4 and then to the piston 5. The piston is made in the form of a cylindrical disk with round holes for technological processes. The piston with oscillating motion mixes, whips and agitates the primary products fed into the cylinder 6 through the nozzle 7. The periodic movement of the piston contributes to the uniform distribution of ferment in the cylinder, the breakdown of protein flakes into fine particles, and the strengthening of enzymatic processes, as a result of which the quality of fermented milk products and aroma are achieved. The whipping process occurs at the moment when the maximum force of mixing and whipping of the piston or its power is reached. The shaking process can be enhanced by means of a communicating tube 8 to the cylinder. The finished products of the technological process are discharged through the nozzle 9 (Figure 28). The mixing and whipping force or its power can be adjusted by varying the torque of the engine, the length of the crank, the number of piston holes and their radius.

The mixing–whipping and stirring device is designed for the production of fermented milk products with healing properties: kumys (fermented milk drink made from mare’s milk) [see Wikipedia] and shubat (fermented milk drink made from camel’s milk) [see Wikipedia]. A mare is milked at hourly intervals, yielding approximately 5 L of milk per day. A small amount of previously prepared kumys (used as a fermentation starter) in the device is added with fresh mare’s milk, etc. The mixture is then regularly mixed, whipped, and stirred over a period of one to two days, for several hours per day. The longer the whipping process continues, the greater its healing effect, i.e., enhancing the flavor, aroma, and overall quality of the kumys.

Camel milk (shubat) is left in the device for fermentation for 24 h. Unlike kumys, shubat is well stirred before consumption (at low motor shaft speeds).

If the power of the engine is equal to or slightly greater than the power of the resulting pressure force, the buoyancy force and gravity, and the friction forces between the piston and the liquid in the round holes and in the gap between the cylinder, then the crank performs the rotational mode of movement; if the torque a of the engine is less than the torque caused by the action of the total forces of pressure and gravity, buoyancy force, friction forces between the piston and the liquid, i.e., not enough for the rotational movement of the crank, then the crank will perform the damping oscillatory process. Thus, the mixing and beating device can operate in two driving modes of the leading link: in rotary and oscillatory damping, depending on the requirements for the quality of the products produced. All this suggested the idea of creating a device based on a crank-slider mechanism, carrying out adjustable technological processes of mixing, whipping and agitating suspensions, from an engine with adjustable torque and power, a driving link of different lengths, a replaceable piston disk with a different number of holes and their radius; a 3D model and an experimental sample of this device are presented in Figure 29. Due to the existing guide (Figure 29) of the slide movement, the reciprocating movement of the piston takes place strictly vertically, parallel to the cylinder forming the production environment. This prevents the devices from dangling the piston and unnecessary contact, friction with the cylinder walls, and knocking. The horizontal platform on which the outer frame rests provides stable operation of the device and the engine in which they are fixed. The presence of support wheels makes it possible for the device to move freely over the production area.

5. Experimental Study of the Dynamics of the Stirring–Beating and Shaking Up Device

An experimental study of the dynamics of the stirring–beating and shaking (Figure 30) up device under the oscillatory- and aperiodic-damping mode of the disk-crank movement was carried out according to the following methodology. The voltage and the motor power were selected at a constant current in the motor circuit, at which the disk-crank rises up, slowing down the movement, stops before reaching 90° of the rotation angle and then descends downward, slowing down the movement, and stops before reaching a static zero equilibrium. This oscillatory- and aperiodic-damping process occurs in the interval of the disk-crank rotation angle φ$\subset$ (0, π/2), as expected, following the results of numerical studies of the dependence φ = φ (t) (Figure 2, Figure 6, Figure 10, Figure 14, Figure 18 and Figure 22) and, after a while, the process repeats again.

In order to determine experimentally the power of the piston and liquid interaction force, it is necessary to measure the force of the piston and liquid interaction and the corresponding piston (slide) speed. The experimental studies in this work were carried out following the methodology proposed by ZETLAB [52]. Calibration of the strain gauge and accelerometer was performed according to the ZETLAB procedure [52]. When using strain gauges, it is necessary to complete a calibration table [52], which will be used in the experimental research. Quantitative comparisons were made with strain gauge calibration tables provided by ZETLAB [52], which showed no significant errors. Based on experience of ZETLAB [52] in measuring normal stresses in rods using a strain gauge, when properly calibrated, deviations in repeated measurements are minimal.

The piston and liquid interaction force was measured by the strain gauge CALT DYLY-103 built into the slide, which was connected to the strain gauge station ZET058 [52] and then to the computer. Using the ZETLAB software [52], an oscillogram of the force acting on the slide was obtained for various cases of oscillatory and aperiodically damped operation of the disk-crank of the prototype stirring–beating device. According to the obtained force oscillogram, the maximum force of interaction of the piston with the liquid was estimated for various cases of the motion mode. To determine the linear acceleration of the slider, the intelligent digital sensor ZET 7052-N by ZETLAB [52] was used. The intelligent digital sensor ZET 7052-N is a vibration sensor equipped with a built-in three-axis sensitive element, which converts the constant component of acceleration into a digital code along three mutually perpendicular axes: X, Y, and Z. The ZET 7052-N digital sensor by ZETLAB [52] is supplied pre-calibrated and accompanied with a calibration certificate. The intelligent digital sensor ZET 7052-N is connected to a computer via the ZET 7076 interface [52]. Using a filtering program [52], the linear velocity of the slider was obtained and then converted into the crank’s angular velocity through the system’s transfer function. The experimental data were processed using ZETLAB software [52] and MATLAB.

The prototype stirring–beating device in combination with the measuring equipment during the experimental studies is shown in Figure 30 and the video material and stored data showing the oscillatory and aperiodically damped mode of motion of the stirring–beating and shaking up device are presented in the appendices [53]. For experimental studies, a disk-crank with holes located at different distances from the center, a piston in the form of a disk with different mass and holes of different numbers and different radii have been prepared. The shape and parameters of the holes can influence flow losses through them and, consequently, affect the pressure difference between the upper and lower surfaces of the piston. Therefore, to minimize flow losses, the piston holes were manufactured using laser technology [54].

The standard parameter values of the mixing–whipping device prototype and the fluid are given in

Table 2. Standard values of the prototype device and fluid parameters.

Parameter	Name	Value
r0	crank length	0.10 m
Lcr	connecting rod length	0.48 m
Mcr	connecting rod mass	1.2 kg
ms	slider mass	2.49 kg
Rc	cylinder radius	0.095 m
m	piston mass	2 kg
R1	piston radius	0.09 m
R2	hole radius	0.02 m
n2	number of holes	4
h	piston height	0.012 m
η	dynamic viscosity of fluid	8.90 × 10−4 Pa·s (20 °C)
ρ	density of fluid	1000 kg⋅m−3

.

The oscillogram of the periodic variation in the force of the piston and liquid interaction, minus the values of the buoyancy force and the force of gravity of the piston, represents the oscillogram of the variation in the force of stirring and beating by the piston. The power of the stirring–beating force is determined by the product of the stirring–beating force with the corresponding speed of the piston (slide). The results of experimental studies are presented in Figure 31, Figure 32, Figure 33 and Figure 34. They show a good agreement between the results of experimental and numerical studies.

As the mass of the piston increases, the torque created by the gravity action with the initial torque remaining unchanged increases, the difference between the engine torque and the torque created by the gravity action, the buoyancy and the friction forces between the piston and the liquid decreases, as do the values of the disk-crank rotation angle and its angular velocity. As a result, the power of the stirring–beating force and its maximum value are reduced (Figure 31).

When the crank is elongated, the torque created by the gravity action increases, as in the previous case, but by increasing the throw of the crank, with the engine torque initially unchanged, the torque created by the action of the stirring–beating force and its power, including its maximum value, decreases (Figure 32), as do the values of the disk-crank rotation angle and its angular velocity.

Both with increasing the number of piston holes (Figure 33), and with the expansion of the piston holes (Figure 34), the resistance to the movement of the piston decreases, the force of the pressure difference on the piston and its power, including its maximum value, decrease, and the values of the rotation angle of the driving link and its angular velocity decrease (see Formula (27)).

6. Conclusions

The differential equations of motion for a nonideal system—a mixing–whipping device based on a crank-slider mechanism—were derived using Lagrange’s equations.

The differential equations of motion are highly nonlinear and are solved numerically by the fourth-order Runge–Kutta method for the oscillation and aperiodic damped mode of motion of the driving member.

The dependences of the rotational speed of the driving member, the angle of rotation of the actuating engine shaft on time and mixing and whipping force power on its angle of rotation, the speed of rotation of the force source shaft, and the parameters of the nonideal mechanical system are obtained.

The result of the interaction of the piston slide-crank mechanism with the excitation source is the variability with the time of the engine shaft rotational speed and subsequent changes in the angle of rotation of the force source shaft with time, the power of the mixing–whipping force depending on the angle of rotation and rotational speed of the excitation source shaft, and the parameters of the nonideal system. This interaction is reflected in how the parameters of the device and the nonideal energy source affect the kinematic, vibrational, and energy characteristics of the system. Thus, for example, increasing the engine’s torque, piston mass, crank length, number and radius of piston holes, and decreasing the fluid density result in a reduction in the maximum crank rotation angle and its limit value, as well as a decrease in the amplitude and period of oscillations in the engine shaft’s angular velocity and in the mixing–whipping force power. The fluid density has little effect on the angular velocity and rotation angle of the engine shaft.

The maximum values of fluctuations of the rotation angle φ and the rotational speed $\dot{\phi }$ of the engine shaft determine the right boundary points of the power graphs of the mixing–whipping force as a function of the values φ and $\dot{\phi }$, respectively. The limit values, to which the rotation angle φ of the engine shaft tends after the time elapses, are the leftmost endpoints of the graphs of the mixing–whipping force power depending on the value of φ, and the minimum values of the rotational speed $\dot{\phi }$ of the excitation source shaft $\dot{\phi }$ are the leftmost limits of the power dependence of the mixing–whipping force as a function of the value of $\dot{\phi }$.

The results of experimental studies are in good agreement with the results of numerical studies. It has been experimentally confirmed that with an increase in the piston mass, a decrease in the number of piston holes and their radius, the maximum power of the mixing and whipping force decreases.

The results of the effects of a nonideal energy source can be utilized in selecting effective system parameters and an energy-saving engine to design a new device that performs the technological processes of mixing and whipping.

Future research will focus on the physical and mathematical modeling of the dynamics (including transient dynamics) of the mixing and shaking device based on a crank-slider mechanism with viscoelastic supports featuring nonlinear stiffness [51] and nonlinear damping.