HyMePre: A Spatial–Temporal Pretraining Framework with Hypergraph Neural Networks for Short-Term Weather Forecasting

Abstract

Accurate short-term weather forecasting plays a vital role in disaster response, agriculture, and energy management, where timely and reliable predictions are essential for decision-making. Graph neural networks (GNNs), known for their ability to model complex spatial structures and relational data, have achieved remarkable success in meteorological forecasting by effectively capturing spatial dependencies among distributed weather stations. However, most existing GNN-based approaches rely on pairwise station connections, limiting their capacity to represent higher-order spatial interactions. Moreover, their dependence on supervised learning makes them vulnerable to spatial heterogeneity and temporal non-stationarity. This paper introduces a novel spatial–temporal pretraining framework, Hypergraph-enhanced Meteorological Pretraining (HyMePre), which combines hypergraph neural networks with self-supervised learning to model high-order spatial dependencies and improve generalization across diverse climate regimes. HyMePre employs a two-stage masking strategy, applying spatial and temporal masking separately, to learn disentangled representations from unlabeled meteorological time series. During forecasting, dynamic hypergraphs group stations based on meteorological similarity, explicitly capturing high-order dependencies. Extensive experiments on large-scale reanalysis datasets show that HyMePre outperforms conventional GNN models in predicting temperature, humidity, and wind speed. The integration of pretraining and hypergraph modeling enhances robustness to noisy data and improves generalization to unseen climate patterns, offering a scalable and effective solution for operational weather forecasting.

1. Introduction

Weather variations have long been one of the most critical external factors influencing societal operations and economic activities. In domains such as agricultural planning, transportation scheduling, energy dispatching, urban management, and public safety, timely and accurate access to meteorological information is a fundamental prerequisite for effective decision-making. The increasing frequency of extreme weather events under climate change further underscores the need for more accurate and robust forecasting systems [1,2]. Consequently, developing scientific and reliable short-term weather forecasting systems is of profound significance, as it supports disaster mitigation, resource optimization, the protection of lives, and the advancement of sustainable development.

In the context of weather forecasting tasks, two primary methodological paradigms are currently employed: traditional numerical weather prediction (NWP) models [3,4] based on physical principles, and data-driven approaches that have gained traction in recent years. The former rely on atmospheric dynamics and thermodynamics to simulate future weather states from initial conditions, offering strong physical interpretability and theoretical rigor. However, these models tend to be computationally intensive and highly sensitive to input precision. In contrast, data-driven methods leverage historical observations to learn statistical patterns among meteorological variables, often through deep neural networks. These methods excel at modeling complex spatiotemporal dependencies and enable rapid inference. Particularly in scenarios with abundant data, data-driven approaches have demonstrated impressive performance in short-term and localized forecasting, making them a valuable complement to traditional models.

Despite the significant progress achieved by deep learning models, their application in weather forecasting still faces several challenges, particularly in leveraging large-scale unlabeled meteorological data. Supervised models require high-quality labeled inputs, yet real-world weather observations often suffer from noise, missing values, and regional inconsistencies. Self-supervised pretraining has emerged as an effective solution, enabling models to extract robust patterns from raw meteorological time series without relying on labeled data. Among various strategies, masked modeling, originally developed in the domains of natural language processing [5] and computer vision [6], has demonstrated strong potential for time series forecasting [7]. These methods reconstruct randomly masked segments of input data, promoting the learning of contextual and structural representations. In meteorological applications, decoupling spatial and temporal masking has proven particularly beneficial, as it encourages the model to separately capture regional correlations and temporal dynamics [8,9]. Decoupling spatial and temporal masking not only improves generalization and robustness but also provides transferable representations for downstream prediction tasks.

Beyond representation learning, modeling spatial interactions among multiple stations is a central challenge in weather forecasting. Conventional graph neural networks (GNNs) have shown strong ability to capture pairwise spatial dependencies by leveraging station graphs [10,11]. These methods naturally encode spatial proximity and correlation structure, offering a principled framework to handle spatially distributed data. Building on this, several large-scale GNN-based models have recently achieved major breakthroughs in global weather prediction. GraphCast [12] models atmospheric evolution using GNNs on a sphere mesh and demonstrates superior medium-range forecasting accuracy compared to traditional NWP systems. NeuralGCM [13] augments physics-based general circulation models with neural components to improve simulation fidelity while maintaining physical constraints. Pangu-Weather [14] further advances this line by applying a 3D Earth-specific deep learning model that achieves fast and highly accurate forecasts on a global scale. These models collectively highlight the potential of data-driven, graph-structured learning in advancing operational weather forecasting. However, a fundamental limitation of conventional GNNs lies in their reliance on pairwise edges, which restricts their ability to capture higher-order spatial dependencies involving multiple stations. Such complex interactions, common in meteorological systems like frontal zones or regional wind patterns, are difficult to express using binary connections alone, especially in the presence of noisy, incomplete, or non-locally correlated data. These challenges underscore the need for more expressive models capable of representing richer spatial structures.

In light of these considerations, there is growing interest in more expressive alternatives that go beyond conventional graphs. The essence of meteorological systems involves high-order spatial interactions (e.g., frontal systems requiring coordinated modeling of multiple stations), where traditional graph neural networks’ binary connections struggle to capture multi-site dependencies. Hypergraph neural networks [15] address this limitation by connecting arbitrary subsets of nodes through hyperedges, explicitly encoding regional clustering behaviors (e.g., station groups under shared synoptic influences like rain belts or wind propagation paths). This capability enables (1) modeling multi-site correlations along moisture transport corridors in short-term precipitation prediction, and (2) capturing nonlinear interactions across climatically similar regions during heatwave propagation. Such high-order expressiveness aligns fundamentally with meteorological physics, providing physically grounded spatial representations. By generalizing traditional GNNs, hypergraphs offer enhanced capacity to model complex multi-station dependencies and collective spatial behaviors. Capturing these higher-order relationships allows more accurate representation of semantic and physical intricacies in weather systems [16,17]. Recent studies have demonstrated the efficacy of HyperGNNs in weather forecasting tasks. The Probabilistic Hypergraph Recurrent Neural Network [18] introduces probabilistic modeling into hypergraph structures, capturing dynamic node–hyperedge relationships and outperforming traditional models in time series forecasting scenarios. These advancements underscore the potential of HyperGNNs to enhance the representation of complex spatial dependencies in meteorological data, leading to more accurate and reliable weather forecasting models.

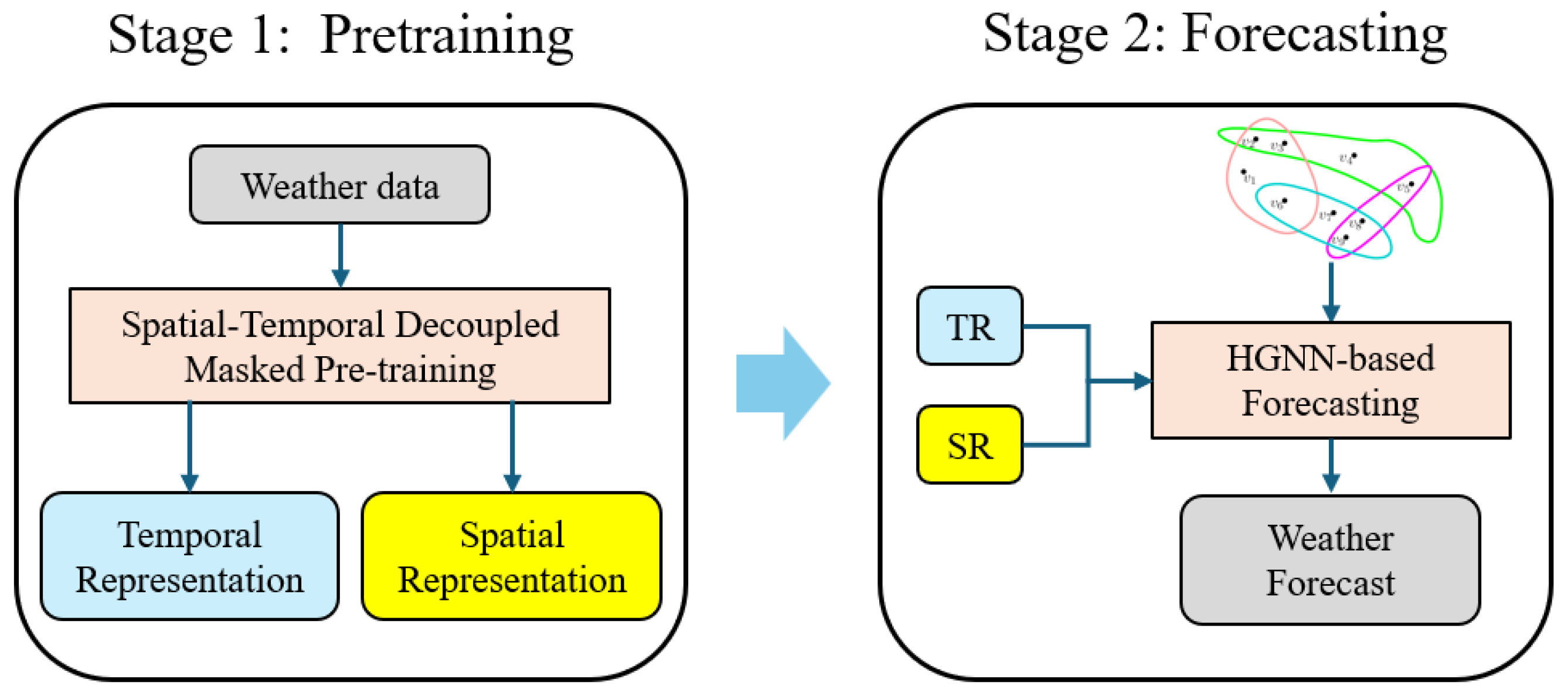
Building upon these insights, we propose Hypergraph-enhanced Meteorological Pretraining (HyMePre), a two-stage framework for short-term weather forecasting, as show in Figure 1. The first stage employs a self-supervised pretraining scheme with separate spatial and temporal masking strategies to learn disentangled representations from unlabeled station-level time series data. In the second stage, a hypergraph neural network-based forecasting module is introduced, where the hypergraph is constructed using time-averaged meteorological features to capture high-order spatial dependencies among weather stations. Through this design, the model not only achieves stronger robustness and generalization in representation learning, but also naturally encodes higher-order spatial dependencies among multiple stations, thereby improving the accuracy and stability of short-term multi-station weather forecasts. In summary, our key contributions are as follows:

• A decoupled spatial–temporal pre-training scheme tailored for meteorological time series is proposed, enabling the model to disentangle and capture long-range spatial patterns and temporal dynamics.
• Hypergraph neural networks are incorporated into the forecasting stage to model spatial dependencies among meteorological data, thereby more effectively capturing higher-order clustering of meteorological phenomena.
• The proposed method is validated on large-scale reanalysis benchmarks and achieved substantial improvements in accuracy compared to multiple models.

2. Related Work

This section provides a brief overview of the key techniques relevant to our research, focusing on deep learning-based spatiotemporal meteorological forecasting, self-supervised masked pretraining for spatiotemporal data, and hypergraph neural networks.

2.1. Spatiotemporal Meteorological Forecasting

Spatiotemporal meteorological forecasting is crucial in disaster warning, environmental management, and sustainable development, and its accuracy is directly related to public safety and energy regulation. To improve prediction capabilities, more and more studies have introduced deep learning methods to model spatial dependencies and temporal dynamics in meteorological data. Lira et al. [11] proposed the GRAST-Frost model, which combines the spatiotemporal attention mechanism with the Internet of Things platform to integrate multi-source data of the target site and 10 surrounding sites, and supports 6, 12, 24, and 48-h low temperature and frost forecasts. Li et al. [19] designed a GNN-based regional heatwave prediction method that can provide accurate real-time high temperature warnings while maintaining low data collection and computing costs, and reveal the spatiotemporal propagation patterns of heat waves and regional climate causal relationships. The authors point out that the framework can also be extended to identifying and forecasting various other severe or intricate weather phenomena. Davidson et al. [20] conducted an empirical study on South Africa, comparing the performance of low-rank weighted graph neural network and Graph WaveNet in predicting the maximum temperature of 21 weather stations, and compared with LSTM and temporal convolutional network (TCN). Liu et al. [21] proposed a spatiotemporal adaptive attention graph convolution model for short-term PM2.5 prediction at the city level, and achieved leading performance on multiple real datasets such as Beijing, Tianjin, and London. For the problem of wind speed modeling, Wu et al. [22] proposed a multidimensional spatiotemporal graph neural network, which integrates local and neighboring node wind speed data, effectively improving the accuracy of local wind speed prediction. Khodayar et al. [23] constructed an undirected graph network with wind power stations as nodes, and achieved robust prediction of short-term wind speed by learning the spatiotemporal characteristics of wind speed and wind direction.

To improve the modeling ability of regional interactions, Ma et al. [10] proposed HiSTGNN, introduced an adaptive graph learning mechanism, constructed a hierarchical structure including a global graph (modeling inter-regional dependencies) and a local graph (modeling the relationship between variables within the region), combined graph convolution and gated temporal convolution to extract complex spatial dependencies and long-term meteorological trends, and enhanced the information flow between the two layers of graphs through a dynamic interaction mechanism. Wilson et al. [24] proposed a WGC-LSTM model that couples weighted graph convolution and long short-term memory network to effectively model spatial relationships in order to deal with the nonlinearity and spatiotemporal autocorrelation problems in meteorological data. Seol et al. [25] proposed the PaGN framework, which improves physical consistency and prediction accuracy by integrating sparse spatial observation data with high-order physical numerical methods. Chen et al. [26] proposed a group-aware GNN that builds both individual city graphs and city-cluster graphs to represent explicit and implicit spatial relationships among urban areas. Their model incorporates differentiable grouping mechanisms to autonomously identify urban clusters, thereby enhancing national-scale air quality forecasting performance. In addition, to deal with the problem of multi-task coupling, Han et al. [27] proposed a multi-adversarial spatiotemporal graph neural network (main GNN), which jointly models air quality and weather forecasts, and uses heterogeneous recursive graph neural networks to capture the complex spatiotemporal dependencies between multiple types of monitoring sites to achieve multi-task collaborative optimization. Sun et al. [28] analyzed the current state of graph neural networks in the field of short- to medium-term weather forecasting and categorized the methods based on different types of datasets.

Deep learning methods such as graph neural networks have greatly enhanced the modeling of spatial and temporal dependencies in meteorological data. However, the conventional pairwise graph structure often struggles to fully capture the intricate and high-order interactions among multiple meteorological stations. This limitation becomes particularly evident in the forecasting of short-term, high-impact weather events where complex spatial correlations are critical. Therefore, there remains an urgent need for more expressive and flexible frameworks that can better represent and propagate these multi-station dependencies, ultimately improving the robustness and accuracy of meteorological forecasts.

2.2. Masked Pretraining

Masked pretraining is now widely adopted as a powerful self-supervised learning strategy in both natural language processing (NLP) and computer vision (CV). Its fundamental principle involves reconstructing the missing portions of input data using the available contextual information. In the field of NLP, Kenton and Toutanova [5] proposed a new language representation model BERT, which is based on the Transformer architecture and can pretrain deep bidirectional semantic representations from large-scale unlabeled text. By considering the left and right contexts across all layers, it achieves stronger semantic modeling capabilities. In subsequent research, Liu et al. [29] reproduced and systematically analyzed the pretraining process of BERT, and found that the original model had the problem of insufficient training, emphasizing the key impact of design details such as hyperparameters and data scale on performance. Lan et al. [30] proposed two parameter reduction techniques to alleviate the memory bottleneck and training efficiency problems faced by BERT when expanding the model scale. By reducing the number of parameters, they significantly improved the scalability and training speed of the model. In the field of CV, similar masking strategies have also been adopted. For example, Bao et al. [8] proposed a self-supervised visual representation model BEiT, drawing on the pretraining strategy of BERT and designing a masked image modeling task. He et al. [6] proposed masked autoencoders (MAE), which mask random areas in the input image and reconstruct based on the unmasked areas. In both areas, mask pretraining has achieved significant improvements in various downstream tasks.

In recent studies, pretraining methods have been applied to time series data to enhance the quality of learned latent features. Nie et al. [9] proposed an efficient Transformer architecture PatchTST for multivariate time series forecasting and self-supervised learning. Shao et al. [31] proposed a scalable pretraining framework that enhances spatiotemporal GNNs by learning fragment-level representations from long-term data to improve multivariate time series forecasting. Li et al. [7] introduced Ti-MAE, which uses masked autoencoding instead of contrastive learning to better align representation learning with downstream prediction, boosting long-term multivariate time series accuracy.

Masked pretraining has proven to be a highly effective self-supervised learning strategy that enables models to capture deep semantic and contextual information from unlabeled data. By leveraging masked reconstruction tasks, it facilitates the learning of rich representations that significantly improve performance across various domains including NLP, computer vision, and time series forecasting. Building on these successes, applying masked pretraining to spatiotemporal meteorological data can enhance feature extraction and improve the robustness and accuracy of downstream forecasting tasks.

2.3. Hypergraph Neural Network

In traditional graph structures, each edge can only connect two nodes and can only represent pairwise relationships. However, in many practical scenarios, entities often have complex relationships that go beyond pairwise interactions. For this reason, hypergraphs are proposed to express high-order topological structures between multiple nodes, where a hyperedge can simultaneously associate any number of nodes [32]. Compared with ordinary graphs, Bretto et al. [33] pointed out that hypergraphs show stronger expressive power and modeling flexibility in depicting high-order dependencies between complex data. It is worth noting that when each hyperedge in a hypergraph only connects two nodes, it will degenerate into a standard graph structure.

With the rise of deep learning, integrating graph neural networks into hypergraph structures has garnered growing interest from the research community. Feng et al. [15] proposed HGNN, which introduces hyperedge convolution to capture high-order dependencies, outperforming traditional GCNs in tasks like citation classification and image recognition. Zhang et al. [34] developed Hyper-SAGNN, a self-attention-based model that supports variable hyperedge sizes and effectively handles both homogeneous and heterogeneous hypergraphs. Yadati et al. [17] introduced HyperGCN, which leverages GCNs for semi-supervised learning on hypergraphs with node attributes, improving classification performance and enabling combinatorial optimization. Yi et al. [35] designed HGC-RNN by integrating hypergraph convolution with RNNs to capture structural and temporal dependencies in sensor network time series. Bai et al. [16] proposed hypergraph convolution and attention operators to enhance the modeling of high-order, non-pairwise relationships, improving adaptability to real-world data structures.

Building on advances in hypergraph-based learning, Sawhney et al. [36] introduced a spatiotemporal hypergraph convolutional framework for capturing stock market trends and industry-level associations, though it treats all node relationships uniformly, potentially limiting its expressiveness. Wang et al. [37] developed a dynamic spatiotemporal hypergraph neural network for subway passenger flow prediction, integrating topology and temporal travel patterns to extract high-order features. Miao et al. [38] introduced a multi-information aggregation hypergraph network that models spatial correlations in meteorological data through adjacency and semantic hypergraphs, and combines aggregation and alienation convolutions with temporal modeling to achieve state-of-the-art prediction performance.

Many atmospheric phenomena, such as frontal systems, monsoonal circulations, and mesoscale convective complexes, involve the simultaneous interaction of multiple spatially dispersed regions. These interactions are inherently group-based and cannot be effectively captured by pairwise relationships alone. Hypergraphs provide a natural mechanism to model such high-order dependencies by allowing a single hyperedge to connect multiple meteorologically similar stations. This facilitates joint reasoning over entire weather patterns, enabling the model to capture the coordinated evolution of regional weather systems. Compared to other higher-order structures such as simplicial complexes or global attention modules, hypergraphs offer a more interpretable and scalable framework that balances expressiveness with computational feasibility. Their flexible construction based on feature similarity makes them particularly well suited for modeling non-local, non-stationary patterns common in meteorological data.

Hypergraph neural networks offer a powerful framework for modeling complex high-order relationships beyond pairwise interactions. Their ability to simultaneously capture multi-node dependencies makes them suitable for spatiotemporal data, enhancing representation learning and forecasting accuracy. In meteorological contexts, this capability is critical: many atmospheric phenomena (e.g., frontal systems, monsoonal circulations, mesoscale convective complexes) involve simultaneous interactions of spatially dispersed regions. These inherently group-based dynamics cannot be fully captured by pairwise graphs. Hypergraphs address this by connecting meteorologically similar stations via hyperedges, enabling joint reasoning over entire weather patterns and modeling coordinated regional evolution. Compared to alternatives like simplicial complexes or global attention, hypergraphs provide a more interpretable and scalable balance of expressiveness and computational feasibility. Their feature-similarity-based construction is particularly adept at handling non-local, non-stationary patterns pervasive in meteorological data.

3. Methodology

We propose HyMePre, a two-stage framework for multi-step weather forecasting. The model consists of a self-supervised pretraining module and a hypergraph-based forecasting module. In the pretraining stage, we apply spatial and temporal masking separately to learn disentangled representations from historical meteorological time series. In the forecasting stage, we construct hypergraphs to capture higher-order spatial dependencies among stations and use hypergraph convolutions to generate future predictions.

3.1. Problem Definition and Network Architecture

The weather forecast predicts future atmospheric conditions by analyzing the historical observation records from monitoring stations. In this paper, the inputs to the HyMePre model include the geographical locations of the weather stations and their historical weather data, the data from all weather stations N at the t-th time step denoted as ${\{X_t=\{x_1^t,x_2^t,\dots ,x_S^t\}\in R^{N\times F}\}}_{t=1}^{T_{in}}$, where $T_{in}$ represents the time dimension and F is the number of meteorological features. The task of the model is based on the historical time series for m time steps as input $\{X_{t-m},\dots \dots ,X_{t-1},X_t\}$ to predict the future time series $\{X_{t+1},\dots \dots ,X_{t+l-1},X_{t+l}\}$ for l time steps. 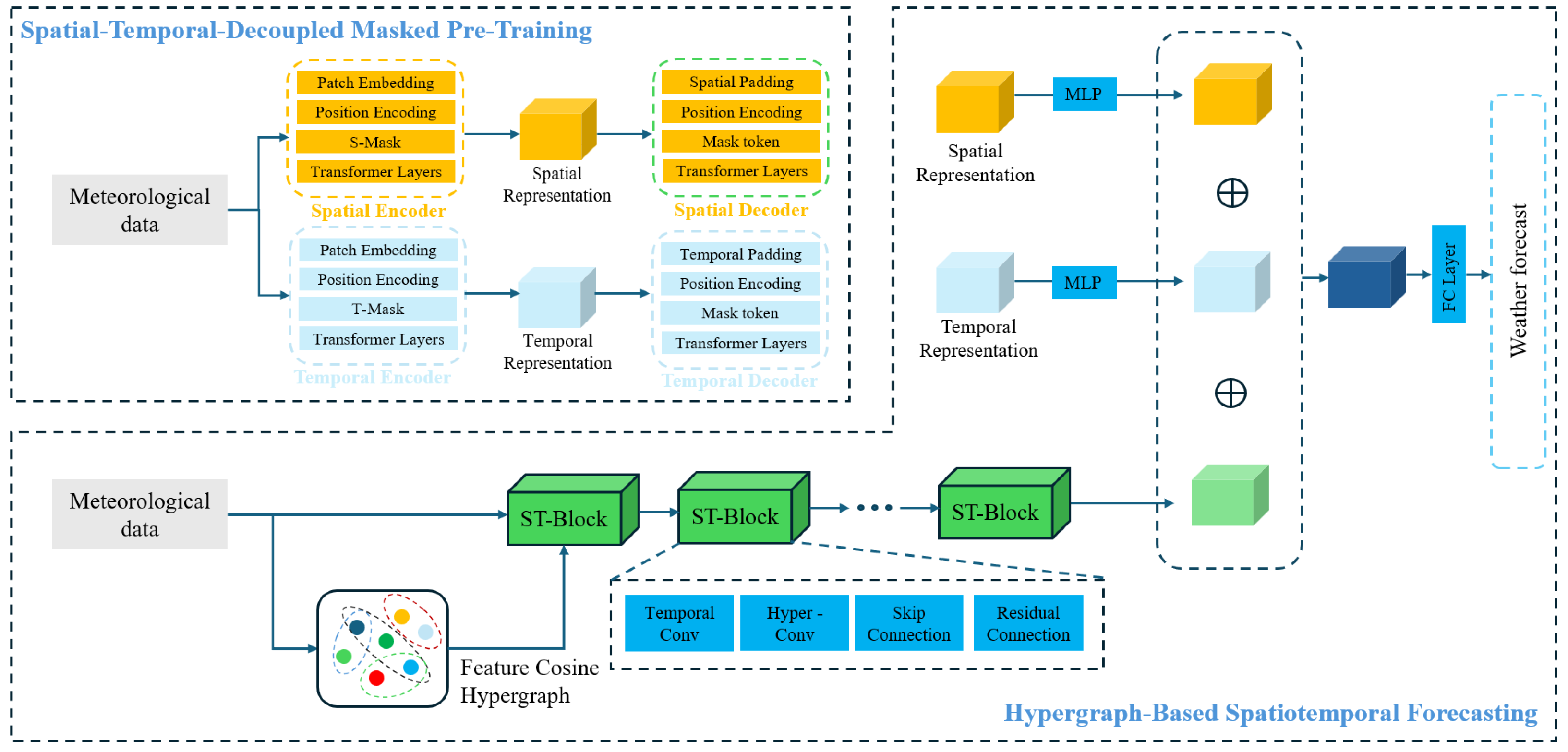As shown in Figure 2, the framework operates through three sequential stages: input representation, preprocessing with masked pretraining, and hypergraph-based forecasting.

Input Representation

The input consists of historical multivariate time series data and station metadata. Each station provides a sequence of observations (e.g., hourly temperature, wind speed) organized as a tensor, where the dimensions correspond to stations, time steps, and meteorological variables. Station metadata includes geographic coordinates (latitude and longitude), which are used to derive spatial relationships. To model complex dependencies between stations, a hypergraph is constructed by connecting groups of stations based on feature similarity. This similarity is computed from historical data, capturing stations with correlated meteorological behavior (e.g., stations experiencing simultaneous rainfall patterns or temperature fluctuations). The hypergraph structure enables the representation of multi-station interactions beyond pairwise connections, such as regional weather systems or clustered microclimates.

Preprocessing with Masked Pretraining

The raw input data undergoes a preprocessing phase where it is mapped into a latent embedding space. A self-supervised pretraining task is applied using a dual-masking strategy: spatial masking randomly occludes observations from a subset of stations, while temporal masking removes contiguous blocks of time steps. The model is trained to reconstruct the masked regions, forcing it to infer missing spatial information from neighboring stations and recover temporal patterns through historical trends. Spatial reconstruction emphasizes learning regional correlations, whereas temporal reconstruction focuses on capturing periodic phenomena. This stage produces disentangled embeddings that separately encode spatial context and temporal dynamics.

Hypergraph-Based Forecasting

The pretrained embeddings are integrated into a hypergraph neural network for final prediction. The hypergraph structure dynamically aggregates features from meteorologically related stations, propagating information through hyperedges that group stations with similar behavioral patterns. For example, a hyperedge might link stations affected by the same frontal system, allowing the model to collectively update their predictions based on shared atmospheric conditions. The forecasting module combines the spatial–temporal embeddings with hypergraph-derived features, refining predictions through iterative message passing. This process ensures that localized weather patterns and large-scale atmospheric dynamics are jointly considered, enhancing the accuracy of multi-step forecasts.

3.2. Spatial–Temporal Decoupled Masked Pretraining

The proposed pretraining framework addresses the challenge of spatiotemporal heterogeneity in meteorological data through a novel dual-masking strategy. The core insight lies in decoupling the learning of spatial and temporal patterns via specialized reconstruction tasks, which forces the model to develop distinct representations for geographic correlations and temporal dynamics. This approach learns disentangled spatial and temporal representations from unlabeled data through a dual masking strategy, which are later integrated into a hypergraph-based predictor.

Given an input spatiotemporal series $\mathbf{X}\in {\mathbb{R}}^{T\times N\times F}$ (where T is the number of time steps, N is the number of stations, and F is the feature dimension), we apply two independent masking strategies: Spatial masking (S-Mask) randomly occludes $r\times 100\%$ of stations across all time steps, forcing the model to reconstruct missing sensor data using spatial correlations. For example, if station i is masked, the model must infer its values from neighboring stations with similar meteorological patterns. Temporal masking (T-Mask) removes $r\times 100\%$ of contiguous time steps, requiring the model to predict missing temporal segments using historical trends. Temporal masking simulates real-world data gaps and enhances the model’s ability to capture periodicity (e.g., daily/weekly cycles).

The masked inputs are processed by two separate autoencoders: Spatial Autoencoder (S-MAE) employs self-attention along the spatial dimension to learn station-wise dependencies. It takes the spatially masked input ${\mathbf{X}}^S\in {\mathbb{R}}^{T\times N(1-r)\times F}$, applies patch embedding and positional encoding, and generates spatial representations ${\mathbf{H}}_s\in {\mathbb{R}}^{T_p\times N\times E}$ (where $T_p$ is the number of patch windows and E is the embedding dimension). Temporal Autoencoder (T-MAE) uses causal self-attention along the temporal dimension to model time series dynamics. It processes the temporally masked input ${\mathbf{X}}^T\in {\mathbb{R}}^{T(1-r)\times N\times F}$ and produces temporal representations ${\mathbf{H}}_t\in {\mathbb{R}}^{T_p\times N\times E}$.

The positional encoding integrates both spatial (e.g., station coordinates) and temporal (e.g., timestamps) information:

$$\left\{\begin{array}{cc}{E}_{[}t,n,2k]=sin\left({\displaystyle \frac{t}{{10000}^{4k/E}}}\right),\hfill & E_{[}t,n,2k+1]=cos\left({\displaystyle \frac{t}{{10000}^{4k/E}}}\right),\hfill \\ E_{[}t,n,2m+E/2]=sin\left({\displaystyle \frac{n}{{10000}^{4m/E}}}\right),\hfill & E_{[}t,n,2m+1+E/2]=cos\left({\displaystyle \frac{n}{{10000}^{4m/E}}}\right),\hfill \end{array}\right.$$

(1)

where t is the time step and n is the station index. The spatial encoding utilizes station indices rather than raw coordinates due to the structured nature of our dataset. The 2048 stations originate from a uniformly discretized global grid (64 longitude bins × 32 latitude bins), where adjacent indices correspond to geographically proximate locations (approximately 5.625° separation per index step). This design enables the model to distinguish spatial proximity (e.g., coastal vs. inland stations) and temporal phases (e.g., morning vs. evening peaks).

During pretraining, the model minimizes the reconstruction loss for masked regions using mean absolute error (MAE):

$${\mathcal{L}}_{\mathrm{pretrain}}={\lambda }_s·\mathrm{MAE}({\widehat{\mathbf{X}}}_s,{\mathbf{X}}_s)+{\lambda }_t·\mathrm{MAE}({\widehat{\mathbf{X}}}_t,{\mathbf{X}}_t),$$

(2)

where ${\widehat{\mathbf{X}}}_s$ and ${\widehat{\mathbf{X}}}_t$ are the reconstructed spatial and temporal segments, and ${\lambda }_s,{\lambda }_t$ balance the two losses. This decoupled training ensures that ${\mathbf{H}}_s$ and ${\mathbf{H}}_t$ capture distinct spatial and temporal patterns.

3.3. Hypergraph-Based Spatiotemporal Forecasting

The forecasting framework leverages hypergraph structures to model complex multi-station interactions while preserving the decoupled spatiotemporal patterns learned during pretraining. This dual-stream architecture combines feature-driven hypergraph construction with temporal dynamics modeling, enabling the capture of both localized weather phenomena and global atmospheric patterns.

Feature Similarity Hypergraph Construction

Let the input multivariate meteorological time series be denoted as $\mathbf{X}\in {\mathbb{R}}^{T\times N\times F}$, where T is the number of time steps, N is the number of stations, and F is the number of meteorological variables (e.g., temperature, humidity, wind speed). For each station i, we compute a feature vector ${\mathbf{f}}_i\in {\mathbb{R}}^F$ by averaging over the temporal dimension:

$${\mathbf{f}}_i={\displaystyle \frac{1}{T}}\sum _{t=1}^T{\mathbf{X}}_{t,i,:}$$

(3)

We then normalize the station features across each variable:

$${\tilde{\mathbf{f}}}_i={\displaystyle \frac{{\mathbf{f}}_i-\mathit{\mu }}{\mathit{\sigma }+ϵ}},\mathit{\mu },\mathit{\sigma }\in {\mathbb{R}}^F$$

(4)

where $\mathit{\mu }$ and $\mathit{\sigma }$ denote the mean and standard deviation over all stations, respectively, and $ϵ$ is a small constant for numerical stability.

Next, a cosine similarity matrix $\mathbf{S}\in {\mathbb{R}}^{N\times N}$ is computed among all normalized station features:

$${\mathbf{S}}_{i,j}={\displaystyle \frac{{\tilde{\mathbf{f}}}_i^{\top }{\tilde{\mathbf{f}}}_j}{{\parallel {\tilde{\mathbf{f}}}_i\parallel }_2·{\parallel {\tilde{\mathbf{f}}}_j\parallel }_2}}$$

(5)

For each station i, we select its top-k most similar stations based on ${\mathbf{S}}_{i,:}$ to form a hyperedge. Repeating this process for all stations yields a hypergraph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where each node represents a station, and each hyperedge $e\in \mathcal{E}$ connects one node to its k most similar peers.

Hypergraph-Aware Forecasting

The forecasting model utilizes the pretrained spatial and temporal embeddings ${\mathbf{H}}_s\in {\mathbb{R}}^{T_p\times N\times E}$ and ${\mathbf{H}}_t\in {\mathbb{R}}^{T_p\times N\times E}$, obtained from Section 3.2, along with the hypergraph $\mathcal{G}$. A hypergraph convolution is applied to propagate information across high-order spatial neighborhoods:

$${\mathbf{H}}^{(l+1)}=\sigma \left({\mathbf{D}}_v^{-1/2}{\mathbf{H}}_G{\mathbf{W}}_h{\mathbf{D}}_e^{-1}{\mathbf{H}}_G^{\top }{\mathbf{D}}_v^{-1/2}{\mathbf{H}}^{\left(l\right)}{\mathbf{W}}_g\right)$$

(6)

where ${\mathbf{H}}_G\in {\mathbb{R}}^{N\times \left|\mathcal{E}\right|}$ is the incidence matrix of $\mathcal{G}$, ${\mathbf{D}}_v$ and ${\mathbf{D}}_e$ are diagonal matrices of node and hyperedge degrees, and ${\mathbf{W}}_h$, ${\mathbf{W}}_g$ are trainable weight matrices.

Temporal dynamics are modeled using dilated causal convolutions over the hypergraph-updated spatial features ${\mathbf{H}}^{(l+1)}$:

$${\mathbf{Z}}_t=\sum _{k=0}^{K-1}{\mathbf{W}}_k\ast {\mathbf{H}}_{t-d·k}^{(l+1)}$$

(7)

where $K=2$ is the kernel size, $d=\{2^0,2^1,\dots ,2^7\}$ are the exponentially growing dilation factors across 8 layers, and * denotes convolution.

The final forecast $\widehat{\mathbf{Y}}$ is computed by fusing the hypergraph-updated features with the pretrained embeddings:

$$\widehat{\mathbf{Y}}=\mathrm{FC}\left(\left[{\mathbf{Z}}_t\parallel {\mathbf{H}}^{(l+1)}\parallel {\mathrm{MLP}}_s\left({\mathbf{H}}_s\right)\parallel {\mathrm{MLP}}_t\left({\mathbf{H}}_t\right)\right]\right)$$

(8)

where ${\mathbf{H}}_s$ and ${\mathbf{H}}_t$ are the spatial and temporal representations extracted via the masked pretraining in Section 3.2, ${\mathrm{MLP}}_s$ and ${\mathrm{MLP}}_t$ are multi-layer perceptrons for dimensionality alignment, and ∥ denotes feature concatenation. This architecture ensures that both high-order spatial interactions and decoupled temporal trends are jointly considered, enhancing the accuracy of multi-step weather forecasts.

By integrating dynamic hypergraph construction with the pretrained spatial–temporal representations, the forecasting module effectively bridges the gap between local meteorological observations and large-scale atmospheric dynamics, providing a robust foundation for short-term weather prediction. In summary, the complete training process of our proposed method is outlined in Algorithm 1.

Algorithm 1 HyMePre: Hypergraph-enhanced Meteorological Pretraining framework

1: Input: Historical meteorological data $\mathbf{X}\in {\mathbb{R}}^{T\times N\times F}$, number of nearest neighbors k, mask rate r   2: Output: Forecasted results $\widehat{\mathbf{Y}}$   3: // Stage 1: Spatial–Temporal Masked Pretraining   4: Apply spatial masking (S-Mask) to occlude $r·N$ stations across all time steps $\to {\mathbf{X}}_S$   5: Apply temporal masking (T-Mask) to occlude $r·T$ time steps for all stations $\to {\mathbf{X}}_T$   6: Encode ${\mathbf{X}}_S$ with spatial autoencoder $\to {\mathbf{H}}_S$   7: Encode ${\mathbf{X}}_T$ with temporal autoencoder $\to {\mathbf{H}}_T$   8: Compute reconstruction loss ${\mathcal{L}}_{\mathrm{pretrain}}={\lambda }_s·\mathrm{MAE}({\widehat{\mathbf{X}}}_S,{\mathbf{X}}_S)+{\lambda }_t·\mathrm{MAE}({\widehat{\mathbf{X}}}_T,{\mathbf{X}}_T)$   9: // Stage 2: Hypergraph-Based Forecasting 10: Compute station-level feature vectors by time-averaging: ${\mathbf{f}}_i={\displaystyle \frac{1}{T}}{\sum }_{t=1}^T{\mathbf{X}}_{t,i,:}$ 11: Normalize ${\mathbf{f}}_i$ across stations and compute cosine similarity matrix $\mathbf{S}$ 12: Construct hypergraph $G=(V,E)$ by connecting each node to its top-k similar neighbors 13: Build incidence matrix ${\mathbf{H}}_G$ and compute degree matrices ${\mathbf{D}}_v$, ${\mathbf{D}}_e$ 14: for each training epoch do 15:     Apply hypergraph convolution using Equation (4) to obtain ${\mathbf{H}}^{(l+1)}$ 16:     Apply dilated causal convolution over ${\mathbf{H}}^{(l+1)}$ to get temporal context ${\mathbf{Z}}_t$ 17:     Fuse embeddings: $\widehat{\mathbf{Y}}=\mathrm{FC}\left(\right[{\mathbf{Z}}_t\parallel {\mathbf{H}}^{(l+1)}\parallel \mathrm{MLP}\left({\mathbf{H}}_S\right)\parallel \mathrm{MLP}\left({\mathbf{H}}_T\right)\left]\right)$ 18:     Compute forecasting loss: ${\mathcal{L}}_{\mathrm{forecast}}=\mathrm{MAE}(\widehat{\mathbf{Y}},\mathbf{Y})$ 19: end for 20: Return: Final prediction $\widehat{\mathbf{Y}}$

4. Experiments

All experiments were performed on a system with an Intel^® Xeon^® Gold 6326 CPU @ 2.90 GHz (Intel Corporation, Santa Clara, CA, USA), an NVIDIA A800 80 GB GPU (NVIDIA Corporation, Santa Clara, CA, USA), and Ubuntu 18.04.1 LTS, with the model implemented in the PyTorch 1.13.1 framework. To assess the performance of the HyMePre model, we conducted comprehensive experiments on four weather datasets, validated the results through ablation studies and various visual analyses, and examined the impact of the number of nodes per hyperedge.

4.1. Experiment Setup

The experiment used the WeatherBench high-resolution dataset with 2048 global nodes, specifically on a 5.625° × 5.625° grid (64 longitude × 32 latitude bins) covering global areas, recording real weather data. The focus of this study is to conduct hourly weather forecasts using a subset extracted from the WeatherBench dataset. This subset covers variables such as temperature, cloud cover, humidity, and ground wind speed. It includes nodes with continuous hourly records from 1 January 2010 to 31 December 2018, to ensure data integrity for model training and testing. For detailed analysis, the prediction results of these four meteorological variables were compared separately. The input and prediction time steps of the HyMePre model were both set to 12 h. The dataset was divided into 1994 training samples, 664 validation samples, and 644 test samples.

HyMePre is a deep learning network used for weather forecasting. To verify the accuracy of our experimental comparisons, we compared it with traditional forecasting models and other deep learning networks. The specific comparison method is as follows:

• HA predicts future values by calculating the average of historical observations at corresponding time steps across previous days or cycles.
• ARIMA models time series data by combining autoregressive terms, differencing operations, and moving average components to capture temporal structures.
• RNN models sequential data by maintaining a hidden state that is updated at each time step, enabling the network to learn temporal dependencies across the input sequence
• STGCN [39] applies one-dimensional convolution along the time axis to learn temporal dependencies from time series inputs. This approach effectively captures both short- and long-term temporal patterns within a predefined window.
• ASTGCN [40] incorporates spatial attention to model spatial dependencies and temporal attention to learn correlations across different time steps, enabling comprehensive spatiotemporal feature extraction.
• AGCRN [41] adaptively captures spatiotemporal dependencies by combining node-level representation learning with dynamic graph construction. It extracts individualized features for each node and generates time-sensitive adjacency structures that reflect evolving relationships among nodes.
• SimpleSTG [42] captures spatiotemporal dependencies through a unified framework that merges spatial and temporal modules. It leverages a simplified Neural Architecture Search method based on stochastic search to optimize model design.
• FCSTGNN [43] provides comprehensive modeling of spatiotemporal dependencies in multi-sensor time series data by constructing fully connected graphs to link all sensors and timestamps. It employs sliding-window-based convolution and pooling GNN layers for efficient feature extraction.

The model was optimized using the AdamW optimizer with an initial learning rate of ${\eta }_0=5\times {10}^{-4}$, adopting a cosine annealing schedule over training epochs. Training employed a dynamic batch size strategy starting from 32 samples and progressively increasing to 128 based on gradient stability. The spatial–temporal attention layers utilized GeLU activation functions, while hypergraph convolution employed Tanh activations for bounded feature propagation. The training protocol ran for 300 maximum epochs with early stopping triggered after 25 epochs of validation plateau ($\Delta <{10}^{-4}$), maintaining dropout rates of $p=0.3$ across all transformer layers for regularization. The model’s effectiveness was evaluated using two metrics: mean absolute error (MAE) and root mean square error (RMSE), as shown below:

$$\begin{array}{c}\hfill MAE={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|\left(y_i^t-{\widehat{y}}_i^t\right)\right|\end{array}$$

(9)

$$\begin{array}{c}\hfill RMSE={\displaystyle \frac{1}{N}}{\left(\sum _{i=1}^N{\left(y_i^t-{\widehat{y}}_i^t\right)}^2\right)}^{1/2}\end{array}$$

(10)

Here, $y_i^t$ represents the predicted value at time t for the i-th meteorological observation station, and ${\widehat{y}}_i^t$ is the corresponding ground truth value. The $MAE$ measures the average absolute errors between predicted values and the ground truth, reflecting their magnitude of difference. The $RMSE$ calculates the square root of the mean squared differences, providing a measure of the model’s stability.

4.2. Performance Comparison

Table 1. Comparison of our method with mainstream spatiotemporal graph neural networks on four weather datasets. Results in bold indicate the best overall performance. The result underlined indicates the second-best overall performance.

Method	Temperature		Cloud Cover		Humidity		Wind
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
HA	8.6710	12.1475	0.3167	0.4343	14.0557	19.1472	5.3825	6.8276
ARIMA	5.5379	68.4896	0.3036	0.5157	7.5307	15.0709	6.1104	7.1914
RNN	5.7892	7.7893	0.2827	0.4289	9.1931	12.6847	3.0875	4.2609
STGCN	5.0880	6.9926	0.2897	0.3777	8.4517	8.7509	5.0770	6.4942
ASTGCN	2.2724	3.0595	0.2890	0.3817	7.0583	9.6149	2.8986	4.2152
AGCRN	1.9150	2.2956	0.2340	0.3368	6.1040	9.6839	3.1805	4.4690
SimpleSTG	1.3500	1.9323	0.2241	0.3235	5.2221	7.9983	3.5102	5.0145
FCSTGNN	1.5854	2.1233	0.2390	0.3403	5.4984	8.4083	2.0154	3.1257
HeMePre	1.4205	1.9777	0.2132	0.3128	5.1625	7.9361	1.7176	2.3126

demonstrates the comparison results of our proposed HyMePre method with other mainstream spatiotemporal graph neural networks on four different meteorological datasets. The specific evaluation metrics include the mean absolute error (MAE) and root mean square error (RMSE) for temperature, cloud cover, humidity, and wind. Smaller values of MAE and RMSE indicate lower prediction errors and better model performance.

As shown in Table 1, HyMePre achieves strong performance across various meteorological variables, particularly in tasks that require modeling complex spatial interactions. The integration of hypergraph neural networks with a decoupled spatiotemporal pretraining approach enables the model to effectively capture higher-order dependencies. This is especially advantageous for variables like wind and cloud patterns, where multi-station correlations play a key role.

By leveraging hyperedges to represent group-level atmospheric behaviors, HyMePre outperforms traditional graph-based methods that rely on pairwise connections, enabling more comprehensive spatial information propagation. The self-supervised pretraining strategy further enhances the model’s ability to generalize, particularly under noisy or incomplete observational conditions.

To ensure the robustness and reliability of these findings, we include error bars in

Table 2. Prediction performance of all models on four meteorological variables (Mean ± Std).

Model	Temperature		Cloud		Humidity		Wind
	MAE ± Std	RMSE ± Std	MAE ± Std	RMSE ± Std	MAE ± Std	RMSE ± Std	MAE ± Std	RMSE ± Std
HA	8.7139 ± 0.2132	12.1906 ± 0.2293	0.3218 ± 0.0074	0.4443 ± 0.0064	14.1265 ± 0.0611	19.2899 ± 0.1361	5.4621 ± 0.0982	6.8627 ± 0.0335
ARIMA	5.4174 ± 0.1409	68.7514 ± 1.6400	0.3086 ± 0.0061	0.5200 ± 0.0030	7.5651 ± 0.0351	15.1049 ± 0.0241	6.2462 ± 0.0645	7.2673 ± 0.0504
RNN	5.6637 ± 0.1494	7.8516 ± 0.1462	0.2890 ± 0.0037	0.4325 ± 0.0015	9.2705 ± 0.0408	12.7762 ± 0.0504	3.1751 ± 0.0651	4.3635 ± 0.0489
STGCN	5.0565 ± 0.1029	7.0719 ± 0.0826	0.2974 ± 0.0062	0.3847 ± 0.0033	8.5065 ± 0.0322	8.7901 ± 0.0182	5.1921 ± 0.0405	6.5567 ± 0.0224
ASTGCN	2.2724 ± 0.0326	3.0698 ± 0.0187	0.2958 ± 0.0028	0.3877 ± 0.0014	7.1219 ± 0.0171	9.6533 ± 0.0321	3.0025 ± 0.0198	4.2784 ± 0.0124
AGCRN	1.9135 ± 0.0450	2.3347 ± 0.0349	0.2376 ± 0.0017	0.3403 ± 0.0011	6.1622 ± 0.0253	9.7646 ± 0.0380	3.2479 ± 0.0363	4.4963 ± 0.0080
SimpleSTG	1.3403 ± 0.0411	1.9494 ± 0.0150	0.2277 ± 0.0019	0.3292 ± 0.0010	5.2537 ± 0.0138	8.0295 ± 0.0191	3.5489 ± 0.0239	5.0314 ± 0.0083
FCSTGNN	1.5719 ± 0.0450	2.1578 ± 0.0302	0.2407 ± 0.0037	0.3429 ± 0.0022	5.5286 ± 0.0155	8.4569 ± 0.0145	2.0412 ± 0.0224	3.1394 ± 0.0098
HeMePre	1.4477 ± 0.0132	1.9951 ± 0.0171	0.2143 ± 0.0017	0.3159 ± 0.0010	5.1791 ± 0.0062	7.9533 ± 0.0087	1.7273 ± 0.0094	2.3321 ± 0.0070

and confidence intervals in

Table 3. Prediction performance of all models on four meteorological variables (Mean ± 95% CI).

Model	Temperature		Cloud		Humidity		Wind
	MAE ± CI	RMSE ± CI	MAE ± CI	RMSE ± CI	MAE ± CI	RMSE ± CI	MAE ± CI	RMSE ± CI
HA	8.7139 ± 0.2552	12.1906 ± 0.3149	0.3218 ± 0.0120	0.4443 ± 0.0086	14.1265 ± 0.0731	19.2899 ± 0.1639	5.4621 ± 0.1168	6.8627 ± 0.0398
ARIMA	5.4174 ± 0.1883	68.7514 ± 2.1966	0.3086 ± 0.0073	0.5200 ± 0.0038	7.5651 ± 0.0419	15.1049 ± 0.0288	6.2462 ± 0.0772	7.2673 ± 0.0570
RNN	5.6637 ± 0.1987	7.8516 ± 0.1935	0.2890 ± 0.0055	0.4325 ± 0.0019	9.2705 ± 0.0487	12.7762 ± 0.0600	3.1751 ± 0.0777	4.3635 ± 0.0584
STGCN	5.0565 ± 0.1385	7.0719 ± 0.1268	0.2974 ± 0.0075	0.3847 ± 0.0048	8.5065 ± 0.0384	8.7901 ± 0.0217	5.1921 ± 0.0484	6.5567 ± 0.0273
ASTGCN	2.2724 ± 0.0484	3.0698 ± 0.0236	0.2958 ± 0.0038	0.3877 ± 0.0019	7.1219 ± 0.0204	9.6533 ± 0.0382	3.0025 ± 0.0236	4.2784 ± 0.0148
AGCRN	1.9135 ± 0.0574	2.3347 ± 0.0482	0.2376 ± 0.0021	0.3403 ± 0.0016	6.1622 ± 0.0299	9.7646 ± 0.0449	3.2479 ± 0.0429	4.4963 ± 0.0099
SimpleSTG	1.3403 ± 0.0552	1.9494 ± 0.0233	0.2277 ± 0.0026	0.3292 ± 0.0014	5.2537 ± 0.0164	8.0295 ± 0.0226	3.5489 ± 0.0281	5.0314 ± 0.0103
FCSTGNN	1.5719 ± 0.0526	2.1578 ± 0.0410	0.2407 ± 0.0048	0.3429 ± 0.0030	5.5286 ± 0.0186	8.4569 ± 0.0171	2.0412 ± 0.0264	3.1394 ± 0.0121
HeMePre	1.4477 ± 0.0171	1.9951 ± 0.0215	0.2143 ± 0.0023	0.3159 ± 0.0013	5.1791 ± 0.0075	7.9533 ± 0.0107	1.7273 ± 0.0116	2.3321 ± 0.0086

. These statistical measures provide a clearer picture of the variability and uncertainty in model performance, supporting more confident comparisons among methods.

While the model may be less optimal for variables influenced by highly localized features, such as temperature, the spatial masking mechanism helps to address this to some extent. Overall, HyMePre presents a promising framework with broad applicability, and future work may further refine its adaptability and efficiency for operational use.

4.3. Ablation Analysis

We conducted ablation tests to validate the effectiveness of the HyMePre design. Five ablation variants were evaluated on temperature, cloud cover, humidity, and wind datasets. The implemented model variants are described as follows:

(1)

w/o S-Mask: Removes temporal masking while retaining spatial masking.

(2)

w/o T-Mask: Disables spatial masking in pretraining, using only temporal masking.

(3)

w/o G: Replaces hypergraph convolution with standard GCN layers.

(4)

w/o Fusion: Replaces the attention fusion module with a simple addition operation for feature fusion.

Table 4. Ablation analysis. Results in bold indicate the best overall performance.

Method	Temperature		Cloud Cover		Humidity		Wind
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
w/o S-Mask	1.4682	2.0423	0.2218	0.3296	5.2357	8.0124	1.7851	2.3940
w/o T-Mask	1.4597	2.0175	0.2184	0.3251	5.1983	7.9886	1.7729	2.3756
w/o G	1.4910	2.0850	0.2942	0.3319	5.2941	8.0317	1.8020	2.4208
w/o-Fusion	1.5326	2.8652	0.2275	0.4156	5.4172	8.2415	1.8645	2.4815
Our	1.4245	1.9762	0.2137	0.3171	5.1723	7.9656	1.7286	2.3369

summarizes the performance degradation patterns across different variants. The full model achieves optimal results on all prediction tasks, demonstrating the necessity of each component. Removing the spatial masking component (w/o S-Mask) leads to a significant drop in prediction accuracy for cloud cover and wind speed. These variables rely on coordinated variations across multiple stations, such as those observed in frontal systems, where inferring missing data requires information from neighboring sites. The absence of temporal masking (w/o T-Mask) weakens the model’s ability to capture periodic humidity dynamics, such as the diurnal evaporation cycle, highlighting the importance of temporal continuity reconstruction.

Replacing hypergraph convolution with conventional graph convolution (w/o G) results in a performance decline across all variables, with the most notable impact on wind speed and cloud cover. Traditional graph structures are limited to pairwise relationships and fail to represent collective behaviors among multiple stations, such as regional wind field propagation. This confirms the essential role of hypergraphs in modeling higher-order spatial dependencies in meteorological phenomena.

Substituting attention-based fusion with simple addition (w/o Fusion) reduces the model’s ability to integrate global and local features effectively. For instance, in temperature prediction, the model struggles to balance localized terrain effects with large-scale atmospheric circulation. In contrast, the fusion mechanism enables dynamic weighting across spatial scales, enhancing the representation of complex weather systems.

The ablation study highlights that each component contributes uniquely to the overall effectiveness of the framework. Excluding any module results in noticeable performance drops, demonstrating that the system’s carefully designed architecture enables distinct yet complementary roles. This coordinated interaction among modules is fundamental to the model’s strong predictive capabilities in meteorological applications.

5. Conclusions

This paper presents HyMePre, a short-term weather forecasting framework that integrates hypergraph neural networks with a decoupled spatiotemporal pretraining strategy. By addressing the limitations of traditional graph neural networks in capturing higher-order spatial dependencies and handling heterogeneous meteorological data, HyMePre significantly improves forecasting performance. The core innovations of the framework lie in its use of a self-supervised pretraining phase with spatial and temporal masking to learn disentangled spatiotemporal representations from unlabeled time series, and a hypergraph-based prediction module that dynamically constructs meteorologically relevant hyperedges to model complex multi-station interactions. Experiments on large-scale reanalysis datasets demonstrate that HyMePre outperforms existing spatiotemporal models across key meteorological variables, including temperature, cloud cover, humidity, and wind speed, achieving the lowest prediction error particularly in wind and cloud-related tasks. Ablation studies further confirm the critical role of each module. These mechanisms enable the model to capture both local microclimate effects and large-scale atmospheric circulation patterns, supporting accurate predictions in complex weather scenarios.

The proposed framework holds strong potential for real-world applications such as extreme weather warning and resource scheduling optimization. Future work will focus on extending the model’s capability to long-term forecasting, improving computational efficiency for deployment in resource-constrained environments, with particular attention to meteorological-adaptive convolutions that auto-tune dilation factors per variable and hypergraph stabilization through density-aware edge weighting. We will also explore physics-informed hypergraph construction methods, potentially integrating HyMePre with numerical weather prediction systems to bridge data-driven and physics-based approaches. By advancing the representation of high-order spatiotemporal dependencies, this study offers a more adaptive and reliable solution to the growing challenges of weather forecasting in the context of climate change.