An Efficient Dropout for Robust Deep Neural Networks

Abstract

Overfitting remains a major difficulty in training deep neural networks, especially when attempting to achieve good generalization in complex classification tasks. Standard dropout is often employed to address this issue; however, its uniform random inactivation of neurons typically leads to instability and insufficient performance increases. This paper proposes an upgraded regularization technique merging adaptive sigmoidal dropout with weight amplification, seeking to dynamically adjust neuron deactivation depending on weight statistics, activation patterns, and neuron history. The proposed dropout process uses a sigmoid function driven by a temperature parameter to determine deactivation likelihood and incorporates a “neuron recovery” step to restore important activations. Simultaneously, the method amplifies high-magnitude weights to select crucial traits during learning. The proposed method is tested on CIFAR-10, and CIFAR-100 datasets using four unique CNN architectures, including deep and residual-based models, to evaluate the approach. Results demonstrate that the suggested technique consistently outperforms both standard dropout and baseline models without dropout, yielding higher validation accuracy and lower, more stable validation loss across all datasets. In particular, it demonstrated superior convergence and generalization performance on challenging datasets such as CIFAR-100. These findings demonstrate the potential of the proposed technique to improve model robustness and training efficiency and provide an alternative in complex classification tasks.

1. Introduction

In recent years, deep learning has become an indispensable tool across various domains such as computer vision, speech recognition, and natural language processing. Despite its effectiveness, a recurrent difficulty in training deep neural networks (DNNs) is overfitting, when a model performs well on training data but fails to generalize effectively to unseen data. To address this issue, several regularization strategies have been developed to improve model robustness and generalization. Among them, dropout [1] has been a commonly utilized method due to its simplicity and effectiveness, particularly in deep networks.

Dropout works by randomly deactivating a part of neurons during training, thereby preventing complicated co-adaptations and indirectly training an ensemble of subnetworks [1,2,3,4]. However, standard dropout applies this deactivation equally, without considering each neuron’s importance or contribution. This indiscriminate strategy may unduly block important neurons and generate instability during training, especially in deeper or more intricate models [5,6].

To confront these restrictions, numerous adaptive dropout variations have been proposed, where dropout probabilities are adjusted based on weight magnitudes, neuron activations, or learned priors [5,7]. While these approaches increase the method’s selectivity, they often come at the cost of increased computational complexity or require architectural redesign and tuning.

This paper introduces a novel regularization method that combines adaptive sigmoidal dropout, neuron recovery, and weight amplification. Unlike standard dropout algorithms, the proposed technique alters dropout behavior dynamically based on neuron activity, weight distributions, and historical inputs. A new neuron recovery mechanism is integrated to restore important neuron activations that would otherwise be blocked. Additionally, weight amplification selectively elevates the most influential weights during training, accelerating learning and enhancing feature extraction, particularly successful in high-complexity datasets.

Importantly, a fundamental practical advantage of the proposed method comes in its implementation flexibility: it may be easily applied to dynamically constructed, pre-trained, or saved models without requiring any architectural changes. This makes it perfect for modern deep learning processes where model structures may vary or be reused across several jobs.

This flexibility, combined with its adaptivity and recovery properties, puts the proposed method as a feasible and robust alternative for regularizing deep networks in real-world applications.

The remainder of this article is organized as follows. Section 2 evaluates related dropout strategies and discusses their strengths and drawbacks in comparison to the proposed method. Section 3 introduces the details of the suggested method. Section 4 discusses the experimental setup, displays the assessment results, and examines the performance across multiple network setups and datasets. Finally, Section 5 concludes the paper.

2. Literature Review

Regularization is a vital component in deep learning, as it mitigates overfitting and increases the generalization capability of models. Among regularization strategies, dropout remains one of the most famous methods. Since its introduction by Srivastava et al. [1], various versions of dropout have been designed to solve its shortcomings and increase performance across diverse architectures and tasks.

Dropout works by randomly deactivating a subset of neurons during training, eliminating excessive co-adaptations and effectively training an ensemble of subnetworks [1,2]. Since its release, various changes have been proposed to overcome its limits and boost adaptability [3]. These include DropConnect [4], which applies dropout to weights instead of activations, and Adaptive Dropout [5], which modifies drop probabilities based on cell activity. Other notable strategies include Maxout [6], Shakeout [7], Soft Dropout [8], and DropBlock [9], which applies structured dropout to continuous spatial regions, especially increasing regularization in convolutional layers.

More recent developments focus on adaptive dropout mechanisms, including Bayesian optimization [10], trainable gradient dropout [11], evolutionary algorithms [12], and biologically inspired models [13]. Methods like Multi-sample Dropout [14], and Guided Dropout [15] improve generalization while minimally adding inference-time complexity. Furthermore, task-specific dropout modifications, such as Clustering-Based Dropout [16], PLACE Dropout [17], and State Dropout for reinforcement learning [18], indicate promise efficacy in some applications.

Despite these developments, traditional dropout techniques still suffer from key constraints. Binary masking causes instability, and uniform dropout probability disregards neuron significance. More recent systems, such as Y-Drop [19], Variational Dropout [20], and Stochastic Delta Rule Dropout [21], aim to address these concerns by applying better control algorithms based on neuron importance, weight distributions, or learned priors.

Table 1. Comparison of Dropout and Dropout-Inspired Regularization Methods.

Method	Key Idea	Advantages	Disadvantages
Standard Dropout [1]	Randomly deactivates neurons during training	Simple, easy to implement; reduces overfitting	Ignores neuron importance; can cause instability
DropConnect [4]	Randomly drops weights instead of activations	Stronger regularization; more flexible	Higher computational cost; complex tuning
Adaptive Dropout [5]	Adjusts dropout rate based on neuron activity	Data-dependent; better adaptability	Requires additional computation
Maxout [6]	Uses maximum across multiple activations	Improves feature learning; strong regularization	Requires architectural changes; increased parameters
Shakeout [7]	Combines dropout and L1 regularization with stochastic noise	Reduces overfitting; improves generalization	Adds complexity to training
Soft Dropout [8]	Uses smooth probability-based deactivation	Reduces randomness-induced instability	Higher computational cost
DropBlock [9]	Drops contiguous regions in feature maps	Effective in CNNs; better spatial regularization	Requires tuning block size; only for CNNs
Trainable Gradient Dropout [11]	Learns dropout rates using gradients during training	Fully adaptive; improves training efficiency	Needs extra parameters and computation
Y-Drop [19]	Conductance-based dropout guided by neuron importance	Focuses on critical neurons; improves stability	Complex implementation; limited use
Variational Dropout [20]	Bayesian inference for adaptive dropout rates	Strong theoretical basis; good regularization	Computationally intensive; complex modeling
Stochastic Delta Rule Dropout [21]	Adds adaptive weight noise during training	Accelerates convergence; reduces overfitting	Requires tuning of noise parameters

outlines numerous dropout and dropout-inspired regularization techniques, comparing their underlying principles, adaptivity, neuron targeting strategies, implementation complexity, and their applicability for dynamic or pre-trained neural network designs.

While existing dropout strategies have improved regularization, many continue to confront issues such as the need for specialized topologies, large processing costs, or poor adaptation to neuron importance.

To address these concerns, this work introduces a novel dropout strategy that promotes adaptive behavior, neuron recovery, and model compatibility. A major strength is that it works directly with dynamically defined, pre-trained, or saved models without needing architectural changes. Unlike other advanced methods that require special layers or retraining, the proposed method can be easily added to most deep learning workflows. Details of the method are explained in Section 3.

3. The Proposed Method

This paper presents an innovative methodology designed to improve the performance of convolutional neural networks (CNNs). The main aim is to achieve higher generalization success and faster convergence by optimizing the model learning process. Advanced techniques such as adaptive dropout and weight amplification are integrated in this method. These methods attempt to address common deep learning issues such as overfitting and inadequate control over model weights during training.

In contrast to standard dropout, which deactivates neurons at random, the recommended method uses an adaptive dropout mask that considers activation magnitude, weight distribution, and previous neuron activity. This mask is dynamically adjusted during training to retain key neurons while selectively eliminating less significant connections.

A key element of this method is the use of a Gaussian-based low-weight mean to identify and mask weakly contributing parameters. For a given weight tensor, the absolute values are taken, and their mean $\left(\mathsf{\mu }\right)$ and standard deviation $\left(\mathsf{\sigma }\right)$ are computed. The threshold for low weights is set as:

$$\mathrm{T}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}=(\mathsf{\mu }+\mathsf{\sigma })/50$$

(1)

Weights below or equal to this threshold are considered low weights, and their mean is used to determine the mask:

$${\mathrm{M}}_{low}=I\left(\left|x\right|>{\mu }_{low}\right)$$

(2)

where $I\left(condition\right)$ is the indicator function and ${\mu }_{low}$ is the calculated low-weight mean.

To control the sharpness of the dropout probability, a temperature parameter is dynamically calculated based on the standard deviation of all trainable weights:

$$\mathrm{T}=1/\left(\mathrm{S}\mathrm{t}\mathrm{d}\mathrm{D}\mathrm{e}\mathrm{v}\right(\mathrm{w})+\mathsf{ϵ})$$

(3)

where $\mathrm{w}$ is the set of all trainable weights, and $\mathsf{ϵ}$ is a small constant for numerical stability.

The proposed method is constructed by integrating multiple components:

• A random mask is generated using a Gaussian distribution:

  $$\mathrm{N}\sim \mathcal{N}\left(\mathsf{\mu },{\mathsf{\sigma }}^2\right)$$

  (4)

  where N denotes a Gaussian noise vector with mean μ and standard deviation σ.
• The dropout probability is adaptively determined based on neuron activity and is defined as:

  $${\mathrm{p}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}=\mathrm{r}\left(1+\mathrm{s}\mathrm{E}\left[\left|\mathrm{x}\right|\right]\right)$$

  (5)

  where $\mathrm{r}$ is the base dropout rate, $\mathrm{s}$ is a stability factor, $\mathrm{E}\left[\left|\mathrm{x}\right|\right]$ denotes the mean (expected value) of the absolute values of the input tensor $x$.
• Sigmoid function is applied to compute the dropout mask as follows:

  $${\mathrm{M}}_{rand}=\mathsf{\sigma }\left({\displaystyle \frac{\mathrm{N}-{\mathrm{p}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}}{\mathrm{T}+\mathsf{ϵ}}}\right)$$

  (6)
• The weight-based mask is defined as:

  $${\mathrm{M}}_{\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}=\mathsf{\sigma }\left(-4\left|\mathrm{x}\right|\right)$$

  (7)

  where ${\mathrm{M}}_{\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}$ denotes the mask generated according to the absolute value of the input tensor x. The scaling factor (−4) sharpens the sigmoid transition, emphasizing the contribution of weights with larger magnitudes.
• The adaptive dropout mask is constructed as a weighted combination of the random and weight-based masks:

  $${\mathrm{M}}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}}=0.7\hspace{0.17em}{\mathrm{M}}_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}+0.3\hspace{0.17em}\left(1-{\mathrm{M}}_{\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}\right)$$

  (8)

The coefficients 0.7 and 0.3 control the influence of each component, allowing the mask to dynamically balance stochasticity and weight information during training.

The adaptive mask is further modulated by recent neuron activity and activation diversity (entropy):

$${\mathrm{M}}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}}\leftarrow {\mathrm{M}}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}}\odot \mathsf{\sigma }\left(2{\mathrm{a}}_{\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}}\right)\odot \mathsf{\sigma }\left(9\hspace{0.17em}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{y}\right)$$

(9)

where ${\mathrm{a}}_{\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}}$ recent is the mean recent activity, $\odot$ is element-wise (Hadamard) multiplication, and $entropy=E\left[\hspace{0.17em}\left|x\right|\hspace{0.17em}\right]/(\max \left(\left|x\right|\right)+\mathsf{ϵ})$. ($E\left[\hspace{0.17em}\left|x\right|\hspace{0.17em}\right]$ is the mean (expected value) of the absolute values of $x$, $\max \left(\left|x\right|\right)$ is the maximum absolute value in $x$, $\mathsf{ϵ}$ is a small constant for numerical stability.)

The masks are applied to compute the dropped and recovered neurons as follows:

$${\mathrm{x}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d}}=\mathrm{x}\odot {\mathrm{M}}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}}\odot {\mathrm{M}}_{\mathrm{l}\mathrm{o}\mathrm{w}}\odot {\mathrm{M}}_{\mathrm{z}\mathrm{e}\mathrm{r}\mathrm{o}}$$

(10)

The recovery factor is calculated as:

$${\mathrm{f}}_{\mathrm{r}\mathrm{e}\mathrm{c}}=\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}\left(1.5\mathrm{E}\left[\left|\mathrm{x}\right|\right],\mathrm{ }0.4,\mathrm{ }0.7\right)$$

(11)

where clip(⋅) restricts the value to the interval [0.4, 0.7], and E[∣x∣] is the mean absolute value of the input tensor.

The recovered neurons are obtained by:

$${\mathrm{x}}_{\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}}={\mathrm{f}}_{\mathrm{r}\mathrm{e}\mathrm{c}}\hspace{0.17em}\left|\mathrm{x}\right|\odot \left(1-{\mathrm{M}}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}}\right)$$

(12)

The final output is computed by combining the dropped and recovered neurons:

$${\mathrm{x}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}=\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\left({\mathrm{x}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d}}=0,\mathrm{ }{\mathrm{x}}_{\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}},\mathrm{ }{\mathrm{x}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d}}\right)$$

(13)

where the $\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}(.)$ operation selects the recovered value when the dropped output is zero; otherwise, it retains the dropped output.

Finally, the output is normalized and masked:

$${\mathrm{x}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=\left({\displaystyle \frac{{\mathrm{x}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}{\mathrm{E}\left[{\mathrm{M}}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}}\right]+\mathsf{ϵ}}}\right)\odot {\mathrm{M}}_{\mathrm{z}\mathrm{e}\mathrm{r}\mathrm{o}}$$

(14)

where $\mathsf{ϵ}$ is a small constant to prevent division by zero.

Also, weight amplification is employed to speed feature learning by selecting elevating the strongest weights, allowing the network quickly understand difficult patterns. A dynamic learning rate schedule is also introduced, which cuts the learning rate at important intervals to maintain consistent convergence. Adaptive correction is provided, and robust generalization is further improved by monitoring weight evolution and neuron activity throughout training.

In summary, the proposed method leverages the statistical aspects of weights, neuron activity history, and dynamic temperature scaling to provide a data-driven, robust, and effective regularization solution for deep neural networks. Illustration of the use of the proposed methodology as presented in

Table 2. Example Applying the Proposed Method.

Step 1: Load and preprocess the dataset Step 2: Define model hyperparameters Step 3: Load the previously saved model Step 4: Define helper functions - Calculates the mean of low magnitude weights using Gaussian distribution principles. - Computes the temperature parameter based on the standard deviation of the model’s weights. - Applies the Proposed Dropout Function, - Amplifies the top percentage of the model’s weights. - Adjusts the learning rate based on the current epoch. - Track neuron activity and weight evolution over recent epochs. - Returns max connections based on the current epoch. Step 5: Training loop Step 6: Save the final model

.

4. Dataset for Comparison

Four different convolutional neural network (CNN) architectures were implemented to thoroughly evaluate the effectiveness of the proposed technique, as shown in

Table 3. Architectural Summary of Network Models.

Model Name	Dataset	Architectural Summary (Flow and Key Components)
Model 1	CIFAR10	Input (32 × 32 × 3) → [5 × (Conv2D: 128 F, 3 × 3 K, ReLU, Same Padding + Batch Norm + MaxPooling: 2 × 2 P)] → Flatten → Dense (512 U, ReLU) → Output (num_classes, Softmax)
Model 2	CIFAR100	Input (32 × 32 × 3) → [5 × (Conv2D: 512 F, 3 × 3 K, ReLU, Same Padding + Batch Norm + (MaxPooling: 2 × 2 P after every 2nd Conv Layer))] → Global Average Pooling 2D → Dense (1024 U, ReLU) → Output (100, Softmax)
Model 3	CIFAR100	Input (32 × 32 × 3) → Conv2D (64 F) → Batch Norm → Conv2D (128 F) → Batch Norm → MaxPooling (2 × 2 P) → Conv2D (256 F) → Batch Norm → Conv2D (512 F) → Batch Norm → MaxPooling (2 × 2 P) → Global Average Pooling 2D → Dense (512 U, ReLU) → Output (100, Softmax) (All Conv2D layers are 3 × 3 K, ReLU, Same Padding)
Model 4	CIFAR100	Input (32 × 32 × 3) → Conv2D (64 F, 3 × 3 K, Same, ReLU) → Batch Norm → 8 × Residual Block: [2 × (64 F), 2 × (128 F, Downsample = 1), 2 × (256 F, Downsample = 1), 2 × (512 F, Downsample = 1)] → Global Average Pooling 2D → Dense (512 U, ReLU) → Dropout (0.5) → Output (100, Softmax) (Each block has 2 × Conv2D (3 × 3 K) and skip connection; downsampled blocks use Conv2D (1 × 1 K) and stride 2)

. These models vary in both depth and architectural complexity to examine the generalizability and robustness of the method. The first three are custom-designed CNNs with unique layer configurations, while the fourth is based on the well-established ResNet architecture, which uses residual connections to enable training of deeper networks. By applying the proposed dropout method to a variety of architectures, including a standard deep residual model, the study shows its adaptability and performance advantages in both simple and complex learning scenarios.

To evaluate the performance of the proposed dropout method, experiments are conducted on CIFAR-10, and CIFAR-100 datasets using convolutional neural network (CNN) architecture. All models were implemented and trained using TensorFlow (version: 2.18.0) on Google Colab with an NVIDIA L4 GPU. This standardized hardware environment ensures consistent runtime measurements and fair comparisons across all experiments.

The architectural elements used in CNN models comprise Conv2D layers for spatial feature extraction via learnable filters; ReLU activations that introduce non-linearity and enhance convergence; Batch Normalization that stabilizes training through activation normalization; MaxPooling and Global Average Pooling that diminish spatial dimensions to mitigate overfitting and computational load; and Dense layers that execute final classification. These components are commonly employed in current convolutional architectures.

4.1. Datasets

CIFAR-10: The CIFAR-10 dataset contains 60,000 32 × 32 color images separated into 10 classes, with 50,000 images for training and 10,000 for testing. The CIFAR-10 dataset contains 60,000 32 × 32 color images divided into 10 classes, with 50,000 images for training and 10,000 for testing.

CIFAR-100: The CIFAR-100 dataset contains 60,000 32 × 32 color images divided into 100 classes, with 50,000 images for training and 10,000 for testing. Each image belongs to one of 100 fine-grained categories, making it a more complex and challenging benchmark compared to CIFAR-10.

4.2. Implementation Details

The CNN architecture was first trained for 20 epochs for the test. The trained network was recorded and compared by continuing training in 3 stages. As shown in Figure 1, the recorded network was trained separately in 3 stages as “No Dropout,” “Proposed Dropout,” and “Standard Dropout.” The naming in the architecture

• No Dropout: The network continues its training in the same way without any additions until it reaches 40 epochs.
• Standard Dropout: The network is trained with random dropout (standard random dropout code) and continues its training until it reaches 40 epochs.
• Proposed Dropout: The network is trained with the recommended method (Table 2) and continues its training until it reaches 40 epochs.

The performance of the models was evaluated using validation accuracy and validation loss. Validation accuracy measures the proportion of correctly classified samples, while validation loss quantifies the divergence between predicted and true distributions using categorical cross-entropy.

$$\mathrm{Validation} \mathrm{Accuracy}={\displaystyle \frac{1}{N}}\sum _{i=1}^N𝟙\left(\arg \max \left(\widehat{y_i}\right)=\arg \max \left(y_i\right)\right)$$

(15)

$$\mathrm{Validation} \mathrm{Loss}=-{\displaystyle \frac{1}{N}}\sum _{i=1}^N\sum _{c=1}^C{y}_{i,c}\log \left(\widehat{y_{i,c}}+\epsilon \right)$$

(16)

where $N$ is the number of validation samples, $c$ is the number of classes, $y_i$ is the one-hot encoded true label, $\widehat{y_i}$ is the predicted probability vector, and $\mathsf{\epsilon }$ is a small constant for numerical stability.

4.3. Results

The performance of the proposed method (“Proposed”) was compared against a baseline model without any dropout (“No Dropout”) and a model using standard random dropout (“Standard Dropout”). The results were evaluated across four experiments conducted on CIFAR-10, and CIFAR-100 (Models 2–4), with validation accuracy and validation loss shown in Figure 2, Figure 3, Figure 4 and Figure 5.

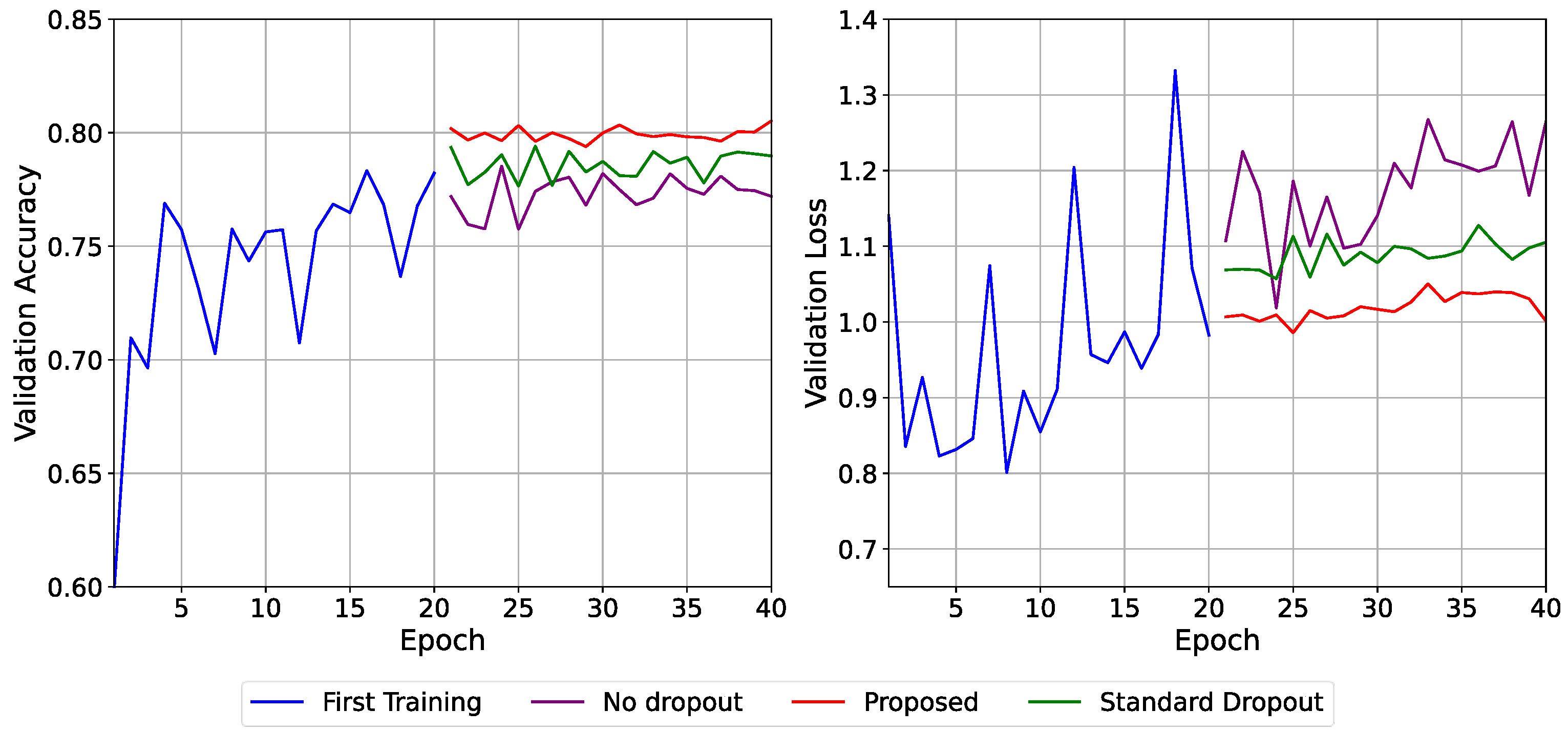
In Figure 2, the “No Dropout” setup rapidly attained reasonable accuracy (~78–79%) but did not progress beyond the initial epochs. The validation loss exhibited significant variations and an upward trend, indicating overfitting. The “Standard Dropout” enhanced generalization by stabilizing accuracy and diminishing loss values (~1.05), while slight variations persisting. The “Proposed” technique outperformed both options, with a steady validation accuracy of 80% and a modest validation loss (between 0.98 and 1.03), indicating more stability and reduced overfitting.

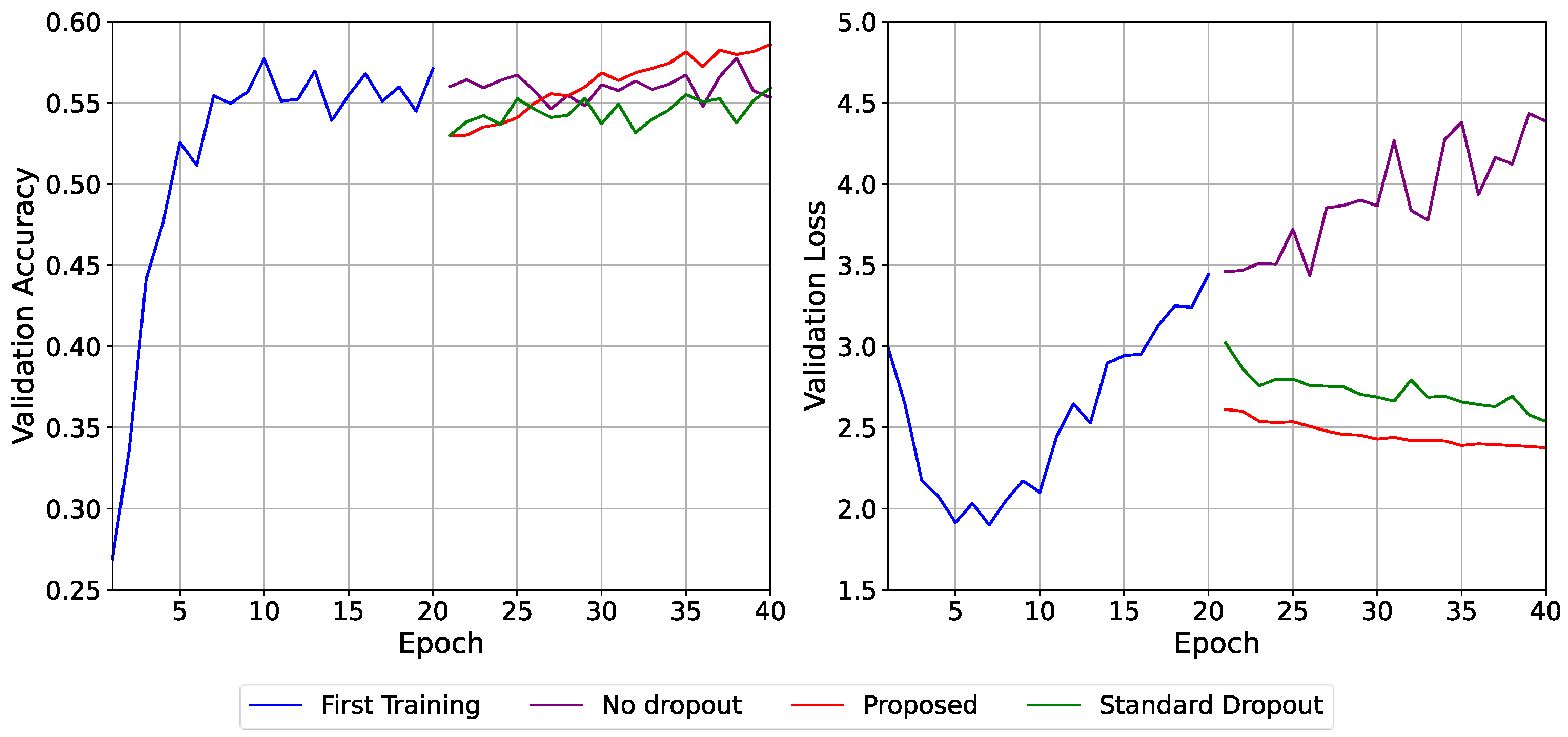
In Figure 3, the proposed method achieved the highest validation accuracy of 58.59%, outperforming both the no dropout (57.75%) and standard dropout (55.91%) configurations. In terms of validation loss, the proposed technique demonstrated a slow and sustained fall, reaching 2.37, compared to 2.54 for standard dropout and a rapid increase to 4.43 for the no-dropout baseline. These results indicate that the proposed dropout technique delivers greater generalization and training stability, notably in managing overfitting during later training phases.

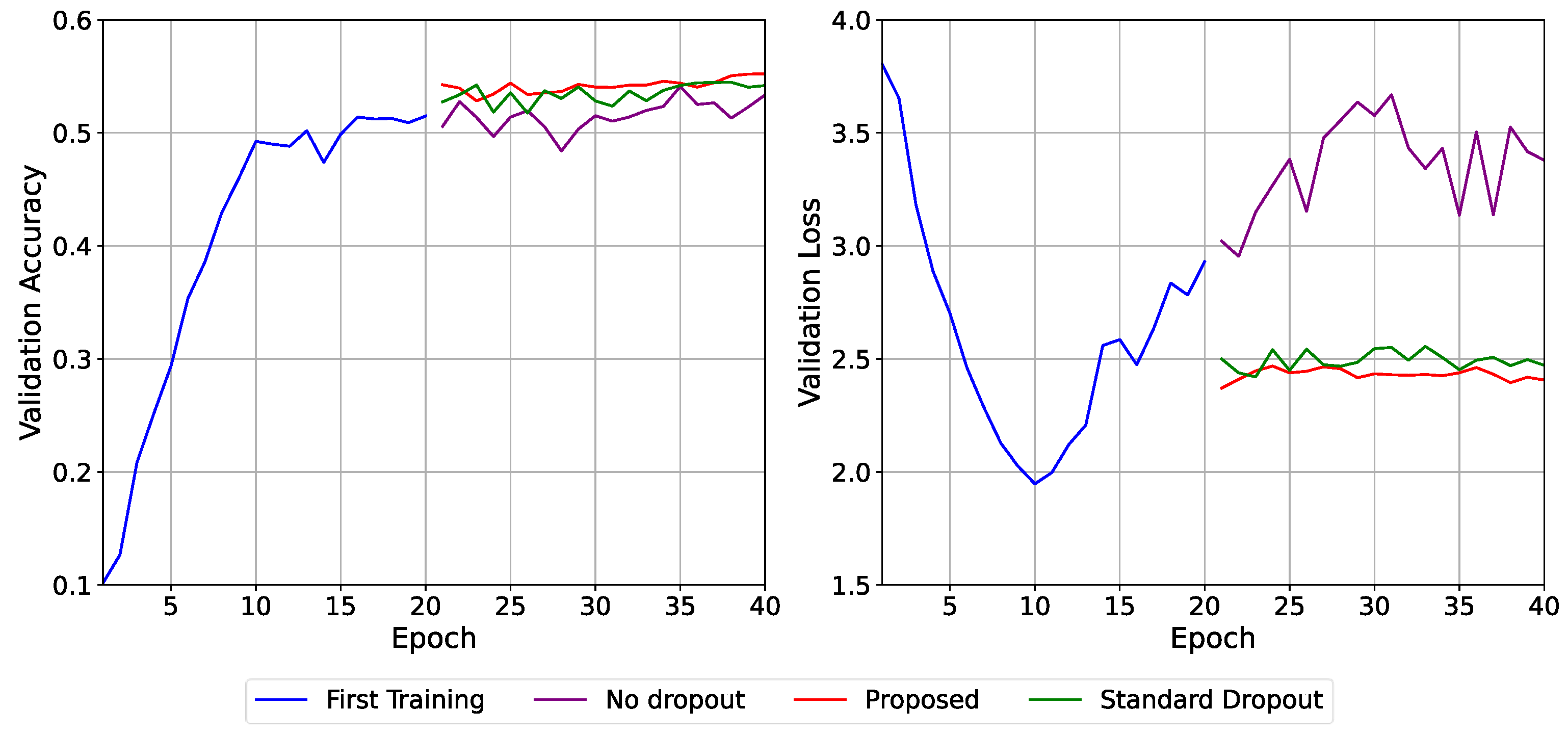
In Figure 4, which used a deeper CNN architecture, the suggested technique obtained a high validation accuracy of 54.4% with a continuously low and steady validation loss of 2.47. The no-dropout baseline obtained a comparable accuracy of 53.75% but suffered from severe overfitting, with validation loss growing to 4.66 by the last epoch. The standard dropout model performed moderately better, reaching 53.87% accuracy and ending with a loss of 2.54. Compared to both alternatives, the proposed method demonstrated better convergence stability, lower loss, and less performance fluctuation, confirming its effectiveness in deeper architectures and its ability to reduce overfitting under complex training conditions.

In Figure 5, a ResNet-inspired architecture with residual blocks is used to test dropout scalability in deeper networks. The proposed method achieved the highest validation accuracy of 55.22%, with a consistently low validation loss of 2.40. In contrast, the baseline model without dropout peaked at 53.36% accuracy and suffered from unstable training, ending with a much higher loss of 3.38. The standard dropout design attained 54.18% accuracy with a final loss of 2.47. These results demonstrate the improved regularization and convergence stability provided by the proposed technique, particularly in deeper and more complex architectural contexts.

To evaluate the consistency and robustness of the suggested dropout method, each of the four CNN models was trained five times under three distinct regularization settings: no dropout, standard dropout, and the proposed method.

Table 4. Mean validation accuracy (±standard deviation) over five runs for each model and methods.

	Model 1	Model 2	Model 3	Model 4
No dropout	0.7772 ± 0.0041	0.5493 ± 0.0043	0.5258 ± 0.0063	0.5214 ± 0.0068
Standard Dropout	0.7852 ± 0.0061	0.5575 ± 0.0032	0.5293 ± 0.0055	0.5397 ± 0.0049
Proposed	0.8002 ± 0.0029	0.5821 ± 0.0034	0.5408 ± 0.0031	0.5490 ± 0.0050

summarizes the mean validation accuracies and accompanying standard deviations across various runs. For instance, in Model 1, the proposed approach produced a mean validation accuracy of 0.8002 ± 0.0029, compared to 0.7852 ± 0.0061 with traditional dropout and 0.7772 ± 0.0041 with no dropout. Similar patterns were obtained in the more complex Model 4, where the proposed technique attained 0.5490 ± 0.0050, significantly outperforming conventional dropout (0.5397 ± 0.0049) and no dropout (0.5214 ± 0.0068). These results reveal that the suggested technique not only enhances generalization performance but also exhibits lower variance over repeated runs, emphasizing its training stability and reliability.

To assess the computational overhead of the proposed method, we compared training durations for Models 2 and 4 using standard dropout and the proposed method. For Model 2, the proposed method completed training approximately 11.6% faster than standard dropout over 20 epochs. Conversely, Model 4, which is a deeper ResNet-based architecture, experienced a roughly 23.3% increase in training time when using the proposed method.

Despite the additional training time in deeper models, the proposed method consistently achieved higher validation accuracy and faster convergence in earlier epochs. This suggests that the performance gains justify the computational cost, particularly in complex architectures where effective regularization has a greater impact.

To further evaluate the effectiveness of the proposed method, an additional experiment was run using the same dataset and network configuration described in a recent study by Avgerinos et al. (the Trainable Gradient Dropout technique) [11]. In this repeat study, the baseline network was trained without utilizing any dropout mechanism. Under these conditions, the model reached a peak validation accuracy of 73.11%, which aligns closely with the results presented in the original study.

Using the identical network structure and dataset, the proposed dropout method was then performed. Remarkably, it achieved a validation accuracy of 74.48% within just 6 epochs, showing significantly faster convergence. Continued training led to a significant gain in performance, reaching 75.09% at epoch 63. These results show the better generalization and training effectiveness of the suggested approach compared to both the dropout-free baseline and the method given by Avgerinos et al. [11].

5. Conclusions

In this study, a novel regularization framework was introduced to enhance the generalization capability of deep neural networks by addressing key limitations of standard dropout. The suggested method combines a flexible dropout system that adjusts based on how active neurons are, how weights are spread out, and their historical activity, together with a strategy to boost critical weights, to help the network learn better and minimize overfitting.

Unlike classic dropout, the adaptive method selectively deactivates neurons based on their relevance and adds a “neuron recovery” step to restore valuable activations. The weight amplification component focuses training on high-magnitude parameters, increasing learning in crucial parts of the network.

Extensive experiments conducted on the CIFAR-10 and CIFAR-100 datasets across four different CNN architectures demonstrated the superiority of the proposed method. In all situations, it achieved higher validation accuracy and reduced validation loss relative to both the no-dropout baseline and conventional dropout. Notably, the approach always maintained consistent convergence, even in deeper architectures.

These results show that the combination of adaptive dropout, dynamic temperature scaling, neuron recovery, and weight amplification gives a more successful regularization technique.

Although the current study focuses on testing the suggested dropout strategy within convolutional neural networks (CNNs) for image classification tasks, its basic principles are broadly applicable. The architecture-agnostic nature and integrative flexibility of the method make it a strong option for extending to other domains such as natural language processing (NLP), time series forecasting, and reinforcement learning. Future research will investigate the method’s performance in these domains by adapting it to recursive and transformer-based structures, allowing for broader use in deep learning applications.