A Resilience Quantitative Assessment Framework for Cyber–Physical Systems: Mathematical Modeling and Simulation
Abstract
1. Introduction
- We develop a diversity-redundancy security architecture tailored to CPSs, incorporating heterogeneous execution units, voting mechanisms, fault isolation, and dynamic recovery. A Markov process model captures probabilistic transitions among cyber states—operational, degraded, detectable failure, and undetectable failure—under persistent threats.
- We formulate a dynamic model that describes the system’s functional evolution in response to cyber disturbances. This model quantifies resilience metrics such as degradation rate, recovery capacity, and long-term steady-state behavior.
- We introduce a segmentation-weighted coupling method that aligns cyber-state sequences with corresponding physical performance phases. By weighting these segments according to their duration and stationary probabilities, the framework supports consistent and interpretable resilience evaluation.
- A case study involving an ICS demonstrates the framework’s effectiveness in comparing design alternatives and identifying critical resilience parameters.
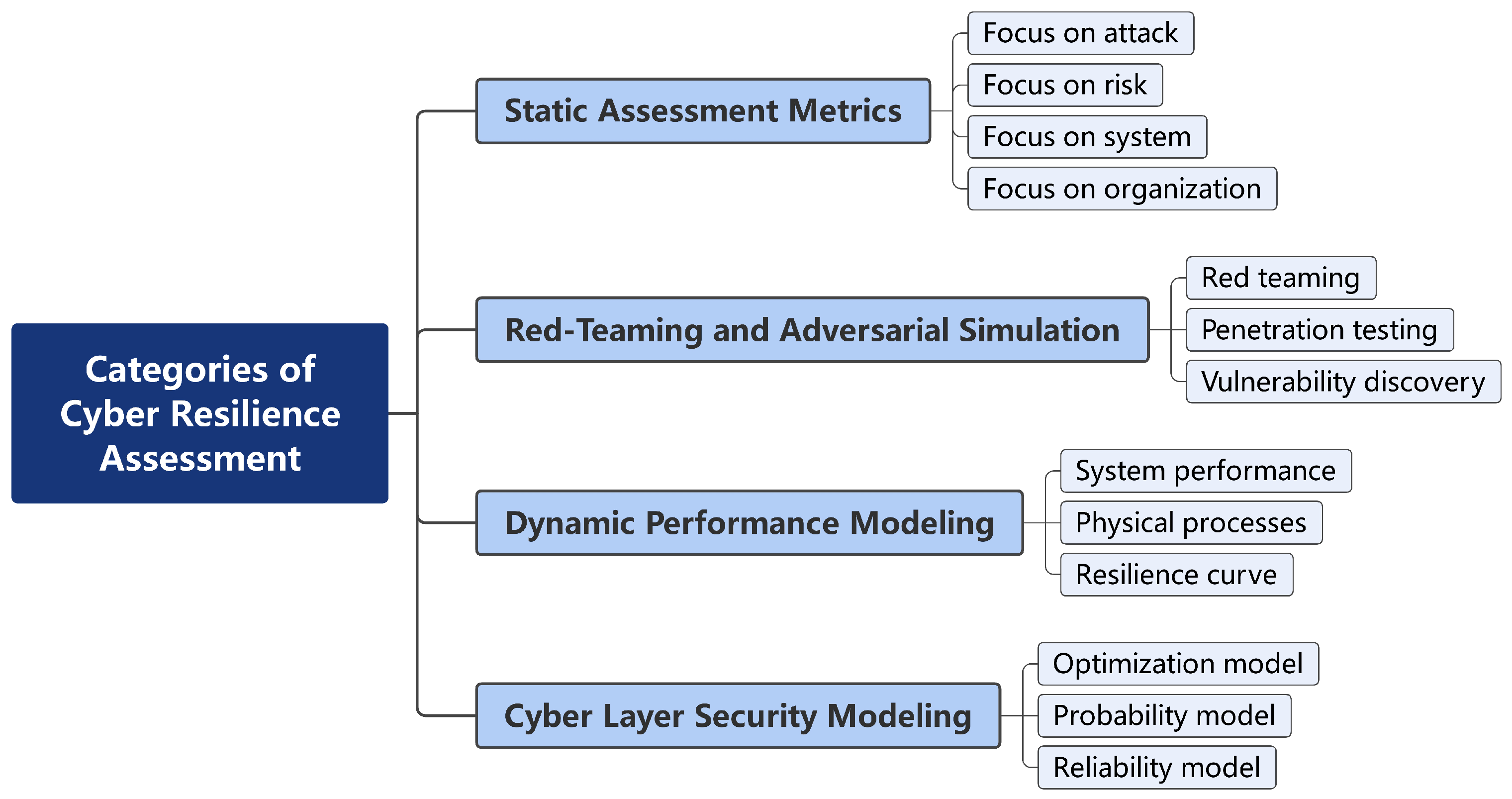
2. Related Work
2.1. Static Assessment Metrics
2.2. Red-Teaming and Adversarial Simulation
2.3. Dynamic Performance Modeling
2.4. Cyber-Layer Security Modeling
3. CPS Resilience Quantitative Assessment Framework
3.1. Quantitative Assessment Framework for Cyber–Physical Coupling
- Physical domain modeling: This component mathematically represents system performance degradation and recovery, reflecting real-time resilience behavior in response to disruptions.
- Cyber-layer modeling: This component uses a Markov-based stochastic process to capture the impact of cyber attacks and evaluate the effectiveness of heterogeneous redundancy strategies.
3.2. Physical Domain: System Performance Modeling
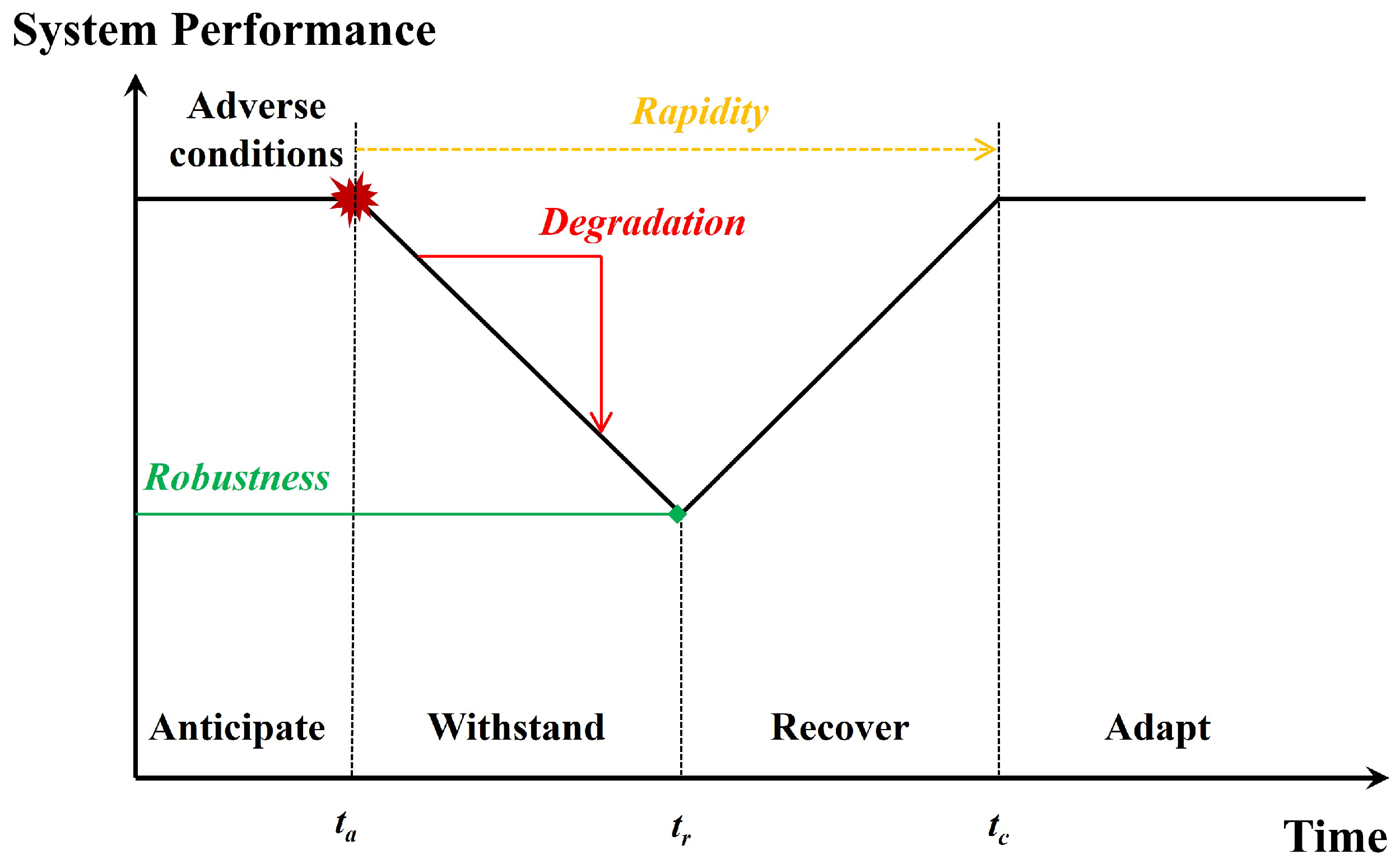
3.2.1. Performance Curve and Resilience Stages
- Prevention Stage: The system operates under normal conditions, employing measures such as intrusion detection, anomaly monitoring, and system hardening to maintain stable performance and minimize exposure to threats.
- Withstanding Stage: Under adverse conditions, performance begins to degrade. The system’s ability to maintain partial functionality during this phase reflects its robustness and fault tolerance.
- Recovery Stage: Following the disruption, the system engages recovery mechanisms—such as redundancy activation, reconfiguration, or manual intervention—to restore performance. The speed and efficiency of this process are key resilience indicators.
- Adaptation Stage: The system adjusts to the new environment by updating configurations, learning from the incident, or strengthening defenses. This adaptive capacity supports long-term resilience enhancement.
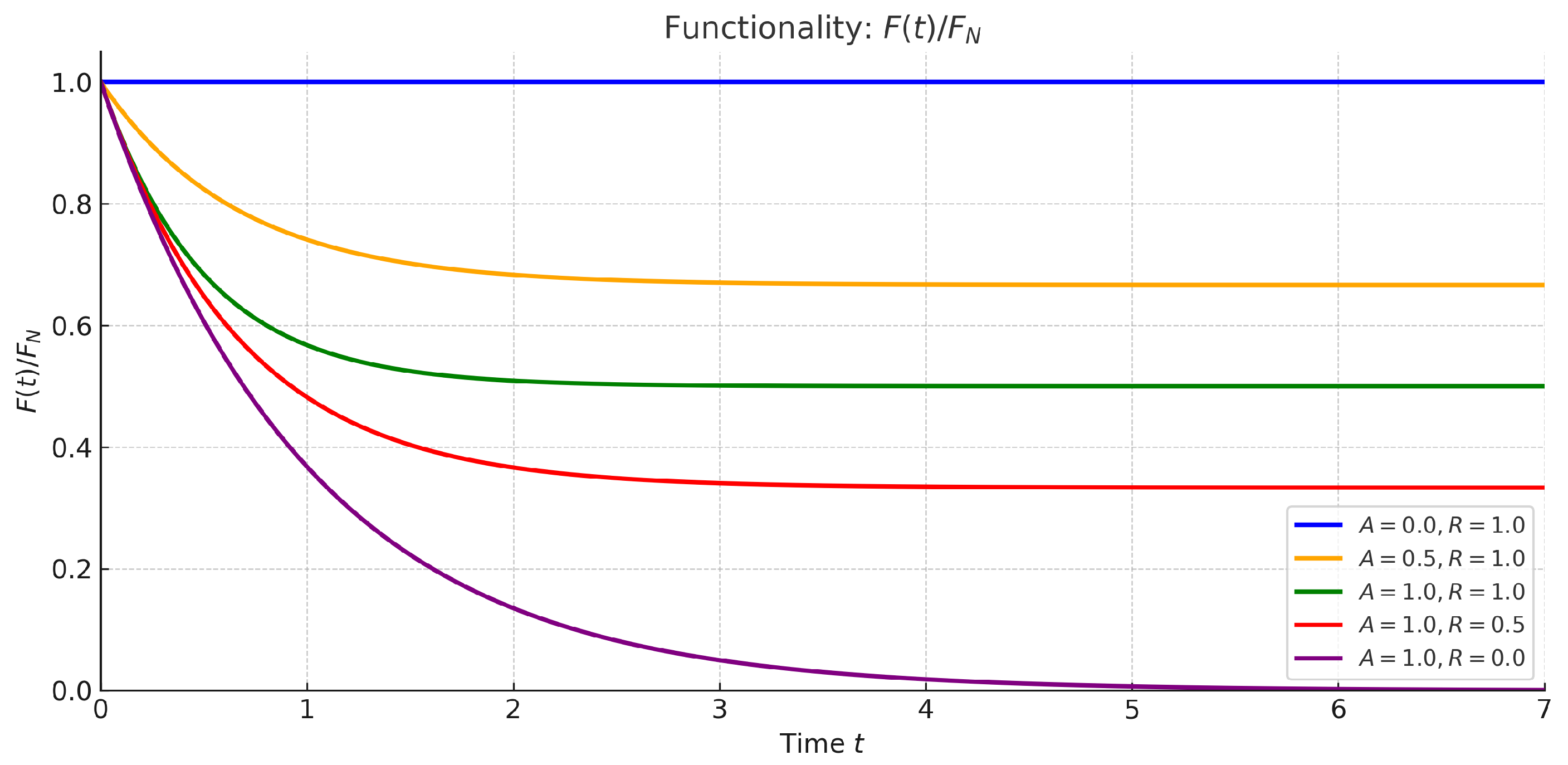
3.2.2. CPS Resilience Mathematical Modeling
- A.
- Constant-coefficient model
- B.
- Piecewise constant-coefficient model
- C.
- Linear (or piecewise linear) coefficient model
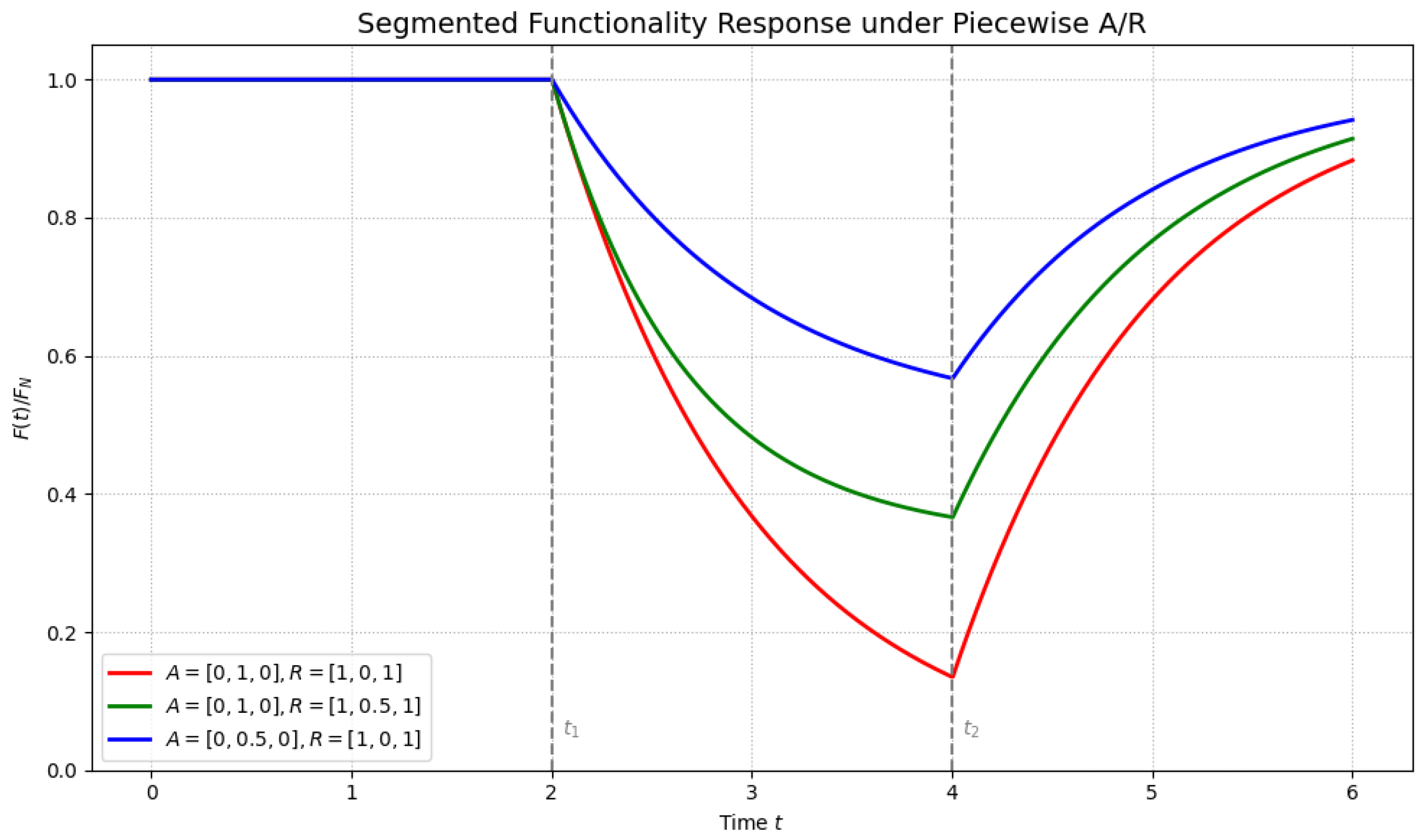
3.2.3. Extension to Time-Varying Dynamics and Physical Interpretations
3.3. Cyber Layer: Security Architecture and Modeling
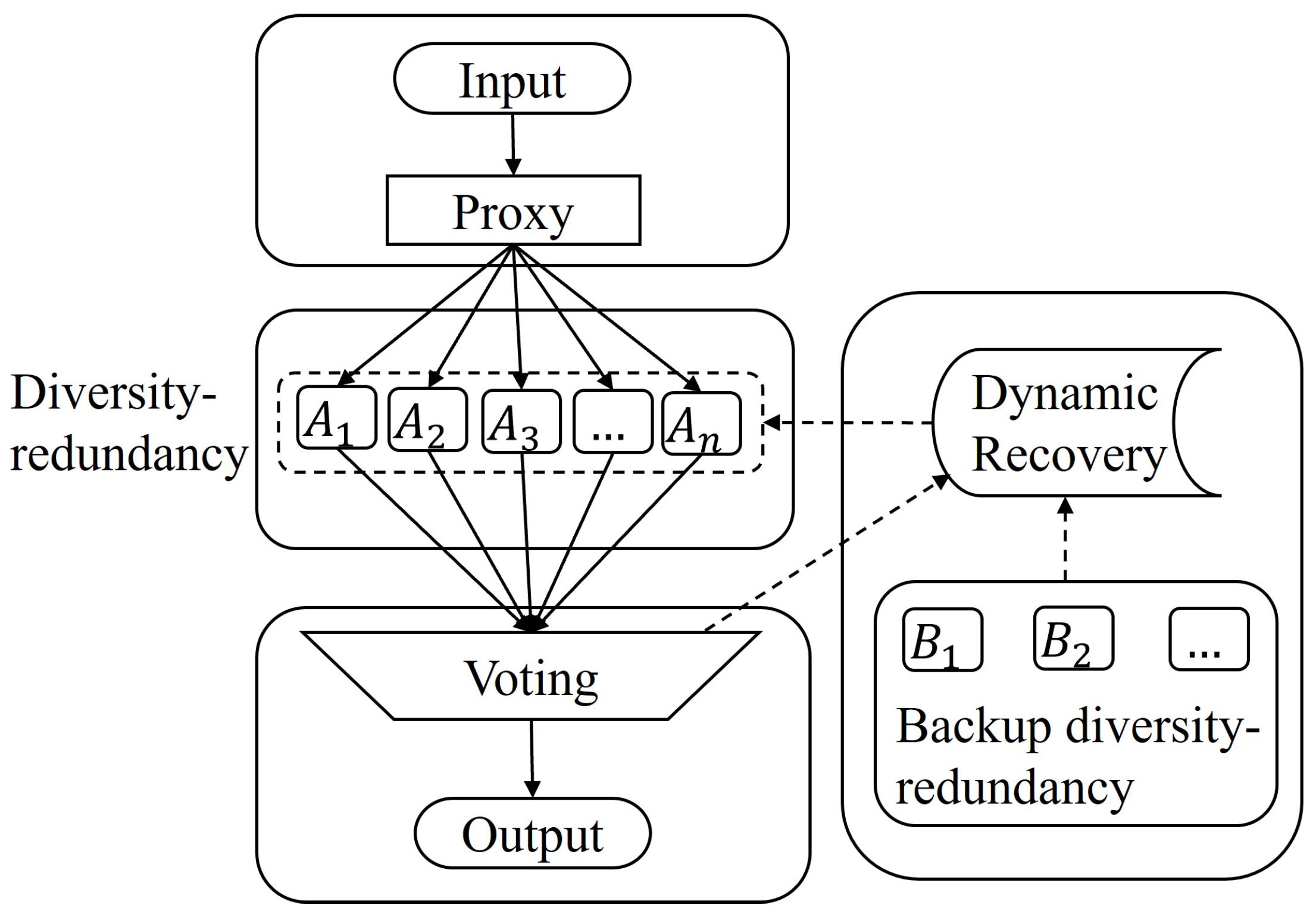
3.3.1. Diversity-Redundancy Security Architecture
- Diverse Redundancy: Multiple redundant units are deployed using heterogeneous implementations (e.g., different hardware platforms, operating systems, or control logic), minimizing the risk of simultaneous compromise due to shared vulnerabilities.
- Voting Awareness: A runtime majority voting mechanism monitors the output consistency of redundant units. Discrepancies are used as indicators of possible compromise or malfunction, serving as an early warning mechanism.
- Fault Isolation and Failover: Upon detection of abnormal behavior, the compromised node is automatically isolated. Control responsibilities are seamlessly handed over to a healthy redundant unit, ensuring uninterrupted operation.
- Dynamic Recovery: The isolated node enters a secure recovery mode, where it is re-initialized using trusted baseline images or reconfigured through remote attestation and software refresh, before being reintegrated into the redundant pool.
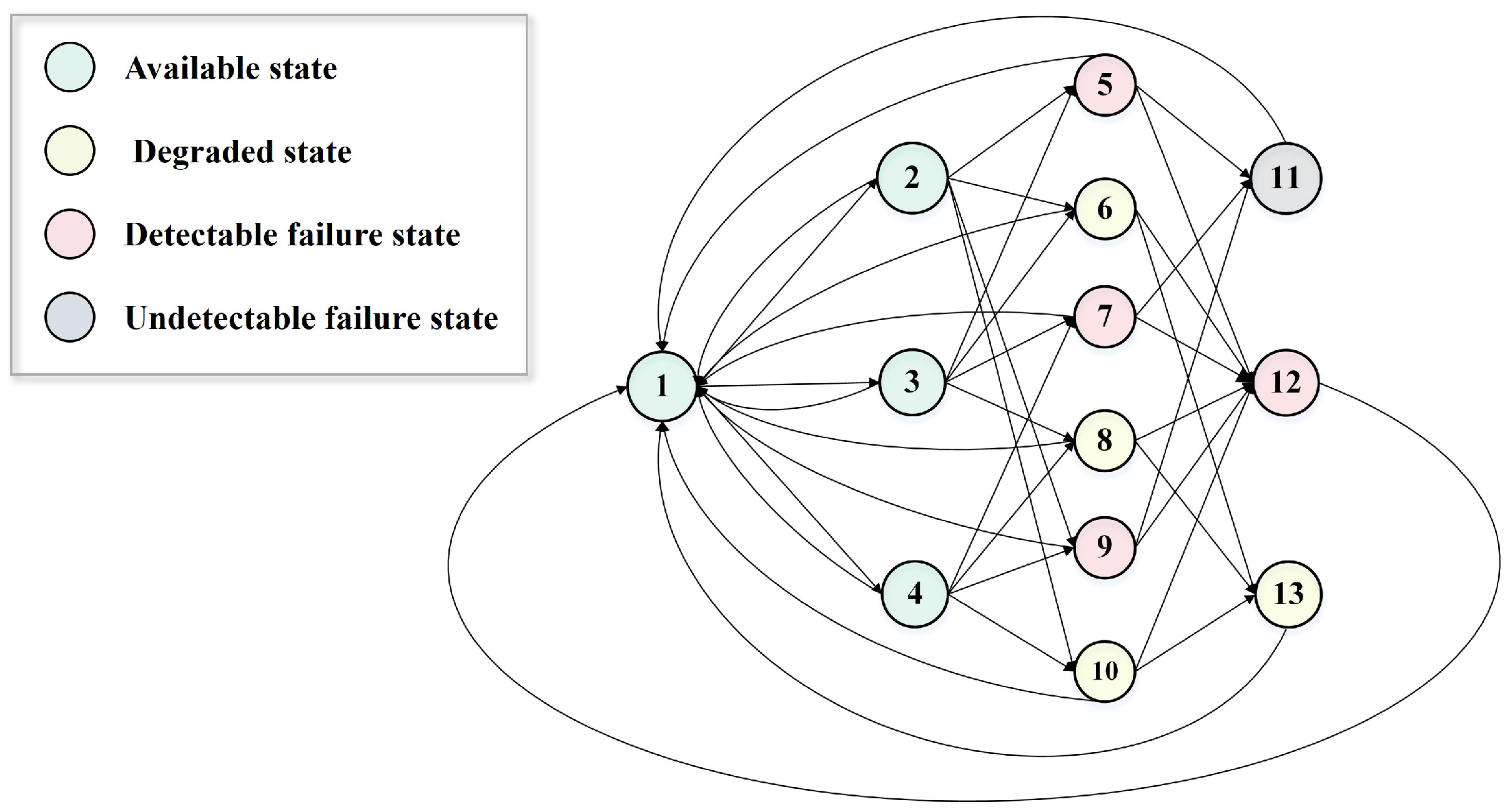
3.3.2. Markov Process Modeling
- Available state: The majority of execution units are functioning correctly.
- Degraded state: The majority of execution units have failed, and their outputs are inconsistent.
- Detectable failure state: The majority of units have failed, but their outputs are consistent, allowing detection.
- Undetectable failure state: All execution units have failed and generate identical (erroneous) outputs, leading to a silent failure.
- States 1–4 represent system availability.
- States 5, 7, 9, 12, and 13 represent detectable failures.
- States 6, 8, and 10 correspond to degraded but observable states.
- State 11 denotes the undetectable failure (stealthy failure) state.
- : Failure rate of the i-th execution unit due to cyber attack-induced disruption.
- : Mean time to recovery when one unit fails with abnormal output.
- : Recovery rate when two units fail with consistent abnormal output vectors (which may include functional outputs, alerts, performance metrics, etc.).
- : Recovery rate when all three units fail and produce identical abnormal outputs—indicating an undetectable, stealthy failure.
- : Recovery rate when all three units fail but their outputs are mutually inconsistent—resulting in an observable degraded state.
- : The uncertainty coefficient that quantifies the likelihood of abnormal output consistency among failed execution units. It reflects how often two faulty nodes produce the same incorrect output vector under adverse conditions.
3.4. Integrated CPS Modeling Strategy and Comparative Advantages
3.4.1. Normalization and Parameterization
- Available states: , representing effective control and recovery.
- Degraded states: These states reflect abnormal but recognizable behavior. Accordingly, and are assigned comparable moderate values, reflecting a balance between degradation and the system’s ability to respond.
- Failure states: ; when the system is in undetectable failure state, take , as the system is unaware of the anomaly and thus cannot initiate recovery.
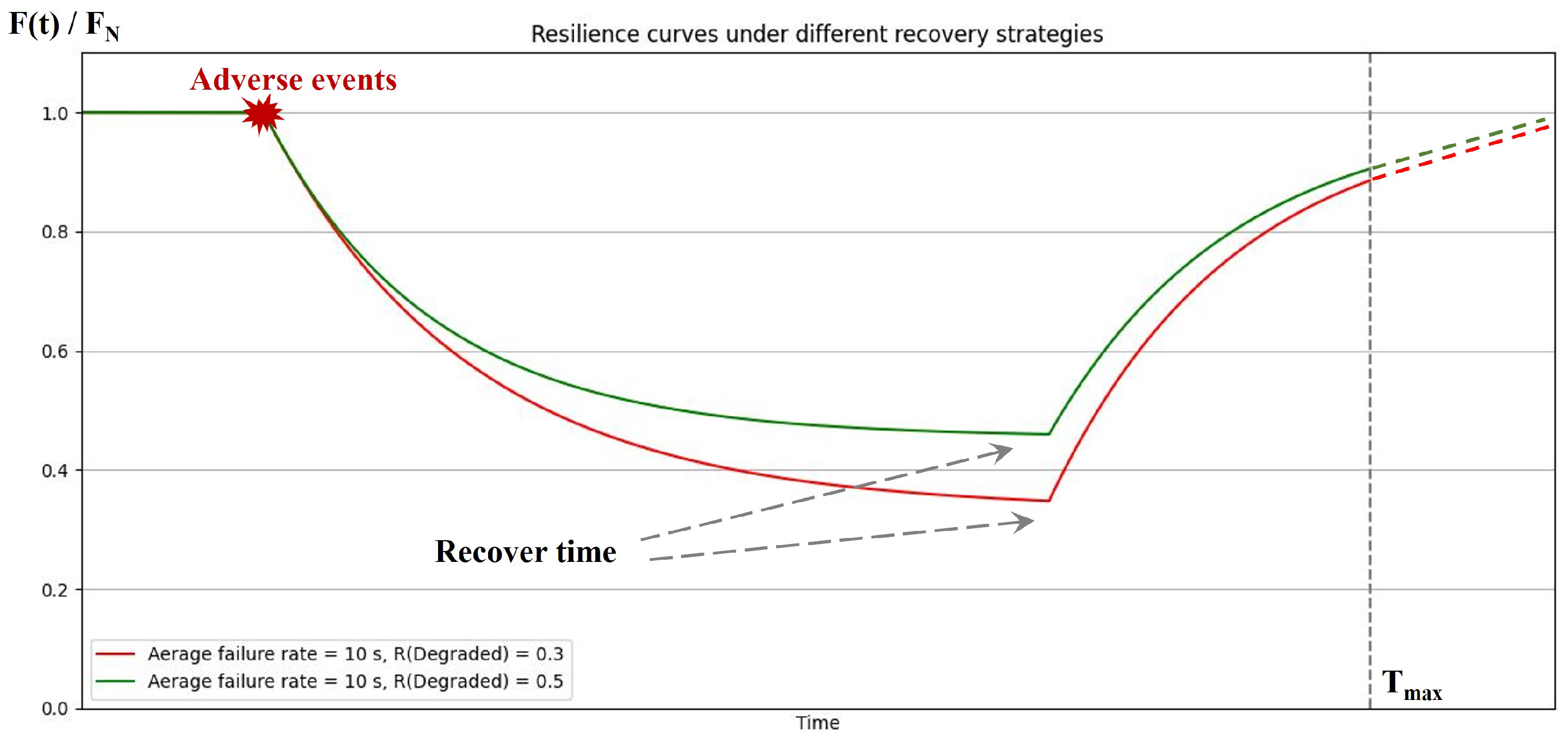
3.4.2. Integrated Benchmarking Process
- Step 1: CTMC parameter settings
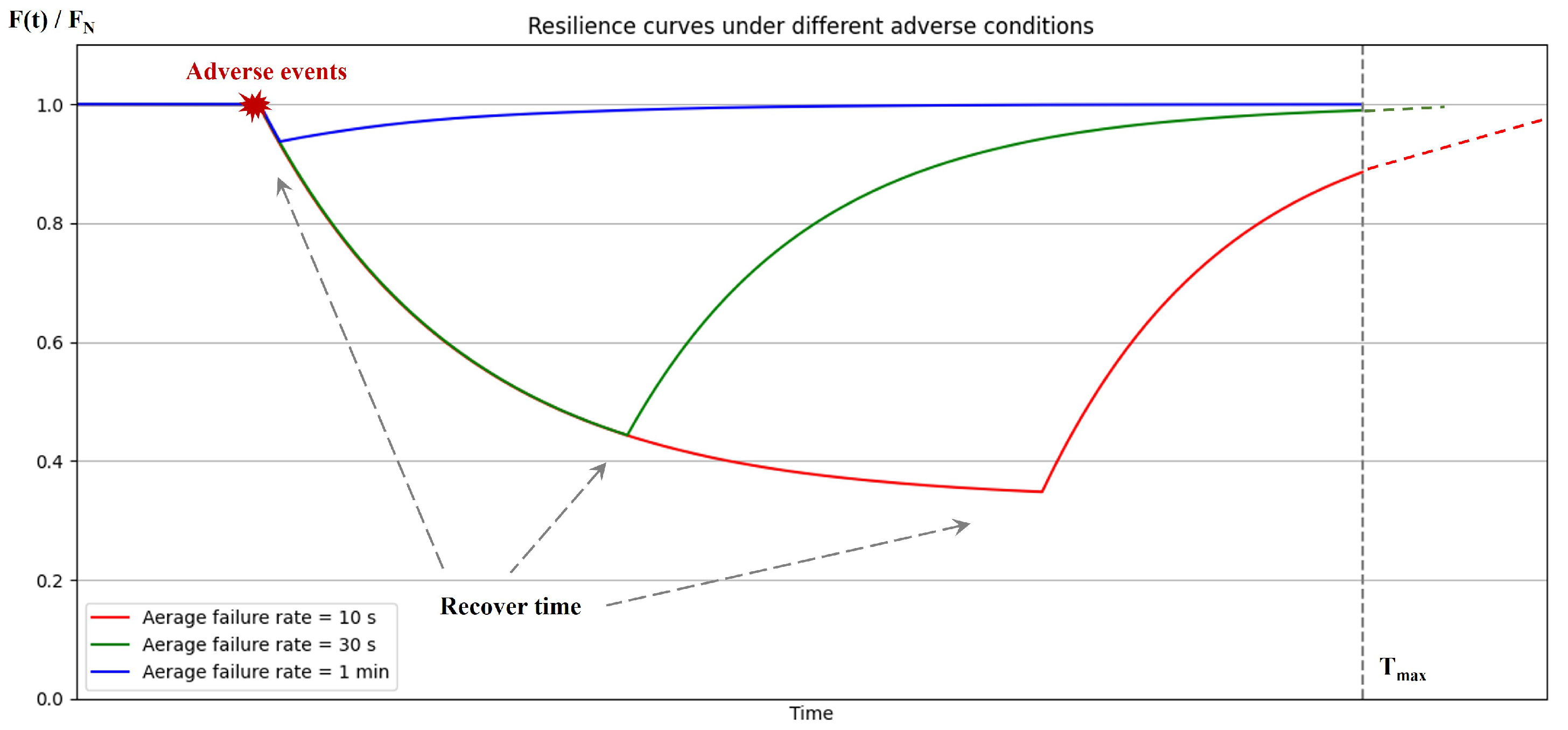
- Step 2: CTMC simulation under different conditions
- Step 3: Standardization of model coupling parameters
- Step 4: Resilience curve display
3.4.3. Comparison with Existing Frameworks
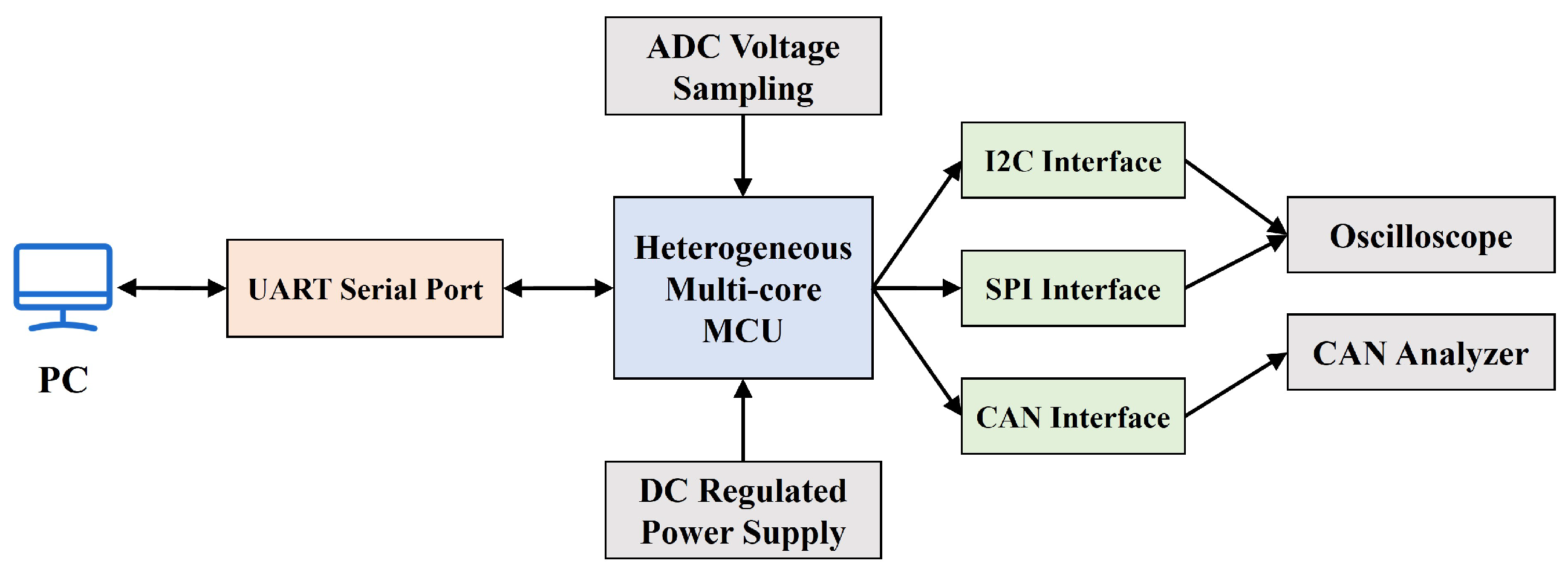
4. Case Study of Industrial Control Systems
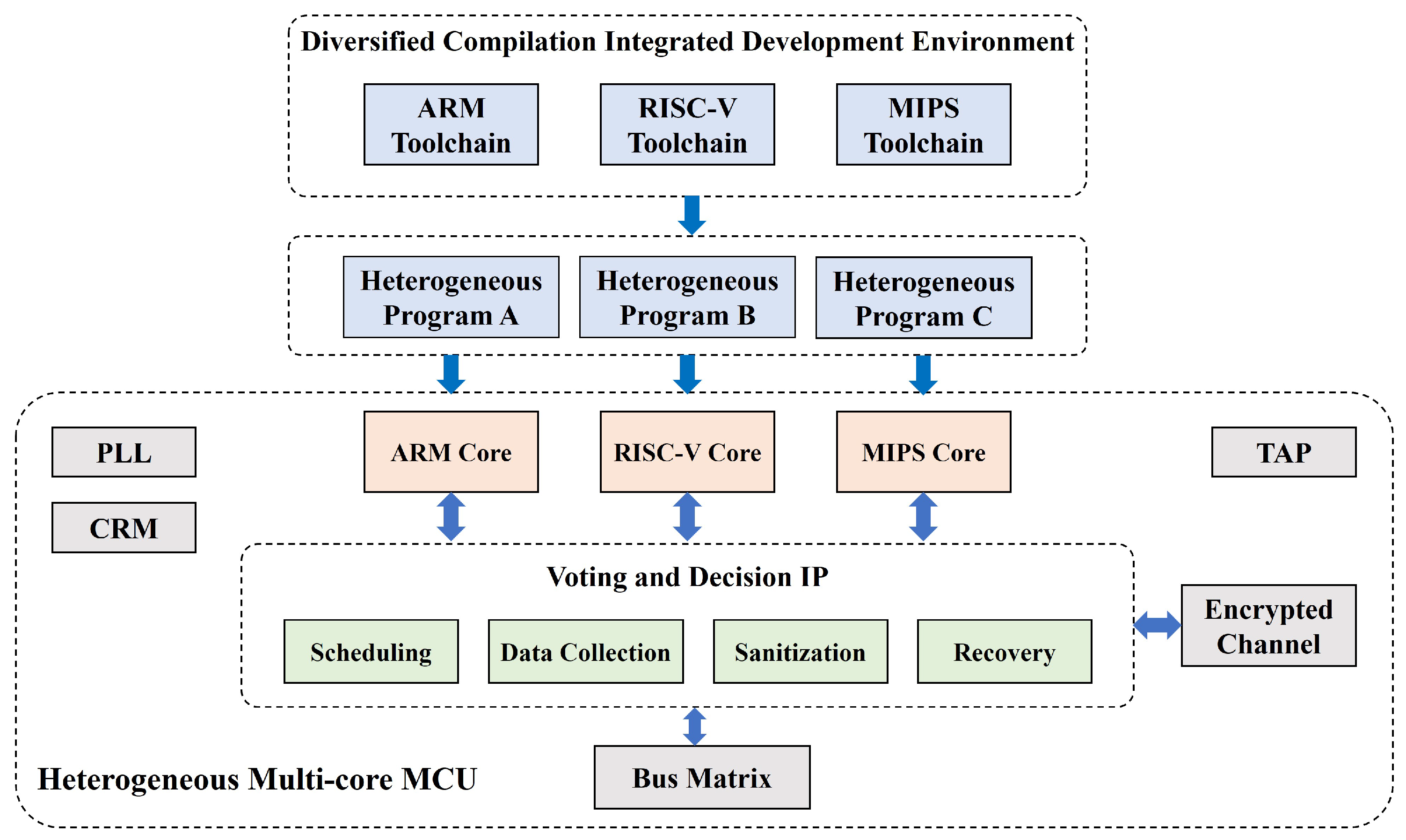
4.1. Application Scenarios and Security Design Implementation
- Trade-offs between performance overhead and security effectiveness in real-time control environments;
- The complexity of coordinating heterogeneous components to achieve fault tolerance and attack resistance;
- Lack of quantitative methods to evaluate how architectural diversity and redundancy translate into resilience benefits under dynamic cyber–physical conditions.
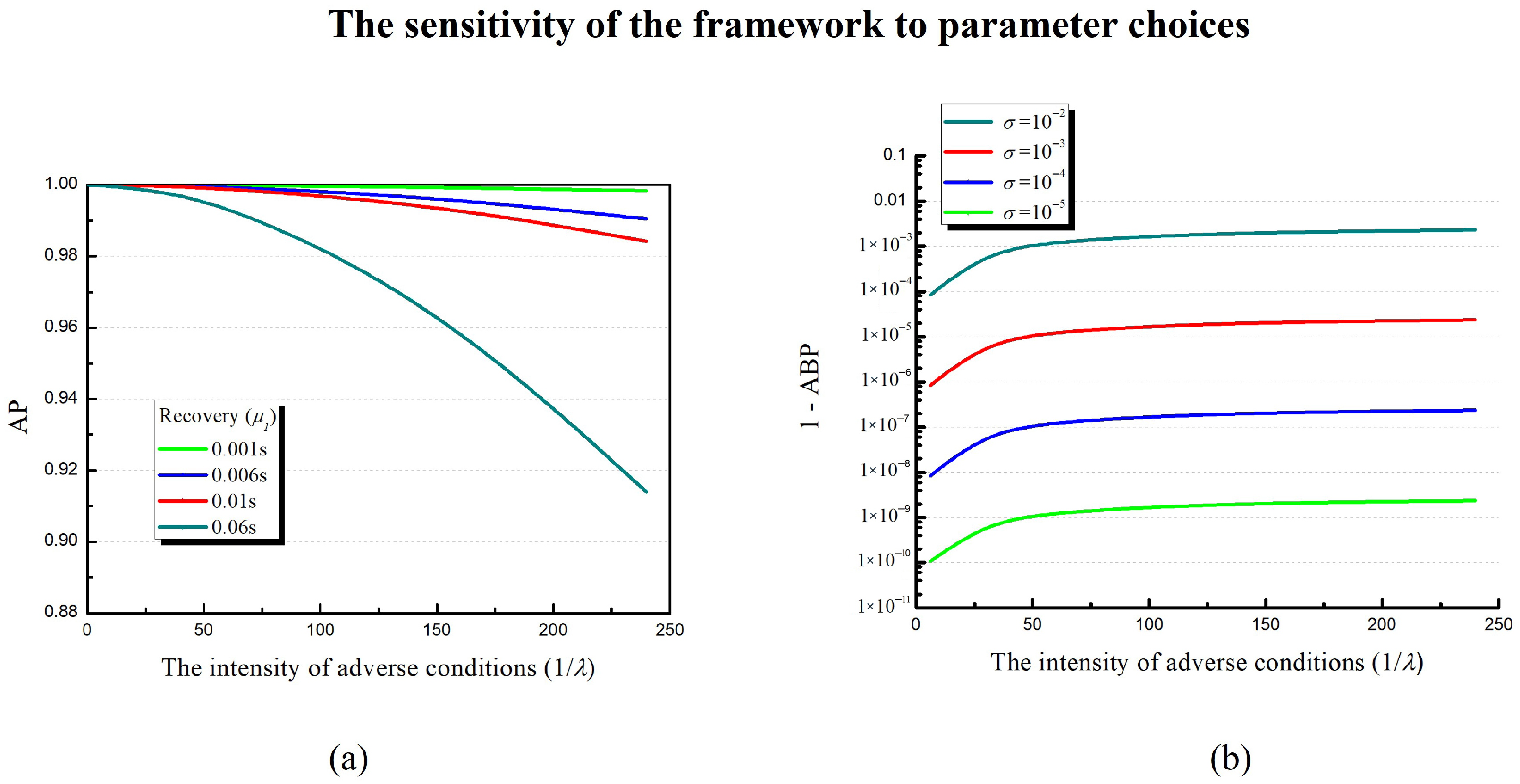
4.2. Modeling and Simulation Results
4.3. Design Optimization and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Almulhim, A.I. Building Urban Resilience Through Smart City Planning: A Systematic Literature Review. Smart Cities (2624-6511) 2025, 8, 22. [Google Scholar] [CrossRef]
- Alhidaifi, S.M.; Asghar, M.R.; Ansari, I.S. A survey on cyber resilience: Key strategies, research challenges, and future directions. ACM Comput. Surv. 2024, 56, 1–48. [Google Scholar] [CrossRef]
- Lee, H.; Kim, S.; Kim, H.K. SoK: Demystifying cyber resilience quantification in cyber-physical systems. In Proceedings of the 2022 IEEE International Conference on Cyber Security and Resilience (CSR), Rhodes, Greece, 27–29 July 2022; pp. 178–183. [Google Scholar]
- Dibaji, S.M.; Pirani, M.; Flamholz, D.B.; Annaswamy, A.M.; Johansson, K.H.; Chakrabortty, A. A systems and control perspective of CPS security. Annu. Rev. Control 2019, 47, 394–411. [Google Scholar] [CrossRef]
- Rus, K.; Kilar, V.; Koren, D. Resilience assessment of complex urban systems to natural disasters: A new literature review. Int. J. Disaster Risk Reduct. 2018, 31, 311–330. [Google Scholar] [CrossRef]
- Gasser, P.; Lustenberger, P.; Cinelli, M.; Kim, W.; Spada, M.; Burgherr, P.; Hirschberg, S.; Stojadinovic, B.; Sun, T.Y. A review on resilience assessment of energy systems. Sustain. Resilient Infrastruct. 2021, 6, 273–299. [Google Scholar] [CrossRef]
- Segovia-Ferreira, M.; Rubio-Hernan, J.; Cavalli, A.; Garcia-Alfaro, J. A survey on cyber-resilience approaches for cyber-physical systems. ACM Comput. Surv. 2024, 56, 1–37. [Google Scholar] [CrossRef]
- Linkov, I.; Fox-Lent, C.; Read, L.; Allen, C.R.; Arnott, J.C.; Bellini, E.; Coaffee, J.; Florin, M.V.; Hatfield, K.; Hyde, I.; et al. Tiered approach to resilience assessment. Risk Anal. 2018, 38, 1772–1780. [Google Scholar] [CrossRef]
- Koh, S.L.; Suresh, K.; Ralph, P.; Saccone, M. Quantifying organisational resilience: An integrated resource efficiency view. Int. J. Prod. Res. 2024, 62, 5737–5756. [Google Scholar] [CrossRef]
- Ross, R.; Pillitteri, V.; Graubart, R.; Bodeau, D.; McQuaid, R. Developing Cyber-Resilient Systems: A Systems Security Engineering Approach; Technical report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2021. [Google Scholar] [CrossRef]
- Bodeau, D.J.; Graubart, R.D.; McQuaid, R.M.; Woodill, J. Cyber Resiliency Metrics Catalog; The MITRE Corporation: Bedford, MA, USA, 2018. [Google Scholar]
- Bodeau, D.J.; Graubart, R.D.; McQuaid, R.M.; Woodill, J. Cyber Resiliency Metrics, Measures of Effectiveness, and Scoring; The MITRE Corporation: Bedford, MA, USA, 2018. [Google Scholar]
- Stouffer, K.; Stouffer, K.; Pease, M.; Tang, C.; Zimmerman, T.; Pillitteri, V.; Lightman, S.; Hahn, A.; Saravia, S.; Sherule, A.; et al. Guide to Operational Technology (OT) Security; Technical report; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023. [Google Scholar]
- White, G.B.; Sjelin, N. The NIST Cybersecurity Framework (CSF) 2.0; Technical report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024. [Google Scholar]
- Juma, A.H.; Arman, A.A.; Hidayat, F. Cybersecurity assessment framework: A systematic review. In Proceedings of the 2023 10th International Conference on ICT for Smart Society (ICISS), Bandung, Indonesia, 6–7 September 2023; pp. 1–6. [Google Scholar]
- Vandezande, N. Cybersecurity in the EU: How the NIS2-directive stacks up against its predecessor. Comput. Law Secur. Rev. 2024, 52, 105890. [Google Scholar] [CrossRef]
- Wu, J. Cyber Resilience System Engineering Empowered by Endogenous Security and Safety; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Abbass, H.; Bender, A.; Gaidow, S.; Whitbread, P. Computational red teaming: Past, present and future. IEEE Comput. Intell. Mag. 2011, 6, 30–42. [Google Scholar] [CrossRef]
- Yulianto, S.; Soewito, B.; Gaol, F.L.; Kurniawan, A. Metrics and Red Teaming in Cyber Resilience and Effectiveness: A Systematic Literature Review. In Proceedings of the 2023 29th International Conference on Telecommunications (ICT), Toba, Indonesia, 8–9 November 2023; pp. 1–7. [Google Scholar]
- Snyder, D.; Heitzenrater, C. Enhancing Cybersecurity and Cyber Resiliency of Weapon Systems: Expanded Roles Across a System’s Life Cycle; Technical report; RAND Corporation: Santa Monica, CA, USA, 2024. [Google Scholar]
- Strom, B.E.; Applebaum, A.; Miller, D.P.; Nickels, K.C.; Pennington, A.G.; Thomas, C.B. Mitre ATT&CK: Design and Philosophy; Technical Report; The MITRE Corporation: McLean, VA, USA, 2018. [Google Scholar]
- Xiong, T.; Lina, G.; Guifen, Z.; Donghong, Q. A intrusion detection algorithm based on improved slime mould algorithm and weighted extreme learning machine. In Proceedings of the 2021 4th International Conference on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, 28–31 May 2021; pp. 157–161. [Google Scholar]
- Yulianto, S.; Soewito, B.; Gaol, F.L.; Kurniawan, A. Enhancing cybersecurity resilience through advanced red-teaming exercises and MITRE ATT&CK framework integration: A paradigm shift in cybersecurity assessment. Cyber Secur. Appl. 2025, 3, 100077. [Google Scholar]
- Fink, G.A.; Griswold, R.L.; Beech, Z.W. Quantifying cyber-resilience against resource-exhaustion attacks. In Proceedings of the 2014 7th International Symposium on Resilient Control Systems (ISRCS), Denver, CO, USA, 19–21 August 2014; pp. 1–8. [Google Scholar]
- Shin, S.; Lee, S.; Burian, S.J.; Judi, D.R.; McPherson, T. Evaluating resilience of water distribution networks to operational failures from cyber-physical attacks. J. Environ. Eng. 2020, 146, 04020003. [Google Scholar] [CrossRef]
- Kott, A.; Linkov, I. Cyber Resilience of Systems and Networks; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1. [Google Scholar]
- Pawar, B.; Huffman, M.; Khan, F.; Wang, Q. Resilience assessment framework for fast response process systems. Process Saf. Environ. Prot. 2022, 163, 82–93. [Google Scholar] [CrossRef]
- Clark, A.; Zonouz, S. Cyber-physical resilience: Definition and assessment metric. IEEE Trans. Smart Grid 2017, 10, 1671–1684. [Google Scholar] [CrossRef]
- Cassottana, B.; Roomi, M.M.; Mashima, D.; Sansavini, G. Resilience analysis of cyber-physical systems: A review of models and methods. Risk Anal. 2023, 43, 2359–2379. [Google Scholar] [CrossRef]
- AlHidaifi, S.M.; Asghar, M.R.; Ansari, I.S. Towards a cyber resilience quantification framework (CRQF) for IT infrastructure. Comput. Netw. 2024, 247, 110446. [Google Scholar] [CrossRef]
- Cheng, Y.; Elsayed, E.A.; Huang, Z. Systems resilience assessments: A review, framework and metrics. Int. J. Prod. Res. 2022, 60, 595–622. [Google Scholar] [CrossRef]
- Almaleh, A. Measuring resilience in smart infrastructures: A comprehensive review of metrics and methods. Appl. Sci. 2023, 13, 6452. [Google Scholar] [CrossRef]
- Weisman, M.J.; Kott, A.; Ellis, J.E.; Murphy, B.J.; Parker, T.W.; Smith, S.; Vandekerckhove, J. Quantitative measurement of cyber resilience: Modeling and experimentation. ACM Trans. Cyber-Phys. Syst. 2025, 9, 1–25. [Google Scholar] [CrossRef]
- Soikkeli, J.; Casale, G.; Muñoz-González, L.; Lupu, E.C. Redundancy planning for cost efficient resilience to cyber attacks. IEEE Trans. Dependable Secur. Comput. 2022, 20, 1154–1168. [Google Scholar] [CrossRef]
- Orojloo, H.; Abdollahi Azgomi, M. Modelling and evaluation of the security of cyber-physical systems using stochastic Petri nets. IET Cyber-Phys. Syst. Theory Appl. 2019, 4, 50–57. [Google Scholar] [CrossRef]
- Chen, C.; Wu, W.; Zhou, H.; Shen, G. A Semi-Markov Survivability Evaluation Model for Intrusion Tolerant Real-Time Database Systems. In Proceedings of the 2011 7th International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 23–25 September 2011; pp. 1–4. [Google Scholar]
- Kotenko, I.; Saenko, I.; Lauta, O. Analytical modeling and assessment of cyber resilience on the base of stochastic networks conversion. In Proceedings of the 2018 10th International Workshop on Resilient Networks Design and Modeling (RNDM), Longyearbyen, Norway, 27–29 August 2018; pp. 1–8. [Google Scholar]
- Hausken, K.; Welburn, J.W.; Zhuang, J. A Review of Attacker–Defender Games and Cyber Security. Games 2024, 15, 28. [Google Scholar] [CrossRef]
- Caetano, H.O.; Desuó, L.; Fogliatto, M.S.; Maciel, C.D. Resilience assessment of critical infrastructures using dynamic Bayesian networks and evidence propagation. Reliab. Eng. Syst. Saf. 2024, 241, 109691. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, S.; Ma, R.; Liu, M.; Luo, H.; Kaynak, O. Monitoring and defense of industrial cyber-physical systems under typical attacks: From a systems and control perspective. IEEE Trans. Ind. Cyber-Phys. Syst. 2023, 1, 192–207. [Google Scholar] [CrossRef]
- Xing, W.; Shen, J. Security Control of Cyber–Physical Systems under Cyber Attacks: A Survey. Sensors 2024, 24, 3815. [Google Scholar] [CrossRef] [PubMed]
- Weisman, M.J.; Kott, A.; Vandekerckhove, J. Piecewise linear and stochastic models for the analysis of cyber resilience. In Proceedings of the 2023 57th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2023; pp. 1–6. [Google Scholar]
- Garcia, M.; Bessani, A.; Gashi, I.; Neves, N.; Obelheiro, R. Analysis of operating system diversity for intrusion tolerance. Softw. Pract. Exp. 2014, 44, 735–770. [Google Scholar] [CrossRef]
- Khan, M.; Babay, A. Making intrusion tolerance accessible: A cloud-based hybrid management approach to deploying resilient systems. In Proceedings of the 2023 42nd International Symposium on Reliable Distributed Systems (SRDS), Marrakesh, Morocco, 25–29 September 2023; pp. 254–267. [Google Scholar]
- Shoker, A.; Rahli, V.; Decouchant, J.; Esteves-Verissimo, P. Intrusion resilience systems for modern vehicles. In Proceedings of the 2023 IEEE 97th Vehicular Technology Conference (VTC2023-Spring), Florence, Italy, 20–23 June 2023; pp. 1–7. [Google Scholar]



| State | |||||||
| 0 | 0 | ||||||
| 0 | 0 | ||||||
| 0 | 0 | ||||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| State | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 |
| Evaluation Dimension | Static Assessment Metrics | Red-Teaming and Adversarial Simulation | Dynamic Performance Modeling | Cyber-Layer Security Modeling | Proposed Framework |
|---|---|---|---|---|---|
| Integrity | ✓ | △ | × | △ | ✓ |
| Availability | × | ✓ | △ | ✓ | ✓ |
| Performance Curve | × | × | ✓ | × | ✓ |
| Cyber–Physical Coupling | △ | △ | △ | × | ✓ |
| Feedback for Design | △ | × | × | △ | ✓ |
| Modeling Scalability | × | × | △ | ✓ | ✓ |
| Parameters | Assignment Methods | Values |
|---|---|---|
| White-box fault injection test | 0.1 s | |
| White-box fault injection test | 3 min | |
| White-box fault injection test | 60 min | |
| White-box fault injection test | 1 min | |
| Historical information evaluation |
| Adverse Conditions | Metrics | Values |
|---|---|---|
| λ = 10 s | AP | 0.7436 |
| EP | 0.0021 | |
| DP | 0.2543 | |
| λ = 30 s | AP | 0.9189 |
| EP | 6.09 × 10−4 | |
| DP | 0.0805 | |
| λ = 1 min | AP | 0.9901 |
| EP | 5.93 × 10−5 | |
| DP | 0.0098 |
| Resilience States | Parameters | Values |
|---|---|---|
| Undetectable failure | A | 1 |
| R | 0 | |
| Detectable failure | A | 0.8 |
| R | 0.1 | |
| Degraded | A | 0.6 |
| R | 0.3 | |
| Available | A | 0 |
| R | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Zhao, H.; Wang, Y.; He, C.; Zhou, D.; Han, X. A Resilience Quantitative Assessment Framework for Cyber–Physical Systems: Mathematical Modeling and Simulation. Appl. Sci. 2025, 15, 8285. https://doi.org/10.3390/app15158285
Cao Z, Zhao H, Wang Y, He C, Zhou D, Han X. A Resilience Quantitative Assessment Framework for Cyber–Physical Systems: Mathematical Modeling and Simulation. Applied Sciences. 2025; 15(15):8285. https://doi.org/10.3390/app15158285
Chicago/Turabian StyleCao, Zhigang, Hantao Zhao, Yunfan Wang, Chuan He, Ding Zhou, and Xiaopeng Han. 2025. "A Resilience Quantitative Assessment Framework for Cyber–Physical Systems: Mathematical Modeling and Simulation" Applied Sciences 15, no. 15: 8285. https://doi.org/10.3390/app15158285
APA StyleCao, Z., Zhao, H., Wang, Y., He, C., Zhou, D., & Han, X. (2025). A Resilience Quantitative Assessment Framework for Cyber–Physical Systems: Mathematical Modeling and Simulation. Applied Sciences, 15(15), 8285. https://doi.org/10.3390/app15158285






