Modeling of Dry Clutch Wear for a Wide Range of Operating Parameters
Abstract
1. Introduction
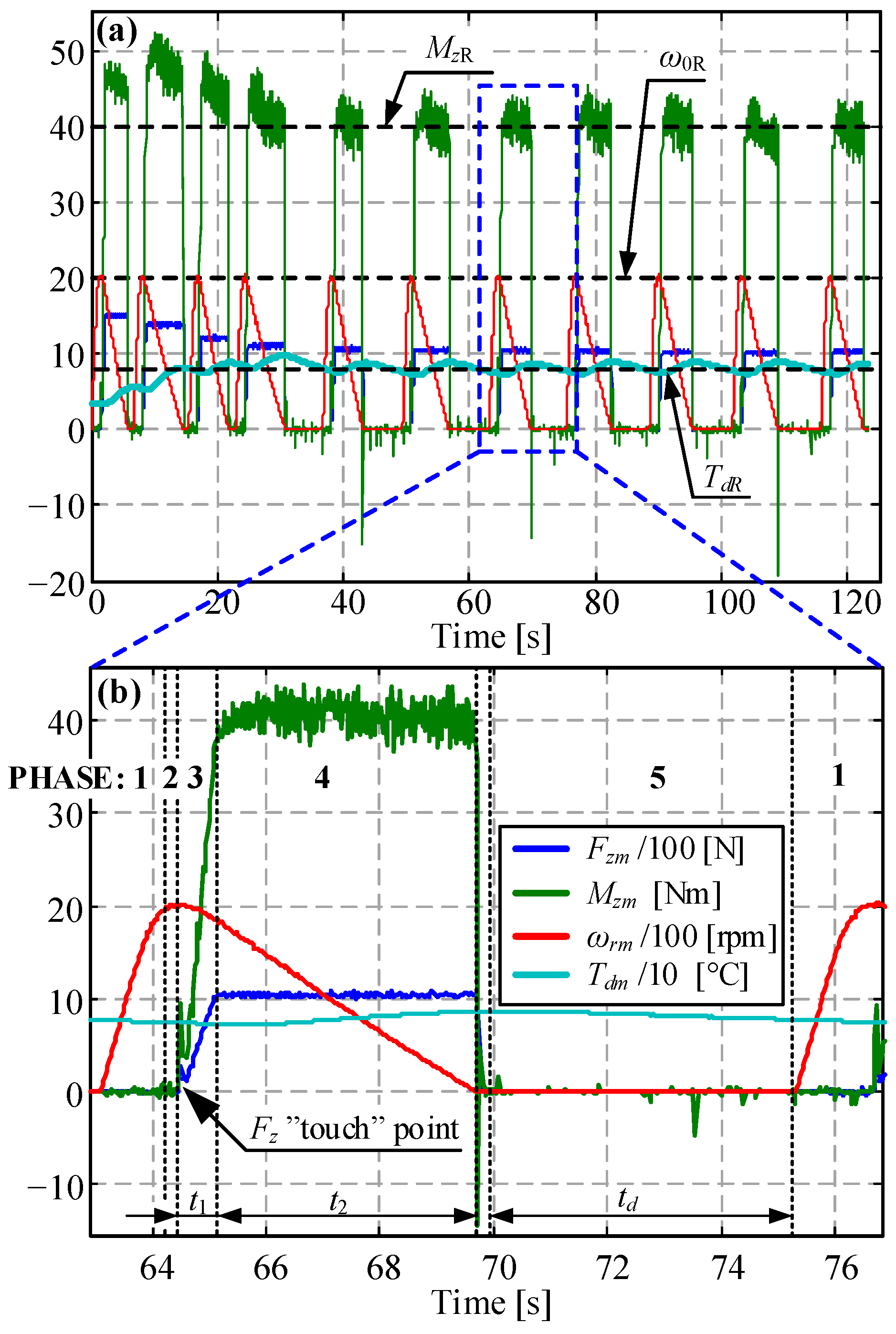
2. Experimental Setup
2.1. Mechanical Subsystem
2.2. Control Subsystem
3. Design of Wear Characterization Experiments
3.1. Static Experiments
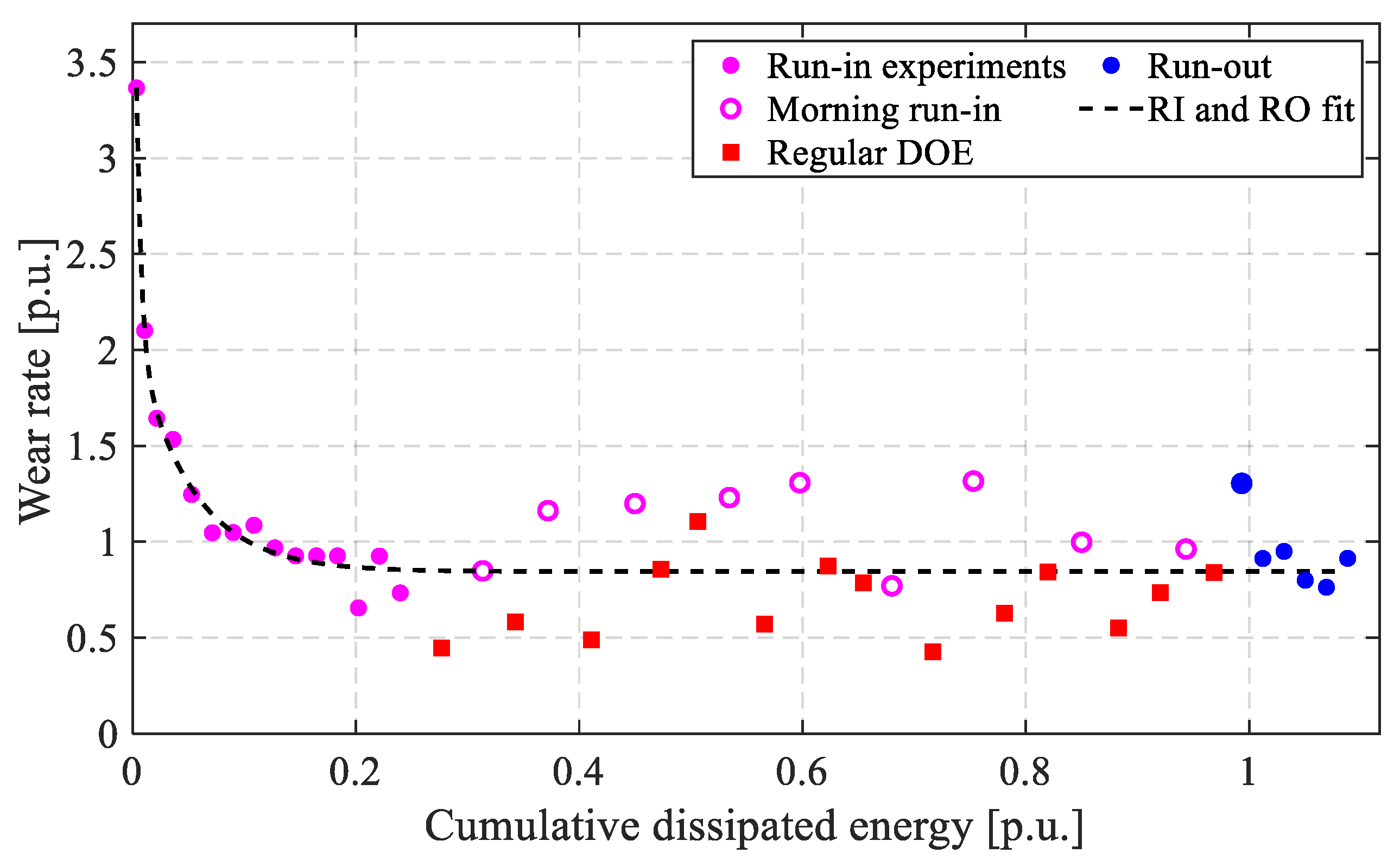
3.2. Run-In Experiments
3.3. Cycle-Wise Validation Experiments
4. Wear Rate Characterization
4.1. Inherent Wear Rate Variability
4.2. Wear Rate Variability Among Different Friction Plates
4.3. Wear Rate Dependences on Individual Operating Parameters
5. Clutch Wear Model and Its Run-In Submodel
5.1. Model Structure
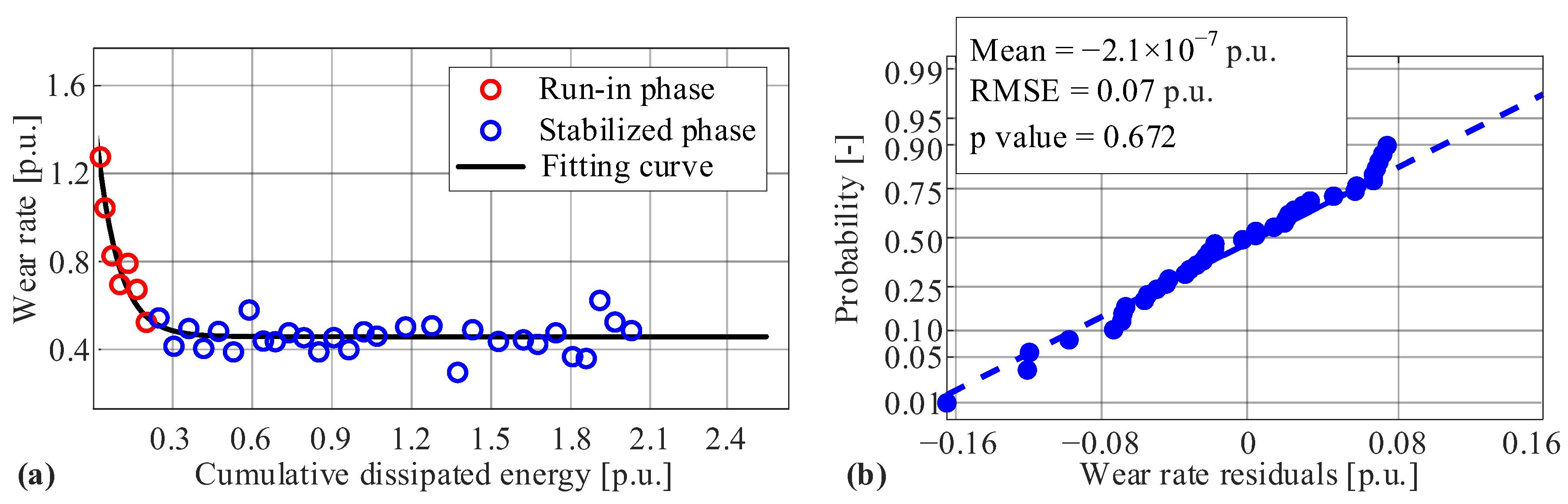
5.2. Run-In Model
6. Wear Rate Expectation Model
6.1. Model Structure
6.2. Model Parametrization
6.3. Model Validation
6.4. Model Analysis
6.5. Comparative Performance Analysis of Models for Three Friction Materials
6.6. Comparison with Baseline Model
7. Wear Rate Variability Model
7.1. Modeling Approach
7.2. Optimization Procedure and Model Candidates
7.3. Model Validation
8. Validation and Analysis of Overall Wear Model
8.1. Model Validation
8.2. Model Analysis
8.3. Implementation Aspects
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Mathematical Symbols and Abbreviations
| Surrogate distance | |
| Cumulative dissipated energy | |
| Dissipated energy | |
| Clutch normal force | |
| Run-in weighting function | |
| Negative log likelihood function | |
| Friction interface temperature | |
| Cycle-wise average pressure plate temperature | |
| Pressure plate temperature reference | |
| Mass of the friction plate | |
| Clutch torque | |
| Cycle-wise average clutch torque | |
| Clutch torque reference | |
| Number of clutch closing cycles | |
| Wear rate variability model parameters | |
| Coefficient of determination | |
| Leave-one-out cross-validation coefficient of determination | |
| Time of ramping up the normal force phase | |
| Clutch closing time | |
| Cycle-wise average clutch closing time | |
| Clutch closing time reference | |
| Cooling delay | |
| Worn volume | |
| Worn volume expectation | |
| Worn volume standard deviation | |
| Worn volume variance | |
| Wear rate | |
| Wear rate expectation | |
| Wear rate standard deviation | |
| General model inputs | |
| Design matrix | |
| Dependent response variable | |
| Input features | |
| Wear rate expectation model parameters | |
| Run-in model energy constants | |
| Normalized model residuals | |
| Wear rate variability model parameter vector | |
| Friction material density | |
| Initial slip speed | |
| Cycle-wise average initial slip speed | |
| Initial slip speed reference | |
| AMT | Automated Manual Transmission |
| CI | Confidence Interval |
| DCT | Dual Clutch Transmission |
| DOE | Design of Experiment |
| KS | Kolmogorov–Smirnov |
| MSE | Mean Square Error |
| NLL | Negative Log Likelihood |
| Probability Density Function | |
| RI | Run-in |
| RMSE | Root Mean Square Error |
| RO | Run-out |
Appendix A. Mathematical Background
Appendix B. Selection of Wear Rate Model Inputs
| Surrogate Inputs | |||
|---|---|---|---|
| Temperature Level | |||
| 120 °C | 0.565 | 0.655 | 0.611 |
| 170 °C | 0.549 | 0.575 | 0.577 |
| 240 °C | 0.753 | 0.690 | 0.596 |
| Average | 0.622 | 0.640 | 0.595 |
Appendix C. Direct Validation of Wear Rate Variability
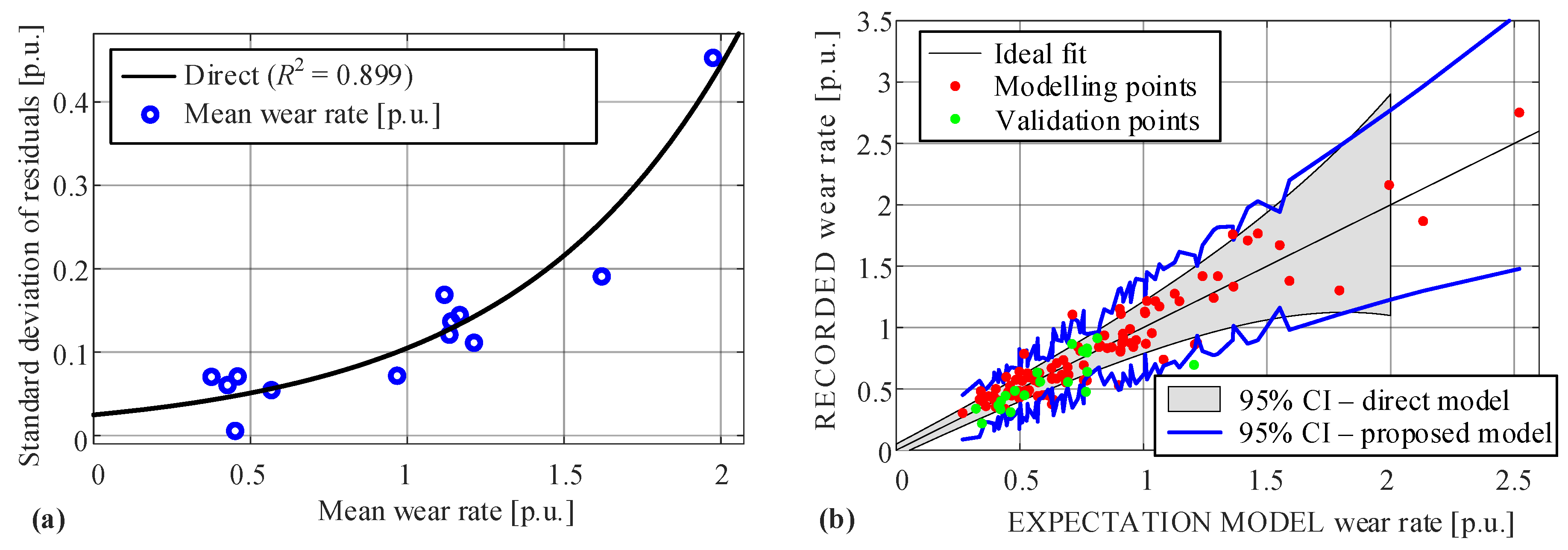
Appendix D. Analysis of Wear Rate Modeling Error Due to Model Inputs Averaging
| Point | Temperature, TdR [°C] | Initial Slip Speed, ω0R [rpm] | Torque, MzR [Nm] | Closing Time, t2R [s] |
|---|---|---|---|---|
| Low-energy, LE | 170 | 1200 | 25 | 3.4 |
| Mid-energy, ME | 170 | 1700 | 50 | 2.15 |
| Run-in, RI | 170 | 2800 | 50 | 3.4 |
| High-energy, HE | 170 | 2800 | 75 | 3.4 |
| Run-in @ 120 °C | 120 | 2800 | 50 | 3.4 |
| Run-in @ 240 °C | 240 | 2800 | 50 | 3.4 |
| Point | Worn Volume for Recorded Inputs [p.u.] | Worn Volume for Averaged Inputs [p.u.] | Relative Worn Volume Difference |
|---|---|---|---|
| LE | 2.903 | 2.901 | −0.080% |
| ME | 3.100 | 3.092 | −0.240% |
| RI | 4.939 | 4.930 | −0.175% |
| HE | 10.544 | 10.511 | −0.317% |
| RI @ 120 °C | 3.386 | 3.363 | −0.636% |
| RI @ 240 °C | 7.874 | 7.861 | −0.160% |
References
- Chen, Y.; Wang, X.; He, K.; Yang, C. Model reference self-learning fuzzy control method for automated mechanical clutch. Int. J. Adv. Manuf. Technol. 2018, 94, 3163–3172. [Google Scholar] [CrossRef]
- Shi, J.; Li, L.; Wang, X.; Liu, C. Robust output feedback controller with high-gain observer for automatic clutch. Mech. Syst. Signal Process. 2019, 132, 806–822. [Google Scholar] [CrossRef]
- Kob, M.; Supriyo, B.; Tawi, K.; Mazali, I. Engagement slip controller development based on actuator displacement for an electro-mechanical friction clutch system. Int. J. Automot. Mech. Eng. 2015, 11, 2664–2674. [Google Scholar] [CrossRef]
- Liauw, Y.; Roozegar, M.; Zou, T.; Morozov, A.; Angeles, J. A topology-change model of multi-speed transmissions in electric vehicles during gear-shifting. Mechatronics 2018, 55, 151–161. [Google Scholar] [CrossRef]
- Della Gatta, A.; Iannelli, L.; Pisaturo, M.; Senatore, A.; Vasca, F. A survey on modeling and engagement control for automotive dry clutch. Mechatronics 2018, 55, 63–75. [Google Scholar] [CrossRef]
- Pisaturo, M.; Senatore, A. Thermal Compensation Control Strategy in Automated Dry Clutch Engagement Dynamics and Launch Manoeuvre. Int. J. Automot. Technol. 2019, 20, 1089–1101. [Google Scholar] [CrossRef]
- Gong, T.; Yao, P.; Xiao, Y.; Fan, K.; Tan, H.; Zhang, Z.; Zhao, L.; Zhou, H.; Deng, M. Wear map for a copper-based friction clutch material under oil lubrication. Wear 2015, 328, 270–276. [Google Scholar] [CrossRef]
- Li, M.; Khonsari, M.M.; McCarthy, D.M.C.; Lundin, J. Parametric analysis of wear factors of a wet clutch friction material with different groove patterns. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 1056–1067. [Google Scholar] [CrossRef]
- Abdullah, O.I.; Schlattmann, J. Temperature analysis of a pin-on-disc tribology test using experimental and numerical approaches. Friction 2016, 4, 135–143. [Google Scholar] [CrossRef]
- Basavarajappa, S.; Ellangovan, S. Dry sliding wear characteristics of glass-epoxy composite filled with silicon carbide and graphite particles. Wear 2012, 296, 491–496. [Google Scholar] [CrossRef]
- Kim, S.; Jang, H. Friction and wear of friction materials containing two different phenolic resins reinforced with aramid pulp. Tribol. Int. 2000, 33, 477–484. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, S.; Tong, J.; Zhao, X.; Zhuang, J.; Liu, Y.; Qi, H. Tribological and mechanical behaviours of rattan-fibre-reinforced friction materials under dry sliding conditions. Mater. Res. Express 2018, 5, 035101. [Google Scholar] [CrossRef]
- Fukuda, K.; Morita, T. Physical model of adhesive wear in early stage of sliding. Wear 2017, 376, 1528–1533. [Google Scholar] [CrossRef]
- Chi, H.T.; Jiang, L.T.; Chen, G.Q.; Kang, P.C.; Lin, X.; Wu, G.H. Dry sliding friction and wear behavior of (TiB2 + h-BN)/2024Al composites. Mater. Des. 2015, 87, 960–968. [Google Scholar] [CrossRef]
- Kumar, I.A.; Kumar, A.; Srinivasan, V.; Raffi, N.M. Wear Study on Basalt, Flax and Hybrid Fiber Reinforced Phenolic Composites. J. Adv. Microsc. Res. 2018, 13, 65–71. [Google Scholar] [CrossRef]
- Fernandez, G.; Zanotto, P.; Sinatora, A. Tribology Applied on Development of New Materials for Dry Clutch System. In Proceedings of the 8th Brazilian Congress of Manufacturing Engineering, Salvador, Bahia, Brazil, 18–22 May 2015. [Google Scholar]
- Biczo, R.; Kalacska, G.; Mankovits, T. Effects of Automotive Test Parameters on Dry Friction Fiber-Reinforced Clutch Facing Surface Microgeometry and Wear. Polymers 2021, 13, 3896. [Google Scholar] [CrossRef]
- Kulkarni, A.; Mahale, R.; Kannan, C. Wear Based Lifetime Estimation of a Clutch Facing using Coupled Field Analysis. Int. J. Automot. Mech. Eng. 2021, 18, 9292–9304. [Google Scholar] [CrossRef]
- Grzelczyk, D.; Awrejcewicz, J. Wear Processes in a Mechanical Friction Clutch: Theoretical, Numerical, and Experimental Studies. Math. Probl. Eng. 2015, 2015, 725685. [Google Scholar] [CrossRef]
- Li, M.; Khonsari, M.M.; Lingesten, N.; Marklund, P.; McCarthy, D.M.C.; Lundin, J. Model validation and uncertainty analysis in the wear prediction of a wet clutch. Wear 2016, 364, 112–121. [Google Scholar] [CrossRef]
- Tabbai, Y.; Alaoui-BeIghiti, A.; El Moznine, R.; Belhora, F.; Hajjaji, A.; El Ballouti, A. Friction and wear performance of disc brake pads and pyroelectric energy harvesting. Int. J. Precis. Eng. Manuf. Green Technol. 2021, 8, 487–500. [Google Scholar] [CrossRef]
- Tabbai, Y.; Sarah, A.; Rjafallah, A.; Alaoui-Belghiti, A.; Hajjaji, A.; El Moznine, R.; Belhora, F.; El Ballouti, A. Pyroelectric generators to harvest energy from disc brake pads for wireless sensors in electric vehicles. Eur. Phys. J. Appl. Phys. 2022, 97, 89. [Google Scholar] [CrossRef]
- Xiao, X.; Yin, Y.; Bao, J.; Lu, L.; Feng, X. Review on the friction and wear of brake materials. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef]
- Hoic, M.; Hrgetic, M.; Kranjcevic, N.; Deur, J.; Tissot, A.; Astolfi, D. Redesign of a Disc-on-Disc Computer Numerical Control Tribometer for a Wide-Range and Shudder-Resistant Operation. Machines 2024, 12, 14. [Google Scholar] [CrossRef]
- Hoic, M.; Hrgetic, M.; Kranjcevic, N.; Kostelac, M.; Deur, J.; Tissot, A. Design of a Disc-on-disc-type CNC Tribometer Targeted at Dry Clutch Friction Plate Wear Characterization. Int. J. Automot. Technol. 2022, 23, 55–71. [Google Scholar] [CrossRef]
- Hoić, M.; Škugor, B.; Deur, J.; Tissot, A. Experimental characterization and modeling of automotive dry clutch friction lining wear. In Proceedings of the Kupplungen und Kupplungssysteme in Antrieben 2019, Ettlingen, Germany, 26–27 March 2019. [Google Scholar]
- Hoic, M.; Miklik, A.; Kostelac, M.; Deur, J.; Tissot, A. Analysis of the Accuracy of Mass Difference-Based Measurement of Dry Clutch Friction Material Wear. Materials 2021, 14, 5356. [Google Scholar] [CrossRef] [PubMed]
- Voelkel, K.; Pflaum, H.; Stahl, K. Running-in Behavior of Wet Multi-plate Clutches: Introduction of a New Test Method for Investigation and Characterization. Chin. J. Mech. Eng. 2020, 33, 34. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009; pp. XXII, 745. [Google Scholar]
- Krunoslav, H.; Branimir, Š.; Nenad, K.; Joško, D.; Matija, H. Characterization and modeling of Dry Friction Clutch Linings Wear using LASSO Method. In Proceedings of the 25th International Conference on Materials, Tribology and Recycling, Vela Luka, Croatia, 27–29 June 2024. [Google Scholar]
- Weisberg, S. Applied Linear Regression, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; p. 368. [Google Scholar]
- Wasserman, L. All of Statistics, A Concise Course in Statistical Inference; Springer Texts in Statistics; Springer: New York, NY, USA, 2004; pp. XX, 442. [Google Scholar]
- Lin, X.; Xi, J.; Hao, S. The calculation model of the friction torque on a dry clutch. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 1796–1805. [Google Scholar] [CrossRef]
- Pavkovic, D.; Deur, J.; Kolmanovsky, I. Adaptive Kalman Filter-Based Load Torque Compensator for Improved SI Engine Idle Speed Control. IEEE Trans. Control Syst. Technol. 2009, 17, 98–110. [Google Scholar] [CrossRef]
- Tong, Q.; Xie, H.; Song, K.; Zou, D. A Control-Oriented Engine Torque Online Estimation Approach for Gasoline Engines Based on In-Cycle Crankshaft Speed Dynamics. Energies 2019, 12, 4683. [Google Scholar] [CrossRef]
- Chen, J.; Yu, J.; Gong, Y. A New Multi-Physics Coupled Method for the Temperature Field of Dry Clutch Assembly. Appl. Sci. 2023, 13, 1165. [Google Scholar] [CrossRef]
- Hoic, M.; Kranjcevic, N.; Herold, Z.; Deur, J.; Ivanovic, V. Modeling of dry dual-clutch axial dynamics. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 220–237. [Google Scholar] [CrossRef]




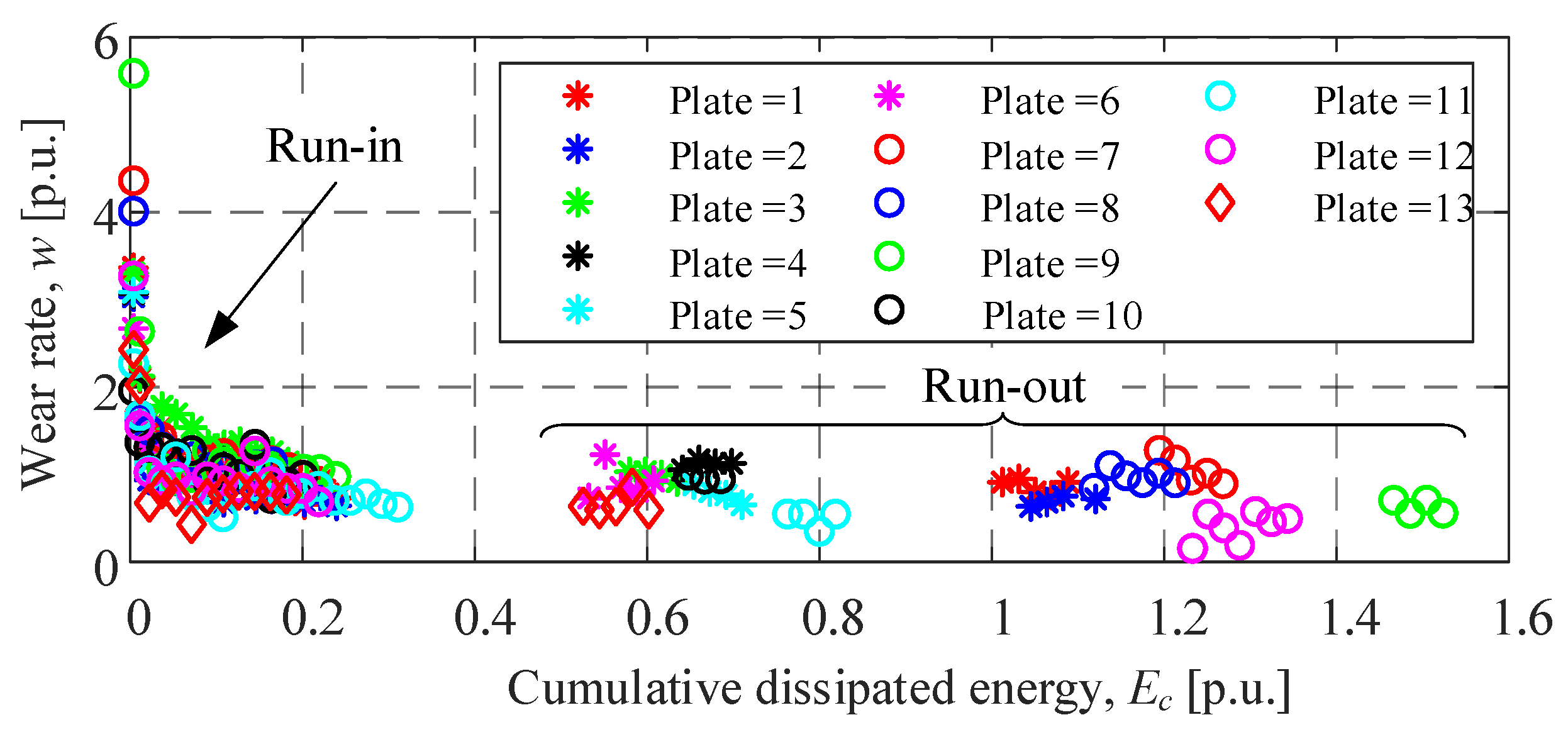
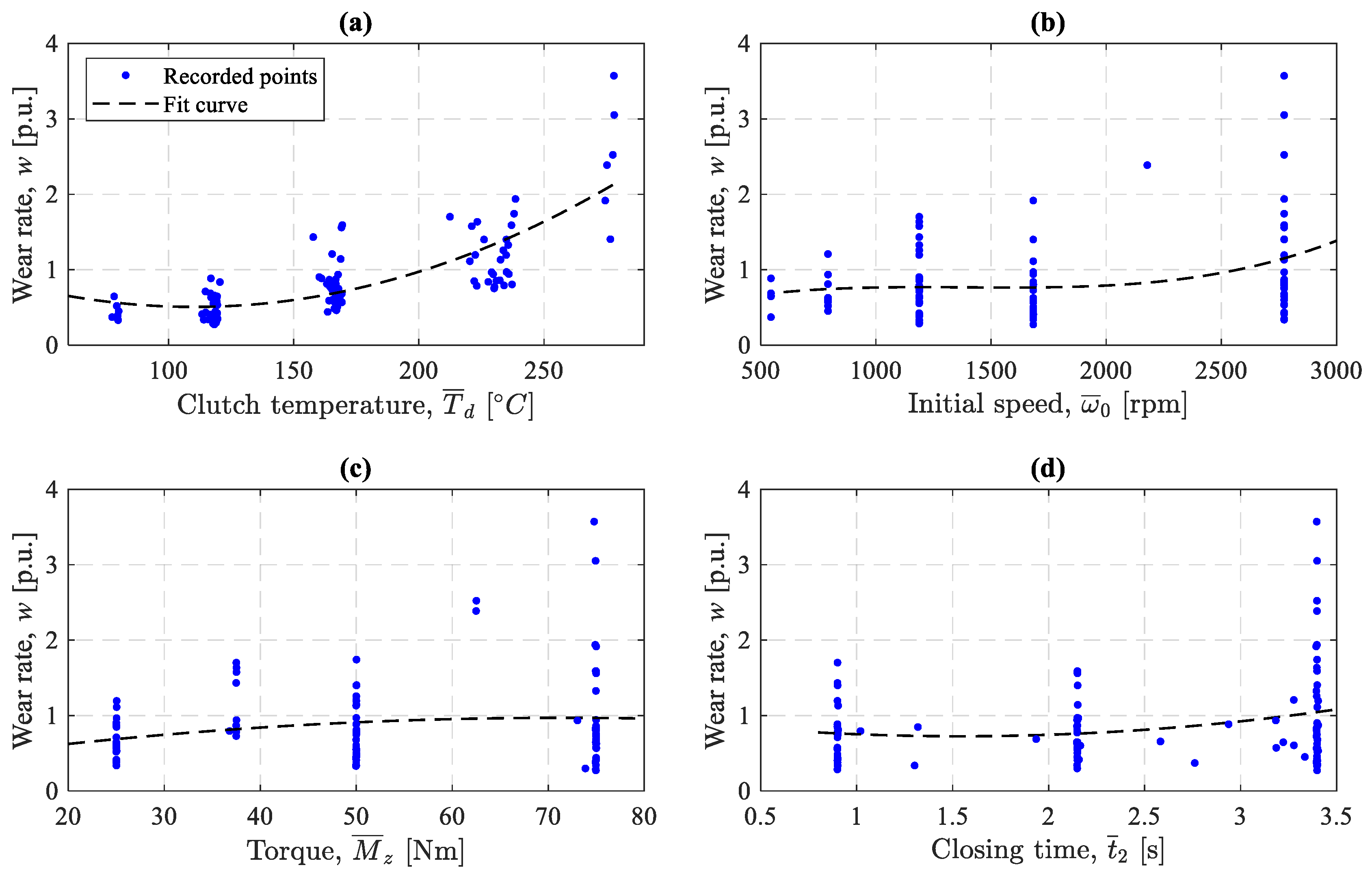

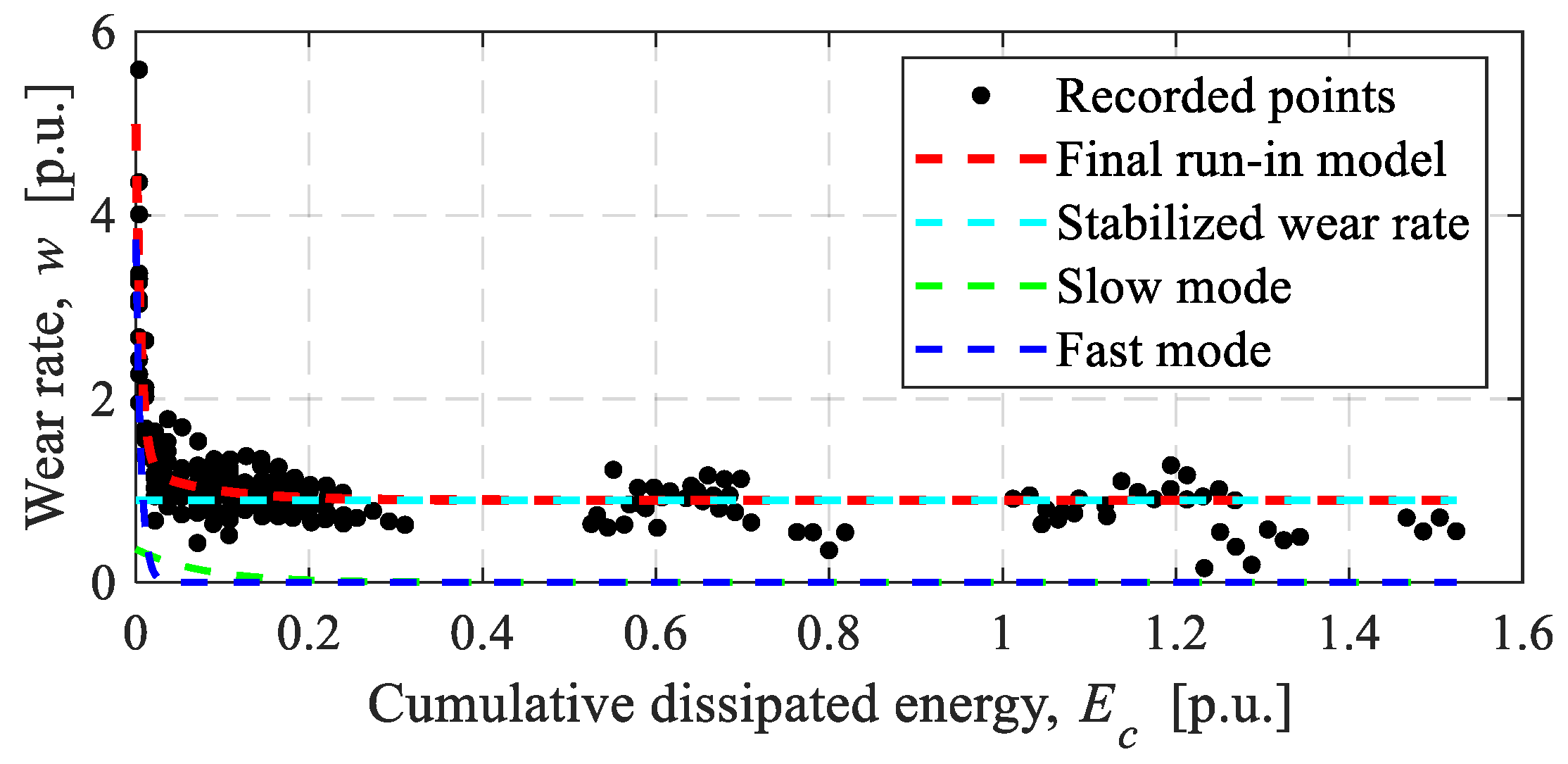
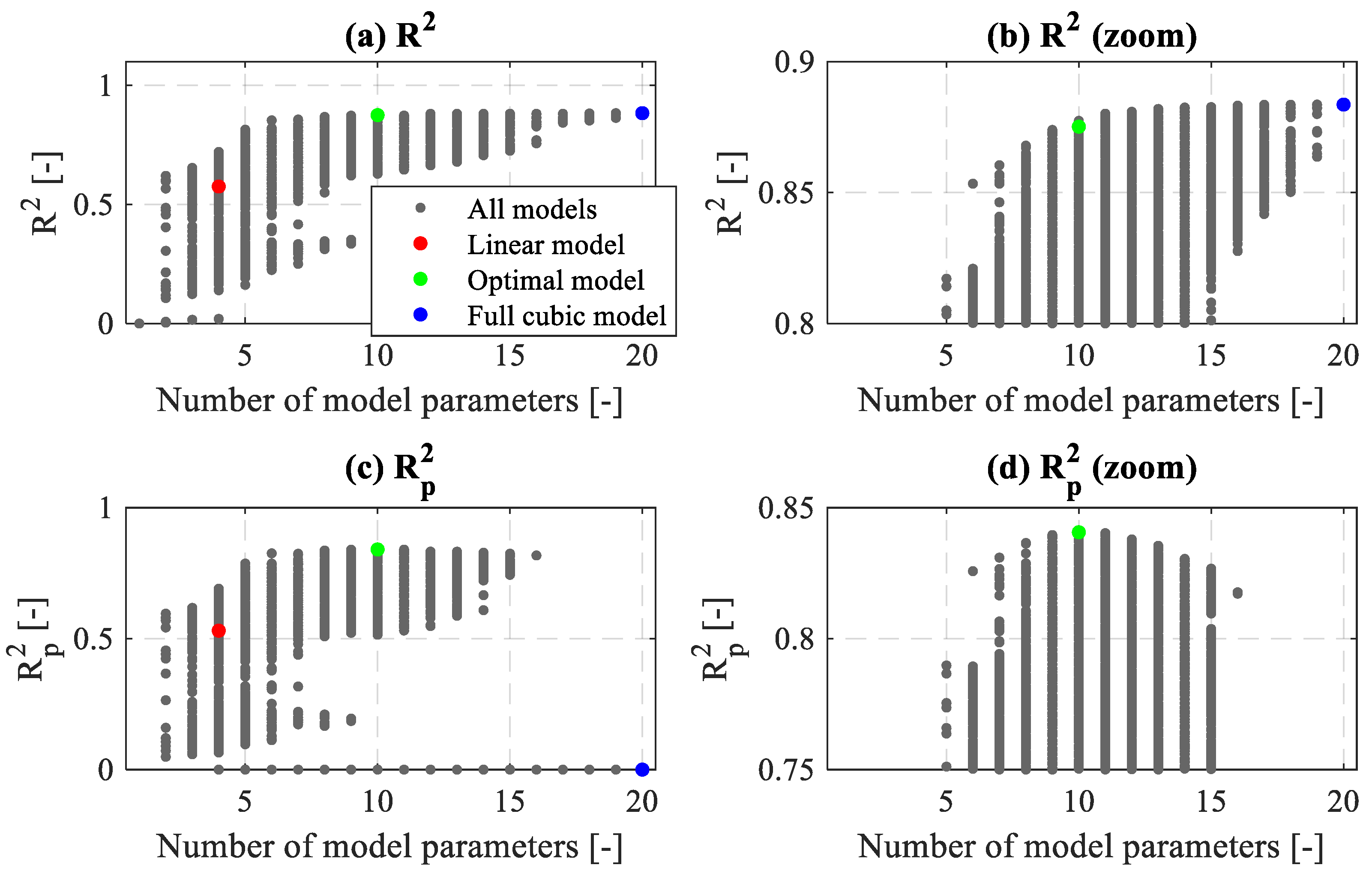
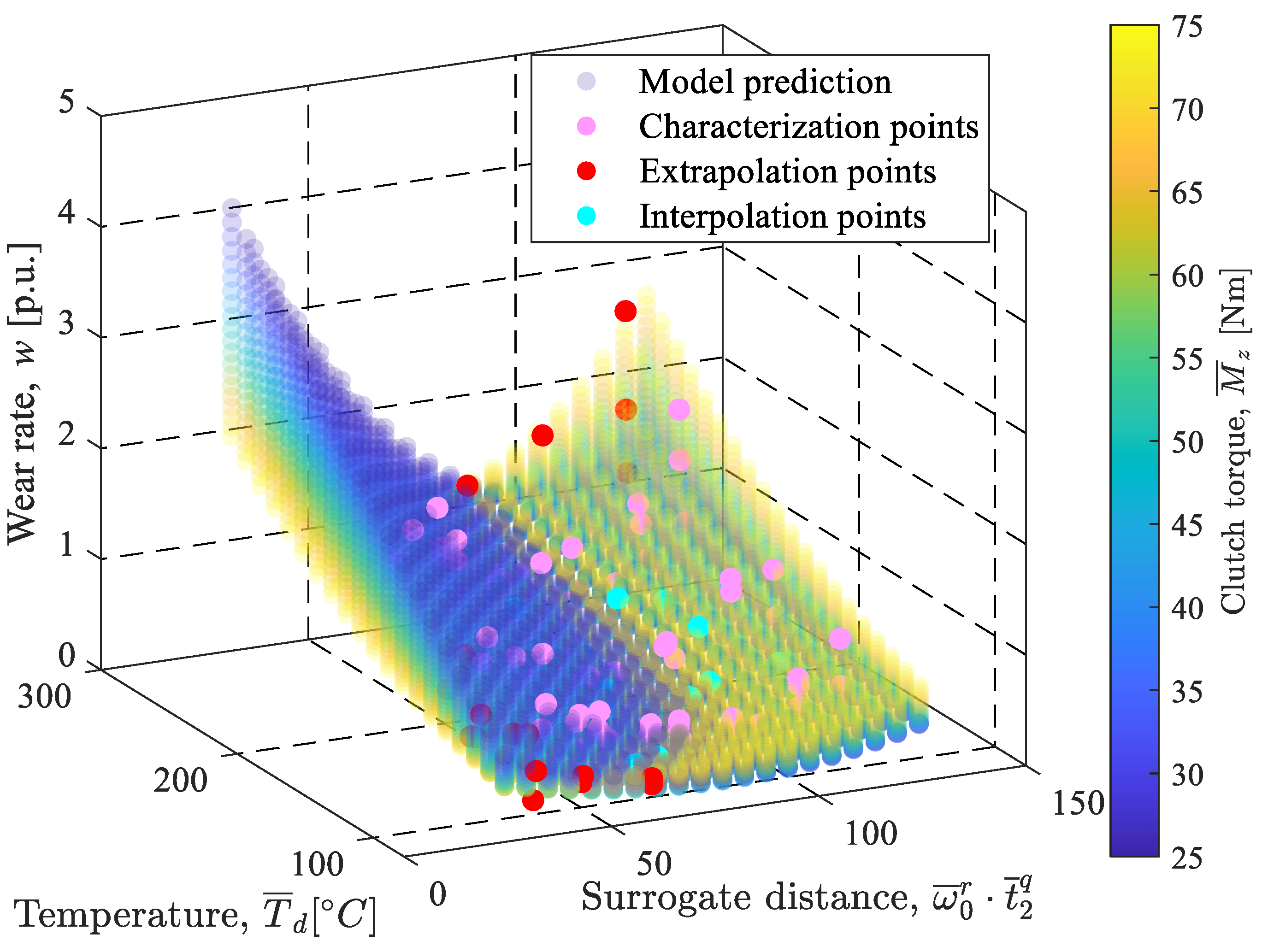
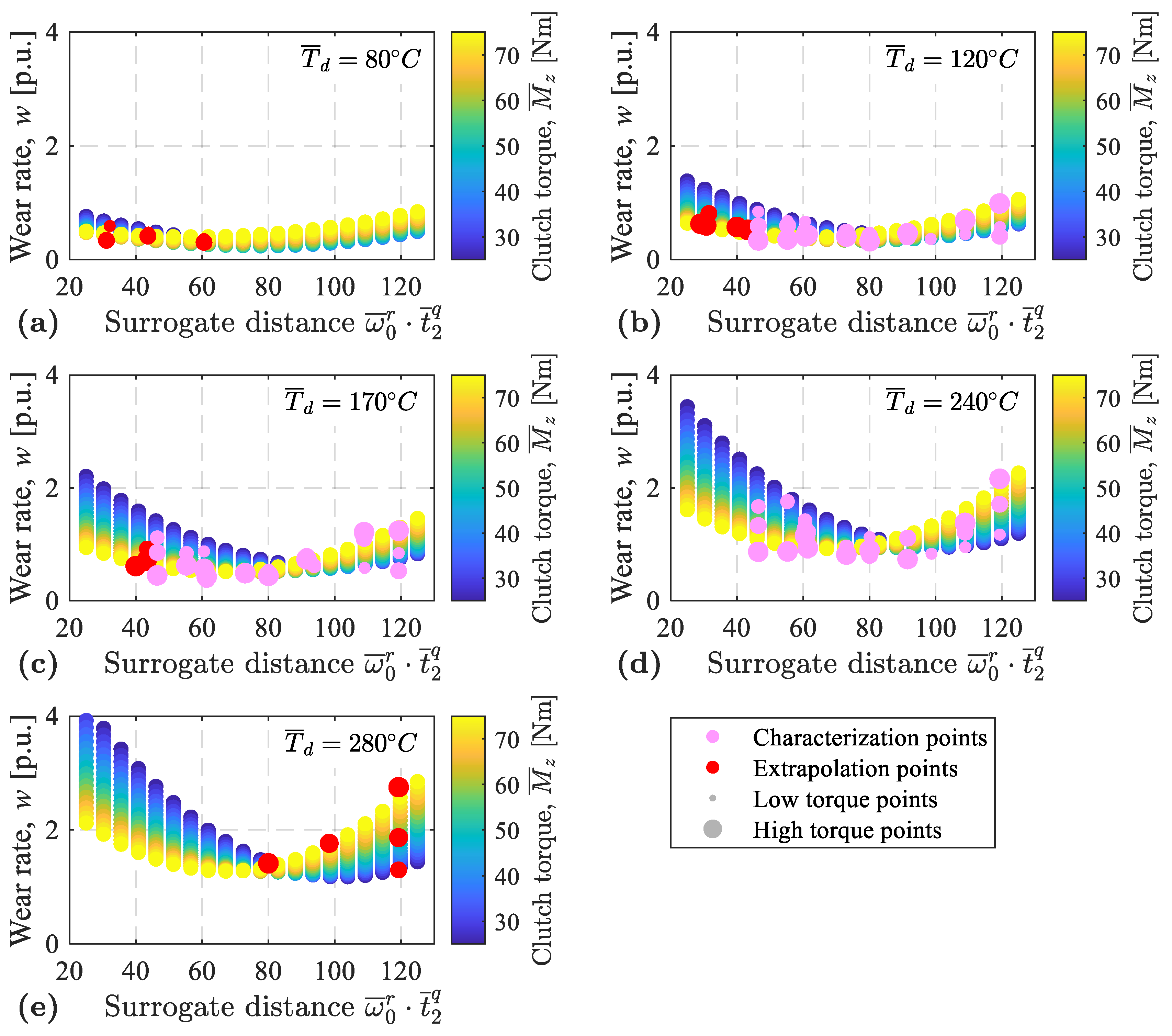
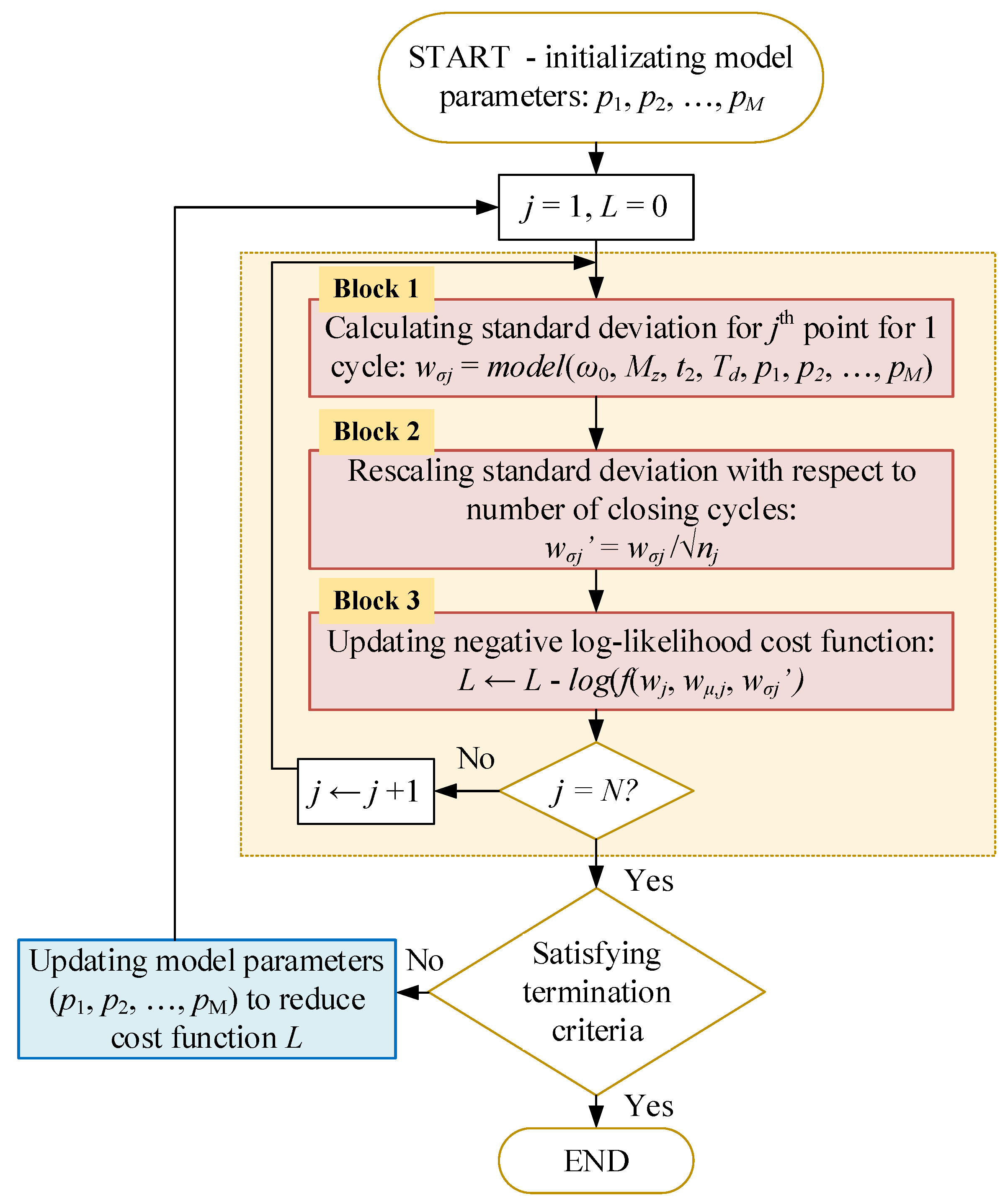

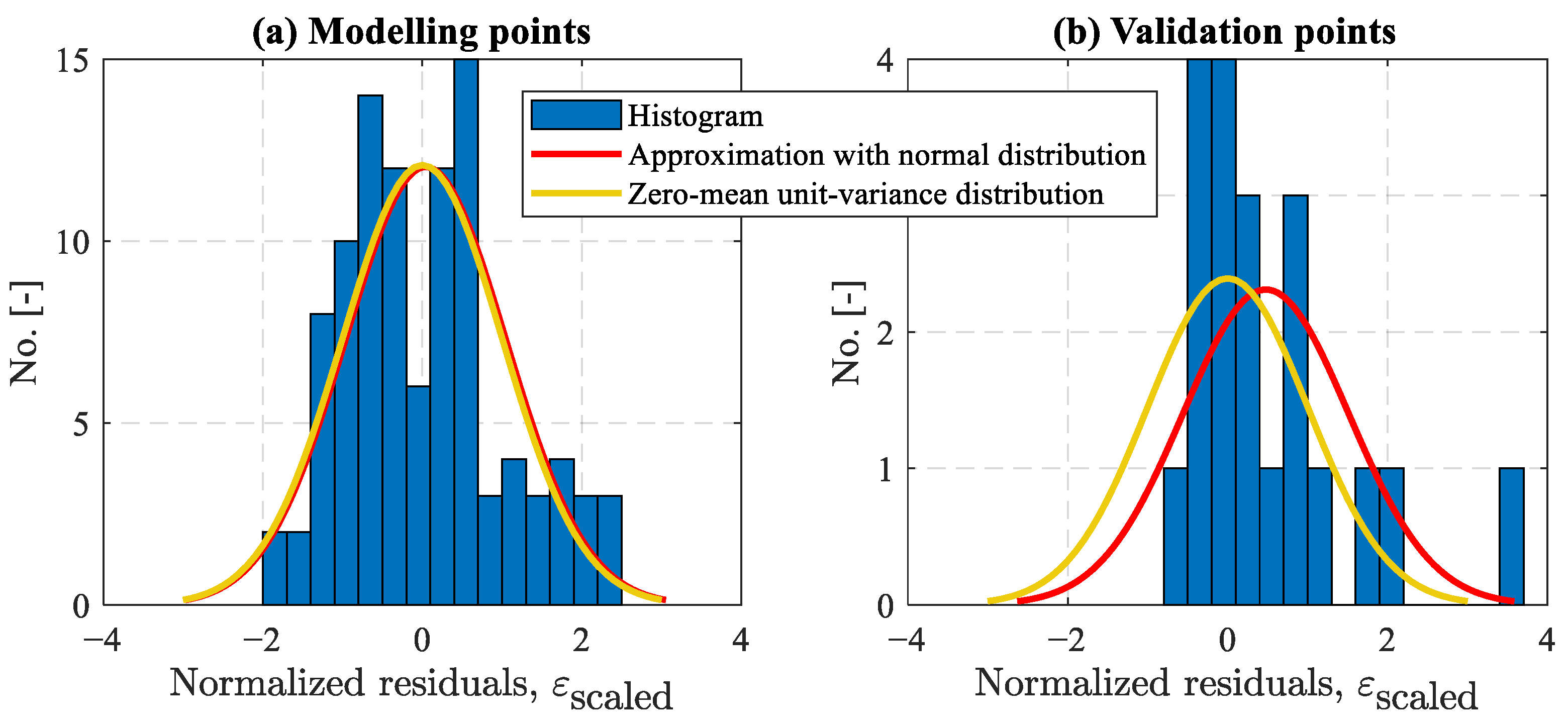


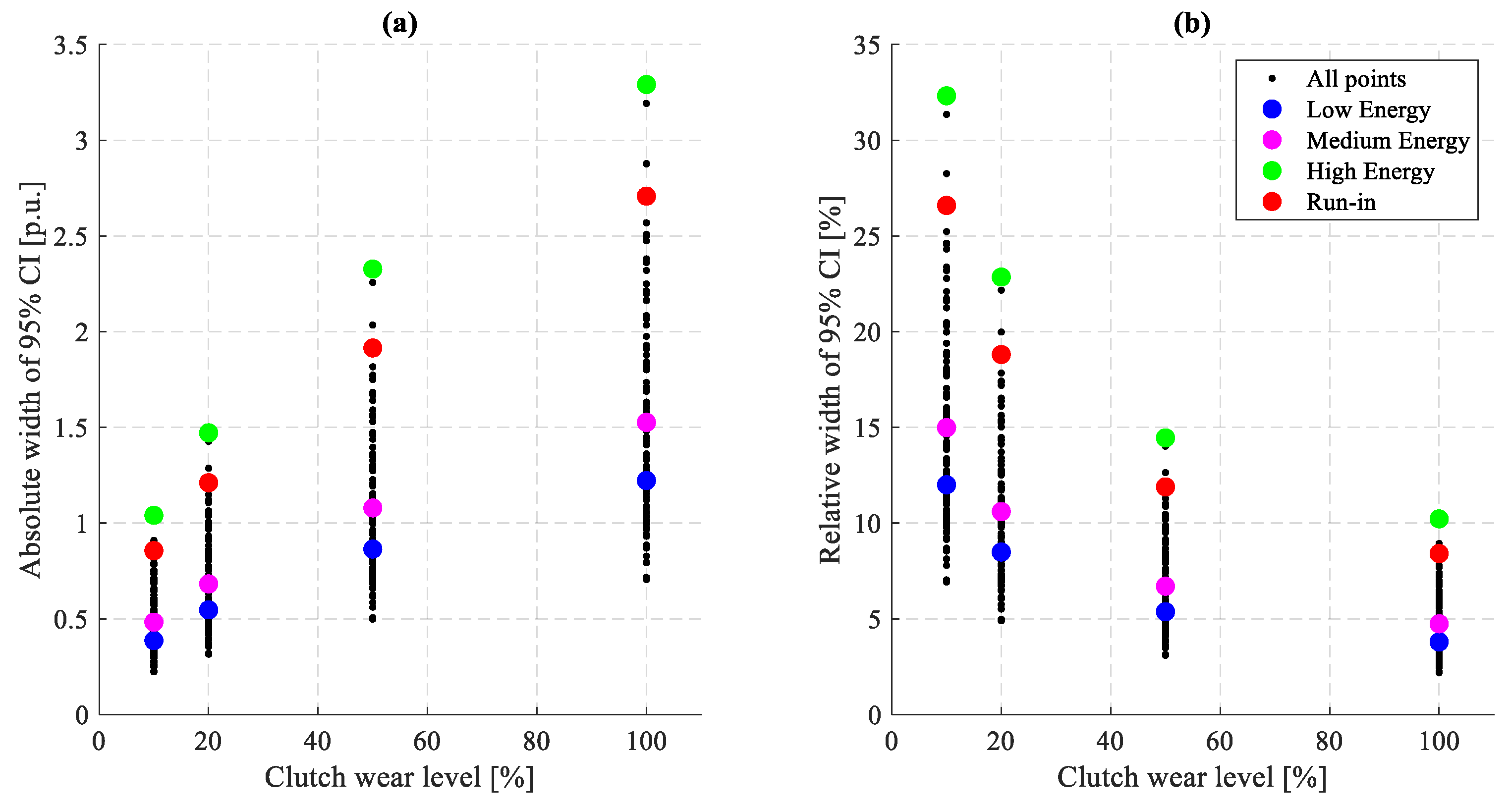
| Correlation of Wear Rate, w, with | Correlation Coefficient |
|---|---|
| Clutch temperature, | 0.744 |
| Initial slip speed, | 0.295 |
| Torque, | 0.210 |
| Closing time, | 0.173 |
| Model | R2 | # | RMSE * [-] | RMSEp *# [-] | Number of Model Parameters |
|---|---|---|---|---|---|
| Linear | 0.576 | 0.531 | 1.853 | 1.939 | 4 |
| Selected/Optimal | 0.875 | 0.841 | 1.000 | 1.130 | 10 |
| Full cubic | 0.884 | 0.790 | 0.966 | 1.297 | 20 |
| Validation Points | Modeling Points | ||
|---|---|---|---|
| All Points | w/o Point 13 | ||
| Residuals mean (p.u.) | 0.057 | 0.033 | 0 |
| Residuals st. dev. (p.u.) | 0.148 | 0.106 | 0.1545 |
| R2 | 0.411 | 0.721 | * 0.875 |
| Friction Material | Modeling Points | Validation Points | Number of Model Parameters | |||
|---|---|---|---|---|---|---|
| Residuals Standard Deviation (p.u.) | R2 | Rp2 | Residuals Standard Deviation (p.u.) | R2 | ||
| A | 0.154 | 0.875 | 0.841 | 0.148 | 0.411 | 10 |
| B | 0.142 | 0.922 | 0.887 | 0.132 | 0.560 | 14 |
| C | 0.149 | 0.865 | 0.820 | 0.125 | 0.724 | 9 |
| Model | Modeling Points | Validation Points | Validation Points w/o Point 13 | |||
|---|---|---|---|---|---|---|
| Residuals Standard Deviation (p.u.) | R2 | Residuals Standard Deviation (p.u.) | R2 | Residuals Standard Deviation (p.u.) | R2 | |
| Baseline model | 0.270 | 0.583 | 0.125 | 0.455 | 0.128 | 0.462 |
| New model | 0.154 | 0.875 | 0.148 | 0.411 | 0.106 | 0.721 |
| Model | Modeling Points | Validation Points | ||||||
|---|---|---|---|---|---|---|---|---|
[-] | [-] | p Value | [-] | [-] | p Value | |||
| Exponential | 267.1 | 0.066 | 1.003 | 0.456 | 58.3 | 0.582 | 1.191 | 0.123 |
| Linear | 266.4 | 0.060 | 1.003 | 0.345 | 57.3 | 0.587 | 1.163 | 0.109 |
| Quadratic | 265.7 | 0.046 | 1.004 | 0.478 | 56.5 | 0.590 | 1.131 | 0.084 |
| Linear w/four inputs | 260.6 | 0.041 | 1.004 | 0.718 | 56.4 | 0.477 | 1.036 | 0.068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haramina, K.; Škugor, B.; Hoić, M.; Kranjčević, N.; Deur, J.; Tissot, A. Modeling of Dry Clutch Wear for a Wide Range of Operating Parameters. Appl. Sci. 2025, 15, 8150. https://doi.org/10.3390/app15158150
Haramina K, Škugor B, Hoić M, Kranjčević N, Deur J, Tissot A. Modeling of Dry Clutch Wear for a Wide Range of Operating Parameters. Applied Sciences. 2025; 15(15):8150. https://doi.org/10.3390/app15158150
Chicago/Turabian StyleHaramina, Krunoslav, Branimir Škugor, Matija Hoić, Nenad Kranjčević, Joško Deur, and Andreas Tissot. 2025. "Modeling of Dry Clutch Wear for a Wide Range of Operating Parameters" Applied Sciences 15, no. 15: 8150. https://doi.org/10.3390/app15158150
APA StyleHaramina, K., Škugor, B., Hoić, M., Kranjčević, N., Deur, J., & Tissot, A. (2025). Modeling of Dry Clutch Wear for a Wide Range of Operating Parameters. Applied Sciences, 15(15), 8150. https://doi.org/10.3390/app15158150








