Establishing Linearity of the MOSkin Detector for Ultra-High Dose-per-Pulse, Very-High-Energy Electron Radiotherapy Using Dose-Rate-Corrected EBT-XD Film
Abstract
1. Introduction
2. Theory and Methods
2.1. Theoretical Framework for MOSFET Detectors
2.2. Film Calibrations and Scanning
2.3. MOSkin Characterisation
2.4. EBT-XD Apparent Dose-Rate Dependence
3. Results
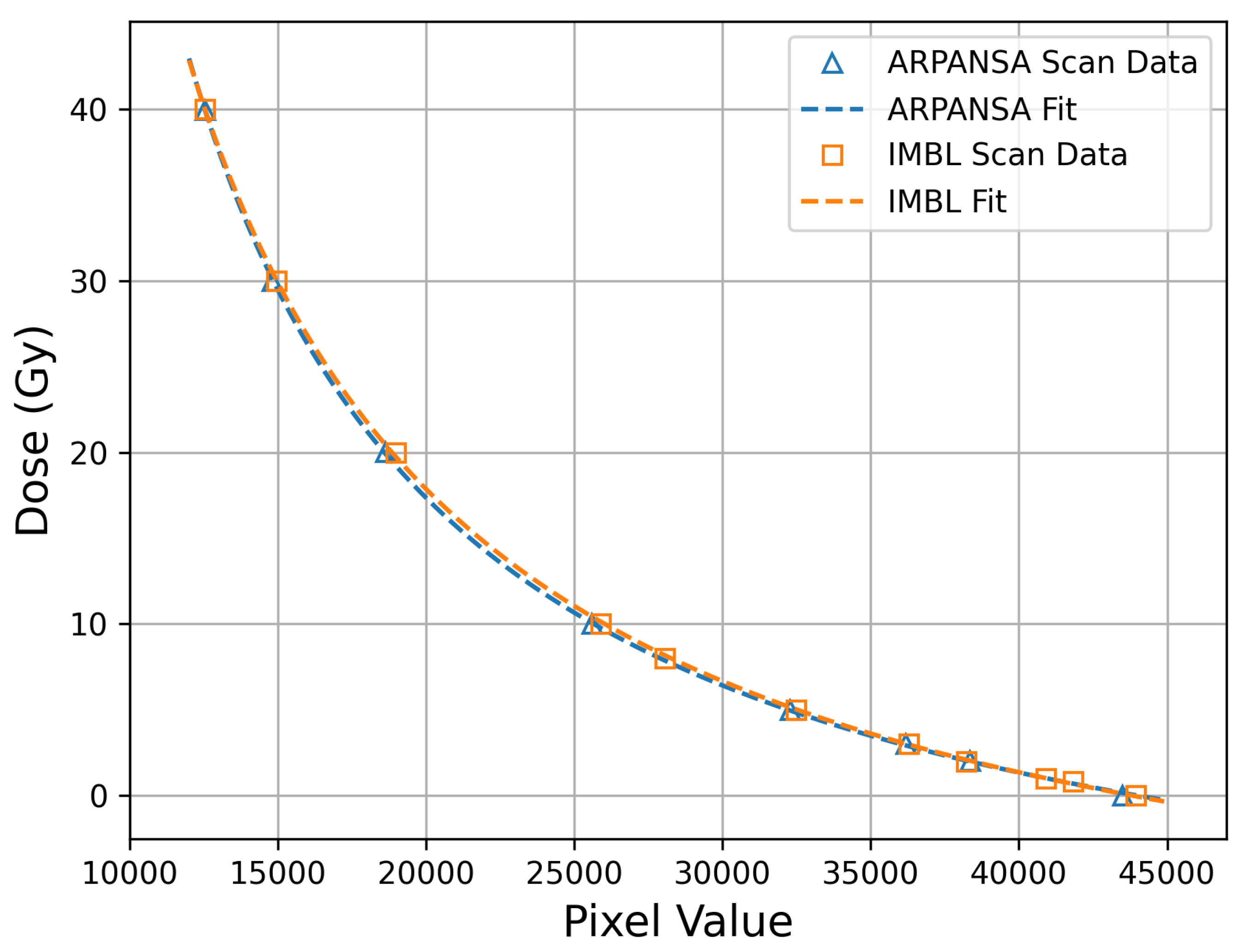
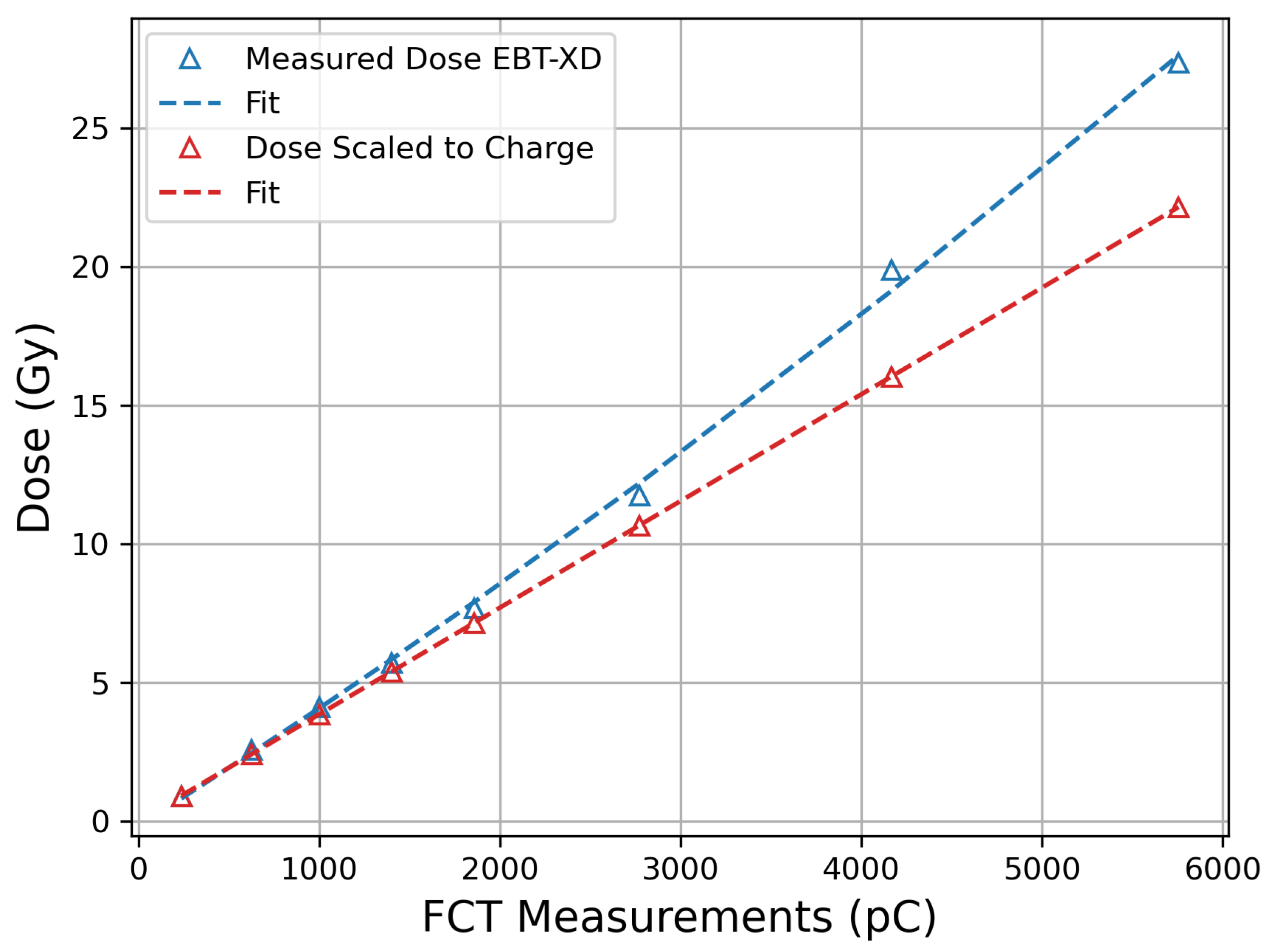
3.1. EBT-XD Film Calibration and Correction
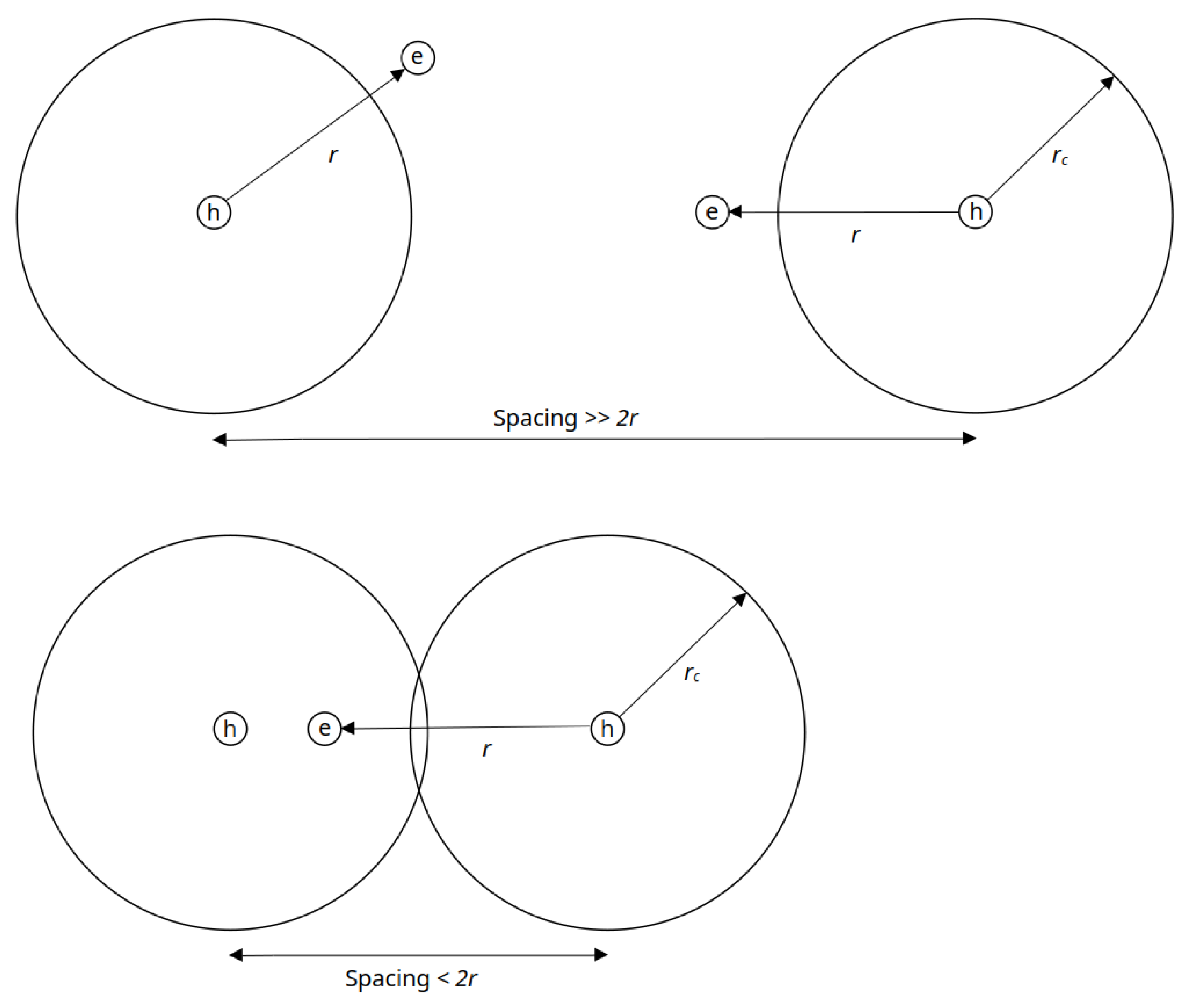
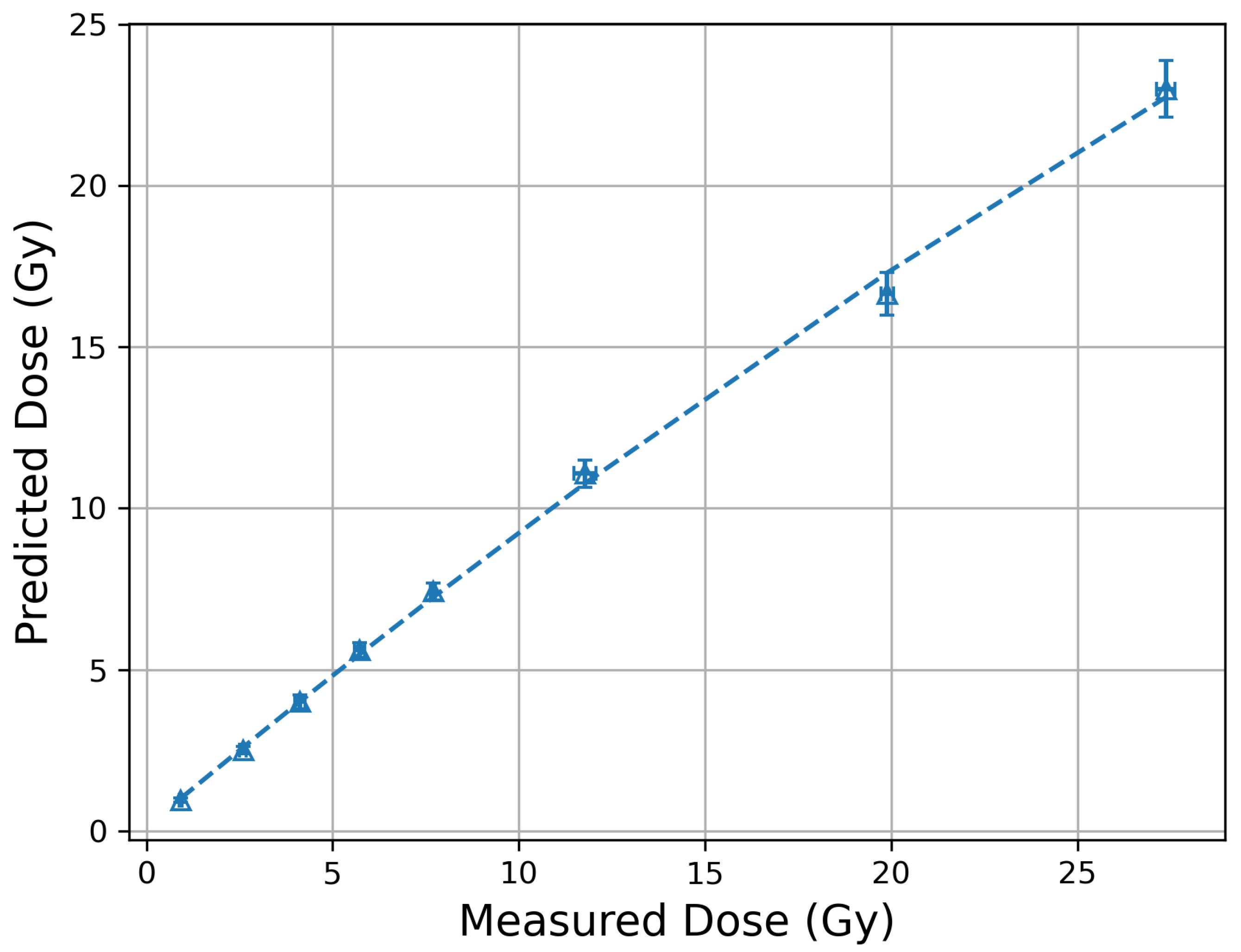
3.2. MOSkin Linearity and Track Spacing
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UHDR | Ultra-high dose rate |
| VHEE | Very-high-energy electrons |
| PEER | Pulsed Energetic Electrons for Research |
| DPP | Dose per pulse |
| MOSFET | Metal oxide semiconductor field-effect transistor |
| CMRP | Centre for Medical Radiation Physics |
| CT | Fast current transformer |
| Shift in threshold voltage | |
| PMMA | Polymethyl methacrylate |
| DPB | Dose per bunch |
| FC | Faraday cup |
| FCT | Fast current transformer |
| PRF | Pulse repetition frequency |
References
- Dewey, D.L.; Boag, J.W. Modification of the Oxygen Effect when Bacteria are given Large Pulses of Radiation. Nature 1959, 183, 1450–1451. [Google Scholar] [CrossRef] [PubMed]
- Field, S.; Bewley, D. Effects of Dose-rate on the Radiation Response of Rat Skin. Int. J. Radiat. Biol. Relat. Stud. Phys. Chem. Med. 1974, 26, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Hendry, J.H.; Moore, J.V.; Hodgson, B.W.; Keene, J.P. The Constant Low Oxygen Concentration in All the Target Cells for Mouse Tail Radionecrosis. Radiat. Res. 1982, 92, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Hornsey, S.; Alper, T. Unexpected Dose-rate Effect in the Killing of Mice by Radiation. Nature 1966, 210, 212–213. [Google Scholar] [CrossRef] [PubMed]
- Favaudon, V.; Caplier, L.; Monceau, V.; Pouzoulet, F.; Sayarath, M.; Fouillade, C.; Poupon, M.F.; Brito, I.; Hupé, P.; Bourhis, J.; et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci. Transl. Med. 2014, 6, 245ra93. [Google Scholar] [CrossRef] [PubMed]
- Bourhis, J.; Montay-Gruel, P.; Gonçalves Jorge, P.; Bailat, C.; Petit, B.; Ollivier, J.; Jeanneret-Sozzi, W.; Ozsahin, M.; Bochud, F.; Moeckli, R.; et al. Clinical translation of FLASH radiotherapy: Why and how? Radiother. Oncol. 2019, 139, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Montay-Gruel, P.; Acharya, M.M.; Gonçalves Jorge, P.; Petit, B.; Petridis, I.G.; Fuchs, P.; Leavitt, R.; Petersson, K.; Gondré, M.; Ollivier, J.; et al. Hypofractionated FLASH-RT as an Effective Treatment against Glioblastoma that Reduces Neurocognitive Side Effects in Mice. Clin. Cancer Res. 2021, 27, 775–784. [Google Scholar] [CrossRef] [PubMed]
- Chabi, S.; To, T.H.V.; Leavitt, R.; Poglio, S.; Jorge, P.G.; Jaccard, M.; Petersson, K.; Petit, B.; Roméo, P.H.; Pflumio, F.; et al. Ultra-high-dose-rate FLASH and Conventional-Dose-Rate Irradiation Differentially Affect Human Acute Lymphoblastic Leukemia and Normal Hematopoiesis. Int. J. Radiat. Oncol. 2021, 109, 819–829. [Google Scholar] [CrossRef] [PubMed]
- Simmons, D.A.; Lartey, F.M.; Schüler, E.; Rafat, M.; King, G.; Kim, A.; Ko, R.; Semaan, S.; Gonzalez, S.; Jenkins, M.; et al. Reduced cognitive deficits after FLASH irradiation of whole mouse brain are associated with less hippocampal dendritic spine loss and neuroinflammation. FLASH Radiother. Int. Workshop 2019, 139, 4–10. [Google Scholar] [CrossRef] [PubMed]
- Vozenin, M.C.; De Fornel, P.; Petersson, K.; Favaudon, V.; Jaccard, M.; Germond, J.F.; Petit, B.; Burki, M.; Ferrand, G.; Patin, D.; et al. The Advantage of FLASH Radiotherapy Confirmed in Mini-pig and Cat-cancer Patients. Clin. Cancer Res. 2019, 25, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Montay-Gruel, P.; Corde, S.; Laissue, J.A.; Bazalova-Carter, M. FLASH radiotherapy with photon beams. Med. Phys. 2022, 49, 2055–2067. [Google Scholar] [CrossRef] [PubMed]
- Schüler, E.; Acharya, M.; Montay-Gruel, P.; Loo, B.W., Jr.; Vozenin, M.C.; Maxim, P.G. Ultra-high dose rate electron beams and the FLASH effect: From preclinical evidence to a new radiotherapy paradigm. Med. Phys. 2022, 49, 2082–2095. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, J.; Bezak, E.; Le, H.; Kempson, I. The current status of FLASH particle therapy: A systematic review. Phys. Eng. Sci. Med. 2023, 46, 529–560. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.; Gao, F.; Yang, Y.; Wu, D.; Zhang, Y.; Feng, G.; Dai, T.; Du, X. FLASH Radiotherapy: History and Future. Front. Oncol. 2021, 11, 644400. [Google Scholar] [CrossRef] [PubMed]
- DesRosiers, C.; Moskvin, V.; Bielajew, A.F.; Papiez, L. 150–250 MeV Electron Beams in Radiation Therapy. Phys. Med. Biol. 2000, 45, 1781. [Google Scholar] [CrossRef] [PubMed]
- Sarti, A.; De Maria, P.; Battistoni, G.; De Simoni, M.; Di Felice, C.; Dong, Y.; Fischetti, M.; Franciosini, G.; Marafini, M.; Marampon, F.; et al. Deep Seated Tumour Treatments With Electrons of High Energy Delivered at FLASH Rates: The Example of Prostate Cancer. Front. Oncol. 2021, 11. [Google Scholar] [CrossRef] [PubMed]
- Böhlen, T.T.; Germond, J.F.; Traneus, E.; Bourhis, J.; Vozenin, M.C.; Bailat, C.; Bochud, F.; Moeckli, R. Characteristics of very high-energy electron beams for the irradiation of deep-seated targets. Med. Phys. 2021, 48, 3958–3967. [Google Scholar] [CrossRef] [PubMed]
- Ronga, M.G.; Cavallone, M.; Patriarca, A.; Leite, A.M.; Loap, P.; Favaudon, V.; Créhange, G.; De Marzi, L. Back to the Future: Very High-Energy Electrons (VHEEs) and Their Potential Application in Radiation Therapy. Cancers 2021, 13, 4942. [Google Scholar] [CrossRef] [PubMed]
- Bazalova-Carter, M.; Qu, B.; Palma, B.; Hårdemark, B.; Hynning, E.; Jensen, C.; Maxim, P.G.; Loo Jr., B.W. Treatment planning for radiotherapy with very high-energy electron beams and comparison of VHEE and VMAT plans. Med. Phys. 2015, 42, 2615–2625. [Google Scholar] [CrossRef] [PubMed]
- Fischer, J.; Whitmore, L.; Desrosiers, C.; Sheehy, S.; Bazalova-Carter, M. Very high-energy electrons as radiotherapy opportunity. Eur. Phys. J. Plus 2024, 139, 728. [Google Scholar] [CrossRef]
- Corsini, R.; Aksoy, A.; Farabolini, W.; Gilardi, A.; Malyzhenkov, A.; Bateman, J.; Dosanjh, M.; Korysko, P.; Robertson, C.; Rieker, V. Medical activites in CLEAR: Studies towards radiotherapy using very high energy electrons (VHEE) in the FLSH regime. In Proceedings of the LINAC2024, Chicago, IL, USA, 25–30 August 2024; pp. 674–677. [Google Scholar] [CrossRef]
- Burkart, F.; Aßmann, R.; Dinter, H.; Jaster-Merz, S.; Kuropka, W.; Mayet, F.; Vinatier, T. The ARES Linac at DESY. In Proceedings of the 31st International Linear Accelerator Conference, LINAC2022, Liverpool, UK, 28 August–2 September 2022. [Google Scholar] [CrossRef]
- Subiel, A.; Moskvin, V.; Welsh, G.H.; Cipiccia, S.; Reboredo, D.; Evans, P.; Partridge, M.; DesRosiers, C.; Anania, M.P.; Cianchi, A.; et al. Dosimetry of Very High Energy Electrons (VHEE) for Radiotherapy Applications: Using Radiochromic Film Measurements and Monte Carlo Simulations. Phys. Med. Biol. 2014, 59, 5811. [Google Scholar] [CrossRef] [PubMed]
- Bazalova-Carter, M.; Liu, M.; Palma, B.; Dunning, M.; McCormick, D.; Hemsing, E.; Nelson, J.; Jobe, K.; Colby, E.; Koong, A.C.; et al. Comparison of Film Measurements and Monte Carlo Simulations of Dose Delivered with Very High-Energy Electron Beams in a Polystyrene Phantom. Med. Phys. 2015, 42, 1606–1613. [Google Scholar] [CrossRef] [PubMed]
- Butler, D.J.; Barnes, M.; McEwen, M.R.; Lerch, M.L.F.; Sheehy, S.L.; Tan, Y.R.E.; Williams, I.M.; Yap, J.S.L. Dosimetry for FLASH and other non-standard radiotherapy sources. Radiat. Meas. 2025, 180, 107330. [Google Scholar] [CrossRef]
- Gonçalves Jorge, P.; Grilj, V.; Bourhis, J.; Vozenin, M.C.; Germond, J.F.; Bochud, F.; Bailat, C.; Moeckli, R. Technical note: Validation of an ultrahigh dose rate pulsed electron beam monitoring system using a current transformer for FLASH preclinical studies. Med. Phys. 2022, 49, 1831–1838. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Cetnar, A.; Woollard, J.; Gupta, N.; Blakaj, D.; Chakravarti, A.; Ayan, A.S. Pulse parameter optimizer: An efficient tool for achieving prescribed dose and dose rate with electron FLASH platforms. Phys. Med. Biol. 2023, 68. [Google Scholar] [CrossRef] [PubMed]
- Cayley, J.; Paino, J.; Guatelli, S.; Rosenfeld, A.; Lerch, M.; Tan, Y.R.E. Simulation and commissioning of a Faraday cup for absolute charge measurements of very high-energy electrons in-air at PEER. Front. Phys. 2024, 12. [Google Scholar] [CrossRef]
- Vozenin, M.C.; Montay-Gruel, P.; Limoli, C.; Germond, J.F. All Irradiations that are Ultra-High Dose Rate may not be FLASH: The Critical Importance of Beam Parameter Characterization and In Vivo Validation of the FLASH Effect. Radiat. Res. 2020, 194, 571–572. [Google Scholar] [CrossRef] [PubMed]
- Bateman, J.J.; Buchanan, E.; Corsini, R.; Farabolini, W.; Korysko, P.; Garbrecht Larsen, R.; Malyzhenkov, A.; Ortega Ruiz, I.; Rieker, V.; Gerbershagen, A.; et al. Development of a novel fibre optic beam profile and dose monitor for very high energy electron radiotherapy at ultrahigh dose rates. Phys. Med. Biol. 2024, 69, 085006. [Google Scholar] [CrossRef] [PubMed]
- Clements, N.; Esplen, N.; Bateman, J.; Robertson, C.; Dosanjh, M.; Korysko, P.; Farabolini, W.; Corsini, R.; Bazalova-Carter, M. Mini-GRID radiotherapy on the CLEAR very-high-energy electron beamline: Collimator optimization, film dosimetry, and Monte Carlo simulations. Phys. Med. Biol. 2024, 69. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, M.R.; Melemenidis, S.; Liu, K.; Grilj, V.; Jansen, J.; Velasquez, B.; Connell, L.; Schulz, J.B.; Bailat, C.; Libed, A.; et al. Multi-Institutional Audit of FLASH and Conventional Dosimetry With a 3D Printed Anatomically Realistic Mouse Phantom. Int. J. Radiat. Oncol. 2024, 120, 287–300. [Google Scholar] [CrossRef] [PubMed]
- Almeida, A.; Togno, M.; Ballesteros-Zebadua, P.; Franco-Perez, J.; Geyer, R.; Schaefer, R.; Petit, B.; Grilj, V.; Meer, D.; Safai, S.; et al. Dosimetric and biologic intercomparison between electron and proton FLASH beams. Radiother. Oncol. J. Eur. Soc. Ther. Radiol. Oncol. 2024, 190, 109953. [Google Scholar] [CrossRef] [PubMed]
- Kranzer, R.; Schüller, A.; Bourgouin, A.; Hackel, T.; Poppinga, D.; Lapp, M.; Looe, H.K.; Poppe, B. Response of diamond detectors in ultra-high dose-per-pulse electron beams for dosimetry at FLASH radiotherapy. Phys. Med. Biol. 2022, 67, 075002. [Google Scholar] [CrossRef] [PubMed]
- Gómez, F.; Gonzalez-Castaño, D.M.; Fernández, N.G.; Pardo-Montero, J.; Schüller, A.; Gasparini, A.; Vanreusel, V.; Verellen, D.; Felici, G.; Kranzer, R.; et al. Development of an ultra-thin parallel plate ionization chamber for dosimetry in FLASH radiotherapy. Med. Phys. 2022, 49, 4705–4714. [Google Scholar] [CrossRef] [PubMed]
- Di Martino, F.; Barca, P.; Barone, S.; Bortoli, E.; Borgheresi, R.; De Stefano, S.; Di Francesco, M.; Faillace, L.; Giuliano, L.; Grasso, L.; et al. FLASH Radiotherapy With Electrons: Issues Related to the Production, Monitoring, and Dosimetric Characterization of the Beam. Front. Phys. 2020, 8. [Google Scholar] [CrossRef]
- Di Martino, F.; Giannelli, M.; Traino, A.C.; Lazzeri, M. Ion recombination correction for very high dose-per-pulse high-energy electron beams. Med. Phys. 2005, 32, 2204–2210. [Google Scholar] [CrossRef] [PubMed]
- Fleetwood, D.; Winokur, P.; Schwank, J. Using laboratory X-ray and cobalt-60 irradiations to predict CMOS device response in strategic and space environments. IEEE Trans. Nucl. Sci. 1988, 35, 1497–1505. [Google Scholar] [CrossRef]
- Su, F.Y.; Biasi, G.; Tran, L.T.; Pan, V.; Hill, D.; Lielkajis, M.; Cutajar, D.; Petasecca, M.; Lerch, M.; Pastuovic, Z.; et al. Characterization of MOSFET Dosimeters for Alpha Particle Therapy. IEEE Trans. Nucl. Sci. 2022, 69, 925–931. [Google Scholar] [CrossRef]
- Alnawaf, H.; Butson, M.; Yu, P.K.N. Measurement and effects of MOSKIN detectors on skin dose during high energy radiotherapy treatment. Australas. Phys. Eng. Sci. Med. 2012, 35, 321–328. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.H.; Cutajar, D.; Metcalfe, P.; Downes, S. Application of MOSkin detector for in vivo dosimetry on total skin electron therapy (TSET). Biomed. Phys. Eng. Express 2018, 4, 024002. [Google Scholar] [CrossRef]
- Jong, W.; Ung, N.; Tiong, A.; Rosenfeld, A.; Wong, J. Characterisation of a MOSFET-based detector for dose measurement under megavoltage electron beam radiotherapy. Radiat. Phys. Chem. 2018, 144, 76–84. [Google Scholar] [CrossRef]
- Jong, W.L.; Wong, J.; Ung, N.M.; Kh, N.; Ho, G.; Cutajar, D.; Rosenfeld, A. Characterization of MOSkin detector for in vivo skin dose measurement during megavoltage radiotherapy. J. Appl. Clin. Med. Phys. Am. Coll. Med. Phys. 2014, 15, 4869. [Google Scholar] [CrossRef] [PubMed]
- Kwan, I.; Rosenfeld, A.; Qi, Z.; Wilkinson, D.; Lerch, M.; Cutajar, D.; Safavi-Naeni, M.; Butson, M.; Bucci, J.; Chin, Y.; et al. Skin dosimetry with new MOSFET detectors. Radiat. Meas. 2008, 43, 929–932. [Google Scholar] [CrossRef]
- Patterson, E.; Stokes, P.; Cutajar, D.; Rosenfeld, A.; Baines, J.; Metcalfe, P.; Powers, M. High-resolution entry and exit surface dosimetry in a 1.5 T MR-linac. Phys. Eng. Sci. Med. 2023, 46, 787–800. [Google Scholar] [CrossRef] [PubMed]
- Tai, M.; Patterson, E.; Metcalfe, P.E.; Rosenfeld, A.; Oborn, B.M. Skin Dose Modeling and Measurement in a High Field In-Line MRI-Linac System. Front. Phys. 2022, 10. [Google Scholar] [CrossRef]
- Thorpe, N.K.; Cutajar, D.; Lian, C.; Pitney, M.; Friedman, D.; Perevertaylo, V.; Rosenfeld, A. A comparison of entrance skin dose delivered by clinical angiographic c-arms using the real-time dosimeter: The MOSkin. Australas. Phys. Eng. Sci. Med. 2016, 39, 423–430. [Google Scholar] [CrossRef] [PubMed]
- Lian, C.P.L.; Othman, M.A.R.; Cutajar, D.; Butson, M.; Guatelli, S.; Rosenfeld, A.B. Monte Carlo study of the energy response and depth dose water equivalence of the MOSkin radiation dosimeter at clinical kilovoltage photon energies. Australas. Phys. Eng. Sci. Med. 2011, 34, 273–279. [Google Scholar] [CrossRef] [PubMed]
- Patterson, E.; Powers, M.; Metcalfe, P.E.; Cutajar, D.; Oborn, B.M.; Baines, J.A. Electron streaming dose measurements and calculations on a 1.5 T MR-Linac. J. Appl. Clin. Med. Phys. 2024, 25, e14370. [Google Scholar] [CrossRef] [PubMed]
- Valentin, J. Basic anatomical and physiological data for use in radiological protection: Reference values: ICRP Publication 89. Ann. ICRP 2002, 32, 1–277. [Google Scholar] [CrossRef]
- Council Directive 2013/59/Euratom of 5 December 2013 Laying Down Basic Safety Standards for Protection Against the Dangers Arising from Exposure to Ionising Radiation, and Repealing Directives 89/618/Euratom, 90/641/Euratom, 96/29/Euratom, 97/43/Euratom and 2003/122/Euratom. 2013. Available online: http://data.europa.eu/eli/dir/2013/59/oj/eng (accessed on 3 February 2025).
- Safari, M.J.; Wong, J.H.D.; Ng, K.H.; Jong, W.L.; Cutajar, D.L.; Rosenfeld, A.B. Characterization of a MOSkin detector for in vivo skin dose measurements during interventional radiology procedures. Med. Phys. 2015, 42, 2550–2559. [Google Scholar] [CrossRef] [PubMed]
- Carrara, M.; Romanyukha, A.; Tenconi, C.; Mazzeo, D.; Cerrotta, A.; Borroni, M.; Cutajar, D.; Petasecca, M.; Lerch, M.; Bucci, J.; et al. Clinical application of MOSkin dosimeters to rectal wall in vivo dosimetry in gynecological HDR brachytherapy. Phys. Medica 2017, 41, 5–12. [Google Scholar] [CrossRef] [PubMed]
- Legge, K.; Cutajar, D.; Wilfert, A.; Martin, J.; Rozenfeld, A.; O’Connor, D.J.; Greer, P. SU-F-T-328: Real-Time in Vivo Dosimetry of Prostate SBRT Boost Treatments Using MOSkin Detectors. Med. Phys. 2016, 43, 3538. [Google Scholar] [CrossRef]
- Poder, J.; Howie, A.; Brown, R.; Bucci, J.; Rosenfeld, A.; Enari, K.; Schreiber, K.; Carrara, M.; Bece, A.; Malouf, D.; et al. Towards real time in-vivo rectal dosimetry during trans-rectal ultrasound based high dose rate prostate brachytherapy using MOSkin dosimeters. Radiother. Oncol. 2020, 151, 273–279. [Google Scholar] [CrossRef] [PubMed]
- Jong, W.; Ung, N.; Wong, J.; Ng, K.; Wan Ishak, W.; Abdul Malik, R.; Phua, V.; Cutajar, D.; Metcalfe, P.; Rosenfeld, A.; et al. In vivo skin dose measurement using MOSkin detectors in tangential breast radiotherapy. Phys. Medica 2016, 32, 1466–1474. [Google Scholar] [CrossRef] [PubMed]
- Souris, J.S.; Cheng, S.H.; Pelizzari, C.; Chen, N.T.; La Riviere, P.; Chen, C.T.; Lo, L.W. Radioluminescence characterization of in situ x-ray nanodosimeters: Potential real-time monitors and modulators of external beam radiation therapy. Appl. Phys. Lett. 2014, 105, 203110. [Google Scholar] [CrossRef] [PubMed]
- Cayley, J.; Tan, Y.R.E.; Petasecca, M.; Cutajar, D.; Breslin, T.; Rosenfeld, A.; Lerch, M. MOSkin dosimetry for an ultra-high dose-rate, very high-energy electron irradiation environment at PEER. Front. Phys. 2024, 12. [Google Scholar] [CrossRef]
- Smyth, L.; Alves, A.; Collins, K.; Beveridge, S. Gafchromic EBT3 Film Provides Equivalent Dosimetric Performance to EBT-XD Film for Stereotactic Radiosurgery Dosimetry. Phys. Eng. Sci. Med. 2024, 47, 1095–1106. [Google Scholar] [CrossRef] [PubMed]
- Szpala, S.; Huang, V.; Zhao, Y.; Kyle, A.; Minchinton, A.; Karan, T.; Kohli, K. Dosimetry with a clinical linac adapted to FLASH electron beams. J. Appl. Clin. Med. Phys. 2021, 22, 50–59. [Google Scholar] [CrossRef] [PubMed]
- Ashland. Ashland EBT-XD Datasheet. Available online: https://www.ashland.com/file_source/Ashland/Documents/PHA21-011_Gafchromic%20EBT-XD%20Protocol.pdf (accessed on 12 May 2024).
- Wanstall, H.C.; Korysko, P.; Farabolini, W.; Corsini, R.; Bateman, J.J.; Rieker, V.; Hemming, A.; Henthorn, N.T.; Merchant, M.J.; Santina, E.; et al. VHEE FLASH sparing effect measured at CLEAR, CERN with DNA damage of pBR322 plasmid as a biological endpoint. Sci. Rep. 2024, 14, 14803. [Google Scholar] [CrossRef] [PubMed]
- Whitmore, L.; Mackay, R.I.; van Herk, M.; Korysko, P.; Farabolini, W.; Malyzhenkov, A.; Corsini, R.; Jones, R.M. CERN-based experiments and Monte-Carlo studies on focused dose delivery with very high energy electron (VHEE) beams for radiotherapy applications. Sci. Rep. 2024, 14, 11120. [Google Scholar] [CrossRef] [PubMed]
- Lagzda, A.; Angal-Kalinin, D.; Jones, J.; Aitkenhead, A.; Kirkby, K.J.; MacKay, R.; Van Herk, M.; Farabolini, W.; Zeeshan, S.; Jones, R.M. Influence of heterogeneous media on Very High Energy Electron (VHEE) dose penetration and a Monte Carlo-based comparison with existing radiotherapy modalities. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2020, 482, 70–81. [Google Scholar] [CrossRef]
- Small, K.L.; Henthorn, N.T.; Angal-Kalinin, D.; Chadwick, A.L.; Santina, E.; Aitkenhead, A.; Kirkby, K.J.; Smith, R.J.; Surman, M.; Jones, J.; et al. Evaluating very high energy electron RBE from nanodosimetric pBR322 plasmid DNA damage. Sci. Rep. 2021, 11, 3341. [Google Scholar] [CrossRef] [PubMed]
- Verona Rinati, G.; Felici, G.; Galante, F.; Gasparini, A.; Kranzer, R.; Mariani, G.; Pacitti, M.; Prestopino, G.; Schüller, A.; Vanreusel, V.; et al. Application of a Novel Diamond Detector for Commissioning of FLASH Radiotherapy Electron Beams. Med. Phys. 2022, 49, 5513–5522. [Google Scholar] [CrossRef] [PubMed]
- Bourgouin, A.; Schüller, A.; Hackel, T.; Kranzer, R.; Poppinga, D.; Kapsch, R.P.; McEwen, M. Calorimeter for Real-Time Dosimetry of Pulsed Ultra-High Dose Rate Electron Beams. Front. Phys. 2020, 8. [Google Scholar] [CrossRef]
- Medina, E.; Ferro, A.; Abujami, M.; Camperi, A.; Centis Vignali, M.; Data, E.; Del Sarto, D.; Deut, U.; Di Martino, F.; Fadavi Mazinani, M.; et al. First Experimental Validation of Silicon-Based Sensors for Monitoring Ultra-High Dose Rate Electron Beams. Front. Phys. 2024, 12. [Google Scholar] [CrossRef]
- Villoing, D.; Koumeir, C.; Bongrand, A.; Guertin, A.; Haddad, F.; Métivier, V.; Poirier, F.; Potiron, V.; Servagent, N.; Supiot, S.; et al. Technical note: Proton beam dosimetry at ultra-high dose rates (FLASH): Evaluation of GAFchromic™ (EBT3, EBT-XD) and OrthoChromic (OC-1) film performances. Med. Phys. 2022, 49, 2732–2745. [Google Scholar] [CrossRef] [PubMed]
- Del Sarto, D.; Masturzo, L.; Cavalieri, A.; Celentano, M.; Fuentes, T.; Gadducci, G.; Giannini, N.; Gonnelli, A.; Milluzzo, G.; Paiar, F.; et al. A systematic investigation on the response of EBT-XD gafchromic films to varying dose-per-pulse, average dose-rate and instantaneous dose-rate in electron flash beams. Front. Phys. 2025, 13. [Google Scholar] [CrossRef]
- Oldham, T.R. Ionizing Radiation Effects in MOS Oxides; International Series on Advances in Solid State Electronics and Technology; World Scientific: Singapore, 2000. [Google Scholar] [CrossRef]
- Oldham, T.R. Basic Mechanisms of TID and DDD Response in MOS and Bipolar Microelectronics; NASA: Washington, DC, USA, 2012.
- Ma, T.; Dressendorfer, P. Ionizing Radiation Effects in MOS Devices and Circuits; INIS Reference Number: 21087484; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Zilio, V.O.; Joneja, O.P.; Popowski, Y.; Rosenfeld, A.; Chawla, R. Absolute depth-dose-rate measurements for an 192Ir HDR brachytherapy source in water using MOSFET detectors. Med. Phys. 2006, 33, 1532–1539. [Google Scholar] [CrossRef] [PubMed]
- Kattner, K. Modelling the effects of heavy charged particles on MOSFETs. Air Force Inst. Technol. 1988. [Google Scholar]
- Ausman, G. Field Dependence of Geminate Recombination in a Dielectric Medium; Defense Technical Information Center: Fort Belvoir, VI, USA, 1987. [Google Scholar]
- Wojcik, M.; Tachiya, M. Geminate charge recombination with distance-dependent intrinsic reaction rate: Escape probability and its electric field effect. Radiat. Phys. Chem. 2005, 74, 132–138. [Google Scholar] [CrossRef]
- Tachiya, M. Breakdown of the Onsager theory of geminate ion recombination. J. Chem. Phys. 1988, 89, 6929–6935. [Google Scholar] [CrossRef]
- The International Commission on Radiation Units and Measurements (ICRU). Stopping Powers for Electrons and Positrons; Technical Report 0-913394-31-9—ICRU–37 INIS Reference Number: 24031395; ICRU: Bethesda, MA, USA, 1984. [Google Scholar]
- Bichsel, H. Stopping Power of Fast Charged Particles in Heavy Elements; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1991.
- NIST. NIST E-Star Database. Available online: https://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html (accessed on 27 June 2024).
- Hughes, R.C. High field electronic properties of SiO2. Solid-State Electron. 1978, 21, 251–258. [Google Scholar] [CrossRef]
- Brown, D.B.; Dozier, C.M. Electron-Hole Recombination in Irradiated SiO2 from a Microdosimetry Viewpoint. IEEE Trans. Nucl. Sci. 1981, 28, 4142–4144. [Google Scholar] [CrossRef]
- Murat, M.; Akkerman, A.; Barak, J. Spatial distribution of electron-hole pairs induced by electrons and protons in SiO/sub 2/. IEEE Trans. Nucl. Sci. 2004, 51, 3211–3218. [Google Scholar] [CrossRef]
- Chan, M.F.; Park, J.; Aydin, R.; Lim, S.B. Technical note: Energy dependence of the Gafchromic EBT4 film: Dose-response curves for 70 kV, 6 MV, 6 MV FFF, 10 MV FFF, and 15 MV x-ray beams. Med. Phys. 2023, 50, 3738–3745. [Google Scholar] [CrossRef] [PubMed]
- Massillon-Jl, G.; Chiu-Tsao, S.T.; Muñoz, I. Energy Dependence of the New Gafchromic EBT3 Film: Dose Response Curves for 50 kV, 6 and 15 MV X-Ray Beams. Int. J. Med. Physics, Clin. Eng. Radiat. Oncol. 2012, 1, 60–65. [Google Scholar] [CrossRef]
- Arce, P.; Bolst, D.; Bordage, M.C.; Brown, J.M.C.; Cirrone, P.; Cortés-Giraldo, M.A.; Cutajar, D.; Cuttone, G.; Desorgher, L.; Dondero, P.; et al. Report on G4-Med, a Geant4 benchmarking system for medical physics applications developed by the Geant4 Medical Simulation Benchmarking Group. Med. Phys. 2021, 48, 19–56. [Google Scholar] [CrossRef] [PubMed]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—a simulation toolkit. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Filipev, I.; Alnaghy, S.; Carolan, M.; Paino, J.; Petasecca, M.; Cutajar, D.; Poder, J.; Davies, J.B.; Oborn, B.M.; Hardcastle, N.; et al. High Spatial Resolution Dosimetry for Radiation Oncology with “MagicPlates”, a New 976-pixel Monolithic Silicon Detector. J. Appl. Clin. Med. Phys. 2025, 26, e70015. [Google Scholar] [CrossRef] [PubMed]


| Varian Truebeam | PEER | |
|---|---|---|
| Bunch Length | Unknown | 100 ps |
| Pulse Length | 3–5 | 20–400 ns |
| DPP | ∼ Gy | 1–23 Gy |
| Max Average Dose rates | ∼ Gy/s | ∼ Gy/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cayley, J.; Engels, E.; Charles, T.; Bennetto, P.; Cameron, M.; Poder, J.; Hausermann, D.; Paino, J.; Butler, D.; Cutajar, D.; et al. Establishing Linearity of the MOSkin Detector for Ultra-High Dose-per-Pulse, Very-High-Energy Electron Radiotherapy Using Dose-Rate-Corrected EBT-XD Film. Appl. Sci. 2025, 15, 8101. https://doi.org/10.3390/app15148101
Cayley J, Engels E, Charles T, Bennetto P, Cameron M, Poder J, Hausermann D, Paino J, Butler D, Cutajar D, et al. Establishing Linearity of the MOSkin Detector for Ultra-High Dose-per-Pulse, Very-High-Energy Electron Radiotherapy Using Dose-Rate-Corrected EBT-XD Film. Applied Sciences. 2025; 15(14):8101. https://doi.org/10.3390/app15148101
Chicago/Turabian StyleCayley, James, Elette Engels, Tessa Charles, Paul Bennetto, Matthew Cameron, Joel Poder, Daniel Hausermann, Jason Paino, Duncan Butler, Dean Cutajar, and et al. 2025. "Establishing Linearity of the MOSkin Detector for Ultra-High Dose-per-Pulse, Very-High-Energy Electron Radiotherapy Using Dose-Rate-Corrected EBT-XD Film" Applied Sciences 15, no. 14: 8101. https://doi.org/10.3390/app15148101
APA StyleCayley, J., Engels, E., Charles, T., Bennetto, P., Cameron, M., Poder, J., Hausermann, D., Paino, J., Butler, D., Cutajar, D., Petasecca, M., Rosenfeld, A., Tan, Y.-R. E., & Lerch, M. (2025). Establishing Linearity of the MOSkin Detector for Ultra-High Dose-per-Pulse, Very-High-Energy Electron Radiotherapy Using Dose-Rate-Corrected EBT-XD Film. Applied Sciences, 15(14), 8101. https://doi.org/10.3390/app15148101






