Multi-View Cluster Structure Guided One-Class BLS-Autoencoder for Intrusion Detection
Abstract
1. Introduction
- 1.
- A multi-view co-association matrix optimization objective function with doubly-stochastic constraints is designed, which systematically unifies view-specific spectral embedding from ensemble partitions and better captures the underlying cluster structure across different views.
- 2.
- A multi-view cluster structure guided one-class BLS-autoencoder (MOCBLSAE) is proposed, which learns discriminative patterns of normal traffic data by preserving the cross-view clustering structure while minimizing the intra-view sample reconstruction errors, thereby enabling the identification of unknown intrusion data.
- 3.
- Based on MOCBLSAE, an intrusion detection framework is constructed and validated on real-world network traffic datasets for multi-view one-class classification tasks, demonstrating its superiority over state-of-the-art one-class methods.
2. Related Works
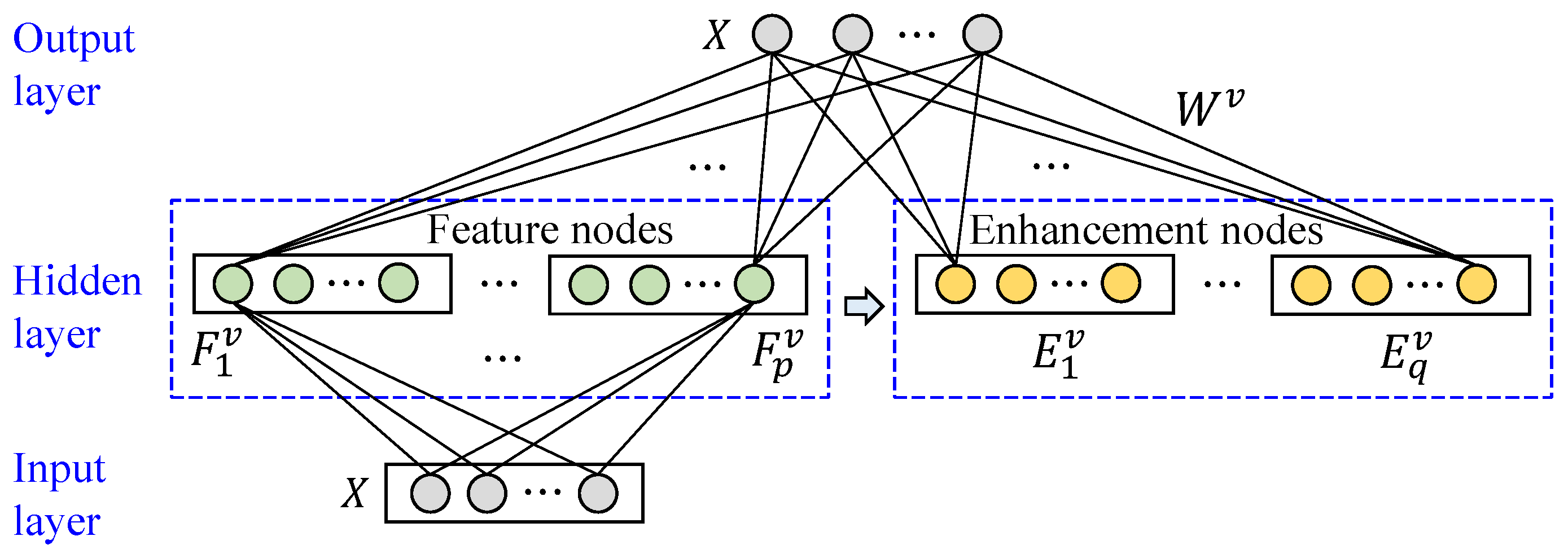
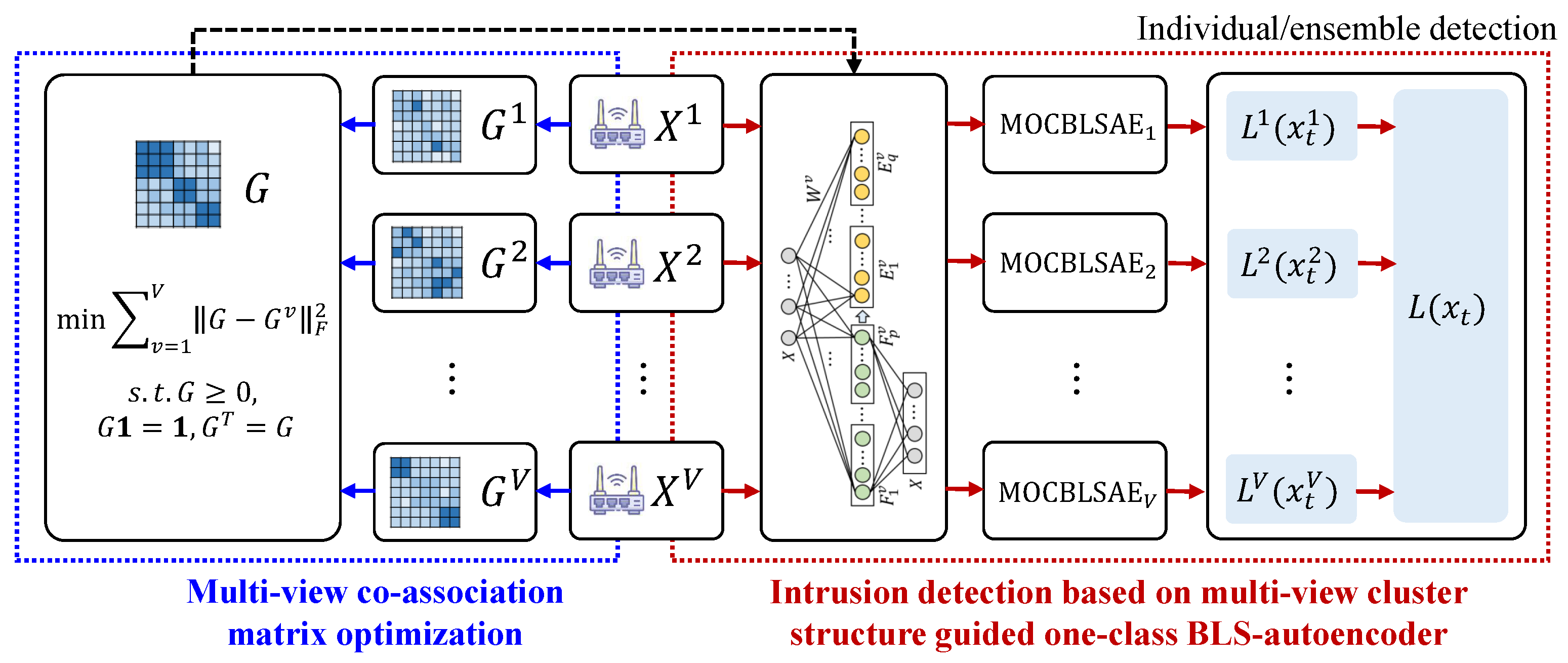
3. Proposed Method
3.1. Definition
3.2. Multi-View Co-Association Matrix Optimization
| Algorithm 1 Multi-view co-association matrix optimization |
|
3.3. Intrusion Detection Framework Based on the Multi-View Cluster Structure Guided One-Class BLS-Autoencoder
| Algorithm 2 Intrusion detection based on multi-view cluster structure guided one-class BLS-autoencoder (IDF-MOCBLSAE) |
|
4. Experiments
4.1. Datasets and Experimental Setup
4.2. Comparison of OCC Methods
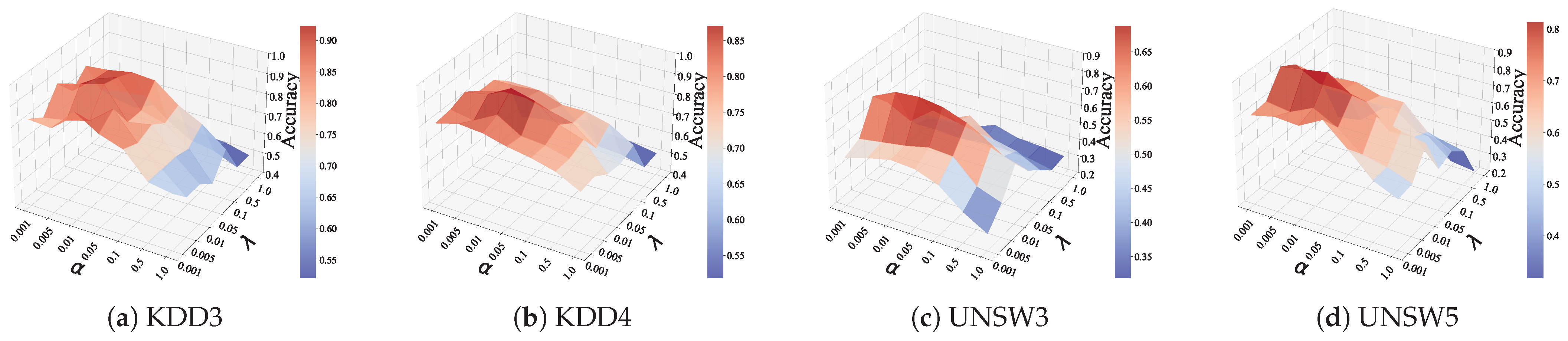
4.3. Parameter Sensitivity Analysis
4.4. Ablation Analysis
4.5. Time Efficiency Analysis
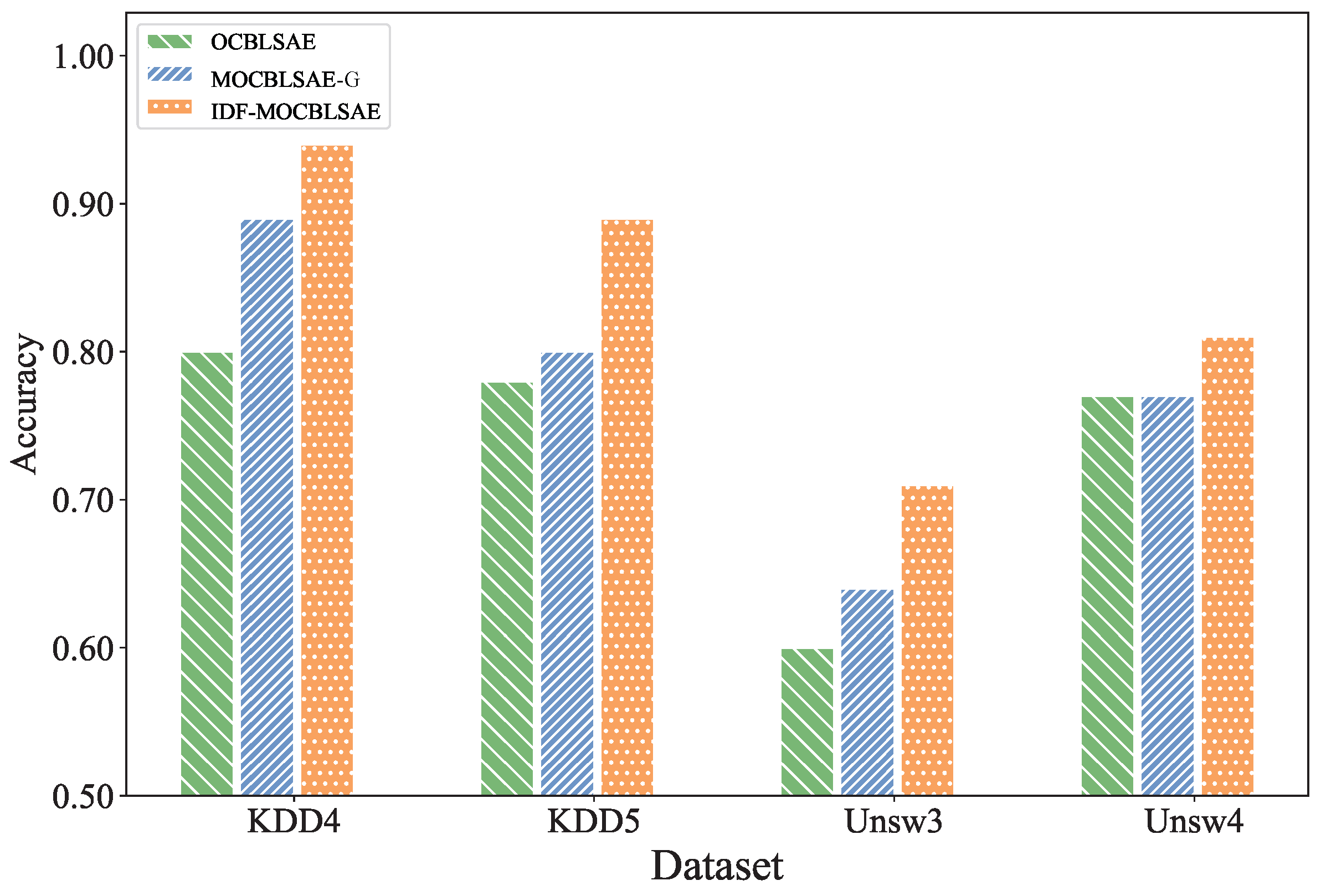

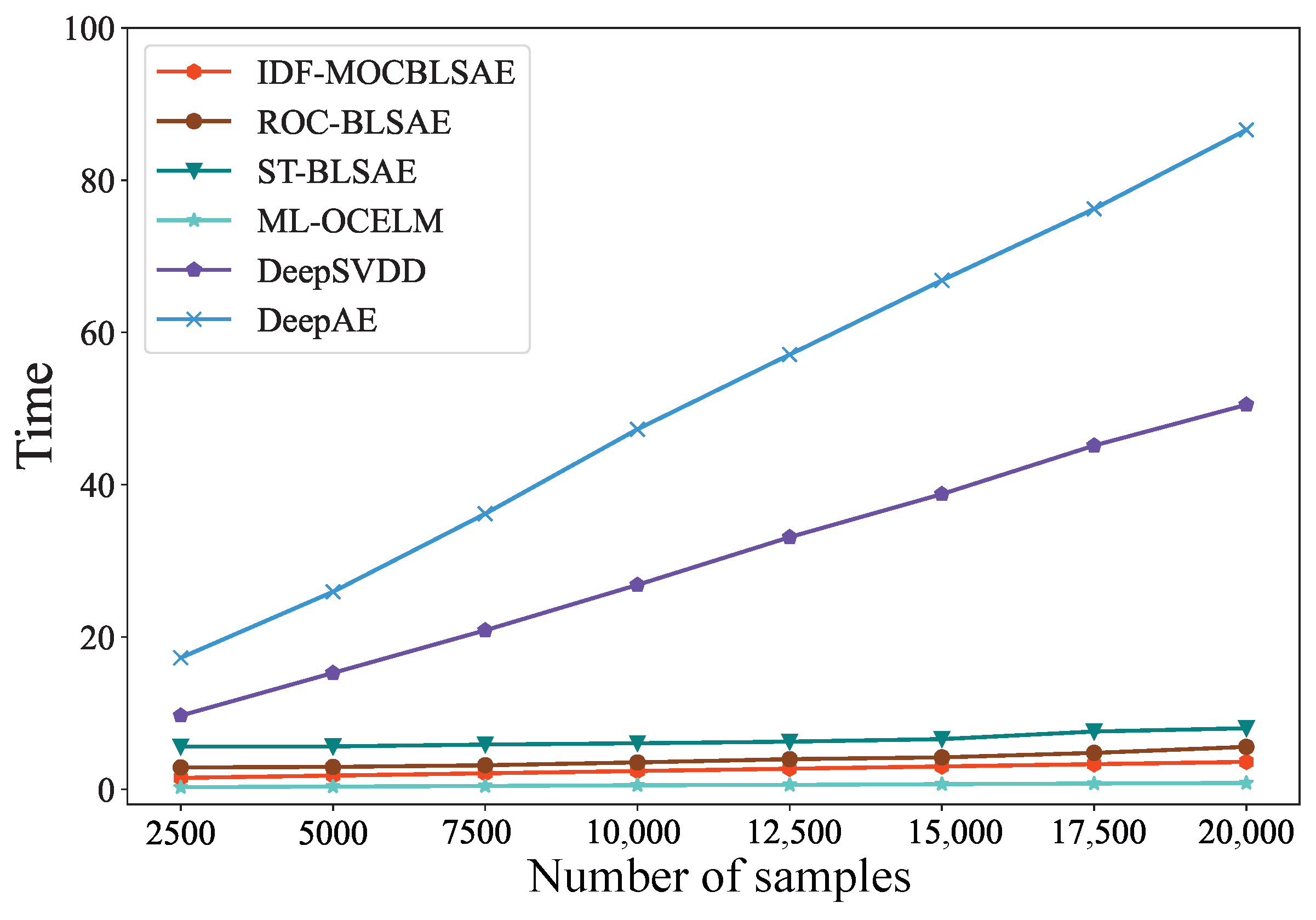
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pang, J.; Pu, X.; Li, C. A Hybrid Algorithm Incorporating Vector Quantization and One-Class Support Vector Machine for Industrial Anomaly Detection. IEEE Trans. Ind. Inform. 2022, 18, 8786–8796. [Google Scholar] [CrossRef]
- Sarmadi, H.; Karamodin, A. A novel anomaly detection method based on adaptive mahalanobis-squared distance and one-class knn rule for structural health monitoring under environmental effects. Mech. Syst. Signal Process. 2020, 140, 106495. [Google Scholar] [CrossRef]
- Li, D.; Xu, X.; Wang, Z.; Cao, C.; Wang, M. Boundary-based Fuzzy-SVDD for one-class classification. Int. J. Intell. Syst. 2022, 37, 2266–2292. [Google Scholar] [CrossRef]
- Dong, X.; Taylor, C.J.; Cootes, T.F. Defect Classification and Detection Using a Multitask Deep One-Class CNN. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1719–1730. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.; Jian, S.; Liao, Q.; Wang, Y.; Pang, G. Calibrated One-Class Classification for Unsupervised Time Series Anomaly Detection. IEEE Trans. Knowl. Data Eng. 2024, 36, 5723–5736. [Google Scholar] [CrossRef]
- Peng, H.; Zhao, J.; Li, L.; Ren, Y.; Zhao, S. One-Class Adversarial Fraud Detection Nets With Class Specific Representations. IEEE Trans. Netw. Sci. Eng. 2023, 10, 3793–3803. [Google Scholar] [CrossRef]
- Pu, Z.; Cabrera, D.; Bai, Y.; Li, C. A One-Class Generative Adversarial Detection Framework for Multifunctional Fault Diagnoses. IEEE Trans. Ind. Electron. 2022, 69, 8411–8419. [Google Scholar] [CrossRef]
- Ding, Y.; Jia, M.; Cao, Y.; Yan, X.; Zhao, X.; Lee, C.G. Unsupervised Fault Detection With Deep One-Class Classification and Manifold Distribution Alignment. IEEE Trans. Ind. Inform. 2024, 20, 1313–1323. [Google Scholar] [CrossRef]
- Leng, Q.; Qi, H.; Miao, J.; Zhu, W.; Su, G. One-Class Classification with Extreme Learning Machine. Math. Probl. Eng. 2015, 2015, 412957. [Google Scholar] [CrossRef]
- Dai, H.; Cao, J.; Wang, T.; Deng, M.; Yang, Z. Multilayer One-Class Extreme Learning Machine. Neural Netw. 2019, 115, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.; Yang, K.; Yu, Z.; Shi, Y.; Chen, C.L.P. Hybrid Ensemble Broad Learning System for Network Intrusion Detection. IEEE Trans. Ind. Inform. 2024, 20, 5622–5633. [Google Scholar] [CrossRef]
- Yang, K.; Shi, Y.; Yu, Z.; Yang, Q.; Sangaiah, A.K.; Zeng, H. Stacked One-Class Broad Learning System for Intrusion Detection in Industry 4.0. IEEE Trans. Ind. Inform. 2023, 19, 251–260. [Google Scholar] [CrossRef]
- Xiao, Y.; Pan, G.; Liu, B.; Zhao, L.; Kong, X.; Hao, Z. Privileged Multi-View One-Class Support Vector Machine. Neurocomputing 2024, 572, 127186. [Google Scholar] [CrossRef]
- Lei, L.; Wang, X.; Zhong, Y.; Zhao, H.; Hu, X.; Luo, C. DOCC: Deep one-class crop classification via positive and unlabeled learning for multi-modal satellite imagery. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102598. [Google Scholar] [CrossRef]
- Golo, M.P.S.; Araujo, A.F.; Rossi, R.G.; Marcacini, R.M. Detecting Relevant App Reviews for Software Evolution and Maintenance Through Multimodal One-Class Learning. Inf. Softw. Technol. 2022, 151, 106998. [Google Scholar] [CrossRef]
- Sohrab, F.; Raitoharju, J.; Iosifidis, A.; Gabbouj, M. Multimodal subspace support vector data description. Pattern Recognit. 2021, 110, 107648. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Ji, Y.; Lee, H. Event-Based Anomaly Detection Using a One-Class SVM for a Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2022, 71, 6032–6043. [Google Scholar] [CrossRef]
- Swarnkar, M.; Hubballi, N. OCPAD: One class Naive Bayes classifier for payload based anomaly detection. Expert Syst. Appl. 2016, 64, 330–339. [Google Scholar] [CrossRef]
- Goernitz, N.; Lima, L.A.; Mueller, K.R.; Kloft, M.; Nakajima, S. Support vector data descriptions and k-means clustering: One class. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3994–4006. [Google Scholar] [CrossRef] [PubMed]
- Massoli, F.V.; Falchi, F.; Kantarci, A.; Akti, Ş.; Ekenel, H.K.; Amato, G. MOCCA: Multilayer one-class classification for anomaly detection. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2313–2323. [Google Scholar] [CrossRef] [PubMed]
- Mauceri, S.; Sweeney, J.; Nicolau, M.; McDermott, J. Dissimilarity-Preserving Representation Learning for One-Class Time Series Classification. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 13951–13962. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Chen, C.P.; Liu, Z. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Dai, H.; Lei, B.; Yin, C.; Zeng, H.; Kummert, A. Maximum Correntropy Criterion-Based Hierarchical One-Class Classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3748–3754. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Long, J.; Zi, Y.; Zhang, S.; Li, C. Incremental Novelty Identification From Initially One-Class Learning to Unknown Abnormality Classification. IEEE Trans. Ind. Electron. 2022, 69, 7394–7404. [Google Scholar] [CrossRef]
- Zhong, Z.; Yu, Z.; Fan, Z.; Chen, C.L.P.; Yang, K. Adaptive Memory Broad Learning System for Unsupervised Time Series Anomaly Detection. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 8331–8345. [Google Scholar] [CrossRef] [PubMed]
- Strehl, A.; Ghosh, J. Cluster ensembles: A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar] [CrossRef]
- Zass, R.; Shashua, A. Doubly stochastic normalization for spectral clustering. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; pp. 1569–1576. [Google Scholar] [CrossRef]
- Kasun, L.; Zhou, H.; Huang, G.; Vong, C. Representational learning with elms for big data. IEEE Intell. Syst. 2013, 28, 31–34. [Google Scholar][Green Version]
- Huang, G.; Song, S.; Gupta, J.N.D.; Wu, C. Semi-Supervised and Unsupervised Extreme Learning Machines. IEEE Trans. Cybern. 2014, 44, 2405–2417. [Google Scholar] [CrossRef] [PubMed]
- Tavallaee, M.; Bagheri, E.; Lu, W.; Ghorbani, A. A Detailed Analysis of the KDD CUP 99 Data Set. In Proceedings of the IEEE Symposium on Computational Intelligence for Security and Defense Applications, Ottawa, ON, Canada, 8–10 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Moustafa, N.; Slay, J. UNSW-NB15: A Comprehensive Data Set for Network Intrusion Detection Systems (UNSW-NB15 Network Data Set). In Proceedings of the Military Communications and Information Systems Conference, Canberra, Australia, 10–12 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Ruff, L.; Vandermeulen, R.; Goernitz, N.; Deecke, L.; Siddiqui, S.A.; Binder, A.; Müller, E.; Kloft, M. Deep one-class classification. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 4393–4402. [Google Scholar]
- Aggarwal, C.C. Outlier Analysis; Springer: Cham, Switzerland, 2015; pp. 75–79. [Google Scholar] [CrossRef]
| Task | Intrusion Type | (Normal + Intrusion) | Dimensions of Each View | |
|---|---|---|---|---|
| KDD1 | Warezclient | 20,000 | 20,000 + 890 | {20, 21} |
| KDD2 | Portsweep | 20,000 | 20,000 + 2931 | {20, 21} |
| KDD3 | Teardrop | 20,000 | 20,000 + 892 | {20, 21} |
| KDD4 | Nmap | 20,000 | 20,000 + 1493 | {20, 21} |
| KDD5 | Pod | 20,000 | 20,000 + 201 | {20, 21} |
| UNSW1 | Reconnaissance | 18,500 | 18,500 + 3496 | {21, 21} |
| UNSW2 | DoS | 18,500 | 18,500 + 4089 | {21, 21} |
| UNSW3 | Exploits | 18,500 | 18,500 + 11,132 | {21, 21} |
| UNSW4 | Fuzzers | 18,500 | 18,500 + 6062 | {21, 21} |
| UNSW5 | Generic | 18,500 | 18,500 + 18,871 | {21, 21} |
| Actual Class | Predicted Class | |
|---|---|---|
| Intrusion (Positive) | Normal (Negative) | |
| Intrusion (Positive) | TP | FN |
| Normal (Negative) | FP | TN |
| Task | IDF-MOCBLSAE | SMC-OCBLS | ST-OCBLS | ML-OCELM | DeepAE | DeepSVDD |
|---|---|---|---|---|---|---|
| KDD1 | 0.9552 | 0.8804 | 0.8018 | 0.7624 | 0.5799 | 0.6261 |
| KDD2 | 0.8711 | 0.9478 | 0.9326 | 0.8425 | 0.9601 | 0.8801 |
| KDD3 | 0.9525 | 0.8964 | 0.8873 | 0.9143 | 0.3616 | 0.7525 |
| KDD4 | 0.9381 | 0.9181 | 0.8891 | 0.7691 | 0.4234 | 0.604 |
| KDD5 | 0.8858 | 0.8001 | 0.7682 | 0.8119 | 0.4728 | 0.7921 |
| UNSW1 | 0.8482 | 0.8481 | 0.8415 | 0.8456 | 0.7699 | 0.7774 |
| UNSW2 | 0.9223 | 0.9455 | 0.9303 | 0.9224 | 0.8559 | 0.8681 |
| UNSW3 | 0.7139 | 0.8639 | 0.8531 | 0.7451 | 0.6817 | 0.7326 |
| UNSW4 | 0.8146 | 0.8108 | 0.8023 | 0.7868 | 0.7489 | 0.7545 |
| UNSW5 | 0.8881 | 0.9831 | 0.9404 | 0.7614 | 0.8328 | 0.7433 |
| Task | IDF-MOCBLSAE | SMC-OCBLS | ST-OCBLS | ML-OCELM | DeepAE | DeepSVDD |
|---|---|---|---|---|---|---|
| KDD1 | 0.9771 | 0.9163 | 0.8531 | 0.7993 | 0.5726 | 0.9163 |
| KDD2 | 0.9309 | 0.9623 | 0.9515 | 0.8671 | 0.9707 | 0.9623 |
| KDD3 | 0.9757 | 0.9281 | 0.9221 | 0.9384 | 0.1691 | 0.9281 |
| KDD4 | 0.9676 | 0.9419 | 0.9205 | 0.7883 | 0.3019 | 0.9419 |
| KDD5 | 0.9428 | 0.8694 | 0.8515 | 0.8759 | 0.3945 | 0.8694 |
| UNSW1 | 0.3121 | 0.2221 | 0.2306 | 0.1552 | 0.1102 | 0.2221 |
| UNSW2 | 0.8987 | 0.8357 | 0.7889 | 0.7643 | 0.3425 | 0.8357 |
| UNSW3 | 0.7679 | 0.7856 | 0.7677 | 0.4965 | 0.4319 | 0.5493 |
| UNSW4 | 0.4784 | 0.4252 | 0.4101 | 0.2761 | 0.3602 | 0.3824 |
| UNSW5 | 0.8581 | 0.9831 | 0.9375 | 0.6581 | 0.8226 | 0.6898 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Chen, Y.-A.; Shi, Y. Multi-View Cluster Structure Guided One-Class BLS-Autoencoder for Intrusion Detection. Appl. Sci. 2025, 15, 8094. https://doi.org/10.3390/app15148094
Yang Q, Chen Y-A, Shi Y. Multi-View Cluster Structure Guided One-Class BLS-Autoencoder for Intrusion Detection. Applied Sciences. 2025; 15(14):8094. https://doi.org/10.3390/app15148094
Chicago/Turabian StyleYang, Qifan, Yu-Ang Chen, and Yifan Shi. 2025. "Multi-View Cluster Structure Guided One-Class BLS-Autoencoder for Intrusion Detection" Applied Sciences 15, no. 14: 8094. https://doi.org/10.3390/app15148094
APA StyleYang, Q., Chen, Y.-A., & Shi, Y. (2025). Multi-View Cluster Structure Guided One-Class BLS-Autoencoder for Intrusion Detection. Applied Sciences, 15(14), 8094. https://doi.org/10.3390/app15148094






