Consensus Guided Multi-View Unsupervised Feature Selection with Hybrid Regularization
Abstract
1. Introduction
- Multiple view-specific basic partitions are integrated into a unified consensus matrix, which guides the feature selection process by preserving comprehensive pairwise constraints across diverse views.
- A hybrid regularization strategy incorporating the -norm and the Frobenius norm is introduced into the feature selection objective function, which not only promotes feature sparsity but also effectively prevents overfitting, thereby improving the stability of the model.
- The proposed CGMvFS framework is extensively evaluated on multiple multi-view datasets, demonstrating superior performance in unsupervised feature selection and robustness compared to existing methods.
2. Related Works
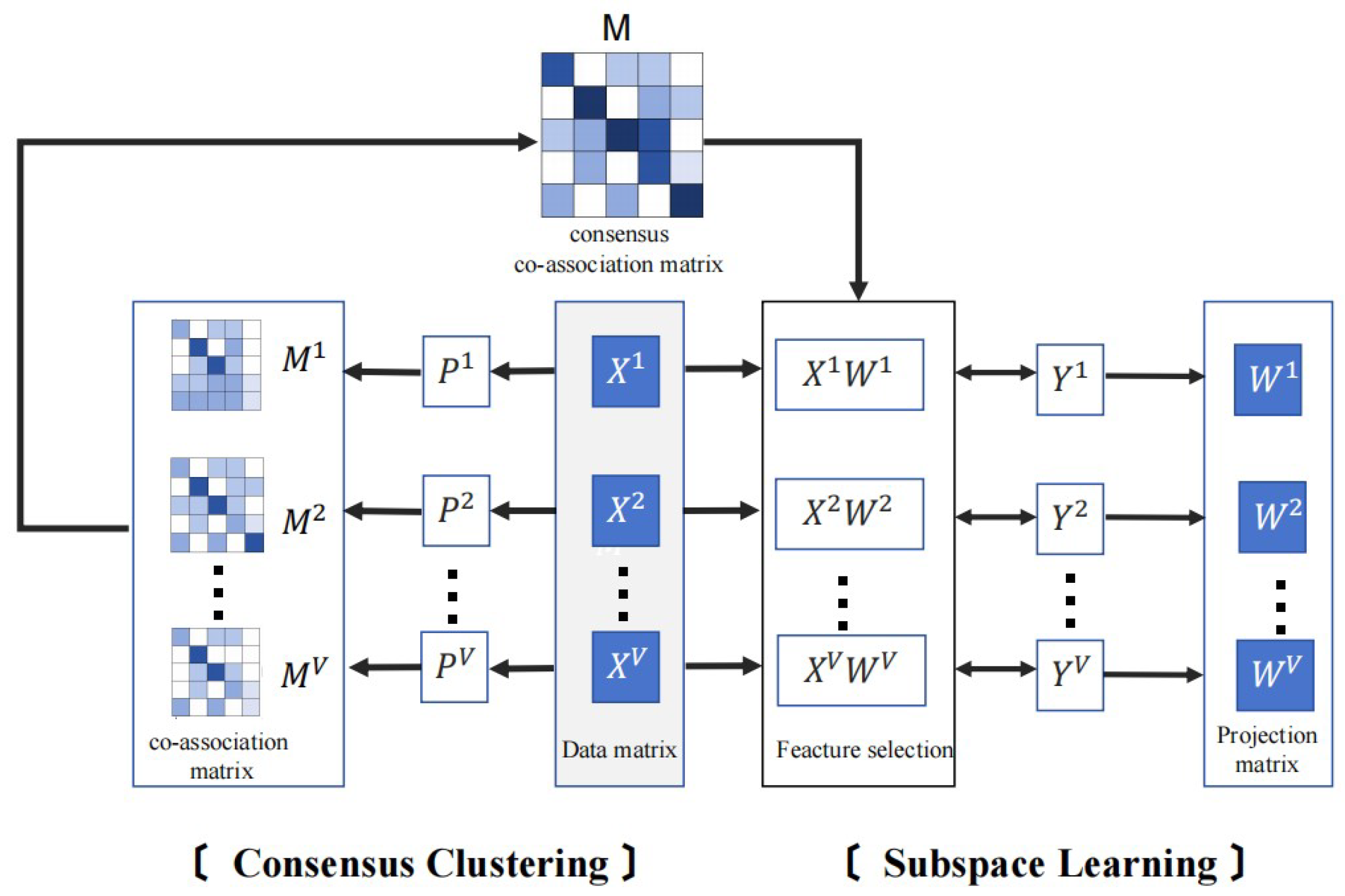
3. Proposed Method
3.1. Framework and Definition
3.2. Formulation
3.3. Optimization
| Algorithm 1 Consensus Guided Multi-view Unsupervised Feature Selection with Hybrid Regularization (CGMvFS) |
| Require: |
| Input: Multi-view dataset ,. |
| Ensure: |
| 1: Initialize ,. |
| 2: for each view to V do |
| 3: Generate basic partition ; |
| 4: Compute the co-affinity matrix and accumulate: ; |
| 5: end for |
| 6: Compute the global consensus matrix ; |
| 7: Calculate the consensus representation matrix through spectral decomposition; |
| 8: for each view to V do |
| 9: repeat |
| 10: Update ; |
| 11: Update ; |
| 12: until converges |
| 13: end for |
| Output Rank the features based on and select the top r most discriminative features. |
3.4. Computational Complexity Analysis
4. Experiments
4.1. Datasets and Experimental Setup
4.2. Comparison Experiment
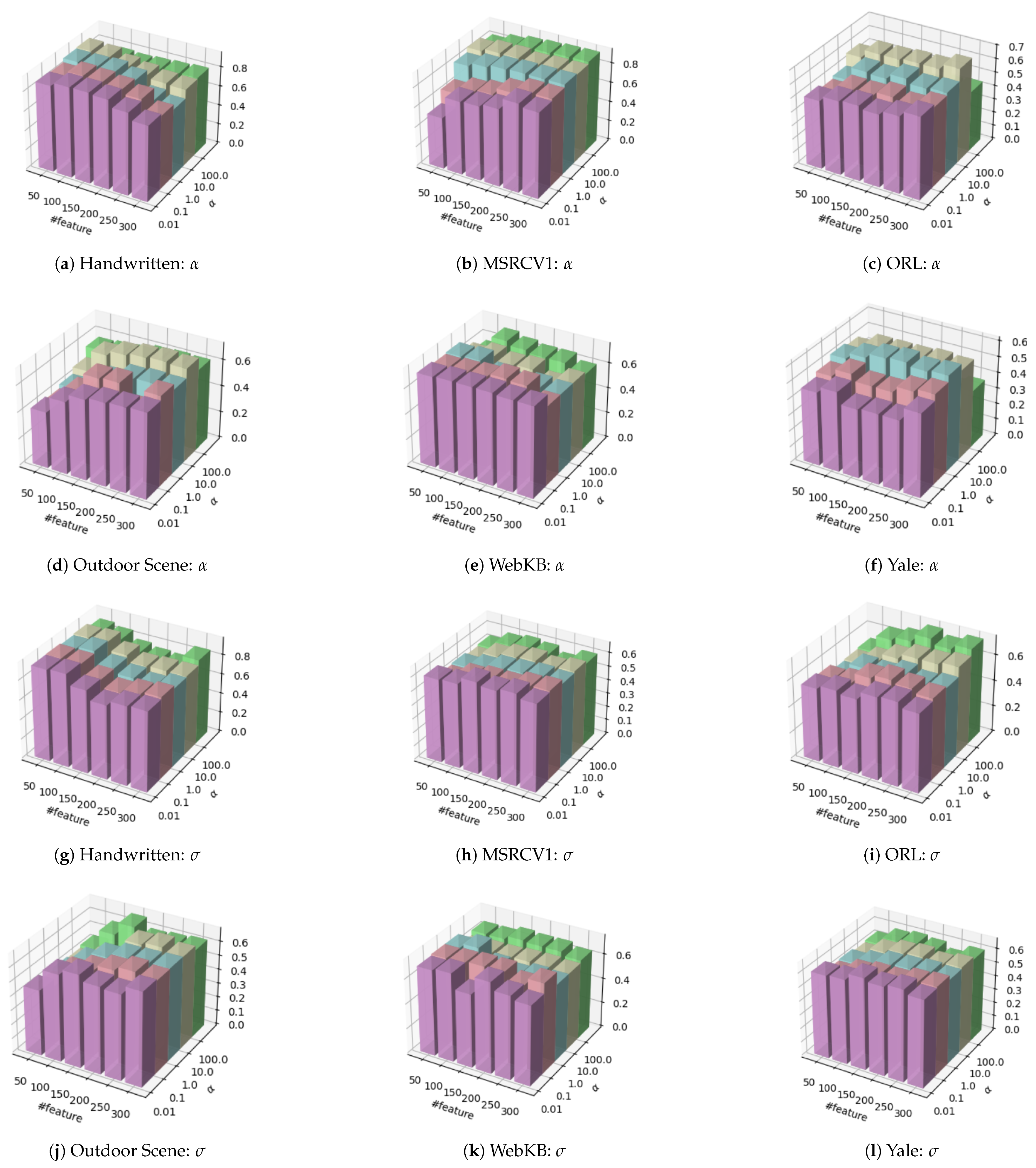
4.3. Parameter Sensitivity Analysis
4.4. Convergence Behavior Analysis
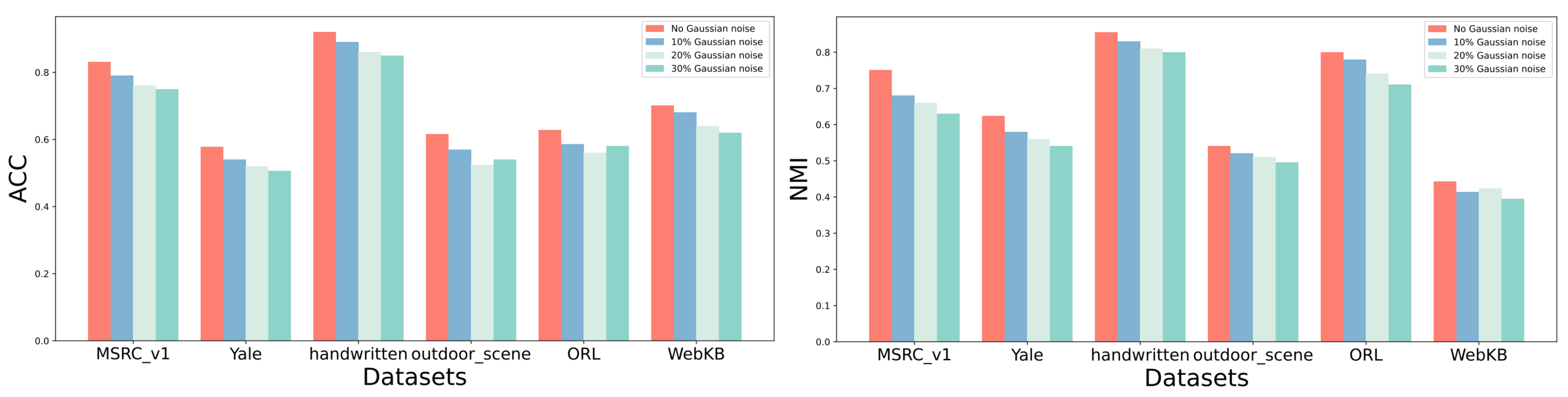
4.5. Robustness Analysis
4.6. Comparison of Running Time
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, Y.; Yu, Z.; Yang, K.; Philip Chen, C.L. Ensemble Denoising Autoencoders Based on Broad Learning System for Time-Series Anomaly Detection. IEEE Trans. Neural Netw. Learn. Syst. 2025, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Zhong, Z.; Yang, K.; Cao, W.; Chen, C.L.P. Broad Learning Autoencoder With Graph Structure for Data Clustering. IEEE Trans. Knowl. Data Eng. 2024, 36, 49–61. [Google Scholar] [CrossRef]
- Chen, W.; Yang, K.; Yu, Z.; Nie, F.; Chen, C.L.P. Adaptive Broad Network With Graph-Fuzzy Embedding for Imbalanced Noise Data. IEEE Trans. Fuzzy Syst. 2025, 33, 1949–1962. [Google Scholar] [CrossRef]
- Yu, Z.; Dong, Z.; Yu, C.; Yang, K.; Fan, Z.; Chen, C.P. A review on multi-view learning. Front. Comput. Sci. 2025, 19, 197334. [Google Scholar] [CrossRef]
- Lin, Q.; Yang, L.; Zhong, P.; Zou, H. Robust Supervised Multi-View Feature Selection with Weighted Shared Loss and Maximum Margin Criterion. Knowl.-Based Syst. 2021, 229, 107331. [Google Scholar] [CrossRef]
- Wang, C.; Song, P.; Duan, M.; Zhou, S.; Cheng, Y. Low-Rank Tensor Based Smooth Representation Learning for Multi-View Unsupervised Feature Selection. Knowl.-Based Syst. 2025, 309, 112902. [Google Scholar] [CrossRef]
- Duan, M.; Song, P.; Zhou, S.; Cheng, Y.; Mu, J.; Zheng, W. High-Order Correlation Preserved Multi-View Unsupervised Feature Selection. Eng. Appl. Artif. Intell. 2025, 139, 109507. [Google Scholar] [CrossRef]
- Yang, K.; Yu, Z.; Chen, W.; Liang, Z.; Chen, C.L.P. Solving the Imbalanced Problem by Metric Learning and Oversampling. IEEE Trans. Knowl. Data Eng. 2024, 36, 9294–9307. [Google Scholar] [CrossRef]
- Shi, C.; Gu, Z.; Duan, C.; Tian, Q. Multi-View Adaptive Semi-Supervised Feature Selection with the Self-Paced Learning. Signal Process. 2020, 168, 107332. [Google Scholar] [CrossRef]
- Zhang, C.; Fang, Y.; Liang, X.; Zhang, H.; Zhou, P.; Wu, X.; Yang, J.; Jiang, B.; Sheng, W. Efficient Multi-view Unsupervised Feature Selection with Adaptive Structure Learning and Inference. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI-24), Jeju, Republic of Korea, 3–9 August 2024. [Google Scholar]
- Cao, Z.; Xie, X.; Sun, F.; Qian, J. Consensus Cluster Structure Guided Multi-View Unsupervised Feature Selection. Knowl.-Based Syst. 2023, 271, 110578. [Google Scholar] [CrossRef]
- Tang, C.; Chen, J.; Liu, X.; Li, M.; Wang, P.; Wang, M.; Lu, P. Consensus Learning Guided Multi-View Unsupervised Feature Selection. Knowl.-Based Syst. 2018, 160, 49–60. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, K.; Wang, M.; Yu, Z.; Zeng, H.; Hu, Y. Boosted Unsupervised Feature Selection for Tumor Gene Expression Profiles. CAAI Trans. Intell. Technol. 2024. [Google Scholar] [CrossRef]
- Hou, C.; Nie, F.; Tao, H.; Yi, D. Multi-View Unsupervised Feature Selection with Adaptive Similarity and View Weight. IEEE Trans. Knowl. Data Eng. 2017, 29, 1998–2011. [Google Scholar] [CrossRef]
- Cao, Z.; Xie, X.; Li, Y. Multi-View Unsupervised Feature Selection with Consensus Partition and Diverse Graph. Inf. Sci. 2024, 661, 120178. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, Z.; Cai, Y.; Yi, X.; Wang, D.; Lv, F.; Li, T. C 2 IMUFS: Complementary and Consensus Learning-Based Incomplete Multi-View Unsupervised Feature Selection. IEEE Trans. Knowl. Data Eng. 2023, 35, 10681–10694. [Google Scholar] [CrossRef]
- Wan, Y.; Sun, S.; Zeng, C. Adaptive Similarity Embedding for Unsupervised Multi-View Feature Selection. IEEE Trans. Knowl. Data Eng. 2021, 33, 3338–3350. [Google Scholar] [CrossRef]
- Gong, X.; Gao, J.; Sun, S.; Zhong, Z.; Shi, Y.; Zeng, H.; Yang, K. Adaptive Compressed-based Privacy-preserving Large Language Model for Sensitive Healthcare. IEEE J. Biomed. Health Inform. 2025, 1–13. [Google Scholar] [CrossRef]
- Gong, X.; Chen, C.L.P.; Hu, B.; Zhang, T. CiABL: Completeness-Induced Adaptative Broad Learning for Cross-Subject Emotion Recognition With EEG and Eye Movement Signals. IEEE Trans. Affect. Comput. 2024, 15, 1970–1984. [Google Scholar] [CrossRef]
- Wang, D.; Wang, L.; Chen, W.; Wang, H.; Liang, C. Unsupervised Multi-View Feature Selection Based on Weighted Low-Rank Tensor Learning and Its Application in Multi-Omics Datasets. Eng. Appl. Artif. Intell. 2025, 143, 110041. [Google Scholar] [CrossRef]
- Xu, S.; Xie, X.; Cao, Z. Graph–Regularized Consensus Learning and Diversity Representation for Unsupervised Multi-View Feature Selection. Knowl.-Based Syst. 2025, 311, 113043. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, J.; Wang, Z.; Zhang, C.; Yang, J.; Wang, Y.; Sheng, W.; Ding, W. Semi-Supervised Multi-View Feature Selection with Adaptive Similarity Fusion and Learning. Pattern Recognit. 2025, 159, 111159. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, M.; Wang, R.; Du, T.; Li, J. Multi-View Unsupervised Feature Selection with Dynamic Sample Space Structure. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 2641–2648. [Google Scholar]
- Zhang, H.; Wu, D.; Nie, F.; Wang, R.; Li, X. Multilevel Projections with Adaptive Neighbor Graph for Unsupervised Multi-View Feature Selection. Inf. Fusion 2021, 70, 129–140. [Google Scholar] [CrossRef]
- Tang, C.; Zheng, X.; Liu, X.; Zhang, W.; Zhang, J.; Xiong, J.; Wang, L. Cross-View Locality Preserved Diversity and Consensus Learning for Multi-View Unsupervised Feature Selection. IEEE Trans. Knowl. Data Eng. 2022, 34, 4705–4716. [Google Scholar] [CrossRef]
- Si, X.; Yin, Q.; Zhao, X.; Yao, L. Consistent and Diverse Multi-View Subspace Clustering with Structure Constraint. Pattern Recognit. 2022, 121, 108196. [Google Scholar] [CrossRef]
- Fang, S.G.; Huang, D.; Wang, C.D.; Tang, Y. Joint Multi-View Unsupervised Feature Selection and Graph Learning. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 16–31. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, Z.; Chen, C.L.P.; You, J.; Wong, H.S.; Wang, Y.; Zhang, J. Transfer Clustering Ensemble Selection. IEEE Trans. Cybern. 2020, 50, 2872–2885. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, Z.; Cao, W.; Chen, C.L.P.; Wong, H.S.; Han, G. Fast and Effective Active Clustering Ensemble Based on Density Peak. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3593–3607. [Google Scholar] [CrossRef]
- Eckart, C.; Young, G. The Approximation of One Matrix by Another of Lower Rank. Psychometrika 1936, 1, 211–218. [Google Scholar] [CrossRef]
- Chan, J.T.; Li, C.K.; Sze, N.S. Isometries for Unitarily Invariant Norms. Linear Algebra Its Appl. 2005, 399, 53–70. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, L.; Liu, H.; Ye, J. On Similarity Preserving Feature Selection. IEEE Trans. Knowl. Data Eng. 2013, 25, 619–632. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, Z.; Chen, C.L.P.; Zeng, H. Consensus Clustering With Co-Association Matrix Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 4192–4205. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Zhu, X.; Liu, X.; Wang, L. Cross-View Local Structure Preserved Diversity and Consensus Learning for Multi-View Unsupervised Feature Selection. Proc. AAAI Conf. Artif. Intell. 2019, 33, 5101–5108. [Google Scholar] [CrossRef]
- Bai, X.; Zhu, L.; Liang, C.; Li, J.; Nie, X.; Chang, X. Multi-view Feature Selection Via Nonnegative Structured Graph Learning. Neurocomputing 2020, 387, 110–122. [Google Scholar] [CrossRef]
- Yuan, H.; Li, J.; Liang, Y.; Tang, Y.Y. Multi-View Unsupervised Feature Selection with Tensor Low-Rank Minimization. Neurocomputing 2022, 487, 75–85. [Google Scholar] [CrossRef]
- Xu, J.; Lange, K. Power K-Means Clustering. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6921–6931. [Google Scholar]



| Feature | Handwritten | WebKB | MSRCV1 | ORL | Outdoor Scene | Yale |
|---|---|---|---|---|---|---|
| 1 | FCCS (76) | view1 (1703) | HOG (576) | View 1 (4096) | GIST (512) | Intensity (4096) |
| 2 | KAR (64) | view2 (230) | CMT (24) | View 2 (3304) | HOG (432) | LBP (3304) |
| 3 | FAC (216) | view3 (230) | GIST (512) | View 3 (6750) | LBP (256) | GABOR (6075) |
| 4 | PA (240) | – | CENTRIST (254) | – | GABOR (48) | – |
| 5 | MOR (6) | – | LBP (256) | – | – | – |
| 6 | ZER (47) | – | – | – | – | – |
| Instance | 2000 | 203 | 210 | 400 | 2688 | 165 |
| Class | 10 | 4 | 7 | 40 | 8 | 15 |
| Method | Datasets | |||||
|---|---|---|---|---|---|---|
| MSRVCV1 | Yale | Handwritten | Outdoor Scene | ORL | WebKB | |
| ASVW [14] | 69.43 ± 6.12 | 44.00 ± 2.25 | 80.12 ± 7.05 | 47.56 ± 1.98 | 33.1 ± 1.54 | 56.11 ± 6.53 |
| CGMV-FS [12] | 68.14 ± 5.41 | 42.88 ± 3.13 | 67.66 ± 4.85 | 26.95 ± 0.65 | 33.49 ± 1.16 | 58.18 ± 5.98 |
| CRV-DGL [34] | 77.05 ± 7.79 | 50.18 ± 5.59 | 79.92 ± 6.75 | 61.15 ± 4.50 | 54.56 ± 3.37 | 73.37 ± 7.38 |
| NSGL [35] | 69.88 ± 4.89 | 39.82 ± 3.52 | 75.91 ± 4.85 | 45.77 ± 3.02 | 40.75 ± 2.62 | 72.02 ± 4.58 |
| TLR [36] | 81.19 ± 7.32 | 48.58 ± 4.82 | 81.74 ± 6.73 | 42.87 ± 3.31 | 55.25 ± 3.39 | 76.82 ± 1.93 |
| CvLP-DGL [25] | 73.57 ± 3.61 | 46.18 ± 4.53 | 73.05 ± 6.55 | 62.83 ± 3.97 | 58.89 ± 2.94 | 70.96 ± 7.91 |
| CCSFS- [11] | 78.36 ± 5.20 | 54.64 ± 4.30 | 84.28 ± 7.30 | 62.16 ± 3.50 | 58.36 ± 3.76 | 75.34 ± 8.06 |
| CDMvFS [15] | 82.46 ± 6.16 | 54.58 ± 5.85 | 86.78 ± 7.69 | 62.58 ± 6.00 | 60.18 ± 2.89 | 75.71 ± 8.86 |
| Our | 83.14 ± 0.79 | 57.82 ± 1.85 | 92.57 ± 0.63 | 61.76 ± 0.66 | 62.80 ± 1.66 | 70.15 ± 1.38 |
| Method | Datasets | |||||
|---|---|---|---|---|---|---|
| MSRVCV1 | Yale | Handwritten | Outdoor Scene | ORL | WebKB | |
| ASVW [14] | 61.29 ± 6.12 | 49.55 ± 1.72 | 78.24 ± 3.34 | 39.76 ± 1.01 | 55.59 ± 1.51 | 11.73 ± 3.99 |
| CGMV-FS [12] | 58.04 ± 3.80 | 48.59 ± 2.26 | 67.31 ± 2.54 | 11.82 ± 0.42 | 55.77 ± 0.96 | 13.92 ± 8.49 |
| CRV-DGL [34] | 68.61 ± 5.18 | 57.72 ± 4.82 | 77.31 ± 2.83 | 49.01 ± 1.46 | 73.76 ± 2.03 | 35.14 ± 9.62 |
| NSGL [35] | 61.29 ± 3.78 | 46.15 ± 2.80 | 72.77 ± 2.83 | 37.59 ± 0.66 | 62.48 ± 1.67 | 33.73 ± 2.36 |
| TLR [36] | 74.67 ± 4.79 | 53.01 ± 3.59 | 81.44 ± 3.69 | 37.66 ± 0.79 | 74.23 ± 1.44 | 39.71 ± 4.79 |
| CvLP-DGL [25] | 64.21 ± 4.03 | 50.05 ± 4.18 | 70.26 ± 3.33 | 49.85 ± 1.28 | 76.43 ± 1.82 | 35.96 ± 5.07 |
| CCSFS [11] | 70.61 ± 3.32 | 58.42 ± 3.42 | 79.77 ± 3.52 | 53.33 ± 0.56 | 76.09 ± 2.17 | 42.71 ± 10.32 |
| CDMvFS [15] | 72.66 ± 5.00 | 59.72 ± 4.29 | 82.69 ± 4.27 | 51.13 ± 2.11 | 77.89 ± 1.20 | 44.04 ± 10.52 |
| Our | 75.10 ± 1.28 | 62.39 ± 2.43 | 85.50 ± 1.51 | 54.05 ± 0.60 | 80.03 ± 0.67 | 44.32 ± 1.27 |
| Method | Handwritten | WebKB | Yale | Outdoor Scene | ORL | MSRCV1 |
|---|---|---|---|---|---|---|
| CCSFS | 268.74 | 9.15 | 138.39 | 256.47 | 275.15 | 3.12 |
| CDMvFS | 938.17 | 4.02 | 138.39 | 1227.69 | 119.69 | 2.65 |
| CGMvFS | 3.76 | 11.34 | 847.02 | 11.88 | 889.06 | 2.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Zeng, H.; Gong, X.; Cai, L.; Xiang, W.; Lin, Q.; Zheng, H.; Zhu, J. Consensus Guided Multi-View Unsupervised Feature Selection with Hybrid Regularization. Appl. Sci. 2025, 15, 6884. https://doi.org/10.3390/app15126884
Shi Y, Zeng H, Gong X, Cai L, Xiang W, Lin Q, Zheng H, Zhu J. Consensus Guided Multi-View Unsupervised Feature Selection with Hybrid Regularization. Applied Sciences. 2025; 15(12):6884. https://doi.org/10.3390/app15126884
Chicago/Turabian StyleShi, Yifan, Haixin Zeng, Xinrong Gong, Lei Cai, Wenjie Xiang, Qi Lin, Huijie Zheng, and Jianqing Zhu. 2025. "Consensus Guided Multi-View Unsupervised Feature Selection with Hybrid Regularization" Applied Sciences 15, no. 12: 6884. https://doi.org/10.3390/app15126884
APA StyleShi, Y., Zeng, H., Gong, X., Cai, L., Xiang, W., Lin, Q., Zheng, H., & Zhu, J. (2025). Consensus Guided Multi-View Unsupervised Feature Selection with Hybrid Regularization. Applied Sciences, 15(12), 6884. https://doi.org/10.3390/app15126884






