A Modified Nonlinear Mohr–Coulomb Failure Criterion for Rocks Under High-Temperature and High-Pressure Conditions

Abstract

In deep, geologically complex environments characterized by high in situ stress and elevated formation temperatures, the mechanical behavior of rocks often transitions from brittle to ductile, differing significantly from that of shallow formations. Traditional rock failure criteria frequently fail to accurately assess the strength of rocks under such deep conditions. To address this, a novel failure criterion suitable for high-temperature and high-pressure conditions has been developed by modifying the Mohr–Coulomb criterion. This criterion incorporates a quadratic function of confining pressure to account for the attenuation rate of strength increase under high confining pressure and a linear function of temperature to reflect the linear degradation of strength at elevated temperatures. This criterion has been used to predict the strength of granite, shale, and carbonate rocks, yielding results that align well with the experimental data. The average coefficient of determination (R²) reached 97.1%, and the mean relative error (MRE) was 5.25%. Compared with the Hoek–Brown and Bieniawski criteria, the criterion proposed in this study more accurately captures the strength characteristics of rocks under high-temperature and high-pressure conditions, with a prediction accuracy improvement of 1.70–4.09%, showing the best performance in the case of carbonate rock. A sensitivity analysis of the criterion parameters n and B revealed notable differences in how various rock types respond to these parameters. Among the three rock types studied, granite exhibited the lowest sensitivity to both parameters, indicating the highest stability in the prediction results. Additionally, the predictive outcomes were generally more sensitive to changes in parameter B than in n. These findings contribute to a deeper understanding of rock mechanical behavior under extreme conditions and offer valuable theoretical support for drilling, completion, and stimulation operations in deep hydrocarbon reservoirs.

1. Introduction

With the continuous advancement of global oil and gas exploration and development into deeper geological formations, ultra-deep reservoirs have become a focal point of attention. Since the 1960s, significant progress has been made in deep reservoir drilling in North America, with successful commercial exploitation in regions such as the Mississippi Basin, the Gulf of Mexico, and the North Sea, where the maximum well depth has reached 10,960 m [1]. Russia has achieved major breakthroughs in the South Kara Sea, discovering world-class oil and gas fields such as the Pobeda Oilfield and the Marshala Zhukova Gas Field. In addition, a deep exploratory well with a total depth of 14,600 m has been successfully drilled in the Sakhalin region [2]. Furthermore, China has made remarkable progress in ultra-deep oil and gas exploration in the Tarim and Sichuan Basins, with a significant increase in the number of wells drilled to depths exceeding 8000 m [3]. With the continuous increase in drilling depths, rocks are subjected to complex geological environments of high in situ stress and elevated temperatures, resulting in mechanical behaviors that differ significantly from those in shallow formations [4,5]. During ultra-deep well drilling, a series of wellbore instability incidents, such as stuck pipe, lost circulation, and wellbore collapse, frequently occur and are showing an increasing trend [6,7]. Currently, there is a lack of systematic and in-depth studies on the characterization of the mechanical properties of ultra-deep reservoir rocks. Therefore, investigating the deformation and failure mechanisms of ultra-deep formations and understanding the influence of temperature and confining pressure on rock strength parameters are essential for providing the fundamental data and a reliable strength evaluation model required for wellbore stability risk assessment during ultra-deep drilling operations.

Many scholars have studied the variations in rock mechanical characteristics under different confining pressure conditions based on triaxial compression tests, revealing the impact of rock mechanical properties on drilling, hydraulic fracturing, and other engineering applications [8,9]. In the ultra-deep high-temperature and high-pressure environment, the transition of rock behavior from brittleness to ductility becomes more pronounced. Understanding the mechanisms underlying the changes in rock mechanical properties in ultra-deep formations is key to addressing wellbore instability issues during drilling in ultra-deep strata [10,11]. Kumari et al. [12] found that the mechanical behavior of granite is influenced by reservoir depth and temperature under in situ stress and temperature conditions, with depth being the primary controlling factor. Sun et al. [13] investigated the effects of temperature–pressure coupling on the porosity, permeability, and mechanical properties of deep shale, revealing that high temperature significantly affects stress-sensitive pore permeability, increases rock plasticity, and exacerbates the compression of pores under high confining pressure. Cheng et al. [14] identified the characteristics of brittle and ductile deformation in organic-rich shale and uncovered the conditions and mechanisms for the transition from brittleness to ductility under deep high-temperature and high-confining pressure conditions.

Rock strength theory primarily focuses on the relationship between the stress state and rock strength parameters, aiming to define the ultimate capacity of rocks to resist deformation and failure and to develop models for determining rock strength [15,16]. Many scholars have conducted in-depth research in this area and proposed numerous rock failure models and criteria. Several classical rock failure criteria include the Mohr–Coulomb (MC) criterion, Drucker–Prager (DP) criterion, and Griffith criterion [17,18,19]. Among these, the MC failure criterion assumes a linear relationship between shear and normal stress on the failure surface. Owing to its simple mathematical form and ease of parameter determination, it has become one of the most widely used models in rock and soil mechanics. It is commonly applied in slope stability, tunneling, wellbore integrity, hydraulic fracturing, and mining excavation analyses. Despite its simplicity, the MC criterion provides valuable insights into the failure behavior of geomaterials across a broad range of geological and engineering contexts [20,21,22]. Abdellah et al. employed the MC failure criterion to investigate the relationships between stress–strain curves, stress ratio, deviatoric stress, and the ratio of volumetric strain to axial strain. Based on numerical simulations, they successfully reproduced the rock failure mechanisms observed in uniaxial and triaxial compression tests, enabling the rapid evaluation of rock strength under different loading conditions. This approach effectively reduced both the time and economic costs associated with rock mechanical strength assessment in mining engineering [23]. Lin et al. proposed a power law-based MC criterion for deep Longmaxi Formation shale and evaluated its reliability, sensitivity, and applicability. Their work provides important references and theoretical support for drilling, completion, and production enhancement in deep shale gas reservoirs [24]. However, as the depth of underground engineering continues to increase, rock mechanics test data indicate that the failure envelope of rocks under high confining pressure is not a linear line, and the MC failure criterion shows significant errors under high confining pressure conditions [25,26,27]. Additionally, some rock failure criteria are developed for the specific rocks taking the special properties of the rocks, such as shale considering the anisotropy and hydration of shale [28,29] and carbonatite considering the hole and pore heterogeneous distribution [30]. Although there are many existing rock failure criteria, few of them can be used for the rock under high-temperature and high-pressure conditions. Under high-temperature conditions, the mismatch in thermal expansion between different minerals in the rock induces shear stresses, which, in turn, trigger the initiation and propagation of microcracks. In addition, cementing materials such as carbonates or clay minerals are prone to thermal decomposition or dehydration at elevated temperatures, leading to a reduction in intergranular bonding strength and compromising the structural integrity of the rock. Moreover, under high confining pressure, the lateral constraint alters the failure mode of the rock from brittle to ductile behavior, and its strength characteristics exhibit pronounced nonlinearity. Scholars have proposed various forms of nonlinear rock failure criteria, which can be categorized into hyperbolic [31], parabolic [32], elliptical [33], and exponential [34,35] failure criteria. Although these nonlinear failure criteria can address the limitations of classical failure criteria under high confining pressure, most of them are empirical formulas that are only applicable to specific regions and rock types. Furthermore, the existing failure criteria rarely account for the effects of temperature, assuming that the nonlinear characteristics of rock strength envelopes in deep formations are solely due to high confining pressure while neglecting the impact of high temperature on rock mechanical properties.

In summary, the current classical rock failure criteria are only applicable under low confining pressure conditions, while nonlinear failure criteria neglect the impact of temperature on rock mechanical properties, making it difficult to accurately assess rock strength under ultra-deep high-temperature and high-confining pressure conditions. As a result, they cannot be widely applied in the wellbore stability evaluation of ultra-deep reservoir oil and gas resources. In this study, based on the MC criterion, a nonlinear rock failure criterion for high-temperature and high-confining pressure conditions is proposed by introducing correction functions related to temperature and confining pressure. The reliability of the new failure criterion is then validated using limited experimental data. The proposed criterion is helpful for evaluating the influence of temperature and confining pressure on rock strength parameters, providing essential baseline data for the development of ultra-deep oil and gas resources, and thus holds significant practical importance.

2. A Nonlinear MC Failure Criterion Considering High-Temperature and High-Pressure Conditions

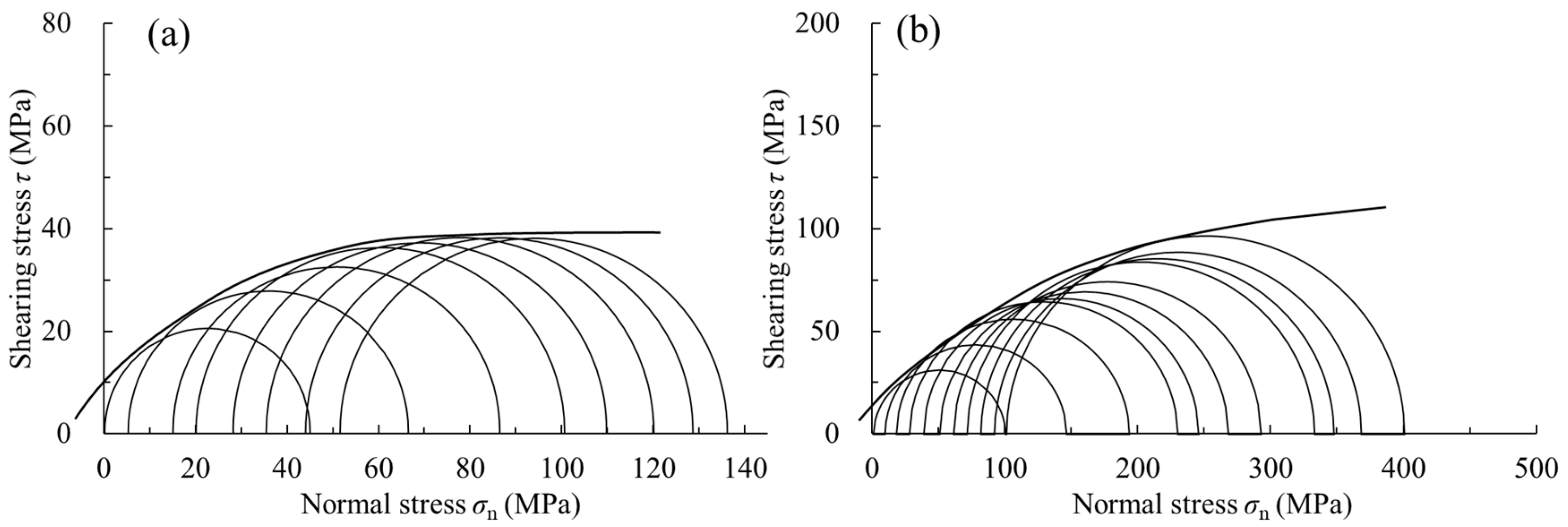
2.1. Nonlinear MC Failure Criterion Under High Stress

The mechanical properties of rock masses and the stress environment are the key factors leading to rock deformation and failure in underground space engineering, such as mining, drilling, and tunnel excavation [12]. To accurately determine rocks’ strength in different formations, various failure criteria have been proposed by scholars. Among them, the MC failure criterion, due to its simplicity and practicality, has become one of the most widely used rock strength theories in geotechnical engineering [17]. This criterion characterizes rock shear strength through cohesion and the internal friction angle, effectively describing failure modes under different stress paths, particularly demonstrating significant advantages in the strength analysis of various rock masses. The MC failure criterion is expressed as follows [36]:

$${\sigma }_1={\displaystyle \frac{2c\cos \phi }{1-\sin \phi }}+{\displaystyle \frac{1+\sin \phi }{1-\sin \phi }}{\sigma }_3$$

(1)

where σ₁ and σ₃ are the major and minor principal stresses applying on the rock, respectively, MPa; c is the rock cohesion, MPa; φ is the rock internal friction angle, °.

Many research results have shown that, as the confining pressure increases, the failure mode of rocks gradually transitions from brittle failure to ductile failure. With the increase in confining pressure, the slope of the Mohr strength envelope decreases gradually, indicating that the rate of increase in shear strength diminishes and eventually approaches zero (as shown in Figure 1) [37,38]. However, the MC criterion assumes that cohesion (c) and the internal friction angle (φ) are constants, which only allows for a linear representation of rock strength variations with confining pressure. It fails to capture the dynamic process of the transition from brittle to ductile failure as the confining pressure increases. To overcome the limitations of the linear MC criterion in predicting rock strength under high confining pressure conditions, many scholars have proposed improvements to the MC criterion. A representative study by Singh et al. [38] introduced a quadratic function of confining pressure to develop a modified MC criterion model that describes the nonlinear coupling relationship between confining pressure and strength. Singh et al. [38] conducted triaxial compression tests on 158 rock samples of various types. Through the experimental data analysis, they found that, as the confining pressure increased, the rock strength gradually increased, but the rate of increase diminished. When the confining pressure reached the uniaxial compressive strength, the rate of increase in the rock strength approached zero. Therefore, the mathematical expression of the modified MC failure criterion is as follows:

$$\left\{\begin{array}{l}\left({\sigma }_1-{\sigma }_3\right)={\displaystyle \frac{2c\cos \phi }{1-\sin \phi }}+{\displaystyle \frac{2\sin \phi }{1-\sin \phi }}{\sigma }_3-{\displaystyle \frac{1}{{\sigma }_c}}.{\displaystyle \frac{\sin \phi }{1-\sin \phi }}{{\sigma }_3}^2, 0\le {\sigma }_3\le {\sigma }_c\\ {\left({\sigma }_1-{\sigma }_3\right)}_{\max }={\displaystyle \frac{2c\cos \phi }{{(1-\sin \phi )}^2}}, {\sigma }_3\ge {\sigma }_c\end{array}\right.$$

(2)

where σ_c is the uniaxial compressive strength of the rock, MPa.

2.2. The Nonlinear MC Failure Criterion

In the 158 triaxial compression test database used for statistical analysis by Singh et al. [38], 53 datasets from sandstone accounted for 33.54% of the total test data. Therefore, the conclusion that the critical confining pressure equals the uniaxial compressive strength may not apply to all rock types [38]. For example, Li et al. [39] found that Solnhofen limestone enters the critical state when the confining pressure is 0.34σ_c, while Bent sandstone does not enter the critical state until the confining pressure reaches 1.5σ_c. Considering that the MC criterion still provides relatively accurate predictions for various rock types under low confining pressure, this study follows the approach of Singh et al. [38] and introduces a correction term based on the MC criterion. However, it assumes that the critical confining pressure under constant compressive strength is nσ_c rather than σ_c. Its mathematical form is as follows:

$$\left({\sigma }_1-{\sigma }_3\right)={\displaystyle \frac{2c\cos \phi }{1-\sin \phi }}+{\displaystyle \frac{2\sin \phi }{1-\sin \phi }}{\sigma }_3-A{{\sigma }_3}^2\begin{array}{ccc}& 0\le {\sigma }_3\le n{\sigma }_c& \end{array}$$

(3)

where A and n are parameters related to rock type, while the meanings of the other parameters are the same as those in the MC criterion.

When the confining pressure reaches the critical condition, i.e., σ₃ = nσ_c, Equation (3) should satisfy the following conditions:

$${\displaystyle \frac{\partial \left({\sigma }_1-{\sigma }_3\right)}{\partial {\sigma }_3}}=0$$

(4)

By solving Equation (4), the following can be obtained:

$$A={\displaystyle \frac{2\sin \phi }{2n{\sigma }_{\mathrm{c}}(1-\sin \phi )}}$$

(5)

In addition, the failure criterion proposed by Singh et al. [38] neglects the impact of temperature on rock mechanical properties and thus does not perform well in predicting rock strength in deep high-temperature and high-pressure environments. Kim et al. [40] analyzed the shear characteristics of saw-cut smooth granite surfaces under various thermal-hydro-mechanical conditions based on the Mohr–Coulomb failure criterion and found that the shear strength of granite gradually decreases with the increasing temperature. The study by Yang et al. [41] on the mechanical properties of sandstone at elevated temperatures also indicated a linear relationship between compressive strength and temperature, with compressive strength decreasing as the temperature increases. Accordingly, a linear model describing the relationship between temperature and rock strength is established as follows:

$${\sigma }^T=B\Delta T+C$$

(6)

where σ^T is the temperature-dependent rock strength, MPa; ΔT is the temperature difference between the actual temperature and room temperature, °C.

We assume that the effect of temperature on the rock mechanical properties is independent of the confining pressure. Therefore, a linear relationship model between temperature and the rock uniaxial compressive strength can be established to represent the temperature-dependent reduction in rock strength. The mathematical form is as follows:

$$\Delta {\sigma }_{\mathrm{c}}^T={\sigma }_{\mathrm{c}}-{\sigma }^T={\sigma }_{\mathrm{c}}-B\Delta T-C$$

(7)

Additionally, from Equation (6), it is known that, when ΔT = 0, Δσ_c^T = 0. Therefore, it can be concluded that C = σ_c. By substituting this into Equation (7), the following can be obtained:

$$\Delta {\sigma }_c^T=B\Delta T$$

(8)

Therefore, the nonlinear MC failure criterion (abbreviated as HTP-MC criterion) can be obtained by combining Equations (3), (5) and (8), as shown in Equation (9):

$$\left({\sigma }_1-{\sigma }_3\right)={\displaystyle \frac{2c\cos \phi }{1-\sin \phi }}+{\displaystyle \frac{2\sin \phi }{1-\sin \phi }}{\sigma }_3-{\displaystyle \frac{2\sin \phi }{2n{\sigma }_c(1-\sin \phi )}}{{\sigma }_3}^2-B\Delta T\begin{array}{cc}& 0\le {\sigma }_3\le n{\sigma }_{\mathrm{c}}\end{array}$$

(9)

2.3. Parameter Determination Method for the HTP-MC Criterion

The principle behind the proposed HTP-MC criterion is to add two correction terms to the MC failure criterion, resulting in a total of four parameters: cohesion c, internal friction angle φ, and rock property-related parameters (n and B).

Determination of cohesion c and internal friction angle φ: In the HTP-MC criterion, cohesion c and internal friction angle φ are consistent with the parameters of the MC failure criterion. To determine the cohesion c and internal friction angle φ without the influence of temperature and confining pressure, at least two triaxial compression tests on rock samples at different low confining pressures under room temperature conditions are required.

Determination of parameter n: Based on the known cohesion c and internal friction angle φ, at least one triaxial compression test data on rock samples under high confining pressure is required. The value of parameter n can then be solved using Equations (3) and (5).

Determination of parameter B: Parameter B characterizes the reduction in rock strength due to temperature. To avoid the influence of confining pressure, parameter B can be determined by conducting uniaxial compression tests at different temperatures. At least two rock samples should be tested under uniaxial compression, one at room temperature and the other at high temperature. Based on the data from these two experiments, parameter B can be solved using Equations (6) and (8).

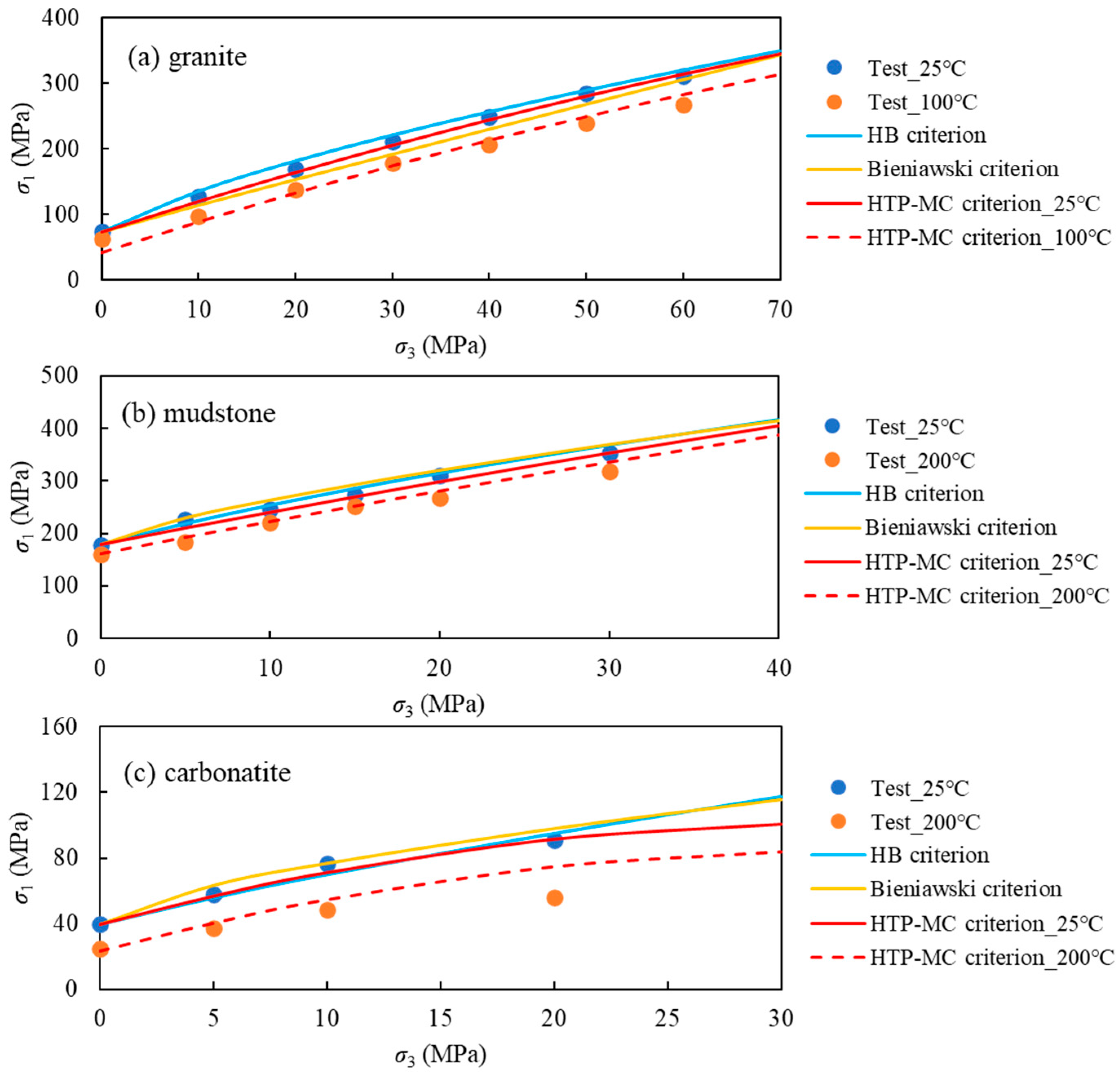
3. Verification of the HTP-MC Criterion

To verify the reliability of the HTP-MC criterion, this study collected high-temperature and high-pressure triaxial compression test data for various types of rocks. As shown in the

Table 1. Confining pressure and strength from triaxial compression tests of rocks used to verify the failure criterion.

Granite a			Mudstone b			Carbonate Rock c
T (°C)	σ3 (MPa)	σ1 (MPa)	T (°C)	σ3 (MPa)	σ1 (MPa)	T (°C)	σ3 (MPa)	σ1 (MPa)
25	0	178.5	20	0	39.7	25	0	73.1
	5	226.5		5	58		10	126.5
	10	246.5		10	76.8		20	169.2
	15	273.6		20	91.1		30	211.1
	30	310.5	200	0	24.8		40	248.9
200	0	354		5	37.3		50	284.3
	5	160.5		10	48.4		60	311.4
	10	183.7		20	55.7	100	0	62.1
	15	221.2					10	97.4
	30	252					20	137
							30	177.7
							40	206.6
							50	239.8
							60	267.6

Data sources: a, [42]; b, [43]; c, [44].

, the rock types include granite, shale, and carbonate rocks. The collected dataset includes two sets of triaxial compression tests. One set was conducted under room temperature conditions, and the other was conducted after high-temperature treatment. Considering those ultra-deep formations, with burial depths greater than 6500 m, typically reach formation temperatures of 160–220 °C, we selected triaxial compression test data for rocks treated at approximately 200 °C as far as the available data allowed.

Currently, in addition to the MC criterion, the Hoek–Brown failure criterion (HB criterion) is also widely applied in rock engineering. Furthermore, Shi et al. [45] and others, through quantitative comparative analysis of five failure criteria, concluded that the Bieniawski failure criterion has distinct advantages in describing the nonlinear strength characteristics of rocks. Therefore, in this study, the proposed HTP-MC criterion, the HB criterion, and the Bieniawski criterion are evaluated by comparing their accuracy in predicting rock triaxial strength. The HB criterion relates rock strength to geological parameters (such as the degree of joint development and disturbance) and rock mechanical parameters (such as uniaxial compressive strength) through empirical formulas, enabling a nonlinear strength representation of rock masses. Its mathematical expression is as follows:

$$\left({\sigma }_1-{\sigma }_3\right)={\sigma }_{\mathrm{c}}{({\displaystyle \frac{m{\sigma }_3}{{\sigma }_{\mathrm{c}}}}+1)}^{0.5}$$

(10)

where m is a constant related to the material, dimensionless; σ_c is the uniaxial compressive strength of the rock, MPa.

According to Bieniawski, the peak σ₁–σ₃ envelope based on rock triaxial test data typically exhibits a concave shape. It is proposed that the relationship between σ₁ and σ₃ should be expressed in an exponential form. Additionally, all stress components should be divided by the uniaxial compressive strength of the rock to ensure dimensional consistency in the mathematical relationship between σ₁ and σ₃ in exponential form. The mathematical expression is as follows:

$${\displaystyle \frac{{\sigma }_1}{{\sigma }_{\mathrm{c}}}}=1+A{({\displaystyle \frac{{\sigma }_3}{{\sigma }_{\mathrm{c}}}})}^k$$

(11)

where A and k are constants related to the rock material, which can be fitted using experimental data, dimensionless; σ_c is the uniaxial compressive strength of the rock, MPa.

To quantify the deviation, the evaluation criteria used in this study are given by Equations (12) and (13), which are the coefficient of determination (R²) and the mean relative error (MRE), respectively. Their expressions are as follows:

$$R^2=1-{\displaystyle \frac{{{\displaystyle \sum _{i=1}^N({\sigma }_{1,i}^T-{\sigma }_{1,i}^p)}}^2}{{{\displaystyle \sum _{i=1}^N({\sigma }_{1,i}^T-{\sigma }_{1,i}^{avg})}}^2}}$$

(12)

$$MRE={\displaystyle \frac{{\displaystyle \sum _{i=1}^N\left|\frac{{\sigma }_{1,i}^T-{\sigma }_{1,i}^p}{{\sigma }_{1,i}^T}\right|}}{N}}\times 100\%$$

(13)

where N is the number of data points in the rock triaxial compression dataset, dimensionless; ${\sigma }_{1,i}^p$ and ${\sigma }_{1,i}^T$ represent the predicted strength and experimental strength of the i-th rock sample under confining pressure σ₃, respectively.

Based on the parameter determination methods of the three rock failure criteria and the triaxial test data, the parameters of the three rock failure criteria were determined, as shown in

Table 2. Parameters in the three failure criteria.

Rock Type	Failure Criteria	Parameters
Granite	HB criterion	m = 15.4
	Bieniawski criterion	A = 4.02; k = 0.74
	HTP-MC criterion	c = 35.44 MPa; φ = 46.68°; n = 0.92; B = 0.103
Mudstone	HB criterion	m = 5.24
	Bieniawski criterion	A = 2.29; k = 0.65
	HTP-MC criterion	c = 10.31 MPa; φ = 35.13°; n = 0.61; B = 0.095
Carbonate rock	HB criterion	m = 15.5
	Bieniawski criterion	A = 3.85; k = 0.97
	HTP-MC criterion	c = 16.67 MPa; φ = 40.96°; n = 1.96; B = 0.42

.

Nate rock (as shown in Figure 2). The predicted results were compared with the actual triaxial compression test data. Additionally, the R² and MRE between the predicted and experimental values were calculated, as presented in Figure 3. The results show that all three failure criteria exhibit high correlation (R² > 0.96, see Figure 2a) in predicting the strength of the three types of rocks, indicating good applicability and accuracy under different lithological conditions. As shown in Figure 3b, when temperature is not considered, the prediction accuracy of the HB criterion, Bieniawski criterion, and HTP-MC criterion for granite and mudstone is relatively high. For granite, the MREs of the predicted strength are 2.67%, 3.87%, and 2.47%, respectively; for mudstone, the MREs are 4.13%, 4.17%, and 2.43%, respectively. However, in the case of carbonate rock, the prediction errors for the HB and Bieniawski criteria are significantly higher, with MREs of 5.27% and 6.27%, respectively, compared to only 2.18% for the HTP-MC criterion. The collected triaxial compression data for granite and mudstone were obtained under relatively low confining pressures, resulting in good applicability for all three criteria. In contrast, the triaxial tests on carbonate rock involved confining pressures up to 60 MPa, making the nonlinear characteristics of the rock failure envelope more prominent. This further demonstrates that the HTP-MC criterion is better suited to describe rock failure behavior under high confining pressure.

High temperatures cause the thermal expansion of mineral grains within the rock. Due to differences in the thermal expansion coefficients of different minerals, uneven deformation and constrained stress develop between grains, resulting in thermal stress. When the thermal stress exceeds the bonding strength between mineral grains, microcrack propagation occurs, reducing the overall strength of the rock. As shown in Figure 2, under high-temperature conditions, the failure strength of granite, mudstone, and carbonate rock decreases significantly. Since the HB and Bieniawski criteria cannot account for the influence of temperature on the rock strength, this study analyzes only the predictions from the HTP-MC criterion. As shown in Figure 3c, the R² values of the HTP-MC criterion for predicting the strength of granite, mudstone, and carbonate rock range from 94.1% to 99.8%, with an average of 97.1%. The MREs range from 2.54% to 8.55%, with an average of 5.25%. These results indicate that the HTP-MC criterion predicts the strength of granite and mudstone more accurately than that of carbonate rock. This discrepancy may be attributed to the heterogeneous nature of carbonate rocks, which increases the prediction error. Overall, the HTP-MC criterion shows low MRE values and high accuracy in predicting rock strength under high-temperature and high-pressure conditions.

It is also worth noting that, in this study, some of the high-temperature and high-pressure triaxial compression data were obtained from rocks that had been subjected to high-temperature treatment prior to testing. This may affect the accuracy of parameter fitting and strength prediction of the proposed criterion. Therefore, in future work, our research will focus on investigating the mechanical behavior of rocks under real-time high-temperature and high-pressure conditions.

4. Discussion

As discussed above, the HTP-MC criterion exhibits high accuracy in predicting rock strength under high-temperature and high-pressure conditions. Compared to the classical MC criterion, which involves only two fitting parameters (cohesion c and internal friction angle φ), the HTP-MC model introduces only two additional parameters (n and B). Theoretically, these parameters can be determined using just four sets of uniaxial or triaxial compression tests. However, in practice, the selection of test data—particularly the number of samples and the temperature and confining pressure conditions—significantly influences the fitting results. These differences reveal the sensitivity of the model parameters to changes in the experimental conditions. If the parameters are highly sensitive to variations in temperature and confining pressure, this may result in decreased predictive accuracy of the model under complex loading environments.

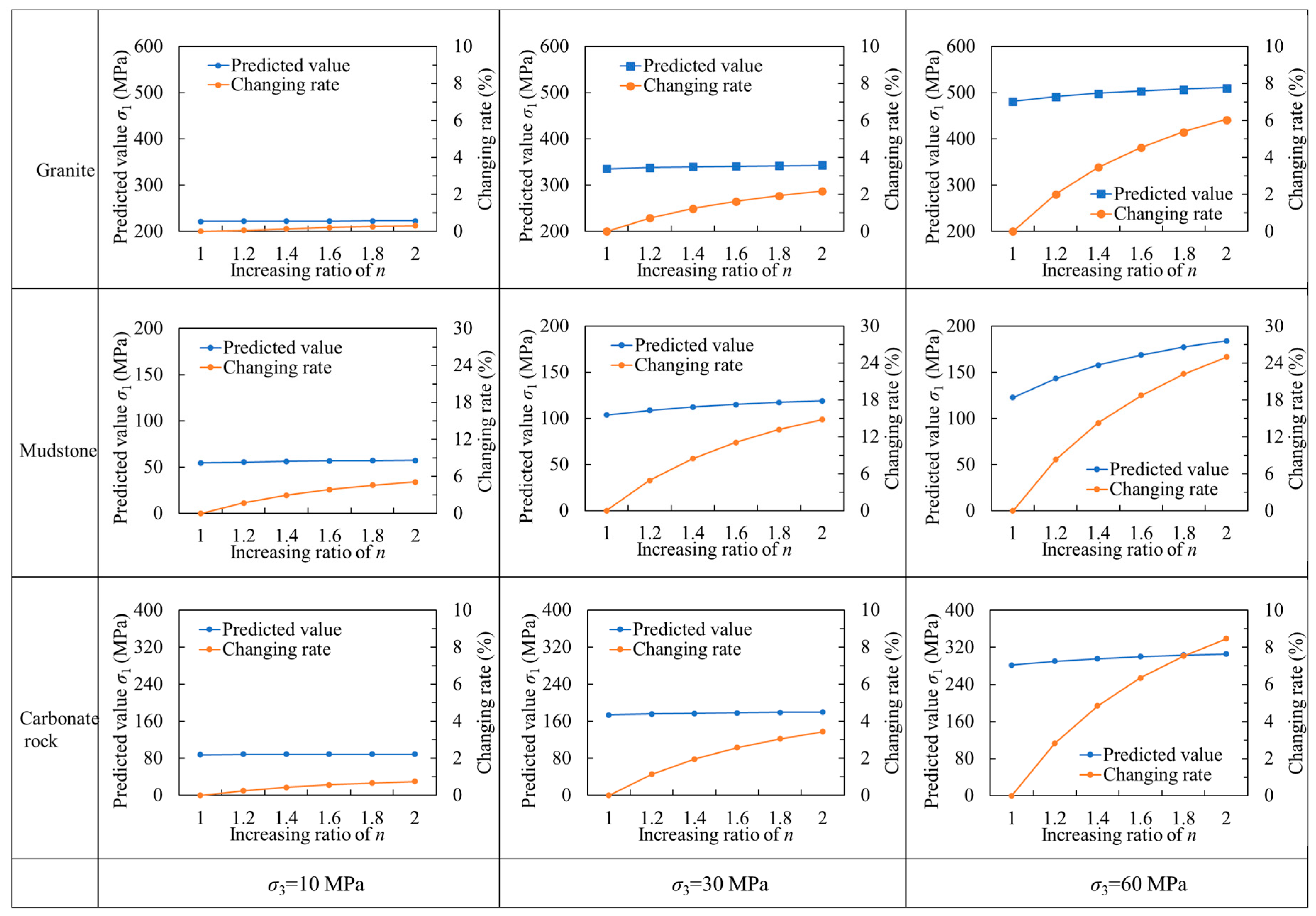
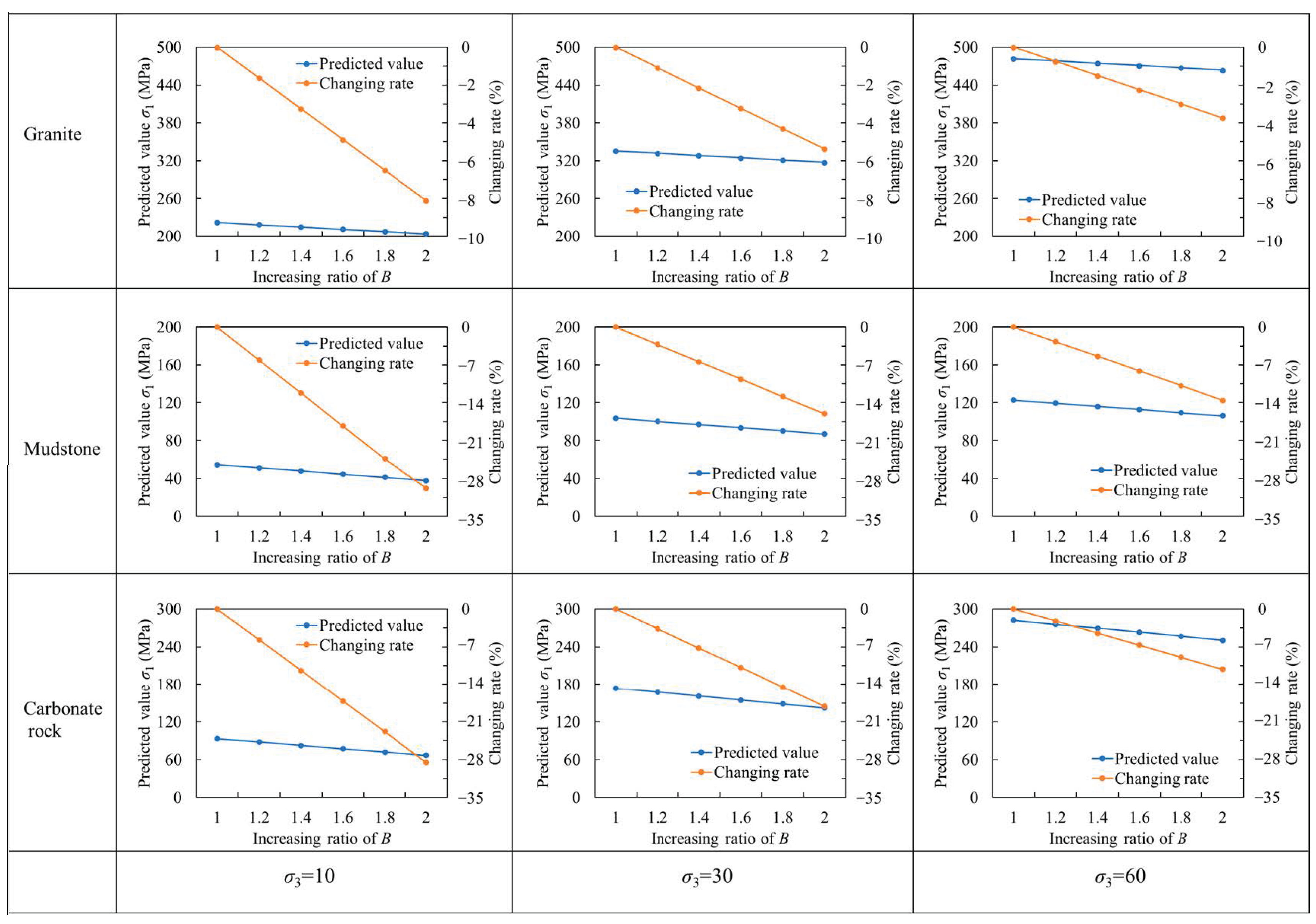
4.1. Sensitivity Analysis of the Parameters on the Predicted Results

To evaluate the contribution of each parameter in the proposed failure criterion to the prediction results, a sensitivity analysis was conducted. The proposed criterion involves four parameters. Among them, the cohesion c and internal friction angle φ are defined in the same way as in the classical MC criterion and are therefore not discussed in detail. The focus of the analysis is on the sensitivity of parameters n and B. For the sensitivity analysis, all other parameters were held constant, as shown in Table 2. Starting from their initial values, parameters n and B were incrementally increased by 20% at each step. The corresponding predicted σ₁ and the rate of change in σ₁ were recorded and used as indicators for the comparative sensitivity analysis.

Figure 4 presents the sensitivity analysis of parameter n on the strength prediction results for three types of rock. In this analysis, the confining pressures were set to 10 MPa, 30 MPa, and 60 MPa, respectively. As shown in Equation (9), all predicted σ₁ increase with the increasing n, indicating a positive correlation between n and σ₁. Parameter n is associated with the critical confining pressure of the rock: a higher n implies a higher critical confining pressure at which the rate of strength increases with respect to the confining pressure, which tends to zero. This also reflects a greater critical compressive strength of the rock. Although all three rock types exhibit an increasing trend in the rate of change of predicted σ₁ with the increasing confining pressure, the rate of increase differs significantly among them. The most pronounced difference in sensitivity to n is observed between granite and shale. When n increases by 2.0, the predicted σ₁ for granite increases by 0.31%, 2.18%, and 6.07% under confining pressures of 10 MPa, 30 MPa, and 60 MPa, respectively. In contrast, for shale, the corresponding increases are 5.13%, 14.82%, and 25.01%.

Figure 5 illustrates the sensitivity analysis of parameter B on the strength prediction results for the three types of rock. Negative values indicate that the predicted σ₁ decreases with the increasing B, which is consistent with Equation (9), showing a negative correlation between B and σ₁. In contrast to parameter n, all three rock types exhibit a decreasing trend in the rate of change of predicted σ₁ with the increasing confining pressure. This is because the model assumes that the strength reduction caused by temperature is independent of the confining pressure, and rocks tend to have higher initial strength under higher confining pressure. Furthermore, the sensitivity of predicted σ₁ to B varies significantly among different rock types. Granite shows considerably lower sensitivity to B compared to shale and carbonate rock. For example, when B increases by 2.0 under confining pressures of 10 MPa, 30 MPa, and 60 MPa, the predicted σ₁ for granite decreases by 8.12%, 5.37%, and 3.74%, respectively. In contrast, for shale, the decreases are 29.80%, 16.04%, and 13.54%, and for carbonate rock, they are 28.54%, 18.13%, and 11.17%, respectively.

In summary, the sensitivity of predicted σ₁ to parameters n and B varies significantly across different rock types. Among them, granite exhibits the lowest sensitivity to both parameters, indicating that the proposed HTP-MC criterion has better adaptability for predicting the strength of granite. This observation is consistent with the results shown in Figure 3c. Moreover, the predicted σ₁ is generally more sensitive to parameter B than to n. For example, under confining pressures ranging from 10 MPa to 60 MPa, an increase of 2.0 n results in σ₁ variation ranges of 0.31~6.07% for granite, 5.13~25.01% for shale, and 0.75~8.47% for carbonate rock. In contrast, a 2.0 increase in B leads to σ₁ variation ranges of approximately −8.12 to −3.74% for granite, −29.80 to −13.54% for shale, and −28.54 to −11.18% for carbonate rock.

4.2. Shortcomings and Suggestions

In this study, some of the high-temperature and high-pressure triaxial compression data used were obtained from rocks subjected to high-temperature treatment prior to testing. This may affect the accuracy of parameter fitting and strength prediction of the proposed criterion. Due to the stringent technical requirements of real-time high-temperature and high-pressure triaxial testing—where both elevated temperature and confining pressure must be maintained simultaneously—many researchers have instead adopted post-heating triaxial compression tests to investigate the effects of temperature and confining pressure on rock mechanical behavior. However, rocks subjected to high-temperature treatment may have undergone irreversible structural changes, such as mineral phase transitions and the development of microcracks. These alterations can result in mechanical behavior under subsequent testing conditions that deviates from the actual in situ response of rocks in deep geological environments.

In addition, this study assumes that the influence of temperature on the mechanical properties of rocks is independent from confining pressure and thus establishes a linear relationship model between temperature and uniaxial compressive strength to characterize the strength degradation induced by temperature. However, some researchers have suggested that the effects of temperature and confining pressure on rock properties are not simply additive. For example, Sun et al. found that, under high-temperature conditions, the plasticity of deep shale is significantly enhanced, which intensifies the compression of pores under high confining pressure and induces thermal stresses between mineral grains in the rock skeleton [13]. As a result, pre-existing bedding planes in shale are more likely to reopen or generate new fractures along these weak planes. This mechanism weakens the reduction in permeability typically caused by the increasing temperature and confining pressure. Mi et al. observed that high temperatures can induce thermal cracking in granite due to differences in thermal expansion among constituent minerals, which significantly reduces the peak strength of the rock. However, this thermal degradation effect can be effectively suppressed under the application of lateral confining pressure [46]. Therefore, future research will continue to investigate the coupled effects of temperature and confining pressure on the mechanical behavior of rocks, with the aim of further improving the failure criterion for rocks under high-temperature and high-pressure conditions.

5. Conclusions

(1)

Based on the classical MC criterion, an improved nonlinear MC criterion was proposed by introducing correction functions for the temperature and confining pressure. This criterion considers the critical confining pressure condition when the compressive strength remains constant as nσ_c rather than σ_c. Additionally, it assumes a linear decrease in rock compressive strength with the temperature, thus establishing a linear relationship model between temperature and rock strength.

(2)

By comparing the strength prediction accuracy of the HB criterion, Bieniawski criterion, and HTP-MC criterion for granite, shale, and carbonate rock, it was found that, under low confining pressure conditions, all three failure criteria show high prediction accuracy. However, under high confining pressure conditions, the HTP-MC criterion better captures the nonlinear characteristics of the rock failure envelope, significantly outperforming the other two failure criteria in terms of strength prediction accuracy.

(3)

The HTP-MC criterion overcomes the limitation of the Hoek–Brown and Bieniawski criteria, which cannot account for the effect of temperature on rock strength. The average MRE value for the prediction of granite, shale, and carbonate rock under high-temperature and high-pressure conditions using the HTP-MC criterion is 5.25%, demonstrating that this criterion provides high prediction accuracy for rock strength under high-temperature and high-pressure conditions.

(4)

All rock types exhibit the general trend that the predicted σ₁ increases with the increasing parameter n and decreases with the increasing parameter B. However, the sensitivity of predicted σ₁ to these parameters varies significantly among different rock types. In particular, granite shows the lowest sensitivity to both n and B, indicating better adaptability of the prediction model for granite strength. Furthermore, the predicted σ₁ is generally more sensitive to changes in parameter B than in n.