Outage Rates and Failure Removal Times for Power Lines and Transformers
Abstract
1. Introduction
- AENS (Average Energy Not Supplied);
- AIT (Average Interruption Time);
- ENS (Energy Not Served).
2. Methods for Determining the Number of Power Line and Transformer Outages
2.1. Factors Influencing the Number of Branch Outages
2.2. Factors Influencing the Transformer Outage Rate
2.3. Methods Used in the Literature to Determine the Number of Outages of Transmission Lines and Transformers
3. Methods of Determining the Time of Failure Removal in Transmission Lines and Power System Transformers
3.1. Factors Influencing the Time of Failure Removal
3.2. Methods Used in the Literature for Determining the Time of Failure Removal in Transmission Lines and Transformers
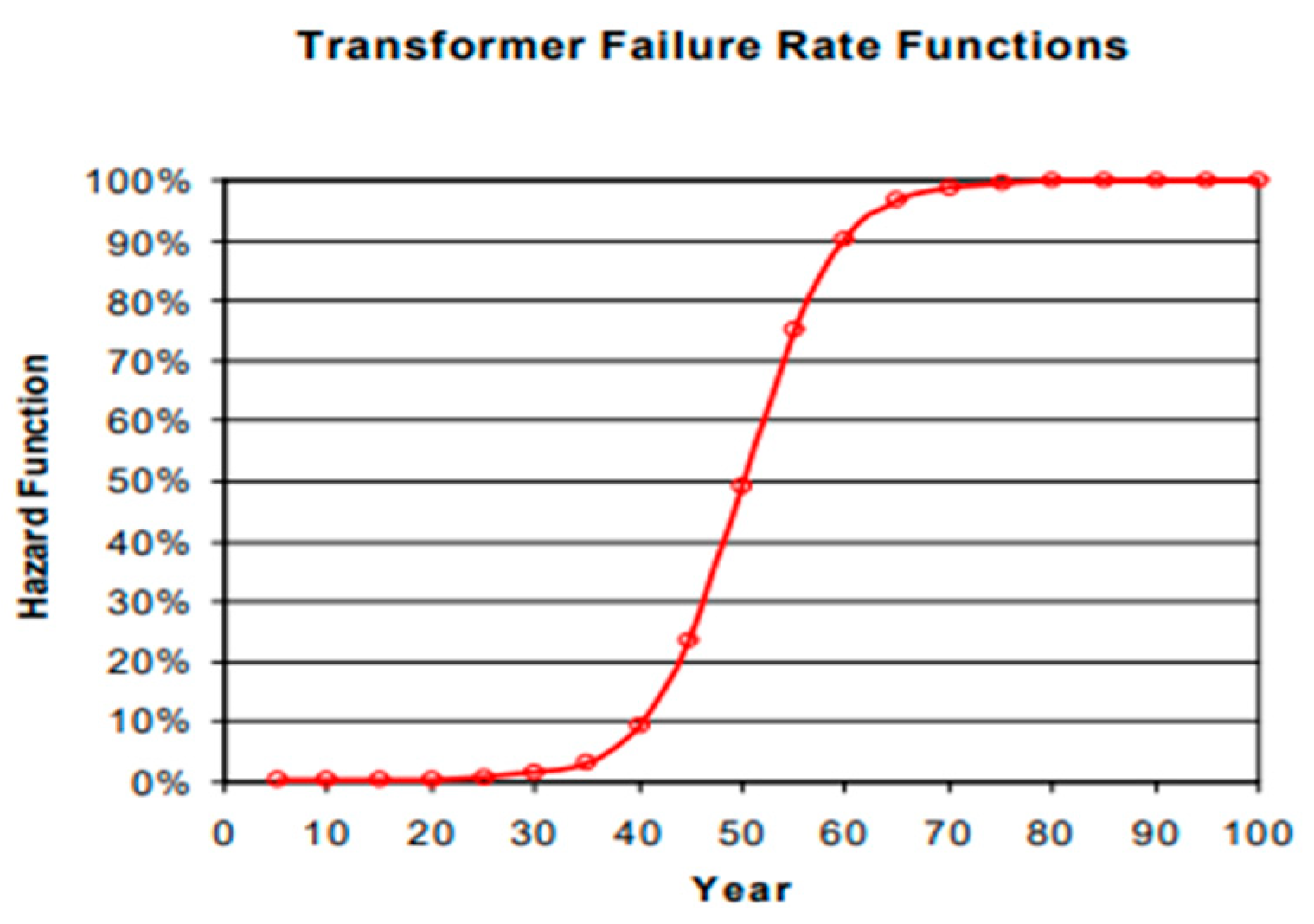
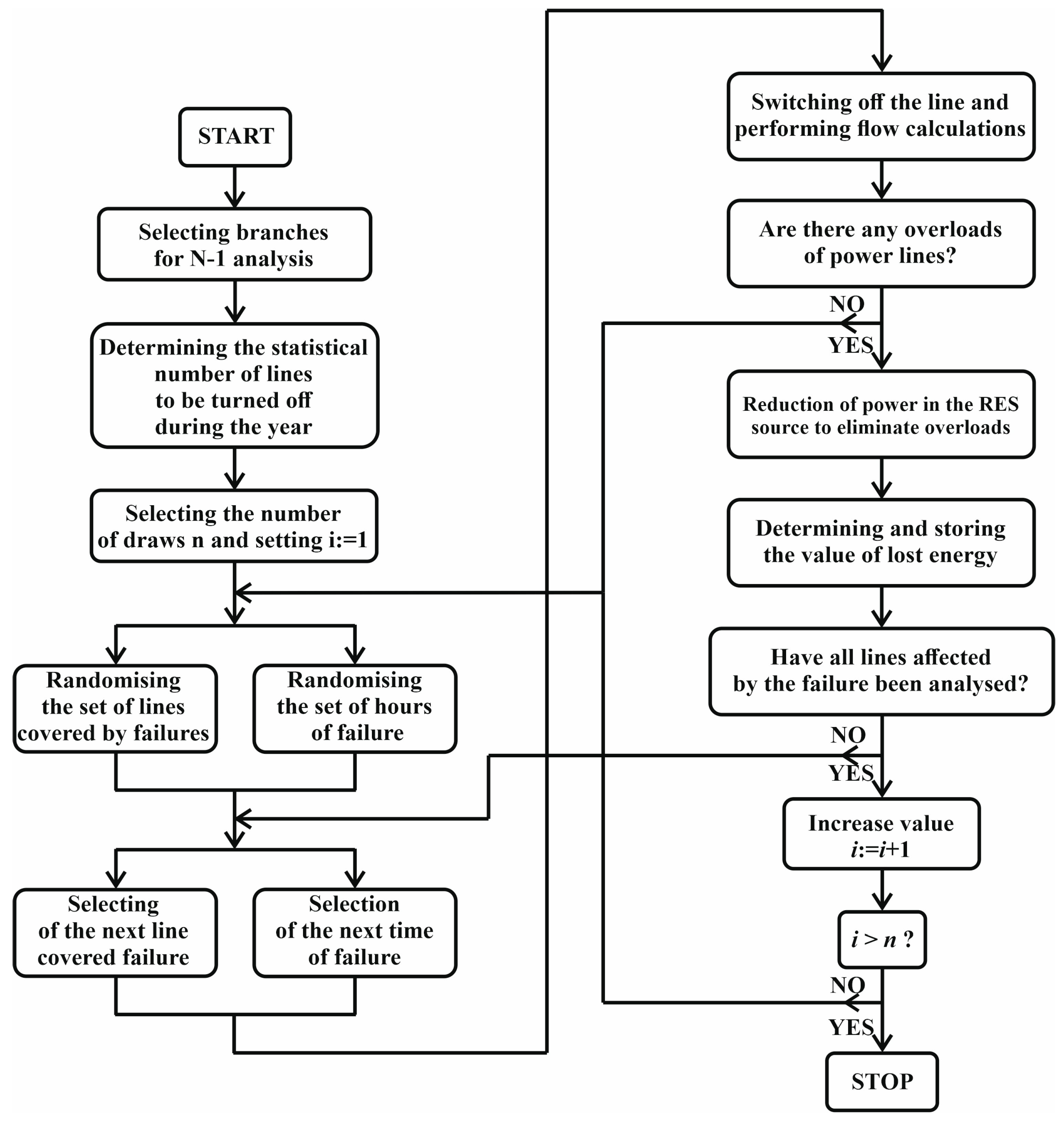
4. Methods of Determining the Reliability Factor and the Time of Failure Removal of HV Lines and Transformers
Failure Removal Time
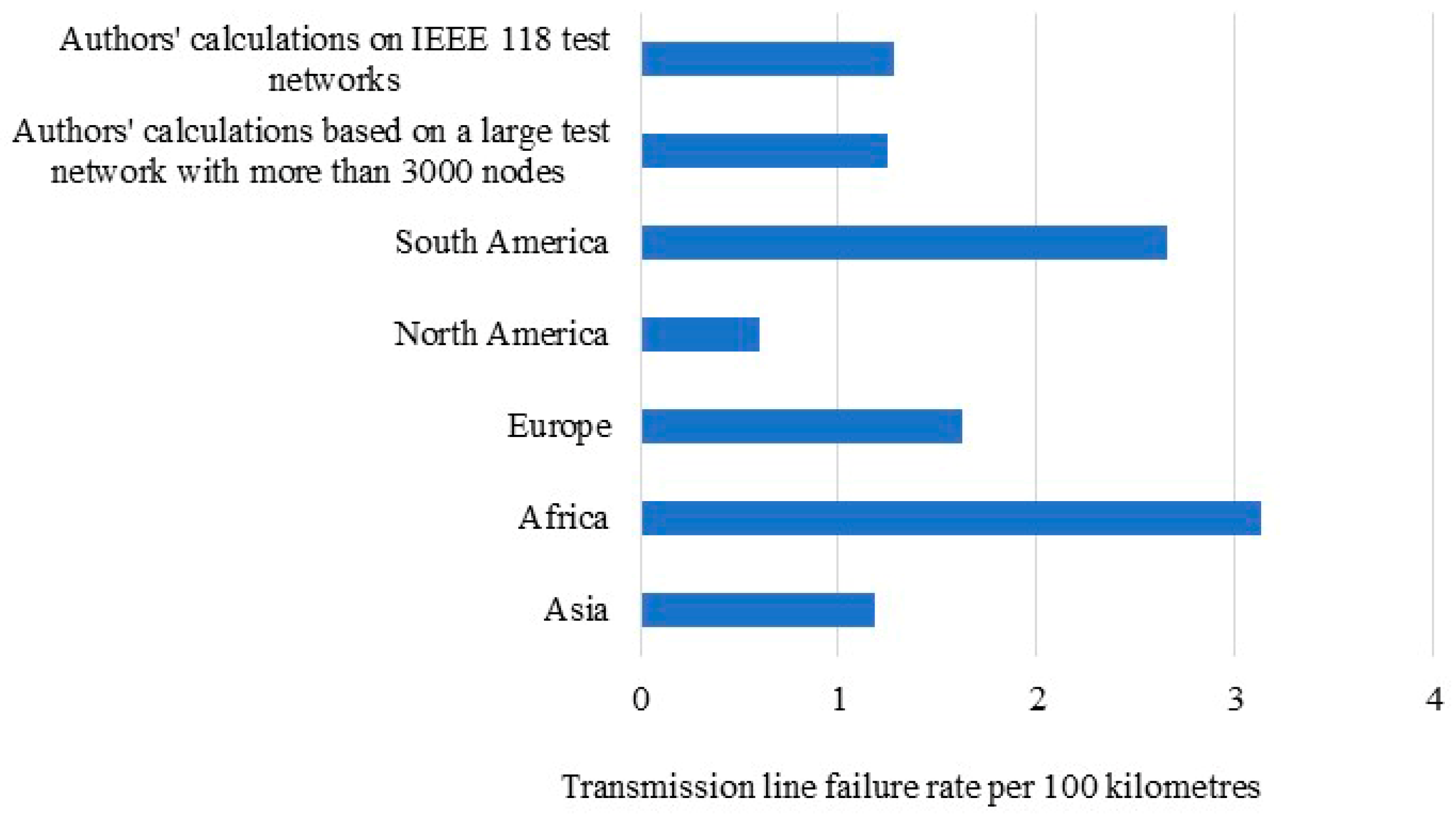
5. Calculations for Different Test Networks
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Michał, B. Analiza Ryzyka Wykonawcy Dotycząca Wybranych Etapów Inwestycji Elektroenergetycznej [Contractors for Selected Phases of an Electricity Project]; SGH: Singapore, 2019. [Google Scholar]
- Borecki, M. A Proposed New Approach for the Assessment of Selected Operating Conditions of the High Voltage Cable Line. Energies 2020, 13, 5275. [Google Scholar] [CrossRef]
- Borecki, M.; Sobolewski, K. An Elimination Method for an Emergency Situation in Gas-Insulated Switchgear in Power Grids. IEEE Trans. Power Deliv. 2021, 36, 3724–3732. [Google Scholar] [CrossRef]
- Hoidalen, H.K. Analytical formulation of lightning-induced voltages on multiconductor overhead lines above lossy ground. IEEE Trans. Electromagn. Compat. 2003, 45, 92–100. [Google Scholar] [CrossRef]
- Kang, Y.-C.; Lee, B.-E.; Zheng, T.-Y.; Kim, Y.-H.; Crossley, P.A. Protection, faulted phase and winding identification for the three-winding transformer using the increments of flux linkages. IET Gener. Transm. Distrib. 2010, 4, 1060. [Google Scholar] [CrossRef]
- Kontroli, N.I. Najwyższa Izba Kontroli. Rozwój Elektroenergetycznej Sieci Dystrybucyjnej [Development of the Electricity Distribution Network]; Najwyższa Izba Kontroli: Warszawa, Poland, 2024.
- Christiaanse, W.; Palmer, A. A Technique for the Automated Scheduling of the Maintenance of Generating Facilities. IEEE Trans. Power Appar. Syst. 1972, PAS-91, 137–144. [Google Scholar] [CrossRef]
- Abbasghorbani, M.; Damchi, Y.; Rajabi Mashhadi, H. Reliability-Centered Maintenance for Overhead Transmission Lines in Composite Power System. Int. Trans. Electr. Energ. Syst. 2022, 2022, 1170269. [Google Scholar] [CrossRef]
- Pandzic, H.; Conejo, A.J.; Kuzle, I.; Caro, E. Yearly Maintenance Scheduling of Transmission Lines Within a Market Environment. IEEE Trans. Power Syst. 2012, 27, 407–415. [Google Scholar] [CrossRef]
- Abiri-Jahromi, A.; Fotuhi-Firuzabad, M.; Abbasi, E. An Efficient Mixed-Integer Linear Formulation for Long-Term Overhead Lines Maintenance Scheduling in Power Distribution Systems. IEEE Trans. Power Deliv. 2009, 24, 2043–2053. [Google Scholar] [CrossRef]
- Alvarez-Alvarado, M.S.; Jayaweera, D. Reliability-based smart-maintenance model for power system generators. IET Gener. Transm. Distrib. 2020, 14, 1770–1780. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, X.; Wu, Y.; Chen, Z.; Gong, H.; Zhu, L.; Liu, Y. Seismic resilience assessment of urban interdependent lifeline networks. Reliab. Eng. Syst. Saf. 2022, 218, 108164. [Google Scholar] [CrossRef]
- Ferrario, E.; Poulos, A.; Castro, S.; La Llera, J.C.d.; Lorca, A. Predictive capacity of topological measures in evaluating seismic risk and resilience of electric power networks. Reliab. Eng. Syst. Saf. 2022, 217, 108040. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, S.; Wu, X.; Chen, D.; He, J. Research on a seismic connectivity reliability model of power systems based on the quasi-Monte Carlo method. Reliab. Eng. Syst. Saf. 2021, 215, 107888. [Google Scholar] [CrossRef]
- Iuliis, M.d.; Kammouh, O.; Cimellaro, G.P.; Tesfamariam, S. Quantifying restoration time of power and telecommunication lifelines after earthquakes using Bayesian belief network model. Reliab. Eng. Syst. Saf. 2021, 208, 107320. [Google Scholar] [CrossRef]
- Venkateswaran, V.B.; Saini, D.K.; Sharma, M. Techno-economic hardening strategies to enhance distribution system resilience against earthquake. Reliab. Eng. Syst. Saf. 2021, 213, 107682. [Google Scholar] [CrossRef]
- Wang, H.; Fang, Y.-P.; Zio, E. Resilience-oriented optimal post-disruption reconfiguration for coupled traffic-power systems. Reliab. Eng. Syst. Saf. 2022, 222, 108408. [Google Scholar] [CrossRef]
- Xie, H.; Tang, L.; Zhu, H.; Cheng, X.; Bie, Z. Robustness assessment and enhancement of deep reinforcement learning-enabled load restoration for distribution systems. Reliab. Eng. Syst. Saf. 2023, 237, 109340. [Google Scholar] [CrossRef]
- Huang, X.; Wang, N. An adaptive nested dynamic downscaling strategy of wind-field for real-time risk forecast of power transmission systems during tropical cyclones. Reliab. Eng. Syst. Saf. 2024, 242, 109731. [Google Scholar] [CrossRef]
- Chłopek, Z. The cognitive interpretation of the Monte Carlo method for the technical applications. Eksploat. I Niezawodn. 2009, 38–46. [Google Scholar]
- Laudyn, D.; Maksymiuk, J. Jakość i Niezawodność w Elektroenergetyce [Quality and Reliability in the Electric Power Industry]; Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 1996. [Google Scholar]
- Paska, J. Niezawodność Systemów Elektroenergetycznych [Reliability of Electricity Systems]; Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 2005. [Google Scholar]
- Zhang, C.; Zeng, Q.; Dui, H.; Chen, R.; Wang, S. Reliability model and maintenance cost optimization of wind-photovoltaic hybrid power systems. Reliab. Eng. Syst. Saf. 2025, 255, 110673. [Google Scholar] [CrossRef]
- Cao, M.; Guo, J.; Xiao, H.; Wu, L. Reliability analysis and optimal generator allocation and protection strategy of a non-repairable power grid system. Reliab. Eng. Syst. Saf. 2022, 222, 108443. [Google Scholar] [CrossRef]
- Meng, X.; Tian, L.; Liu, J.; Jin, Q. Failure prediction of overhead transmission lines incorporating time series prediction model for wind-ice loads. Reliab. Eng. Syst. Saf. 2025, 259, 110927. [Google Scholar] [CrossRef]
- Dikshit, S.; Alipour, A. A moment-matching method for fragility analysis of transmission towers under straight line winds. Reliab. Eng. Syst. Saf. 2023, 236, 109241. [Google Scholar] [CrossRef]
- Meng, X.; Tian, L.; Li, C.; Liu, J. Copula-based wind-induced failure prediction of overhead transmission line considering multiple temperature factors. Reliab. Eng. Syst. Saf. 2024, 247, 110138. [Google Scholar] [CrossRef]
- Du, W.-L.; Fu, X.; Shao, S.; Li, G.; Li, H.-N.; Yang, F.-L. Wind hazard reliability assessment of a transmission tower-line system incorporating progressive collapse. Reliab. Eng. Syst. Saf. 2025, 257, 110878. [Google Scholar] [CrossRef]
- Du, W.-L.; Fu, X.; Zhu, D.-J.; Li, G.; Li, H.-N.; Huang, Z.-H.; Liu, Y.-Z. Nataf-based probabilistic buffeting prediction of overhead transmission lines under multi-dimensional turbulent wind excitation. Reliab. Eng. Syst. Saf. 2025, 257, 110846. [Google Scholar] [CrossRef]
- Chen, L.J.; Li, X. Statistic analysis on reliability of power transmission and transformation facilities in China in 2011. Elect. Power 2012, 45, 89–93. [Google Scholar]
- Chen, L.J.; Hu, X.Z. Statistic analysis on reliability of power transmission and transformation facilities in China in 2010. Elect. Power 2011, 44, 71–77. [Google Scholar]
- Alminhana, F.; Mason, M.; Albermani, F. Transmission line failure propagation under extreme wind scenarios: Extratropical cyclones. Eng. Struct. 2023, 284, 115942. [Google Scholar] [CrossRef]
- Dikshit, S.; Dobson, I.; Alipour, A. Cascading structural failures of towers in an electric power transmission line due to straight line winds. Reliab. Eng. Syst. Saf. 2024, 250, 110304. [Google Scholar] [CrossRef]
- Ma, L.; Christou, V.; Bocchini, P. Framework for probabilistic simulation of power transmission network performance under hurricanes. Reliab. Eng. Syst. Saf. 2022, 217, 108072. [Google Scholar] [CrossRef]
- Bi, W.; Tian, L.; Li, C.; Ma, Z.; Pan, H. Wind-induced failure analysis of a transmission tower-line system with long-term measured data and orientation effect. Reliab. Eng. Syst. Saf. 2023, 229, 108875. [Google Scholar] [CrossRef]
- Billinton, R.; Singh, G. Application of adverse and extreme adverse weather: Modelling in transmission and distribution system reliability evaluation. IEE Proc. Gener. Transm. Distrib. 2006, 153, 115. [Google Scholar] [CrossRef]
- Billinton, R.; Singh, G.D. Reliability assessment of transmission and distribution systems considering repair in adverse weather conditions. In Proceedings of the IEEE CCECE2002 Canadian Conference on Electrical and Computer Engineering. Conference Proceedings (Cat. No.02CH37373), Winnipeg, MB, Canada, 12–15 May 2002; IEEE: New York, NY, USA, 2002; pp. 88–93, ISBN 0-7803-7514-9. [Google Scholar]
- Chernysheva, A.; Adamec, V.; Tulsky, V.; Vanin, A. Calibration of the distribution network reliability model based on failure data. Case Study. In Proceedings of the 2019 International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 14–15 March 2019; IEEE: New York, NY, USA, 2019; pp. 1–5, ISBN 978-1-5386-9334-6. [Google Scholar]
- Christodoulou, C.A.; Ekonomou, L.; Fotis, G.P.; Gonos, I.F.; Stathopulos, I.A. Assessment of surge arrester failure rate and application studies in Hellenic high voltage transmission lines. Electr. Power Syst. Res. 2010, 80, 176–183. [Google Scholar] [CrossRef]
- Malik, H.; Yadav, A.K.; Mishra, S.; Mehto, T. Application of neuro-fuzzy scheme to investigate the winding insulation paper deterioration in oil-immersed power transformer. Int. J. Electr. Power Energy Syst. 2013, 53, 256–271. [Google Scholar] [CrossRef]
- Borecki, M. Analiza Zagrożenia Piorunowego i Sposobów Jego Ograniczenia w Liniach Napowietrznych 110 kV–400 kV [Analysis of the Lightning Danger and Ways to Reduce It in 110 kV–400 kV Overhead Lines], 1st ed.; Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 2024. [Google Scholar]
- Sundararaman, B.; Jain, P. Fault Detection and Classification in Electrical Power Transmission System Using Wavelet Transform. In RAiSE-2023; MDPI: Basel, Switzerland, 2023; p. 71. [Google Scholar]
- Chojnacki, A.Ł. Analiza Niezawodności Eksploatacyjnej Elektroenergetycznych Sieci Dystrybucyjnych [Analysis of the Operational Reliability of Electricity Distribution Networks]; Politechnika Świętokrzyska: Kielce, Poland, 2013. [Google Scholar]
- Mahmoud, S.A. Reliability Assessment for Overhead Power Transmission Lines Using Failure Rate Analysis. Aust. J. Basic Appl. Sci. 2016, 10, 34–49. [Google Scholar]
- Chojnacki, A. Właściwości niezawodnościowe napowietrznych linii dystrybucyjnych 110 kV [Reliability characteristics of 110 kV overhead distribution lines]. Przegląd Elektrotechniczny 2017, 85, 15–19. [Google Scholar] [CrossRef]
- Chojnacki, A. Impact of ambient temperature on the failure intensity of overhead MV power lines. Przegląd Elektrotechniczny 2022, 1, 309–313. [Google Scholar] [CrossRef]
- Mesić, M.; Plavšić, T. The contribution of failure analyses to transmission network maintenance preferentials. Eng. Fail. Anal. 2013, 35, 262–271. [Google Scholar] [CrossRef]
- Mesic, M.; Toljan, I.; Tesnjak, S. The role of transmission network maintenance in achieving power system reliability. In Proceedings of the MELECON 2008—The 14th IEEE Mediterranean Electrotechnical Conference. MELECON 2008—2008 IEEE Mediterranean Electrotechnical Conference, Ajaccio, France, 5–7 May 2008; IEEE: New York, NY, USA, 2008; pp. 688–693, ISBN 978-1-4244-1632-5. [Google Scholar]
- Melodi, A.O.; Momoh, J.A.; Oyinlola, A.O. Transmission system reliability modeling and assessment for Nigerian electric grid. In Proceedings of the 2017 IEEE PES PowerAfrica, Accra, Ghana, 27–30 June 2017; IEEE: New York, NY, USA, 2017; pp. 40–45, ISBN 978-1-5090-4746-8. [Google Scholar]
- Gaver, D.P.; Montmeat, F.E.; Patton, A.D. Power System Reliability I-Measures of Reliability and Methods of Calculation. IEEE Trans. Power Appar. Syst. 1964, 83, 727–737. [Google Scholar] [CrossRef]
- Liu, Y.; Singh, C. Evaluation of Hurricane Impact on Failure Rate of Transmission Lines Using Fuzzy Expert System. In Proceedings of the 2009 15th International Conference on Intelligent System Applications to Power Systems (ISAP), Curitiba, Brazil, 8–12 November 2009; IEEE: New York, NY, USA, 2009; pp. 1–6, ISBN 978-1-4244-5097-8. [Google Scholar]
- Ahmadi, R.; Wu, S.; Sobhani, A. Reliability Modeling and Maintenance Optimization for a Repairable System with Heterogeneity Population. IEEE Trans. Rel. 2022, 71, 87–99. [Google Scholar] [CrossRef]
- Enjavimadar, M.; Rastegar, M. Optimal reliability-centered maintenance strategy based on the failure modes and effect analysis in power distribution systems. Electr. Power Syst. Res. 2022, 203, 107647. [Google Scholar] [CrossRef]
- Heo, J.H.; Kim, M.K.; Lyu, J.K. Implementation of Reliability-Centered Maintenance for transmission components using Particle Swarm Optimization. Int. J. Electr. Power Energy Syst. 2014, 55, 238–245. [Google Scholar] [CrossRef]
- Heo, J.-H.; Kim, M.-K.; Park, G.-P.; Yoon, Y.T.; Park, J.K.; Lee, S.-S.; Kim, D.-H. A Reliability-Centered Approach to an Optimal Maintenance Strategy in Transmission Systems Using a Genetic Algorithm. IEEE Trans. Power Deliv. 2011, 26, 2171–2179. [Google Scholar] [CrossRef]
- Zhang, D.; Li, W.; Xiong, X. Overhead Line Preventive Maintenance Strategy Based on Condition Monitoring and System Reliability Assessment. IEEE Trans. Power Syst. 2014, 29, 1839–1846. [Google Scholar] [CrossRef]
- Wang, J.; Xiong, X.; Zhou, N.; Li, Z.; Weng, S. Time-varying failure rate simulation model of transmission lines and its application in power system risk assessment considering seasonal alternating meteorological disasters. IET Gener. Transm. Distrib. 2016, 10, 1582–1588. [Google Scholar] [CrossRef]
- Liu, Y.; Singh, C. Reliability Evaluation of Composite Power Systems Using Markov Cut-Set Method. IEEE Trans. Power Syst. 2010, 25, 777–785. [Google Scholar] [CrossRef]
- Chojnacki, A. Funkcje niezawodnościowe napowietrznych linii dystrybucyjnych 110 kV, SN oraz nn [Reliability functions of 110 kV, MV and LV overhead distribution lines]. Przegląd Elektrotechniczny 2024, 1, 196–200. [Google Scholar] [CrossRef]
- Yellen, J.; Al-Khamis, T.M.; Vemuri, S.; Lemonidis, L. A decomposition approach to unit maintenance scheduling. IEEE Trans. Power Syst. 1992, 7, 726–733. [Google Scholar] [CrossRef]
- Al-Khamis, T.M.; Vemuri, S.; Lemonidis, L.; Yellen, J. Unit maintenance scheduling with fuel constraints. IEEE Trans. Power Syst. 1992, 7, 933–939. [Google Scholar] [CrossRef]
- Billinton, R.; Bollinger, K. Transmission System Reliability Evaluation Using Markov Processes. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 538–547. [Google Scholar] [CrossRef]
- Han, S.-R.; Guikema, S.D.; Quiring, S.M.; Lee, K.-H.; Rosowsky, D.; Davidson, R.A. Estimating the spatial distribution of power outages during hurricanes in the Gulf coast region. Reliab. Eng. Syst. Saf. 2009, 94, 199–210. [Google Scholar] [CrossRef]
- Mo, H.; Sansavini, G. Impact of aging and performance degradation on the operational costs of distributed generation systems. Renew. Energy 2019, 143, 426–439. [Google Scholar] [CrossRef]
- Azadeh, A.; Asadzadeh, S.M.; Salehi, N.; Firoozi, M. Condition-based maintenance effectiveness for series–parallel power generation system—A combined Markovian simulation model. Reliab. Eng. Syst. Saf. 2015, 142, 357–368. [Google Scholar] [CrossRef]
- IEEE. 2007 International Power Engineering Conference (IPEC 2007); IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- IEEE Std C57.125-2015; (Revision of IEEE Std C57.125-1991): IEEE Guide for Failure Investigation, Documentation, Analysis, and Reporting for Power Transformers and Shunt Reactors. IEEE: New York, NY, USA, 2015; ISBN 978-0-7381-9901-6.
- Bossi, A.; Dind, J.; Frisson, J.; Khoudiakov, U.; Light, H. An International Survey on Failures in Large Power Transformers in Service; Electra: London, UK, 1983. [Google Scholar]
- Tenbohlen, S.; Jagers, J.; Vahidi, F. Standardized survey of transformer reliability: On behalf of CIGRE WG A2.37. In Proceedings of the 2017 International Symposium on Electrical Insulating Materials (ISEIM), Toyohashi, Japan, 11–15 September 2017; IEEE: New York, NY, USA, 2017; pp. 593–596, ISBN 978-4-88686-099-6. [Google Scholar]
- Tenbohlen, S. VDE-Hochspannungstechnik: Vorträge der ETG-Fachtagung 14.–16. November 2016 in Berlin; VDE Verlag: Berlin/Offenbach, Germany, 2016; ISBN 978-3-8007-4310-0. [Google Scholar]
- Abdelfatah, M.; EL-Shimy, M.; Ismail, H.M. Reliability analysis of 220 kV power transformers in Egypt. Ain Shams Eng. J. 2011, 2, 183–194. [Google Scholar] [CrossRef][Green Version]
- Klistala, T. Przegląd metod diagnostycznych układów izolacyjnych transformatorów dużej mocy w eksploatacji [Overview of diagnostic methods for insulating systems of high-power transformers in service]. Pomiary Autom. Kontrola 2008, 54, 754–759. [Google Scholar]
- Bagiński, A.; Domżalski, T.; Kaźmierski, M.; Łukaszewski, J.; Olech, W.; Olejniczak, H.; Owczarek, J.; Sieradzki, S.; Szymański, Z. Ramowa Instrukcja Eksploatacji Transformatorów [Framework for the Operation of Transformers]; ELEKTRYKA Sp. z o. O: Gliwice, Poland, 2001. [Google Scholar]
- Jagers, J.N.; Khosa, J.; De Klerk, P.J.; Gaunt, C.T. Transformer reliability and condition assessment in a South African utility. In Proceedings of the XVth International Symposium on High Voltage Engineering, Ljubljana, Slovenia, 27–31 August 2007. [Google Scholar]
- Petersen, A.A.P.L. Impact of recent transformer failures and fires Australian and New Zealand experiences. In Proceedings of the CIGRE-Session 2004 Elektrotech, Inftech, Paris, France, 29 August–3 September 2004; pp. 1–10. [Google Scholar]
- Martin, D.; Marks, J.; Saha, T. Survey of Australian power transformer failures and retirements. IEEE Electr. Insul. Mag. 2017, 33, 16–22. [Google Scholar] [CrossRef]
- Minhas, M.S.A.; De Klerk, P.J.; Reynders, J.P. Failures in Large Power Transformers. In Proceedings of the CIGRE International Conference on Large High Voltage Systems, Cairo, Egypt, 27–30 September 1997. [Google Scholar]
- Siderakis, K.; Pylarinos, D.; Thalassinakis, E. Power Transformers Management in the Power System of Crete. In Proceedings of the 9th International Conference on Deregulated Electricity Market Issues in South Eastern Europe, Nicosia, Cyprus, 25–26 September 2014. [Google Scholar]
- Kogan, V.I.; Fleeman, J.A.; Provanzana, J.H.; Shih, C.H. Failure analysis of EHV transformers. IEEE Trans. Power Deliv. 1988, 3, 672–683. [Google Scholar] [CrossRef]
- Chafai, M.; Refoufi, L.; Bentarzi, H. Large power transformer reliability modeling. Int. J. Syst. Assur. Eng. Manag. 2016, 7, 9–17. [Google Scholar] [CrossRef]
- Soleimani, M.; Kezunovic, M.; Butenko, S. Linear Arrhenius-Weibull Model for Power Transformer Thermal Stress Assessment. IEEE Access 2022, 10, 19013–19021. [Google Scholar] [CrossRef]
- Behzadirafi, S.; Salehfar, H.; Aravindan, V. Impact of Power System Protection and Fault Current Limiters on Component Failure Rates. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018; IEEE: New York, NY, USA, 2018; pp. 1–6, ISBN 978-1-5386-3596-4. [Google Scholar]
- Behzadirafi, S.; Salehfar, H. Preventive Maintenance Scheduling Based on Short Circuit and Overload Currents. IEEE Trans. Smart Grid 2015, 6, 1740–1747. [Google Scholar] [CrossRef]
- Zhao, S.; Singh, C. A reliability evaluation method for line switching operations in power systems. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; IEEE: New York, NY, USA, 2016; pp. 1–7, ISBN 978-88-941051-2-4. [Google Scholar]
- Singh, C.; Mitra, J. Composite system reliability evaluation using state space pruning. IEEE Trans. Power Syst. 1997, 12, 471–479. [Google Scholar] [CrossRef]
- Chojnacki, A. Ocena wskaźników niezawodnościowych stacji 110 kV/SN i rozdzielni sieciowych SN w oparciu o metody analityczne oraz symulacyjne [Reliability assessment of 110 kV/SN substations and MV network switchgear based on analytical and simulation methods]. Przegląd Elektrotechniczny 2016, 1, 182–187. [Google Scholar] [CrossRef]
- Chojnacki, A. Parametry i właściwości niezawodnościowe stacji GPZ i RS [Parameters and reliability characteristics of GPZ and RS substations]. Przegląd Elektrotechniczny 2016, 1, 198–204. [Google Scholar] [CrossRef]
- Chojnacki, A. Podstawowe funkcje niezawodnościowe stacji 110 kV/SN oraz rozdzielni sieciowych SN [Basic reliability functions of 110 kV/SN substations and MV network switchgear]. Przegląd Elektrotechniczny 2016, 1, 240–243. [Google Scholar] [CrossRef]
- Stępień, J. Kompleksowy model niezawodnościowy głównych punktów zasilających 110/15 kV [Comprehensive reliability model of 110/15 kV main supply points]. Przegląd Elektrotechniczny 2008, 1, 128–131. [Google Scholar]
- Pijarski, P.; Belowski, A. Application of Methods Based on Artificial Intelligence and Optimisation in Power Engineering—Introduction to the Special Issue. Energies 2024, 17, 516. [Google Scholar] [CrossRef]
- Alvarez-Alvarado, M.S.; Donaldson, D.L.; Recalde, A.A.; Noriega, H.H.; Khan, Z.A.; Velasquez, W.; Rodriguez-Gallegos, C.D. Power System Reliability and Maintenance Evolution: A Critical Review and Future Perspectives. IEEE Access 2022, 10, 51922–51950. [Google Scholar] [CrossRef]
- Safdarian, F.; Wert, J.L.; Cyr, D.; Overbye, T.J. Power System Resiliency and Reliability Issues from Renewable Resource Droughts. In Proceedings of the 2024 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2024; IEEE: New York, NY, USA, 2024; pp. 1–6, ISBN 979-8-3503-7240-3. [Google Scholar]
- Mahdavi, M.; Javadi, M.S.; Catalão, J.P. Integrated generation-transmission expansion planning considering power system reliability and optimal maintenance activities. Int. J. Electr. Power Energy Syst. 2023, 145, 108688. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, H. Wind power system reliability and maintenance optimization considering turbine and wind uncertainty. JQME 2022, 28, 252–273. [Google Scholar] [CrossRef]
- Garip, S.; Özdemir, Ş.; Altin, N. Power System Reliability Assessment—A Review on Analysis and Evaluation Methods. J. Energy Syst. 2022, 6, 401–419. [Google Scholar] [CrossRef]
- Chojnacki, A.L. Assessment of the Risk of Damage to 110 kV Overhead Lines Due to Wind. Energies 2021, 14, 556. [Google Scholar] [CrossRef]
- Chojnacki, A. Analysis of Seasonality and Causes of Equipment and Facility Failures in Electric Power Distribution Networks. Przegląd Elektrotechniczny 2023, 1, 159–165. [Google Scholar] [CrossRef]
- Rexhepi, V. An Analysis of Power Transformer Outages and Reliability Monitoring. Energy Procedia 2017, 141, 418–422. [Google Scholar] [CrossRef]
- Minhas, M. Failures in power system transformers and appropriate monitoring techniques. In Proceedings of the 11th International Symposium on High-Voltage Engineering (ISH 99), London, UK, 23–27 August 1999; IEEE: New York, NY, USA, 1999. v1-94-v1-94. ISBN 0-85296-719-5. [Google Scholar]
- Chojnacki, A.Ł.; Chojnacka, K.J. Niezawodność Elektroenergetycznych Sieci Dystrybucyjnych [Reliability of Electricity Distribution Networks]; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2018. [Google Scholar]
- Jongen, R.A.; Morshuis, P.H.F.; Smit, J.J.; Janssen, A.L.J.; Gulski, E. A Statistical Approach to Processing Power Transformer Failure Data. In Proceedings of the 19th International Conference on Electricity Distribution (CIRED), Vienna, Austria, 21–24 May 2007. [Google Scholar]
- Jongen, R.; Gulski, E.; Morshuis, P.; Smit, J.; Janssen, A. Statistical analysis of power transformer component life time data. In Proceedings of the 2007 International Power Engineering Conference (IPEC 2007), Singapore, 3–6 December 2007. [Google Scholar]
- Khalil, M. Qualitative and Quantitative FMECA on 220 kV Power Transformers. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–8, ISBN 978-1-5386-5186-5. [Google Scholar]
- Li, W. Risk Assessment of Power Systems; Wiley: New York, NY, USA, 2014; ISBN 9781118686706. [Google Scholar]
- Airoboman, A. Reliability Assessment of Power System Network: A Detailed Review. IJET 2022, 7, 90–103. [Google Scholar] [CrossRef]
- Zhou, Y.; Pahwa, A.; Yang, S.-S. Modeling Weather-Related Failures of Overhead Distribution Lines. IEEE Trans. Power Syst. 2006, 21, 1683–1690. [Google Scholar] [CrossRef]
- Pahwa, A. Modeling Weather-Related Failures of Overhead Distribution Lines. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; IEEE: New York, NY, USA, 2007; p. 1, ISBN 1-4244-1296-X. [Google Scholar]
- Yang, S.; Zhou, W.; Zhu, S.; Le Wang, Y.E.L.; Xia, X.; Li, H. Failure probability estimation of overhead transmission lines considering the spatial and temporal variation in severe weather. J. Mod. Power Syst. Clean Energy 2019, 7, 131–138. [Google Scholar] [CrossRef]
- Tenbohlen, S.; Jagers, J.; Gebauer, J.; Müller, P.; Lapworth, J.; Yukiyasu, S.; Desai, B.; McIntosh, A.; Bastos, G.; Bo, L. Transformer Reliability Survey: Interim Report. Electra 2012, 46–49. [Google Scholar]
- Hachimenum, N.; Amadi, F.I.I. Analysis of Transformer Loadings and Failure Rate in Onitsha Electricity Distribution Network. Am. J. Electr. Electron. Eng. 2016, 4, 157–163. [Google Scholar]
- Farzaneh Vahidi, S.T. Statistical Failure Analysis of European Substation Transformers. In Proceedings of the Diagnostik elektrischer Betriebsmittel 2014—Beiträge der 6, Berlin, Germany, 25–26 November 2014. [Google Scholar]
- William, H.B. Analysis of transformer failures WGP 33 (03). In Proceedings of the 36th Annual Conference on International Association of Engineering Insurers (IMIA), Stockholm, Sweden, 15–17 September 2003. [Google Scholar]
- Hernandez, R.D.; Hancock, B.; Salmeron, M. Lessons Learned from Analysis of Power Transformer Failure Rates. In Proceedings of the 2022 IEEE 40th Central America and Panama Convention (CONCAPAN), Panama City, Panama, 9–12 November 2022; IEEE: New York, NY, USA, 2022; pp. 1–6, ISBN 978-1-7281-6715-2. [Google Scholar]
- Jagers, J.T.S. Evaluation of transformer reliability data based on national and utility statistics. In Proceedings of the 16th International Symposium on High Voltage Engineering, Cape Town, South Africa, 24–28 August 2009. [Google Scholar]
- Kowalski, Z. Niezawodność Zasilania Odbiorców Energii Elektrycznej [Reliability of Power Supply to Electricity Consumers], 1st ed.; Wydawnictwo Politechniki Łódzkiej: Łódź, Poland, 1992. [Google Scholar]
- Sozański, J. Niezawodność i Jakość Pracy Systemu Elektroenergetycznego [Reliability and Quality of Power System Operation]; WNT: Warszawa, Poland, 1990. [Google Scholar]
- Dąbrowska-Kauf, G. Niezawodność dostaw energii elektrycznej jako miara efektywności diagnostyki technicznej w sieciach elektroenergetycznych [Reliability of electricity supply as a measure of the effectiveness of technical diagnostics in electricity networks]. Diagnostyka 2005, 33, 203–208. [Google Scholar]
- Abdelfatah, M.; EL-Shimy, M.; Ismail, H.M. Outage data analysis of utility power transformers based on outage reports during 2002–2009. Int. J. Electr. Power Energy Syst. 2013, 47, 41–51. [Google Scholar] [CrossRef]
- Li, W.; Zhou, J.; Xiong, X. Fuzzy Models of Overhead Power Line Weather-Related Outages. IEEE Trans. Power Syst. 2008, 23, 1529–1531. [Google Scholar] [CrossRef]
- Kacejko, P.; Pijarski, P.; Wancerz, M.; Adamek, S. Risk Assessment of Generation Curtailment in RES for Emergency States of Power Grids. AEZ 2023, 14, 10–34. [Google Scholar] [CrossRef]
- Wang, P.; Billinton, R. Reliability cost/worth assessment of distribution systems incorporating time-varying weather conditions and restoration resources. IEEE Trans. Power Deliv. 2002, 17, 260–265. [Google Scholar] [CrossRef]
- Alvehag, K.; Soder, L. A Reliability Model for Distribution Systems Incorporating Seasonal Variations in Severe Weather. IEEE Trans. Power Deliv. 2011, 26, 910–919. [Google Scholar] [CrossRef]
- Murray, K.; Bell, K.R.W. Wind related faults on the GB transmission network. In Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, UK, 7–10 July 2014; IEEE: New York, NY, USA, 2014; pp. 1–6, ISBN 978-1-4799-3561-1. [Google Scholar]
- Ulrich, M. The Characterisation and Automatic the Characterisa and Automatic Classification of Transmission Line Faults. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 2014. [Google Scholar]
- Bargiel, J.; Goc, W.; Teichman, B. Dane do oceny niezawodności sieci Elektroenergetycznych wysokiego napięcia [Data for reliability assessment of high-voltage electricity networks]. Zeszyty Naukowe Politechniki Śląskiej 2000, 174, 119–130. [Google Scholar]
- Tenbohlen, S.; Hanif, Z.; Martin, D. Analysis of Major Failures of Power Transformers. In Proceedings of the ICTRAM, Split, Croatia, 29 November–2 December 2023. [Google Scholar]
- Energiforsk. High Voltage Equipment Reliability Data. 2023. Available online: https://energiforsk.se/media/32998/2023-974-high-voltage-equipment-reliability-data.pdf (accessed on 15 April 2025).
- Kjolle, G.H. What Do Fault Statistics Tell Us What Do Fault Statistics Tell Us Regarding Causes Resulting in Power Outages? CESI: Milan, Italy, 2011. [Google Scholar]
- Enel Foundation. Assessment of the Impact of International Interconnection Lines on the Resilience of Argentina and Chile; CESI: Milan, Italy, 2020. [Google Scholar]
- Polskie Sieci Elektroenergetyczne PSE S.A. Available online: https://www.pse.pl (accessed on 15 April 2025).
- PTPiREE. Energetyka, Dystrybucja, Przesył—Edycja 2024, Poznań, 2024. Available online: https://ptpiree.pl/raport-ptpiree/ (accessed on 15 April 2025).
- Waldemar, D. Zagrożenia i wyzwania dla krajowej sieci przesyłowej [Threats and challenges to the national transmission network]. Rynek Energii 2018, 138, 48–54. [Google Scholar]
- Waldemar, D. Krajowe Stacje Najwyższych i Wysokich Napięć—Przegląd Rozwiązań i Technologii [National High and High Voltage Substations—Overview of Solutions and Technologies]. In Proceedings of the XLIII Konferencja Naukowo Techniczna Nowoczesne Technologie w Stacjach i Liniach Elektroenergetycznych, Gdańsk, Polska, 9–10 May 2019. [Google Scholar]
- Waldemar, D. Krajowa sieć elektroenergetyczna—Analiza stanu i zagrożeń funkcjonowania [National electricity grid—Analysis of status and risks of operation]. Rynek Energii 2023, 166, 3–10. [Google Scholar]
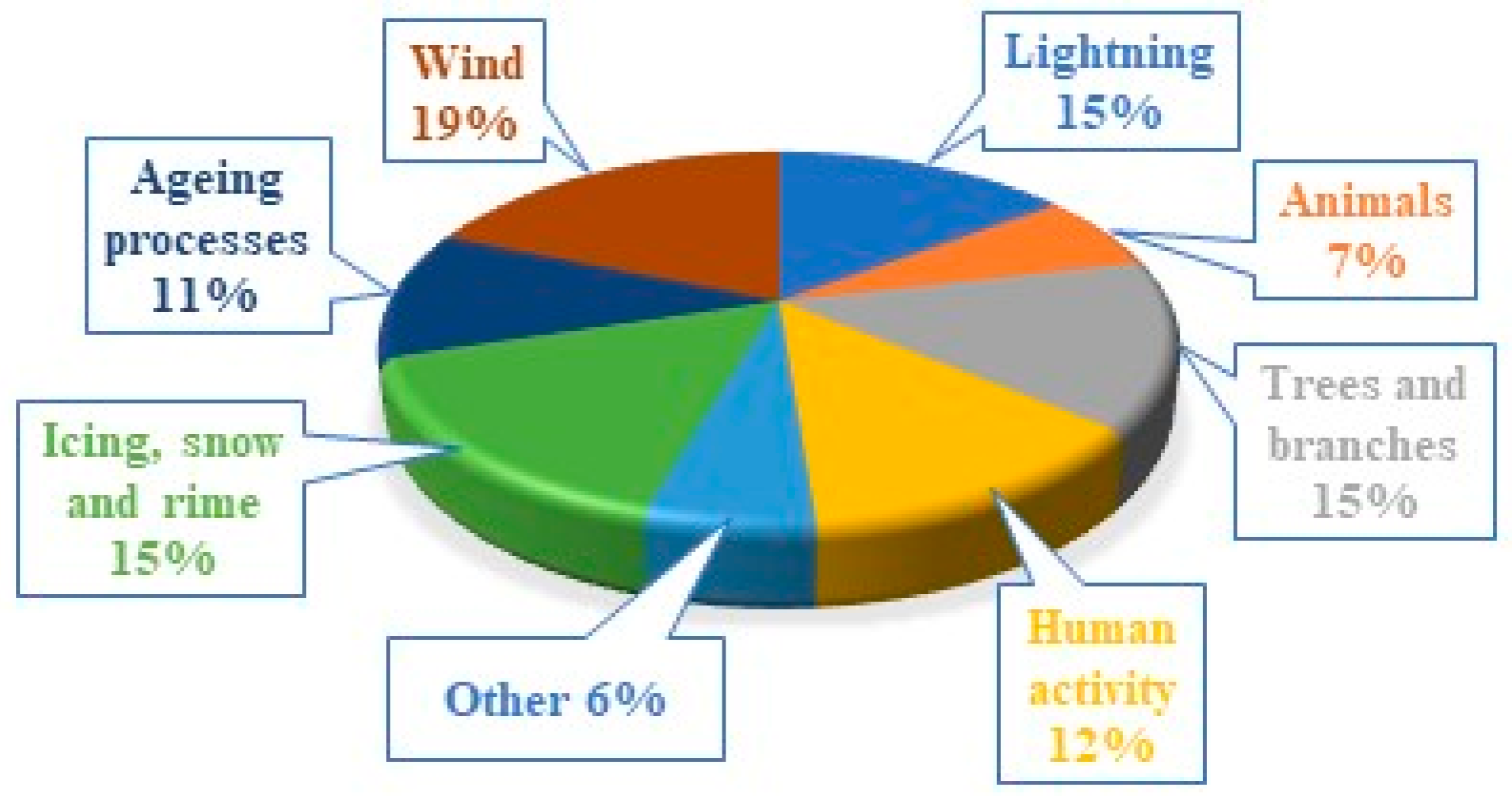
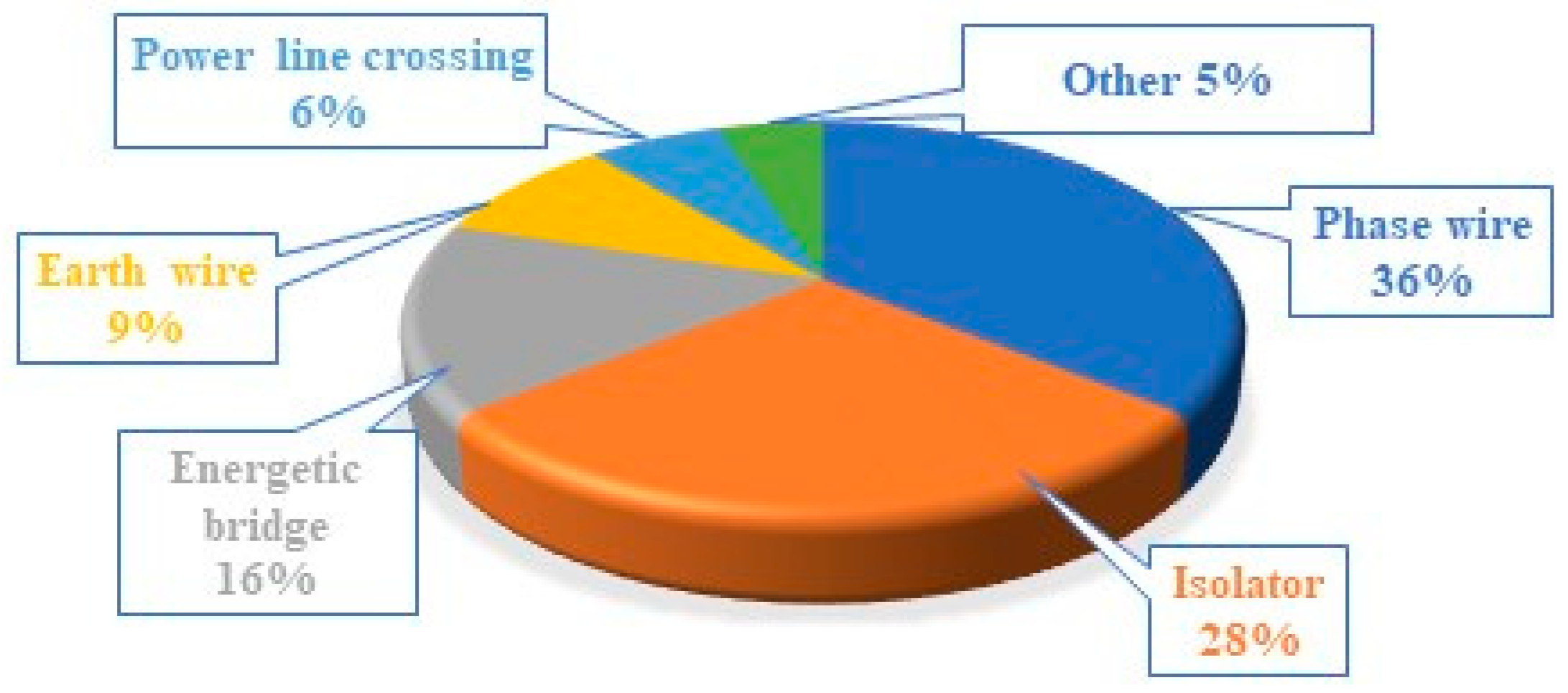





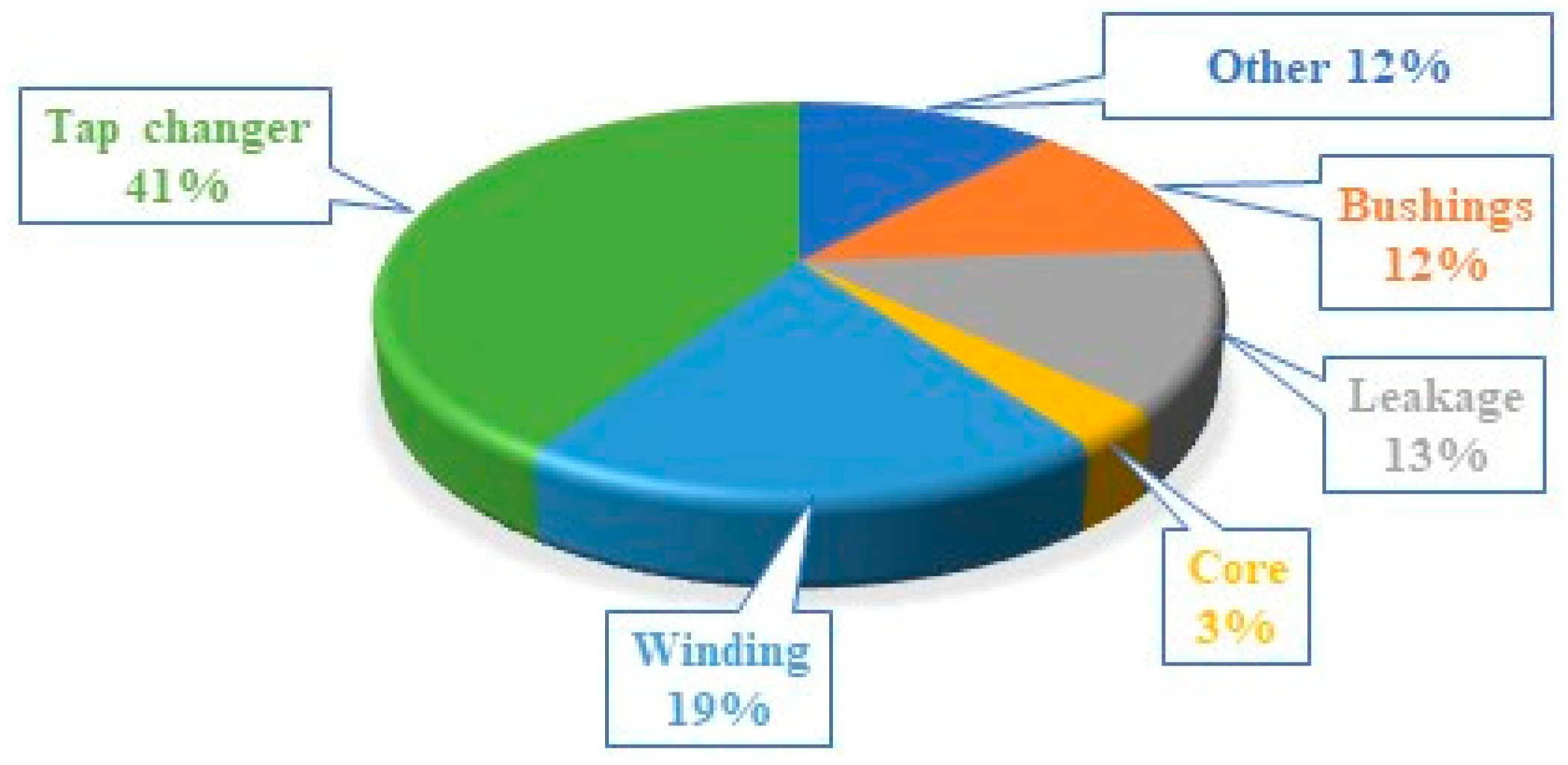
| Method Used | Continent | References |
|---|---|---|
| Empirical formula | Europe | [2,3,4,38,39,40,41,43,44,45,46,47,48,59,70,86,87,89,90,91,92,100,110,111,112,116,122,123,124,125,126,127] |
| Asia | [5,8,30,31,44,56,108,110,118,121] | |
| North America | [44,50,103,113,128] | |
| Africa | [49,71,80,105,118,129] | |
| Australia and Oceania | [70,76] | |
| Weibull distribution | Europe | [11,81] |
| Asia | [50,54] | |
| North America | [82] | |
| Markov processes | Asia | [51,52,53,55,65] |
| North America | [58,62,82] | |
| Australia and Oceania | [64] | |
| Poisson distribution | Asia | [97,99] |
| North America | [98] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pijarski, P.; Belowski, A. Outage Rates and Failure Removal Times for Power Lines and Transformers. Appl. Sci. 2025, 15, 8030. https://doi.org/10.3390/app15148030
Pijarski P, Belowski A. Outage Rates and Failure Removal Times for Power Lines and Transformers. Applied Sciences. 2025; 15(14):8030. https://doi.org/10.3390/app15148030
Chicago/Turabian StylePijarski, Paweł, and Adrian Belowski. 2025. "Outage Rates and Failure Removal Times for Power Lines and Transformers" Applied Sciences 15, no. 14: 8030. https://doi.org/10.3390/app15148030
APA StylePijarski, P., & Belowski, A. (2025). Outage Rates and Failure Removal Times for Power Lines and Transformers. Applied Sciences, 15(14), 8030. https://doi.org/10.3390/app15148030