Abstract
This article addresses the problem of increasing the energy efficiency of electromechanical systems driven by asynchronous electric drives. In this context, one of the promising areas is the application of a predictive control strategy that allows for reducing energy losses in dynamic modes of electric drives. This paper proposes a computerised method for the multiparameter optimisation of predictive control algorithms for asynchronous electric drives. A computer model was designed in MATLAB and Simulink R2024a based on the gradient-based model predictive control strategy. A series of simulation experiments were carried out by varying the sampling step, number of iterations, prediction horizon, loss function parameters, and maximum linear search step to identify their impact on the control quality indicators. A taxonomic approach was used for multi-criteria optimisation. The study results show that the optimal setting of the algorithmic parameters improves the accuracy of task processing, reduces energy consumption, and reduces computation time. The results obtained can be used to design and operate energy-efficient control systems for asynchronous electric drives in industrial and transport applications. Prospects for further research will focus on hybrid intelligent architectures to enhance adaptability and integration into automated systems.
1. Introduction
1.1. Relevance of the Topic and Research Motivation
Improving the energy efficiency of electromechanical devices and systems, specifically with the use of an electric drive, is one of the key tasks of the industrial, energy, and transport sectors in the context of global requirements and sustainable development goals to improve energy efficiency and the rational use of resources during technological and production processes [1]. According to recent research data, the share of electricity consumed by electric drives is up to 46% of the total, with the vast majority of this use coming from dynamic modes of operation (up to 80%) in the context of the industrial and commercial sectors [2]. The most typical example that proves the above statistical indicators is the functioning of electric vehicle drives, where the speed and torque dynamically change throughout the entire operating cycle [3,4,5], specifically in response to variations in electrical parameters (e.g., stator current, rotor flux, voltage) and the subsequent impact on energy efficiency and control precision.
In practical terms, electric drives with model predictive control are widely used in diverse applications where dynamic performance and energy efficiency are critical. For example, in electric vehicle systems, MPC allows for better transient response, torque tracking, and disturbance tolerance [6]. In industrial belt systems, predictive control allows for cost-optimal operation in terms of coordination between the operation status of belt conveyors and the time-of-use tariff [7]. Additionally, water utilities benefit from the MPC of water supply systems to minimize energy costs [8]. These cases demonstrate the relevance of parameter-optimised MPC in modern electromechanical infrastructure.
In dynamic modes, power losses are not constant and significantly depend on changes in the stator current, rotor flux, switching frequency, and other parameters of electromechanical systems. While steady-state modes are already well researched and in most cases, provided with energy-efficient solutions (maximum torque per ampere (MTPA) strategy, field-oriented control (FOC) methods, direct torque control (DTC) methods), the vast majority of available technological solutions require further development to optimise transient losses, which in most production processes of industrial facilities and electric transport, account for a significant proportion of the operating time [9,10,11,12].
The above problem is further complicated by the limitations associated with the need to take into account factors as voltage and current limits, as well as nonlinear effects such as magnetic circuit saturation, losses in the core, etc. Most existing models do not allow for the implementation of hardware and software accounting for these parameters and effects in real time, which reduces the overall efficiency and adaptability of control systems. All this proves the relevance and necessity of solving the scientific and applied problem of the development and further elaboration of adaptive methods and model predictive control algorithms of electric drives capable of minimising energy losses in dynamic modes, taking into account destabilising factors and limitations.
1.2. Analysis of the Latest Research and Publications
The results of the analysis of the scientific and technical literature show significant progress in the research of algorithms for the predictive control of electric drives to minimise losses, both on the basis of offline and online control strategies. For example, a scientific article [13] proposes the use of model predictive control by means of dynamic programming methods to design optimal rotor flux and current trajectories based on an approach in which templates are predefined offline and then adapted to a profile specific to each application. The studies in Refs. [14,15] demonstrate approaches to determine the optimal motor size and duty cycle duration through loss minimisation. However, although offline methods provide significant results in terms of efficiency, they have certain limitations in terms of versatility and adaptability.
The well-known online methods, which are described in detail in scientific publications [16,17,18,19], are based on the application of adaptive models using various control laws. For example, the authors of Ref. [17] studied the efficiency of the ANFIS controller under variable load conditions. The authors of Ref. [18] considered the combination of direct torque control (DTC), fuzzy logic, and teamwork optimisation (TOA) algorithms, which provides an increase in the efficiency of an asynchronous motor by 10–15% under dynamic operating conditions. The study described in Ref. [19] focuses on the practical increase in the mileage of an electric vehicle through the development and implementation of energy-efficient control methods and tools.
A significant step forward is the development of model predictive control (MPC) strategies that take into account a number of nonlinear constraints [20]. To date, a significant number of high-quality research results are available regarding various approaches to control electromechanical systems using MPC algorithms with a fixed optimisation horizon, sliding window, adaptive strategies, etc. [21,22,23]. The authors of these scientific publications demonstrated that adaptive schemes allow better adaptation to changing conditions, but require flexible mechanisms for recalculating constraints and loss models in real time, which under practical conditions, requires significant computing resources using specialised DSP and FPGA modules. Also, the authors of Ref. [24] studied approaches and models for the probabilistic analysis of dynamical systems, which at random moments in time, transit from one state to another, taking into account limited computing resources [25].
Today, the interest of the scientific and engineering community in using computer modelling methods to accelerate online optimisation is growing rapidly. In particular, the latest approaches use various methods of fast optimisation, which allow for implementing predictive control using even computationally limited platforms [26]. However, the accuracy of such simplified models largely depends on the correct identification of model parameters and the consideration of constraints, which negatively affects their universality.
In addition, recent studies of the use of predictive control for a permanent magnet synchronous motor (PMSM) drives contribute valuable insights that are potentially transferable to asynchronous drives. In Ref. [27], a nonlinear extended state observer was used to enhance the robustness of model predictive current control against model uncertainties and disturbances. Another work [28] proposed a motor-parameter-free model predictive voltage control based on an incremental model, which significantly reduces sensitivity to motor parameters and simplifies implementation. These developments highlight the ongoing trend toward increasing robustness and reducing model dependency in MPC strategies.
In addition, studies that combine MPC methods with neural network predictive models are of particular interest [29,30]. Such hybrid architectures allow for the compensation of the inaccuracies of mathematical models caused by magnetic circuit saturation, temperature effects, or material degradation. Such models demonstrate an increase in the accuracy and adaptability of automated control performance, without a significant increase in computational load.
Therefore, based on the logical generalisation of the above-mentioned known scientific works in the subject area, it is worth emphasising the fact that, taking into account the significant progress in the development and application of predictive control methods, including asynchronous electric drives, the vast majority of approaches display limitations associated with insufficient consideration of destabilising factors (iron losses, saturation, etc.) or the lack of practical solutions for hardware and software implementation of models due to high real-time computation power requirements. Consequently, the known research results require further development to create models for the formation of control influences for asynchronous electric motors, taking into account multifactorial constraints in real time.
1.3. Aim, Objectives, Object, and Subject of the Study
Based on the above reviewed scientific works, it has been established that for the application of MPC algorithms, these algorithms must be parametrised by the user and that this parametrisation determines the quality of the results. Therefore, the main aim of this article is to improve the hardware and software provisions for controlling asynchronous motors by developing and validating a computerised method for the multiparameter optimisation of predictive control algorithms based on the criteria of reducing computational costs and increasing the accuracy of task development, which is achieved by applying methods and approaches of multiple-criteria decision making (MCDM) in determining the optimal combinations of control parameters and influences. This is particularly important because the selected parameters of the MPC algorithms, such as the number of sampling points over the prediction horizon, the weighting coefficients of the cost function, the maximum number of gradient search iterations, and others, directly affect the control system’s ability to generate energy-optimal trajectories. Improperly tuned parameters may lead to overcorrection, oscillations, or inefficient voltage commands, all of which increase energy consumption during dynamic operation. A key innovative aspect of this research lies in the integration of the GRAMPC predictive control framework with a taxonomic multiple-criteria decision-making method for systematic multiparameter optimisation.
The objectives of this study are as follows:
- –
- Analysis of the influence of the main parameters of the prediction algorithm (length of the prediction horizon, sampling step, number of iterations, indicators of the loss function) on the efficiency of electric drive control in the dynamic mode;
- –
- Development of a computer model that allows for conducting a series of simulation experiments to identify and configure the parameters of predictive control tools, followed by a comparative analysis of the results in terms of accuracy, computation time, and energy efficiency;
- –
- Studying the feasibility of using the taxonomic method as a basic mechanism for the multiparameter selection of optimal combinations of control parameters;
- –
- Analysis of computer experiment results at qualitative and quantitative levels for different sets of parameters in order to identify those configurations that provide the best balance between speed, accuracy, and energy consumption;
- –
- Validation of the obtained research results through a series of simulation experiments with a modelled load on the electric drive and variable control settings.
The object of the study is the process of multiparameter optimisation of gradient algorithms for the predictive control of electric drives with a rotating magnetic field in real time.
The subject of the study comprises algorithms and methods for reducing the computation time, improving the control accuracy, and reducing the energy consumption of electromechanical systems based on electric drives with a rotating magnetic field.
2. Materials and Methods
The methodological basis for solving the formulated scientific and practical problem and achieving the main aim of the article is a set of interrelated theoretical and applied research methods that combine the general scientific principles of systematicity, modelling, formalisation, optimisation, and structural and functional analysis. In particular, a critical review and logical and analytical generalisation of modern scientific approaches and practical results in the field of the energy-efficient control of asynchronous electric machines is carried out. The basic research approaches are based on the theory of electromechanical systems, including electric drives, as well as on the concepts of optimal and predictive control of nonlinear dynamic systems. The formalisation, verification, and validation of the research hypotheses were carried out using a computer experiment and numerical analysis of electromechanical control systems. The proposed approach focuses on electrical dynamics and the optimisation of control parameters in the model predictive framework.
The present study aims at improving the methods and means of energy-efficient and precision control of asynchronous electric drives, the results of which were previously reported in Ref. [31].
In the course of this article, an asynchronous machine with the technical characteristics given in Table 1, which correspond to typical parameters for electric motors with the rated power of 370 W, is considered as a controlled electromechanical object. It offers a balanced trade-off between model simplicity and realistic dynamic behaviour, making it well-suited for detailed control algorithm development and parametric optimisation.

Table 1.
Typical technical and functional characteristics of an electric motor with the rated power of 370 W.
The following notations are used in Table 1: PN—nominal power; Zp—number of pole pairs; nN—nominal speed; TN—nominal torque; JM—total moment of inertia of the asynchronous machine and the load machine, as well as the coupling between the two machines and the torque sensor; R1—stator winding resistance; R2—equivalent rotor winding resistance; Lσ—stray inductance in the inverse gamma equivalent diagram; Lμ—magnetisation inductance in the inverse gamma equivalent diagram; P1–P6—coefficients of the magnetisation inductance polynomial , where is the d-component of the stator current vector ; C1, C2—coefficients for setting the torque dependence on speed reference trajectory; , —the initial and final values of the speed reference trajectory, respectively.
The functional basis for the parametric optimisation of predictive control algorithms based on the criteria for reducing computational costs and increasing the accuracy of task execution is the developed computer model in the MATLAB and Simulink simulation environment. The GRAMPC toolbox [32] is used as the framework for the MPC algorithm implementation. In order to reduce computational time and improve the accuracy of electric drive control, a set of parameters was selected for optimisation within the GRAMPC predictive algorithm, specifically the number of sampling points over the prediction horizon (Nhorizon), the maximum number of gradient search iterations (NMaxGradIter), the weighting coefficients of the cost function (PCost), the prediction horizon (Thorizon), and the maximum optimisation search step (LineSearchMax). For each of these parameters, numerical simulations with variable combinations were conducted to determine the impact on the following:
- –
- Accuracy of system operation in accordance with a given reference trajectory;
- –
- Computation time;
- –
- Energy consumption.
To objectively assess the effectiveness of various combinations of parameters, the taxonomic method of multicriteria analysis (MCDM) was applied. This approach is based on building a matrix of initial indicators for each test object, normalising the data, forming a reference vector, calculating the distance to the reference, and ranking the results based on the deviation from the optimal value using the least squares method [33].
The algorithmic implementation included the following steps:
1. Formation of the input matrix of indicators for ranking N objects by M indicators (accuracy of system operation in accordance with a given speed trajectory—Ns (Accuracy, in %), calculation time for parameters—Ts (Calculation time, in seconds), energy consumption—EL, accuracy of system operation in accordance with the magnetisation current trajectory—R2), as shown below in the form of a generalised matrix (1). In this case, the indicators were compared with the reference values obtained using the fmincon algorithm [34].
where X is the matrix of indicators for each object under study; i is the current indicator number; j is the current object number; M is the number of indicators; N is the number of objects.
2. Normalisation of indicators, which is a mandatory stage due to the fact that the indicators reflect different, incomparable values, which allows for the elimination of the influence of absolute values, as shown below using Formulas (2)–(5):
where Xnorm is the matrix of normalised indicators for each object under study; is the average value of the i-th indicator for the corresponding number of objects; is the standard deviation of the i-th indicator for the corresponding number of objects; i is the current number of the indicator; j is the current number of the object; M is the number of indicators; N is the number of objects.
3. Generation of a vector of benchmark values based on the optimal values of the indicators for each row of the Xnorm matrix. Based on this, the vector (6) will be shaped, as shown in a generalised form below:
where is a vector of normalised benchmark values for each studied indicator.
4. Selection of the best object, which is carried out on the basis of the least squares method, comparing each normalised indicator with the corresponding benchmark value according to (7):
where aj is the weighting coefficient of the significance of the respective indicator (with aj = 1, if all indicators are equivalent).
The best object is the one characterised by the minimum value of the parameter Rj calculated by (7).
Therefore, the application of the above-mentioned methodology based on the taxonomic approach allowed for the formation of an objective integral assessment of the quality of the GRAMPC implementation of the algorithm for the predictive control of asynchronous electric motors, which, in the course of further studies of the article, became the basis for selecting parameters that provide multiparameter optimisation based on the simultaneous consideration of accuracy, computation time, and energy consumption.
3. Results
3.1. Computer Model
To implement the model of predictive control of an asynchronous machine, shown in Figure 1 and Figure 2, the MATLAB and Simulink R2024a simulation environment was used. The developed architecture includes both the control subsystem and the model of the control object (asynchronous machine), which is built in the form of structurally connected blocks.
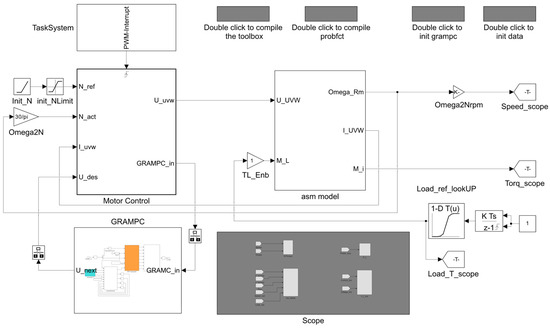
Figure 1.
The top level of the structure of a predictive control computer model.
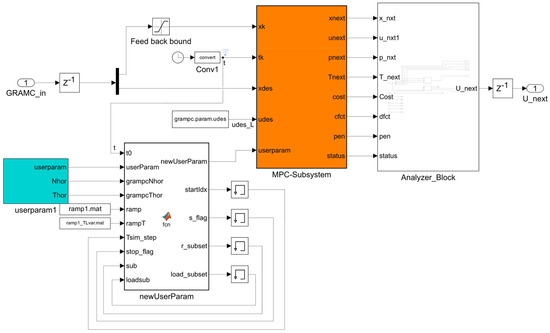
Figure 2.
GRAMPC subsystem of the predictive control computer model.
The top level of the system architecture is shown in Figure 1. The GRAMPC subsystem implements the predictive control algorithm with the subsequent generation of the control signal of the three-phase voltage U_uvm in the Motor Control subsystem, based on measured values and the desired speed N_ref. The asynchronous machine model asm model receives the control signals U_uvm and the load level M_L. In addition, the currents I_uvm and the angular velocity Omega_Rm are measured in the asm model. The Load_ref_lookUP block generates the load torque as a function of time. The PWM-Interrupt and initialisation blocks provide system setup before starting the simulation, as well as the compilation and initialisation of the GRAMPC library.
The GRAMPC subsystem from Figure 1 is illustrated in detail in Figure 2. Here, the main component is the MPC-Subsystem block, which is the GRAMPC kernel [32] that accepts the vector of the current system state, the vector of desired values, and the configuration of userparam parameters. The output is the optimal control action U_next (two components of the stator voltage phasor ud and uq), which is fed to the Motor Control subsystem. Userparam1, ramp1.mat, and ramp1_TLvar.mat provide individual optimisation parameters and desired trajectories in the form of vectors containing the values of the desired speed and load torque at each of the discretisation steps. The Analyzer_Block monitors and records simulation parameters for further analysis. This allows for tracking the stability and efficiency of the model during computer experiments. The newUserParam parameter generation module is responsible for determining the depth of the ‘look ahead’ in the predictive control task for the desired trajectories of speed and load torque. In this implementation, the desired values of the speed from the ramp1.mat file and the load torque from the ramp1_TLvar.mat file are fed into the MPC-Subsystem as arrays of Nhorizon length as components of the userparam vector. This allows the MPC-Subsystem controller with modified probfct.c not only to react to the current system state, but also to proactively take into account future operating conditions, such as expected torque fluctuations or speed setpoint changes. This extension to the GRAMPC made by the authors of this study is critical for improving stability and energy efficiency under dynamic operating conditions.
Thus, the developed computer model makes it possible to evaluate the performance of commands by speed and torque in the MPC closed loop.
3.2. Results of the Analysis of the Influence of the Prediction Algorithm Parameters
For each set of the varying parameters to be optimised within the GRAMPC predictive algorithm described in Section 2, ten simulations (with the same set of the parameters) were performed to avoid random errors. The average values were used in the process of finding the optimal values. A visualisation of the obtained measurements is shown in Figure 3, Figure 4, Figure 5 and Figure 6.
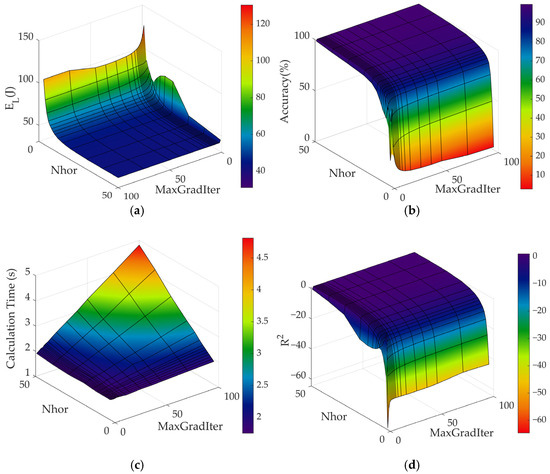
Figure 3.
Plots of EL, Accuracy, Calculation time, and R2 versus Nhorizon and NMaxGradIter.
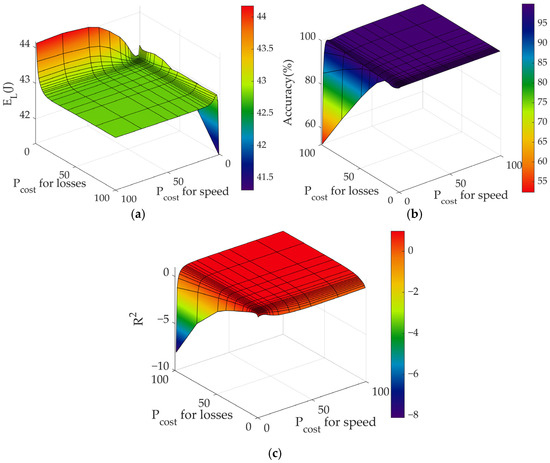
Figure 4.
Plots of EL, Accuracy, and R2 versus PCost (loss) and PCost (speed).
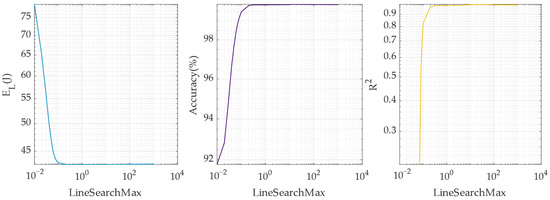
Figure 5.
Plots of EL, Accuracy, and R2 versus LineSearchMax.
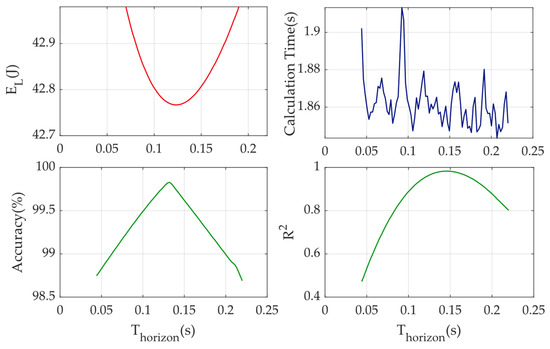
Figure 6.
Plots of EL, Accuracy, Calculation time, and R2 versus Thorizon.
The accuracy of system operation in accordance with a given speed trajectory—Ns (Accuracy, in %)—is calculated using Formula (8) below:
where N is the total number of sampling points; nramp,j is the speed setpoint at sampling instant j; nj is the result of the actual model execution at sampling instant j.
The coefficient of determination (R2), calculated using (9), was used as a quantitative measure of the accuracy of system operation in accordance with the magnetisation current trajectory:
where N is the total number of sampling points; I1d,j is the desired result at sampling instant j; is the result of the actual model execution at sampling instant j; I1d,avg is the average value of the desired result.
The weighting coefficients of the significance of the indicators (accuracy of system operation in accordance with a given speed trajectory—Ns (Accuracy, in %), calculation time for parameters—Ts (Calculation time, in seconds), energy consumption—EL, accuracy of system operation in accordance with the magnetisation current trajectory—R2) with varying different algorithmic parameters are given in Table 2. The initial values of the algorithmic parameters are given in Table 3.

Table 2.
Weighting coefficients.
In Figure 3, the dependence of the indicators on the parameters Nhorizon and NMaxGradIter is shown. Figure 4 displays the dependence on PCost, whereas in Figure 5, the effect of the variation of the LineSearchMax parameter is shown, and in Figure 6, the effect of the Thorizon is given.
The Nhorizon parameter determines the number of sampling points on the Thorizon prediction horizon. According to Ref. [32], this parameter is one of the key parameters that affects both the performance and computational load of the MPC. A larger number of points usually improves stability and control accuracy, but increases the amount of computation.
The energy consumption EL is shown in Figure 3a. For each fixed NMaxGradIter, the generalised trend is a decrease in energy consumption with increasing Nhorizon. For example, at NMaxGradIter = 4, the EL decreases from ~80.5 J (Nhorizon = 5) to ~44.3 J (Nhorizon = 20), which indicates more efficient operation with a larger number of Nhorizon points. At the same time, with a small number of NMaxGradIter iterations, anomalies arose: for example, for NMaxGradIter = 1, EL was initially ~82 J at Nhorizon = 20, and at NMaxGradIter = 2, the value of EL sharply decreased to 45.6 J. In general, the smallest EL is provided by the largest Nhorizon and NMaxGradIter, indicating that a deeper gradient search allows for finding better solutions.
The results for the Ns metric for Nhorizon and NMaxGradIter are shown in Figure 3b. It is evident that with an increase in Nhorizon, the accuracy of the speed increases: for example, for a fixed number of NMaxGradIter iterations, the Ns (accuracy, in %) increases to almost 100% with sufficient values of Thorizon. At the same time, anomalies can be seen: for high NMaxGradIter and small values of Nhorizon, this leads to a sharp drop in Ns, which indicates the instability of optimisation when the number of discretisation points Nhorizon on the Thorizon prediction horizon is insufficient.
In Figure 3c, the Calculation time, in seconds Ts is shown. It is nearly independent of the influence of Nhorizon within the studied range of values: for all combinations of parameters, Ts remains within a narrow range of approximately 1.8–2.1 s at small values of NMaxGradIter. Thus, an increase in the number of sampling points does not lead to a significant increase in computation time (the computer load hardly changes) at small values of NMaxGradIter.
The dependence of R2 on NMaxGradIter and Nhorizon is illustrated in Figure 3d. At small values of NMaxGradIter and Nhorizon, R2 displays large negative values (up to –74), which means that the model shows a very poor fit. As Nhorizon increases, R2 gradually increases (approaching zero and even +0.5 … +0.9 at large parameter values). NMaxGradIter > 2 has almost no effect on R2.
From the results in Figure 3, it can be seen that a larger number of Nhorizon points reduces the tracking error in the speed profile (higher Ns) and improves current fitting (higher R2) with a sufficient number of iterations NMaxGradIter > 1. In practice, this means that Nhorizon should be chosen to match the dynamics of the system, without overcomplicating the solution. On the other hand, increasing the number of gradient iterations NMaxGradIter improves the convergence of optimisation, resulting in higher solution accuracy. However, after a certain threshold (approximately 2–3 iterations), the improvements are minor, such that an additional increase is not justified.
The PCost parameter consists of two weighting factors: PCost(speed) for speed deviation and PCost(loss) for energy loss. It determines the compromise in the cost function between the accuracy of the speed profile and energy efficiency.
In Figure 4a, it is shown that increasing the weight of PCost(speed) leads to a slight increase in EL: for example, when PCost(loss) = 1, EL increases from ~43.1 J (PCost(speed) = 1) to ~44.1 J (PCost(speed) = 100). This is due to the priority of maintaining speed, resulting in higher energy consumption. On the other hand, increasing PCost(loss) reduces EL (for example, when PCost(speed) = 1, EL drops from 43.1 J (PCost(loss) = 1) to 42.2 J (PCost(loss) = 75)). However, these changes are quite small.
Figure 4b shows Ns depending on the ratio of PCost(loss) and PCost(speed). For nearly all combinations, Ns ≈ 99–100%, i.e., the speed setpoint is successfully achieved. The accuracy only drops significantly for combinations of PCost(speed) = 1 and PCost(loss) > 40. Thus, the balance of PCost weights has a negligible effect on the accuracy of the speed profile itself, and it remains high.
Figure 4c illustrates R2 depending on PCost. Here, a clear compromise can be seen, as in the case of Figure 4b: at high PCost(loss) weight, R2 drops significantly (even to negative values), indicating a deterioration in current regulation. Conversely, at low PCost(loss) weight and moderate PCost(speed) weight, R2 approaches 1.0 (the best values ~1.0 are observed at PCost(loss) ≥ 2 and PCost(speed) ≤ 10). Thus, prioritising speed accuracy leads to better current regulation and vice versa.
Setting the PCost weight allows for achieving a balance between two objectives. Higher weights for speed ensure almost perfect profile tracking (Ns ≈ 100%), but result in increased energy consumption. Conversely, focusing on minimising energy consumption slightly reduces speed accuracy. This trade-off is to be expected with multidimensional functionality, i.e., increasing one indicator stochastically harms the others.
The LineSearchMax parameter sets the maximum possible step size of the line search algorithm in the gradient method. This is critical for the convergence speed and stability of the optimisation. GRAMPC uses specialised line search strategies optimised for fast and resource-efficient implementation [32].
Figure 5 shows that at very low values of LineSearchMax (0.01–0.05) the system demonstrates unsatisfactory results: Ns ≈ 92–97%, losses EL are very high (78.9–47.1 J), and the R2 indicator is equal 0, and in some cases, negative values are observed, i.e., the model clearly did not converge. With an increase in LineSearchMax to 0.1–0.4, Ns grows rapidly (up to ≈99.8%), EL drops to ≈42.8 J, and R2 becomes positive and reaches 1.0. With LineSearchMax ≥ 0.5, all indicators stabilise: Ns ≈ 99.8%, EL ≈ 42.8 J, R2 = 1.0, and Ts ≈ 2.4 s. Thus, a line search with a larger maximum permissible step ensured a stable and rapid transition to the optimal solution.
A small maximum step size (LineSearchMax < 0.1) will ‘lock’ the algorithm with a small NMaxGradIter and lead to an inefficient solution (low accuracy Ns, high energy consumption EL, and unstable R2). Increasing LineSearchMax allows for wider gradient steps, which significantly speeds up convergence and stabilises the solution. This is consistent with practical experiments, which show that in some cases, it is necessary to increase LineSearchMax for reliable convergence.
The parameter Thorizon specifies the prediction horizon (the end time of the control segment). Figure 6 shows the following trends: when Thorizon is increased from very small values ≈ 0.09 s, there is a noticeable improvement in performance. In particular, the accuracy of Ns increases from ≈ 98.7% (Thorizon ≈ 0.044 s) to ≈ 99.3% (Thorizon ≈ 0.088 s). At the same time, energy consumption decreases (from 43.3 J to 42.9 J), and R2 improves significantly (from ≈ 0.5 to ≈ 0.8). Moreover, in the range Thorizon ≈ 0.13–0.20 s, the metrics nearly stabilise: Ns ≈ 99.2–99.3%, EL ≈ 42.8–42.9 J, and R2 ≈ 0.9. At a very large Thorizon (greater than 0.20 s), R2 decreases slightly (~0.8). In general, Thorizon ≈ 0.14 s proved to be optimal in terms of the accuracy/cost ratio. Increasing the time horizon of the predictions usually allows for longer system behaviour to be taken into account, which improves control quality and increases stability.
The analysis showed that optimising GRAMPC parameters significantly affects the performance of the electric drive control. In particular, increasing Nhorizon and to a lesser extent, NMaxGradIter, contributed to an increase in profile tracking accuracy (increase in Ns), improved current control (increase in R2), and reduced energy consumption. Increasing Thorizon improved performance to a certain level (Thorizon ≈ 0.14 s), after which the gains plateaued. This is consistent with MPC theory, as a longer prediction horizon and a deeper search allow for better control actions to be found. LineSearchMax is a critical convergence parameter, i.e., a too small LineSearchMax value significantly worsened all metrics, while LineSearchMax = 40 provided nearly perfect results, without a significant increase in computation time. Adjusting the PCost weighting coefficients revealed a balance between two objectives: with a high weighting of speed, the profile accuracy increased to almost 100%, but at the same time, the energy consumption increased, and the accuracy of the desired magnetisation current waveform decreased slightly.
3.3. Results of Applying the Taxonomic Approach and Simulation Experiment
To determine the optimal combination of values for the algorithmic parameters Nhorizon, NMaxGradIter, Thorizon, and LineSearchMax, as well as the weight coefficients PCost of the cost function, it is necessary to thoroughly analyse the empirical data obtained. Given the large dimension of the option space and the presence of multiple evaluation criteria, such a task is difficult to perform using visual methods alone.
According to the proposed methodology given in Section 2, the taxonomic method involves normalising indicators using Formulas (2)–(5), forming a benchmark vector (6), and calculating the distances between the objects of observation and the benchmark, taking into account the weighting coefficients of the criteria. As a result, for each set of parameters, the integral distance Rj was calculated using Formula (7), which serves as a measure of the distance from the conditionally best option. The results are shown in Figure 7.
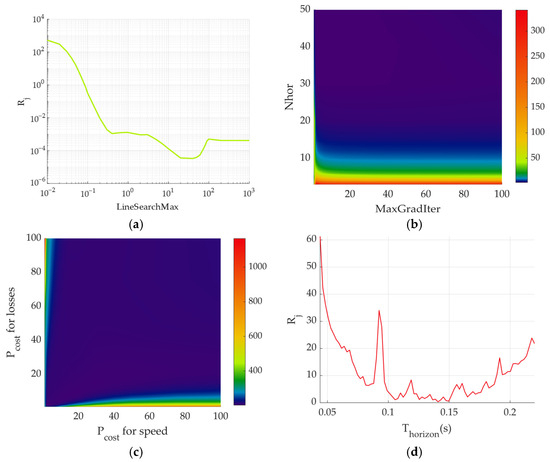
Figure 7.
Plots of Rj versus LineSearchMax, Nhorizon, NMaxGradIter, PCost, and Thorizon.
The value of Rj as a function of the LineSearchMax parameter is shown in Figure 7a. There is a sharp drop in Rj when the parameter increases from 0.01 to ≈ 40, after which the values stabilise at a minimum level. This indicates the need to use a sufficiently large maximum line search step to ensure effective convergence of the algorithm at low values of NMaxGradIter.
The distribution of Rj values for different combinations of Nhorizon and NMaxGradIter parameters is shown in Figure 7b. There is a clear minimisation of the distance Rj at medium or moderately large values of both parameters: in particular, Nhorizon ≈ 35–50; NMaxGradIter ≥ 2. This corresponds to the zone in which a good compromise between accuracy, energy consumption, and current control quality is achieved. At the periphery of the diagram, where the parameters display extreme values (too low or too high), Rj increases, indicating a deterioration in overall performance.
The dependence of Rj on the values of the weight coefficients PCost, i.e., the ratio between loss and speed deviation, is shown in Figure 7c. The lowest values of Rj are observed for sets where Pcost(loss) ≈ 2 and Pcost(speed) ≈ 2–3, which demonstrates an optimal balance between energy saving and dynamic quality. At the same time, excessive growth of any of the components (for example, a speed weight up to 100 or more) causes a deterioration in the overall Rj index, i.e., overloading the cost function with one goal leads to degradation in other criteria.
Figure 7d shows Rj when Thorizon changes. The curve has a clear minimum at Thorizon ≈ 0.14 s, which is approximately in 3.18 times greater than the rotor time constant. This confirms the earlier conclusion about the existence of an optimal prediction zone. Values less than 0.1 s or greater than 0.2 s led to an increase in Rj, indicating insufficient or excessive consideration of the future dynamics of the system.
The application of the taxonomic method made it possible to form an objective rating assessment of the parameters of predictive control (see Table 3).
This approach ensured comprehensive multi-factor optimisation, taking into account conflicting criteria such as speed accuracy, energy consumption, calculation time, and current trajectory quality. The method can be extended to other model variants or control configurations and is a promising tool for automated system configuration in multi-criteria optimisation mode.

Table 3.
Comparison of algorithmic parameters.
Table 3.
Comparison of algorithmic parameters.
| Parameter | Initial Guess | Optimal Values |
|---|---|---|
| Nhorizon | 50 | 50 |
| NMaxGradIter | 2 | 2 |
| PCost (loss) | 10 | 2 |
| PCost (speed) | 5 | 2 |
| Thorizon | 0.1302 | 0.1408 |
| LineSearchMax | 0.5 | 40 |
Figure 8 shows the results of the developed model (see Figure 1 and Figure 2), where a comparison of the benchmark (calculation using fmincon [34]) with the indicators from Table 3 based on GRAMPC, before and after optimisation of the algorithmic parameters, is presented. In this case, the initial guess of the algorithmic parameters was chosen by the authors to be quite close to the optimal values, so the difference between the trajectories is minimal.
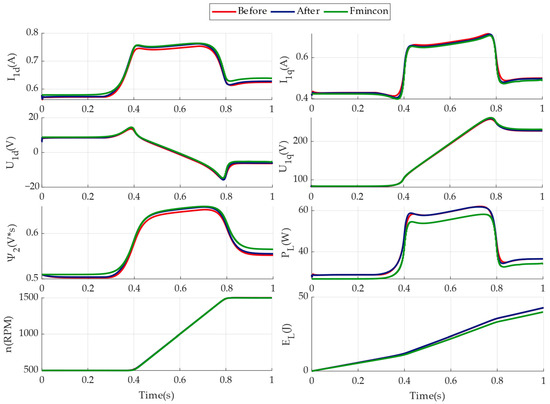
Figure 8.
Simulation results, where Fmincon indicates plots obtained using fmincon; Before indicates plots obtained using GRAMPC with initial guess settings; After indicates plots obtained using GRAMPC with optimised settings.
Table 4 presents the percentage fit of two optimisation results, Before and After (see Figure 8), for each state variable, compared to the benchmark solution obtained using fmincon. The fit is evaluated using the coefficient of determination R2, expressed as a percentage.

Table 4.
Fit percentage of optimisation results compared to fmincon reference.
Thus, the final results show that the objective multiparameter optimisation of the GRAMPC settings can improve the performance of the control system. This is confirmed by a comparison of the initial and optimal parameters in Table 3 and Table 4, where, for example, a decrease in PCost weights and an increase in LineSearchMax led to better control quality, with almost unchanged Thorizon and NMaxGradIter. In general, the optimal parameters provide high tracking accuracy and system stability with minimal energy consumption, which proves the effectiveness of the chosen approach to MPC tuning.
4. Discussion and Prospects for Further Research
The presented results clearly demonstrate that energy efficiency in asynchronous drive systems is not only a function of hardware or basic control strategy, but also of how well the predictive control parameters are tuned. The study proved that the proposed computerised method of multi-criteria optimisation of predictive control parameters for asynchronous electric drives, which includes a formalised description, a simulation model, and algorithmic principles of predictive control, allows for effective coordination of the main performance indicators of electromechanical systems, such as the accuracy of system operation in accordance with a setpoint trajectory, energy consumption, and computational costs. The proposed combination of taxonomic analysis with computer modelling in the MATLAB and Simulink environment provided the possibility for the adaptive and optimised adjustment of the main technical and functional parameters of the predictive algorithm, which is confirmed by the quantitative results obtained.
The practical value of the presented approach lies in the creation of a computer model, which is a means of configuring algorithmic software for predictive control of asynchronous electric drives for various purposes, allowing automated control systems to be adapted to changes in operating conditions, without significantly complicating the process of deployment and integration into existing technological and production processes. This is particularly relevant for industrial sectors in which electric drives operate under variable load conditions and require flexible control to ensure optimal energy efficiency.
Although the presented study focuses on standard squirrel-cage induction motors with cylindrical geometry (typical asynchronous electric motor with a rated power of 370 W, which represents standard industrial configurations), the proposed optimisation methodology can, under additional experiments and investigations, be extended to other electric machines such as PMSMs, flat or pancake motors, and others. The proposed parameter tuning approach remains applicable, provided that their specific electromagnetic characteristics are accurately reflected in the model.
At the same time, the scientific and applied results obtained open up prospects for further research in the following areas:
- –
- Scaling up the proposed method by introducing hybrid methods, specifically by using neural networks and machine learning methods for automatic real-time adjustment of predictive models;
- –
- Researching the effectiveness of the developed method in regards to electric drives with other types of motors;
- –
- Validating and adjusting the results obtained based on practical experiments in various industry applications;
- –
- Integrating the developed approach into modern automation and digitalisation complexes for production and technological processes.
A main focus of future work will be given to conducting a real-world case study involving prototype-based validation of the proposed MPC approach in order to demonstrate its practical applicability under realistic operating conditions. Additionally, further research will focus on profiling and optimising the computational load of the control algorithm on embedded platforms, including microcontrollers and FPGA-based systems, to assess the feasibility for low-power or resource-constrained industrial applications.
Therefore, the results of this study form the technical and technological basis for the further development and improvement of computer technologies for controlling electric drives.
5. Conclusions
Based on the results of our research conducted to develop and validate a computerised method for the multiparameter optimisation of algorithms for predictive control of asynchronous electric drives, the following results have been obtained:
1. The effectiveness of applying a multiparameter optimisation method for the parameters of predictive control algorithms, based on a combination of computer modelling and taxonomic analysis methods, has been proposed and proven. This has made it possible to comprehensively take into account the criteria of accuracy of system operation in accordance with a setpoint trajectory, energy consumption, and computational costs.
2. A computer model of a predictive control system for an asynchronous electric drive has been developed and validated in MATLAB and Simulink based on the GRAMPC strategy, which provides an adequate model of the dynamic behaviour of an asynchronous electric drive under a wide range of operating modes.
3. During a series of computer experiments, the optimal parameters of the predictive control algorithm have been established: Nhorizon = 50, NMaxGradIter = 2, Thorizon = 0.14 s, and LineSearchMax = 40, which ensures stable operation of the algorithm when controlling an asynchronous motor with a power of 370 W in dynamic modes.
4. It has been demonstrated that the application of a taxonomic approach to effectiveness analysis allows for the automated determination of optimal combinations of control algorithm parameters for different operating modes, which increases the adaptability and practical applicability of the proposed method of predictive control in industrial electric drives.
5. The results obtained form a methodological and applied basis for the further development of hybrid intellectualised predictive algorithms with increased adaptability to changing operating conditions and integration into real industrial automated control systems.
6. The study’s novelty is highlighted by the integration of a real-time-capable MPC tool (GRAMPC) with a taxonomic MCDM-based optimisation process, providing a structured methodology for selecting algorithm parameters. This approach enables a more precise, energy-efficient, and computationally viable control of asynchronous drives under dynamic conditions, distinguishing the proposed solution from existing approaches.
Author Contributions
Conceptualization, S.S. and I.L.; methodology, G.D. and I.L.; software, G.D.; validation, S.S., G.D. and I.L.; formal analysis, K.M.; investigation, S.S., K.M., G.D. and I.L.; data curation, G.D. and I.L.; writing—original draft preparation, G.D.; writing—review and editing, G.S. and G.D.; visualization, K.M. and G.D.; supervision, S.S., G.S. and G.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out as part of the joint Ukrainian–German R&D project ‘Model Predictive Dynamic Energy Efficient Control in Rotating Field Machines’, funded by the Ministry of Education and Science of Ukraine (state registration number 0124U003745) and the German Federal Ministry of Education and Research under grant number 01DK24020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Koval, V.; Kryshtal, H.; Udovychenko, V.; Soloviova, O.; Froter, O.; Kokorina, V.; Veretin, L. Review of mineral resource management in a circular economy infrastructure. Min. Miner. Depos. 2023, 17, 61–70. [Google Scholar] [CrossRef]
- Farrag, M.; Lai, C.S.; Darwish, M.; Taylor, G. Improving the Efficiency of Electric Vehicles: Advancements in Hybrid Energy Storage Systems. Vehicles 2024, 6, 1089–1113. [Google Scholar] [CrossRef]
- Rjabtšikov, V.; Rassõlkin, A.; Kudelina, K.; Kallaste, A.; Vaimann, T. Review of Electric Vehicle Testing Procedures for Digital Twin Development: A Comprehensive Analysis. Energies 2023, 16, 6952. [Google Scholar] [CrossRef]
- Roy, S.; Pandey, R. A Review on Motor and Drive System for Electric Vehicle. In Planning of Hybrid Renewable Energy Systems, Electric Vehicles and Microgrid; Bohre, A.K., Chaturvedi, P., Kolhe, M.L., Singh, S.N., Eds.; Energy Systems in Electrical Engineering; Springer: Singapore, 2022; pp. 601–628. [Google Scholar] [CrossRef]
- Statista: Estimated Number of Electric Vehicles in Use Worldwide Between 2016 and 2023. Available online: https://www.statista.com/statistics/1101415/number-of-electric-vehicles-by-type/#statisticContainer (accessed on 11 June 2025).
- Krupa, T.M.; Koraddi, S.; Raju, A.B. Model Predictive Torque Control of Induction Motor for Electric Vehicle Application. In Proceedings of the 2024 International Conference on Innovation and Novelty in Engineering and Technology (INNOVA), Vijayapura, India, 20–21 December 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Luo, J.; Huang, W.; Zhang, S. Energy cost optimal operation of belt conveyors using model predictive control methodology. J. Clean. Prod. 2015, 105, 196–205. [Google Scholar] [CrossRef]
- Reis, A.L.; Andrade-Campos, A.; Matos, P.; Antunes, C.H.; Lopes, M.A.R. An energy and cost efficiency Model Predictive Control framework to optimize Water Supply Systems operation. Appl. Energy 2025, 384, 125478. [Google Scholar] [CrossRef]
- Gallert, B.; Choi, G.; Jing, X.; Lee, K.; Son, Y. Maximum efficiency control strategy of PM traction machine drives in GM hybrid and electric vehicles. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 566–571. [Google Scholar] [CrossRef]
- Piriienko, S.; Ammann, U.; Neuburger, M.; Bertele, F.; Röser, T.; Balakhontsev, A.; Neuberger, N.; Cheng, P.-W. Influence of the control strategy on the efficiency of SynRM-based small-scale wind generators. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, Australia, 13–15 February 2019; pp. 280–285. [Google Scholar] [CrossRef]
- Fan, Y.; Ma, H.; Zhu, G.; Luo, J. Improved MTPA and MTPV optimal criteria analysis based on IPMSM nonlinear flux-linkage model. Energies 2024, 17, 3494. [Google Scholar] [CrossRef]
- Sinchuk, O.; Strzelecki, R.; Beridze, T.; Peresunko, I.; Baranovskyi, V.; Kobeliatskyi, D.; Zapalskyi, V. Model studies to identify input parameters of an algorithm controlling electric supply/consumption process by underground iron ore enterprises. Min. Miner. Depos. 2023, 17, 93–101. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Yang, S.M. Efficiency–Optimized Flux Trajectories for Closed–Cycle Operation of Field-Orientation Induction Machine Drives. In Proceedings of the Conference Record of the 1988 IEEE Industry Applications Society Annual Meeting, Pittsburgh, PA, USA, 2–7 October 1988; pp. 457–462. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Yang, S.M. AC Induction Servo Sizing for Motion Control Applications via Loss Minimizing Real–Time Flux Control. IEEE Trans. Ind. Appl. 1992, 28, 589–593. [Google Scholar] [CrossRef]
- Klenke, F.; Hofmann, W. Energy-Efficient Control of Induction Motor Servo Drives with Optimized Motion and Flux Trajectories. In Proceedings of the Proceedings of the 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–7.
- Weis, R.; Gensior, A. A Model-Based Loss-Reduction Scheme for Transient Operation of Induction Machines. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Alitasb, G.K. Integer PI, Fractional PI and Fractional PI data trained ANFIS Speed Controllers for Indirect Field Oriented Control of Induction Motor. Heliyon 2024, 10, e37822. [Google Scholar] [CrossRef]
- Nandy, S.; Das, S.; Pal, A. Online Golden Section Method based Loss Minimization Scheme for Direct Torque Controlled Induction Motor Drive. In Proceedings of the 2018 8th IEEE India International Conference on Power Electronics (IICPE), Jaipur, India, 13–15 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Sahoo, A.; Jena, R. Loss model based controller of fuzzy DTC driven induction motor for electric vehicles using optimal stator flux. e-Prime Adv. Electr. Eng. Electron. Energy 2023, 6, 100304. [Google Scholar] [CrossRef]
- Englert, T.; Graichen, K. Nonlinear model predictive torque control and setpoint computation of induction machines for high performance applications. Control Eng. Pract. 2020, 99, 104415. [Google Scholar] [CrossRef]
- Janisch, G.; Kugi, A.; Kemmetmüller, W. A high-performance model predictive torque control concept for induction machines for electric vehicle applications. Control Eng. Pract. 2024, 153, 106128. [Google Scholar] [CrossRef]
- Brix, A.; Muller, V.; Hofmann, W. Energy Efficient Predictive Rotor Flux Control of Induction Machines in Autonomous Driving Electric Vehicles. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Abdelati, R.; Mimouni, M.F. Optimal control strategy of an induction motor for loss minimization using Pontryaguin principle. Eur. J. Control 2019, 49, 94–106. [Google Scholar] [CrossRef]
- Meleshko, Y.; Raskin, L.; Semenov, S.; Sira, O. Methodology of probabilistic analysis of state dynamics of multi-dimensional semi-Markov dynamic systems. East Eur. J. Enterp. Technol. 2019, 6, 6–13. [Google Scholar] [CrossRef]
- Moskalenko, V.; Kharchenko, V.; Semenov, S. Model and Method for Providing Resilience to Resource-Constrained AI-System. Sensors 2024, 24, 5951. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, C.; Wang, Q.; Dong, S.; Xiao, A. Research on Simplified Design of Model Predictive Control. Actuators 2025, 14, 191. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Liang, X.; Guo, H.; Zhuang, X. Robust Model Predictive Current Control of PMSM Based on Nonlinear Extended State Observer. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 862–873. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L. A Simple Motor-Parameter-Free Model Predictive Voltage Control for PMSM Drives Based on Incremental Model. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 2845–2854. [Google Scholar] [CrossRef]
- Jaguemont, J.; Darwiche, A.; Bardé, F. Model Predictive Control Using an Artificial Neural Network for Fast-Charging Lithium-Ion Batteries. World Electr. Veh. J. 2025, 16, 231. [Google Scholar] [CrossRef]
- Li, Y.; Liu, L. Physics-Informed Neural Network-Based Nonlinear Model Predictive Control for Automated Guided Vehicle Trajectory Tracking. World Electr. Veh. J. 2024, 15, 460. [Google Scholar] [CrossRef]
- Schullerus, G. Modellprädiktive dynamisch energieeffiziente Betriebsführung einer Asynchronmaschine. In Proceedings of the SPS IPC DRIVES 2014, Nürnberg, Germany, 25–27 November 2014; pp. 366–374. (In German). [Google Scholar]
- GRAMPC Documentation Version 2.2. Available online: https://sourceforge.net/p/grampc/blog/2019/10/grampc-v22/ (accessed on 5 June 2025).
- Samorodov, B.V. Modification of the taxonomic method with regard to the competence of experts in the rating of banks. Bull. Ukr. Acad. Bank. 2011, 2, 62–67. (In Ukrainian) [Google Scholar]
- Dominic, A.; Schullerus, G.; Winter, M. Optimal Flux and Current Trajectories for Efficient Operation of Induction Machines. In Proceedings of the 2019 20th International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 23–26 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).