A Comprehensive Review of Propeller Design and Propulsion Systems for High-Altitude Pseudo-Satellites
Abstract
1. Introduction
2. Methodology
3. Propulsion Systems for HAPSs
3.1. Combustion Propulsion
3.2. Electric Propulsion
3.3. Hybrid Propulsion
3.4. Future Propulsion Concepts
4. Propeller Theory for HAPSs
4.1. Development on Theoretical Background
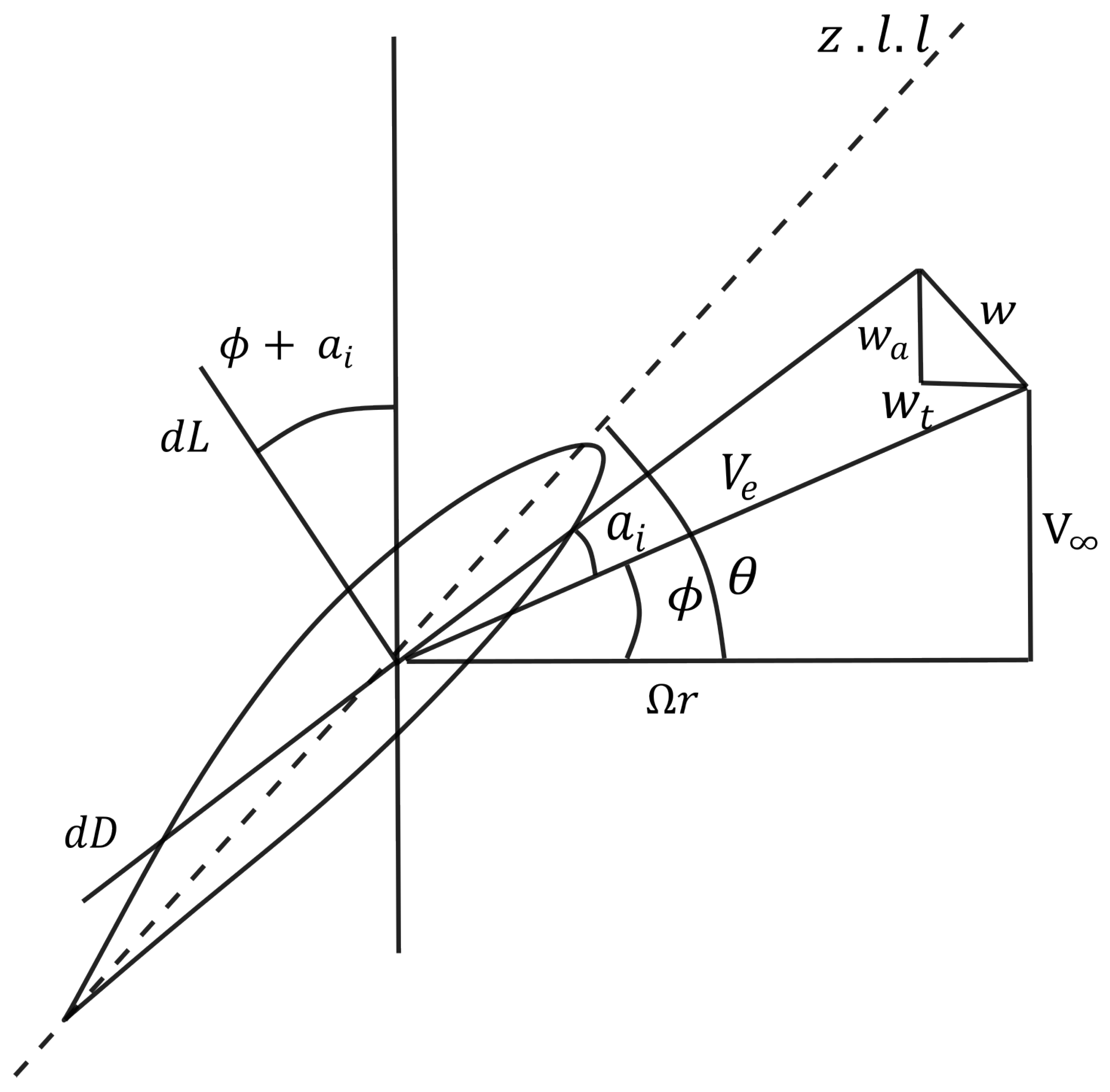
4.2. Blade Element Momentum Theory
4.3. Solidity
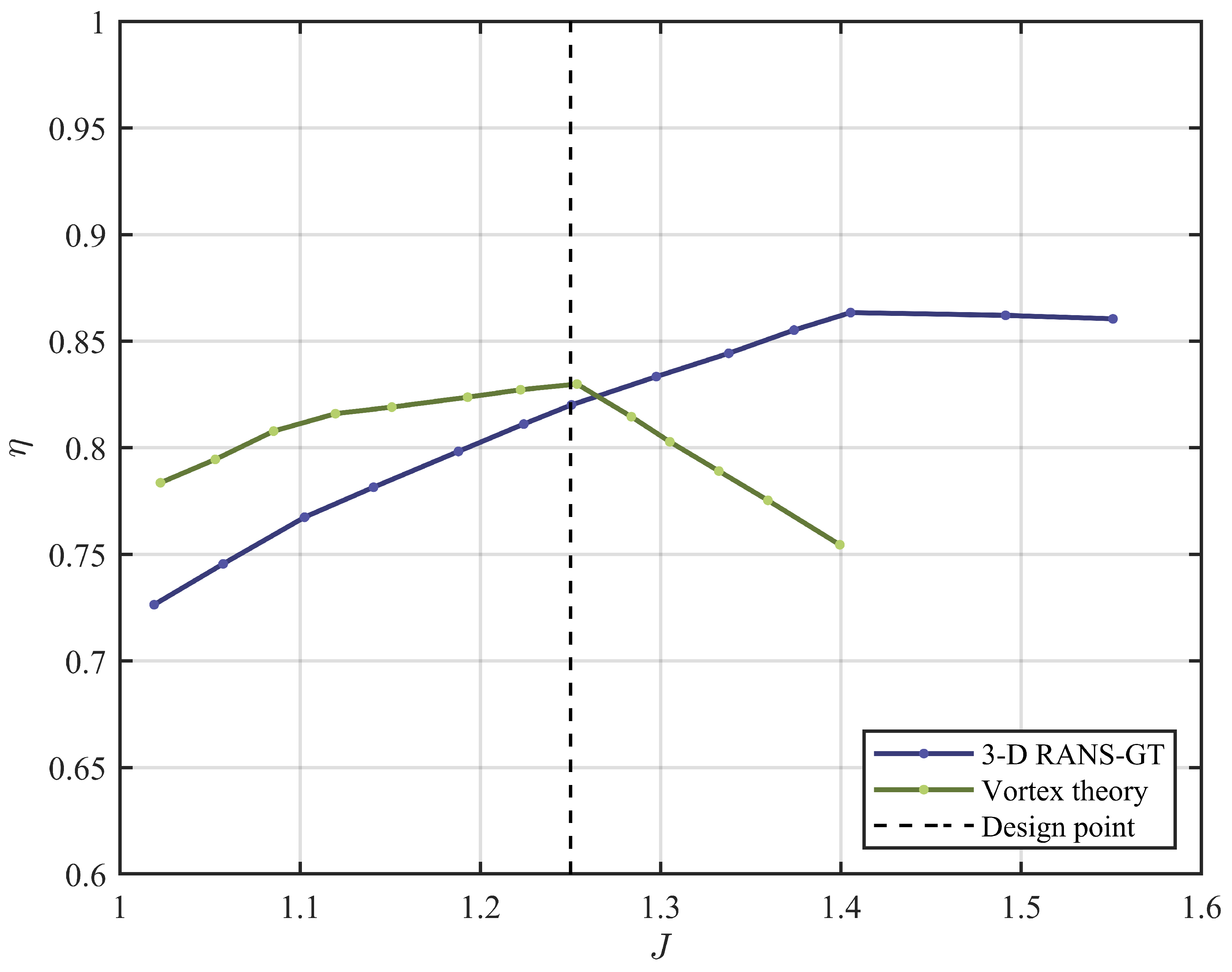
4.4. Vortex Theory
5. Propeller Design for HAPS Operation
5.1. Design Issues for High Altitude Propellers
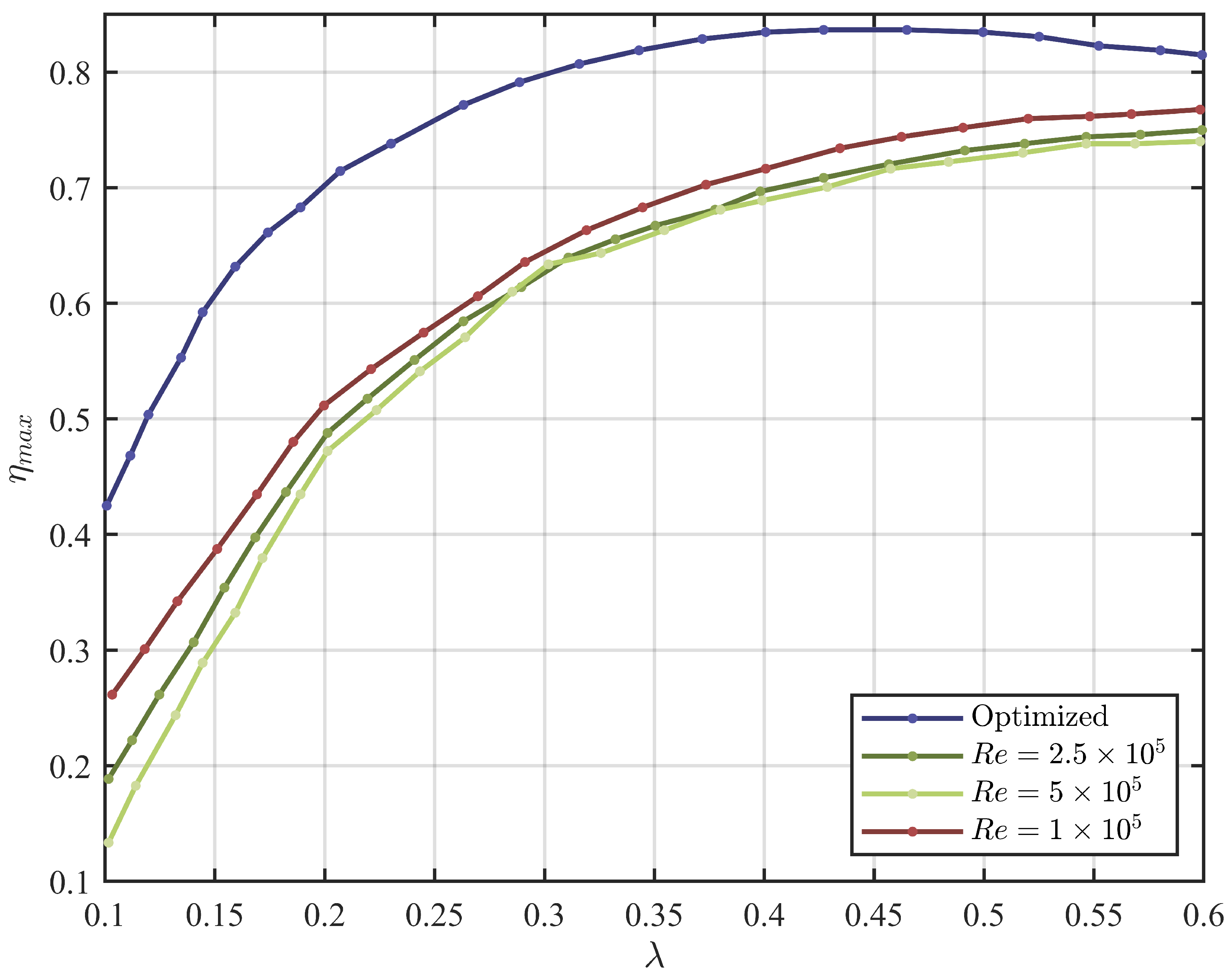
5.2. Recent Development on Propeller Design Methodology
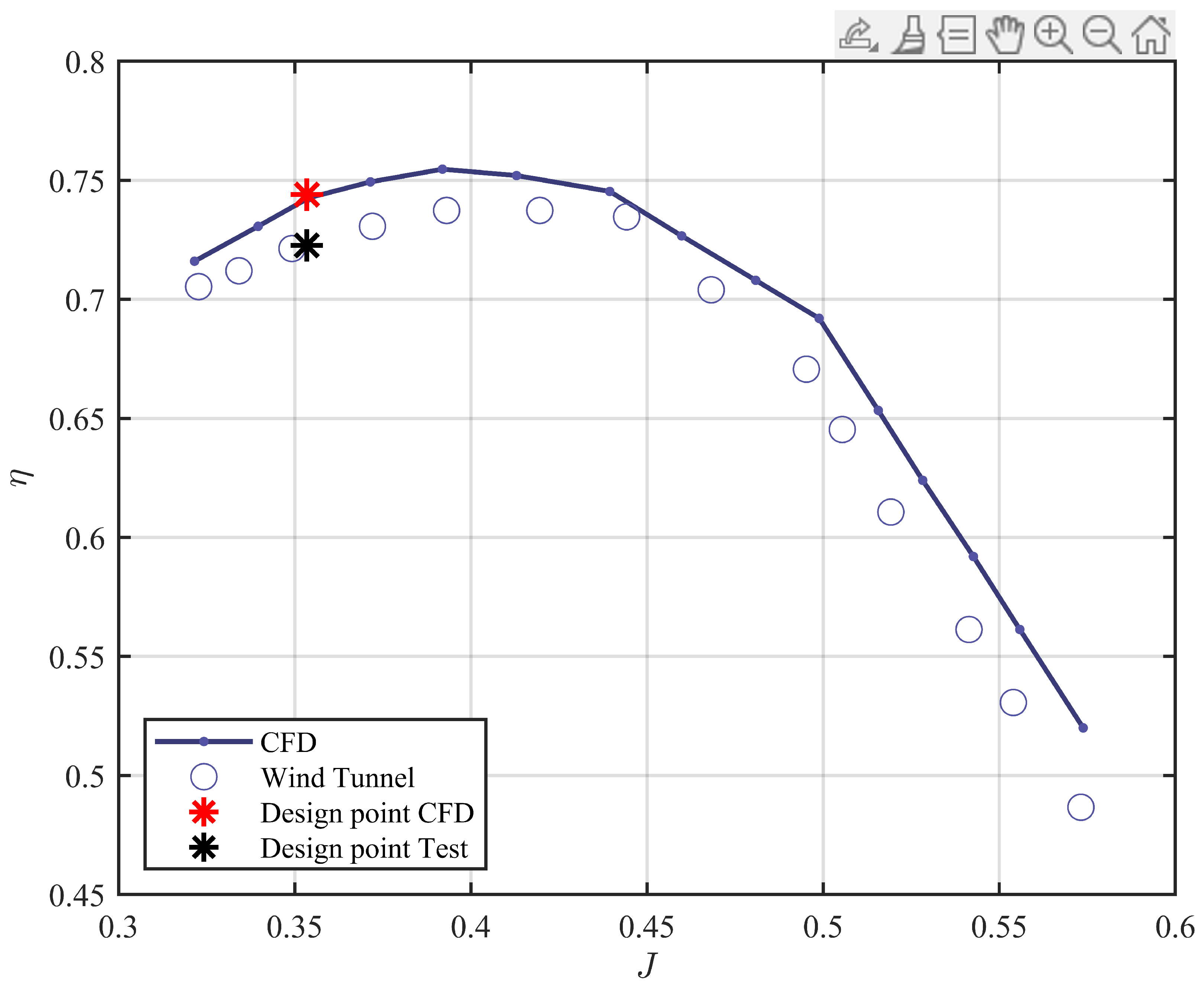
6. Experimental Methods for Evaluating HAPS Propeller Performance
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AF | Activity Factor |
| AMI | Arbitrary Mesh Interface |
| BEMT | Blade Element Momentum Theory |
| BET | Blade Element Theory |
| BLDC | Brushless Direct Current |
| CIRA | Italian Aerospace Research Centre |
| CFD | Computational Fluid Dynamics |
| CST | Class-Shape Transformation |
| DMSoD | Deep Mean Subset of Data |
| DOE | Design of Experiments |
| EPS | Electric Propulsion System |
| FR | Frozen Rotor |
| GT | Gamma Transition |
| HAA | High Altitude Airship |
| HALE | High Altitude Long Endurance |
| HAPS | High Altitude Pseudo Satellite |
| MFNN | Multi-Fidelity Neural Network |
| MIGA | Multi-Island Genetic Algorithm |
| MIL | Minimum Induced Loss |
| PCE | Polynomial Chaos Expansion |
| Probability Density Function | |
| PMSM | Permanent Magnet Synchronous Motors |
| PSO | Particle Swarm Optimization |
| RANS | Reynolds-Averaged Navier–Stokes |
| RFC | Regenerative Fuel Cells |
| RPAS | Remotely Piloted Aircraft Systems |
| UAV | Unmanned Aerial Vehicle |
| UQ | Uncertainty quantification |
| VFEIM | Variable Fidelity Expected Improvement Matrix |
| Nomenclature | |
| a | axial induction factor |
| Induced angle | |
| Tangential induction factor | |
| c | Local blade chord |
| Axial force coefficient | |
| 2D drag coefficient | |
| Drag coefficient | |
| Volumetric drag coefficient | |
| 2D lift coefficient | |
| Lift coefficient | |
| Normal force coefficient | |
| Power coefficient | |
| Thrust coefficient | |
| D | Drag, propeller diameter |
| f | Prandtl tip–loss factor, airship fitness ratio |
| Stall delay factor | |
| F | Momentum loss factor |
| h | Altitude |
| J | Advance ratio |
| l | 2D lift |
| Electric motor mass | |
| n | Rotational speed in rev s−1 |
| Number of blades | |
| P | Power |
| Q | Torque |
| r | Propeller radial coordinate |
| R | Propeller radius and radial coordinate |
| S | Reference wing area |
| T | Thrust |
| Airship volume | |
| Total relative velocity | |
| Free stream velocity | |
| w | Induced velocity |
| Induced velocity (tangential component) | |
| Induced velocity (axial component) | |
| Angle of attack | |
| Circulation | |
| Propeller efficiency | |
| Electric motor efficiency | |
| Propeller induced efficiency | |
| Propeller viscous efficiency | |
| Pitch angle | |
| Advance ratio () | |
| Air density | |
| Solidity | |
| Advance angle | |
| Advance angle at blade tip | |
| Angular velocity in rad s−1 |
References
- Botti, J. Airbus Group: A Story of Continuous Innovation. Aeronaut. J. 2016, 120, 3–12. [Google Scholar] [CrossRef]
- BAE Systems. PHASA-35 Completes First Successful Stratospheric Flight. 2024. Available online: https://www.baesystems.com/en/article/phasa-35-completes-first-successful-stratospheric-flight (accessed on 4 January 2024).
- Mumford, R. Stratobus Project Takes Off. Microw. J. 2016, 59, 6. [Google Scholar]
- Sceye. High Altitude Platform Systems (HAPS). 2024. Available online: https://www.sceye.com/platform (accessed on 5 February 2024).
- Baraniello, V.R.; Persechino, G.; Borsa, R. Tools for the Conceptual Design of a Stratospheric Hybrid Platform; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Baraniello, V.R.; Persechino, G.; Angelino, C.V.; Tufano, F. The Application of High-Altitude Pseudo-Satellites for a Rapid Disaster Response. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA, 2021; pp. 8400–8403. [Google Scholar] [CrossRef]
- Riccio, E.; Giaquinto, C.; Baraniello, V.R.; Coiro, D. Preliminary Conceptual Design for a Box-Wing High Altitude Pseudo Satellite. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; p. 0461. [Google Scholar]
- Gallington, R.; Schoenung, S.; Papadales, B. Possibilities for Very High-Altitude Subsonic Propulsion. In Proceedings of the 30th Joint Propulsion Conference and Exhibit, Indianapolis, IN, USA, 27–29 June 1994. [Google Scholar] [CrossRef]
- Hendrick, P.; Hallet, L.; Verstraete, D. Comparison of Propulsion Technologies for a HALE Airship. In Proceedings of the 7th AIAA ATIO Conference, 2nd CEIAT International Conference on Innovation and Integration in Aerospace Sciences, Belfast, Northern Ireland, 18–20 September 2007. [Google Scholar] [CrossRef]
- Young, M. An Overview of Advanced Concepts for Near Space Systems. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009. [Google Scholar] [CrossRef]
- Townsend, A.; Jiya, I.N.; Martinson, C.; Bessarabov, D.; Gouws, R. A Comprehensive Review of Energy Sources for Unmanned Aerial Vehicles, Their Shortfalls and Opportunities for Improvements. Heliyon 2020, 6, 11. [Google Scholar] [CrossRef] [PubMed]
- Deloitte. Research Study on High-Altitude Pseudo-Satellites. 2022. Available online: https://www.frontex.europa.eu/assets/EUresearchprojects/News/2023/Frontex_HAPS_KoM.pdf (accessed on 20 December 2023).
- Boaretto, N.; Garbayo, I.; Valiyaveettil-SobhanRaj, S.; Quintela, A.; Li, C.; Casas-Cabanas, M.; Aguesse, F. Lithium Solid-State Batteries: State-of-the-Art and Challenges for Materials, Interfaces and Processing. J. Power Sources 2021, 502, 229919. [Google Scholar] [CrossRef]
- Amprius. Amprius Technologies Ships First Commercially Available 450 WH/KG, 1150 Wh/L Batteries. 2022. Available online: https://amprius.com/amprius-technologies-ships-first-commercially-available-450-wh-kg-1150-wh-l-batteries (accessed on 20 December 2023).
- MicroLink Devices Recognized as Airbus Key Supplier. 2019. Available online: https://mldevices.com/test-news/ (accessed on 20 December 2023).
- Hydrogen-Powered Aviation. A Fact-Based Study of Hydrogen Technology, Economics, and Climate Impact by 2050. Available online: https://www.clean-hydrogen.europa.eu/document/download/754333a6-070d-4954-bda6-9ca4a3637a5d_en?filename=20200720_Hydrogen%20Powered%20Aviation%20report_FINAL%20web.pdf (accessed on 20 December 2023).
- Alves, P.; Silvestre, M.; Gamboa, P. Aircraft Propellers—Is There a Future? Energies 2020, 13, 4157. [Google Scholar] [CrossRef]
- Nixon, D. The Boeing Condor; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2001. [Google Scholar] [CrossRef]
- Halawi, S. Zephyr’s Next Chapter, Airbus Trade Media Briefing 2022, Madrid, Spain. 2022. Available online: https://mediaassets.airbus.com/pm_38_602_602492-ie1gtafyip.pdf?dl=true (accessed on 20 December 2023).
- Boeing. Boeing Phantom Eye Completes 1st Autonomous Flight. 2012. Available online: https://boeing.mediaroom.com/2012-06-04-Boeing-Phantom-Eye-Completes-1st-Autonomous-Flight (accessed on 20 December 2023).
- NASA. Perseus B. 1999. Available online: https://www.nasa.gov/wp-content/uploads/2021/09/120313main_FS-059-DFRC.pdf (accessed on 20 December 2023).
- NASA. Pathfinder: Leading the Way in Solar Flight. 2022. Available online: https://www.nasa.gov/wp-content/uploads/2021/09/120291main_FS-034-DFRC.pdf (accessed on 20 December 2023).
- U.S. Air Force. RQ-4 Global Hawk. 2014. Available online: https://www.af.mil/About-Us/Fact-Sheets/Display/Article/104516/rq-4-global-hawk/ (accessed on 20 December 2023).
- Taylor, M.J.H. World Aircraft & Systems Directory; Brassey’s Ltd.: London, UK, 1999. [Google Scholar]
- Fédération Aéronautique Internationale. Class C-1e (Landplanes: Take-Off Weight 3000 to 6000 kg)—Altitude. 1988. Available online: https://www.fai.org/record/1388 (accessed on 20 December 2023).
- Lobner, P. Sceye Stratospheric Airship. 2022. Available online: https://lynceans.org/wp-content/uploads/2021/04/Sceye_stratospheric-airship-converted.pdf (accessed on 4 January 2024).
- Colozza, A. High Altitude Propeller Design and Analysis Overview; NASA-CR-1998-208520; NASA: Washington, DC, USA, 1998.
- Gonzalo, J.; López, D.; Domínguez, D.; García, A.; Escapa, A. On the Capabilities and Limitations of High-Altitude Pseudo-Satellites. Prog. Aerosp. Sci. 2018, 98, 37–56. [Google Scholar] [CrossRef]
- NASA. Helios Prototype: The Forerunner of 21st Century Solar-Powered Atmospheric Satellites. 2022. Available online: https://www.nasa.gov/wp-content/uploads/2021/09/120318main_FS-068-DFRC.pdf (accessed on 20 December 2023).
- Hwang, S.J.; Kim, S.G.; Kim, C.W.; Lee, Y.G. Aerodynamic Design of the Solar-Powered High Altitude Long Endurance (HALE) Unmanned Aerial Vehicle (UAV). Int. J. Aeronaut. Space Sci. 2016, 17, 132–138. [Google Scholar] [CrossRef]
- Zuckerberg, M. The Technology Behind Aquila. 21 July 2016. Available online: https://www.facebook.com/notes/mark-zuckerberg/the-technology-behind-aquila/10153916136506634/ (accessed on 29 November 2017).
- Zephyr. The High-Altitude Pseudo-Satellite. 2017. Available online: https://www.airbus.com/en/newsroom/news/2016-04-zephyr-the-high-altitude-pseudo-satellite-is-taking-off (accessed on 29 November 2017).
- Smith, I.S.; Lee, M. The HiSentinel Airship. In Proceedings of the 7th AIAA Aviation Technology, Integration and Operations Conference (ATIO), Belfast, Northern Ireland, 18–20 September 2007. [Google Scholar] [CrossRef]
- Maekawa, S.; Nakadate, M.; Takegaki, A. Structures of the Low Altitude Stationary Flight Test Vehicle. J. Aircr. 2007, 44, 662–666. [Google Scholar] [CrossRef]
- United States Government Accountability Office. Future Aerostat and Airship Investment Decisions Drive Oversight and Coordination Needs; GAO-13–81; U.S. Government Accountability Office: Washington, DC, USA, 2012.
- Winslow, J.; Otsuka, H.; Govindarajan, B.; Chopra, I. Basic Understanding of Airfoil Characteristics at Low Reynolds Numbers (104–105). J. Aircr. 2018, 55, 1050–1061. [Google Scholar] [CrossRef]
- Ma, R.; Zhong, B.; Liu, P. Optimization Design Study of Low-Reynolds-Number High-Lift Airfoils for the High-Efficiency Propeller of Low-Dynamic Vehicles in Stratosphere. Sci. China Technol. Sci. 2010, 53, 2792–2807. [Google Scholar] [CrossRef]
- Maulana, F.A.; Amalia, E.; Moelyadi, M.A. Computational Fluid Dynamics (CFD) Based Propeller Design Improvement for High Altitude Long Endurance (HALE) UAV. Int. J. Intell. Unmanned Syst. 2023, 11, 425–438. [Google Scholar] [CrossRef]
- Lissaman, P.B.S. Low-Reynolds-Number Airfoils. Annu. Rev. Fluid Mech. 1983, 15, 223–239. [Google Scholar] [CrossRef]
- Yao, Y.; Ma, D.; Yang, X. Optimization Design of Propeller for Ultra-High-Altitude Unmanned Aerial Vehicle. J. Phys. Conf. Ser. 2022, 2364, 012009. [Google Scholar] [CrossRef]
- Khedr, A.; Castellani, F. Large Eddy Simulation of the Effect of Blade Rotation on Laminar Separation Bubbles in Horizontal Axis Wind Turbines. Phys. Fluids 2025, 37, 041604. [Google Scholar] [CrossRef]
- Goyal, J.; Sinnige, T.; Avallone, F.; Ferreira, C. Benchmarking of Aerodynamic Models for Isolated Propellers Operating at Positive and Negative Thrust. AIAA J. 2024, 62, 3758–3775. [Google Scholar] [CrossRef]
- Melani, P.F.; Mohamed, O.S.; Cioni, S.; Balduzzi, F.; Bianchini, A. An Insight into the Capability of the Actuator Line Method to Resolve Tip Vortices. Wind Energy Sci. 2024, 9, 601–622. [Google Scholar] [CrossRef]
- Mueller, T.J. Fixed and Flapping Wing Aerodynamics for Micro Air Vehicle Applications; AIAA: Reston, VA, USA, 2001. [Google Scholar] [CrossRef]
- Yao, Y.; Ma, D.; Zhang, L.; Yang, X.; Yu, Y. Aerodynamic Optimization and Analysis of Low Reynolds Number Propeller with Gurney Flap for Ultra-High-Altitude Unmanned Aerial Vehicle. Appl. Sci. 2022, 12, 3195. [Google Scholar] [CrossRef]
- Monk, J.S. A Propeller Design and Analysis Capability Evaluation for High Altitude Application. Ph.D. Dissertation, University of the Witwatersrand, Johannesburg, South Africa, 2010. [Google Scholar]
- Schawe, D.; Rohardt, C.H.; Wichmann, G. Aerodynamic Design Assessment of Strato 2C and Its Potential for Unmanned High Altitude Airborne Platforms. Aerosp. Sci. Technol. 2002, 6, 43–51. [Google Scholar] [CrossRef]
- Grob Aircraft. G520 NG Egrett. Available online: https://grob-aircraft.com/en/g-520ng.html (accessed on 10 July 2025).
- Larrabee, E.E. Practical Design of Minimum Induced Loss Propellers. SAE Trans. 1979, 88, 2053–2062. [Google Scholar]
- Merlin, P.W. Crash Course: Lessons Learned from Accidents Involving Remotely Piloted and Autonomous Aircraft; No. AFRC-E-DAA-TN5128; NASA: Washington, DC, USA, 2013.
- Morgado, J.; Abdollahzadeh, M.; Silvestre, M.A.R.; Páscoa, J.C. High Altitude Propeller Design and Analysis. Aerosp. Sci. Technol. 2015, 45, 398–407. [Google Scholar] [CrossRef]
- McCormick, B.W. Aerodynamics, Aeronautics, and Flight Mechanics; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Haque, A.U.; Asrar, W.; Omar, A.A.; Sulaeman, E.; Ali, J.M. Assessment of Engine’s Power Budget for Hydrogen Powered Hybrid Buoyant Aircraft. Propuls. Power Res. 2016, 5, 34–44. [Google Scholar] [CrossRef][Green Version]
- Harmats, M.; Weihs, D. Hybrid-Propulsion High-Altitude Long-Endurance Remotely Piloted Vehicle. J. Aircr. 1999, 36, 321–331. [Google Scholar] [CrossRef]
- Bentz, J.C. Fuel Cell Powered Electric Propulsion for HALE Aircraft. In Proceedings of the ASME 1992 International Gas Turbine and Aeroengine Congress and Exposition, Cologne, Germany, 1–4 June 1992; ASME: New York, NY, USA, 1992; Volume 2. Paper No. V002T02A027. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Song, B. Modeling and Dynamic Simulation Study of Big Inertia Propulsion System of High-Altitude Airship. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce, Dengleng, China, 8–10 August 2011. [Google Scholar] [CrossRef]
- Colozza, A.J.; Dolce, J. Initial Feasibility Assessment of a High-Altitude Long Endurance Airship; NASA Technical Reports Server (NTRS), NASA/CR-2003-212724; NASA: Washington, DC, USA, 2003.
- Yu, K.; Guo, H.; Sun, Z.; Wu, Z. Efficiency Optimization Control of Permanent Magnet Synchronous Motor for Electric Propulsion System. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Republic of Korea, 26–29 October 2013; IEEE: New York, NY, USA, 2014; pp. 56–61. [Google Scholar] [CrossRef]
- Lee, J.; Nam, K.; Choi, S.; Kwon, S. Loss Minimizing Control of PMSM with the Use of Polynomial Approximations. IEEE Trans. Power Electron. 2009, 24, 1071–1082. [Google Scholar] [CrossRef]
- McElroy, T.; Landrum, D.B. Simulated High-Altitude Testing of a COTS Electric UAV Motor. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Wrobel, R.; Scholes, B.; Mustaffer, A.; Ullah, S.; Reay, D.; Mecrow, B.; Hussein, A. Design and Experimental Characterization of an Additively Manufactured Heat Exchanger for the Electric Propulsion Unit of a High-Altitude Solar Aircraft. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; IEEE: New York, NY, USA, 2019; pp. 753–760. [Google Scholar] [CrossRef]
- Wrobel, R.; Scholes, B.; Hussein, A.; Law, R.; Mustaffar, A.; Reay, D. A Metal Additively Manufactured (MAM) Heat Exchanger for Electric Motor Thermal Control on a High-Altitude Solar Aircraft—Experimental Characterization. Thermal Sci. Eng. Prog. 2020, 19, 100629. [Google Scholar] [CrossRef]
- Gallo, L.; Tashie-Lewis, B.; Laskaridis, P.; Miller, P.; Husband, M. Modelling of Distributed-Propulsion Low-Speed HALE UAVs Burning Liquid Hydrogen; SAE Technical Paper No. 2015-01-2467; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Belan, M.; Cacciola, S.; Terenzi, R.; Trovato, S.; Usuelli, D.; Familiari, G. Preliminary Sizing of High-Altitude Airships Featuring Atmospheric Ionic Thrusters: An Initial Feasibility Assessment. Aerospace 2024, 11, 590. [Google Scholar] [CrossRef]
- Benford, G.; Benford, J. An Aero-Spacecraft for the Far Upper Atmosphere Supported by Microwaves. Acta Astronaut. 2005, 56, 529–535. [Google Scholar] [CrossRef]
- Xie, C.; Tao, G.; Wu, Z. Performance Prediction and Design of Stratospheric Propeller. Appl. Sci. 2021, 11, 4698. [Google Scholar] [CrossRef]
- Liu, X.; He, W.; Wei, F. Design of High-Altitude Propeller Using Multilevel Optimization. Int. J. Comput. Methods 2020, 17, 1950004. [Google Scholar] [CrossRef]
- Marinus, B.G.; Mourousias, N.; Malim, A. Exploratory Optimizations of Propeller Blades for a High-Altitude Pseudo-Satellite. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020. [Google Scholar] [CrossRef]
- Zheng, X.K.; Wang, X.L.; Cheng, Z.J.; Han, D. The Efficiency Analysis of High-Altitude Propeller Based on Vortex Lattice Lifting Line Theory. CEAS Aeronaut. J. 2017, 8, 141–162. [Google Scholar] [CrossRef]
- Rankine, W.J.M. On the Mechanical Principles of the Action of Propellers. Trans. R. Inst. Nav. Archit. 1865, 6, 13–39. [Google Scholar]
- Froude, W. On the Elementary Relation between Pitch, Slip, and Propulsive Efficiency. Trans. R. Inst. Nav. Archit. 1878, 19, 22–33. [Google Scholar]
- Drzewiecki, S. Méthode pour la détermination des éléments mécaniques des propulseurs hélicoïdaux. Bull. ATM 1892, 3, 11–13. [Google Scholar]
- Betz, A. Schraubenpropeller mit geringstem Energieverlust. Mit einem Zusatz von L. Prandtl. Nachrichten Ges. Wiss. GöTtingen 1919, 1919, 193–217. [Google Scholar]
- Goldstein, S. On the Vortex Theory of Screw Propellers. Proc. R. Soc. Lond. A 1929, 123, 440–465. [Google Scholar]
- Theodorsen, T. Theory of Propellers; McGraw–Hill: New York, NY, USA, 1948. [Google Scholar]
- Glauert, H. Airplane Propellers. In Aerodynamic Theory; Durand, W.F., Ed.; Springer: Berlin/Heidelberg, Germany, 1935; pp. 169–360. [Google Scholar]
- Larrabee, E. Propellers of Minimum Induced Loss, and Water Tunnel Tests of Such a Propeller. In Proceedings of the NASA, Industry, University, General Aviation Drag Reduction Workshop, Lawrence, KS, USA, 14–16 July 1975. [Google Scholar]
- D’Angelo, S.; Berardi, F.; Minisci, E. Aerodynamic Performances of Propellers with Parametric Considerations on the Optimal Design. Aeronaut. J. 2002, 106, 313–320. [Google Scholar] [CrossRef]
- Li, X.; Li, Q.; Zhang, J. Aerodynamic Design of a High Efficient Solar Powered UAV Propeller. Adv. Aeronaut. Sci. Eng. 2020, 11, 02. [Google Scholar] [CrossRef]
- Ning, A. Using Blade Element Momentum Methods with Gradient-Based Design Optimization. Struct. Multidiscip. Optim. 2021, 64, 991–1014. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, Z.; Fan, Z. A Method of Propeller Design with Given Thrust Distribution and Its Application. J. Aerosp. Power 2020, 35, 1238–1246. [Google Scholar] [CrossRef]
- Hu, B.; Gao, Y.; Wei, B. Propeller Design Rule Extraction Based on Rough Set Theory. J. Aerosp. Power 2023, 38, 1901–1908. [Google Scholar] [CrossRef]
- Liu, X.; He, W. Performance Calculation and Design of Stratospheric Propeller. IEEE Access 2017, 5, 14358–14368. [Google Scholar] [CrossRef]
- García-Gutiérrez, A.; Gonzalo, J.; Domínguez, D.; López, D.; Escapa, A. Aerodynamic Optimization of Propellers for High Altitude Pseudo-Satellites. Aerosp. Sci. Technol. 2020, 96, 105562. [Google Scholar] [CrossRef]
- Jiao, J.; Song, B.F.; Zhang, Y.G.; Li, Y.B. Optimal Design and Experiment of Propellers for High Altitude Airship. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2018, 232, 1887–1902. [Google Scholar] [CrossRef]
- Zhang, T.; Barakos, G.N.; Foster, M. Multi-Fidelity Aerodynamic Design and Analysis of Propellers for a Heavy-Lift eVTOL. Aerosp. Sci. Technol. 2023, 135, 108185. [Google Scholar] [CrossRef]
- Hu, Y.; Xiang, J.Q.; Liu, Z.H.; Conrad, Z.J.; Cao, J.N.; Zhang, X.P. Hovering Efficiency Optimization of the Ducted Propeller with Weight Penalty Taken into Account. Aerosp. Sci. Technol. 2021, 117, 106937. [Google Scholar] [CrossRef]
- Yu, P.; Peng, J.; Bai, J.; Han, X.; Xiang, S. Aeroacoustic and Aerodynamic Optimization of Propeller Blades. Chin. J. Aeronaut. 2020, 33, 826–839. [Google Scholar] [CrossRef]
- Peters, N.; Silva, C.; Ekaterinaris, J. A Data-Driven Reduced-Order Model for Rotor Optimization. Wind Energy Sci. 2023, 8, 1201–1223. [Google Scholar] [CrossRef]
- Geng, X.; Liu, P.; Hu, T.; Akkermans, J. Multi-Fidelity Optimization of a Quiet Propeller Based on Deep Deterministic Policy Gradient and Transfer Learning. Aerosp. Sci. Technol. 2023, 137, 108288. [Google Scholar] [CrossRef]
- Kou, Q.; Wang, H.; Liu, K.; Zhi, X. Aerodynamic Design of High-Altitude Propellers within a Bayesian Optimization Framework. Acta Aerodyn. Sin. 2023, 41, 96–103. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, Z.; Fan, Z. A Quick Design Method of Propeller Coupled with CFD Correction. Acta Aeronaut. Astronaut. Sin. 2020, 41, 123216. [Google Scholar] [CrossRef]
- Kwon, H.I.; Yi, S.; Choi, S.; Kim, K. Design of Efficient Propellers Using Variable Fidelity Aerodynamic Analysis and Multilevel Optimization. J. Propuls. Power 2015, 31, 1057–1072. [Google Scholar] [CrossRef]
- Yang, X.; Ma, D.; Zhang, L. High-Fidelity Multi-Level Efficiency Optimization of Propeller for High Altitude Long Endurance UAV. Aerosp. Sci. Technol. 2023, 133, 108142. [Google Scholar] [CrossRef]
- Wu, X.; Zuo, Z.; Ma, L.; Zhang, W. Multi-Fidelity Neural Network-Based Aerodynamic Optimization Framework for Propeller Design in Electric Aircraft. Aerosp. Sci. Technol. 2024, 146, 108963. [Google Scholar] [CrossRef]
- Wang, X.; Ning, C.; Wang, W.; Zhang, W. Intelligent Fusion Method of Multi-Source Aerodynamic Data for Flight Tests. Acta Aerodyn. Sin. 2023, 41, 12–20. [Google Scholar] [CrossRef]
- Mourousias, N.; Malim, A.; Marinus, B.G.; Runacres, M. Multi-Fidelity Multi-Objective Optimization of a High-Altitude Propeller. In Proceedings of the AIAA Aviation 2023 Forum, San Diego, CA, USA, 12–16 June 2023; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2023. Paper No. 2023-3590. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics, Proceedings of the Conference, Notre Dame, IN, USA, 5–7 June 1989; Mueller, T.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar] [CrossRef]
- Marinus, B.G.; Akila, H.; Constantin, L.; Cracana, S. Effect of Rotation on the 3D Boundary Layer around a Propeller Blade. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2017. Paper No. 2017-3866. [Google Scholar] [CrossRef]
- Liu, P.; Ma, L.; Duan, Z.; Ma, R. Study and Verification on Similarity Theory for Propellers of Stratospheric Airships. J. Beijing Univ. Aeronaut. Astronaut. 2012, 7, 957. [Google Scholar]
- Sodja, J.; Stadler, D.; Kosel, T. Computational Fluid Dynamics Analysis of an Optimized Load-Distribution Propeller. J. Aircr. 2012, 49, 955–961. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Tao, G. Numerical Simulation of High-Altitude Propeller’s Aerodynamic Characteristics and Wind Tunnel Test. J. Beijing Univ. Aeronaut. Astronaut. 2013, 39, 1102. [Google Scholar]
- Nigam, N.; Tyagi, A.; Chen, P.; Alonso, J.J.; Palacios, F.; Ol, M.V.; Byrnes, J. Multi-Fidelity Multi-Disciplinary Propeller/Rotor Analysis and Design. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2015. Paper No. 2015-0029. [Google Scholar] [CrossRef]
- Mourousias, N.; García-Gutiérrez, A.; Malim, A.; Fernández, D.D.; Marinus, B.G.; Runacres, M.C. Uncertainty Quantification Study of the Aerodynamic Performance of High-Altitude Propellers. Aerosp. Sci. Technol. 2023, 133, 108108. [Google Scholar] [CrossRef]
- Ledoux, J.; Riffo, S.; Salomon, J. Analysis of the Blade Element Momentum Theory. SIAM J. Appl. Math. 2021, 81, 2596–2621. [Google Scholar] [CrossRef]
- Fan, Z.; Zhou, Z.; Zhu, X.; Wang, R.; Wang, K. High-Robustness Nonlinear-Modification Method for Propeller Blade Element Momentum Theory. Acta Aeronaut. Astronaut. Sin. 2018, 39, 32–45. [Google Scholar] [CrossRef]
- Mahmuddin, F. Rotor Blade Performance Analysis with Blade Element Momentum Theory. Energy Procedia 2017, 105, 1123–1129. [Google Scholar] [CrossRef]
- Loureiro, E.V.; Oliveira, N.L.; Hallak, P.H.; de Souza Bastos, F.; Rocha, L.M.; Delmonte, R.G.P.; de Castro Lemonge, A.C. Evaluation of Low-Fidelity and CFD Methods for the Aerodynamic Performance of a Small Propeller. Aerosp. Sci. Technol. 2021, 108, 106402. [Google Scholar] [CrossRef]
- Fiddes, S.P.; Brown, K.; Bunniss, P.C. Optimum Propellers Revisited—Beyond Blade Element Theory. In Proceedings of the 19th Congress of the International Council of the Aeronautical Sciences (ICAS), Anaheim, CA, USA, 18–23 September 1994. [Google Scholar]
- Adkins, C.N.; Liebeck, R.H. Design of Optimum Propellers. J. Propuls. Power 1994, 10, 676–682. [Google Scholar] [CrossRef]
- Rwigema, M.K. Propeller Blade Element Momentum Theory with Vortex Wake Deflection. In Proceedings of the 27th International Congress of the Aeronautical Sciences, Nice, France, 19–24 September 2010. [Google Scholar]
- MacNeill, R.; Verstraete, D. Blade Element Momentum Theory Extended to Model Low Reynolds Number Propeller Performance. CEAS Aeronaut. J. 2017, 121, 835–857. [Google Scholar] [CrossRef]
- Montgomerie, B. Methods for Root Effects, Tip Effects and Extending the Angle of Attack Range to ±180 deg, with Application to Aerodynamics for Blades on Wind Turbines and Propellers; TR FOI-R-1305; Swedish Defence Research Agency: Stockholm, Sweden, 2004. Available online: https://www.osti.gov/etdeweb/biblio/20607079 (accessed on 10 July 2025).
- Viterna, L.A.; Corrigan, R.D. Fixed Pitch Rotor Performance of Large Horizontal Axis Wind Turbines. In Proceedings of the Large Horizontal-Axis Wind Turbines Workshop, Cleveland, OH, USA, 28–30 July 1981; Available online: https://ntrs.nasa.gov/citations/19830010962 (accessed on 10 July 2025).
- Liu, Z.; Liu, P.; Hu, T.; Qu, Q. Experimental Investigations on High Altitude Airship Propellers with Blade Planform Variations. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2018, 232, 2952–2960. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P.; Qu, Q.; Hu, T. Effect of Advance Ratio and Blade Planform on the Propeller Performance of a High-Altitude Airship. J. Appl. Fluid Mech. 2016, 9, 2993–3000. [Google Scholar] [CrossRef]
- Fradenburgh, E.A.; Matuska, D.G. Advancing Tiltrotor State-of-the-Art with Variable Diameter Rotors. In Proceedings of the 48th American Helicopter Society International Annual Forum, Washington, DC, USA, 3–5 June 1992. [Google Scholar]
- Beemer, J.D. POBAL-S, the Analysis and Design of a High-Altitude Airship; DTIC Document, ADA012292; Air Force Cambridge Research Laboratories: Bedford, MA, USA, 1975.
- Okuyama, M.; Shibata, M.; Yokokawa, A.; Kimura, K. Study of Propulsion Performance and Propeller Characteristics for Stratospheric Platform Airship; PB2007105559; Japan Aerospace Exploration Agency (JAXA): Tokyo, Japan, 2006. [Google Scholar]
- Kim, D.M. Korea Stratospheric Airship Program and Current Results. In Proceedings of the AIAA 3rd Annual Aviation Technology, Integration, and Operations (ATIO) Forum, Denver, CO, USA, 17–19 November 2003. [Google Scholar] [CrossRef]
- Liu, P.; Duan, Z.; Ma, L.; Ma, R. Aerodynamics Properties and Design Method of High Efficiency-Light Propeller of Stratospheric Airships. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE), Nanjing, China, 24–26 June 2011; IEEE: New York, NY, USA, 2011; pp. 8041–8044. [Google Scholar] [CrossRef]
- Dumas, A.; Pancaldi, F.; Anzillotti, F.; Trancossi, M. High Altitude Platforms for Telecommunications: Design Methodology; SAE Technical Paper No. 2009-01-3159; SAE International: Warrendale, PA, USA, 2009. [Google Scholar] [CrossRef]
- Mattingly, J.D.; Heiser, W.H.; Pratt, D.T. Aircraft Engine Design; AIAA: Reston, VA, USA, 2002. [Google Scholar] [CrossRef]
- Morgado, J.; Silvestre, M.Â.R.; Páscoa, J.C. Validation of New Formulations for Propeller Analysis. J. Propuls. Power 2015, 31, 467–477. [Google Scholar] [CrossRef]
- Svorcan, J.; Hasan, M.S.; Baltić, M.; Simonović, A. Optimal Propeller Design for Future HALE UAV. Sci. Tech. Rev. 2019, 69, 25–31. [Google Scholar] [CrossRef]
- Dumitrescu, H.; Cardoş, V.; Dumitrache, A. Modelling of Inboard Stall Delay Due to Rotation. J. Phys. Conf. Ser. 2007, 75, 012022. [Google Scholar] [CrossRef]
- Morgado, J.C.P.J.; Vizinho, R.; Silvestre, M.A.R.; Páscoa, J.C. XFOIL vs CFD Performance Predictions for High Lift Low Reynolds Number Airfoils. Aerosp. Sci. Technol. 2016, 52, 207–214. [Google Scholar] [CrossRef]
- Park, D.; Lee, Y.; Cho, T.; Kim, C. Design and Performance Evaluation of Propeller for Solar-Powered High-Altitude Long-Endurance Unmanned Aerial Vehicle. J. Aerosp. Eng. 2018, 2018, 5782017. [Google Scholar] [CrossRef]
- Tang, J.; Wang, X.; Duan, D.; Xie, W. Optimization and Analysis of Efficiency for Contra-Rotating Propellers for High-Altitude Airships. CEAS Aeronaut. J. 2019, 123, 706–726. [Google Scholar] [CrossRef]
- Oliveira, L.; Muñoz, H.; Catalano, F. Aerodynamic Analysis of High Rotation and Low Reynolds Number Propeller. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 August 2012. [Google Scholar] [CrossRef]
- Breton, S.P.; Coton, F.N.; Moe, G. A Study on Rotational Effects and Different Stall Delay Models Using a Prescribed Wake Vortex Scheme and NREL Phase VI Experiment Data. Wind Energy Int. J. Progr. Appl. Wind Power Convers. Technol. 2008, 11, 459–482. [Google Scholar] [CrossRef]
- Lanzafame, R.; Messina, M. BEM Theory: How to Take into Account the Radial Flow Inside of a 1-D Numerical Code. J. Renew. Energy 2012, 39, 440–446. [Google Scholar] [CrossRef]
- Bak, C.; Johansen, J.; Andersen, P.B. Three-Dimensional Corrections of Airfoil Characteristics Based on Pressure Distributions. In Proceedings of the 2006 European Wind Energy Conference and Exhibition, Athens, Greece, 27 February–2 March 2006. [Google Scholar]
- Corrigan, J.J.; Schillings, J.J. Empirical Model for Stall Delay Due to Rotation. In Proceedings of the American Helicopter Society Aeromechanics Specialists Conference, San Francisco, CA, USA, 19–21 January 1994. [Google Scholar]
- Snel, H.; Houwink, R.; Bosschers, J.; Piers, W.J.; Van Bussel, G.J.W.; Bruining, A. Sectional Prediction of 3-D Effects for Stalled Flow on Rotating Blades and Comparison with Measurements; ECN-RX-93-028; Netherlands Energy Research Foundation (ECN): Petten, The Netherlands, 1993. [Google Scholar]
- Du, Z.; Selig, M.S. A 3-D Stall-Delay Model for Horizontal Axis Wind Turbine Performance Prediction. In Proceedings of the 1998 ASME Wind Energy Symposium, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- Chaviaropoulos, P.K.; Hansen, M.O.L. Investigating Three-Dimensional and Rotational Effects on Wind Turbine Blades by Means of a Quasi-3D Navier–Stokes Solver. J. Fluids Eng. 2000, 122, 330–336. [Google Scholar] [CrossRef]
- Wauters, J.; Degroote, J. On the Study of Transitional Low-Reynolds Number Flows over Airfoils Operating at High Angles of Attack and Their Prediction Using Transitional Turbulence Models. Prog. Aerosp. Sci. 2018, 103, 52–68. [Google Scholar] [CrossRef]
- Koch, L.D. Design and Performance Calculations of a Propeller for Very High-Altitude Flight; NASA-TM-1998-206637; NASA: Washington, DC, USA, 1998.
- Coiro, D.P.; de Nicola, C. Prediction of Aerodynamic Performance of Airfoils in Low Reynolds Number Flows. In Low Reynolds Number Aerodynamics, Proceedings of the Conference, Notre Dame, IN, USA, 5–7 June 1989; Mueller, T.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Mourousias, N.; Marinus, B.G.; Runacres, M.C. A novel multi-fidelity optimization framework for high-altitude propellers. Aerosp. Sci. Technol. 2024, 153, 109407. [Google Scholar] [CrossRef]
- Xu, J.; Han, Z.; Song, W.; Li, K. Efficient Aerodynamic Optimization of Propeller Using Hierarchical Kriging Models. J. Phys. Conf. Ser. 2020, 1519, 012019. [Google Scholar] [CrossRef]
- Mourousias, N.; Malim, A.; Marinus, B.G.; Runacres, M. Surrogate-Based Optimization of a High-Altitude Propeller. In Proceedings of the AIAA Aviation 2021 Forum, Virtual Event, 2–6 August 2021. [Google Scholar] [CrossRef]
- Mourousias, N.; Malim, A.; Marinus, B.G.; Runacres, M. Assessment of Multi-Fidelity Surrogate Models for High-Altitude Propeller Optimization. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Traub, L.W. Considerations in Optimal Propeller Design. J. Aircr. 2021, 58, 950–957. [Google Scholar] [CrossRef]
- Jiménez, J.H.; Hoyos, J.D.; Echavarría, C.; Alvarado, P. Exhaustive Analysis on Aircraft Propeller Performance through a BEMT Tool. J. Aeronaut. Astronaut. Aviat. 2022, 54, 13–23. [Google Scholar] [CrossRef]
- Clarke, M.A.; Erhard, R.M.; Smart, J.T.; Alonso, J. Aerodynamic Optimization of Wing-Mounted Propeller Configurations for Distributed Electric Propulsion Architectures. In Proceedings of the AIAA Aviation 2021 Forum, Virtual Event, 2–6 August 2021; p. 2471. [Google Scholar] [CrossRef]
- García-Gutiérrez, A.; Gonzalo, J.; López, D.; Delgado, A. Stochastic design of high-altitude propellers. Aerosp. Sci. Technol. 2020, 107, 106283. [Google Scholar] [CrossRef]
- Xu, J.; Song, W.; Yang, X.; Nie, H. Aerodynamic Performance of Variable-Pitch Propellers for High-Altitude UAVs. IOP Conf. Ser. Mater. Sci. Eng. 2019, 686, 012019. [Google Scholar] [CrossRef]
- Wald, Q.R. The aerodynamics of propellers. Prog. Aerosp. Sci. 2006, 42, 85–128. [Google Scholar] [CrossRef]
- Wolowicz, C.H.; Brown, J.S., Jr.; Gilbert, W.P. Similitude Requirements and Scaling Relationships as Applied to Model Testing; NASA-TP-1435; NASA: Washington, DC, USA, 1979.
- Jiao, J.; Song, B.; Li, Y. Development of a testing methodology for high-altitude propeller. Aircr. Eng. Aerosp. Tec. 2017, 9, 1486–1494. [Google Scholar] [CrossRef]
- Baltazar, J.; Rijpkema, D.; Falcão de Campos, J. Prediction of the propeller performance at different Reynolds number regimes with RANS. J. Mar. Sci. Eng. 2021, 9, 115. [Google Scholar] [CrossRef]
- Müller, S.B.; Abdel-Maksoud, M.; Hilbert, G. Scale effects on propellers for large container vessels. In Proceedings of the First International Symposium on Marine Propulsors—SMP’09, Trondheim, Norway, 22–24 June 2009. [Google Scholar]
- Wang, X.; Walters, K. Computational analysis of marine-propeller performance using transition-sensitive turbulence modelling. J. Fluids Eng. 2012, 134, 071107. [Google Scholar] [CrossRef]
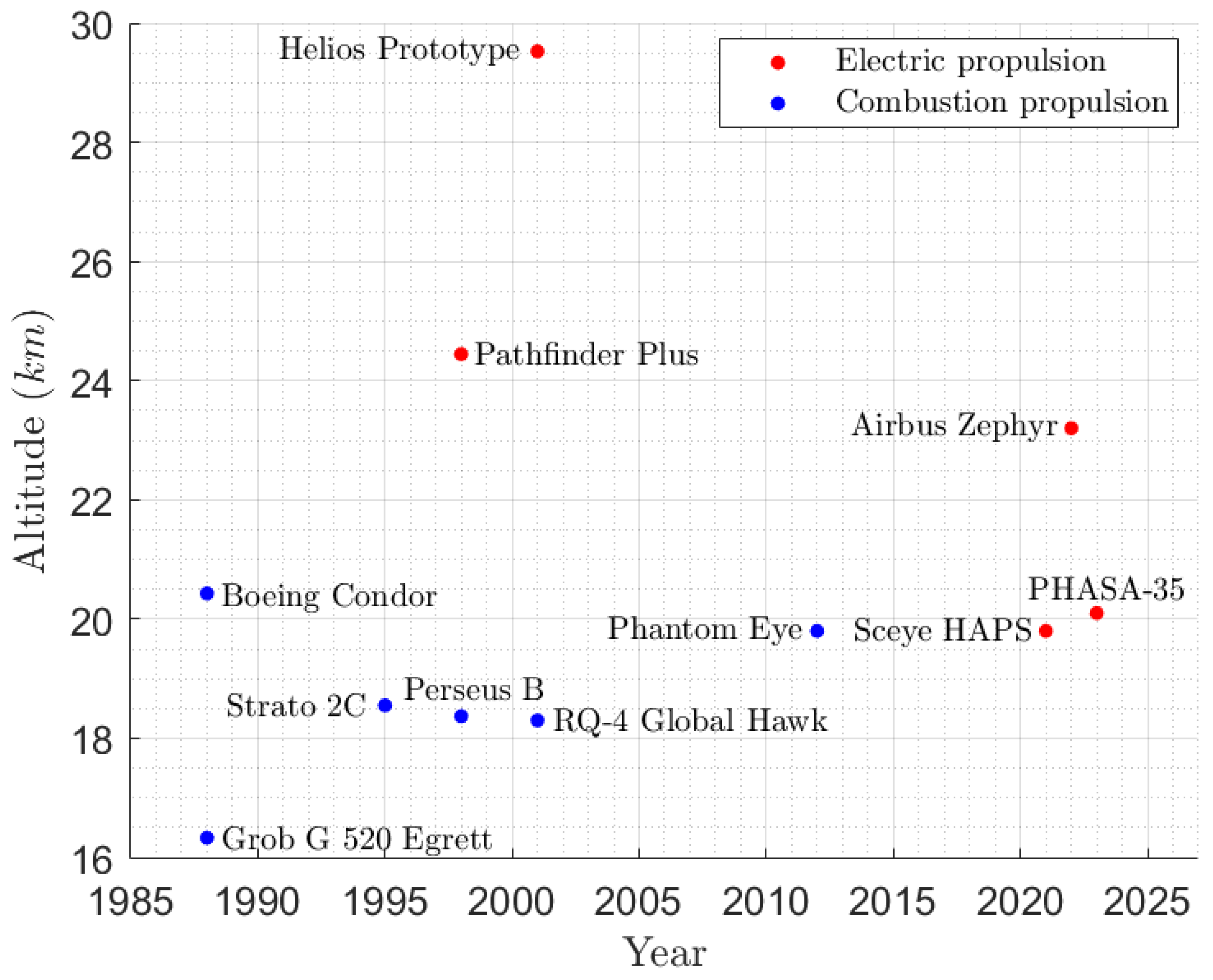





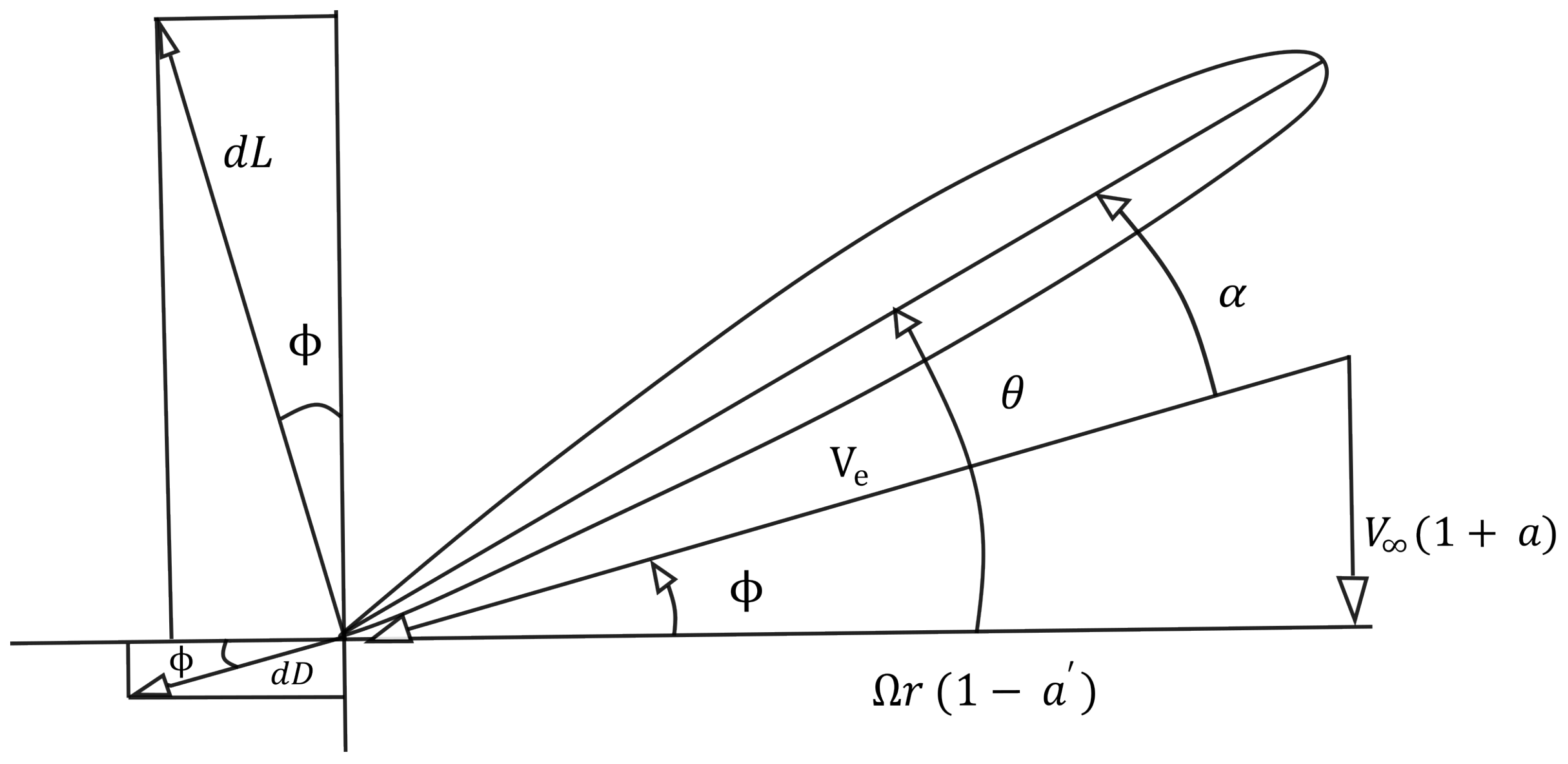

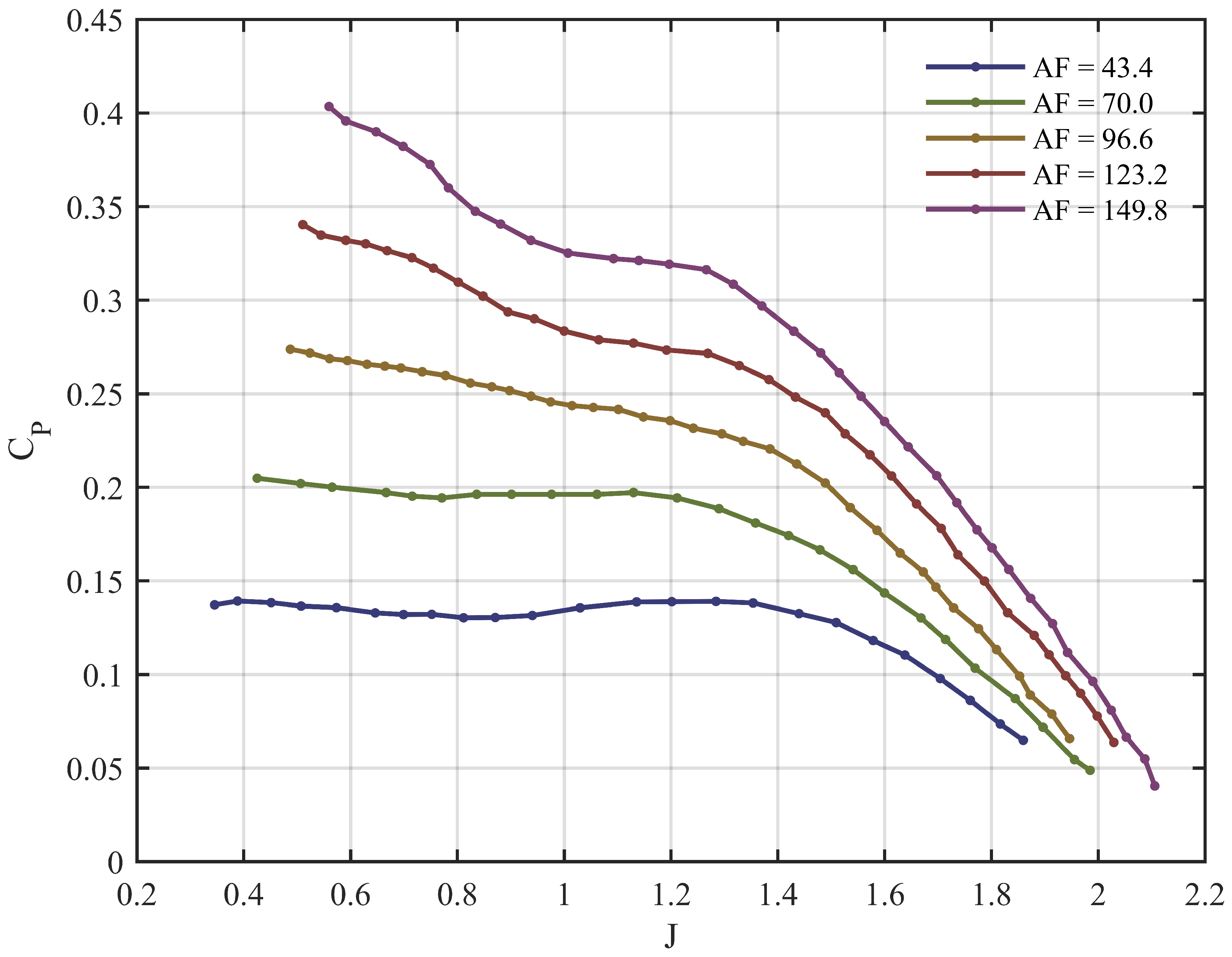
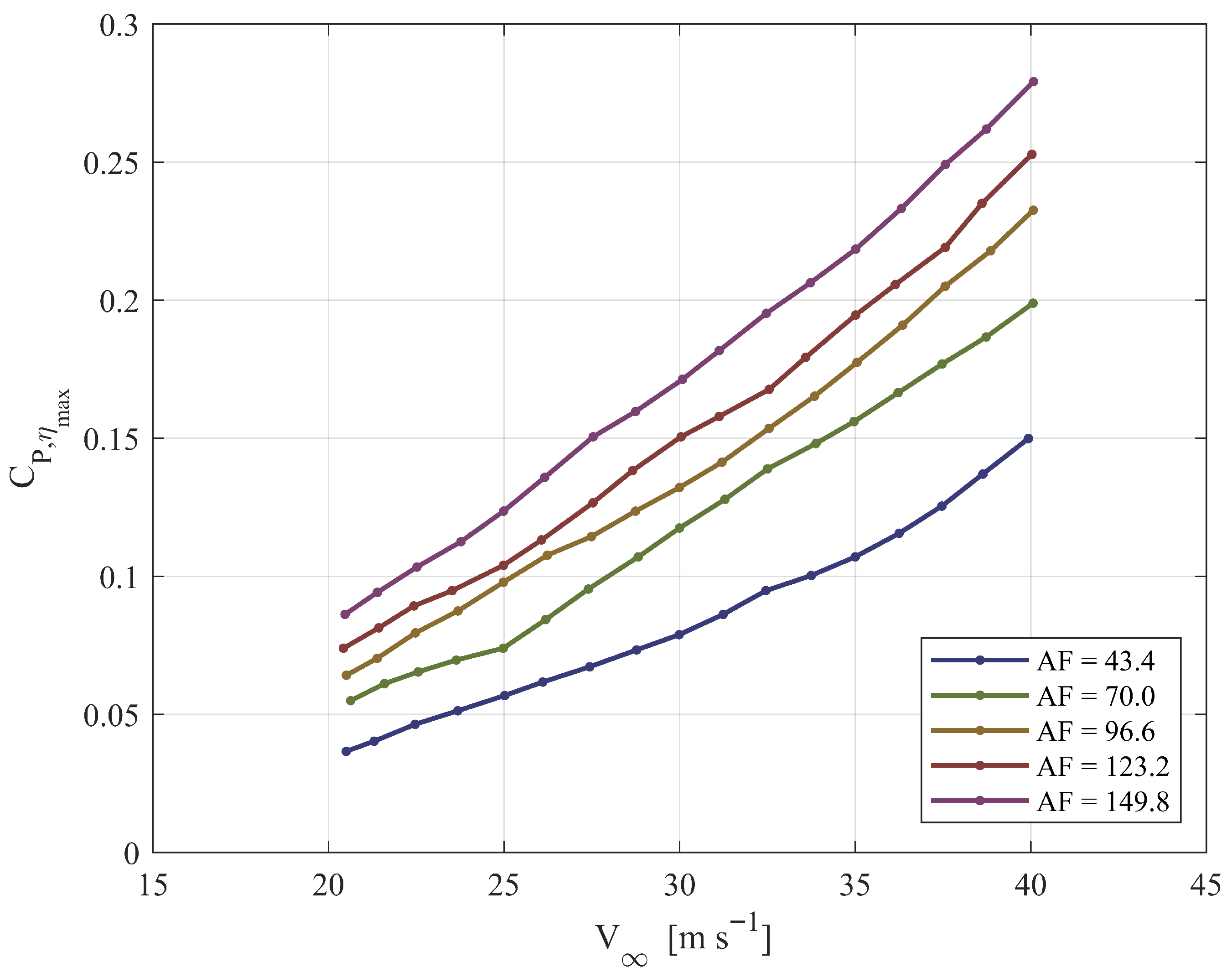
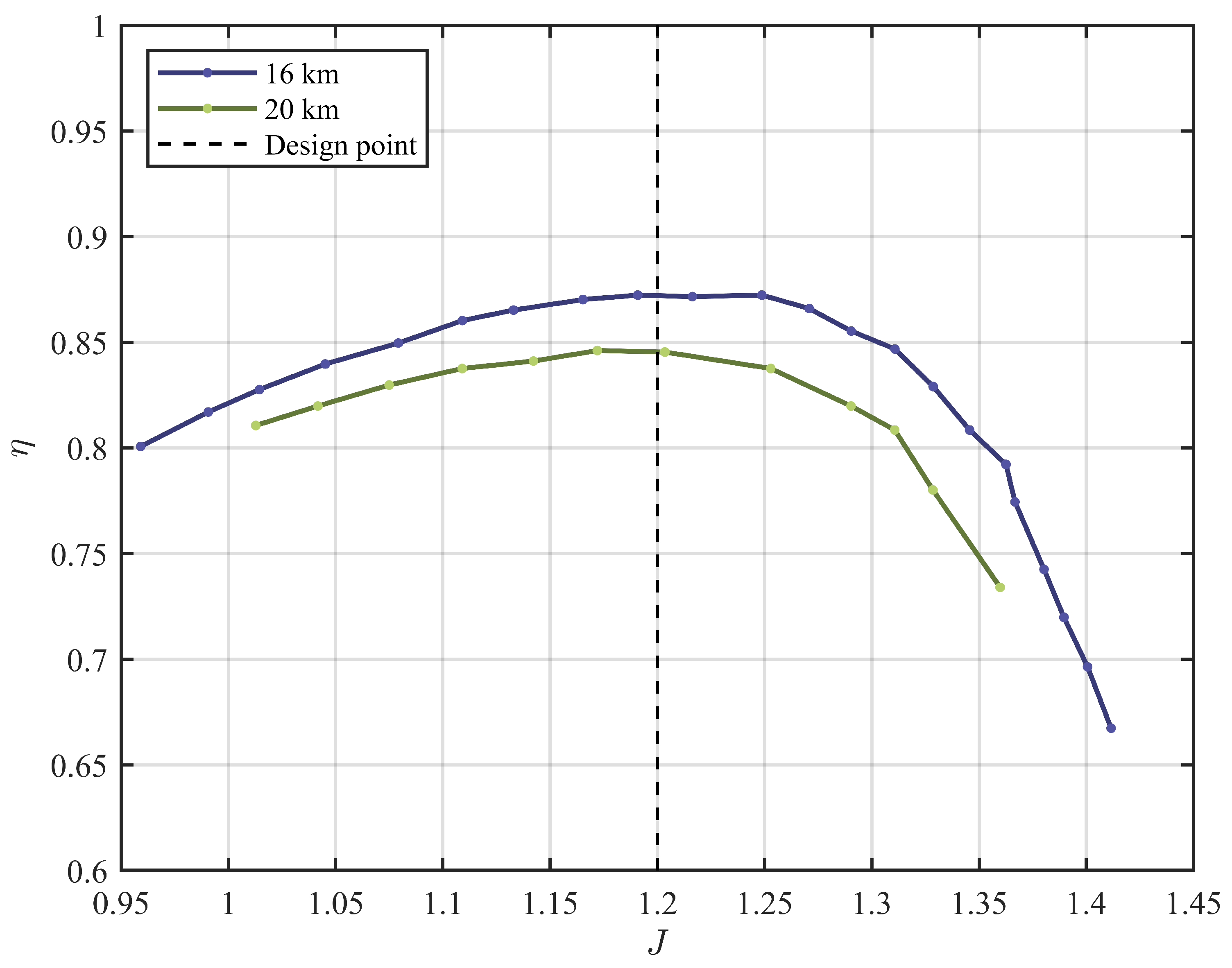
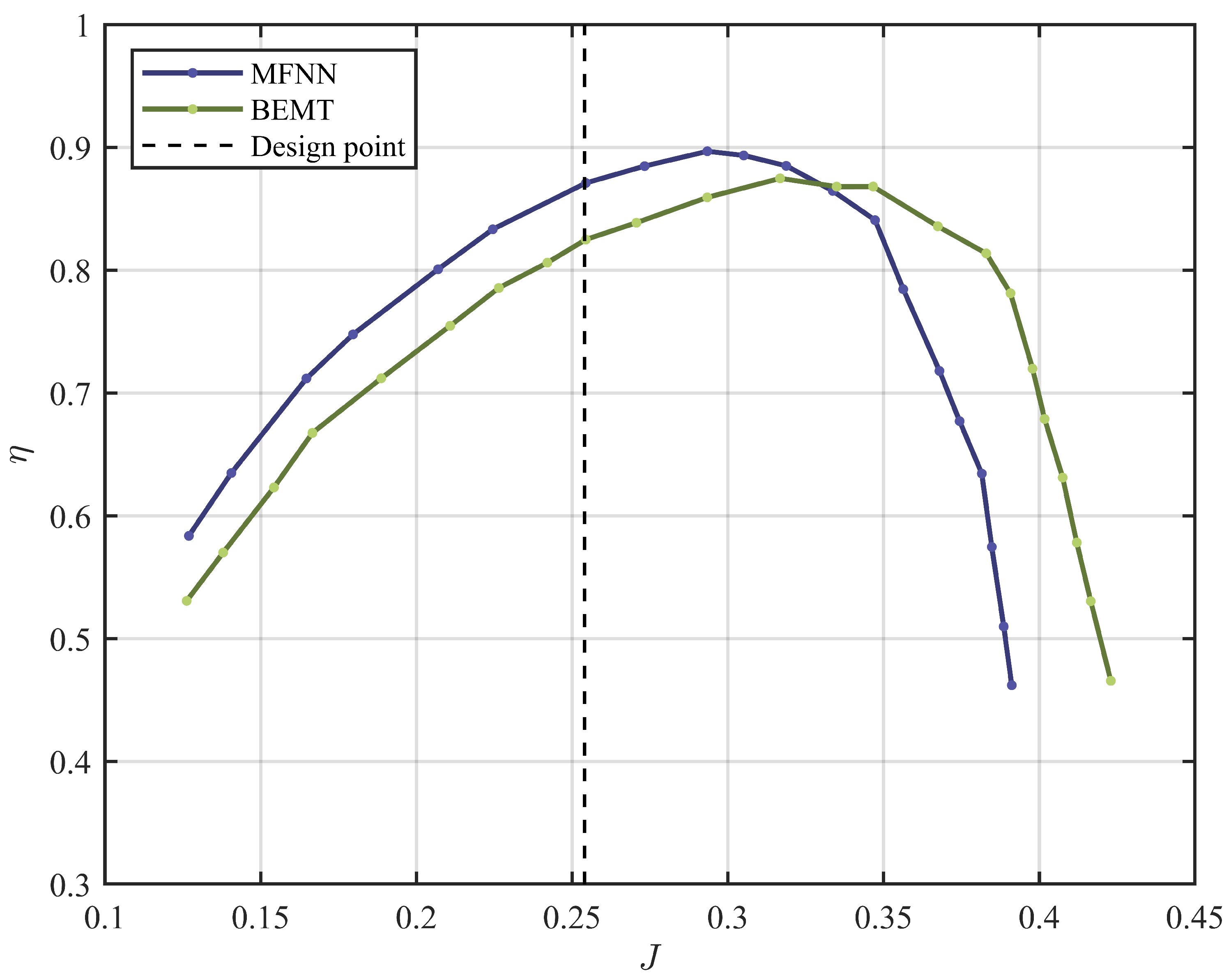

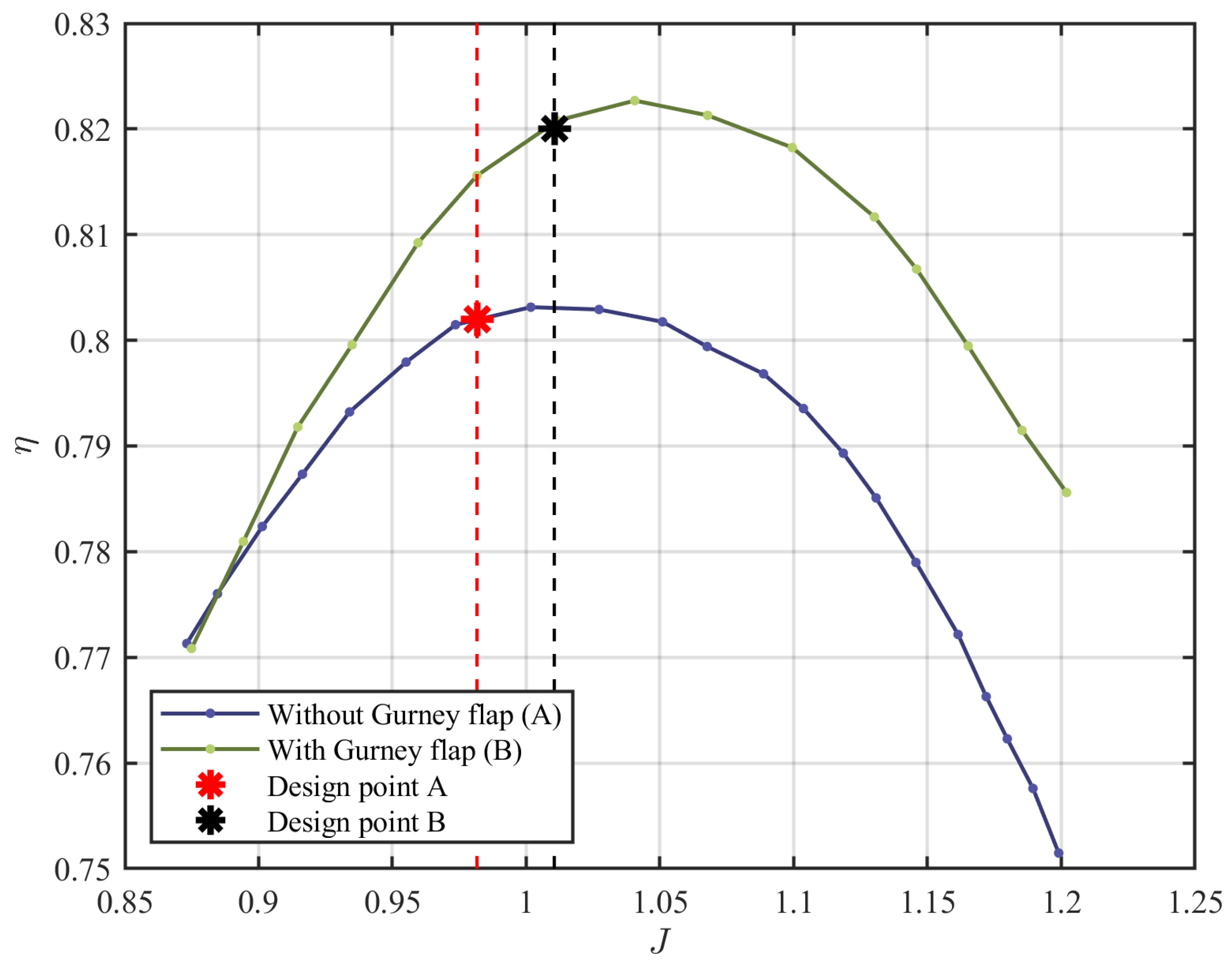
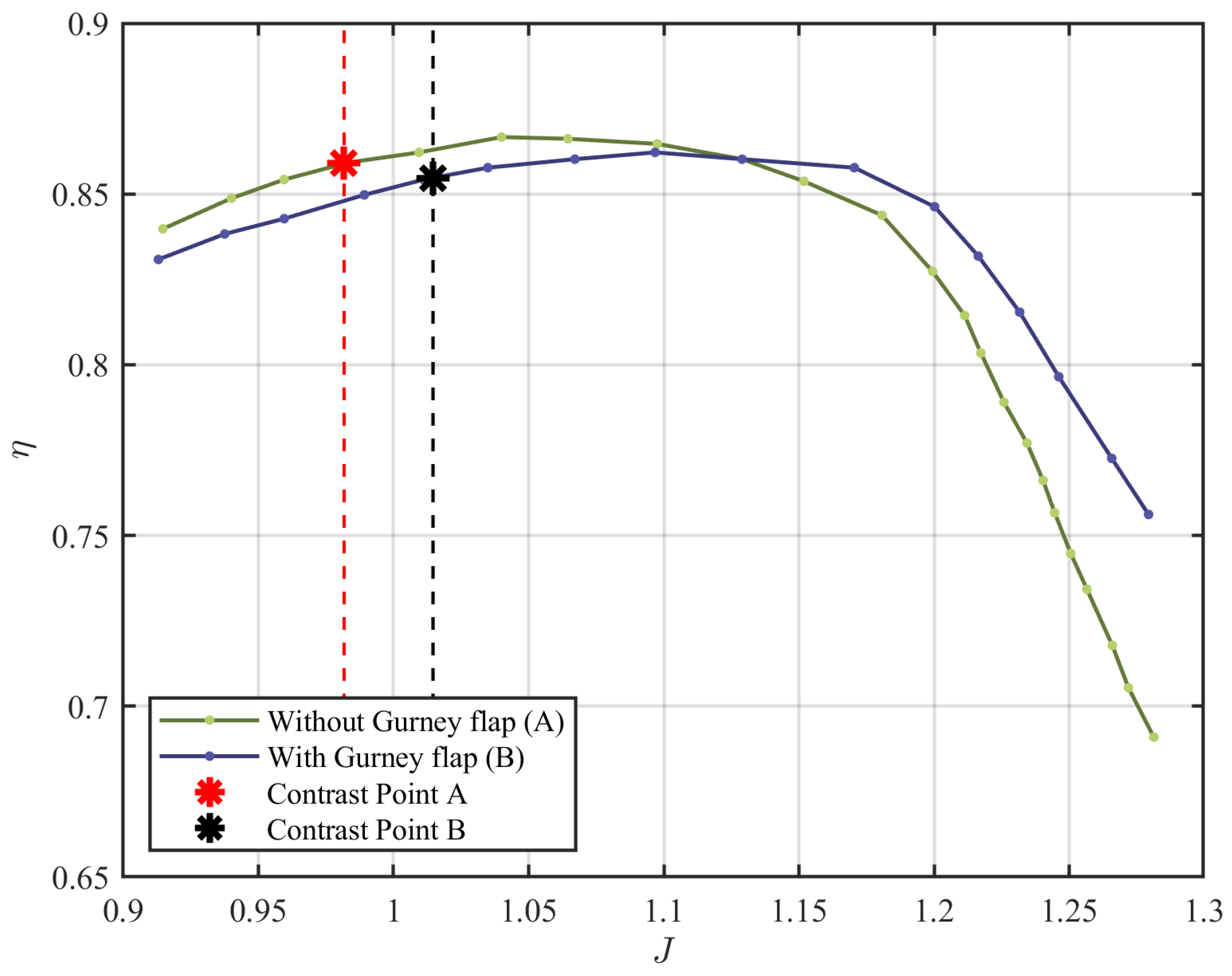


| Year | Aircraft Name | Nominal Thrust [N] | Propeller Diameter [m] |
|---|---|---|---|
| 1987 | Egrett [48] | 2773 | 3.04 |
| 1988 | Condor [27] | 1129 | 4.90 |
| 1993 | Pathfinder [27,46] | 23 | 2.01 |
| 1994 | Perseus [21] | 388 | 4.40 |
| 1995 | Strato2C [46,47] | 2500 | 6.00 |
| 1996 | Theseus [50] | 409 | 2.74 |
| Propeller | AF | D (m) | ||
|---|---|---|---|---|
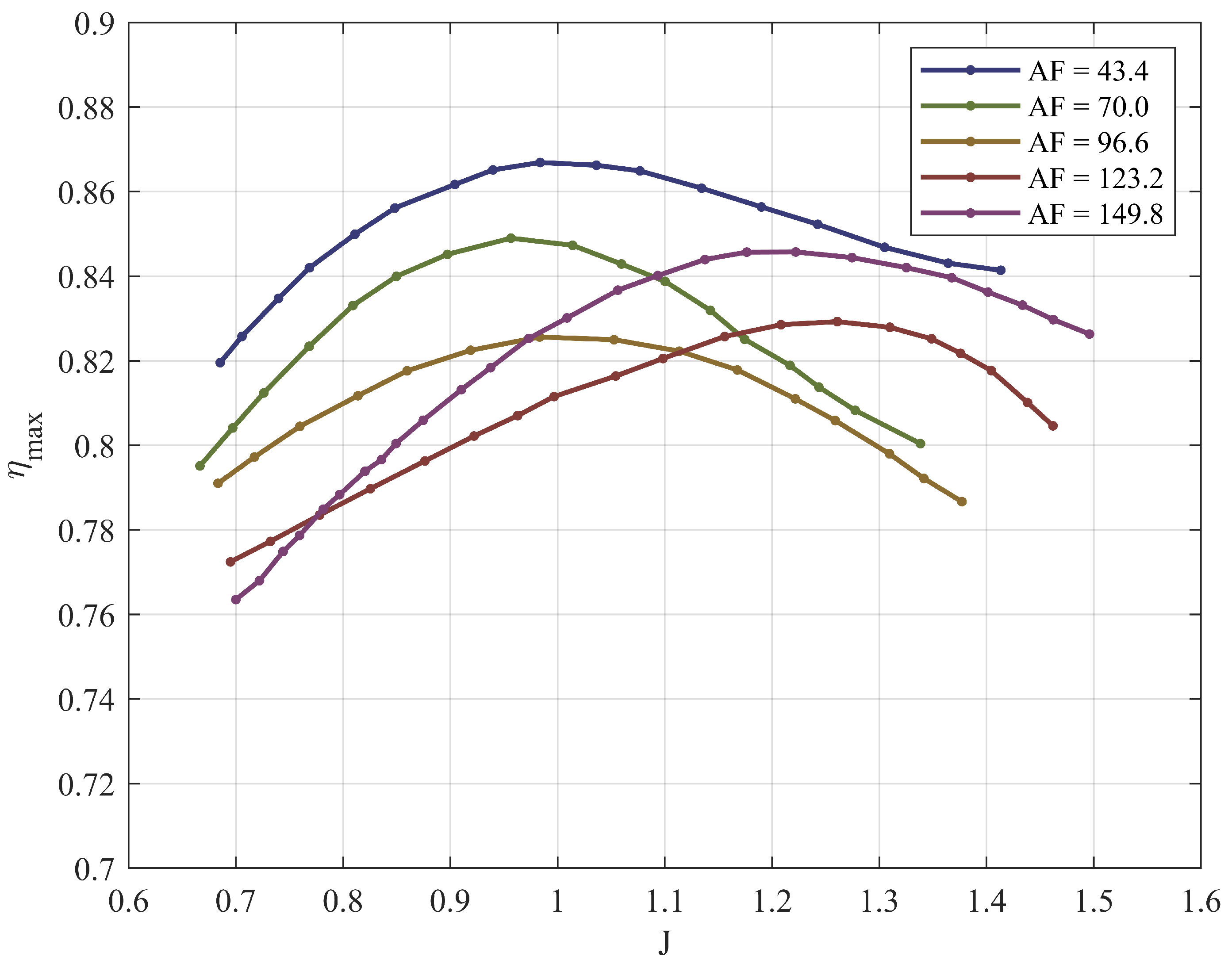
| Propeller 1 | 43.4 | 0.85 | 2 | 0.87 |
| Propeller 2 | 70.0 | 0.85 | 2 | 0.85 |
| Propeller 3 | 96.6 | 0.85 | 2 | 0.83 |
| Propeller 4 | 123.2 | 0.85 | 2 | 0.83 |
| Propeller 5 | 149.8 | 0.85 | 2 | 0.85 |
| Altitude (km) | Wind Speed (m/s) | rpm | Shaft Power | Max Thrust | Efficiency |
|---|---|---|---|---|---|
| 20 | 25 | +43.54% | +42.35% | +36.47% | −4.06% |
| 15 | 15 | +112.17% | +112.11% | +75.06% | −17.48% |
| 10 | 10 | +139.89% | +140.66% | +83.14% | −23.85% |
| 5 | 8 | +141.37% | +141.38% | +79.46% | −29.19% |
| 0 | 6 | +156.81% | +159.09% | +78.85% | −30.86% |
| References | Max Efficiency [%] | Optimization Technique and Design Method | Model Used in Optimization | Operating Condition | Diameter and | Airfoil |
|---|---|---|---|---|---|---|
| Mourousias et al. [141], 2024 | 86.11 | Multi-fidelity multi-objective Bayesian optimization | 3D RANS/Vortex Theory | V = 55 m/s, h = 16 km, T = 185 N | D = 3 m, = 3 | Optimized airfoil |
| Mourousias et al. [97], 2023 | 85.25 | Multi-fidelity Bayesian optimization | 3D RANS/Vortex Theory | V = 55 m/s, h = 16 km, T = 217 N | D = 2.7 m, = 3 | Optimized airfoil |
| Gutiérrez et al. [84], 2020 | 85 | Based on Wald design method [150] | BEMT | V = 10 m/s, T = 100 N, h = 20 km | D = 8 m, = 4 | NACA4412 |
| Mourousias et al. [144], 2022 | 84.2 | Bayesian optimization | 3D RANS | V = 55 m/s, h = 16 km, T = 220 N | D = 3.4 m, = 4 | Optimized airfoil |
| Marinus et al. [68], 2020 | 82.3 | Genetic algorithm (PSO) | Vortex Theory | V = 77.64 m/s, T = 318 N, h =16 km | D = 1.9 m, = 3 | Clark-Y |
| Yao et al. [45], 2022 | 82/80.2 (with/without Gurney Flap) | Multi-level: Level 1 Betz method, Level 2 GA, Level 3 GA | 2D RANS/3D RANS | V = 32 m/s, T = 20 N, h = 20 km | D = 2 m, = 2 | Optimized airfoil |
| Xu et al. [149], 2019 | 81.84/78.52 (Fixed/Variable Pitch propeller) | Bayesian optimization | 3D RANS | V = 25 m/s, T = 22.89–31.24 N, h = 20 km | D = 2 m, = 2 | E387 |
| Yang et al. [94], 2023 | 79.29 | Multi-level: adjoint, perturbation, flow reconstruction | 2D RANS/3D RANS/BEMT | V = 17 m/s, T = 13.3 N, h = 15 km | D = 1.4 m, = 2 | Optimized airfoil |
| Tang et al. [129], 2019 | 78.07 (VLM), 65.2 (CFD) | Kerwin method with VLM for contra-rotating props | VLM | V = 20 m/s, T = 380 N, h = 20 km | D = 6 m, = 4 | S1223 |
| Jiao et al. [85], 2018 | 75 (calc), 70.5 (exp) | Genetic algorithm (NSGA-II) | Vortex Theory | V = 20 m/s, T = 900 N, h = 20 km | D = 6.8 m, = 2 | Custom airfoil sections |
| Zheng et al. [69], 2017 | 73.48 (VLM), 66 (CFD) | Coney method with VLM | VLM | V = 20 m/s, T = 484 N, h = 20 km | D = 7.2 m, = 3 | S1223 |
| Morgado et al. [51], 2015 | 73.2 | Adkins–Liebeck design method | BEMT | V = 30 m/s, T = 6790 N, h = 16 km | D = 6 m, = 2 | Custom airfoil |
| Park et al. [128], 2018 | 65.4 | Inverse design based on Adkins and Liebeck + RSM + desirability function | BEMT | V = 14.6 m/s, T = 21 N, h = 15 km | D = 1.2 m, = 2 | DAE51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riccio, E.; Alifano, F.; Baraniello, V.R.; Coiro, D. A Comprehensive Review of Propeller Design and Propulsion Systems for High-Altitude Pseudo-Satellites. Appl. Sci. 2025, 15, 8013. https://doi.org/10.3390/app15148013
Riccio E, Alifano F, Baraniello VR, Coiro D. A Comprehensive Review of Propeller Design and Propulsion Systems for High-Altitude Pseudo-Satellites. Applied Sciences. 2025; 15(14):8013. https://doi.org/10.3390/app15148013
Chicago/Turabian StyleRiccio, Eleonora, Filippo Alifano, Vincenzo Rosario Baraniello, and Domenico Coiro. 2025. "A Comprehensive Review of Propeller Design and Propulsion Systems for High-Altitude Pseudo-Satellites" Applied Sciences 15, no. 14: 8013. https://doi.org/10.3390/app15148013
APA StyleRiccio, E., Alifano, F., Baraniello, V. R., & Coiro, D. (2025). A Comprehensive Review of Propeller Design and Propulsion Systems for High-Altitude Pseudo-Satellites. Applied Sciences, 15(14), 8013. https://doi.org/10.3390/app15148013






