Study of Online Testing of Void Defects in AM Components with Grating Laser Ultrasonic Spectrum Method
Abstract
1. Introduction
2. Methodology
3. Numerical Simulations and Experiment Validation
3.1. Theoretical Basis for Laser Ultrasonics Generation
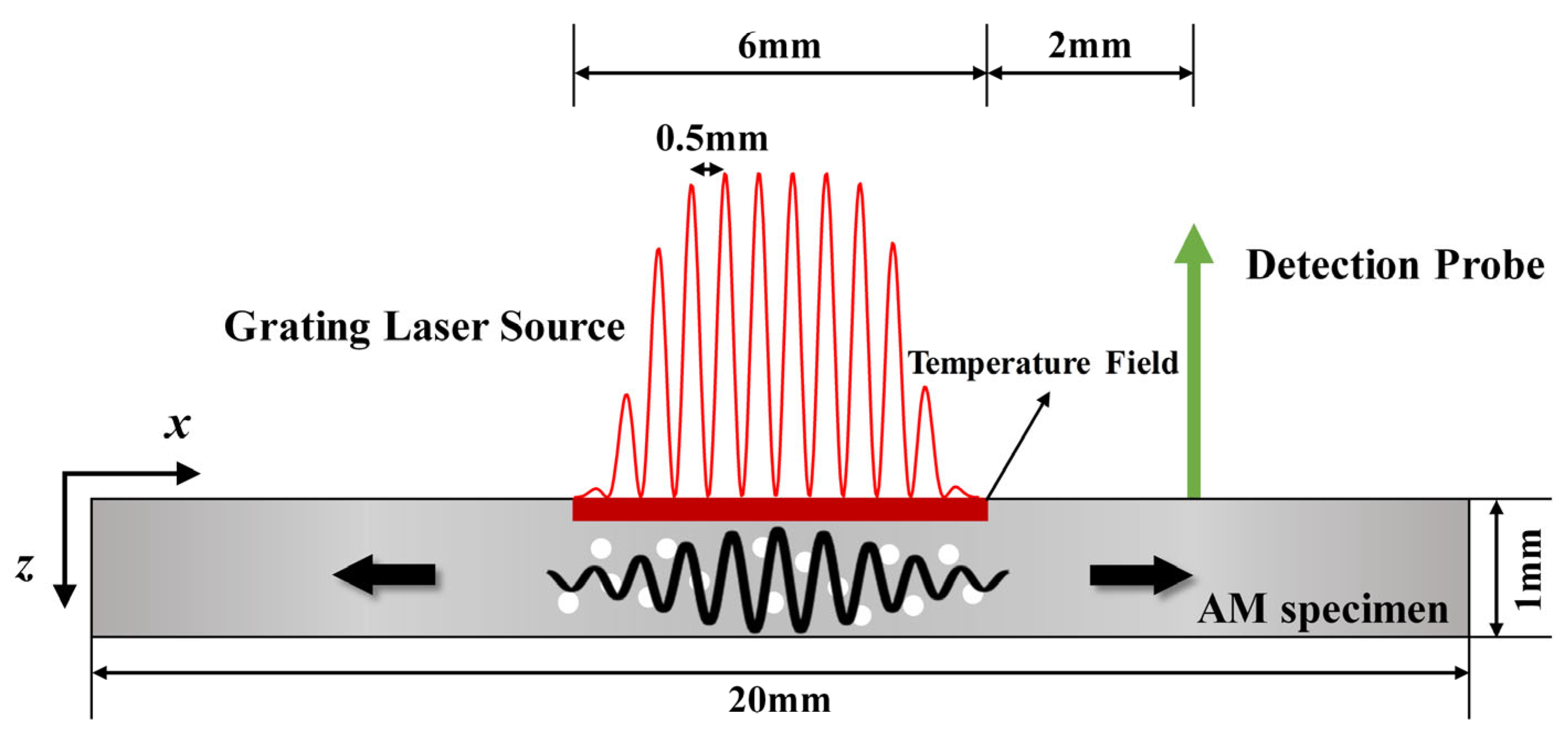
3.2. Finite Element Simulation Model
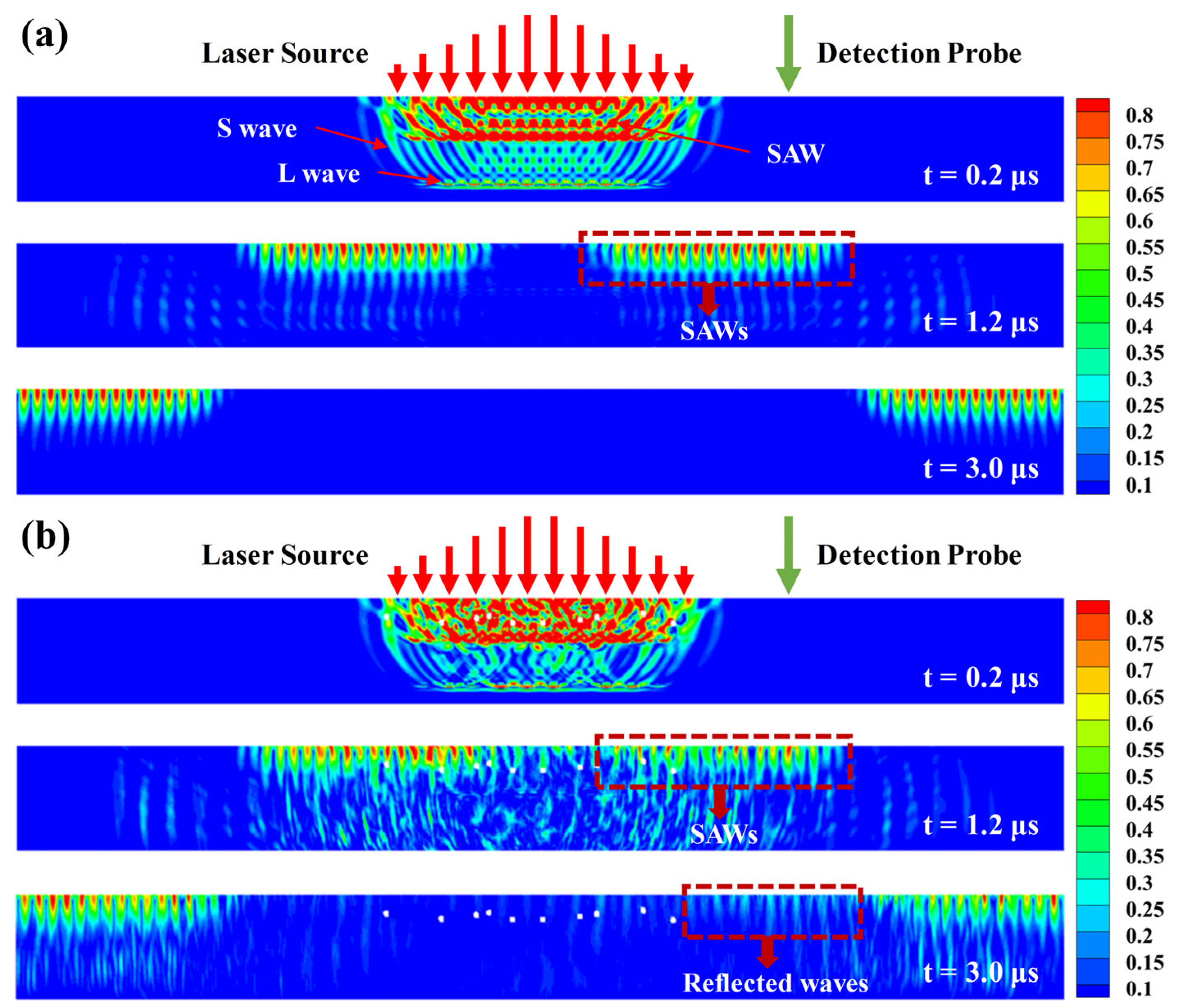
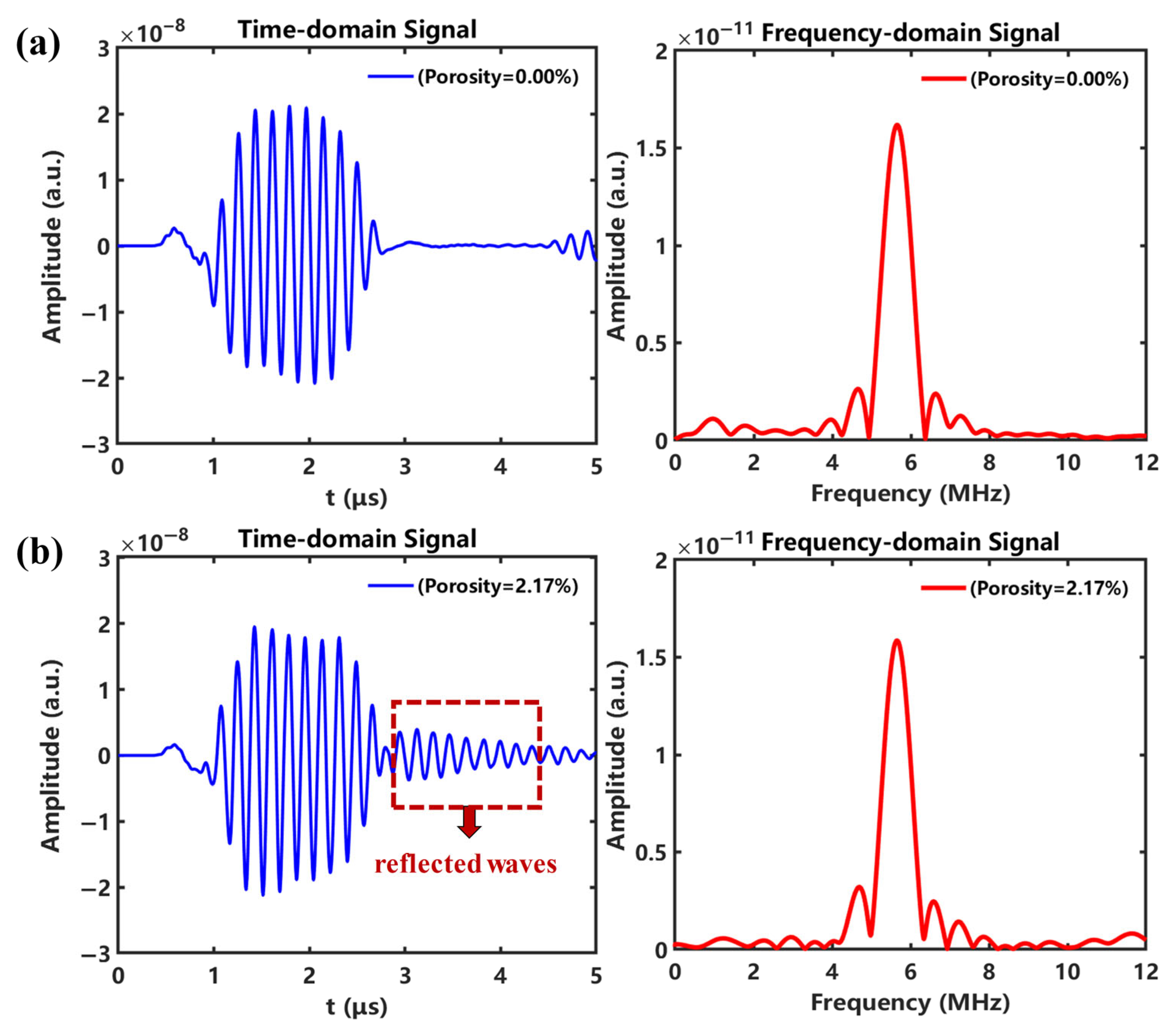
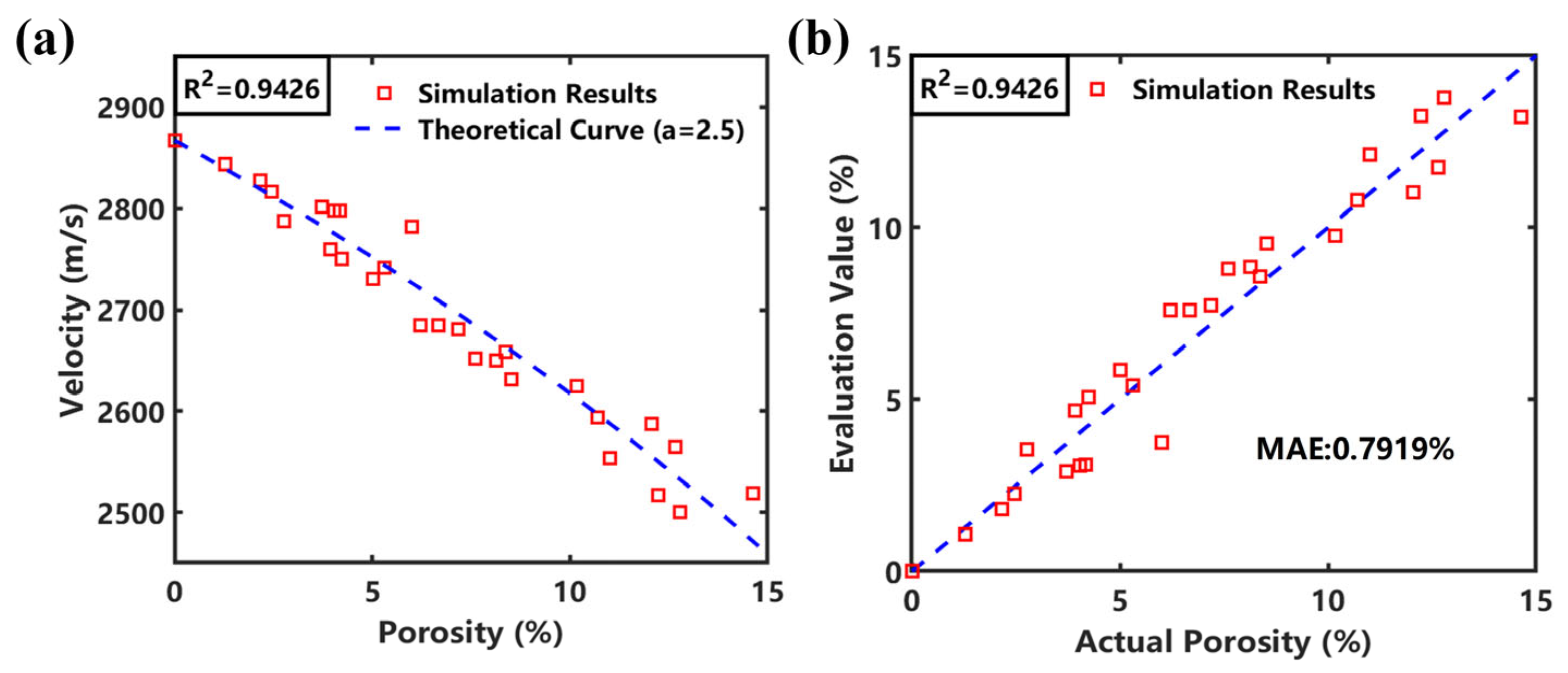
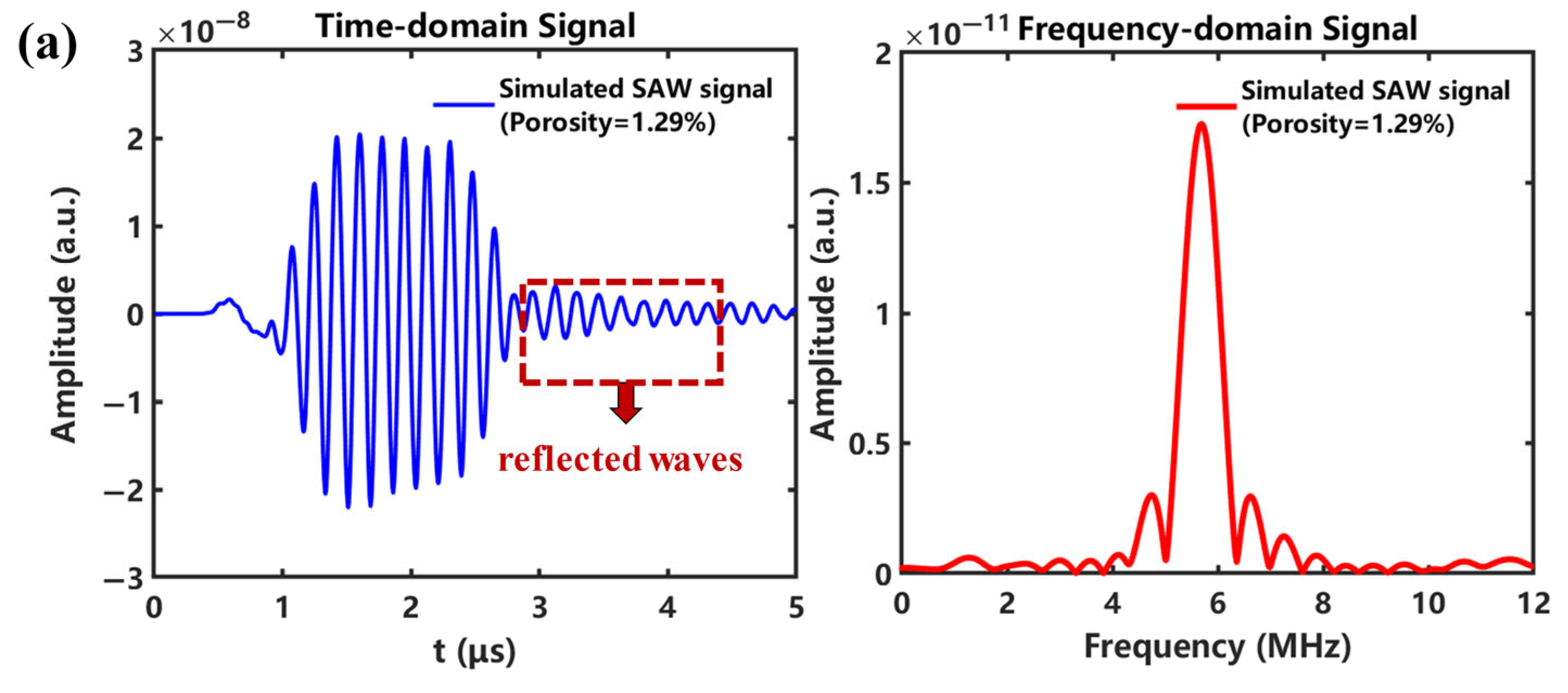
3.3. Simulation Results and Analysis
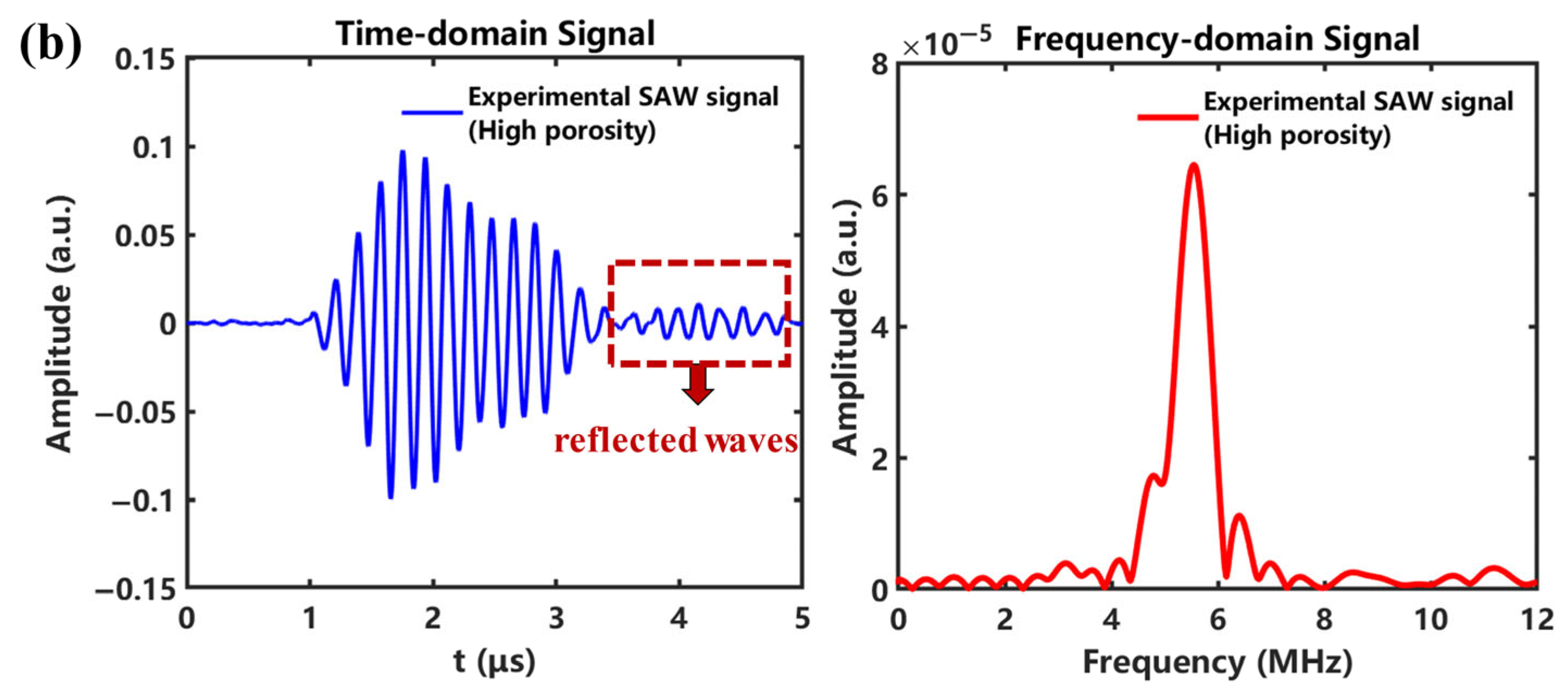
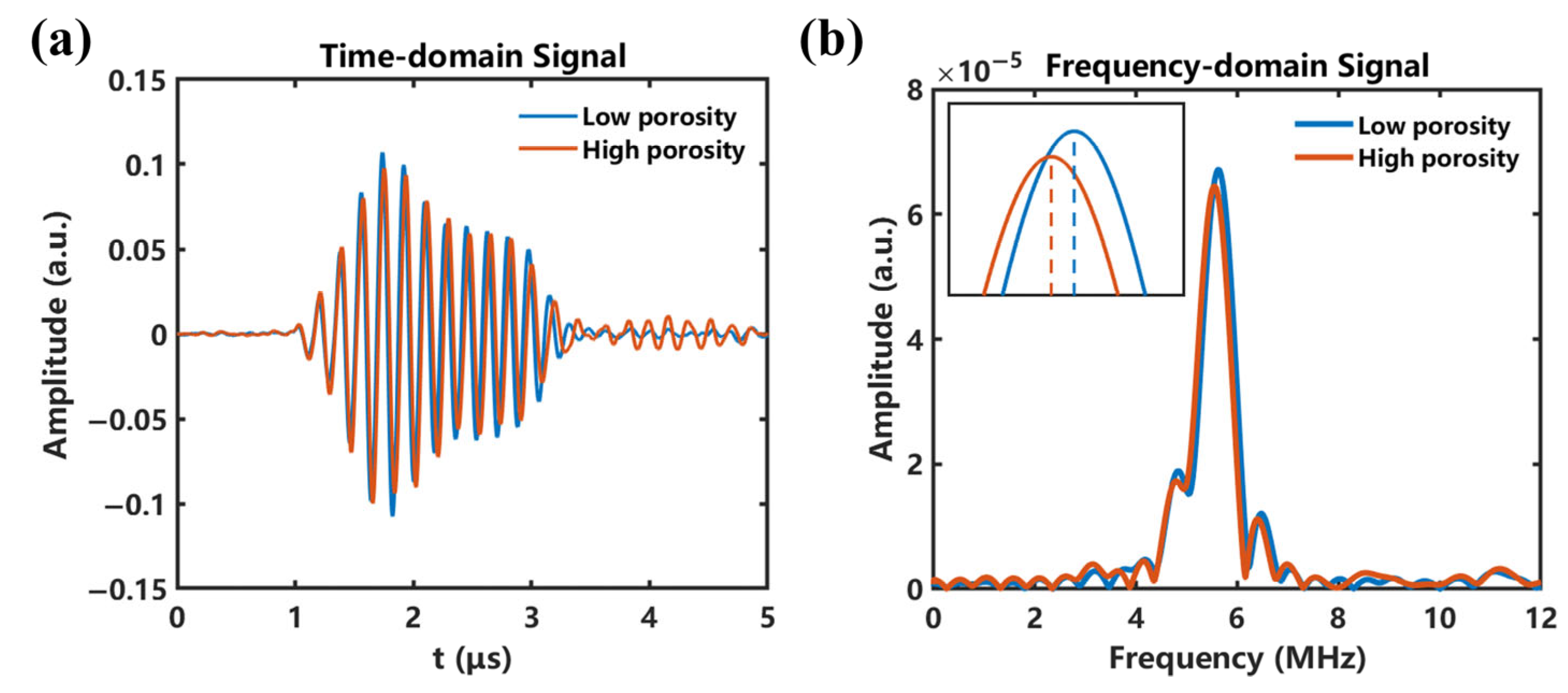
3.4. Experiment Validation
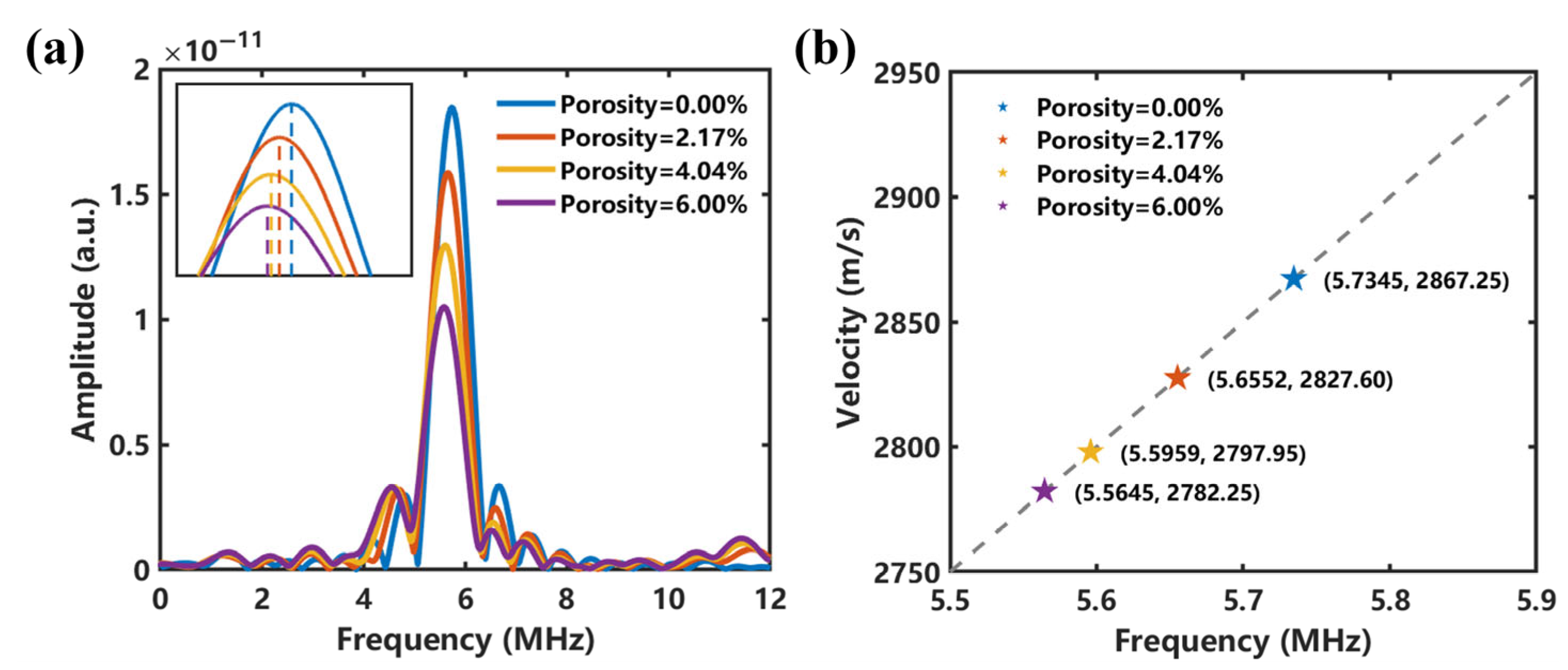
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khajavi, S.H.; Deng, G.; Holmström, J.; Puukko, P.; Partanen, J. Selective laser melting raw material commoditization: Impact on comparative competitiveness of additive manufacturing. Int. J. Prod. Res. 2018, 56, 4874–4896. [Google Scholar] [CrossRef]
- Wu, B.; Pan, Z.; Ding, D.; Cuiuri, D.; Li, H.; Xu, J.; Norrish, J. A review of the wire arc additive manufacturing of metals: Properties, defects and quality improvement. J. Manuf. Process. 2018, 35, 127–139. [Google Scholar] [CrossRef]
- Hauser, T.; Reisch, R.T.; Breese, P.P.; Lutz, B.S.; Pantano, M.; Nalam, Y.; Bela, K.; Kamps, T.; Volpp, J.; Kaplan, A.F. Porosity in wire arc additive manufacturing of aluminium alloys. Addit. Manuf. 2021, 41, 101993. [Google Scholar] [CrossRef]
- Ramírez, I.S.; Márquez, F.P.G.; Papaelias, M. Review on additive manufacturing and non-destructive testing. J. Manuf. Syst. 2023, 66, 260–286. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Z.; Li, Y. Application of ultrasonic array method for the inspection of TC18 addictive manufacturing titanium alloy. Sensors 2019, 19, 4371. [Google Scholar] [CrossRef]
- Kim, C.; Yin, H.; Shmatok, A.; Prorok, B.C.; Lou, X.; Matlack, K.H. Ultrasonic nondestructive evaluation of laser powder bed fusion 316L stainless steel. Addit. Manuf. 2021, 38, 101800. [Google Scholar] [CrossRef]
- Sun, X.; Huang, L.; Xiao, B.; Zhang, Q.; Li, J.; Ding, Y.; Fang, Q.; He, W.; Xie, H. X-ray computed tomography in metal additive manufacturing: A review on prevention, diagnostic, and prediction of failure. Thin-Walled Struct. 2024, 207, 112736. [Google Scholar] [CrossRef]
- Rahman, O.; Rakhmonov, J.; Bahl, S.; Frederick, C.; Shyam, A.; Dehoff, R.; Plotkowski, A.; Ziabari, A. Dual X-ray computed tomography-aided classification of melt pool boundaries and flaws in crept additively manufactured parts. Mater. Charact. 2024, 217, 114317. [Google Scholar] [CrossRef]
- Sun, W.; Kasa, T.; Hatsukade, Y.; Yonehara, M.; Ikeshoji, T.; Kyogoku, H. Quality assessment of SUS316L fabricated by metal additive manufacturing with eddy current inspection. NDT E Int. 2023, 138, 102901. [Google Scholar] [CrossRef]
- Zimermann, R.; Mohseni, E.; Foster, E.A.; Vasilev, M.; Loukas, C.; Vithanage, R.K.; Macleod, C.N.; Lines, D.; Silva, M.P.E.E.; Fitzpatrick, S. In-process non-destructive evaluation of metal additive manufactured components at build using ultrasound and eddy-current approaches. J. Manuf. Process. 2023, 107, 549–558. [Google Scholar] [CrossRef]
- Caiazzo, F.; Cardaropoli, F.; Alfieri, V.; Sergi, V.; Cuccaro, L. Experimental analysis of selective laser melting process for Ti-6Al-4V turbine blade manufacturing. In Proceedings of the XIX International Symposium on High-Power Laser Systems and Applications 2012, Istanbul, Turkey, 10–14 September 2012; pp. 381–390. [Google Scholar]
- Strantza, M.; Aggelis, D.G.; De Baere, D.; Guillaume, P.; Van Hemelrijck, D. Evaluation of SHM system produced by additive manufacturing via acoustic emission and other NDT methods. Sensors 2015, 15, 26709–26725. [Google Scholar] [CrossRef]
- Lu, Q.Y.; Wong, C.H. Applications of non-destructive testing techniques for post-process control of additively manufactured parts. Virtual Phys. Prototyp. 2017, 12, 301–321. [Google Scholar] [CrossRef]
- Mandache, C. Overview of non-destructive evaluation techniques for metal-based additive manufacturing. Mater. Sci. Technol. 2019, 35, 1007–1015. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Xia, C.; Pan, Z.; Polden, J.; Li, H.; Xu, Y.; Chen, S.; Zhang, Y. A review on wire arc additive manufacturing: Monitoring, control and a framework of automated system. J. Manuf. Syst. 2020, 57, 31–45. [Google Scholar] [CrossRef]
- Jeon, I.; Yang, L.; Ryu, K.; Sohn, H. Online melt pool depth estimation during directed energy deposition using coaxial infrared camera, laser line scanner, and artificial neural network. Addit. Manuf. 2021, 47, 102295. [Google Scholar] [CrossRef]
- Ma, H.; Mao, Z.; Feng, W.; Yang, Y.; Hao, C.; Zhou, J.; Liu, S.; Xie, H.; Guo, G.; Liu, Z. Online in-situ monitoring of melt pool characteristic based on a single high-speed camera in laser powder bed fusion process. Appl. Therm. Eng. 2022, 211, 118515. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Y.; Bai, Q. Defect formation mechanisms in selective laser melting: A review. Chin. J. Mech. Eng. 2017, 30, 515–527. [Google Scholar] [CrossRef]
- Cerniglia, D.; Montinaro, N. Defect detection in additively manufactured components: Laser ultrasound and laser thermography comparison. Procedia Struct. Integr. 2018, 8, 154–162. [Google Scholar] [CrossRef]
- Cai, Y.; Xiong, J.; Chen, H.; Zhang, G. A review of in-situ monitoring and process control system in metal-based laser additive manufacturing. J. Manuf. Syst. 2023, 70, 309–326. [Google Scholar] [CrossRef]
- Pieris, D.; Stratoudaki, T.; Javadi, Y.; Lukacs, P.; Catchpole-Smith, S.; Wilcox, P.D.; Clare, A.; Clark, M. Laser Induced Phased Arrays (LIPA) to detect nested features in additively manufactured components. Mater. Des. 2020, 187, 108412. [Google Scholar] [CrossRef]
- Honarvar, F.; Varvani-Farahani, A. A review of ultrasonic testing applications in additive manufacturing: Defect evaluation, material characterization, and process control. Ultrasonics 2020, 108, 106227. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhao, X.; Yang, B.; Li, J.; Liu, Y.; Ma, G.; Yuan, S.; Wu, J. Nondestructive evaluation of porosity in additive manufacturing by laser ultrasonic surface wave. Measurement 2022, 193, 110944. [Google Scholar] [CrossRef]
- Lv, G.; Yao, Z.; Chen, D.; Li, Y.; Cao, H.; Yin, A.; Liu, Y.; Guo, S. Fast and high-resolution laser-ultrasonic imaging for visualizing subsurface defects in additive manufacturing components. Mater. Des. 2023, 225, 111454. [Google Scholar] [CrossRef]
- Stratoudaki, T.; Javadi, Y.; Kerr, W.; Wilcox, P.D.; Pieris, D.; Clark, M. Laser induced phased arrays for remote ultrasonic imaging of additive manufactured components. In Proceedings of the 57th Annual Conference of the British Institute of Non-Destructive Testing, NDT 2018, Nottingham, UK, 10–12 September 2018; pp. 174–182. [Google Scholar]
- Davis, G.; Nagarajah, R.; Palanisamy, S.; Rashid, R.A.R.; Rajagopal, P.; Balasubramaniam, K. Laser ultrasonic inspection of additive manufactured components. Int. J. Adv. Manuf. Technol. 2019, 102, 2571–2579. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, D.; Li, H.; Song, C.; Zhou, X.; Shen, S.; Zhang, G.; Yang, Y.; Wang, H. Detection of internal holes in additive manufactured Ti-6Al-4V part using laser ultrasonic testing. Appl. Sci. 2020, 10, 365. [Google Scholar] [CrossRef]
- Qian, C.; Chen, Y.; Pei, C.; Chen, Z. Remote measurement of material elastic property at elevated temperature with grating laser ultrasonic testing. Nondestruct. Test. Eval. 2024, 39, 2316–2329. [Google Scholar] [CrossRef]
- Dai, T.; Jia, X.; Zhang, J.; Wu, J.; Sun, Y.; Yuan, S.; Ma, G.; Xiong, X.; Ding, H. Laser ultrasonic testing for near-surface defects inspection of 316L stainless steel fabricated by laser powder bed fusion. China Foundry 2021, 18, 360–368. [Google Scholar] [CrossRef]
- Qian, C.; Kou, X.; Pei, C.; Chen, Z. Topcoat thickness measurement of thermal barrier coating using grating laser acoustic spectrum method. Ceram. Int. 2022, 48, 3676–3684. [Google Scholar] [CrossRef]
- Li, W.; Dryburgh, P.; Pieris, D.; Patel, R.; Clark, M.; Smith, R.J. Imaging microstructure on optically rough surfaces using spatially resolved acoustic spectroscopy. Appl. Sci. 2023, 13, 3424. [Google Scholar] [CrossRef]
- Pieris, D.; Patel, R.; Dryburgh, P.; Hirsch, M.; Li, W.; Sharples, S.; Smith, R.; Clare, A.; Clark, M. Spatially resolved acoustic spectroscopy towards online inspection of additive manufacturing. Insight Non Destr. Test. Cond. Monit. 2019, 61, 132–137. [Google Scholar] [CrossRef]
- Cao-Rial, M.T.; Moreno, C.; Quintela, P. Determination of Young modulus by using Rayleigh waves. Appl. Math. Model. 2020, 77, 439–455. [Google Scholar] [CrossRef]
- Ternero, F.; Rosa, L.G.; Urban, P.; Montes, J.M.; Cuevas, F.G. Influence of the total porosity on the properties of sintered materials—A review. Metals 2021, 11, 730. [Google Scholar] [CrossRef]
- Kim, F.H.; Kim, F.H.; Moylan, S.P. Literature Review of Metal Additive Manufacturing Defects; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Wang, Y.; Chen, J.; Wu, X.; Chen, M.; Su, H.; Wang, L.; Wu, C. Investigation on high-deposition-rate directed energy deposition of Al-5% Mg alloy via external compound magnetic fields. Addit. Manuf. 2023, 61, 103299. [Google Scholar] [CrossRef]



| Density (kg·m−3) | Specific Heat (J·kg−1·K−1) | Thermal Conductivity (W·m−1·K−1) | Thermal Expansion (K−1) | Elastic Modulus (Pa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| 4.35 × 103 | 540 | 7.0 | 8.8 × 10−5 | 1.1 × 1011 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, Y.; Yang, J.; Guo, Q.; Gan, Z.; Pei, C. Study of Online Testing of Void Defects in AM Components with Grating Laser Ultrasonic Spectrum Method. Appl. Sci. 2025, 15, 7995. https://doi.org/10.3390/app15147995
Li H, Liu Y, Yang J, Guo Q, Gan Z, Pei C. Study of Online Testing of Void Defects in AM Components with Grating Laser Ultrasonic Spectrum Method. Applied Sciences. 2025; 15(14):7995. https://doi.org/10.3390/app15147995
Chicago/Turabian StyleLi, Hengtao, Yan Liu, Jinfeng Yang, Qinghua Guo, Zhichao Gan, and Cuixiang Pei. 2025. "Study of Online Testing of Void Defects in AM Components with Grating Laser Ultrasonic Spectrum Method" Applied Sciences 15, no. 14: 7995. https://doi.org/10.3390/app15147995
APA StyleLi, H., Liu, Y., Yang, J., Guo, Q., Gan, Z., & Pei, C. (2025). Study of Online Testing of Void Defects in AM Components with Grating Laser Ultrasonic Spectrum Method. Applied Sciences, 15(14), 7995. https://doi.org/10.3390/app15147995







