Abstract
The purpose of this research was to indicate the importance of an efficient design of steel frame structures, taking into account the fire design situation. In the case of steel frame structures, the typical mechanisms of failure (sway, beam, and mixed) are well known. Using this knowledge, combined with a reliability assessment of single nodes, may let designers reduce both the amount of material used for a structure and the total cost of the structure. In this article, one-story, single-nave frames with different loads were analyzed. Two types of loads were analyzed: symmetrical and unsymmetrical. Both cases resulted in different failure paths. The static analysis of the structure in the following minutes of the fire duration was carried out in the Robot Structural Analysis programme. The temperature load was computed according to the Eurocode recommendation with the assumption that the temperature of fire gases is described by the standard fire curve. Afterward, the system reliability analysis for the selected failure paths was conducted. Additionally, the displacement analysis was performed in the following minutes of the fire. The biggest challenge in the proposed method is that there are many potential failure paths, and checking all of them is very time-consuming, even when using advanced computers. Therefore, only selected collapse modes were analyzed.
1. Introduction
The present article is focused on the optimal design of a plane steel frame structure in a fire design situation with the use of system reliability analysis. Previous research [1,2] has proven that system reliability analysis may be a valuable tool that allows anyone to design truss structures in a more effective way. However, the structural behavior in terms of reliability may be completely different for structures with pinned and rigid connections [3]. Therefore, the reliability analysis of the frame structures under fire influence has to be conducted separately.
The analysis, including reliability methods, enables us to design a safety structure with less material compared to the traditional method based on partial safety factors. Therefore, it appears that similar groups of methods can be used to reduce the mass and final cost of frame steel structures. The present research initially characterizes the issue as the considered problem is complex and has many limitations, which will be described in the following sections. To make this and further research easier to compare with other results, the analyzed structure was inspired by publications [4,5].
The design of a structure in a deterministic way for fire conditions is well established not only by normative documents [6,7] but also in handbooks [8,9]. The present article combines a static analysis of a steel frame during fire with a reliability analysis. The basics of the reliability theory are well known; the real flowering of this field of science appeared after introduction of the Hasofer–Lind index [10], which, to this day, is the most popular measure of the safety of a structure. In the following years, many “classical” publications were published [11,12,13,14].
The present research focuses on the analysis of system reliability. For the analyzed frame structures, three typical mechanisms of failure (collapse modes) are known: sway (outward), beam (inward), and combined (Figure 1).
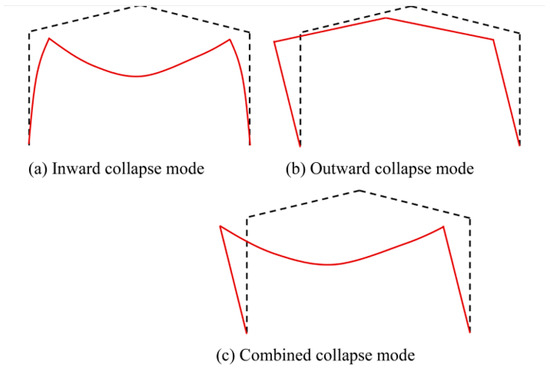
Figure 1.
The typical collapse modes for frame structures [4].
Fire analysis of a frame structure is not an easy task, as the fire process is very unpredictable, and even small details in construction may determine the structural response. Therefore, the best way to design the structure is to perform a parallel numerical and experimental analysis. A very interesting publication that analyzes a one-story single-nave steel frame was presented in [4]. The partial results of this analysis, i.e., the inward collapse mode, are presented in Figure 2.

Figure 2.
Inward collapse mode—experimental research [4].
Another detailed analysis of the structural behavior of a steel frame under fire influence was described in [5]. The structures analyzed in this article were inspired by the last two mentioned publications. The details will be described in the following part of this article, although the presented analyses will be developed upon in the future, so the author would like to compare some results. Therefore, it should be underlined that the simplifications made in the present research may have a significant influence on the results. This subject in the context of steel frames was thoroughly analyzed by the authors of [15]. Nevertheless, at the present stage of research, simplified assumptions are essential to narrow down the analyzed tasks and obtain some initial results.
Reliability methods in the last years have been applied more and more willingly in engineering analyses, and also in civil engineering problems [16,17]. Furthermore, a reliability analysis enables the optimization of the structure, not only in the persistent design situation [18] but also under fire influence [19]. As the reliability analysis may be quite a complex task, dedicated software is still being developed not only in Poland [20] but also abroad [21].
The reliability analysis of a steel frame system has been the subject of two publications [22,23]. The use of this method for the structure under fire load is also discussed in [24,25]. Fire safety nowadays is such an established subject that the newest scientific research willingly focuses on it. In [26], the authors conducted a deep coupled CFD-FEA (computational fluid dynamics–finite element method) analysis for the ductile failure analysis of a steel structure, and the efficiency of the proposed method was verified through two practical studies (a frame and transmission tower).
This topic is also important in the context of structures and human safety. There are numerous publications that focus on assessing the collapse time of structures under fire load, which is important information about the structural safety from the users’ point of view. An interesting analysis of a steel portal frame is presented in [27], where analytical research was compared with an experiment. One of the most modern approaches to conducting research connected with structural safety under fire employs machine learning algorithms, including neural networks [28,29]. The subject is so wide and so willingly analyzed by scientists that it is impossible to mention all the scientific publications. Many of the abovementioned articles focus on a few-story frame structures, which is, in fact, the most important case from the practical point of view. In the presented article, the analyzed structure has a simplified geometry to enable the deep mechanical-fire-reliability analysis. It should be underlined that the presented analysis has initial character and the research will be further developed in the further author’s scientific work. In the current analysis, only a few collapse modes were taken into account. The most typical of them for the frame structure were taken into account. This choice is supported by both theoretical and experimental research [4,26,28].
2. Materials and Methods
The presented method combines fire and reliability analysis of a plane steel frame. As the task is very complex, some reductive assumptions had to be made. They are as follows:
- The temperature of fire gases is uniformly distributed and computed according to standard fire curve.
- The temperature of steel elements is uniformly distributed in all directions and is computed according to the Eurocode.
- The structure will become unreliable because of the formation of plastic hinges, before exceeding bearing capacity in any rod.
- Randomness is not taken into account during temperature computation.
- The geometric and mechanical characteristics are assumed to be random values with a normal distribution.
- Random variables are assumed to be not correlated.
- Changes in the rigidity of the nodes under temperature are neglected.
The assumptions presented above are very strong, and in the obvious way introduce some discrepancy between obtained theoretical results and realistic situation. Nevertheless, they are essential to narrow down the task, find out some fundamental dependencies, and identify potential problems that may occur during system reliability analysis of frame structures under fire influence. Modeling the temperature of fire gases is a separate, extensive field of science; this is why it was computed according to Eurocode, without probabilistic description. This article focuses on the structural response of the frame, not on fire modeling. Because of the formulation of the research, where bearing capacity and effect of action are values used for the reliability index assessment, the choice of random variables seems to be quite natural. The last two assumptions (uncorrelated variables and neglecting the changes in the nodes’ rigidity) may generate the biggest doubts. They are introduced to focus directly on the system reliability method. In further research, the author will resign from them and compare the results with those obtained currently.
In this paper, two types of plane, one-story single-nave steel frames, are analyzed (Figure 3). They are assumed to have the same dimensions and fire insulation, but different loads and steel profiles of the top chord, which is essential due to another concentrated load in this area.
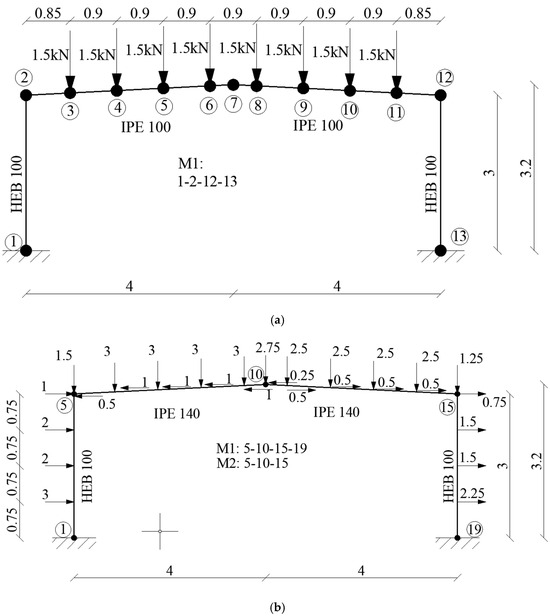
Figure 3.
Steel frames analyzed: (a) frame A, (b) frame B.
The calculations were made in three steps. First, the temperature of the fire gases and the single elements was calculated according to Eurocode [6]. The temperature of fire gases was assumed to be uniformly distributed according to the standard fire curve, and the fire insulation was assumed to have the following characteristics: , , . Then, static analysis in following minutes of fire duration was conducted in the Robot Structural Analysis program. Self-weight, temperature load, and concentrated forces (according to Figure 3) were taken into account. In the schemes (Figure 3), the analyzed mechanism are presented (M1, M2), but they will be described later in this article. Finally, the principal part of the research-system reliability analysis was carried out. The set of random variables is presented in Table 1, and their characteristics were assumed according to [30]. All other variables were treated as deterministic. Additionally, the displacement analysis was conducted in the following minutes of the fire duration.

Table 1.
Random variables.
In the presented research, the failure of the whole frame was analyzed as the result of creating plastic hinges in the most stressed nodes, which finally leads to transforming the structure into mechanisms. To realize this task, it is essential to know the bending moment resistance () for individual cross-sections. In a fire design situation, this value can be computed according to the following formula [6]:
where —effective yield strength; —bending moment resistance in persistent design situation [31] according to Equation (2).
In Equation (1), the partial safety factor is intentionally uncredited, because the further computation takes into account randomness.
where —yield strength of steel; —plastic section modulus of cross-section according to the y (horizontal) axis.
Formulation of the probabilistic model makes it necessary to approximate the coefficient of variation for the bending moment resistance. According to Ref. [32], this value can be computed as follows:
The first step of reliability analysis is the assessment of the reliability of a single node. This value in the following minutes of fire duration was computed according to the formulas presented below. It should be noted that at nodes when different profiles were connected (the corners), the characteristics of the “weaker” element were taken into account. The computation of reliability for the single i-th element was computed according to the following equations:
- Coefficient of variation for effect of action and bearing capacity:
- Safety margin (SMi):
- Coefficient of variation for safety margin:
- Reliability index of a single element (βi):
- Probability of failure for a single element (pfi):
where is the inverse cumulative standard normal distribution.
- Reliability of element (Ri):
Knowing the reliability of a single element (node) makes it possible to assess the reliability of the whole structure. The mechanisms connected with frame structures have parallel character, which means that all the elements in one set have to become unreliable to result in the failure of the whole structure. Therefore, the reliability for a single mechanism (failure path) is computed according to the following formula [1]:
where —reliability of the structure for the n-th failure path (parallel system); —reliability of single node according to Equations (4)–(10); i—number of nodes that create the analyzed failure path.
All analyzed mechanisms are connected with each other in a series way; therefore, final reliability for the structure with analyzed mechanism is computed as follows:
where k—the total number of analyzed mechanisms.
3. Results
Both frames (A and B) were analyzed similarly. There were computed reduction factors for yield strength and Young’s modulus [6], a decrease in bending resistance, and changes in effect of action in characteristic nodes of frames. These values enabled the author to assess the safety of structures according to the system reliability analysis, taking into account the previously defined most characteristic failure paths (M1 and M2). After that, displacement analysis with fire development was also conducted.
3.1. Frame A
The temperature increase in the following minutes of fire duration and related reduction factors for yield strength and Young’s modulus [6] for frame A are presented in Table 2 and Table 3. These show the values of effect of action and bending moment resistance in following minutes of fire duration. In the table, only the values for the most stressed elements (nodes) are presented. The number of nodes is consistent with that presented in Figure 3. The analysis was carried out with timesteps of 5 min.

Table 2.
Temperature analysis of elements of frame A.

Table 3.
Resistance to bending moment and effect of action for single nodes in the following minutes of fire duration for frame A.
For frame A in the 45th minute of the fire duration, the bending moment resistance was exceeded; therefore, the previous step was analyzed. The most stressed elements were nodes no. 2 and 12 (corners of the frame). After introducing their hinges, the moment distribution in the 40th minute of fire would look similar to that shown in Figure 4a. It is easy to notice (see Table 3) that in this case, the bearing capacity in the ridgepole area was exceeded, which decided the failure of the structure. Nevertheless, before introducing hinges, the moment distribution looked like that shown in Figure 4b. The highest values of the bending moments occurred in the columns’ bases and in the corners. Therefore, in the reliability computation, two mechanisms that combined these nodes (M1, M2—Figure 3a) were analyzed. Of course, in the case of frame structures there is an unlimited number of failure paths, because plastic hinges may be created in any point of frame. But it is generally known and checked by the experiment mentioned in the Introduction that the most typical are sway and beam mechanisms. Therefore, those mechanisms were particularly chosen for further analysis.
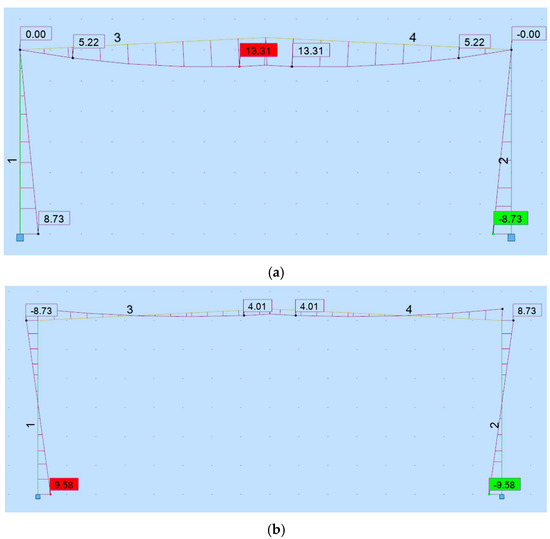
Figure 4.
Bending moments in frame A in the 40th minute of fire: (a) after introducing plastic hinges; (b) without plastic hinges.
According to the method presented in the previous chapter, at the beginning of the fire (0–15 min), the reliability of the structure (according to mechanism M1) was so high that it was mathematically impossible to compute the value of the reliability index. The reliability indices for the following minutes of fire duration are presented in Figure 5. Between the 35th and 40th minutes, a rapid decrease in the reliability index is observed (according to the M1 mechanism). This is the direct result of the ky reduction coefficient that influences the decrease in the bending moment resistance value. On the other hand, the analysis of the beam mechanism (M2) shows that the reliability increases slightly with the fire duration, which is the result of unburdening the bent. It is noteworthy that the combined mechanism (M1M2) computed according to Equation (12) gave the same results as the mechanism M2.
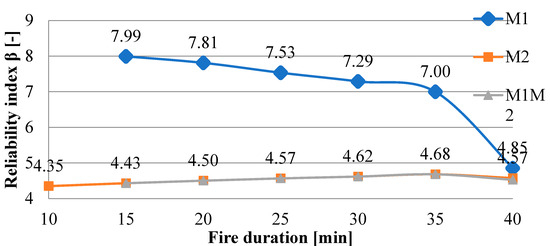
Figure 5.
Reliability indices for frame A in the following minutes of fire duration.
Simultaneously with the main part of the research, i.e., reliability analysis of the frame structure under fire, the analysis of displacement was conducted. The direction of the X-axis was assumed to be right and the Z-axis upward. The following graphs (Figure 6a,b) present the results obtained for the “A” frame. Figure 6a shows the classical effect of stretching of the frame. The deflection of corners according to the X-axis increases in the following minutes of fire duration, and the position of the ridgepole is invariable. Figure 6b shows the unburdening of the bent. As the structure is symmetrical, the displacement of nodes no. 2 and 12 (according to Figure 3a) towards the Z-axis has the same value. It is clearly visible that the temperature load causes the displacement opposite to that typical for the gravity load.
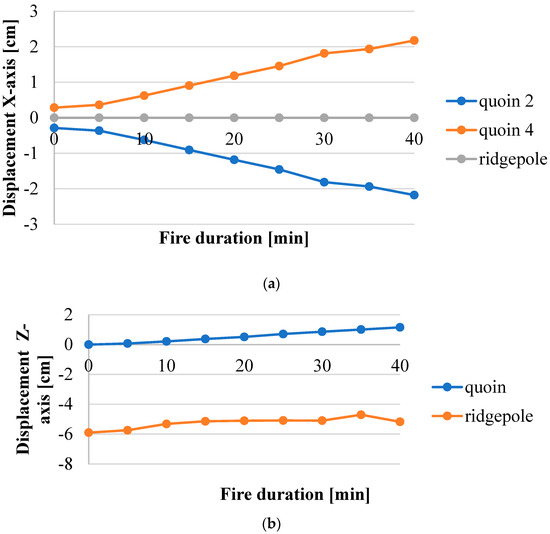
Figure 6.
The displacements of selected nodes of frame A in following minutes of fire duration: (a) in horizontal direction; (b) in vertical direction.
3.2. Frame B
The temperature increase in the following minutes of fire duration and related reduction factors for yield strength and Young’s modulus [6] for frame B are presented in Table 4 and Table 5. These show the values of effect of action and bending moment resistance in following minutes of fire duration. In the table, only the values for the most stressed elements (nodes) are presented. The number of nodes is consistent with that presented in Figure 3. The analysis was carried out with timesteps of 5 min.

Table 4.
Temperature analysis of elements of frame B.

Table 5.
Resistance to bending moment and effect of action for single nodes in the following minutes of fire duration for frame B.
In the case of frame B, because of the type of load, the beam mechanisms seems to be the least probable. Therefore, mixed (M1) and sway mechanisms were considered to be the most likely to occur.
Structural response analysis indicated that in the 30th minute of fire duration, the resistance of the bending moment in node no. 15 was exceeded. After introducing the hinge in this place, the bending moment distribution looked like that shown in Figure 7a. Similarly, as in the case of frame A, the reliability analysis was conducted until the previous timestep before the failure of the structure. In the 25th minute, the bending moment distribution looked like that shown in Figure 7b. For frame B, two types of mechanism were analyzed (Figure 3b). The results of analysis for mechanisms M1 and M2 and the combination of both of them are presented in Figure 8. It can be easily noticed that the M2 mechanism, which is typically the beam mechanism, gives lower values of the reliability index. Furthermore, the combination of this mechanism with mechanism M1 gives exactly the same values as in the case of individual analysis.
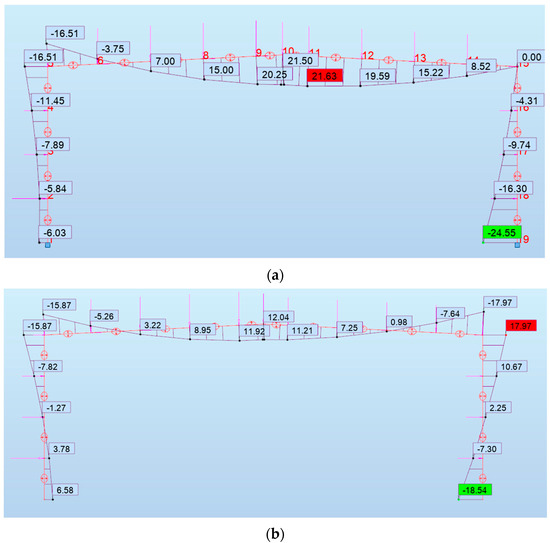
Figure 7.
Bending moments in frame B in the 25th minute of fire: (a) after introducing plastic hinges; (b) without plastic hinges.
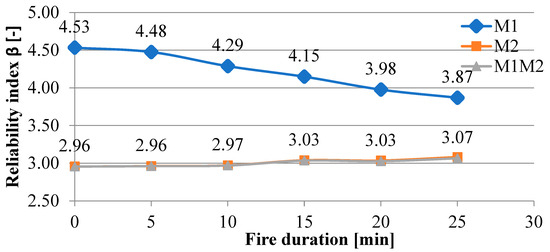
Figure 8.
Reliability indices for frame B in the following minutes of fire duration.
For frame B, displacement analysis was also performed. The results are presented in Figure 9. Analysis of the X-axis displacements shows symmetrical displacement of the nodes of corners and the invariable position of the central node no. 10. In the case of frame B, the load was not symmetrical; therefore, some initial displacement (in minute “0” of fire duration) is observed. The deflections according to the Z-axis are of a similar type to those in the case of A frame; the unburdening effect is observed.
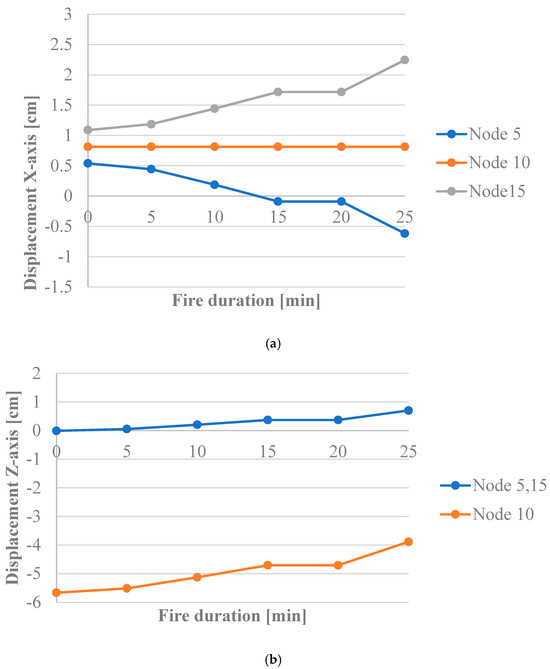
Figure 9.
The displacements of selected nodes of frame B in the following minutes of fire duration: (a) in the horizontal direction; (b) in the vertical direction.
4. Conclusions
System reliability analysis seems to be an appropriate tool to assess the reliability of the steel plane frame in a fire design situation. The behavior of the structure during fire was examined in detail, but the probabilistic model was quite simple, so only the most possible failure paths were considered. It is important to note that in the analyzed examples, only a few values were treated as random; a better assessment would be possible in the case of a more detailed probabilistic description. In such a case, the identification of the most probable failure path is difficult, or even impossible, to identify. Then, the task becomes more complex, so computational methods have to be applied. The more the failure paths are analyzed, the better the reliability assessment that could be obtained. Nevertheless, the possibilities of creating plastic hinges in frames are unlimited, so some strategies of failure path limitations have to be developed. Finally, it should be underlined that although in building structures some benefits of high redundancy are known, each case should be analyzed individually.
Although the presented analyses have initial character, some conclusions may be drawn. First of all, the system reliability analysis for the individual collapse mode can be conducted easily. In this article, the most typical failure modes for frame structures were analyzed. It is obvious that, in fact, possible failure paths are unlimited, but it seems (based on a review of the literature) that inward, outward, or mixed collapse modes are the most important to assess the reliability of the frame structure. This hypothesis will be checked in the author’s future work.
The analyzed portal frame is a very simple structure, but it is necessary to examine the basic structure in depth to continue research. Such an approach may help to identify the typical behavior and dependencies during the analysis of more complex structures, as they can be easily overlooked. During computation, the typical behavior of the steel frame was observed. Under temperature load, the girder elements elongated due to the additional forces that are typically generated under fire load. Also, these forces were the reason for the unburdening of the beam, which can be observed in Figure 6b and Figure 9b. Figure 6b indicates that this effect disappears between the 35th and 40th minutes, which is a direct result of the decrease in reduction factor for yield strength (see Table 4). The decrease in the reliability indices in following minutes of fire duration is the result of the increase in effect of action and the decrease in bearing capacity, and this is typical behavior that anyone can expect. Nevertheless, it is noteworthy that during temperature load (especially in statically indeterminate structures), force redistributions are observed. Each failure mode consists of a few elements; some of them may be temporarily unburdened, which can result in an increase in the reliability index in the following minutes of fire duration. Such a situation was observed for both the analyzed frames during inward collapse mode analysis (M2, Figure 5 and M2, Figure 8).
It is generally known that designers may benefit from the redundancy of the structure. This fact was also confirmed by the authors of [1,2] in the context of steel trusses; the unreliable element in the fire did not decide the failure of the whole structure, but a new static scheme was created. The currently conducted research did not enable us to find a similar dependency. On the contrary, for a portal frame, the creation of one plastic hinge leads directly to the failure of the whole structure.
The research presented confirms that the reliability analysis may be helpful during the design of frame structures for fire situations. This enables anyone to predict the possible activity of the structure during the temperature load. However, the whole analysis is complex and combines many aspects. Therefore, as the presented analysis is preliminary in nature, many limitations have been determined, and the author will gradually resist them in further research. The directions of future works are as follows:
- Reliability analysis including full interaction between bending and axial forces.
- Progressive resignation from reductive assumptions.
- Preparation of C++ computer code that enables parallel static, fire, and reliability analysis and allows the introduction of different sets of random variables.
- Steady development of the code, especially in the context of possible failure paths reduction.
- Similar research focusing on spatial frames.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Kubicka, K. The probabilistic model for system reliability analysis of a steel plane and spatial trusses. J. Theor. Appl. Mech. 2024, 62, 269–278. [Google Scholar] [CrossRef] [PubMed]
- Kubicka, K.; Sokol, M. Fire safety of plane steel truss according to system reliability analysis combined with FORM method: The probabilistic model and SYSREL computation. Appl. Sci. 2023, 13, 2647. [Google Scholar] [CrossRef]
- Kubicka, K.; Radoń, U.; Szaniec, W.; Pawlak, U. Comparative analysis of the reliability of steel structure with pinned and rigid nodes subjected to fire. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 022051. [Google Scholar] [CrossRef]
- Lou, G.-B.; Hou, J.; Qi, H.-H.; Jiang, Y.; Zhong, B.; Pang, Y.; Li, G.-Q. Experimental numerical and analytical analysis of a single-span steel portal frame exposed to fire. Eng. Struct. 2024, 302, 117417. [Google Scholar] [CrossRef]
- Tkaczyk, A. Ultimate Load-Bearing Capacity of Steel Frame Structures in Developed Fire-Kinematic Method Assessment. Ph.D. Dissertation, Cracow University of Technology, Kraków, Poland, 2017. (In Polish). [Google Scholar]
- EN 1993-1-2; Eurocode 3: Design of Steel Structures-Part 1-2: General Rules-Structural Fire Design. European Committee for Standardization (CEN): Brussels, Belgium, 1993.
- EN 1991-1-2; Eurocode 1: Actions on Structures-Part 1-2: General Actions—Actions on Structure Exposed to Fire. European Committee for Standardization (CEN): Brussels, Belgium, 1991.
- Kodur, V.; Naser, M. Structural Fire Engineering; McGraw Hill: Grand Rapids, MI, USA, 2020. [Google Scholar]
- Turkowski, P.; Sulik, P. Design of Steel Structures with Regard to Fire Conditions According to Eurocode; Instytut Techniki Budowlanej: Warszawa, Poland, 2015. (In Polish) [Google Scholar]
- Hasofer, A.; Lind, N.C. Exact and invariant second moment code format. J. Eng. Mech. Div. 1974, ASCE 100, 111–121. [Google Scholar] [CrossRef]
- Ditlevsen, O.; Madsen, H. Structural Reliability Methods; John Wiley & Sons Ltd.: Chichester, UK, 1996. [Google Scholar]
- Thoft-Christensen, P.; Baker, M. Structural Reliability Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Thoft-Christensen, P.; Murotsu, Y. Application of Structural Reliability Theory; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Fiessler, B.; Neumann, H.-J.; Rackwitz, R. Quadratic limit states in structural reliability. J. Eng. Mech. 1979, ASCE 105, 661–676. [Google Scholar] [CrossRef]
- Maślak, M.; Pazdanowski, M.; Suchodała, M.; Woźniczka, P. Fire resistance evaluation for a steel hall transverse frame depending on the simplification degree of the computational model applied. Arch. Civ. Eng. 2022, 68, 219–235. [Google Scholar] [CrossRef]
- Potrzeszcz-Sut, B.; Dudzik, A.; Radoń, U. Implicit neural state functions in hybrid reliability analysis of plane frame. Arch. Civ. Eng. 2023, 69, 55–71. [Google Scholar] [CrossRef]
- Radoń, U.; Zabojszcza, P. The aaplication of Sobol indices in structural reliability and sensivity analysis of models with uncertainty in practice engineering. Appl. Sci. 2025, 15, 342. [Google Scholar] [CrossRef]
- Zabojszcza, P.; Radoń, U. Optimization of steel roof framing taking into account the random nature of design parameters. Materials 2023, 15, 5017. [Google Scholar] [CrossRef] [PubMed]
- Akaa, O.; Abu, A.; Spearpoint, M.; Giovinazzi, S. Optimising design decision-making for steel structures in fire using a hybrid analysis technique. Fire Saf. J. 2017, 91, 532–541. [Google Scholar] [CrossRef]
- Available online: http://numpress.ippt.gov.pl/ (accessed on 8 July 2025).
- Available online: www.strurel.de (accessed on 8 July 2025).
- Zhang, H.; Shayan, S.; Rasmussen, K.J.R.; Ellingwood, B.R. System-based design of planar steel frames, I: Reliability framework. J. Constr. Steel Res. 2016, 123, 135–143. [Google Scholar] [CrossRef]
- Zhang, H.; Shayan, S.; Rasmussen, K.J.R.; Ellingwood, B.R. System-based design of planar steel frames, II: Reliability results and design recommendations. J. Constr. Steel Res. 2016, 123, 154–161. [Google Scholar] [CrossRef]
- Venkatachari, S.; Kodur, V.K.R. System level response of braced frame structures under fire exposure scenarios. J. Constr. Steel Res. 2020, 170, 106073. [Google Scholar] [CrossRef]
- Chen, W.; Ye, J. The most adverse fire scenario research of steel frame structure fire-resistant design based on structural vulnerability analysis. Structures 2021, 34, 2861–2875. [Google Scholar] [CrossRef]
- Shi, Z.; Feng, Y.; Egbelakin, T.; Yang, C.; Gao, W. Computational fluid dynamics-informed virtual safety assessment of steel-framed structure with fire-induced ductile failure. Reliab. Eng. Syst. Saf. 2025, 258, 110918. [Google Scholar] [CrossRef]
- Qi, H.-H.; Lou, G.-B.; Pang, Y.; Li, G.-Q. Early warning approach for fire-induced collapse of steel portal frame based on overall deformation. J. Build. Eng. 2025, 101, 111835. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.-Q.; Zhu, S. Graph recurrent neural networks-integrated real-time prediction of key displacements for fire-induced collapse early warning of steel frames. Appl. Soft Comput. 2024, 163, 111942. [Google Scholar] [CrossRef]
- Wei, X.; Liu, J.; Xu, L. Intelligent prediction method for the collapse time of steel frame structures under fire. J. Constr. Steel Res. 2024, 219, 108798. [Google Scholar] [CrossRef]
- Maślak, M. The Fire Durability of Steel Bar Structures; Politechnika Krakowska: Kraków, Poland, 2008. (In Polish) [Google Scholar]
- EN 1993-1-1; Eurocode 3: Design of Steel Structures-Part 1-1:General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 1993.
- Biegus, A. Probabiliastic Analysis of Steel Structures; PWN: Warszawa, Poland, 1999. (In Polish) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).