Time–Frequency-Domain Fusion Cross-Attention Fault Diagnosis Method Based on Dynamic Modeling of Bearing Rotor System
Abstract
1. Introduction
2. Relevant Theoretical Models
2.1. Bearing Dynamics Modeling
- (1)
- The outer ring is fastened to the bearing housing.
- (2)
- The inner ring rotates smoothly along with the shaft.
- (3)
- The elements are arranged at equal intervals on the raceway for pure rolling.
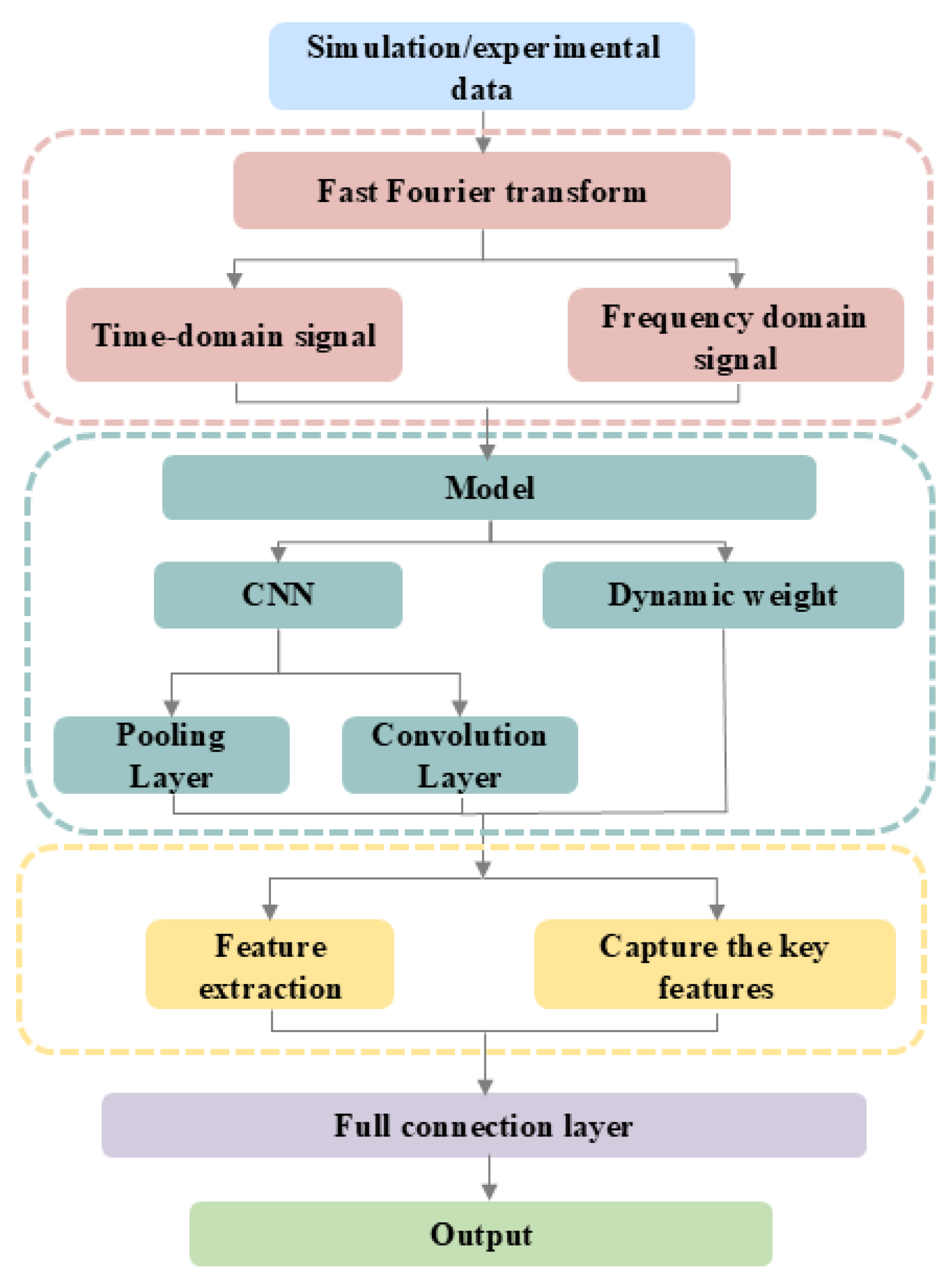
2.2. CNN + Transformer Network Architecture
2.3. Transformer Feature Fusion
2.3.1. Attention Mechanism
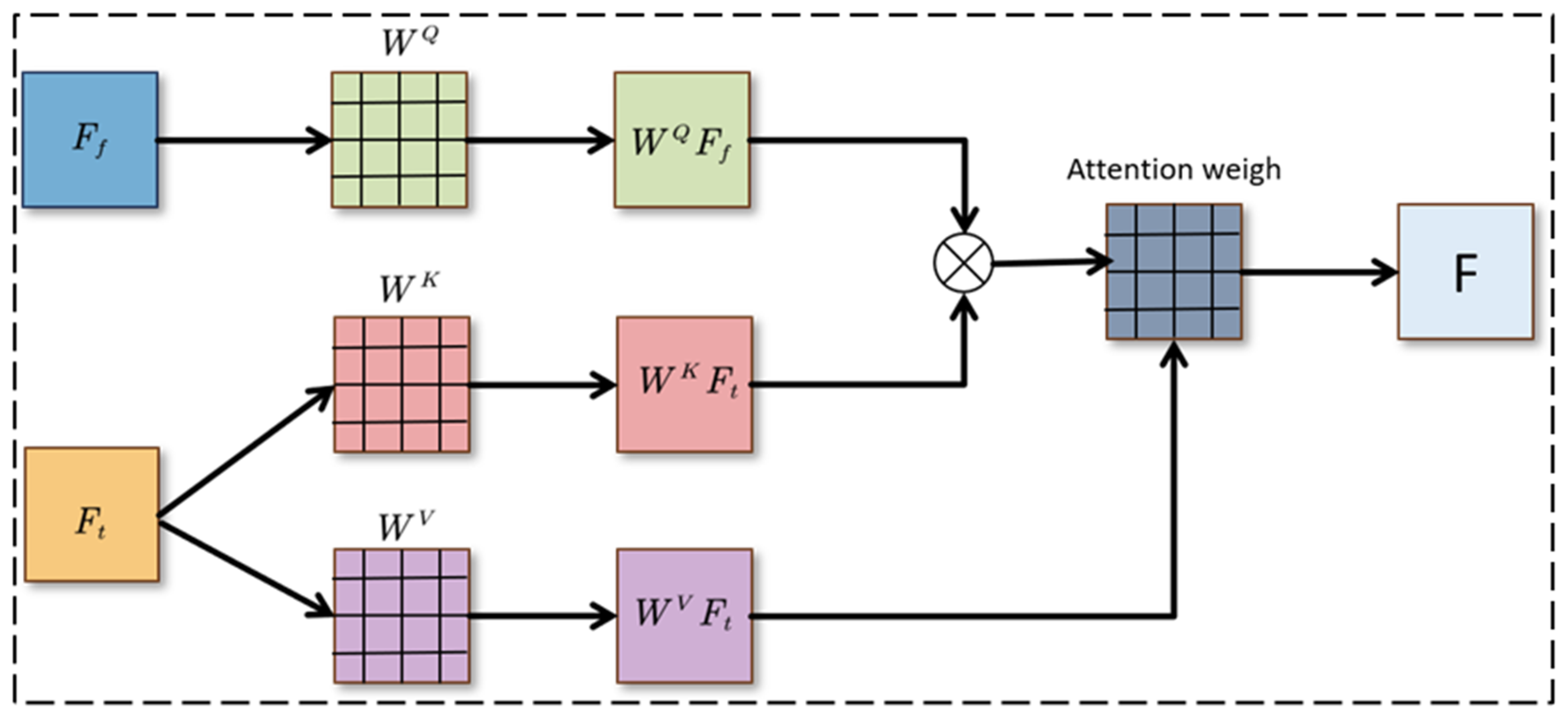
2.3.2. Cross-Attention Mechanism
2.3.3. Domain Adaptive Classifier
3. Dynamics Simulation and Experimental Verification
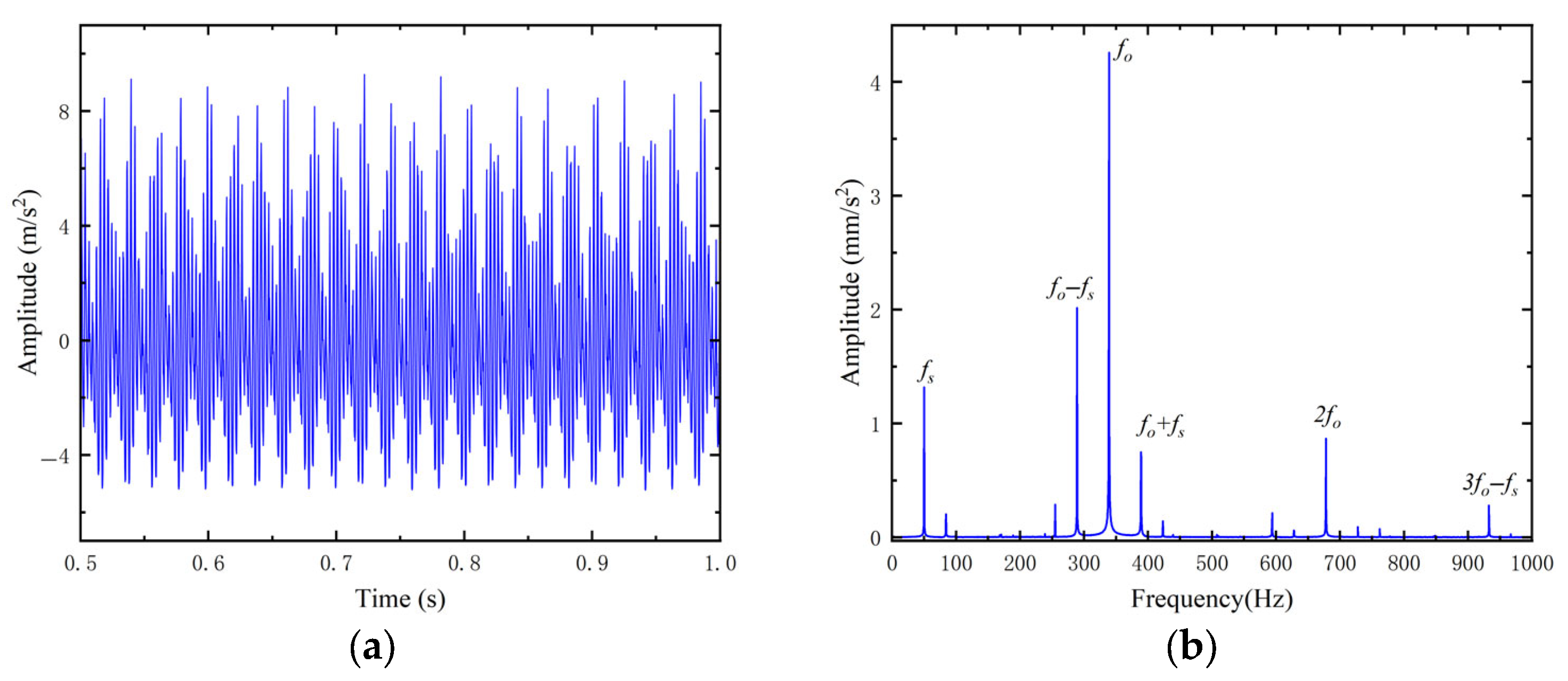
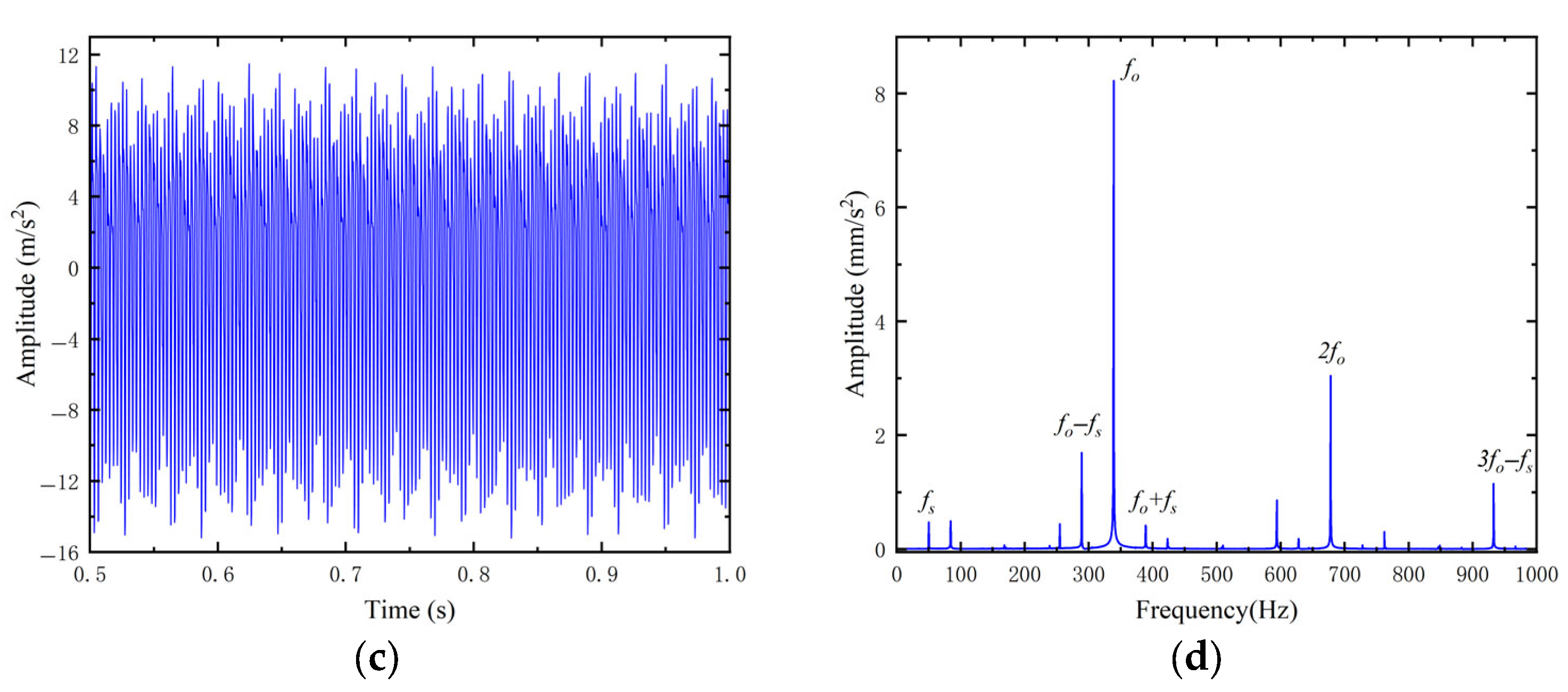
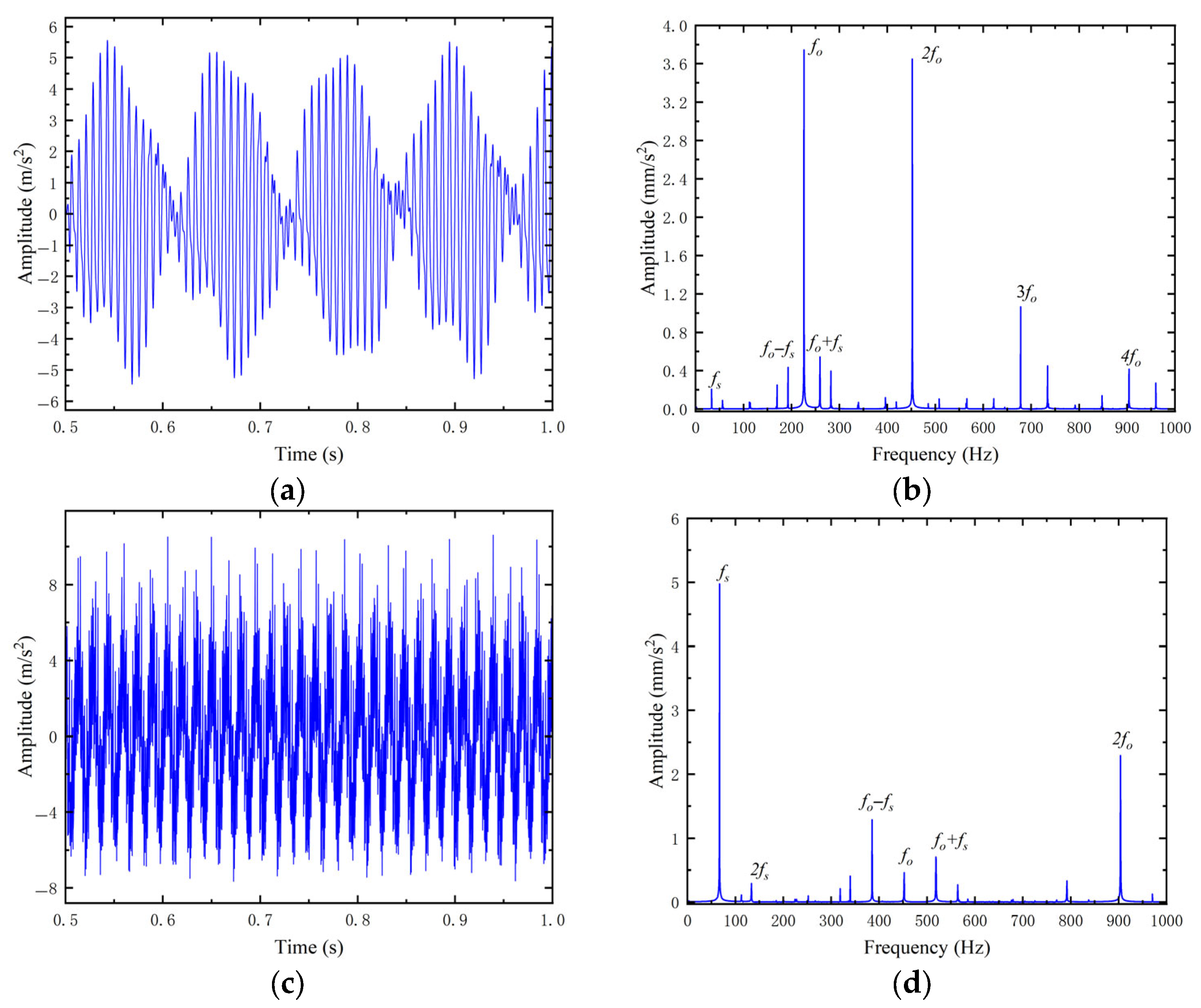
3.1. Dynamics Simulation Analysis
3.2. Experiment Setup
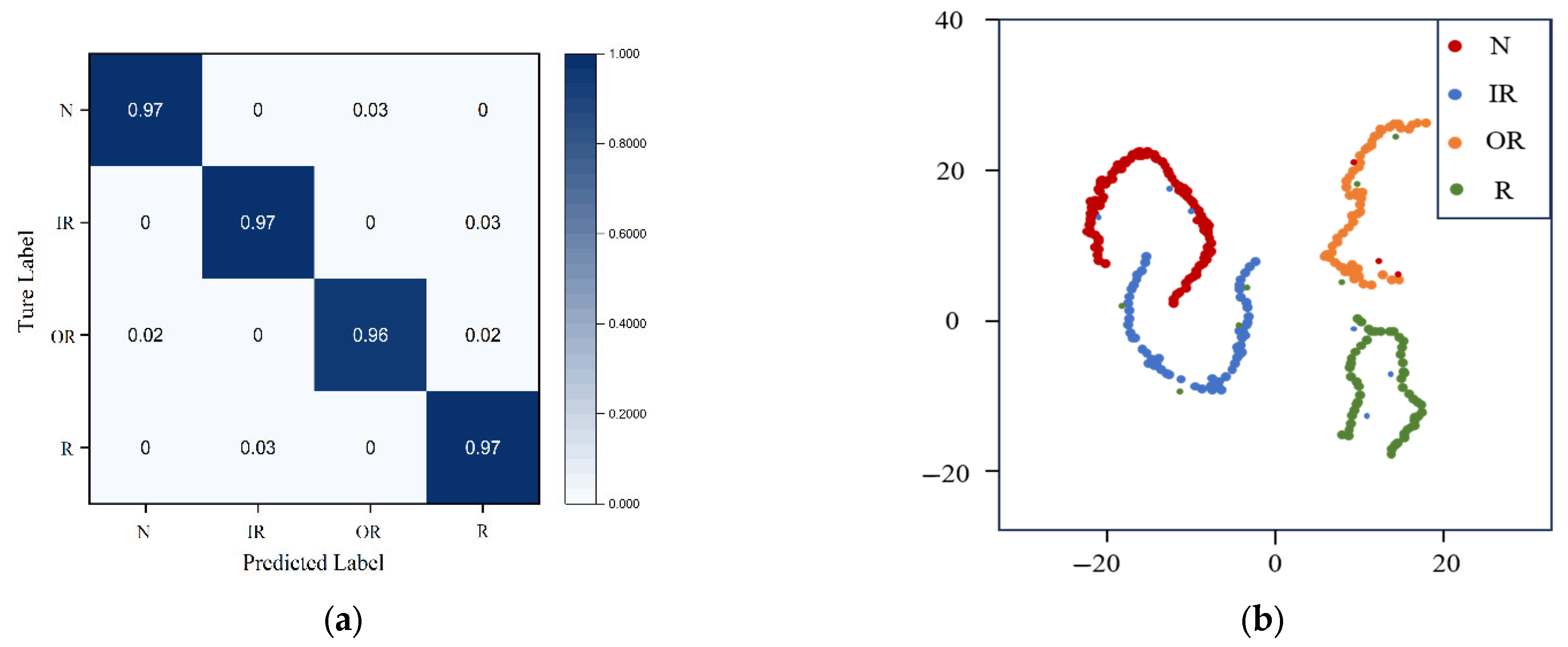
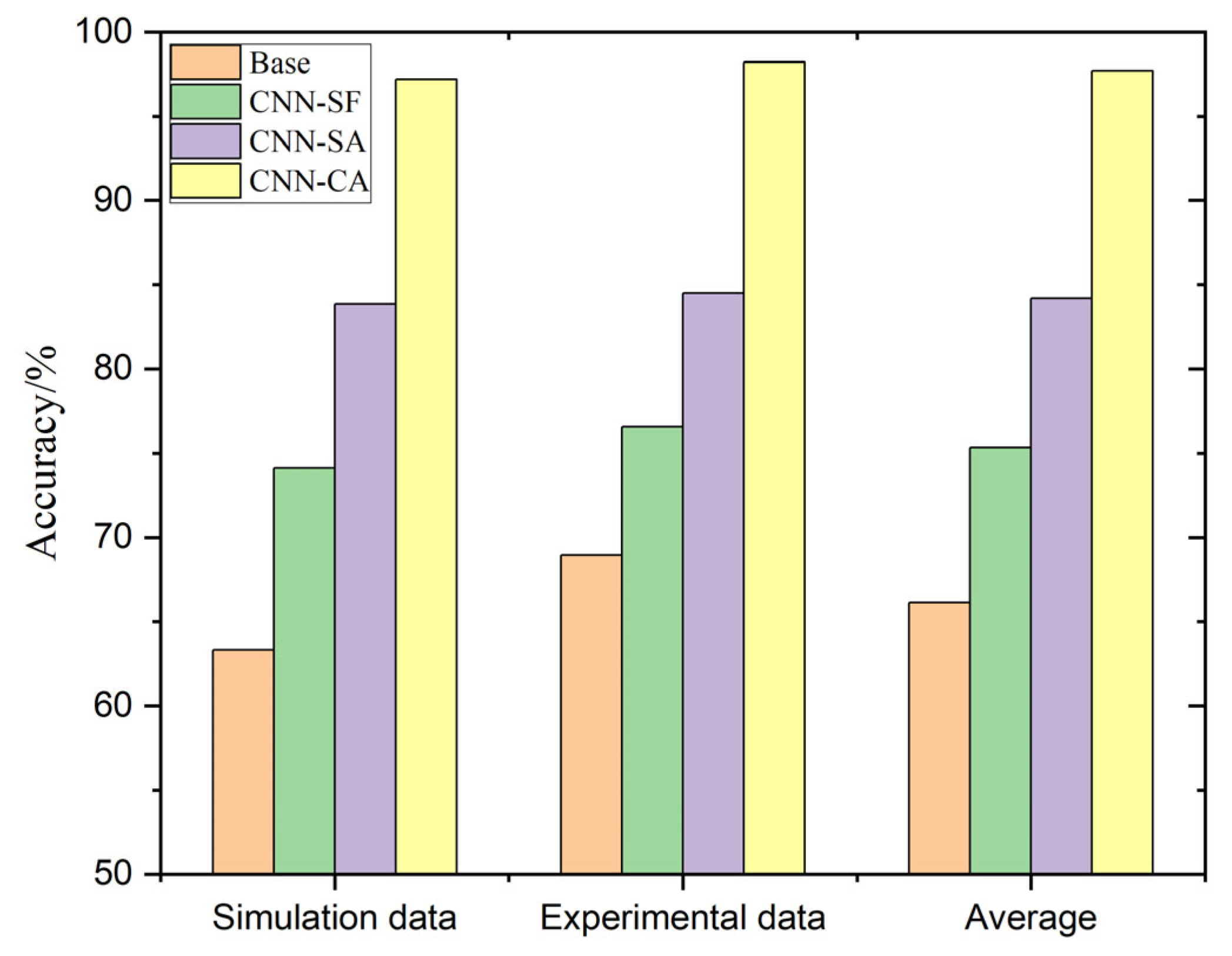
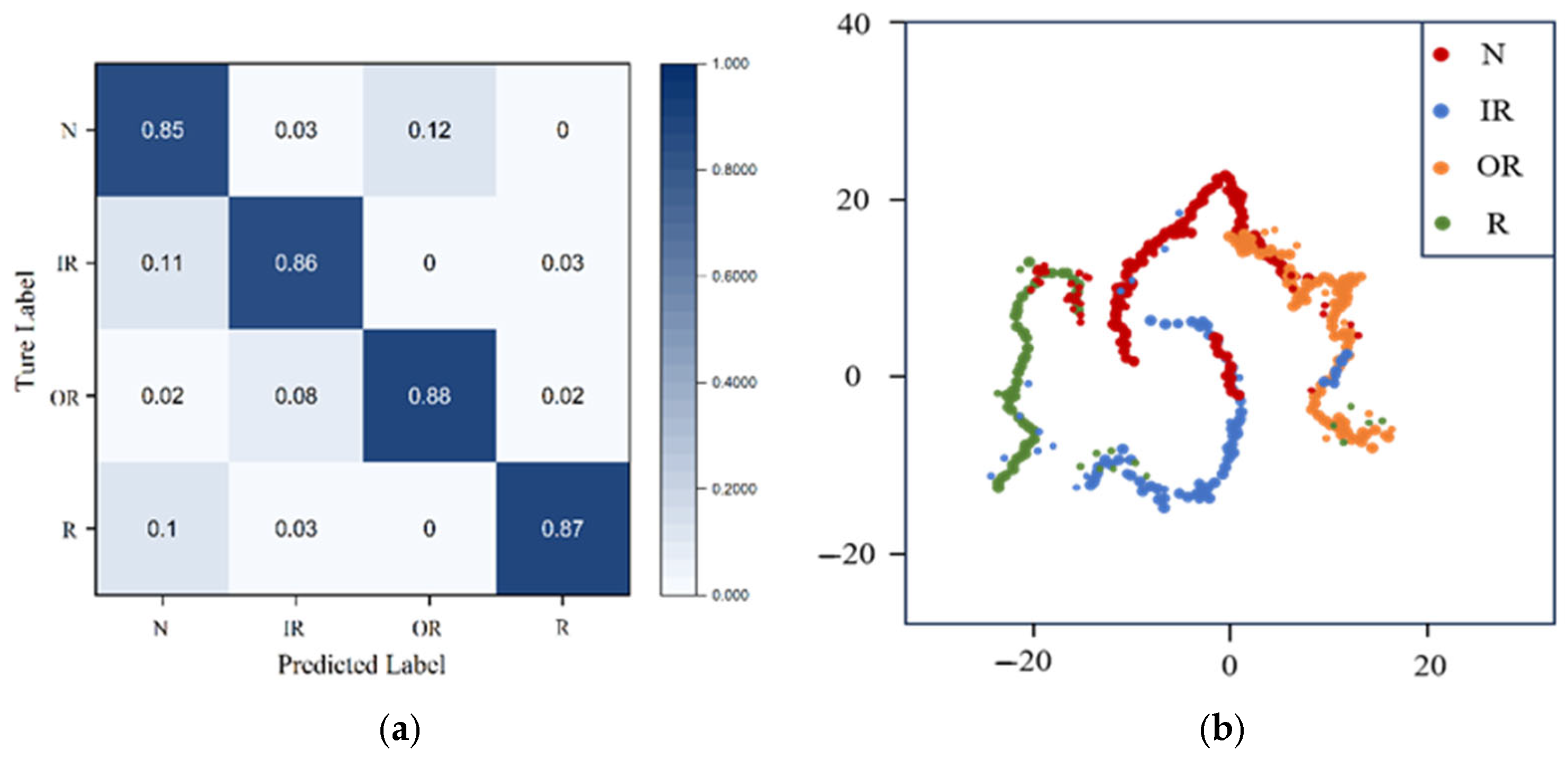
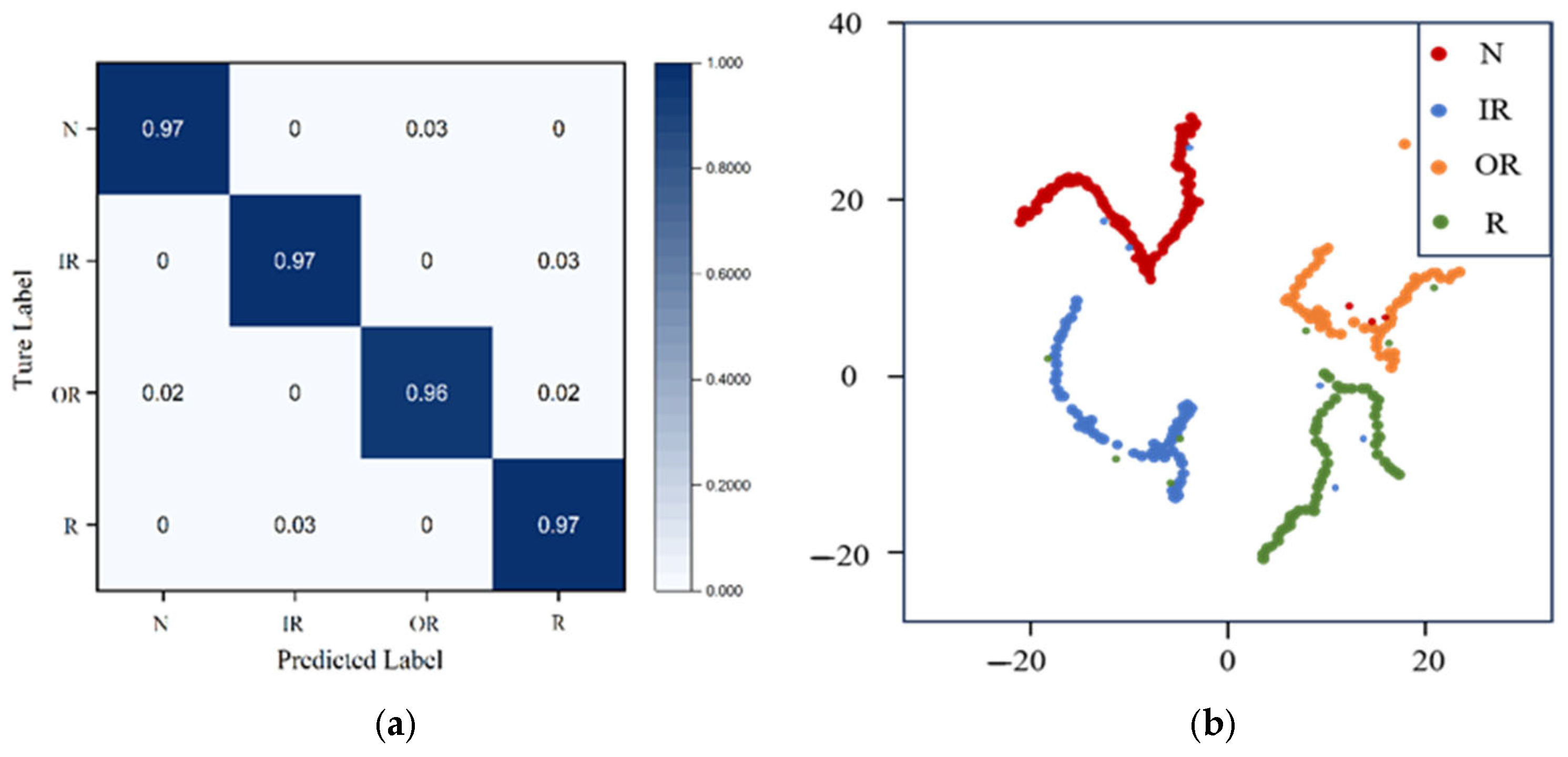
3.3. Method Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shang, L.; Zhang, Z.; Tang, F.; Cao, Q.; Pan, H.; Lin, Z. CNN-LSTM hybrid model to promote signal processing of ultrasonic guided lamb waves for damage detection in metallic pipelines. Sensors 2023, 23, 7059. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, N.; Zhang, Z.; Xu, X. Bearing fault diagnosis based on mel frequency cepstrum coefficient and deformable space-frequency attention network. IEEE Access 2023, 11, 34407–34420. [Google Scholar] [CrossRef]
- Zegai, M.L.; Bendjebbar, M.; Belhadri, K.; Doumbia, M.L.; Hamane, B.; Koumba, P.M. Direct torque control of Induction Motor based on artificial neural networks speed control using MRAS and neural PID controller. In Proceedings of the 2015 IEEE Electrical Power and Energy Conference (EPEC), London, ON, Canada, 26–28 October 2015; pp. 320–325. [Google Scholar] [CrossRef]
- Douiri, M.R.; Cherkaoui, M.; Douiri, S.M. Rotor resistance and speed identification using extended kalman filter and fuzzy logic controller for induction machine drive. In Proceedings of the 2012 International Conference on Multimedia Computing and Systems, Tangiers, Morocco, 10–12 May 2012; pp. 1182–1187. [Google Scholar] [CrossRef]
- Douiri, M.R.; Cherkaoui, M.; Nasser, T.; Essadki, A. A neuro fuzzy PI controller used for speed control of a direct torque to twelve sectors controlled induction machine drive. In Proceedings of the 2011 International Conference on Multimedia Computing and Systems, Ouarzazate, Morocco, 7–9 April 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, Y.; He, C.; Liu, Y.; Liu, X.; Cao, Z. Feature extraction based on hierarchical improved envelope spectrum entropy for rolling bearing fault diagnosis. IEEE Trans. Instrum. Meas. 2023, 72, 1–12. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Zhou, X.; Zhang, H.; Lin, Z.; Jia, S. Dynamic analysis of deep groove ball bearing with localized defects and misalignment. J. Sound Vib. 2024, 568, 118071. [Google Scholar] [CrossRef]
- Liu, K.; Wang, D.; Chen, B.; Shi, X.; Feng, Y.; Li, W. Vibration characteristics investigation of a single/dual rotor-bearing-casing system with local bearing defects. Mech. Syst. Signal Process. 2025, 225, 112227. [Google Scholar] [CrossRef]
- Jafari, S.M.; Rohani, R.; Rahi, A. Experimental and numerical study of an angular contact ball bearing vibration response with spall defect on the outer race. Arch. Appl. Mech. 2020, 90, 2487–2511. [Google Scholar] [CrossRef]
- Alkomy, H.; Shan, J. Modeling and validation of reaction wheel micro-vibrations considering imbalances and bearing disturbances. J. Sound Vib. 2021, 492, 115766. [Google Scholar] [CrossRef]
- Dipen, S.S.; Patel, V.N. Theoretical and experimental vibration studies of lubricated deep groove ball bearings having surface waviness on its races. Measurement 2018, 129, 405–423. [Google Scholar] [CrossRef]
- Larizza, F.; Howard, C.Q.; Grainger, S.; Wang, W. A nonlinear dynamic vibration model of a defective bearing: The importance of modelling the angle of the leading and trailing edges of a defect. Struct. Health Monit. 2020, 20, 2604–2625. [Google Scholar] [CrossRef]
- Mufazzal, S.; Muzakkir, S.M.; Khanam, S. Theoretical and experimental analyses of vibration impulses and their influence on accurate diagnosis of ball bearing with localized outer race defect. J. Sound Vib. 2021, 513, 116407. [Google Scholar] [CrossRef]
- Tingarikar, G.; Choudhury, A. Vibration analysis-based fault diagnosis of a dynamically loaded bearing with distributed defect. Arab. J. Sci. Eng. 2021, 47, 8045–8058. [Google Scholar] [CrossRef]
- Govardhan, T.; Choudhury, A. Amplitudes of components in vibration spectra of rolling bearings with localized defects under harmonic loads. J. Vib. Control 2020, 27, 1537–1547. [Google Scholar] [CrossRef]
- Luo, M.; André, H.; Guo, Y.; Peng, Y. Analysis of contact behaviours and vibrations in a defective deep groove ball bearing. J. Sound Vib. 2024, 570, 118104. [Google Scholar] [CrossRef]
- Zhang, X.; Bai, C.; Jin, Y.; Wang, J. Nonlinear vibration characteristics of a rotor bearing system with irregular raceway defect. Nonlinear Dyn. 2025, 113, 11259–11281. [Google Scholar] [CrossRef]
- Song, X.; Li, Z.; Liu, Y. MVB fault diagnosis based on time-frequency analysis and convolutional neural networks. Sci. Rep. 2025, 15, 5271. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Chen, R.; Yang, L.; Zou, Y.; Gao, L. Recent progress in digital twin-driven fault diagnosis of rotating machinery: A comprehensive review. Neurocomputing 2025, 634, 129914. [Google Scholar] [CrossRef]
- Han, T.; Zhang, L.; Yin, Z.; Tan, A.C. Rolling bearing fault diagnosis with combined convolutional neural networks and support vector machine. Measurement 2021, 177, 109022. [Google Scholar] [CrossRef]
- Chen, S.; Yang, R.; Zhong, M. Graph-based semi-supervised random forest for rotating machinery gearbox fault diagnosis. Control Eng. Pract. 2021, 117, 104952. [Google Scholar] [CrossRef]
- Wang, X.; Gu, H.; Wang, T.; Zhang, W.; Li, A.; Chu, F. Deep convolutional tree-inspired network: A decision-tree-structured neural network for hierarchical fault diagnosis of bearings. Front. Mech. Eng. 2021, 16, 814–828. [Google Scholar] [CrossRef]
- Lee, D.; Choo, H.; Jeong, J. Gcn-based lstm autoencoder with self-attention for bearing fault diagnosis. Sensors 2024, 24, 4855. [Google Scholar] [CrossRef]
- Borré, A.; Seman, L.O.; Camponogara, E.; Stefenon, S.F.; Mariani, V.C.; Coelho, L.d.S. Machine fault detection using a hybrid CNN-LSTM attention-based mode. Sensors 2023, 23, 4512. [Google Scholar] [CrossRef] [PubMed]
- Djaballah, S.; Saidi, L.; Meftah, K.; Hechifa, A.; Bajaj, M.; Zaitsev, I. A hybrid LSTM random forest model with grey wolf optimization for enhanced detection of multiple bearing faults. Sci. Rep. 2024, 14, 23997. [Google Scholar] [CrossRef] [PubMed]
- Thuan, N.D. A novel bearing fault diagnosis method for compound defects via zero-shot learning. J. Mech. Sci. Technol. 2024, 38, 4603–4610. [Google Scholar] [CrossRef]
- Hassannejad, R.; Ettefagh, M.M.; Mossayebi, Y.B. Adaptive wavelet-informed physics-based CNN for bearing fault diagnosis. Int. J. Progn. Health Manag. 2025, 16, 1–20. [Google Scholar] [CrossRef]
- Gao, H.; Ma, J.; Zhang, Z.; Cai, C. Bearing fault diagnosis method based on attention mechanism and multi-channel feature fusion. IEEE Access 2024, 12, 45011–45025. [Google Scholar] [CrossRef]
- Li, Y.; Men, Z.; Bai, X.; Xia, Q.; Zhang, D. A bearing fault diagnosis method based on M-SSCNN and M-LR attention mechanism. Struct. Health Monit. 2025, 24, 830–852. [Google Scholar] [CrossRef]
- Lee, S.K.; Kim, H.; Chae, M.; Oh, H.J.; Yoon, H.; Youn, B.D. Self-supervised feature learning for motor fault diagnosis under various torque conditions. Knowl.-Based Syst. 2024, 288, 111465. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, Y.K. Physics-informed time-frequency fusion network with attention for noise-robust bearing fault diagnosis. IEEE Access 2024, 12, 12517–12532. [Google Scholar] [CrossRef]
- Snyder, Q.; Jiang, Q.; Tripp, E. Integrating self-attention mechanisms in deep learning: A novel dual-head ensemble transformer with its application to bearing fault diagnosis. Signal Process. 2025, 227, 109683. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, J.; Hu, J.; Shen, C.; Huang, W.; Zhu, Z. Simulation data driven time-frequency fusion 1D convolutional neural network with multiscale attention for bearing fault diagnosis. Meas. Sci. Technol. 2025, 36, 035109. [Google Scholar] [CrossRef]
- Hou, W.; Zhang, C.; Jiang, Y.; Cai, K.; Wang, Y.; Li, N. A new bearing fault diagnosis method via simulation data driving transfer learning without target fault data. Measurement 2023, 215, 112879. [Google Scholar] [CrossRef]
- Xie, J.; Tian, L.; Lin, M.; Yang, B.; Yang, J.; Wang, T. A small sample diagnosis method driven by simulation and test data: Applied to axle box bearings of high-speed train. Meas. Sci. Technol. 2023, 34, 125044. [Google Scholar] [CrossRef]
- Elouaham, S.; Latif, R.; Nassiri, B.; Dliou, A.; Laaboubi, M.; Maoulainine, F. Analysis electroencephalogram signals using ANFIS and periodogram techniques. Int. Rev. Comput. Softw. 2013, 8, 2959–2966. [Google Scholar]








| Healthy State | Label | Sample Number |
|---|---|---|
| N | 0 | 238 |
| IR | 1 | 236 |
| OR | 2 | 235 |
| R | 3 | 237 |
| Module | Layer | Parameters | Output Shape | Comment |
|---|---|---|---|---|
| Input Layer | Original Signal | (32, 1, 1024) | Batch Size = 32 Signal = 1024 | |
| FFT | (32, 1, 512) | |||
| CNN | Convolution 1 | (2, 16) | (32, 16, 512) | |
| Convolution 2 | (2, 32) | (32, 32, 512) | ||
| Convolution 3 | (1, 64) | (32, 64, 128) | ||
| Transformer (Attention) | Input Dimension | 64 | (32, 128, 64) | |
| Encoder Layer | 2 | (32, 128, 64) | ||
| Attention Head | 4 | (32, 128, 64) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, S.; Wang, Z.; Zhao, R.; Guo, X.; Liu, A.; Liang, W. Time–Frequency-Domain Fusion Cross-Attention Fault Diagnosis Method Based on Dynamic Modeling of Bearing Rotor System. Appl. Sci. 2025, 15, 7908. https://doi.org/10.3390/app15147908
Xing S, Wang Z, Zhao R, Guo X, Liu A, Liang W. Time–Frequency-Domain Fusion Cross-Attention Fault Diagnosis Method Based on Dynamic Modeling of Bearing Rotor System. Applied Sciences. 2025; 15(14):7908. https://doi.org/10.3390/app15147908
Chicago/Turabian StyleXing, Shiyu, Zinan Wang, Rui Zhao, Xirui Guo, Aoxiang Liu, and Wenfeng Liang. 2025. "Time–Frequency-Domain Fusion Cross-Attention Fault Diagnosis Method Based on Dynamic Modeling of Bearing Rotor System" Applied Sciences 15, no. 14: 7908. https://doi.org/10.3390/app15147908
APA StyleXing, S., Wang, Z., Zhao, R., Guo, X., Liu, A., & Liang, W. (2025). Time–Frequency-Domain Fusion Cross-Attention Fault Diagnosis Method Based on Dynamic Modeling of Bearing Rotor System. Applied Sciences, 15(14), 7908. https://doi.org/10.3390/app15147908






