Failure Mechanism and Structural Analysis of Chain Slings with Non-Standard Connections
Abstract
1. Introduction
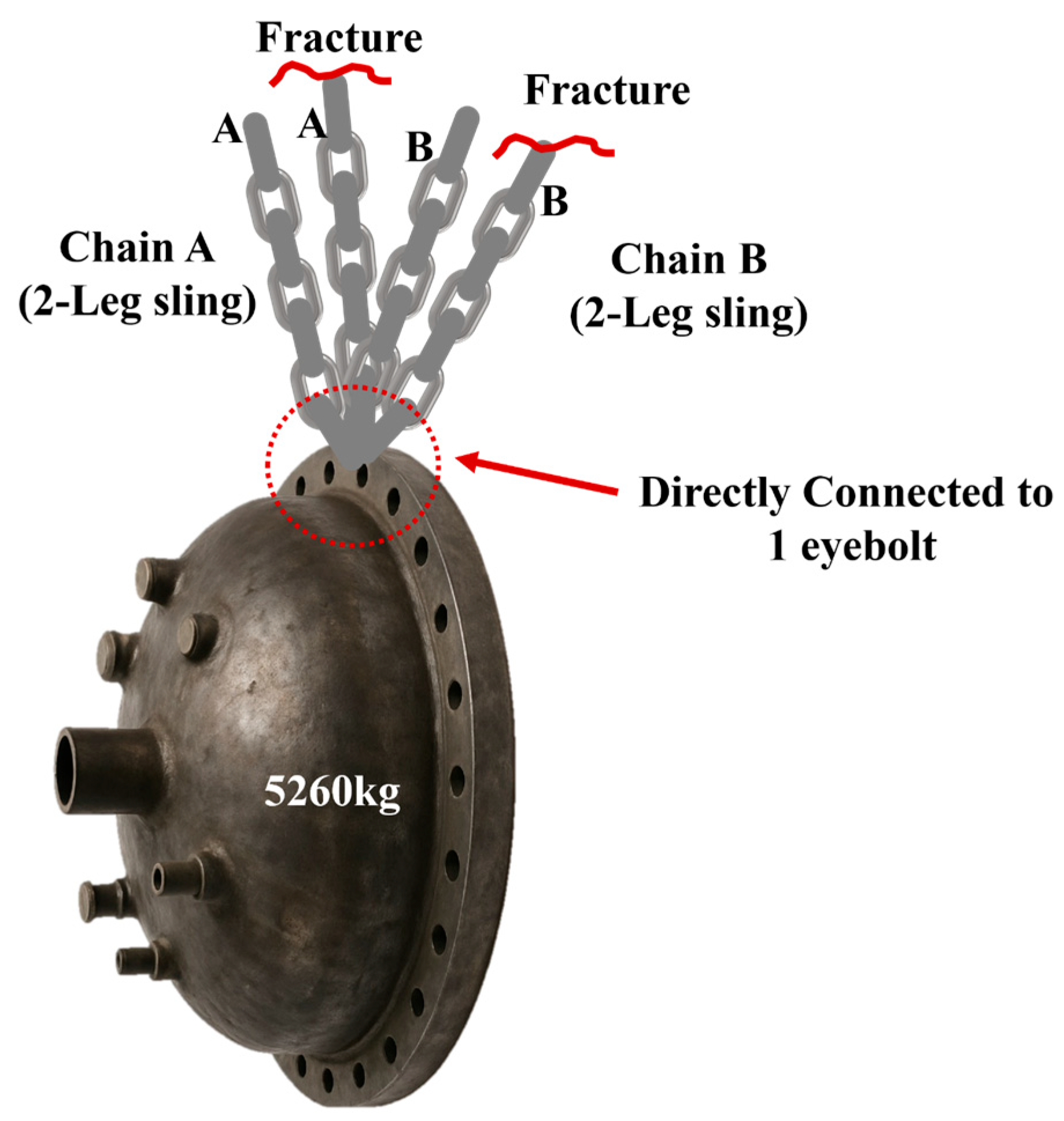
2. Overview
3. Failure Cause Analysis
3.1. Fracture Surface Analysis
3.2. Dimensional Measurement and Analysis of Chain Slings
3.3. Experimental Evaluation of Chain Fracture
3.4. Review of Safety Factor
3.5. Evaluation of the Eye Bolt
3.6. Comprehensive Review of Chain Failure (Cause)
3.6.1. Use of Auxiliary Chains Without Load Marking and Below Standard Specifications
3.6.2. Use of Chains Without Considering Safety Factor Requirements
3.6.3. Use of Chains with Degraded Durability
3.6.4. Use of Eye Bolt Exceeding Its Rated Lifting Capacity
4. Structural Analysis
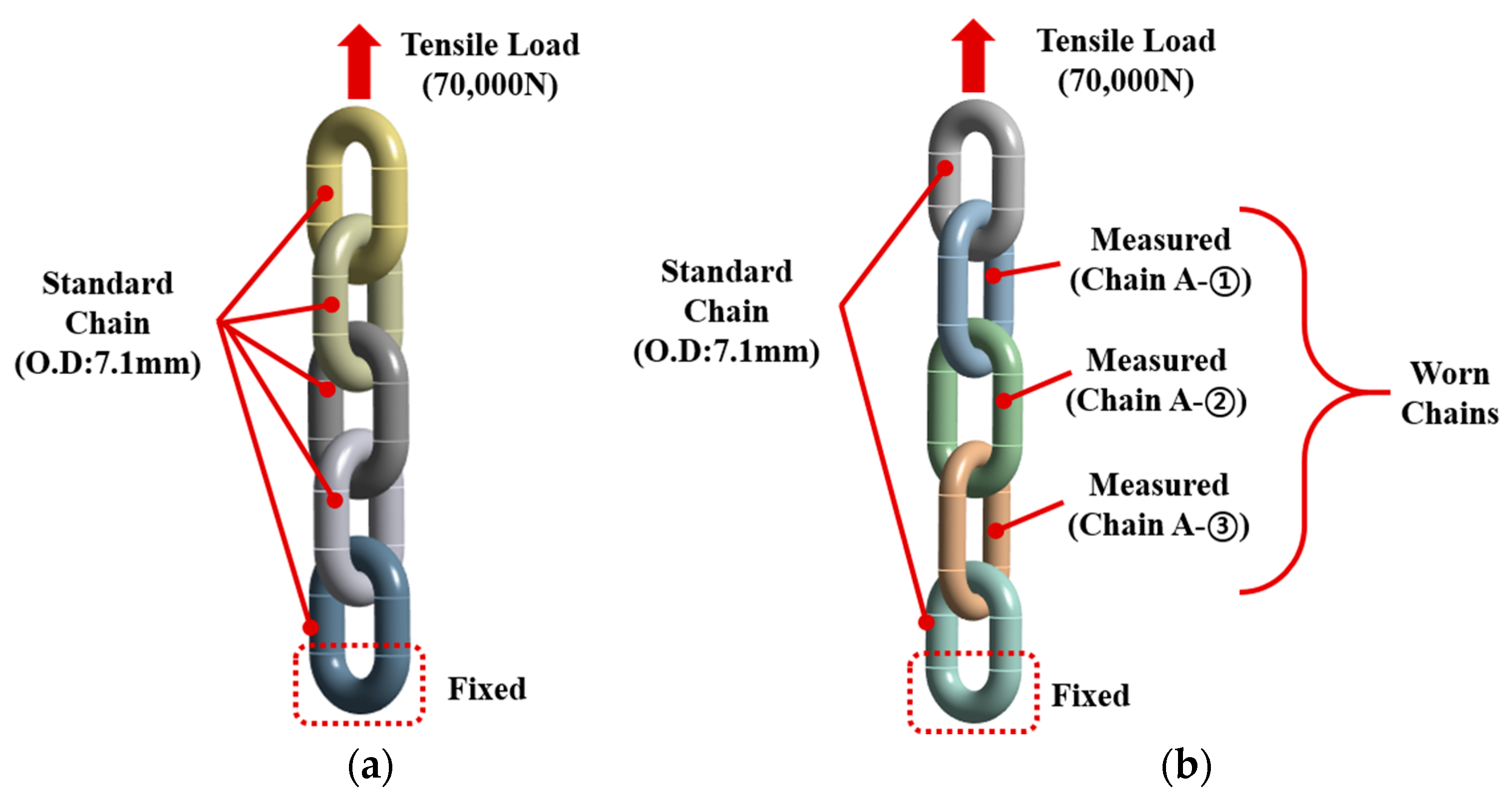
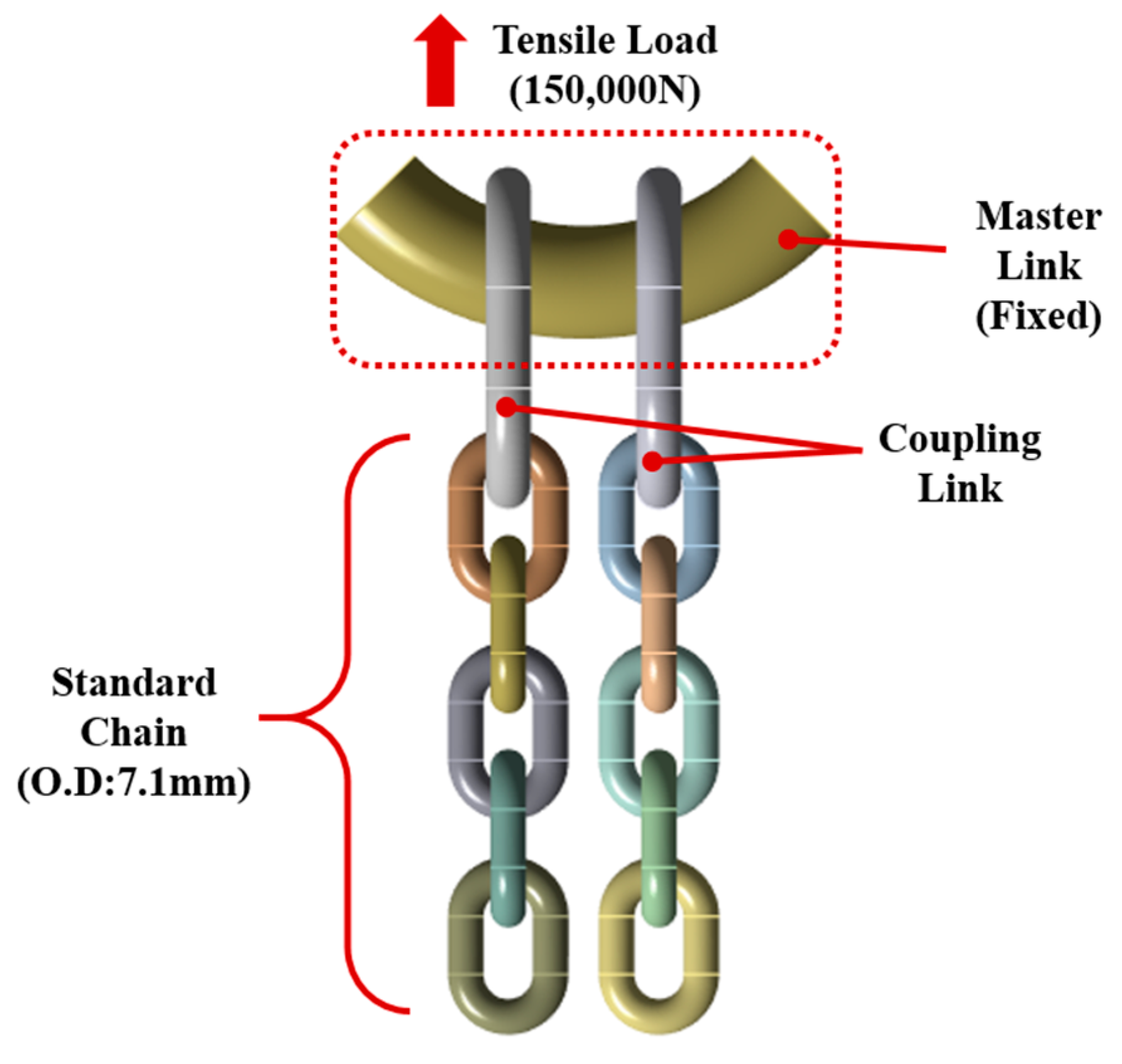
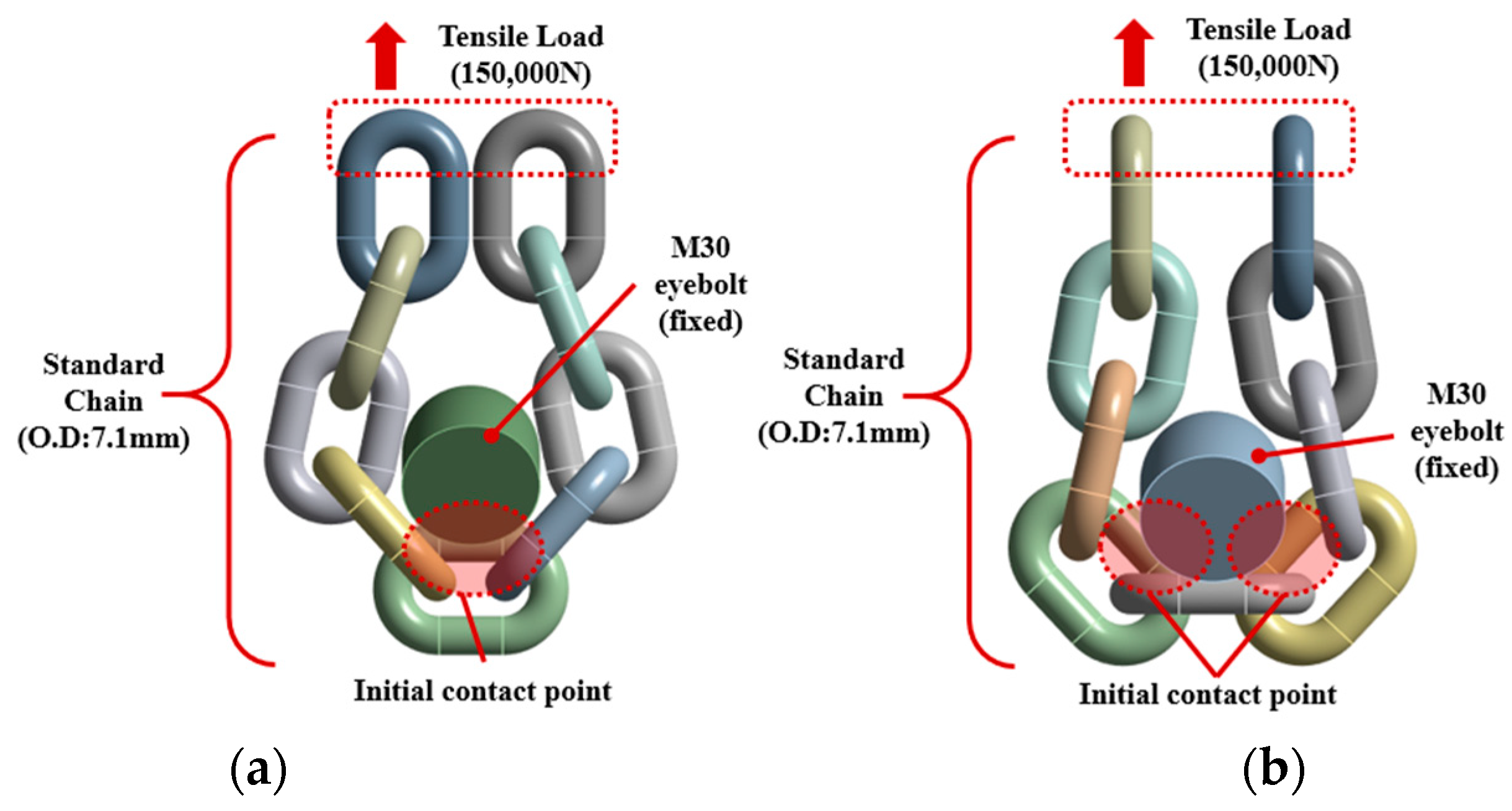
4.1. Analysis Model and Boundary Conditions
4.2. Analysis Model
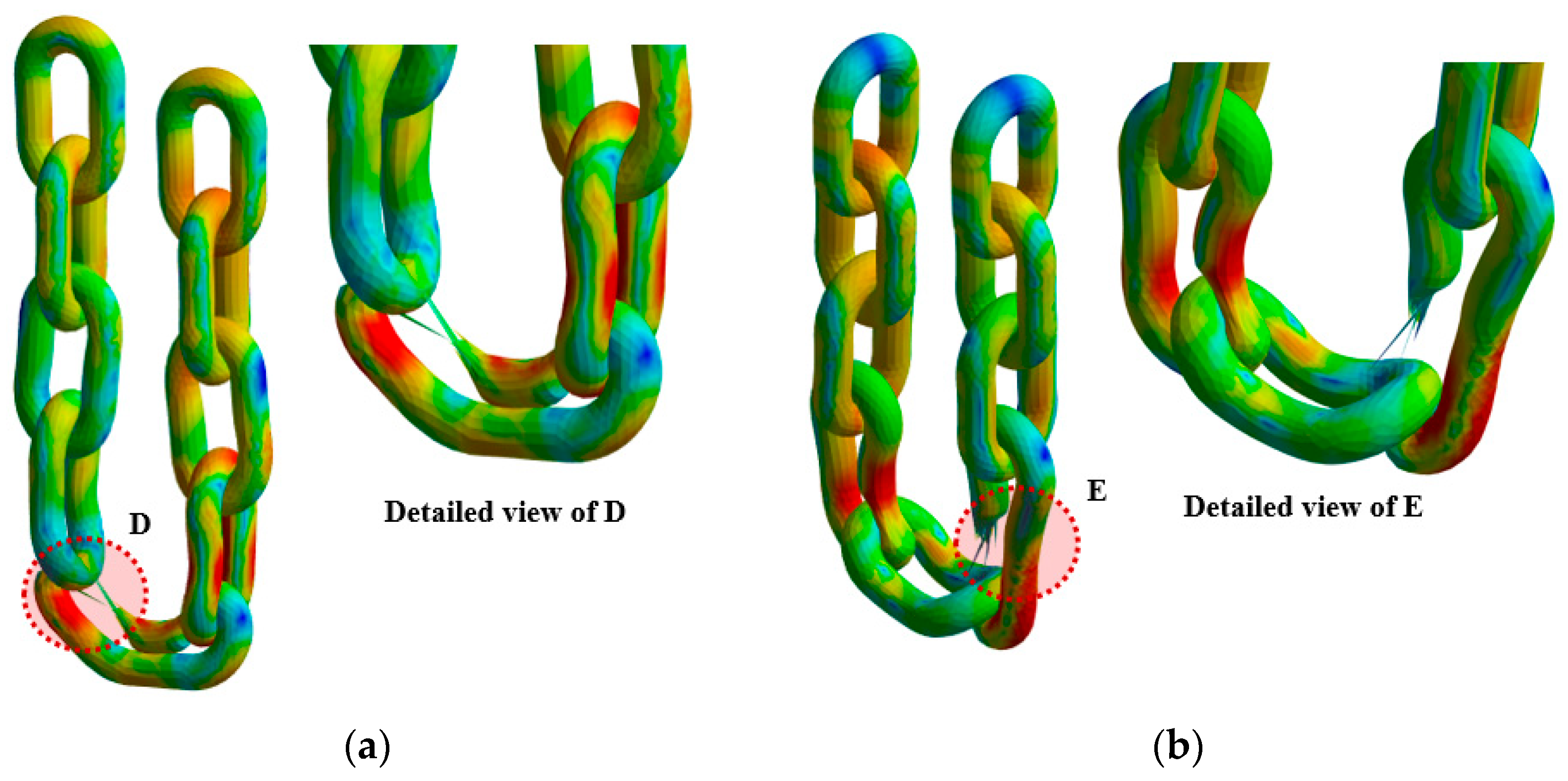
4.3. Analysis Results
5. Guidelines for On-Site Implementation
6. Conclusions
- Dimensional measurements of the chain slings revealed that in some cases, the wire diameter had decreased by more than 10%, or the pitch had increased by more than 5%, compared to standard values. In particular, the diameter of Chain A-③ had decreased by approximately 15% to 6.03 mm compared to the standard 7.1 mm, exceeding the discard criteria. This indicates that plastic deformation and elongation occurred during repeated use, highlighting the necessity of dimensional inspections and immediate disposal of non-compliant products before use.
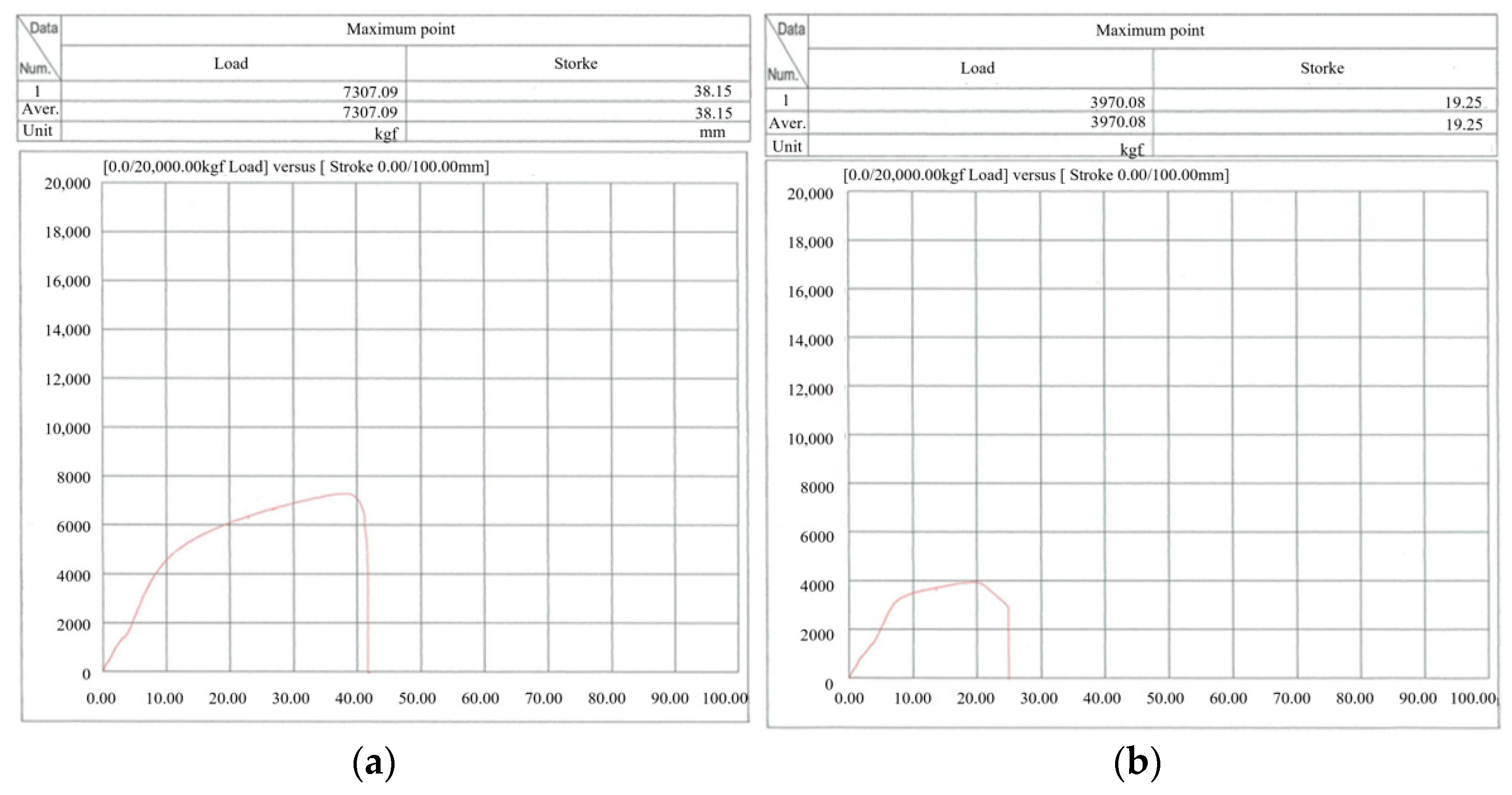
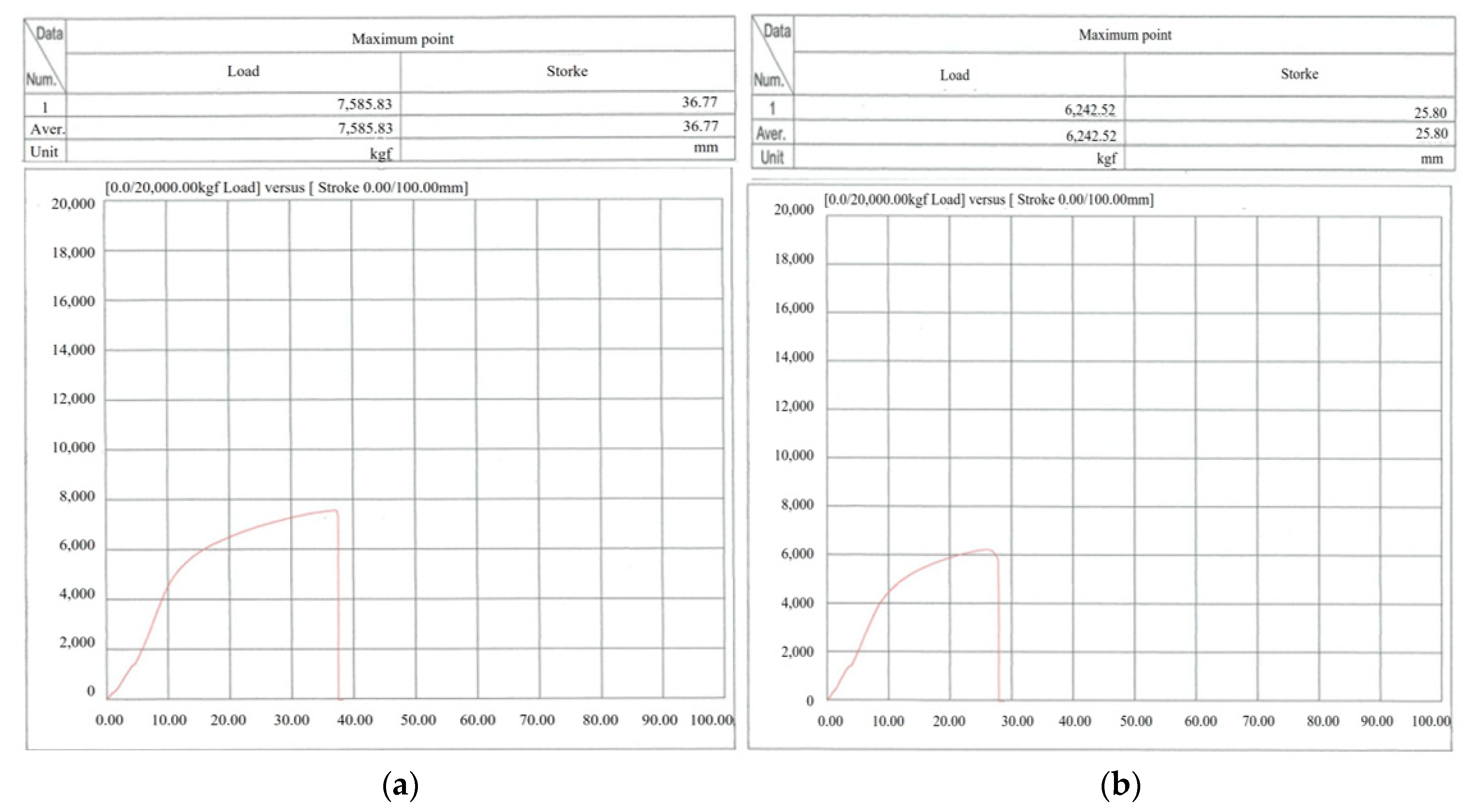
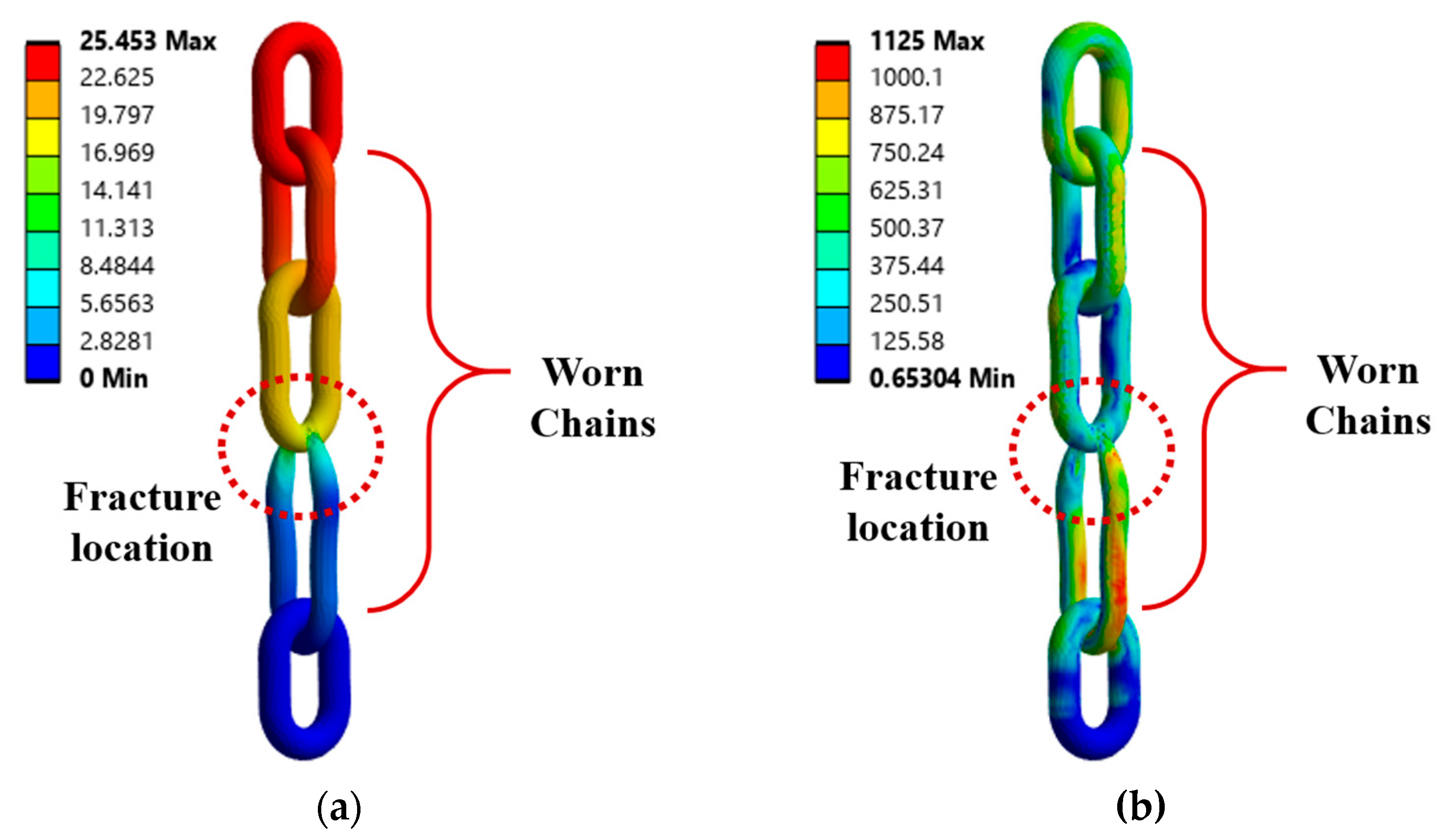
- The fracture test results showed that the aged Chain A failed at 3970 kgf during the second test—only about 62% of the standard fracture load of 6400 kgf. Chain B also failed at 6242 kgf, falling below the standard. These results demonstrate that external and dimensional degradation directly leads to reduced strength, emphasizing the importance of strictly enforcing discard criteria.
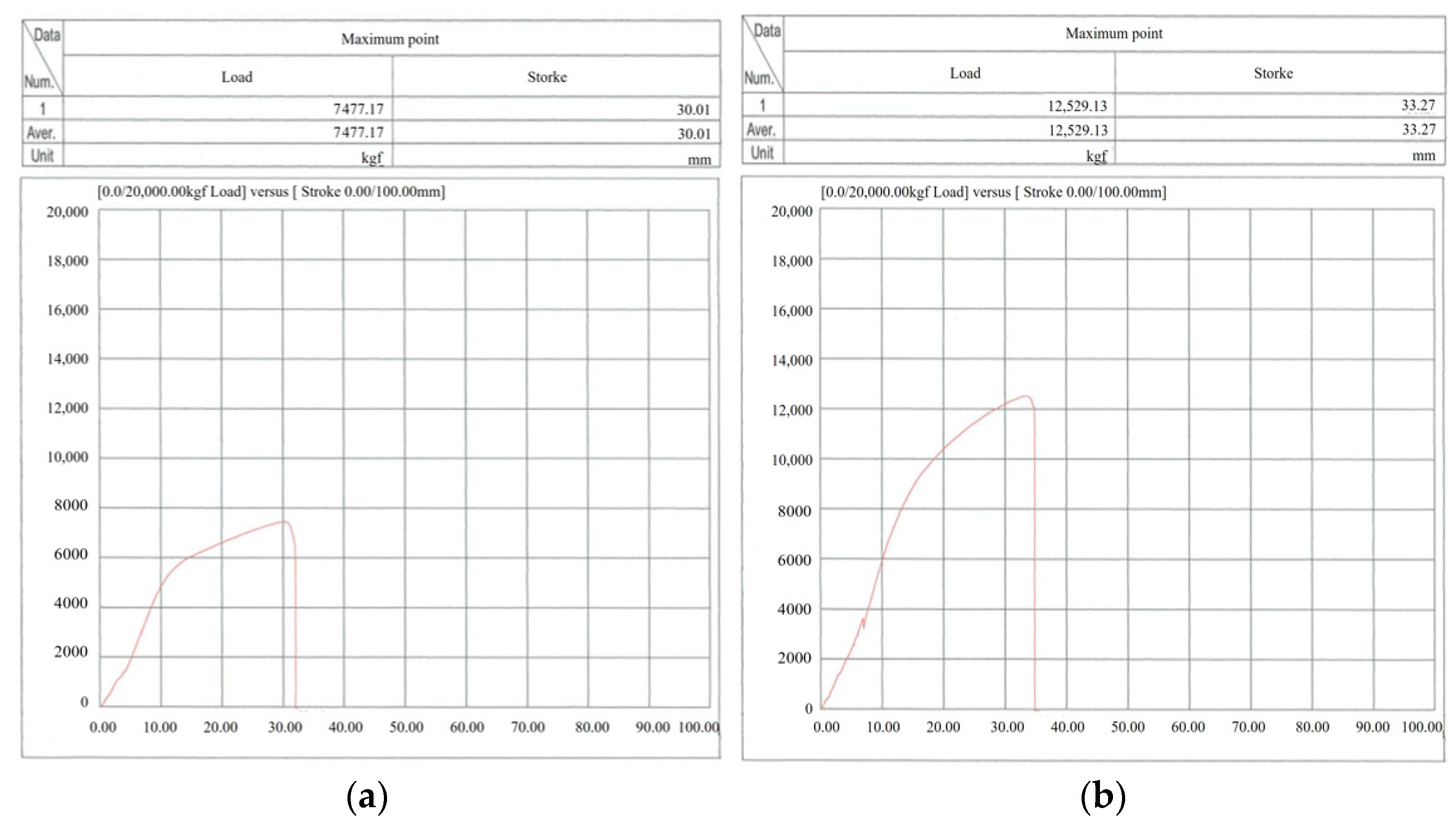
- Clear differences emerged based on the fastening method. When the new chain was used in a single-leg configuration, the fracture load was 7477 kgf. In contrast, when configured as a two-leg sling using a non-standard method, the fracture load was 12,529 kgf—only 83.8% of the theoretical value of 14,954 kgf. This reduction is attributed to the combined bending and torsional loads applied to the chain wrapped around the eyebolt. Notably, in the four-leg sling configuration (theoretically 25,600 kgf), failure occurred at just 5260 kgf, indicating a severe reduction in strength.
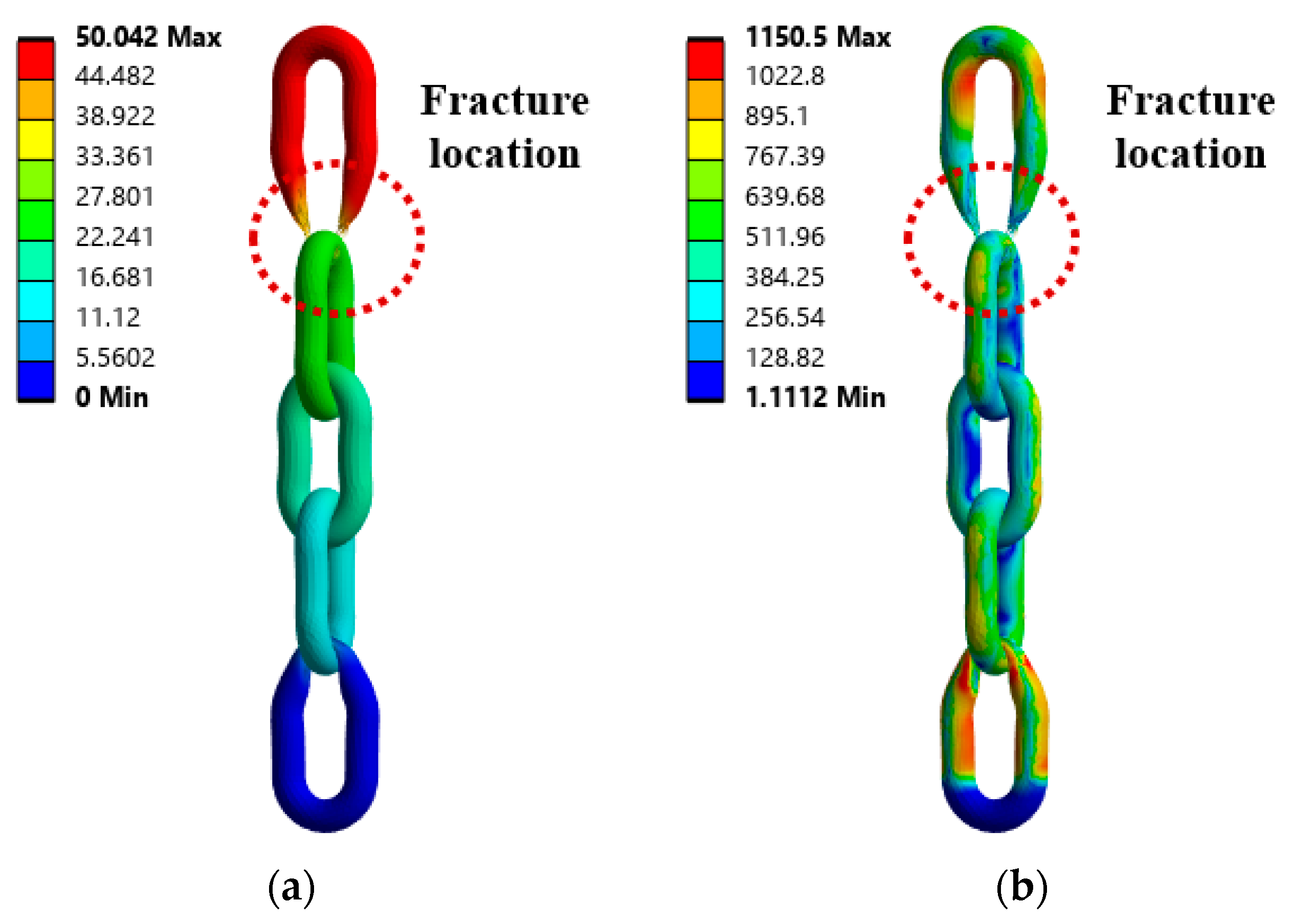
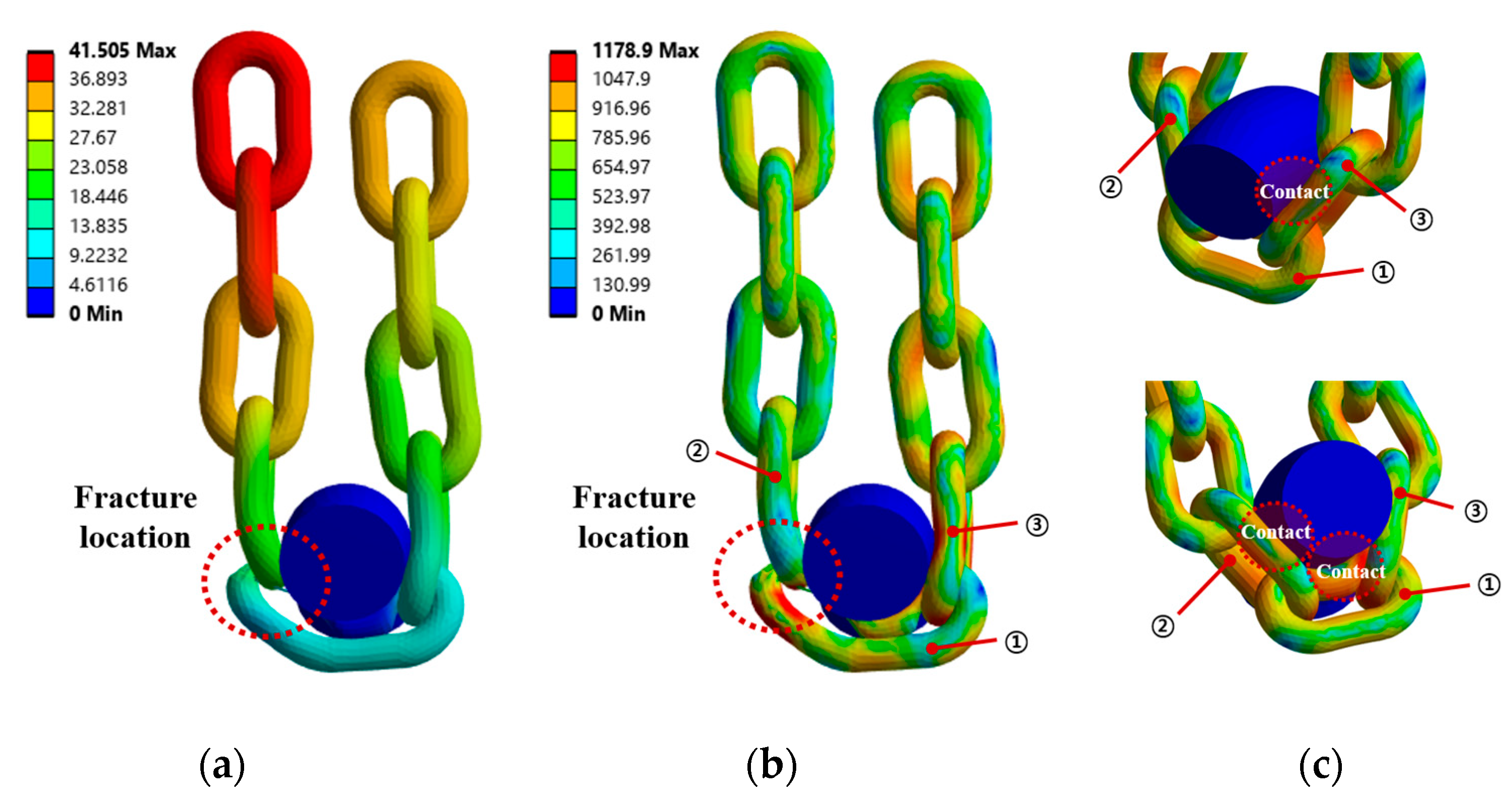
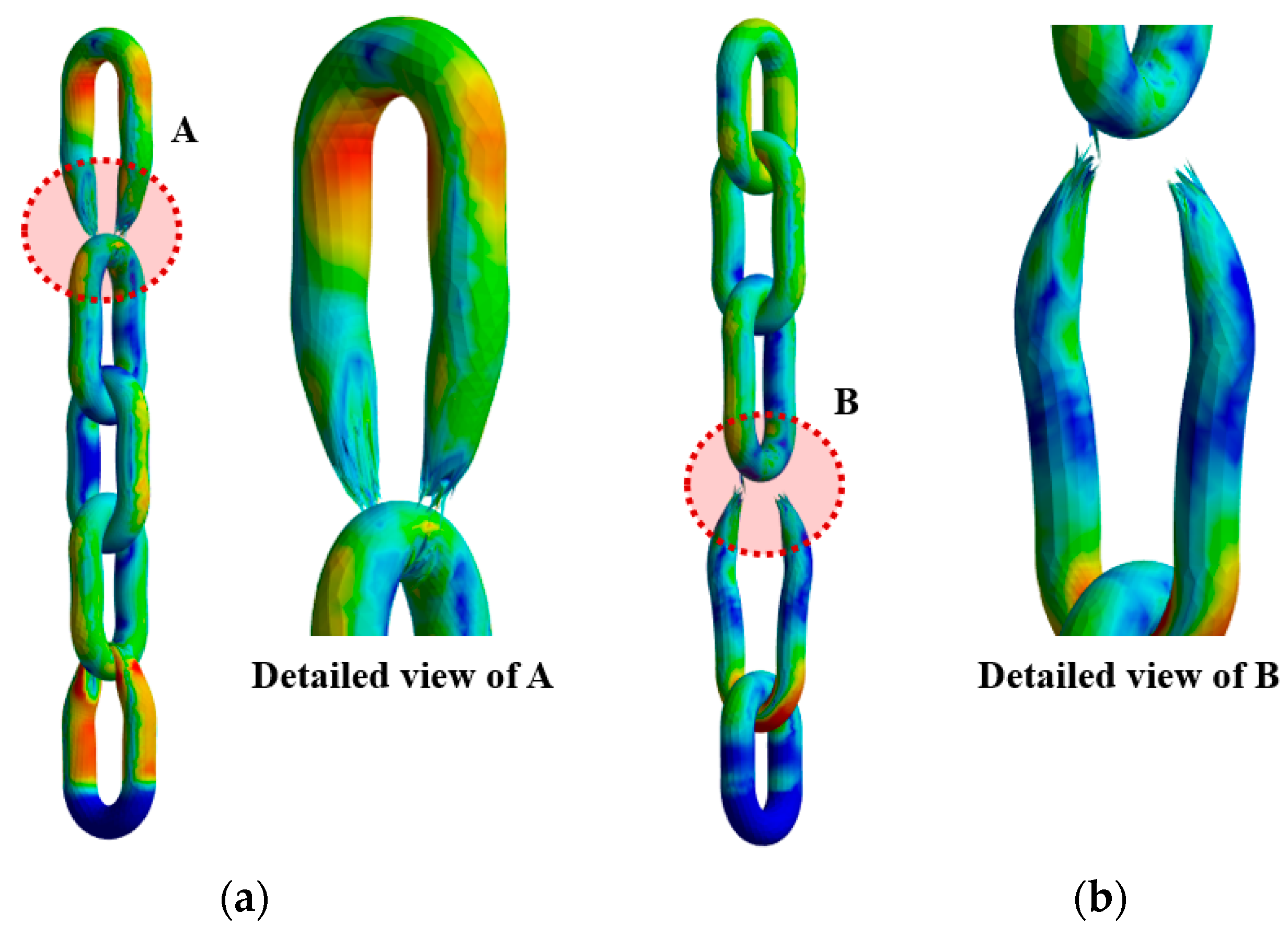
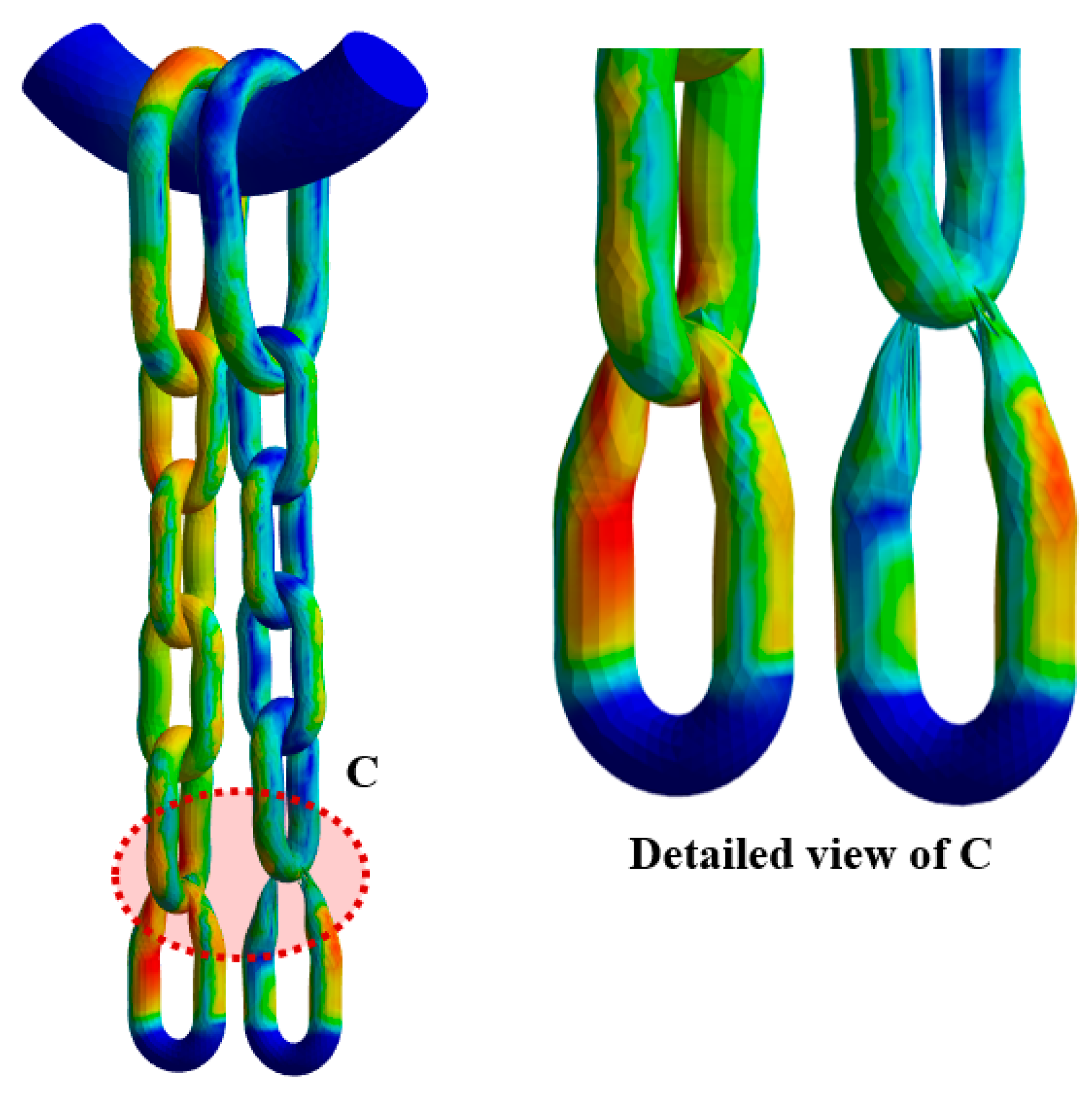
- Structural analysis showed that Case 3 (standard fastening) allowed the load to be evenly distributed throughout the chain, with a maximum stress of approximately 1156 MPa and a maximum tensile load of about 124,500 N. This aligns with the chain’s design strength, and fracture occurred in a region with appropriate stress distribution rather than at the joints. In contrast, in Cases 4 and 5 (non-standard fastening), the chain was directly wrapped around the eyebolt, resulting in combined bending and compressive loads. The maximum stresses reached approximately 1179 MPa and 1213 MPa, while the maximum tensile loads were reduced to 106,500 N and 105,000 N, respectively—more than a 15% decrease. The failure points were located near the eyebolt contact area, clearly indicating nonlinear stress concentration and structural weakness.
- This performance degradation was caused by the complex loading conditions—local bending, compressive stress, and contact friction—arising from wrapping the chain around the curved surface of the eyebolt. These conditions are consistent with the local plastic deformation and stress concentration predicted by the Johnson–Cook damage accumulation model. In particular, the non-standard fastening method distorts the chain’s intended load path, significantly reducing structural strength and increasing the likelihood of unexpected failures.
- This study structurally validated the fastening methods prescribed by international standards such as DIN EN 818-4 and ISO 3056 (using shackles or master links), and quantitatively analyzed the impact of non-standard fastening methods on chain strength and service life, making it a meaningful practical case.
- The findings provide the following practical implications:
- Standard fastening methods (using auxiliary connectors) must always be followed.
- Wrapping chains directly around eyebolts should be strictly prohibited due to high local stress concentrations and structural damage risks.
- Fatigue life and fracture behavior vary significantly depending on the fastening method; thus, these factors must be considered in both design and field application.
- Subtle differences in chain curvature, contact angle, and friction conditions affect overall durability, necessitating regular inspections and clear discard criteria.
- Future research should focus on fatigue analysis and the development of damage-accumulation-based life prediction models that incorporate additional parameters not considered in this study, such as cyclic loads, impact loads, and asymmetric loading. Further investigations are also needed into optimizing contact surface geometry, improving friction conditions, and designing auxiliary fastening components.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Solazzi, L.; Danzi, N.; Gelfi, M.; Zavanella, L.E. Failure Analysis of a Pair of Failed Chain Links. Eng. Fail. Anal. 2023, 152, 107481. [Google Scholar] [CrossRef]
- U.S. Occupational Safety and Health Administration (OSHA). Sling Safety—Safe Sling Use. 2021. Available online: https://www.osha.gov/safe-sling-use (accessed on 4 April 2025).
- Japanese Industrial Safety and Health Association (JISHA). Slinging Work—Safety Guidelines for Sling Use. 2019. Available online: https://www.jisha.or.jp/international/jicosh/english/topics/slinging/slinging.html (accessed on 7 April 2025).
- Peerless Chain. Available online: https://peerlesschain.com/news/the-anatomy-of-an-alloy-chain-sling-failure (accessed on 3 April 2025).
- Steel Image Inc. Available online: https://steelimage.com/wp-content/uploads/2019/02/Fatigue-Failure-of-Automotive-Assmebly-Plant-Chain.pdf (accessed on 2 May 2025).
- Zarandi, E.P.; Skallerud, B.H. Experimental and Numerical Study of Mooring Chain Residual Stresses and Implications for Fatigue Life. Int. J. Fatigue. 2020, 135, 105530. [Google Scholar] [CrossRef]
- Lone, E.N.; Sauder, T.; Larsen, K.; Leira, B.J. Probabilistic Fatigue Model for Design and Life Extension of Mooring Chains, Including Mean Load and Corrosion Effects. Ocean Eng. 2022, 245, 110396. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Smedley, P. Fatigue Performance of High Strength and Large Diameter Mooring Chain in Seawater. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, UK, 9–14 June 2019. [Google Scholar]
- Fernández, J.; Arredondo, A.; Storesund, W.; González, J.J. Influence of the Mean Load on the Fatigue Performance of Mooring Chains. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. [Google Scholar]
- Gabrielsen, Ø.; Larsen, K.; Dalane, O.; Lie, H.B.; Reinholdtsen, S.-A. Mean Load Impact on Mooring Chain Fatigue Capacity: Lessons Learned From Full Scale Fatigue Testing of Used Chains. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, UK, 9–14 June 2019. [Google Scholar]
- Bergara, A.; Arredondo, A.; Altuzarra, J.; Martínez-Esnaola, J.M. Fatigue Crack Propagation Analysis in Offshore Mooring Chains and the Influence of Manufacturing Residual Stresses. Ocean Eng. 2022, 257, 111605. [Google Scholar] [CrossRef]
- Lone, E.N.; Sauder, T.; Larsen, K.; Leira, B.J. Fatigue Assessment of Mooring Chain Considering the Effects of Mean Load and Corrosion. In Proceedings of the ASME 2021 40th International Conference on Ocean, Offshore and Arctic Engineering, Virtual Conference, 21–30 June 2021. [Google Scholar]
- Kim, Y.; Kim, M.S.; Park, M.J. Fatigue Analysis on the Mooring Chain of a Spread Moored FPSO Considering the OPB and IPB. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 178–201. [Google Scholar] [CrossRef]
- Lone, E.N.; Sauder, T.; Larsen, K.; Leira, B.J. Fatigue reliability of mooring chains, including mean load and corrosion effects. Ocean Eng. 2022, 266, 112621. [Google Scholar] [CrossRef]
- Zarandi, E.P.; Skallerud, B.H. Cyclic behavior and strain energy-based fatigue damage analysis of mooring chains high strength steel. Mar. Struct. 2020, 70, 102703. [Google Scholar] [CrossRef]
- Qvale, P.; Nordhagen, H.O.; Ås, S.K.; Skallerud, B.H. Effect of Long Periods of Corrosion on the Fatigue Lifetime of Offshore Mooring Chain Steel. Mar. Struct. 2022, 85, 103236. [Google Scholar] [CrossRef]
- Aursand, M.; Haagensen, P.J.; Skallerud, B.H. Remaining Fatigue Life Assessment of Corroded Mooring Chains Using Crack Growth Modelling. Mar. Struct. 2023, 90, 103446. [Google Scholar] [CrossRef]
- Lone, E.N.; Mainçon, P.; Gabrielsen, Ø.; Sauder, T.; Larsen, K.; Leira, B.J. Analysis of S–N Data for New and Corroded Mooring Chains at Varying Mean Load Levels Using a Hierarchical Linear Model. Mar. Struct. 2023, 91, 103466. [Google Scholar] [CrossRef]
- Pressas, I.; Pantazopoulos, G. Failure Analysis and Numerical Modeling of a Fractured Chain Element from a Drawing Machine in a Metallurgical Production Plant. Eng. Fail. Anal. 2025, 171, 109406. [Google Scholar] [CrossRef]
- Gabrielsen, Ø.; Larsen, K.; Reinholdtsen, S.A. Fatigue Testing of Used Mooring Chain. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 19–24 June 2017. [Google Scholar]
- Zarandi, E.P.; Lee, T.L.; Skallerud, B.H. Data on residual stresses of mooring chains measured by neutron diffraction and hole drilling techniques. Data Brief. 2020, 30, 105587. [Google Scholar] [CrossRef] [PubMed]
- Park, J.S.; Yi, M.S. Nonlinear Structural Strength of Steel Chain Contacted with Knuckle-Shaped Plate under Lifting Conditions. Ships Offshore Struct. 2024, 1–13. [Google Scholar] [CrossRef]
- Kim, T.G.; Lee, S.B.; Lee, H.C. A Case Study on Engineering Failure Analysis of Link Chain. Saf. Health Work. 2010, 1, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Angulo, Á.; Allwright, J.; Mares, C.; Gan, T.H.; Soua, S. Finite Element Analysis of Crack Growth for Structural Health Monitoring of Mooring Chains using Ultrasonic Guided Waves and Acoustic Emission. Procedia Struct. Integr. 2017, 5, 217–224. [Google Scholar] [CrossRef]
- Cheng, X.Y.; Zhang, H.X.; Li, H.; Shen, H.P. Effect of Tempering Temperature on the Microstructure and Mechanical Properties in Mooring Chain Steel. Mater. Sci. Eng. A 2015, 636, 164–171. [Google Scholar] [CrossRef]
- Ma, K.T.; Shu, H.; Smedley, P.; L’Hostis, D.; Duggal, A. A Historical Review on Integrity Issues of Permanent Mooring Systems. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2013. [Google Scholar]
- Riccioli, F.; Gabrielsen, Ø.; Høgsæt, I.S.; Barros, P.S.; Pahlavan, L. Corrosion-Fatigue Damage Identification in Submerged Mooring Chain Links Using Remote Acoustic Emission Monitoring. Mar. Struct. 2024, 98, 103685. [Google Scholar] [CrossRef]
- Lee, J.W.; Han, C.H.; Lee, S.W.; Jeon, Y.H.; Lee, C.H. A Study on the Safety Improvement of Lifting Purpose Chain Sling. J. Korean Soc. Saf. 2023, 38, 60–67. [Google Scholar]
- Yeom, C.H.; Lee, J.H.; Park, H. A Study on the Introduction of a Rigging and Slinging Certificate System to Reduce a Struck by Object Accidents. J. Korean Soc. Saf. 2018, 33, 92–100. [Google Scholar]
- Lee, W.; Han, C.H.; Woo, Y.J.; Lee, J.H.; Lee, C.H. A Study on the Development of Rigging and Slinging Course for Seafarers. J. Fish. Mar. Sci. Educ. 2016, 28, 1561–1572. [Google Scholar]
- Fontaine, E.; Kilner, A.; Carra, C.; Washington, D.; Ma, K.-T.; Phadke, A.; Laskowski, D.; Kusinski, G. Industry Survey of Past Failures, Pre-emptive Replacements and Reported Degradations for Mooring Systems of Floating Production Units. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. [Google Scholar]
- KS B 6243; Chain Blocks. Korean Standards Association: Seoul, Republic of Korea, 2016.
- Regulations on Occupational Safety and Health Standards; Ministry of Employment and Labor: Sejong-si, Republic of Korea, 2025.
- KS B 2818; Leaf Chains—Welded Type. Korean Standards Association: Seoul, Republic of Korea, 2016.
- DIN 580: 2010-09; Lifting Eye Bolts. Deutsches Institut für Normung: Berlin, Germany, 2010.
- ISO 16872:2015; Round Steel Short Link Chains for Lifting Purposes—Fine Tolerance Hoist Chains for Hand Operated Chain Hoists—Grade VH. International Organization for Standardization: Geneva, Switzerland, 2015.
- EN 818-4:1996+A1:2008; Short Link Chain for Lifting Purposes—Safety—Part 4: Chain Slings—Grade 8. European Committee for Standardization: Brussels, Belgium, 2008.
- ISO 3056:1986; Non-calibrated Round Steel Link Lifting Chain and Chain Slings—Use and Maintenance. International Organization for Standardization: Geneva, Switzerland, 1986.












| Diameter (d) | Pitch (p) | Inner (a) | Outer (d) | ||
|---|---|---|---|---|---|
| 7.1 | +0.14 | 21.3 | +3.6 | 8.9 or more | 24.9 or more |
| −0.43 | −1.8 | ||||
| Diameter (d) | Pitch (p) | Inner (a) | Outer (d) | ||
|---|---|---|---|---|---|
| Chain A | ① | 6.63 | 25.78 | 10.97 | 24.51 |
| ② | 6.61 | 26.22 | 10.70 | 24.52 | |
| ③ | 6.03 | 27.31 | 10.94 | 24.80 | |
| Chain B | ① | 6.63 | 21.10 | 9.12 | 23.30 |
| ② | 6.64 | 20.65 | 8.92 | 23.18 | |
| ③ | 6.71 | 21.31 | 9.20 | 23.08 | |
| S.W.L | Proof Load | Breaking Load |
|---|---|---|
| 1600 kgf | 3200 kgf | 6400 kgf |
| Slinging Method | Breaking Load | ||
|---|---|---|---|
| Chain A | ① | 1-Leg | 7307.09 kgf (71,683 N) |
| ② | 1-Leg | 3970.08 kgf (38,946 N) | |
| Chain B | ① | 1-Leg | 7585.83 kgf (74,471 N) |
| ② | 1-Leg | 6242.52 kgf (61,239 N) | |
| New Chain Sling | ① | 1-Leg | 7477.17 kgf (73,351 N) |
| ② | 2-Leg 1 | 12,529.13 kgf (122,911 N) | |
| Description | Safety Factor |
|---|---|
| Suspension wire rope or chain for a worker transport unit | 10 or more |
| Suspension wire rope or chain in direct contact with the cargo load | 5 or more |
| Hook, shackle, and lifting beam | 3 or more |
| In other cases | 4 or more |
| Sling Type | Description | S.W.L |
|---|---|---|
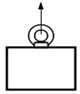 | Lifting capacity Axial (S.W.L) per lifting eye bolt | 3200 kgf |
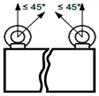 | Lifting capacity per lifting eye bolt ≤ 45° | 2300 kgf |
 | Lifting capacity per lifting eye bolt, with bolt fitted at sides of load ≤ 45° | 1600 kgf |
| Product Type | Slinging Method | Chain Connection Method | Maximum Tensile Load | |
|---|---|---|---|---|
| Case 1 | Standard | 1-Leg | Standard connection | 70,000 N |
| Case 2 | Chain A | |||
| Case 3 | Standard | 2-Leg | Standard connection 1 | 150,000 N |
| Case 4 | Non-Standard connection 2 | |||
| Case 5 |
| Structural Properties | |
|---|---|
| Young’s modulus | 205 GPa |
| Poisson’s ratio | 0.29 |
| Mass density | 7850 kg/m3 |
| Johnson-Cook Strength Model | |
|---|---|
| Initial yield stress (A) | 792 MPa |
| Hardening constant (B) | 510 MPa |
| Hardening exponent (n) | 0.26 |
| Strain rate sensitivity (C) | 0.014 |
| Thermal softening exponent (m) | 1.03 |
| Reference strain rate (/s) | 1 |
| Melting temperature (°C) | 1519.9 |
| Johnson-Cook Failure Model | |
|---|---|
| Initial failure strain (D1) | 0.05 |
| Exponential factor (D2) | 3.44 |
| Triaxiality factor (D3) | −2.12 |
| Strain rate factor (D4) | 0.002 |
| Temperature factor (D5) | 0.61 |
| Maximum Stress (MPa) | Displacement (mm) | Breaking Load (N) | Comparison of Breaking Loads | |
|---|---|---|---|---|
| Case 1 | 1150.5 | 50.042 | 62,300 | - |
| Case 2 | 1125.0 | 25.453 | 46,800 | Comparison with Case 1: 75.12% |
| Case 3 | 1156.1 | 50.037 | 124,500 | - |
| Case 4 | 1178.9 | 41.505 | 106,500 | Comparison with Case 3: 85.54% |
| Case 5 | 1213.3 | 32.007 | 105,000 | Comparison with Case 3: 84.34% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.; Lee, J. Failure Mechanism and Structural Analysis of Chain Slings with Non-Standard Connections. Appl. Sci. 2025, 15, 7841. https://doi.org/10.3390/app15147841
Choi Y, Lee J. Failure Mechanism and Structural Analysis of Chain Slings with Non-Standard Connections. Applied Sciences. 2025; 15(14):7841. https://doi.org/10.3390/app15147841
Chicago/Turabian StyleChoi, Yujun, and Jaesun Lee. 2025. "Failure Mechanism and Structural Analysis of Chain Slings with Non-Standard Connections" Applied Sciences 15, no. 14: 7841. https://doi.org/10.3390/app15147841
APA StyleChoi, Y., & Lee, J. (2025). Failure Mechanism and Structural Analysis of Chain Slings with Non-Standard Connections. Applied Sciences, 15(14), 7841. https://doi.org/10.3390/app15147841








