Numerical Simulation and Analysis of Heart–Aorta Fluid–Structure Interaction Based on S-ALE Method
Abstract
1. Introduction
2. Materials and Methods
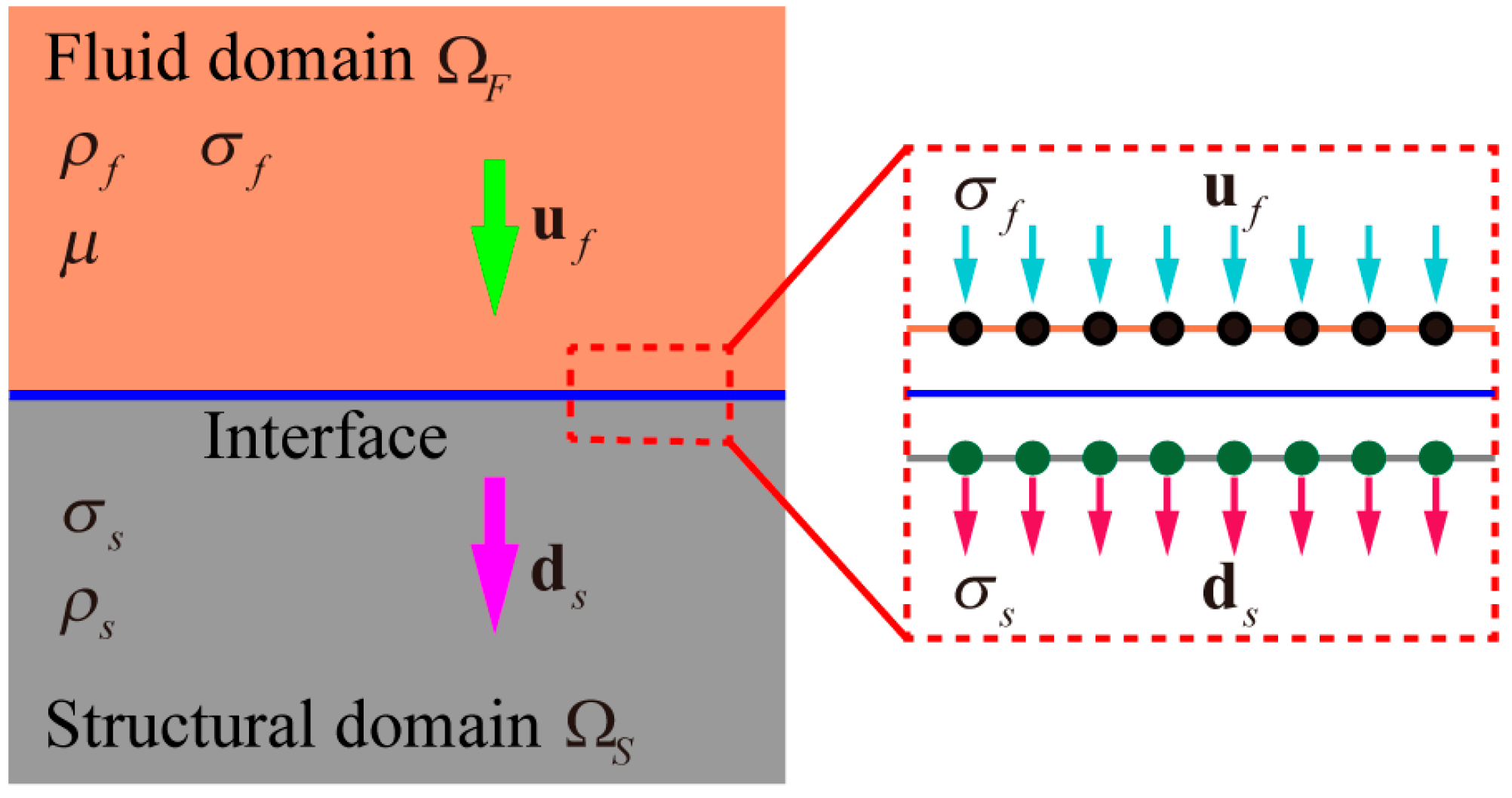
2.1. S-ALE Method Fundamentals and Coupling Conditions
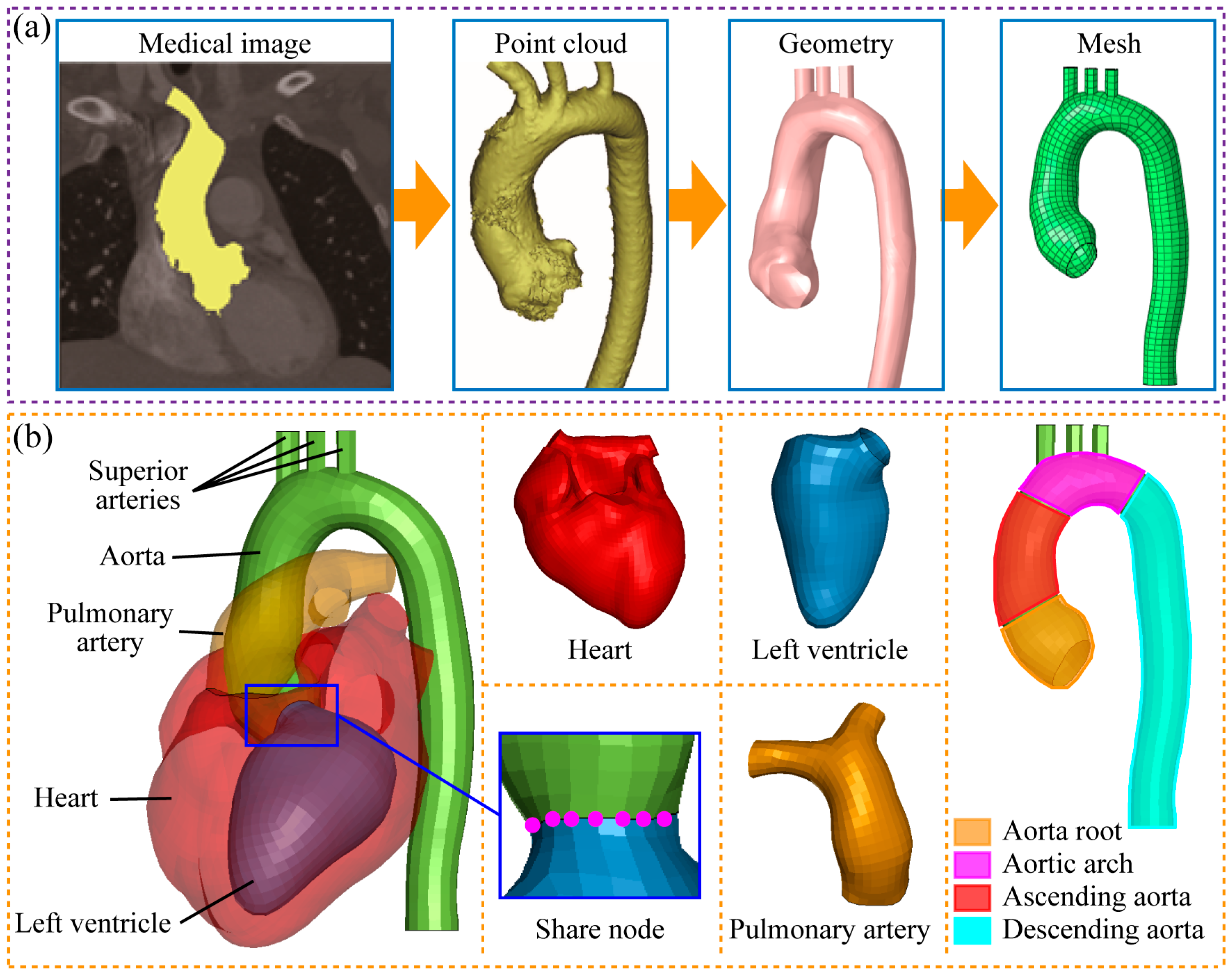
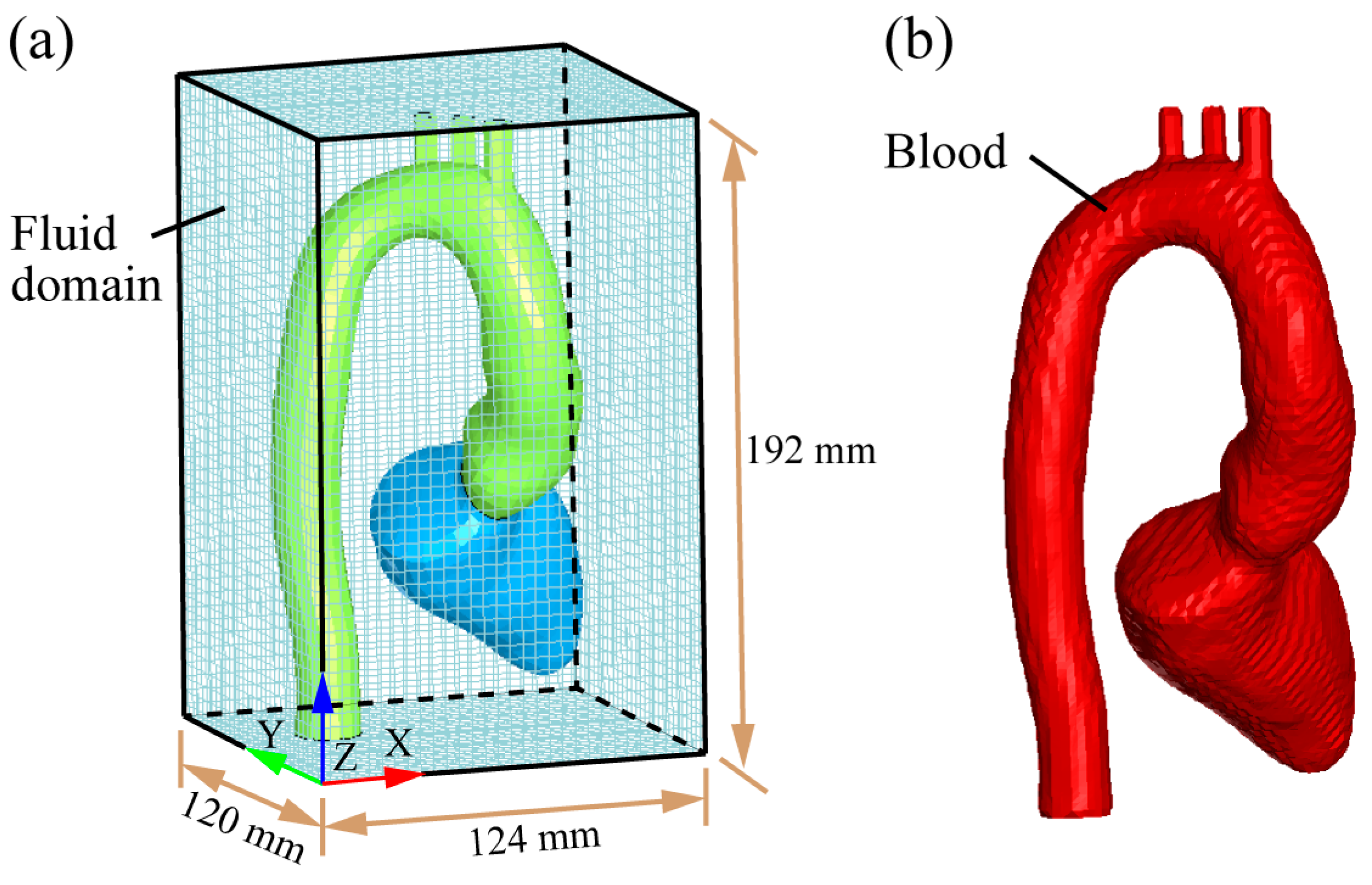
2.2. Establishment of Heart–Aorta FSI Model
| Sinus of Valsalva | Sinotubular Junction | Mid Ascending | Mid Descending | Diaphragm | |
|---|---|---|---|---|---|
| Nevsky et al. 2011 [31] | 31.1–33.2 | 26.7–28.5 | 27.2–29.1 | 20.3–22.1 | 19.3–20.8 |
| Wei et al. 2019 [23] | 27.4 | 27.8 | 27.1 | 20.8 | 18.1 |
| Section diameters | 32.3 ± 0.8 | 27.1 ± 0.3 | 26.8 ± 0.6 | 21.2 ± 0.5 | 19.4 ± 0.1 |
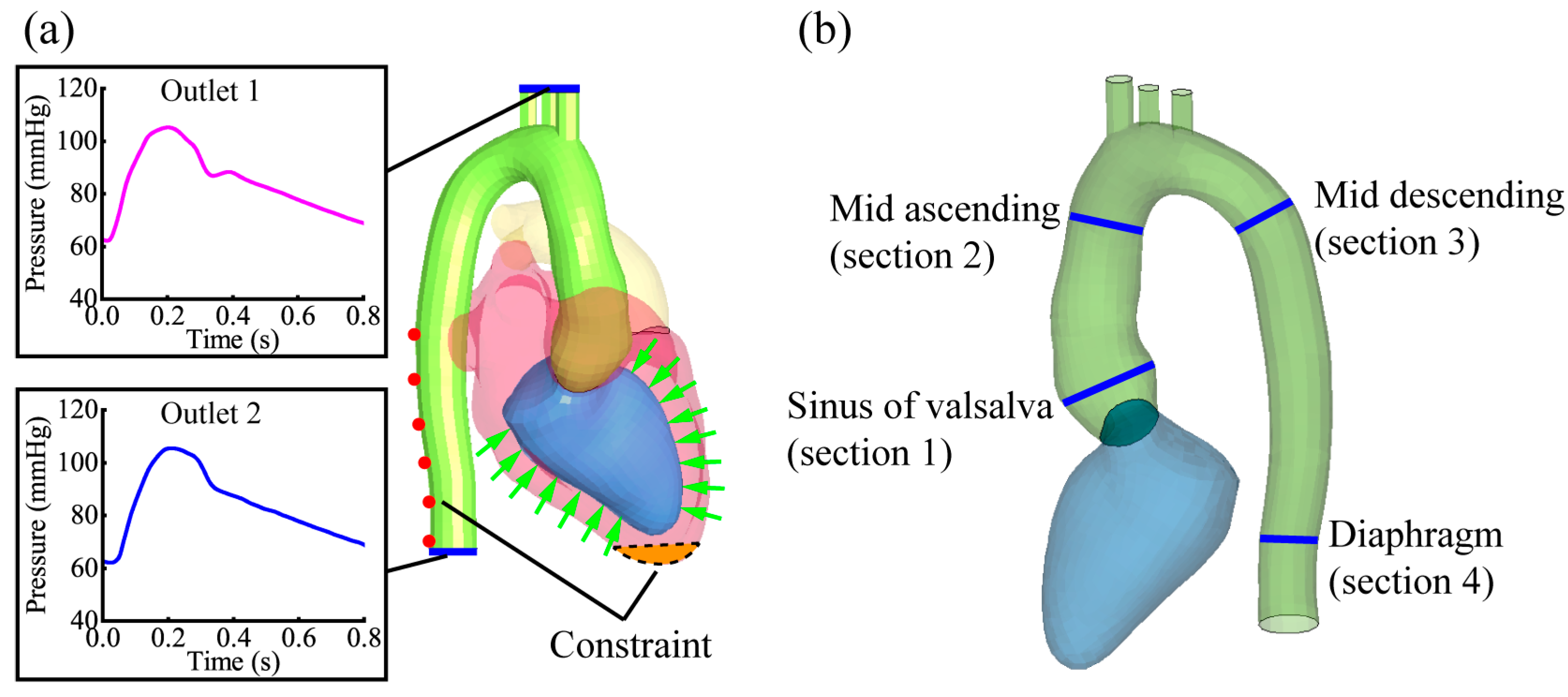
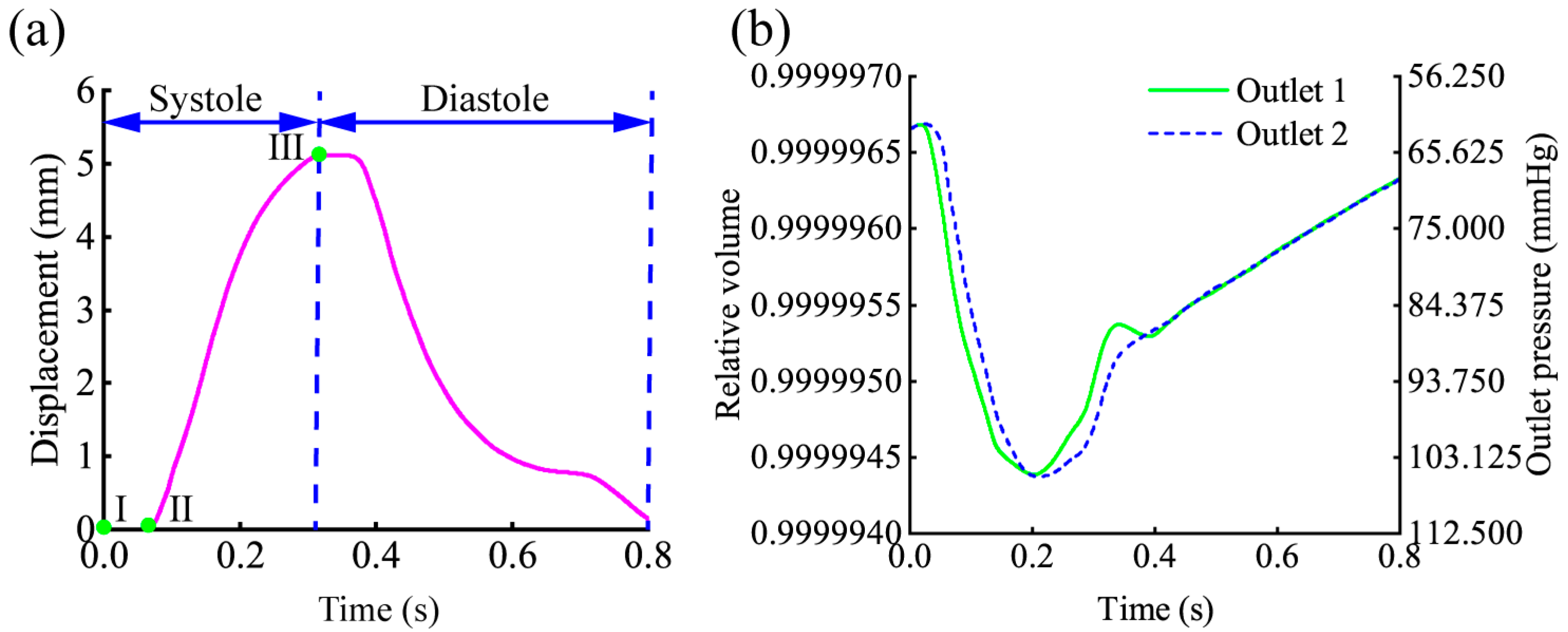
2.3. Simulation Boundary and Output Settings
2.4. Analysis of Heart–Aorta FSI at Different Physiological States
3. Results and Discussion
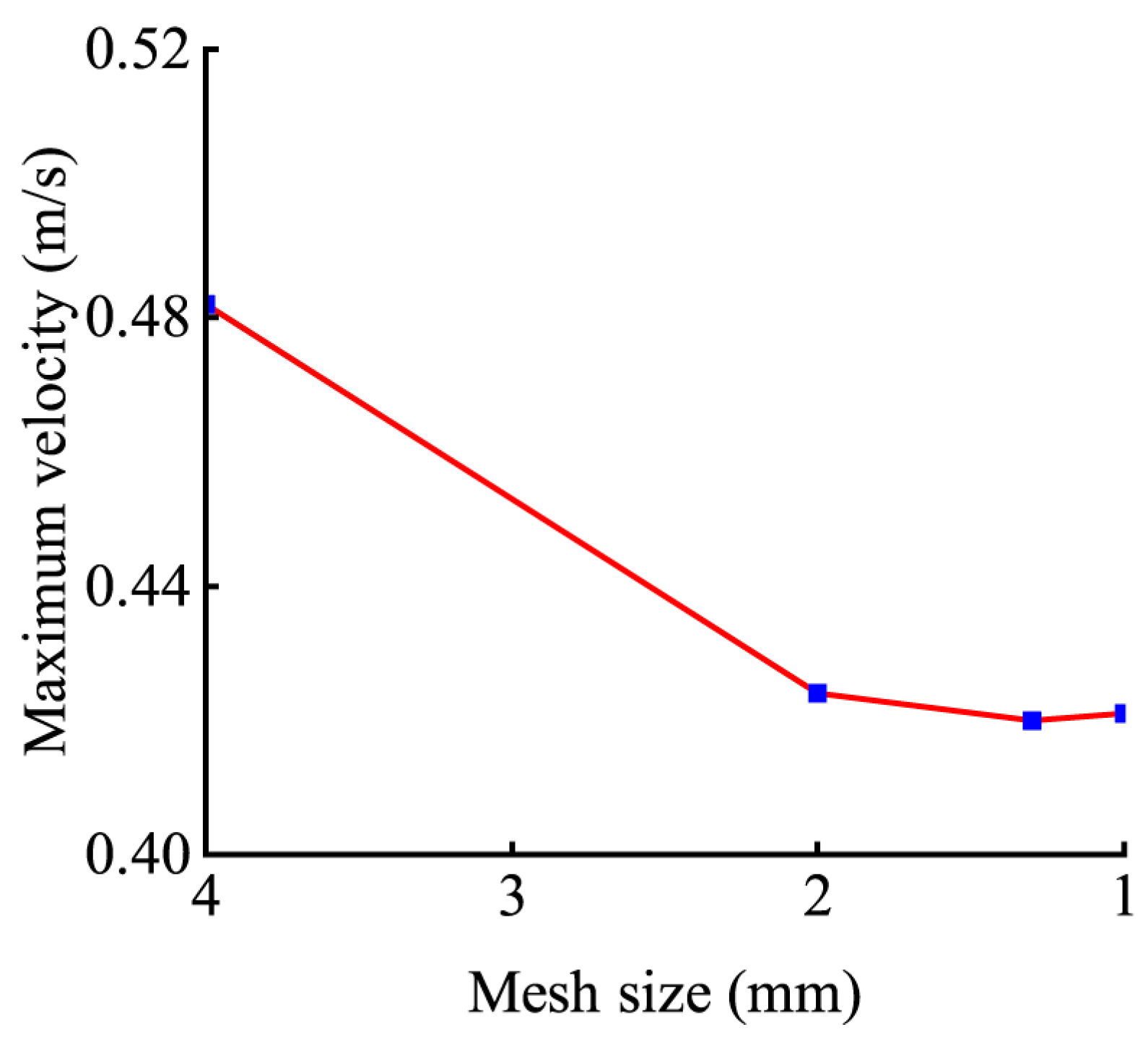
3.1. Mesh Sensitivity Analysis
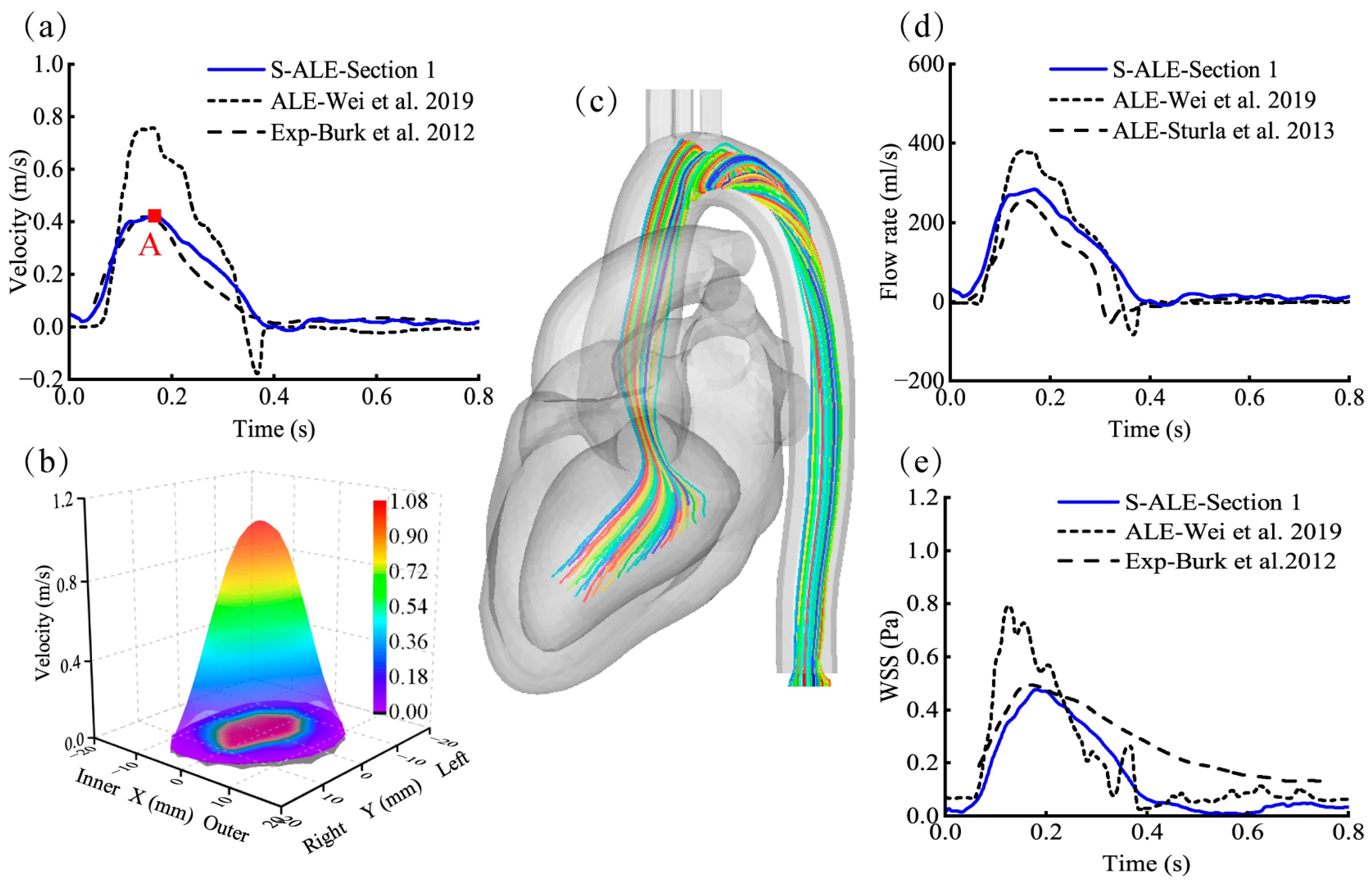
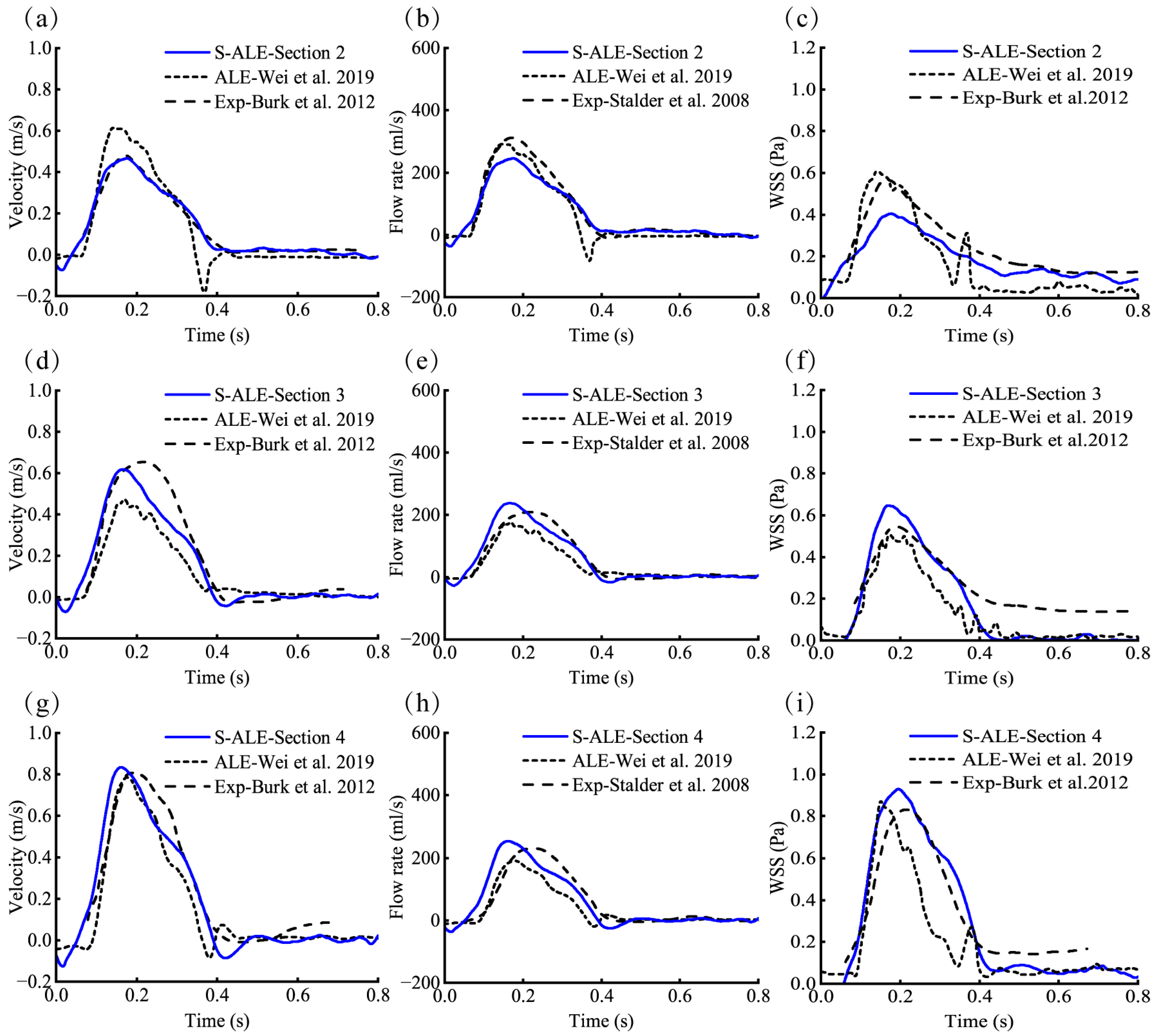
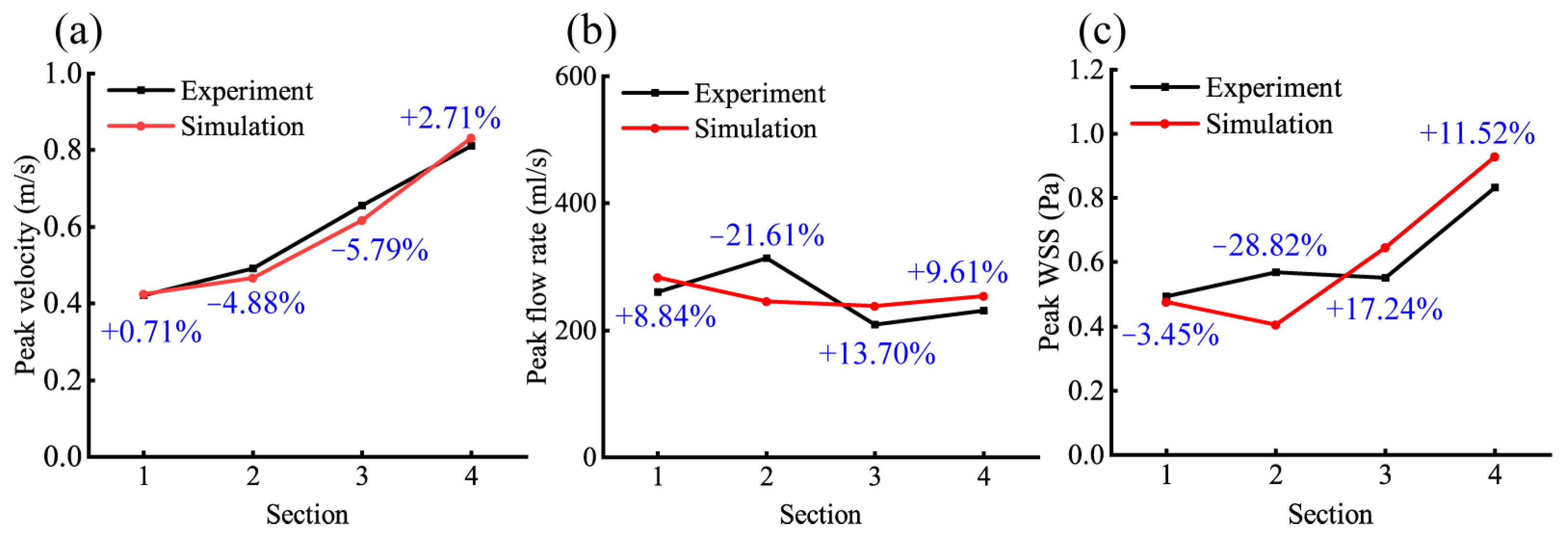
3.2. Validation of the FSI Numerical Model
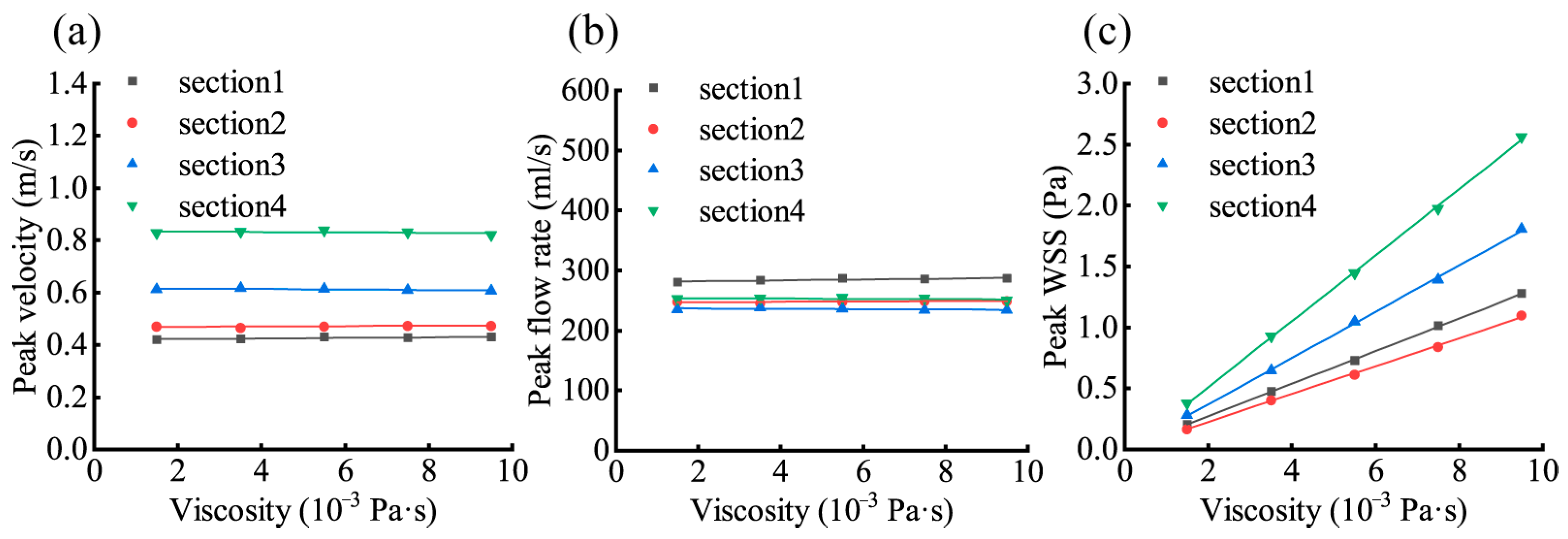
3.3. Effect of Changes in Blood Viscosity on the Aortic Hemodynamic Response
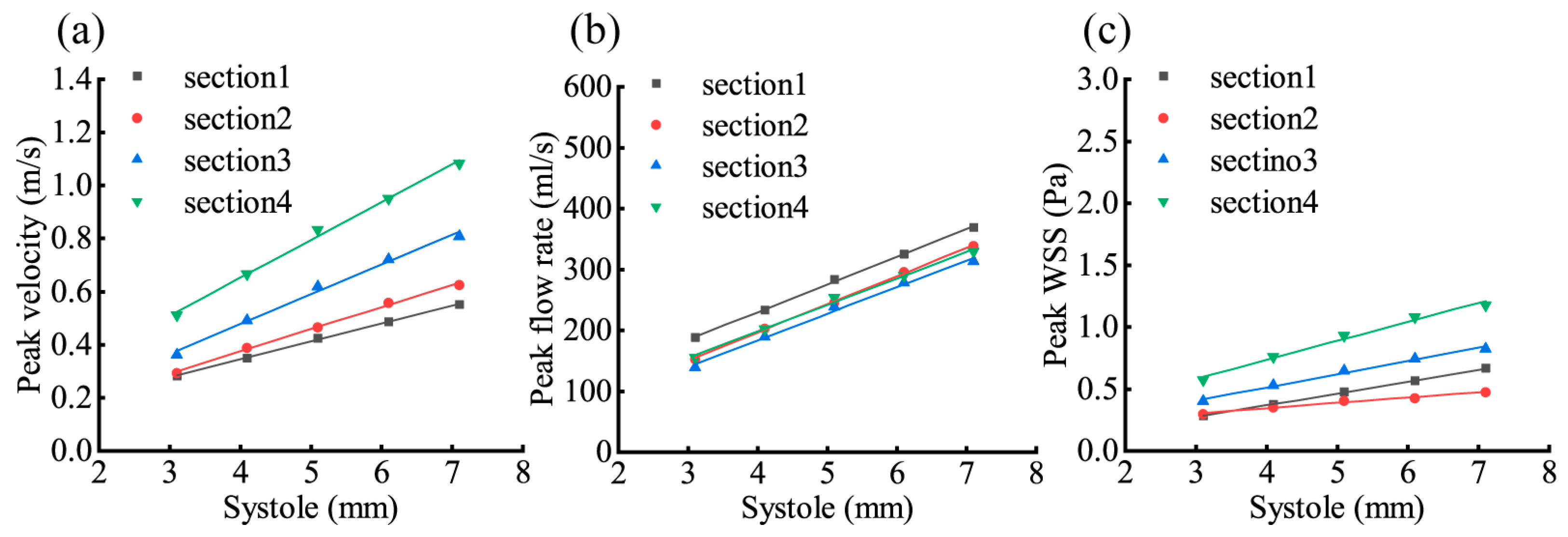
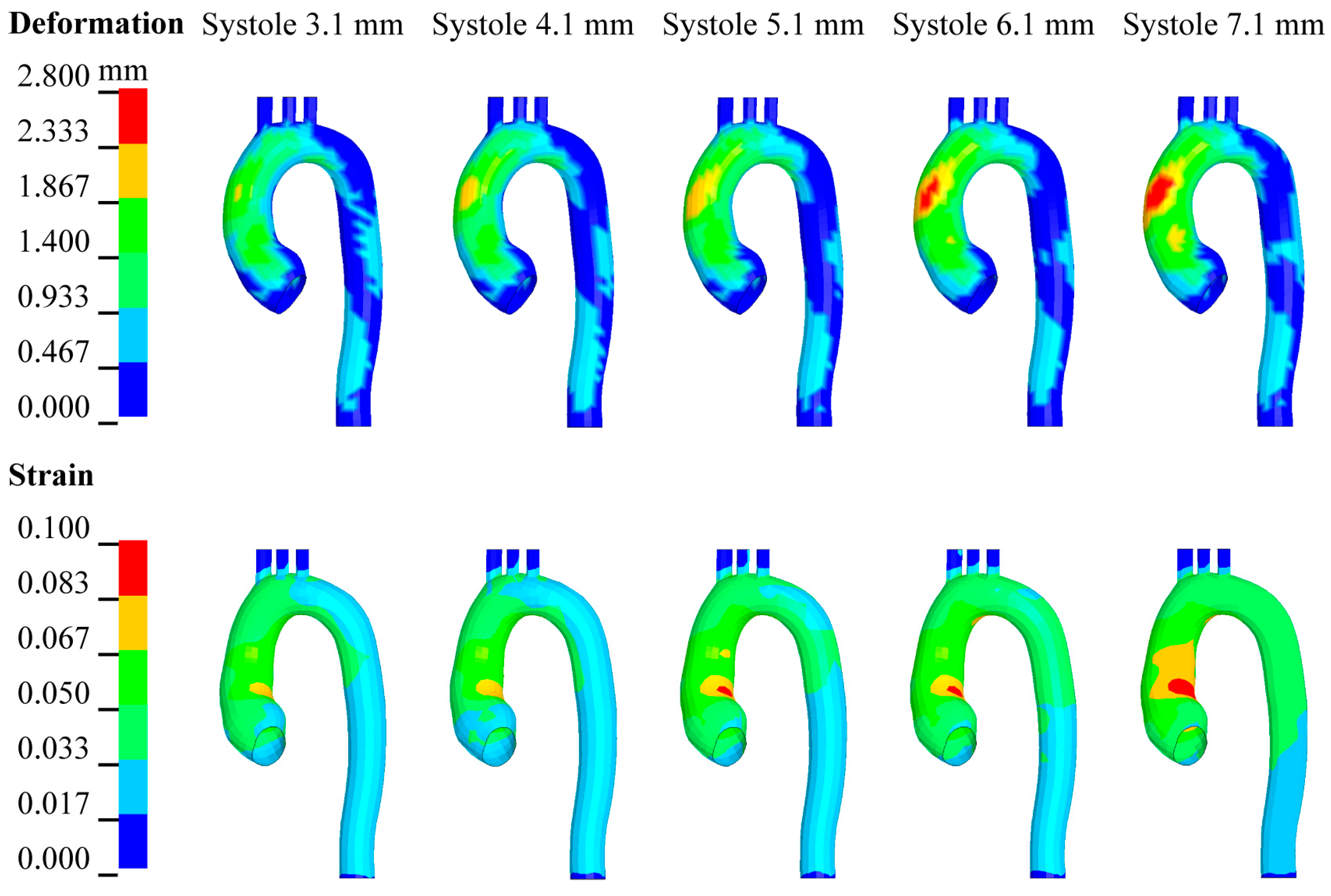
3.4. Effect of Changes in LV Systole on Aortic Hemodynamic Response
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Ghayesh, M.H.; Kotousov, A.; Zander, A.C.; Dawson, J.A.; Psaltis, P.J. Fluid-structure interaction study for biomechanics and risk factors in Stanford type A aortic dissection. Int. J. Numer. Meth. Biomed. Eng. 2023, 39, e3736. [Google Scholar] [CrossRef] [PubMed]
- Mesri, A.; Niazmand, H.; Deyranlou, A.; Reza, S.M. Fluid-structure interaction in abdominal aortic aneurysms: Structural and geometrical considerations. Int. J. Mod. Phys. C 2015, 26, 1550038. [Google Scholar] [CrossRef]
- Burk, J.; Blanke, P.; Stankovic, Z.; Barker, A.; Russe, M.; Geiger, J.; Frydrychowicz, A.; Langer, M.; Markl, M. Evaluation of 3D blood flow patterns and wall shear stress in the normal and dilated thoracic aorta using flow-sensitive 4D CMR. J. Cardiovasc. Magn. Reson. 2012, 14, 84. [Google Scholar] [CrossRef]
- Stalder, A.F.; Russe, M.F.; Frydrychowicz, A.; Bock, J.; Hennig, J.; Markl, M. Quantitative 2D and 3D phase contrast MRI: Optimized analysis of blood flow and vessel wall parameters. Magn. Reson. Med. 2008, 60, 1218–1231. [Google Scholar] [CrossRef]
- Hirschhorn, M.; Tchantchaleishvili, V.; Stevens, R.; Rossano, J.; Throckmorton, A. Fluid-structure interaction modeling in cardiovascular medicine-A systematic review 2017–2019. Med. Eng. Phys. 2020, 78, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Syed, F.; Khan, S.; Toma, M. Modeling dynamics of the cardiovascular system using fluid-structure interaction methods. Biology 2023, 12, 1026. [Google Scholar] [CrossRef]
- Hou, T.; Wei, X.; Iqbal, A.A.; Yang, X.; Wang, J.; Ren, Y.; Yan, S. Advances in biomedical fluid–structure interaction: Methodologies and applications from an interfacing perspective. Phys. Fluids 2024, 36, 21301. [Google Scholar] [CrossRef]
- Mourato, A.; Valente, R.; Xavier, J.; Brito, M.; Avril, S.; de Sá, J.C.; Tomás, A.; Fragata, J. Computational modelling and simulation of fluid structure interaction in aortic aneurysms: A systematic review and discussion of the clinical potential. Appl. Sci. 2022, 12, 8049. [Google Scholar] [CrossRef]
- Abbas, S.S.; Nasif, M.S.; Al-Waked, R. State-of-the-art numerical fluid–structure interaction methods for aortic and mitral heart valves simulations: A review. Simul.-Trans. Soc. Mod. Sim. 2022, 98, 3–34. [Google Scholar] [CrossRef]
- Wu, Q.; He, Y.; Yu, Z.; Wang, J.; Fan, W. Fluid-structure interaction analysis of vessel-bridge-steel floating fender collisions. Ocean Eng. 2024, 295, 116828. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, D.; Wu, W. Numerical analysis method of ship-ice collision-induced vibration of the polar transport vessel based on the full coupling of ship-ice-water-air. J. Ocean Eng. Sci. 2023, 8, 323–335. [Google Scholar] [CrossRef]
- Lopes, D.; Agujetas, R.; Puga, H.; Teixeira, J.; Lima, R.; Alejo, J.P.; Ferrera, C. Analysis of finite element and finite volume methods for fluid-structure interaction simulation of blood flow in a real stenosed artery. Int. J. Mech. Sci. 2021, 207, 106650. [Google Scholar] [CrossRef]
- Ong, C.W.; Kabinejadian, F.; Xiong, F.; Wong, Y.R.; Toma, M.; Nguyen, Y.N.; Chua, K.J.; Cui, F.S.; Ho, P.; Leo, H. Pulsatile flow investigation in development of thoracic aortic aneurysm: An in-vitro validated fluid structure interaction analysis. J. Appl. Fluid Mech. 2019, 12, 1855–1872. [Google Scholar] [CrossRef]
- Kemp, I.; Dellimore, K.; Rodriguez, R.; Scheffer, C.; Blaine, D.; Weich, H.; Doubell, A. Experimental validation of the fluid–structure interaction simulation of a bioprosthetic aortic heart valve. Australas. Phys. Eng. S. 2013, 36, 363–373. [Google Scholar] [CrossRef]
- Scotti, C.M.; Finol, E.A. Compliant biomechanics of abdominal aortic aneurysms: A fluid-structure interaction study. Comput. Struct. 2007, 85, 1097–1113. [Google Scholar] [CrossRef]
- Valente, R.; Mourato, A.; Brito, M.; Xavier, J.; Tomás, A.; Avril, S. Fluid-structure interaction modeling of ascending thoracic aortic aneurysms in SimVascular. Biomechanics 2022, 2, 189–204. [Google Scholar] [CrossRef]
- Hsu, M.; Bazilevs, Y. Blood vessel tissue prestress modeling for vascular fluid-structure interaction simulation. Finite Elem. Anal. Des. 2011, 47, 593–599. [Google Scholar] [CrossRef]
- Wang, X.; Li, X. Fluid-structure interaction based study on the physiological factors affecting the behaviors of stented and non-stented thoracic aortic aneurysms. J. Biomech. 2011, 44, 2177–2184. [Google Scholar] [CrossRef]
- Fadhil, N.A.; Hammoodi, K.A.; Jassim, L.; Al-Asadi, H.A.; Habeeb, L.J. Multiphysics analysis for fluid–structure interaction of blood biological flow inside three-dimensional artery. Curved Layer. Struct. 2023, 10, 20220187. [Google Scholar] [CrossRef]
- Issakhov, A.; Sabyrkulova, A.; Abylkassymova, A. Numerical modeling of the fluid-structure interaction during blood flow in a flexible stenotic aorta. Int. Commun. Heat Mass 2024, 158, 107857. [Google Scholar] [CrossRef]
- Taheri, R.A.; Razaghi, R.; Bahramifar, A.; Morshedi, M.; Mafi, M.; Karimi, A. Interaction of the blood components with ascending thoracic aortic aneurysm wall: Biomechanical and fluid analyses. Life 2022, 12, 1296. [Google Scholar] [CrossRef] [PubMed]
- Tango, A.M.; Salmonsmith, J.; Ducci, A.; Burriesci, G. Validation and extension of a fluid-structure interaction model of the healthy aortic valve. Cardiovasc. Eng. Technol. 2018, 9, 739–751. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Kahn, C.J.F.; Behr, M. Fluid-structure interaction simulation of aortic blood flow by ventricular beating: A preliminary model for blunt aortic injuries in vehicle crashes. Int. J. Crashworthiness 2019, 3, 229–306. [Google Scholar] [CrossRef]
- Sturla, F.; Votta, E.; Stevanella, M.; Conti, C.A.; Redaelli, A. Impact of modeling fluid-structure interaction in the computational analysis of aortic root biomechanics. Med. Eng. Phys. 2013, 35, 1721–1730. [Google Scholar] [CrossRef]
- Lee, S.H.; Kent, R. Blood flow and fluid-structure interactions in the human aorta during traumatic rupture conditions. Stapp Car Crash J. 2007, 51, 211–233. [Google Scholar]
- Tong, F.; Lan, F.; Chen, J.; Li, D.; Li, X. Numerical study on the injury mechanism of blunt aortic rupture of the occupant in frontal and side-impact. Int. J. Crashworthiness 2023, 28, 270–279. [Google Scholar] [CrossRef]
- Maceira, A.M.; Prasad, S.K.; Khan, M.; Pennell, D.J. Normalized left ventricular systolic and diastolic function by steady state free precession cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 2006, 8, 417–426. [Google Scholar] [CrossRef]
- Crosetto, P.; Reymond, P.; Deparis, S.; Kontaxakis, D.; Stergiopulos, N.; Quarteroni, A. Fluid-structure interaction simulation of aortic blood flow. Comput. Fluids 2011, 43, 46–57. [Google Scholar] [CrossRef]
- Brown, S.; Wang, J.; Ho, H.; Tullis, S. Numeric simulation of fluid-structure interaction in the aortic arch. In Book Computational Biomechanics for Medicine; Wittek, A., Miller, K., Nielsen, P.M., Eds.; Springer: New York, NY, USA, 2013; pp. 13–23. [Google Scholar]
- Ruan, J.; El-Jawahri, R.; Chai, L.; Barbat, S.; Prasad, P. Prediction and analysis of human thoracic impact responses and injuries in cadaver impacts using a full human body finite element model. Stapp Car Crash J. 2003, 47, 299–321. [Google Scholar]
- Nevsky, G.; Jacobs, J.E.; Lim, R.P.; Donnino, R.; Babb, J.S.; Srichai, M.B. Sex-specific normalized reference values of heart and great vessel dimensions in cardiac CT angiography. AJR Am. J. Roentgenol. 2011, 196, 788–794. [Google Scholar] [CrossRef]
- Katritsis, D.; Kaiktsis, L.; Chaniotis, A.; Pantos, J.; Efstathopoulos, E.P.; Marmarelis, V. Wall shear stress: Theoretical considerations and methods of measurement. Prog. Cardiovasc. Dis. 2007, 49, 307–329. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Guo, Z.; Sakamoto, M.; Matsuzawa, T. Fluid-structure interaction within a layered aortic arch model. J. Biol. Phys. 2006, 32, 435–454. [Google Scholar] [CrossRef] [PubMed]
- LSTC. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2021. [Google Scholar]
- Kim, H.J.; Vignon-Clementel, I.E.; Figueroa, C.A.; Ladisa, J.F.; Jansen, K.E.; Feinstein, J.A.; Taylor, C.A. On coupling a lumped parameter heart model and a three-dimensional finite element aorta model. Ann. Biomed. Eng. 2009, 37, 2153–2169. [Google Scholar] [CrossRef] [PubMed]
| Weakened Systole | Normal Systole | Enhanced Systole | |||
|---|---|---|---|---|---|
| LV systole schematic | 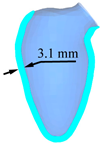 | 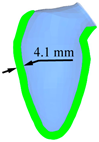 | 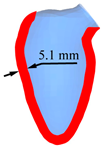 | 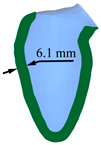 | 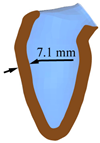 |
| Peak displacement | 3.1 mm | 4.1 mm | 5.1 mm | 6.1 mm | 7.1 mm |
| Ejection volume | 49.4 ml | 58.3 ml | 66.6 ml | 74.2 ml | 81.2 ml |
| Section | Peak Velocity | Peak Flow Rate | Peak WSS | |||
|---|---|---|---|---|---|---|
| r | ε | r | ε | r | ε | |
| 1 | 0.8746 | 0.0025 | 0.8810 | 0.0025 | 0.9999 | 0.1814 |
| 2 | 0.6510 | 0.0013 | 0.6852 | 0.0013 | 0.9996 | 0.1840 |
| 3 | −0.6318 | −0.0015 | −0.6581 | −0.0013 | 0.9997 | 0.1836 |
| 4 | −0.6260 | −0.0010 | −0.6020 | −0.0010 | 0.9997 | 0.1858 |
| Section | Peak Velocity | Peak Flow Rate | Peak WSS | |||
|---|---|---|---|---|---|---|
| r | ε | r | ε | r | ε | |
| 1 | 0.9996 | 0.1620 | 0.9996 | 0.1622 | 0.9998 | 0.2028 |
| 2 | 0.9998 | 0.1786 | 0.9996 | 0.1869 | 0.9935 | 0.1090 |
| 3 | 0.9968 | 0.1869 | 0.9971 | 0.1891 | 0.9957 | 0.1701 |
| 4 | 0.9978 | 0.1767 | 0.9978 | 0.1770 | 0.9932 | 0.1695 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Lan, F.; Chen, J.; Chen, X. Numerical Simulation and Analysis of Heart–Aorta Fluid–Structure Interaction Based on S-ALE Method. Appl. Sci. 2025, 15, 7769. https://doi.org/10.3390/app15147769
Li X, Lan F, Chen J, Chen X. Numerical Simulation and Analysis of Heart–Aorta Fluid–Structure Interaction Based on S-ALE Method. Applied Sciences. 2025; 15(14):7769. https://doi.org/10.3390/app15147769
Chicago/Turabian StyleLi, Xiong, Fengchong Lan, Jiqing Chen, and Xinzhe Chen. 2025. "Numerical Simulation and Analysis of Heart–Aorta Fluid–Structure Interaction Based on S-ALE Method" Applied Sciences 15, no. 14: 7769. https://doi.org/10.3390/app15147769
APA StyleLi, X., Lan, F., Chen, J., & Chen, X. (2025). Numerical Simulation and Analysis of Heart–Aorta Fluid–Structure Interaction Based on S-ALE Method. Applied Sciences, 15(14), 7769. https://doi.org/10.3390/app15147769






