Improved Hybrid A* Algorithm Based on Lemming Optimization for Path Planning of Autonomous Vehicles
Abstract
1. Introduction
- (1)
- Graph Search-Based Algorithms
- (2)
- Sampling-Based Algorithms
- (3)
- Interpolation-Based Algorithms
- (4)
- Numerical Optimization-Based Algorithms
- (5)
- Machine Learning-Based Algorithms
2. Algorithm Overview
2.1. Hybrid A* Algorithm
2.2. Lemming Optimization Algorithm
2.2.1. Position Initialization
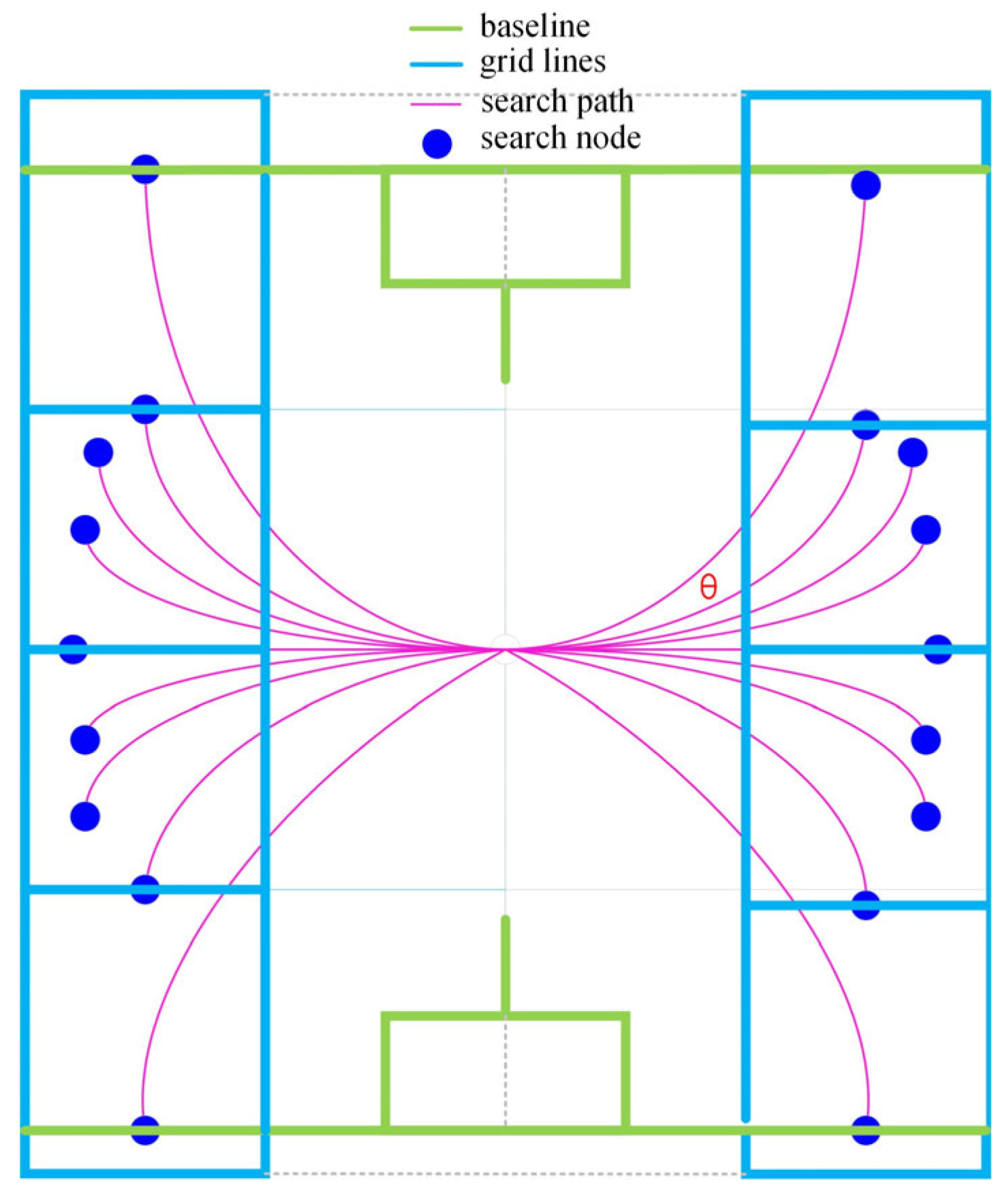
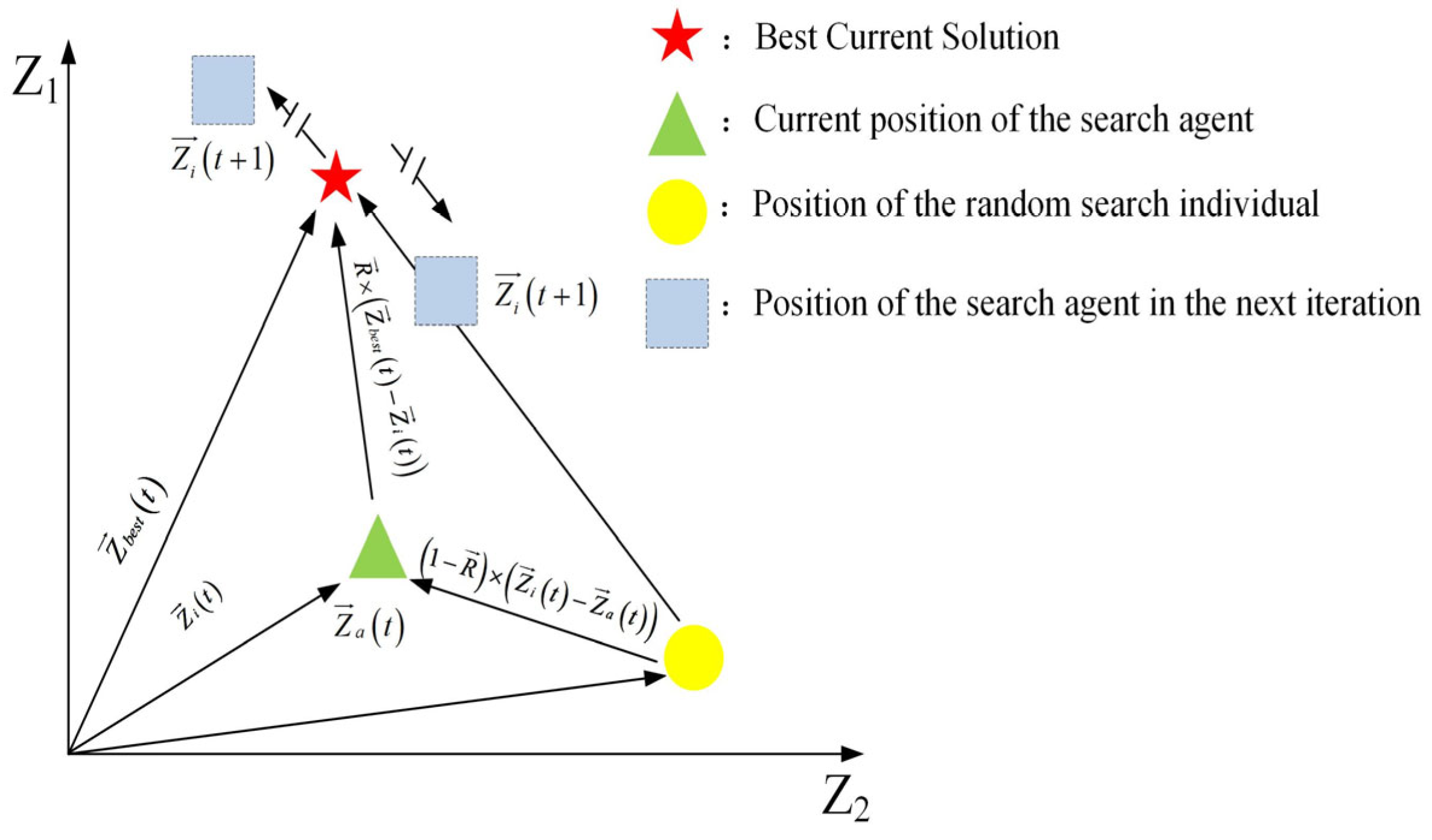
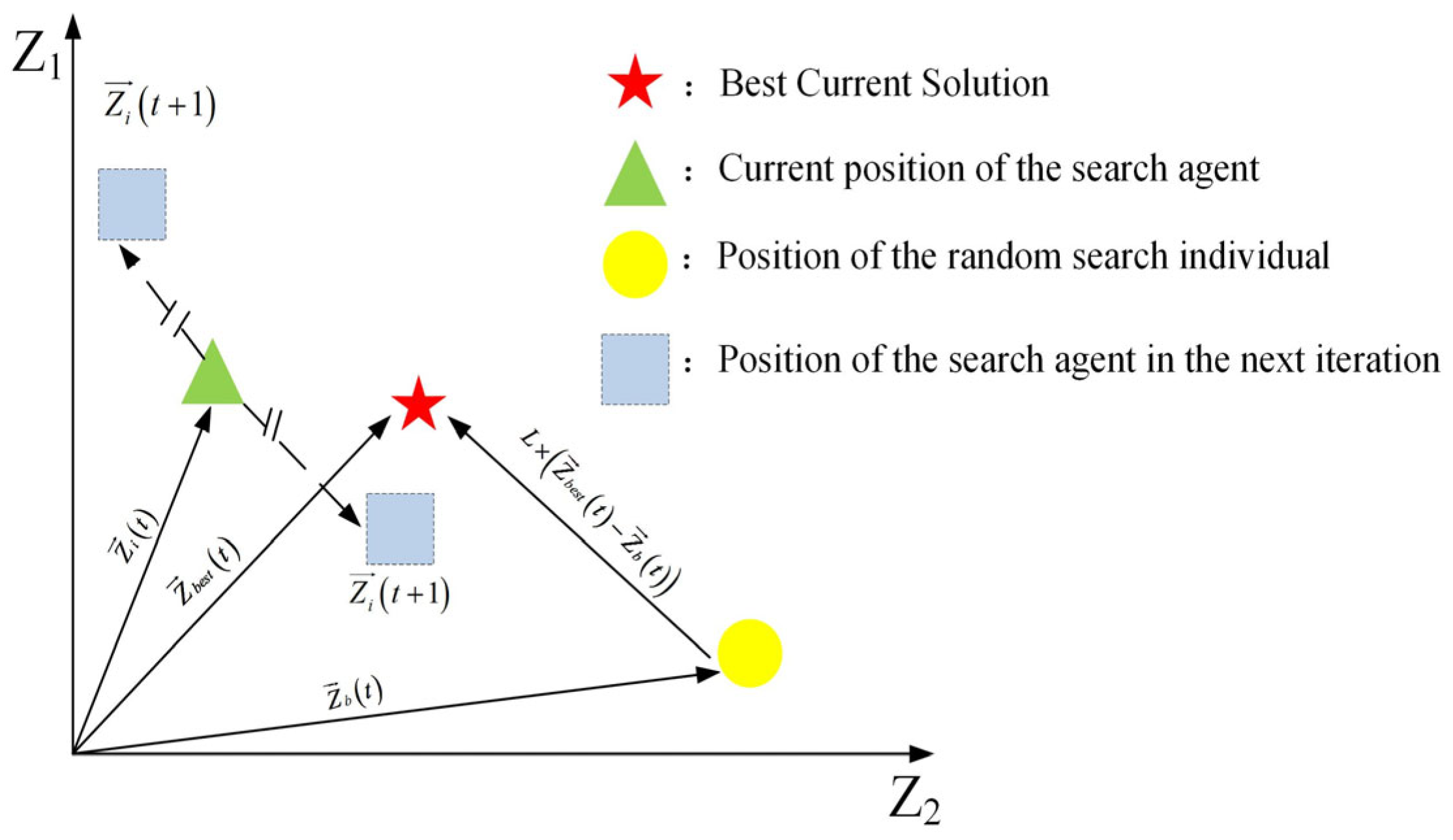
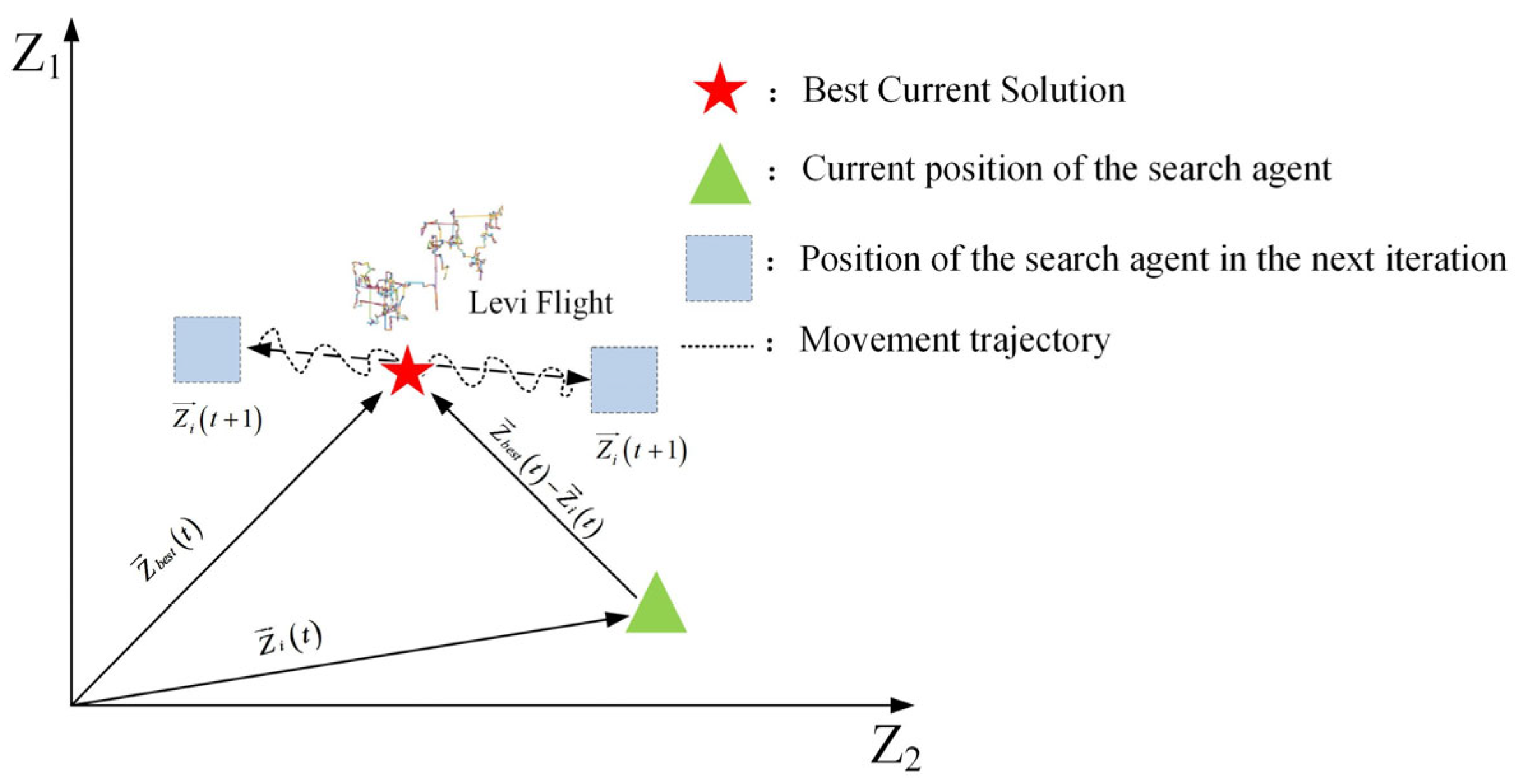
2.2.2. Behavioral Patterns
- (1)
- Long-distance migration
- (2)
- Digging holes
- (3)
- Gathering food
- (4)
- Evading predators
3. Improved Hybrid A* Algorithm
3.1. Distance Heuristic Function
- (1)
- Manhattan distance:
- (2)
- Euclidean distance:
- (1)
- When d1 = d2
- (2)
- When d1 > d2
- (3)
- When d1 < d2
3.2. Steering Penalty Term
3.3. Reeds–Shepp Curves
4. Hybrid Path Planning Algorithm
4.1. Framework of Integrated Algorithms
| Algorithm 1. Layered optimization framework construction |
|
| Algorithm 2. Initialization of elite reserved stock |
|
4.2. Mechanism of Algorithm Fusion
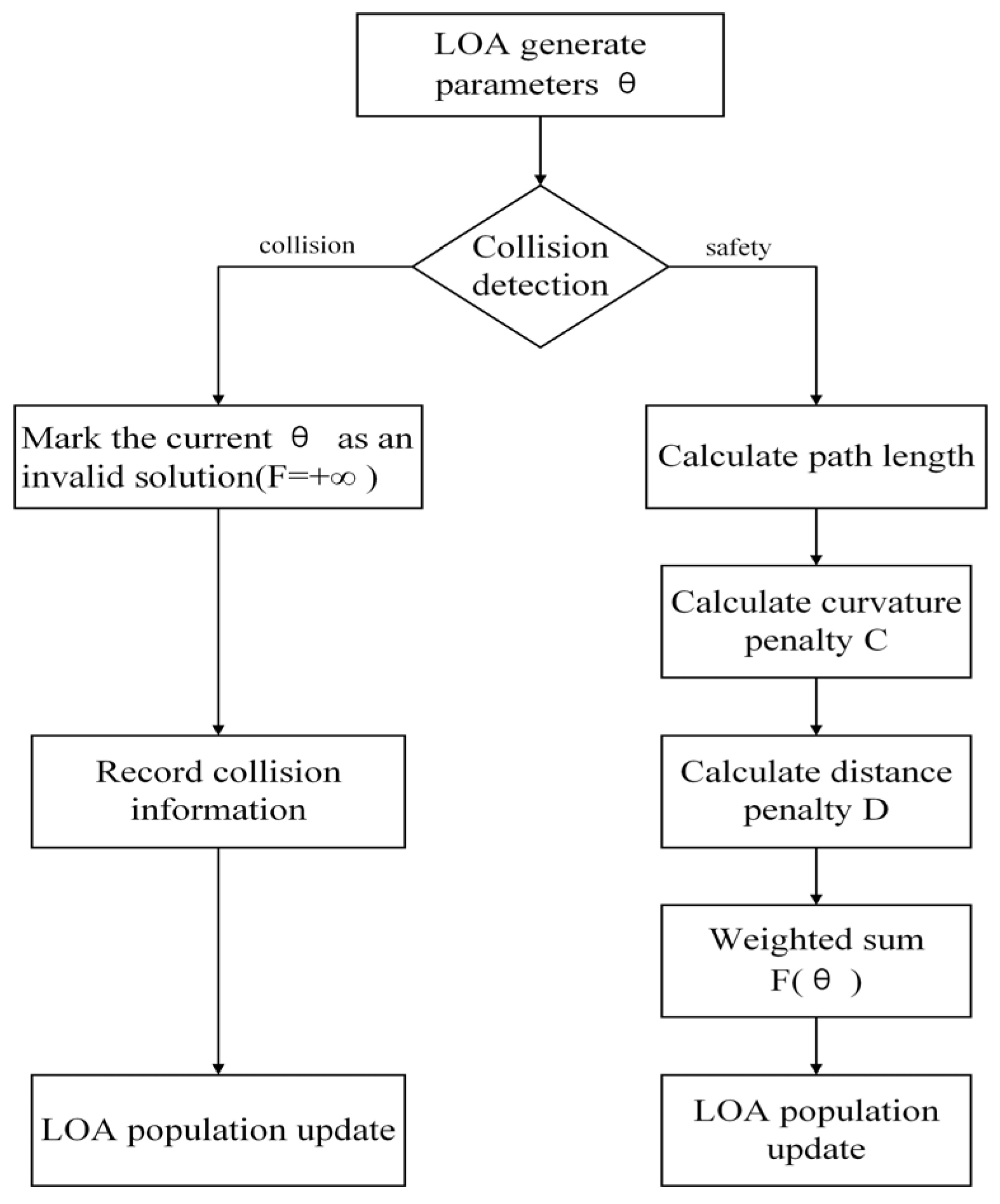
4.2.1. Objective Function (Fitness Function)
- (1)
- Global search phase (exploring diversity)
- (2)
- Local search phase (developing optimality)
4.2.2. Penalty Function
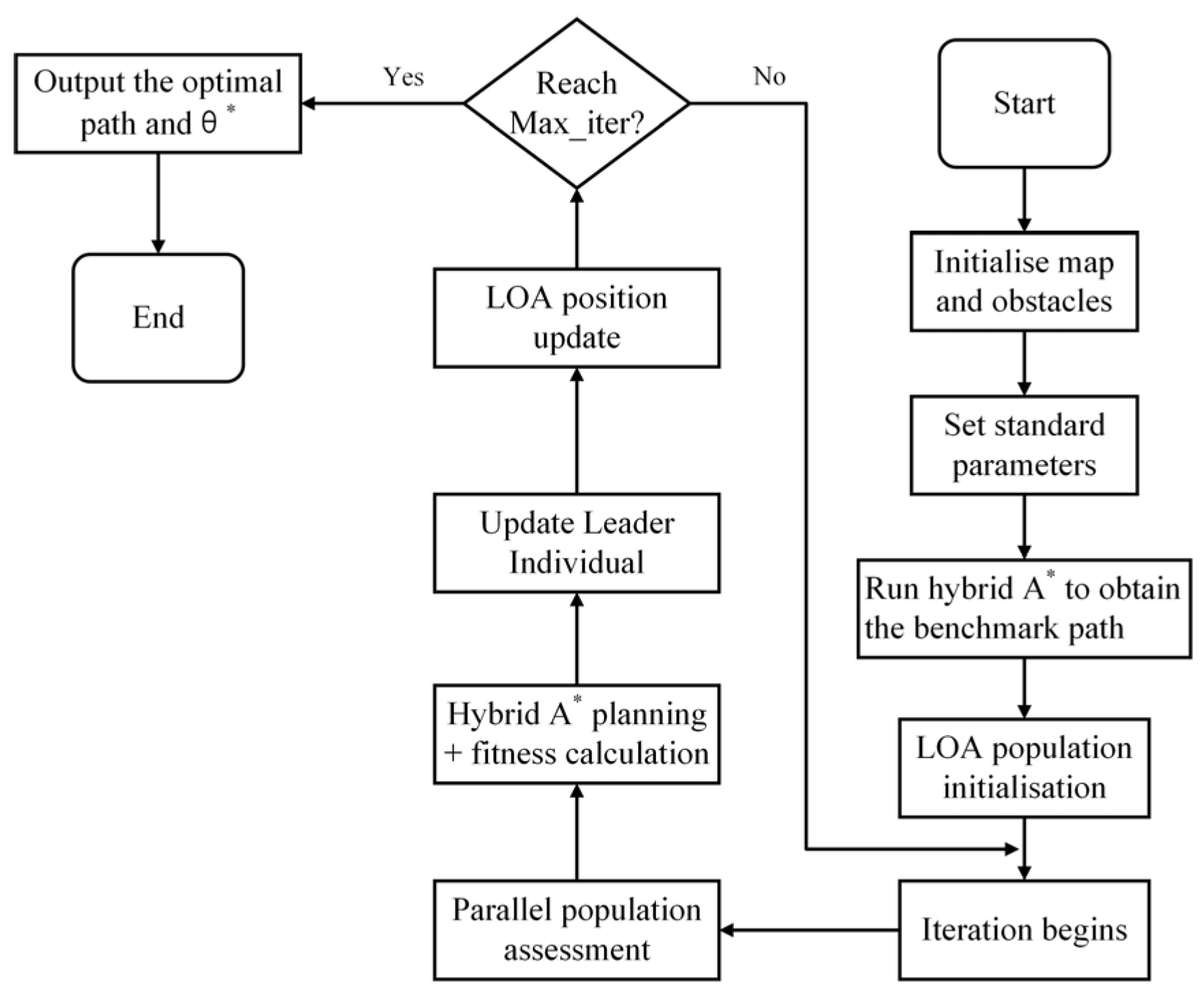
4.3. Fusion Algorithm Workflow
5. Simulation Experiments
5.1. Map Construction
5.2. Selection of Algorithm Parameters
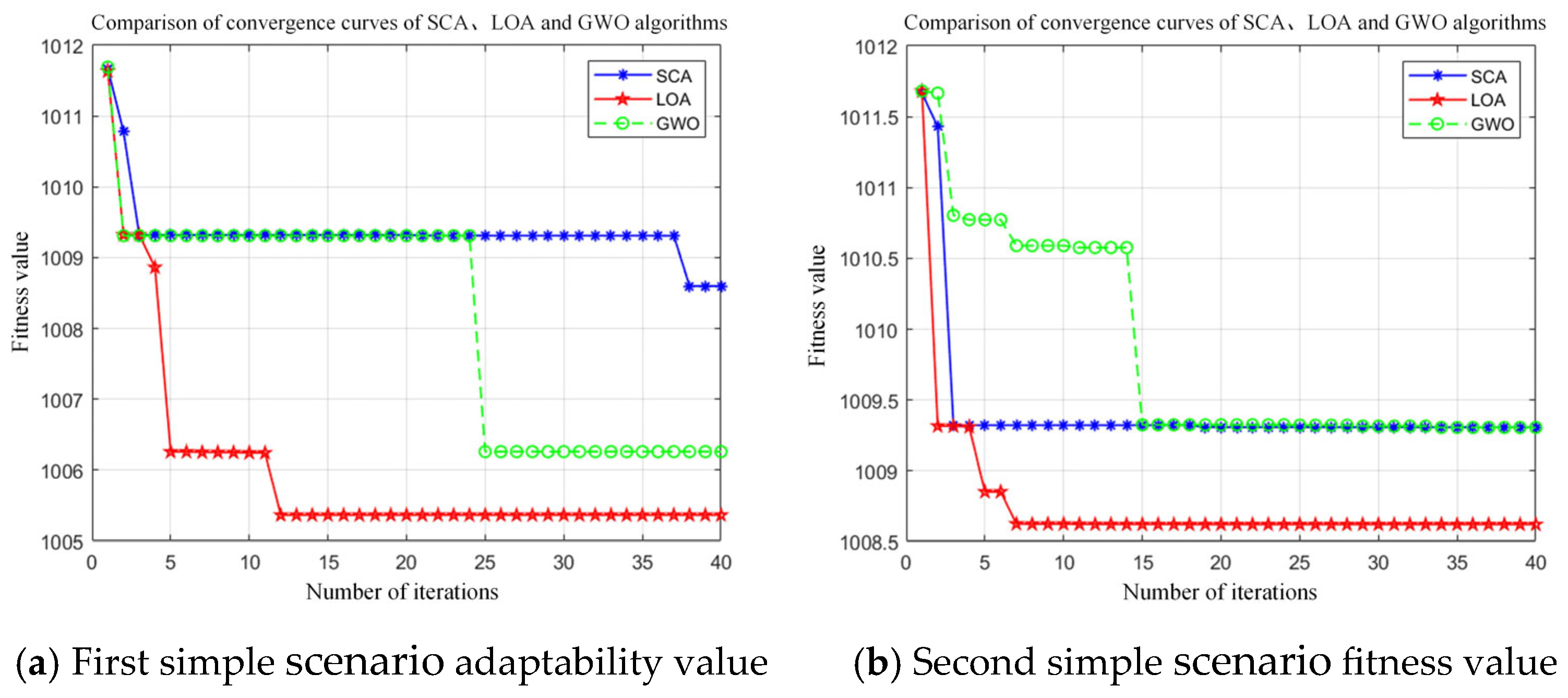
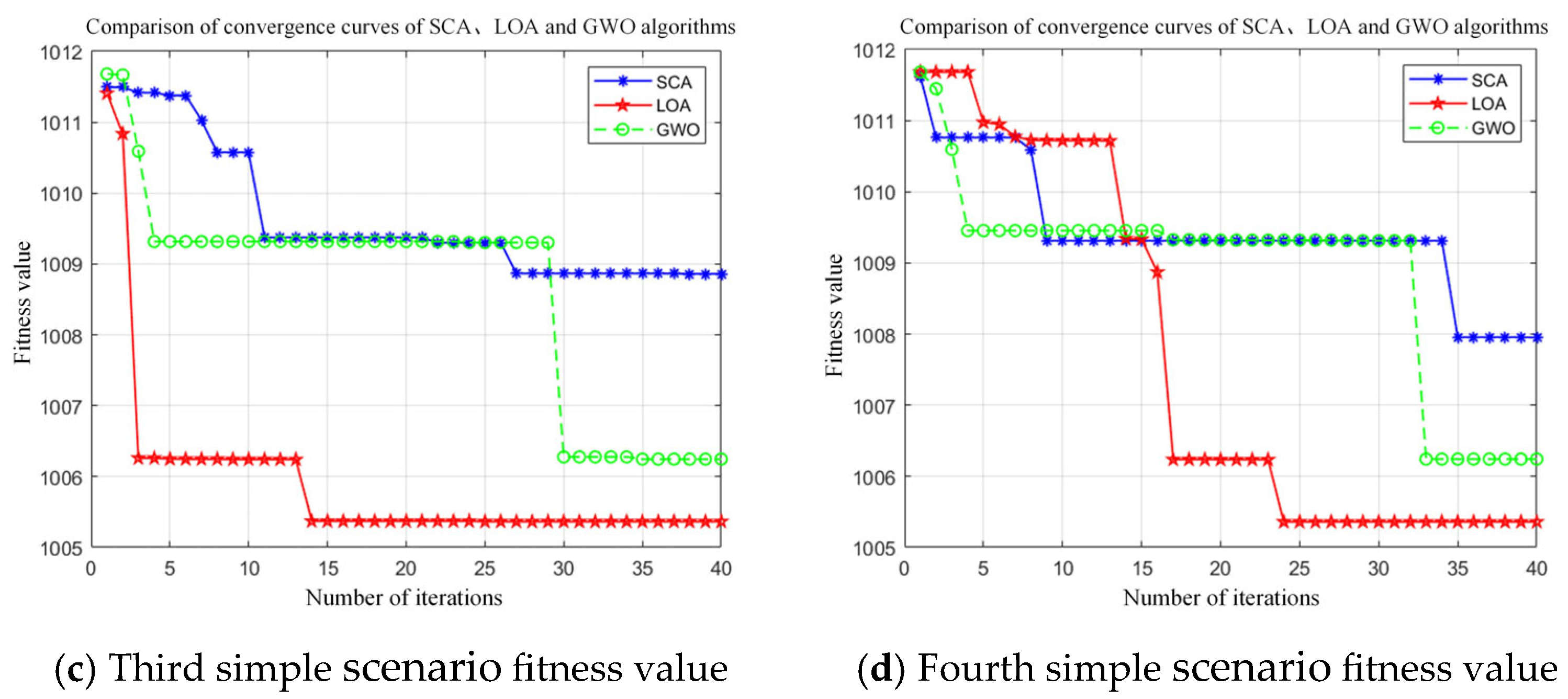
5.3. Simulation Result Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, F.Y. Driverless cars and their development. China High New Technol. 2019, 24–27. [Google Scholar] [CrossRef]
- Yuan, S.Z.; Li, J. Summary of Research on Path Planning of Driverless Vehicles. Auto Eng. 2019, 5, 11–13. [Google Scholar]
- Zhu, D.Q.; Yan, M.Z. A Review of Mobile Robot Path Planning Techniques. J. Control Decis. 2010, 25, 961–967. [Google Scholar] [CrossRef]
- Teng, S.; Hu, X.; Deng, P.; Li, B.; Li, Y.; Ai, Y.; Yang, D.; Li, L.; Xuanyuan, Z.; Zhu, F.; et al. Motion planning for autonomous driving: The state of the art and future perspectives. IEEE Trans. Intell. Veh. 2023, 8, 3692–3711. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, R.Y.; Zhang, Y.F.; Zhang, G. Autonomous Vehicle Trajectory Generation Based on Hybrid A* Algorithm. Automot. Dig. 2023, 44–54. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; Association for Computing Machinery: New York, NY, USA, 2022. [Google Scholar]
- Marchese, F.M. Multiple mobile robots path-planning with MCA. In Proceedings of the International Conference on Autonomic and Autonomous Systems (ICAS), Silicon Valley, CA, USA, 19–21 July 2006. [Google Scholar]
- Zhu, D.-D.; Sun, J.-Q. A new algorithm based on Dijkstra for vehicle path planning considering intersection attribute. IEEE Access 2021, 9, 19761–19775. [Google Scholar]
- Sang, W.; Lin, M. Research on AGV path planning integrating an improved A* algorithm and DWA algorithm. Appl. Sci. 2024, 14, 7551. [Google Scholar]
- Zhou, H.; Shang, T.; Wang, Y.; Zuo, L. Salp Swarm Algorithm Optimized A* Algorithm and Improved B-Spline Interpolation in Path Planning. Appl. Sci. 2025, 15, 5583. [Google Scholar]
- Shim, T.; Adireddy, G.; Yuan, H. Autonomous vehicle collision avoidance system using path planning and model predictive control based active front steering and wheel torque control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2012, 226, 767–778. [Google Scholar]
- Taghavifar, H. Optimal reinforcement learning and probabilistic-risk-based path planning and following of autonomous vehicles with obstacle avoidance. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 1427–1439. [Google Scholar]
- Reda, M.; Onsy, A.; Haikal, A.Y.; Ghanbari, A. Path planning algorithms in the autonomous driving system: A comprehensive review. Robot. Auton. Syst. 2024, 174, 104630. [Google Scholar]
- Zhu, S. Obstacle-Avoidance path planning of unmanned vehicles based on polynomial optimization. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 6988–6992. [Google Scholar]
- Zhou, W.; Li, J. Research on obstacle avoidance path planning of automatic driving vehicle. Auto Eng. 2018, 55–58. Available online: https://www.sohu.com/a/239903213_99949100 (accessed on 4 July 2025).
- Li, X.C. Smooth and collision-free trajectory generation in cluttered environments using cubic B-spline. Mech. Mach. Theory 2022, 169, 104606. [Google Scholar]
- Zheng, L.; Zeng, P.; Yang, W.; Li, Y.; Zhan, Z. Bézier curve-based trajectory planning for autonomous vehicles with collision avoidance. IET Intell. Transp. Syst. 2020, 14, 1882–1891. [Google Scholar]
- Zhu, Y.J.; Li, J.S.; Fen, M.Y.; Xu, Y.C. Autonomous parking path planning algorithm for intelligent vehicles based on numerical optimization. J. Mil. Transp. 2019, 21, 84–89. [Google Scholar]
- Hu, C.; Zhao, L.; Qu, G. Event-Triggered model predictive adaptive dynamic programming for road intersection path planning of unmanned ground vehicle. IEEE Trans. Veh. Technol. 2021, 70, 11228–11243. [Google Scholar]
- Ji, J.; Khajepour, A.; Melek, W.W.; Huang, Y. Path planning and tracking for vehicle collision avoidance based on model predictive control with mult constraints. IEEE Trans. Veh. Technol. 2016, 66, 952–964. [Google Scholar]
- Li, Y.; Liu, Y. Research on Path Planning Based on the Integrated Artificial Potential Field-Ant Colony Algorithm. Appl. Sci. 2025, 15, 4522. [Google Scholar]
- Bojarski, M.; Del Testa, D.; Dworakowski, D.; Firner, B.; Flepp, B.; Goyal, P.; Jackel, L.D.; Monfort, M.; Muller, U.; Zhang, J.; et al. End to end learning for self-driving cars. Comput. Sci. 2022. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Chao, T. Autonomous vehicle path planning algorithm based on improved Q-learning. In International Conference on Guidance, Navigation and Control; Springer Nature: Singapore, 2024. [Google Scholar]
- Zhang, L.; Zhang, Y.; Li, Y. Path planning for indoor mobile robot based on deep learning. Optik 2020, 219, 165096. [Google Scholar]
- Chen, L.; Wu, P.; Chitta, K.; Jaeger, B.; Geiger, A.; Li, H. End-to-end autonomous driving: Challenges and frontiers. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 10164–10183. [Google Scholar] [PubMed]
- Rodríguez, N.; Gupta, A.; Zabala, P.L.; Cabrera-Guerrero, G. Optimization algorithms combining (meta) heuristics and mathematical programming and its application in engineering. Math. Probl. Eng. 2018. [Google Scholar] [CrossRef]
- Bu, Z.; Korf, R.E. A*+ BFHS: A hybrid heuristic search algorithm. Proc. AAAI Conf. Artif. Intell. 2022, 36, 10138–10145. [Google Scholar]
- Hoel, C.J.; Driggs-Campbell, K.; Wolff, K.; Laine, L.; Kochenderfer, M.J. Combining planning and deep reinforcement learning in tactical decision making for autonomous driving. IEEE Trans. Intell. Veh. 2019, 5, 294–305. [Google Scholar]
- Nielsen, I.; Bocewicz, G.; Saha, S. Multi-agent path planning problem under a multi-objective optimization framework. In Distributed Computing and Artificial Intelligence, Special Sessions, 17th International Conference, L’Aquila, Italy, 17–19 June 2020; Springer International Publishing: Cham, Switzerland, 2021; pp. 5–14. [Google Scholar]
- Badue, C.; Guidolini, R.; Carneiro, R.V.; Azevedo, P.; Cardoso, V.B.; Forechi, A.; Jesus, L.; Berriel, R.; Paixao, T.M.; Mutz, F.; et al. Self-driving cars: A survey. Expert Syst. Appl. 2021, 165, 113816. [Google Scholar]
- Hu, J.; Wu, H.; Zhong, B.; Xiao, R. Swarm intelligence-based optimization algorithms: An overview and future research issues. Int. J. Autom. Control 2020, 14, 656–693. [Google Scholar]
- Xiao, Y.; Cui, H.; Abu Khurma, R.; Castillo, P.A. Artificial lemming algorithm: A novel bionic meta-heuristic technique for solving real-world engineering optimization problems. Artif. Intell. Rev. 2025, 58, 84. [Google Scholar]





| Algorithm Type | Core Technology | Advantageous Scenarios | Application |
|---|---|---|---|
| Layered planning framework | Hybrid A* + MPC | Structured roads | Benz DRIVEPILOT3.0 |
| Deep learning-driven | BEV-Transformer | Complex urban road conditions | Huawei ADS 3.0 |
| Hybrid enhancement | RRT + reinforcement learning | Extreme obstacle scenarios | Waymo Driver 5 |
| End-to-end architecture | Multimodal large model | Adaptation to all scenarios | Tesla Dojo platform |
| Algorithm | Advantages | Drawbacks | Applicable Scenarios |
|---|---|---|---|
| LOA | Strong global search capabilities for high-dimensional optimization problems | Slow convergence Sensitive parameter tuning | Multi-objective optimization problems Path planning |
| GWO | Simple structure with few parameters Fast convergence | Easy to fall into local optimality Strong dependence on initial population | Continuous space optimization Engineering design problems |
| SCA | Clear mathematical principles No gradient information required | Weak development capabilities Poor adaptability to dynamic environments | Low-dimensional nonlinear optimization Initial path generation |
| Hybrid A* algorithm | High path feasibility Better real-time performance | Higher computational complexity Insufficient path smoothing | Autopilot path planning Motion planning |
| Type of Punishment | Effect | Technical Implementation |
|---|---|---|
| Incomplete constraint penalty | Ensures that the path complies with the vehicle kinematics | Reeds–Shepp curve generation Hermit satisfaction |
| Obstacle collision penalty | Avoid paths that cross obstacles | Grid map (sign) and continuous monitoring (isPathClear) |
| Path length penalty | Prefers shorter paths | Fitness function (length_penalty) |
| Scene | Applicable Algorithm | Reeds–Shepp Advantage | Limitations |
|---|---|---|---|
| Structured roads | Hybrid A* | Fast calculation speed | Path may not be smooth |
| Extremely confined spaces | Reeds–Shepp + LOA | Kinematic assurance and global optimization | Parameter adjustment required |
| Highly dynamic environments | RRT | Quick obstacle avoidance | Low path quality |
| Off-road terrain | Reeds–Shepp + MPC | Good terrain adaptability | Need to predict coefficient of friction |
| Parameter Name | Function |
|---|---|
| Path length | Normalizes the path length, encouraging the generation of shorter paths |
| Curvature penalty | Penalizes sharp turns to ensure that the path satisfies the vehicle’s kinematic constraints (for example, min_r) |
| Distance penalty | Ensures that the path is free of obstacles to improve the safety |
| Collision penalty | If the path collides with an obstacle, the system returns directly to +∞ and infeasible solutions are eliminated |
| Parameter/Variable | Function | Expression Value |
|---|---|---|
| Max_iter | Maximum number of iterations | Set by yourself (40) |
| progress | Iteration progress | Iter/Max_iter |
| theta | Exploration angle adjustment | 2 × atan(1 − progress0.8) |
| No_improve_count | Early stop counter | Threshold(10) |
| E | Exploration–exploitation Switching threshold | 2 × log(1/(rand() + 1 × 10−10)) × theta |
| N | Population size | 25 |
| Parameter | Function | Expression Value |
|---|---|---|
| Local_weight | Current optimal solution guidance weight | 0.5 + 0.5 × progress |
| Learn_rate | Historical optimal learning rate | Max(0.2, 1 − progress) |
| Parameters | Function | Expression value |
| Spiral_coef | Spiral search coefficient | 1 − 0.5 × progress |
| G | Global jump strength | 2 × (sign(rand−0.5)) × (1 − progress2) |
| global_mean | Population mean guidance | 0.1 × rand |
| best_history | Historical optimal solution guidance | 0.05 |
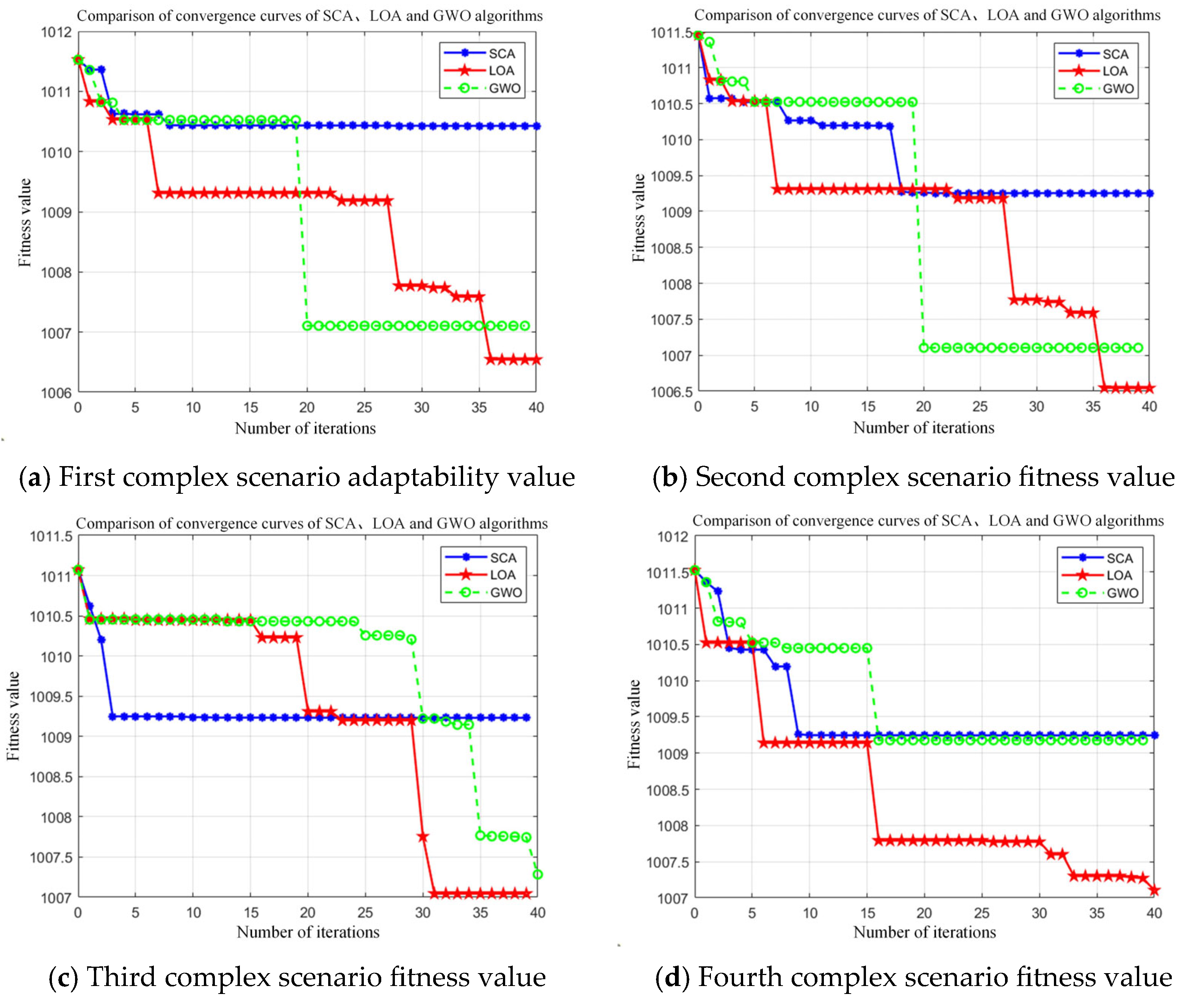
| Optimization Algorithm | LOA Fitness Value | SCA Fitness Value | GWO Fitness Value |
|---|---|---|---|
| Number of tests 1 | 1,008.63 | 1,009.30 | 1,009.00 |
| Number of tests 2 | 1,008.58 | 1,009.31 | 1,009.01 |
| Number of tests 3 | 1,008.59 | 1,009.38 | 1,009.31 |
| Number of tests 4 | 1,008.62 | 1,009.34 | 1,009.31 |
| Number of tests 5 | 1,006.26 | 1,008.59 | 1,006.27 |
| Number of tests 6 | 1,006.24 | 1,009.02 | 1,008.59 |
| Number of tests 7 | 1,006.29 | 1,009.30 | 1,008.65 |
| Number of tests 8 | 1,006.25 | 1,008.60 | 1,007.96 |
| Number of tests 9 | 1,005.37 | 1,008.60 | 1,006.28 |
| Number of tests 10 | 1,005.36 | 1,008.85 | 1,006.25 |
| Average optimal fitness value | 1,007.02 | 1,009.09 | 1,008.06 |
| Optimization Algorithm | LOA Fitness Value | SCA Fitness Value | GWO Fitness Value |
|---|---|---|---|
| Number of tests 1 | 1,007.22 | 1,010.42 | 1,009.24 |
| Number of tests 2 | 1,005.68 | 1,010.43 | 1,007.06 |
| Number of tests 3 | 1,007.59 | 1,010.43 | 1,009.24 |
| Number of tests 4 | 1,006.54 | 1,010.43 | 1,007.24 |
| Number of tests 5 | 1,007.07 | 1,011.35 | 1,009.24 |
| Number of tests 6 | 1,006.54 | 1,010.43 | 1,007.72 |
| Number of tests 7 | 1,007.07 | 1,009.25 | 1,007.07 |
| Number of tests 8 | 1,006.55 | 1,009.23 | 1,007.26 |
| Number of tests 9 | 1,007.07 | 1,010.43 | 1,009.25 |
| Number of tests 10 | 1,006.55 | 1,009.24 | 1,007.25 |
| Average optimal fitness value | 1,006.79 | 1,010.14 | 1,008.06 |
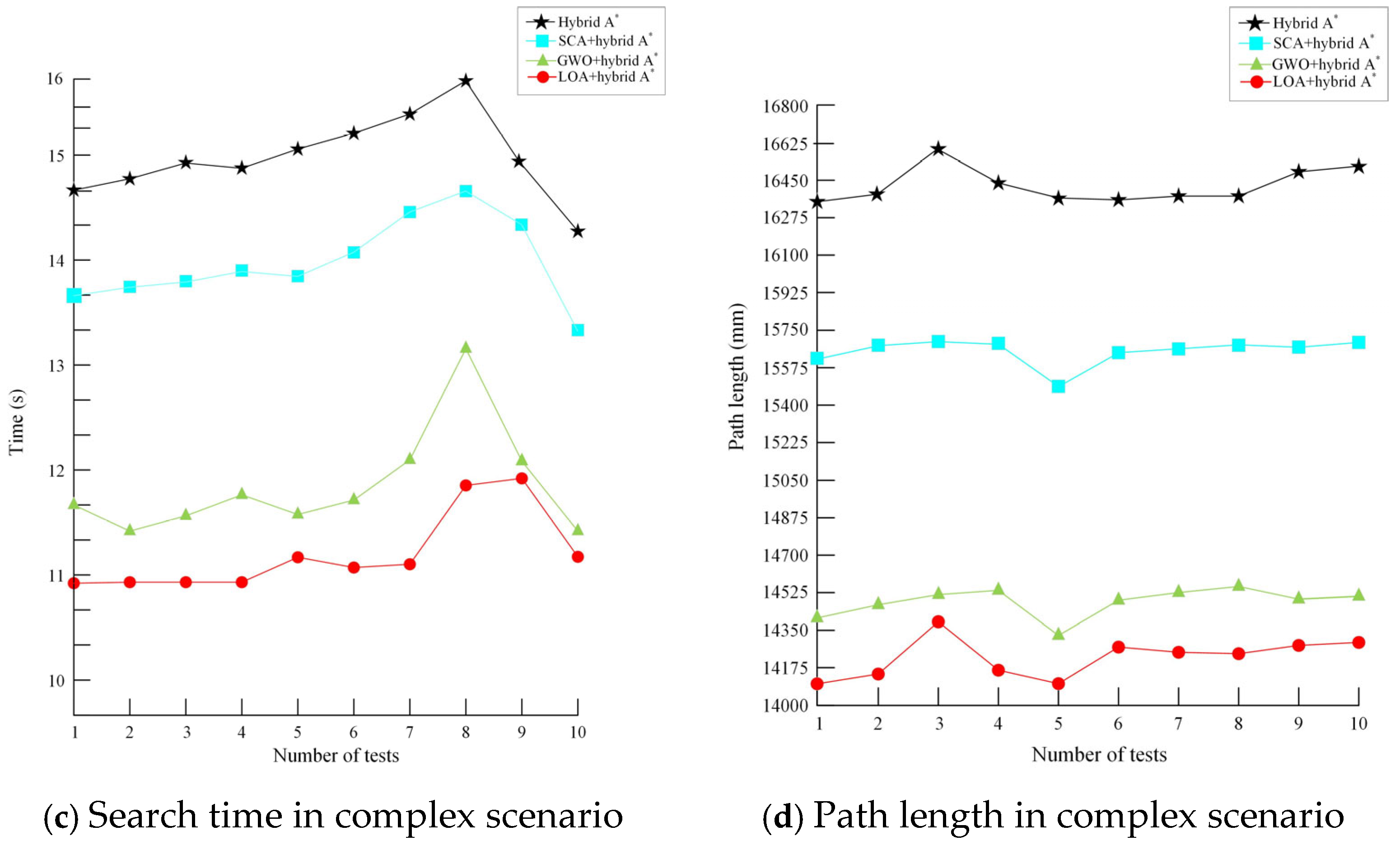
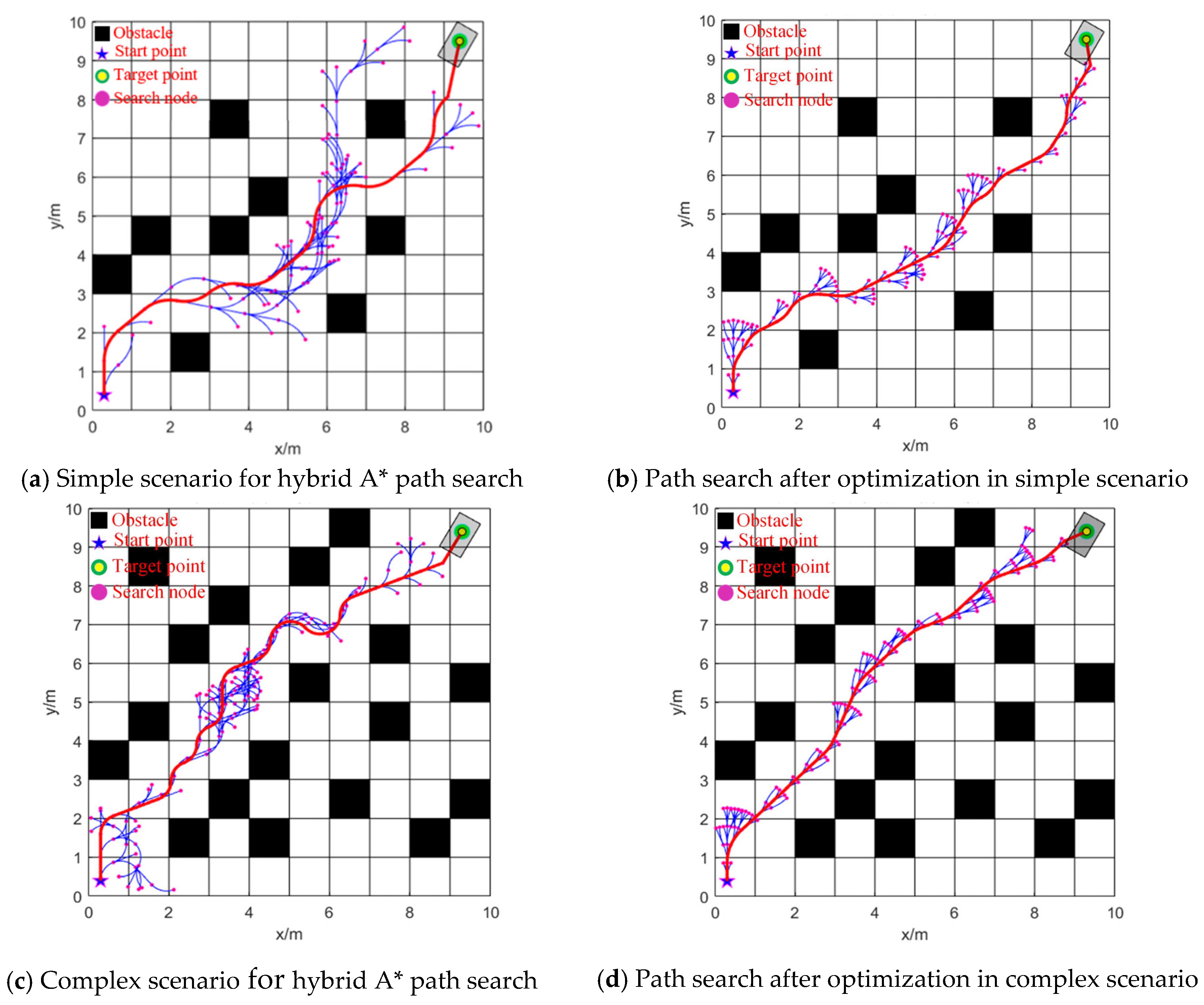
| Scenario | Algorithm | Path Length/mm | Planning Time/s | Number of Nodes |
|---|---|---|---|---|
| Simple scenario | Hybrid A* | 15,730.5 | 7.39 | 1150 |
| SCA + Hybrid A* | 14,422.9 | 6.74 | 840 | |
| GWO + Hybrid A* | 14,175.6 | 6.38 | 820 | |
| LOA + Hybrid A* | 13,980.6 | 4.93 | 800 | |
| Complex scenario | Hybrid A* | 16,421.2 | 14.79 | 1650 |
| SCA + Hybrid A* | 15,700.0 | 14.01 | 1580 | |
| GWO + Hybrid A* | 14,433.5 | 11.86 | 1260 | |
| LOA + Hybrid A* | 14,188.2 | 11.31 | 1260 |
| Parameter | Suitable Value for Simple Scenario | Suitable Value for Complex Scenario | Adjustment Logic |
|---|---|---|---|
| Population size (N) | Minimum value (10–20) | Maximum value (20–30) | Complex scenarios require more diverse exploration. |
| Maximum number of iterations () | Minimum value (20–30) | Maximum value (40–60) | Complex scenarios require longer convergence times. |
| Lévy flight intensity | Lower value (levy_strength = 0.1) | Higher value (levy_strength = 0.3) | Complex scenarios require stronger global leap capabilities. |
| Local search weight | Higher value (local_weight = 0.8) | Lower value (local_weight = 0.5) | Simple scenarios converge quickly, while complex scenarios require balance. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Liu, Y.; Xu, W. Improved Hybrid A* Algorithm Based on Lemming Optimization for Path Planning of Autonomous Vehicles. Appl. Sci. 2025, 15, 7734. https://doi.org/10.3390/app15147734
Chen Y, Liu Y, Xu W. Improved Hybrid A* Algorithm Based on Lemming Optimization for Path Planning of Autonomous Vehicles. Applied Sciences. 2025; 15(14):7734. https://doi.org/10.3390/app15147734
Chicago/Turabian StyleChen, Yong, Yuan Liu, and Wei Xu. 2025. "Improved Hybrid A* Algorithm Based on Lemming Optimization for Path Planning of Autonomous Vehicles" Applied Sciences 15, no. 14: 7734. https://doi.org/10.3390/app15147734
APA StyleChen, Y., Liu, Y., & Xu, W. (2025). Improved Hybrid A* Algorithm Based on Lemming Optimization for Path Planning of Autonomous Vehicles. Applied Sciences, 15(14), 7734. https://doi.org/10.3390/app15147734






