Multiscale Eight Direction Descriptor-Based Improved SAR–SIFT Method for Along-Track and Cross-Track SAR Images
Abstract
1. Introduction
- (1)
- A method is put forward to obtain high-precision feature points that are not affected by threshold values by combining current scale information.
- (2)
- A more robust feature descriptor is constructed using the Gradient Location and Orientation Histogram (GLOH) method with multiple scales and directions.
- (3)
- An acceleration algorithm based on both CPU and GPU is proposed to develop the matching efficiency of large-area images.
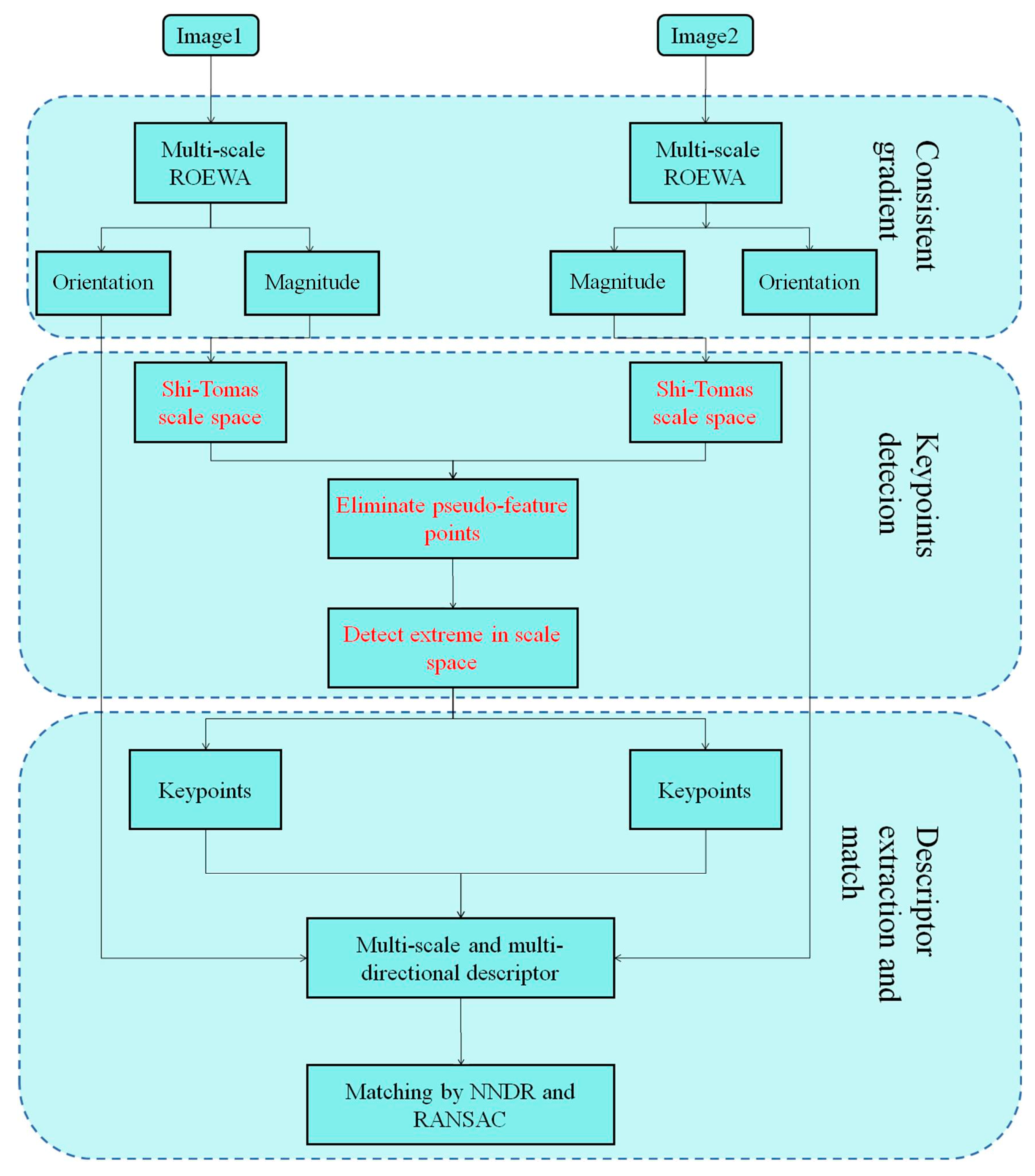
2. Materials and Methods
| Algorithm 1: High precision SAR image matching |
| Input: k: Scale number of spatial layers i: Current cycle number s: SUSAN st: Shi–Tomasi Output: Matchpoints: Matching points of SAR images |
| Begin Constructing scale pyramid For k <= i Use s to reduce noise effects Detect corner points using st End for Build feature descriptors Feature point matching according to descriptor Return Matchpoints |
2.1. SAR–SIFT
2.2. Improved Feature Extraction Algorithm
2.2.1. Threshold-Free Multiscale Response Function
2.2.2. Removing Non-Scale Key Points and Key Points Detected
2.2.3. Improved Eight-Direction Multi-Scale Feature Descriptor
2.3. Algorithm Efficiency Improvement
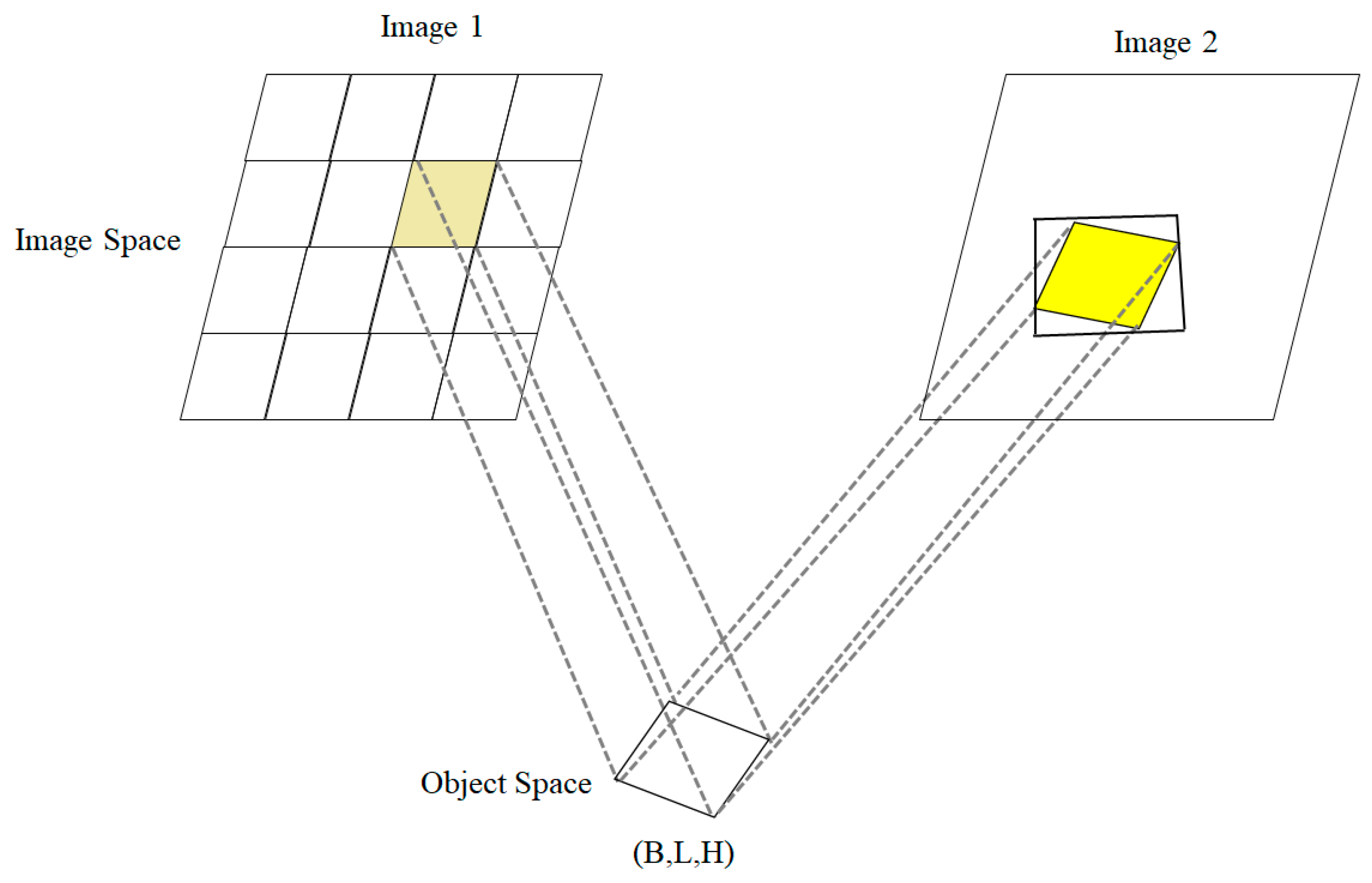
2.3.1. Extracting Overlapping Regions of Primary and Secondary Images Based on Block Matching Strategy
- (1)
- First, the corner points of the images are mapped to the world coordinate system to determine if there is an intersection between the two images. If no intersection exists, subsequent steps are not executed to avoid unnecessary computations.
- (2)
- After identifying the overlapping region between the images, one image is selected as the main image, which is then divided into blocks. The image coordinates of the corner points of each block are computed using the Rational Polynomial Coefficients (RPC) model. Next, the corner points of each block in the main image are substituted into the auxiliary image, and the row and column coordinates of the overlapping region in the auxiliary image are calculated using the RPC model, as shown in Figure 4.
- (3)
- The STSU–SAR–SIFT matching algorithm is applied to obtain the connecting points in the overlapping area.
- (4)
- The connecting points in the overlapping area are mapped back to the original images. By multiplying the size of each image block by the row and column number and adding the connecting point coordinates, the coordinates are obtained on the corresponding image.
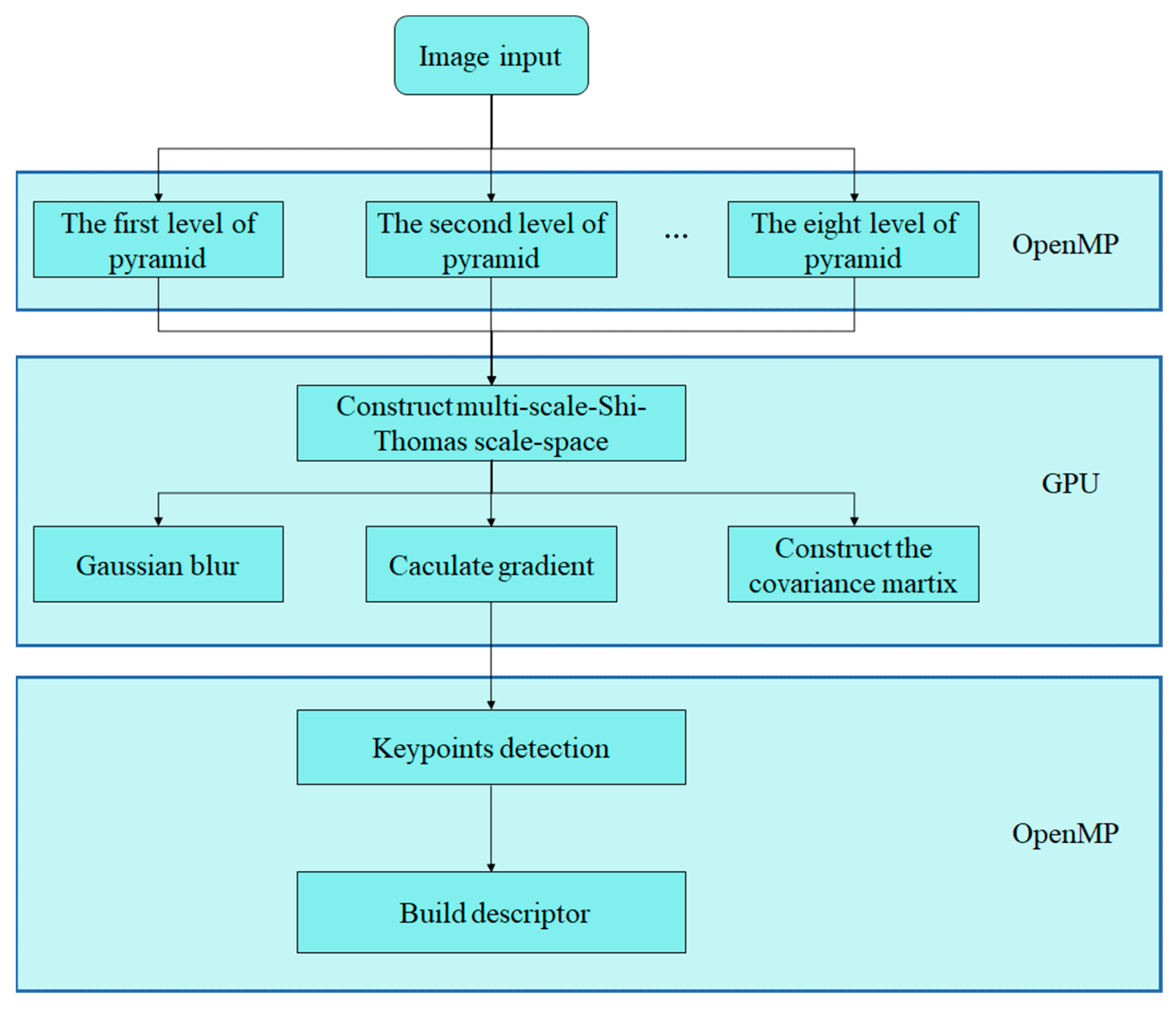
2.3.2. OpenMP and GPU Collaborative Acceleration Strategy
3. Results
3.1. Parameter Introduction and Experimental Data
3.2. Comparative Analysis
3.2.1. Feature Extraction Results Under Different Descriptors
3.2.2. Descriptor Dimensionality Analysis
3.2.3. Distribution of Feature Points Under Different Parameters
3.2.4. Match Point Precision Analysis
- (1)
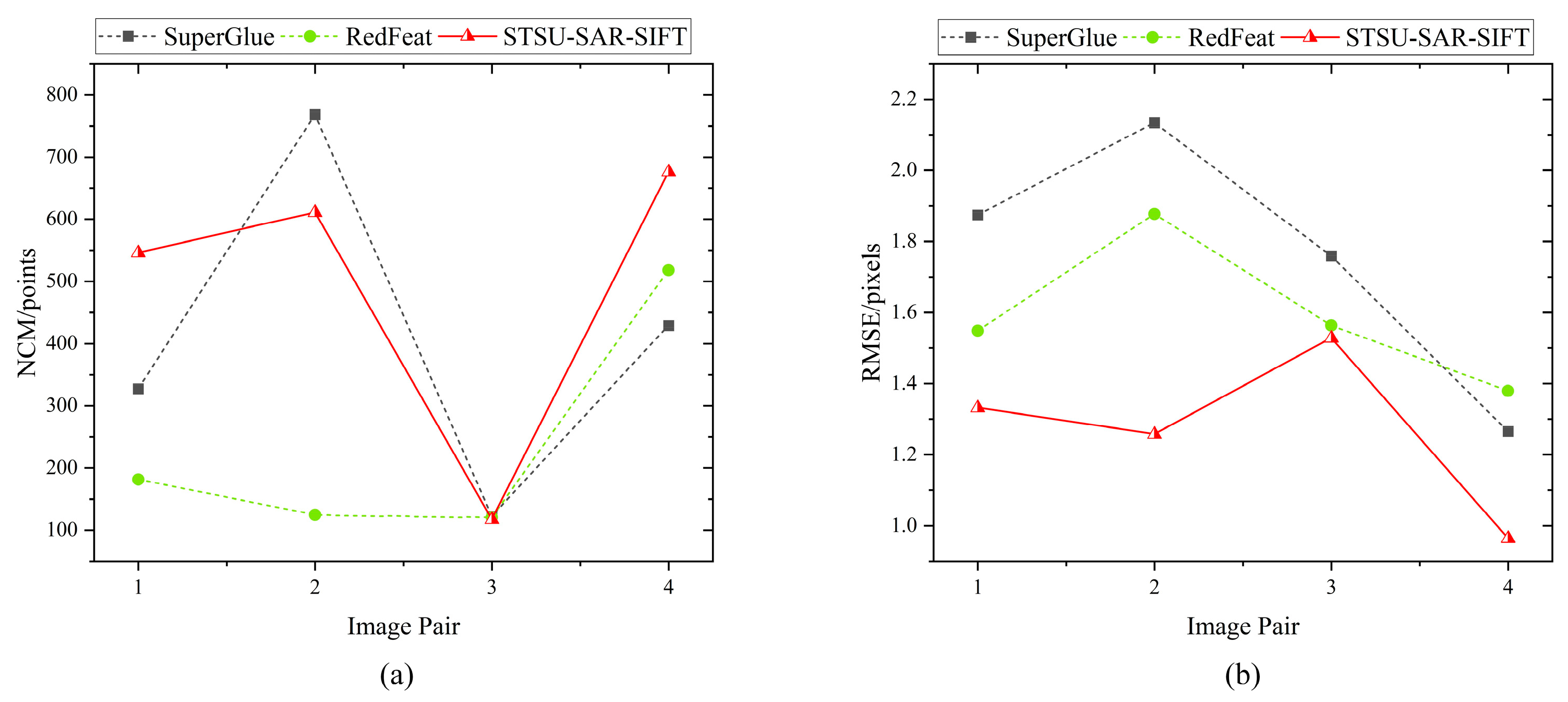
- For both GF-3 and Sentinel-1 images, our proposed STSU–SAR–SIFT algorithm consistently achieved the lowest RMSE values. Even when compared with the state-of-the-art deep learning-based matching algorithms such as SuperGlue and RedFeat, our algorithm demonstrated distinct advantages and was significantly superior to SAR–SIFT.
- (2)
- Given the minimal variability in SAR images captured during the same orbital imaging period, all algorithms perform adequately in extracting tie points from the same orbit. However, SIFT, SURF, and AKAZE are more sensitive to noise, resulting in comparatively higher root mean square errors. Meanwhile, the two deep learning-based methods have shown excellent results across both datasets. Nevertheless, according to the data in the table, STSU–SAR–SIFT exhibits the best performance, indicating its superior suitability for extracting tie points from SAR images.
- (3)
- When extracting tie points from vertical orbits, the SAR–SIFT algorithm generates a large number of false corners, and its feature descriptors fail to adequately represent terrain features, resulting in higher RMSE values. In contrast, the proposed STSU–SAR–SIFT algorithm eliminates many false corners and provides robust feature descriptions, significantly outperforming the SAR–SIFT algorithm. Due to the different imaging times on vertical orbits, severe image distortions occur, preventing the SIFT, SURF, and AKAZE algorithms from accurately extracting tie points.
- (4)
- While extracting dual-matching tie points, although the similarity in same orbit images is high, significant variations in vertical orbit images result in much lower accuracy of tie points on vertical orbits compared to same orbit images. Hence, the accuracy of dual-matching tie points lies between those of the same and vertical orbits. Given that STSU–SAR–SIFT exhibits superior accuracy on both same and vertical orbits compared to SAR–SIFT, it also surpasses SAR–SIFT in accuracy for dual-matching tie points.
- (5)
- When extracting triple-matching tie points, STSU–SAR–SIFT continues to perform better than SAR–SIFT, although the difference is not particularly significant. One reason is that in the experimental data, triple-matching points typically occur only in configurations of “two-left-one-right” or “two-right-one-left,” resulting in a relatively small number of such tie points.
3.2.5. Comparison with Deep Learning-Based Methods
3.2.6. Efficiency Analysis of Parallel Computing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake Damage Assessment of Buildings Using VHR Optical and SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef]
- Bruzzone, L.; Bovolo, F. A Novel Framework for the Design of Change-Detection Systems for Very-High-Resolution Remote Sensing Images. Proc. IEEE 2013, 101, 609–630. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.; Du, J.; Luo, B. Unified Framework for the Joint Super-Resolution and Registration of Multiangle Multi/Hyperspectral Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2369–2384. [Google Scholar] [CrossRef]
- Wu, P.; Wang, Z.; Zheng, B.; Li, H.; Alsaadi, F.E.; Zeng, N. AGGN: Attention-based glioma grading network with multi-scale feature extraction and multi-modal information fusion. Comput. Biol. Med. 2023, 152, 106457. [Google Scholar] [CrossRef]
- Paul, S.; Pati, U.C. Remote Sensing Optical Image Registration Using Modified Uniform Robust SIFT. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1300–1304. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-Modal Image Matching Based on Radiation-Variation Insensitive Feature 698 Transform. IEEE Trans. Image Process. 2020, 29, 3296–3310. [Google Scholar] [CrossRef]
- Ahakonye, L.A.C.; Nwakanma, C.I.; Lee, J.M.; Kim, D.S. SCADA intrusion detection scheme exploiting the fusion of modified decision tree and Chi-square feature selection. Internet Things 2023, 21, 100676. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Y. A Fast Offset Estimation Approach for InSAR Image Subpixel Registration. IEEE Geosci. Remote Sens. Lett. 2012, 9, 267–271. [Google Scholar] [CrossRef]
- Cole-Rhodes, A.A.; Johnson, K.L.; LeMoigne, J.; Zavorin, I. Multiresolution registration of remote sensing imagery by optimization of mutual information using a stochastic gradient. IEEE Trans. Image Process 2003, 12, 1495–1511. [Google Scholar] [CrossRef]
- Chen, S.; Li, X.; Zhao, L.; Yang, H. Medium-low resolution multisource remote sensing image registration based on SIFT and robust regional mutual information. Int. J. Remote Sens. 2018, 39, 3215–3242. [Google Scholar] [CrossRef]
- Beier, T.; Neely, S. Feature-based image metamorphosis. In Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, Chicago, IL, USA, 27–31 July 1992; ACM: Singapore, 1992; pp. 35–42. [Google Scholar] [CrossRef]
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Chen, S.; Zhong, S.; Xue, B.; Li, X.; Zhao, L.; Chang, C.I. Iterative Scale-Invariant Feature Transform for Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3244–3265. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform Robust Scale-Invariant Feature Matching for Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Wang, S.; You, H.; Fu, K. BFSIFT: A Novel Method to Find Feature Matches for SAR Image Registration. IEEE Geosci. Remote Sens. Lett. 2012, 9, 649–653. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE Features. In Computer Vision—ECCV; Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7577, pp. 214–227. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-Like Algorithm for SAR Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef]
- Hong, Y.; Leng, C.; Zhang, X.; Yan, H.; Peng, J.; Jiao, L.; Cheng, I.; Basu, A. SAR Image Registration Based on ROEWA-Blocks and Multiscale Circle Descriptor. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10614–10627. [Google Scholar] [CrossRef]
- Pallotta, L.; Giunta, G.; Clemente, C. SAR Image Registration in the Presence of Rotation and Translation: A Constrained Least Squares Approach. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1595–1599. [Google Scholar] [CrossRef]
- Pallotta, L.; Giunta, G.; Clemente, C.; Soraghan, J.J. SAR Coregistration by Robust Selection of Extended Targets and Iterative Outlier Cancellation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperGlue: Learning Feature Matching With Graph Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4937–4946. [Google Scholar] [CrossRef]
- Lindenberger, P.; Sarlin, P.E.; Pollefeys, M. LightGlue: Local Feature Matching at Light Speed. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 17581–17592. [Google Scholar] [CrossRef]
- Xu, W.; Yuan, X.; Hu, Q.; Li, J. SAR-optical feature matching: A large-scale patch dataset and a deep local descriptor. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103433. [Google Scholar] [CrossRef]
- Deng, Y.; Ma, J. ReDFeat: Recoupling Detection and Description for Multimodal Feature Learning. IEEE Trans. Image Process 2023, 32, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Zhi, X.; Yan, J.; Hang, Y.; Wang, S. Realization of CUDA-based real-time registration and target localization for high-resolution video images. J. Real-Time Image Proc. 2019, 16, 1025–1036. [Google Scholar] [CrossRef]
- Feng, H.; Li, E.; Chen, Y.; Zhang, Y. Parallelization and characterization of SIFT on multi-core systems. In Proceedings of the 2008 IEEE International Symposium on Workload Characterization, Seattle, WA, USA, 14–16 September 2008; pp. 14–23. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Guoping, L.; Yan, S.; Jia, H. CLSIFT: An Optimization Study of the Scale Invariance Feature Transform on GPUs. In Proceedings of the 2013 IEEE 10th International Conference on High Performance Computing and Communications & 2013 IEEE International Conference on Embedded and Ubiquitous Computing, Zhangjiajie, China, 13–15 November 2013; pp. 93–100. [Google Scholar] [CrossRef]
- Al-Saadi, A.; Paraskevakos, I.; Gonçalves, B.C.; Lynch, H.J.; Jha, S.; Turilli, M. Comparing workflow application designs for high resolution satellite image analysis. Future Gener. Comput. Syst. 2021, 124, 315–329. [Google Scholar] [CrossRef]
- Shi, J.; Tomasi, C. Good features to track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR-94, Seattle, WA, USA, 21–23 June 1994; IEEE Computer Society Press: Los Alamitos, CA, USA, 1994; pp. 593–600. [Google Scholar] [CrossRef]


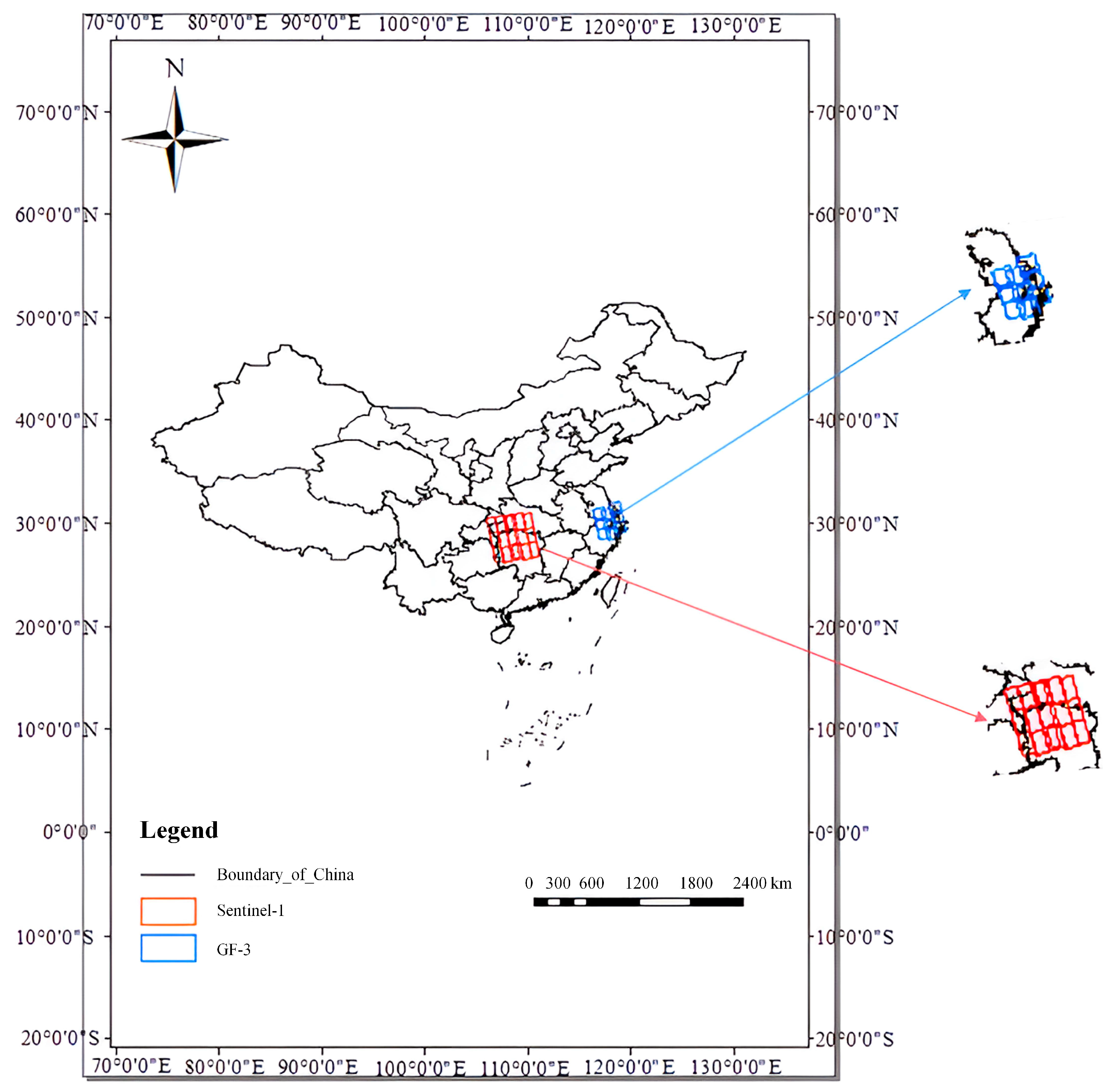





| Satellite | Image Date | Image Scenes | Image Size (Pixels) | Resolution (m) | Region |
|---|---|---|---|---|---|
| GF-3 | 21 April 2018 | 9 | 28,744 × 26,550 | 2.25 and 4.77 | Taihu |
| Sentinel-1 | 20 March 2020 | 15 | 17,144 × 13,112 | 20 and 20 | Hunan |
| Methods | GF-3 | Sentiel-1 | ||||
|---|---|---|---|---|---|---|
| NCM | TCM | CMR | NCM | TCM | CMR | |
| This paper | 288 | 459 | 62.75% | 22 | 49 | 44.33% |
| SAR–SIFT | 250 | 449 | 54.62% | 10 | 25 | 40.72% |
| I–SAR–SIFT | 259 | 442 | 55.68% | 12 | 30 | 41.19% |
| PSO–SIFT | 252 | 465 | 55.89% | 19 | 44 | 42.95% |
| Dimensionality | 3 × 8 × 8 | 3 × 8 × 6 | 3 × 6 × 8 | 3 × 6 × 6 |
|---|---|---|---|---|
| NCM | 428 | 387 | 424 | 437 |
| RMSE | 1.31 | 1.44 | 1.46 | 1.53 |
| TIME (seconds) | 21.93 | 21.66 | 21.57 | 21.43 |
| Data | Different Algorithms | RMSE (All) | RMSE (Same Orbit) | RMSE (Vertical Orbit) | RMSE (Two-Overlapping) | RMSE (Three-Overlapping) |
|---|---|---|---|---|---|---|
| GF-3 | STSU–SAR–SIFT | 0.43 | 0.27 | 0.58 | 0.40 | 0.41 |
| SAR–SIFT | 0.68 | 0.28 | 1.14 | 0.66 | 0.67 | |
| SIFT | 0.71 | 1.72 | None | 0.31 | None | |
| SURF | 0.75 | 1.79 | None | 0.35 | None | |
| AKAZE | 0.77 | 1.04 | None | 0.37 | None | |
| SuperGlue | 0.65 | 0.33 | 0.75 | 0.69 | 0.71 | |
| RedFeat | 0.58 | 0.31 | 0.67 | 0.58 | 0.64 | |
| Sentinel-1 | STSU–SAR–SIFT | 1.27 | 0.59 | 2.36 | 1.37 | None |
| SAR–SIFT | 1.87 | 0.37 | 2.77 | 1.87 | None | |
| SIFT | None | None | None | None | None | |
| SURF | None | None | None | None | None | |
| AKAZE | None | 0.79 | None | 3.64 | None | |
| SuperGlue | 1.61 | 0.74 | 2.56 | 1.65 | None | |
| RedFeat | 1.54 | 0.62 | 2.54 | 1.63 | None |
| Datasate | CPU (Hours) | Multi-Thread CPU (Hours) | CPU and GPU (Hours) |
|---|---|---|---|
| Sentinel-1 | 2.7 | 1.3 | 0.75 |
| GF-3 | 8.3 | 5 | 3.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Chen, J.; Hong, Z. Multiscale Eight Direction Descriptor-Based Improved SAR–SIFT Method for Along-Track and Cross-Track SAR Images. Appl. Sci. 2025, 15, 7721. https://doi.org/10.3390/app15147721
Wang W, Chen J, Hong Z. Multiscale Eight Direction Descriptor-Based Improved SAR–SIFT Method for Along-Track and Cross-Track SAR Images. Applied Sciences. 2025; 15(14):7721. https://doi.org/10.3390/app15147721
Chicago/Turabian StyleWang, Wei, Jinyang Chen, and Zhonghua Hong. 2025. "Multiscale Eight Direction Descriptor-Based Improved SAR–SIFT Method for Along-Track and Cross-Track SAR Images" Applied Sciences 15, no. 14: 7721. https://doi.org/10.3390/app15147721
APA StyleWang, W., Chen, J., & Hong, Z. (2025). Multiscale Eight Direction Descriptor-Based Improved SAR–SIFT Method for Along-Track and Cross-Track SAR Images. Applied Sciences, 15(14), 7721. https://doi.org/10.3390/app15147721






